1. Introduction
The advancement in propulsion technology has led to increased interest in low-thrust orbit design for its efficient fuel consumption. Electric thrusters have been successfully utilized in numerous accomplished missions, such as Deep Space 1, Hayabusa, Smart 1, Dawn, etc.; however, finding the optimal orbit with electric propulsion is quite challenging as it exhibits strong non-linear characteristics, which arise from the application of continuous long-term low thrust. While there is no analytical solution available for general low-thrust orbits, three primary numerical methods are commonly used: direct [
1,
2], indirect [
3,
4], and hybrid methods [
5,
6]. Direct methods involve discretizing the original optimal control problem to convert it into a non-linear programming problem (NLP). Subsequently, numerical optimization techniques are applied to solve the NLP problem and determine the optimal solution for the original optimal control problem. However, direct methods are computationally intensive. Indirect methods utilize Pontryagin’s maximum principle (PMP) to establish the necessary conditions for optimal control, thereby transforming the optimal control problem into a two-point boundary-value problem (TPBVP). Resolving TPBVP is challenging due to its limited convergence radius and sensitivity to initial values. Shooting methods could be employed to solve the corresponding TPBVP [
7,
8,
9]. Hybrid methods combine the strengths of both direct and indirect methods, requiring a priori knowledge of the thrust structure and conditions derived from PMP.
This work explores an improved version of the indirect method, focusing on fuel-optimal continuous low-thrust rendezvous scenarios with a fixed flight time. The original version [
10] has been widely applied in resolving numerous low-thrust fuel-optimal orbits.
Satisfactory initial guess values play a crucial role in low-thrust trajectory optimization, given the highly non-linear nature of the problem. To address the challenges posed by bang-bang control problems, smoothing techniques—also referred to as homotopic approaches—have been introduced [
11]. Such similar techniques, alternatively known as continuation methods, have been extensively explored by researchers [
12,
13,
14,
15].
A rapid homotopic method was developed by Jiang et al. [
10]. This method integrates the homotopic method with PSO, the normalization technique, the switching detection method, and the shooting method. PSO can enlarge the probability of finding out the global solution by searching the initial values [
16]. Although the PSO results are difficult to satisfy a high-accuracy requirement because of the introduction of the penalty term into the objective function, it is not a problem to apply PSO here as PSO results are just utilized as an initial value guess. As an efficient approach, the normalization technique can map the unbounded unknown multipliers to the surface of a unit hypersphere, which can provide good convergence performance. The probability of finding convergent solutions can be increased several times by applying the normalization technique. For example, an a priori switching detection technique was developed by Jiang et al. In addition, Saghamanesh et al. presented a modified methodology of the switching detection process [
17]. These switching detection techniques are embedded in the Runge–Kutta algorithm with fixed step sizes. Tang et al. embedded the detection technique in a Runge–Kutta method with adaptive step sizes [
18]. The switching detection technique helps improve the integration accuracy for bang-bang control and the robustness of the solution. Moreover, while the Min Pack-1 [
19]—a FORTRAN subprogram that uses the classical Levenberg–Marquardt method—can be utilized to solve the shooting function, MATLAB’s “
fsolve” can also be utilized as an alternative. The trust-region algorithms employed by “
fsolve” are highly efficient in solving the fuel-optimal problem. The Jacobian matrix of the shooting function can be approximated using finite differences or computed by integrating the variational equations for greater accuracy [
20]. These techniques are effective in solving the fuel-optimal problem with a much higher convergence rate, a higher probability of achieving a globally optimal solution, and with less time required in comparison to methods that do not use these techniques.
This study concentrates on improving the efficiency of solving the fuel-optimal problem with the use of techniques described in [
10]. Traditionally, PSO stops only when the number of iterations is greater than the maximum number of iterations. But often, after a certain number of iterations, the particles will be concentrated to a small range, and there is not much point in continuing the iteration as it will only waste computing power. Thus, to enhance computational efficiency in the PSO process, a diversity termination term is additionally introduced. Although the switching detection technique is very useful, the integration process with switch detection is notably intricate and problematic. Instead, we choose a quite easy but competent integrator in MATLAB. The version of MATLAB we used is R2023b. In some sense, the propagation of the low-thrust orbit with bang-bang control can be deemed as an ordinary differential equation (ODE) problem with stiffness. In our work, to propagate the orbit, a stiff ODE solver with adaptive step sizes—which can guarantee the accuracy of integrating general low-thrust orbits—is used to handle incomplete differentiation of dynamic motion. Furthermore, a new parameter, the maximum thrust to initial mass ratio (
), is introduced and its impact on the problem is examined. This study also establishes relationships among the Lagrange multipliers for scenarios with different
in the energy-optimal auxiliary problem, which can be leveraged in scenarios with high
, e.g., several times the least value of
, to reduce the variable search space, thereby significantly improving computational efficiency. In the energy-optimal problem with the least value of
, the largest thrust is exactly the maximum allowable thrust.
Nonetheless, to the authors’ knowledge, few research studies have been conducted on proposing a clearly defined strategy for the homotopic process. An efficient iterative strategy plays a crucial role in improving the efficiency of resolving fuel-optimal problems. In our work, a robust step size adjustment strategy is proposed. This strategy encompasses two main key techniques: the determination of the maximum step size and the distinction of sub-optimal solutions. As each iteration succeeds, the step size is increased to expedite progress. Setting a maximum step size constrains the step size in each iteration, increasing the likelihood of successful iterations and facilitating a rapid and smooth advancement of the homotopic process. The distinction of sub-optimal solutions ensures a robust convergence toward the optimal solutions. If the outcome is sub-optimal, then the step size is reduced, and the iteration is repeated until no sub-optimal solutions occur.
The rest of this paper is organized as follows. In
Section 2, the concepts of the fuel-optimal problem with fixed boundary conditions are given and some practical techniques are presented. In
Section 3, the energy-optimal problem with PSO selected as the global optimization method is introduced. In
Section 4, the parameter
is introduced, and relationships among the Lagrange multipliers with different
in the energy-optimal problem are given. In
Section 5, a well-defined and efficient strategy in the homotopic procedure is constructed, and distinction equations of sub-optimal solutions are derived. In
Section 6, the settings of the integrator and the shooting function solver are presented. A numerical example and discussion are given in
Section 7.
Section 8 concludes this paper.
2. Statement of the Problem with Quadratic Penalty Smoothing Technique and Normalization Technique
We only consider the Sun’s gravity and the electric propulsion. Consequently, the motion of the spacecraft can be described by Equation (1).
where
and
represent the position and velocity vectors, respectively, in the heliocentric ecliptic reference frame (HERF);
denotes the instantaneous mass of the spacecraft;
denotes the maximal thrust magnitude;
is the thruster’s specific impulse;
is the standard acceleration of gravity at sea level,
;
is the gravitational constant. The sun’s gravitational constant
is equal to
. The control variable consists of the unit vector representing the thrust direction, denoted as
, and the engine throttle, denoted as
.
It is very difficult to directly solve the fuel-optimal low-thrust problem because of the highly non-linear characteristics and consequently small convergence radius. To overcome this obstacle, the quadratic penalty smoothing technique is used. The performance index of the fuel-optimal problem is constructed by Equation (2), while the new performance index is constructed in the variant quadratic homotopic function Equation (3), where the homotopic parameter
links the fuel-optimal criterion
with the energy-optimal criterion
.
is a series of decreasing values. Multiplying the performance index by an auxiliary Lagrange multiplier
does not change the essence of the optimal control problem. In this way, a series of auxiliary problems are constructed. The purpose of employing this smoothing technique is to initially tackle the less-complex energy-optimal auxiliary problem, which possesses a relatively broad convergence domain. Subsequently, a sequence of auxiliary problems is solved to iteratively approximate the fuel-optimal problem by adjusting the
. This approach is implemented to mitigate the challenge posed by the narrow convergence domain resulting from the bang-bang control.
where
and
denote the fixed initial and final times, respectively.
The Hamiltonian function is built as Equation (4). In order to minimize it, the optimal thrust direction unit vector
and engine throttle
are established through Equations (5) and (6). The optimal thrust direction lies along the opposite direction of the vector
, termed as the primer vector [
21]. The functional Lagrange multipliers are denoted as the co-state vector
.
where
is the switching function (SF), which holds the following form:
It should be noted that, if is equal to 0 and is equal to , then a singularity will occur in the calculation of the value of ; therefore, if this situation arises, we set equal to 0.
The vector dynamical function consisting of the spacecraft’s motion equations and the ordinary differential equations of
(Euler–Lagrange equations) has the following form:
If the boundary state is fixed, its corresponding boundary co-state is free; however, if the boundary state is free, the corresponding co-state must be equal to 0. In this optimization problem, the mass at the last moment is free, and thus the corresponding co-state needs to be equal to 0. Therefore, the transversality condition holds the following form:
Utilization of the normalization technique can confine the unknown co-state vectors
from an unbounded space to the surface of a unit hypersphere, which could notably enhance the efficiency and convergence of the optimization algorithm. The new co-state vector can be redefined by the following:
Note that both the initial and final states are fixed. Finally, a two-point boundary-value problem (TPBVP) is formulated by applying Pontryagin’s minimum principle, which leads to the development of a shooting function comprising eight components:
Provided with initial states and tentative values for the co-states, Equation (8) can be numerically integrated from to . Subsequently, the discrepancies in the boundary conditions can be ascertained.
The unknown co-state variables
can be defined as outlined below:
where the seven angle variables are calculated by the following:
The search variable vector
comprises seven separate components and is defined within the interval
. Equation (12) inherently satisfies
, which consequently allows it to be excluded from the shooting function. Thus, Equation (11) can be rewritten as follows:
The normalization technique is utilized throughout the entire homotopic process.
3. Optimal Energy Problem
To start the homotopic procedure, it is first necessary to solve the energy optimization problem corresponding to the homotopic parameter
. The objective function containing a penalty term that takes into account the residuals of the shooting function is constructed:
According to [
10], penalty factor
can be generated randomly in the domain
. Subsequently, the particle swarm optimization (PSO) algorithm is applied to find out a global solution of the energy-optimal problem. Parameters of the PSO are shown in
Table 1.
The swarm size
is set to 20; the maximal iteration
is 1000; the maximal velocity
is 0.8; the “self-confidence”
declines linearly from
to
; the “swarm-confidence”
increases linearly from
to
; the inertial factor
declines linearly from
to
. These parameters are similar to those in [
10]. Additionally, a diversity term
is introduced here.
is defined as the standard deviation of the Euclidean distances from each particle to the centroid.
represents the diversity threshold. If
is lower than
, then the algorithm is considered to be trapped in a local optimum and the iteration of the PSO is terminated. To utilize the performance of the computer more efficiently, it is feasible to simultaneously run multiple PSOs through parallel computations. Then, the best outcome is selected for further processing.
After the PSO is terminated, the obtained result is utilized as the initial guess to solve the shooting function (14), employing the aforementioned techniques in the preceding sections.
4. Maximum Thrust to Initial Mass Ratio
In this paper, HERF is used to describe the motion of spacecraft and celestial bodies. For the convenience of computation and convergence of algorithms, distance, time, and mass need to be nondimensionalized and the units of these variables can be defined as , , and , where is the sun’s gravitational constant, and after nondimensionalization, it is equal to 1; is the initial mass of the spacecraft in kilograms.
When performing dimensionless processing on the units, the spacecraft propulsion system’s maximum allowable thrust in units Newtons needs to be divided by , yielding , while the initial mass of the spacecraft needs to be divided by itself, resulting in a value of 1. Through dimensionless processing of the units, the influences of and on Equations (3)–(8) can be reflected in exactly one parameter . Introducing a parameter , the expression for can be defined as . With held constant, i.e., and can be scaled by any positive constant, the solutions to the problem are the same.
In the energy-optimal problem, is set to 1. According to Equation (8), the derivative of is negative and is required to be equal to 0 at moment . Consequently, the remains consistently above 0, and the switch function remains consistently below 1, resulting in the status of the thruster being ”on” all the time. Therefore, the energy-optimal problem is a problem of continuous thrust.
Assuming that the spacecraft’s propulsion system can provide a large enough thrust, then, during the entire trajectory, the thrust throttle
can hold the form outlined below:
The energy-optimal performance index is built as follows:
In an energy-optimal problem where
R times the maximum thrust is provided, then Equation (18) can be obtained.
R does not change the essence of the optimal control problem. Consequently, it can be inferred that assuming the propulsion system is capable of delivering a sufficiently high thrust, the maximum allowable thrust does not influence the solutions of the problem. In other words, the energy-optimal orbits derived under varying maximum allowable thrust conditions are expected to be the same.
Differentiating Equation (7) yields the following:
Considering Equations (5), (7), (9), (16) and (19), the following conversion relations can be derived:
The subscript A represents an energy-optimal problem, while the subscript B represents an energy-optimal problem with a maximum thrust that is R times the maximum thrust of problem A. It is assumed that both problems A and B are provided with a sufficiently large maximum allowable thrust. The subscript AUX signifies a constructed auxiliary vector.
If a fuel-optimal orbit with a large needs to be determined, the initial stage of the homotopic process for solving the energy-optimal orbit will require exploration within a significantly extensive solution space. This will escalate the complexity of the solution and the computational workload. Typically, energy-optimal orbits do not necessitate very high acceleration. Therefore, it may be advantageous to first solve the energy-optimal orbit by assuming a lower and subsequently calculate the numerical values of the solution with the targeted higher by applying Equation (20). This approach can reduce the solution space and enhance the efficiency of problem-solving. However, it is a little challenging to assume an appropriate small value of , which may require sufficient experience.
5. Iteration Strategy in Homotopic Procedure
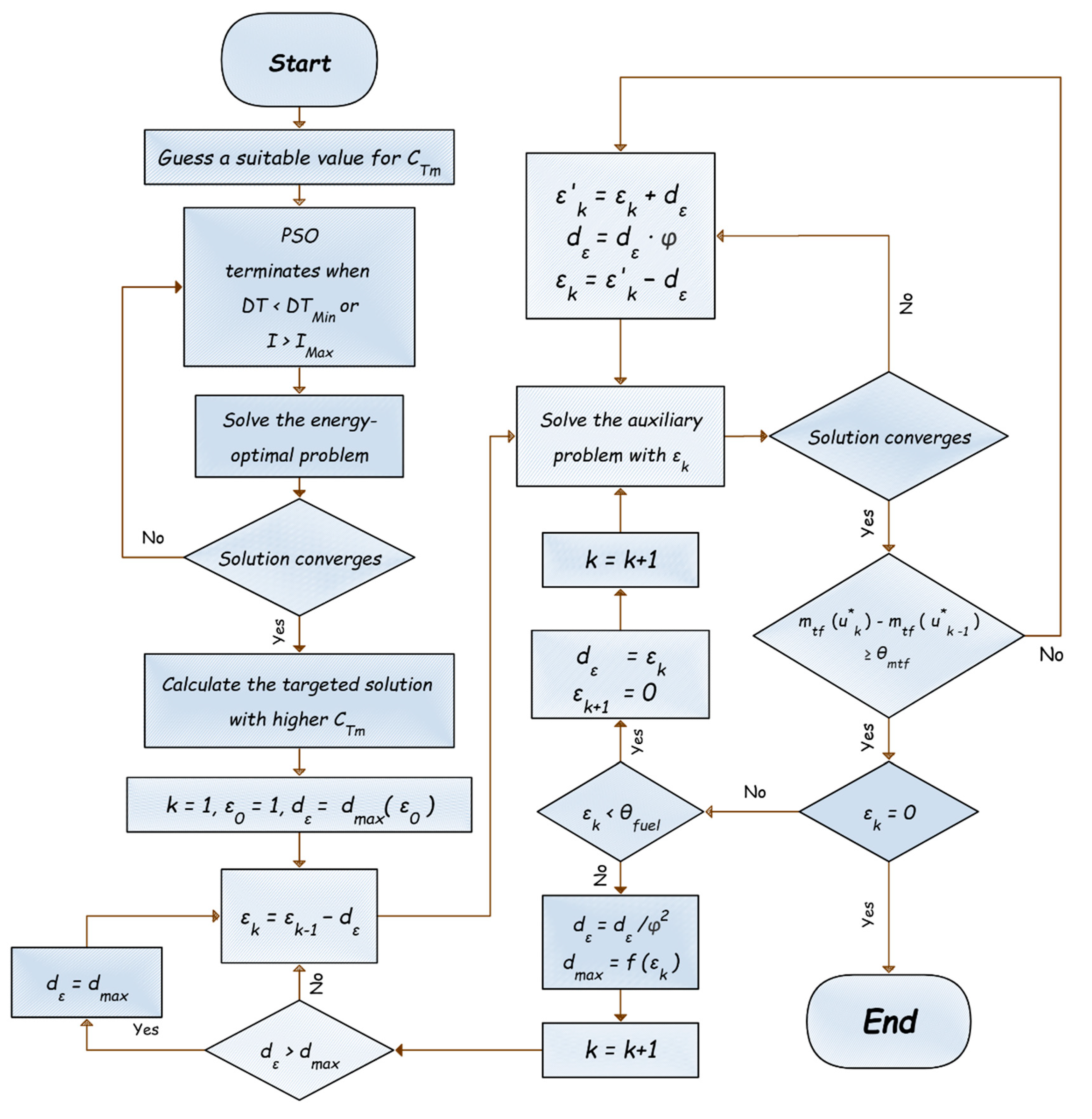
5.1. Iteration Step Size
During the homotopic process, the converged solution of each iteration serves as the tentative values to initiate the next iteration with a smaller
. If an iteration fails to converge, the step size
needs to be decreased by multiplying it by a scaling factor
, and the computation should be repeated. Conversely, if the iteration successfully converges,
is divided by
. If the adjusted
exceeds the predefined maximum step size
,
is set to
, and the next iteration is carried out. It is recommended to select
as the initial step size and 0.8 as the scaling factor
. For each
, the maximum iterative step size
is determined by the following equation:
The maximum iteration step values corresponding to different
are listed in
Table 2.
5.2. Distinction of Sub-Optimal Solutions
During the homotopic process, we can derive the following properties:
Proposition 1. With optimal control, the final mass of the spacecraft at the end of the flight increases as the declines.where represents the optimal control associated with ; and represents the final mass of the spacecraft at the end of the flight. Proof of Proposition 1. Construct an equation as follows:
where
According to [
11], a conclusion can be drawn, as presented in Equation (25):
Based on Equation (25), Equation (26) can be derived:
so
because
so
and then
so
thus, the desired result is obtained. □
We can use Equation (22), which is a necessary condition for the homotopic process toward the optimal direction, to assess the quality of the solution.
Construct the following equation:
If Equation (32) is not satisfied, the solution may be deemed to have converged to a sub-optimal solution. In such cases, it is necessary to decrease the step size , update the homotopic parameters , and redo the computation.
Taking into account factors such as computational errors, the threshold can be set to . Hence, the direction toward the optimal solutions during the homotopic process can be guaranteed.
5.3. Threshold for the Fuel-Optimal Problem
When the homotopic parameter falls below a certain threshold, the iteration step size can be adjusted to be equal with and is set to 0. In other words, the subsequent iteration attempts to solve the fuel optimization problem. This threshold value can be set to .
The entire iterative strategy is summarized in the flowchart in
Figure 1.
6. Settings of Programming Algorithms
6.1. Integrator for Orbital Propagation
In an auxiliary problem constructed using a quadratic penalty term and the fuel-optimal problem, trajectories remain continuous throughout but exhibit non-differentiability at the thrust switch moment. The switching detection technique can be used to tackle this challenge. Nevertheless, this approach is fairly complex; for simplicity, we employ a MATLAB stiff integrator to propagate orbits instead.
Some ordinary differential equation (ODE) problems may demonstrate stiffness, typically arising from disparities in scaling within the problem [
22]. The stiffness characteristic of the problem can be inferred from Equations (6) and (8). Consequently, we opt for a stiff ODE solver with adaptive steps, such as ode15s [
23], known for its ability to efficiently and accurately handle ODEs exhibiting stiffness. Throughout the computational process, the stiff ODE solver ode15s is utilized. The relative and absolute tolerances of the ode15s settings can both be set to be
or even smaller.
6.2. Settings of the Shooting Function Solver
The shooting function (14) can be solved by the subroutine “fsolve” in MATLAB, which can employ trust-region and Levenberg–Marquardt algorithms, etc.
In the problem of solving the low-thrust fuel-optimal orbit, the setup of the solver is crucial, and various factors need to be considered to achieve high solving efficiency. A forward-difference approximation, which is deemed sufficient to ensure convergence for the simple problem considered, is employed to calculate the Jacobian matrix. In the problem-solving process, the solver’s accuracy must be adjusted to ensure solution quality. However, in the homotopic process, setting the accuracy too small is unnecessary as it significantly increases computation time, making the problem harder to solve. During the homotopic process, upon solving each auxiliary problem, the following outcomes may arise: (1) no solution found; (2) exceeding the maximum number of iterations; (3) obtaining a sub-optimal solution; (4) obtaining an optimal solution. If the step size in the homotopic process is too large, results 1–3 are more likely. Therefore, it is advisable to set a suitable maximum number of iterations for the solver. When the iteration count surpasses this limit, the iteration stops, decreases, and the problem is re-solved with an updated homotopic parameter to enhance solving efficiency. This strategy is particularly beneficial for solving problems with small thrust orbits, especially those with a high maximum allowable thrust and low initial spacecraft mass. When approaches 0, the shooting function becomes highly sensitive, and its convergence domain narrows. Determining the appropriate maximum number of iterations is influenced by various factors, such as the solver’s algorithm and accuracy. This number should guarantee the successful solution of a general problem.
Table 3 outlines our solver parameter settings. In general, it is unnecessary to set the solver to a very high accuracy during the homotopic process. If higher accuracy is required, then after successfully obtaining the solution to the fuel-optimal problem, it is feasible to reset the solver to a higher accuracy and re-solve the problem in accordance with the specified task requirements.
7. Numerical Example and Discussion
One example of fuel-optimal rendezvous problems with fixed boundary conditions, previously addressed in [
10,
11,
17,
24], is provided. The parameters of this example are summarized in
Table 4. The computations were conducted on a personal laptop computer with processor
i5-13500H CPU @ 2.60 GHz and a
memory of
30 GB. The orbital elements, heliocentric position, and velocity of the planets can be computed online using the Jet Propulsion Laboratory Horizons system [
25].
To illustrate the characteristics of our algorithm, we have chosen a typical demonstration of the solution outcomes, depicted in
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9. The final dimensionless mass obtained is 0.8603. This indicates that if the initial mass is 1500 kg, the final mass would be 1290.5 kg. The average time required to solve the given example using the presented strategy is approximately 70 s. In our work, we used MATLAB Coder to convert M functions, e.g., “
fsolve” and the integrator, into C/C++ code and compile them into MEX files, thereby greatly improving computational speed.
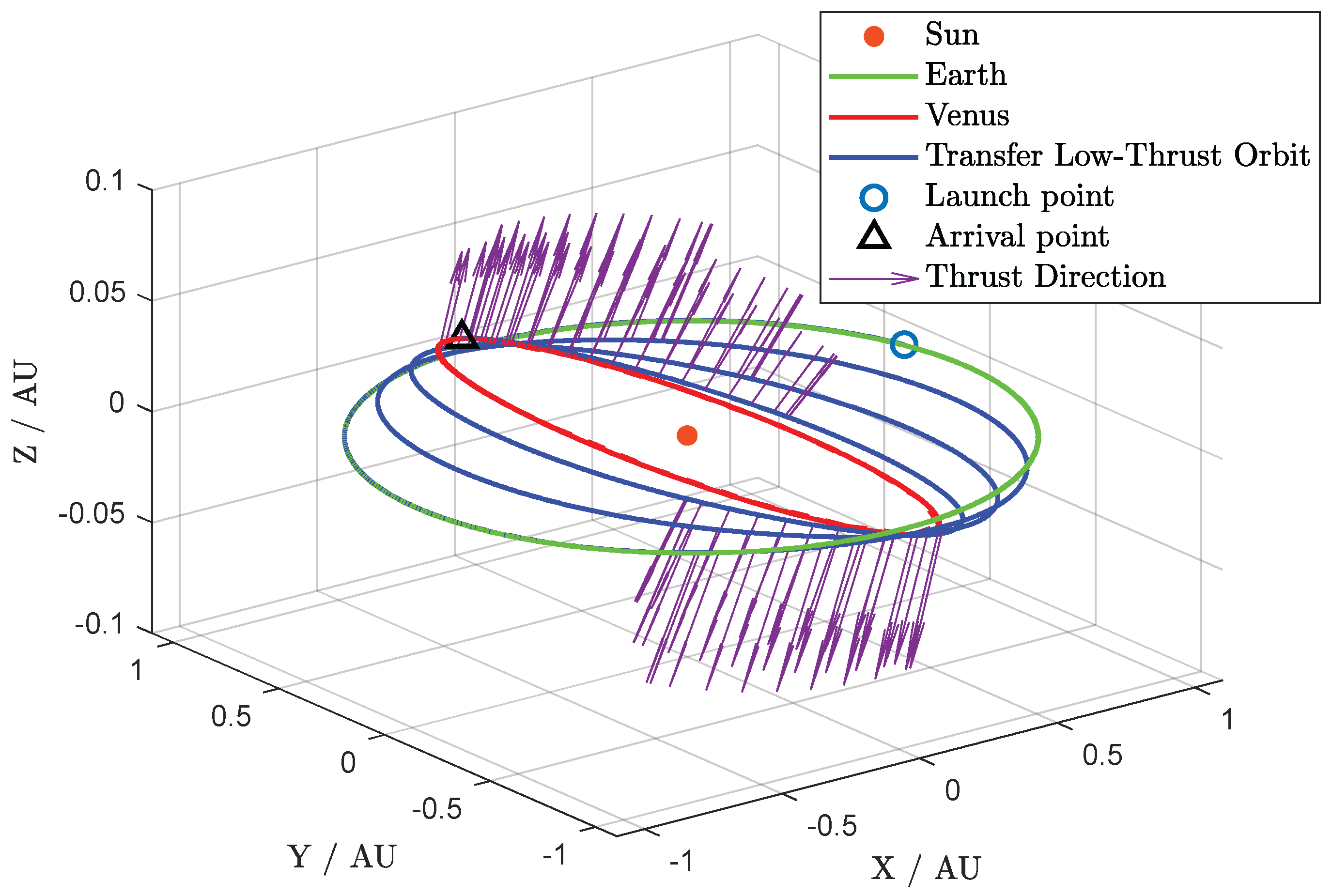
Figure 2 illustrates the 3D fuel-optimal transfer trajectory. The figure also indicates the thrust direction during the flight. However, it should be noted that the z-axis scale is magnified approximately tenfold in comparison to the xy-axis. The thrust continuously and slowly changes the semi-major axis and inclination of the orbit at appropriate positions (perihelion and aphelion).
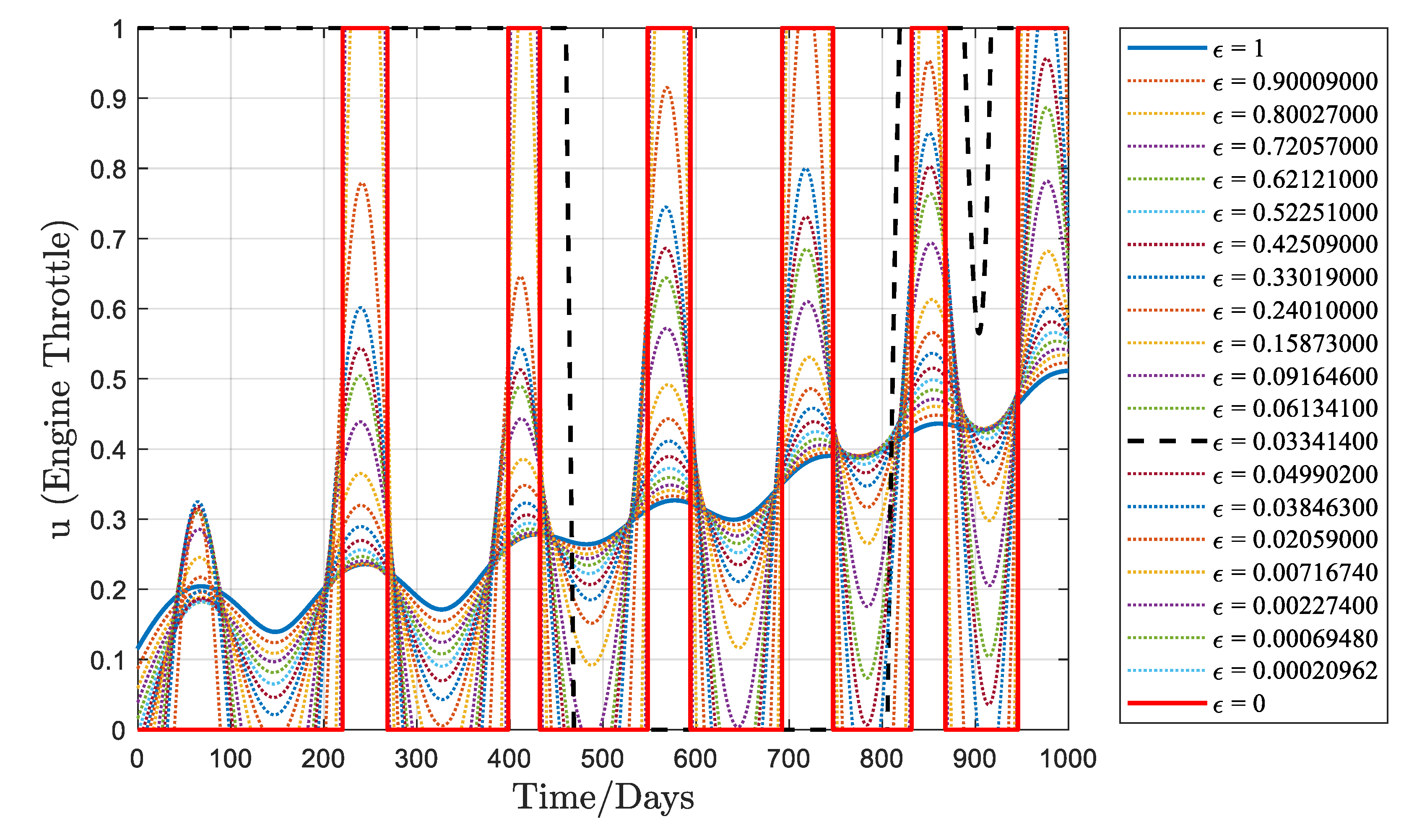
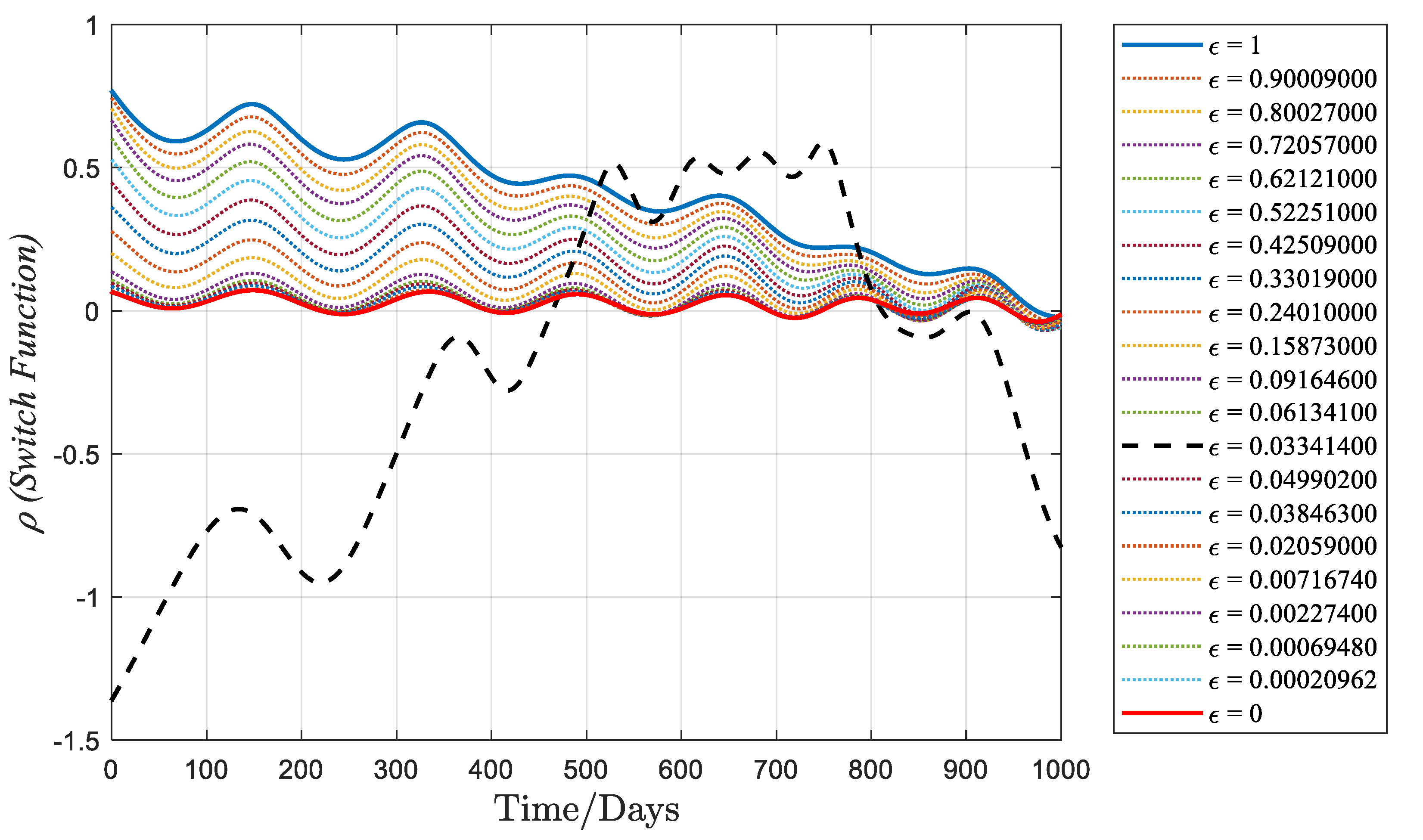
Figure 3 and
Figure 4 depict the thrust and switching function profiles during the homotopic process, respectively. With
equal to 0, the thrust mode transitions to bang-bang control.
Figure 4 illustrates that with
at 0,
fluctuates with small amplitudes around the value of 0. If
is below 0, the spacecraft thrusters are fully open; if
exceeds 0, the thrusters are closed. Additionally, in the fuel-optimal problem, variation in the value of
leads to fluctuations in the valleys of the
curve, causing changes in the number of arc segments intersecting 0. This alteration results in the disappearance or increase in thrust arc segments, consequently altering the switching strategy of the spacecraft thrusters.
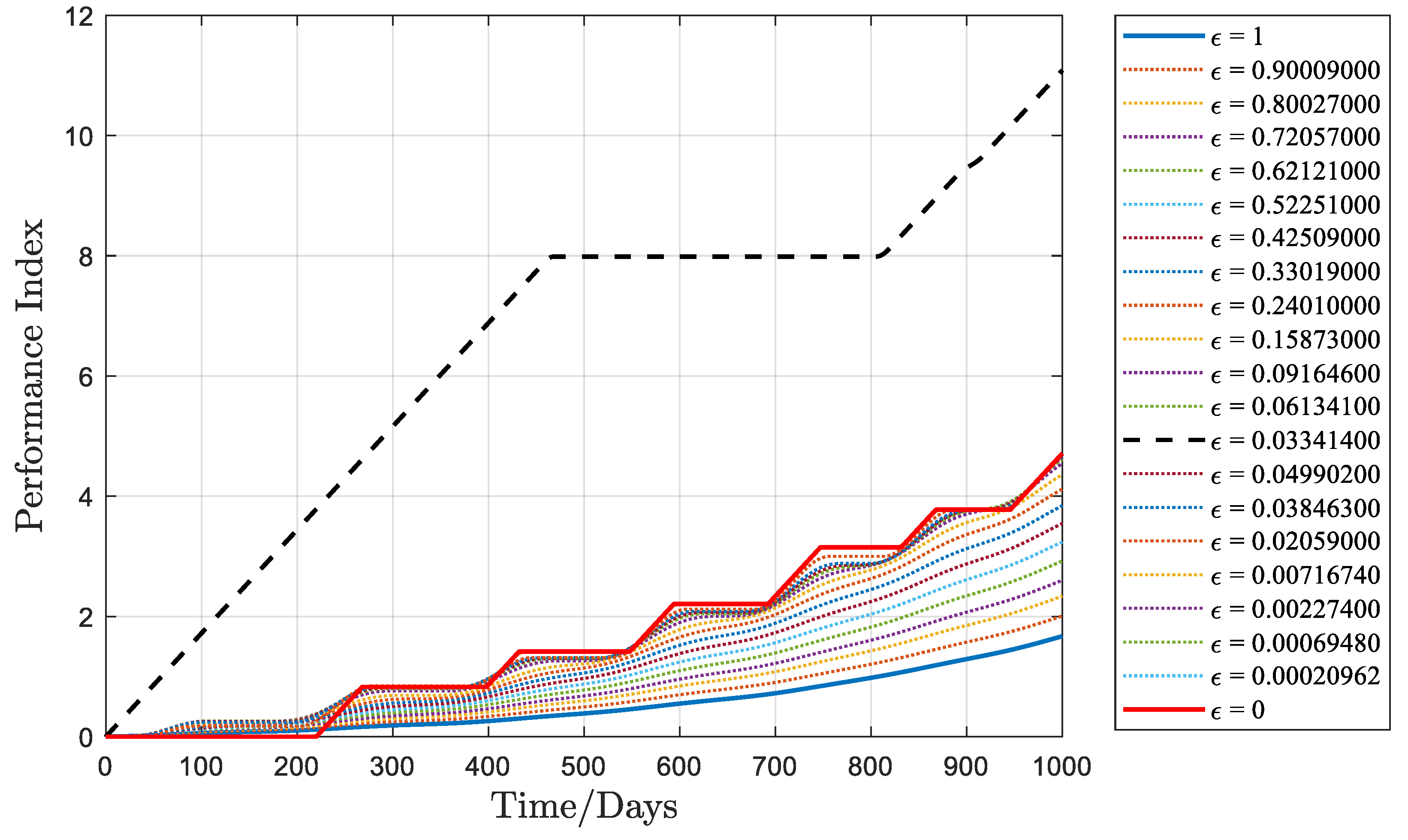
Figure 5 depicts a schematic representation of the performance index over time with different
, validating Equation (25). As
decreases, the performance index at the final moment for the optimal solution of each auxiliary problem grows. With
equal to 0, the performance index remains unchanged during the coasting arcs.
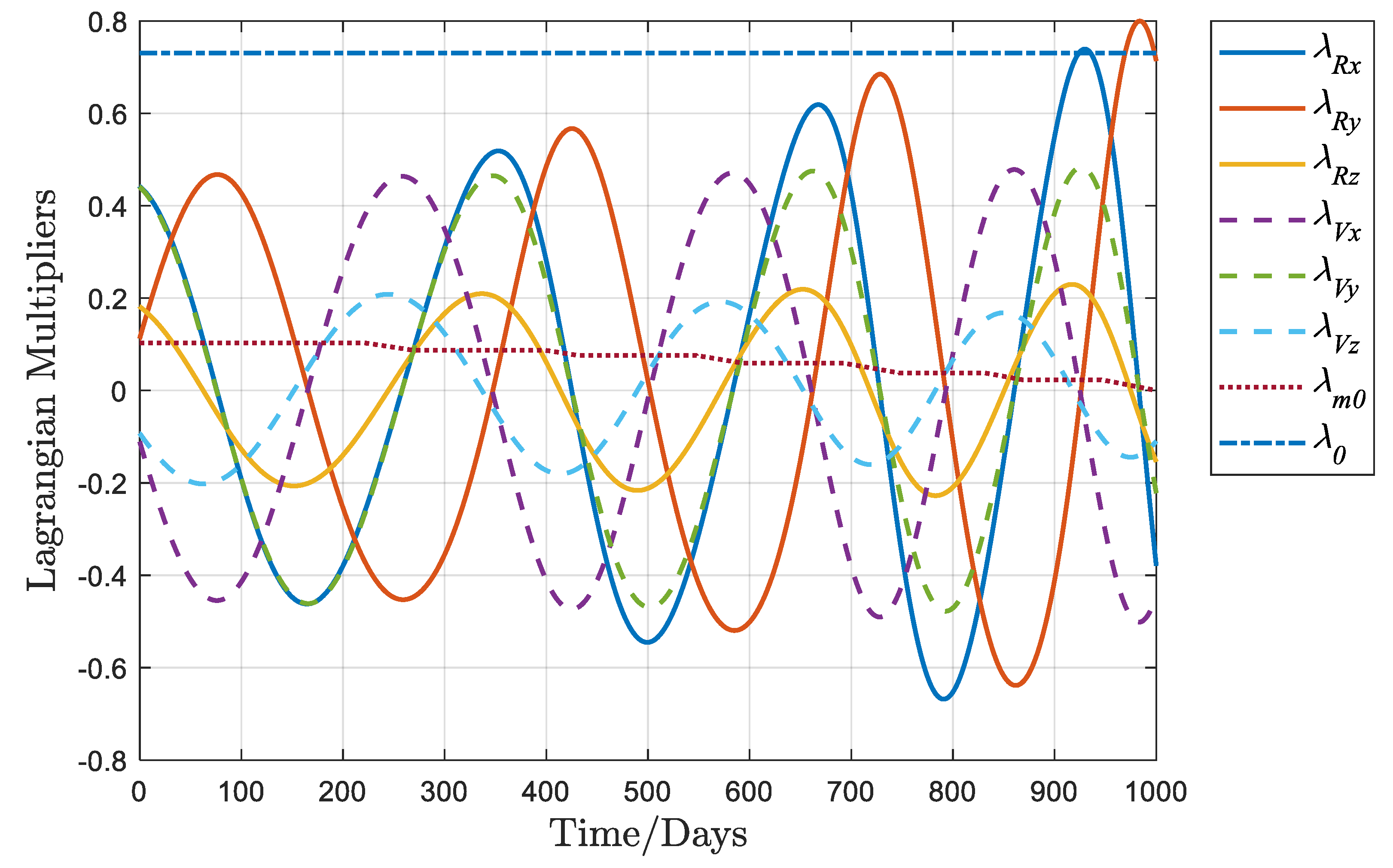
Figure 6 depicts the curves representing the eight Lagrange multipliers
of the fuel-optimal orbit with
equal to 0. Abrupt changes in the parameters are evident at the moment of thrust switching.
remains constant throughout;
decreases solely during the thrust arcs, remains constant during the coasting arcs, and reaches 0 at the terminal moment; the other Lagrange multipliers exhibit, to a certain extent, the fluctuating properties of the sinusoidal function.
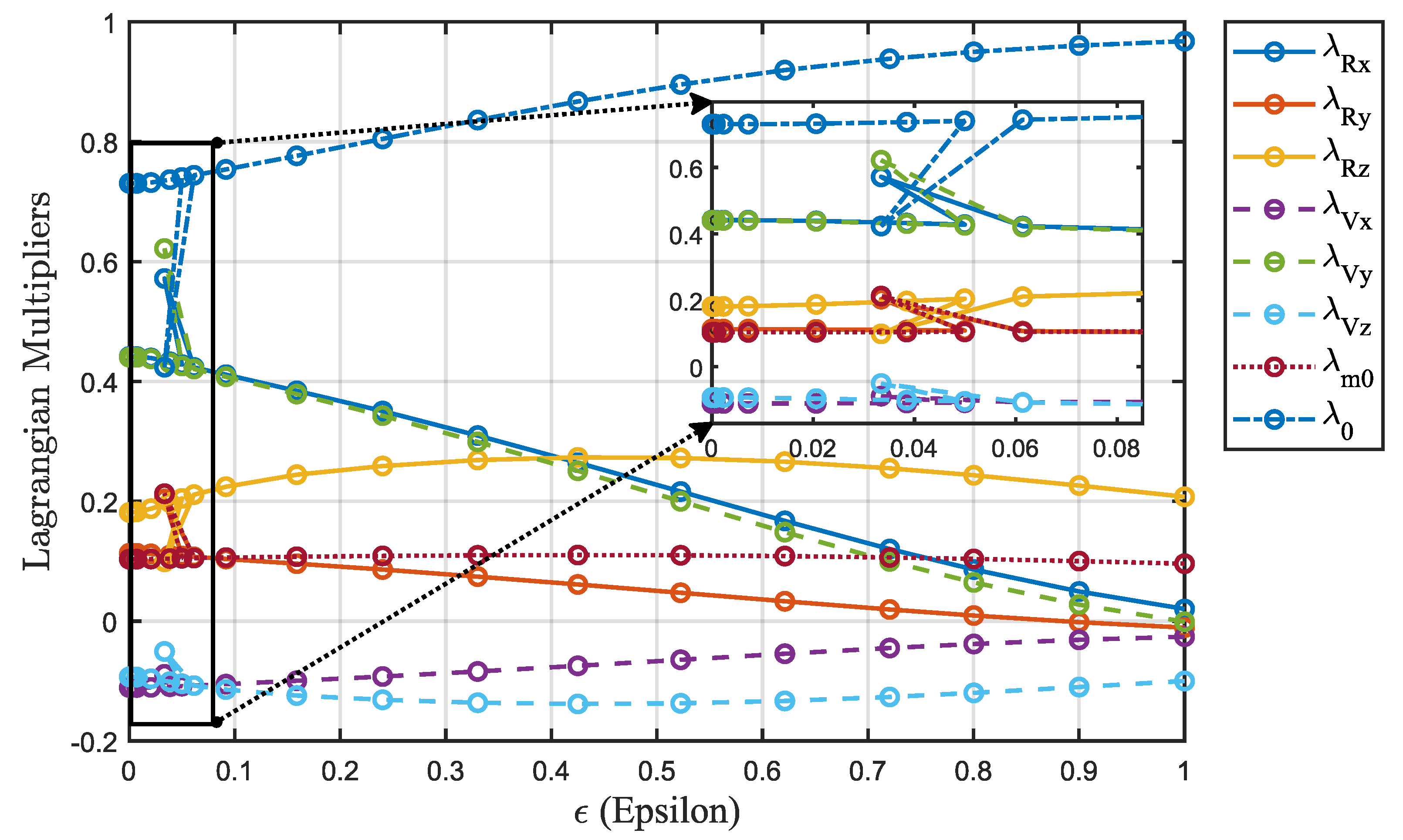
Figure 7 depicts the curves of
as
decreases during the homotopic process. The effectiveness of the smoothing technique in resolving the fuel-optimal bang-bang control problem is evident. The entire homotopic process approximates from the solution with
equal to 1 to the solution with
equal to 0.
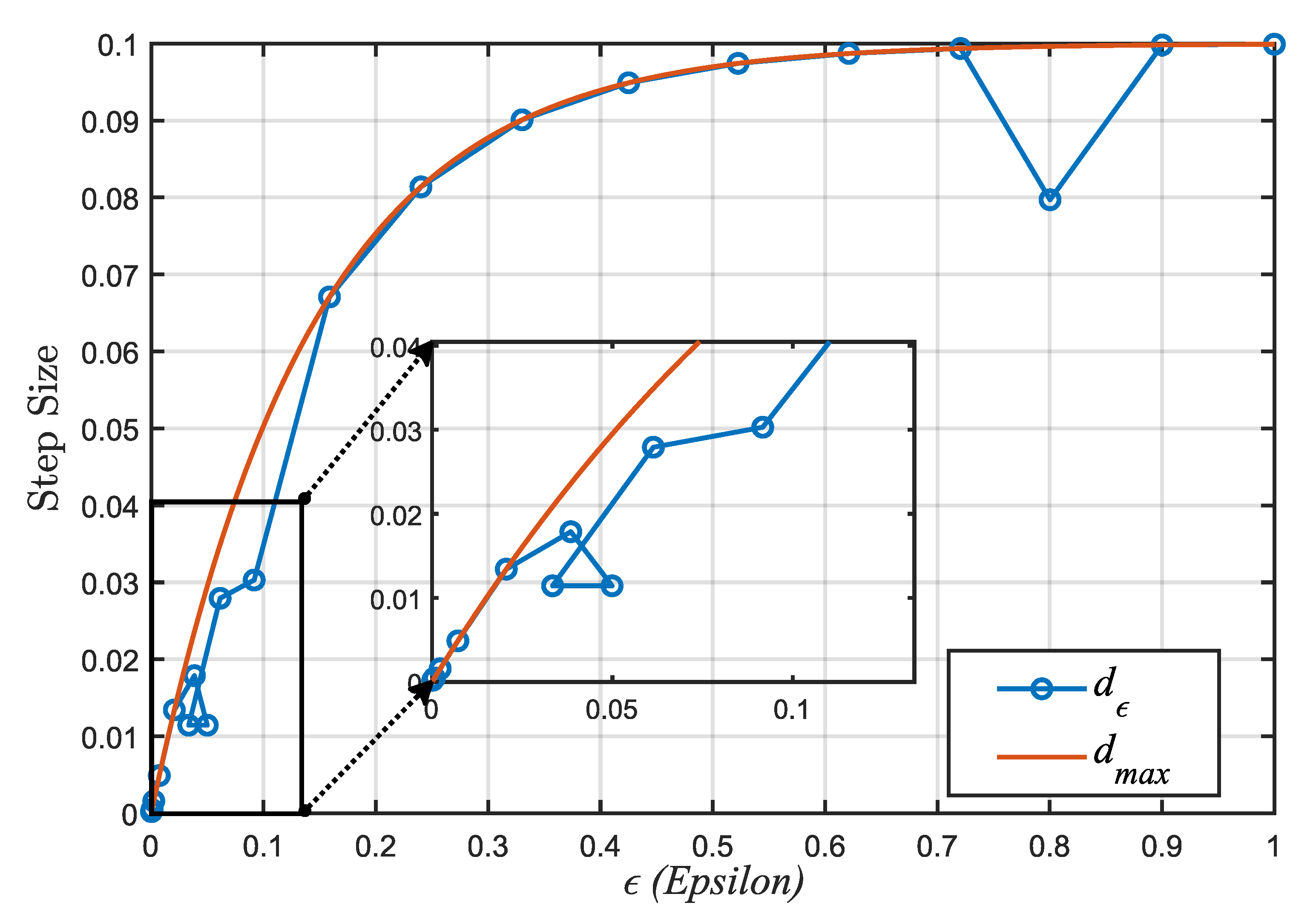
Figure 8 and
Figure 9 illustrate the variation in the step size
with respect to
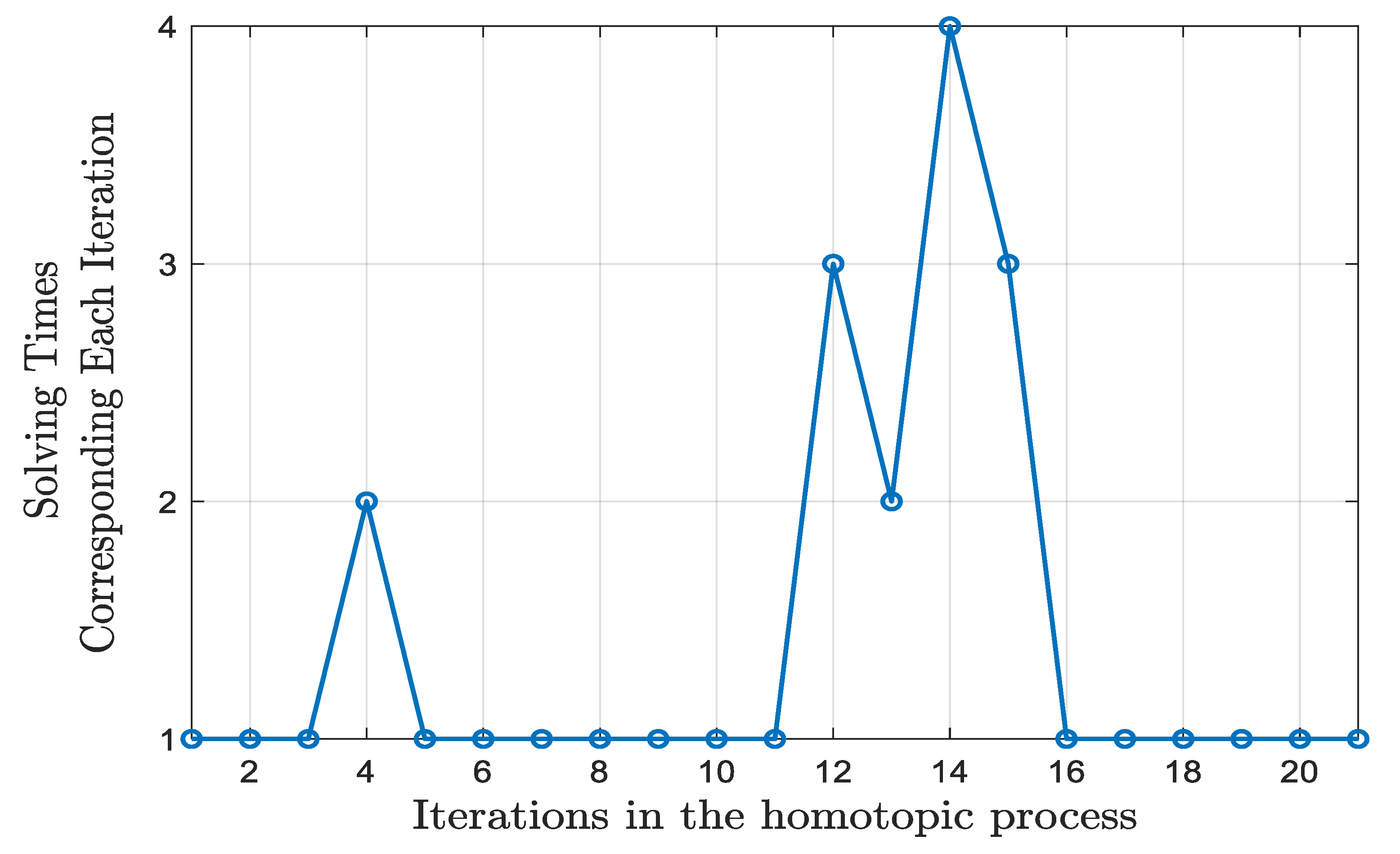
and the number of solving times necessary for a successful resolution of each auxiliary problem, respectively. During iterations 11 to 16, i.e., when
falls within the range of [0.02, 0.09], the resolution fails many times and the
decreases to a relatively small degree. If
only can be reduced, this is likely to result in a situation where
is too small, thus hindering the progression of the homotopic process. In our algorithm,
increases after each successful resolution, as depicted in
Figure 8. This approach not only mitigates the difficulty of a stagnant homotopic process but also improves the speed of homotopic iterations, thereby enhancing the efficiency of problem-solving.
Notice that in
Figure 3,
Figure 4 and
Figure 5, there is a black dashed line, which represents a sub-optimal converged solution obtained with
equal to 0.0334 during the homotopic iteration process. In our algorithm, whether the result converges to a sub-optimal solution is determined through Equation (32). If convergence to a sub-optimal solution occurs, the homotopic process ensures progression toward a good direction by re-solving the problem with an updated
using a reduced
. The enlarged views of the regions in
Figure 7 and
Figure 8 illustrate how the algorithm jumps out of the missteps of the sub-optimal solution.
Additionally, the average time required to compute the PSO part is reduced from 3 s to 0.6 s after the introduction of the diversity term, while still achieving comparable results. To address the energy-optimal problem, we initially set to 0.12, and after obtaining the solution, we utilized the relations (20) to calculate the numerical values of the co-states at corresponding to equal to 0.22. This approach allowed us to reduce the average time required to solve the energy-optimal problem from 25 s to 15 s. To better illustrate this approach’s efficiency, the following example is given. When addressing a problem with a large value of , both the computation of the PSO and the resolution of Equation (14) require a significant amount of time. In the given scenario, if a problem with equal to 1 needs to be solved, the process of calculating the energy-optimal orbit takes approximately 130 s to complete. In contrast, if we initially solve the problem with equal to 0.12 and utilize Equation (20), the total time needed for the entire process could be just approximately 15 s. Equation (20) can be used to significantly reduce calculation time in the resolution of the energy-optimal problem, especially when is quite large.
8. Conclusions
This paper presents a comprehensive analysis of a modified indirect method for addressing the fuel-optimal orbital control problem in low-thrust propulsion systems. By leveraging the quadratic penalty smoothing technique and the normalization technique, the complexity and non-linearity inherent in low-thrust orbital control are effectively managed, considerably increasing the possibility of fuel-optimal solutions’ convergence in comparison with methods that do not use these techniques. The implementation of PSO facilitates the global search for optimal solutions. The introduction of a diversity termination term within the PSO process enhances computational efficiency, demonstrating a significant reduction in computation time. A stiff ODE solver is competent to propagate general interplanetary low-thrust orbits with sufficient accuracy. Moreover, the effect of the maximum thrust to initial mass ratio parameter is investigated. The relationships among the Lagrange multipliers for different can be utilized, especially in scenarios with high , to achieve a decrease in computation time. The proposed homotopic strategy, involving the determination of the maximum step size and the distinction of sub-optimal solutions, could ensure robust convergence toward the fuel-optimal solution when a sub-optimal solution is obtained. The practical application of these techniques is substantiated through an interplanetary rendezvous example, affirming the method’s efficacy and potential for broader implementation in advanced space mission planning.
Although the strategy mentioned is applied within the two-body model in HERF, and combined with the quadratic penalty smoothing technique, the underlying concept of this strategy can be extended to problems described by other models in various coordinate systems, as well as to problems employing different homotopic approaches.