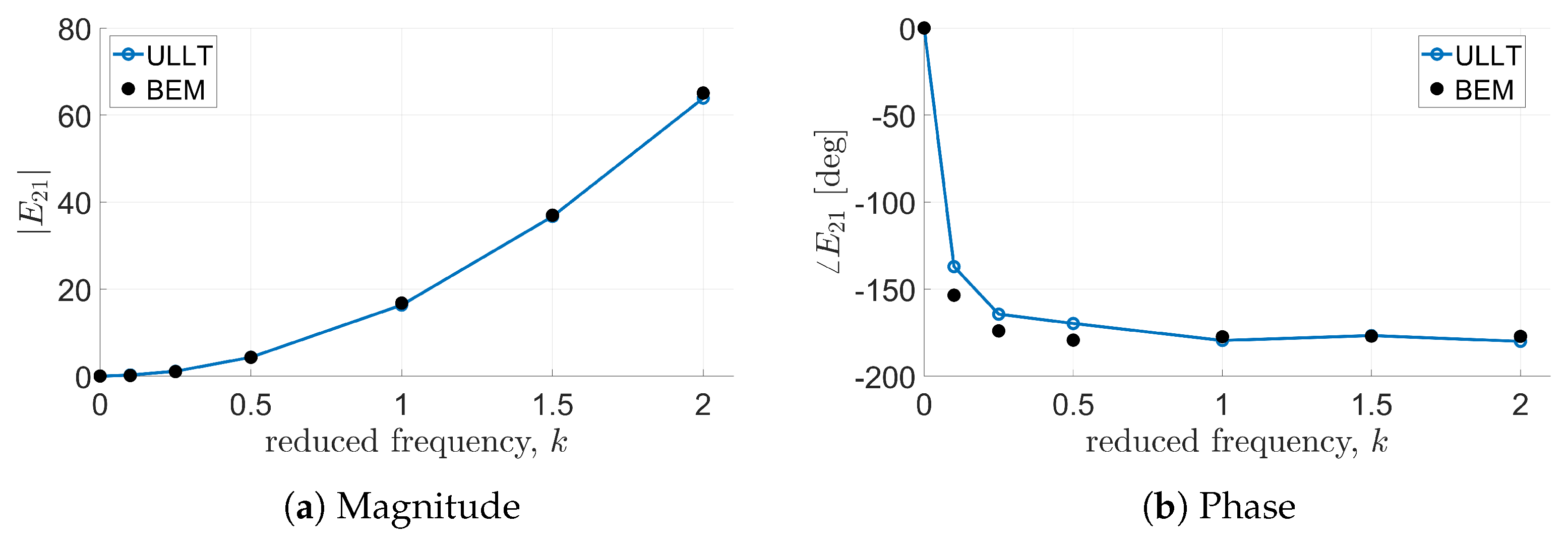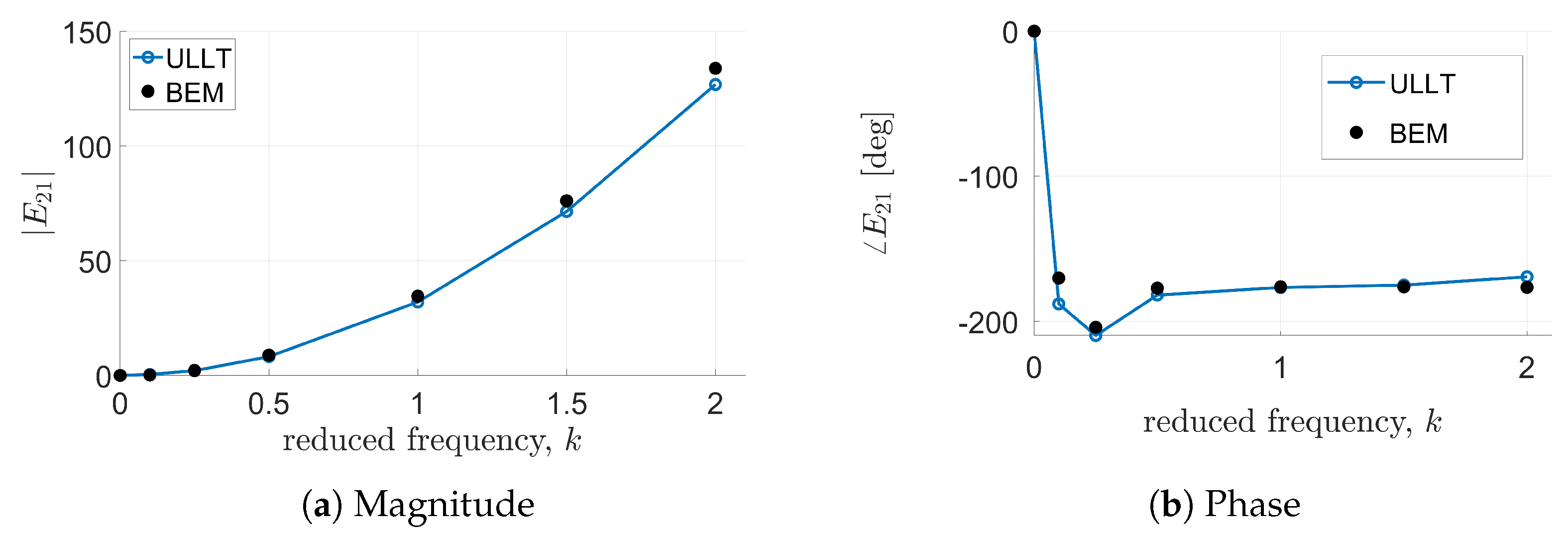Unsteady Lifting-Line Free-Wake Aerodynamic Modeling for Morphing Wings

Abstract

A time-stepping, lifting-line solution algorithm for the prediction of the unsteady aerodynamics of morphing wings is presented. The velocity induced by the wake vorticity is determined through a free-wake vortex-lattice model, whereas the Küssner and Schwarz’s unsteady airfoil theory is used to evaluate the sectional loads, and the generalized aerodynamic loads related to body deformation including camber morphing. The wake vorticity released at the trailing edge derives from the bound circulation and is convected downstream as a vortex ring to form the vortex-lattice wake structure. The local bound circulation is obtained by the application of the Kutta–Joukowski theorem extended to unsteady flows. The accuracy of the loads predicted by the proposed solver is assessed by comparison with the predictions obtained by a three-dimensional boundary-element-method solver for potential flows. The two sets of results agree very well for a wide range of reduced frequencies.

1. Introduction

In the earliest stages of aircraft design, the availability of a reliable computational tool able to examine lifting bodies is a crucial point in evaluating the aerodynamic performance of the aircraft [1]. This becomes even more important when interactional aerodynamics embodies a relevant performance aspect. Moreover, a simpler description of the bodies allows for a flexible approach when optimizing geometries and trying out different solutions; for this reason, a one-dimensional representation becomes the natural model of choice. To this aim, describing lifting bodies through spanwise distributions of sectional properties leaves the analyst free to test various solutions while avoiding the need to process or re-mesh at every iteration. Concerning the canonical lifting-line solution [2,3] many hypotheses are challenged when such a description is applied to wings undergoing an arbitrary and unsteady flowfield, making it necessary to recast the problem in a different formulation.

The earliest attempts to address this topic began at the beginning of the last century by Theodorsen [4] and Wagner [5], among several others, who developed theoretical methods to calculate analytically the lift, drag and pitching moment of airfoils for unsteady flows. Subsequently, the technological advancements in computer science led to the definition of aerodynamic solvers based on a discrete description of the differential problems underneath, letting numerical methods take the spotlight thanks to their ability to describe a wide range of flight conditions. Finite differences and finite volumes CFD solvers do not benefit from any of the analytical formulations derived in the past, somewhat agnostically addressing the problem at hand, but with the inconvenience of carrying high computational costs and complex topological descriptions.

A valid middle ground can be found in hybrid methods such as the Lifting-Line Theory (LLT), which proved to be a very effective tool for the preliminary design of aircraft aerodynamics; although less accurate than high-resolution solvers, the method provides reliable aerodynamic load predictions at a significantly lower computational cost.

Introduced by Prandtl [3] for steady-state flows applications to straight slender wings, the LLT was later modified to deal with arbitrary wing geometry, with the inclusion of sweep angle, arbitrary chord distribution and airfoil cross-sections (see, for instance, Refs. [6,7,8,9]), and simulate nonlinear aerodynamic effects [10,11,12,13]. In the last decades, several unsteady-flow versions have been developed and presented in the literature. These are known as Unsteady Lifting-Line Theories (ULLTs) and are typically based on airfoil unsteady aerodynamics for rigid wing sections, either described by Theodorsen’s or Wagner’s theories. Among these, the first methodology was presented by Sclavounos [14], which combines the three-dimensional trailed vorticity effects with the evaluation of the sectional aerodynamic loads through the Theodorsen theory [4]. Later, Drela provided a similar model with the inclusion of an approximate low-frequency, unsteady-flow version of the Kutta–Joukowski theorem to define the vorticity released along the wake [15], which was extended in [16] to develop a ULLT suitable for the analysis of complex wing geometries. In addition, the approach introduced by Sclavounos was improved for high-frequency applications by Bird and Ramesh [17], Boutet and Dimitriadis proposed a state-space ULLT model enhancing the original Prandtl LLT by combining it with Wagner’s theory for the evaluation of the sectional unsteady loads and Drela’s low-frequency, unsteady-flow version of the Kutta–Joukowski theorem [18], while Izraelevitz et al. [19] presented a ULLT model based on a state-space form of the Wagner indicial response function.

Following this line of research, the present paper aims to propose a time-domain ULLT formulation based on distributed sectional loads given by the unsteady airfoil theory of Küssner and Schwarz [20,21], combined with the velocity induced by the wake vorticity, which, in turn, is derived from the unsteady formulation of the Kutta–Joukowski theorem [22] and is free to move under the action of the self-induced velocity field. The main novelty of the proposed aerodynamic formulation is the capability to examine arbitrarily deforming wings (with the inclusion of morphing camber) and take into account the effects of wake vorticity distortion (free-wake modeling). Indeed, the present model can be considered as the time-domain extension of that recently presented in [23], which was developed in the frequency domain and, therefore, could only consider a fixed wake geometry. Free-wake modeling is present in other ULLT formulations proposed in the literature. It may have a crucial influence in problems where the wake is close to the lifting bodies, like in rotorcraft applications. Note, that in the proposed formulation the shed vorticity contributes to the definition of the self-induced velocity that deforms the wake. Still, it is not taken into account to evaluate the induced velocity on the wing since this effect is already present in the theory of Küssner and Schwarz. The proposed solver is applied to evaluate the generalized aerodynamic loads due to wing deformation and camber morphing and, thus, can be used for aeroelastic applications. In particular, it can be used to determine the aerodynamic matrix collecting the transfer functions that relate the Lagrangian coordinates of a deforming-morphing wing to the corresponding generalized aerodynamic forces.

Although several types of morphing wings have been considered in the literature (see, for instance, [24,25]), those based on camber morphing are the most diffuse and versatile ones. Their aerodynamic modeling is often based on 2D airfoil theories neglecting the effect of the wake vorticity or, on the contrary, applying extremely accurate and computationally expensive CFD tools [26,27,28,29,30]. Indeed, the lack of medium-fidelity aerodynamic solvers for camber-morphing wings inspired both the present work and the model introduced in [23].

The proposed aerodynamic solution approach is similar to the Vortex-Lattice Method. This method considers the body and wakes described by vortex rings: the wake vortices are free to move according to the corresponding velocity field, while the intensity of the body vortices is the unknown of the problem [1]. Thus, its computational cost is greater than that of the ULLT methods where the sectional aerodynamics are solved analytically. A similar correlation exists between the frequency-domain ULLT proposed in [23] and the Doublet-Lattice Methods which describe the aerodynamic solution in terms of a discrete distribution of acceleration potential (namely, pressure jump) over the wing mean surface [1]. Both are frequency-domain solvers considering fixed wake surfaces.

In the following, the derivation of the proposed time-domain ULLT aerodynamic modeling is described. Then, the numerical investigation examines the magnitude and phase of the components of the aerodynamic matrix evaluated by the present approach and the predictions determined by a computational tool based on a boundary element method (BEM) for three-dimensional potential-flows extensively validated in the past [31,32,33,34,35,36,37,38]. In addition, time-marching responses to arbitrary inputs obtained by the proposed formulation from undeformed-wake and free-wake modeling are compared.

2. Time-Domain ULLT Modeling for Camber Morphing Wings

The model hereafter described is a fully unsteady lifting-line model, capable of releasing a vortex-lattice wake free to move according to the self-induced velocity field while computing the sectional aerodynamic loads via Küssner–Schwarz’s model in a completely dynamic manner. To close the lifting-line problem it features a fourth-order formulation of the unsteady extension of the K-J theorem.

2.1. Küssner–Schwarz Sectional Model

In order to gather the aerodynamic forces on each section of the lifting body, the only formulation capable of providing results for arbitrary wing deformation including morphing camber and inflow distribution of the incoming wind is Küssner–Schwarz’s solution [20,21]. All other formulations are indeed based on a particular profile of downwash, some assuming constant or linear distributions [4], some others making hypotheses on the gust shapes encountered by the airfoil [39,40,41].

To go into the detail of the model’s implementation at hand, the explanation shall start from the definition in the frequency domain of the Fourier transform coefficients, as derived by Küssner and very well reformulated in [21].

For a complete description of the problem let us define $\rho$ as the air density, and V as the undisturbed flow speed; hence, let us consider a coordinate system, $(x,z)$, with the origin located at the mid-point of the airfoil, the x-axis aligned with the unperturbed flow of velocity V (as well as with the airfoil), positive from the leading to the trailing edge, and the z-axis positive upward. Moreover, calling b the semichord of the airfoil and $\omega$ the angular frequency, we can define the key nondimensional parameter $k=\omega b/V$, the reduced frequency. In particular, let us define a physical downwash as a function of the vertical displacement, w

$$v=V{\displaystyle \frac{\partial w}{\partial x}}+\dot{w}$$

(1)

In this formulation, the vertical velocity component must be expressed in the cosine Fourier Series. Therefore, we express the displacement as a linear combination of M-suitable shape functions

$$w(x,t)=\sum _{m=1}^M{\psi }_m\left(x\right)q_m\left(t\right)$$

(2)

where $q_m$ represents the m-th generalized Lagrangian coordinates. At the same time, by rewriting Equation (1) in the frequency domain, indicating with (^~) the variables in the new domain, and combining with Equation (2), we can rewrite the downwash as

$$\tilde{v}\left(\xi \right)={\displaystyle \frac{V}{b}}\left[{\displaystyle \frac{\partial \tilde{w}}{\partial \xi }}+ik\tilde{w}\right]={\displaystyle \frac{V}{b}}\sum _{m=1}^M\left[{\displaystyle \frac{\partial {\psi }_m}{\partial \xi }}+ik{\psi }_m\right]{\tilde{q}}_m$$

(3)

where, the $\xi =x/b$ is the nondimensional chordwise coordinate (which is related to the one used in [21] through $\xi =cos\theta$), with the leading and trailing edges of the airfoil, respectively, identified by the values $\xi =-1$ and $\xi =1$.

Next, defining the N Fourier velocity coefficients

$${\tilde{P}}_n=-{\displaystyle \frac{1}{\pi }}\sum _{m=1}^M\left[{\int }_{-1}^1\left({\displaystyle \frac{\partial {\psi }_m}{\partial \xi }}+ik{\psi }_m\right){\displaystyle \frac{cosn[arccos(\xi \left)\right]}{\sqrt{1-{\xi }^2}}}\mathrm{d}\xi \right]{\tilde{q}}_m$$

(4)

and the corresponding pressure coefficients

$$\left\{\begin{array}{c}{\tilde{a}}_0\left(k\right)=C\left(k\right)({\tilde{P}}_0+{\tilde{P}}_1)-{\tilde{P}}_1\hfill \\ {\tilde{a}}_n\left(k\right)={\tilde{P}}_n+ik\left({\tilde{P}}_{n-1}-{\tilde{P}}_{n+1}\right)/2n\mathrm{for}n\ge 1\hfill \end{array}\right.$$

(5)

the pressure jump distribution along the chord can be defined as

$$\begin{array}{c}\hfill \Delta \tilde{p}\left(\xi \right)=-2\rho V^2\left[{\tilde{a}}_0\left(k\right){\displaystyle \frac{\sqrt{1-\xi }}{\sqrt{1+\xi }}}+2\sum _{n=1}^N{\tilde{a}}_n\left(k\right)sin\left(narccos\xi \right)\right]\end{array}$$

(6)

It can be split into its non-circulatory and circulatory parts. The former is defined as

$$\begin{array}{cc}\hfill \Delta {\tilde{p}}^{nc}\left(\xi \right)=-2\rho V^2& \left[\left(ik\sqrt{1-{\xi }^2}\right){\tilde{P}}_0+\left((2+ik\xi )\sqrt{1-{\xi }^2}-{\displaystyle \frac{\sqrt{1-\xi }}{\sqrt{1+\xi }}}\right){\tilde{P}}_1\right.\hfill \\ \hfill & \left.+2\sum _{n=2}^N{S}_n(\xi ,k){\tilde{P}}_n\right]\hfill \end{array}$$

(7)

having defined the function $S_n(\xi ,k)$ as

$$\begin{array}{cc}\hfill S_n(\xi ,k)=& -{\displaystyle \frac{ik}{2(n-1)}}sin\left[\right(n-1)arccos\xi ]+sin[narccos\xi ]\hfill \\ & +{\displaystyle \frac{ik}{2(n+1)}}sin\left[\right(n+1)arccos\xi ]\hfill \end{array}$$

(8)

while the latter is

$$\Delta {\tilde{p}}^c\left(\xi \right)=-2\rho V^2\sqrt{{\displaystyle \frac{1-\xi }{1+\xi }}}C\left(k\right)\tilde{Q}$$

(9)

where $C\left(k\right)$ represents the lift deficiency function formulated by Theodorsen [4], while the term Q is defined as

$$\begin{array}{c}\hfill \tilde{Q}={\tilde{P}}_0+{\tilde{P}}_1=-{\displaystyle \frac{1}{\pi }}\sum _{m=1}^M\left[{\int }_{-1}^1\left({\displaystyle \frac{\partial {\psi }_m}{\partial \xi }}+ik{\psi }_m\right)\sqrt{{\displaystyle \frac{1+\xi }{1-\xi }}}\mathrm{d}\xi \right]{\tilde{q}}_m\end{array}$$

(10)

Then, to have a time-domain description of the aerodynamic formulation suitable for describing the loads corresponding to arbitrary inputs, let us now introduce a second-order rational approximation of the lift deficiency function [42]

$$C\left(k\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{(ik-z_1)(ik-z_2)}{(ik-{\sigma }_1)(ik-{\sigma }_2)}}$$

(11)

where $z_1$, $z_2$ represent the two zeros and ${\sigma }_1$, ${\sigma }_2$ the poles of the second order approximation. This leads to a new system of equations for the two added states required by the rational approximation

$$\left\{\begin{array}{c}\Delta {\tilde{p}}^c\left(\xi \right)=-2\rho V^2\sqrt{{\displaystyle \frac{1-\xi }{1+\xi }}}{\displaystyle \frac{1}{2}}\left[-k^2-(z_1+z_2)ik+z_1{z}_2\right]\tilde{r}\hfill \\ \left[-k^2-({\sigma }_1+{\sigma }_2)ik+{\sigma }_1{\sigma }_2\right]\tilde{r}=\tilde{Q}\hfill \end{array}\right.$$

(12)

where $\tilde{r}$ is an aerodynamic added state introduced by the poles of the rational approximation of $C\left(k\right)$.

Next, the sectional generalized aerodynamic loads can be obtained by projecting the pressure jump on the set of shape functions used to express the displacement

$${\tilde{f}}_m={\tilde{f}}_m^c+{\tilde{f}}_m^{nc}=-b{\int }_{-1}^1\left[\Delta {\tilde{p}}^c\left(\xi \right)+\Delta {\tilde{p}}^{nc}\left(\xi \right)\right]{\psi }_m\left(\xi \right)\mathrm{d}\xi$$

(13)

being ${\tilde{f}}_m^c$ and ${\tilde{f}}_m^{nc}$ the circulatory and non-circulatory parts of the generalized aerodynamic loads, respectively.

Starting from the circulatory part, combining Equations (10), (12) and (13) and rearranging them in vector form yields

$$\left\{\begin{array}{c}{\tilde{\mathbf{f}}}^c=2b\rho V^2\mathbf{g}\left[-k^2-(z_1+z_2)ik+z_1{z}_2\right]\tilde{r}\hfill \\ \left[-k^2-({\sigma }_1+{\sigma }_2)ik+{\sigma }_1{\sigma }_2\right]\tilde{r}=\left({\mathbf{h}}^T+ik{\mathbf{l}}^T\right)\tilde{\mathbf{q}}\hfill \end{array}\right.$$

(14)

where g, h, l are $[M\times 1]$ vectors, whose component are expressed as

$$\left\{\begin{array}{c}{\displaystyle g_m={\displaystyle \frac{1}{2}}{\int }_{-1}^1\frac{\sqrt{1-\xi }}{\sqrt{1+\xi }}{\psi }_m\mathrm{d}\xi }\hfill \\ {\displaystyle h_m=-{\displaystyle \frac{1}{\pi }}{\int }_{-1}^1{\displaystyle \frac{\sqrt{1-{\xi }^2}}{1-\xi }}{\displaystyle \frac{\partial {\psi }_m}{\partial \xi }}\mathrm{d}\xi }\hfill \\ {\displaystyle l_m=-{\displaystyle \frac{1}{\pi }}{\int }_{-1}^1{\displaystyle \frac{\sqrt{1-{\xi }^2}}{1-\xi }}{\psi }_m\mathrm{d}\xi }\hfill \end{array}\right.$$

(15)

In the same way, the non-circulatory part of the generalized aerodynamic loads is obtained by the combination of Equations (4), (7) and (13), that provides, after rearranging in vector form

$${\tilde{\mathbf{f}}}^{nc}=2b\rho V^2\left[-k^2\mathbf{CB}+ik(\mathbf{CA}+\mathbf{DB})+\mathbf{DA}\right]\tilde{\mathbf{q}}$$

(16)

where the matrices D and C and have dimensions $[M\times N]$, while A and B are $[N\times M]$, and their components are defined as

$$\left\{\begin{array}{c}{\displaystyle A_{nr}=-\frac{1}{\pi }{\int }_{-1}^1\frac{cos\left[n(arccos\xi )\right]}{\sqrt{1-{\xi }^2}}\frac{\partial {\psi }_r\left(\xi \right)}{\partial \xi }\mathrm{d}\xi }\hfill \\ {\displaystyle B_{nr}=-\frac{1}{\pi }{\int }_{-1}^1\frac{cos\left[n(arccos\xi )\right]}{\sqrt{1-{\xi }^2}}{\psi }_r\left(\xi \right)\mathrm{d}\xi }\hfill \\ {\displaystyle C_{m0}={\int }_{-1}^1\sqrt{1-{\xi }^2}{\psi }_m\left(\xi \right)\mathrm{d}\xi }\hfill \\ {\displaystyle C_{m1}={\int }_{-1}^1\xi \sqrt{1-{\xi }^2}{\psi }_m\left(\xi \right)\mathrm{d}\xi }\hfill \\ {\displaystyle C_{mn}={\int }_{-1}^1\left(\frac{sin\left[\right(n+1)arccos\xi ]}{(n+1)}-\frac{sin\left[\right(n-1)arccos\xi ]}{(n-1)}\right){\psi }_m\left(\xi \right)\mathrm{d}\xi \mathrm{for}n>1}\hfill \\ D_{m0}=0\hfill \\ {\displaystyle D_{m1}={\int }_{-1}^1(2\xi +1)\frac{\sqrt{1-\xi }}{\sqrt{1+\xi }}{\psi }_m\left(\xi \right)\mathrm{d}\xi }\hfill \\ {\displaystyle D_{mn}=2{\int }_{-1}^{1}sin(narccos\xi ){\psi }_m\left(\xi \right)\mathrm{d}\xi \mathrm{for}n>1}\hfill \end{array}\right.$$

(17)

Finally, combining Equations (14) and (16) and performing the inverse Fourier transform we obtaining the following definition in the time domain

$$\left\{\begin{array}{c}\mathbf{f}\left(\tau \right)=2b\rho V^2\left[\mathbf{C}\mathbf{B}\ddot{\mathbf{q}}+(\mathbf{CA}+\mathbf{DB})\dot{\mathbf{q}}+\mathbf{DA}\mathbf{q}+\mathbf{g}(\ddot{r}-(z_1+z_2)\dot{r}+z_1{z}_{2}r)\right]\hfill \\ \ddot{r}-({\sigma }_1+{\sigma }_2)\dot{r}+{\sigma }_1{\sigma }_{2}r={\mathbf{l}}^T\dot{\mathbf{q}}+{\mathbf{h}}^T\mathbf{q}\hfill \end{array}\right.$$

(18)

where $\tau$ is the non-dimensional time variable, defined as $\tau =tV/b$. This expression of the aerodynamic loads is the key element of the proposed approach, which derives from the rational approximation of the lift deficiency function in Equation (11) and represents a state-space formulation particularly suitable for aeroelastic applications.

2.2. Relation between Bound Circulation and Circulatory Lift

The canonical formulation for lifting-line models exploits the widely-known Glauert formulation and Kutta–Joukowski theorem [1,2]. Using this formulation in a time-stepping simulation tool including wake effects would result in a quasi-steady approach. In this case, to achieve the balance between circulatory lift and released vorticity, there is the need to iteratively modify the bound circulation, $\mathrm{\Gamma }$, until appropriate matching is reached. To take into account the unsteady effects of this approach, the Kutta–Joukowski theorem extended to unsteady linear aerodynamics [22] must be used. Indeed, for each section of the wing, the following relation holds

$$\tilde{\mathrm{\Gamma }}={\displaystyle \frac{1}{\rho V}}H\left(k\right){\tilde{L}}_c$$

(19)

where $H\left(k\right)$ represents the reciprocal of the Kutta–Joukowski frequency response function, which is given in terms of transcendental functions (namely Bessel functions) of the reduced frequency, making it unsuitable for deriving state-space time-domain formulations. To achieve this objective, it is convenient to express it through an approximated rational form. Since $H\left(k\right)\to 0$ as $k\to \infty$, for the bound circulation frequency response function this expression can be used (considering $N_H>M_H$)

$$H\left(k\right)\cong H_0{\displaystyle \frac{{\prod }_{m=1}^{M_H}(ik-z_m)}{{\prod }_{n=1}^{N_H}(ik-p_n)}}$$

(20)

where the constant $H_0$, the $N_H$ poles $p_n$, and the $M_H$ zeroes $z_m$ are determined to obtain an adequate accuracy. Combining Equation (20) with (19) and performing the inverse Fourier transform yields the following expression

$$\left\{\begin{array}{c}{\displaystyle \mathrm{\Gamma }\left(\tau \right)={\displaystyle \frac{1}{\rho V}}\sum _{n=1}^{N_H}{c}_n{r}_n\left(\tau \right)}\hfill \\ {\dot{r}}_n\left(\tau \right)=p_n{r}_n\left(\tau \right)+L_c\left(\tau \right)n=1,...,N_H\hfill \end{array}\right..$$

(21)

which provides, in nondimensional time $\tau$, the bound circulation as a function of the circulatory lift time history (with the coefficients $c_n$ obtained from the partial fraction decomposition). The added states $r_n$ are introduced by the poles of the rational approximation. In the method developed for this study, $M_H=3$ and $N_H=4$ showed a satisfactory correlation with the exact solution through the entire range of application of the reduced frequency k. Note, that the application of lower-order rational forms for the description of the function $H\left(k\right)$ would decrease the quality of the approximation, while not reducing significantly the computational cost of the proposed formulation.

It is worth noting that a finite-state approximation of unsteady aerodynamic formulations can be found since the work of [43]. Thereafter, several approaches have been developed for the finite-state modeling of airfoil unsteady aerodynamics, many of which are outlined and compared in [44]. From that study it can be gathered that the number of states introduced by this present finite-state approximation of the Kutta–Joukowski theorem is in line with the number of states typically introduced for lift response modeling.

2.3. Three-Dimensional Formulation

To include three-dimensional effects into the sectional solution via Küssner–Schwarz’s model, it becomes necessary to take into account the effects of the velocity induced by the wake vorticity. Specifically, this contribution is included by numerically evaluating its chordwise distribution due to the trailing vortices (the effects from the shed vortices are already taken into account by the Küssner–Schwarz’s theory).

Dividing the wing into a prescribed number, $N_B$, of finite sections, discretizing the wake into $N_W$ streamwise elements (corresponding to the number of timesteps of the simulation), and evaluating the induced velocity onto $N_C$ collocation points along the chord of each section, it is possible to derive an expression of the following type

$${\mathbf{v}}_{ind}=\mathbf{F}\left(t\right)\mathsf{\Gamma }$$

(22)

where ${\mathbf{v}}_{ind}$ denotes the vector collecting the wake-induced normalwash at the $N_B\times N_C$ control points and Γ collects the $N_B$ values of the discretized spanwise bound circulation distribution.

Note, that we consider only the normal component of the induced velocity

$$v_i(x,y,t)={\mathbf{v}}_{ind}(x,y,t)·\widehat{\mathbf{n}}$$

(23)

where $\widehat{\mathbf{n}}$ represents the unit vector normal to the chord airfoil. This contribution modifies Equation (1) as

$$v=V{\displaystyle \frac{\partial w}{\partial x}}+\dot{w}+v_i$$

(24)

and thus the coefficients $P_n$ in Equation (4), the pressure jump distribution and, therefore, the generalized aerodynamic loads. Overall, the contribution of the induced velocity modifies Equation (18) as

$$\left\{\begin{array}{c}\mathbf{f}\left(\tau \right)=2b\rho V^2\left[\mathbf{CB}\ddot{\mathbf{q}}+(\mathbf{CA}+\mathbf{DB})\dot{\mathbf{q}}+\mathbf{DA}\mathbf{q}+\mathbf{C}\dot{\mathbf{t}}+\mathbf{D}\mathbf{t}+\mathbf{g}(\ddot{r}-(z_1+z_2)\dot{r}+z_1{z}_{2}r)\right]\hfill \\ \ddot{r}-({\sigma }_1+{\sigma }_2)\dot{r}+{\sigma }_1{\sigma }_{2}r={\mathbf{l}}^T\dot{\mathbf{q}}+{\mathbf{h}}^T\mathbf{q}+j\hfill \end{array}\right.$$

(25)

where t is a $[N\times 1]$ vector, whose components are expressed as follows, along with the scalar j

$$\left\{\begin{array}{cc}{t}_n(y,t)\hfill & {\displaystyle =-{\displaystyle \frac{1}{\pi V}}{\int }_{-1}^1\frac{cos\left[n(arccos\xi )\right]}{\sqrt{1-{\xi }^2}}{v}_i\left(x\left(\xi \right),y,t\right)\mathrm{d}\xi }\hfill \\ j(y,t)\hfill & {\displaystyle =-{\displaystyle \frac{1}{\pi V}}{\int }_{-1}^1{\displaystyle \frac{\sqrt{1-{\xi }^2}}{1-\xi }}{v}_i(x\left(\xi \right),y,t)\mathrm{d}\xi }\hfill \end{array}\right.$$

(26)

2.4. Time-Stepping Formulation for the Closure of LLT Model

In a time-marching method, convergence must be reached within each timestep before advancing the time variable.

In more detail, this convergence evaluates the change in circulation due to the variation in the lift generated by the wake released at that particular instant.

The iterative process starts at the beginning of a new timestep, computing the aerodynamic forces (with Küssner–Schwarz’s model) due to freestream, kinematic and induced velocity—with the induced velocity at first only determined by previous timestep wake elements. All the actions are computed specifically for each airfoil.

The newly computed value of sectional circulatory lift enters the unsteady Kutta–Joukowsky added states model and computes the value of bound circulation of each airfoil. Once all values are available on all wing sections, the new wake can be released. However, since this wake being released should be affecting the flowfield that is generating it, the algorithm proceeds adjourning the induced velocities.

The new values of induced velocity trigger a new computation of sectional forces and subsequently all other passages until the normalized difference between each section’s circulation is negligible with respect to the one computed at the previous iteration step.

At this point, time is increased, wake is convected downstream and a new timestep can begin its loop (see the graphical description of the iterative process in Figure 1).

3. Numerical Investigation

In this section, first, the accuracy of the proposed ULLT formulation to evaluate the aerodynamic matrix collecting the transfer functions relating the generalized aerodynamic loads to the Lagrangian coordinates, $E_{ij}\left(k\right)$, is assessed by comparison with the predictions provided by a frequency-domain BEM computational tool for three-dimensional lifting bodies in arbitrary motion. It is worth reminding that this computational tool was extensively validated against both experimental and numerical literature data, concerning both fixed and rotary wing configurations [31,32,33,34,35,36,37,38]. Next, the influence of wake modeling on load predictions is examined.

The numerical results concerning the assessment of accuracy present the magnitude and phase of the aerodynamic matrix components within the reduced frequency range $k\in [0,2]$. These are derived from time-marching predictions for suitable harmonic inputs and consider a simple test case consisting of untwisted rectangular wings with chord length $c=1$ m and two different aspect ratios corresponding to half-span lengths $l=5$ m, $l=10$ m. The undisturbed flow has freestream velocity equal to $V=50$ m/s and ISA-SL air density ($\rho =1.225$ kg/m³).

Pitching and torsion motions are assumed to occur around the local aerodynamic center line. Both the results presented obtained by the ULLT tool and those provided by the BEM solver are numerically converged ones, in terms of body and wake discretization elements. In particular, at $N_C=80$ chordwise nodes and with $N_B\ge 20$ spanwise sections for the $l=5$ case, the results were already converged; timewise, a timestep of around $\Delta t=T/50$ with T period of the harmonic motion, was adequate throughout all cases.

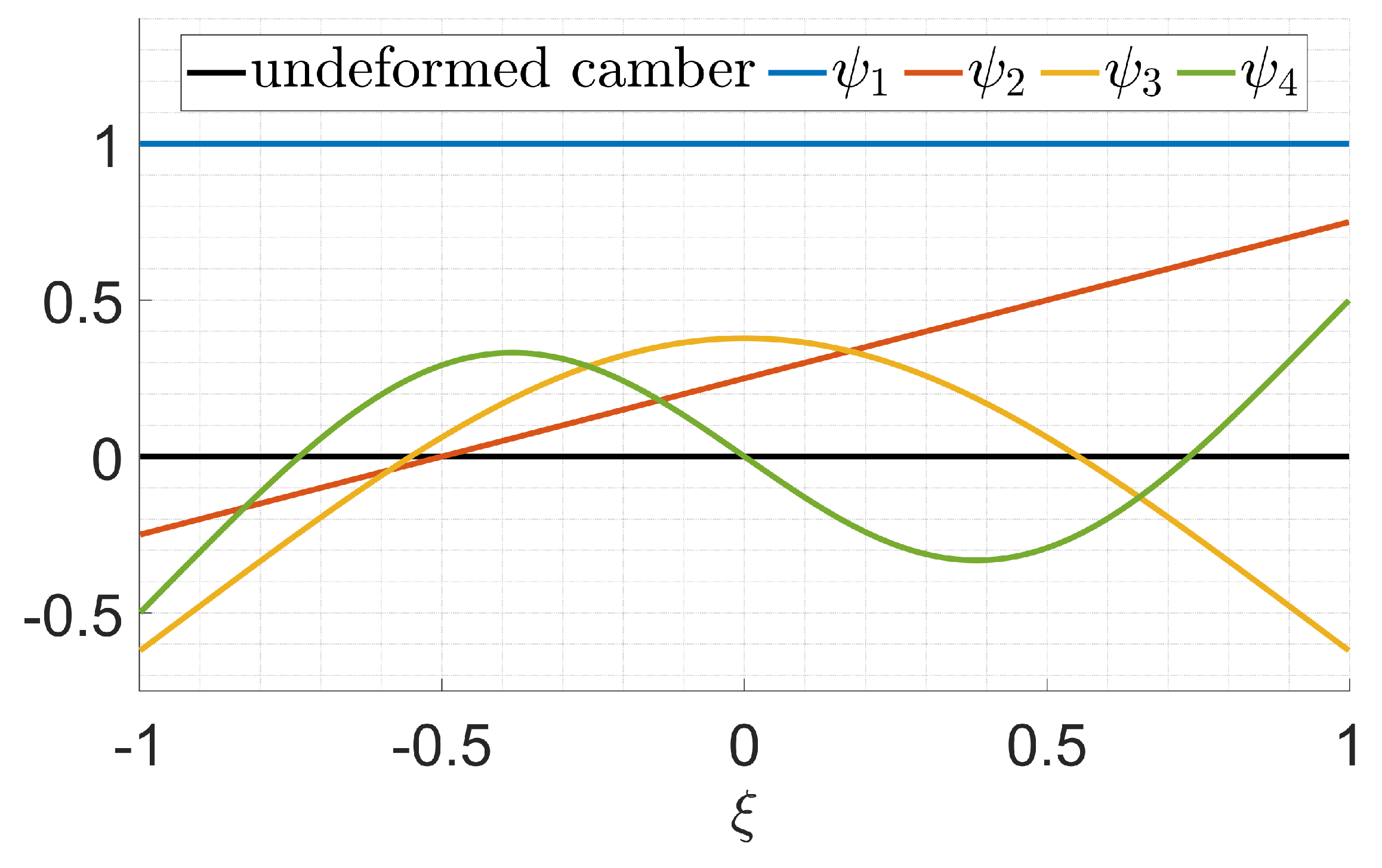
Four different spanwise-uniform shape functions of increasing complexity are considered, namely ${\psi }_{1,2,3,4}$:

• shape functions representing plunging and pitching rigid-body motions (corresponding to the first and second natural bending modes of vibration of a free-free beam)

  $$\left\{\begin{array}{c}{\psi }_1\left(\xi \right)=1\hfill \\ {\psi }_2\left(\xi \right)=(\xi -{\xi }_0)b\hfill \end{array}\right.$$

  (27)

  with ${\xi }_0$ representing the nondimensional coordinate of the aerodynamic center; the corresponding generalized forces are the total lift and pitching moment around the aerodynamic center line;
• shape functions representing camber morphing and corresponding to the third and fourth natural bending modes of vibration of a free-free beam

  $$\left\{\begin{array}{c}{\psi }_3\left(\xi \right)=c_{1}cos\left({\mu }_1\xi \right)+c_{2}cosh\left({\mu }_1\xi \right)\hfill \\ {\psi }_4\left(\xi \right)=c_{3}sin\left({\mu }_2\xi \right)+c_{4}sinh\left({\mu }_2\xi \right)\hfill \end{array}\right.$$

  (28)

  with $c_1=0.4360$, $c_2=-0.0579$, $c_3=-0.3537$, $c_4=0.0099$ and ${\mu }_1=2.3650$, ${\mu }_2=3.9266$ as coefficients of the approximation.

Note, that these shape functions are not related to any real wing configuration, and are introduced to represent a generic motion of the wing sections (for simplicity, all wing sections are assumed to undergo the same motion). Arbitrarily, but legitimately, they are defined through the natural modes of vibration of a free-free beam to comply with the absence of geometric constraints at the edges of each wing section. Their shapes are depicted in Figure 2.

3.1. Validation of the Proposed KS-LLT Model

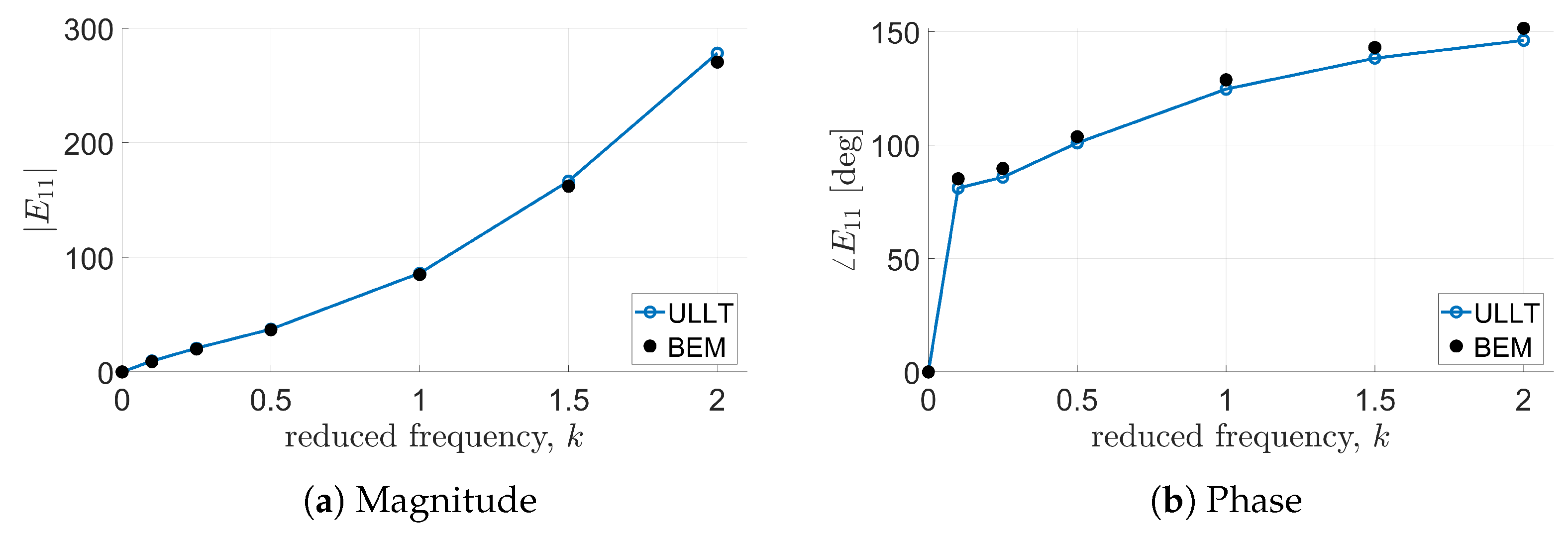
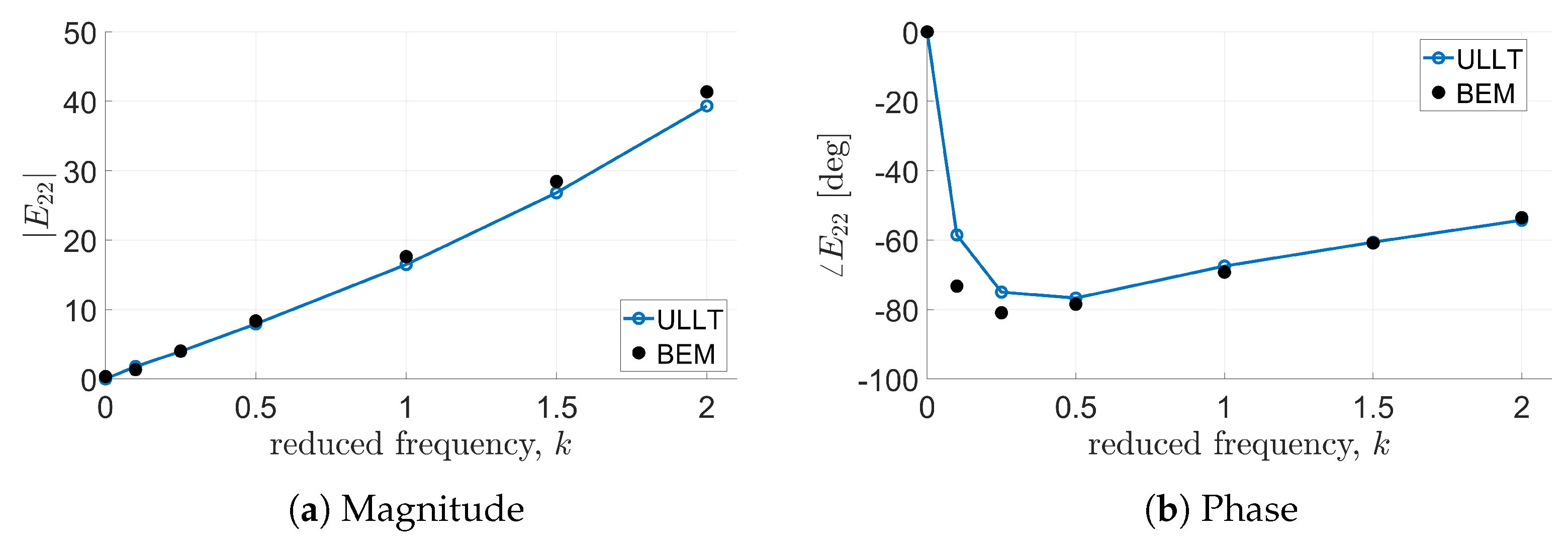
For $l=5$ m, Figure 3 and Figure 4 present the transfer functions $E_{11}$ and $E_{12}$ (namely, lift due to plunging motion and lift due to pitching motion), whereas Figure 5 and Figure 6 show the transfer functions $E_{21}$ and $E_{22}$ relating pitching moment to plunging and pitching motion, respectively.

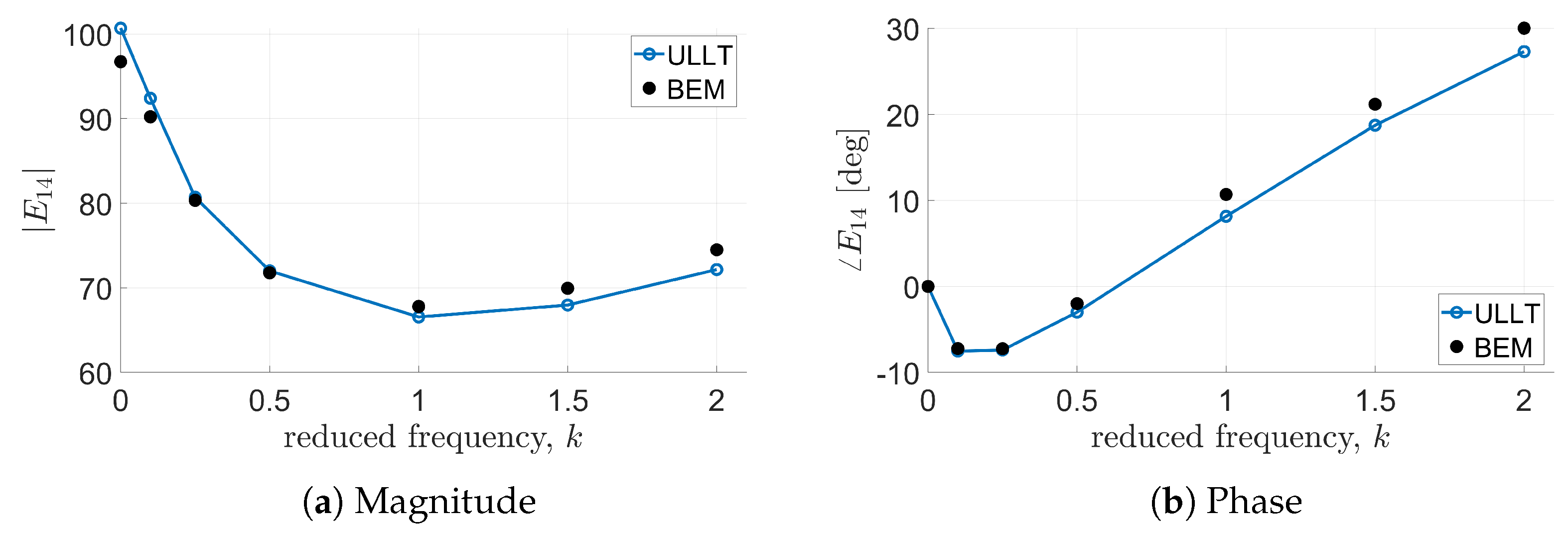
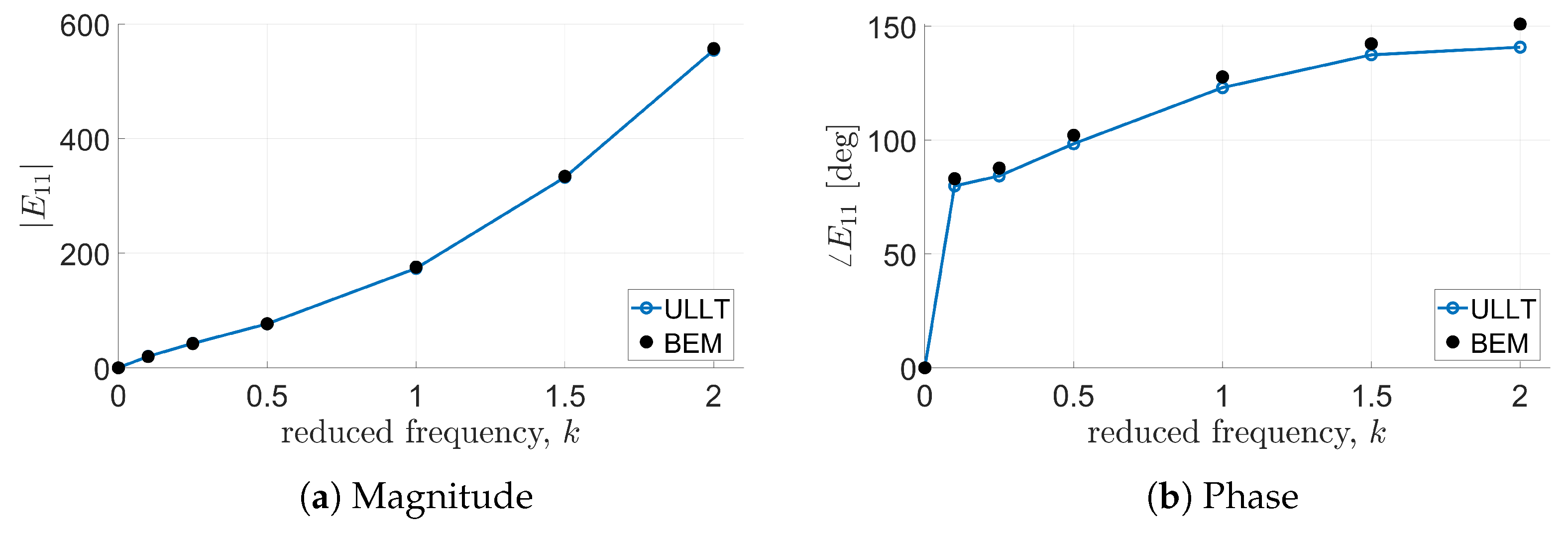
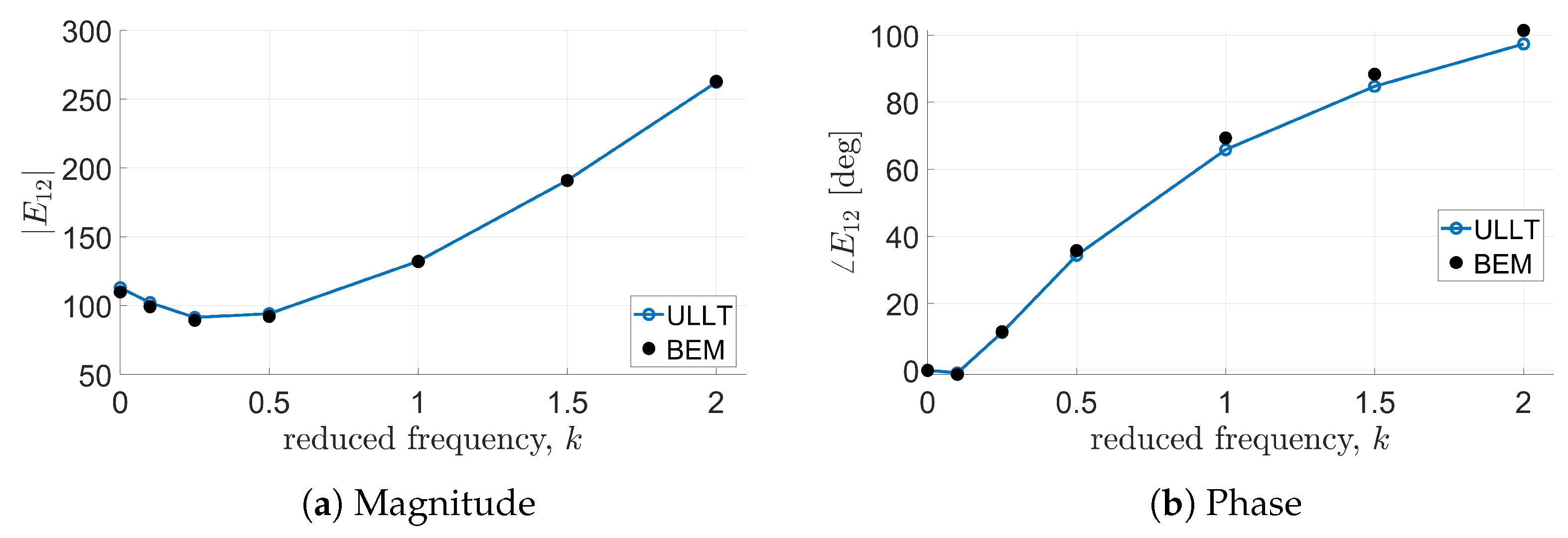
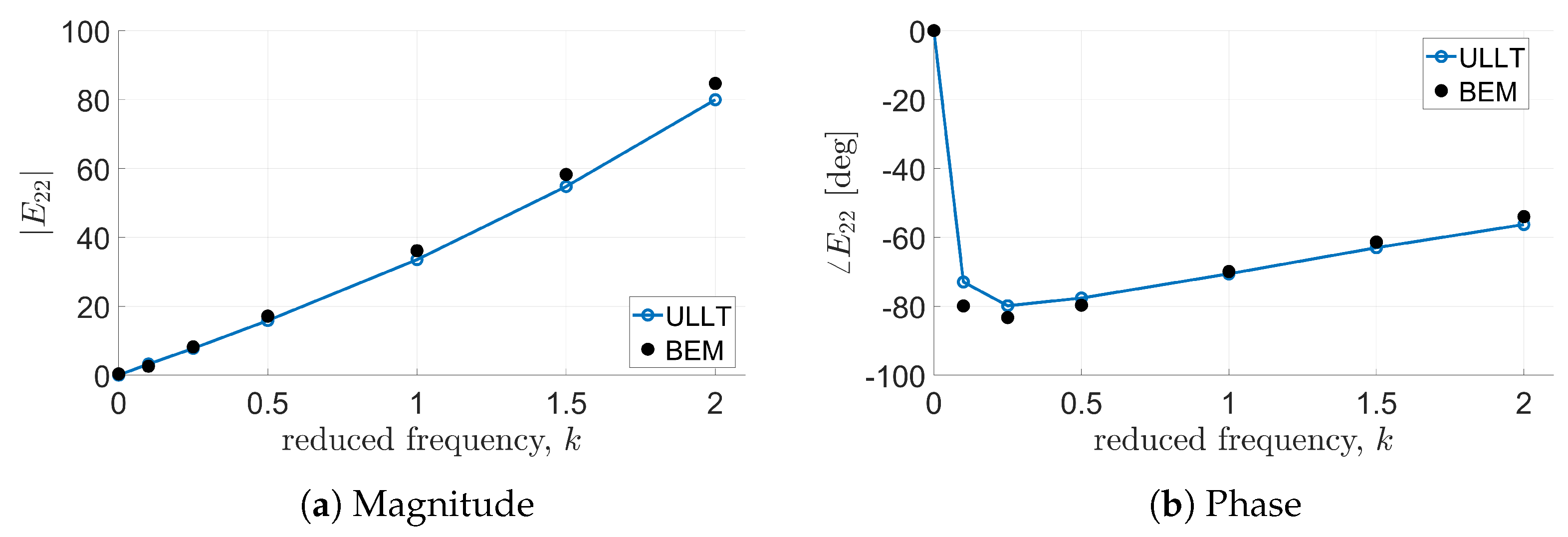
In these cases, all solvers considered provide almost identical results. Predictions from the ULLT solver and the BEM tool are in very good agreement, with some discrepancies appearing at high values of reduced frequency in most of the cases and at lower frequencies only for $E_{21}$ and $E_{22}$ phases correlation. It is worth noting that the transfer functions’ magnitude and phase determined by the present ULLT approach are evaluated through an FFT of the computed time-domain evolution of the loads.

The same level of agreement between ULLT predictions and BEM predictions is observed in Figure 7 and Figure 8 which show the transfer functions relating lift generation to the third and fourth bending modes, respectively.

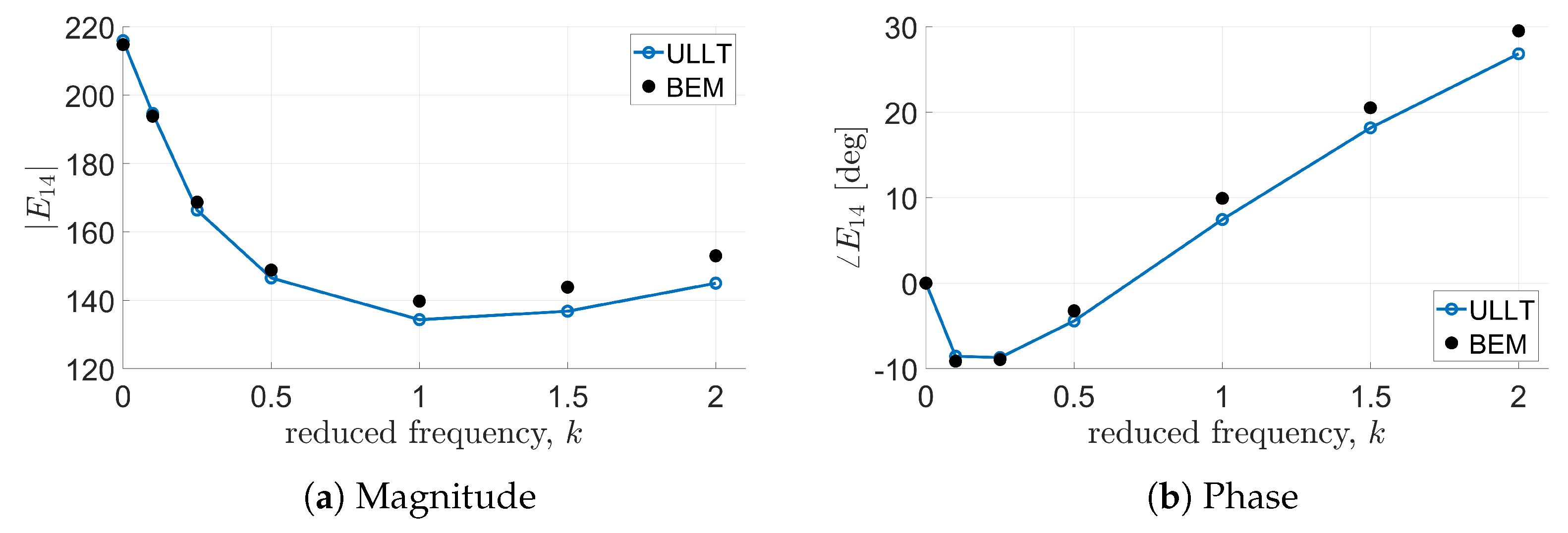
Now, the capability of the proposed ULLT solver to predict unsteady aerodynamic loads is assessed for a higher aspect ratio wing, still considering the same shape functions for the definition of the aerodynamic matrix. For $l=10\mathrm{m}$, ULLT predictions are compared with BEM solutions in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, and the quality of the correlations is very similar to that already observed for the wing having a smaller aspect ratio.

It is worth noting that, the correlations between the simulations given by the proposed ULLT solver and the BEM outcomes are of a quality very similar to that of the correlations presented in [17] for rectangular thin wings, between the results provided by the LLT models discussed in that work and CFD outputs.

3.2. Time-Domain Results

Next, the proposed ULLT formulation is applied for the determination of the time response to an arbitrary input by using both a flat fixed wake shape and the free-wake mode solution. We consider the following damped harmonic time evolution of the generic Lagrangian coordinate

$$q_m\left(t\right)=e^{-\beta t}{h}_{0}sin\left(\omega t\right)$$

(29)

where $\beta$ denotes the damping factor and $h_0$ is the amplitude of the undamped signal.

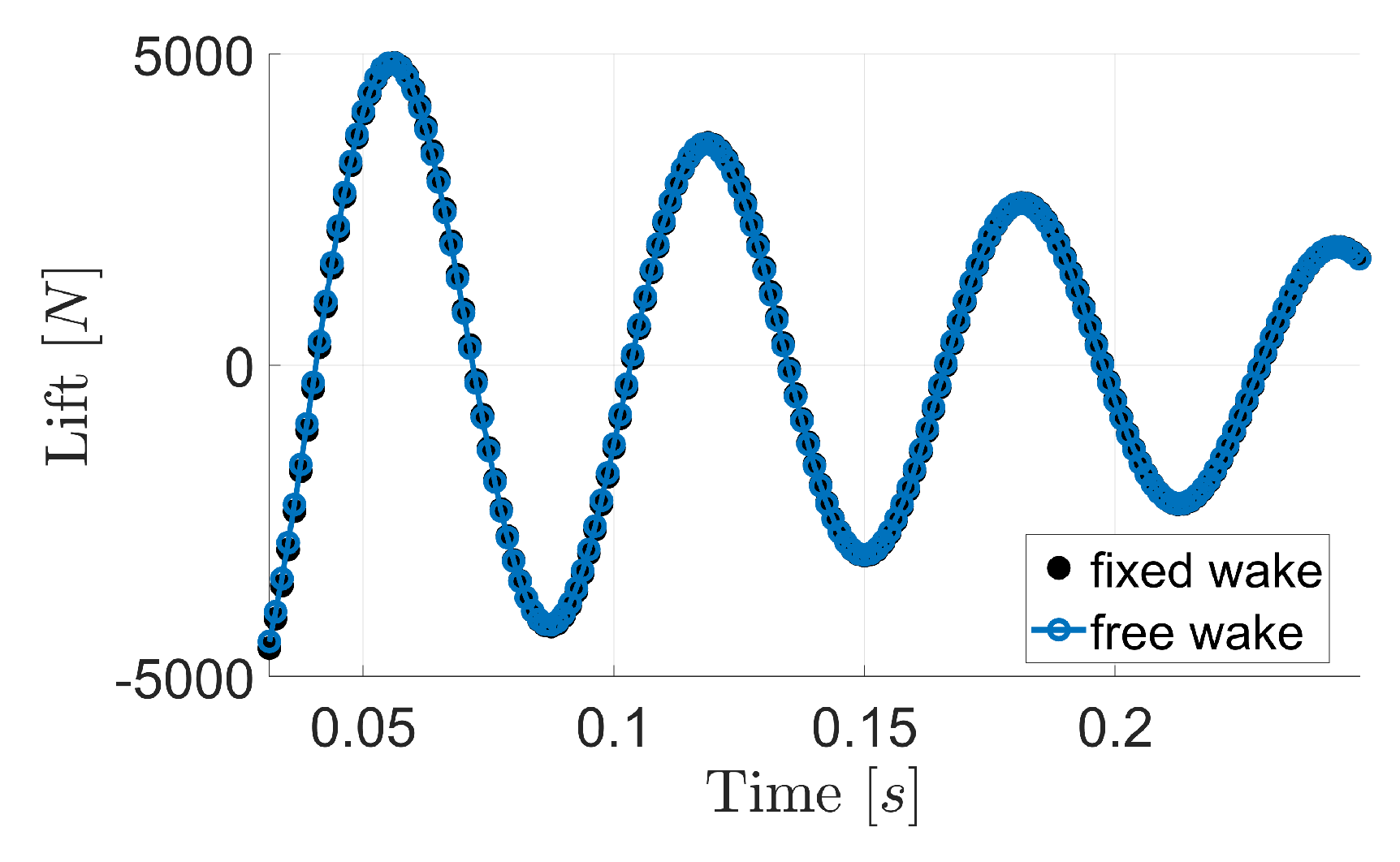
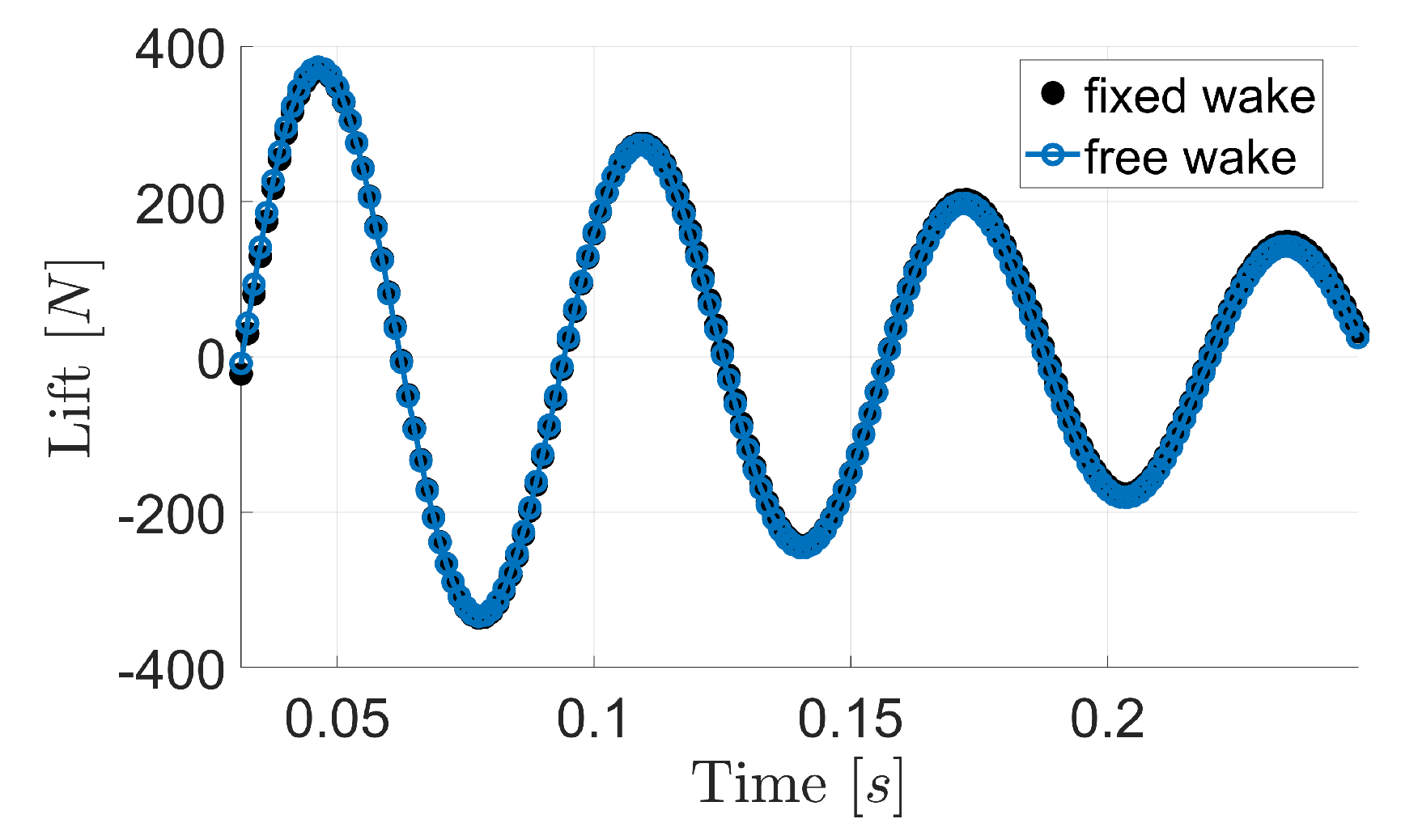
For the wing with $l=5$ m, reduced frequency equal to $k=1.0$ and $\beta =5.0$ Figure 15 and Figure 16 show the lift generated by, respectively, $q_1$ (with amplitude $h_0=0.05$ m) and $q_3$ (with amplitude $h_0=0.005$ m) (see Equation (29)) as obtained through the proposed solver under fixed-wake and free-wake assumptions.

The results from the two wake models are very close, as expected. Indeed, for a translating wing, the wake roll-up generated by the distribution of vorticity yields a significant wake distortion at a distance from the wing such that its effects are almost negligible. This is apparent in Figure 17 which depicts the wake shape given by the free-wake mode solution corresponding to the $q_1$ input (plunging motion). In this picture, the quadrilateral rings representing the vortices released at each time step are colored by their intensity.

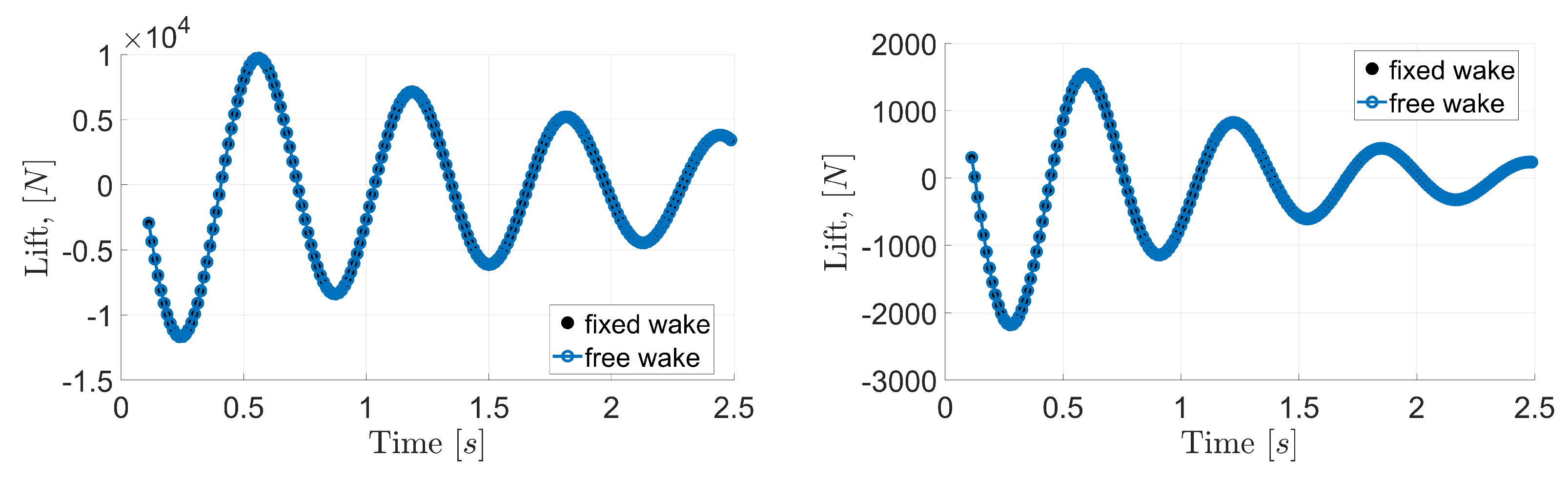
Note, that it was proven that the effects of wake distortion on wing loads are negligible for several wing motions compatible with the sectional aerodynamic model applied. For instance, this can be observed in Figure 18 which, for plunging motion, shows the comparisons between fixed-wake and free-wake simulations for a doubled amplitude of wing oscillation ($h_0=0.1$ m, left-hand-side picture), and for a halved reduced frequency ($k=0.5$, right-hand-side picture), with respect to the motion considered for Figure 15.

However, it is worth noting that the free-wake effects may be relevant for rotorcraft aerodynamic analyses or, more generally, for the simulation of complex configurations like, for instance, wings in tandem where the mutual influence can significantly alter the aerodynamic field. Thus, the solver developed in this work opens the path towards extensions to those kinds of applications, for which the availability of an efficient computational tool with a good level of accuracy, like the one proposed here, can be of great help to designers.

Finally, note that for the wing configurations considered here, the computational cost of the proposed ULLT solver is significantly lower than that required by the BEM tool. Although the performance of the applied computational tool has not been specifically optimized, it is about ten times faster than the BEM.

4. Conclusions

A novel time-domain ULLT approach for wings’ unsteady aerodynamics has been presented. The element of novelty resides in the application of the Küssner–Schwarz’s sectional solution model represented in the time domain through the rational approximation of the lift deficiency function, suited for the computation of responses to arbitrary wing deformation (camber morphing included) without the need for a complex lifting bodies tridimensional approach. This also allows for a free-wake approach and the general applicability of such a solver in all kinds of applications. Along with that, the completion of the unsteadiness representation of the loads is fulfilled with the application of the unsteady extension of the K-J theorem expressed in state-space form. To validate the model, correlation results are presented for four different Lagrangian coordinates and corresponding generalized forces at different frequencies, against a well-validated, frequency-domain BEM solver. The results agree well with the reference data, confirming the generality of the approach and its applicability for aeroelastic modeling of arbitrarily deforming wings. An investigation of the influence of free-wake modeling on the predicted aerodynamic loads is accomplished by correlating its results with the outcomes from the flat-wake assumption for an arbitrary damped harmonic input. It has been shown that the free-wake effects are negligible in the translating wing configurations analyzed but they might be of great importance for rotorcraft applications.