Coupling Analysis between the Transonic Buffeting Flow and a Heaving Supercritical Airfoil Based on Dynamic Mode Decomposition
Abstract
1. Introduction
2. Numerical Model
2.1. CFD Method
2.2. Heave Motion of the Airfoil
2.3. Mesh-Moving Technique
2.4. CFD Validation
3. Dynamic Model Decomposition
4. Interaction between Buffeting Flow and the Heaving Airfoil
4.1. Case Description
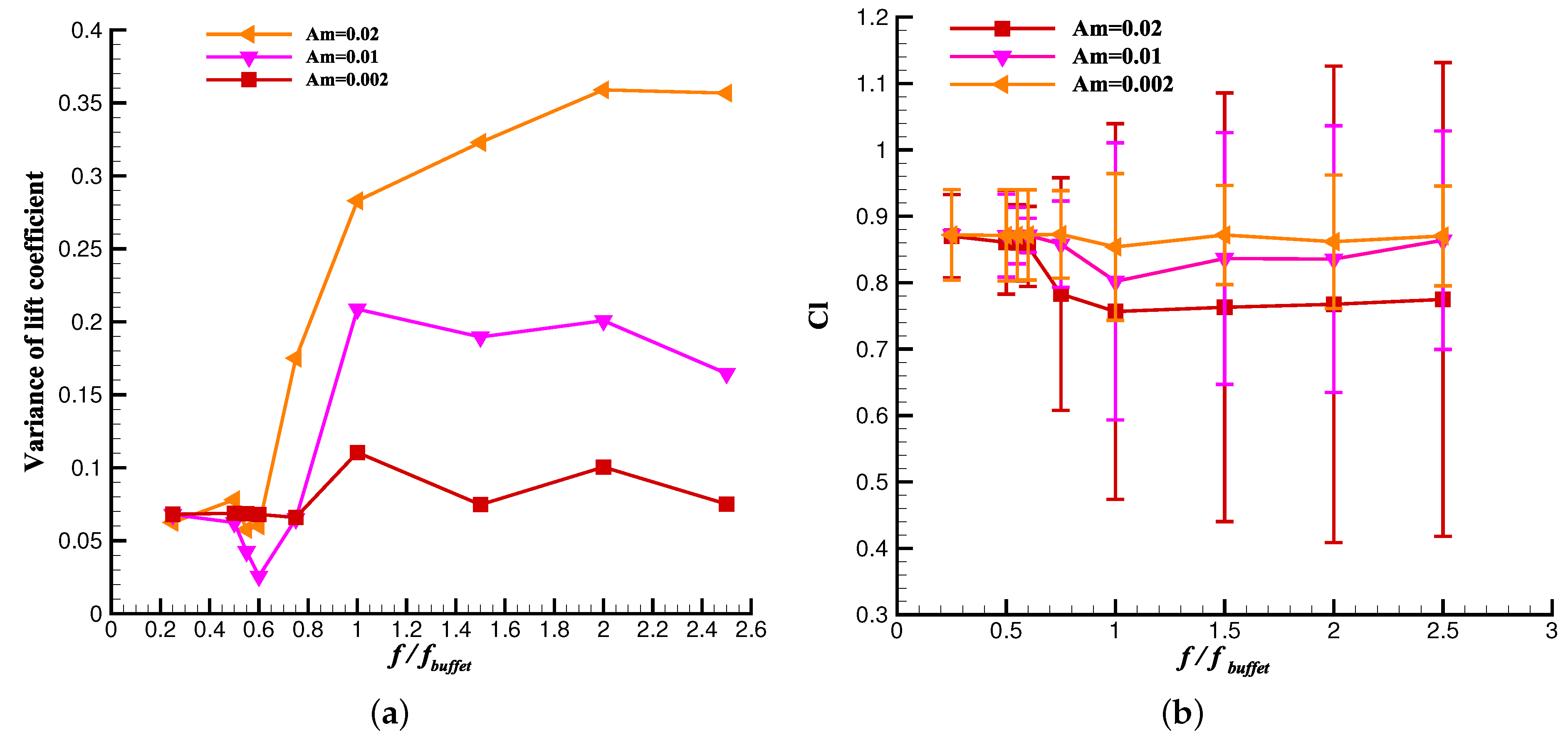
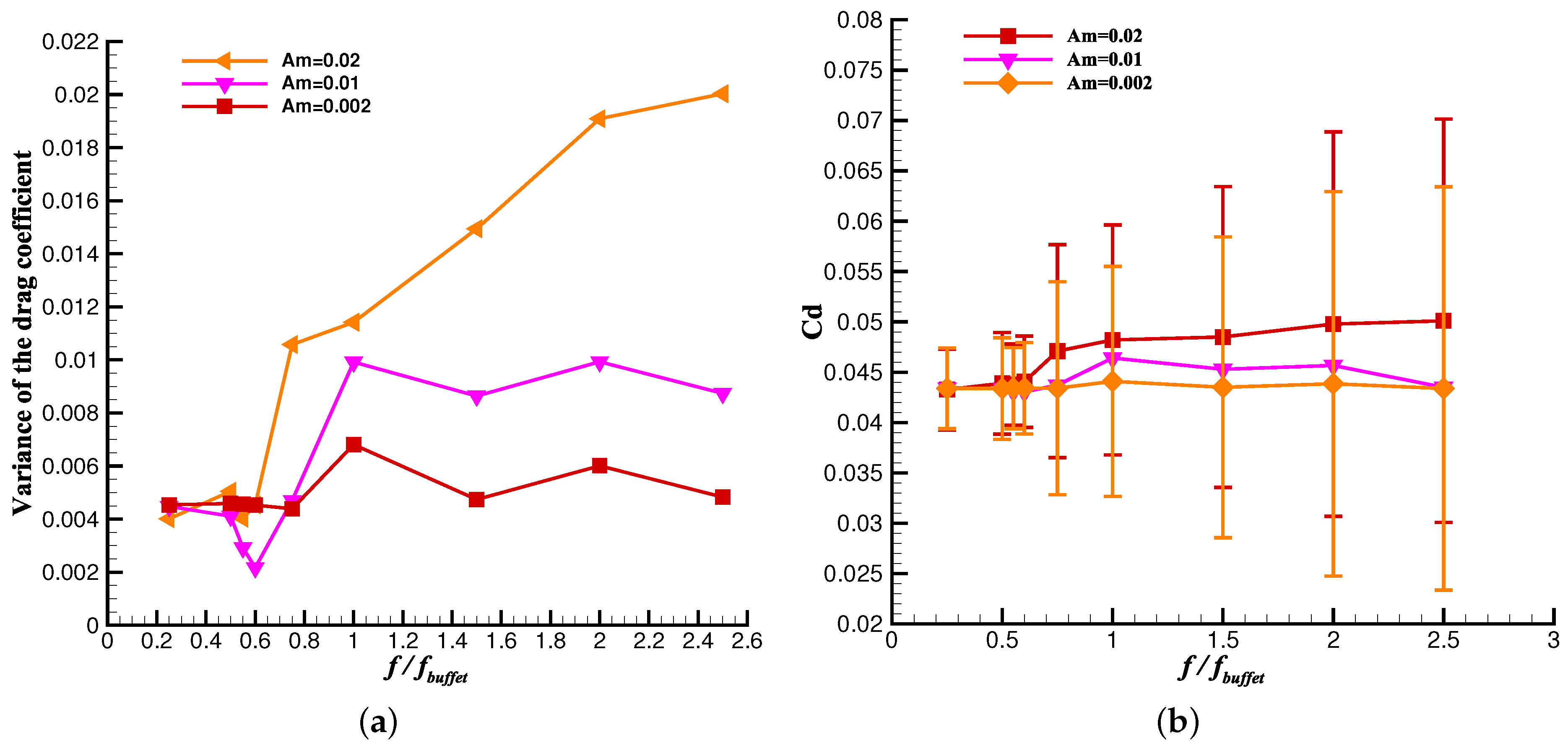
4.2. Aerodynamic Analysis
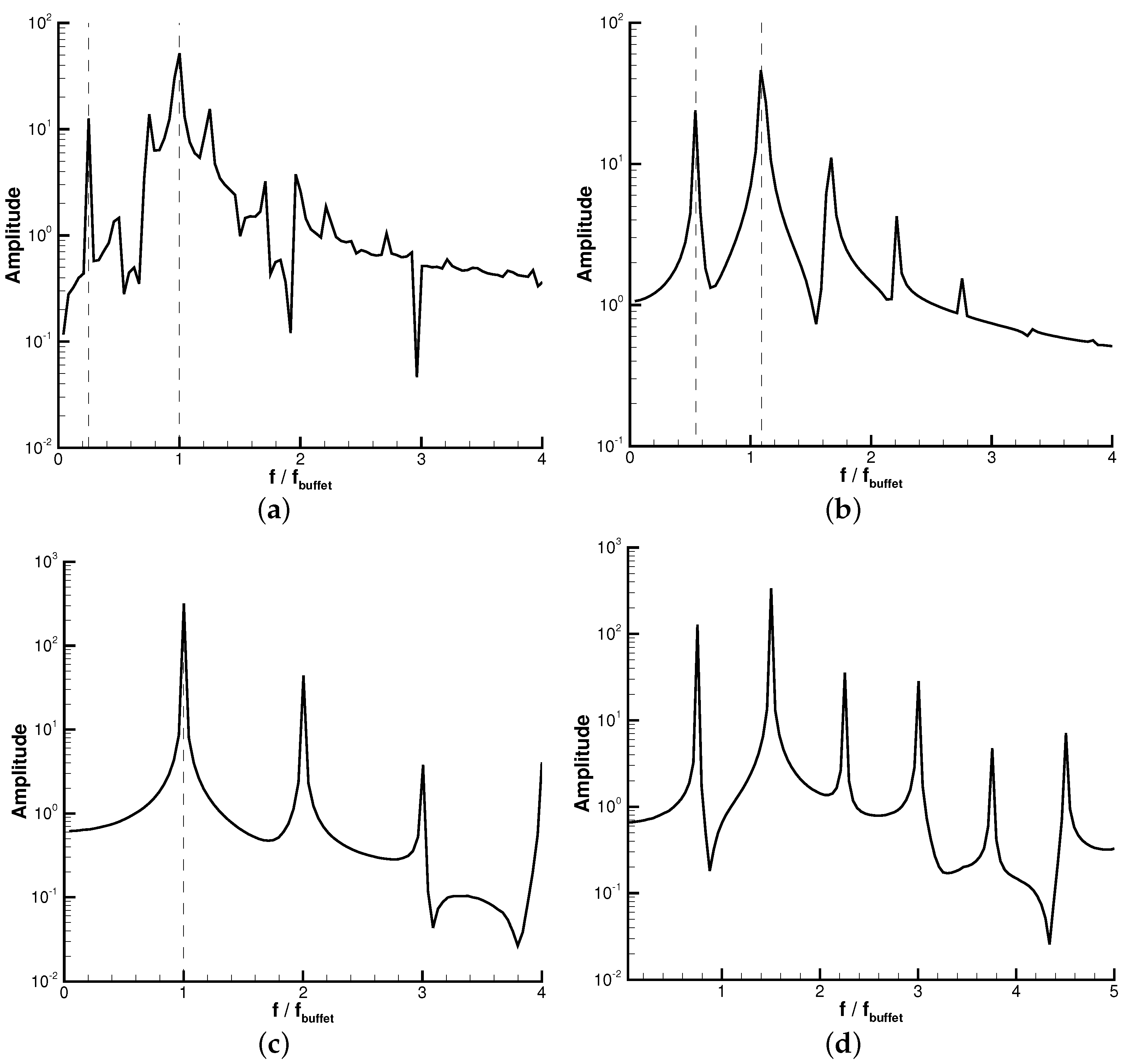
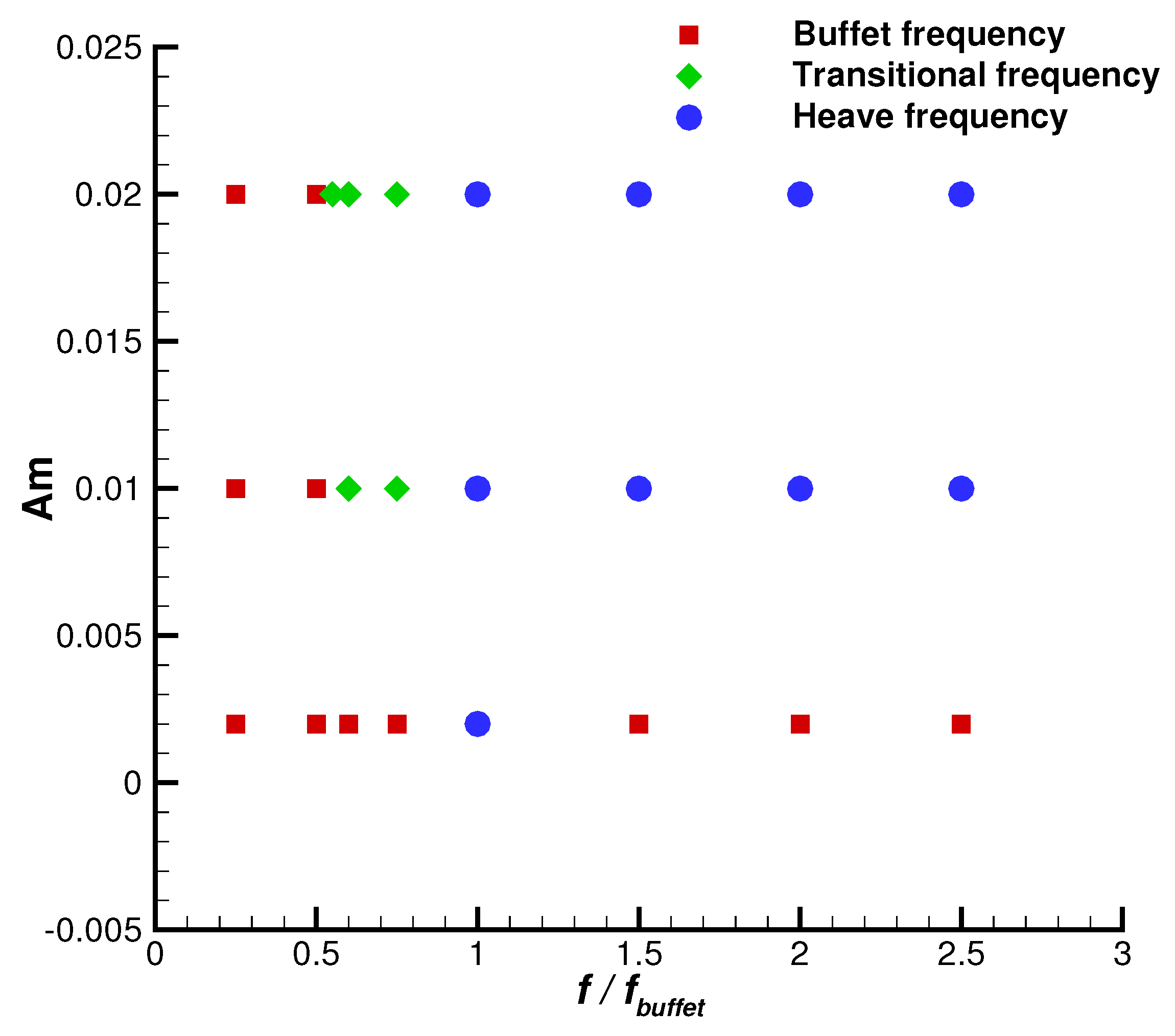
4.3. Frequency Analysis
- Buffet frequency response in Figure 8a: The flow response was characterized by the buffet reduced frequency for the transonic shock wave boundary layer interaction. The impact of the heave motion was negligible. The spectrum amplitude corresponding to the frequency spectrum was relatively small.
- Transitional response in Figure 8b: The heave frequency and its double harmonics are observed in the spectrum. However, the dominant frequency was near the buffet range. This is a transition phase where the impact of heave motion became competitive with the inherent oscillating shock wave boundary layer interaction. In this phase, the lift coefficient experienced a significant drop of 12% from to .
- Heaving frequency lock-in response in Figure 8c,d: The spectral amplitude with the inherent buffet frequency was weakened. The flow response exhibited the harmonic motion of a given heave frequency with super-harmonics.
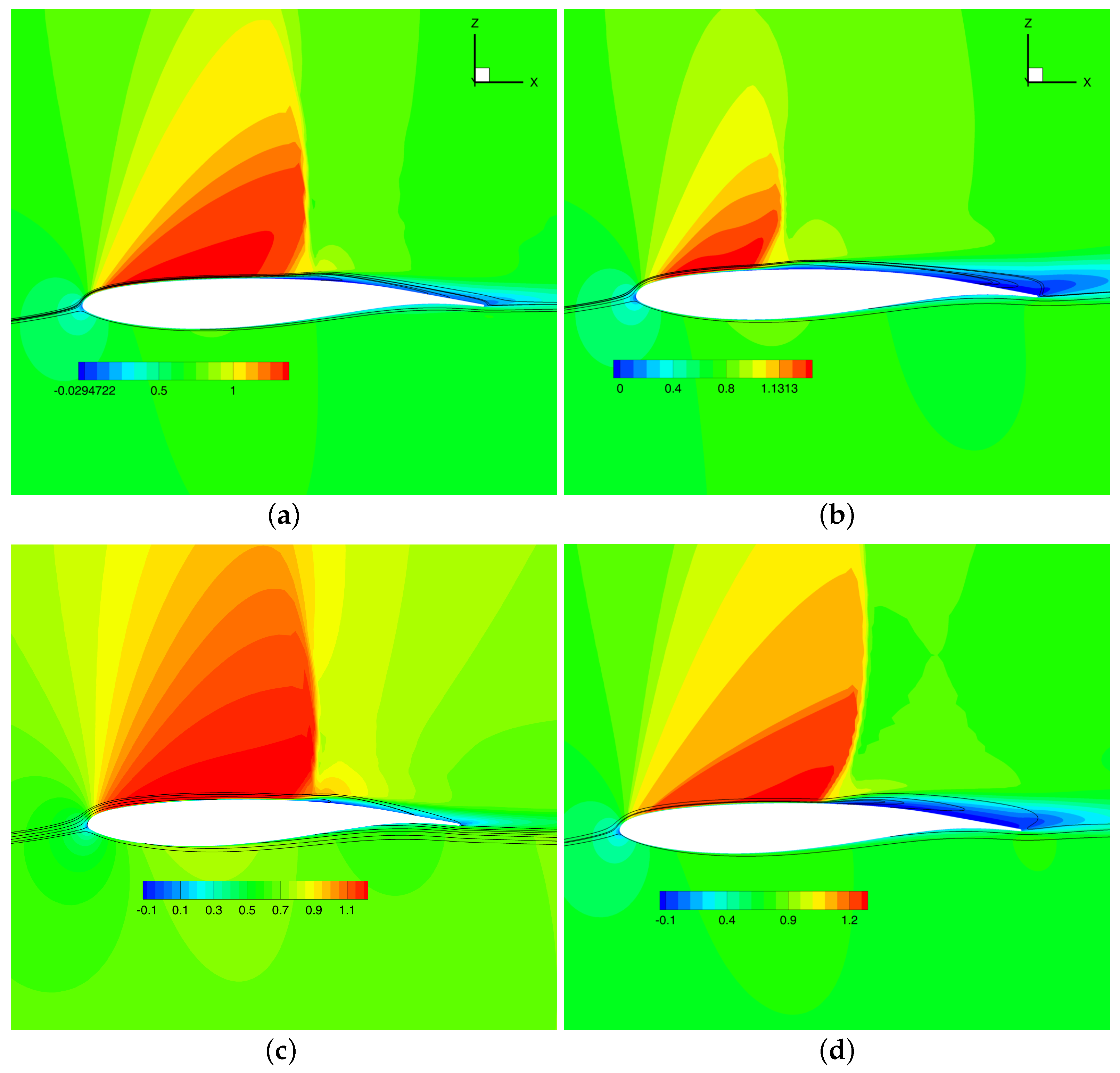
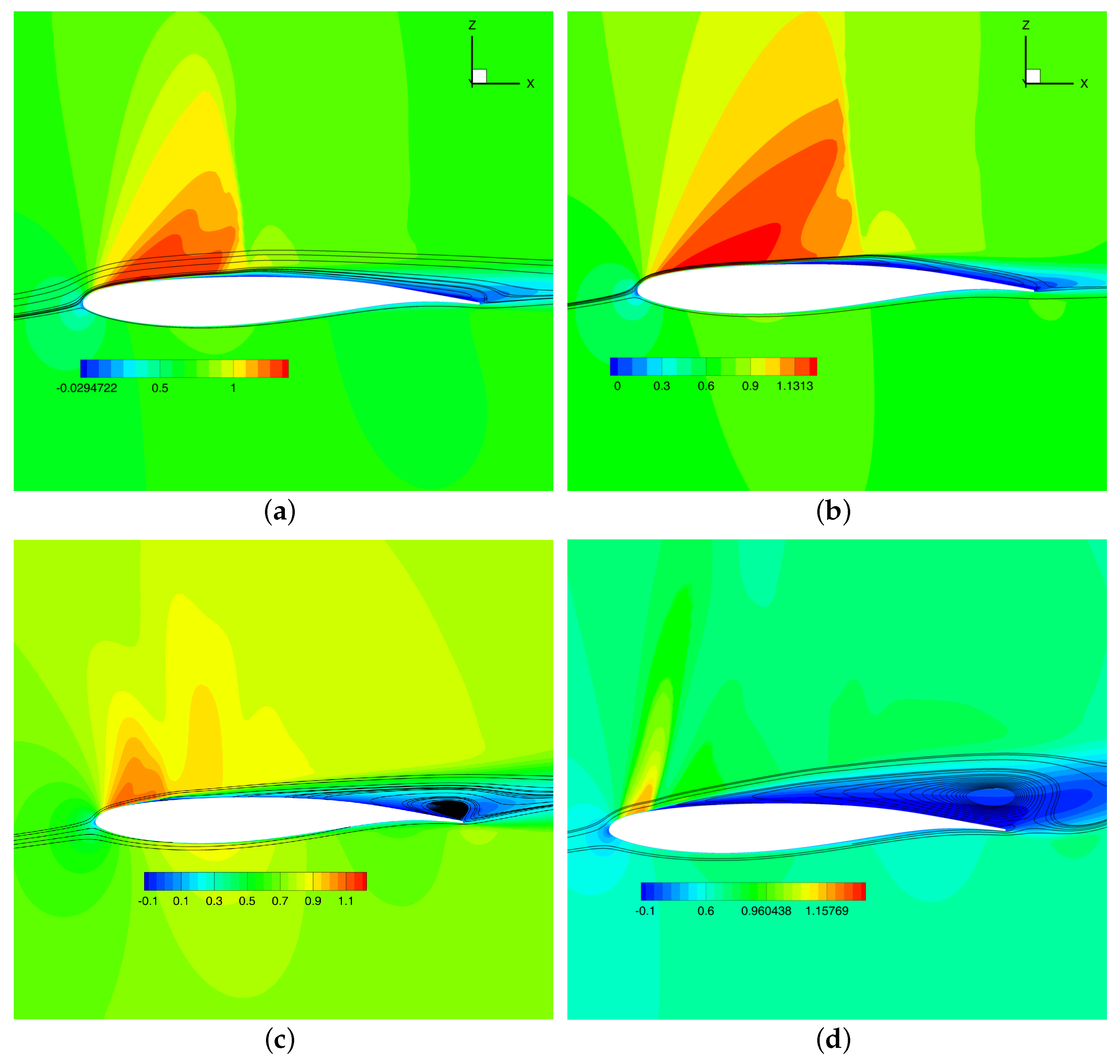
4.4. Flow Pattern Analysis
4.4.1. Flow Field Analysis
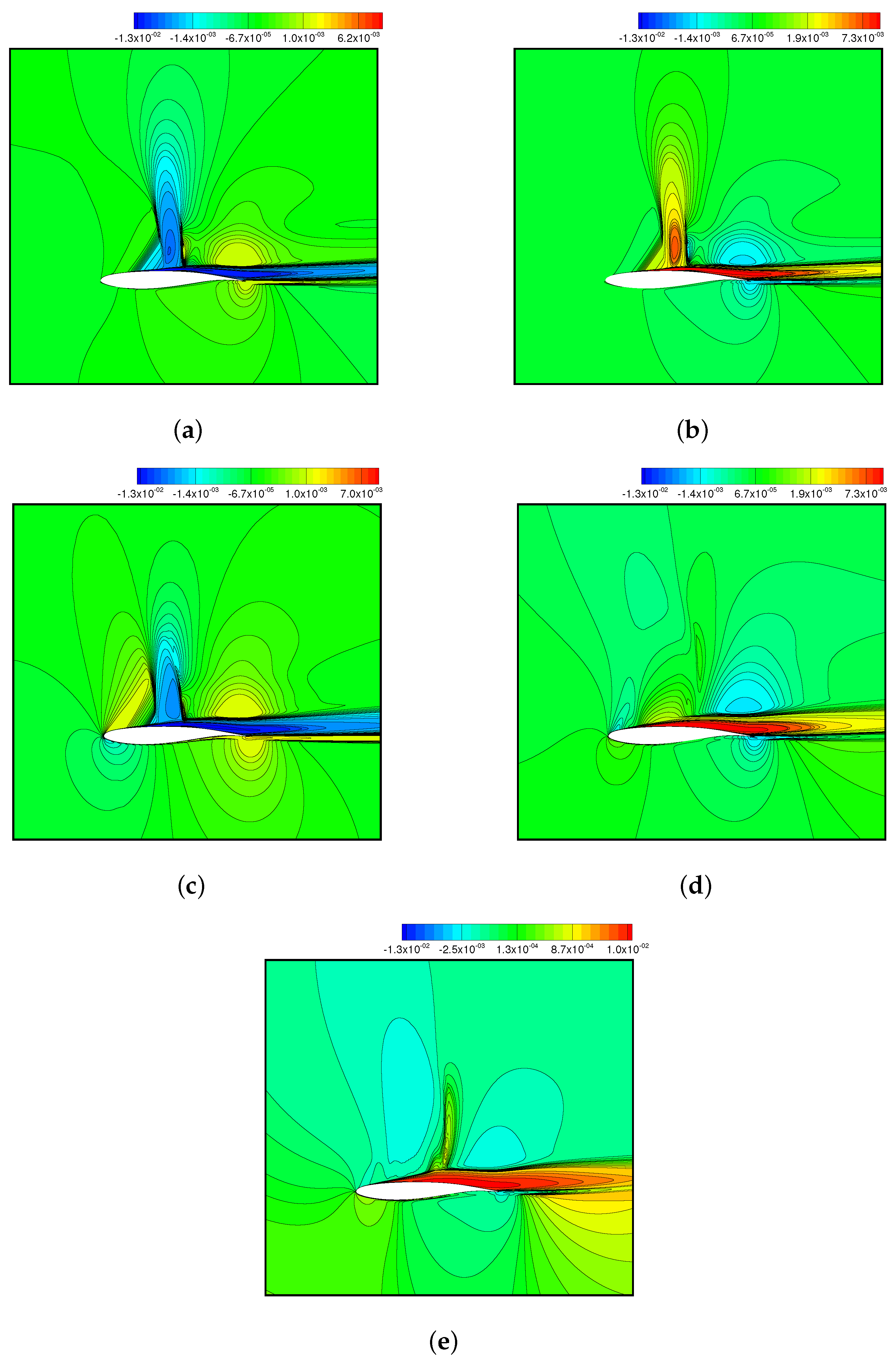
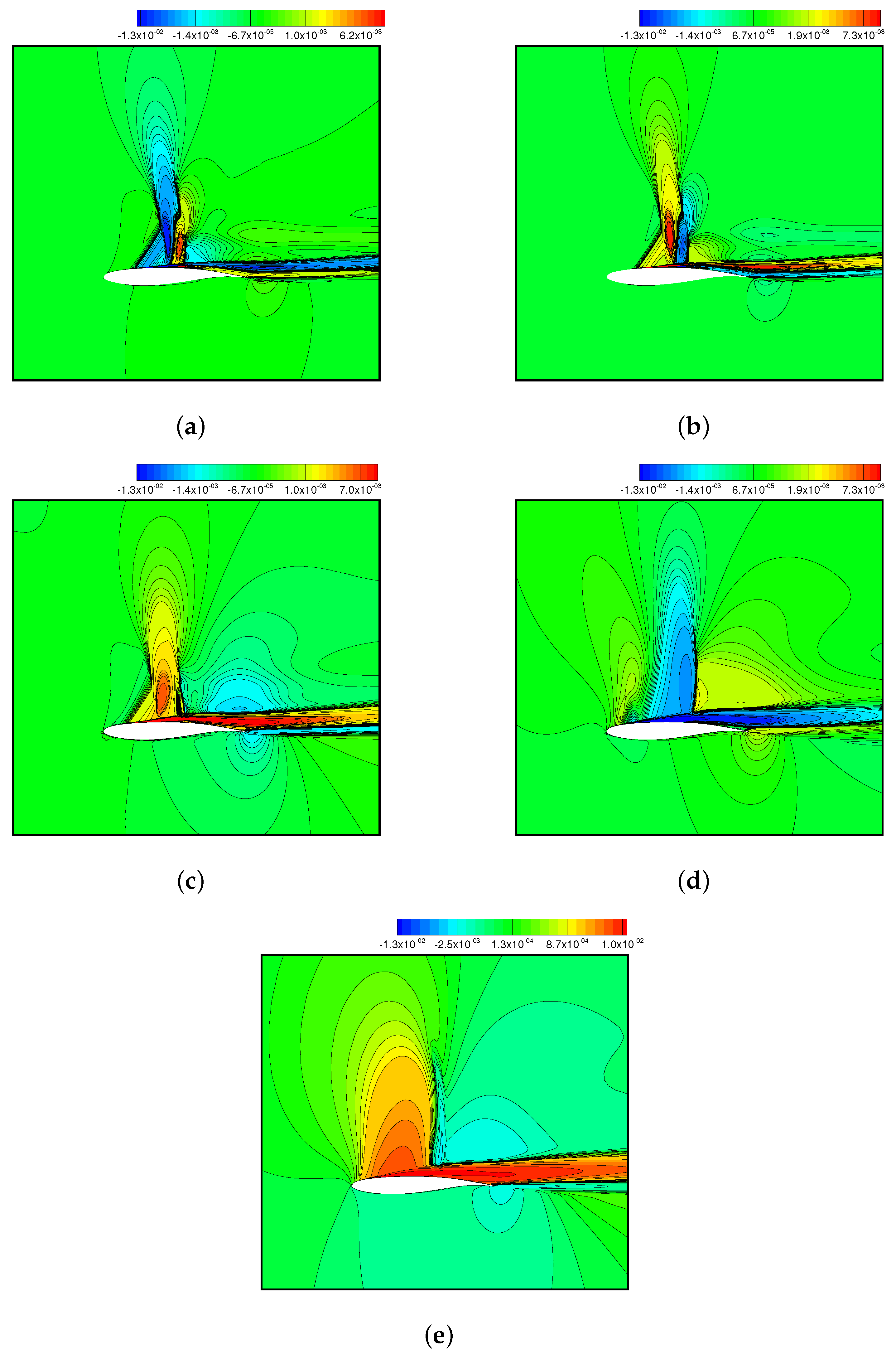
4.4.2. Dynamic Mode Decomposition Analysis
5. Conclusions
- (1)
- Both the time-averaged lift and drag coefficient experienced a remarkable deterioration at for and . The time-averaged lift coefficient decreased by a maximum of 13.3% for . However, when the motion amplitude was small for , the changes in the time-averaged and variance of the lift and drag coefficient were minor.
- (2)
- A parametric study of the heave frequency and amplitude indicates that the flow response under the heave motion could be categorized into three types: (a) A buffet frequency response, where the impact of the heave motion was negligible. (b) A transitional response, i.e., a transition phase for the increasing impact of the heave motion. The aerodynamic performance changed remarkably in this stage. (c) A heaving frequency lock-in response, where the flow oscillation exhibited a harmonic motion of a given frequency with super-harmonics. These three types of flow responses were associated with the change in the aerodynamic performance.
- (3)
- The energy contribution of the DMD modes shows that the buffet mode accounted for more than 95% of the entire fluid system when the motion frequency was relatively low (e.g., ). As the frequency increased to , the airfoil motion gradually became influential with an increased energy percentage of the boundary layer mode. When the motion frequency , the energy transferred from the buffet mode to the boundary layer with a more even balance for each mode due to the predominantly heaving motion.
- (4)
- The dynamic mode decomposition was used to identify the characteristic flow pattern in the coupling. It shows that the buffet mode was a pair of marginally stable modes with the frequency featured the shock motion and the pulsating recirculation. For the transitional response, the -shaped shock structure was weakened and the boundary layer became thicker in the first-order DMD mode, whilst the recirculation was merged with a double shock in the second-order DMD mode. As the motion frequency increased to , the merger of the shock wave and boundary layer that was observed in the first-order mode and the second-order DMD mode exhibited a similar pattern to the buffet mode. At , the heave motion dominated the flow response with the heave frequency and its super-harmonics. The mode was characterized with the boundary layer that formed near the leading edge, rather than the shock foot.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AOA | Angle of attack |
| DMD | Dynamic mode decomposition |
| SVD | Singular value decomposition |
| f | Reduced frequency, |
| Buffet reduced frequency | |
| DES | Detached eddy simulation |
| POD | Proper orthogonal decomposition |
| Convective flux | |
| Diffusive flux | |
| Freestream density | |
| Freestream viscosity | |
| Freestream velocity | |
| c | Airfoil chord length |
| Dimensional time, s | |
| t | Non-dimensional time, |
| Dimensional displacement of the heaving airfoil | |
| Dimensional equilibrium of the heave motion | |
| Dimensional heave amplitude | |
| A | Non-dimensional displacement of the heaving airfoil |
| Equilibrium of the heave motion | |
| Non-dimensional heave amplitude, | |
| Circular frequency | |
| Dimensional heave frequency, Hz | |
| New position of node | |
| New position of node | |
| Total number of nodes near the ith node | |
| Spring stiffness coefficient related to the and the nodes | |
| Coefficient for the enhancement of the spring stiffness on the boundary | |
| Minimum interior angle of the triangle element for torsional stiffness | |
| TI | Turbulent intensity |
| Snapshots of the flow fields | |
| Flow field data matrix | |
| Linear operator | |
| Unitary matrix | |
| Diagonal matrix | |
| DMD modes matrix | |
| Eigenvector matrix of | |
| b | Amplitude of the DMD modes |
Appendix A
References
- Gao, C.; Zhang, W. Transonic aeroelasticity: A new perspective from the fluid mode. Prog. Aerosp. Sci. 2020, 113, 100596. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Vio, G.A.; Levinski, O. A review of recent developments in the understanding of transonic shock buffet. Prog. Aerosp. Sci. 2017, 92, 39–84. [Google Scholar] [CrossRef]
- Lee, B.H. Self-sustained shock oscillations on airfoils at transonic speeds. Prog. Aerosp. Sci. 2001, 37, 147–196. [Google Scholar] [CrossRef]
- Knipfer, A.; Schewe, G. Investigations of an oscillating supercritical 2D wing section in a transonic flow. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; pp. 1–12. [Google Scholar]
- Deck, S. Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J. 2005, 43, 1556–1566. [Google Scholar] [CrossRef]
- Dietz, G.; Schewe, G.; Mai, H. Amplification and amplitude limitation of heave/pitch limit-cycle oscillations close to the transonic dip. J. Fluids Struct. 2006, 22, 505–527. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D.; Travin, A. Origin of transonic buffet on aerofoils. J. Fluid Mech. 2009, 628, 357–369. [Google Scholar] [CrossRef]
- Accorinti, A.; Baur, T.; Scharnowski, S.; Kähler, C.J. Experimental investigation of transonic shock buffet on an OAT15A profile. AIAA J. 2022, 60, 6289–6300. [Google Scholar] [CrossRef]
- Ramey, J.M.; Sekula, M.K.; Piatak, D.J.; Heaney, P.S.; Soranna, F. Development of Buffet Forcing Functions using Frequency-Dependent Coherence Factors. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15, 19–21 January 2021; pp. 1–13. [Google Scholar]
- Timme, S. Global instability of wing shock-buffet onset. J. Fluid Mech. 2020, 885, A37. [Google Scholar] [CrossRef]
- Raveh, D.E.; Dowell, E.H. Frequency lock-in phenomenon for oscillating airfoils in buffeting flows. J. Fluids Struct. 2011, 27, 89–104. [Google Scholar] [CrossRef]
- Hartmann, A.; Klaas, M.; Schröder, W. Coupled airfoil heave/pitch oscillations at buffet flow. AIAA J. 2013, 51, 1542–1552. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Strelets, M. Global instability in the onset of transonic-wing buffet. J. Fluid Mech. 2019, 881, 3–22. [Google Scholar] [CrossRef]
- Kang, W.; Zhang, J.-Z.; Ren, S.; Lei, P.-F. Nonlinear galerkin method for low-dimensional modeling of fluid dynamic system using POD modes. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 943–952. [Google Scholar] [CrossRef]
- Szubert, D.; Grossi, F.; Garcia, A.J.; Hoarau, Y.; Hunt, J.C.; Braza, M. Shock-vortex shear-layer interaction in the transonic flow around a supercritical airfoil at high reynolds number in buffet conditions. J. Fluids Struct. 2015, 55, 276–302. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. An improved criterion to select dominant modes from dynamic mode decomposition. Eur. J. Mech.-B/Fluids 2017, 62, 109–129. [Google Scholar] [CrossRef]
- Poplingher, L.; Raveh, D.E.; Dowell, E.H. Modal analysis of transonic shock buffet on 2D airfoil. AIAA J. 2019, 57, 2851–2866. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Levinski, O.; Vio, G.A. Origins of atypical shock buffet motions on a supercritical aerofoil. Aerosp. Sci. Technol. 2020, 107, 106304. [Google Scholar] [CrossRef]
- Zauner, M.; Sandham, N.D. Modal analysis of a laminar-flow airfoil under buffet conditions at re = 500,000. Flow Turbul. Combust. 2020, 104, 509–532. [Google Scholar] [CrossRef]
- Kang, W.; Hu, S.; Wang, Y. Lift enhancement mechanism study of the airfoil with a dielectric elastic membrane skin. J. Fluids Struct. 2024, 125, 104083. [Google Scholar] [CrossRef]
- Kang, W.; Lei, P.; Zhang, J.; Xu, M. Effects of local oscillation of airfoil surface on lift enhancement at low reynolds number. J. Fluids Struct. 2015, 57, 49–65. [Google Scholar] [CrossRef]
- Kang, W.; Xu, M.; Yao, W.; Zhang, J. Lock-in mechanism of flow over a low-reynolds-number airfoil with morphing surface. Aerosp. Sci. Technol. 2020, 97, 105647. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, C.; Liu, Y. The interaction between flutter and buffet in transonic flow. Nonlinear Dyn. 2015, 82, 1851–1865. [Google Scholar] [CrossRef]
- Jacquin, L.; Molton, P.; Deck, S.; Maury, B.; Soulevant, D. Experimental study of shock oscillation over a transonic supercritical profile. AIAA J. 2009, 47, 1985–1994. [Google Scholar] [CrossRef]
- Landon, R. NACA 0012 oscillating and transient pitching, Compendium of unsteady aerodynamic measurements. In Data Set 3 in AGARD Report No. 702; Defense Technical Information Center: Fort Belvoir, VA, USA, 1982; pp. 3.1–3.25. [Google Scholar]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Weiner, A.; Semaan, R. Robust dynamic mode decomposition methodology for an airfoil undergoing transonic shock buffet. AIAA J. 2023, 61, 4456–4467. [Google Scholar] [CrossRef]
- Feldhusen-Hoffmann, A.; Lagemann, C.; Loosen, S.; Meysonnat, P.; Klaas, M.; Schröder, W. Analysis of transonic buffet using dynamic mode decomposition. Exp. Fluids 2021, 62, 66. [Google Scholar] [CrossRef]
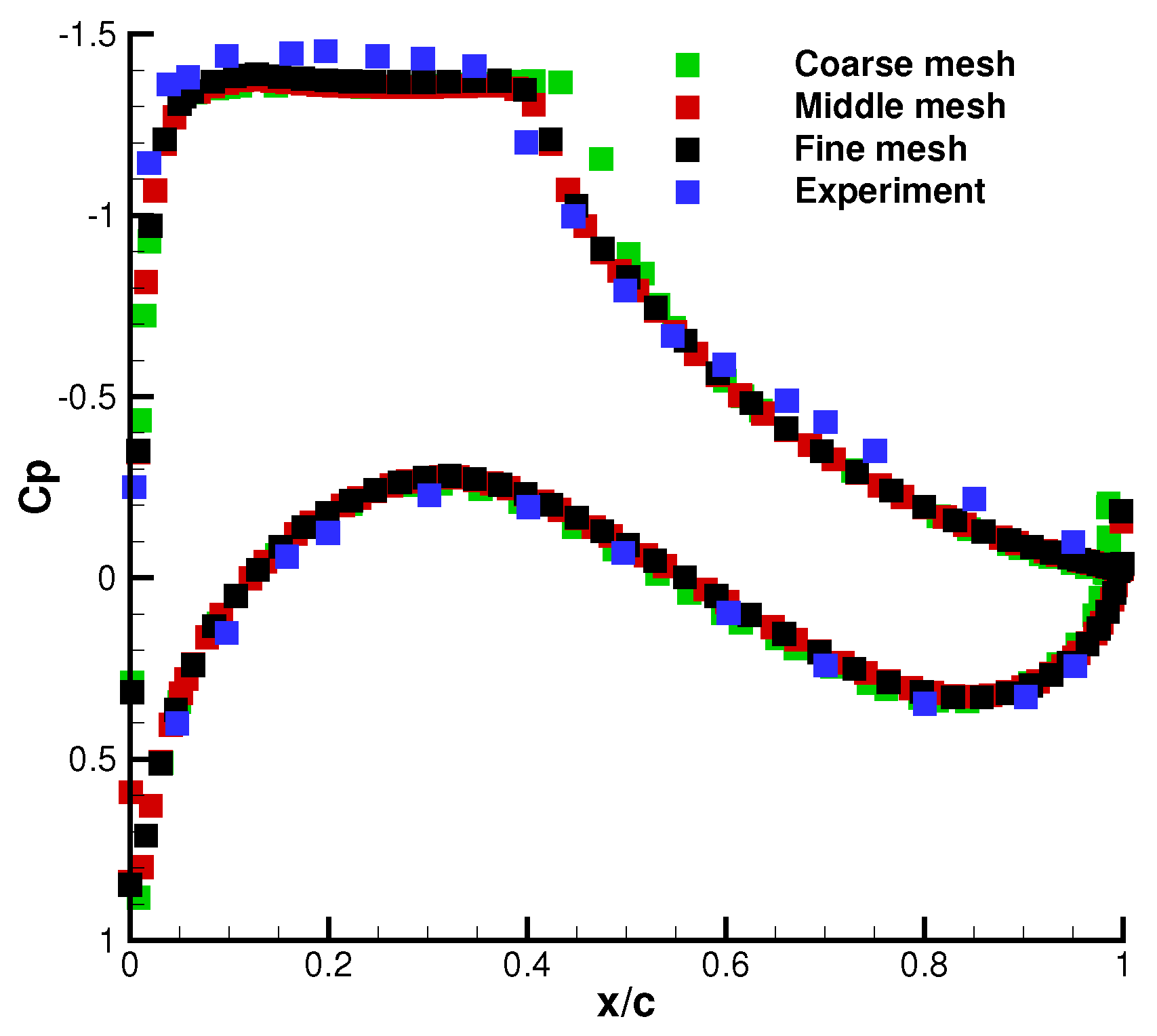
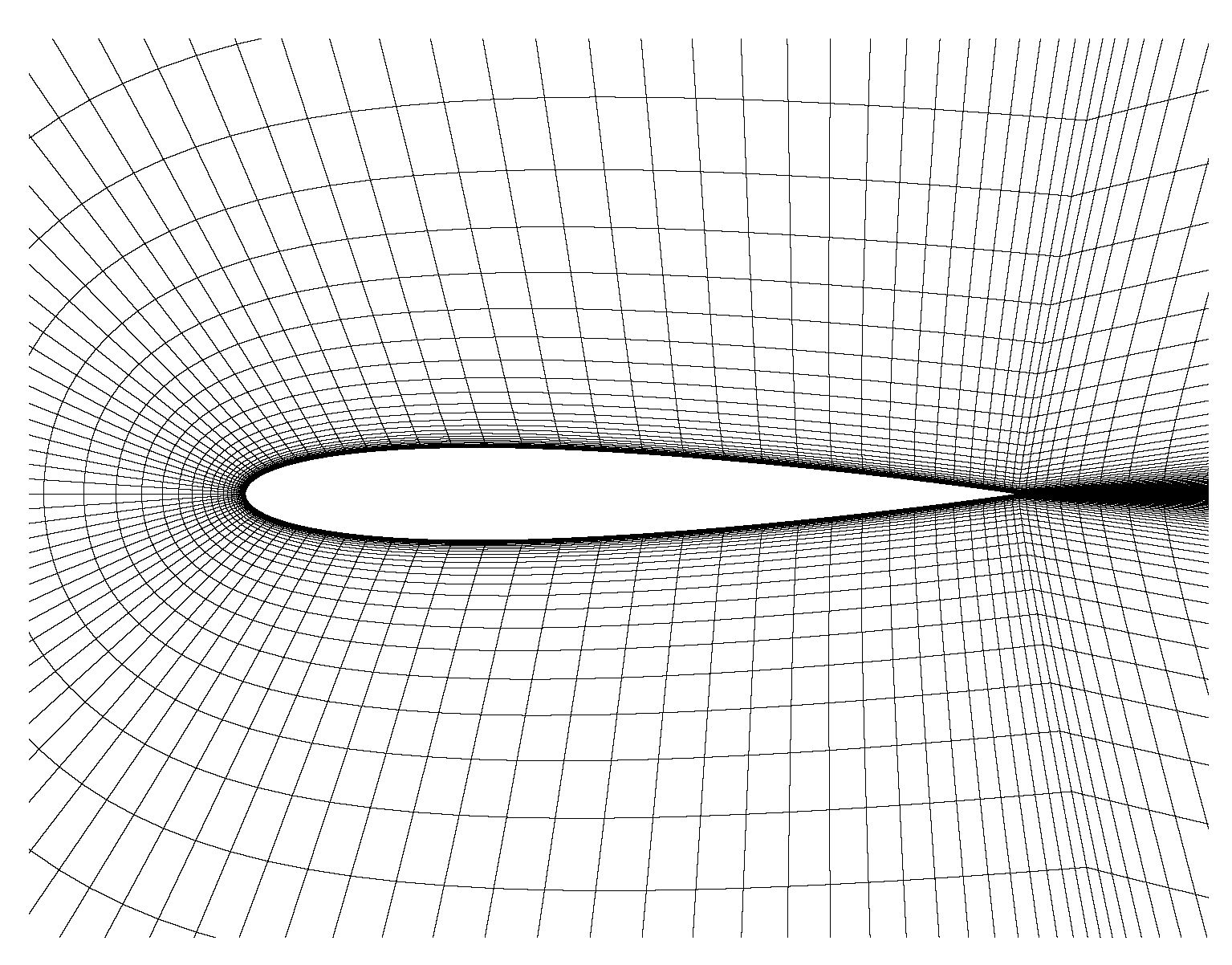
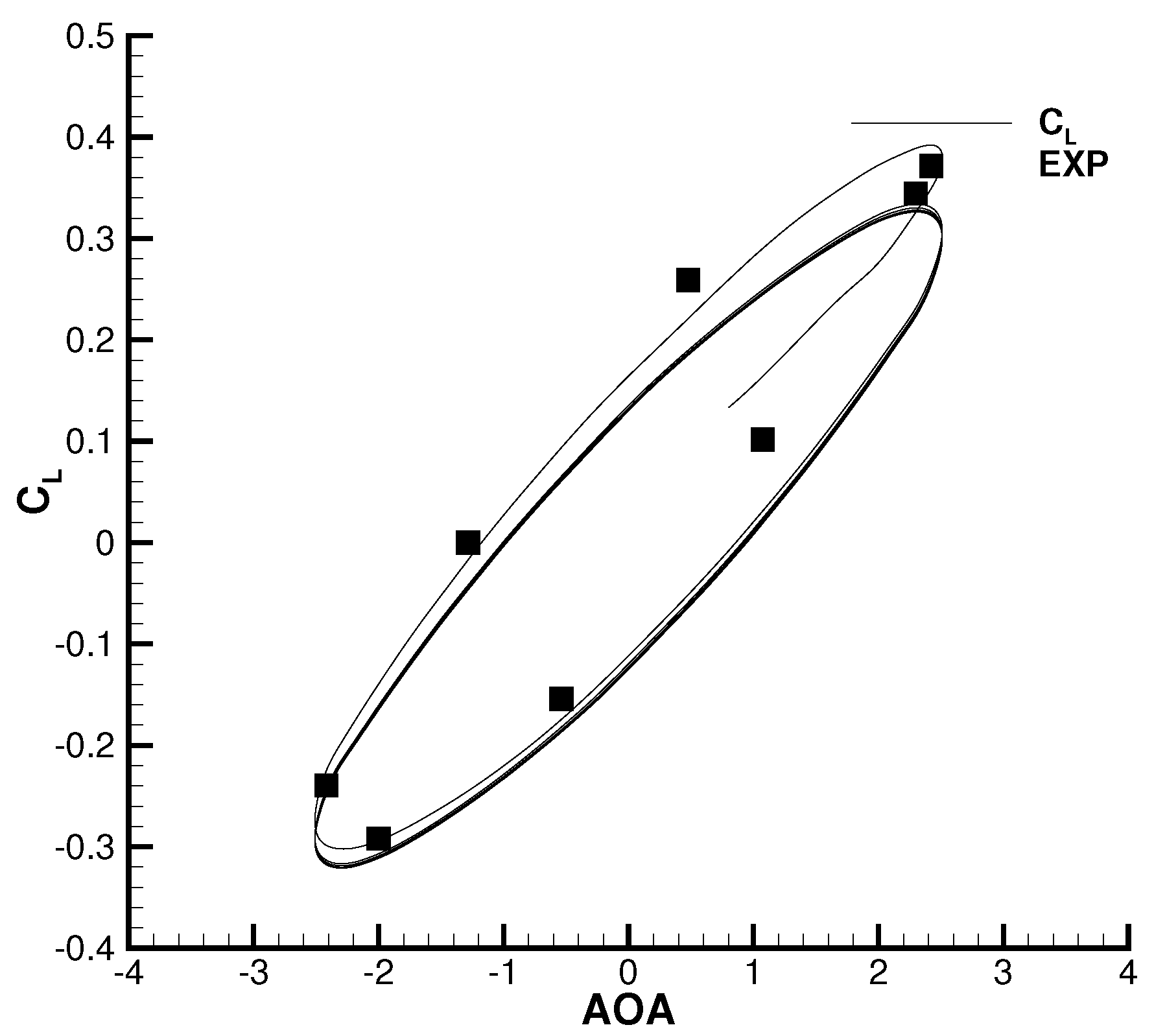
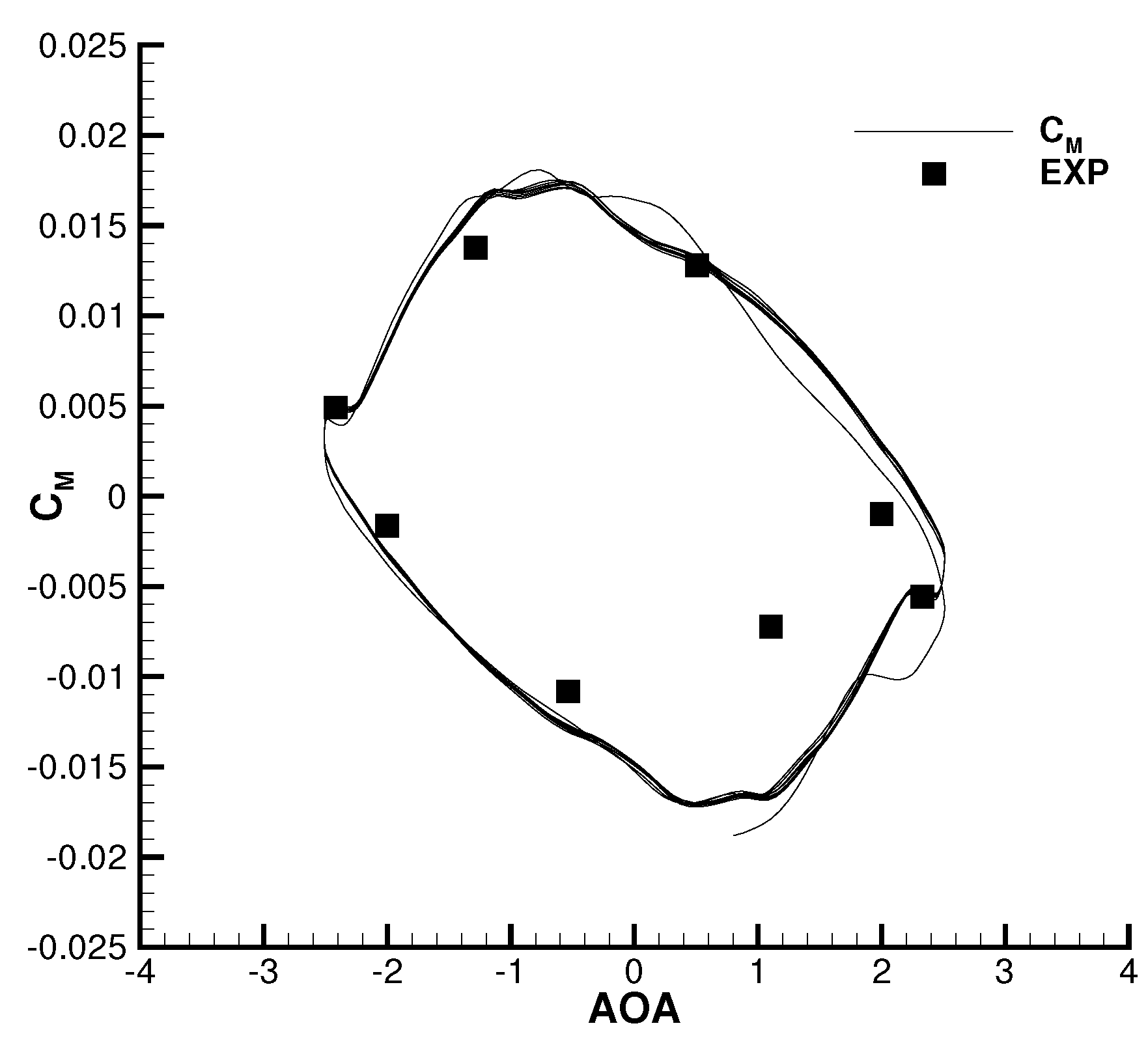


| Cases | Grid Size | |||
|---|---|---|---|---|
| Coarse-sized grid | 345 × 65 | 0.904 | 0.0462 | 0.205 |
| Middle-sized grid | 529 × 129 | 0.871 | 0.0439 | 0.205 |
| Fine-sized grid | 855 × 201 | 0.882 | 0.044 | 0.206 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, W.; Chen, B.; Hu, S. Coupling Analysis between the Transonic Buffeting Flow and a Heaving Supercritical Airfoil Based on Dynamic Mode Decomposition. Aerospace 2024, 11, 722. https://doi.org/10.3390/aerospace11090722
Kang W, Chen B, Hu S. Coupling Analysis between the Transonic Buffeting Flow and a Heaving Supercritical Airfoil Based on Dynamic Mode Decomposition. Aerospace. 2024; 11(9):722. https://doi.org/10.3390/aerospace11090722
Chicago/Turabian StyleKang, Wei, Bingzhou Chen, and Shilin Hu. 2024. "Coupling Analysis between the Transonic Buffeting Flow and a Heaving Supercritical Airfoil Based on Dynamic Mode Decomposition" Aerospace 11, no. 9: 722. https://doi.org/10.3390/aerospace11090722
APA StyleKang, W., Chen, B., & Hu, S. (2024). Coupling Analysis between the Transonic Buffeting Flow and a Heaving Supercritical Airfoil Based on Dynamic Mode Decomposition. Aerospace, 11(9), 722. https://doi.org/10.3390/aerospace11090722






