1. Introduction
Unmanned Aerial Vehicles (UAVs) are playing an important role both in the civil and military fields. In particular, they are becoming indispensable as main combat equipment in modern warfare [
1]. One type of high-performance UAV is propelled by tail propellers, such as the U.S. Predator MQ and China Pterodactyl. As a key aerodynamic component of such vehicles, the inlet has to provide high-quality airflow with the required flow rate for the engine and to meet the constraints and limitations from the shape fusion and structure layout of the vehicle; thus, there exist huge challenges in the design of the flow channel of such inlets [
2,
3,
4]. In particular, the compact flow channel layout with a horizontal inlet entrance, a vertical volute entrance and a horizontal engine entrance requires the airflow to pass two 90° bends before entering the engine core with high quality, i.e., with minimized total pressure losses and maximized flow uniformity at the entrance of the engine. In view of the fact that the degree of deflection and the inlet area expansion ratio (usually below 1.5) of a conventional S-bend inlet are small, it is difficult to apply the relatively mature S-bend inlet design methods to UAV inlets with double 90° bends [
5]. Therefore, this motivated us to conduct the present study on the aerodynamic performance and swirl flow characteristics of a UAV inlet with double 90° bends, which is also integrated with the aircraft fuselage and a volute.
In terms of flow characteristics and mechanisms of conventional subsonic S-bend inlets, scholars all over the world have conducted fruitful investigations [
6,
7,
8,
9,
10]. Researchers from Georgia Institute of Technology [
11,
12,
13] combined the fluid visualization methods of oil flow and pressure-sensitive paint to reveal the causes of the swirl flow at the first and second bends inside the S-bend inlet and the flow mechanism of the swirl characteristics at the outlet. Additionally, they also proposed active flow control measures to alleviate the strength of the internal secondary flow to reduce the distortion and total pressure losses. For S-bend inlets with different offsets, Cranfield University [
14,
15,
16] used Particle Image Velocimetry (PIV) to obtain the three-dimensional velocity field of the inlet and adopted swirl intensity SI [
17] as a quantitative index to investigate the effect of the unsteady swirl distortion characteristics at the exit. Nanjing University of Aeronautics and Astronautics [
18,
19,
20] designed a variety of ultra-compact serpentine inlets and boundary-layer ingestion inlets, and carried out in-depth simulations and experimental studies on their internal flow mechanisms and performance rules. China Aerodynamic Research and Development Center [
21] analyzed the strong swirl flow field at the outlet of a backed large S-bend inlet using a rotary measurement section based on a five-hole probe.
Most of the research studies on volute inlet flow are focused on the field coupled with compressors. Hariharan et al. [
22,
23] designed a compressor volute with different cross-sectional profiles and numerically investigated the flow characteristics such as the cross-sectional pressure distributions, velocity distributions, pressure recovery coefficients, and physical mechanisms of the flow losses in the volute. Yang et al. [
24,
25] conducted hydrostatic pressure measurements and performance tests for a compact volute with different inlet bending shapes. The mechanism of the internal destabilization due to the non-axisymmetric geometry of the volute, causing stall and surge of the compressor, was revealed. Vagnoli and Verstraete [
26] and Zhang et al. [
27] studied the internal flow characteristics of the volute by unsteady numerical simulation methods. The results indicated that the distortion matching between the inlet and outlet of the volute with non-symmetric geometrical shapes has a large impact on the aerodynamic performance and flow field characteristics of the compressor.
It can be found from the state-of-the-art literature that most of the studies on subsonic inlets so far have focused on the S-bend inlet with a relatively gentle transition of the flow channel. Inlets with double 90° bends of the flow channel and coupled with volutes and aircraft fuselages are seldom reported. In this paper, an inlet/volute configuration with double 90° bends is designed and integrated with an aircraft fuselage. The aerodynamic performance and internal swirl flow characteristics are investigated experimentally. Finally, the possibility of improving the aerodynamic performance and swirl flow characteristics of the inlet is explored by adding deflectors and baffles inside the inlet. The second chapter describes the experimental setup, including the experimental wind tunnel, model parameters, measurement devices, and measurement systems. The third chapter defines the performance parameters involved in the text. The fourth chapter analyzes the results of inlet performance and swirl in terms of angle of attack, sideslip angle, AIP Mach number, freestream air speed, deflector and baffle height, respectively. This paper proposes a double 90° large deflection S-bend inlet design, which exhibits the following characteristics: compact structure, small deflection, excellent stealth performance, and the ability to maintain good aerodynamic performance. In view of the strong swirl flow observed in the volute, an innovative initiative is proposed, namely the addition of deflectors before the first bend of the inlet and baffles at the bottom of the volute, with the aim of inhibiting the swirl intensity.
2. Experimental Setup
2.1. Test Model
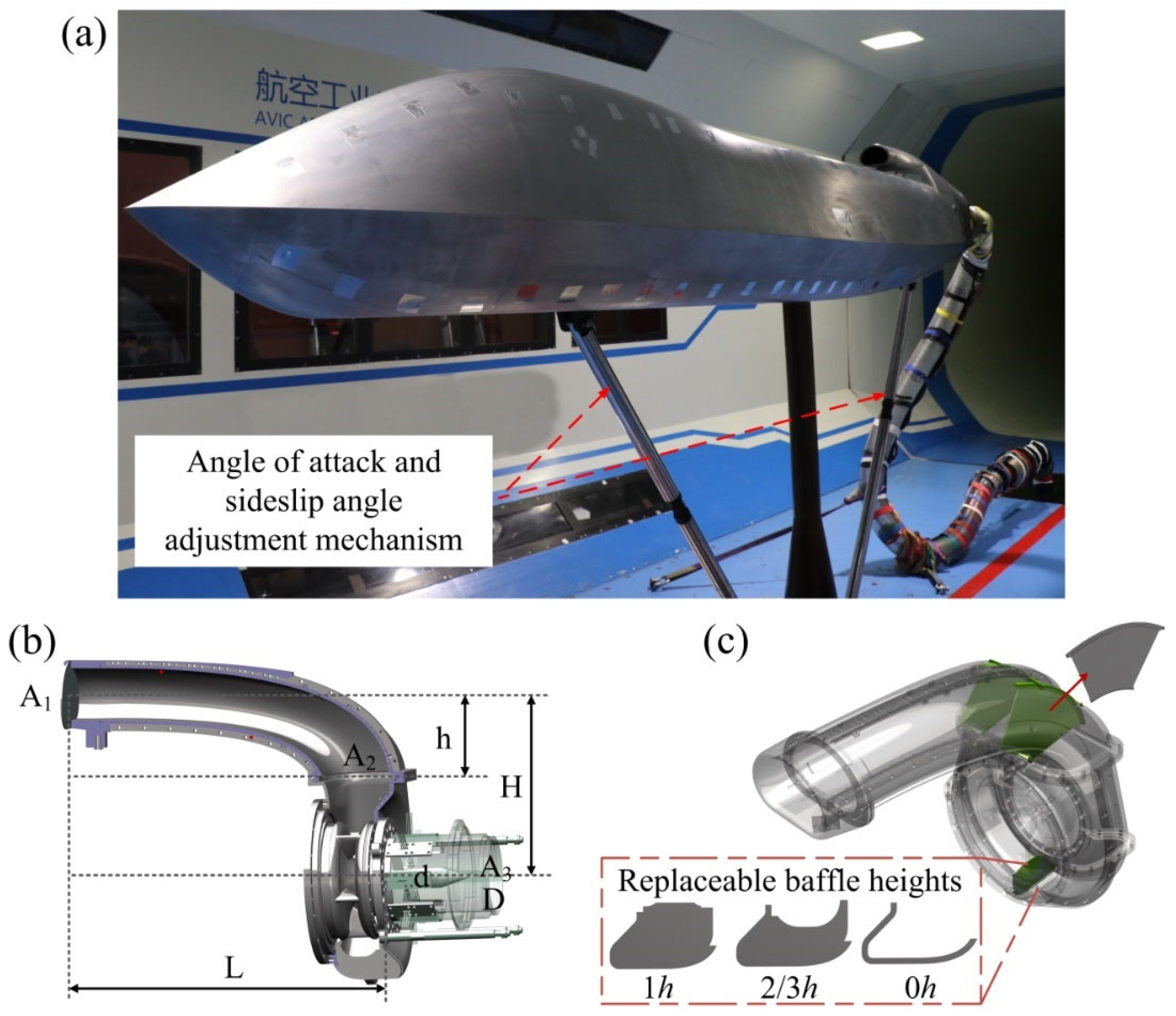
The inlet test model installed in the wind tunnel, as shown in
Figure 1a, has double 90° flow bends and is integrated with a fuselage, a truncated wing and a volute. The main geometric variables are defined in
Figure 1b with their values tabulated in
Table 1. The size of the overall mold is 3.67 m × 0.5 m × 0.7 m, and an opening was cut at the tail of the model to facilitate the connection of the suction pipe with the inlet duct. The straight sections of the fuselage and wing were cut off to meet the room requirements of the wind tunnel test site. The model adopts an abdominal bracing mode, taking the wind tunnel support as the point of support, with auxiliary diagonal bracing members added at the front and back to improve the stability of the model. To reduce the weight of the model, the interior of the model is made hollow with load-bearing frames. To explore the potential measures to alleviate the intensity of the swirl flow inside the inlet, two removable deflectors are installed right ahead of the first 90° bend, as well as one removable baffle installed at the bottom of the volute, as shown in
Figure 1c. Three different heights of the baffle were designed for the test, namely, 0 h, 2/3 h, and 1 h. The basic configuration of the tested inlet has the deflectors and the baffle of height 2/3 h. It is clarified here that all the results discussed in
Section 4 of the paper except
Section 4.5 are based on the experimental measurements for the basic configuration.
2.2. Wind Tunnel
The test wind tunnel is a closed loop single reflux low-speed wind tunnel called FL-9. The model inlet adopts a suction method. The wind tunnel’s angle of attack and sideslip angle adjustment mechanism are connected to the model through an abdominal brace to ensure the experiments are conducted within the range of sideslip angle of ±16° and angle of attack of ±14°. The maximum wind speed simulated under the normal pressure condition is 130 m/s, and 90 m/s under 0.4 MPa pressure. The cross-sectional dimensions of the wind tunnel experimental section are 3.5 m high and 4.5 m wide.
All the tests were run under the normal pressure condition without pressurization. The tested wind speed range is 0 to 90 m/s, angle of attack range is −8° to 12°, and sideslip angle range is 0 to 16°. The tail suction pipe adopts the boundary layer suction pipeline systems, one set of which is a pressurized exhaust pipeline system, and the other set is an atmospheric pressure injection pipeline system.
2.3. Measurement System
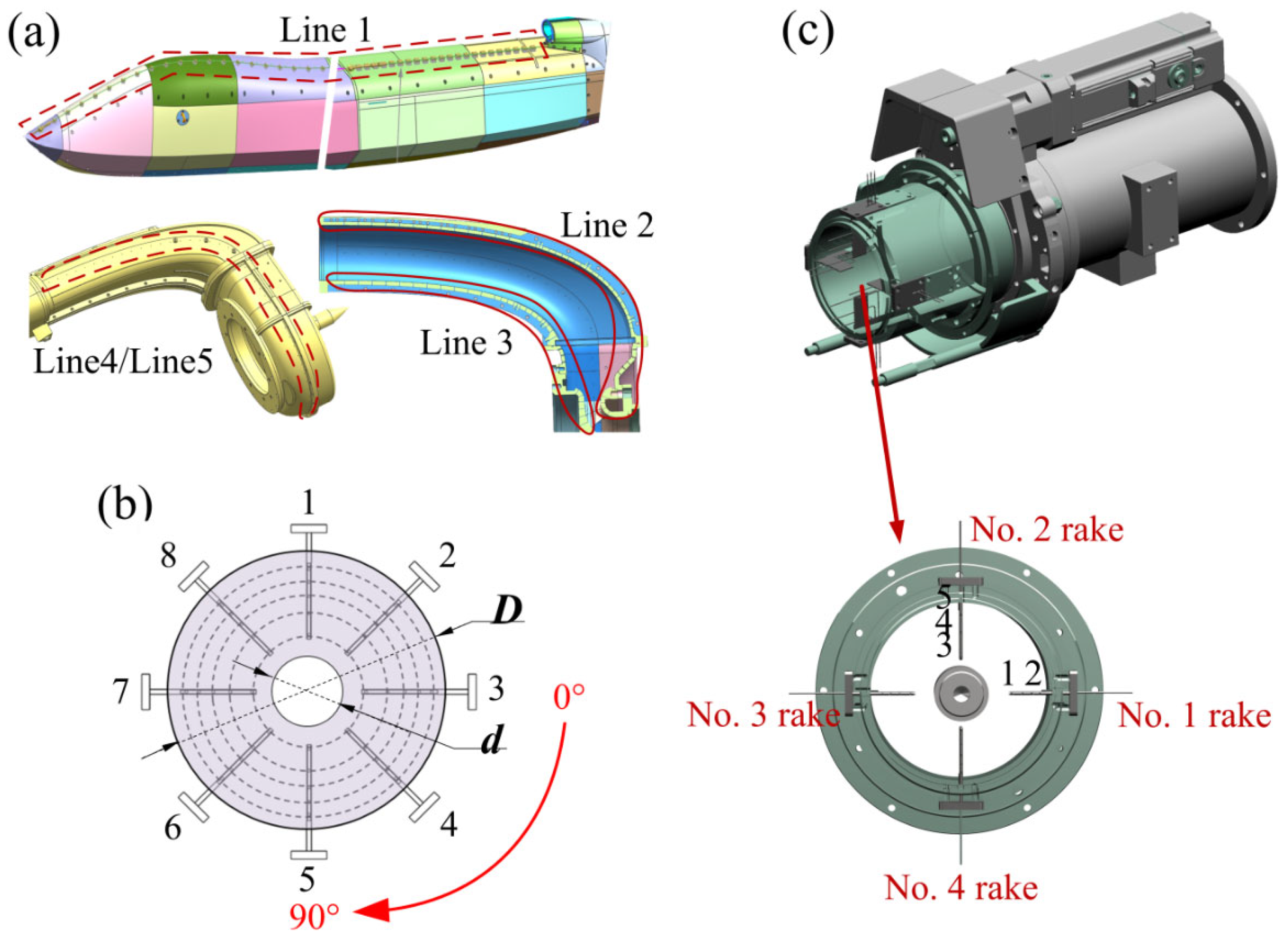
Figure 2a shows the distribution of the static pressure probes on the test model, which has a total of five static pressure curves. There are 45 pressure measurement points distributed at the centerline of the upper surface of the aircraft, which is named Line 1. There are four pressure measurement lines distributed on the surface of the inlet/volute. Forty-three measurement points are distributed along Line 2 on the upper part of the inlet/volute, and 30 measurement points distributed along Line 3 on the lower part. Forty points are symmetrically distributed on each of the left and right sides, which are named Line 4 and Line 5, respectively.
In order to obtain the aerodynamic data such as total pressure and swirl angle simultaneously in the main measurement section, i.e., the Aerodynamic Interface Plane (AIP), two methods were used: a conventional measurement rake and a rotary measurement rake. The conventional rake is designed as a cross shape with eight rakes, as shown in
Figure 2b. Each rake has five probes distributed radially according to an equal ring area. The azimuthal angle of the swirl flow starts from the position where the No. 3 rake is located. The rotary rake adopts a five-hole probe, as shown in
Figure 2c. Four rakes are arranged on the rotating mechanism with a total of 10 probes. In order to maximize the spacing of the probes, two rakes in the opposite direction have three probes, and the other two rakes have two probes. The probes are located complementarily in the radial isotropic distribution and are spaced every 22.5°. They rotate within a 180° range so that the data for the 16 rake positions on the entire measurement surface are obtained. The probe is rotated over a 180° range, with a 22.5° increment per revolution, and remains stationary for a period of 5 s before initiating a data acquisition process to obtain data for 16 rake positions across the entire measurement cross-section AIP. The wind tunnel test parameters are collected by a VXI data acquisition system, and the steady-state total/static pressure of the inlet is measured by a PSI9000 pressure acquisition system from the United States, including four 15PSI valve blocks with a measurement accuracy better than 0.1% FS. Prior to installation in the measurement section, the five-hole probe is calibrated, and the calibration is carried out on a special calibration table.
During the test, the wind tunnel is activated to reach the target freestream air speed. The pressure of the air supply to the ejector is then controlled to ensure that the ejector enters the pre-set working state. Finally, the pressure difference between the front and rear of the inlet piping system is stabilized. Subsequently, the position of the throttle cone of the flow regulating valve in the ventilation pipeline is altered in order to modify the flow rate of the inlet. Concurrently, the steady/dynamic pressure of the inlet is quantified at each flow rate, while the gas flow in the ventilation pipeline is meticulously quantified by a high-precision flow meter installed within the wind tunnel.
3. Performance Parameter Definitions
Based on the measurements of the flow field parameters, the average total pressure recovery coefficient σ, and the total pressure distortion index DC60, the average swirl angle on the AIP at the inlet outlet can be calculated, and the average Mach number MAIP can also be calculated. The specific definitions are expressed as follows.
- (1)
The average total pressure recovery coefficient is defined as
where
is the freestream total pressure,
is the area-weighted average of the total pressure at the AIP of the inlet.
- (2)
The average Mach number at the AIP is defined as
where
and
are the wall static pressure points at the location of AIP with a total of 8 arranged,
.
- (3)
The total pressure distortion index is defined as
where
is the minimum total pressure in any sector region with an azimuthal angle of 60°.
is the average dynamic pressure of the AIP.
- (4)
The maximum swirl angle is defined as follows:
The maximum swirl angle
is the rotation angle
when
is taken to its maximum value, i.e.,
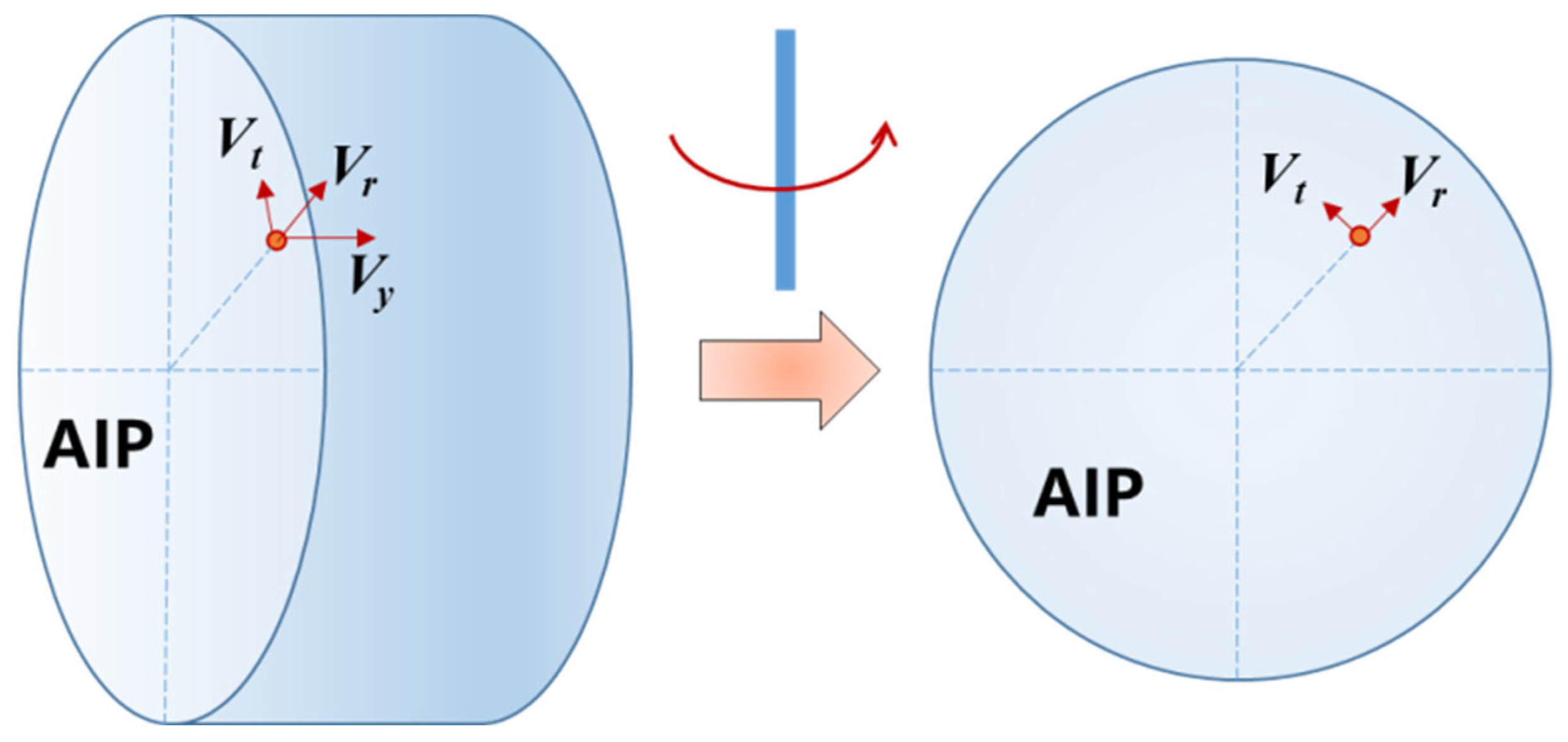
where
, where
is the tangential velocity of the airflow at the
j-th probe position of the
i-th rake at the AIP,
is the meridional velocity at the point where
is the radial velocity, and
is the axial velocity, as shown in
Figure 3.
- (5)
The swirl distortion index,
, is the ratio of the sum of the areas of each measurement point with an absolute value of the swirl angle at the AIP
greater than 15° to the total area of the AIP. Since the cross-sectional area represented by each measurement point is equal in the experiments:
In the calculations, each angle is in the unit of degree and is positive when viewed counterclockwise in the direction of flow.
is the total number of measurement points at the AIP where
.
- (6)
The pressure coefficient along the wall is defined as
where
is the static pressure at the measurement point,
is the incoming static pressure,
is the dynamic pressure of the incoming flow defined as
, where
is the air density and
is the freestream velocity.
- (6)
The standard deviation is defined as
where
represents the standard deviation of a specific parameter within a given data set, e.g.,
is the standard deviation of the total pressure recovery coefficient,
is the standard deviation of the total pressure distortion index,
is the standard deviation of the swirl distortion index, and
is the standard deviation of the maximum swirl angle. n is the number of groups of repetitive data, and
is the sample data.
is the mean of the sample data, defined as
.
4. Results and Discussion
4.1. Measurement Repeatability Analysis of Tests
Prior to conducting the test, a repeatability test was conducted for a typical working condition with a constant control flow rate. This was done in order to measure the aerodynamic performance and swirl characteristics of the outlet cross section in a repeatable manner.
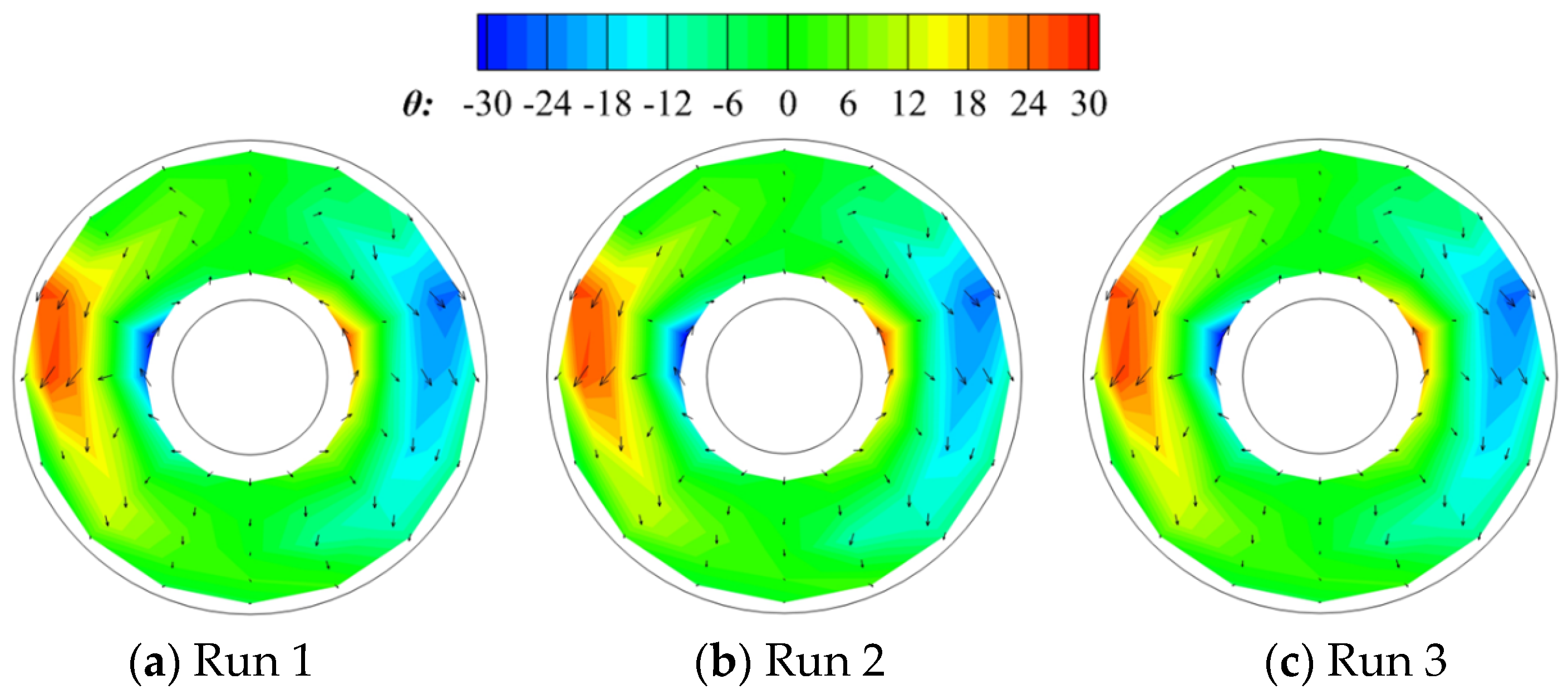
Table 2 presents a comparative analysis of the repeatability test data for one of the working conditions.
As illustrated in
Table 2, the standard deviation of the total pressure recovery coefficient, total pressure distortion index, swirl index, and maximum swirl angle in the three repeatability experiments is maintained within a narrow range. This indicates that the variations in these quantities are not related to measurement uncertainty, thereby providing evidence that the reproducibility of the test device is reliable.
Figure 4 and
Figure 5 illustrate the comparison of the total pressure recovery coefficient cloud and swirl angle velocity vector cloud for the three groups of data. It can be observed that the repeatability of the cloud is relatively good, with the pressure regions, as well as the region with larger swirl angle, all situated in the corresponding position. Furthermore, the difference in the total pressure recovery coefficient is less than 0.001. The difference in the total pressure distortion index is less than 0.0011, the difference in the swirl angle distortion index is less than 1.25%, and the repeatability is satisfactory.
4.2. Effects of Angle of Attack
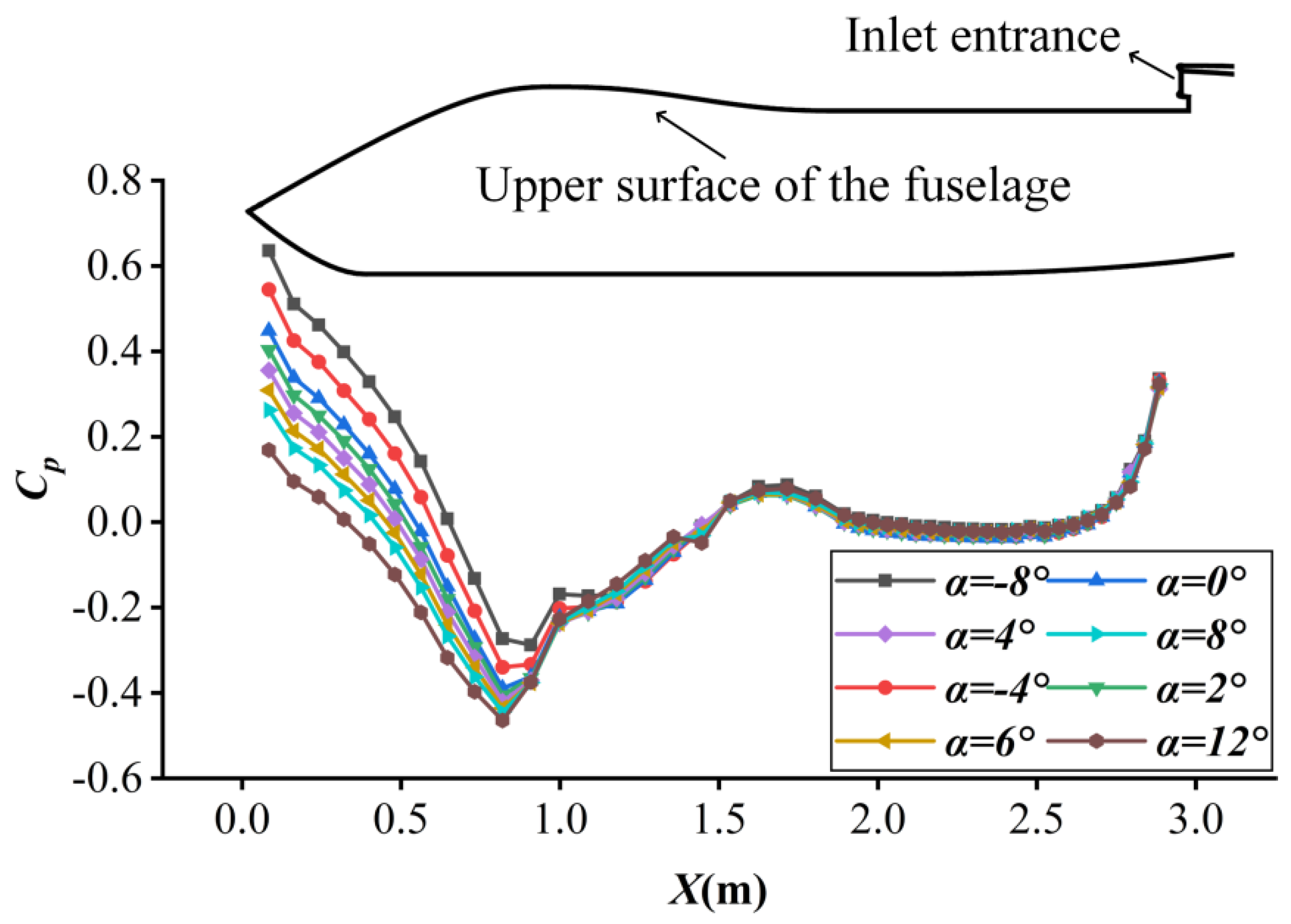
Figure 6 illustrates the pressure distribution along Line 1 on the upper surface of the fuselage at a freestream speed of
V0 = 90 m/s and sideslip angle of
β = 0°. Across all the angles of attack examined, a consistent trend is observed in the variation of wall pressure. Initially, there is a decrease attributed to the suction effect of the converging nose profile, followed by an increase due to the inward concavity of the center profile. The pressure reaches the peak at the location with the maximum flow passage area over the fuselage. Afterwards, the pressure undergoes a short and slight decrease followed by a long plateau until the inlet entrance, where a sharp rise occurs due to the deceleration effect induced by the inlet. Overall, the most significant variation in wall pressure happens at the nose section, which is a result of the large local flow angle incorporating the inclination angle of the nose profile.
Figure 7 presents the static pressure distributions along the inlet and volute. The inlet, serving as a flow decelerator, consistently exhibits adverse pressure gradients along its wall from X = 3.025 m to X = 3.250 m; however, the pressure on the upper surface of the inlet remains almost unchanged as angle of attack increases (
Figure 7a). Conversely, significant variations are noted on the lower surface, especially in the region near the first bend (
Figure 7b). This increased suction pressure and adverse pressure gradient can lead to separation of the boundary layer on the lower part of the inlet, causing flow separation and reducing the efficiency of the inlet. As angle of attack is increased to and beyond
α = 8°, a slight surge is observed at the end of the first bend along Line 3, which is caused by the ingested shedding separation vortices created by the most drastic change in the flow at the nose. The airflow in close proximity to the lower surface of the volute wall exhibits a smaller turning radius, thus is more prone to be separated. Inside the volute, both pressure curves along Line 4 and Line 5 show a gradual rise (
Figure 7c,d). As the flow approaches the bottom of the volute, the pressure experiences a sudden rise until the bottom, which is attributed to the blockage effect of the baffle at the bottom of the volute. Additionally, the pressure distributions along Line 4 and Line 5 are nearly identical, indicating the fundamental symmetry of the flow within the volute.
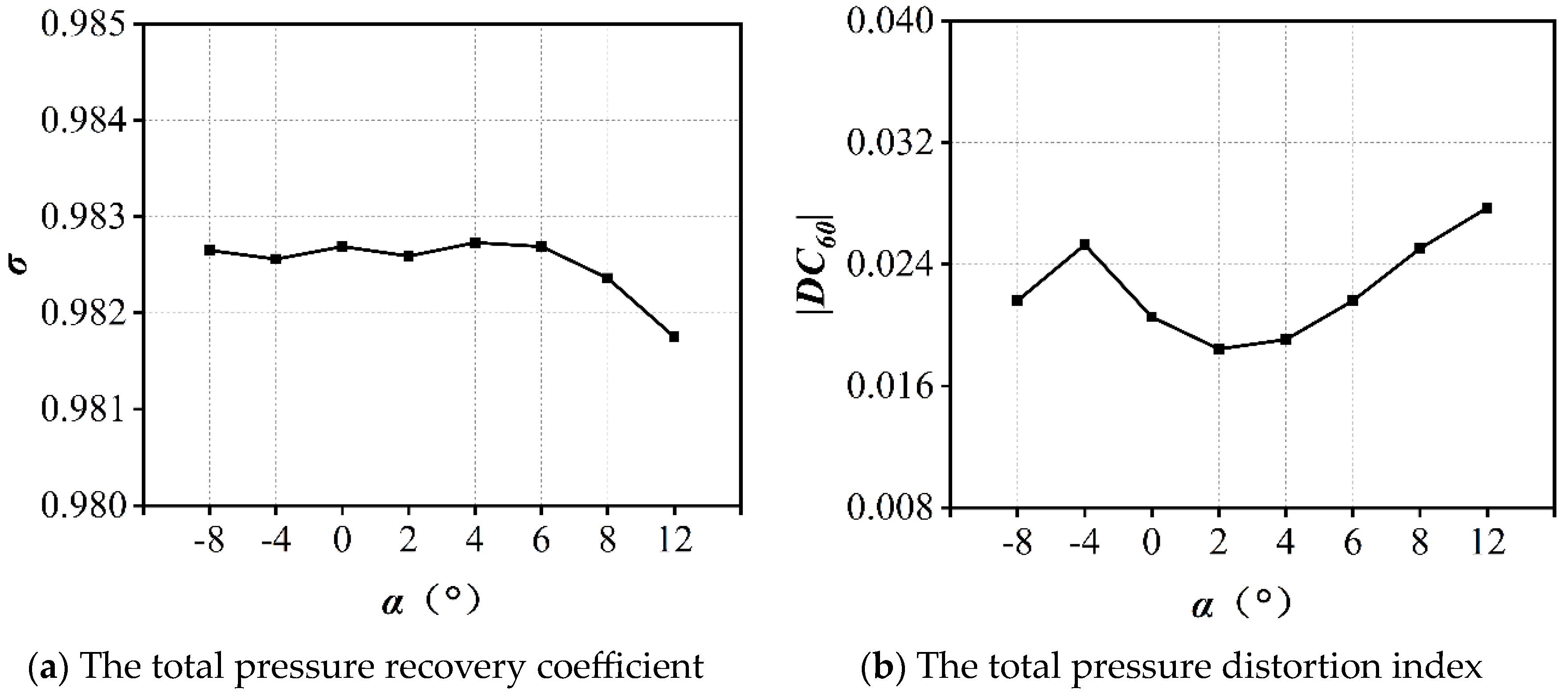
Figure 8 shows the aerodynamic performance of the inlet at various angles of attack. The total pressure recovery coefficient remains unchanged until
α = 8°, at which it begins to fall slightly due to the increased drag of the airflow. However, the overall total pressure recovery coefficient remains near 0.98, indicating that the inlet performance can adapt to a large change in the angle of attack at cruise. Moreover, the total pressure distortion
DC60 also remains at a fairly low level over all tested angles of attack. As shown in
Figure 9, the values of the maximum swirl angle and the swirl distortion index at the AIP are also stable. The separation vortices at the nose were sucked in by the inlet, leading to a slight increase in the total pressure distortion at the AIP as well as an increase in the intensity of the swirl flow.
4.3. Effects of Sideslip Angle
The impact of sideslip angle on inlet performance is investigated at an angle of attack of
α = 0° and
V0 = 50 m/s.
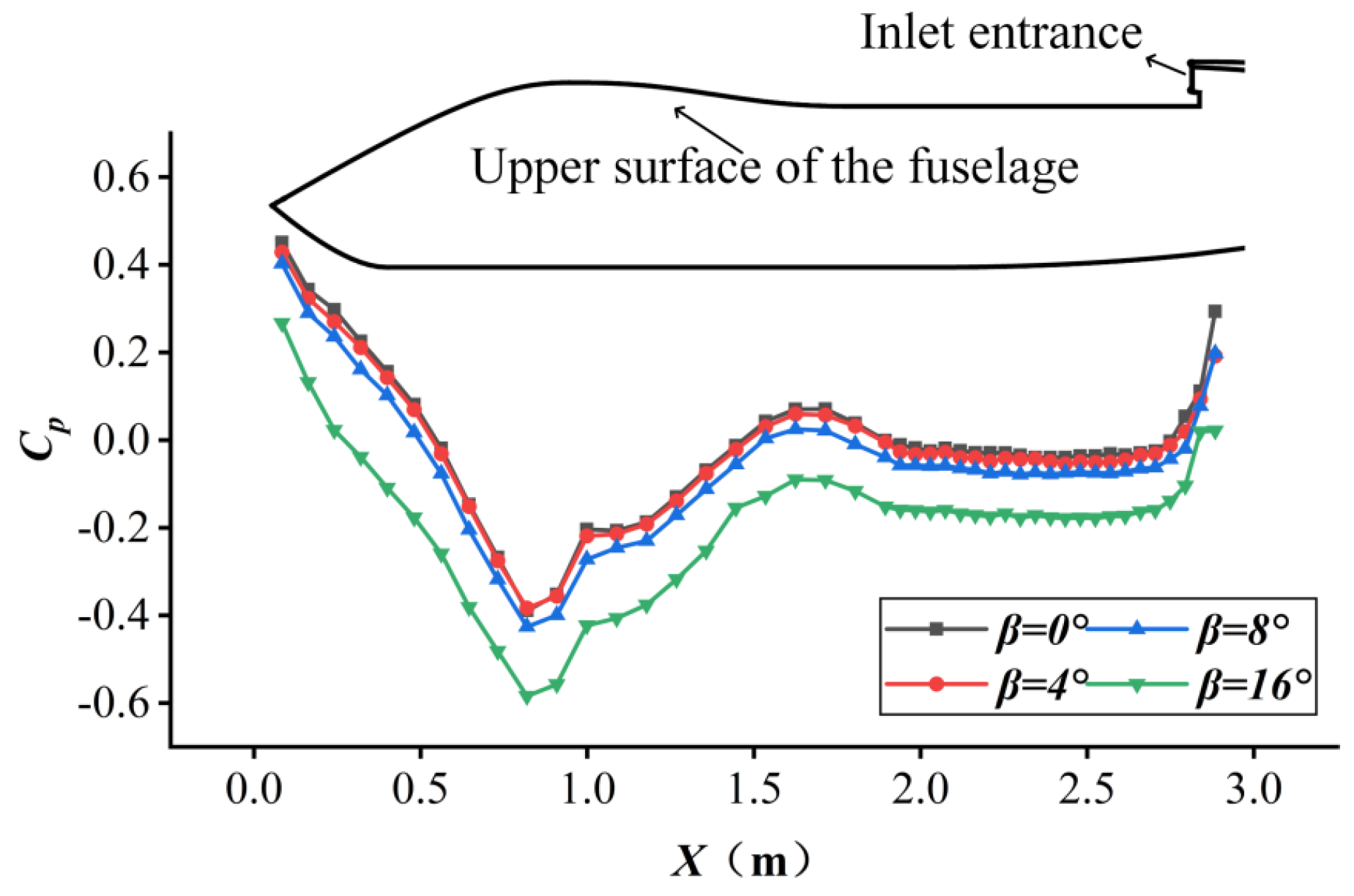
Figure 10 displays the pressure distribution along Line 1 on the upper surface of the fuselage. It is observed that there is a minimal change within the range of
β = 0°~8°. However, as the sideslip angle increases to
β = 16°, the pressure curve exhibits a pronounced downward shift. This is due to the large decrease in the longitudinal velocity component at such large sideslip angles, releasing the suction effect of the upper surface of the fuselage.
Figure 11 shows the pressure coefficient distribution along Line 2 to Line 5 at different sideslip angles. The pressure profile inside the inlet does not shift as significantly with increasing sideslip angle, probably because at lower freestream speeds, even large sideslip angles do not lead to higher intake losses. Especially after passing the first turn into the volute, the pressure curves at different sideslip angles almost coincide. The pressure curves undergo a notable downward shift, resulting in a considerable total pressure loss and distortion increase in the inlet, as illustrated in
Figure 12. As depicted in
Figure 11b, the pressure at the junction of the inlet and the volute experiences a sudden surge followed by a sharp decline. This location marks the conclusion of the initial significant deflection, where a robust transverse flow in the airflow is driven by the centrifugal force. The transverse flow interacts with the deflector end, resulting in flow separation and the formation of vortices. In
Figure 12, the effect of increasing sideslip angle on the pressure distortion is significantly larger than the effect on the total pressure recovery, which suggests that the homogeneity of the total pressure distortion is more sensitive to the factor of sideslip angle.
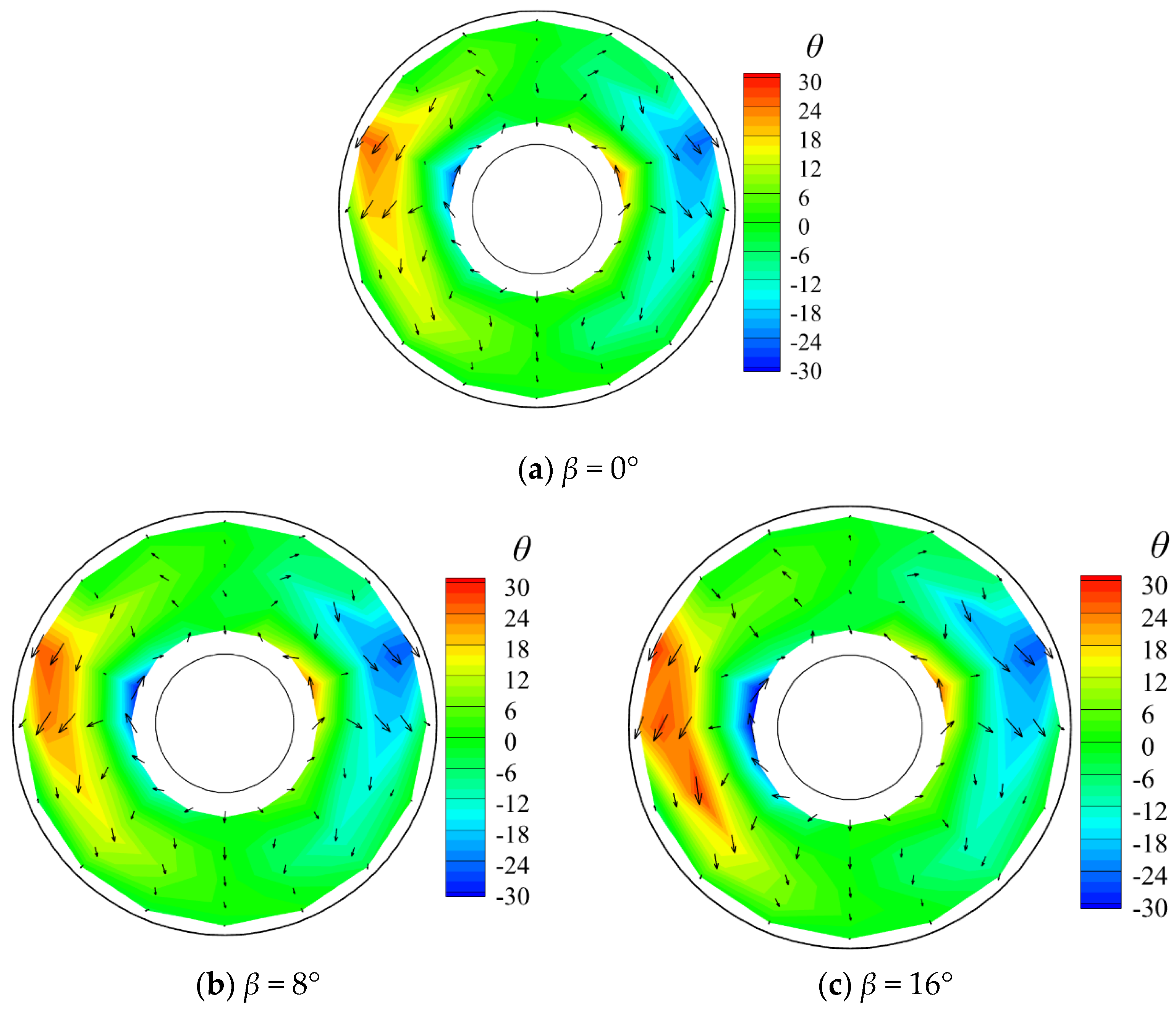
Figure 13 illustrates the contour of the total pressure recovery coefficient at the AIP at four sideslip angles. As the sideslip angle increases, the symmetry of the distribution gradually deteriorates, with the low-pressure region on the left side gradually increased. In contrast, the high-pressure region near the central axis keeps shrinking. The flow momentum on the right side is evidently greater than that on the left side, which gives rise to a twisted flow tendency about the center body axis. The process of flow field twisting intensifies flow separation and diffusion, leading to more energy losses of the inlet. This further elucidates why the total pressure distortion index intensifies while the total pressure recovery remains essentially unaltered with the increase in sideslip angle.
As illustrated in
Figure 14, the asymmetry of the swirl angle distribution at the AIP becomes more pronounced as the sideslip angle increases, as well as the symmetry of the secondary flow velocity distribution at the AIP. As the sideslip angle increases, the secondary flow rotates clockwise, resulting in the position of the maximum swirl angle continuously moving towards the left side of the AIP for stacking. As shown in
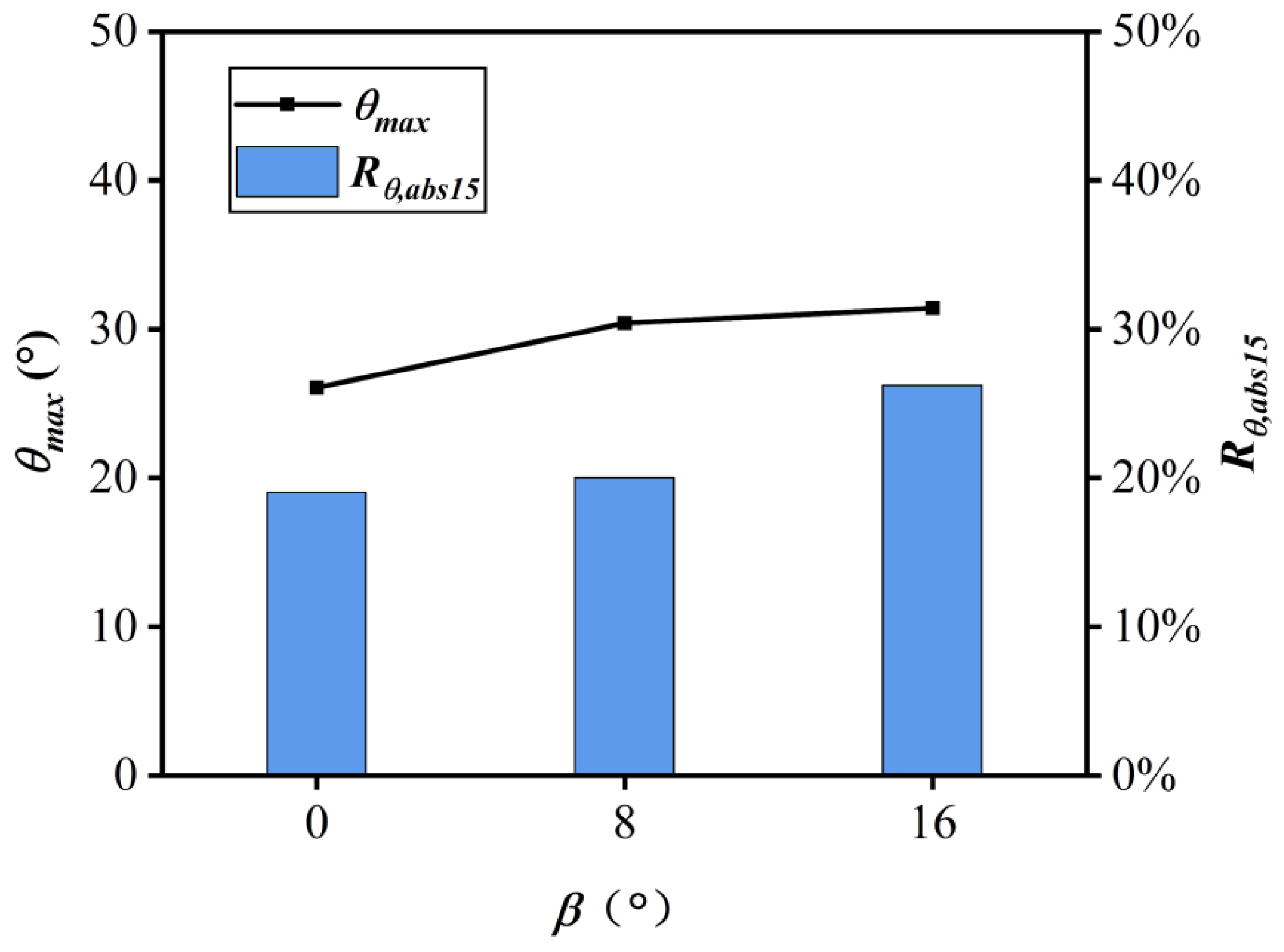
Figure 15, the magnitudes of the swirl distortion index and the maximum swirl angle increase significantly with the increase in sideslip angle. This implies that the two indices can effectively reflect the characteristics of the swirl flow at the exit of the UAV inlet.
4.4. Effects of AIP Mach Number
The performance of the inlet under various Mach numbers at the AIP,
MAIP, for the testing condition of
V0 = 50 m/s,
α = 0° and
β = 0° is plotted in
Figure 16. The two performance variables generally exhibit a rational response to
MAIP, with deteriorations in both as
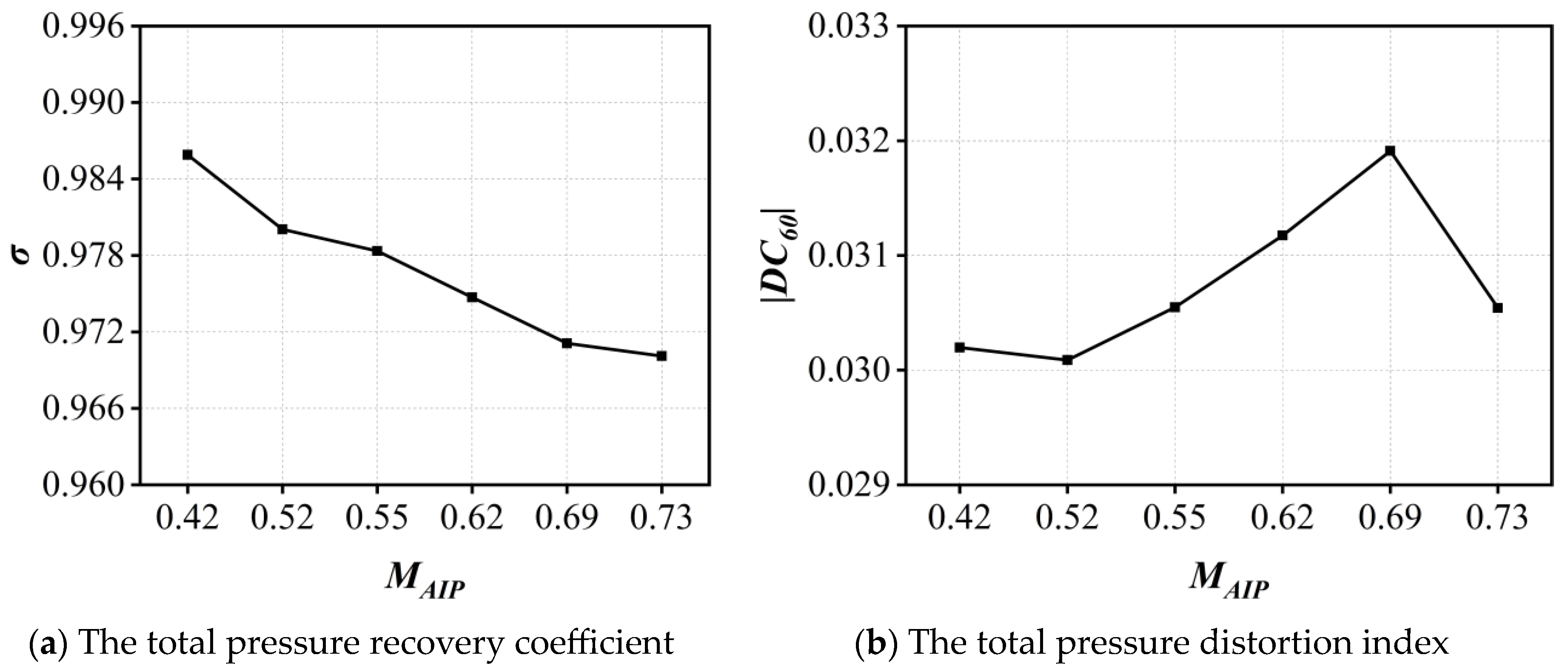
MAIP increases. Nevertheless, the total pressure recovery coefficients are all above 0.97, and the total pressure distortion remains at a low level within the operating Mach number range of air-breathing engines, indicating that the current design of the inlet is satisfactory.
Figure 17 qualitatively shows the reduction in the total pressure recovery coefficient with the increasing Mach number at the AIP, with a significant shrinkage in the size of the high total pressure area. At azimuths of 45°, 135°, 225°, and 315°, significant low total pressure areas emerge around
MAIP = 0.55 and further expand with the increase in
MAIP. Further, it can be seen that the regions of low total pressure are all located closer to the outer wall of the inlet, because the airflow is faster near the outer wall (
Figure 14), causing the airflow to stagnate or be obstructed in this region. The notable discrepancy between the high and low total pressure distributions leads to decreased flow homogeneity within the inlet.
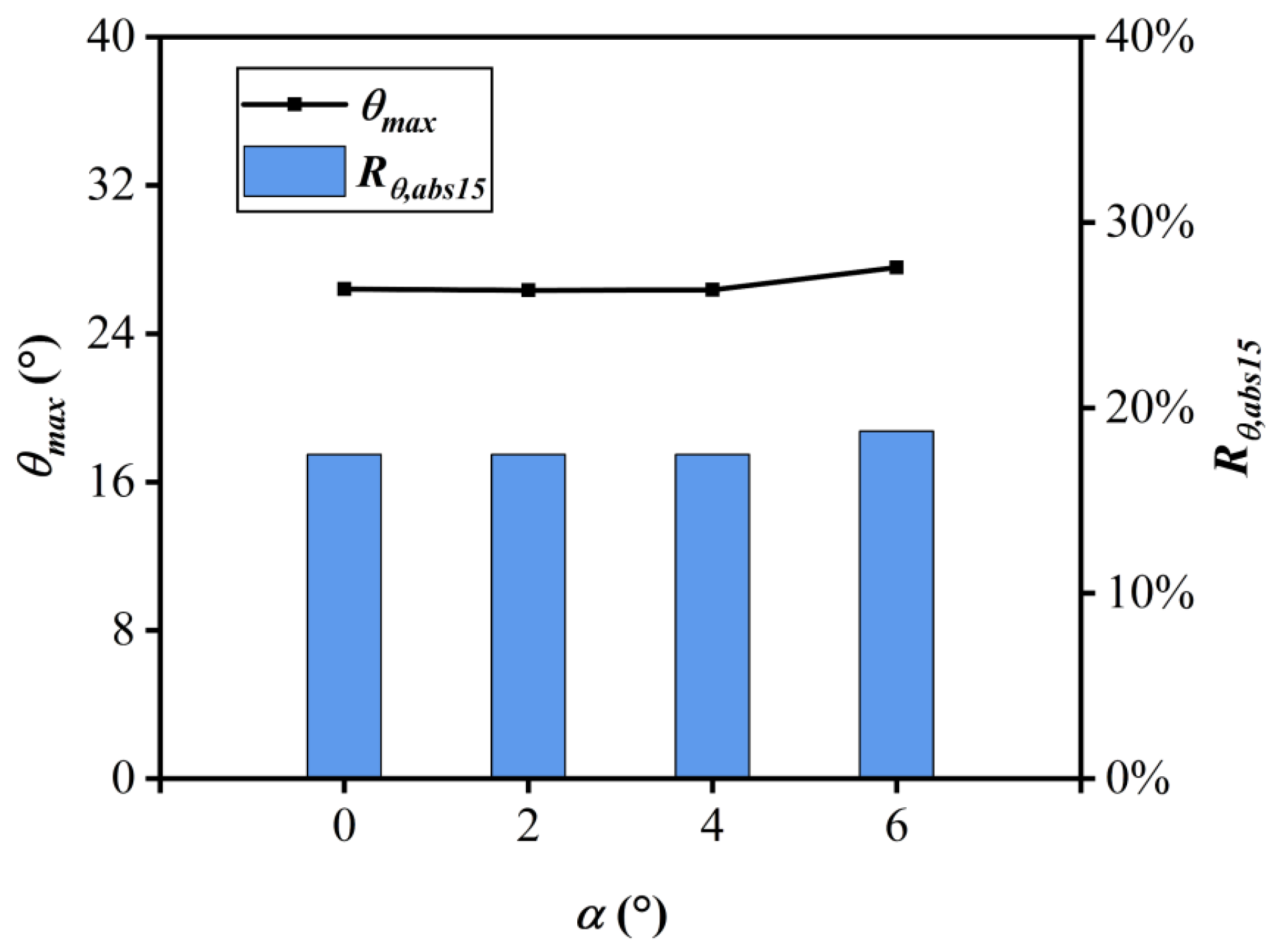
Figure 18 illustrates that the swirl distortion index
at AIP, in contrast to the overall decreasing trend in the total pressure recovery factor, exhibits a gradual decline with increasing
MAIP. The maximum swirl angle at AIP, on the other hand, demonstrates a more gentle decrease with
MAIP around 26.5°. Consequently, it can be concluded that the vortex characteristics improve with increasing
MAIP, accompanied by a reduction in both vortex area and maximum swirl angle. It demonstrates that the total pressure distortion is not necessarily related to the strength of the swirl flow. Rather, the total pressure distortion reflects the uniformity of the pressure distribution.
4.5. Effects of Freestream Speed
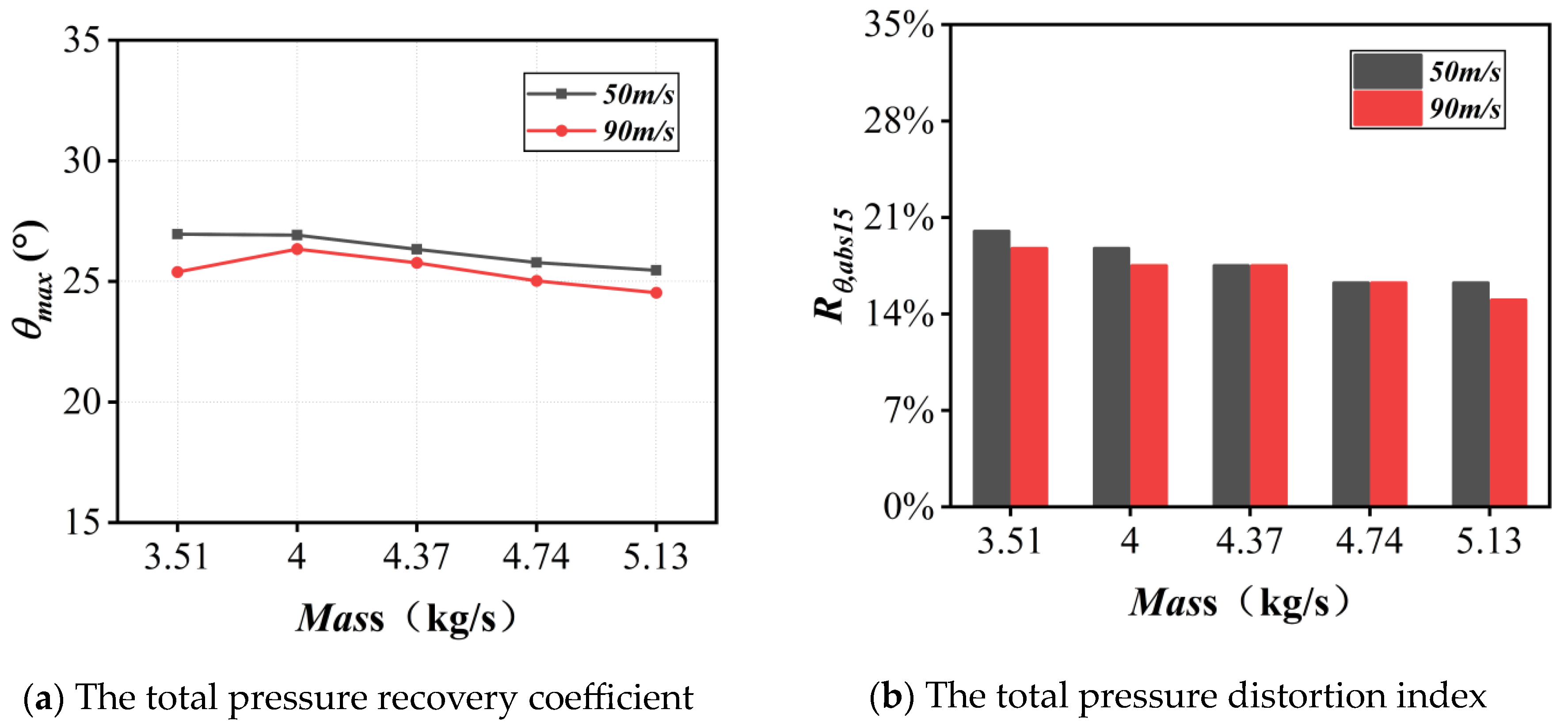
Figure 19 illustrates the aerodynamic performance of the inlet for two freestream speeds (i.e., flight speeds) while
α = 2° and
β = 0°. As the freestream speed increases, the total pressure recovery performance improves due to the enhanced ram effect of the incoming flow. The total pressure recovery coefficients at
V0 = 90 m/s are all higher than at
V0 = 50 m/s. In regard to total pressure distortion, it seems that the difference between different freestream air speeds is amplified as the mass flow rate increases, especially for mass flow rates beyond 4.37 kg/s, where a higher freestream speed causes a slightly larger total pressure distortion. In conclusion, increasing freestream air speed is beneficial for improvement of the total pressure recovery performance, but the total pressure distortion is also increased. In addition, it can also be obtained from
Figure 19 that both the total pressure recovery and distortion deteriorate with the increasing mass flow rate of the inlet.
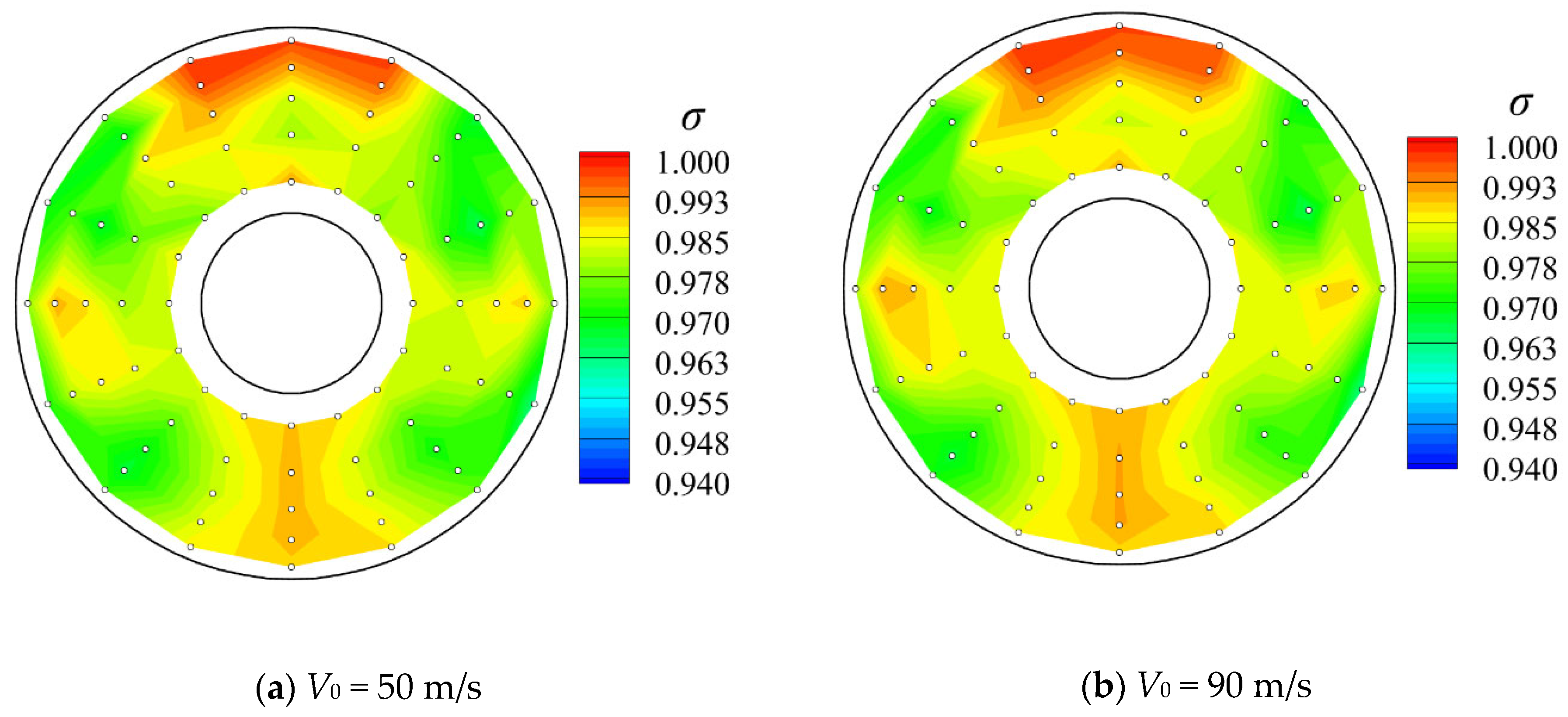
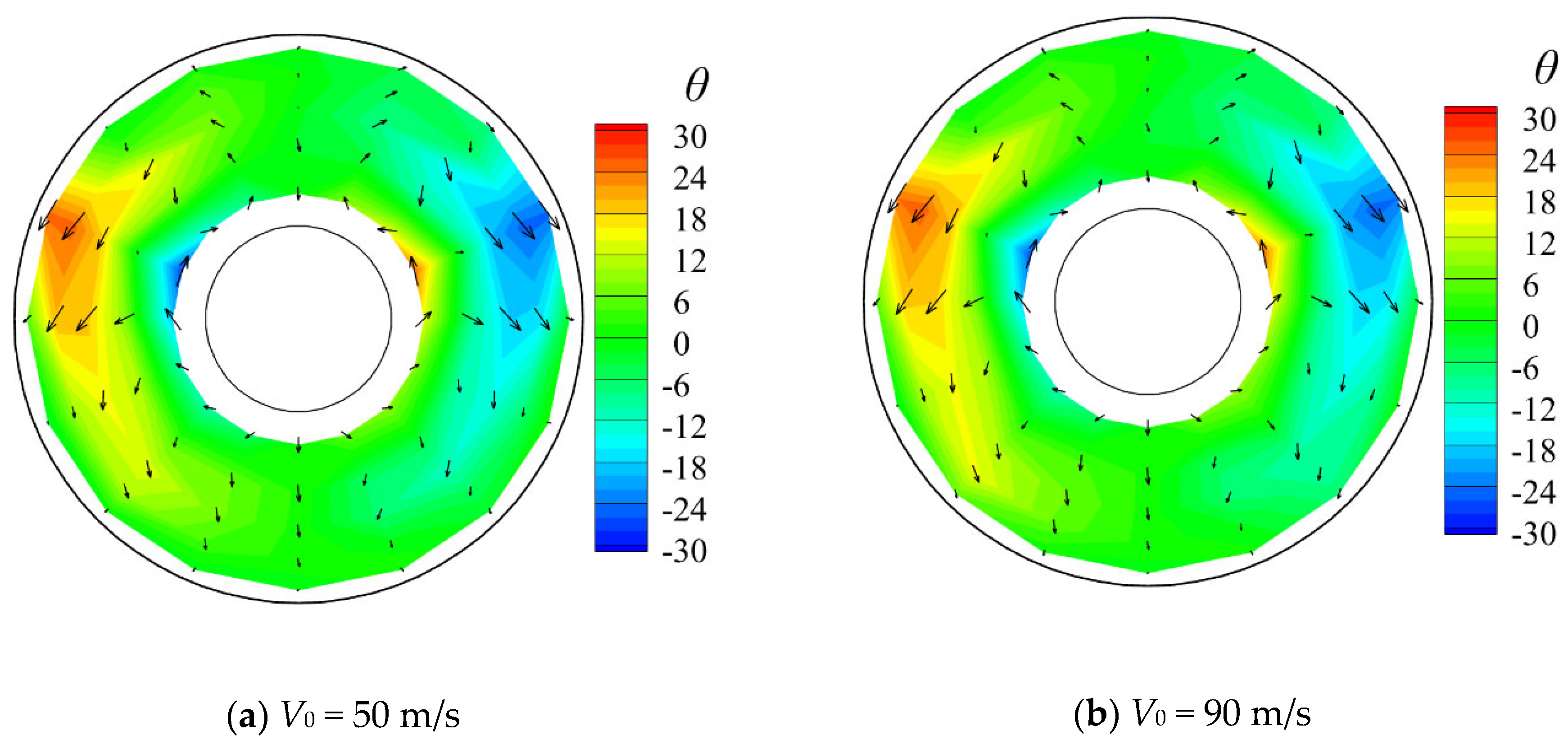
Figure 20 illustrates the swirl flow characteristics at both freestream speeds. It can be observed that both the swirl distortion index and the maximum swirl angle decrease at the higher freestream speed of
V0 = 90 m/s, indicating an enhancement of the swirl flow characteristics at higher freestream speeds. The increase in freestream air speed intensifies the kinetic energy of the flow in the inlet and simultaneously alleviates the vortex and turbulence phenomena in the flow, thereby optimizing the swirl flow condition.
Figure 21 and
Figure 22 illustrate the total pressure and the swirl angle contours at the incoming mass flow rate of 4 kg/s. It can be seen that as the freestream speed increases, the area of high-pressure region continues to increase and gradually overwhelms the low total pressure region. In terms of swirl flow characteristics, as the freestream speed increases, the magnitude of the maximum swirl angle decreases, and the area of the absolute swirl angle decreases, indicating the improvement in the swirl flow characteristics inside the inlet. In short, the aerodynamic performance of the inlet is generally improved as the freestream air speed increases.
4.6. Effects of the Deflectors and Baffle
The study of the effect of the deflectors was conducted under a fixed freestream flow velocity of
V0 = 90 m/s. The results for the aerodynamic performance and swirl characteristics of the model state at
α = 0° and
β = 8° with and without the deflectors are presented in
Table 3. Although the total pressure recovery coefficient exhibited a slight decline in the presence of the deflector, the total pressure distortion
DC60 was reduced by 29.75%, 19.89%, and 34.38% at the three increasing mass flow rates, respectively. As qualitatively shown in
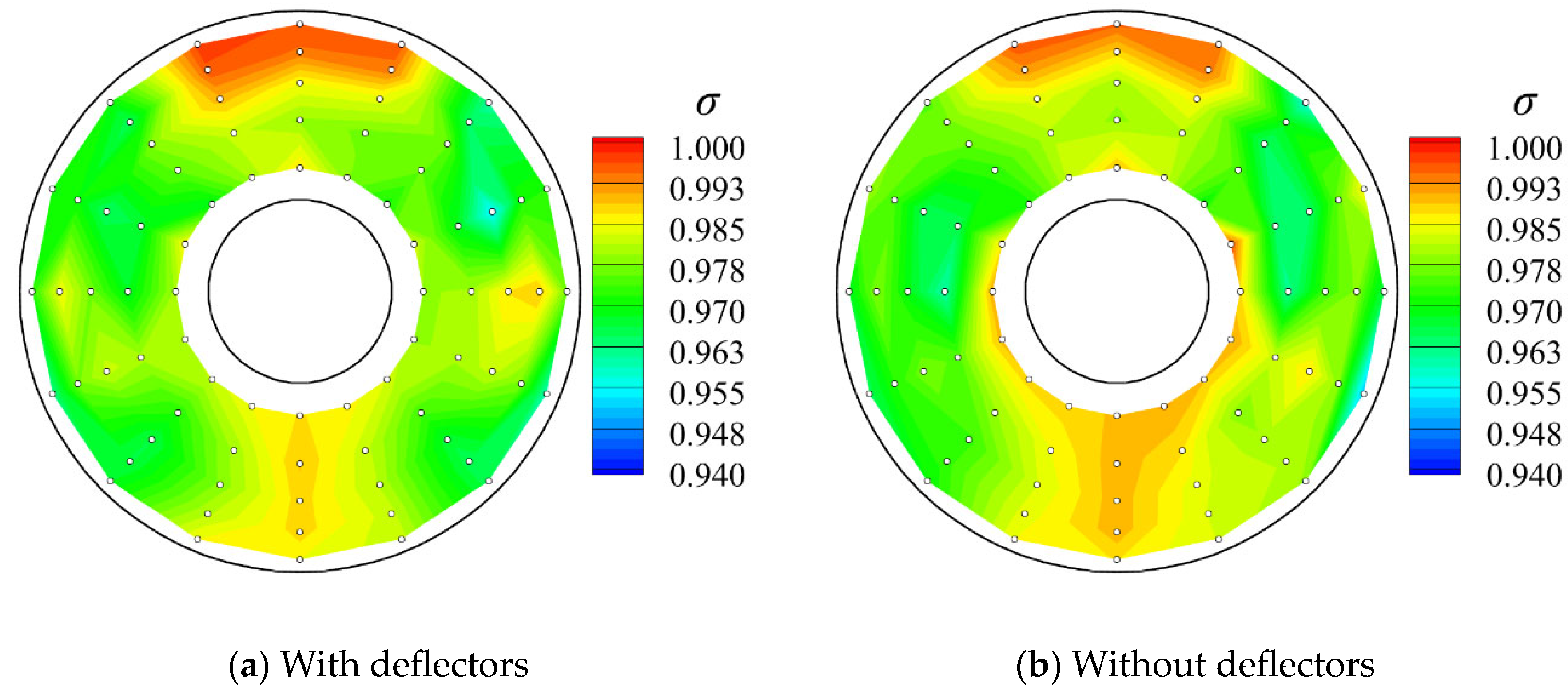
Figure 23, the addition of the deflectors results in a more symmetrical distribution of the total pressure at the AIP.
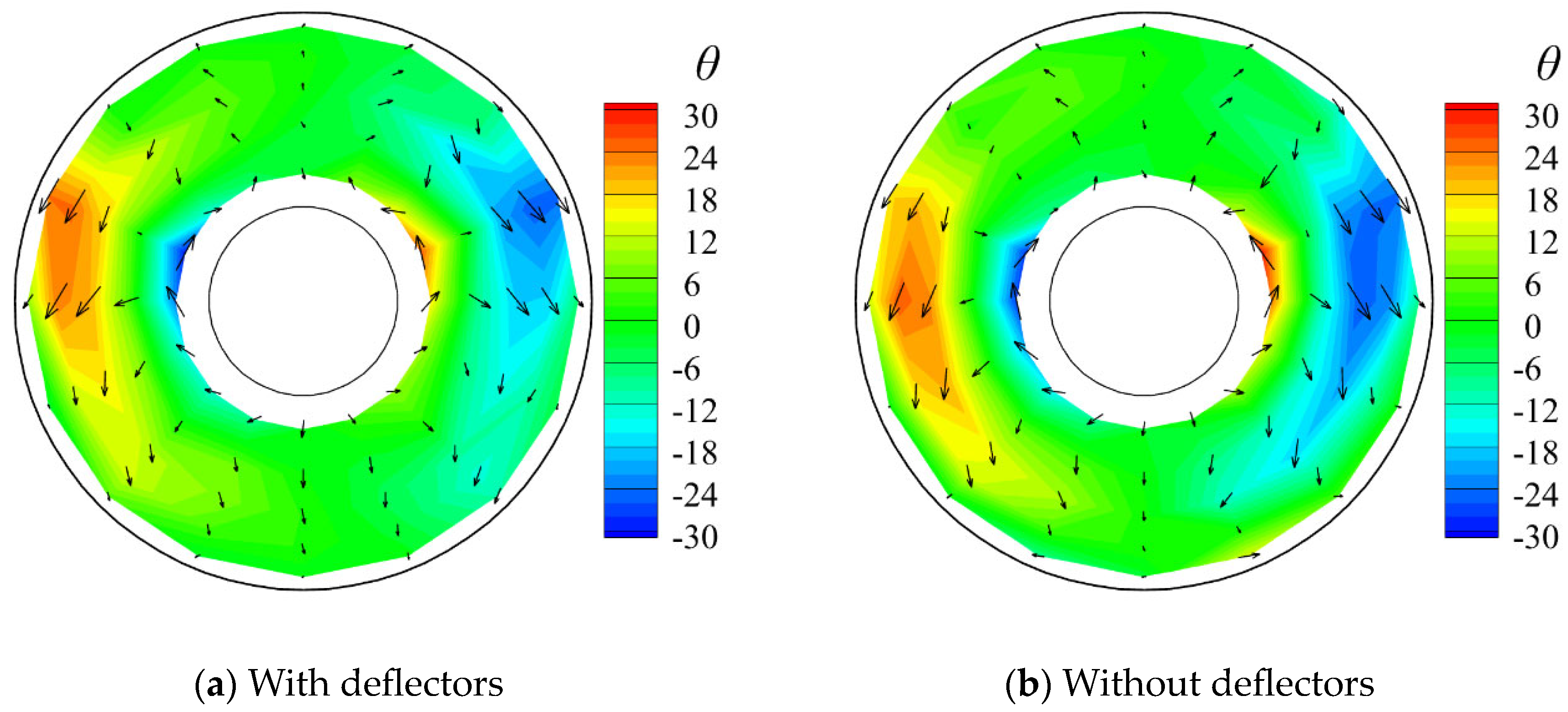
Furthermore, the addition of the deflectors resulted in an improvement in the swirl characteristics of the inlet, as illustrated in
Figure 24. Quantitatively, the swirl distortion index decreased by 14.29%, 15%, and 28.57% at the three increasing mass flow rates, respectively. However, the maximum swirl angle increased slightly, by 5.2%, 1.19%, and 1.29%, respectively. This illustrates the importance of the choice of the reference quantity when characterizing the swirl flow in a complex inlet such as the one in the present study. The addition of the deflectors results in a significant improvement in the secondary flow characteristics, as it separates the inlet flow before it reaches the first 90° bend of the inlet. Therefore, the magnitude of the swirl angle at the AIP is overall decreased.
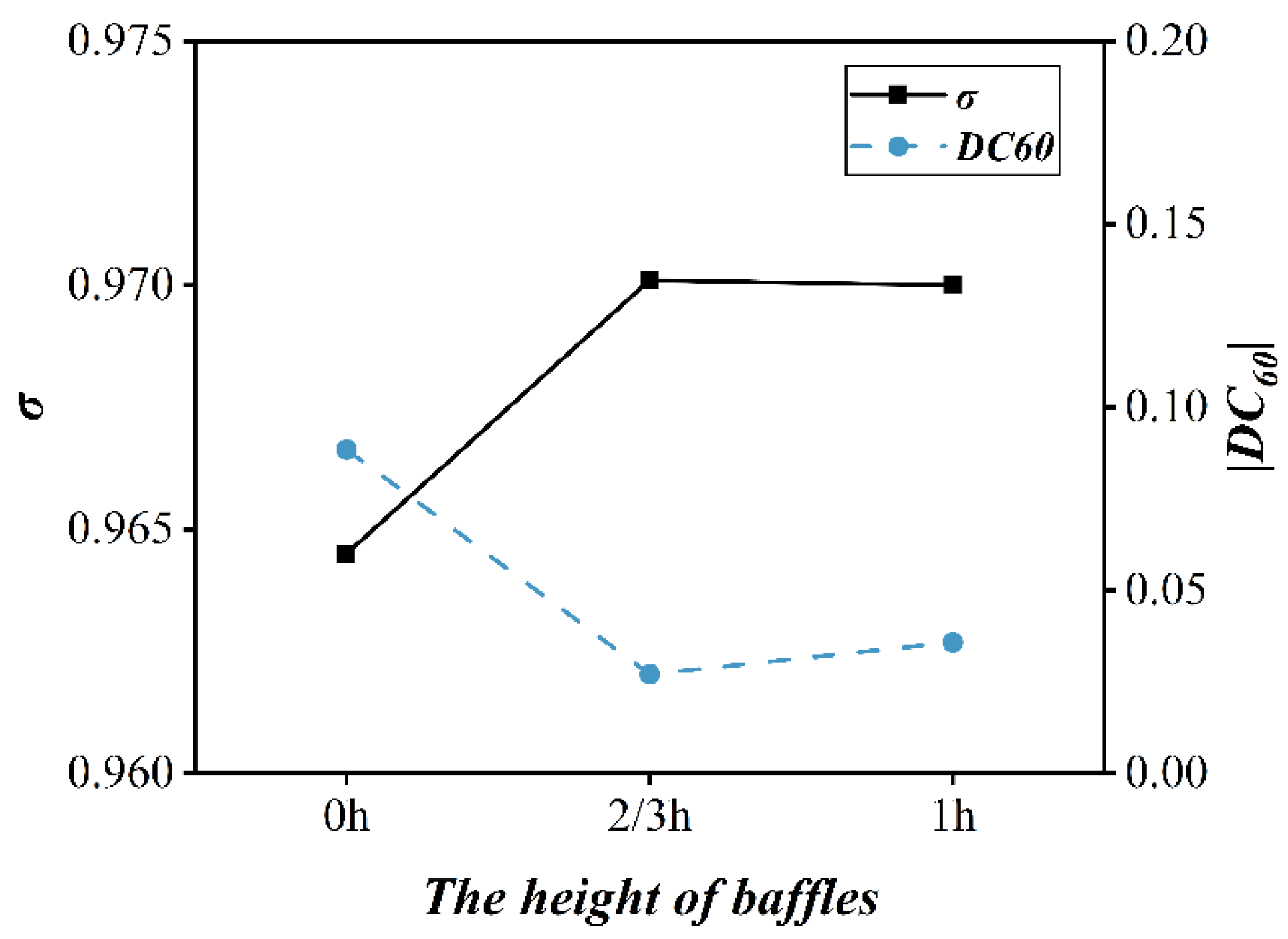
Figure 25 and
Figure 26 show the performance of the inlet with varying heights of the baffle installed at the bottom of the volute under the specified test conditions of
V0 = 90 m/s,
α = 0°, and
β = 8°. It is evident that the incorporation of the baffle significantly enhances the aerodynamic performance of the inlet. A baffle with a height of 2/3 h improves the total pressure recovery by about 0.58% in comparison with the result in the absence of baffle. Further increasing the baffle height to 1 h contrarily worsens the total pressure distortion performance slightly.
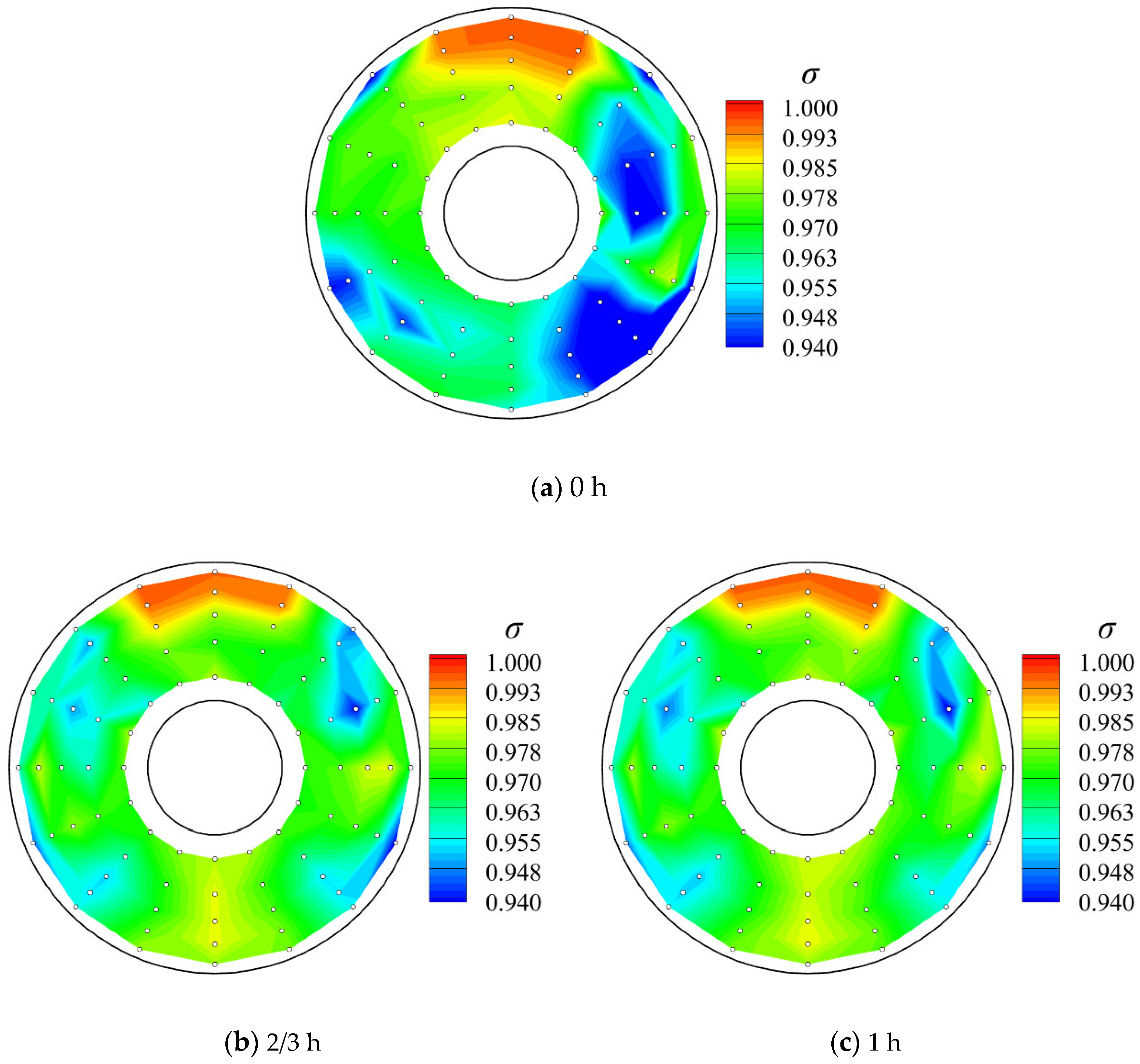
Figure 27 illustrates the vortex characteristics of the inlets with baffles of varying heights under conditions identical to those in
Figure 25. It is evident from
Figure 27 that the utilization of a baffle with a height of 2/3 h had the most significant effect in mitigating the intensity of the swirl flow inside the volute.
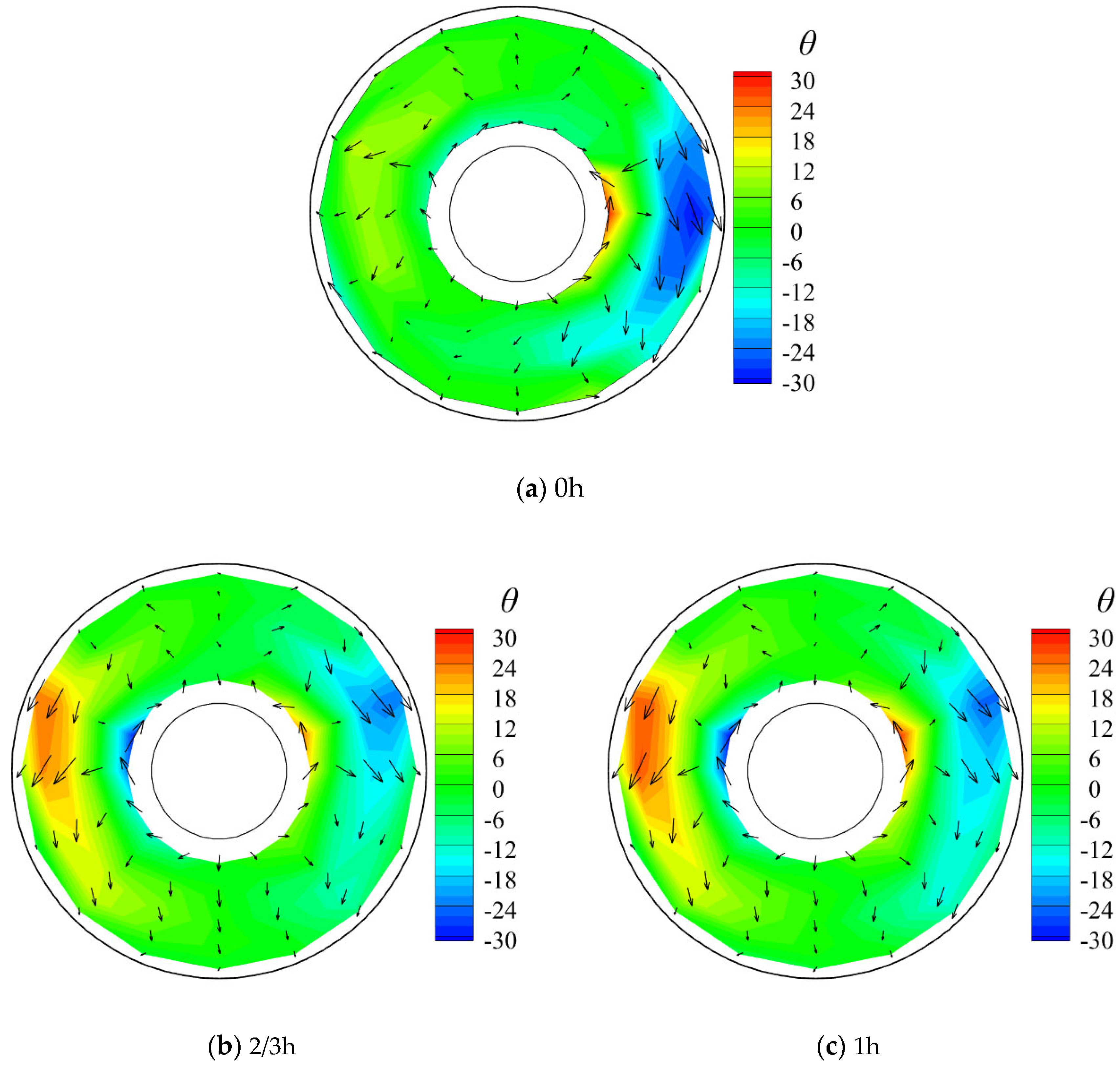
Figure 28 also demonstrates that the baffle with a height of 2/3 h produced the least swirl angle intensity at the AIP, with a significant reduction in magnitude and area. The absence of the baffle results in the formation of a strong swirl flow in the volute. The presence of the sideslip angle directly leads to the concentration of the large swirl angle at the optimal position of the AIP, resulting in a strong inhomogeneity in the distribution of the swirl flow. Conversely, the addition of the baffle causes the blockage of the swirling flow at the bottom, thereby improving both the strength and uniformity of the distribution. In comparison to the results for the baffle-absent volute shown in
Figure 27, the baffle with a height of 2/3 h reduces the maximum swirl angle by 4.36%. The above results collectively indicate that the addition of a baffle with height of 2/3 h at the bottom of the volute represents the optimal strategy for enhancing the inlet aerodynamic performance and swirl flow characteristics.
5. Conclusions
This study experimentally investigated the aerodynamic performance and internal swirl flow characteristics of an unmanned aircraft inlet with double 90° bends and integrated with an aircraft fuselage and a volute. It primarily focused on the performance of the total pressure recovery coefficient σ and total pressure distortion index DC60, as well as the swirl characteristics of the swirl angle and swirl distortion index. The influences of various factors, including angle of attack, sideslip angle, AIP Mach number, freestream speed, deflectors mounted ahead of the first 90° bend of the inlet, and the baffle mounted at the bottom of the volute, were carefully investigated. The following conclusions can be drawn from the above results.
(1) The change in the wall static pressure with angle of attack primarily occurs in the nose section of the fuselage and on the lower surface of the inlet/volute. The total pressure recovery coefficient is less affected by angle of attack, while the total pressure distortion exhibits an initial decrease and a subsequent increase with the increase in angle of attack. Additionally, the maximal swirl angle and the swirl distortion index have a tendency to rise with the increase in angle of attack.
(2) An increase in the sideslip angle to 16° results in a significant negative impact on the overall performance of the inlet, with a notable decline in the wall static pressure on the fuselage but a minimal change in the static pressure on the inlet and volute. Furthermore, the increase in sideslip angle exerts a more pronounced influence on the total pressure recovery than the total pressure distortion, as well as increases in both the maximum swirl angle and the swirl distortion index.
(3) As the AIP Mach number increases, the aerodynamic performance of the inlet decreases, while the swirl flow characteristics improve slightly. As the AIP Mach number exceeds 0.62, distinct regions of low total pressure appear at 45°, 135°, 225°, and 315° azimuths near the outer wall of the inlet. The maximum swirl angle and the swirl distortion index at the AIP decrease slightly with the increasing AIP Mach number, but this improvement effect becomes weaker beyond a Mach number of 0.62.
(4) As the freestream speed increases, the total pressure recovery performance is slightly improved due to the enhanced ram effect of the inlet airflow, and simultaneously, the total pressure distortion remains at a low level. Further, the swirl distortion index at the AIP is improved, with a maximum reduction of 7.69% as the freestream speed is increased from 50 m/s to 90 m/s.
(5) Although the total pressure recovery coefficient exhibits a slight decline with the addition of the deflectors, the total pressure distortion DC60 undergoes a notable improvement in the tested mass flow rate range, with the maximum reduction of 34.38% comparing with that without deflectors. In addition, the total pressure distribution becomes markedly symmetrical with the addition of the deflector. The addition of the baffle at the bottom of the volute also significantly enhances the aerodynamic performance and swirl flow characteristics of the inlet. A baffle with height of 2/3 h installed at the bottom of the volute represents the optimal strategy for enhancing the inlet aerodynamic performance and swirl flow characteristics.
Author Contributions
Conceptualization, X.H. and D.L.; Methodology, J.R., H.T. and X.H.; Formal analysis, Z.W. (Zhenlong Wu); Investigation, J.R., H.T. and D.L.; Data curation, J.R. and Z.W. (Ziyun Wang); Writing—original draft, J.R.; Writing—review and editing, Z.W. (Zhenlong Wu); Visualization, Z.W. (Ziyun Wang); Supervision, Z.W. (Zhenlong Wu); Project administration, Z.W. (Zhenlong Wu) and H.T.; Funding acquisition, H.T. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National High-Level Talent Project (YQR23019) and the Postdoctoral Fellowship Program of CPSF (GZB20230970).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Dongpo Li and Yi Zhou was employed by the company AVIC (Chengdu) Unmanned Aerial Vehicle System Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lei, L.; Fu, C.; Kun, L.; Huachen, P.; Huawei, Q.; Fang, W.; Maoying, Z.; Xiaoqing, T. Blowing–suction control in S-shaped inlet and its impact on fan-stage performance. AIAA J. 2019, 57, 3954–3968. [Google Scholar] [CrossRef]
- Cheng, D.-S.; Tan, H.-J.; Sun, S.; Tong, Y. Computational study of a high-performance submerged inlet with bleeding vortex. J. Aircr. 2012, 49, 852–860. [Google Scholar] [CrossRef]
- Li-fang, Z.; Jian-xin, H.; Ding-yi, P. Multi-Points and Multi-Objective Optimization Design of Subsonic UAV S-Shaped Inlet. J. Propuls. Technol. 2021, 42, 495–504. [Google Scholar]
- Vyas, J.; Braun, V.; Andreoli, G.J. Paniagua and Technology, Short engine intakes: Design and trade-off aerodynamic recommendations. Aerosp. Sci. Technol. 2023, 134, 108164. [Google Scholar] [CrossRef]
- Berens, T.M.; Delot, A.-L.; Chevalier, M.; van Muijden, J. Numerical simulations for high offset intake diffuser flows. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–14 January 2014. [Google Scholar]
- Chiereghin, N.; MacManus, D.G.; Savill, M.; Dupuis, R. Dynamic distortion simulations for curved aeronautical intakes. In Proceedings of the Applied Aerodynamics Conference 2014 (RAeS): Advanced Aero Concepts, Design and Operations, Bristol, UK, 22–24 July 2014; pp. 384–402, ISBN 9781510802698. [Google Scholar]
- Rein, M.; Koch, S.; Ruetten, M. Experimental investigations on the influence of ingesting boundary layers into a diverterless S-duct intake. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–14 January 2014. [Google Scholar]
- Zhulin, X.U.; Rongzhao, G.A.; Xingya, D.A. Assessment and measurement of total pressure distortion based on five-hole-probe for S-shaped inlet. J. Exp. Fluid Mech. 2018, 32, 78–86. [Google Scholar]
- Rein, M.; Koch, S. Experimental study of boundary-layer ingestion into a diverterless S-duct intake. AIAA J. 2015, 53, 3487–3492. [Google Scholar]
- Wang, K.; Liu, L.; Huang, H.X.; Tan, H.J.; Tang, X.B.; Zheng, G.J. Technology, Behavior of Flow Distortion within a Boundary Layer Ingestion Inlet. Aerosp. Sci. Technol. 2024, 146, 108947. [Google Scholar]
- Burrows, T.J.; Gong, Z.; Vukasinovic, B.; Glezer, A. Investigation of trapped vorticity concentrations effected by hybrid actuation in an offset diffuser. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Burrows, T.J.; Vukasinovic, B.; Glezer, A. Flow dynamics effected by active flow control in an offset diffuser. In Proceedings of the 2018 Flow Control Conference, Toronto, ON, Canada, 15–19 October 2018. [Google Scholar]
- Burrows, T.J.; Vukasinovic, B.; Glezer, A.; Lakebrink, M.T.; Mani, M. Experimental and numerical investigation of active flow control of a serpentine diffuser. AIAA J. 2021, 59, 607–620. [Google Scholar]
- Gil-Prieto, D.; MacManus, D.G.; Zachos, P.K.; Tanguy, G.; Menzies, K.R. Convoluted intake distortion measurements using stereo particle image velocimetry. AIAA J. 2017, 55, 1878–1892. [Google Scholar]
- Rütten, M.; Koch, S.; Kuckenburg, S.; Rein, M. Investigation of the flow within partially submerged scoop type air intakes. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Tanguy, G.; MacManus, D.G.; Zachos, P.; Gil-Prieto, D.; Garnier, E. Passive flow control study in an S-duct using stereo particle image velocimetry. AIAA J. 2017, 55, 1862–1877. [Google Scholar]
- Zachos, P.K.; MacManus, D.G.; Prieto, D.G.; Chiereghin, N. Flow distortion measurements in convoluted aeroengine intakes. AiAA J. 2016, 54, 2819–2832. [Google Scholar]
- Sun, S.; Tan, H.-J.; Wang, C.-X. Submerged inlet performance enhancement using a unique bump-shaped vortex generator. J. Propuls. Power 2016, 32, 1275–1280. [Google Scholar]
- Sun, S.; Tan, H.-J. Flow characteristics of an ultracompact serpentine inlet with an internal bump. J. Aerosp. Eng. 2018, 31, 04017089. [Google Scholar]
- Wang, K.; Huang, H.-X.; Liu, L.; Zheng, G.-J.; Lin, Z.-K.; Sun, S.; Tan, H.-J. A new distortion evaluation method based on geometric association for arbitrary cross-sectional shape of inlet. Aerosp. Sci. Technol. 2022, 128, 107728. [Google Scholar]
- Xu, Z.; Da, X.; Fan, Z. Assessment of swirl distortion of serpentine inlet based on five-hole probe. Acta Aeronaut Astronaut. Sin. 2017, 38, 48–57. [Google Scholar]
- Hariharan, C.; Govardhan, M. Improving performance of an industrial centrifugal blower with parallel wall volutes. Appl. Therm. Eng. 2016, 109, 53–64. [Google Scholar]
- Hariharan, C.; Govardhan, M. Aerodynamic performance and flow characteristics of an industrial centrifugal blower volute with varied cross-sectional shapes/area ratios. Int. J. Turbo Jet-Engines 2019, 36, 89–106. [Google Scholar]
- Yang, C.; Wang, Y.; Tong, D.; Yang, C.; Li, Y. Stall inception induced by the volute tongue at centrifugal compressor inlet Proceedings of the Institution of Mechanical Engineers, Part G. J. Aerosp. Eng. 2017, 231, 931–940. [Google Scholar]
- Zhang, H.; Yang, C.; Yang, C.; Zhang, H.; Wang, L.; Chen, J. Inlet bent torsional pipe effect on the performance and stability of a centrifugal compressor with volute. Aerosp. Sci. Technol. 2019, 93, 105322. [Google Scholar] [CrossRef]
- Vagnoli, S.; Verstraete, T. URANS analysis of the effect of realistic inlet distortions on the stall inception of a centrifugal compressor. Comput. Fluids 2015, 116, 192–204. [Google Scholar]
- Zhang, M.; Zheng, X. Criteria for the matching of inlet and outlet distortions in centrifugal compressors. Appl. Therm. Eng. 2018, 131, 933–946. [Google Scholar] [CrossRef]
Figure 1.
Schematic diagram of the UAV test model inlet installed in the wind tunnel. (a) Test model installed in the wind tunnel; (b) Schematic diagram of inlet and volute; (c) Schematic diagram of deflectors and baffles of different heights.
Figure 1.
Schematic diagram of the UAV test model inlet installed in the wind tunnel. (a) Test model installed in the wind tunnel; (b) Schematic diagram of inlet and volute; (c) Schematic diagram of deflectors and baffles of different heights.
Figure 2.
Illustration of the arrangement of pressure measurement probes on the test model: (a) static pressure tap distribution, (b) conventional total pressure rakes, (c) rotary total pressure rakes.
Figure 2.
Illustration of the arrangement of pressure measurement probes on the test model: (a) static pressure tap distribution, (b) conventional total pressure rakes, (c) rotary total pressure rakes.
Figure 3.
Schematic diagram of the velocity vector for calculation of swirl angle.
Figure 3.
Schematic diagram of the velocity vector for calculation of swirl angle.
Figure 4.
Contours of total pressure recovery coefficients for repetitive trips.
Figure 4.
Contours of total pressure recovery coefficients for repetitive trips.
Figure 5.
Contours of swirl angle and velocity vector (arrows indicate the direction and size of the velocity) for repetitive trips.
Figure 5.
Contours of swirl angle and velocity vector (arrows indicate the direction and size of the velocity) for repetitive trips.
Figure 6.
Pressure coefficient distribution along Line 1 at different angles of attack.
Figure 6.
Pressure coefficient distribution along Line 1 at different angles of attack.
Figure 7.
Pressure coefficient distribution along Line 2 to Line 5 at different angles of attack.
Figure 7.
Pressure coefficient distribution along Line 2 to Line 5 at different angles of attack.
Figure 8.
Aerodynamic performance of the inlet at different angles of attack.
Figure 8.
Aerodynamic performance of the inlet at different angles of attack.
Figure 9.
Swirl flow characteristics of the inlet at different angles of attack.
Figure 9.
Swirl flow characteristics of the inlet at different angles of attack.
Figure 10.
Pressure coefficient distribution along Line 1 at different sideslip angles.
Figure 10.
Pressure coefficient distribution along Line 1 at different sideslip angles.
Figure 11.
Pressure coefficient distribution along Line 2 to Line 5 at different sideslip angles.
Figure 11.
Pressure coefficient distribution along Line 2 to Line 5 at different sideslip angles.
Figure 12.
Aerodynamic performance of the inlet at different sideslip angles.
Figure 12.
Aerodynamic performance of the inlet at different sideslip angles.
Figure 13.
Contours of total pressure recovery coefficients at the AIP at different sideslip angles.
Figure 13.
Contours of total pressure recovery coefficients at the AIP at different sideslip angles.
Figure 14.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP at different sideslip angles.
Figure 14.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP at different sideslip angles.
Figure 15.
Swirl flow characteristics of the inlet at different sideslip angles.
Figure 15.
Swirl flow characteristics of the inlet at different sideslip angles.
Figure 16.
Aerodynamic performance of the inlet at different AIP Mach numbers.
Figure 16.
Aerodynamic performance of the inlet at different AIP Mach numbers.
Figure 17.
Contours of total pressure recovery coefficients at the AIP at different AIP Mach numbers.
Figure 17.
Contours of total pressure recovery coefficients at the AIP at different AIP Mach numbers.
Figure 18.
Swirl flow characteristics of the inlet at different AIP Mach numbers.
Figure 18.
Swirl flow characteristics of the inlet at different AIP Mach numbers.
Figure 19.
Aerodynamic performance of the inlet at different AIP mass flow rates.
Figure 19.
Aerodynamic performance of the inlet at different AIP mass flow rates.
Figure 20.
Swirl flow characteristics of the inlet at different AIP mass flow rates.
Figure 20.
Swirl flow characteristics of the inlet at different AIP mass flow rates.
Figure 21.
Contours of total pressure recovery coefficients at the AIP at different freestream speeds.
Figure 21.
Contours of total pressure recovery coefficients at the AIP at different freestream speeds.
Figure 22.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP at different freestream speeds.
Figure 22.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP at different freestream speeds.
Figure 23.
Contours of total pressure recovery coefficients at the AIP of the inlet with and without the deflectors at a nominal mass flow rate of 4.4 kg/s.
Figure 23.
Contours of total pressure recovery coefficients at the AIP of the inlet with and without the deflectors at a nominal mass flow rate of 4.4 kg/s.
Figure 24.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP of the inlet with and without the deflectors at a nominal mass flow rate of 4.4 kg/s.
Figure 24.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP of the inlet with and without the deflectors at a nominal mass flow rate of 4.4 kg/s.
Figure 25.
Aerodynamic performance of the inlet with different baffles at different sideslip angles.
Figure 25.
Aerodynamic performance of the inlet with different baffles at different sideslip angles.
Figure 26.
Contours of total pressure recovery coefficients at the AIP of the inlet with different baffles at a nominal mass flow rate of 5.2 kg/s.
Figure 26.
Contours of total pressure recovery coefficients at the AIP of the inlet with different baffles at a nominal mass flow rate of 5.2 kg/s.
Figure 27.
Swirl flow characteristics of the inlet with different baffles at different sideslip angles.
Figure 27.
Swirl flow characteristics of the inlet with different baffles at different sideslip angles.
Figure 28.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP of the inlet with different baffles at a nominal mass flow rate of 5.2 kg/s.
Figure 28.
Contours of swirl angle and velocity vectors (arrows indicate the direction and size of the velocity) at the AIP of the inlet with different baffles at a nominal mass flow rate of 5.2 kg/s.
Table 1.
The geometric parameters of the test model inlet.
Table 1.
The geometric parameters of the test model inlet.
| Model Parameter | Numerical Value |
|---|
| D | 87.82 mm |
| d | 0.33D |
| L | 5D |
| h | 1.32D |
| H | 2.92D |
| A1 | (0.96D)2 |
| A2 | (1.5D)2 |
| A3 | (0.84D)2 |
Table 2.
Comparison of repeatability test data.
Table 2.
Comparison of repeatability test data.
| Run | V0 (m/s) | α (°) | β (°) | Mass (kg/s) | σ | | DC60 | | | | (°) | |
|---|
| 1 | 90 | 0 | 12 | 3.45 | 0.9856 | 0.0001 | −0.0460 | 0.00061 | 22.50% | 0.722% | 31.75 | 0.14572 |
| 2 | 3.44 | 0.9857 | −0.0461 | 21.25% | 32.03 |
| 3 | 3.44 | 0.9855 | −0.0450 | 21.25% | 31.82 |
Table 3.
Comparison of the inlet performance with and without deflectors.
Table 3.
Comparison of the inlet performance with and without deflectors.
| | Mass (kg/s) | σ | DC60 | | (°) |
|---|
| With deflectors | 3.461 | 0.9863 | −0.0307 | 22.50% | 30.17 |
| 4.387 | 0.9782 | −0.0294 | 21.25% | 29.74 |
| 5.213 | 0.9701 | −0.0271 | 18.75% | 29.16 |
| Without deflectors | 3.431 | 0.9868 | −0.0437 | 26.25% | 28.67 |
| 4.347 | 0.9797 | −0.0367 | 25.00% | 29.39 |
| 5.155 | 0.9718 | −0.0413 | 26.25% | 27.87 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).