Abstract
System architecture design is crucial for forward design in aerostat system engineering, yet a comprehensive research framework has been lacking. This paper presents a new method for stratospheric airship architecture preliminary design and optimization trade-off, grounded in Model-Based Systems Engineering (MBSE) theory. Firstly, a requirement analysis for a stratospheric airship is conducted using SysML, leading to the analysis and acquisition of the airship’s mission architecture design. Additionally, a multidisciplinary coupling simulation platform is developed with MATLAB, and the architecture preliminary design’s Pareto front is derived using the NSGA-II algorithm. Finally, based on the Pareto optimization set, the TOPSIS algorithm is applied to derive the optimal architecture preliminary design scheme for the airship. The optimization results validate the accuracy of the architecture preliminary design obtained from the requirement analysis, the reliability of the multidisciplinary coupling simulation platform, and the feasibility of the optimization algorithms. This comprehensive study spans the requirement analysis to the optimal architecture scheme, providing theoretical reference and design guidance for the forward design of airship systems engineering.
1. Introduction
The airship is a lighter-than-air aircraft, primarily consisting of the hull system, energy system, propulsion system, flight control system, safety control system, deployment and recovery system, and payload system. It offers advantages such as high flight altitude, strong survivability, and wide-range communication [1]. Interest in studying stratospheric airships has grown in recent years due to their potential for scientific and civilian applications in communications, scientific observation, and scientific experiments [2,3,4].
Airship is a complex engineering task that necessitates the use of systems engineering methods. Compared with traditional document-based systems engineering methods, Model-Based Systems Engineering (MBSE) integrates all information into an interconnected set of models, allowing the system to be described and represented from various perspectives. MBSE has already made significant progress in areas such as space exploration [5], spacecraft fault management [6], commercial aircraft design [7], and tropospheric airships [8].
The design, optimization, and trade-off of system architecture involve a series of decision-making processes [9]. The key task in architecture design is transforming mission requirements and objectives into a coherent system architecture. This process requires carefully planned decision points to confirm the system architecture, ensuring decisions are made cautiously and rationally to maximize system value.
The design of an airship is a complex system of engineering involving many disciplines. At present, there is a lack of research systems for stratospheric airships using MBSE. Therefore, the architecture preliminary design and tradeoff optimization of stratospheric airship architecture using MBSE in this paper is of engineering significance for the relevant research of airship system engineering design.
This paper employs a multi-objective optimization method based on NSGA-II. It also utilizes a decision-solving and trade-off method using TOPSIS (Technique for Order Preference by Similarity to the Ideal Solution). Together, these methods aim to find the optimal architecture solution for complex systems characterized by large scale, numerous alternatives, multiple indicators, and strong constraints. This approach aims to enhance the efficiency and effectiveness of decision-making in complex system architecture design.
As shown in Figure 1, the basic forward design process for a stratospheric airship consists of three components: requirements analysis, architecture design, and application verification. The main tasks are distributed as follows:
1. Model Construction Based on SysML: Utilize SysML to formally standardize and model the system architecture, completing requirements analysis and architecture design.
2. Multi-Objective Optimization and Trade-Off:
a. After describing the system architecture, use MATLAB to model key disciplines within the system architecture.
b. Employ NSGA-II to compute the Pareto front solution set for architecture decisions that meet the established system design goals and constraints, followed by a brief analysis of the Pareto front and rank correlation.
c. Explore the optimal solution for target weights using the TOPSIS to determine the final architecture scheme.
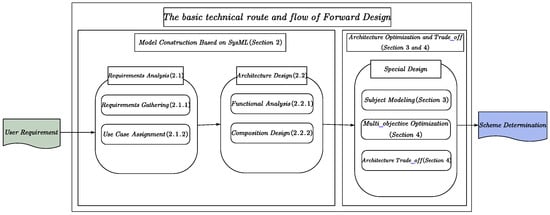
Figure 1.
The basic technical route and flow of forward design.
2. SysML-Based Architecture Preliminary Design for Stratospheric Airship
The forward design of a stratospheric airship begins with user requirements and adheres to the principles of systems engineering, including holism, hierarchy, and development stages. This approach yields architectural solutions that meet efficiency requirements and spatial environment constraints [10]. The SysML model is built using MWorks.Sysbuilder 2023. This section introduces the MBSE methodology in the forward design of stratospheric airships:
Step 1: Capture system requirements and their relationships—Section 2.1.1.
Step 2: Develop use-case diagrams to outline the functionalities needed to meet these requirements—Section 2.1.2.
Step 3: Use activity and sequence diagrams to map out the behaviors and interactions needed—Section 2.2.1.
Step 4: Create BDDs to define the high-level structure of the system, ensuring it satisfies the requirements; develop IBDs to show the internal composition and interactions of the system’s components—Section 2.2.2.
2.1. Requirements Analysis
2.1.1. Requirements Gathering
The basic design requirements of this study include fulfilling the fundamental functions of the stratospheric airship, such as scientific experiments, communication relays, and high-altitude aerial photography. Additionally, the design must feature long endurance, high altitude, etc.
Based on the design requirements and demand segmentation theory, and combined with previous design experience and user needs, a stakeholder requirement list is established. This list is divided into functional and non-functional requirements. Functional requirements refer to the specific functions the system must achieve, supporting specific operations and processing certain data, which are the primary objectives of the system design. Non-functional requirements refer to attributes such as security, reliability, and usability, which are important for the system’s overall performance. The requirement list is shown in Table 1.

Table 1.
List of requirements.
2.1.2. Use-Case Assignment
Based on the requirements and metrics obtained during the requirements collection phase, the stakeholders’ needs are further refined through use cases and the system’s functional scenarios are analyzed. When analyzing the functional profile of the stratospheric airship, the use-case scenarios are primarily decomposed according to the operational logic sequence. This includes five main scenarios: pre-launch preparation, launch and entry into the designated airspace, execution of the flight mission, mission completion and return, and airship recovery. The involved use-case participants, and their basic functions are shown in Table 2.

Table 2.
Use-Case Assignment.
Based on the MBSE methodology, Use-Case Diagrams (UCD) are employed to describe the functional scenarios of the airship. The purpose of the UCD is to define the interaction between external actors and the system to fulfill a requirement, which will help in identifying system functionalities and how they fulfill user needs [10]. A top-level use-case view is established based on the basic functional roles of the task participants, as shown in Figure 2. The use-case diagram captures the stakeholders’ requirements for the stratospheric airship by depicting the interactions between system use cases and use-case participants (task participants).
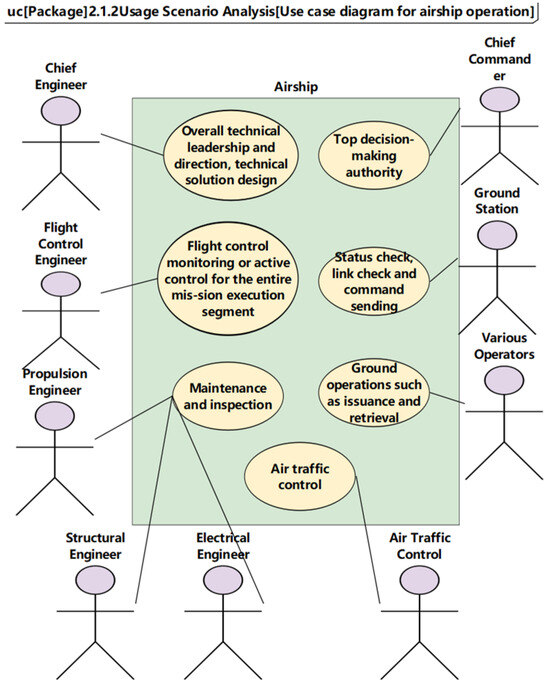
Figure 2.
Stratospheric airship basic use cases and functional division.
Here are some explanations of Figure 2. In Figure 2, the “Stickmen” represent mission participants. Although the image of the “Stick man” is human, it can represent not only a person but a device or an organization. Furthermore, some ellipses with specific missions are the duties of the “Stickmen”. The duties may be the tasks of engineers or the functions of organizations.
2.2. Architecture Preliminary Design
2.2.1. Functional Analysis
For the floating platform use case, an Activity Diagram (ACT) is utilized for scenario analysis to construct the functional activities of the system. Before the stratospheric airship launch, the environmental monitoring department first needs to conduct a meteorological consultation to safeguard the meteorological conditions of the mission. Then, the folded hull will be moved to the launch site and the pods will be mounted. Next, the capsule will be inflated. After reaching the predefined inflation amount, the anchoring cables will be cut off one after another, and the airship will lift off. The airship will ascend due to buoyancy and, upon reaching the target altitude, will switch to float mode to conduct scientific tasks. After completing the tasks, the airship will fly to the predetermined landing airspace, actively trigger the capsule cutting, and land within the predetermined range. Finally, the airship will be recovered and a follow-up analysis will be conducted. The operation flow is shown in Table 3.

Table 3.
Mission node breakdown.
According to the overall stage division of the stratospheric airship mission, the ACT is established as shown in Figure 3. The overall mission is mainly divided into 10 stages: “Store in the hanger”, “Transfer to issuance site”, “Mount payload”, “Inflate”, “Launch”, “Take off”, “Climb”, “Mission fly”, “Return and Land”, and “Invent and Recycle”. Additionally, “Emergency landing” is considered a special mission phase. In short, the purpose of the ACT is to capture the flow of activities and control the flow between them, so an ACT is similar to a flow chart, but in some ways is more complex.
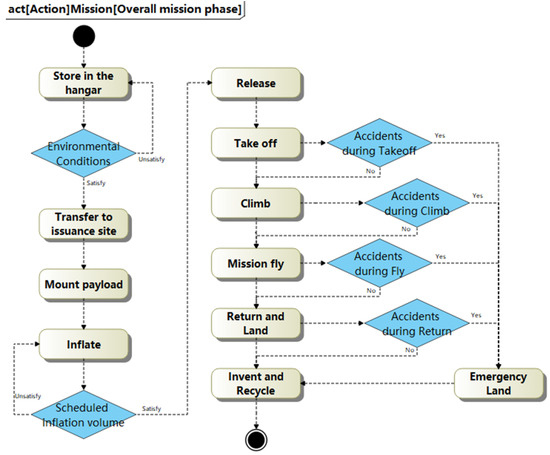
Figure 3.
Activity diagram for overall mission phase activity diagram.
After the stratospheric airship climbs to altitude, it will begin to carry out the mission. The “Mission Fly” activity diagram is shown in Figure 4. Under normal conditions, the airship will perform various maneuvers according to the instructions obtained from the ground station. The flight control subsystem mainly controls the buoyancy, attitude, speed, and flight direction of an airship. The actuator of airship buoyancy control is helium airbag and ballast (for balance weight); the actuator of attitude control is the tail fin of the airship; the actuator of speed control is the main propulsion unit; the actuator of flight direction control is the yaw propulsion unit.
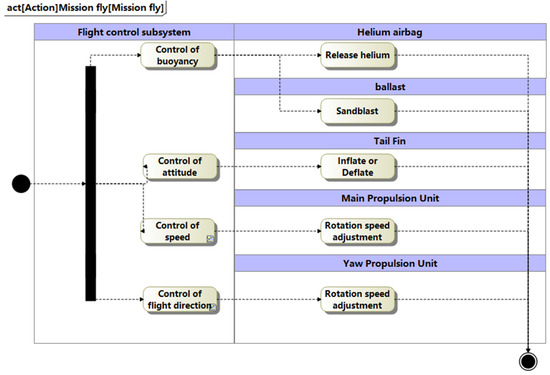
Figure 4.
Activity diagram for Mission Fly.
The different flight statuses of airships rely on the control of the tail fin, airbags, propulsion units, and other equipment to perform maneuvers such as area stopping, climbing and descending altitude, and trajectory flight. The SQD includes the following elements: (a) Lifelines: Represent objects or components in the system; (b) Messages: Represent the interaction between objects or components; (c) Activation: Displays the actions performed by an object or component during a certain period; (d) Interaction Frame: Encapsulate a set of interactions, often to represent the if–else structure, parallel structure, or loop structure [10]. Figure 5 illustrates the SQD of an operational scenario where a blimp faces different conditions during a mission.

Figure 5.
Sequence diagram for Mission Fly.
It can be seen from Figure 5 that data interaction, fault decision, and mission fly are in parallel. Under normal conditions, the airship will maintain data interaction with the ground station. The airship switches between autonomous control mode and ground station active control mode according to the command of the ground station. In the event of a failure of the airship, emergency procedures are immediately implemented and emergency operations are carried out according to the state of the airship and the instructions of the ground station.
2.2.2. Composition Design
For the system-level design of the stratospheric airship, the overall composition of the system is defined by the Block Definition Diagram (BDD) [10]. The purpose of the BDD is to define the system’s structure in terms of its blocks and relationships. Based on the descriptions in the previous sections, combined with the design experience, the system architecture can be initially divided as shown in Figure 6. The stratospheric airship consists of eight subsystems: hull subsystem, structure subsystem, energy subsystem, propulsion subsystem, avionics subsystem, flight control subsystem, measurement subsystem, and security subsystem. All components of these subsystems need to be represented in the BDD. It is worth noting that the BDD establishes the high-level structure of the system, so it does not show the flow of information between the subsystems.
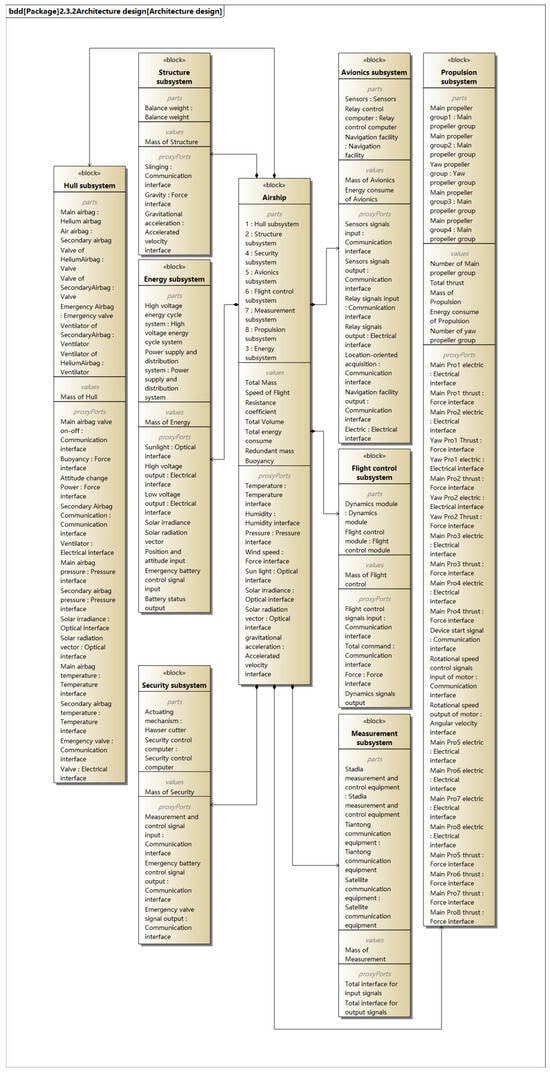
Figure 6.
Airship architecture design.
In conjunction with the airship architecture design, the internal structure of the stratospheric airship is defined through the Internal Block Diagram (IBD) [10], as shown in Figure 7. The IBD’s purpose is to detail the internal structure of a block, showing its parts, ports, and connections. Furthermore, the IBD describes the transfer of information flow among the subsystems. It added details not shown in the BDD. Combining BDD and IBD makes a more detailed description of the composition of a system.
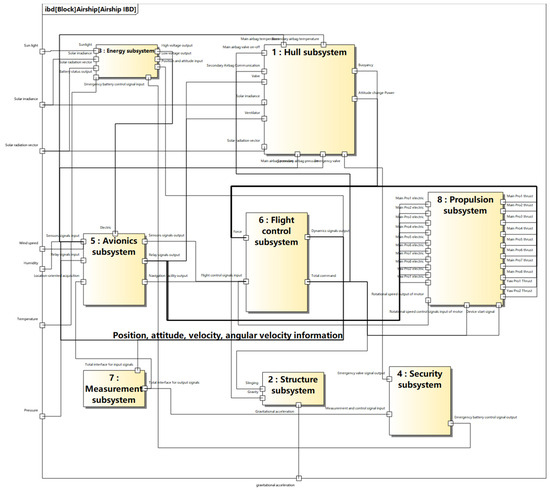
Figure 7.
Description of airship internal relationships.
3. Multidisciplinary Theoretical Modeling
In this section, a multidisciplinary theoretical coupled simulation platform is constructed using MATLAB R2023b in conjunction with the architectural model from Section 2. The platform is designed for the airship design process and contains three equilibria: Buoyancy–Gravity equilibrium, Thrust–Drag equilibrium, and Energy Consumption equilibrium. The relevant discipline models include the environment model, geometry model, structure model, thrust and resistance model, and energy model. Figure 8 illustrates the relationship between the multidisciplinary theoretical models, the architecture design model, and the three balances.
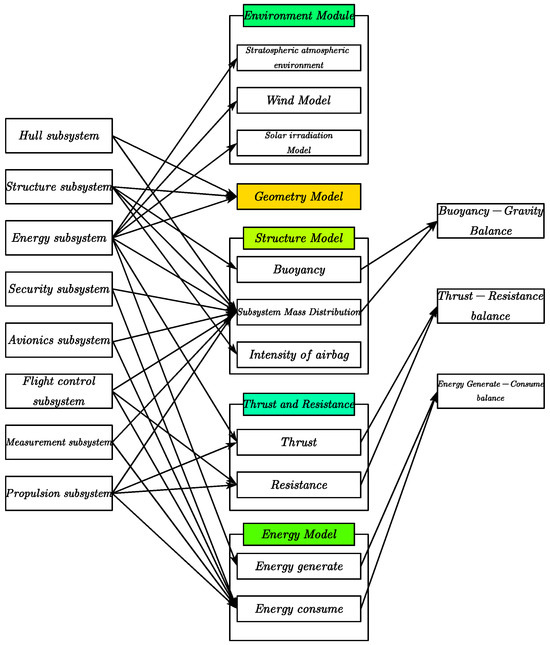
Figure 8.
Relationship of architecture, subject models, and three equilibria.
3.1. Environment Model
3.1.1. Stratospheric Atmospheric Environment
The stratospheric atmospheric environment is modeled using the U.S. Standard Atmosphere 1976 model [11]. The changing patterns of stratospheric atmospheric temperature (), pressure (), and density () with altitude are expressed as follows:
3.1.2. Wind Model
Li [12] developed an equation to describe the relationship between annual mean horizontal wind speed and height, based on the distribution of annual mean wind speed with height in China, as follows:
where ; ; ; ; ; ; ; ; ; ; .
3.1.3. Solar Radiation Model
Several models have been developed in recent years. Carlson proposed a solar model in 1983 [13]. However, it was oversimplified. A comprehensive solar model, which is not that accurate at high altitudes, has been proposed by Ran [14]. The solar radiation on an arbitrary object varies with the day of the year, the time of day, and the location of the airship deployment. In this model, the solar radiation () can be estimated as the sum of the direct irradiation () and the diffuse irradiation () [15]:
The direct irradiation () and the diffuse irradiation () can be expressed as:
where is the solar radiation at the top of the atmosphere, which can be expressed as:
where is the solar constant, whose yearly average value is 1367 W/m2. is the true anomaly, which can be expressed as:
where is the day number in a year. is the number of days in a year, whose default value is 365.
The relative air mass, , and the absolute air mass, , can be expressed as:
where is the solar elevation angle.
The vertical water vapor column () and the aerosol optical depth () can be expressed as:
where is the aerosol optical depth at the measurement site, is the water vapor column at the measurement site, and (km) is the height above the measurement site.
3.2. Geometry Model
There are some descriptions of the curve of the airship’s envelope, such as GNVR [16], GARG [17], Wang [18], etc. In this article, the curve of stratospheric airship envelopes proposed by Landweber and Gertler [19] as follows:
where , , , and can be expressed as:
where
where
where is the distance of the maximum diameter from the nose, is the length, is the maximum diameter, is the radius of curvature at the nose, is the radius of curvature at the tail, and is the volume. The schematic diagram of the shape parameters of the airship is as follows:
3.3. Structure Model
3.3.1. Buoyancy
Buoyancy of the airship can be expressed as:
3.3.2. Mass Distribution
The total mass of the airship () can be expressed as:
where is the mass of the structure subsystem, is the mass of the solar array, is the mass of storage batteries, is the mass of the propulsion subsystem, is the mass of other subsystems, and is the mass of the payload.
The mass of the structure subsystem can be expressed as:
The mass of gas can be expressed as:
where and are the molecular mass of helium and air, respectively.
The mass of the airship envelope can be expressed as:
where is the areal density of the envelope, the coefficient is a factor considering the internal compositions of the envelope, and is the surface area of the envelope.
The mass of the tail can be expressed as:
where the coefficient is a factor considering the attachments of the tail.
The mass of the solar array can be expressed as:
where is the surface area of the solar array and is the areal density of the solar array.
The mass of storage batteries can be expressed as:
where is the energy density of the batteries.
The mass of the propulsion subsystem can be expressed as:
where is the power density of the propulsion subsystem.
For stratospheric airship subsystems, the mass of the avionics subsystem, the flight control subsystem, the measurement and control subsystem, and the security control subsystem can be calculated as percent of the mass of the envelope, the tail, the energy subsystem, and the propulsion subsystem. can be expressed as:
3.3.3. Intensity of Airbag
To ensure the safe flight of the stratospheric airship, the von Mises stress of the envelope should be lower than the maximum allowable stress of the envelope’s material [20,21]. Considering an equivalent cylindrical envelope with the same surface area and volume as the actual airship, the longitudinal stress () and the circumferential hoop stress () can be expressed as:
where is the thickness of the envelope and is the total pressure difference value, which can be expressed as:
The bending moment of the envelope can be expressed as:
Von Mises stress can be expressed as:
Because the thickness of the film material is very small compared to the diameter of the envelope, the stresses are considered only in the two-dimensional plane. In addition, the shear stresses in the plane of the material are neglected in this section, so the principal stress and can be replaced by and . The equations are simplified and organized as:
Furthermore, the maximum allowable stress is .
3.4. Thrust and Resistance
3.4.1. Thrust
The thrust unit of a stratospheric airship consists of several main thruster packs and yaw thruster packs. The propeller groups consist of motors, propellers, and connecting mechanisms. The total thrust can be expressed as:
where is the number of propeller groups, is the power of one propeller, and is the efficiency of the propeller.
3.4.2. Resistance
Resistance is the most crucial aspect of any airship. There are some analyses of airship aerodynamics, such as experimental investigation [22,23] and numerical investigation [24,25]. The resistance of airships can be expressed as:
where ρa is the density of the ambient air, v is the speed of the airship, and is the drag coefficient of the airship [26,27]. can be expressed as:
where is the drag coefficient of the naked airship itself; after obtaining the drag coefficient of the naked airship, the total drag coefficient, , of the airship can be obtained according to the empirical coefficient [28]; is the fineness ratio. is the Reynolds number:
where is the dynamic viscosity of ambient air.
3.5. Energy Model
3.5.1. Energy Generation
The layout of the solar array is determined by three variables, which are solar array start position coefficient, , solar array end position coefficient, , and solar array start angle, . and are the start position and end position of the solar array on the airship, respectively. The layout schematic is shown in Figure 9.

Figure 9.
Schematic diagram of the shape parameters of the airship.
The solar array is divided into 100 × 100 cells. Figure 10 shows the analysis for any cell in the airship reference system at any point in time [29].
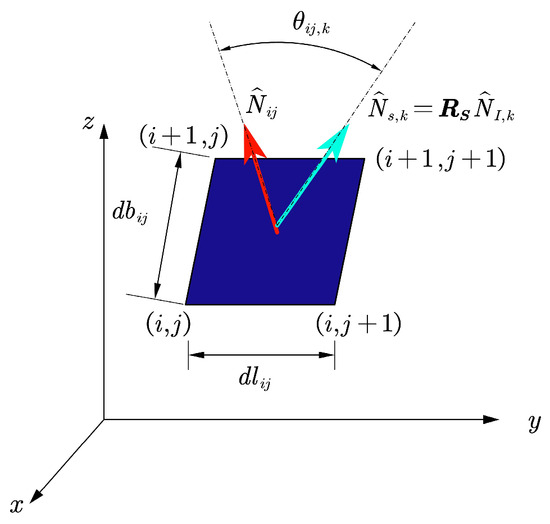
Figure 10.
The analysis for any cell of the solar array.
Assuming that any element is a plane, then the surface unit normal vector of any element is obtained by cross product, and the surface area of any element is obtained by dot product:
where The angle between the Sun and the normal vector on the surface of the unit solar array can be calculated as:
where is the rotation matrix from the Earth coordinate system to the airship coordinate system and is the direction vector of the solar rays at a certain latitude and longitude at a certain time concerning the Earth’s coordinate system. The total energy generated by a solar array on any given day can be calculated as:
where is the solar radiation at a given moment. is the power generation efficiency of the solar array. The length of one day is divided into 120 periods to improve calculation accuracy.
3.5.2. Energy Consumption
The total power required consists mainly of the power of the propulsion subsystem, , the power of the remaining electrical subsystems, , and the payload power, , which can be described as follows:
Equation (36) is organized to obtain the power used by the airship to counter drag consumption:
where is the overall efficiency of the propulsion subsystem:
where is the efficiency of the propeller and is the efficiency of the motor.
Finally, the total energy consumed by the stratospheric airship on any given day is expressed as:
where is the energy conversion efficiency of storage batteries.
3.6. Integration of Models
The models’ integration relationship of a stratospheric airship is organized as shown in Figure 11. The red characters represent the design variables that need to be optimized. The brown boxes represent different subject models. The white boxes indicate the constraints that need to be met.
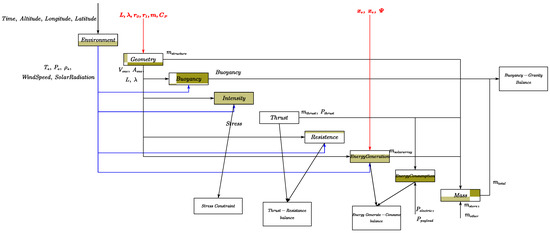
Figure 11.
The integration of different models.
4. Methodology and Problem Description
Two problems need to be addressed in this section. The first challenge involves solving the Pareto frontier from the initial design space, focusing on obtaining multiple alternative schemes that meet the design requirements and constraints. The second challenge is selecting the optimal solution from the Pareto frontier, centering on choosing the best option among the viable schemes. This section proposes an optimization and trade-off method combining the NSGA-II algorithm with the TOPSIS algorithm to achieve the optimal design. Initially, the Pareto frontier is derived from the design space using NSGA-II, followed by selecting the optimal solution from this frontier using TOPSIS. Figure 12 illustrates the process from design space to optimal solution.
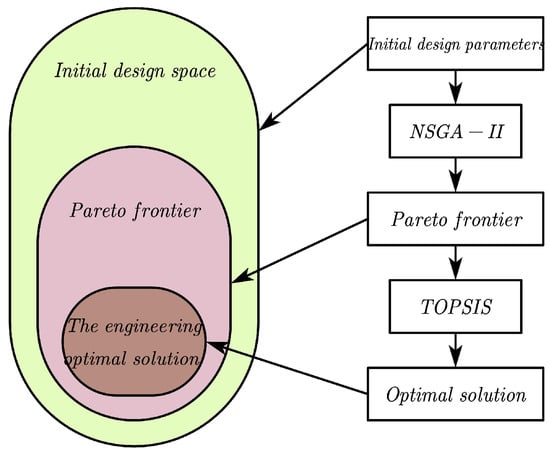
Figure 12.
Total solution process.
4.1. Methodology
4.1.1. Multi-Objective Optimization Algorithm
At present, multidisciplinary optimization of stratospheric airships has made some progress [29,30,31]. In this paper, NSGA-II, a non-dominant sorting genetic algorithm, is adopted for the multidisciplinary optimization of stratospheric airships. NSGA-II is a widely used multi-objective optimization genetic algorithm [32] with significant advantages in many aspects:
- It introduces a fast non-dominated sorting algorithm to reduce computational complexity;
- An elite strategy is included to improve the accuracy of optimization results;
- The crowding degree and the crowding degree comparison operator ensure that individuals in the quasi-Pareto domain uniformly extend across the entire Pareto domain.
However, when the population of NSGA-II is large, the calculations can still be quite time-consuming [33]. In engineering, the requirements for result convergence and accuracy are higher than those for calculation time. Using a server can help mitigate calculation time issues, making the NSGA-II multi-objective optimization algorithm a suitable choice. The flowchart of the NSGA-II algorithm is shown in Figure 13.
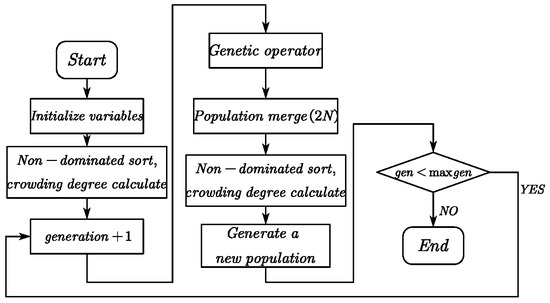
Figure 13.
NAGS-II solution process.
4.1.2. Architectural Tradeoffs Algorithm
The TOPSIS method, widely used in management science and economic decision-making, is a multi-attribute decision-making method designed to evaluate and rank multiple alternative solutions by comparing the distances between each option and the ideal solution. Here are the detailed steps of the TOPSIS algorithm [34]:
The TOPSIS method is a multi-criteria decision analysis method used to rank alternatives based on their closeness to an ideal solution. Here is a step-by-step process for calculating TOPSIS [35]:
Step 1—Construct the Decision Matrix: Assume there are alternatives and criteria. Construct an decision matrix, , where represents the score of the i-th alternative concerning the j-th criterion.
Step 2—Normalize the Decision Matrix: Normalize the decision matrix to eliminate the inconsistencies due to different units of measurement among criteria. After normalization, all data values are scaled to fall within the range [0, 1]. The normalized matrix is calculated as follows:
Step 3—Calculate the Weighted Normalized Decision Matrix: Assign weights to each criterion based on their importance and calculate the weighted normalized matrix :
where is the weight of the -th criterion.
Step 4—Determine the Ideal and Negative-Ideal Solutions: Determine the positive ideal solution, , and the negative ideal solution, :
Step 5—Calculate the Separation Measures: Calculate the separation distance of each alternative from the ideal solution, , and the negative ideal solution, , using the Euclidean distance:
Step 6—Calculate the Relative Closeness to the Ideal Solution: Calculate the relative closeness of each alternative to the ideal solution :
The value ranges between 0 and 1, which is closer to 1, indicating a better alternative.
Step 7—Rank the Alternatives: Rank the alternatives based on their relative closeness, . The higher the value of , the higher the ranking of the alternative.
4.2. Multi-Objective Optimization Description
Multi-objective optimization problems often do not have a unique optimal solution but a set of balanced solutions known as the Pareto front, also called the Pareto efficient frontier or Pareto optimal set. The Pareto front describes a state in which improving one objective cannot be achieved without regressing another. It is widely used in economics, engineering, and operations research to find the best solution set [36]. Figure 14 illustrates the flowchart from the design space to the final solution.
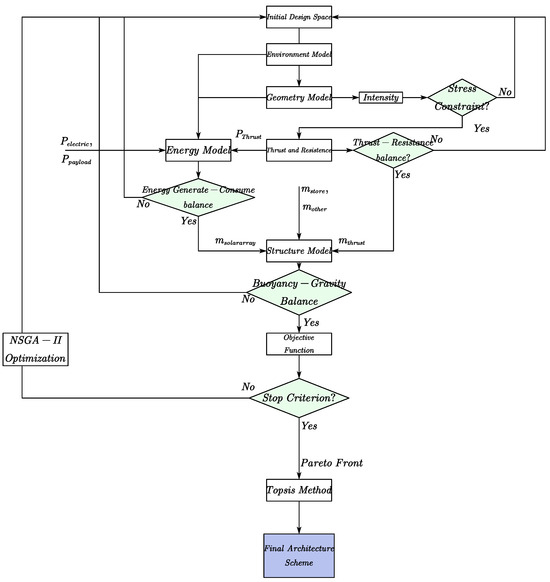
Figure 14.
Flowchart of optimization and trade-off.
A multi-objective optimization problem needs to be solved in this study. According to the design expectation and importance, the objectives are to minimize the drag coefficient, , the total mass, , and the area–volume ratio, of the airship (the smaller the value is, the greater the effective utilization of buoyancy). The corresponding weights of the three objectives are 1/3, and the corresponding initial conditions are , , and , respectively. This multi-objective optimization problem is formulated as follows:
The design variables consist of a series of parameters, and this study involves parameters from multiple disciplines. Nine design variables are considered; the first six design variables are related to the airship envelope curve and size, and the next three are related to the size and layout of the solar array. Table 4 lists a total of nine design variables and their value ranges.

Table 4.
Design variables and their range.
Table 5 illustrates the values of the partially determined parameters. Among the stakeholder requirements is the requirement of “flight duration 360 days”. To meet this requirement, it is necessary to ensure that energy consumption can be balanced, even on days of minimum solar radiation throughout the year. The day with the minimum solar radiation in the whole year is the winter solstice, so the parameter “” is set to 23 December 2024.

Table 5.
Determined parameters and their values.
4.3. Architecture Trade-Off Description
Before performing TOPSIS analysis, appropriate evaluation metrics need to be selected. Index selection needs to satisfy relevance, quantifiability, and comprehensiveness [34]. In the design of the first-stage and second-stage rocket separation system architecture, cost, quality, and reliability are selected as indicators [37]. In this case, the architecture evaluation problem selects the cost of the envelope, , and the reliability of the airship envelope material, , as the evaluation indicators.
can be expressed as:
where is the unit areal cost of the airship envelope. The weight, , is set to 0.5.
For the reliability index, , using the damage accumulation method, the stress applied on the flexible material will cause damage accumulation in the material. As damage accumulates, the reliability of the material decreases, leading to potential failure. The residual strength model and residual stiffness model are proposed in the article [38] for the life prediction of airship envelope materials:
where is the residual strength; is the strength without damage; is the residual stiffness; is the material constant, ; is the cycle number; is the applied load; and is the applied stress. The article mentions that when and , the material will be destroyed completely. Therefore, the formula can be arranged as:
It is not difficult to see that the applied stress and the applied load are inversely related to the material life. Therefore, the von Mises stress, , was used as the calculated variable according to Equation (41). The weight, , was set to 0.5.
In summary, the architecture trade-off problem can be expressed as:
5. Results and Discussion
5.1. Analysis of Multi-Objective Optimization Results
According to the process proposed in Section 4, the multi-objective optimization NSGA-II algorithm is used to obtain the Pareto solutions. The figures are drawn using origin 2018 and AxGlyph Figure 15 shows the Pareto solution trigram of the resistance coefficient, total mass, and area–volume ratio of the stratospheric airship hull contour. Each point represents a design solution, with red points indicating infeasible solutions, black points representing feasible solutions, and green points denoting Pareto solutions. Figure 15 illustrates that feasible solutions are concentrated within a specific solution space.
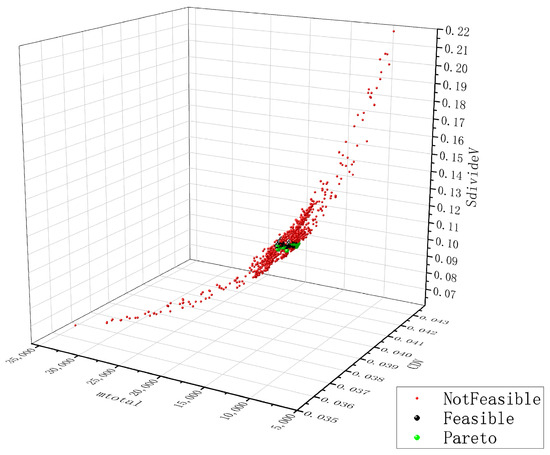
Figure 15.
Ternary graph of Pareto frontier for airship.
The feasible solutions in Figure 15, as well as the points represented by the Pareto solutions, are plotted as binary graphs, as shown in Figure 16. Plot (a) of Figure 16 shows a negative correlation between drag coefficient, , and total mass, ; Plot (b) of Figure 16 shows a positive correlation between the total mass, , and the airship area–volume ratio, ; Plot (c) of Figure 16 depicts a negative correlation between the area–volume ratio, , and drag coefficient, , of the airship. The figure demonstrates that the total mass, drag coefficient, and airship area–volume ratio of the three objectives are mutually restrictive. Therefore, it is necessary to make a trade-off between the total mass, , drag coefficient, , and the airship area–volume ratio, , to ensure the best balance point among multiple objectives.

Figure 16.
Binary graphs of Pareto frontier for airship: (a) is the CDV–mtotal binary graph, (b) is the mtotal–SdV binary graph, (c) is the SdV–CDV binary graph.
5.1.1. Correlation Analysis
Correlation analysis is a statistical method that determines whether or not there is a relationship between variables and the direction of the relationship (positive or negative correlation) [39]. Through correlation analysis, we can identify variables that have a significant influence on the target variables and improve the explanatory power of the model [40]. The Spearman correlation coefficient is a non-parametric method used to measure the correlation between two variables. It is calculated by converting the original values of a variable into ranks (i.e., their positions after ranking by size) to obtain the correlation between the two variables [32]. According to statistical law [33], the correlation coefficient ranges from −1 to 1, where 1 indicates a complete positive correlation, −1 indicates a complete negative correlation, and 0 indicates no correlation. Variables can be classified as highly correlated, strongly correlated, moderately correlated, weakly correlated, or not correlated. The rank correlation coefficient is shown in Figure 16. According to correlation theory, the correlations between design parameters and objectives in feasible solutions and Pareto solutions are analyzed, as shown in Figure 17.
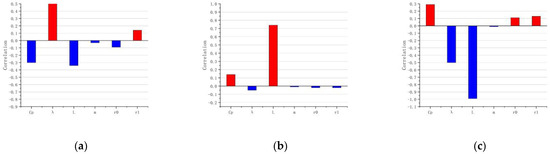
Figure 17.
Analysis of Spearman correlation coefficient: (a) is the area–volume ratio, , correlation coefficient, (b) is the total mass, , correlation coefficient, (c) is the drag coefficient, , correlation coefficient.
Plot (a) of Figure 17 describes the correlation coefficient of the airship area–volume ratio, , in which the correlation coefficient of the airship slenderness ratio is 0.51, indicating a moderate positive correlation. The correlation coefficient of airship length is −0.34, showing a weak negative correlation. The correlation coefficient of other parameters is less than 0.2, indicating no significant correlation. Among all the parameters, is the largest in absolute value. When considering the of airships, the design of should be given the highest priority. In this way, and should be designed subsequently because their correlation coefficient absolute values are secondary. Another parameter’s correlation coefficient is too small to influence the value of the airship in a certain way.
Plot (b) of Figure 17 describes the correlation coefficient of the total mass , where the correlation coefficient of airship length is 0.74, showing a strong positive correlation. The correlation coefficient of other parameters is less than 0.2, indicating no significant correlation. When considering the of airships, should be designed firstly because of its largest absolute value among all the parameters. Furthermore, other parameters’ correlation coefficient absolute values are all under 0.2, which means they are too small to influence the value of in a certain way, so these parameters should not be given too much attention.
Plot (c) of Figure 17 describes the correlation coefficient of the drag coefficient, , where the correlation coefficient of airship length is −0.99, indicating a high negative correlation. The correlation coefficient of the slenderness ratio is −0.5, showing a moderate negative correlation. The correlation coefficient of the prismatic coefficient is 0.29, indicating a weak positive correlation. The correlation coefficient of other parameters is less than 0.2, indicating no significant correlation. It is not hard to see that the correlation coefficient of has the largest absolute value and is secondary among all the parameters. Therefore, when considering , the design of should be given the highest priority and λ should be given the secondary priority. Furthermore, the correlation coefficient of is 0.29, which means that the change of ’s value can influence the value of in a low degree. cannot be ignored, although the influence degree of is low. Another parameter’s correlation coefficient is too small to influence the value of in a certain way, so they could be ignored when considering the drag coefficient.
All in all, the correlation coefficients of the three parameters , , and are too small, and it is difficult for them to affect , , or of the airship in a certain way, so they should not be given too much attention when determining the , , and of the airship. We need to pay more attention to the design of , , and because their impact on , , and is obvious.
5.1.2. Comparison Analysis of Airship Envelope Curve
Solutions on the Pareto front often show trade-offs between different goals. A solution may excel in one goal but be slightly inferior in another, while another solution may be balanced across multiple goals. For comparison analysis, the solutions with the smallest drag coefficient, the smallest total mass, and the smallest airship area–volume ratio were selected from the Pareto front in Figure 15.
- The drag coefficient is at its lowest
The comparison of the smallest drag coefficient is shown in Figure 18, and the data for the comparison is shown in Table 6. When the drag coefficient is lowest, the , , and of the airship become larger, while , , and become smaller. At the same time, the total mass and area–volume ratio of the airship are reduced simultaneously.

Figure 18.
Comparison with the lowest drag coefficient.

Table 6.
Comparison with the lowest drag coefficient.
- 2.
- Total mass is at its lowest
The comparison of the boat type with the minimum total mass is shown in Figure 19, and the data for the comparison is shown in Table 7. When the total mass is minimized, , , , and of the airship decreases and increases, while has very little change. Simultaneously, the drag coefficient of the airship increases and the area–volume ratio decreases.

Figure 19.
Comparison with the lowest total mass.

Table 7.
Comparison with the lowest total mass.
- 3.
- The area–volume ratio is at its lowest.
The comparison of the airship type with the smallest area–volume ratio is shown in Figure 20, and the data for the comparison is shown in Table 8. When the area–volume ratio of the airship is minimized, the , , , and of the airship decrease and and increase. The total mass of the airship decreases, and the drag coefficient increases.
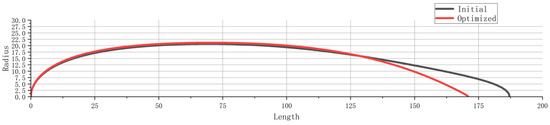
Figure 20.
Comparison with the lowest area–volume ratio.

Table 8.
Comparison with the lowest area–volume ratio.
From the above data, it can be seen that no matter what goal is pursued, will be larger than the original design parameter and and will be smaller, which is consistent with the results of the correlation analysis in Section 5.1.1, that is, changes in , , and do not affect the goal pursued more clearly. By contrast, the changes in , , and are very predictable. When pursuing the minimum drag coefficient, the and of the airship become larger, while becomes smaller. These results are consistent with the analysis in Section 5.1.1. In addition, there are inherent constraints between the three goals being pursued, and it is necessary to ensure that all three meet the design requirements. The choice must be made according to the actual design situation. Above all, these results show a similarity to the results of Yang [41], Yin [42], and Alam [29].
5.2. Analysis of Architecture Trade-Off Results
According to the Pareto frontier solution set in Section 5.1 and the implementation method of the TOPSIS method in Section 4.3, the relative closeness of each option is calculated. Table 9 shows the raw and processed data. and are the raw data, and and are the relative closeness.

Table 9.
Data of architecture tradeoff.
The relative closeness of the obtained cost, , and reliability, , is constructed as a binary graph and the curve is fitted with logarithmic data points. Visualization of the solution space, as shown in Figure 20, assists the designer in determining weight combinations. The fitted linear curve is and the coefficient of determination is 0.96473. The fitting curve shows that cost, , is positively correlated with reliability, , in the range of weight combination selection.
The selection range is determined according to the binary graph of the relative closeness and the fitting curve, and the selection in this range can meet the requirements. In this case, the correlation between cost, , and reliability, , is positive, and the relative closeness of cost, , will increase with the increase of the relative proximity of reliability, . Formula (65) describes the objective function of architecture tradeoff. The scheme with the largest sum of relative proximity is the final architecture scheme, as shown in Figure 21. Figure 22 shows the final schematic and the corresponding set of parameters.
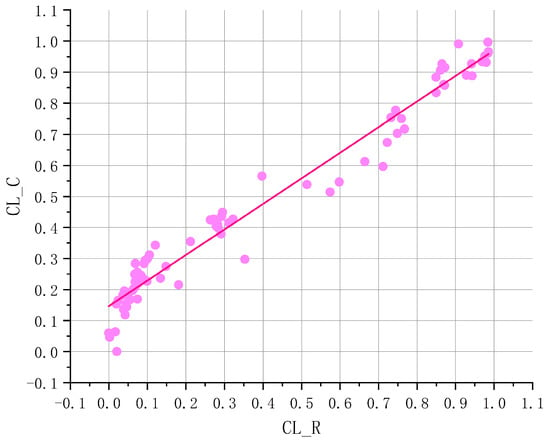
Figure 21.
Binary graph of cost, C, and reliability, R.

Figure 22.
The final shape of the airship.
Table 10 shows the comparison between the final shape and the original shape. It can be seen that the total weight and area–volume ratio of the airship is reduced compared with the original shape, and the drag coefficient is increased.

Table 10.
Comparison with the final shape.
6. Conclusions
System architecture, as the core of complex system engineering, is crucial to the success of the entire system design. The results of architectural preliminary decision trade-off directly affect the progress of subsequent design and system implementation, as well as the quality and performance of the system. This paper proposes a new method that supports the design and trade-off of stratospheric airship architecture. This method enables the modeling and characterization of system architecture, optimization of the design space, and Pareto frontier trade-off, helping designers find solutions that satisfy multiple stakeholders.
1. Using MBSE, we completed the requirements analysis and architecture preliminary design of the stratospheric airship forward design. This allowed us to achieve the formalization, standardization, and modeling of the system architecture. Additionally, it helped optimize and balance the design space, assisting designers in finding solutions that meet the needs of multiple stakeholders.
2. The multidisciplinary theoretical formula and program model of the stratospheric airship were established, and a multidisciplinary simulation program was built with MATLAB to realize the rapid and efficient initial design of the airship.
3. Using the multidisciplinary theoretical simulation computing platform, NSGA-II and TOPSIS algorithms can quickly obtain the optimal architecture at the system level. Additionally, the algorithm has scalable functions; after the system-level architecture parameters are fixed, subsystem-level optimization and analysis can be further refined.
As one of the ways to solve system engineering problems, MBSE can transform some engineering problems into digital models. To understand MBSE in a broader sense, whether it is the architecture design in the early stage or the verification and even the digital simulation in the later stage, it can be realized by building the corresponding model in the computer. It is important to take full advantage of MBSE’s “model-based” thinking to solve engineering problems faster and better. In summary, this paper systematically studies the forward design of airships, from requirements analysis to the selection of the optimal scheme, providing theoretical guidance and reference for the system engineering design of airships.
Author Contributions
Conceptualization, W.L., Y.Y. and J.M.; methodology, W.L., Y.Y. and J.M.; software, W.L.; validation, W.L. and L.K.; formal analysis, W.L. and L.K.; investigation, W.L. and L.K.; resources, W.L. and S.C.; data curation, W.L. and S.C.; writing—original draft preparation, W.L. and S.C.; writing—review and editing, W.L. and S.C.; visualization, W.L. and S.C.; supervision, Y.Y. and J.M.; project administration, Y.Y. and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research is funded by National Key R&D Program of China, 2022YFB3903000, 2022YFB3903005. The article processing charge was funded by the Aerospace Information Research Institute, Chinese Academy of Sciences.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. Data are not available due to commercial restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lambert, C. Developing architectures for high altitude airships. In Proceedings of the AIAA’s 3rd Annual Aviation Technology, Integration, and Operations (ATIO) Forum, Denver, CO, USA, 17–19 November 2003. [Google Scholar]
- Du, H.; Lyu, M.; Yu, C.; Wu, Y.; Wu, Y.; Sun, K. Numerical simulation of fluid-thermal-structural coupling characteristics of stratospheric non-rigid airship. Chin. J. Aeronaut. 2024; in press. [Google Scholar] [CrossRef]
- Zheng, B.; Zhu, M.; Guo, X.; Ou, J.; Yuan, J. Path planning of stratospheric airship in dynamic wind field based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 150, 109173. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, X.; Wang, Q. Rules and Design Criterion of Airship Stability and Modes. Adv. Space Res. 2023, 73, 3179–3194. [Google Scholar] [CrossRef]
- McVittie, T.I.; Sindiy, O.V.; Simpson, K.A. Model-based system engineering of the Orion flight test 1 end-to-end information system. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012. [Google Scholar]
- Izygon, M.; Wagner, H.; Okon, S.; Wang, L.; Sargusingh, M.; Evans, J. Facilitating R&M in spaceflight systems with MBSE. In Proceedings of the 2016 Annual Reliability and Maintainability Symposium (RAMS), Tucson, AZ, USA, 25–28 January 2016. [Google Scholar]
- Wang, Y.; Zhang, W.B.; Zhan, C. DoDAF-based civil aircraft MBSE development method. Syst. Eng. Electron. 2021, 43, 3579–3585. [Google Scholar]
- Chen, Z.; Wu, H.; Luo, Z.; Wang, J. Research on the concept of operation for tropospheric airship based on MBSE. Syst. Eng. Electron. 2024, 46, 1004–1012. [Google Scholar]
- Crawley, E.; Cameron, B.; Selva, D. System Architecture: Strategy and Product Development for Complex Systems; Prentice Hall Press: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Delligatti, L. A Brief Guide to the Systems Modeling Language; China Machine Press: Beijing, China, 2014. [Google Scholar]
- National Oceanic and Atmospheric Administration. US Standard Atmosphere, 1976; Technical Report; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1976. [Google Scholar]
- LI, X. Numerical Simulation of Thermal-Structure Coupling for Near Space Airship; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2013. [Google Scholar]
- Carlson, L.A.; Horn, W.J. New thermal and trajectory model for high-altitude balloons. J. Aircr. 1981, 20, 500–507. [Google Scholar] [CrossRef]
- Ran, H.; Thomas, R.; Mavris, D.N. A Comprehensive Global Model of Broadband Direct Solar Radiation for Solar Cell Simulation. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Dai, Q.; Fang, X. A simple model to predict solar radiation under clear sky conditions. Adv. Space Res. 2014, 53, 1239–1245. [Google Scholar] [CrossRef]
- Ram, C.V.; Pant, R.S. Multidisciplinary Shape Optimization of Aerostat Envelopes. J. Aircr. 2010, 47, 1073–1076. [Google Scholar] [CrossRef]
- Garg, A.K.; Burnwal, S.; Pallapothu, A.; Alawa, R.; Ghosh, A. Solar Panel Area Estimation and Optimization for Geostationary Stratospheric Airships. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Wang, Q.; Chen, J.; Fu, G.; Duan, D.; Zhao, H. A methodology for optimisation design and analysis of stratosphere airship. Aeronaut. J. 2009, 113, 533–540. [Google Scholar] [CrossRef]
- Landweber, L.; Gertler, M. Mathematical Formulation of Bodies of Revolution; The David W. Taylor Model Basin: Bethesda, MD, USA, 1950. [Google Scholar]
- Gawale, A.C.; Pant, R.S. Design, fabrication and flight testing of remotely controlled airship. In Proceedings of the National Conference on LTA Technologies, Aerial Delivery R&D Establishment, Agra, India, 20–22 October 2002. [Google Scholar]
- Gawande, V.N.; Bilaye, P.; Gawale, A.; Pant, R.; Desai, U. Design and Fabrication of an Aerostat for Wireless Communication in Remote Areas. In Proceedings of the 7th AIAA ATIO Conf, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf; followed by 2nd TEOS Forum, Belfast, Ireland, 18–20 September 2007. [Google Scholar]
- Wang, X.; Fu, G.-Y.; Duan, D.-P.; Shan, X.-X. Experimental Investigations on Aerodynamic Characteristics of the ZHIYUAN-1 Airship. J. Aircr. 2010, 47, 1463–1468. [Google Scholar] [CrossRef]
- Andan, A.D.; Asrar, W.; Omar, A.A. Investigation of Aerodynamic Parameters of a Hybrid Airship. J. Aircr. 2012, 49, 658–662. [Google Scholar] [CrossRef]
- Jalasabri, J.; Romli, F.I.; Harmin, M.Y. Mathematical Modelling for Effects of Fineness Ratio, Altitude and Velocity on Aerodynamic Characteristics of an Airship Design using Computational Fluid Dynamics. CFD Lett. 2020, 12, 90–110. [Google Scholar] [CrossRef]
- Gonzalo, J.; Domínguez, D.; García-Gutiérrez, A.; Escapa, A. On the development of a parametric aerodynamic model of a stratospheric airship. Aerosp. Sci. Technol. 2020, 107, 106316. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Liselotte A. Hoerner: Brick Town, NJ, USA, 1965. [Google Scholar]
- Khoury, G.A. Airship Technology; Cambridge University Press: Cambridge, UK, 2012; Volume 10. [Google Scholar]
- Pant, R.S. A methodology for determination of baseline specifications of a non-rigid airship. J. Aircr. 2008, 45, 2177–2182. [Google Scholar] [CrossRef]
- Alam, M.I.; Pant, R.S. Multi-objective multidisciplinary design analyses and optimization of high altitude airships. Aerosp. Sci. Technol. 2018, 78, 248–259. [Google Scholar] [CrossRef]
- Ming, Z.; Shi, Y.; Liang, H.; Zhang, X. Near space airship conceptual design and optimization. J. Commun. Inf. Netw. 2016, 1, 125–133. [Google Scholar] [CrossRef]
- Manikandan, M.; Shah, R.R.; Priyan, P.; Singh, B.; Pant, R.S. A parametric design approach for multi-lobed hybrid airships. Aeronaut. J. 2024, 128, 1–36. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications: A State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Ploskas, N.; Papathanasiou, J. A decision support system for multiple criteria alternative ranking using TOPSIS and VIKOR in fuzzy and nonfuzzy environments. Fuzzy Sets Syst. 2019, 377, 1–30. [Google Scholar] [CrossRef]
- Dunford, R.; Su, Q.; Tamang, E. The Pareto Principle; Plymouth University: Plymouth, UK, 2014. [Google Scholar]
- Yu, H.; Wang, G.; Wang, R.; Wei, Z.; Zhang, W.; Liu, A.; Yan, Y. Architecture decision solving and tradeoffs method supporting complex system design. Comput. Integr. Manuf. Syst. 2023, 1–27. Available online: https://link.cnki.net/urlid/11.5946.TP.20230928.1832.005 (accessed on 12 July 2024).
- Xianghong, B. Research on the Evolution of Mechanical Properties of Airship Envelopes; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Fieller, E.C.; Hartley, H.O.; Pearson, E.S. Tests for rank correlation coefficients. I. I. Biom. 1957, 44, 470–481. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Yan, Y. Study on the Multidisciplinary Optimization Design Method of Near Space Airship Platform. 2012 CSTR:35001.37.01.33236.20120123.
- Yin, S.; Zhu, M.; Liang, H. Multi-disciplinary design optimization with variable complexity modeling for a stratosphere airship. Chin. J. Aeronaut. 2019, 32, 1244–1255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).