A Time-Domain Calculation Method for Gust Aerodynamics in Flight Simulation
Abstract
1. Introduction
2. Review of Existing Time-Domain Gust Load Calculation Methods
2.1. Frequency-Domain Inverse Fourier Transform Analysis Method
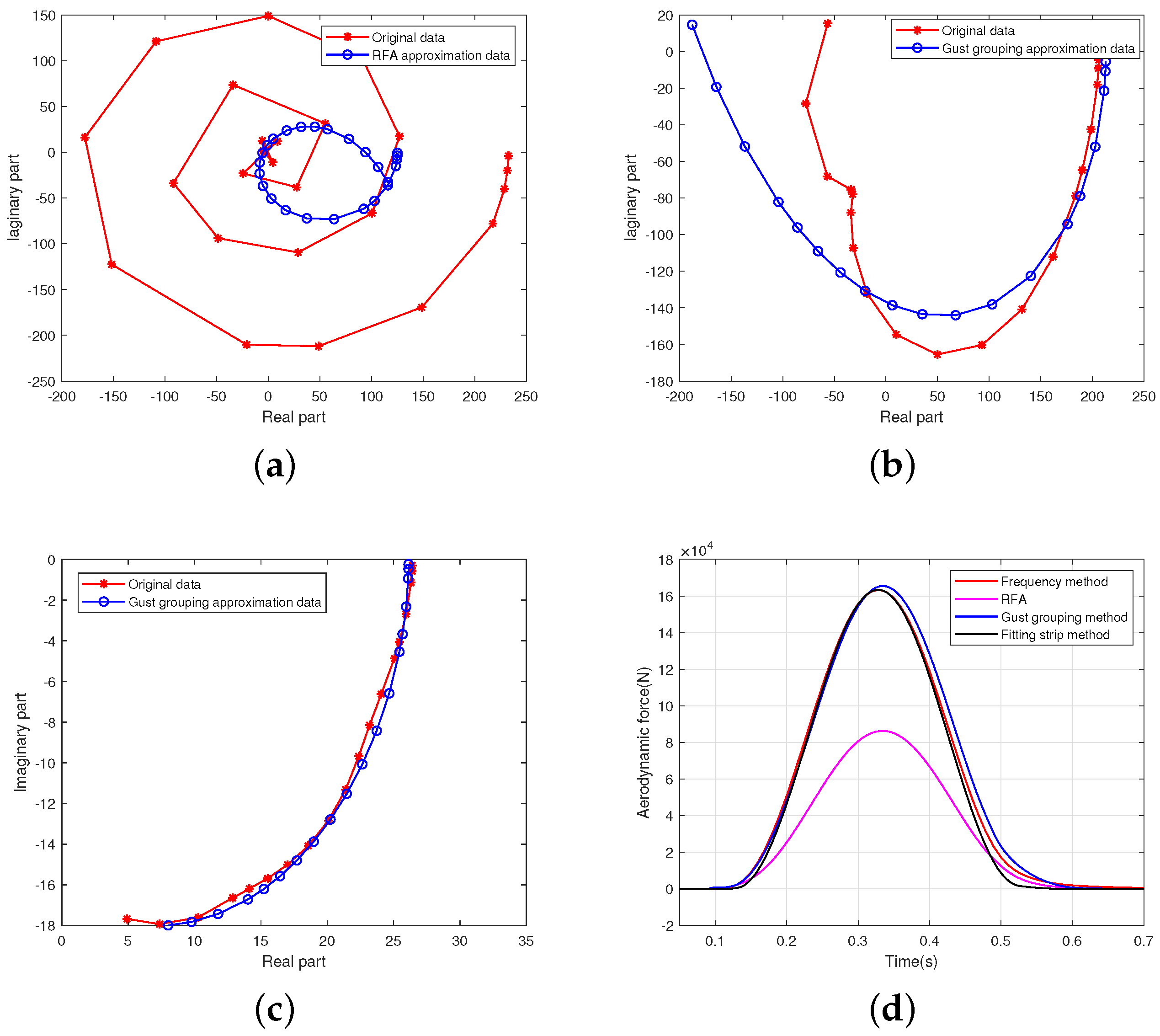
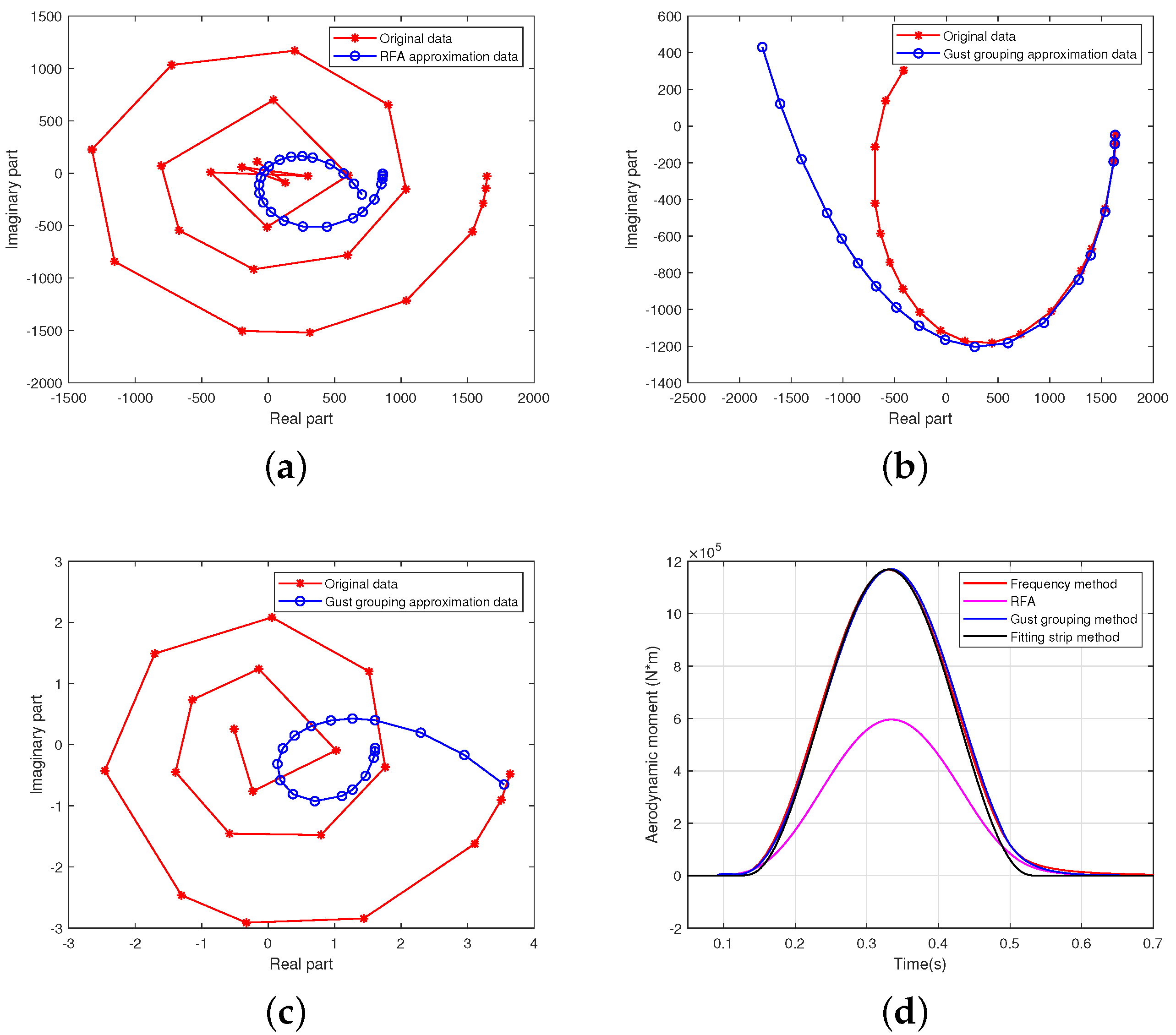
2.2. Rational Function Approximation
2.3. Time-Domain Solution Method for Gust Grouping
2.4. CFD
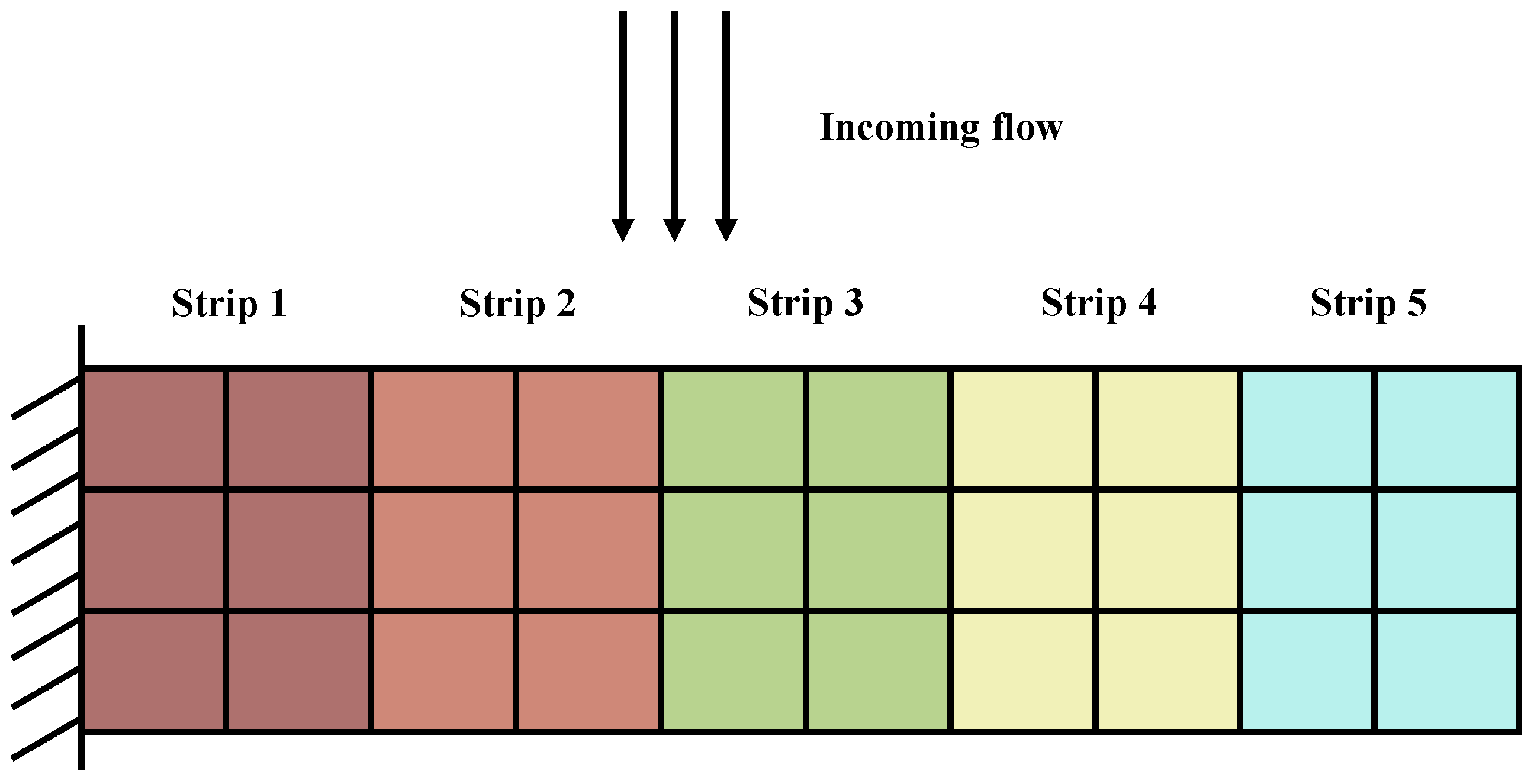
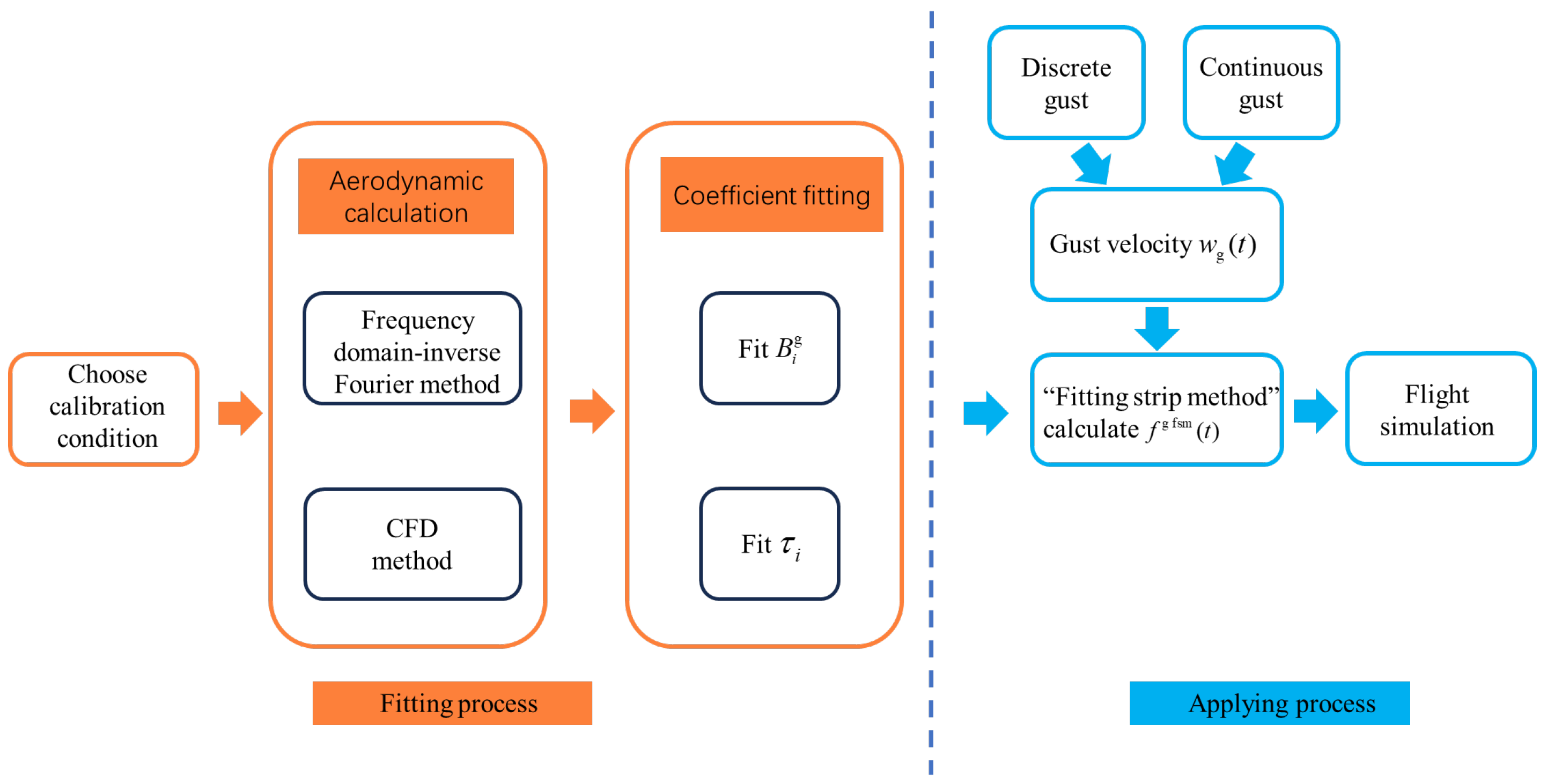
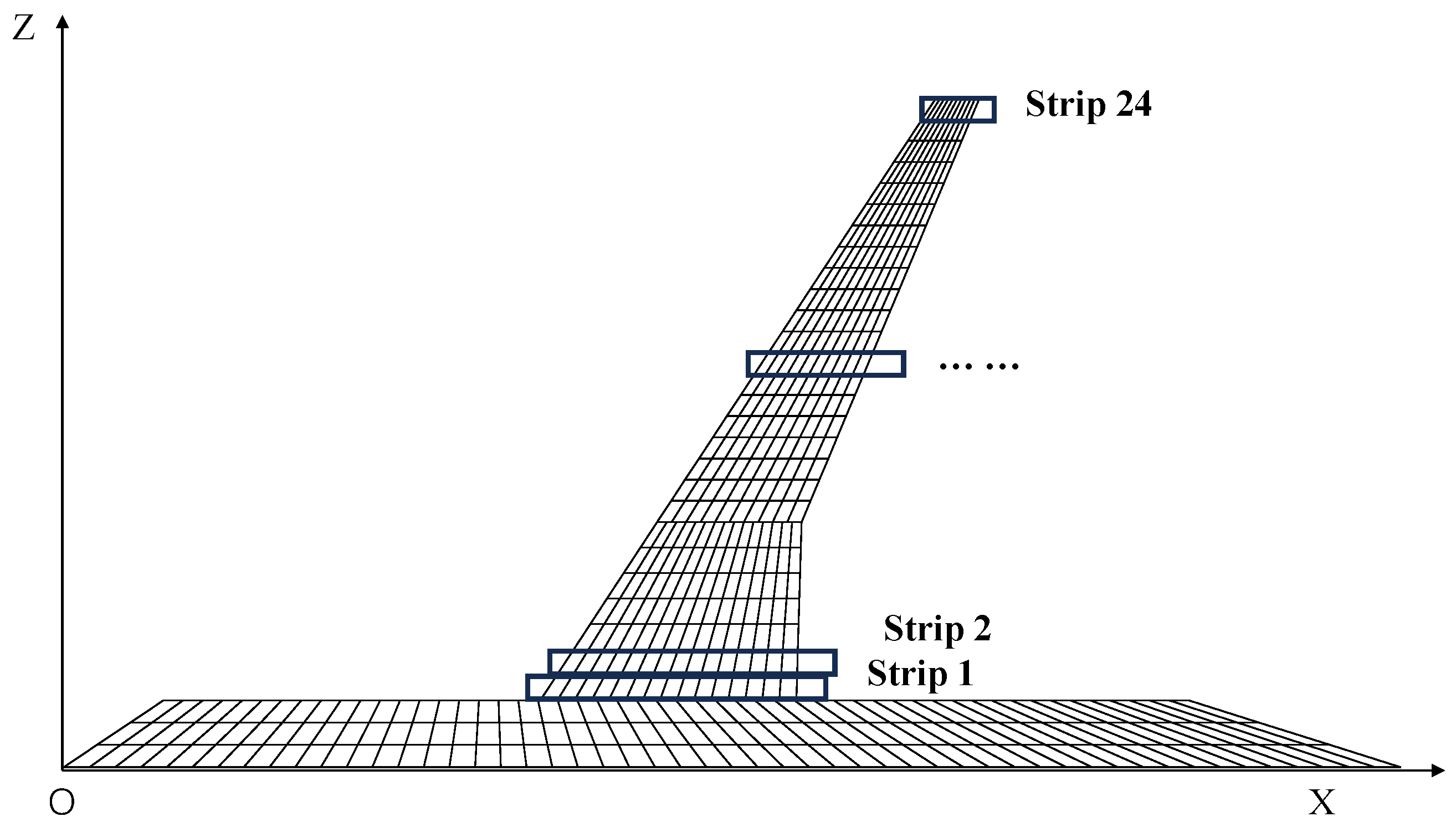
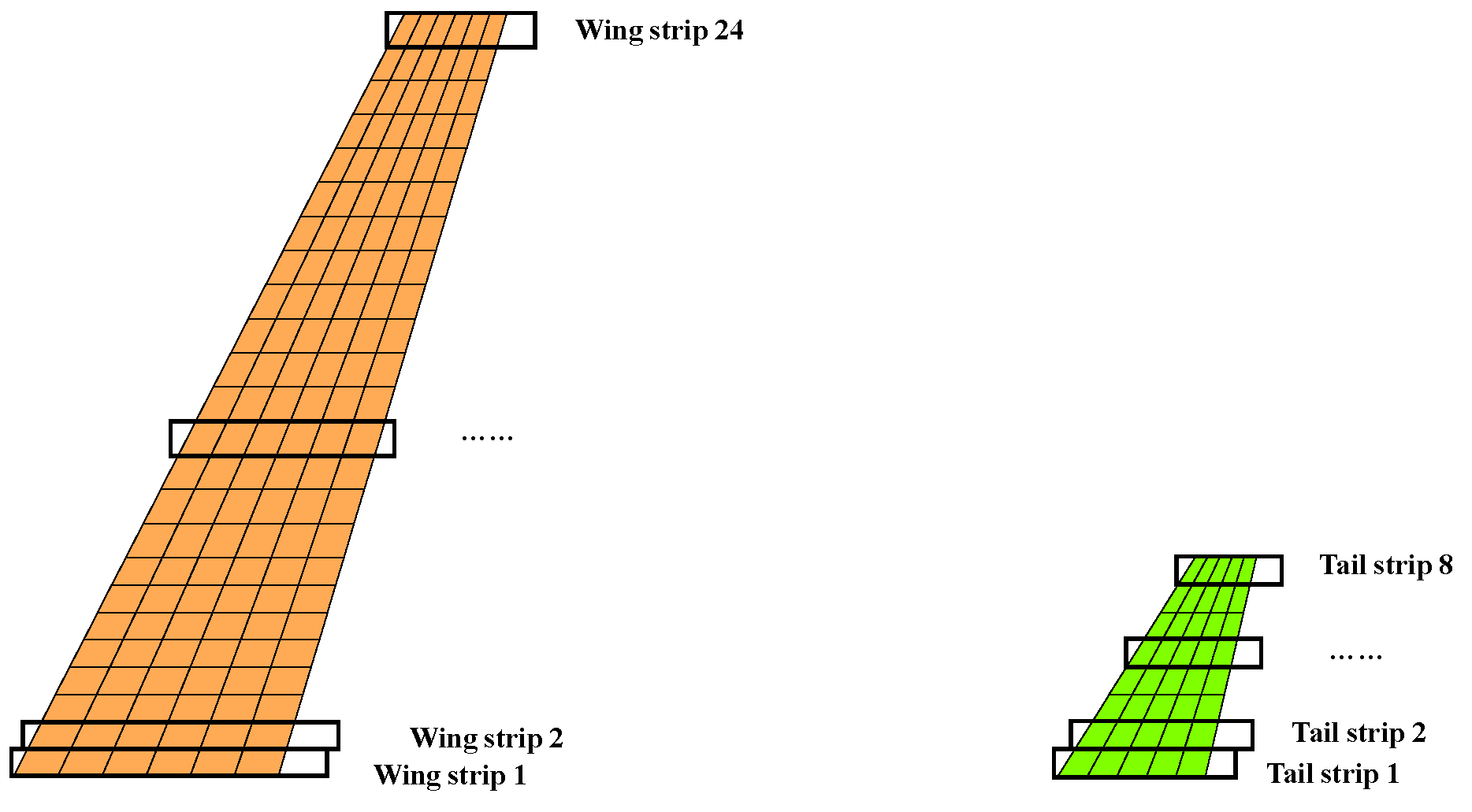
3. Fitting Strip Method
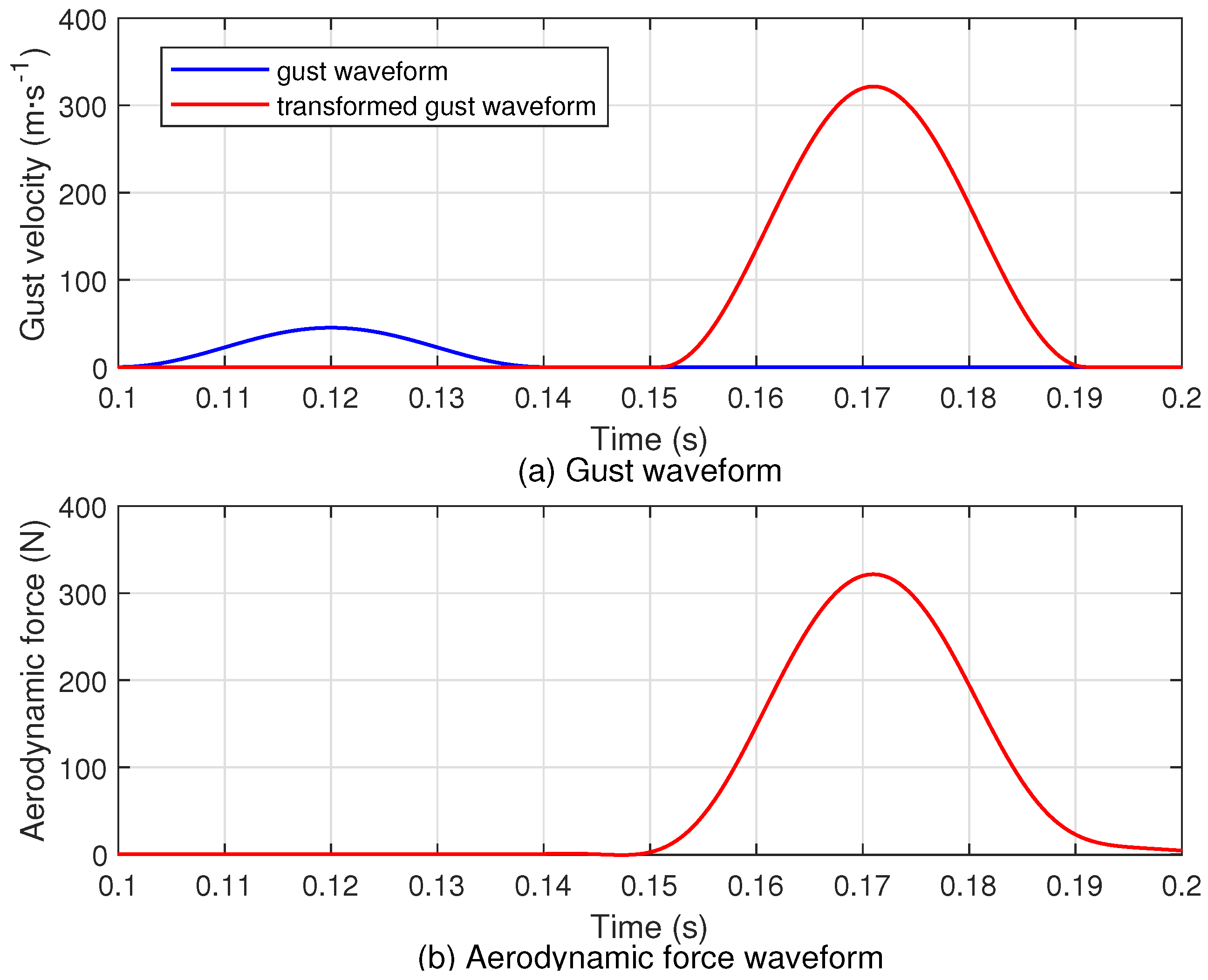
3.1. Proposal of the Method
3.2. Specific Steps of the Method
4. Validation of the Method
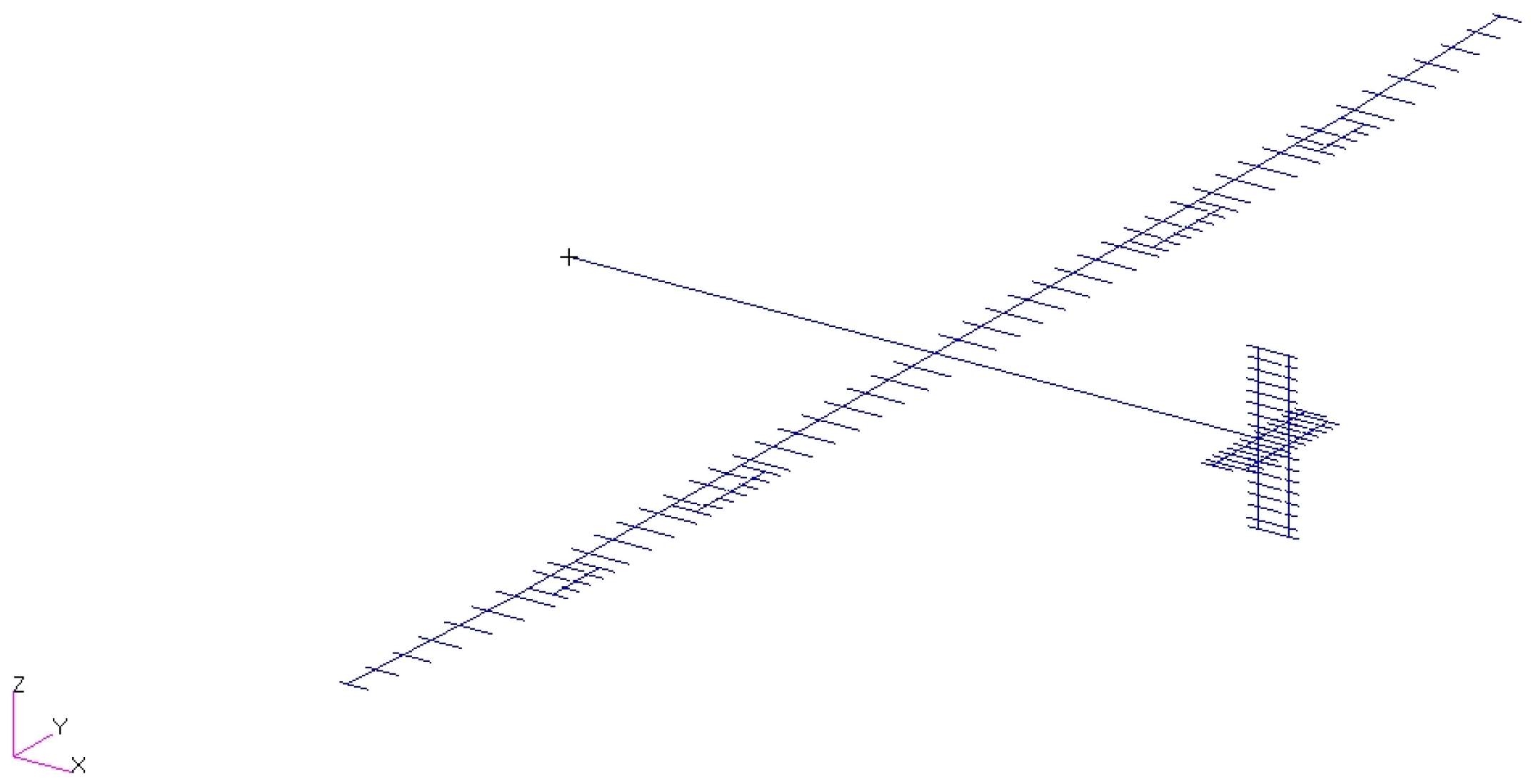
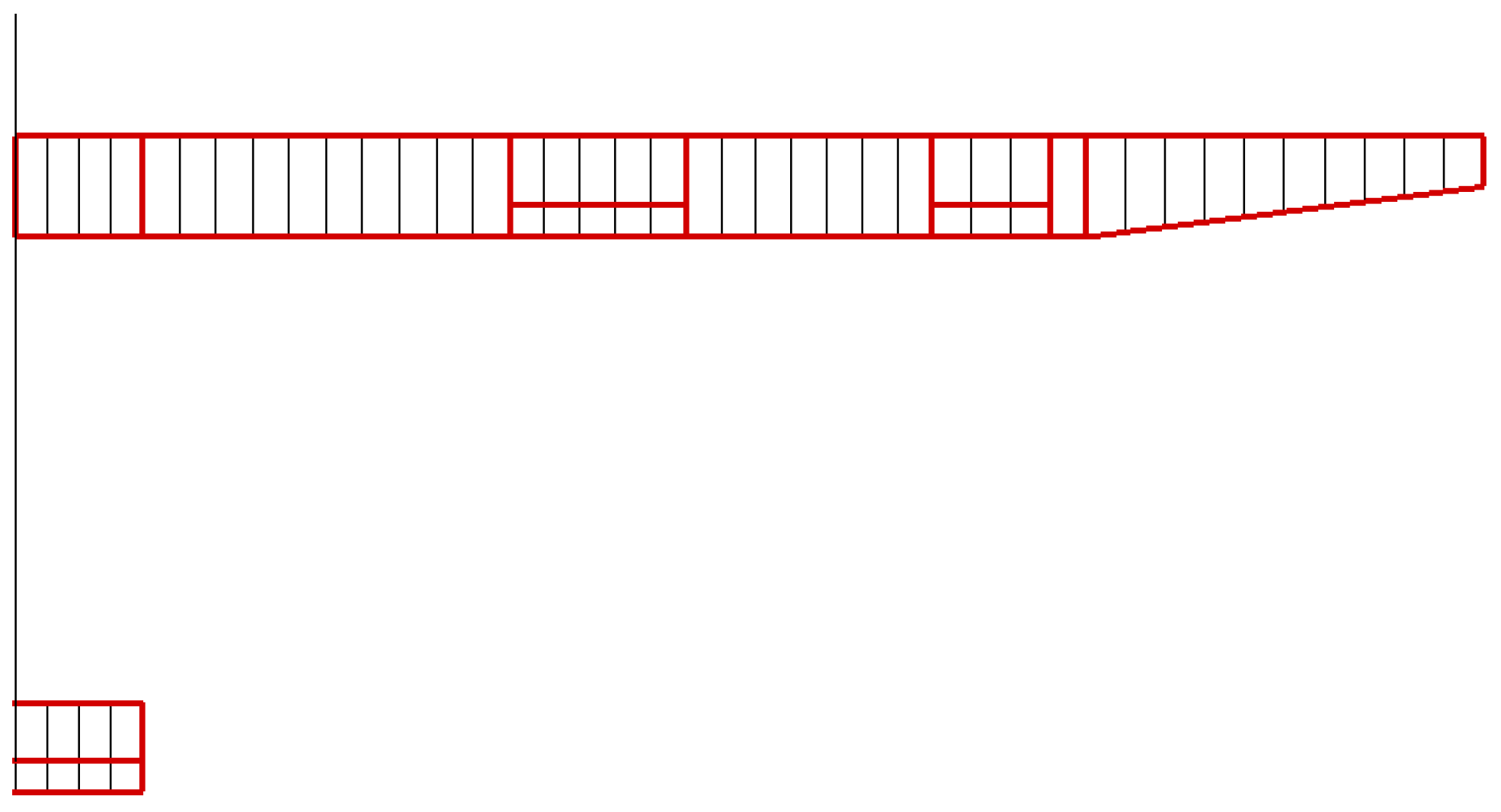
4.1. Swept-Wing Model
4.2. Experimental Model of the Swept Wing
4.3. Results of the Calculation of Discrete Gusts
4.4. Calculation Results for Continuous Gusts
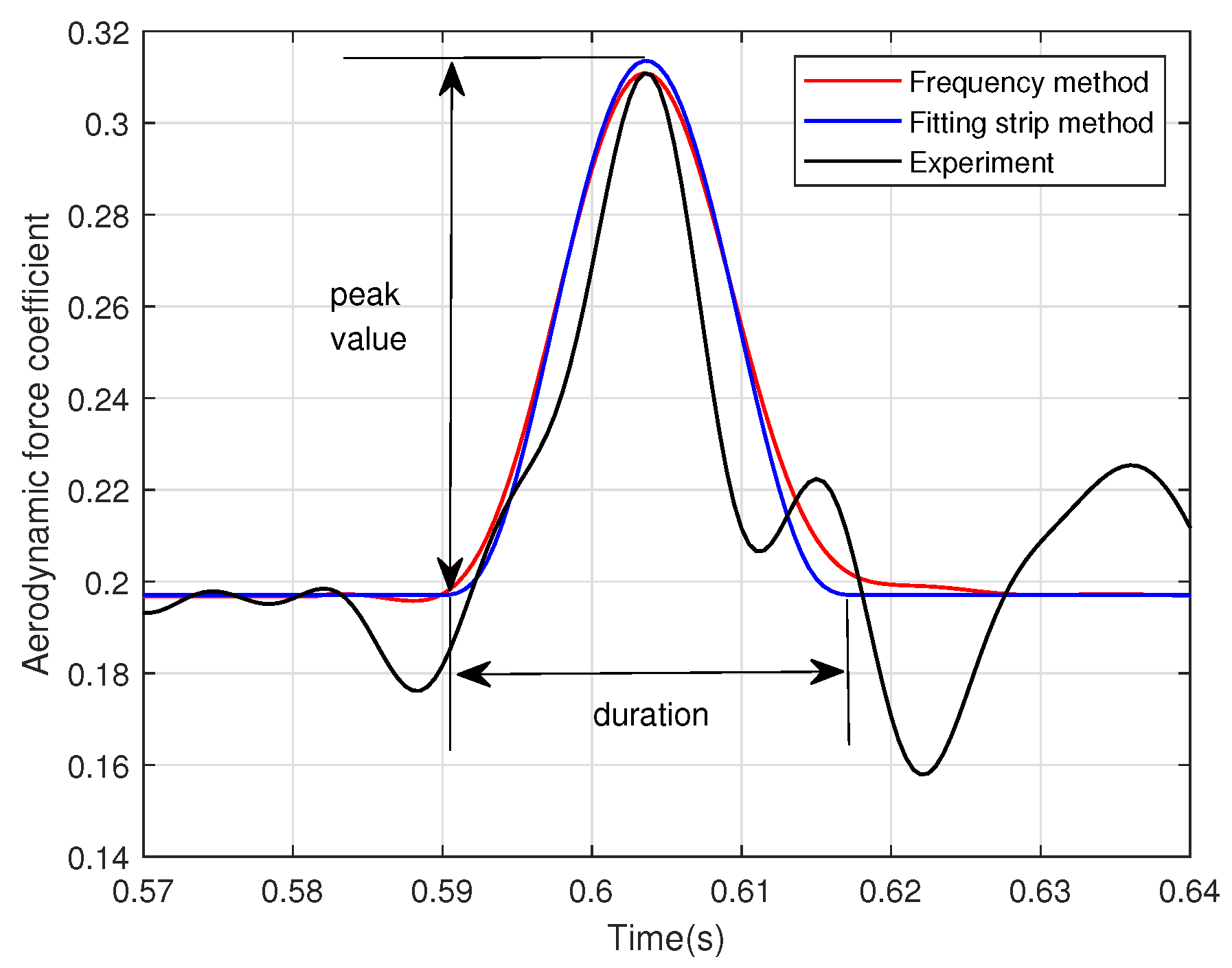
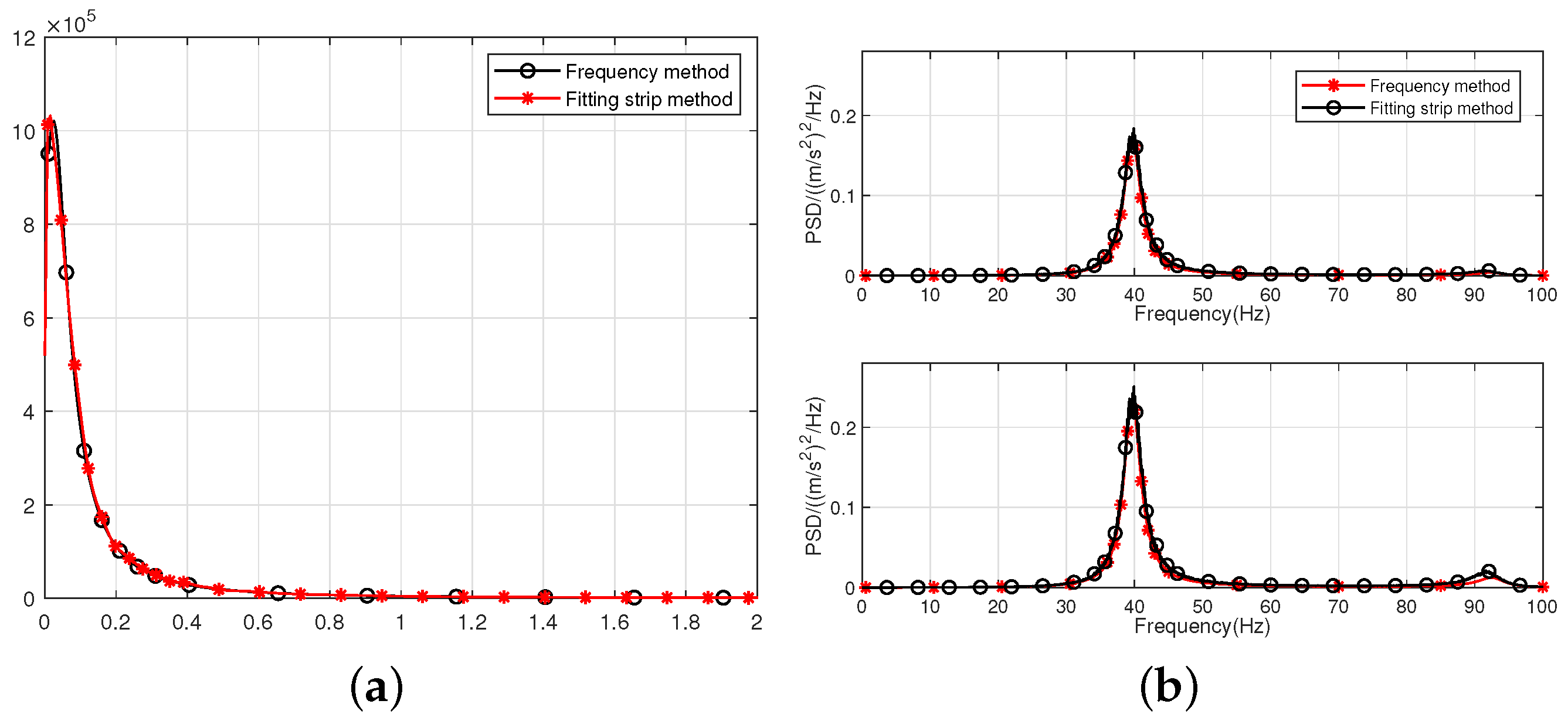
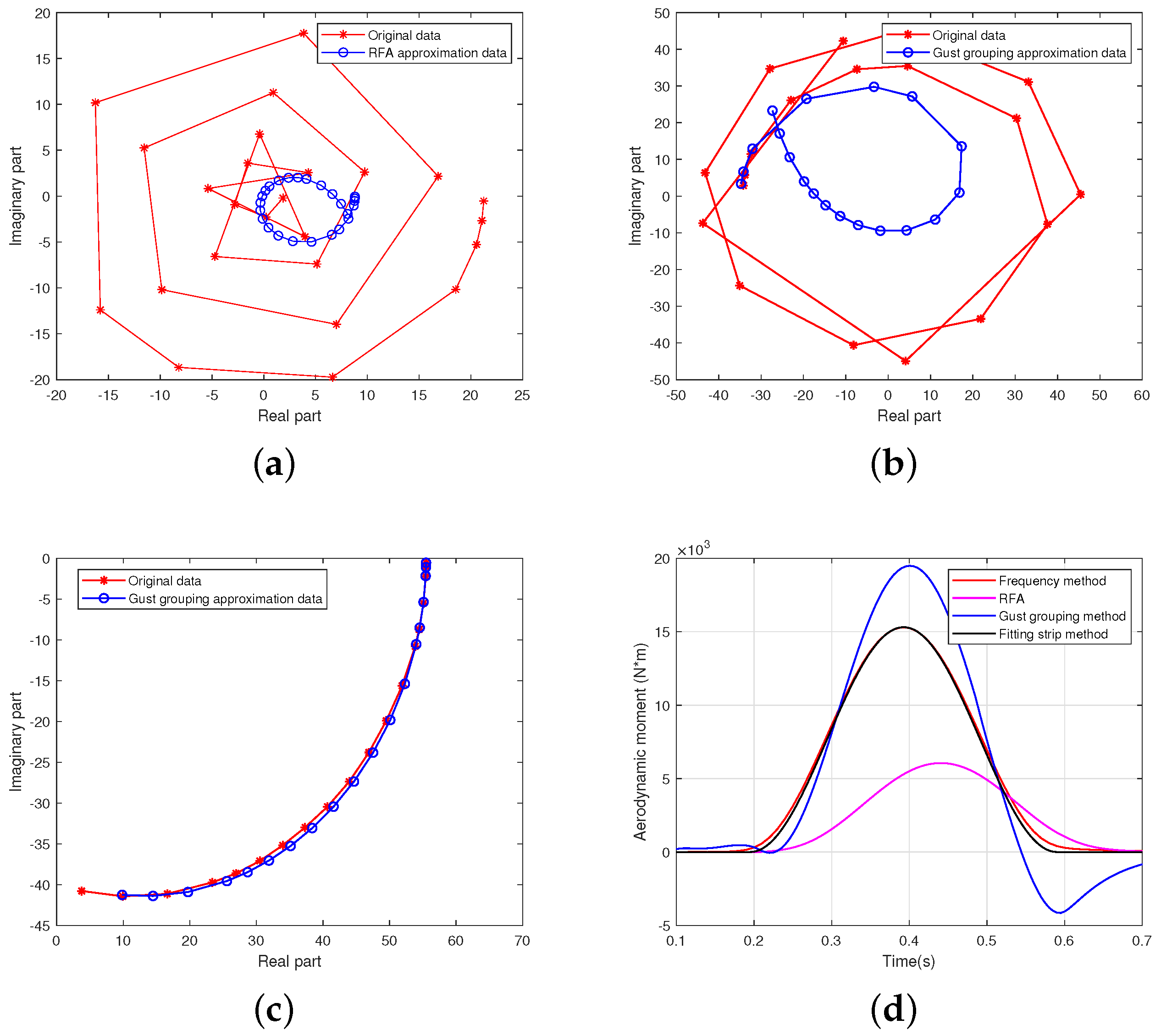
5. Comparison of Different Methods
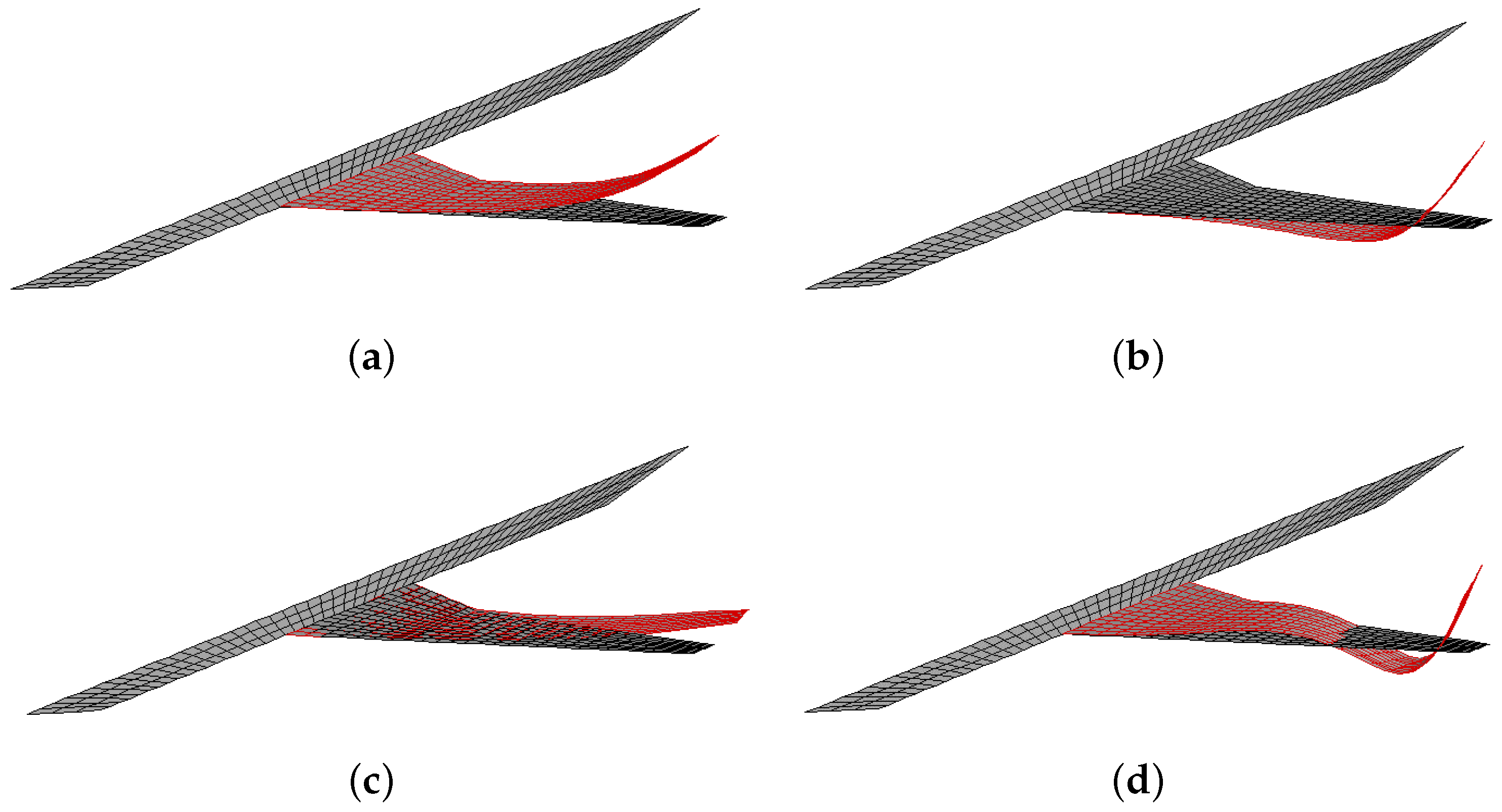
5.1. Model of a Normal-Layout Aircraft
5.2. Calculation Results
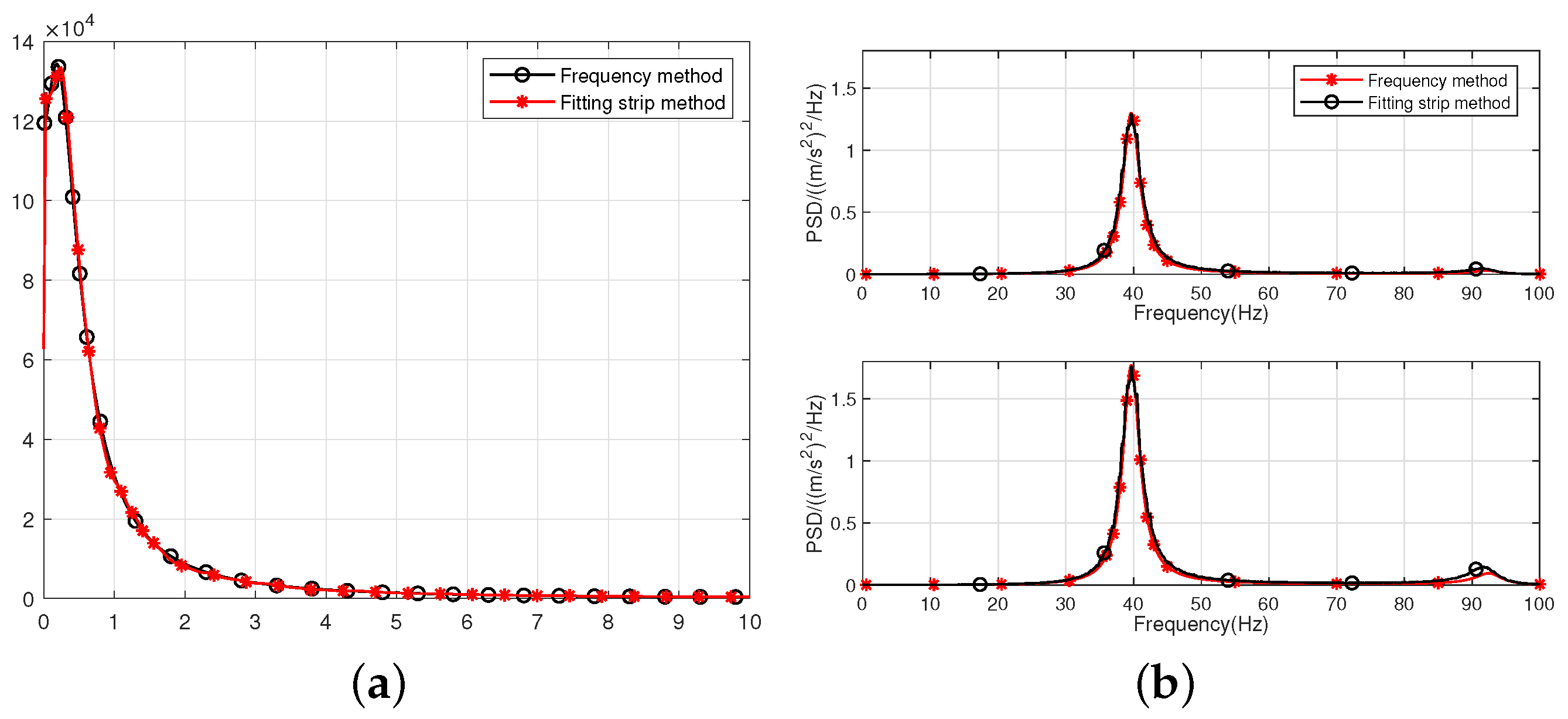
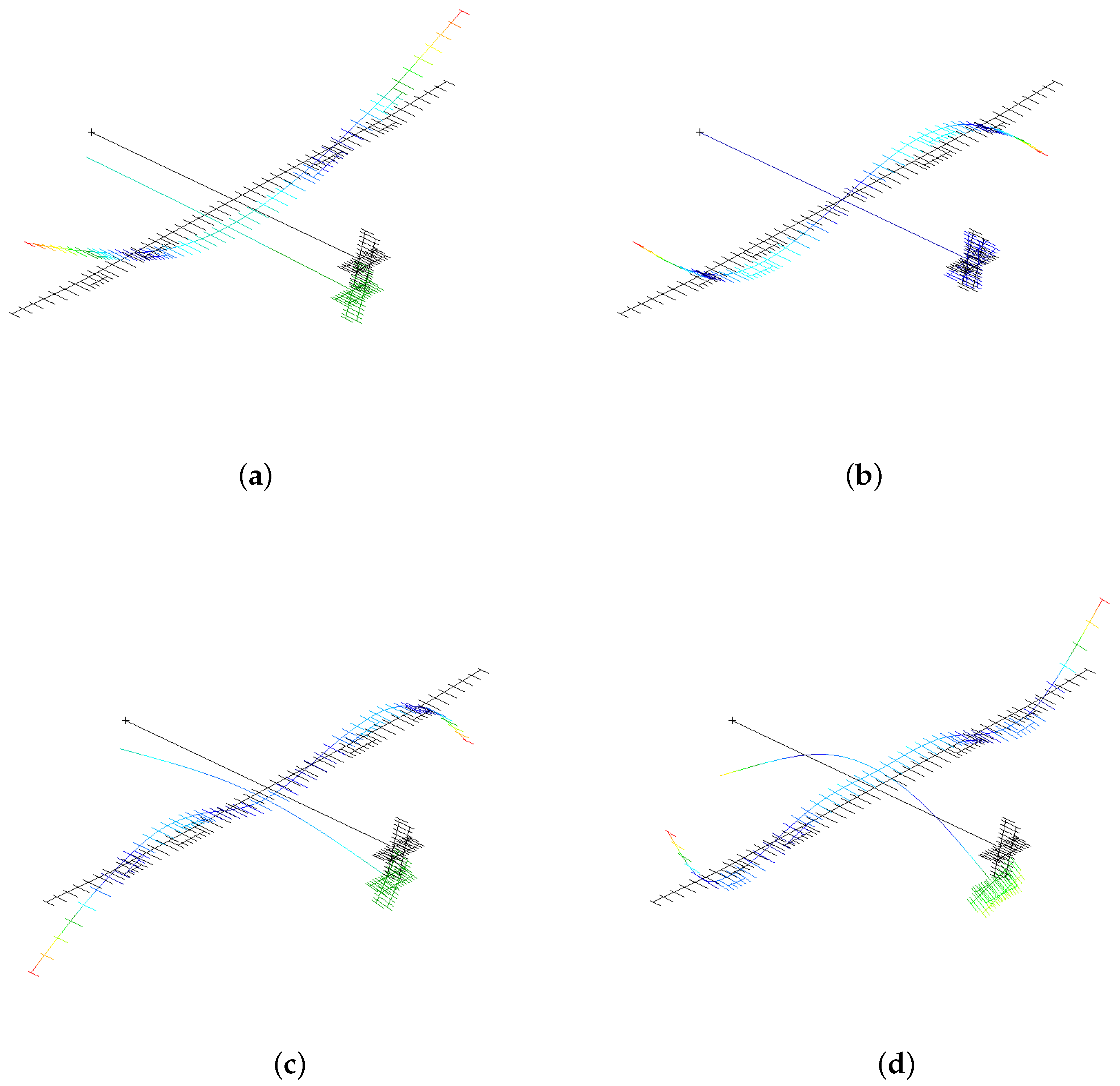
6. Application
6.1. Calculation Model
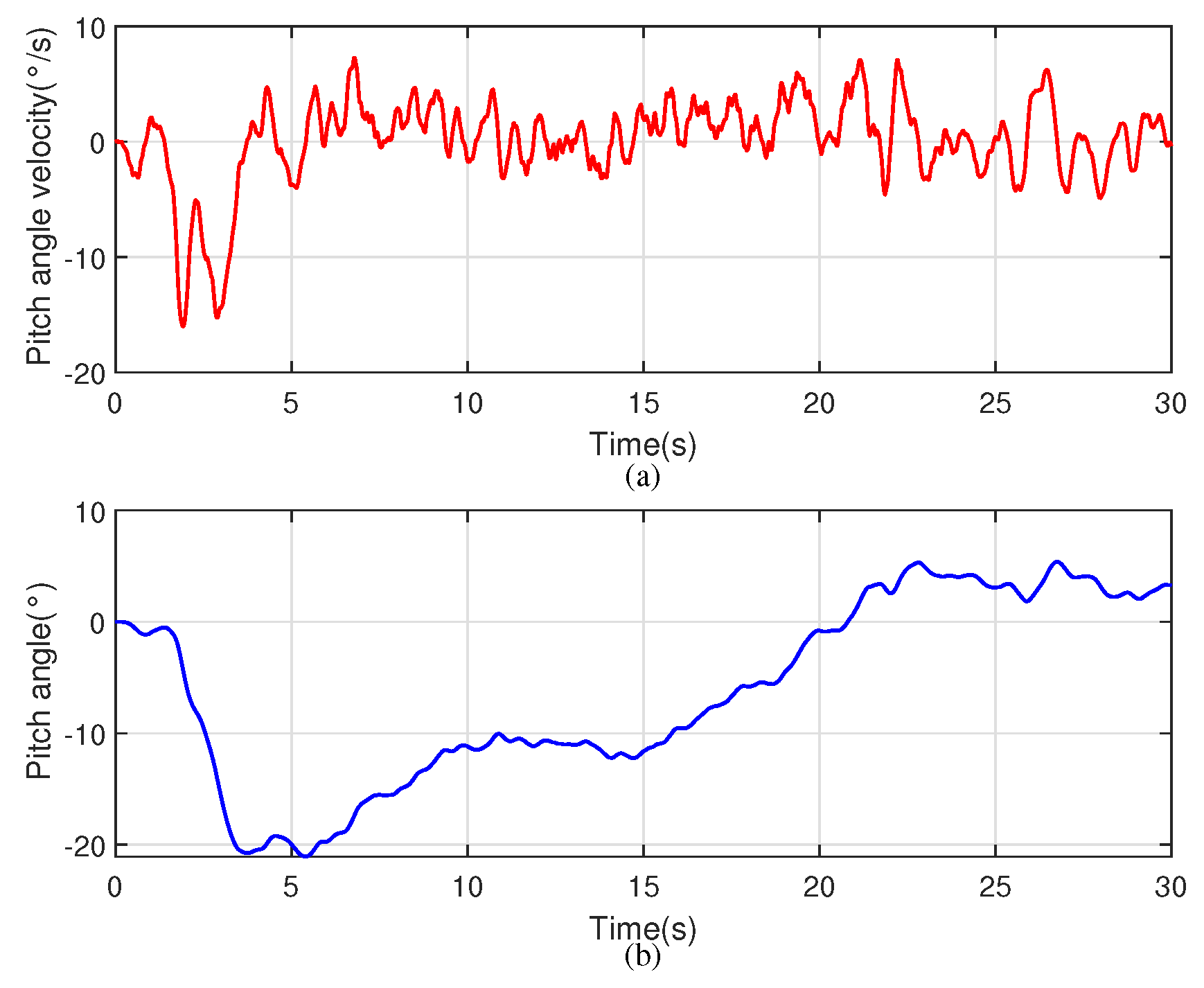
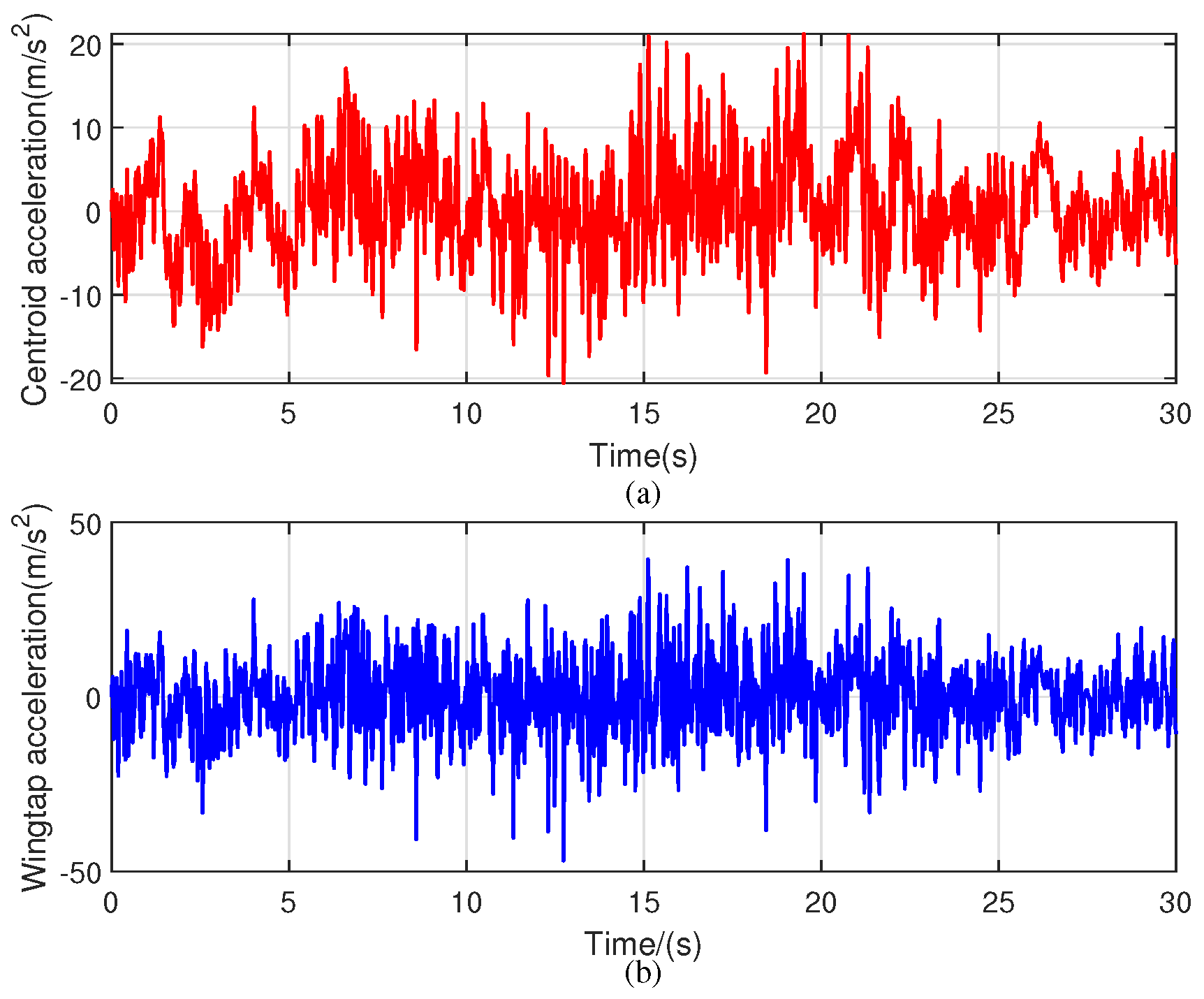
6.2. Calculation Results of the Flight Simulation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hunsaker, J.C.; Wilson, E.B. Report on Behavior of Aeroplanes in Gusts; Technical Report; NASA: Washington, DC, USA, 1915.
- Houbolt, J.C. Atmospheric turbulence. AIAA J. 1973, 11, 421–437. [Google Scholar] [CrossRef]
- Richardson, J.R.; Atkins, E.M.; Kabamba, P.T.; Girard, A.R. Scaling of Airplane Dynamic Response to Stochastic Gusts. J. Aircr. 2014, 51, 1554–1566. [Google Scholar] [CrossRef][Green Version]
- Karpel, M. Time-domain aeroservoelastic modeling using weighted unsteady aerodynamic forces. J. Guid. Control. Dyn. 1990, 13, 30–37. [Google Scholar] [CrossRef]
- Zole, A.; Karpel, M. Continuous gust response and sensitivity derivatives using state space models. J. Aircr. 1994, 13, 30–37. [Google Scholar] [CrossRef]
- Karpel, M.; Moulin, B.; Presente, E. Dynamic Gust Loads Analysis for Transport Aircraft with Nonlinear Control Effects. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 16th AIAA/ASME/AHS Adaptive Structures Conference, 10th AIAA Non-Deterministic Approaches Conference, 9th AIAA Gossamer Spacecraft Forum, 4th AIAA Multidisciplinary Design Optimization Specialists Conference, Schaumburg, IL, USA, 7–10 April 2008. [Google Scholar]
- Wu, Z.; Yang, C. Continuous and Discrete Gust Responses of Elastic missiles. J. Beijing Univ. Aeronaut.-Tronautics 2007, 33, 136–140. (In Chinese) [Google Scholar]
- Qiu, Q.; Wu, Z.; Yang, C. An equivalent emulation method of gust response for flight tests. Aerosp. Sci. Technol. 2023, 142, 108649. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Y. Adaptive Feed-Forward Control for Gust Load Alleviation on a Flying-Wing Model Using Multiple Control Surfaces. Aerospace 2023, 10, 981. [Google Scholar] [CrossRef]
- Parameswaran, V.; Baeder, J.D. Indicial Aerodynamics in Compressible Flow-Direct Computational Fluid Dynamic Calculations. J. Aircr. 1997, 34, 131–133. [Google Scholar] [CrossRef]
- De Nayer, G.; Breuer, M. A source-term formulation for injecting wind gusts in CFD simulations. J. Wind. Eng. Ind. Aerodyn. 2020, 207, 104405. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, C.; Huang, K.; Yang, C. Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System. Aerospace 2022, 9, 813. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, C.; Wang, W.; An, C. An Experimental and Numerical Evaluation of the Aerodynamic Performance of a UAV Propeller Considering Pitch Motion. Drones 2023, 7, 447. [Google Scholar] [CrossRef]
- Pflüger, J.; Breitsamter, C. Gust response of an elasto-flexible morphing wing using fluid–structure interaction simulations. Chin. J. Aeronaut. 2024, 37, 45–57. [Google Scholar] [CrossRef]
- Schmidt, D.K.; Raney, D.L. Modeling and simulation of flexible flight vehicles. J. Guid. Control Dyn. 2001, 24, 539–546. [Google Scholar] [CrossRef]
- Saltari, F.; Riso, R.; De Matteis, G.; Mastroddi, F. Finite element-based modeling for flight dynamics and aeroelasticity of flexible aircraft. J. Aircr. 2017, 54, 2350–2366. [Google Scholar] [CrossRef]
- Albano, E.; Hodden, W.P. A doublet lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Bera, K.K.; Chandiramani, N.K. An element dependent multiple lag rational function approximation for aeroelastic analysis of cable bridge. Appl. Math. Model. 2022, 105, 95–113. [Google Scholar] [CrossRef]
- Karpel, M.; Moulin, B.; Chen, P.C. Dynamic Response of Aeroservoelastic Systems to Gust Excitation. J. Aircr. 2005, 42, 1264–1272. [Google Scholar] [CrossRef]
- Boulbrachene, K.; Breuer, M. Aeroelastic response of an elastically mounted 2-DOF airfoil and its gust-induced oscillations. J. Fluids Struct. 2023, 117, 103828. [Google Scholar] [CrossRef]
- Balatti, D.; Khodaparast, H.H.; Friswell, M.I.; Manolesos, M.; Castrichini, A. Experimental and numerical investigation of an aircraft wing with hinged wingtip for gust load alleviation. J. Fluids Struct. 2023, 119, 103892. [Google Scholar] [CrossRef]
- Yan, S.; Zhiqiang, W.; Zhigang, W.U.; Chao, Y. Gust response analysis and verification of elastic aircraft based on nonlinear aerodynamic reduced-order model. Acta Aeronaut. Astronaut. Sin. 2022, 43, 327–346. (In Chinese) [Google Scholar]
- He, T.; Su, W. Robust control of gust-induced vibration of highly flexible aircraft. Aerosp. Sci. Technol. 2023, 143, 108703. [Google Scholar] [CrossRef]
- Friedewald, D. Numerical Simulations on Unsteady Nonlinear Transonic Airfoil Flow. Aerospace 2021, 8, 7. [Google Scholar] [CrossRef]
- Peihan, W.; Zhigang, W.U.; Chao, Y.; Xiaoxu, S. Patch module method for flight simulation of flexible aircraft. Acta Aeronaut. ET Astronaut. Sin. 2023, 44, 80–96. (In Chinese) [Google Scholar]
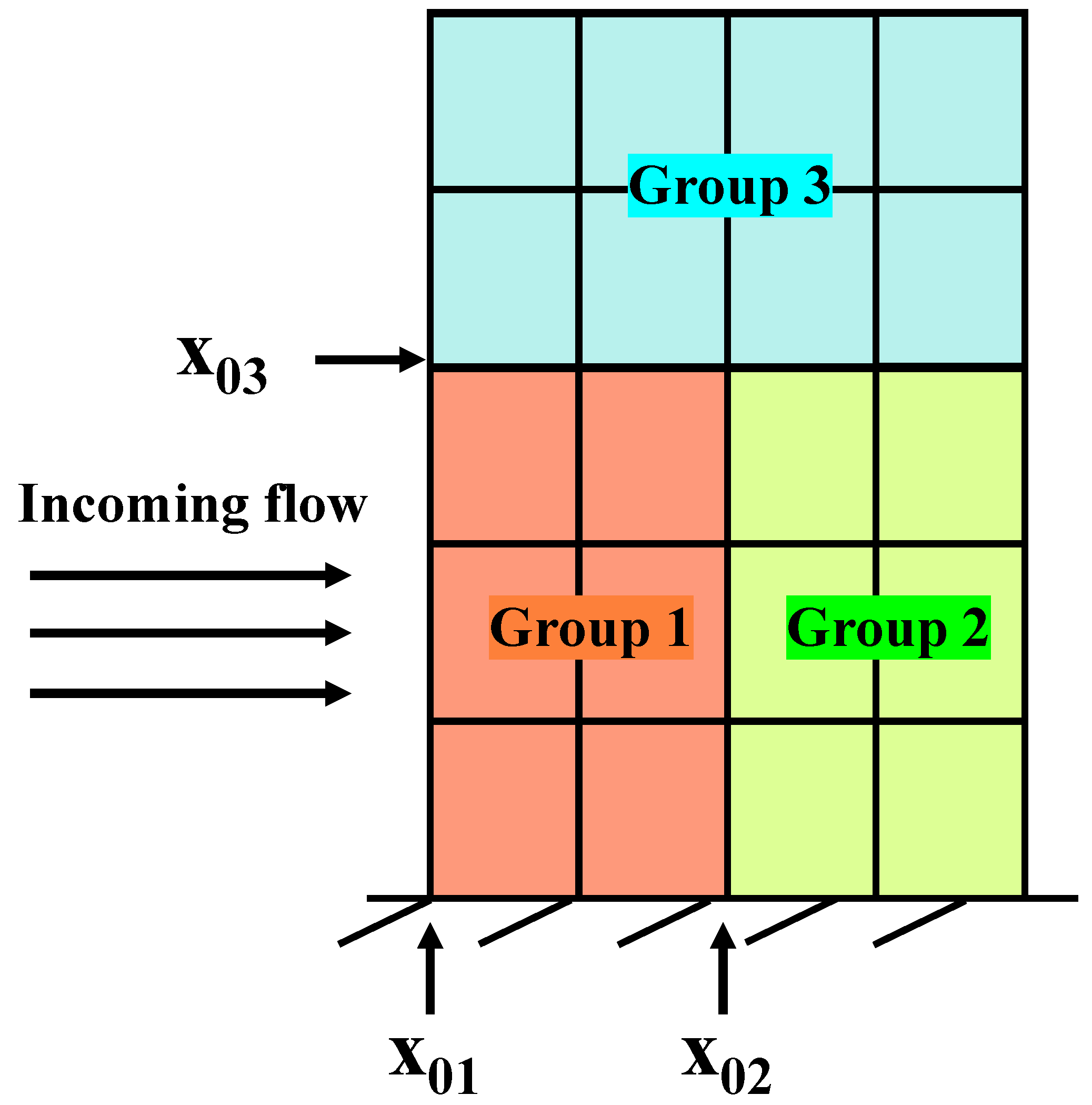





| Mode Order | Frequency (Hz) | Mode Name |
|---|---|---|
| 1 | 38.3 | First-order bending mode |
| 2 | 92.3 | Second-order bending mode |
| 3 | 140.6 | In-plane mode |
| 4 | 186.6 | Third-order bending mode |
| Number | Mach Number | Dynamic Pressure (Pa) | Maximum of Gust Velocity () | Gust Scale (m) |
|---|---|---|---|---|
| 1 | 0.5 | 14,324 | 5 | 4.2 |
| 2 | 0.5 | 14,324 | 5 | 6.8 |
| 3 | 0.6 | 20,018 | 3.5 | 5 |
| 4 | 0.85 | 31,763 | 3.4 | 14.6 |
| Method | Condition 1 | Condition 2 | Condition 3 | Condition 4 | |
|---|---|---|---|---|---|
| Frequency method | peak value | 0.114 | 0.106 | 0.073 | 0.064 |
| duration (s) | 0.032 | 0.047 | 0.031 | 0.051 | |
| Fitting strip method | peak value | 0.117 | 0.106 | 0.071 | 0.047 |
| duration (s) | 0.027 | 0.041 | 0.026 | 0.049 | |
| Experiment | peak value | 0.114 | 0.100 | 0.070 | 0.042 |
| duration (s) | 0.019 | 0.035 | 0.025 | 0.042 | |
| CFD | peak value | / | / | / | 0.047 |
| duration (s) | / | / | / | 0.065 |
| Method | Condition 1 | Condition 2 | Condition 3 | Condition 4 | |
|---|---|---|---|---|---|
| Frequency method | peak value | 0.056 | 0.047 | 0.034 | 0.026 |
| duration (s) | 0.030 | 0.046 | 0.031 | 0.044 | |
| Fitting strip method | peak value | 0.056 | 0.046 | 0.035 | 0.020 |
| duration (s) | 0.026 | 0.040 | 0.026 | 0.050 | |
| Experiment | peak value | 0.056 | 0.044 | 0.036 | 0.021 |
| duration (s) | 0.020 | 0.030 | 0.021 | 0.042 | |
| CFD | peak value | / | / | / | 0.022 |
| duration (s) | / | / | / | 0.065 |
| Method | CFD | Inverse Fourier Transform Method | Fitting Strip Method |
|---|---|---|---|
| Time (s) | 37,800 | 1.03 | 0.09 |
| Mode Order | Frequency (Hz) | Mode Name |
|---|---|---|
| 1 | 0.48 | Symmetrical first bending mode of the wing |
| 2 | 1.34 | Antisymmetric second bending mode of the wing |
| 3 | 2.00 | Symmetrical third bending mode of the wing |
| 4 | 3.32 | First bending mode of the fuselage |
| 5 | 3.55 | Antisymmetric fourth bending mode of the wing |
| 6 | 4.72 | Symmetrical fifth bending mode of the wing |
| 7 | 5.58 | Antisymmetric sixth bending mode of the wing |
| 8 | 5.94 | First bending mode of the wing in plane |
| 9 | 9.02 | First bending mode of the horizontal tail |
| 10 | 9.30 | Second bending mode of the fuselage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yang, C.; Wen, D.; Zhou, W.; Wu, Z. A Time-Domain Calculation Method for Gust Aerodynamics in Flight Simulation. Aerospace 2024, 11, 583. https://doi.org/10.3390/aerospace11070583
Yang Z, Yang C, Wen D, Zhou W, Wu Z. A Time-Domain Calculation Method for Gust Aerodynamics in Flight Simulation. Aerospace. 2024; 11(7):583. https://doi.org/10.3390/aerospace11070583
Chicago/Turabian StyleYang, Zexuan, Chao Yang, Daxin Wen, Wenbo Zhou, and Zhigang Wu. 2024. "A Time-Domain Calculation Method for Gust Aerodynamics in Flight Simulation" Aerospace 11, no. 7: 583. https://doi.org/10.3390/aerospace11070583
APA StyleYang, Z., Yang, C., Wen, D., Zhou, W., & Wu, Z. (2024). A Time-Domain Calculation Method for Gust Aerodynamics in Flight Simulation. Aerospace, 11(7), 583. https://doi.org/10.3390/aerospace11070583






