A Graph Reinforcement Learning-Based Handover Strategy for Low Earth Orbit Satellites under Power Grid Scenarios
Abstract
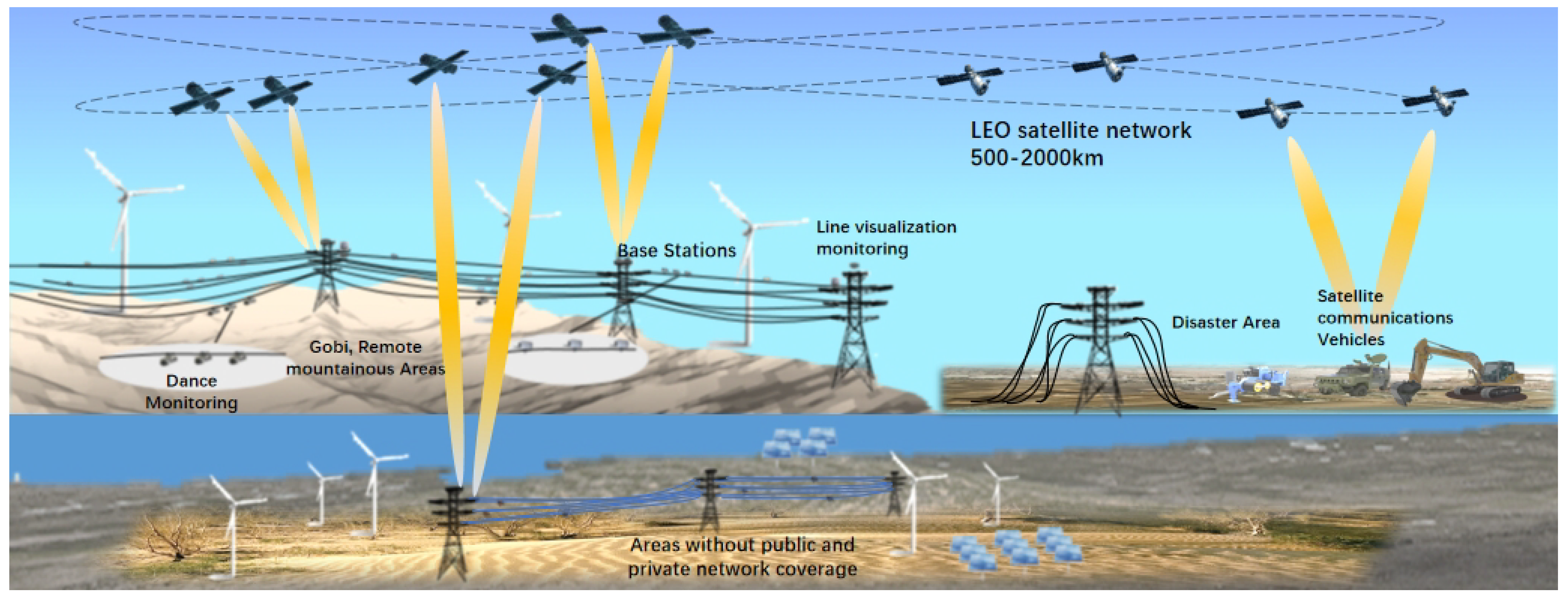
1. Introduction
2. Materials and Methods
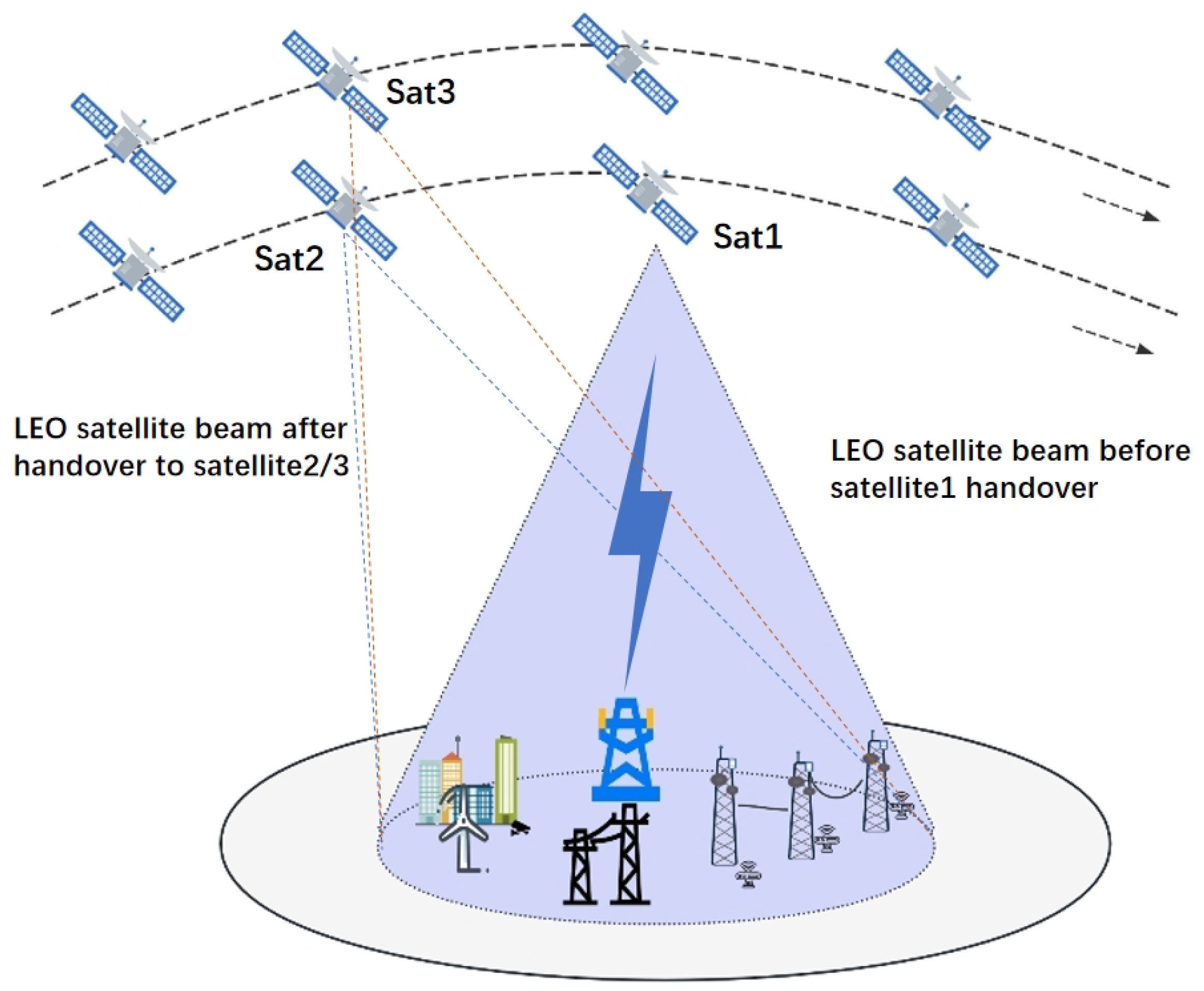
2.1. System Model
2.2. Analysis of Handover Decision Factors
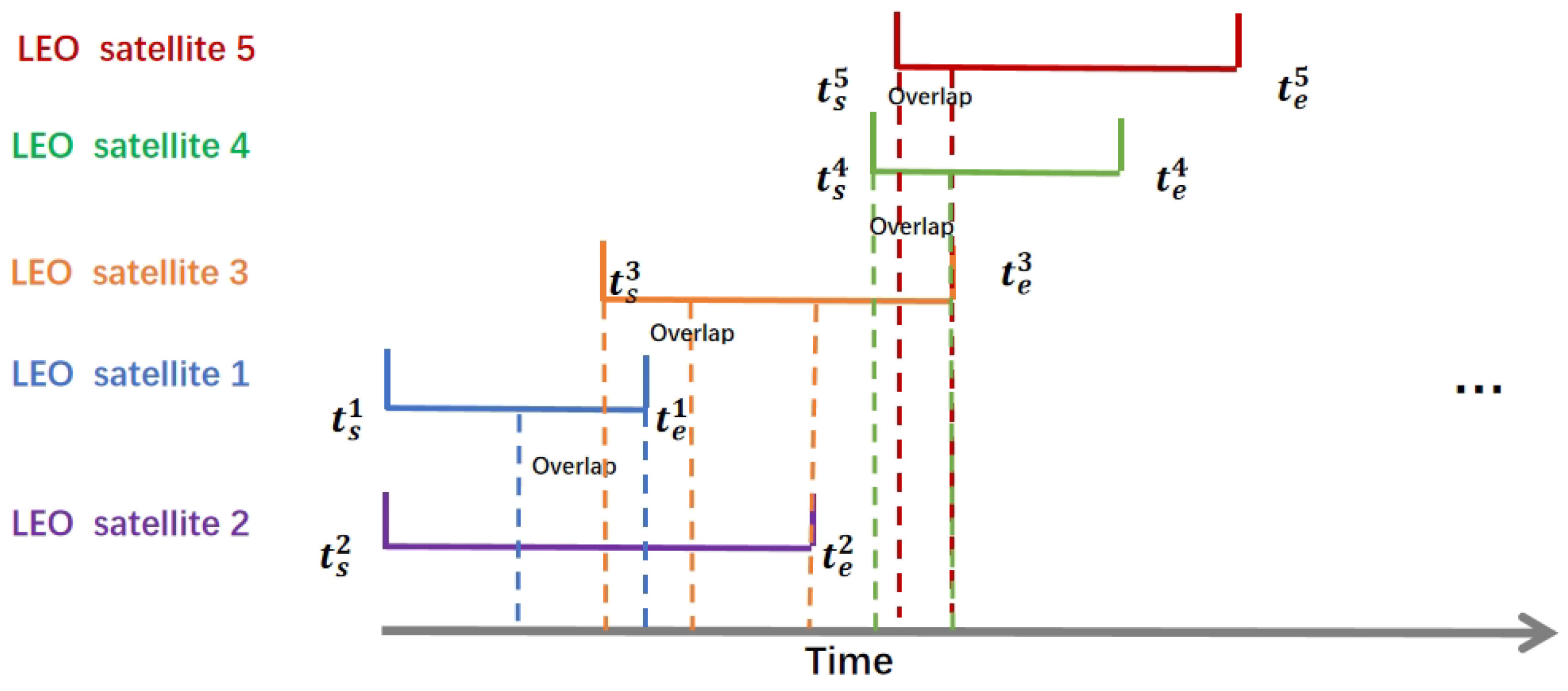
2.2.1. Remaining Service Time
2.2.2. Transmission Delay
2.2.3. Data Rate
2.3. Problem Description
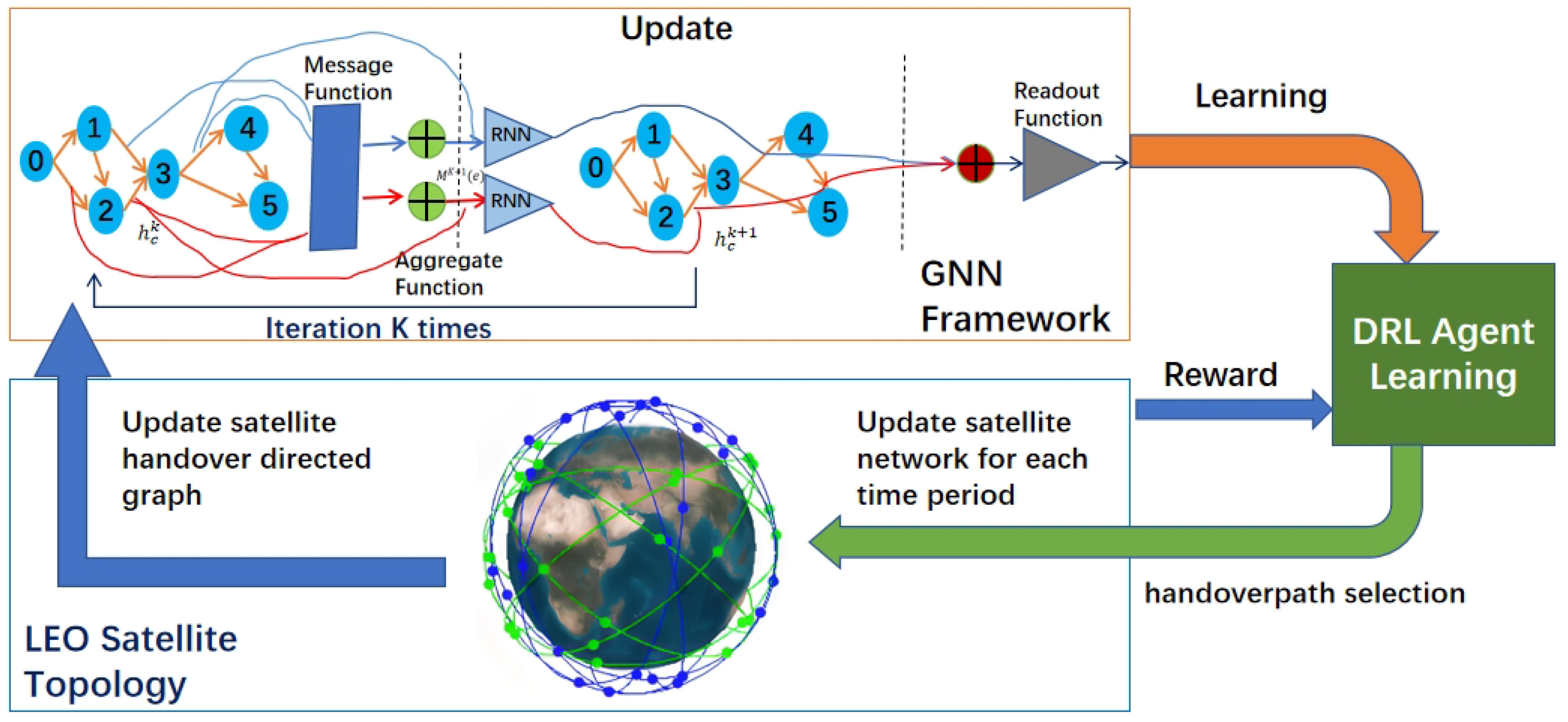
3. The Proposed DRL + GNN-Based Handover Scheme
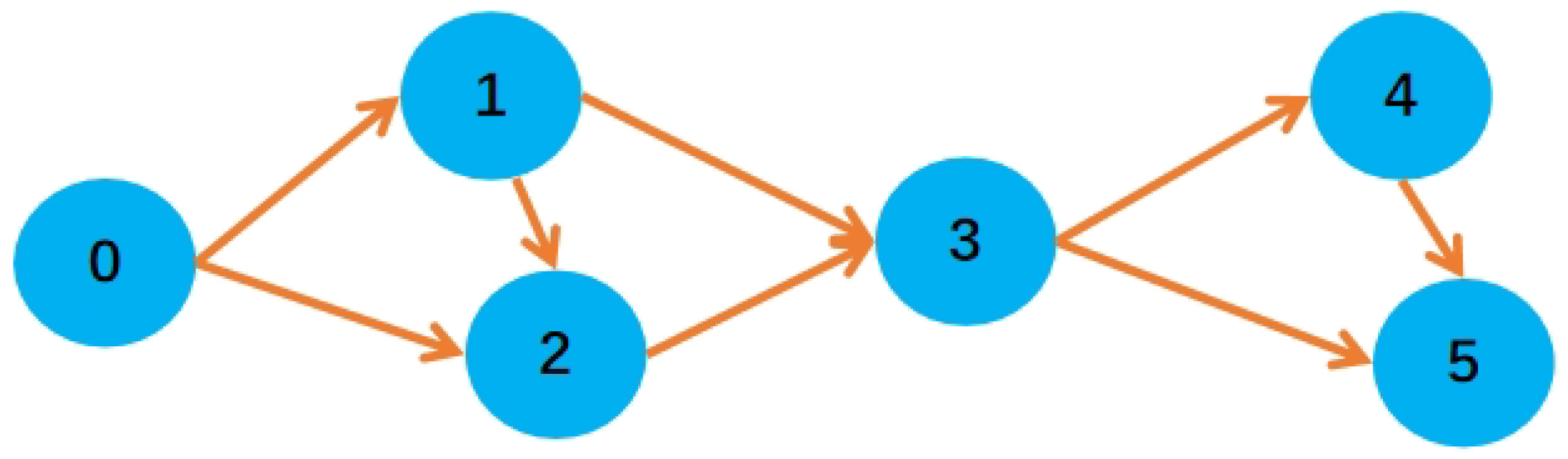
3.1. GNN Architecture
| Algorithm 1 LEO satellite handover graph state representation learning |
|
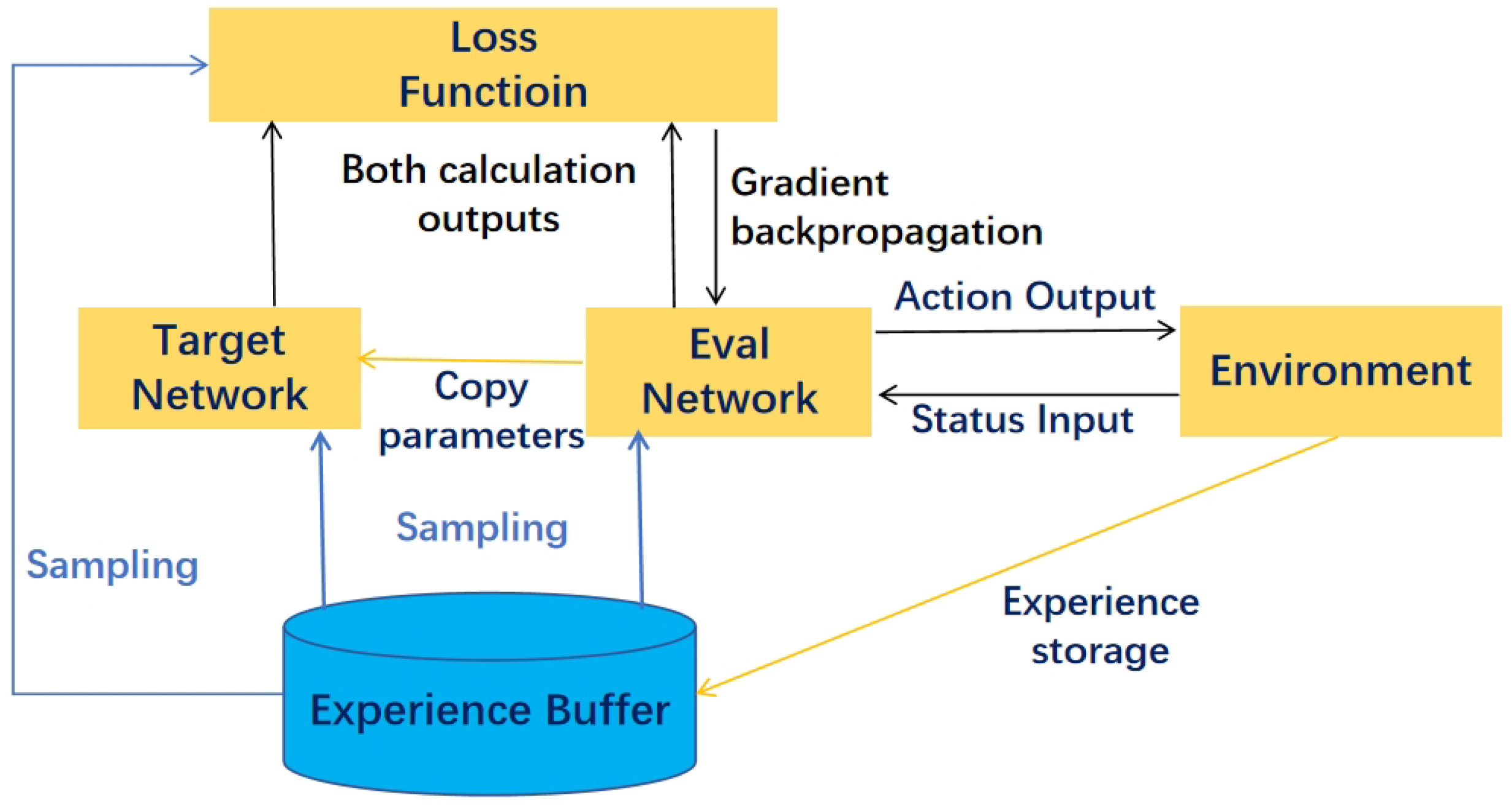
3.2. DQN Framework
- State space
- Action space
- Reward function
3.3. MPNN-DQN Based Handover Scheme
| Algorithm 2 Satellite handover decision algorithm based on MPNN-DQN |
|
4. Results
4.1. Experimental Setup
4.2. Learning Convergence Analysis
4.3. Comparison of Algorithm Performance
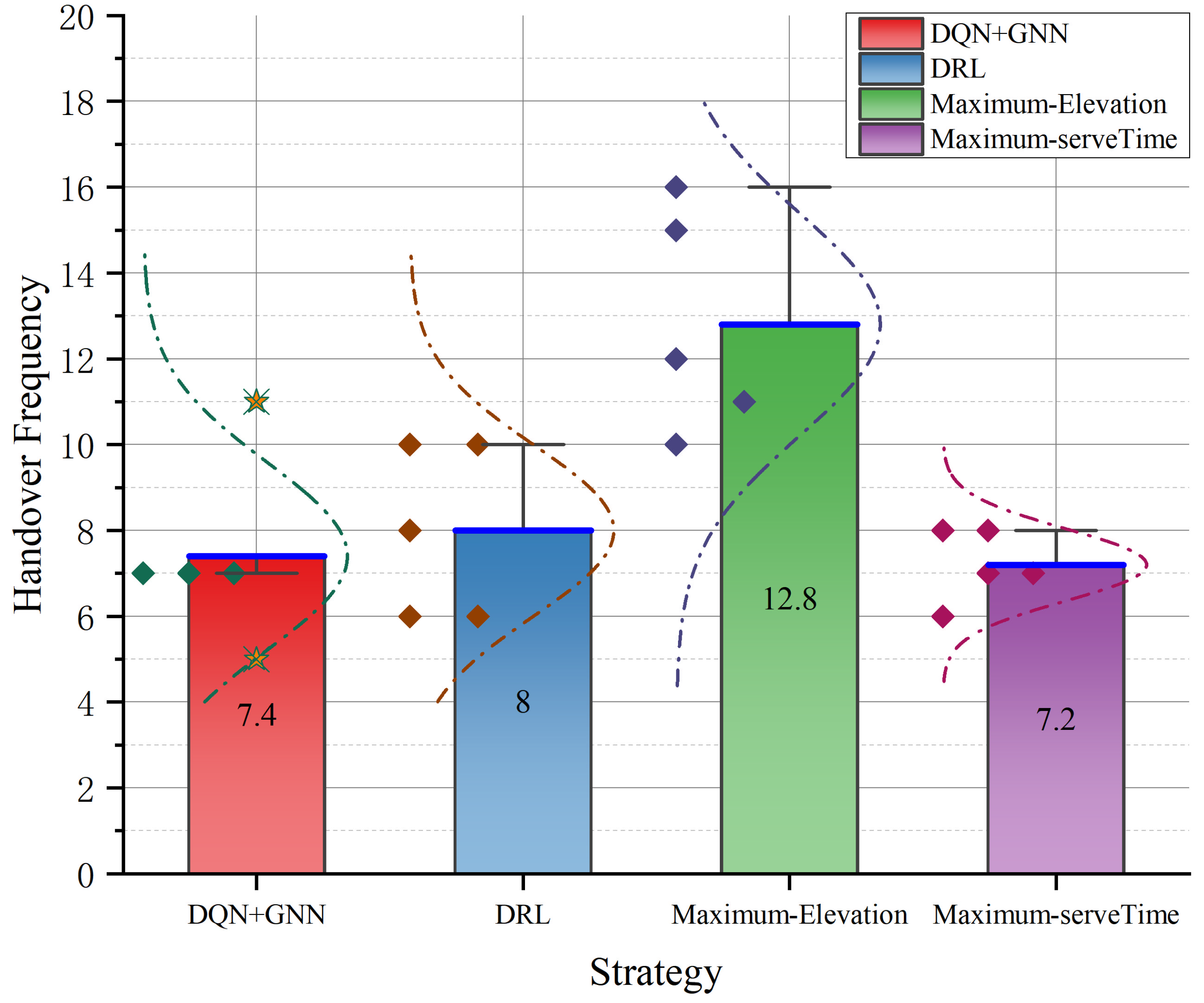
4.3.1. Handover Frequency Comparison
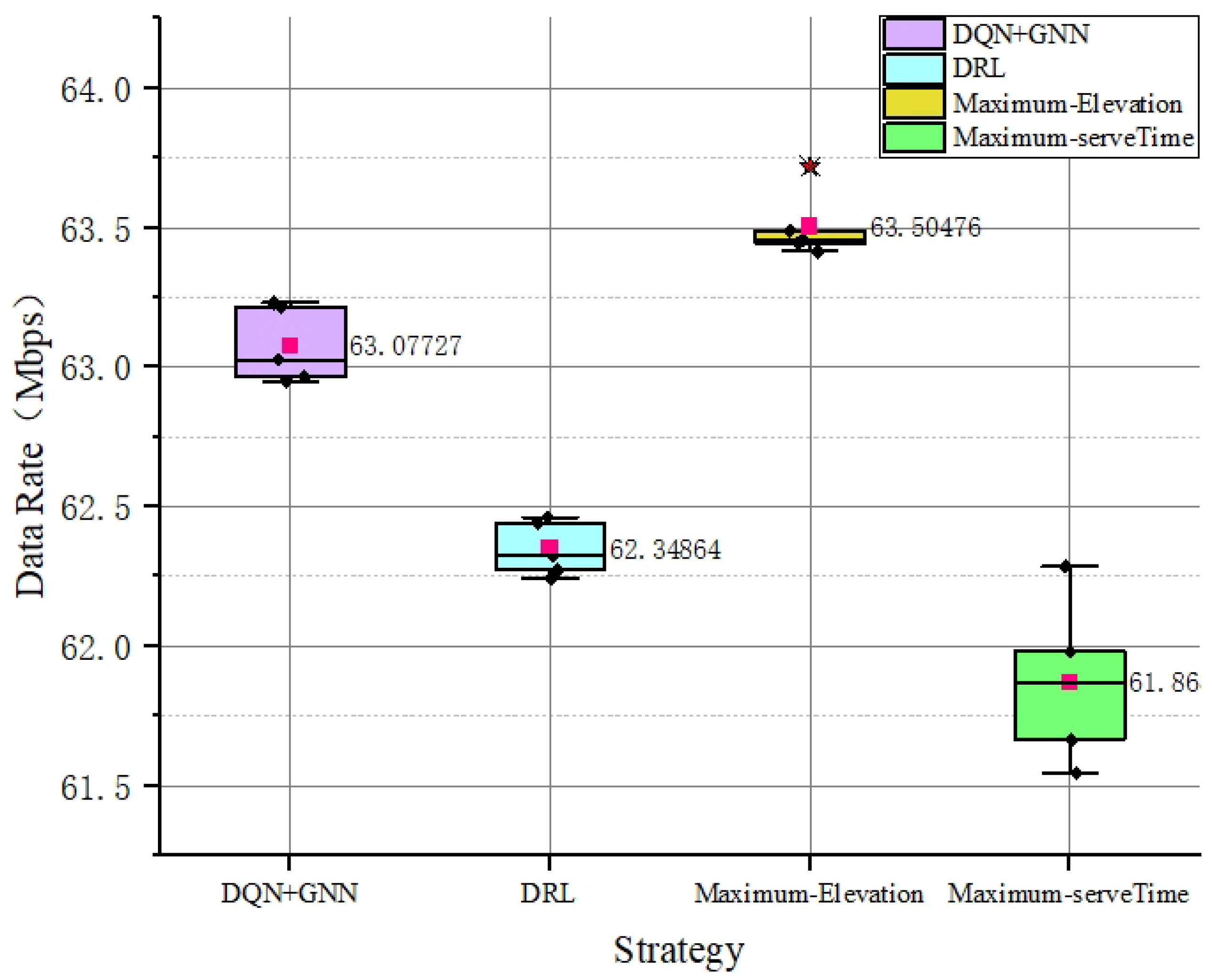
4.3.2. Data Rate Comparison
4.3.3. Handover Delay Comparison
4.3.4. Complexity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, H.; Li, P.; Zhang, L.; Zhu, Y.; Al-Zahrani, F.A.; Ahmed, K. Application of optical fiber nanotechnology in power communication transmission. Alex. Eng. J. 2020, 59, 5019–5030. [Google Scholar] [CrossRef]
- Cao, J.; Liu, J.; Li, X.; Zeng, L.; Wang, B. Performance analysis of a new power wireless private network in intelligent distribution networks. In Proceedings of the 2012 Power Engineering and Automation Conference, Wuhan, China, 18–20 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Li, Z.; Wang, Y.; Liu, M.; Sun, R.; Chen, Y.; Yuan, J.; Li, J. Energy efficient resource allocation for UAV-assisted space-air-ground Internet of remote things networks. IEEE Access 2019, 7, 145348–145362. [Google Scholar] [CrossRef]
- Zhu, Q.; Sun, F.; Hua, Z. Research on hybrid network communication scheme of high and low orbit satellites for power application. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 9, pp. 460–466. [Google Scholar]
- Berger, L.T.; Iniewski, K. Smart Grid Applications, Communications, and Security; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-air-ground integrated network: A survey. IEEE Commun. Surv. Tutor. 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- De Sanctis, M.; Cianca, E.; Araniti, G.; Bisio, I.; Prasad, R. Satellite communications supporting internet of remote things. IEEE Internet Things J. 2015, 3, 113–123. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Zhou, H.; Chen, X.; Peng, Y.; Yu, P.; Wang, Y.; Feng, X. A system of power emergency communication system based BDS and LEO satellite. In Proceedings of the 2021 Computing, Communications and IoT Applications (ComComAp), Shenzhen, China, 26–28 November 2021; IEEE: Hoboken, NJ, USA, 2021; pp. 286–291. [Google Scholar]
- Liu, J.; Shi, Y.; Zhao, L.; Cao, Y.; Sun, W.; Kato, N. Joint placement of controllers and gateways in SDN-enabled 5G-satellite integrated network. IEEE J. Sel. Areas Commun. 2018, 36, 221–232. [Google Scholar] [CrossRef]
- Giordani, M.; Zorzi, M. Satellite communication at millimeter waves: A key enabler of the 6G era. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; IEEE: Hoboken, NJ, USA, 2020; pp. 383–388. [Google Scholar]
- Liu, Z.; Zha, X.; Ren, X.; Yao, Q. Research on Handover Strategy of LEO Satellite Network. In Proceedings of the 2021 2nd International Conference on Big Data and Informatization Education (ICBDIE), Hangzhou, China, 2–4 April 2021; IEEE: Hoboken, NJ, USA, 2021; pp. 188–194. [Google Scholar]
- Gong, Y. A Review of Low Earth Orbit Satellite Communication Mobility Management. Commun. Technol. 2023, 56, 923–928. [Google Scholar]
- Ilčev, S.D. Global Mobile Satellite Communications Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Han, Z.; Xu, C.; Zhao, G.; Wang, S.; Cheng, K.; Yu, S. Time-varying topology model for dynamic routing in LEO satellite constellation networks. IEEE Trans. Veh. Technol. 2022, 72, 3440–3454. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, X.; Sun, J.; Gu, X.; Guo, Q. Intelligent resource management for satellite and terrestrial spectrum shared networking toward B5G. IEEE Wirel. Commun. 2020, 27, 54–61. [Google Scholar] [CrossRef]
- Bottcher, A.; Werner, R. Strategies for handover control in low earth orbit satellite systems. In Proceedings of the IEEE Vehicular Technology Conference (VTC), Stockholm, Sweden, 8–10 June 1994; IEEE: Hoboken, NJ, USA, 1994; pp. 1616–1620. [Google Scholar]
- Xu, J.; Wang, Z.; Zhang, G. Design and transmission of broadband LEO constellation satellite communication system based on high-elevation angle. Commun. Technol. 2018, 51, 1844–1849. [Google Scholar]
- Papapetrou, E.; Karapantazis, S.; Dimitriadis, G.; Pavlidou, F.N. Satellite handover techniques for LEO networks. Int. J. Satell. Commun. Netw. 2004, 22, 231–245. [Google Scholar] [CrossRef]
- Gkizeli, M.; Tafazolli, R.; Evans, B.G. Hybrid channel adaptive handover scheme for non-GEO satellite diversity based systems. IEEE Commun. Lett. 2001, 5, 284–286. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Xu, Y.; Tian, H.; Cui, S. Handover control in wireless systems via asynchronous multiuser deep reinforcement learning. IEEE Internet Things J. 2018, 5, 4296–4307. [Google Scholar] [CrossRef]
- Duan, C.; Feng, J.; Chang, H.; Song, B.; Xu, Z. A novel handover control strategy combined with multi-hop routing in LEO satellite networks. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Vancouver, BC, Canada, 21–25 May 2018; IEEE: Hoboken, NJ, USA, 2018; pp. 845–851. [Google Scholar]
- Rehman, T.; Khan, F.; Khan, S.; Ali, A. Optimizing satellite handover rate using particle swarm optimization (pso) algorithm. J. Appl. Emerg. Sci. 2017, 7, 53–63. [Google Scholar]
- Zhou, J.; Ye, X.; Pan, Y.; Xiao, F.; Sun, L. Dynamic channel reservation scheme based on priorities in LEO satellite systems. J. Syst. Eng. Electron. 2015, 26, 1–9. [Google Scholar] [CrossRef]
- Huang, F.; Xu, H.; Zhou, H.; Wu, S.Q. QoS based average weighted scheme for LEO satellite communications. J. Electron. Inf. Technol. 2008, 30, 2411–2414. [Google Scholar] [CrossRef]
- Miao, J.; Wang, P.; Yin, H.; Chen, N.; Wang, X. A multi-attribute decision handover scheme for LEO mobile satellite networks. In Proceedings of the 2019 IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019; IEEE: Hoboken, NJ, USA, 2019; pp. 938–942. [Google Scholar]
- Wu, Z.; Jin, F.; Luo, J.; Fu, Y.; Shan, J.; Hu, G. A graph-based satellite handover framework for LEO satellite communication networks. IEEE Commun. Lett. 2016, 20, 1547–1550. [Google Scholar] [CrossRef]
- Hu, X.; Song, H.; Liu, S.; LI, X.; Wang, W.; Wang, C. Real-time prediction and updating method for LEO satellite handover based on time evolving graph. J. Commun. 2018, 39, 43–51. [Google Scholar]
- Hozayen, M.; Darwish, T.; Kurt, G.K.; Yanikomeroglu, H. A graph-based customizable handover framework for LEO satellite networks. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; IEEE: Hoboken, NJ, USA, 2022; pp. 868–873. [Google Scholar]
- Li, H.; Liu, R.; Hu, B.; Ni, L.; Wang, C. A multi-attribute graph based handover scheme for LEO satellite communication networks. In Proceedings of the 2022 IEEE 10th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 22–23 October 2022; IEEE: Hoboken, NJ, USA, 2022; pp. 127–131. [Google Scholar]
- Wang, J.; Mu, W.; Liu, Y.; Guo, L.; Zhang, S.; Gui, G. Deep reinforcement learning-based satellite handover scheme for satellite communications. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; IEEE: Hoboken, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Zhang, C.; Zhang, N.; Cao, W.; Tian, K.; Yang, Z. An AI-based optimization of handover strategy in non-terrestrial networks. In Proceedings of the 2020 ITU Kaleidoscope: Industry-Driven Digital Transformation (ITU K), Ha Noi, Vietnam, 7–11 December 2020; IEEE: Hoboken, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Liang, J.; Zhang, D.; Qiu, F. Multi-attribute Handoff Control Methodfor LEO Satellite Internet. J. Army Eng. Univ. 2022, 1, 14–20. [Google Scholar]
- 3GPP. Study on Architecture Aspects for Using Satellite Access in 5G. Technical Report, 3rd Generation Partnership Project (3GPP), Technical Specifcation (TS) 23.737, March 2021. Available online: https://itecspec.com/archive/3gpp-specification-tr-23-737/ (accessed on 23 June 2024).
- Vallado, D.; Crawford, P.; Hujsak, R.; Kelso, T. Revisiting spacetrack report# 3. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Big Sky, MT, USA, 21–24 August 2006; p. 6753. [Google Scholar]
- Liu, M. Research on Handover Strategy in Low Earth Orbit Mobile Satellite Network. Master’s Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 2021. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Networks 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the INTERNATIONAL Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Almasan, P.; Suárez-Varela, J.; Rusek, K.; Barlet-Ros, P.; Cabellos-Aparicio, A. Deep reinforcement learning meets graph neural networks: Exploring a routing optimization use case. Comput. Commun. 2022, 196, 184–194. [Google Scholar] [CrossRef]
- Zhang, Z. Research on LEO Satellite Handover Technology Based on 5G Architecture. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2023. [Google Scholar]



| Symbol | Description |
|---|---|
| dk | Transmission delay |
| rk | Data Rate |
| tk | remaining service time |
| Zero padding |
| Parameter | Value |
|---|---|
| UE position (Latitude, Longitude, Altitude) | (−62°, 50°, 0 m) |
| Simulation time (minutes) | 30 |
| Number of total time slots | 60 |
| Number of total satellites providing coverage | 15 |
| Satellite altitude (km) | 400–600 |
| Minimum coverage elevation angle | 10° |
| Simulation starting time | 1 May 2023 09:30 a.m. (UTC) |
| Parameter | Value |
|---|---|
| Discount factor | 0.95 |
| Learning rate | 0.001 |
| Experience replay pool size | 4000 |
| Initial exploration rate | 1 |
| Termination of exploration rate | 0.005 |
| Training batch size | 32 |
| Q-target network parameter update step size (episodes) | 50 |
| DQN iterations | 1600 |
| Loss Function | Mean-Squared Error (MSE) |
| Optimizer | Stochastic Gradient Descent (SGD) |
| Method | Training Size | Computing Time | Training Required |
|---|---|---|---|
| DQN + GNN | 5000 episodes | 24 h | Yes |
| DRL | 5000 episodes | 18 h | Yes |
| Max-Elevation | N/A | N/A | No |
| Max-ServeTime | N/A | N/A | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Gao, W.; Zhang, K. A Graph Reinforcement Learning-Based Handover Strategy for Low Earth Orbit Satellites under Power Grid Scenarios. Aerospace 2024, 11, 511. https://doi.org/10.3390/aerospace11070511
Yu H, Gao W, Zhang K. A Graph Reinforcement Learning-Based Handover Strategy for Low Earth Orbit Satellites under Power Grid Scenarios. Aerospace. 2024; 11(7):511. https://doi.org/10.3390/aerospace11070511
Chicago/Turabian StyleYu, Haizhi, Weidong Gao, and Kaisa Zhang. 2024. "A Graph Reinforcement Learning-Based Handover Strategy for Low Earth Orbit Satellites under Power Grid Scenarios" Aerospace 11, no. 7: 511. https://doi.org/10.3390/aerospace11070511
APA StyleYu, H., Gao, W., & Zhang, K. (2024). A Graph Reinforcement Learning-Based Handover Strategy for Low Earth Orbit Satellites under Power Grid Scenarios. Aerospace, 11(7), 511. https://doi.org/10.3390/aerospace11070511






