Design and Analysis of Low-Gravity Simulation Scheme for Mars Ascent Vehicle
Abstract
1. Introduction
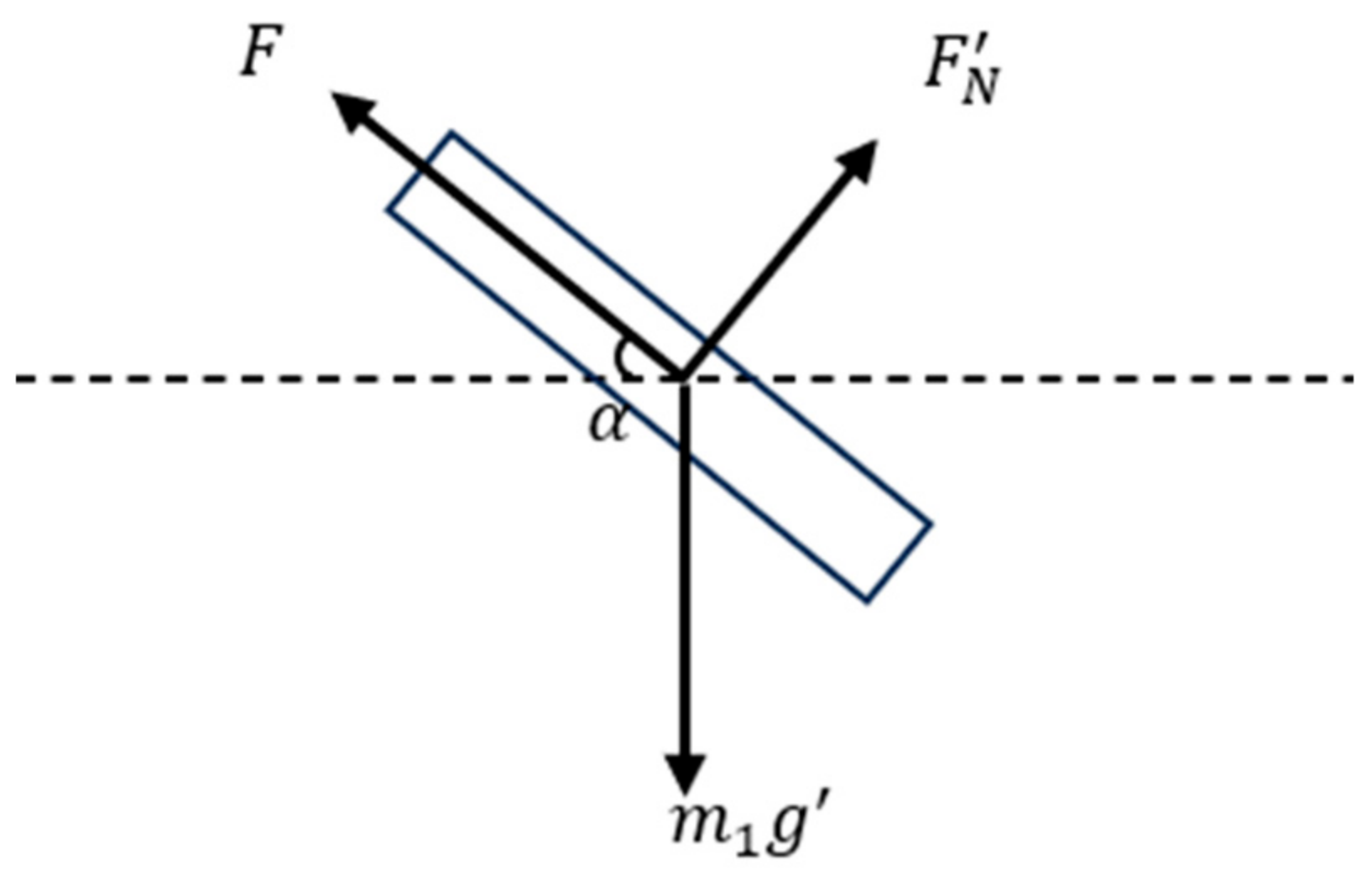
2. MAV Kinematic Analysis
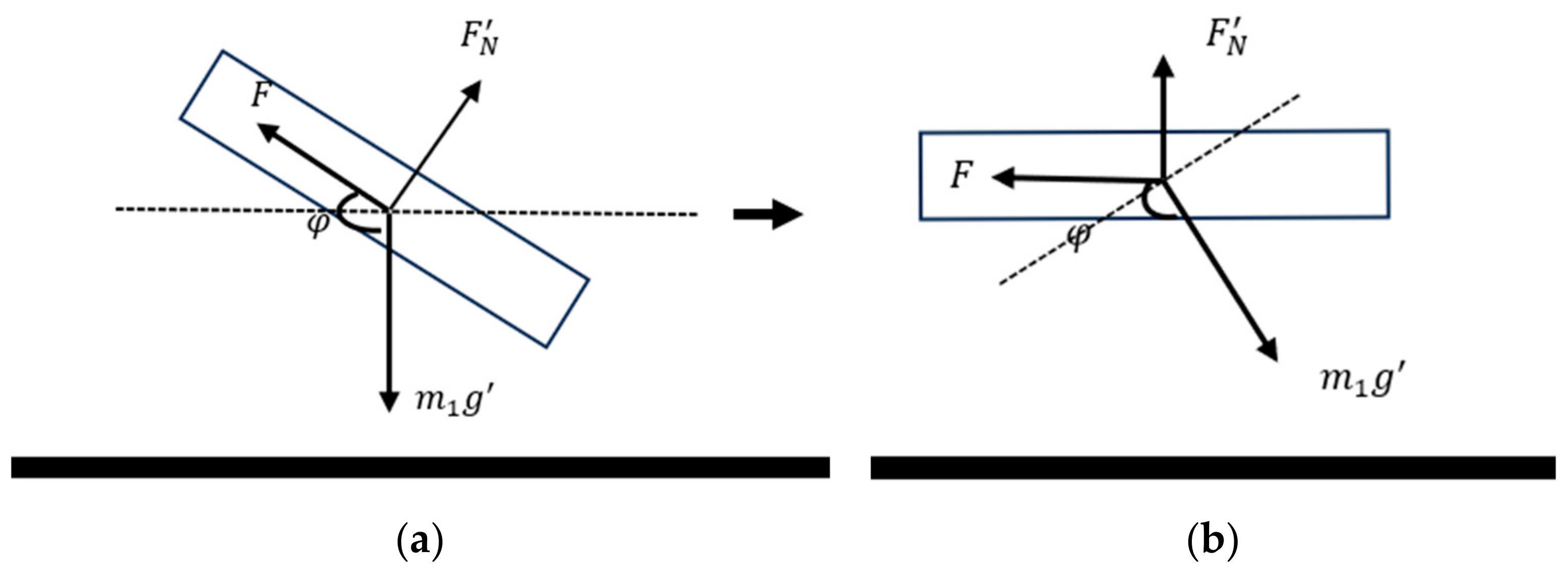
3. Uniqueness of MAV Low-Gravity Simulation
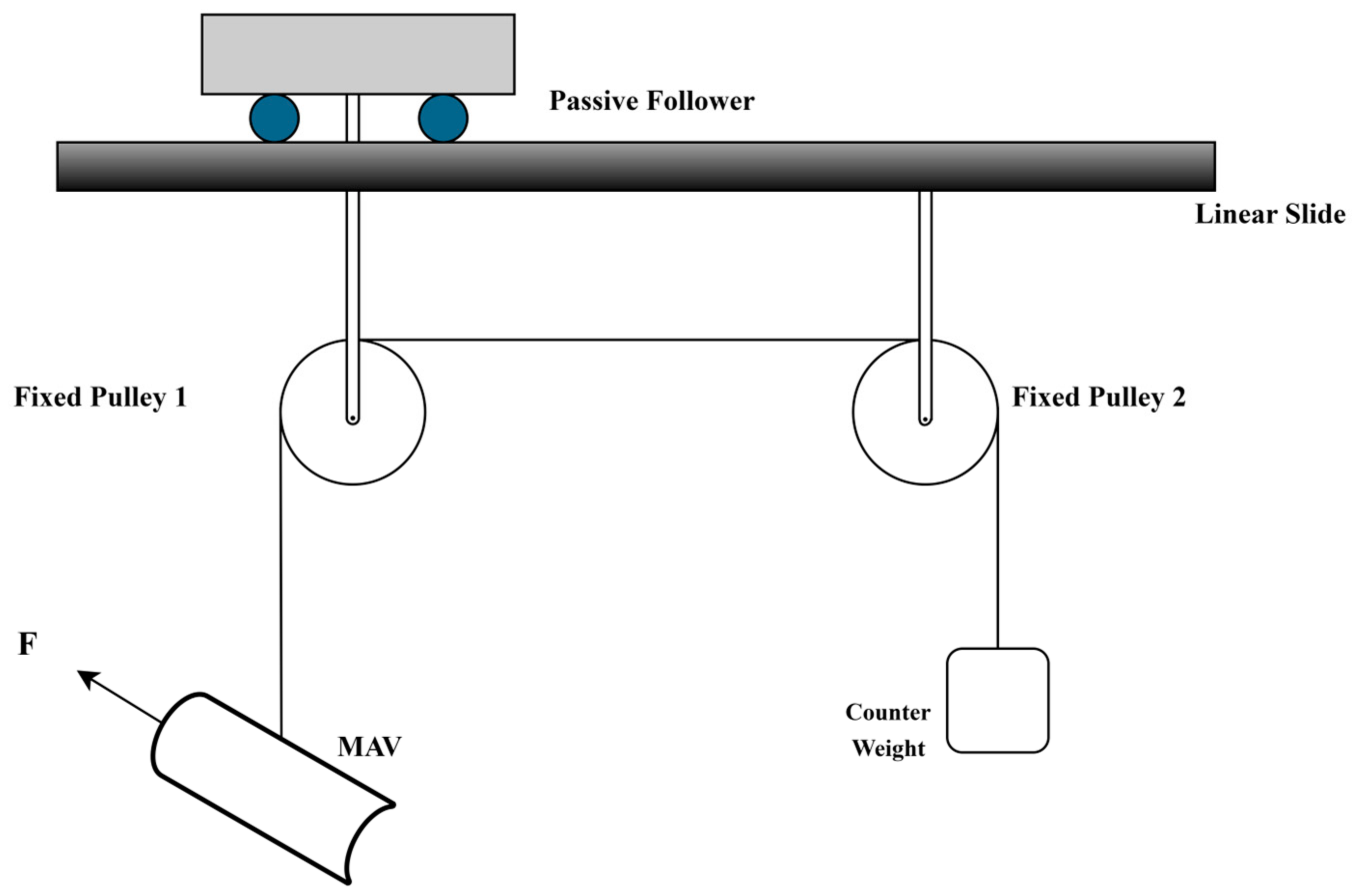
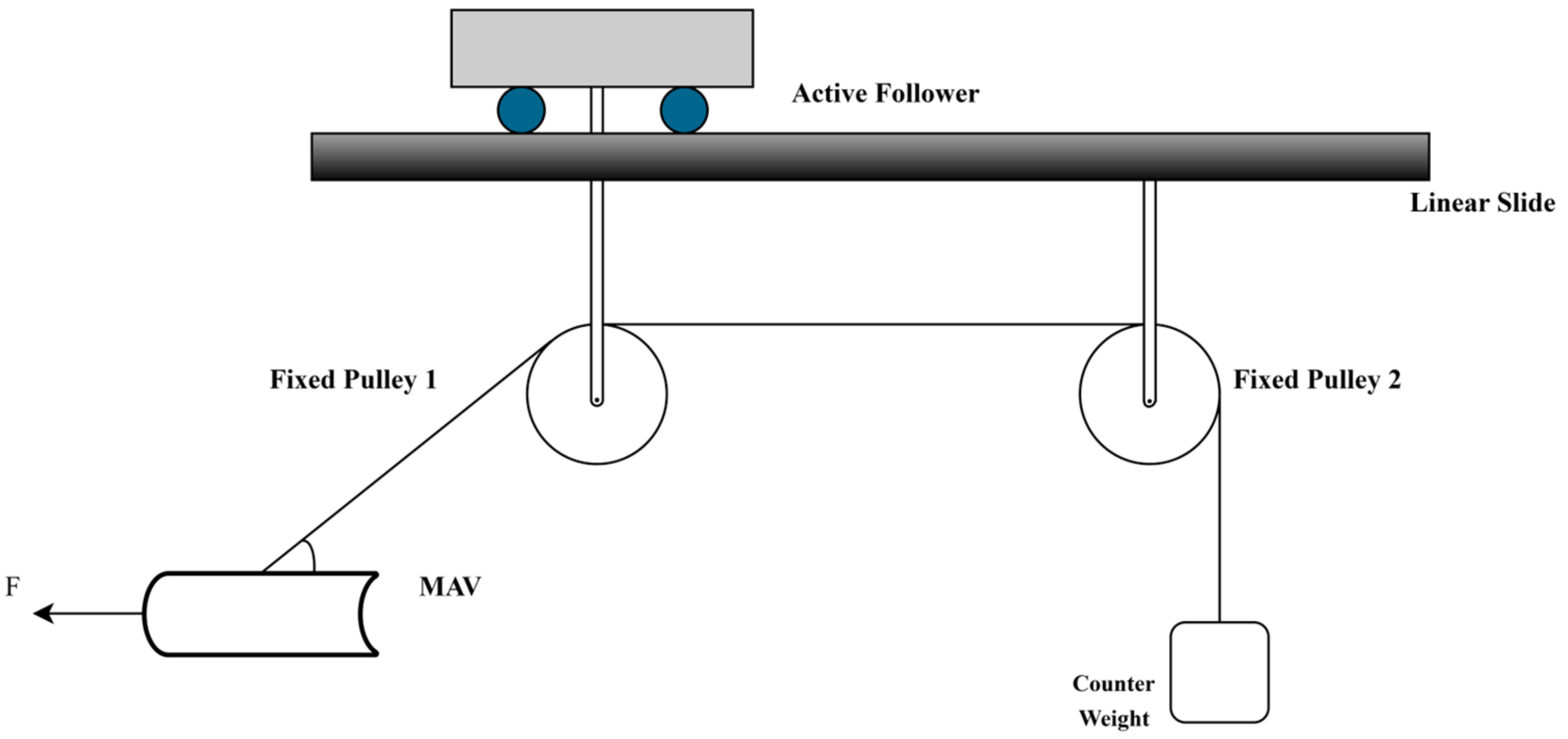
Classical Pulley Balancing Cable Suspension Scheme
4. Cable Suspension Scheme Design
4.1. Improved Pulley Balancing Cable Suspension Scheme
4.2. Cable Suspension Scheme Based on Coordinate Transformation
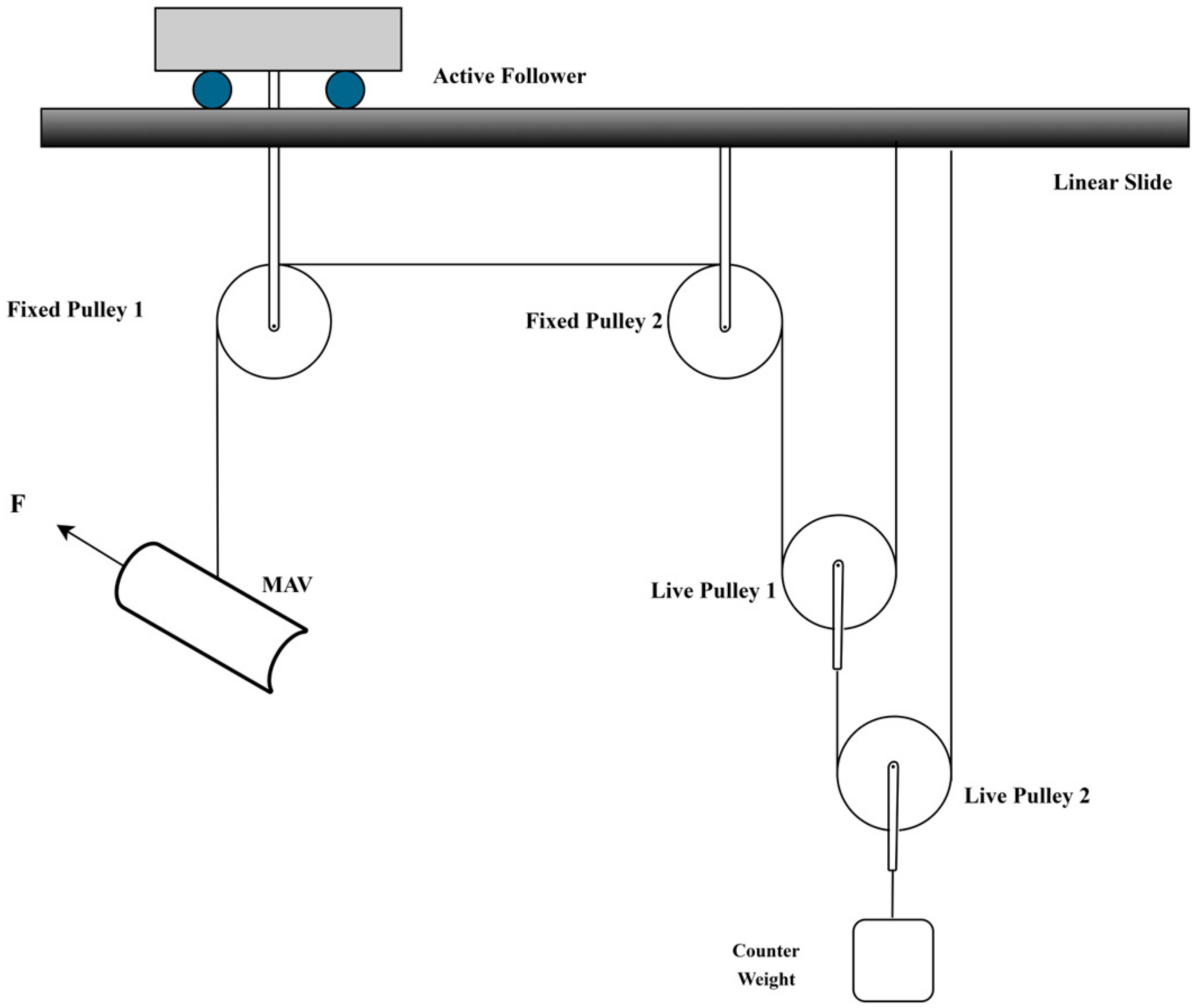
4.3. Cable Suspension Scheme Based on Movable Pulley Block
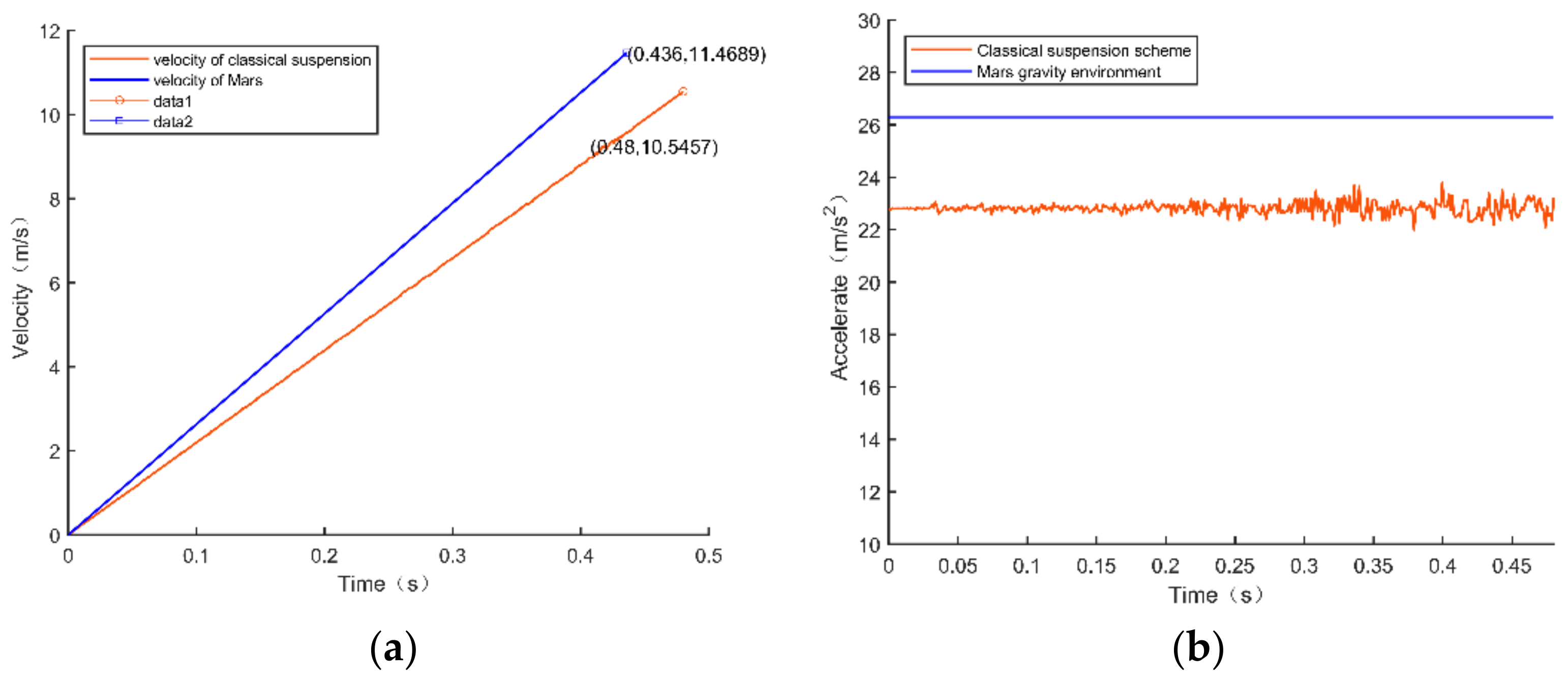
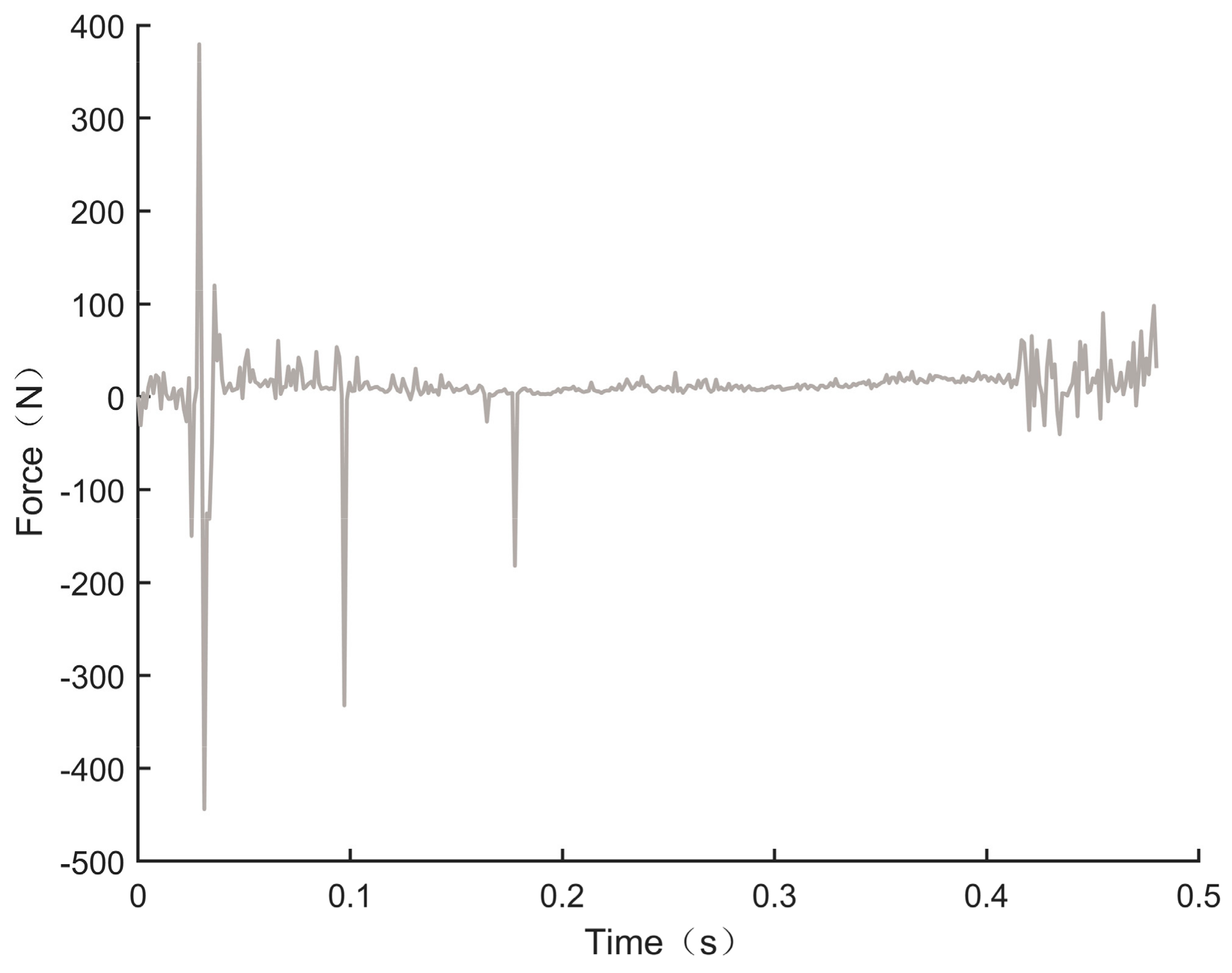
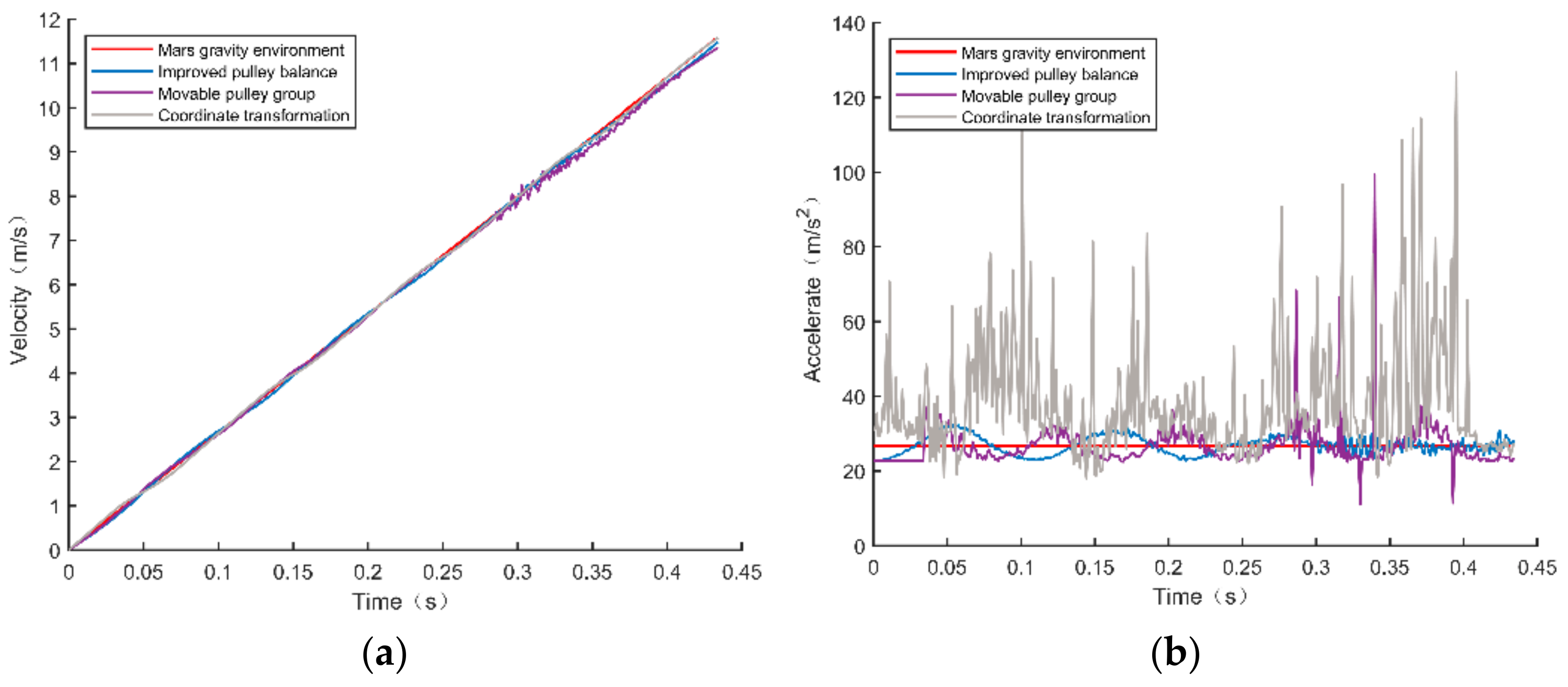
5. Simulation Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McCollum, L.T.; Schnell, A.; Yaghoubi, D.; Bean, Q.; McCauley, R.; Prince, A. Development Concepts for Mars Ascent Vehicle (MAV) Solid and Hybrid Vehicle Systems. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Shotwell, R. History of Mars Ascent Vehicle Development over the Last 20 Years. In Proceedings of the 2016 IEEE Aerospace Conferenc, Big Sky, MT, USA, 5–12 March 2016; pp. 1–11. [Google Scholar] [CrossRef]
- Prince, A.; Kibbey, T.; Karp, A. A Design for a Two-Stage Solid Mars Ascent Vehicle. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; pp. 1–18. [Google Scholar] [CrossRef]
- Wang, W.; Tang, X.; Shao, Z.; Yang, J.; Yi, W. Design and Analysis of a Wire-Driven Parallel Mechanism for Low-Gravity Environment Simulation. Adv. Mech. Eng. 2014, 6, 810606. [Google Scholar] [CrossRef]
- Xu, B.; Shi, J.; Zhang, J.; Zhao, C.; Hou, W.; Zhao, B. Design and Implementation of Ultra-Large Inertia Spacecraft Micro-Low Gravity Simulation Test System. J. Mach. Des. 2022, 39, 107–113. [Google Scholar] [CrossRef]
- Gao, H.; Niu, F.; Liu, Z.; Yu, H.; Li, N. Suspended Micro-Low Gravity Environment Simulation Technology: Status Quo and Prospect. Acta Areonaut. Astronaut. Sin. 2021, 42, 523911. [Google Scholar] [CrossRef]
- Sun, J.; Wei, C.; Chen, H.; Wang, B.; Li, X.; Zhang, Q. Design of Gravity Compensation Scheme for Passive Lifting Method of Multi-Degree Freedom Robotic Arm. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 447–451. [Google Scholar] [CrossRef]
- Jia, J.; Jia, Y.; Sun, S. Modeling and Control of a Suspended Gravity Compensation System with Rigid-Flexible Coupling. Proc. Int. Conf. Artif. Life Robot. 2016, 21, 369–372. [Google Scholar] [CrossRef]
- Jia, J.; Jia, Y.; Sun, S. Preliminary Design and Development of an Active Suspension Gravity Compensation System for Ground Verification. Mech. Mach. Theory 2018, 128, 492–507. [Google Scholar] [CrossRef]
- De Stefano, M.; Vijayan, R.; Stemmer, A.; Elhardt, F.; Ott, C. A Gravity Compensation Strategy for On-Ground Validation of Orbital Manipulators. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 11859–11865. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Y.; Ju, C.; Xue, X.; Zhang, J. A New Force Control Method by Combining Traditional PID Control with Radial Basis Function Neural Network for a Spacecraft Low-Gravity Simulation System. Aerospace 2023, 10, 520. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, H.B.; Deng, Z.Q. Design and Implementation of a Large-Scale Gravity Compensation System for Lunar Rover. Appl. Mech. Mater. 2013, 385–386, 759–767. [Google Scholar] [CrossRef]
- Li, L.; Deng, Z.; Gao, H.; Guo, P. Active Gravity Compensation Test Bed for a Six-DOF Free-Flying Robot. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 3135–3140. [Google Scholar] [CrossRef]
- Jiang, B.; Hussain, M.T.; Zeng, X. Attitude-Adjusting Dynamical Behavior of Cubic Rover on Low-Gravity Testbed. Astrodynamics 2024, 8, 149–159. [Google Scholar] [CrossRef]
- Hou, W.; Hao, Y.; Wang, C.; Chen, L.; Li, G.; Zhao, B.; Wang, H.; Wei, Q.; Xu, S.; Feng, K.; et al. Theoretical and Experimental Investigations on High-Precision Micro-Low-Gravity Simulation Technology for Lunar Mobile Vehicle. Sensors 2023, 23, 3458. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.B.; Nie, H.; Wan, J.L.; Lin, Q. Investigation on Landing Impact Dynamic and Low-Gravity Experiments for Deep Space Lander. Sci. China Physics Mech. Astron. 2014, 57, 1987–1997. [Google Scholar] [CrossRef]
- Zhao, Z.; Fu, K.; Li, M.; Li, J.; Xiao, Y. Gravity Compensation System of Mesh Antennas for In-Orbit Prediction of Deployment Dynamics. Acta Astronaut. 2020, 167, 1–13. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, L.; Liu, Y.; Jia, S. Dynamics of Circular Thin Membrane Solar Arrays Based on Ground Zero-Gravity Simulation Test. IET Conf. Proc. 2022, 2022, 847–851. [Google Scholar] [CrossRef]
- Xiang, S.; Gao, H.; Liu, Z.; Yu, H.; Deng, Z. A Novel Active Suspension Gravity Compensation System for Physically Simulating Human Walking in Microgravity. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1052–1057. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, J.; Wang, N.; Zhu, A.; Wang, X.; Zhang, Z.; Xu, H. Design and Analysis of a Novel Weight Reduction System for Simulating Astronauts Walking in Low-Gravity Environment. In Proceedings of the International Conference on Advanced Robotics and Mechatronics (ICARM), Sanya, China, 8–10 July 2023; pp. 1119–1124. [Google Scholar] [CrossRef]
- Shotwell, R.; Benito, J.; Karp, A.; Dankanich, J. A Mars Ascent Vehicle for Potential Mars Sample Return. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–12. [Google Scholar] [CrossRef]
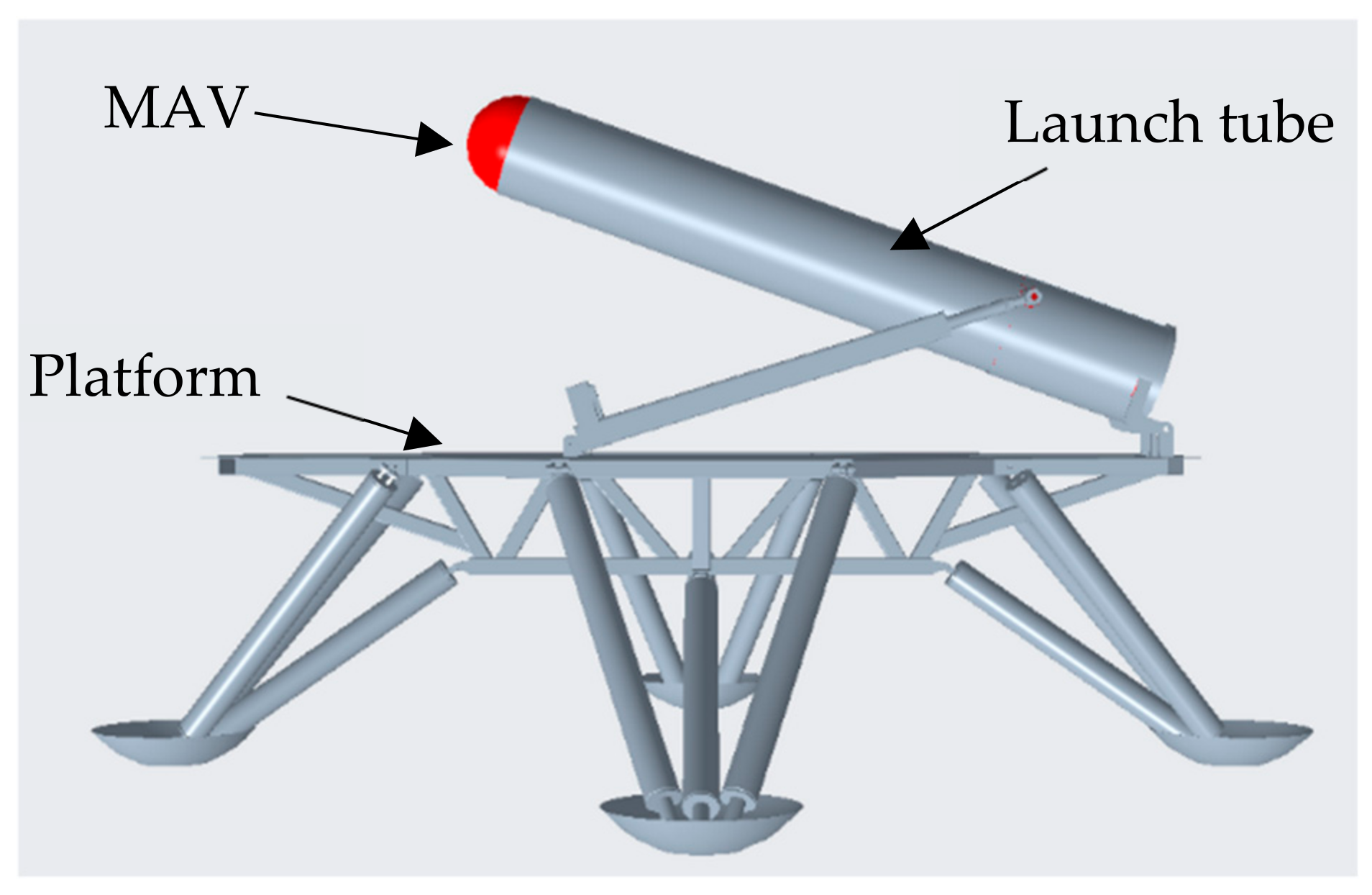


| Property | Shape | Thrust (N) | Mass (kg) | Length (m) | Diameter (m) |
|---|---|---|---|---|---|
| MAV | Cylindrical | 10,000 | 340 | 2.4 | 0.515 |
| Launch tube | Cylindrical | None | 128 | 2.5 | 0.555 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, H.; Hu, Z.; Wang, C.; Chen, J. Design and Analysis of Low-Gravity Simulation Scheme for Mars Ascent Vehicle. Aerospace 2024, 11, 424. https://doi.org/10.3390/aerospace11060424
Li C, Wang H, Hu Z, Wang C, Chen J. Design and Analysis of Low-Gravity Simulation Scheme for Mars Ascent Vehicle. Aerospace. 2024; 11(6):424. https://doi.org/10.3390/aerospace11060424
Chicago/Turabian StyleLi, Chen, Huijuan Wang, Zhicheng Hu, Chen Wang, and Jinbao Chen. 2024. "Design and Analysis of Low-Gravity Simulation Scheme for Mars Ascent Vehicle" Aerospace 11, no. 6: 424. https://doi.org/10.3390/aerospace11060424
APA StyleLi, C., Wang, H., Hu, Z., Wang, C., & Chen, J. (2024). Design and Analysis of Low-Gravity Simulation Scheme for Mars Ascent Vehicle. Aerospace, 11(6), 424. https://doi.org/10.3390/aerospace11060424






