Figure 1.
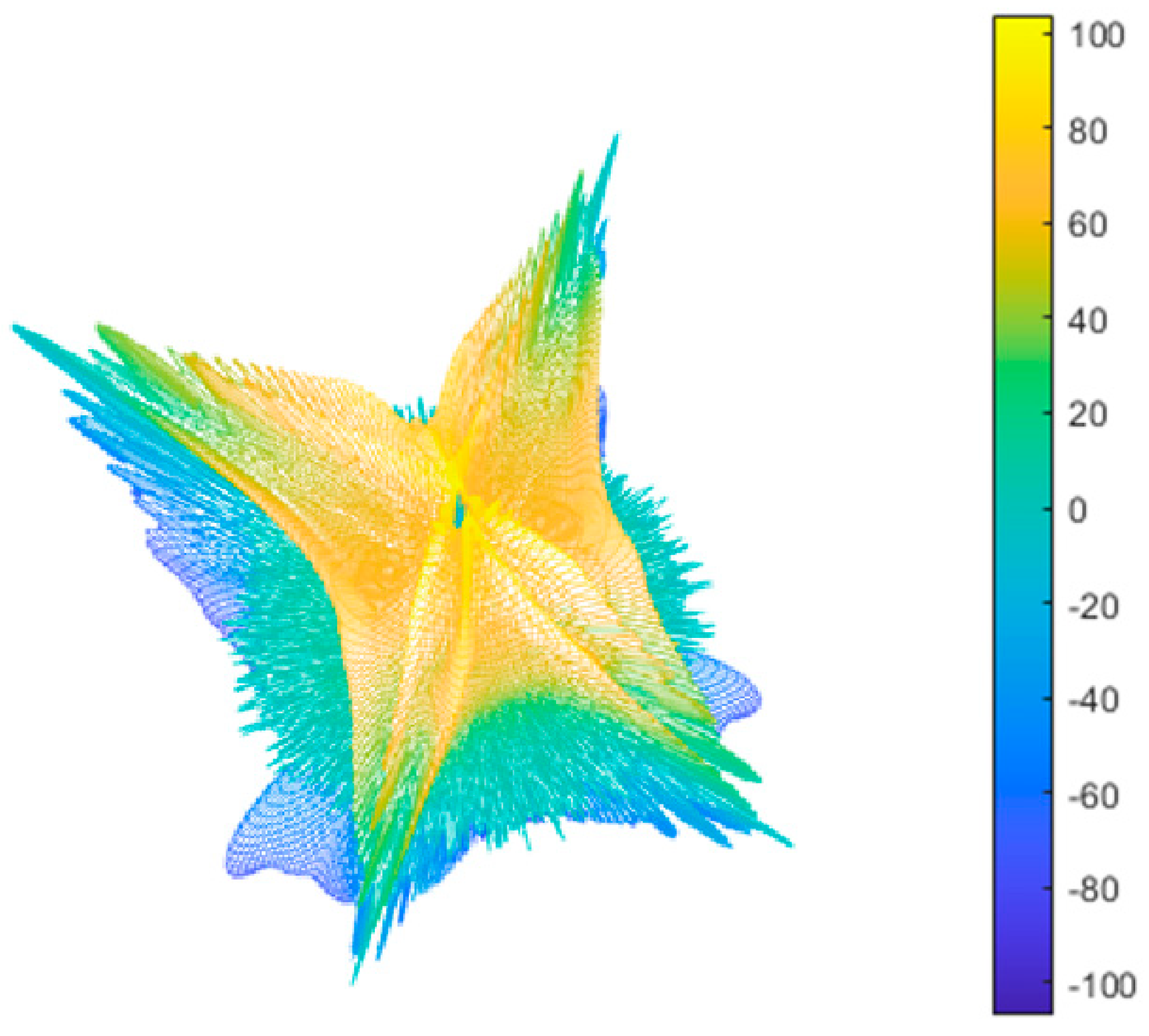
Typical Stealth Aircraft 3D RCS.
Figure 1.
Typical Stealth Aircraft 3D RCS.
Figure 2.
RCS variations with changes in azimuth angle.
Figure 2.
RCS variations with changes in azimuth angle.
Figure 3.
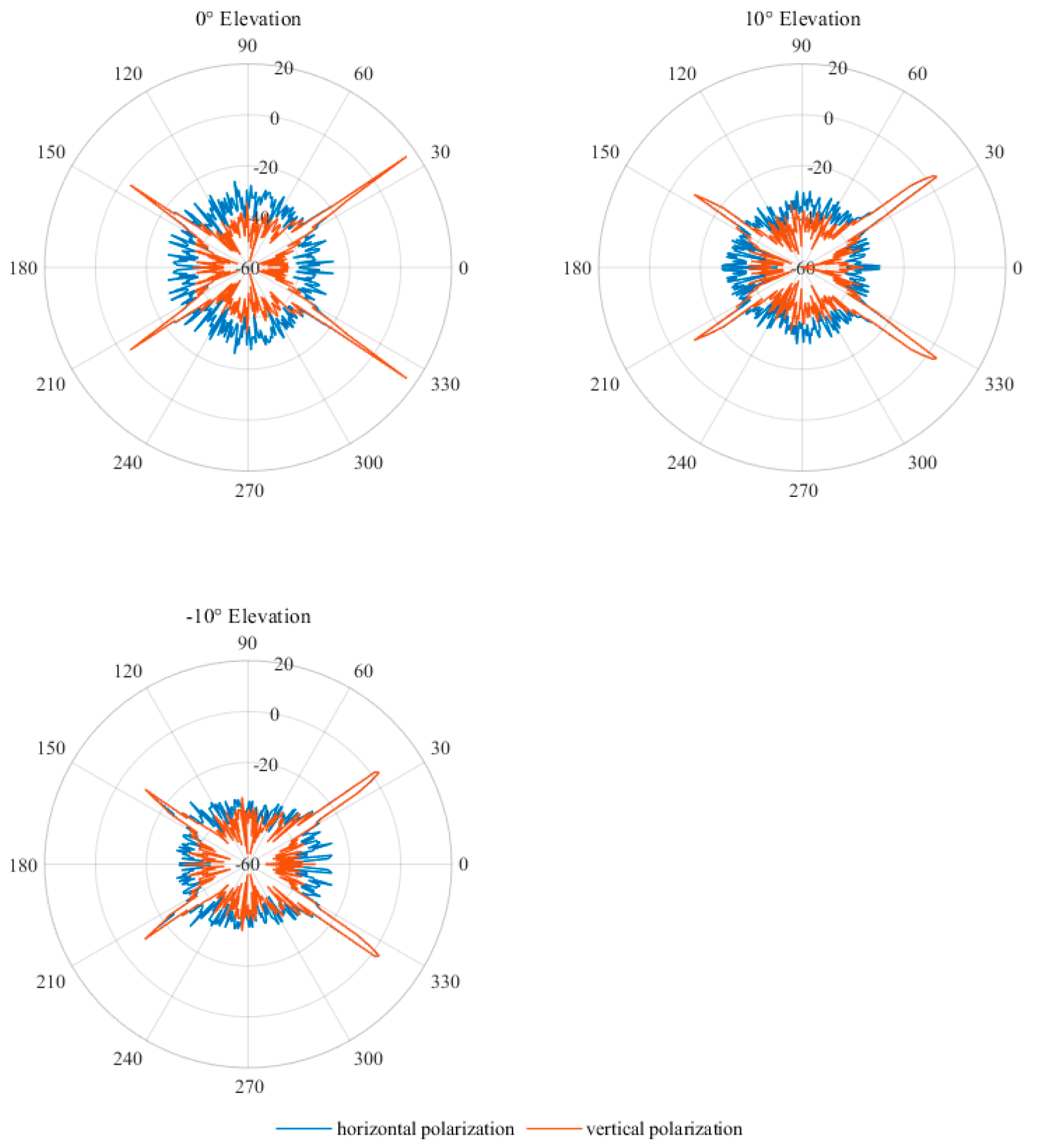
RCS variations with changes in elevation angle: (a) 0° azimuth angle, (b) 25° azimuth angle, and (c) 35° azimuth angle.
Figure 3.
RCS variations with changes in elevation angle: (a) 0° azimuth angle, (b) 25° azimuth angle, and (c) 35° azimuth angle.
Figure 4.
Aerodynamic model: (a) lift coefficient variation curve with angle of attack; (b) drag coefficient variation curve with lift coefficient.
Figure 4.
Aerodynamic model: (a) lift coefficient variation curve with angle of attack; (b) drag coefficient variation curve with lift coefficient.
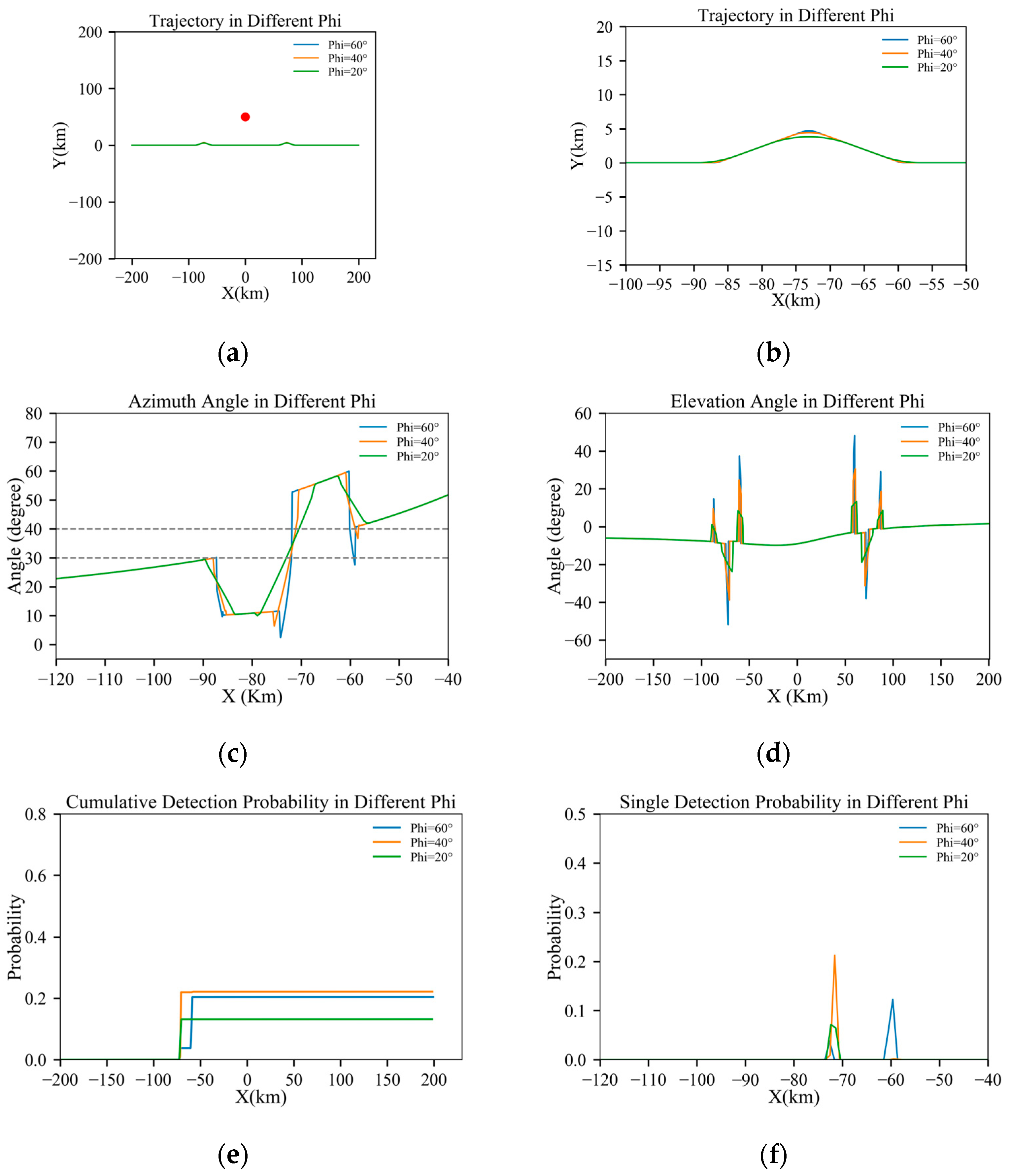
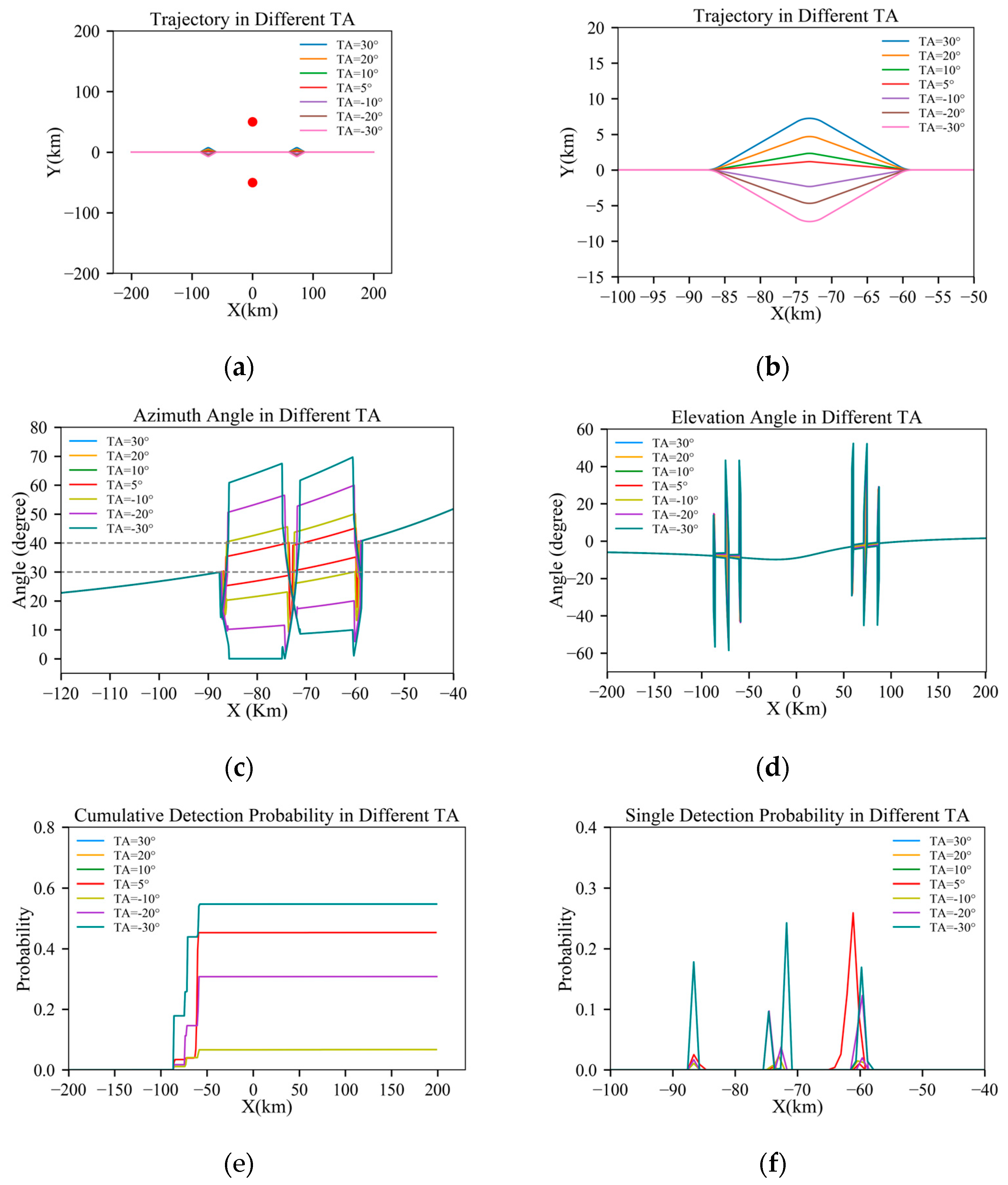
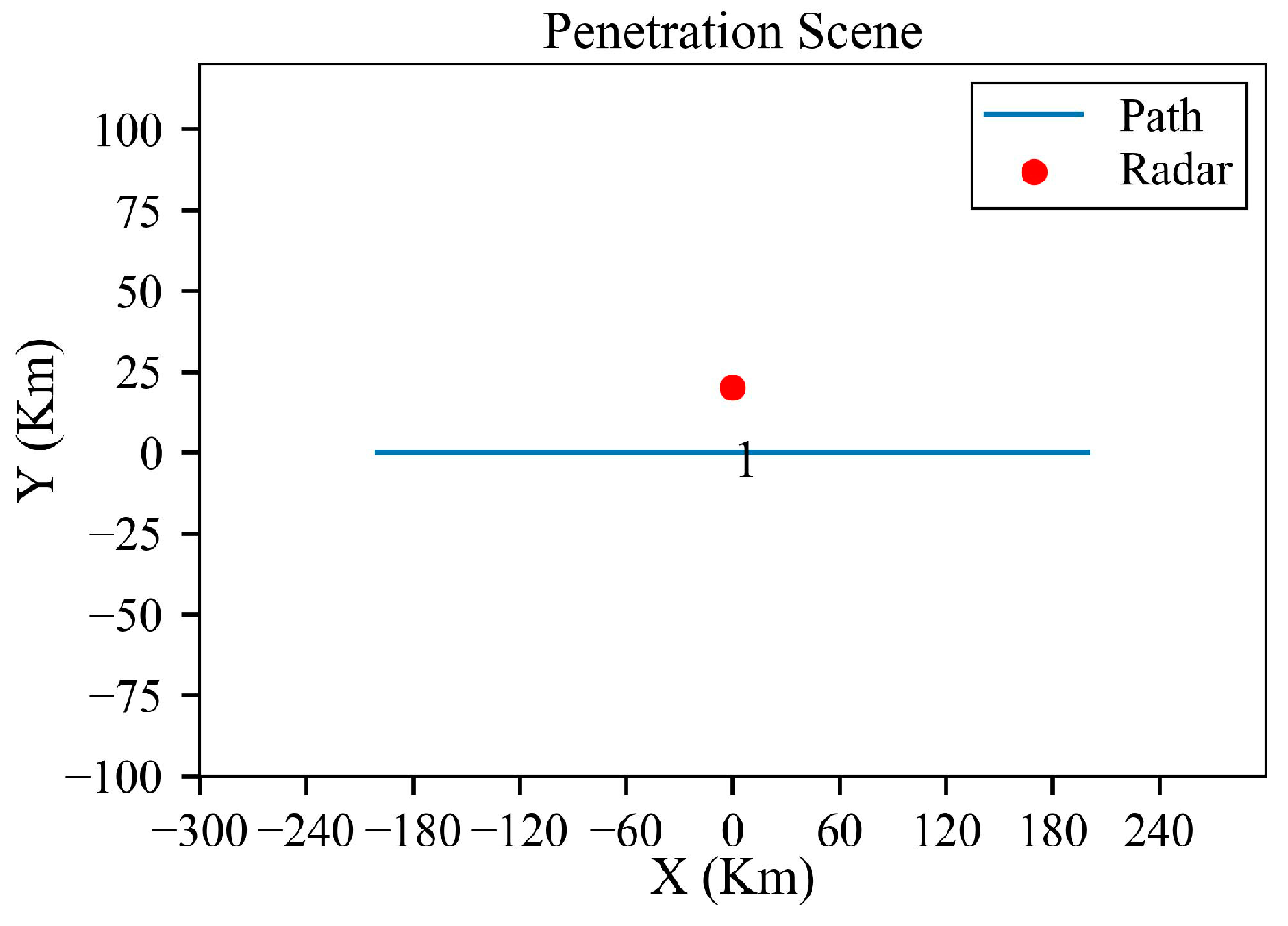
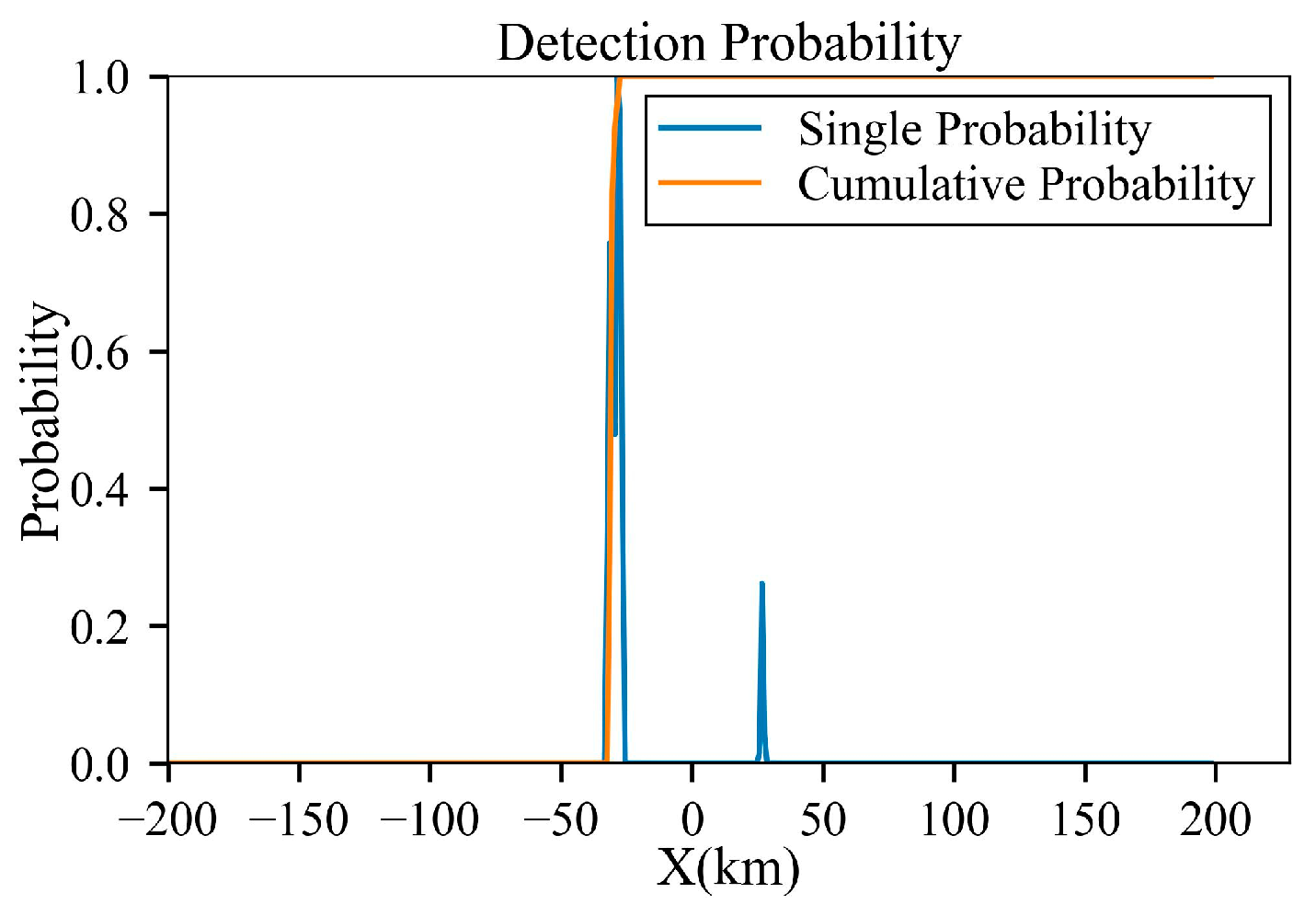
Figure 5.
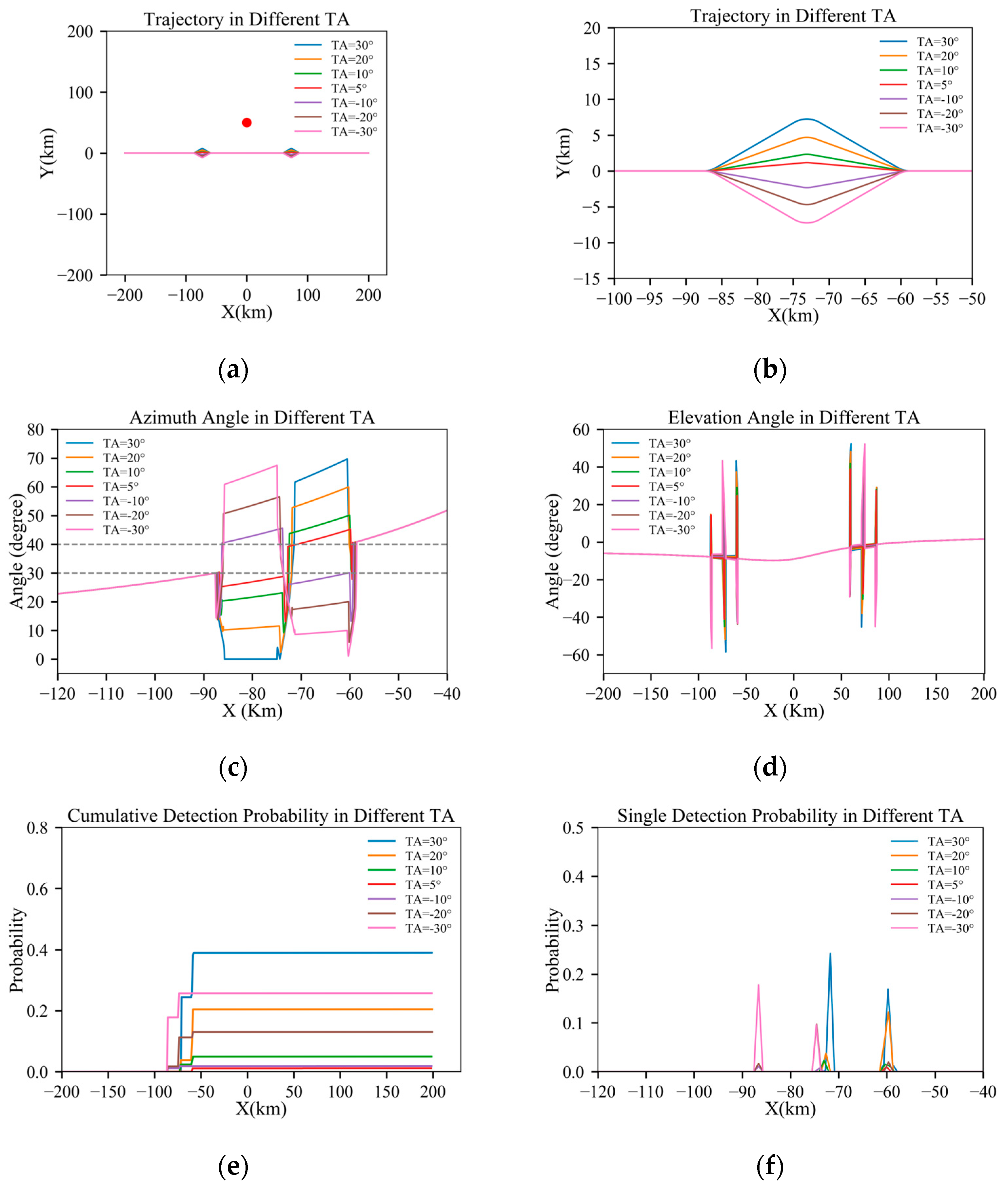
Results under D = 20 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 5.
Results under D = 20 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
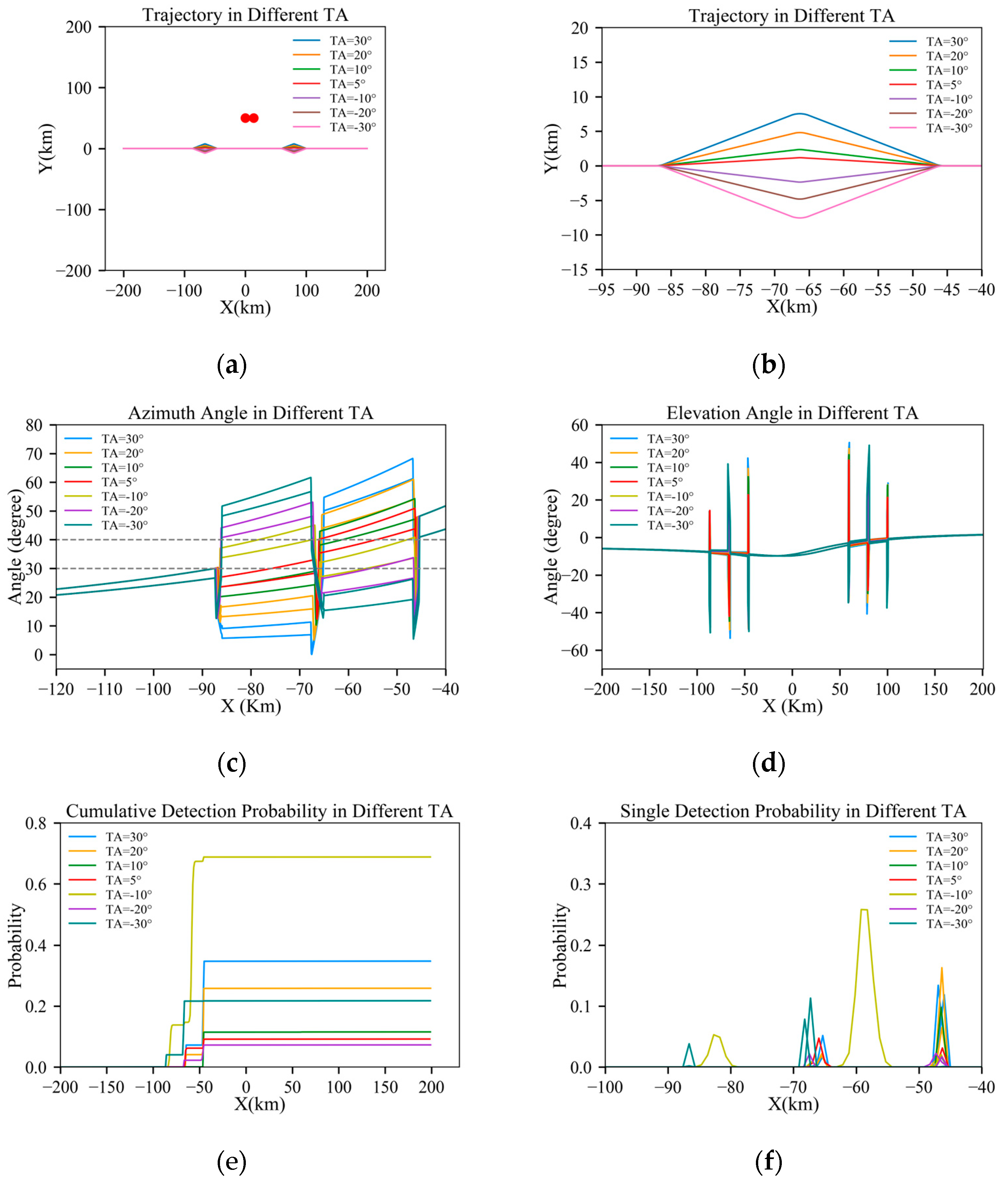
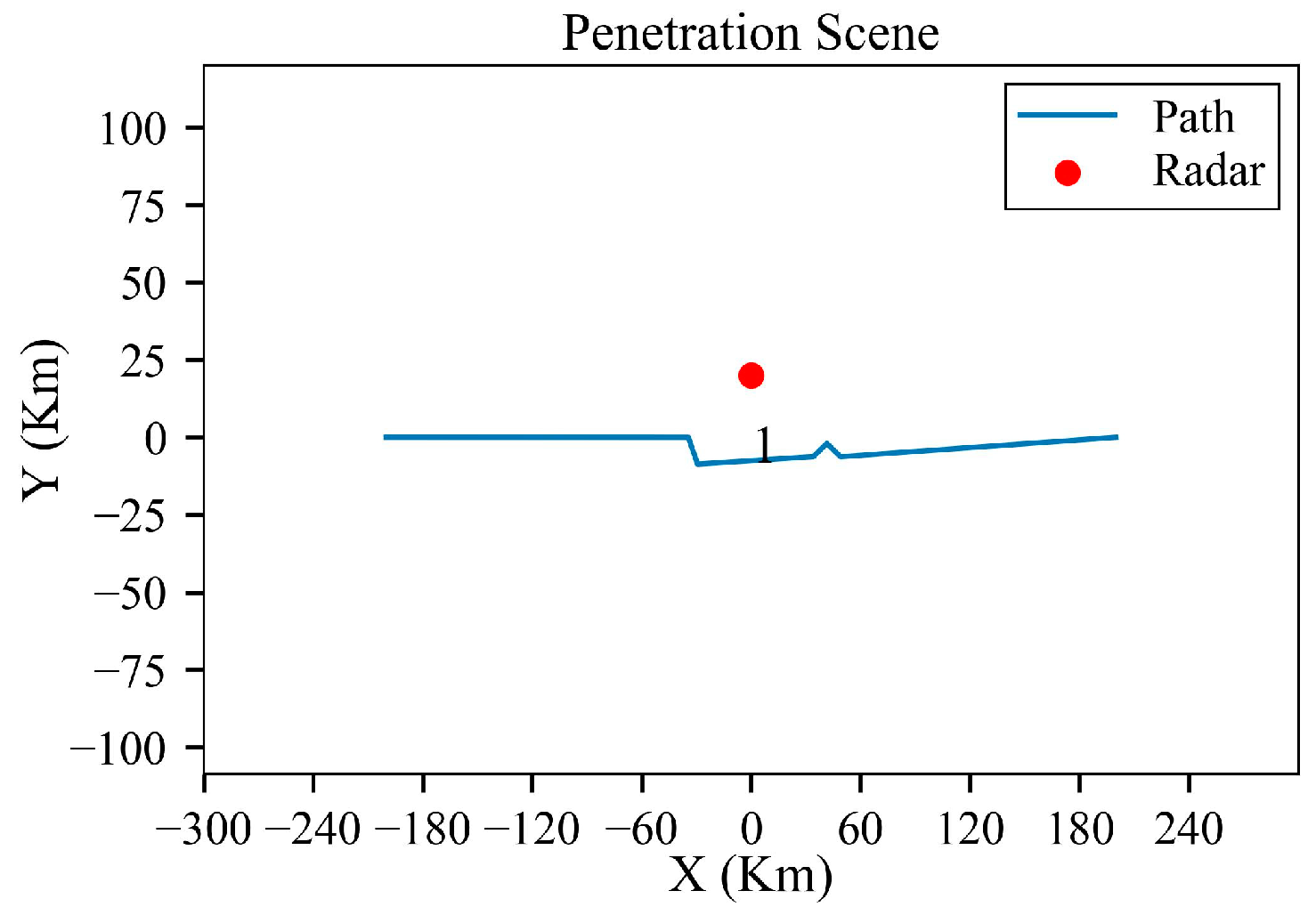
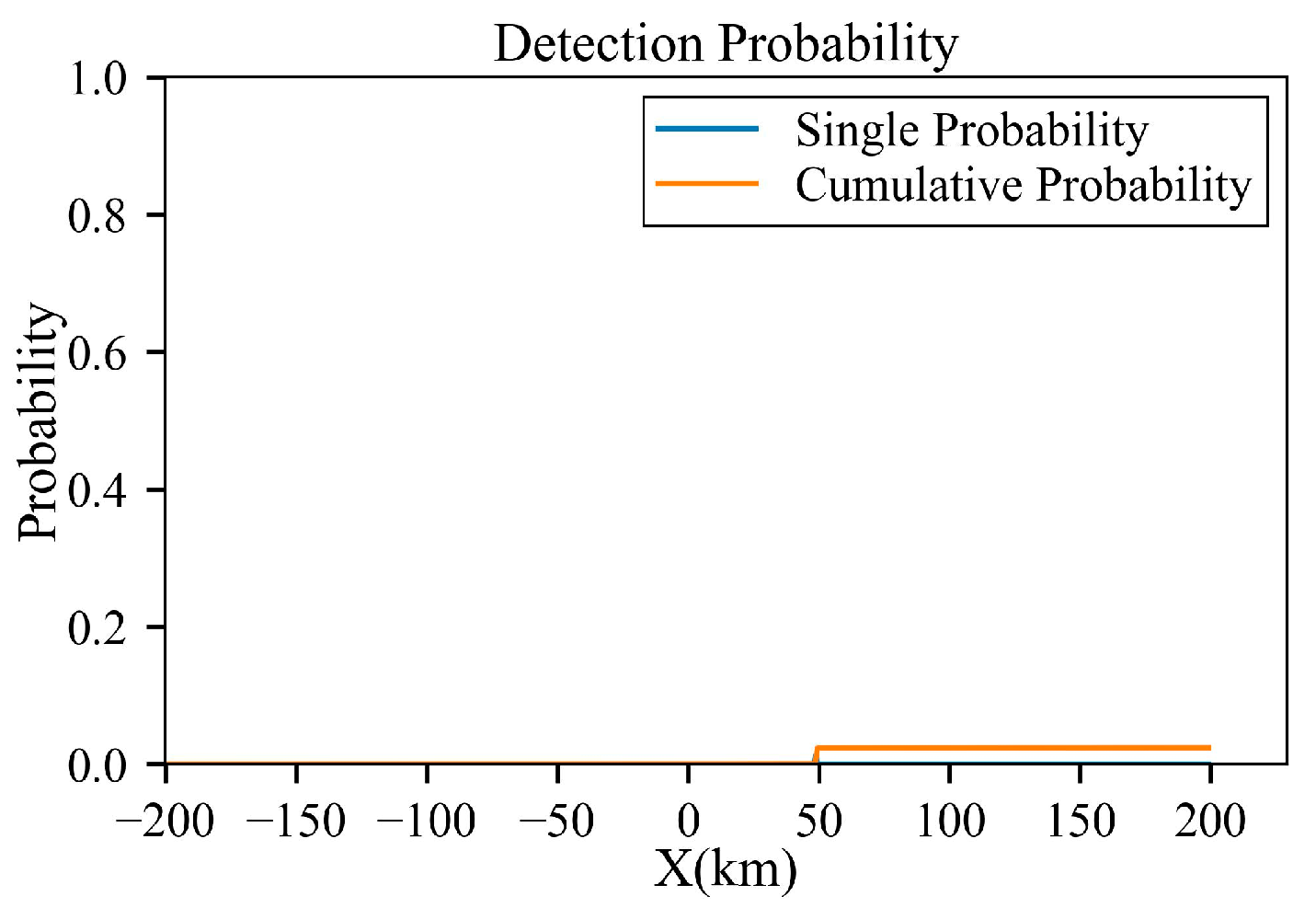
Figure 6.
Results under D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 6.
Results under D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 7.
Results under D = 100 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 7.
Results under D = 100 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 8.
Results under TA = 5°, D = 20 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 8.
Results under TA = 5°, D = 20 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 9.
Results under TA = 5°, D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 9.
Results under TA = 5°, D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 10.
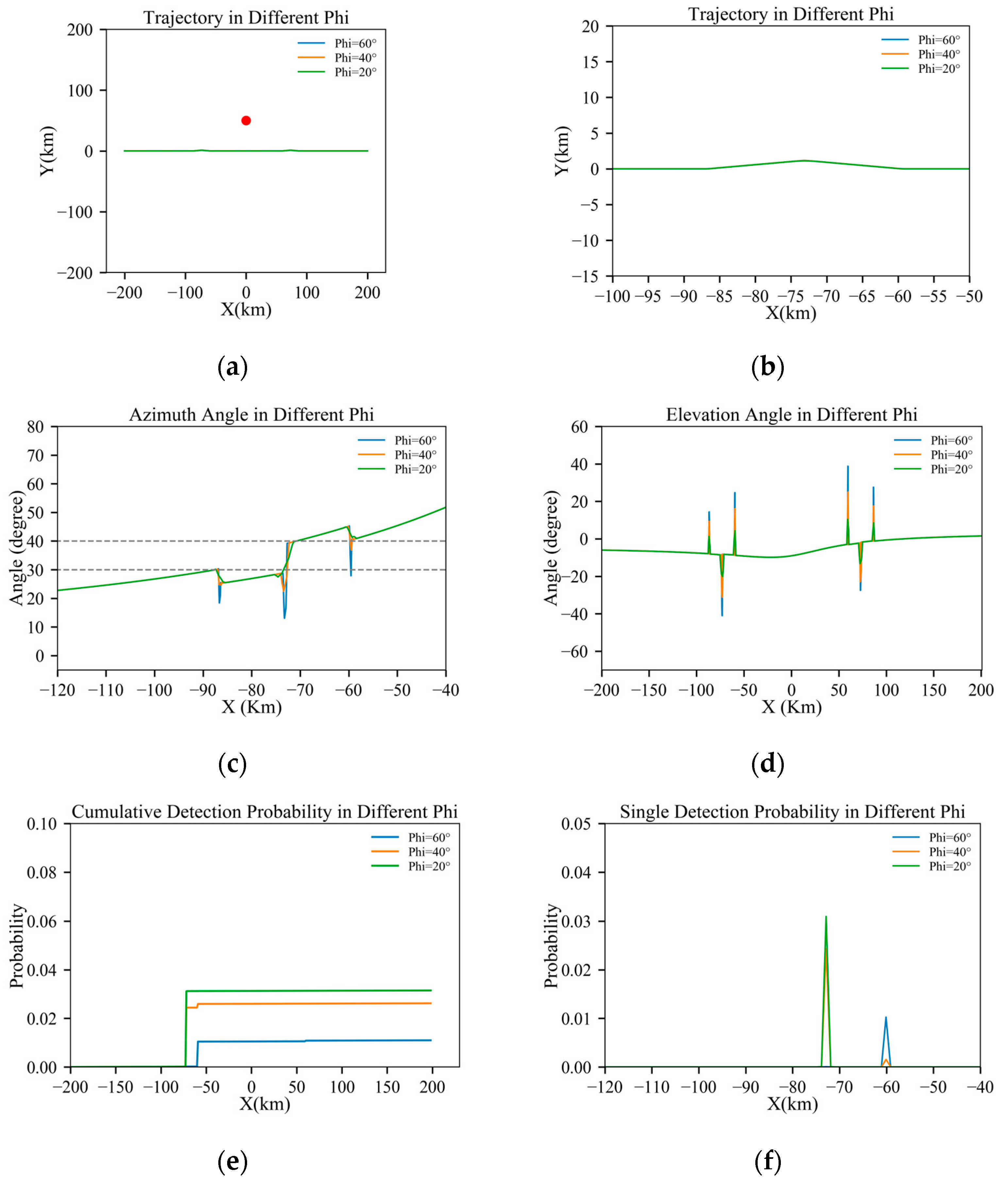
Results under TA = 20°, D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 10.
Results under TA = 20°, D = 50 km: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
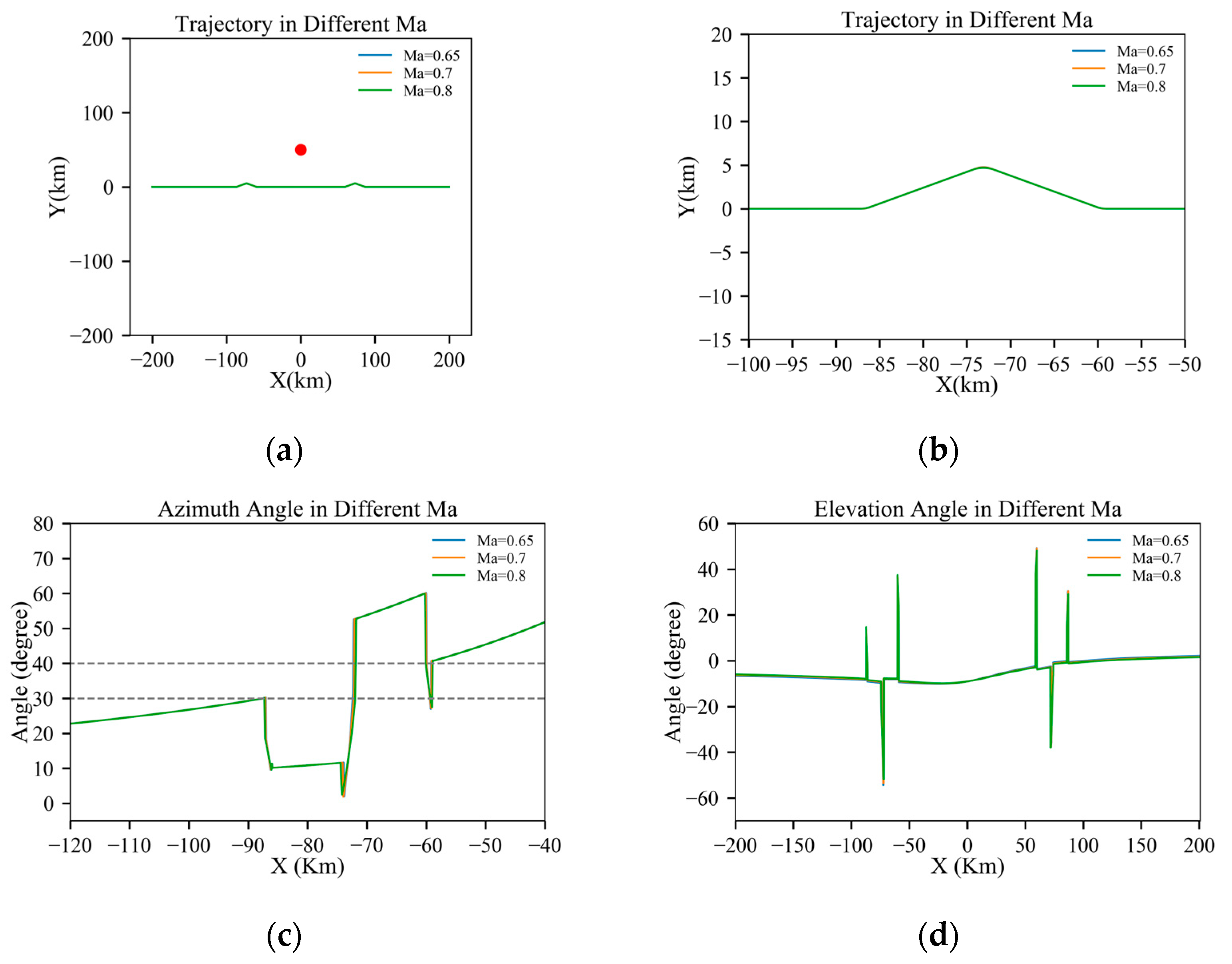
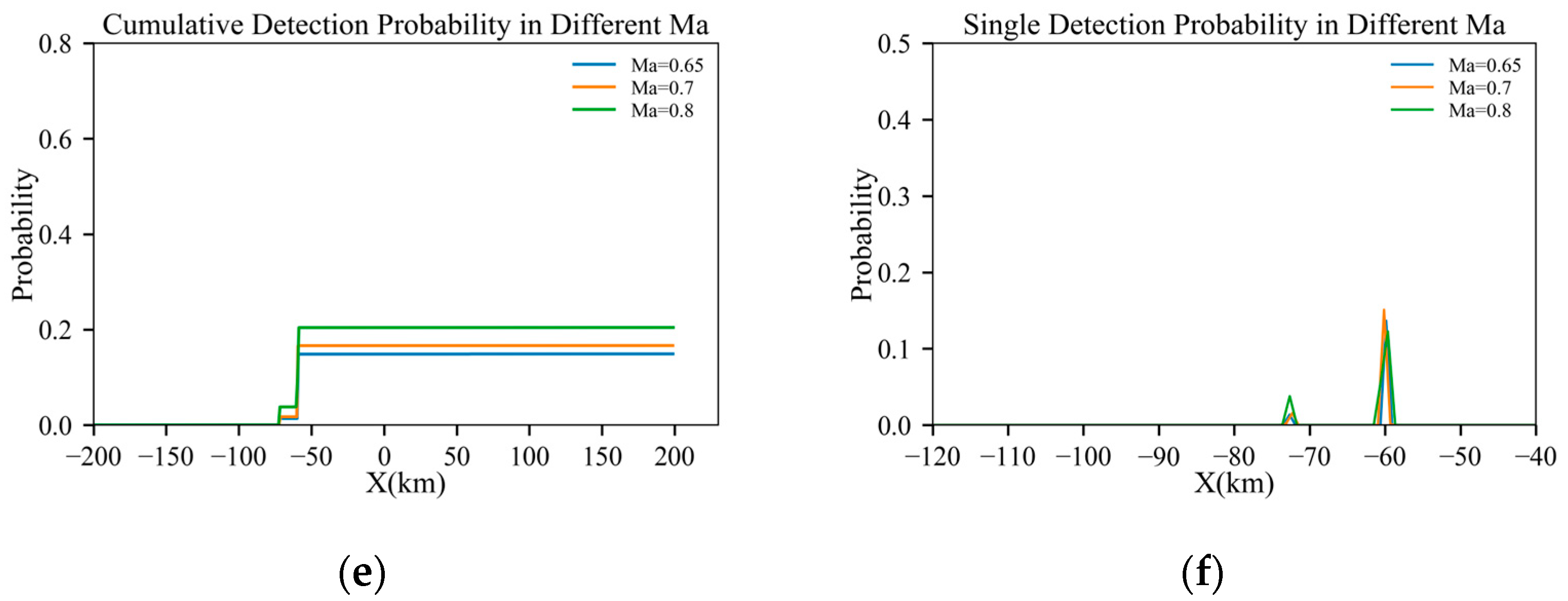
Figure 11.
Results under different Mach numbers: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 11.
Results under different Mach numbers: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
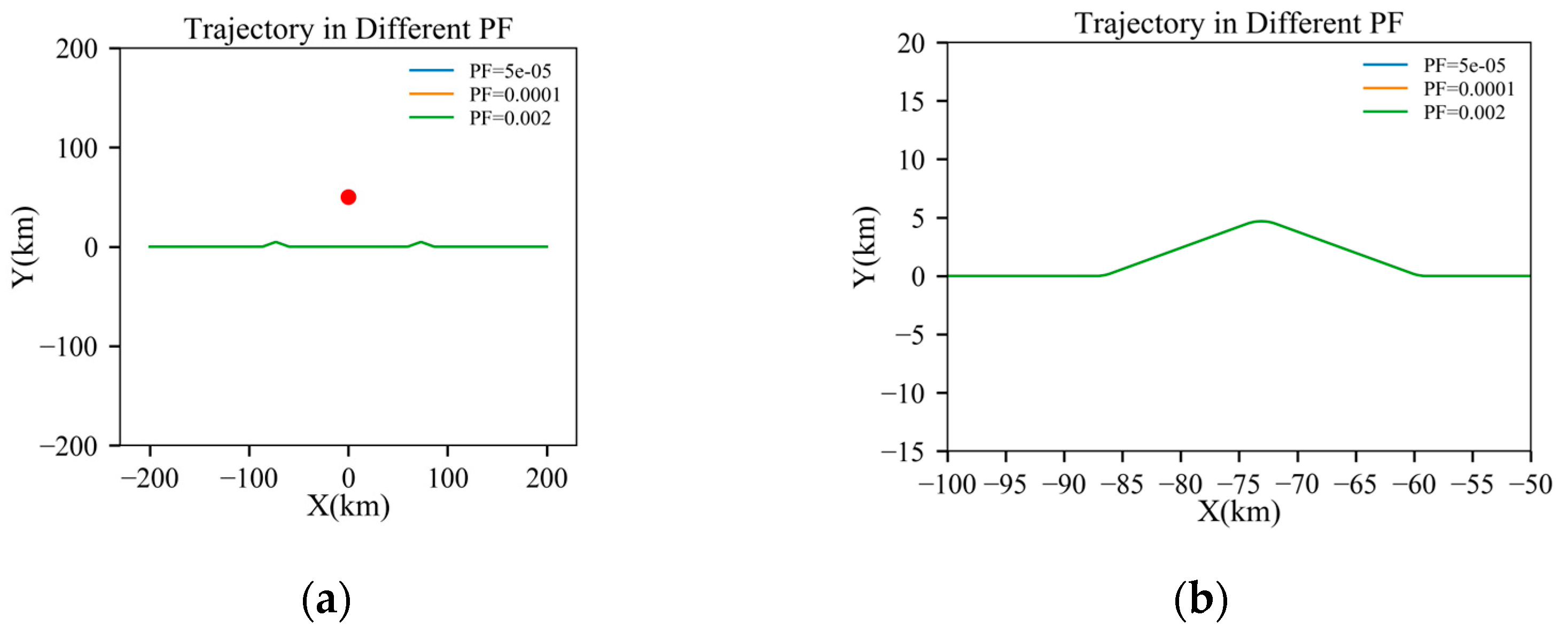
Figure 12.
Results under different radar power factors: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 12.
Results under different radar power factors: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 13.
Results of a cross-side radar scenario: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 13.
Results of a cross-side radar scenario: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 14.
Results of a closely positioned radar scenario: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 14.
Results of a closely positioned radar scenario: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 15.
Results of radars positioned further apart: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
Figure 15.
Results of radars positioned further apart: (a) full trajectory view; (b) magnified view of the turning section; (c) azimuth angle through the trajectory; (d) elevation angle through the trajectory; (e) cumulative detection probabilities through the trajectory; and (f) single-detection probabilities through the trajectory.
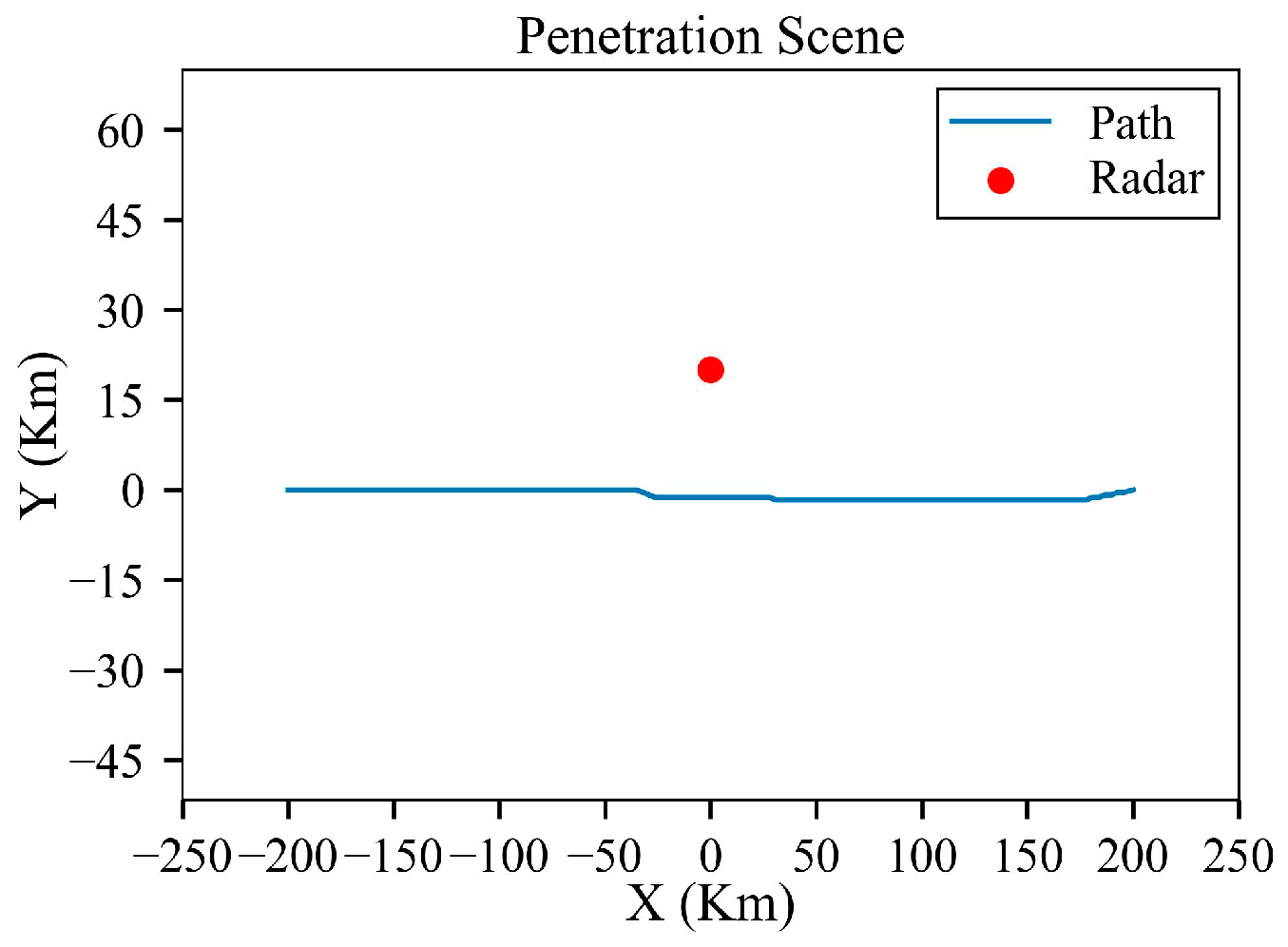
Figure 16.
Turning maneuver trajectory after planning.
Figure 16.
Turning maneuver trajectory after planning.
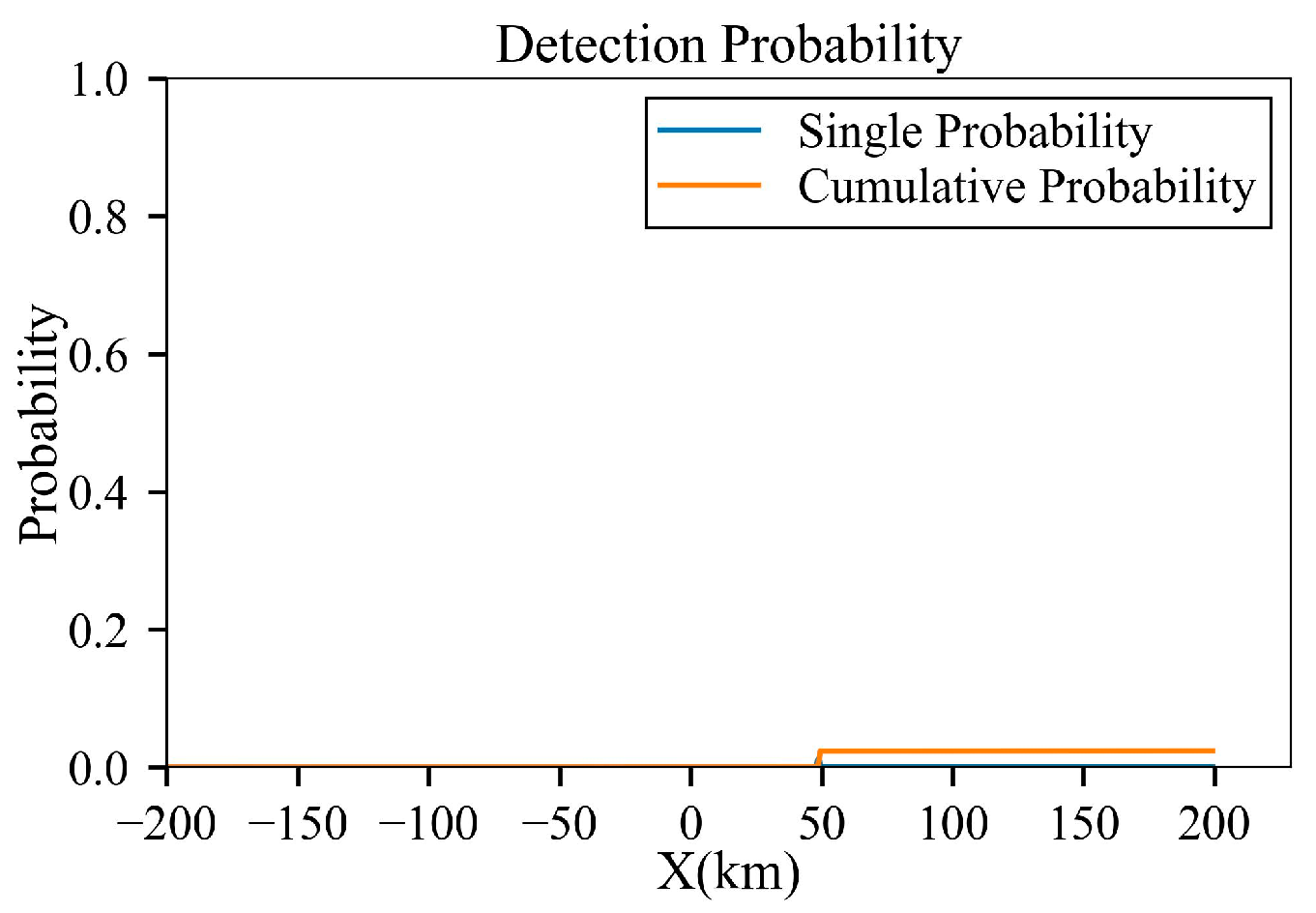
Figure 17.
Detection probability of the trajectory after planning under low-power radar.
Figure 17.
Detection probability of the trajectory after planning under low-power radar.
Figure 18.
The azimuth and elevation angles to the radar of the trajectory before planning: (a) azimuth angle and (b) elevation angle.
Figure 18.
The azimuth and elevation angles to the radar of the trajectory before planning: (a) azimuth angle and (b) elevation angle.
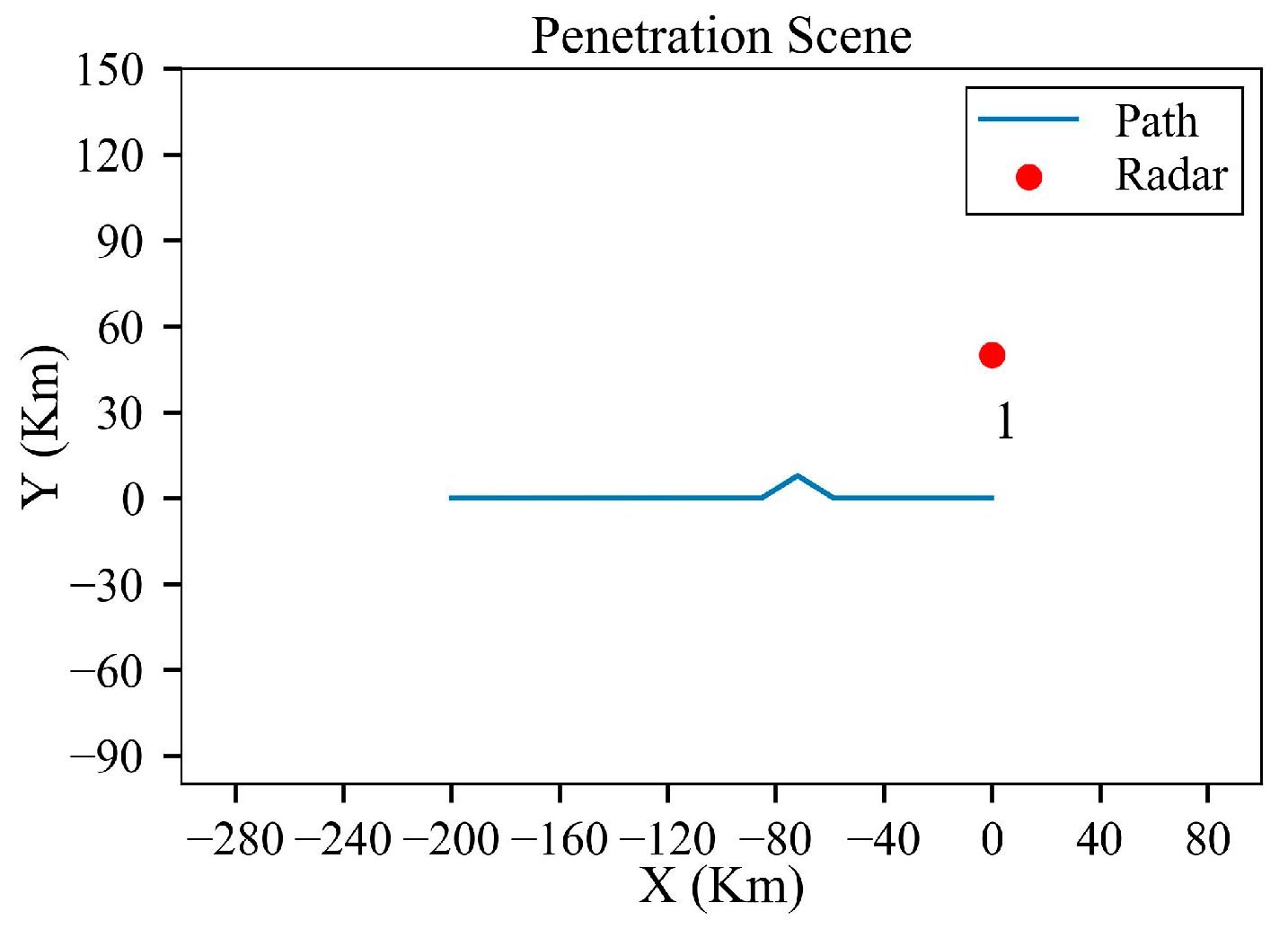
Figure 19.
Straight trajectory before planning in single-radar scenario.
Figure 19.
Straight trajectory before planning in single-radar scenario.
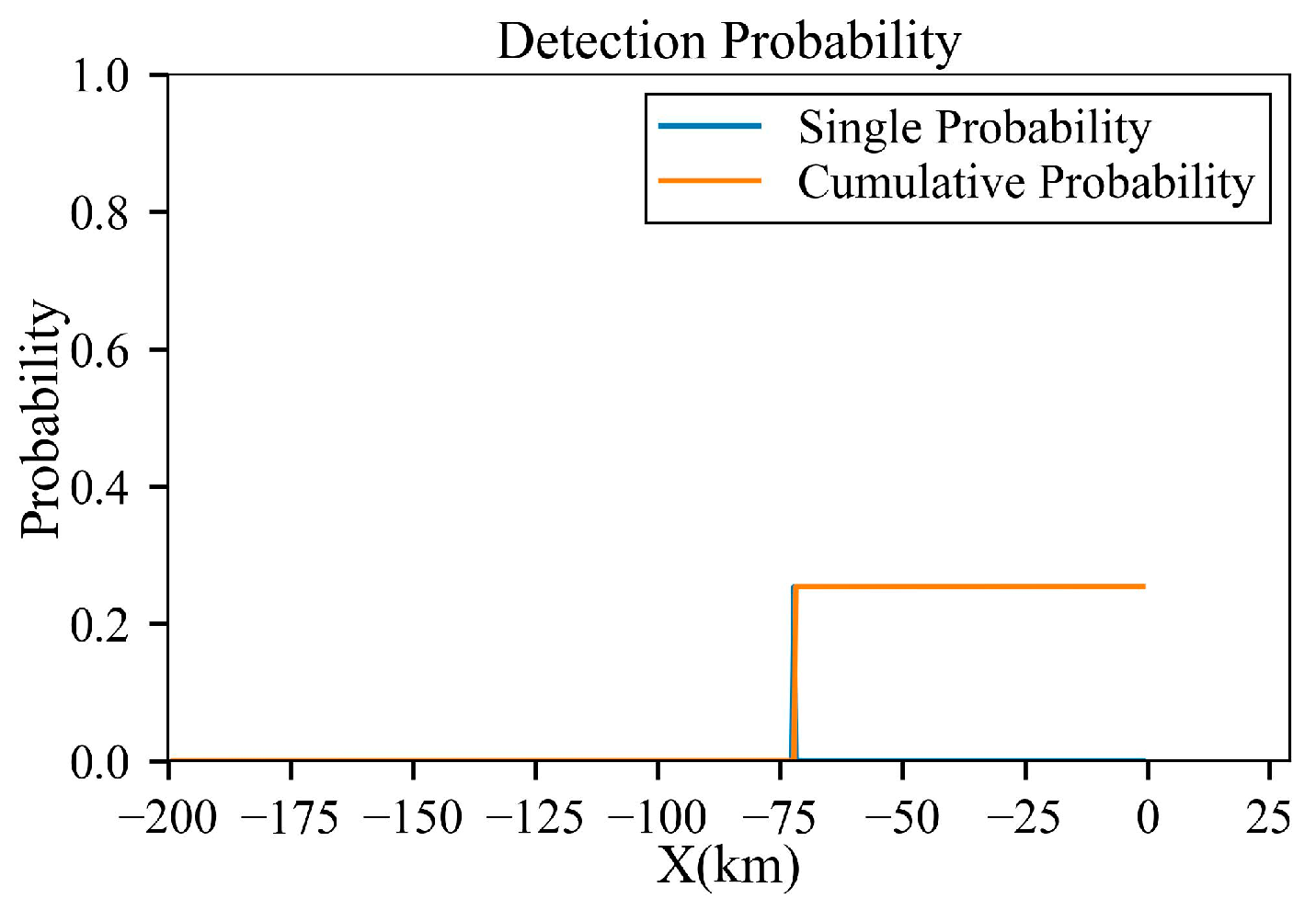
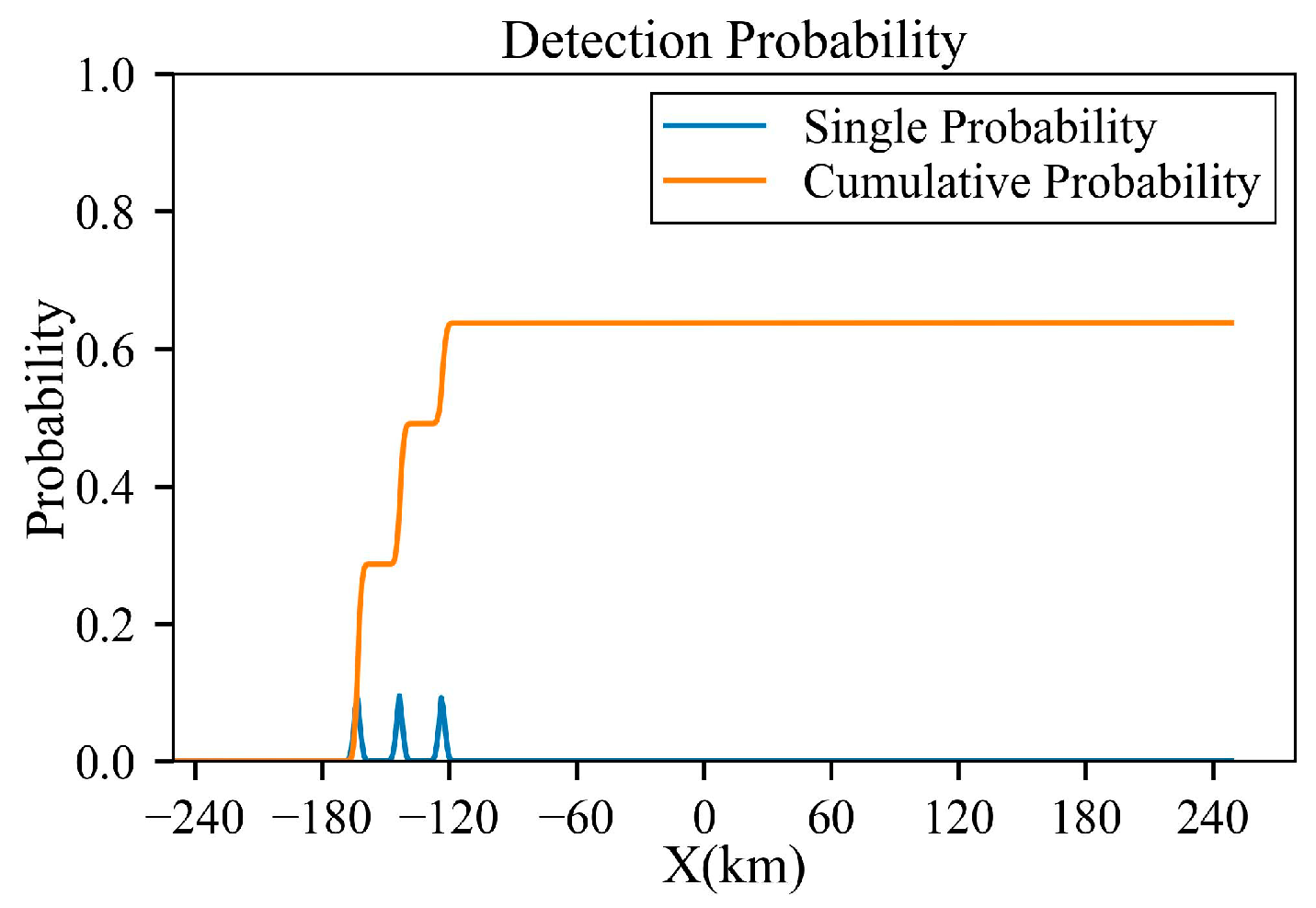
Figure 20.
Detection probability of the trajectory before planning under low-power radar.
Figure 20.
Detection probability of the trajectory before planning under low-power radar.
Figure 21.
The azimuth and elevation angles to the radar of the trajectory before planning in single-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 21.
The azimuth and elevation angles to the radar of the trajectory before planning in single-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 22.
Turning maneuver trajectory after RVR-TM method planning in single-radar scenario.
Figure 22.
Turning maneuver trajectory after RVR-TM method planning in single-radar scenario.
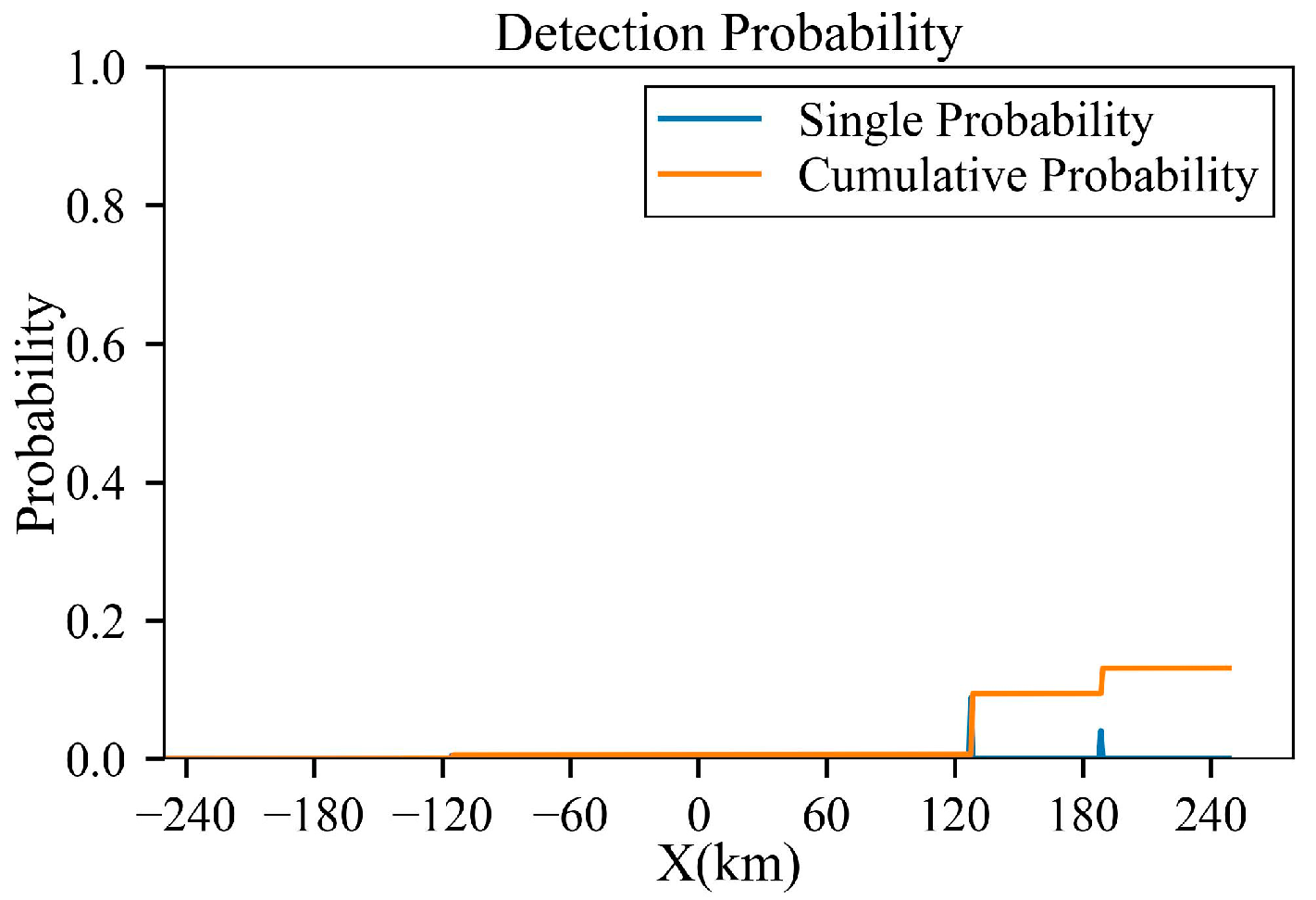
Figure 23.
Detection probability of the trajectory after RVR-TM method planning under a single radar.
Figure 23.
Detection probability of the trajectory after RVR-TM method planning under a single radar.
Figure 24.
The azimuth and elevation angles to the radar of the trajectory after RVR-TM method planning in single-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 24.
The azimuth and elevation angles to the radar of the trajectory after RVR-TM method planning in single-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 25.
Turning maneuver trajectory after 3D-SASLRM method planning in single-radar scenario.
Figure 25.
Turning maneuver trajectory after 3D-SASLRM method planning in single-radar scenario.
Figure 26.
Detection probability of the trajectory after 3D-SASLRM method planning in single-radar scenario.
Figure 26.
Detection probability of the trajectory after 3D-SASLRM method planning in single-radar scenario.
Figure 27.
Straight trajectory before planning in a three-radar scenario.
Figure 27.
Straight trajectory before planning in a three-radar scenario.
Figure 28.
Detection probability of the trajectory before planning under a single radar.
Figure 28.
Detection probability of the trajectory before planning under a single radar.
Figure 29.
The azimuth and elevation angles to the radar of the trajectory before planning in a three-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 29.
The azimuth and elevation angles to the radar of the trajectory before planning in a three-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 30.
Turning maneuver trajectory after RVR-TM method planning in a three-radar scenario.
Figure 30.
Turning maneuver trajectory after RVR-TM method planning in a three-radar scenario.
Figure 31.
Detection probability of the trajectory after RVR-TM method planning under three radars.
Figure 31.
Detection probability of the trajectory after RVR-TM method planning under three radars.
Figure 32.
The azimuth and elevation angles to the radar of the trajectory after RVR-TM method planning in a three-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 32.
The azimuth and elevation angles to the radar of the trajectory after RVR-TM method planning in a three-radar scenario: (a) azimuth angle and (b) elevation angle.
Figure 33.
Turning maneuver trajectory after 3D-SASLRM method planning in a three-radar scenario.
Figure 33.
Turning maneuver trajectory after 3D-SASLRM method planning in a three-radar scenario.
Figure 34.
Detection probability of the trajectory after 3D-SASLRM method planning in a three-radar scenario.
Figure 34.
Detection probability of the trajectory after 3D-SASLRM method planning in a three-radar scenario.
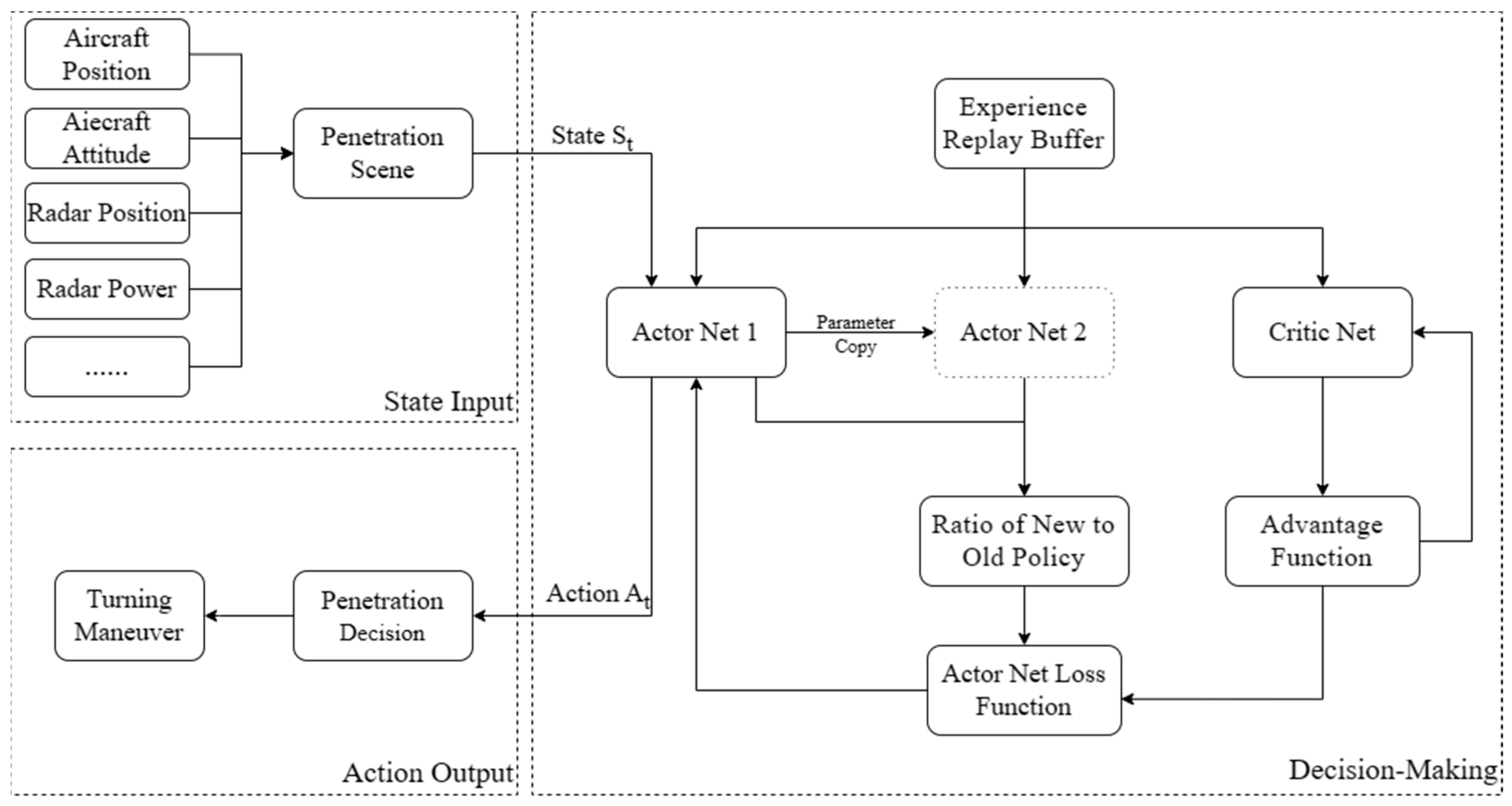
Figure 35.
Decision model based on PPO algorithm.
Figure 35.
Decision model based on PPO algorithm.
Figure 36.
Results under different distance penalties: (a) with no distance penalty and (b) with distance penalty.
Figure 36.
Results under different distance penalties: (a) with no distance penalty and (b) with distance penalty.
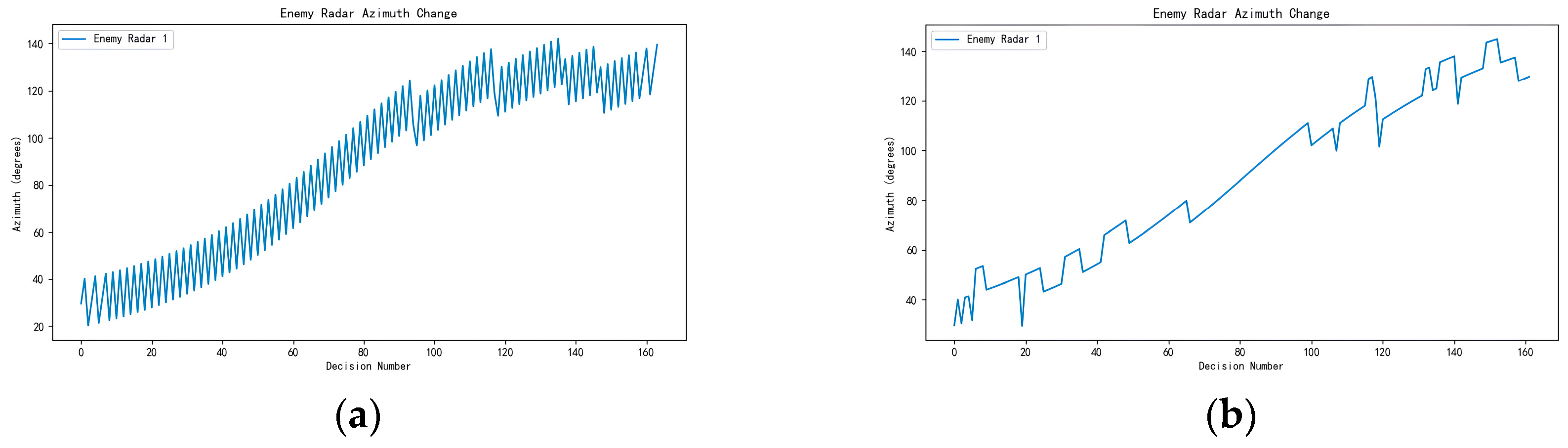
Figure 37.
Azimuth under different action penalties: (a) with no action penalty and (b) with action penalty.
Figure 37.
Azimuth under different action penalties: (a) with no action penalty and (b) with action penalty.
Figure 38.
Trajectory and azimuth with reward shaping: (a) trajectory and (b) azimuth angle.
Figure 38.
Trajectory and azimuth with reward shaping: (a) trajectory and (b) azimuth angle.
Figure 39.
Process of imitation learning.
Figure 39.
Process of imitation learning.
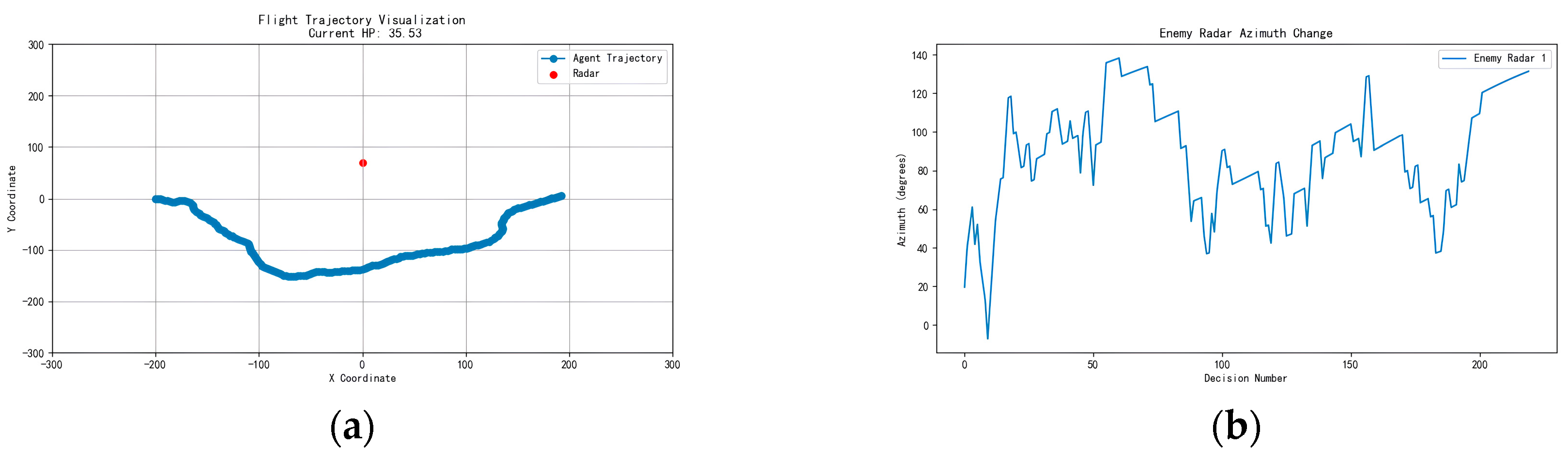
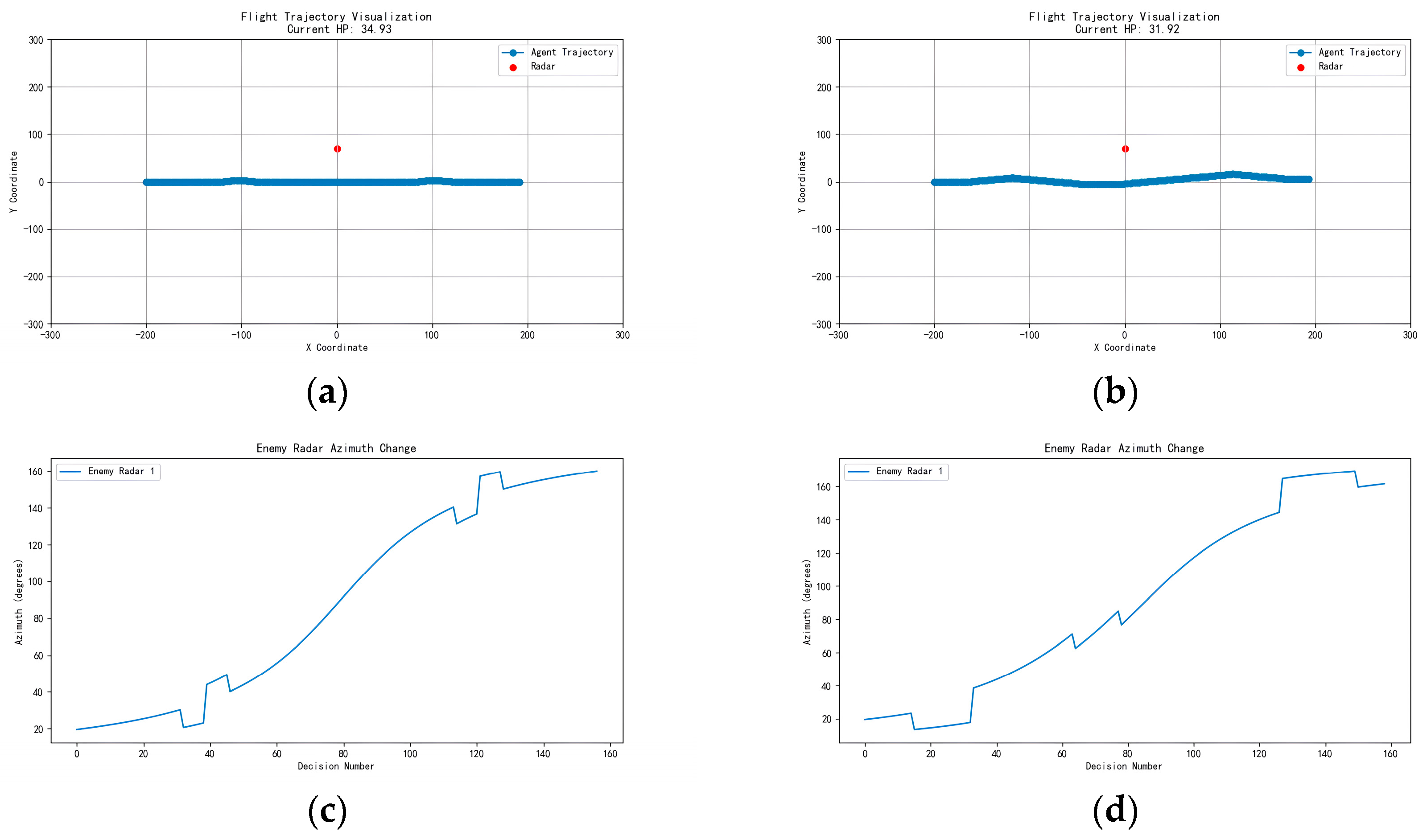
Figure 40.
Results after incorporating imitation learning: (a) trajectory before incorporating imitation learning; (b) trajectory after incorporating imitation learning; (c) azimuth angle before incorporating imitation learning; and (d) azimuth angle after incorporating imitation learning.
Figure 40.
Results after incorporating imitation learning: (a) trajectory before incorporating imitation learning; (b) trajectory after incorporating imitation learning; (c) azimuth angle before incorporating imitation learning; and (d) azimuth angle after incorporating imitation learning.
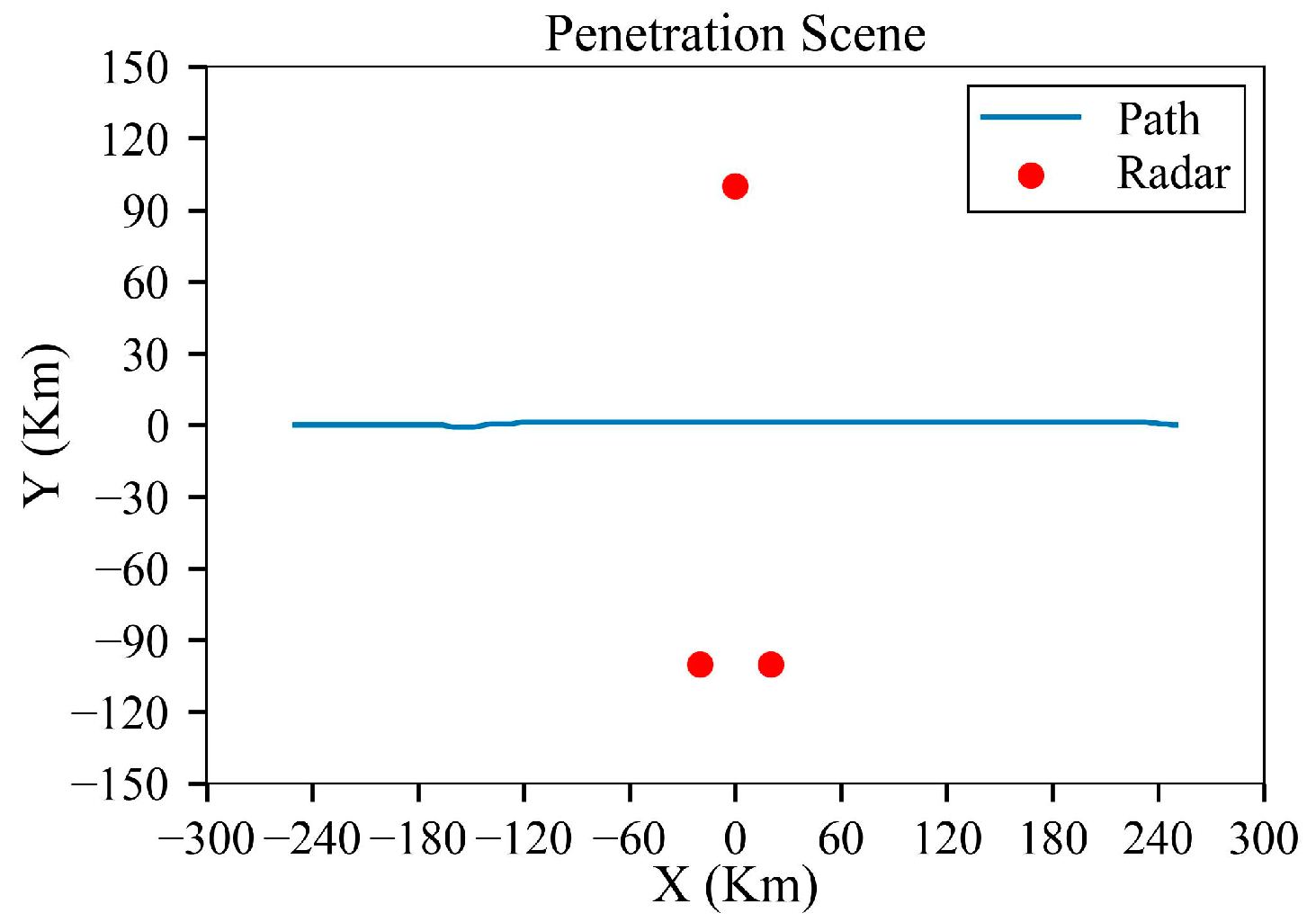
Table 1.
Scene parameter settings in different TAs when D = 20 km.
Table 1.
Scene parameter settings in different TAs when D = 20 km.
| Phi | Ma | | Power Factor |
|---|
| 60° | 0.8 | 20 km | |
Table 2.
Scene parameter settings in different TAs when D = 50 km.
Table 2.
Scene parameter settings in different TAs when D = 50 km.
| Phi | Ma | | Power Factor |
|---|
| 60° | 0.8 | 50 km | |
Table 3.
Scene parameter settings in different TAs when D = 100 km.
Table 3.
Scene parameter settings in different TAs when D = 100 km.
| Phi | Ma | | Power Factor |
|---|
| 60° | 0.8 | 100 km | |
Table 4.
Scene parameter settings in different rolling angles when TA = 5° and D = 20 km.
Table 4.
Scene parameter settings in different rolling angles when TA = 5° and D = 20 km.
| TA | Ma | | Power Factor |
|---|
| 5° | 0.8 | 20 km | |
Table 5.
Scene parameter settings in different rolling angles when TA = 5° and D = 50 km.
Table 5.
Scene parameter settings in different rolling angles when TA = 5° and D = 50 km.
| TA | Ma | | Power Factor |
|---|
| 5° | 0.8 | 50 km | |
Table 6.
Scene parameter settings in different rolling angles when TA = 20° and D = 50 km.
Table 6.
Scene parameter settings in different rolling angles when TA = 20° and D = 50 km.
| TA | Ma | | Power Factor |
|---|
| 20° | 0.8 | 50 km | |
Table 7.
Scene parameter settings in different flight speeds.
Table 7.
Scene parameter settings in different flight speeds.
| TA | Phi | | Power Factor |
|---|
| 20° | 60° | 50 km | |
Table 8.
Scene parameter settings in different power factors.
Table 8.
Scene parameter settings in different power factors.
Table 9.
Scene parameter settings in a scenario with dual radars.
Table 9.
Scene parameter settings in a scenario with dual radars.
| Power Factor | Phi | | Ma |
|---|
| 60° | 50 km | 0.8 |
Table 10.
Radar parameters for single-radar threat environment for RVR-TM algorithm.
Table 10.
Radar parameters for single-radar threat environment for RVR-TM algorithm.
| Index | (s) | | N | | | | Power Factor |
|---|
| 1 | 4 | | 2 | 0.5 | 0 | 0 | |
Table 11.
Specific definition of the state space.
Table 11.
Specific definition of the state space.
| Identifier | Name | Range | Description |
|---|
| AgentAzi | Aircraft Azimuth | [−π, π] (rad) | The azimuth angle of the aircraft’s direction of movement relative to the map’s X-axis |
| AgentVelocity | Aircraft Velocity | 0–10 (km/10 s) | The flight distance of aircraft between each decision |
| AgentHP | Aircraft Health | 0–100 | Represents the highest acceptable probability of radar detection |
| EnemyAzi | Radar Azimuth Angle | [−π, π] (rad) | The angle between the aircraft-radar vector and the X-axis in the aircraft’s body coordinate system |
| EnemyDis | Radar Relative Distance | (−∞, +∞) (km) | The magnitude of the vector from the aircraft to the radar |
| EnemyPow | Radar Power | 0–1 | Radar power factor |
| TargtAzi | Target Azimuth Angle | [−π, π] (rad) | The angle between the aircraft-target vector and the X-axis in the aircraft’s body coordinate system |
| TargtDis | Target Relative Distance | (−∞, +∞) (km) | The magnitude of the vector from the aircraft to the target |
Table 12.
Radar parameters for single-radar threat environment.
Table 12.
Radar parameters for single-radar threat environment.
| Index | Location | (s) | | N | | | | Power Factor |
|---|
| 1 | (0,60,0) | 4 | | 2 | 0.5 | 0 | 0 | |