1. Introduction
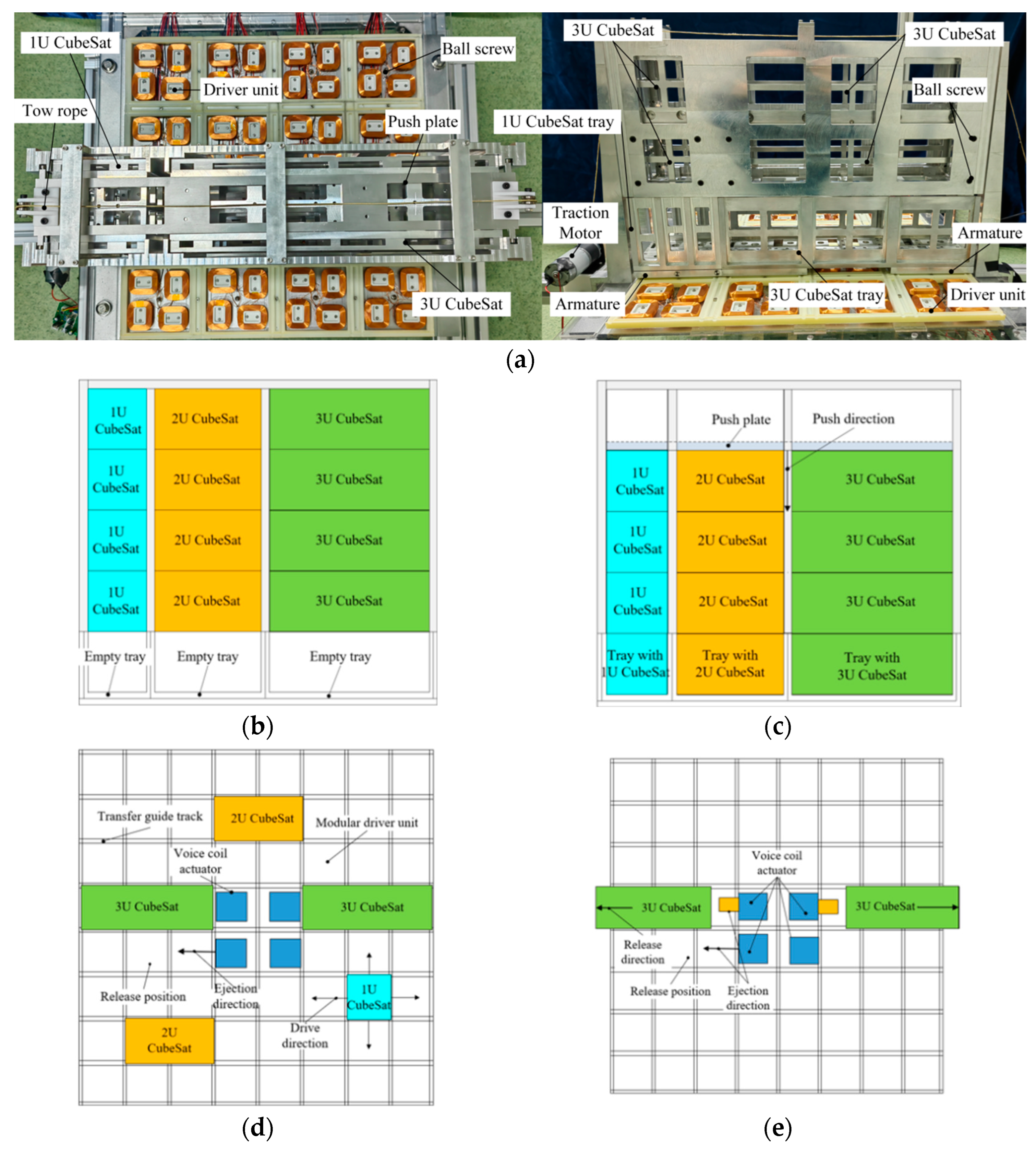
CubeSats possess several advantages, including their compact size, being lightweight, and rapid development cycles. When deployed in groups, they can undertake complex tasks, such as constellation formation and formation flying, which would be challenging for a single large satellite [
1,
2]. Typically launched as secondary payloads using box-type deployers and released into orbit via internal springs, individual CubeSats reach their designated orbits. However, to accommodate the increasing demand for large-scale CubeSat applications, future deployers must support the deployment of a greater number of CubeSats and enable cluster releases in orbit [
3].
The current multi-satellite deployment scheme primarily utilizes box-type deployers with compressed spring ejection mechanisms. Among the notable developments in this area, the P-POD CubeSat deployer stands out. Developed jointly by the California Institute of Technology and Stanford University in the United States, the P-POD is capable of accommodating three standard 1U CubeSats. It is the earliest developed and most widely used CubeSat release mechanism to date. To date, this deployer has successfully launched over 150 CubeSats into orbit [
4,
5,
6,
7,
8]. The University of Toronto in Canada has developed the Generic Nanosatellite Bus (GNB), a deployment device specifically designed for releasing the CanX series nanosatellites, which are each sized at 200 mm × 200 mm × 200 mm [
9,
10]. The GNB deployer operates on a similar principle to the U.S. P-POD, but it features an open-sided casing that allows for the storage and deployment of nanosatellites equipped with antennas, enhancing its functionality. The DRAGON small satellite deployment device, pioneered by the Space Research Center of the Polish Academy of Sciences, is designed to release nanosatellites measuring 200 mm × 200 mm × 200 mm [
11]. The NASA WWF deployer accommodates rectangular payloads of 10 × 23 × 35 cm and can release 6U CubeSats. Using linear springs for propulsion, this system halts the satellite midway to allow orbit-guidance systems to complete the trajectory [
12]. Meanwhile, the JEM Small Satellite Orbital Deployer (J-SSOD), developed by the Japan Aerospace Exploration Agency, managed to separate 1U CubeSats weighing 1 kg from the International Space Station in 2015, achieving separation velocities between 1.1 m/s and 1.7 m/s. This deployer uses a box storage mechanism with compressed springs and linear guide rails to release up to three 1U CubeSats simultaneously [
13]. Although the design of CubeSat box-type deployers is simple and well-researched, they have limitations, such as a maximum capacity of three 1U CubeSats and a lack of reusability. To deploy a large number of CubeSats simultaneously, the use of multiple deployers is required, which significantly increases space occupancy. Currently, to expand deployer capacity, configurations often involve either multi-row combinations or enlargements within a two-dimensional plane. Essentially, these setups integrate multiple single-row deployers, equipping each CubeSat with an independent launch window and separation mechanism. However, the constraints imposed by the separation mechanism’s layout and operation hinder the possibility of three-dimensional deployer combinations or the direct, large-scale storage and release of stacked CubeSats. References [
14,
15,
16,
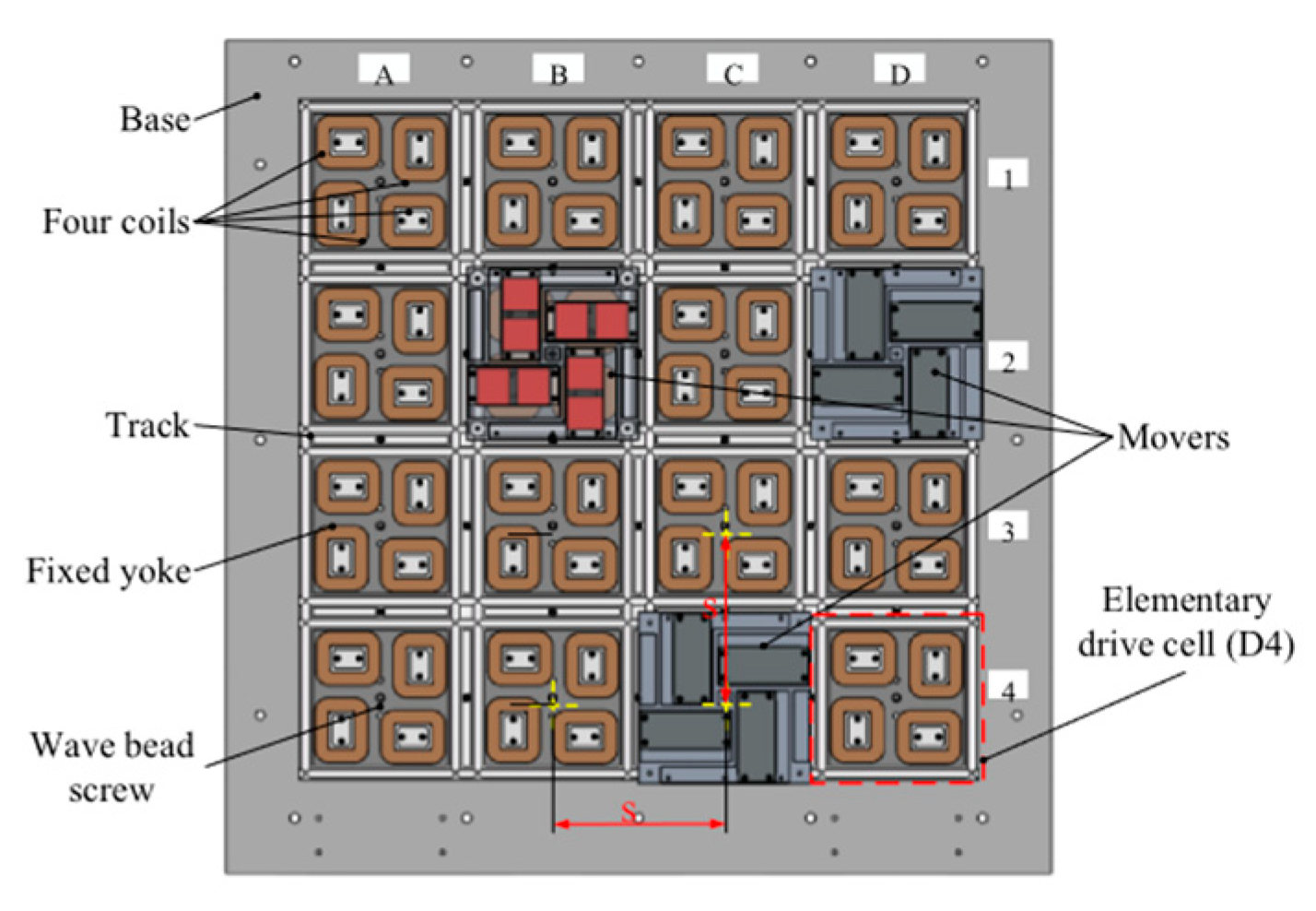
17] introduce a new deployment approach for large-scale, stacked CubeSats for in-orbit transfer and release. This scheme enhances storage capacity by tightly stacking CubeSats in three dimensions and utilizes the CubeSats in-orbit electromagnetic transfer system to methodically push these stacked CubeSats from a three-dimensional arrangement onto a two-dimensional transfer platform. The CubeSats are then moved to the release window using a planar two-dimensional drive, effectively transforming a three-dimensional transfer challenge into a two-dimensional platform issue. Due to the high number and significant mass of the CubeSats, dynamic shifts in the system’s center of mass occur during the transfer process within the deployer. Additionally, the actuation forces generated during the movement can disturb the electromagnetic conveying platform’s attitude and decrease pointing accuracy, resulting in discrepancies between the CubeSats’ actual and intended positions post-separation. To tackle this, in-orbit path planning for CubeSats is essential to ensure the stability of the electromagnetic conveying platform’s attitude during transfers. This strategic planning helps mitigate the effects of mass center shifts and actuation forces, thereby enhancing both the stability of the platform’s attitude and the precision of CubeSat deployment.
For CubeSat in-orbit transfer path planning, the objective is to minimize disturbances to the electromagnetic conveying platform’s attitude while also reducing the number of steps CubeSats need to reach their designated positions. This involves considering multiple factors such as transfer torque, the platform’s angular velocity, and the number of CubeSat movement steps, making it a multi-objective path planning challenge. Researchers have developed several solutions to address this complex problem, including well-known algorithms like A*, ant colony optimization, and Dijkstra’s algorithm. The A* algorithm is particularly noted for its efficiency in path optimization, as it integrates global information while assessing each potential node along the shortest path. It creates a cost function between the start and end points, estimates the distance from the current node to the endpoint, and uses this estimate to assess the node’s likelihood of being on the shortest route. This targeted approach not only speeds up the search process but also makes it more directed [
18]. Significant advancements have been made in refining the A* algorithm. For instance, Baoying Li et al. [
19] enhanced the algorithm to address issues like redundant nodes, slow search speeds, and frequent abrupt turns, resulting in smoother paths for mobile robots. Huanwei Wang et al. [
20] introduced modifications like extended distance, bidirectional search, and path smoothing methods to improve the algorithm’s efficiency and decrease the number of sharp turns. Chenguang Liu et al. [
21] tailored an improved A* algorithm for ship route planning to balance path length with navigation safety. Guozheng Fan et al. [
22] tackled UAV path planning challenges such as computational burdens, response delays, and obstacle avoidance during missions with an improved A* algorithm. Yunfeng Fan et al. [
23] proposed an improved A* algorithm for multi-robot systems in warehouse logistics to ensure collision-free and optimal path planning for each robot. Similarly, Minghao Li et al. [
24] developed a version of the A* algorithm to swiftly detect explosives in scenarios where their locations are unknown, demonstrating that this enhanced algorithm can find the shortest path faster and more efficiently than other models. Due to the traditional A* algorithm’s issues with excessive path turning points and slow search speeds in spatial obstacle path planning, Yangqi Ou et al. [
25] proposed an enhanced version of the A* algorithm, which incorporates a path smoothing strategy and an adaptive cost function into the traditional A* algorithm framework. These additions help reduce the number of path steps turning points and increase the search efficiency. Despite their effectiveness, these methods did not consider dynamic factors, which are crucial in the CubeSat in-orbit electromagnetic transfer system where path planning is based on dynamic models. Unlike other applications that prioritize shorter paths and quicker computation times, CubeSat path planning focuses on minimizing the impact on the electromagnetic conveying platform. The primary goal is to reduce disturbances during transfers, with the secondary aim of achieving shorter paths and faster execution times. Thus, dynamic parameters like transfer torque, angular velocity, and center of mass position are critical in selecting the most suitable CubeSat transfer paths, ensuring the stability and precision of the platform’s operations.
Given the limitations of existing path planning algorithms, this paper proposes an improved A* algorithm to address the path planning problem for CubeSat in-orbit transfer. The improved A* algorithm considers both the degree of disturbance to the attitude of the electromagnetic conveying platform caused by CubeSat transfer and the efficiency of CubeSat transfer. It aims to minimize the disturbance to the attitude of the electromagnetic conveying platform while minimizing the number of steps required for CubeSats to reach their expected positions. The main contributions and innovations of the paper are the following three aspects:
(1) Establish a Cost Model for Attitude Disturbance: Develop a model considering dynamic parameters such as transfer torque, angular velocity, and angular acceleration that the electromagnetic conveying platform experiences. Determine the position of the center of mass to assess the extent of attitude disturbance caused by CubeSat transfers and refine the cost function based on these findings.
(2) Introduce Path Coordination Strategy: Adapt the traditional A* algorithm by incorporating a path coordination strategy. This strategy addresses potential blockages caused by other CubeSats during transfer, ensuring smooth progress to intended release positions and avoidance of local optima.
(3) Optimize Management of the Open List: Enhance the computational speed and search efficiency by pre-filtering node information in the open list to reduce its size.
The remainder of the paper is structured to provide a comprehensive overview of the CubeSat in-orbit transfer system, starting with
Section 2, which introduces the working principles of the system and the initial environment modeling.
Section 3 delves into the foundational principles and limitations of the traditional A* algorithm. In
Section 4, enhancements made to the A* algorithm are detailed.
Section 5 presents a comparative analysis of test results from the improved A* algorithm to determine the optimal transfer path for specific CubeSat scenarios. Finally,
Section 6 concludes the paper with summarizing remarks.
3. Traditional A* Algorithm
3.1. Basic Principles
The A* algorithm establishes a cost function between the start point and the target point, giving the search a sense of purpose. The cost function of the traditional A* algorithm typically consists of two parts, formulated as follows:
In the formula, g0(n) represents the cost for the CubeSat to move from the start point to the current grid n; h0(n) represents the heuristic function for the CubeSat to move from the current grid n to the endpoint; f0(n) represents the cost function for the CubeSat to move from the start point to the endpoint.
In the traditional A* algorithm, considering the movement characteristics of the CubeSat on the electromagnetic conveying platform, which means the CubeSat can only move horizontally or vertically one grid at a time, the Manhattan distance is chosen as the heuristic function. The Manhattan distance represents the sum of the horizontal and vertical distances between two points, meaning that movement can only occur in four directions: up, down, left, and right within the grid. The formula is as follows:
In Equations (3) and (4), (xn, yn) represents the coordinates of the current cell n, (xs, ys) represents the coordinates of the starting point s, and (xe, ye) represents the coordinates of the endpoint e.
In the traditional A* algorithm, two lists are involved: the open list, containing the cost function values f0(n) for the four adjacent cells of the current cell, sorted in ascending order, and the closed list, encompassing all cells visited by the CubeSat. The path formed by connecting these cells in the closed list constitutes the final transfer path. Initially, the open list includes the coordinates of the start cell along with its corresponding f0(n) value, while the closed list starts empty.
3.2. Traditional A* Algorithm Logic
The traditional A* algorithm works as follows:
(1) Firstly, check if the open list is empty. If the open list is not empty, return the coordinates of the cell with the minimum f0(n) in the open list and add this coordinate to the closed list.
(2) Next, check if the current cell is the goal cell. If the current cell is the goal cell, the path is found. If the current cell is not the goal cell, search for adjacent reachable cells. If an adjacent reachable cell is not in the open list or the closed list, calculate the cost f0(n) for the adjacent reachable cell, add the coordinates and the f0(n) of the adjacent reachable cell to the open list, and set the current cell as the parent cell of the adjacent reachable cell.
(3) Repeat the above process. If the current cell is the goal cell, the optimal path is found, and the path is outputted. If the open list is empty, it indicates that no path is found.
The logic of the traditional A* algorithm is summarized as shown in
Figure 4.
3.3. The Limitations of the Traditional A* Algorithm
The traditional A* algorithm is a heuristic search algorithm for finding the shortest path in a static road network, capable of quickly identifying the shortest path from a start point to a destination on a map. However, the traditional A* algorithm is not suitable for CubeSat in-orbit transfer path planning due to three reasons:
Firstly, the traditional A* algorithm’s cost function does not align with the application requirements of CubeSat in-orbit transfer systems. According to the application requirements of CubeSat in-orbit transfer systems, the goal is to minimize the disturbance to the attitude of the electromagnetic conveying platform during CubeSat transfer while reducing the number of steps CubeSats take to reach their target positions as much as possible. However, the cost function of the traditional A* algorithm only focuses on minimizing path length and lacks cost estimation for the disturbance of the electromagnetic conveying platform’s attitude caused by CubeSat transfer paths. Therefore, it is necessary to introduce a model for estimating the disturbance of the electromagnetic conveying platform’s attitude and redesign the cost function of the improved A* algorithm to ensure that it meets the application requirements of CubeSat in-orbit transfer systems.
Secondly, the traditional A* algorithm cannot solve path-planning problems in dynamic road networks and is only suitable for planning paths in static road networks. However, the CubeSat in-orbit transfer system plans to utilize the transfer torque generated by the movement of other CubeSats to balance some of the transfer torque of the target CubeSat, aiming to minimize the disturbance to the attitude of the electromagnetic conveying platform during the transfer process. Therefore, the path planning problem for CubeSat in-orbit transfer is a multi-point, multi-objective path planning problem in a dynamic road network environment, which the traditional A* algorithm cannot solve.
Thirdly, the traditional A* algorithm fails to meet the efficiency requirements of multi-point, multi-objective path planning problems. The traditional A* algorithm stores all the information of the cells searched in the open list and arranges them in descending order. However, for a multi-point problem, each step corresponds to too many combinations of CubeSats, resulting in a large volume of data in the open list, which reduces the search efficiency.
In summary, the traditional A* algorithm cannot address the multi-point, multi-objective path planning challenges inherent in CubeSat in-orbit transfer. It falls short of meeting the application requirements, such as minimizing attitude interference and maximizing transfer efficiency in the CubeSat in-orbit transfer system. Therefore, it is imperative to improve the traditional A* algorithm.
4. Improved A* Algorithm
To accommodate the increasing future demand for CubeSats in orbit, the enhanced A* algorithm is pivotal for managing the simultaneous deployment of large batches of these satellites across a variety of applications, including routine operations, emergency services, and specialized scenarios such as space-based defense strategies. When instructed to deploy specific CubeSats, the electromagnetic transport system utilizes its built-in pusher to transfer them from storage to the transport platform. The enhanced A* algorithm then activates to identify the optimal path for moving the target CubeSats in conjunction with movable units. After the path is determined, the transport platform shifts the target CubeSats towards the launch window following this optimal route. The deployment concludes with the coil-type electromagnetic actuator ejecting and releasing the CubeSats into orbit, effectively executing the task of deploying numerous satellites simultaneously.
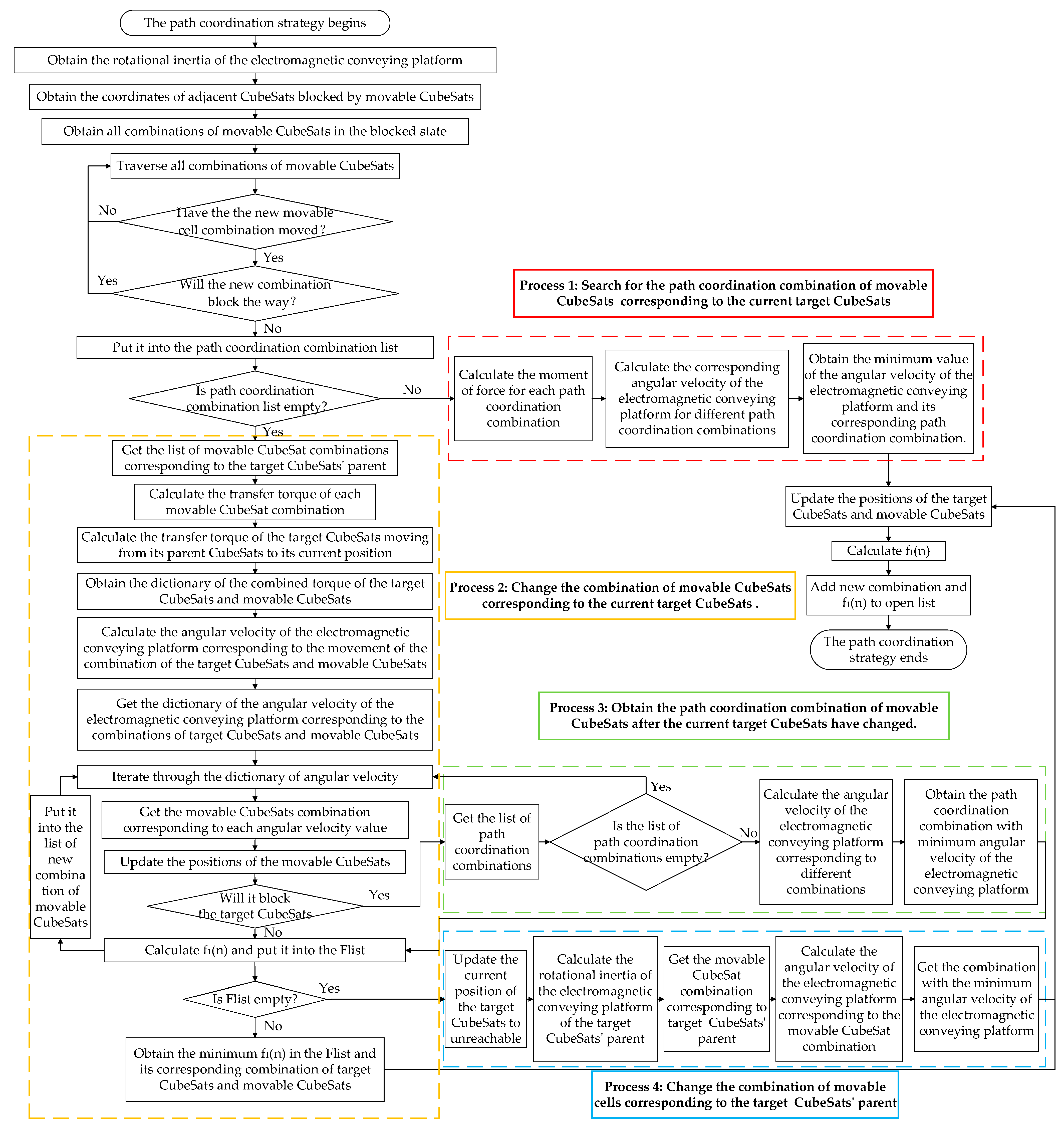
4.1. The Improved A* Algorithm Process Introduction
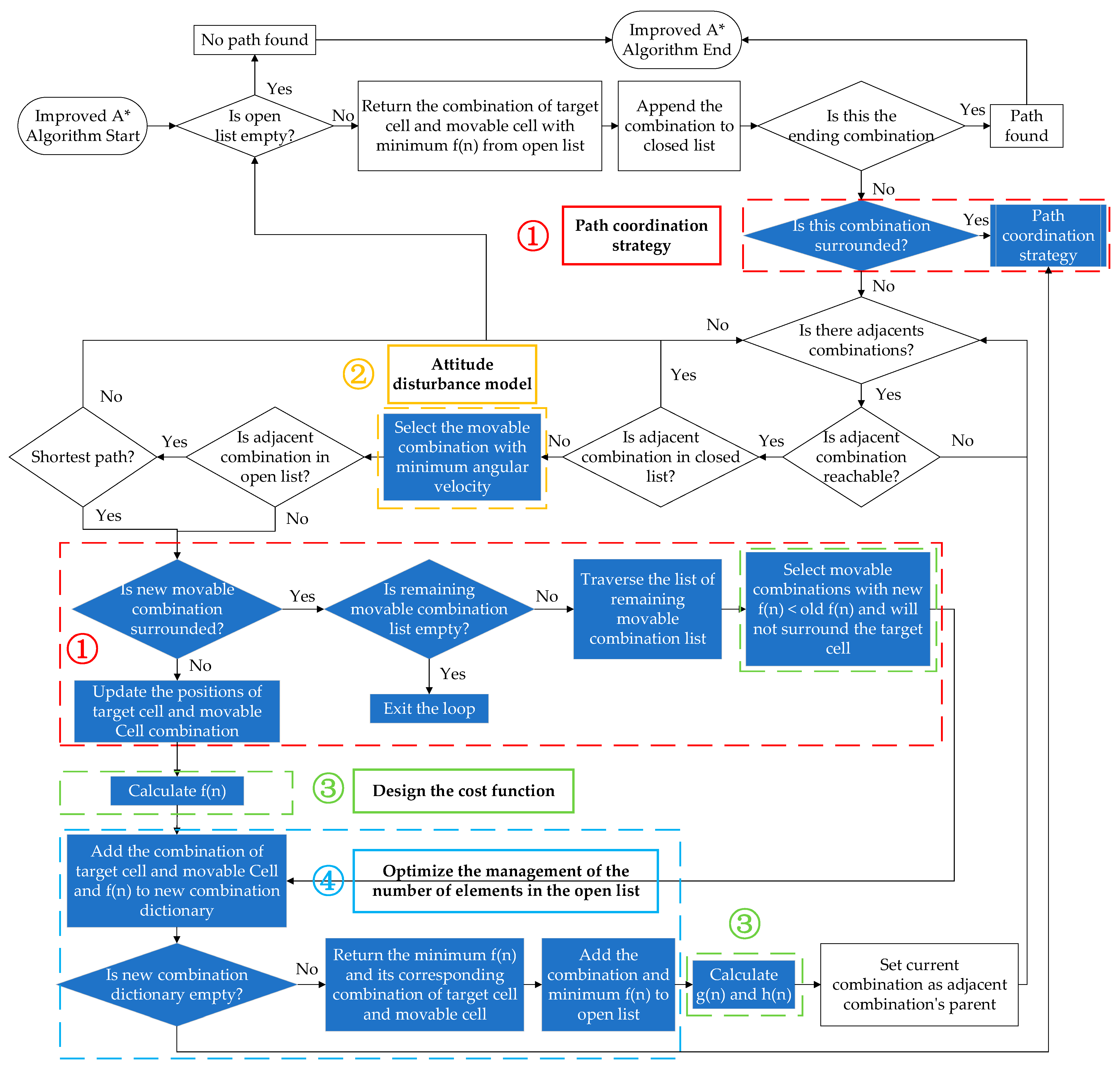
Considering the limitations of the traditional A* algorithm mentioned above, improvements should focus on establishing an attitude interference model, designing cost functions, introducing path coordination strategies, and optimizing the open list. The improved A* algorithm process is summarized in
Figure 5, where the blue boxes represent the enhancements compared to the traditional A* algorithm. The CubeSats on the electromagnetic conveying platform are classified into two categories: target CubeSats and movable CubeSats. Target CubeSats are those that need to be transported to the CubeSat release window, while movable CubeSats refer to the other CubeSats on the platform, excluding the target CubeSats.
Firstly, considering the capability of the CubeSat’s in-orbit electromagnetic transfer system to achieve large-scale deployment of payloads in orbit, there are typically a considerable number of CubeSats on the electromagnetic conveying platform, which can easily lead to congestion situations, thereby affecting the efficiency of CubeSat transfer. This article addresses this issue by introducing a check for whether the current combination of target CubeSats is congested before obtaining adjacent target CubeSat combinations. It proposes the introduction of a path coordination strategy to find alternative routes for congested target CubeSats, ensuring that they can reach their intended release positions smoothly, as depicted in
Figure 5①. If no feasible detour combination is found, the status of the target CubeSat combination is modified to unreachable to avoid unnecessary, redundant calculations, thereby enhancing the algorithm’s operational efficiency and resource utilization.
Next, since CubeSat in-orbit transfer path planning involves a multi-point, multi-objective problem, before placing the target CubeSat combination into the open list, it is necessary to find the corresponding movable CubeSat combination. The newly established electromagnetic conveying platform attitude interference model can quantify the degree of CubeSat transfer process disturbance to the platform. This serves as the basis for filtering movable CubeSat combinations, ensuring that the torque generated by the transfer of movable CubeSat combinations can maximize the offset of the torque generated by the transfer of target CubeSats. This achieves the objective of minimizing the attitude interference of each step of CubeSat transfer to the electromagnetic conveying platform, as depicted in
Figure 5②.
Section 5 verifies the effectiveness of movable CubeSats combinations in reducing attitude disturbance of the electromagnetic conveying platform through comparative case studies.
If the new combination of target CubeSat and movable CubeSats is not in the open list (never visited before) or in the closed list but not part of the shortest path (previously visited but not the shortest path), before calculating the new cost function f
1(n), a new judgment on whether the movable CubeSats will block the target CubeSat is added, as shown in
Figure 5①. If the new movable CubeSats will block the target CubeSat, obtain the corresponding detour combination and add the transfer cost f
1(n) of the detour combination to the transfer cost f
1(n) of the movable CubeSats combination. Revisit the list of movable CubeSats combinations, filtering for the one with the minimum cost f
1(n) to avoid falling into a local optimum and improve algorithm performance. If the new movable CubeSats do not block the target CubeSat, then calculate the transfer cost f
1(n) for the new combination, as shown in
Figure 5③. The transfer cost f
1(n) needs to consider both the efficiency of CubeSat transfer and the degree of attitude interference caused by the transfer process on the electromagnetic conveying platform. To achieve this, a refined cost function should be devised, integrating the attitude interference model of the electromagnetic conveying platform into the A* algorithm’s cost function. This entails setting separate coefficients k
h to represent CubeSat transfer efficiency and k
ω to denote the electromagnetic conveying platform attitude interference. By adjusting the ratio k
ω/k
h of these coefficients, the balance between the two factors in the cost function can be altered, thereby influencing CubeSat’s in-orbit transfer path planning.
Finally, unlike the traditional A* algorithm, the improved A* algorithm does not directly add the coordinates of the new target CubeSat and movable CubeSat combination, along with the transfer cost f
1(n), to the open list. Instead, they are first placed in a new combination dictionary. After traversing the adjacent reachable cells of the current target CubeSat and their corresponding movable CubeSat combinations, the improved A* algorithm returns the combination with the minimum transfer cost f
1(n) from the new combination dictionary. This combination, along with its f
1(n) value, is then added to the open list. This optimization effectively manages the number of elements in the open list, thereby enhancing the efficiency of the algorithm, as depicted in
Figure 5④.
4.2. Establishing an Attitude Interference Model
The degree of attitude interference of CubeSats on the electromagnetic conveying platform during transfer can be measured by the torque generated by CubeSat transfer, the angular velocity and angular acceleration of the electromagnetic conveying platform, and the variation in the center of mass of the CubeSat in the in-orbit transfer system.
4.2.1. The Calculation of CubeSat Transfer Torque and Center of Mass Position
The movement of multiple CubeSats on the electromagnetic conveying platform can be approximated as a system of n mass points. The real-time center of gravity coordinates of the CubeSats in-orbit electromagnetic transfer system can be calculated using the formula for the center of mass of a mass point system, as shown in Equation (5).
In Equation (5), (xc, yc) represents the center of mass coordinates of the electromagnetic conveying platform, mi represents the mass of the ith CubeSat on the electromagnetic conveying platform, and (xi, yi) represents the coordinates of the ith CubeSat on the electromagnetic conveying platform.
According to reference [
15], the movement of CubeSats on the electromagnetic conveying platform relies on electromagnetic force transfer provided by the transfer platform, where the transfer force for 1U, 2U, and 3U CubeSats can be approximately considered as F, 2F, and 3F, respectively. The degree of attitude disturbance to the electromagnetic conveying platform caused by CubeSat transfer can be measured by the magnitude of the torque exerted by the electromagnetic force on the central axis of the electromagnetic conveying platform during CubeSat transfer. The simplification of its dynamic model refers to the moment of spatial forces about the axis, measuring the change in the rotational state of an object around a certain axis. The calculation formula is shown in Equation (6). The magnitude of the torque is calculated according to Formula (6), and the sign is determined by the right-hand rule.
In Equation (6), Mz represents the torque exerted by the CubeSat transfer force on the electromagnetic conveying platform, F represents the electromagnetic transfer force of the CubeSat, and d represents the distance from the center of mass of the electromagnetic conveying platform to the line of action of the CubeSat transfer force.
According to the movement of the CubeSat on the electromagnetic conveying platform, the torque magnitude and sign generated by the CubeSat’s movement in the right, down, left, and up directions are summarized in
Table 1. In
Table 1, (x, y) represents the centroid coordinates of the CubeSat, and (x
c, y
c) represents the centroid coordinates of the electromagnetic conveying platform.
4.2.2. Angular Velocity and Angular Acceleration of the Electromagnetic Conveying Platform
The magnitude of the angular velocity and angular acceleration of the electromagnetic conveying platform can, to some extent, characterize the degree of attitude interference of the electromagnetic conveying platform. According to the differential equation of rigid body rotation about a fixed axis, it is known that the product of the moment of inertia of the rigid body about the rotation axis and the angular acceleration is equal to the algebraic sum of all the torques acting on the rigid body about the rotation axis. The formula is shown in (7).
In Equation (7), Jz represents the moment of inertia of the electromagnetic conveying platform about its center axis, Lz denotes the angular momentum of the CubeSat transfer with respect to the center axis of the electromagnetic conveying platform, ω stands for the angular velocity of the electromagnetic conveying platform, and α represents the angular acceleration of the electromagnetic conveying platform.
From Equation (7), it can be observed that for different rigid bodies, assuming the same torque applied by the external force system to their axes, the larger the moment of inertia of the body about the axis, the smaller the angular acceleration α, and thus, the smaller the change in its rotational state; conversely, the smaller the moment of inertia of the body about the axis, the larger the angular acceleration α, and hence, the greater the change in its rotational state. Therefore, the moment of inertia of a rigid body is a measure of the rotational inertia of the body, just as mass is a measure of inertia for a particle.
According to the parallel axis theorem, the moment of inertia of a rigid body about any axis is equal to the moment of inertia about a parallel axis passing through the center of mass plus the product of the body’s mass and the square of the distance between the two axes, as shown in Equation (8).
In Formula (8), M represents the mass of the electromagnetic conveying platform, and d represents the distance between the current center of mass position (x
c, y
c) and the geometric center (x
o, y
o) of the electromagnetic conveying platform.
In Formula (8), J
zC represents the moment of inertia of the electromagnetic conveying platform about the axis passing through the center of mass, and J
z represents the moment of inertia of the electromagnetic conveying platform about the axis passing through the geometric center of the electromagnetic conveying platform. According to the relevant technical manual, J
z can be expressed as follows:
In Formula (10), M represents the mass of the electromagnetic conveying platform, and a and b, respectively, represent the length and width of the electromagnetic conveying platform.
Therefore, the angular acceleration of the electromagnetic conveying platform can be expressed as follows:
Thus, the angular velocity of the electromagnetic conveying platform can be expressed as follows:
Combining the analysis of the application scenarios of CubeSats in-orbit electromagnetic transfer system, it can be inferred that the maximum angular velocity of the electromagnetic conveying platform during the transfer process and the final angular velocity after transfer play a crucial role in the attitude stability of the CubeSats in-orbit electromagnetic transfer system.
In Equation (13), P1(n) represents the attitude disturbance model of the electromagnetic conveying platform, ω1(n) denotes the real-time angular velocity of the electromagnetic conveying platform, and kω represents the weight coefficient corresponding to the cost of the attitude disturbance level of the electromagnetic conveying platform.
4.3. Design the Cost Function
The cost function can be expressed as a comprehensive consideration of both the disturbance level of the CubeSat in-orbit electromagnetic transfer system to the attitude of the electromagnetic conveying platform and the efficiency of the CubeSat in-orbit transfer.
In Equation (14), k
h represents the weighting coefficient of the cost associated with the efficiency of CubeSat in-orbit transfer. By adjusting the ratio between kh and kω, the paper can change how much CubeSat’s transfer system prioritizes efficiency versus minimizing attitude disturbance to the electromagnetic conveying platform in the overall transfer cost. Increasing k
h favors finding the shortest transfer path for CubeSat, somewhat overlooking the potential disturbance to the electromagnetic conveying platform’s attitude caused by the path. Conversely, raising k
ω prompts the system to prioritize minimizing attitude disturbance to the electromagnetic conveying platform when choosing a path, potentially overlooking CubeSat transfer efficiency and leading to locally optimal solutions. The function g
1(n) represents the Manhattan distance for a CubeSat to move from the starting point (x
s, y
s) to the current cell (x
n, y
n). It can be expressed as:
h
1(n) represents the heuristic function for the CubeSat to move from the current position (x
n, y
n) to the destination (x
e, y
e), and it can be expressed as follows:
Based on the cost function, the initial conditions for the improved A* algorithm for CubeSat’s in-orbit transfer path planning are designed, as shown in
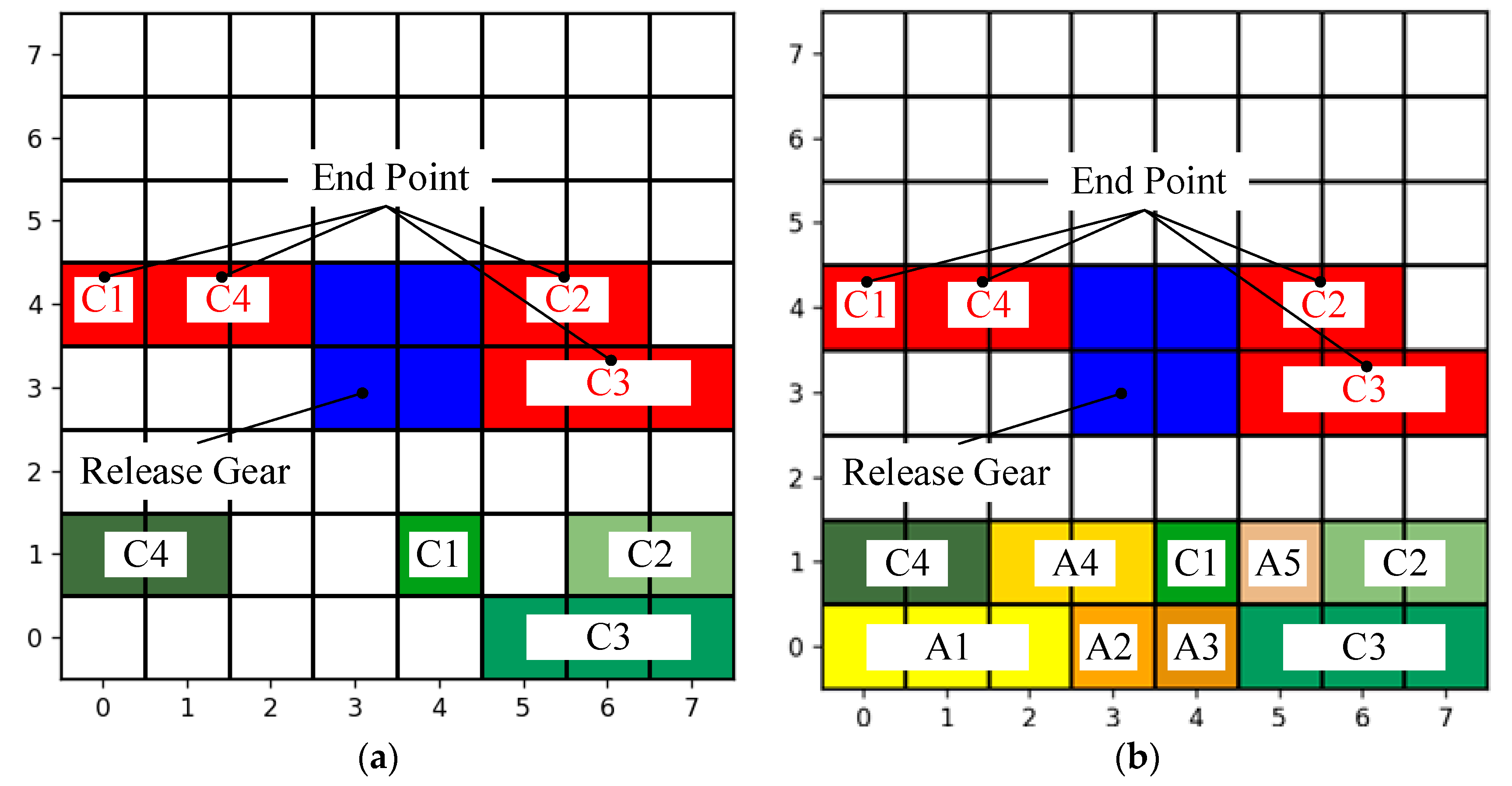
Table 2.
The initial conditions for each example are shown in
Figure 6.
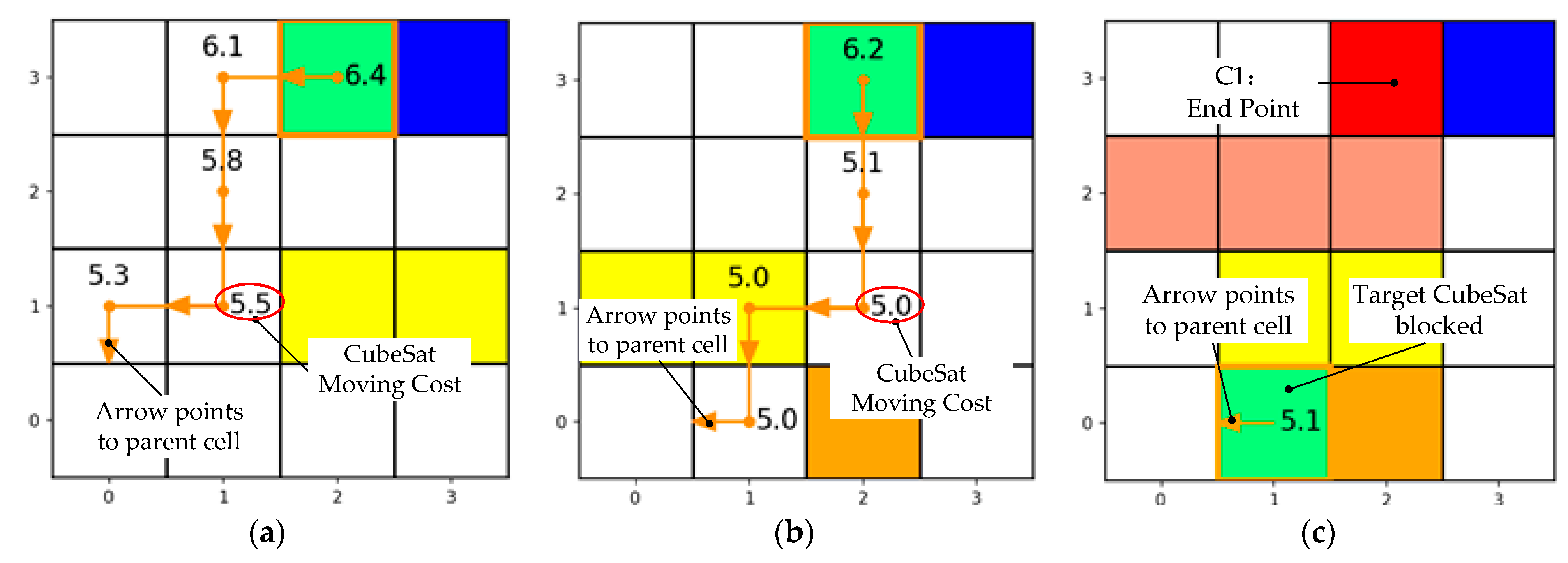
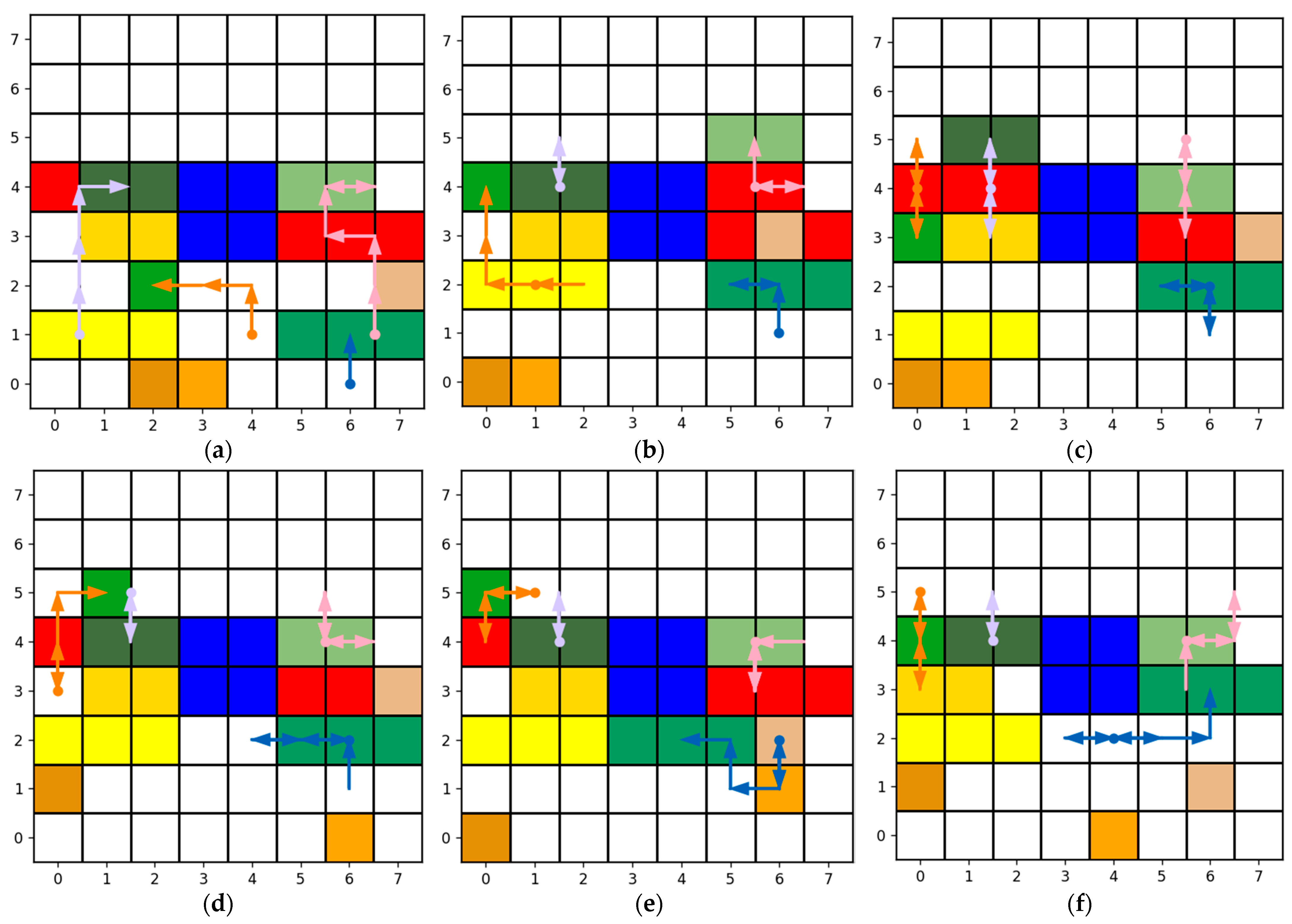
The results of the algorithm’s operational testing are shown in
Figure 7. In
Figure 7, arrows point to the current cell’s parent.
From
Figure 7c, it can be observed that the CubeSat shown in Example 3 is surrounded by other CubeSats during the transfer process, resulting in the interruption of the algorithm and the failure to reach the destination. Analysis indicates that as the number of CubeSats on the electromagnetic conveying platform increases, it is inevitable that situations where the target CubeSat is surrounded by other CubeSats will occur. Therefore, introducing the path coordination strategy to address this situation is necessary.
4.4. The Path Coordination Strategy
The application scenarios for path coordination strategies in CubeSat deployment can broadly be categorized into two types: those where the deployment sequence is known and those where it is unknown. In the first scenario, where the deployment sequence of CubeSats is known, such as in routine deployment tasks, the CubeSats’ in-orbit electromagnetic transfer system pushes entire layers of CubeSats simultaneously to the transport platform. This approach means that both target and movable CubeSats are moved to the platform together. However, as the number of CubeSats on the platform increases, issues such as path congestion inevitably arise. Path coordination strategies are then crucial for ensuring that target CubeSats can efficiently reach the launch window without disruptions. In the second scenario, where the deployment sequence is unknown, the role of path coordination strategies becomes even more critical. These strategies prevent the transport process from getting bogged down in local optima. As shown in the operational logic of the improved A* algorithm (illustrated in
Figure 5), before implementing a transport plan that offers the lowest transport cost for the target CubeSat and movable CubeSat at that step, it is vital to assess whether the plan might cause path blockages. If potential blockages are identified, path coordination strategies are employed to devise alternative plans that circumvent these issues. This proactive integration of path coordination strategies into the improved A* algorithm helps to avoid local optima and significantly boosts the efficiency of CubeSat in-orbit transportation.
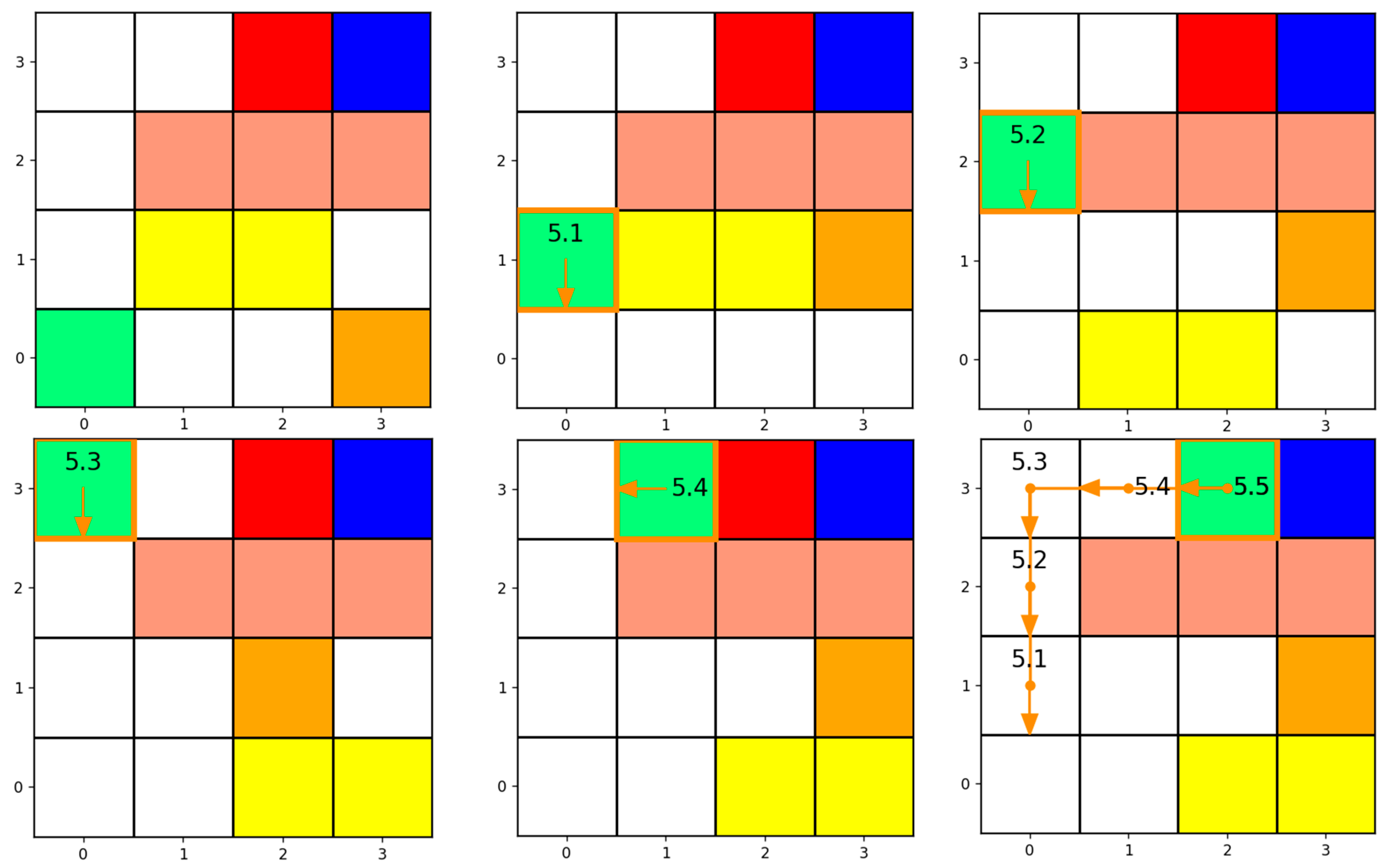
The path coordination strategy mainly consists of four levels. Firstly, it checks whether the target CubeSats are blocked. If the current target CubeSats are blocked, it then identifies which movable CubeSat is blocking it and subsequently obtains the path coordination combination corresponding to the current target CubeSats’ associated movable CubeSats, which is process 1. Next, it should be determined whether the path coordination combination of the target CubeSats and movable CubeSats will block the path. If the path coordination combination of the movable CubeSats does not block the path, it indicates that the combination is feasible; otherwise, it indicates that the combination is not feasible. If a feasible path coordination combination cannot be found, indicating that Process 1 is not feasible, it means that the position of the movable CubeSats combination corresponding to the current target CubeSats needs to be changed, which is Process 2. If the current target CubeSats are still blocked after changing the position of the movable CubeSats, the path coordination combination corresponding to the changed position of the movable CubeSats is obtained, which is Process 3. If no path coordination combination is found corresponding to the changed position of the movable CubeSats, it indicates that none of the movable CubeSats combinations corresponding to the current target star are feasible. Therefore, it is necessary to change the position of the movable CubeSats corresponding to the target CubeSat combination’s parent, which is Process 4. The flowchart of the path coordination strategy is shown in
Figure 8.
The key points of the path coordination strategy lie in how to determine if the target CubeSat combination is blocked, by whom, and whether the new combination obstructs the path. The specific solution is as follows:
(1) Determine if the target CubeSat combination is blocked: Firstly, obtain the coordinates and accessibility of the adjacent cells from the current position of the target CubeSat combination. If all adjacent cells are inaccessible, then the target CubeSat combination is considered blocked; otherwise, if at least one adjacent cell is accessible, then the target CubeSat combination is not blocked.
(2) Determine which movable CubeSat blocks the target CubeSat combination: Since the target CubeSat combination’s transfer strategy involves traversing adjacent cell coordinates, moving only one step at a time without backtracking, the adjacent cell coordinates of the target CubeSat combination does not include cases where all four directions (right, down, left, up) have been visited. In other words, if all adjacent cell coordinates are already in the closed list, it implies that the target CubeSat combination is blocked by another CubeSat. Therefore, the key to this problem lies in determining which movable CubeSat blocks the target CubeSat combination. Firstly, obtain the coordinates of the adjacent cells of the target CubeSat combination and remove the visited coordinates. Obtain the current movable CubeSat coordinate dictionary, where the movable CubeSat name serves as the key and the list of occupied cell coordinates serves as the value. Traverse the coordinates of the adjacent cells of the target CubeSat combination and check if they are in the movable CubeSat coordinate dictionary. If found, return the corresponding key of the coordinate, which represents the movable CubeSat name, indicating that the target CubeSat combination is blocked by this movable CubeSat.
(3) Determine whether the given combination of the target CubeSats and movable CubeSats will block the path: Firstly, obtain the coordinates of the adjacent cells of the target CubeSats and remove the coordinates that have been visited. Then, obtain the list of cell coordinates occupied by the movable CubeSat combination. Finally, traverse the adjacent cell coordinates of the target CubeSats. If there are adjacent cell coordinates that are not in the list of movable CubeSat coordinates, it indicates that this combination will not block the path. Conversely, if all adjacent cell coordinates are in the list of movable CubeSat coordinates, it indicates that this combination will block the path.
Following the implementation of the path coordination strategy, the test results for Example 3 are depicted in
Figure 9 (with k
ω/k
h = 1).
4.5. Optimize the Open List
During the algorithm testing process, it was observed that as the number of CubeSats increased, the algorithm runtime also increased, failing to meet the requirement for quick response. Optimization of the algorithm is necessary. During the execution of the traditional A* algorithm, expanding a node involves computing the transfer cost f0(n) for all adjacent nodes and sorting them in the open list in descending order. Due to the numerous combinations of target CubeSats and movable CubeSats, the size of the open list is large. Consequently, the computation time required to return the combination with the minimum f0(n) value from the open list also increases, thus reducing the speed of open list expansion. In the improved A* algorithm, this paper optimizes the management of the number of nodes in the open list by introducing a new combination dictionary. The positions and corresponding transfer costs f1(n) obtained from traversing the target CubeSat combinations at each step are first placed into the new combination dictionary. This allows for the comparison of f1(n) values before placing them into the open list, ensuring that only the combination with the minimum f1(n) and its corresponding f1(n) are placed into the open list. This reduces the number of nodes in the open list and effectively improves the efficiency of the algorithm.
6. Conclusions
The paper introduces an improved A* algorithm tailored for path planning within the CubeSats in-orbit electromagnetic transfer system, aimed at minimizing disturbances to the platform’s attitude caused by CubeSat transfers while also reducing the number of steps required for CubeSats to reach their designated positions.
The enhancement of the A* algorithm involves four key improvements: developing an attitude disturbance model, crafting a refined cost function, implementing a path coordination strategy, and optimizing the management of the open list. The first step involves creating a model to quantify the level of attitude disturbance on the electromagnetic conveying platform during CubeSat transfers and integrating this model into the cost function to better reflect the trade-offs between transfer efficiency and disturbance. In response to potential blockages caused by the high number of CubeSats on the platform, a path coordination strategy is introduced to effectively manage and plan the transfer route, ensuring smooth delivery of CubeSats to their target locations. To improve the efficiency of the algorithm, this study also refines how the elements in the open list are managed, enhancing the overall execution speed of the algorithm. Ultimately, the comparative analysis of the optimal transport paths demonstrates the crucial role of movable CubeSats in maintaining the stability of the platform’s attitude. The improved A* algorithm plays a key role in optimizing these paths, significantly mitigating disturbances.
On the 8 × 8 electromagnetic conveying platform, Case 1 only involves the transfer of target CubeSats, whereas Case 2 includes both target and movable CubeSats, moving four and nine CubeSats, respectively, to the launch window. In Case 2, the platform’s final angular acceleration is 0.0009 rad·s−2, its final angular velocity is −0.0026 rad·s−1, and its maximum angular velocity reaches −0.029 rad·s−1. In contrast, Case 1’s final angular acceleration is approximately 80 times, the final angular velocity is about 77 times, and the maximum angular velocity is about 7 times that of those observed in Case 2. This stark contrast underscores the indispensable role of movable CubeSats in reducing disturbances to the platform’s attitude. The improved A* algorithm specifically tailors transport path planning for the joint movement of target and movable CubeSats, ensuring a stable platform attitude and balanced transport efficiency, thereby enabling effective large-scale CubeSat in-orbit transfer path planning.









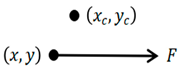
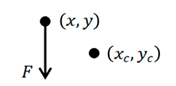
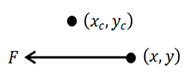
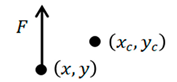


_Zhu.png)



