Abstract
The autonomous control of landing procedures can provide the efficiency and precision that
are vital for the successful, safe completion of space operations missions. Controlling a lander with
this precision is challenging because the propellants, which will be expended during the operations,
represent a significant fraction of the lander’s mass. The mass variation of each tank profoundly
influences the inertia and mass characteristics as thrust is generated and complicates the precise
control of the lander state. This factor is a crucial consideration in our research and methodology. The
dynamics model for our lander was developed where the mass, inertia, and center of mass (COM)
vary with time. A feed-forward neural network (NN) is incorporated into the dynamics to capture
the time-varying inertia tensor and COM. Moreover, the propellant takes time to travel through the
feed lines from the storage tanks to the engine; also, the solenoid valves require time to open and
close. Therefore, there are time delays between the actuator and the engine response. To take into
account these sources of variations, a combined time delay is also included in the control loop to
evaluate the effect of delays by fluid and mechanisms on the performance of the controller. The
time delay is estimated numerically by a Computational Fluid Dynamics (CFD) model. As part of
the lander’s control mechanism, a thrust vector control (TVC) with two rotational gimbals and a
reaction control system (RCS) are incorporated into the dynamics. Simple proportional, integral, and
derivative (PID) controllers are designed to control the thrust, the gimbal angles of the TVC, and the
torque required by the RCS to manipulate the lander’s rotation and altitude. A complex mission with
several numerical examples is presented to verify the hover and rotational motion control.
Keywords:
dynamics with time-varying mass; inertia; COM; CFD; lunar lander; PID control; neural network 1. Introduction
The race to establish a presence on the lunar surface has grown in recent years, with both commercial companies and national agencies competing [1,2,3,4]. However, this pursuit has been fraught with setbacks and challenges, as evidenced by the numerous failed attempts that have characterized recent endeavors in lunar exploration [5]. While significant research has been conducted on landing technologies such as propulsion systems, guidance algorithms, and landing mechanisms [6,7,8,9,10,11,12], there appears to be comparatively limited focus on modeling dynamics, stability, and control.
This paper focus on propulsion systems that use liquid oxygen and liquid methane (LO2-LCH4) as propellants [13]. It is important to note that for this iteration of the study, the model employs the properties of the Earth’s gravitational environment. A significant portion of the total mass of such a lunar lander is the mass of the cryogenic propellants. As the lander operates, propellant is consumed to fuel the propulsion system, which leads to the reduction in the mass of each propellant in the lander. Properties such as mass, moment of inertia, and center of mass in the dynamics are crucial in the modeling and control of the system. The stability of the lunar lander is very sensitive to the moment of inertia and the COM as rotational motion is highly coupled with these two time-varying properties. This variation requires the careful consideration and adjustment of control strategies to maintain stability and ensure the successful execution of lunar landing missions. In earlier studies [14], researchers explored the control of a lunar lander’s position and orientation using a single thruster, without knowledge of its mass and velocity measurements. They proposed a controller with an invariance-based mass estimator and a sliding velocity observer but did not account for variations in the center of mass and inertia. Sliding-mode control has also been used to reduce the effect of noise without considering time-varying mass and moment of inertia [15]. In [16], the control system designed does not incorporate a mechanism that accounts for the change in mass, center of mass, and inertia that affect the lander dynamics during descent and landing. In [17], numerical optimization and bending filters are employed to increase control robustness under uncertainty, but again without considering time-varying mass properties. Ref. [18] employs a nonlinear controller divided into the thrust vector control and the position control that is based on the sliding mode theory. The test conducted to prove the functioning of the controller for the altitude, attitude, and position did not consider the variation of mass and moment of inertia. Ref. [19] introduced the design, modelling and control of a lander with semi-active control, assuming also that inertia parameters do not vary during the entire landing maneuver. The use of neural networks along with reinforcement learning and augmented optimization algorithms has proved beneficial for solving nonlinearities during a landing procedure. In [20,21], the use of neural networks and deep reinforcement learning for optimal control proves an improvement for real-time performance, while augmented convex–concave decomposition (ACCD) developed by [22] enhances the feasibility of optimization by ensuring a more robust convergence.
There are additional nonlinearities that must be managed by a lunar lander control system. For instance, it takes time for the fluid to travel through the pipeline to reach the engine. In addition, valve actuation is not instantaneous but has a time delay. These effects combine to create a time delay between the actuator and the engine response. To take into account these sources of variation, a control-oriented model for a lunar lander is developed where a time-varying mass, the moment of inertia, and COM are modeled in the dynamics. A combined time delay is also incorporated into the TVC responses to evaluate the effect of the delays and the controller’s performance. The time delay is estimated numerically by a computational fluid dynamics (CFD) model. As a part of the control mechanism of the lander, a TVC with two rotational gimbals and an RCS are incorporated into the dynamics. A combination of PID controllers are designed to control the TVC gimbal angles and RCS torque input to manipulate the rotation and the altitude of the lander.
Furthermore, a complex flight path mission is introduced to test the lander altitude and attitude motion control. The mission individually tests each controller at different time intervals.
2. Modeling the Dynamics
In Figure 1, a conceptual diagram of the lunar lander model is shown. This lander is developed and integrated as a testbed of a LO2 and LCH4 propulsion system [23]. The model shows three vertical cylinders containing liquid oxygen, liquid methane, and pressurized helium. Fully fueled, the lander has a gross mass of 372 kg, of which 103.7 kg is tank propellants and pressurizing fluids. The height of the lander is 3.7 m, and the diameter at the base of the legs is 1.3 m. The helium tank is at the top and the oxygen tank is at the bottom. The lander model is oriented with the reference frame where the z-axis is vertical and passes through the center of gravity of the lander when standing vertically up, see Figure 1a. A TVC is installed directly below the liquid oxygen tank, 0.6 m below the center of mass of the fully-fueled lander, see Figure 1b. Individual fuel lines are directly routed from the liquid methane and liquid oxygen tanks to the engine located between the liquid oxygen tank and the TVC.
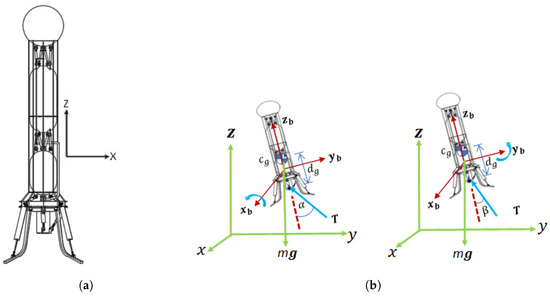
Figure 1.
The model shows three vertical cylinders containing oxygen, liquid methane, and pressurized helium. The gimbal angles and are the angular rotations of the thrust vector T with respect to and axes, respectively. (a) Lunar lander concept. (b) Gimbal angle orientation.
The TVC manipulates the direction of the thrust and the magnitude of the thrust to control the lander’s angular motions and attitude. The TVC has a gimbal that controls the roll and pitch angular directions. The gimbal angle manipulates the roll, and the gimbal angle manipulates the pitch. The TVC is placed so that the thrust vector results at an offset distance from the model’s center of gravity on the center-line (on axis). This distance is represented as in Figure 1b. As the propellant constitutes a large fraction of the vehicle’s mass, the mass properties are expected to change dramatically as the propellant is burned off during the landing maneuver. Realistically, simulations and control of the lander’s dynamics must thus account for changes in mass, COM, and inertia.
2.1. Modeling the Mass Variation
The change in mass is related to the thrust required by the controller to perform desired outputs or maneuvers. Assuming specific impulse is constant throughout achievable throttle settings, the rate of change of the mass as a function of thrust is given by
where is the nominal mass flow rate of the fuel (different for LOX and LCH4), is the throttle, T is the magnitude of the thrust and is the maximum thrust that the engine can produce. Applying Forward Euler approximation to Equation (1), the instantaneous mass can be written as
where is time step and is the mass at the previous time step. The mass flow rate of the two fuels is different. Since the mass of the pressurant fluid is so small, only the concentrated depletion of pressurant mass and volume in its original tank is observed, but the addition of pressurant fluid mass in each of the two fuel tanks is not simulated.
2.2. Modeling the Variation in COM and Moment of Inertia
The lander computer aided design (CAD) model is used to calculate the inertia tensor and the COM. As seen in Figure 2, the lander is positioned with the gimbal pivot axes aligned with the environment x and y axes. This ensures that the calculated COM will be with respect to the gimbal pivot axes. The resulting distance between the model origin and the calculated COM, , is the moment arm of the thrust actuation with respect to the estimated COM.
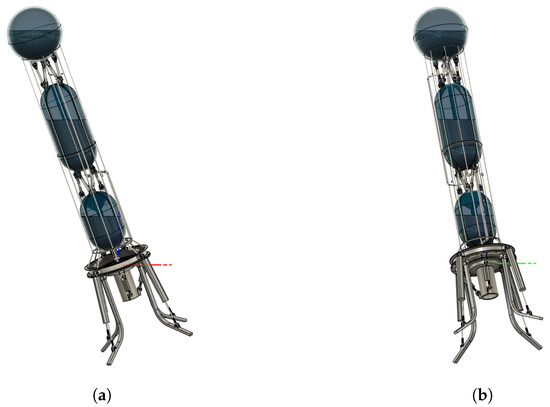
The reason for changes in center of mass of the lander and in inertia tensor is fuel consumption. The change in COM will affect the TVC as the distance and the inertia varies with time. Each tank is initially filled with fluid of different physical properties, which makes it difficult to estimate how the center of mass and inertia tensor change over time as the fuel is consumed. Our analysis employs different mass flow rates for each liquid in each tank. Using the CAD model, we then calculate the change in COM and inertia tensor matrix of the lander by emptying each tank. The fuel depletion is achieved in 6 separate stages, where the same amount of fuel is consumed in each subsequent stage until all tanks are empty, refer to Table 1. This data only captures part of the COM and inertia change, specifically when the lander is in its upright orientation. The COM and inertia are affected by the different orientations the lander could be in as it is performing its flight mission. For this reason, the same procedure was performed for various orientations, particularly changes in the x and y axes, refer to Table 2.

Table 1.
Lander fuel levels for LOX, LCH4 and He.

Table 2.
Orientations for COM and inertia tensor approximation.
Combining each orientation with all 6 fuel levels yields 132 fuel-level/orientation combinations. Figure 2 depicts the lander with an arbitrary fuel-level/orientation combination of L-3 and O-16. The internal shape of the liquids is assumed to be level towards the negative Z direction. At this point, we are not simulating any other fluid movements due to viscosity or external accelerations. The COM with respect to the TVC gimbal pivot location and the inertia tensors for each combination are captured.
The captured data are then used to train a feed-forward neural network to estimate the COM and inertia tensor of the lander live as the Simulink simulation runs. The network is first trained and tested in a MATLAB algorithm before generating a Simulink block containing the trained network for use in the model. The input signals for the network block are the individual masses of the three fluids and the attitude of the lander . The output of the network block consists of the COM coordinates and the 3 × 3 inertia tensor estimated by the NN block with the instantaneous lander properties for fluid masses and orientation. The COM coordinates are normalized to calculate the magnitude, .
2.3. Modeling the Time Delay of the Engine
When the engine receives the signal from the TVC controller to produce the required thrust T, the engine opens a valve at each tank, and propellant flows through the feed lines to the engine to produce required thrust. This process is subject to two sources of time-delay; one is the time to open the valve, and another one is the time that the propellants take to travel through the feed lines. As the properties of LCH4 cause it to flow more slowly than LOX we compute the overall feed time-delay from the LCH4 response. To compute this delay, a 3D transient CFD model of a fuel pipeline is used to estimate the time LCH4 takes to travel through the line. The pipe diameter is considered to be 1 in. by 4 ft. of length. The boundary conditions include inlet velocity and outlet pressure equal to 0 gauge. The inlet velocity is approximated from the known mass flow rate by enforcing the continuity condition:
where is the density of liquid LCH4, A is the cross sectional area and is the fluid velocity. Figure 3 below shows CFD results indicating that the LCH4 takes 0.035 s to pass half the distance from inlet towards the outlet. The inset scale shows the volume fraction of LCH4. Therefore, LCH4 takes 0.07 s to travel the pipeline from inlet to the outlet.

Figure 3.
CFD model results the LCH4 take 0.035 s to reach half way of the line from inlet towards the outlet. The inset scale shows the volume fraction the LCH4.
To include the valve and other miscellaneous delays, a total delay is approximated by considering the total delay to be twice of the pipeline delay obtained in the CFD simulation; that is s. This time delay is incorporated in resulting engine force (and torque as well) from the TVC as follows:
where is the resulting force from the TVC without time-delay. The associated resulting torque is given by
where .
2.4. Modeling the Dynamics
The lander’s dynamics are modeled through the use of the 6 degrees of freedom (DOF) variable mass block that is part of the Aerospace Blockset in Simulink [24]. The block is modeled after the Flat-Earth Equations of Motion by Stevens et al. [25] and the lander’s dynamics in inertial frame are described by 12 ordinary differential equations (ODEs) [26]. The block considers the rotation of a body-fixed frame (, , ) about a flat Earth reference frame (, , ). The lander’s COM position is described by its inertial Cartesian coordinates, , and its orientation with respect to the inertial reference frame by three Euler angles (roll), (pitch), (yaw). For this effort, our system assumes forces and moments due to gravity and propulsion only. For the propulsion effects on the vehicle, the TVC and the RCS are assumed to be working in parallel where the RCS controls only the yaw of the vehicle.
2.5. Control Mechanism
In this section, we present the dynamics of the lunar lander with TVC and RCS mechanisms active. Figure 4 depicts a block diagram that shows the dynamics of the lunar lander with a time-delayed TVC and RCS controllers. The TVC consists of three components: PID controllers, a gimbal mechanism, and the engine. The controller sends the signals , , and based on the absolute error of the current and desired set positions of the lander’s roll, pitch, and altitude, respectively. The gimbal mechanism calculates the required gimbal angles and , and the engine calculates the required thrust. As the pipeline has a time delay, the resulting force and torque are computed by incorporating the time delay as discussed in Section 2.3.
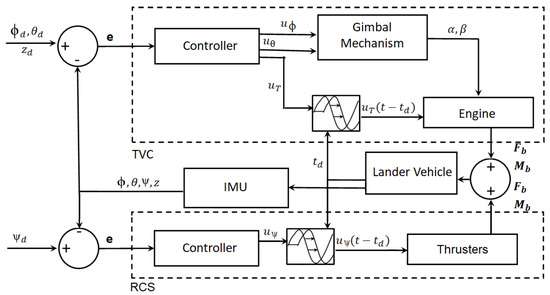
Figure 4.
Block diagram of the lunar lander system with a time-delayed TVC controller and instantaneous RCS controller.
The RCS consists of two components: PID controller and thrusters. The controller sends the signal based on the absolute error of the current and desired set positions of the lander’s yaw. Note that the RCS thrusters for this platform and analysis have not been designed. For this reason, the RCS input to the system is considered to be a moment rather than a thrust. The thrust could be approximated to be the moment commanded by the PID divided by the distance , which is the distance from the z-axis of the lander to the thrust output location of the RCS. It is assumed that an even number of RCS units would be attached to the lander. The total thrust required would then be divided by the number of RCS units present. A time delay for the RCS thrusters has not been modeled, but we approximate it by using the same delay as the TVC. The lander’s inertial measurement unit (IMU) evaluates the current position and orientation and sends the state feedback to the controllers.
3. Numerical Results
In order to verify how the dynamics and control of the lander work in the presence of time varying mass, moment of inertia, COM, and the engine’s time delay, we employ a complex flight mission with various changes in altitude and orientation. Table 3 provides the values of the parameters used in modeling the lander’s dynamics. In addition, both of the gimbal mechanisms’ saturation limits are set to . The angular actuation speed of the gimbal angles is assumed to be 0.3218 rad/s (about /s) based on similar work [27]. This is implemented to keep the PID controller from attempting to command the TVC gimbal angles to go from 0– instantly.

Table 3.
Parameters used in the dynamics modeling.
It is important to note that the lander’s initial position is meters while its initial orientation is degrees. This initial orientation is set to test the controller capabilities at take-off and replicate a take-off where the lander is not perfectly vertical.
3.1. Mission
The mission consists of specific maneuvers: change in altitude for ascent and descent (), rotation about x (), rotation about y (), and rotation about z (). Figure 5 shows a diagram of the maneuvers performed by the lander. The desired altitude and orientation changes for our complex mission are depicted in Figure 6.
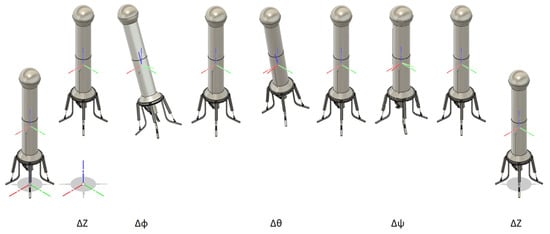
Figure 5.
Visualization of desired mission maneuvers.
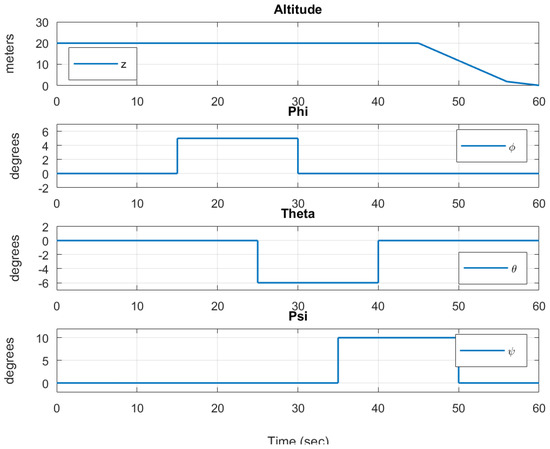
Figure 6.
Mission control with variable desired altitude and orientation.
3.2. Altitude Control
To test the altitude control, we specify desired altitude changes at s. The total simulation run time is 60 s. No external disturbances take place as we are already testing the controller capabilities with a complex mission path plan. The PID gains for the altitude controller are set to , , and . The resulting altitude response is plotted in Figure 7 along with the commanded altitude by the mission planner. The thrust resulting from the altitude controller is also plotted. Figure 7 also helps display how the thrust input directly affects the changes in altitude. Figure 8 displays the vertical velocity of the lander throughout the mission. Note that the altitude controller maintains a hover of height 20 m at s. The vertical velocity is near zero during that time. Also, it can be seen that the landing procedure produces a soft landing depicted in the last seconds of the simulation where also nears 0 m/s. Recall that the mass properties vary for each propellant, as seen on Table 3. Figure 9 depicts the mass variation with time of each of the propellants.
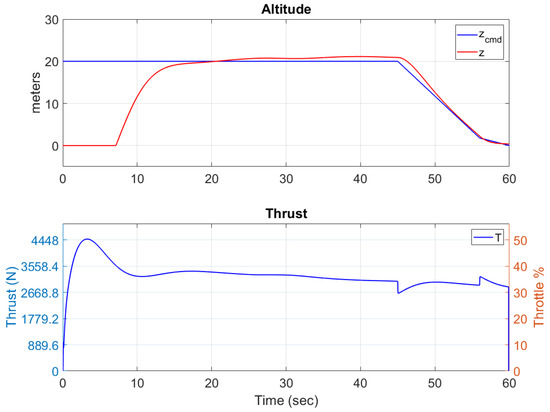
Figure 7.
Altitude control with commanded and response altitude.
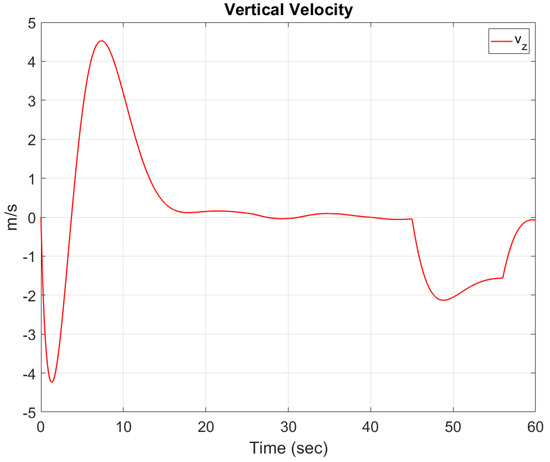
Figure 8.
Vertical velocity ().
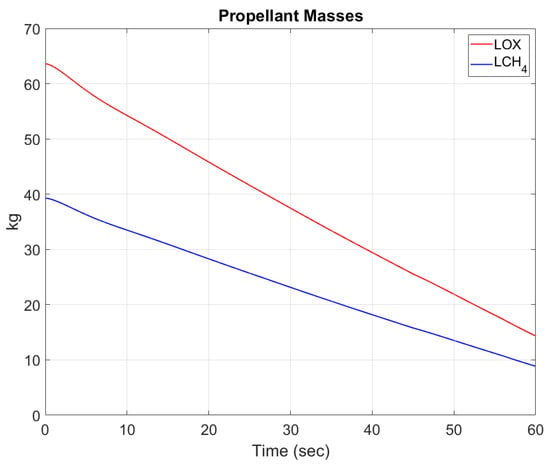
Figure 9.
Time history of the lander propellant mass.
3.3. Rotational Control
The complex flight mission also tests the lander’s roll, pitch, and yaw performance. The PID controllers’ gains are given in Table 4. The resulting roll response is plotted in Figure 10 along with the roll angle commanded by the mission planner. The TVC gimbal angle is also depicted in that figure. Note how the gimbal angle is limited to 10 degrees in each direction and how it directly affects the angle . Figure 11 displays the same but for the TVC angle and lander orientation angle . Figure 12 depicts the commanded and response angles for the yaw control, as well as the RCS moment generated to reach the desired angle .

Table 4.
PID gains used in TVC and RCS controllers.
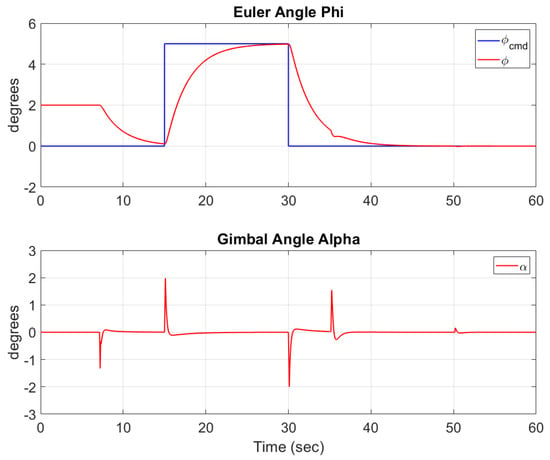
Figure 10.
The roll commanded and TVC gimbal response as mass, inertia, and COM change with time.
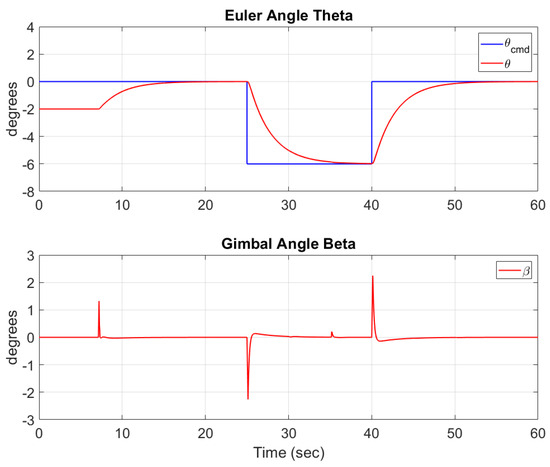
Figure 11.
The pitch commanded and TVC gimbal response as mass, inertia, and COM change with time.
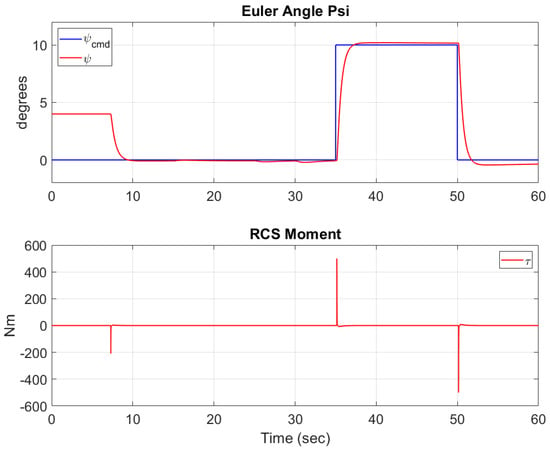
Figure 12.
The yaw commanded and RCS moment response as mass, inertia, and COM change with time.
Although a normal force acting on the lander from the ground is not simulated at this time, a PID actuation delay is applied to prevent the lander TVC and RCS systems from attempting to control the lander attitude before the lander loses contact with the ground. In order to thoroughly test the controllers, the mission planner employs overlaps in orientation adjustments. That is, each subsequent orientation maneuver begins before the previous one has finished executing. This provides the controller execution of two separate angles at the same time. This process can be seen at for interaction, for interaction, and for interaction, as seen in Figure 6. We see that the lander reaches the desired orientations proving the efficiency of the controllers.
4. Discussion
This paper introduces the dynamic modeling of a lunar lander considering time-varying mass, moment of inertia, and center of mass. It is important to note that mass depletion is considered for two individual propellants and one pressurant liquid in their respective tanks and different mass flow rates are assumed for each liquid depletion. Our model employs a feed-forward neural network trained with calculated COM and inertia tensor data for the lander at various fuel levels and orientations. The neural network provides live approximation of the COM and inertia for use in the propulsion and plant blocks of the lander system. Time delays between the actuator and engine have also been taken into account and a delayed response for the thrust has been incorporated.
A complex flight mission was planned and executed which test the individual altitude and attitude controllers. Both the altitude and attitude controllers account for the thrust time delay and the time variation in mass, moment of inertia, and COM. Although the thrust time delay and the variable mass, moment of inertia, and COM have a major influence on the dynamics of the lander, the controllers are capable of reaching the desired altitude and attitude. In the altitude graph, Figure 7, it is observed that the thrust required to maintain the desired altitude decreases as propellants are depleted. Figure 7 and Figure 8 depict the hover capabilities of the controllers. It is also evident that the velocity of climb and descent of the lander can be controlled by adjusting the rate of climb and descent in the altitude mission control. No external translational disturbances were executed as the flight mission is complex enough to test the altitude controller capabilities.
Because the mass of the propellants are dependent on the individual mass flow rates of depletion and the throttle of the thruster, Equation (2), we are able to see that the mass variations in Figure 9 are non-linear.
The attitude control of our model is also tested. Initially, all the orientations are set to arbitrary degrees to simulate a takeoff where the lander is not placed perfectly vertically. Since all three orientation angles are set to non-zero values, the attitude controller must maneuver the lander in the first seconds after takeoff to align the lander perfectly vertically with the TVC and RCS systems. This is achieved without issues as depicted in Figure 10, Figure 11 and Figure 12. The mission planer then tests the attitude control for each angle individually. No external rotational disturbances were executed as the flight mission is complex enough to test the attitude controller capabilities. Although lateral control of the vehicle with a desired landing position has not been developed for this system, it could be developed in a future iteration of this model. The position PID control could be coupled in cascade to the existing orientation PID control of the TVC. The lateral position control would provide desired roll and pitch angles for the TVC control that would reduce the position error between the current and the desired position.
This article has focused on the modeling the dynamics of the lander in a realistic way. The implemented control algorithm is conventional and, in the future, the authors intend to design an optimal control problem to achieve more robust maneuvering with a minimum amount of fuel.
Author Contributions
Conceptualization, A.S. and A.F.-A.; methodology, A.G.O., A.S. and A.E.-F.; software, A.G.O., C.G. and A.E.-F.; validation, A.G.O. and A.S.; formal analysis, A.G.O. and A.S.; investigation, A.G.O., A.S. and A.E.-F.; resources, A.S., A.F.-A. and A.C.; data curation, A.G.O. and A.S.; writing—original draft preparation, A.G.O., A.S. and C.G.; writing—review and editing, A.G.O., A.S., C.G., A.F.-A., A.C. and A.E.-F.; visualization, A.G.O. and A.S.; supervision, A.S.; project administration, A.S., A.F.-A. and A.C.; funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This project is sponsored by NASA under award No. 80NSSC20M0237.
Data Availability Statement
Data sharing is not applicable as the article describes entirely theoretical research.
Acknowledgments
We would like to thank the support given by Jack Chessa by providing guidance and technical data on the lander platform. We would also like to thank Amzad Hossain for his valuable insights and positive discussion regarding propulsion applications.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyre, N.; Goodliff, K. The Artemis program: An overview of NASA’s activities to return humans to the moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–10. [Google Scholar]
- Cohen, B.A.; Chavers, D.G.; Ballard, B.W. NASA’s robotic lunar lander development project. Acta Astronaut. 2012, 79, 221–240. [Google Scholar] [CrossRef]
- Gambone, E.A. Morpheus Lander Roll Control System and Wind Modeling. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 0330. [Google Scholar]
- Li, C.; Wang, C.; Wei, Y.; Lin, Y. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef] [PubMed]
- Pozza, M.A.; Dennerley, J.A. Risk Management in Outer Space Activities; Springer: Singapore, 2022. [Google Scholar]
- Hurlbert, E.A.; Ueno, H.; Alexander, L.; Klem, M.D.; Daversa, E.; Rualt, J.M.; Manfletti, C.; Caruana, J.N.; Asakawa, H.; Whitley, R.J. International space exploration coordination group assessment of technology gaps for LOX/Methane propulsion systems for the global exploration roadmap. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016; p. 5280. [Google Scholar]
- Hurlbert, E.A.; Atwell, M.J.; Melcher, J.C.; Morehead, R.L. Integrated pressure-fed liquid oxygen/methane propulsion systems-Morpheus experience, MARE, and future applications. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 4681. [Google Scholar]
- Smith, T.; Klem, M.; Fisher, K. Propulsion risk reduction activities for non-toxic cryogenic propulsion. In Proceedings of the AIAA Space 2010 Conference & Exposition, Anaheim, CA, USA, 30 August–2 September 2010; p. 8680. [Google Scholar]
- Klem, M.D.; Smith, T.D.; Wadel, M.F.; Meyer, M.L.; Free, J.M.; Cikanek, H.A., III. Liquid oxygen/liquid methane propulsion and cryogenic advanced development. In Proceedings of the 62nd International Aeronautical Congress, Cape Town, South Africa, 3–7 October 2011; number E-17931. [Google Scholar]
- Olansen, J.B.; Munday, S.; Devolites, J.; Baine, M. Project Morpheus: Lessons learned in lander technology development. In Proceedings of the AIAA SPACE 2013 Conference and Exposition, San Diego, CA, USA, 10–12 September 2013; p. 5310. [Google Scholar]
- Weiss, S.P. Apollo Experience Report: Lunar Module Structural Subsystem; Technical Report; NASA Technical Reports Server: Hampton, VA, USA, 1973. [Google Scholar]
- Choe, Y.; Park, C.G. LiDAR-Inertial-Based Absolute Positioning with Sparse DEM for Accurate Lunar Landing. IEEE Trans. Aerosp. Electron. Syst. 2024, 1–14. [Google Scholar] [CrossRef]
- Mohon, L. NASA Tests Methane Engine Components for Next Generation Landers. 2015. Available online: https://www.nasa.gov/technology/space-travel-tech/nasa-tests-methane-powered-engine-components-for-next-generation-landers/ (accessed on 15 January 2024).
- Cortés-Martínez, R.; Kumar, K.D.; Rodríguez-Cortés, H. Precise power descent control of a lunar lander using a single thruster. Acta Astronaut. 2021, 186, 473–485. [Google Scholar] [CrossRef]
- Sagliano, M.; Dumke, M.; Theil, S. Simulations and flight tests of a new nonlinear controller for the EAGLE lander. J. Spacecr. Rocket. 2019, 56, 259–272. [Google Scholar] [CrossRef]
- Rew, D.Y.; Ju, G.; Lee, S.; Kim, K.; Kang, S.W.; Lee, S.R. Control system design of the Korean lunar lander demonstrator. Acta Astronaut. 2014, 94, 328–337. [Google Scholar] [CrossRef]
- Jang, J.; Yang, L.; Fritz, M.; Nguyen, L.; Johnson, W.R.; Hart, J. Design and analysis of morpheus lander flight control system. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014; p. 4115. [Google Scholar]
- De Oliveira, A.; Lavagna, M. Development of a Controlled Dynamics Simulator for Reusable Launcher Descent and Precise Landing. Aerospace 2023, 10, 993. [Google Scholar] [CrossRef]
- Wang, C.; Nie, H.; Chen, J.; Lee, H.P. The design and dynamic analysis of a lunar lander with semi-active control. Acta Astronaut. 2019, 157, 145–156. [Google Scholar] [CrossRef]
- Li, W.; Song, Y.; Cheng, L.; Gong, S. Closed-loop deep neural network optimal control algorithm and error analysis for powered landing under uncertainties. Astrodynamics 2023, 7, 211–228. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, Z.; Jiang, F. Real-time control for fuel-optimal moon landing based on an interactive deep reinforcement learning algorithm. Astrodynamics 2019, 3, 375–386. [Google Scholar] [CrossRef]
- Sagliano, M.; Seelbinder, D.; Theil, S.; Lu, P. Six-degree-of-freedom rocket landing optimization via augmented convex–concave decomposition. J. Guid. Control Dyn. 2024, 47, 20–35. [Google Scholar] [CrossRef]
- Ponce, R. Development and Integration of the Janus Robotic Lander: A Liquid Oxygen-Liquid Methane Propulsion System Testbed; The University of Texas at El Paso: El Paso, TX, USA, 2017. [Google Scholar]
- MathWorks. Custom Variable Mass 6DOF (Euler Angles). 2006. Available online: https://www.mathworks.com/help/aeroblks/customvariablemass6dofeulerangles.html (accessed on 1 February 2024).
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hughes, P.C. Spacecraft Attitude Dynamics; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Bernacchia, D. Design of Thrust Vectoring Attitude Control System for Lunar Lander Flying Testbed. Ph.D. Thesis, Universita’ Di Bologna, Bologna, Italy, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).