Aerodynamic Characteristics of the Novel Two-Dimensional Enhanced Shock Vector Nozzle
Abstract
1. Introduction
2. Numerical Method
2.1. Flow Solver
2.2. Governing Equations
2.3. Definitions of Nozzle Performance Parameters
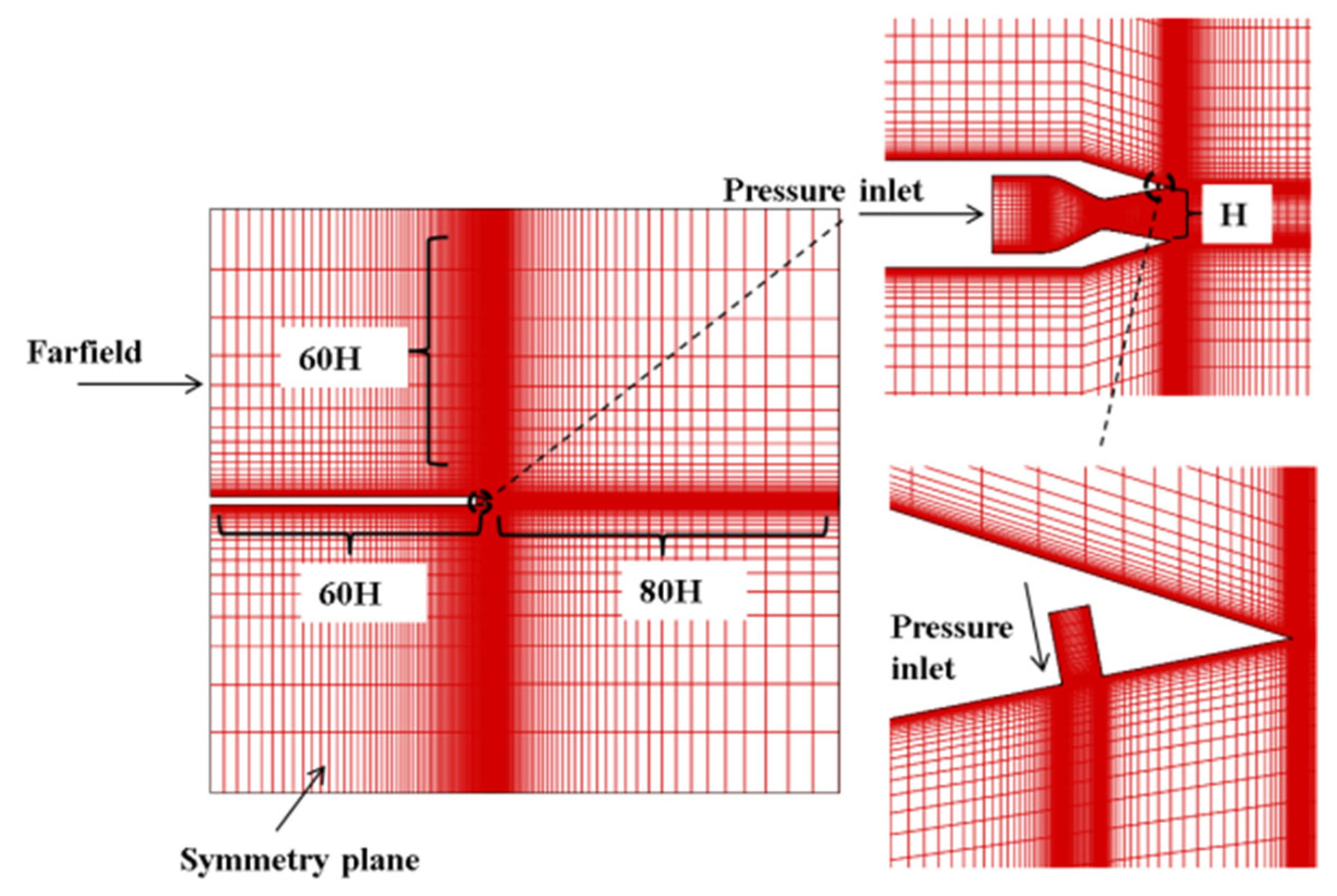
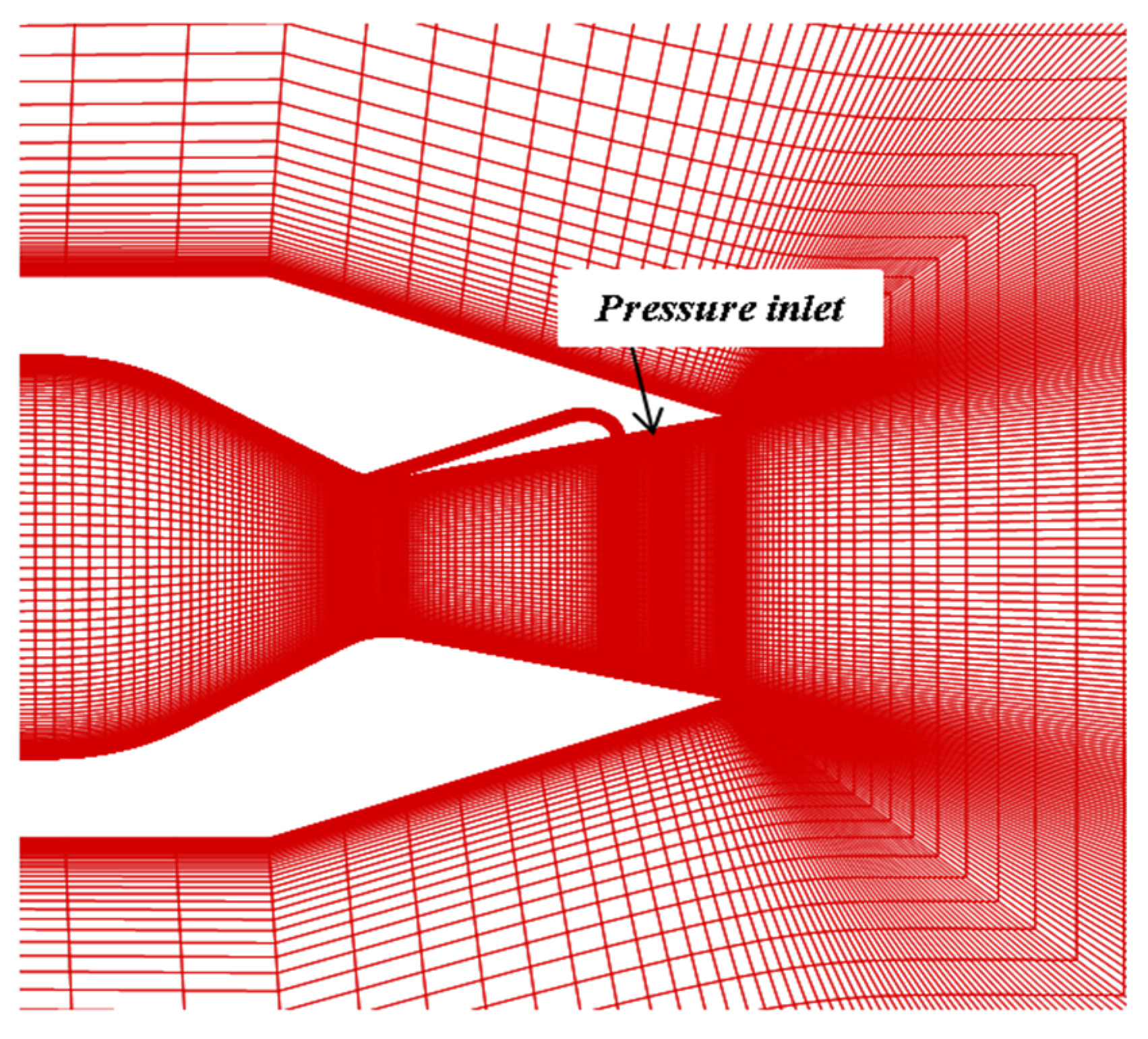
2.4. Computational Domain and Boundary Conditions
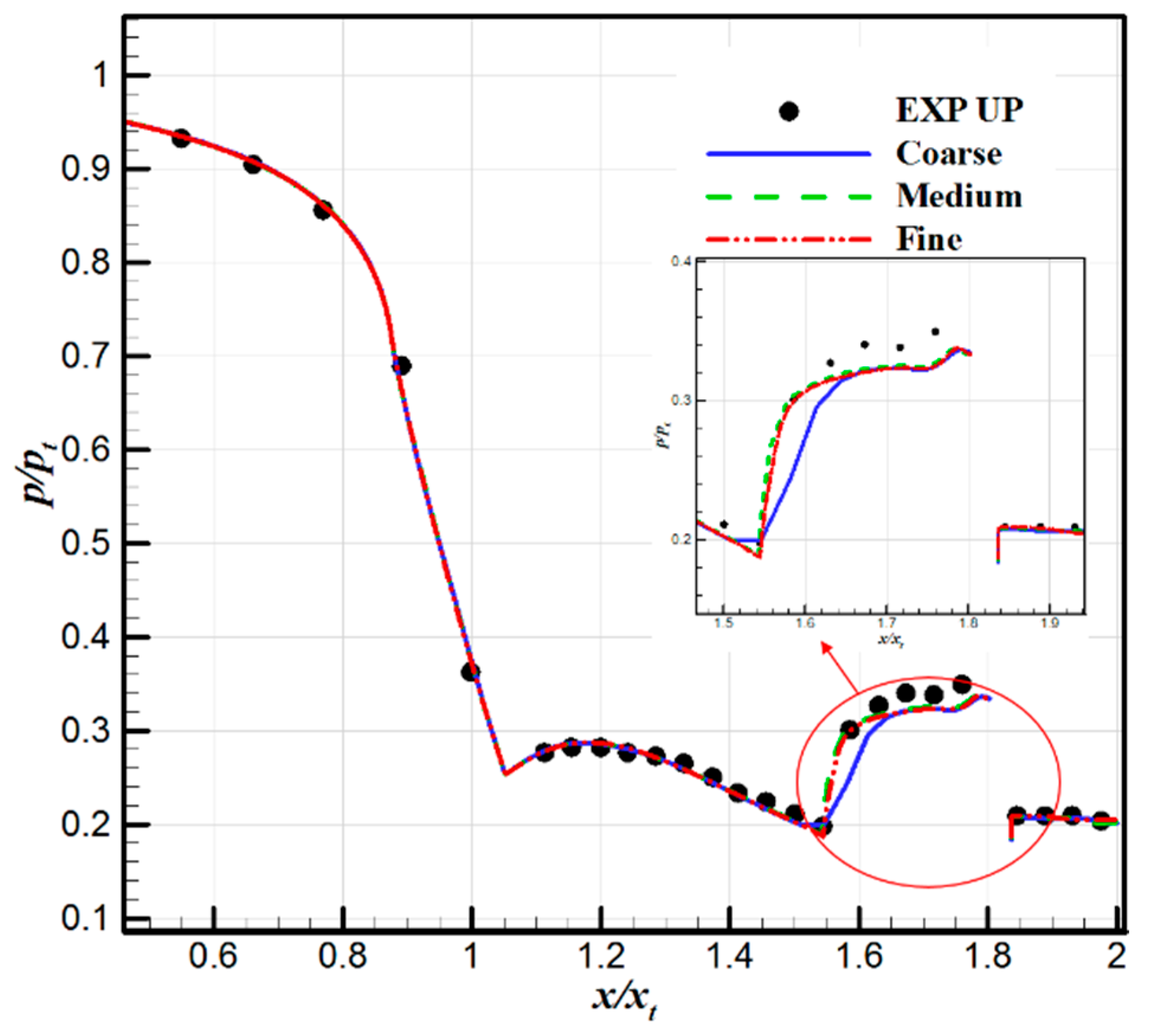
2.5. Grid Independence Analysis
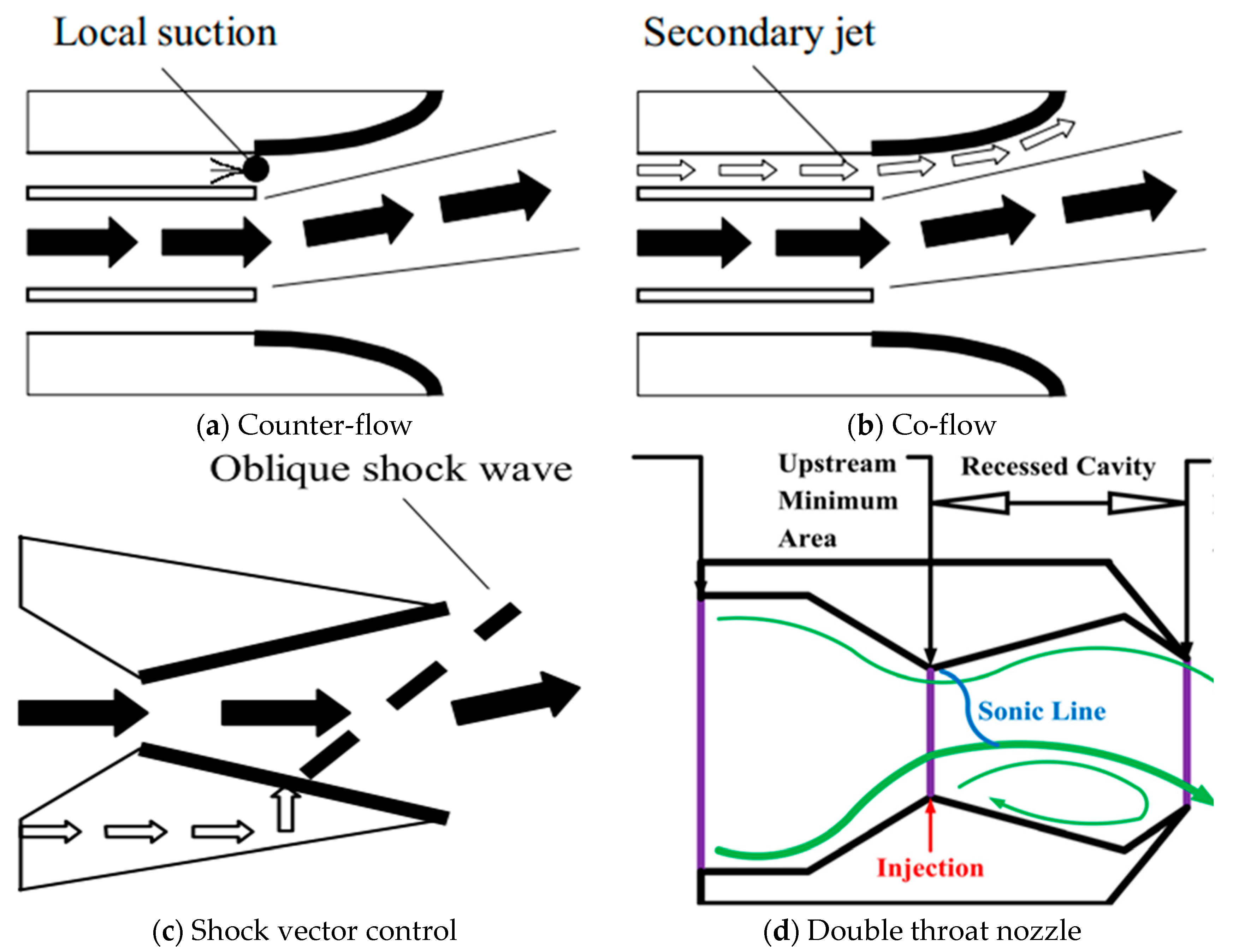
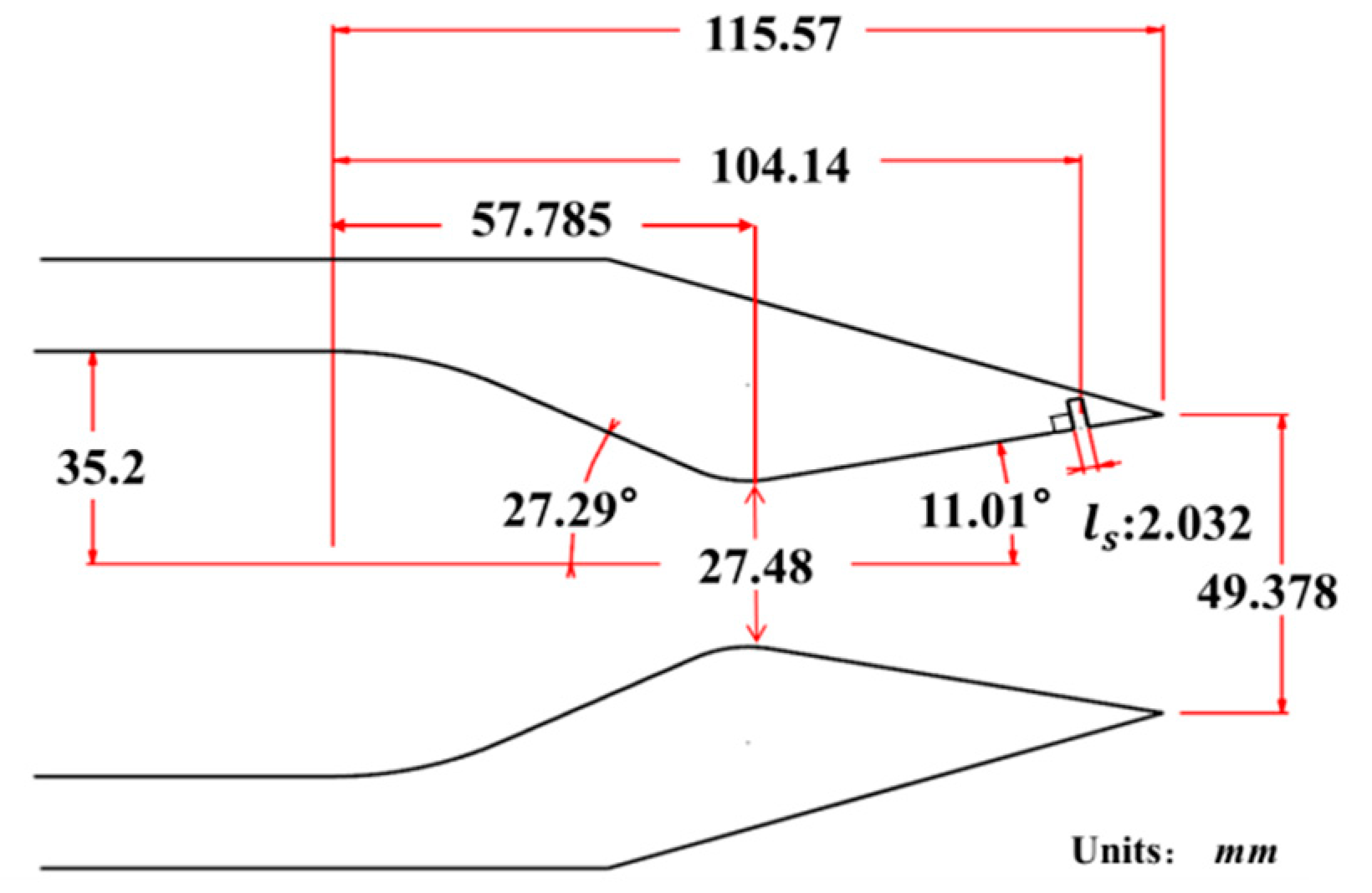
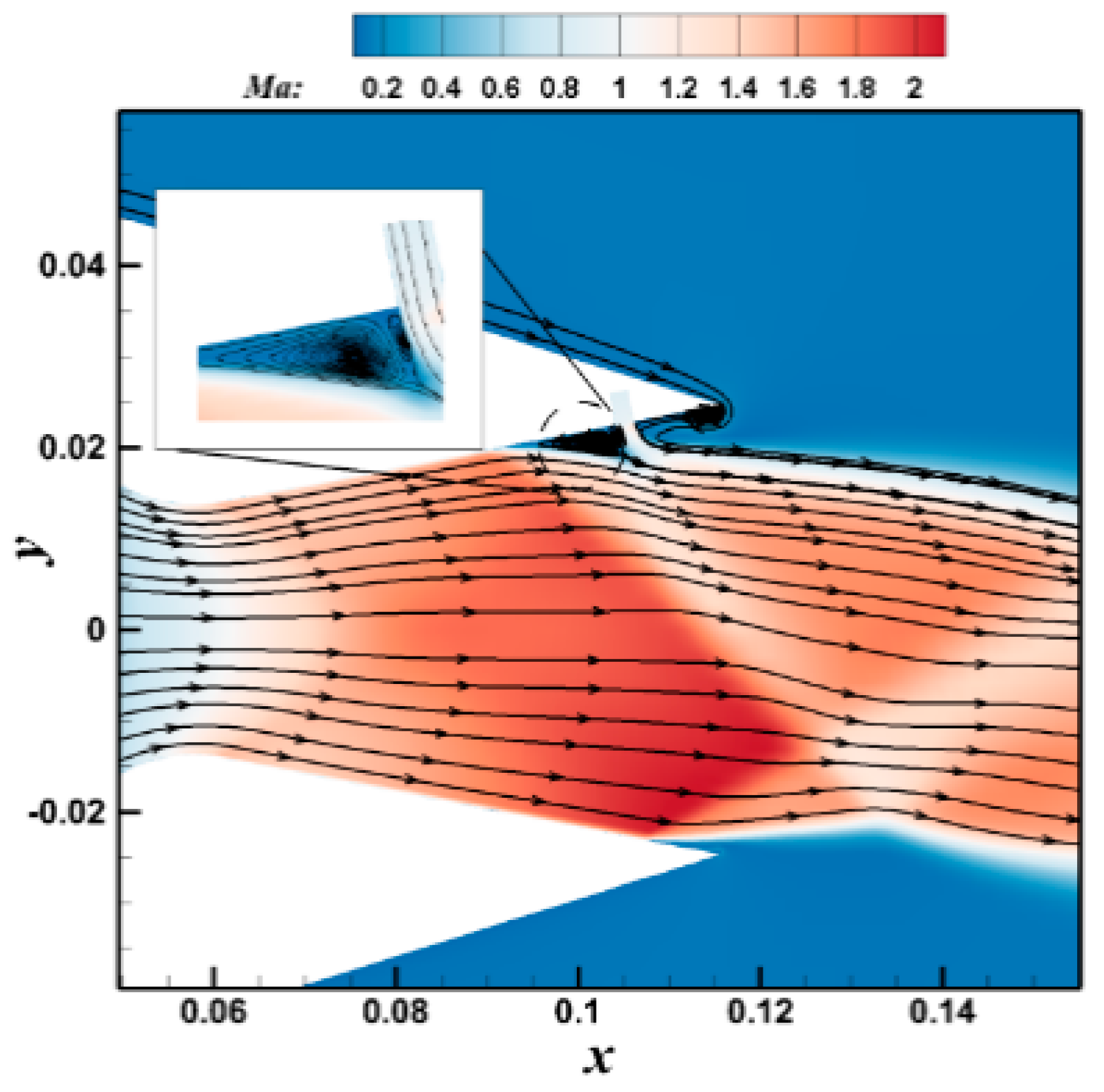
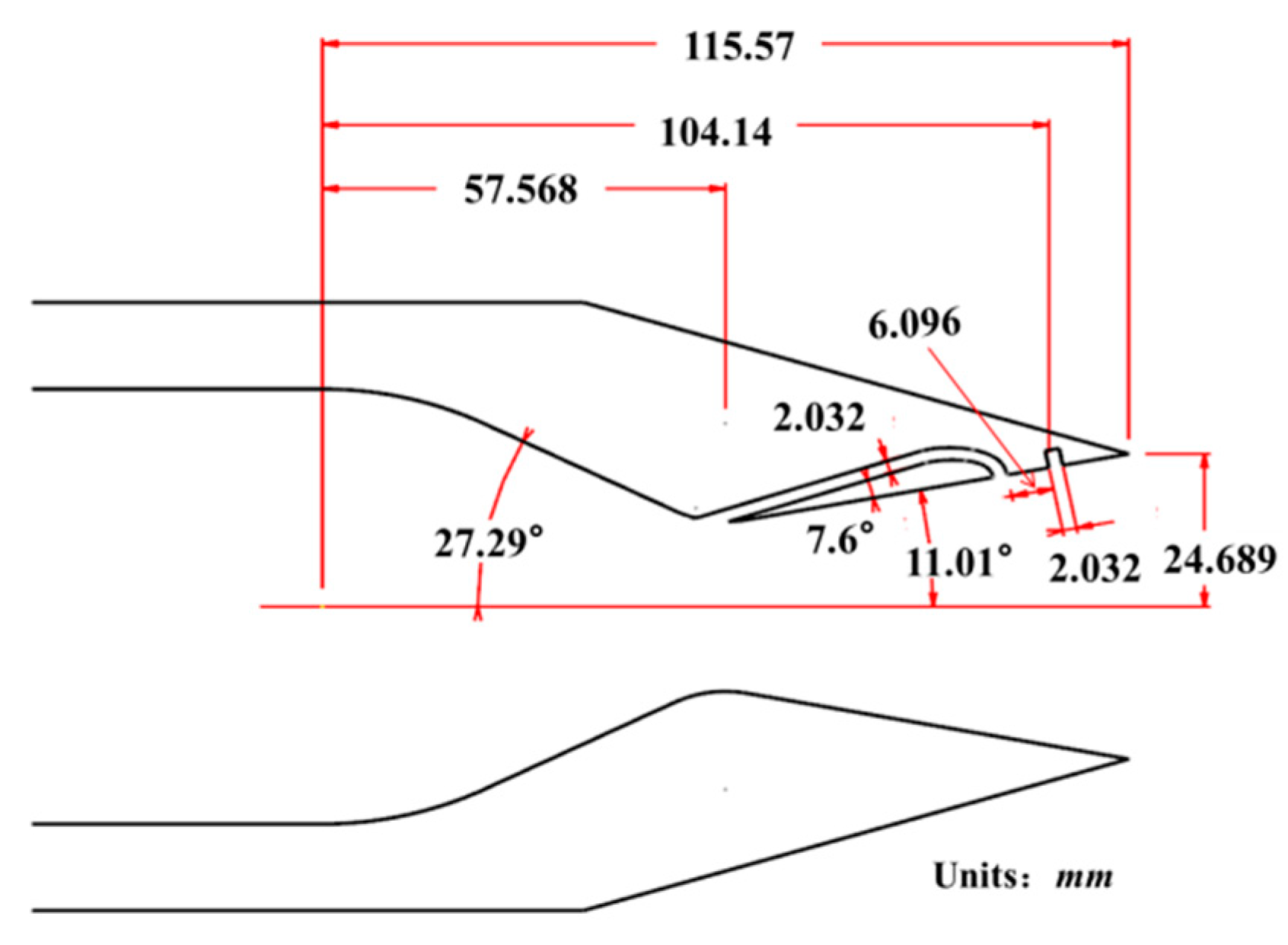
3. Design of the ESVC
4. Vector Performance of ESVC
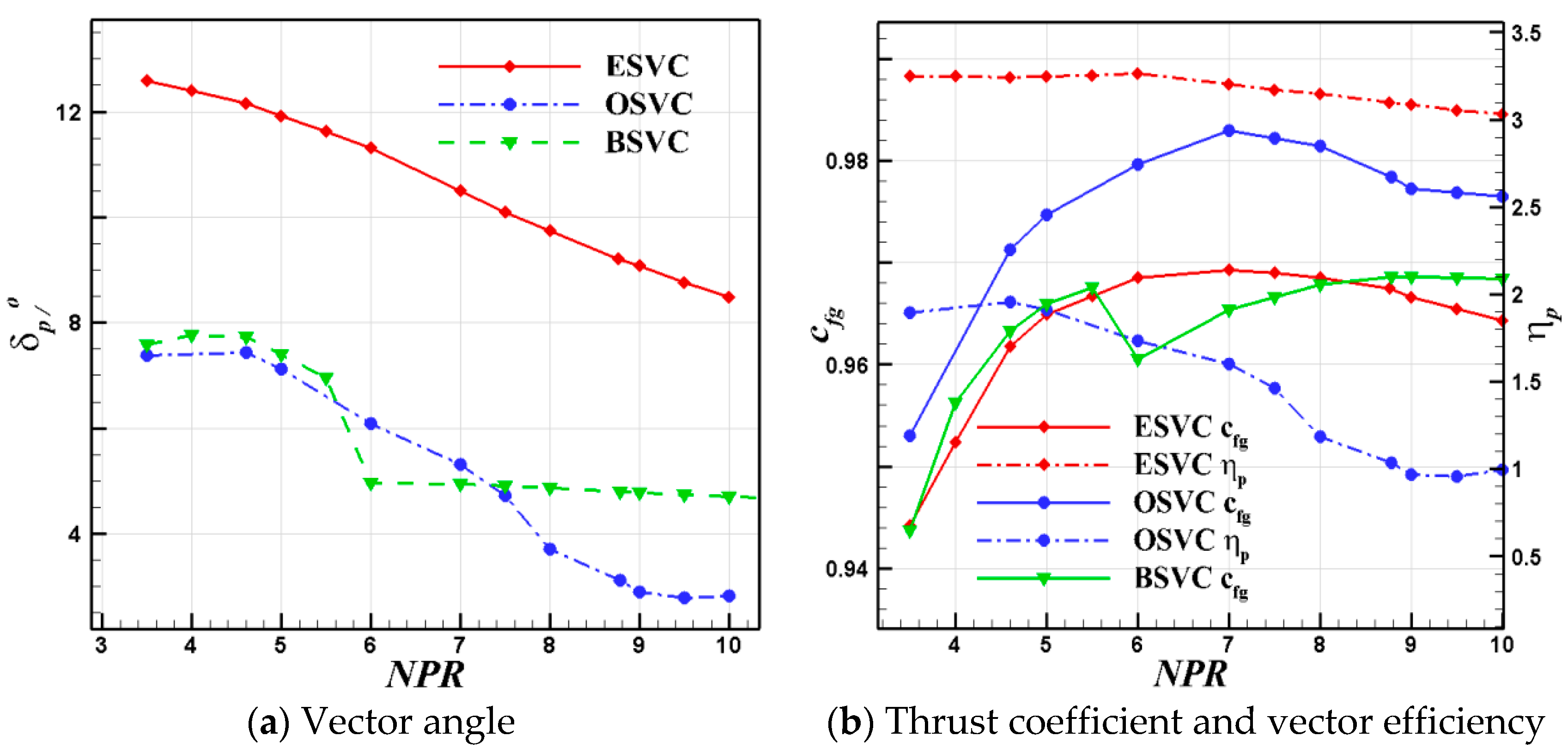
4.1. Effect of NPR
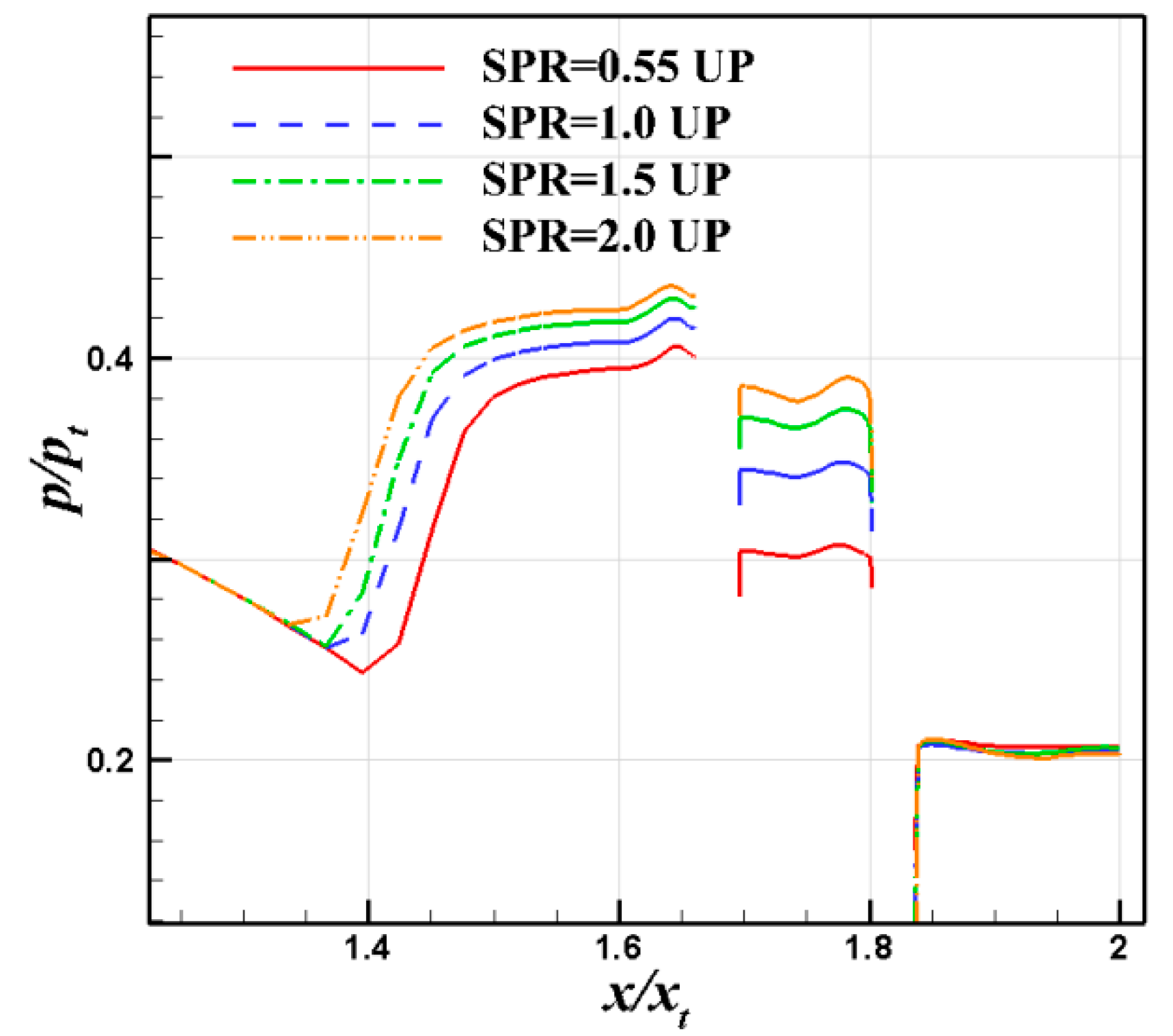
4.2. Effect of SPR
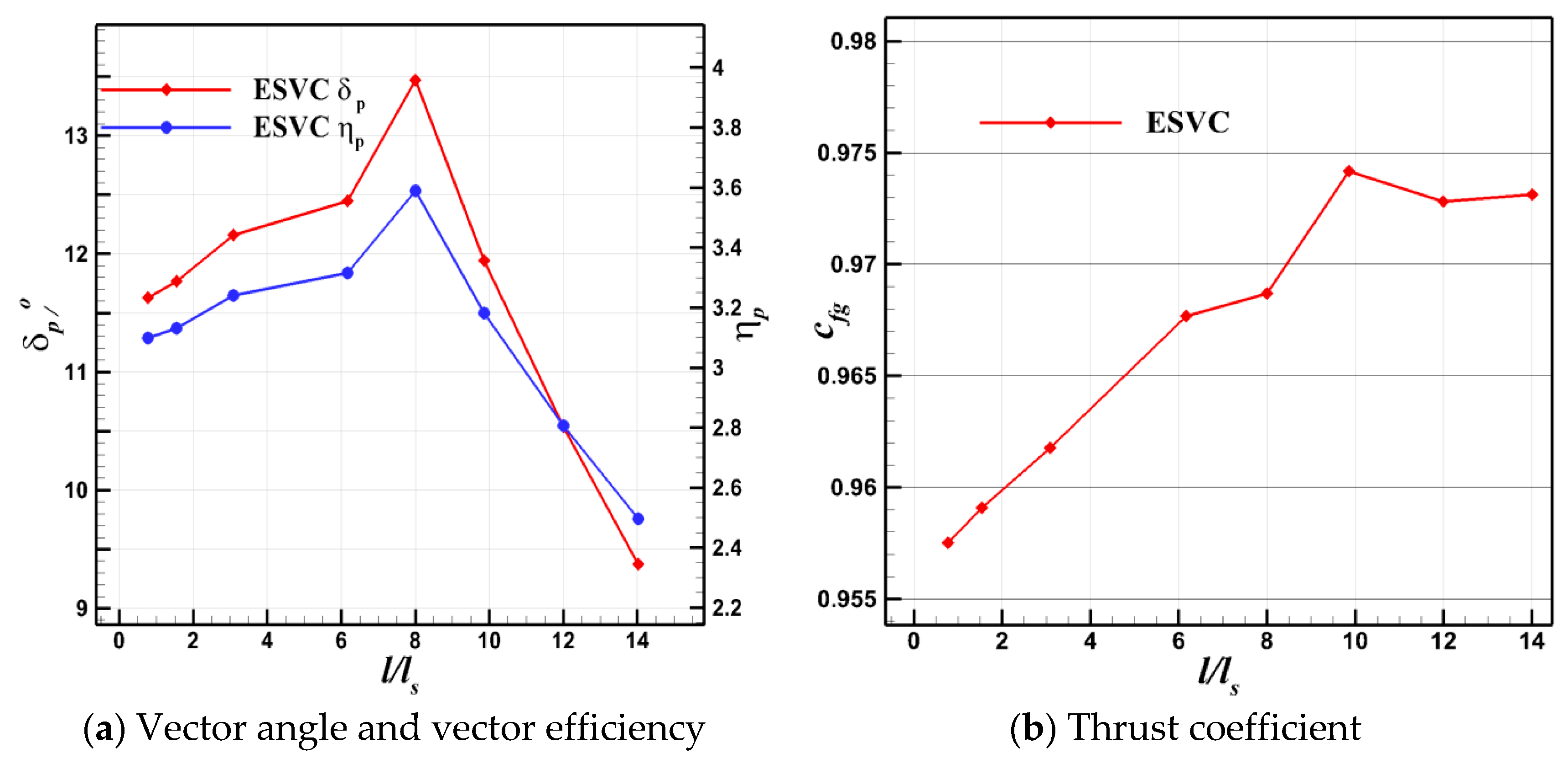
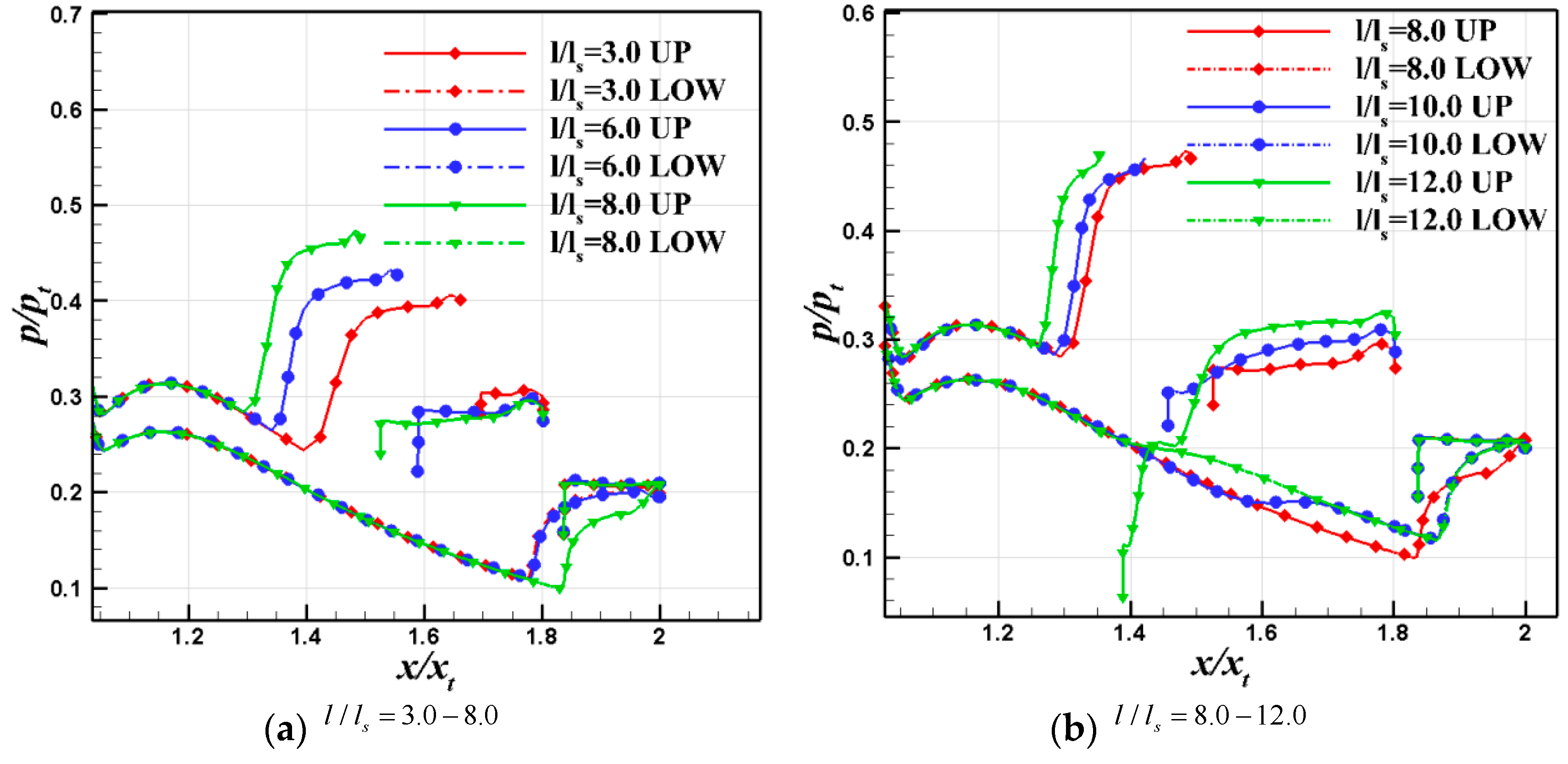
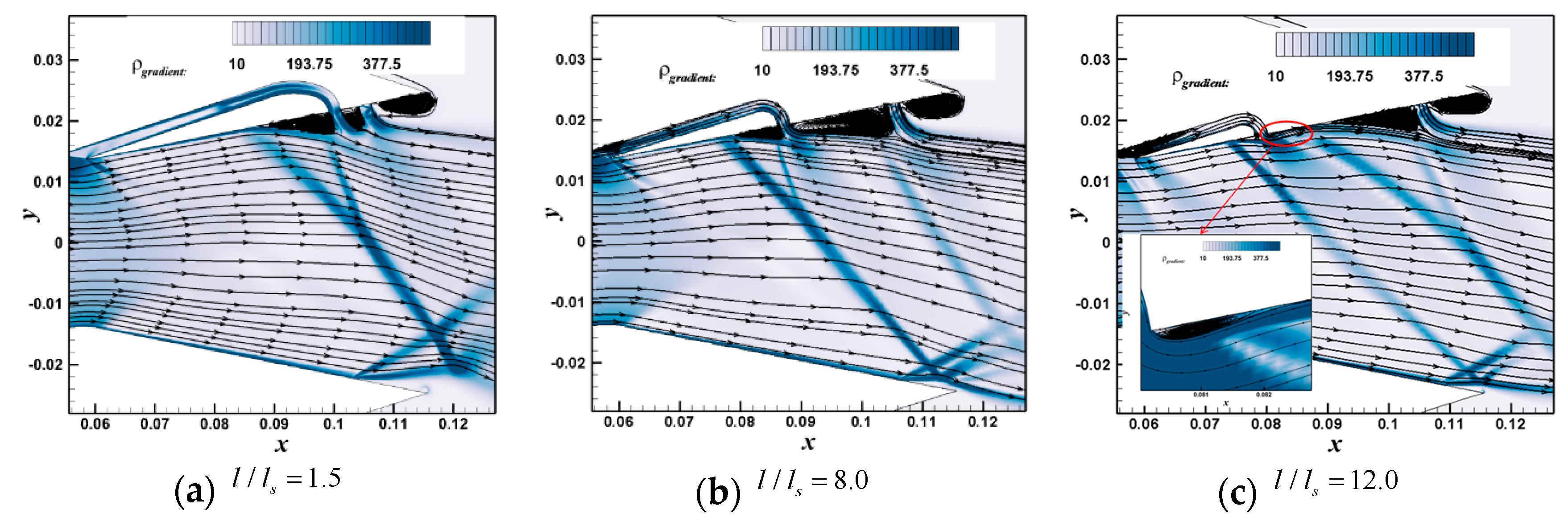
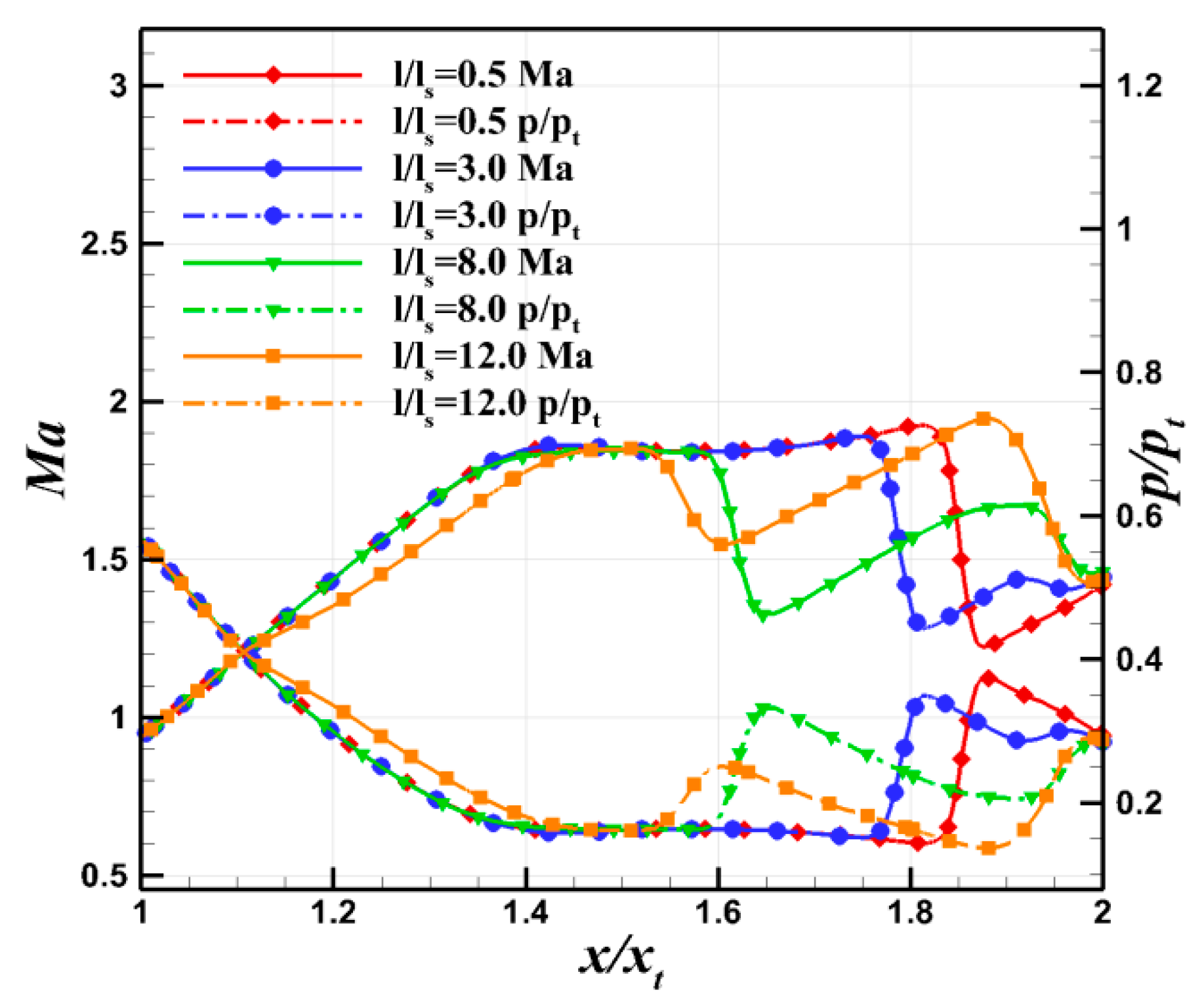
4.3. Effect of Spacing between Two Jets
5. Conclusions
- (1)
- The ESVC integrates features from both throat skewing and SVC nozzles, capitalizing on the priming effect of the original secondary flow. This integration effectively eliminates the separation and reattachment phenomena observed in the BSVC after injection at specific pressure ratios. Consequently, the vectoring performances of both the BSVC and OSVC are significantly enhanced without necessitating an increase in the induced airflow from the engine.
- (2)
- The linearity of the vector angle variation with the NPR in the ESVC surpasses that of both the OSVC and BSVC, facilitating easier control. The vector angle and vector efficiency of the ESVC are more than twice as favorable as those of the OSVC, significantly enhancing the performance of the SVC nozzle under under-expansion conditions. Furthermore, within a specified SPR range, the vector angle and vector efficiency of the ESVC are substantially improved compared to the OSVC, achieving a vector angle exceeding 18° and a thrust coefficient surpassing 0.95.
- (3)
- The distance between two jets is a critical parameter influencing the vector performance of the ESVC. The vector performance of the ESVC initially increases and then decreases with the widening spacing between the two jets, indicating the existence of optimal jet spacing. To ensure that the separation between the two jets does not reattach, it is observed that the vector performance achieved by the flow traversing through two weaker shocks is superior to that resulting from passing through a single strong excitation. Consequently, the design should strategically avoid the reattachment of separation following the jet.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Francis, M.S. Air vehicle management with integrated thrust-vector control. AIAA J. 2018, 56, 4741–4751. [Google Scholar] [CrossRef]
- Kowal, H.J. Advances in thrust vectoring and the application of flow-control technology. Can. Aeronaut. Space J. 2002, 48, 145–151. [Google Scholar] [CrossRef]
- Xiao, Z.Y.; Jiang, X.; Mou, B.; Chen, Z. Advances in fluidic thrust vectoring technique research. J. Exp. Fluid Mech. 2017, 31, 8–15. [Google Scholar]
- Walker, S. Lessons learned in the development of a national cooperative program. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; p. 3348. [Google Scholar]
- Clyde, W.; William, J.C. Fludic flow effectors for flight control. AIAA J. 2018, 56, 3808–3823. [Google Scholar]
- Deere, K.A. Summary of fluidic thrust vectoring research conducted at NASA Langley research center. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3800. [Google Scholar]
- Wen, X.; Zhou, K.W.; Liu, P.; Zhu, H.; Wang, Q.; Liu, Y. Schlieren Visualization of Coflow Fluidic Thrust Vectoring Using Sweeping Jets. AIAA J. 2022, 60, 435–444. [Google Scholar] [CrossRef]
- Mason, M.S.; Crowther, W.J. Fluidic thrust vectoring for low observable air vehicles. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004; p. 2210. [Google Scholar]
- Wang, Y.S.; Xu, J.L.; Huang, S. Study of starting problem of axisymmetric divergent dual throat nozzle. J. Eng. Gas Turbines Power 2017, 139, 062602. [Google Scholar] [CrossRef]
- Yagle, P.J.; Miller, D.N.; Ginn, K.B.; Hamstra, J.W. Demonstration of fluidic throat skewing for thrust vectoring in structurally fixed nozzles. J. Eng. Gas Turbines Power 2001, 123, 502–507. [Google Scholar] [CrossRef]
- Flamm, J.; Deere, K.; Mason, M.; Berrier, B.; Johnson, S. Experimental study of an axisymmetric dual throat flu-idic thrust vectoring nozzle for supersonic aircraft application. In Proceedings of the 43rd AI-AA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007; p. 5084. [Google Scholar]
- Ferlauto, M.; Marsilio, R. Numerical investigation of the dynamic characteristics of a du-al-throat-nozzle for fluidic thrust-vectoring. AIAA J. 2017, 55, 86–98. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Huang, S.; Jiang, J.; Pan, R. Design and preliminary analysis of the variable axisym-metric divergent bypass dual throat nozzle. J. Fluids Eng. 2020, 142, 061204. [Google Scholar] [CrossRef]
- Wu, K.; Kim, H.D.; Jin, Y.Z. Fluidic thrust vector control based on counter-flow concept. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1412–1422. [Google Scholar] [CrossRef]
- Jegede, O. Dual-Axis Fluidic Thrust Vectoring of High Aspect Ratio Supersonic Jets. Ph.D. Thesis, Manchester University, Manchester, UK, 2016. [Google Scholar]
- Shi, N.X.; Gu, Y.S.; Zhou, Y.H.; Wang, L.X.; Feng, C.; Li, L.K. Mechanism of hysteresis and uncontrolled deflection in jet vectoring control based on Coanda effect. Phys. Fluids 2022, 34, 084107. [Google Scholar] [CrossRef]
- Shi, J.W. Investigation on Flow Mechanism and Performance Estimation of Fixed-Geometric Thrust Vectoring Nozzle. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2015. [Google Scholar]
- Emelyanov, V.N.; Teterina, I.V.; Volkov, K.N.; Garkushev, A.U. Pressure oscillations and instability of working processes in the combustion chambers of solid rocket motors. Acta Astronaut. 2017, 135, 183–195. [Google Scholar] [CrossRef]
- Waithe, K.; Deere, K. An experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3802. [Google Scholar]
- Viti, V.; Neel, R.; Schetz, J.A. Detailed flow physics of the supersonic jet interaction flow field. Phys. Fluids 2009, 21, 046101. [Google Scholar] [CrossRef]
- Zmijanovic, V.; Lago, V.; Sellam, M.; Chpoun, A. Thrust shock vector control of an axisymmetric conical supersonic nozzle via secondary transverse gas injection. Shock Waves 2014, 24, 97–111. [Google Scholar] [CrossRef]
- Zmijanovic, V.; Leger, L.; Depussay, E. Experimental-numerical Parametric investigation of a rocket nozzle secondary injection thrust vectoring. J. Propuls. Power 2016, 32, 196–213. [Google Scholar] [CrossRef]
- Forghany, F.; Taeibe-Rahni, M.; Asadollahi-Ghohieh, A.; Banazdeh, A. Numerical investigation of in-jection angle effects on shock vector control performance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 405–417. [Google Scholar] [CrossRef]
- Chen, J.L.; Liao, Y.H. Parametric study on thrust vectoring with a secondary injection in a convergent–divergent nozzle. J. Aerosp. Eng. 2020, 33, 04020020. [Google Scholar] [CrossRef]
- Emelyanov, V.; Yakovchuk, M.; Volkov, K. Multiparameter optimization of thrust vector con-trol with transverse injection of a supersonic underexpanded gas jet into a convergent diver-gent nozzle. Energies 2021, 14, 4359. [Google Scholar] [CrossRef]
- Younes, K.; Hickey, J.P. Fludic thrust shock-vectoring control: A sensitivity analysis. AIAA J. 2020, 58, 1887–1890. [Google Scholar] [CrossRef]
- Shu, B.W.; Huang, J.T.; Gao, Z.H.; Liu, G.; He, C.; Xia, L. Sensitivity analysis of vector performance of two-dimensional shock vector control nozzle. Acta Aeronaut. Astronaut. Sin. 2023, 44, 127831. [Google Scholar]
- Gu, R.; Xu, J.; Guo, S. Experimental and numerical investigations of a bypass dual throat nozzle. J. Eng. Gas Turbines Power 2014, 136, 084501. [Google Scholar] [CrossRef]
- Huang, S.; Xu, J.; Yu, K.; Wang, Y.; Pan, R. Design and experimental study of a bypass dual throat nozzle with the ability of short/vertical takeoff and landing. Aerosp. Sci. Technol. 2022, 121, 107301. [Google Scholar] [CrossRef]
- Huang, S.; Xu, J.L.; Yu, K.K.; Wang, Y.; Pan, R.; Chen, K.; Zhang, Y. Numerical study of a trapezoidal bypass dual throat nozzle. Chin. J. Aeronaut. 2023, 36, 42–62. [Google Scholar] [CrossRef]
- Deng, R.; Kim, H.D. A study on the thrust vector control using a bypass flow passage. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1722–1729. [Google Scholar] [CrossRef]
- Deng, R.; Setoguchi, T.; Kim, H.D. Large eddy simulation of shock vector control using bypass flow passage. Int. J. Heat Fluid Flow 2016, 62, 474–481. [Google Scholar] [CrossRef]
- Shi, J.W.; Wang, Z.X.; Zhou, L. Numerical investigation on a new concept of shock vector control nozzle. J. Eng. Gas Turbines Power 2019, 141, 091004. [Google Scholar]
- Ferlauto, M.; Marsilio, R. On the use of synthetic jet actuators to induce jet-vectoring in nozzles. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1627. [Google Scholar]
- Huang, J.T.; Zhou, Z.; Yu, J.; Gao, Z.H.; Yu, L. Sensitivity analysis of design variables considering intake and exhaust effects. J. Propuls. Technol. 2019, 40, 250–258. [Google Scholar]
- Zhou, Z.; Yu, Y.G.; Liu, G.; Chen, Z.B.; Heng, K.F. Comprehensive study on yaw control characteristic of com-bined control surfaces of flying wing configuration. Acta Aeronaut. Astronaut. Sin. 2020, 41, 523422. [Google Scholar]
- Liu, G.; Xiao, Z.Y.; Wang, J.T.; Liu, F. Numerical simulation of missile air-launching process under rail slideway constraints. Acta Aerodyn. Sin. 2015, 33, 192–197. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Mangin, B.; Chopun, A.; Jacquin, L. Experimental and numerical study of the fluidic thrust vectoring of a two-dimensional supersonic nozzle. In Proceedings of the 24th Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006; p. 3666. [Google Scholar]
- Jakirlic, S.; Maduta, R. Extending the bounds of steady rans closures: Toward an instability sensitive Reynolds stress model. Int. J. Heat Fluid Flow 2015, 51, 175–194. [Google Scholar] [CrossRef]

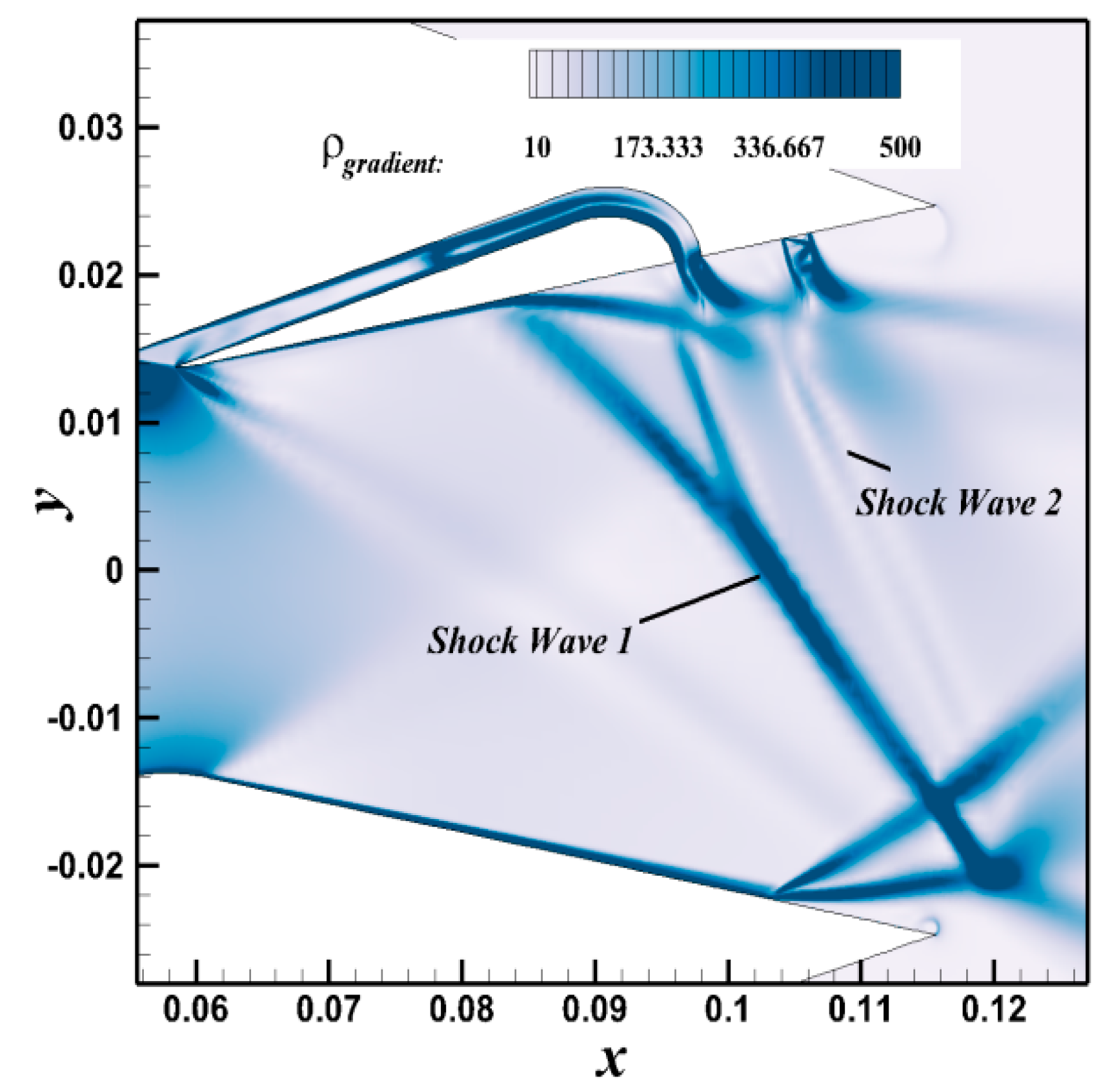



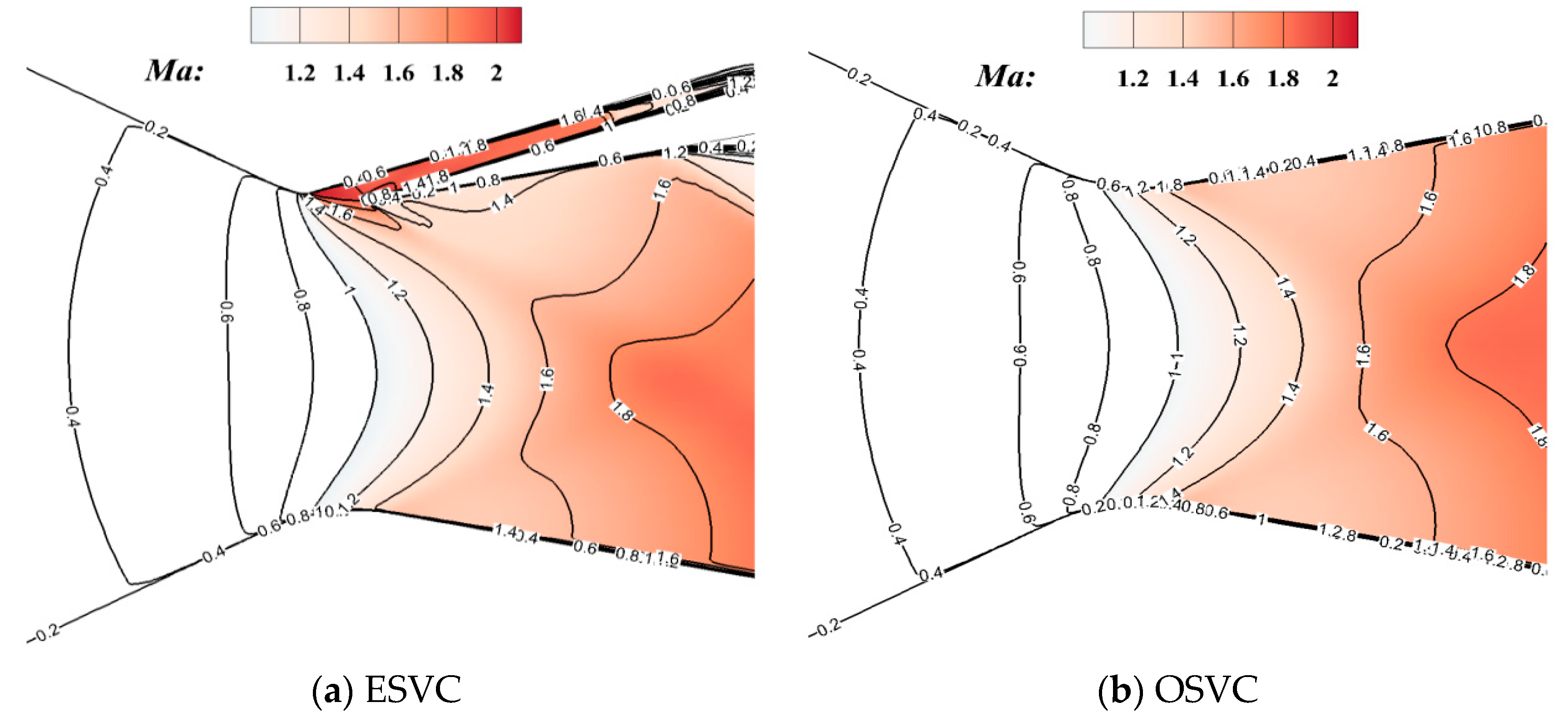
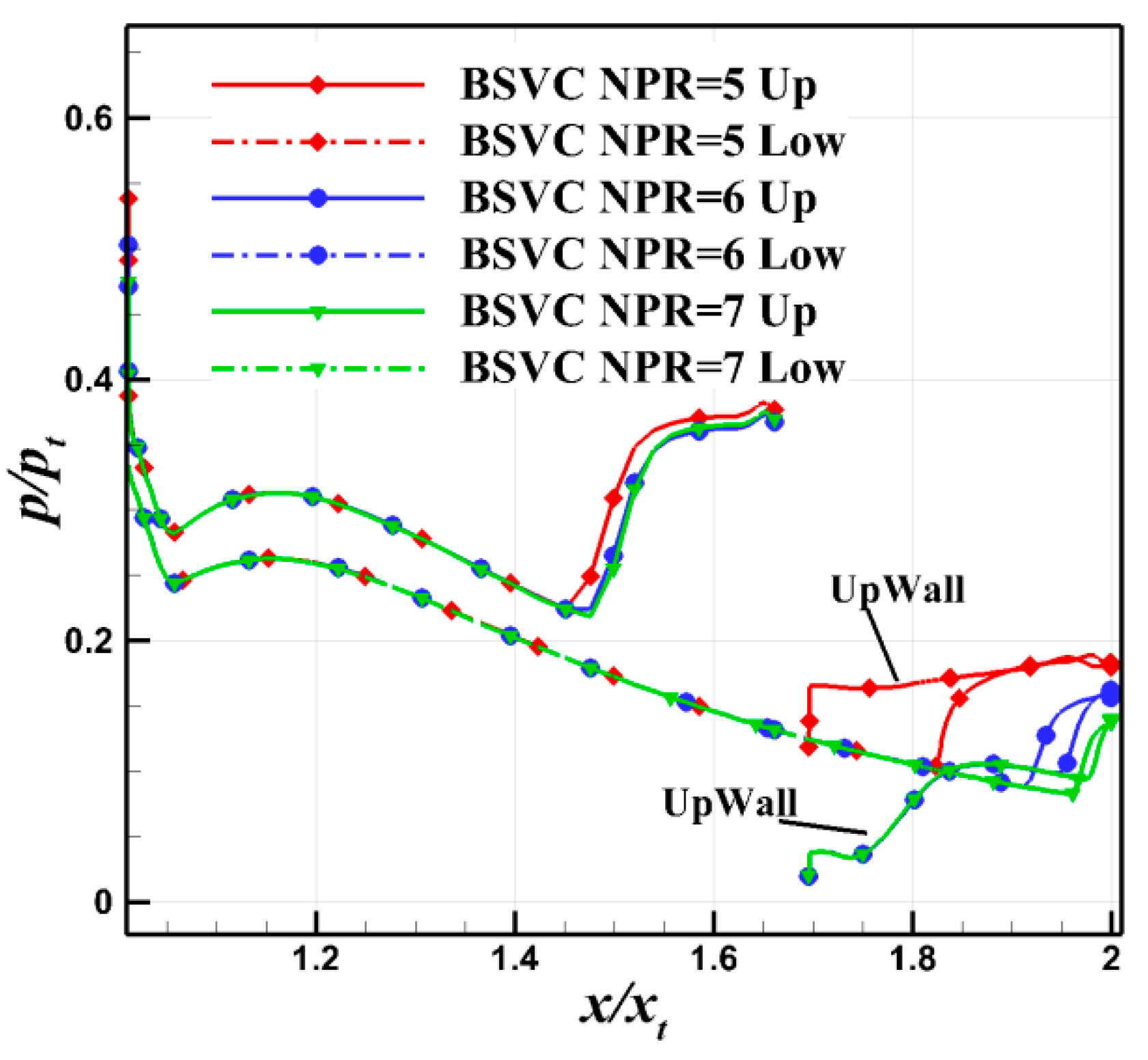
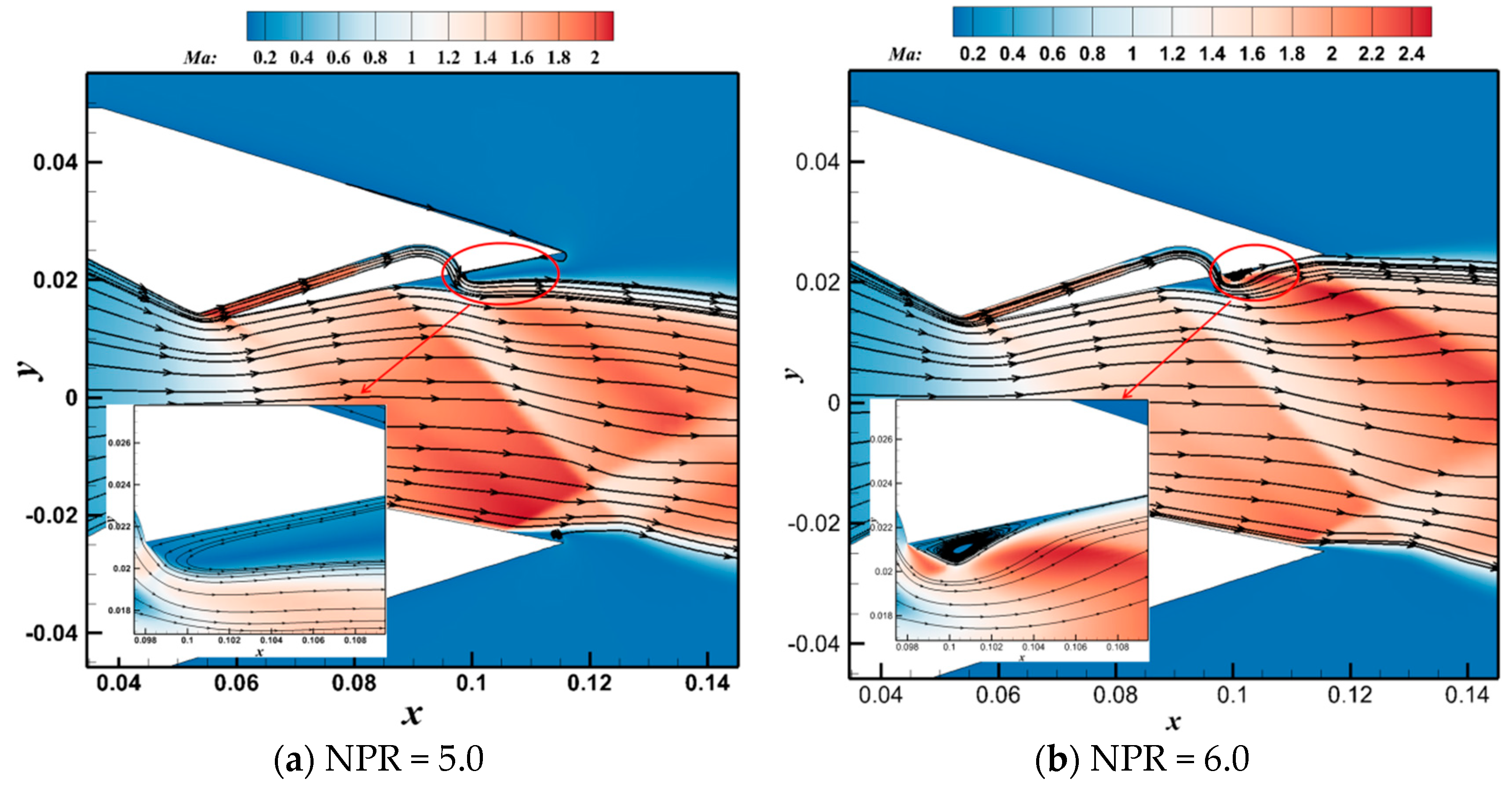


| (°) | ||
|---|---|---|
| coarse | 0.975 | 7.0 |
| medium | 0.972 | 7.42 |
| fine | 0.971 | 7.46 |
| Exp | 0.969 | 7.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, B.; Gao, Z.; Huang, J.; He, C.; Zheng, H.; Xia, L. Aerodynamic Characteristics of the Novel Two-Dimensional Enhanced Shock Vector Nozzle. Aerospace 2024, 11, 369. https://doi.org/10.3390/aerospace11050369
Shu B, Gao Z, Huang J, He C, Zheng H, Xia L. Aerodynamic Characteristics of the Novel Two-Dimensional Enhanced Shock Vector Nozzle. Aerospace. 2024; 11(5):369. https://doi.org/10.3390/aerospace11050369
Chicago/Turabian StyleShu, Bowen, Zhenghong Gao, Jiangtao Huang, Chengjun He, Haibo Zheng, and Lu Xia. 2024. "Aerodynamic Characteristics of the Novel Two-Dimensional Enhanced Shock Vector Nozzle" Aerospace 11, no. 5: 369. https://doi.org/10.3390/aerospace11050369
APA StyleShu, B., Gao, Z., Huang, J., He, C., Zheng, H., & Xia, L. (2024). Aerodynamic Characteristics of the Novel Two-Dimensional Enhanced Shock Vector Nozzle. Aerospace, 11(5), 369. https://doi.org/10.3390/aerospace11050369





