Numerical Simulation of Water Film Flow and Breakup on Anti-Icing Surface
Abstract
1. Introduction
2. Mathematical Model and Calculation Method
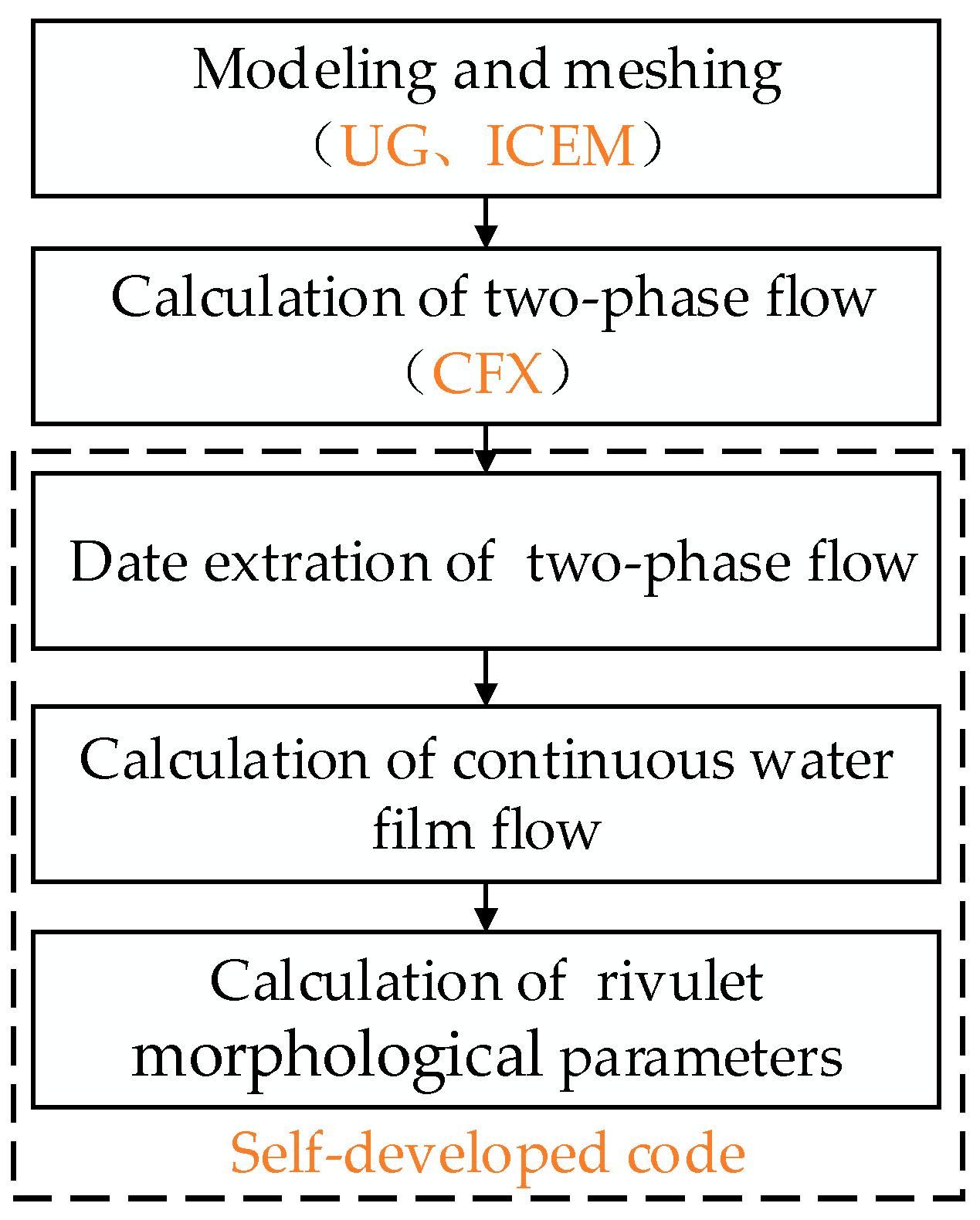
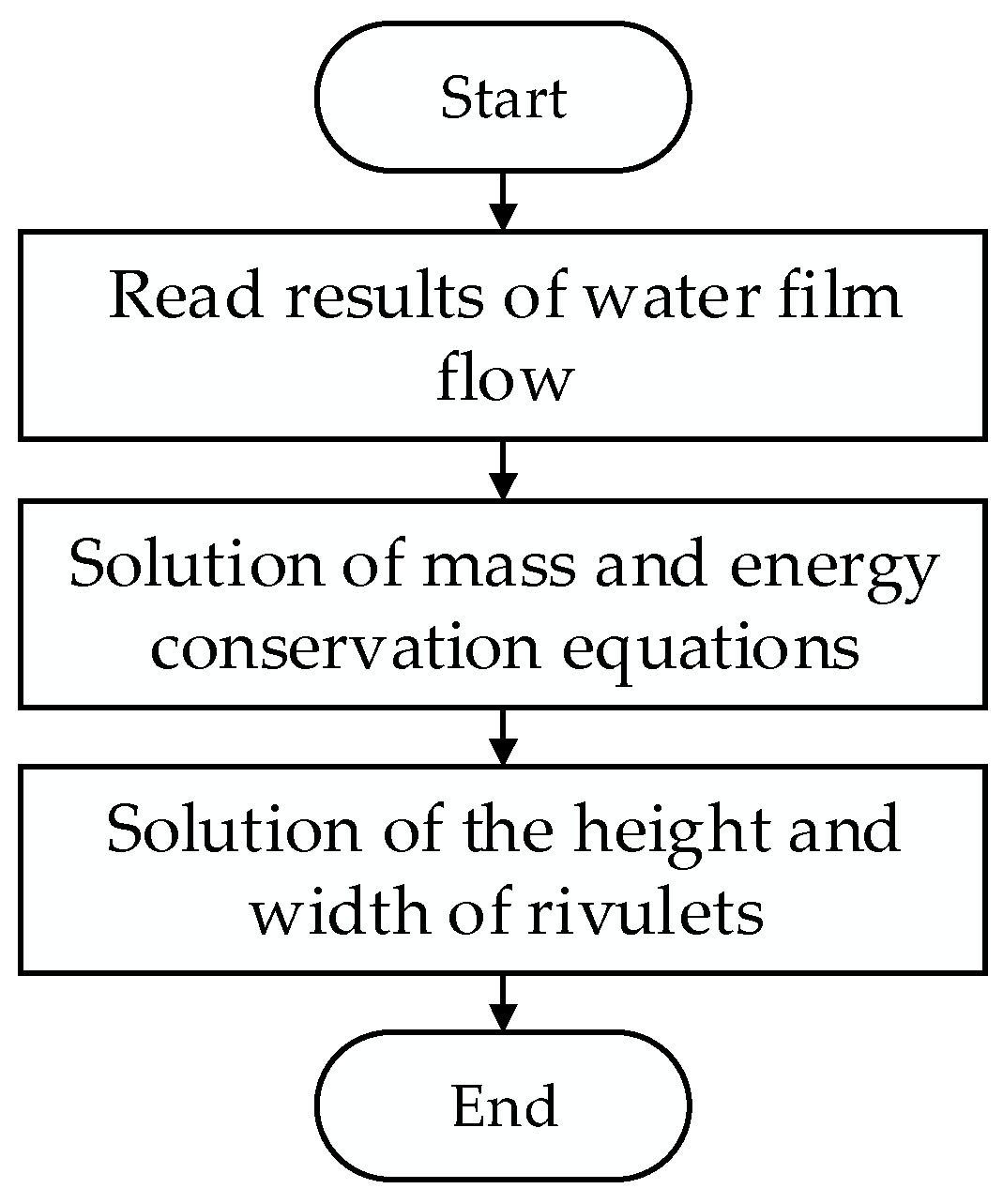
2.1. Physical Process and Overall Calculation Process
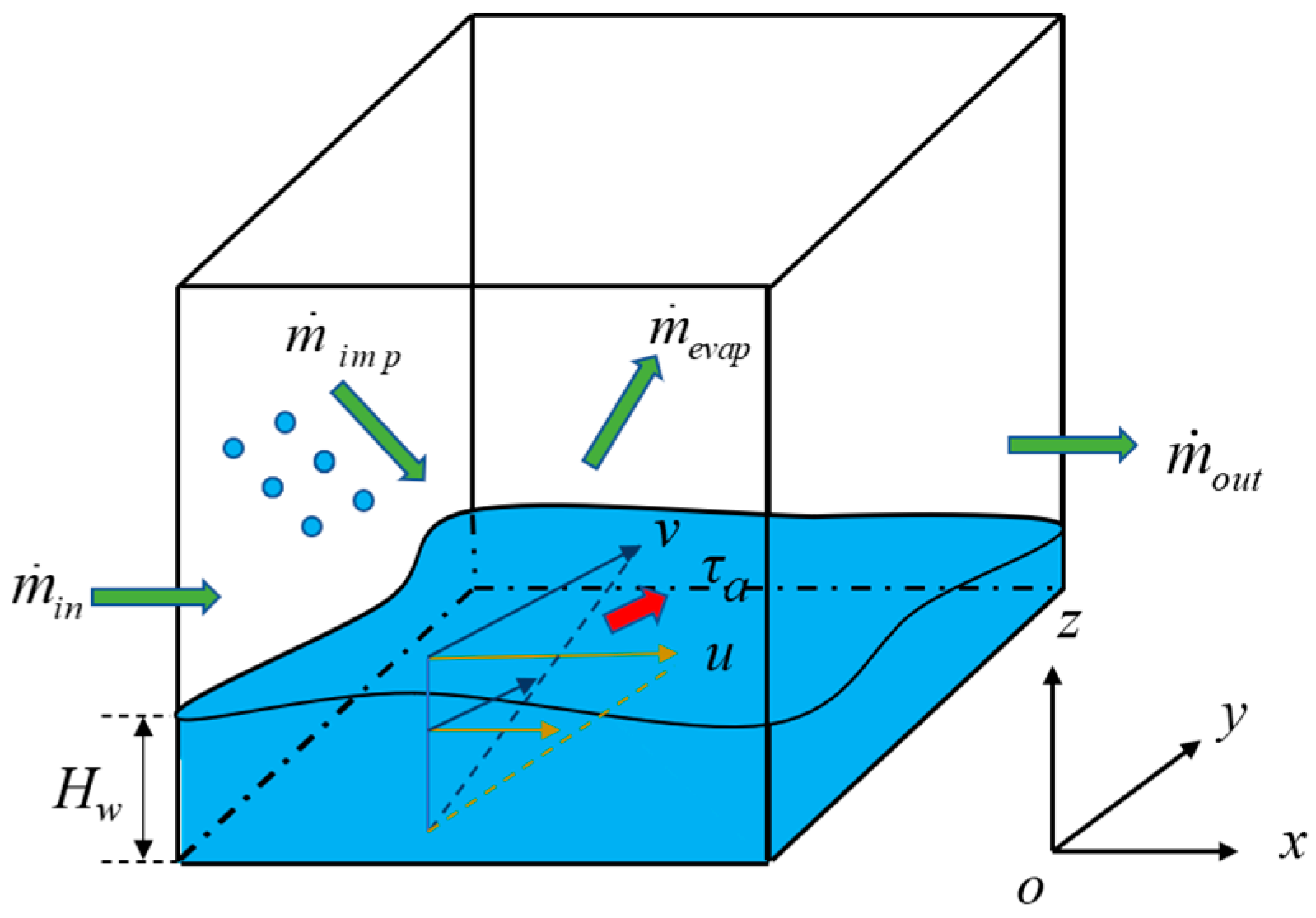
2.2. Continuous Water Film Flow
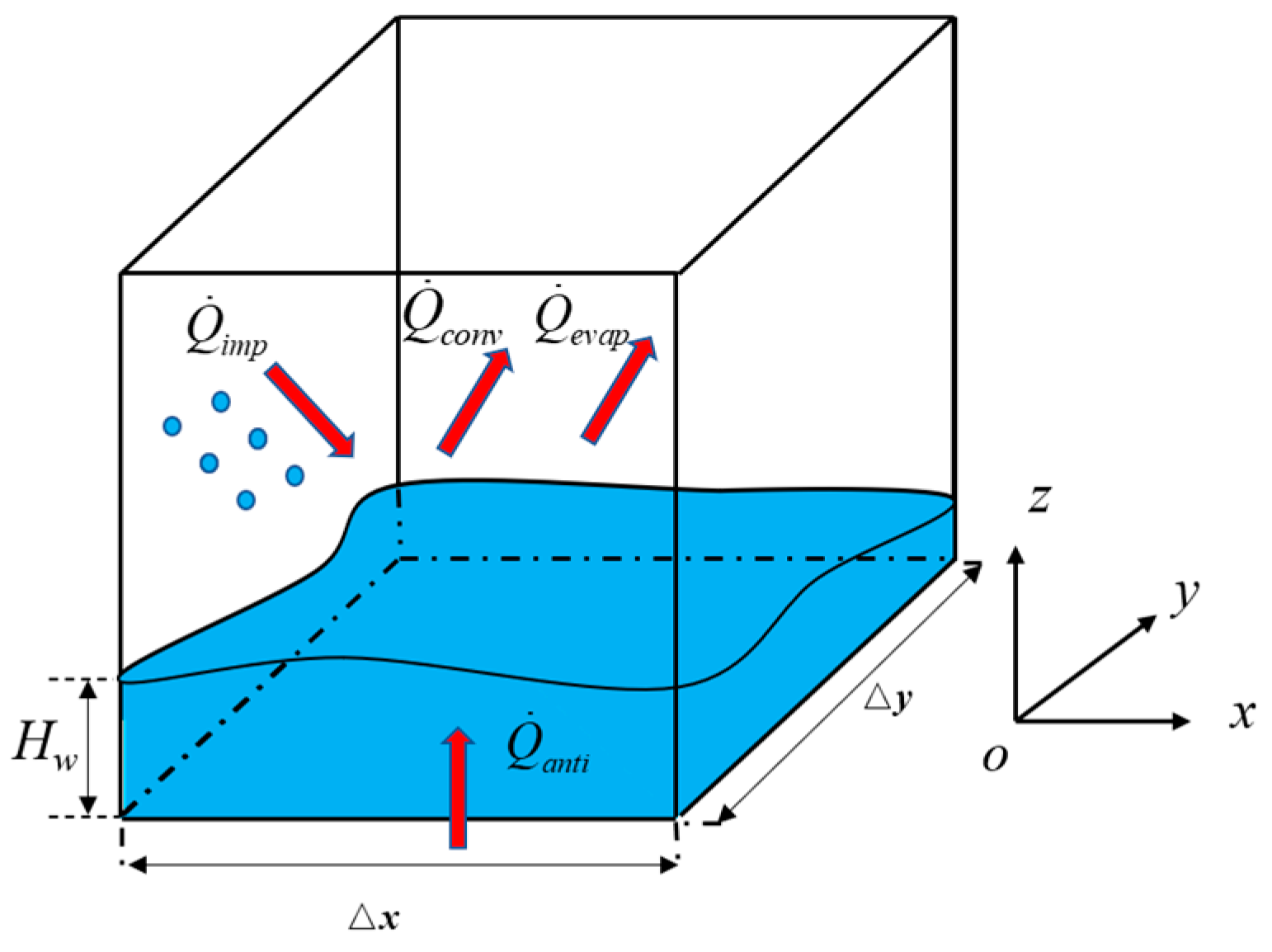
2.2.1. Mathematical Model
2.2.2. Discretization of Equations
2.2.3. Model Solving
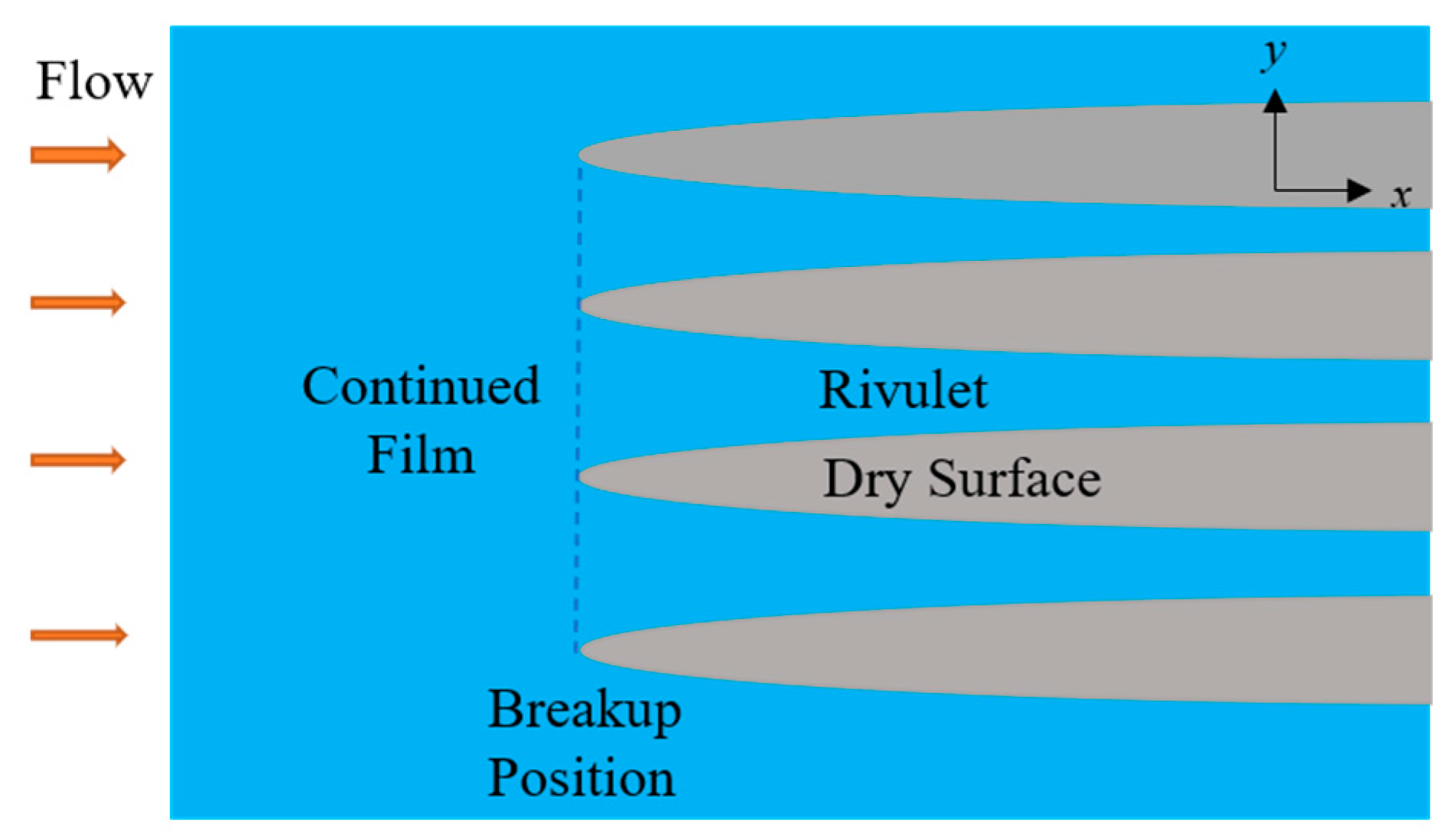
2.3. Continuous Water Film Breakup and Rivulet Formation
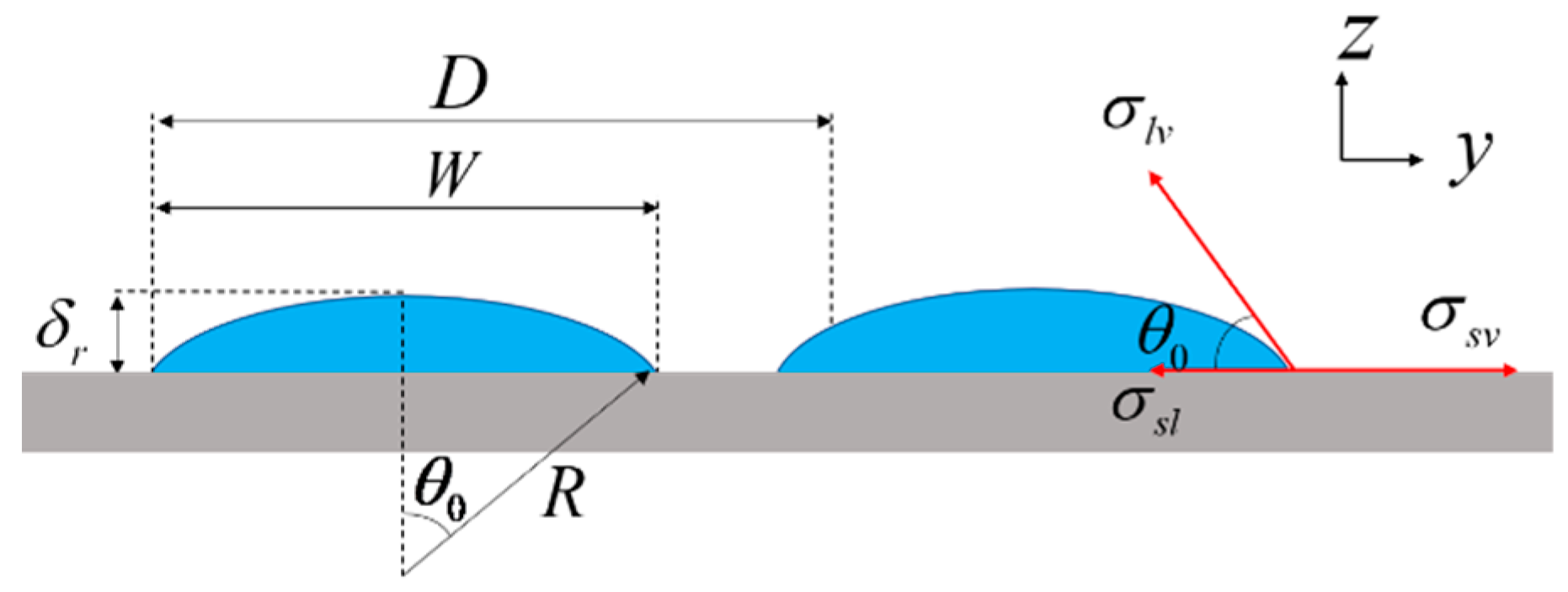
2.3.1. Mathematical Model
2.3.2. Model Solving
3. Example Analysis and Verification
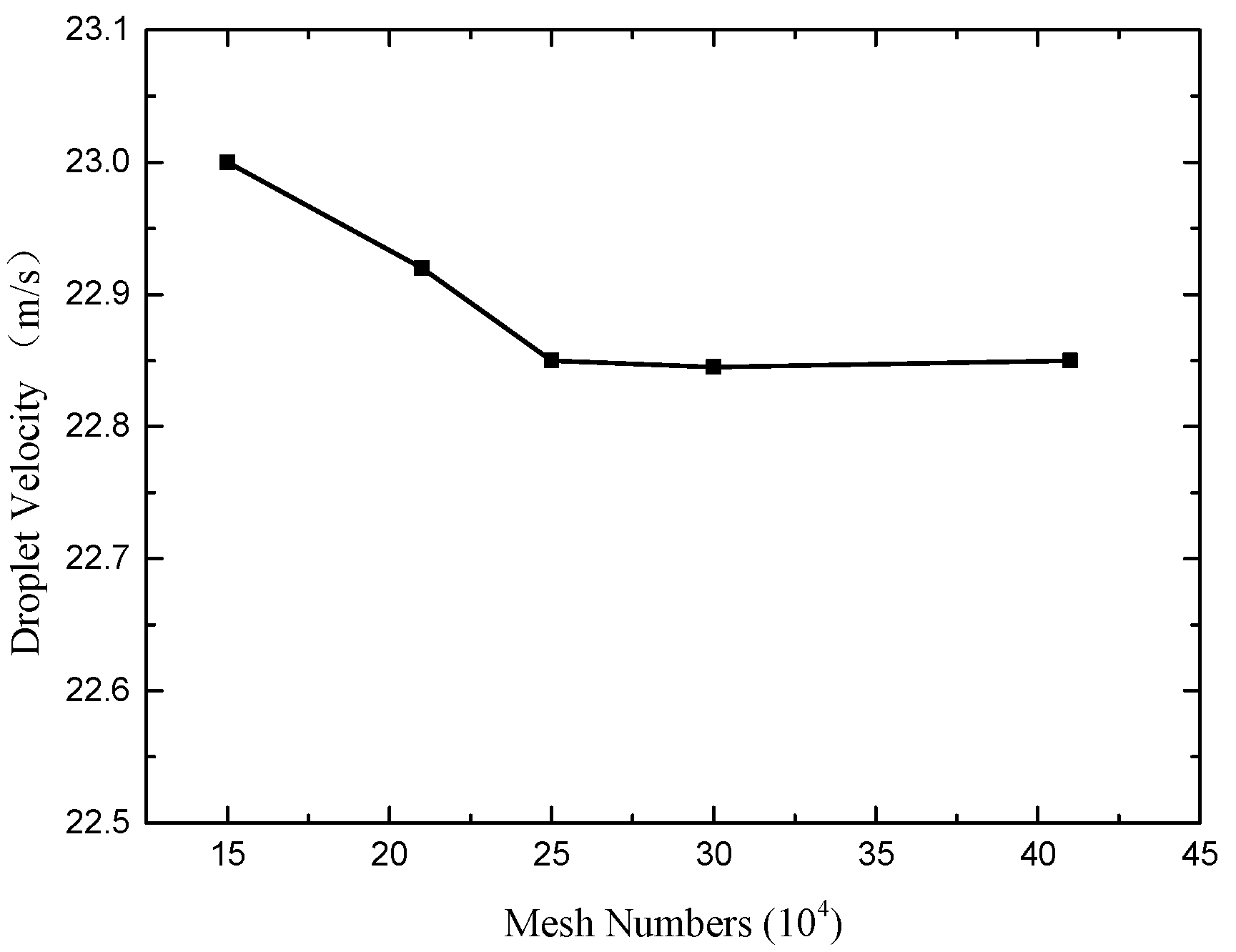
3.1. Computational Model
3.2. Calculation Results and Analysis
3.2.1. Impingement Characteristics
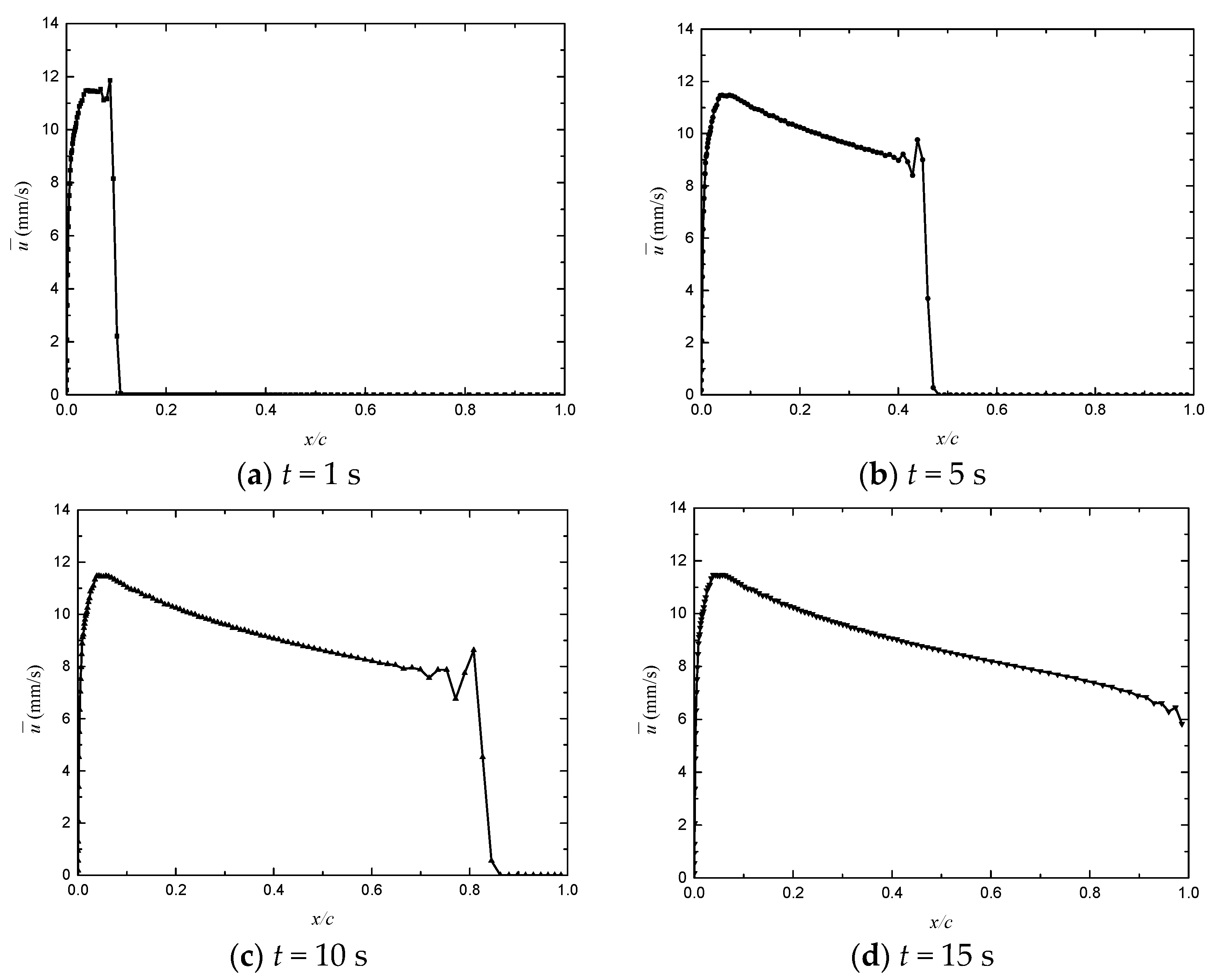
3.2.2. Transient Characteristics of Continuous Water Film Flow
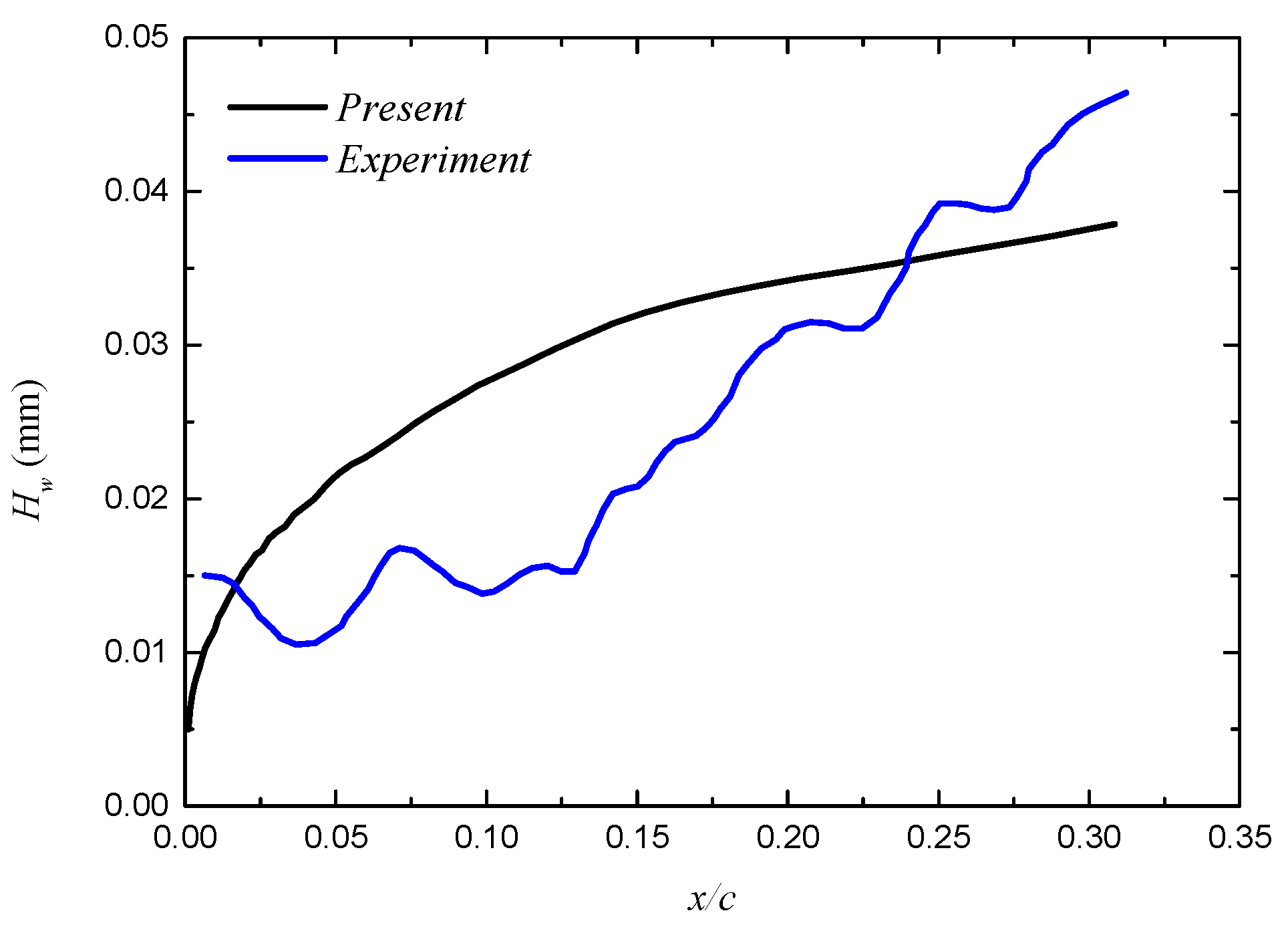
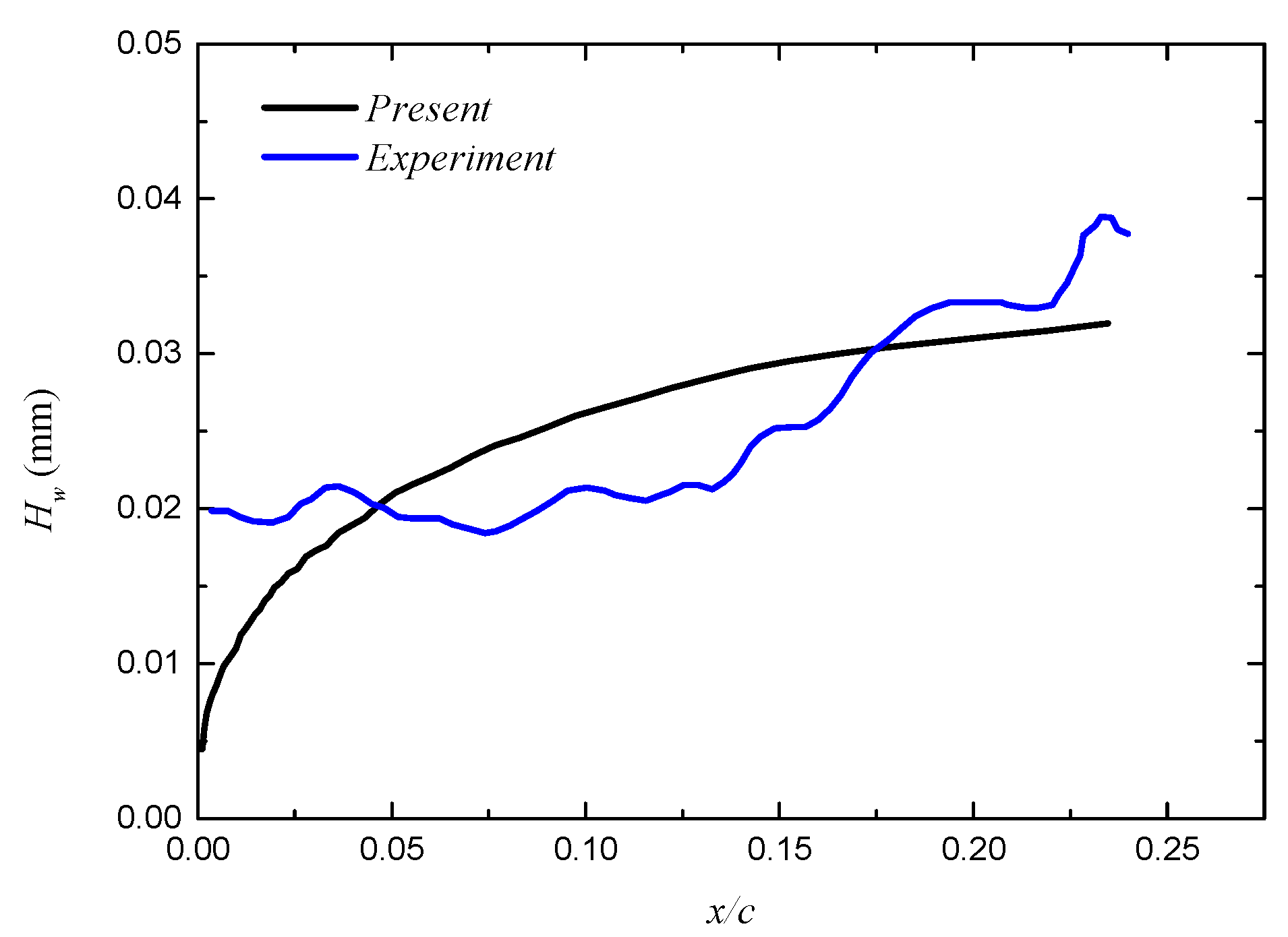
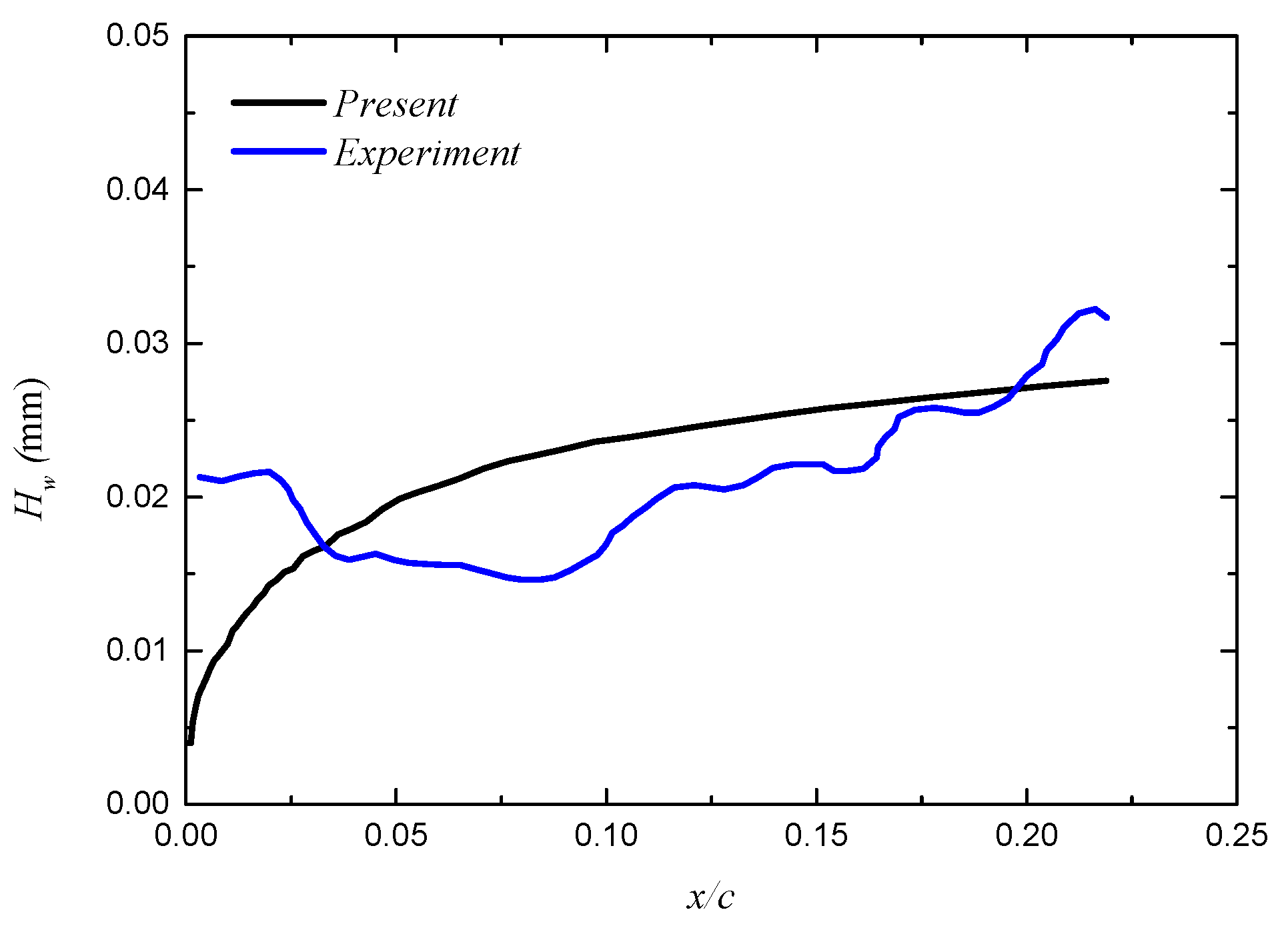
3.2.3. Steady State Continuous Water Film Height Verification
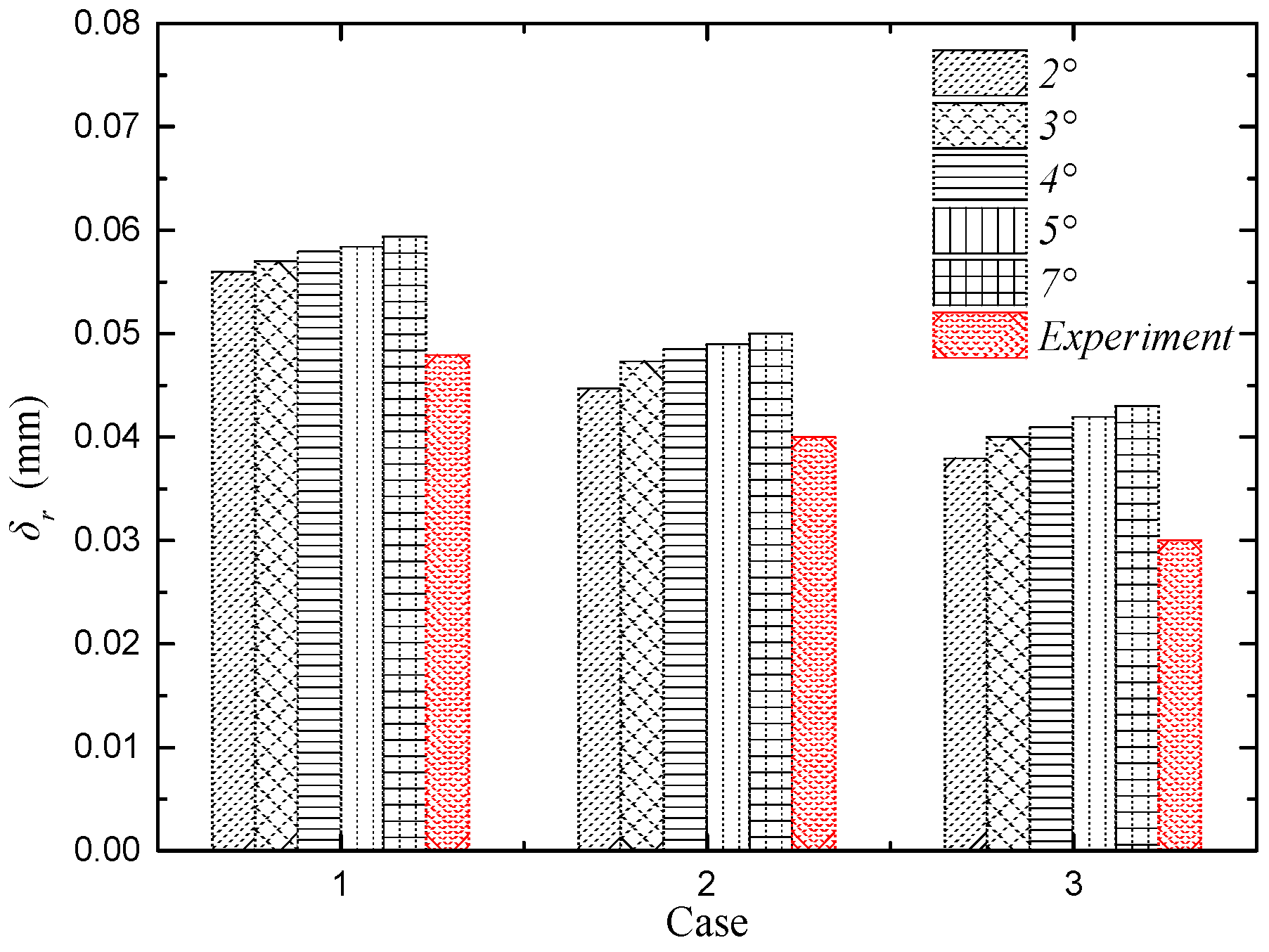
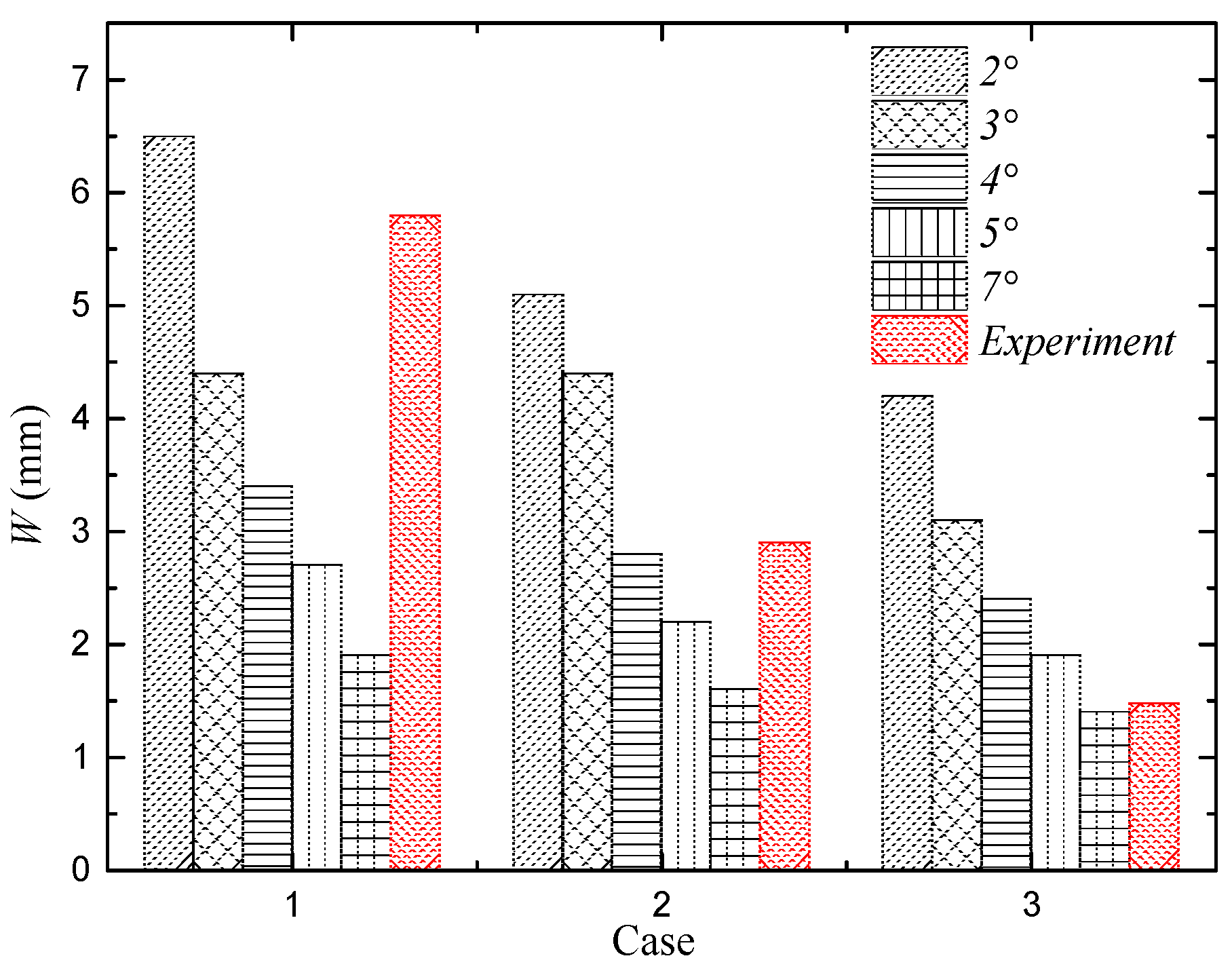
3.2.4. Verification of Rivulet Morphological Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AOA | Angle of Attack |
| c | chord length of the airfoil |
| D | distance between each rivulet and its adjacent rivulets |
| h | convective heat transfer coefficient between the air and the water film |
| L | spanwise height |
| LWC | Liquid Water Content |
| MVD | Mean Volume Diameter |
| NACA | National Advisory Committee for Aeronautics |
| p | pressure of the water film |
| R | radius of the outer profile of a rivulet |
| t | Time |
| T∞ | Temperature of the incoming flow |
| u∞ | incoming flow velocity |
| u | flow velocity of the water film in the x-direction |
| v | flow velocity of the water film in the y-direction |
| W | width of each stream |
| specific heat capacity of water | |
| energy passing through the water film per unit time | |
| energy passing through the stream per unit time | |
| gravitational acceleration in the x-direction | |
| gravitational acceleration in the y-direction | |
| gravitational acceleration in the z-direction | |
| height of the water film | |
| water film height solved in the last time step | |
| initial water film height | |
| new water film height | |
| evaporation flow rate of the water film per unit area of the control body | |
| impact flow rate of the water film per unit area of the control body | |
| flow rate along the flow direction of the water film into of the control body | |
| flow rate along the flow direction of the water film out of the control body | |
| mass flow of the water film | |
| mass flow of the rivulets | |
| air pressure acting on the upper surface of the water film | |
| anti-icing heat flow per unit area in the control body | |
| convective heat transfer between the water film and air per unit area in the control body | |
| latent heat released by water film evaporation per unit area in the control body | |
| energy from impingement of the droplets per unit area in the control body | |
| temperature of the water film | |
| kinematic viscosity of water | |
| time step size | |
| length of control volume in the x-direction | |
| length of control volume in the y-direction | |
| average velocity in the x-direction of the water film along its height | |
| average velocity in the y-direction of the water film along its height | |
| flow velocity of the stream | |
| drag force at the air–water film interface | |
| air shear force in the x-direction | |
| air shear force in the y-direction | |
| dynamic viscosity of water | |
| density of water | |
| thermal conductivity of water | |
| solid–liquid contact angle between the wall and rivulet | |
| the height of each stream | |
| surface tension coefficients of the gas–liquid interface | |
| surface tension coefficients of the solid–liquid interface | |
| surface tension coefficients of the gas–solid interface | |
| an auxiliary function |
Appendix A. The Water Film Height and Velocity Distribution at Different Times
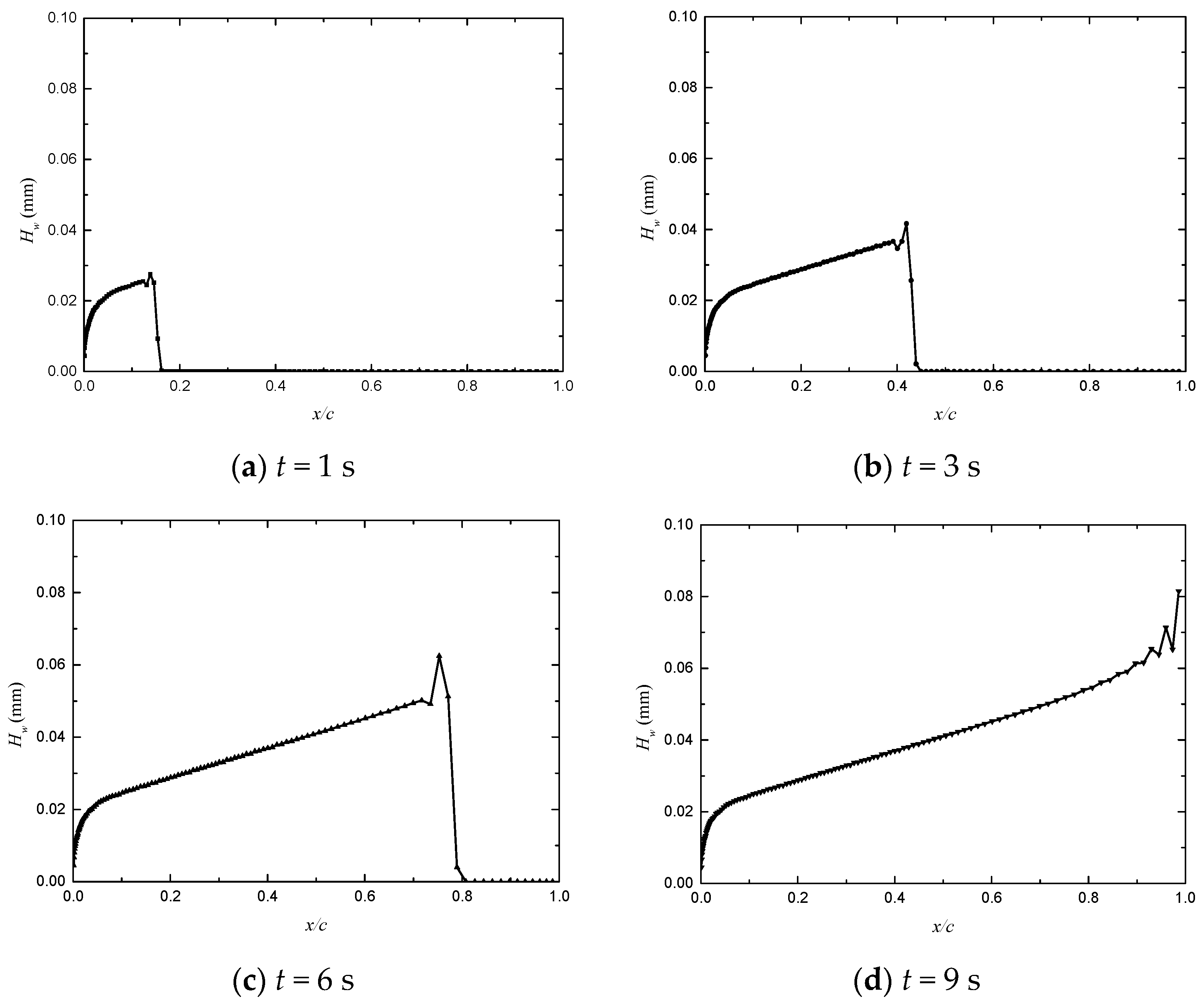

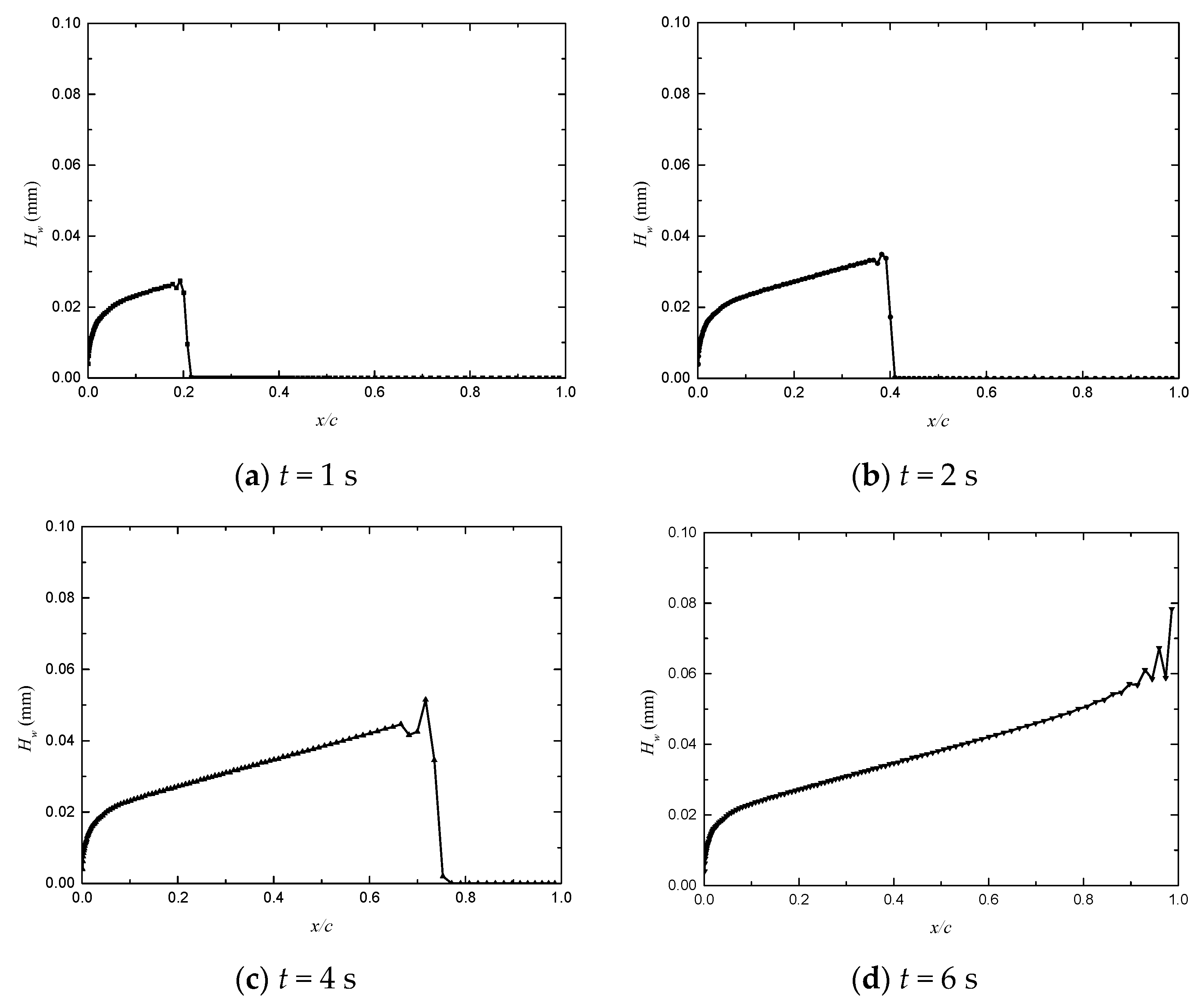
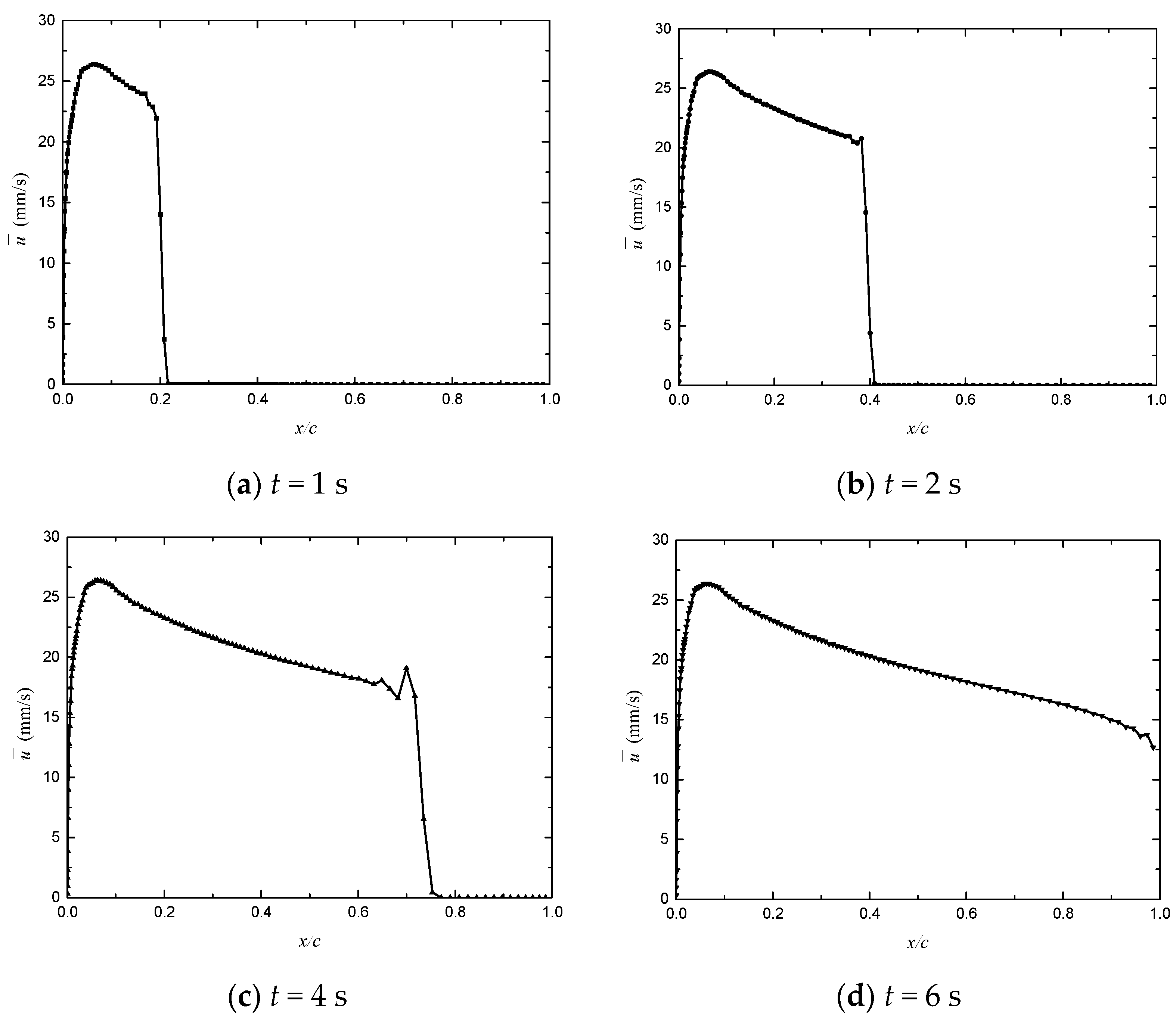
References
- Goraj, Z. An overview of the deicing and antiicing technologies with prospects for the future. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]
- He, Q.; Li, K.; Xu, Z.; Wang, J.; Wang, X.; Li, A. Research progress on construction strategy and technical evaluation of aircraft icing accretion protection system. Chin. J. Aeronaut. 2023, 36, 1–23. [Google Scholar] [CrossRef]
- Hansman, R.J., Jr.; Turnock, S.R. Investigation of surface water behavior during glaze ice accretion. J. Aircr. 1989, 26, 140–147. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear driven rivulet dynamics on surfaces with various wettabilities. In Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition, Montreal, QC, Canada, 14–20 November 2014. IMECE2014-38665. [Google Scholar]
- Zhang, K.; Johnson, B.; Rothmayer, A.P.; Hu, H. An Experimental investigation on wind-driven rivulet/film flows over a NACA0012 airfoil by using digital image projection technique. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA 2014-0741. [Google Scholar]
- Zhang, K.; Tian, W.; Hu, H. An experimental investigation on the surface water transport process over an airfoil by using a digital image projection technique. Exp. Fluids 2015, 56, 173. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Tian, W.; Hu, H. An experimental study to characterize the effects of initial ice roughness on the wind-driven water runback over an airfoil surface. Int. J. Multiph. Flow 2020, 126, 103254. [Google Scholar] [CrossRef]
- Lou, Y.; Bu, X.; Shen, X.; Lin, G.; Zhang, R.; Zeng, F.; Jin, H.; Ma, K.; Wen, D. Simulation of and Experimental Research on Rivulet Model on Airfoil Surface. Aerospace 2022, 9, 570. [Google Scholar] [CrossRef]
- Messinger, B.L. Equilibrium temperature of an unheated icing surface as a function of airspeed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Al-Khalil, K.M. Numerical Simulation of an Aircraft Anti-Icing System Incorporating a Rivulet Model for the Runback Water. Ph.D. Thesis, University of Toledo, Toledo, OH, USA, 1991. [Google Scholar]
- Al-Khalil, K.M.; Keith, J.T.G.; De Witt, K.J. Further development of an anti-icing runback model. In Proceedings of the 29th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 7–10 January 1991. AIAA 91-0266. [Google Scholar]
- Fortin, G.; Perron, J.; Mingione, G.; Perron, J. CIRAAMIL Ice accretion code improvement. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009. AIAA-2009-3968. [Google Scholar]
- Hedde, T.; Guffond, D. ONERA Three-dimensional icing model. AIAA J. 1995, 33, 1038–1045. [Google Scholar] [CrossRef]
- Silva, G.; Silvares, O.; Zerbini, E. Water film breakdown and rivulets formation effects on thermal anti-ice operation simulation. In Proceedings of the 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, San Francisco, CA, USA, 5–8 June 2006. AIAA-2006-3785. [Google Scholar]
- Dong, W.; Zheng, M.; Zhu, J.; Lei, G. Calculation and analysis of runback water flow on anti-icing airfoil surface. J. Aircr. 2016, 53, 1597–1605. [Google Scholar] [CrossRef]
- Bu, X.; Ma, W.; Lin, G. Numerical simulation of runback film breakup on two-dimentional anti-icing airfoil surface. J. Aerosp. Power 2015, 30, 368–375. [Google Scholar]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a shallow-water icing model in FENSAP-ICE. J. Aircr. 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Myers, T.G.; Charpin, J.P.; Thompson, C.P. Slowly accreting ice due to supercooled water impacting on a cold surface. Phys. Fluids 2002, 14, 240–256. [Google Scholar] [CrossRef]
- Cao, G.; Ji, H.; Hu, Y.; Pang, L.; Si, R.; Feng, X. An icing model for simulating three dimentional ice accretion on the upwind surface of a plane. J. Aerosp. Power 2011, 26, 1953–1963. [Google Scholar]
- Cao, G.; Ji, H.; SI, R. Computational methodology of water film flow in three dimensional ice accretion on upwind surface. J. Aerosp. Power 2015, 30, 677–685. [Google Scholar]
- Su, C.; Hu, Y.; Cao, G.; Ji, H. Numerical investigation on glaze ice accretion with the evaporation of the water film. Tuijin Jishu/J. Propuls. Technol. 2018, 39, 1540–1548. [Google Scholar]
- Jian, J.; Ji, H.; Cao, G.; Hu, Y.; Chen, N. Numerical study on water film flow and shedding in horn glaze ice accretion. J. Eng. Thermophys. 2018, 39, 2284–2293. [Google Scholar]
- Gosset, A. Prediction of rivulet transition in anti-icing applications. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences, Milan, Italy, 3–6 July 2017. EUCASS2017-482. [Google Scholar]
- Lei, M.; Chang, S.; Yang, B. Three-dimensional numerical simulation of icing using Myers model. Acta Aeronaut. Astronaut. Sin. 2018, 39, 36–46. [Google Scholar]
- Xin, M.; Zhong, G.; Cao, Y. Caculation of airfoil anti-icing/deicing characteristics based on water film flow and coupled heat transfer. J. Aerosp. Power 2021, 36, 783–794. [Google Scholar]
- Ferro, C.G.; Maggiore, P.; Champvillair, D. Development of a computational fluid dynamics model for ice formation: Validation and parameter analysis. Atmosphere 2023, 14, 834. [Google Scholar] [CrossRef]
- Samad, A.; Villeneuve, E.; Morency, F.; Béland, M.; Lapalme, M. A preliminary approach towards rotor icing modeling using the unsteady vortex lattice method. Drones 2024, 8, 65. [Google Scholar] [CrossRef]
- Andros, F.E. Heat Transfer Characteristics of the Two-Phase Closed Thermosyphon (Wickless Heat Pipe) Including Direct Flow Observation; Technical Report; Arizona State University: Tempe, AZ, USA, 1980. [Google Scholar]
- Brumby, R.E. The effect of wing ice contamination on essential flight characteristics. In AGARD Conference Proceedings; AGARD-CP-496; University of Michigan: Ann Arbor, MI, USA, 1991. [Google Scholar]
- Hedde, T.; Guffond, D. Development of a three-dimensional icing code, comparison with experimental shapes. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. AIAA-92-0041. [Google Scholar]
- Mirabedini, S.M.; Rahimi, H.; Hamedifar, S.; Mohseni, S.M. Microwave irradiation of polypropylene Surface: A study on wettability and adhesion. Int. J. Adhes. Adhes. 2004, 24, 163–170. [Google Scholar] [CrossRef]


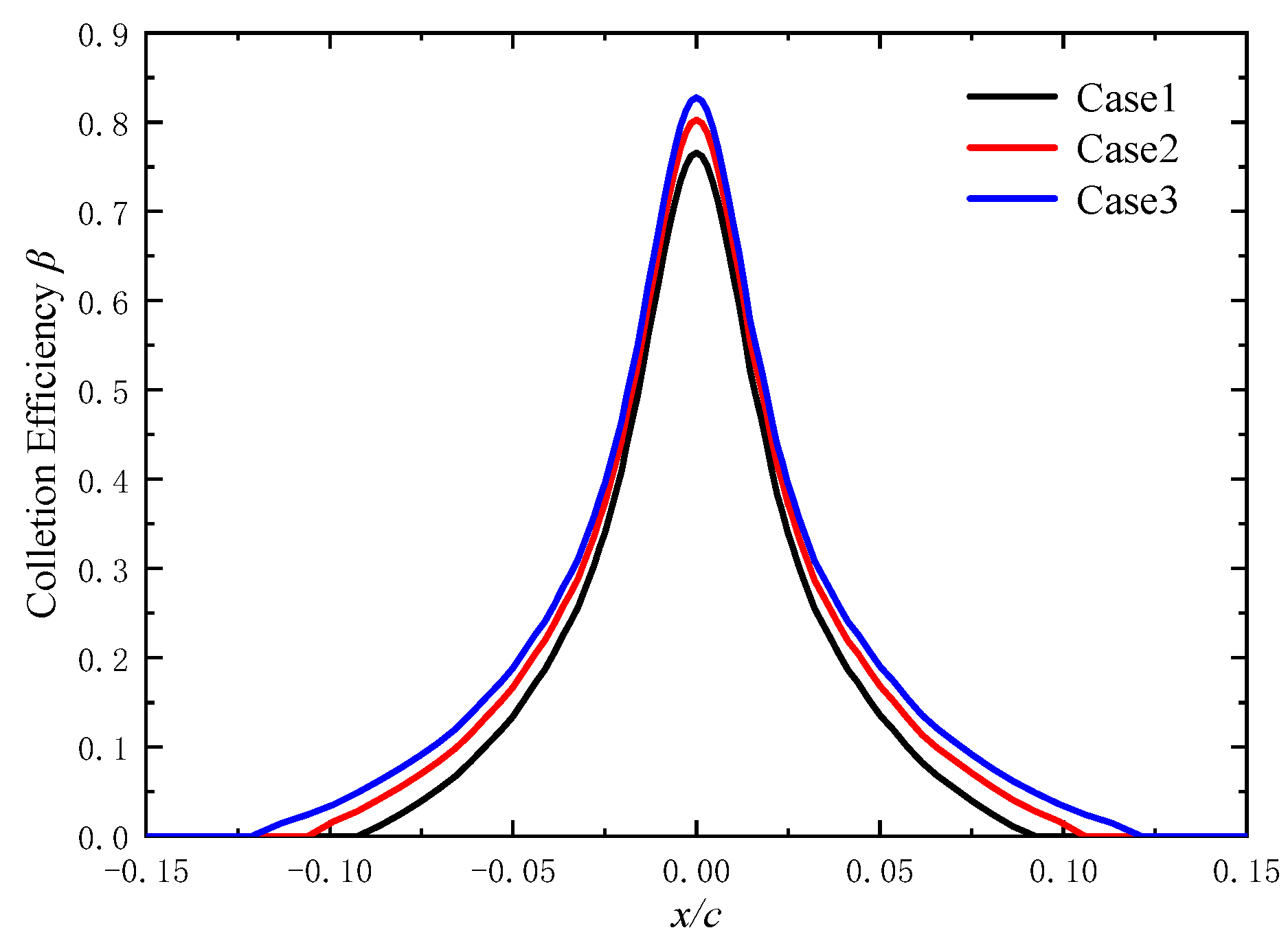
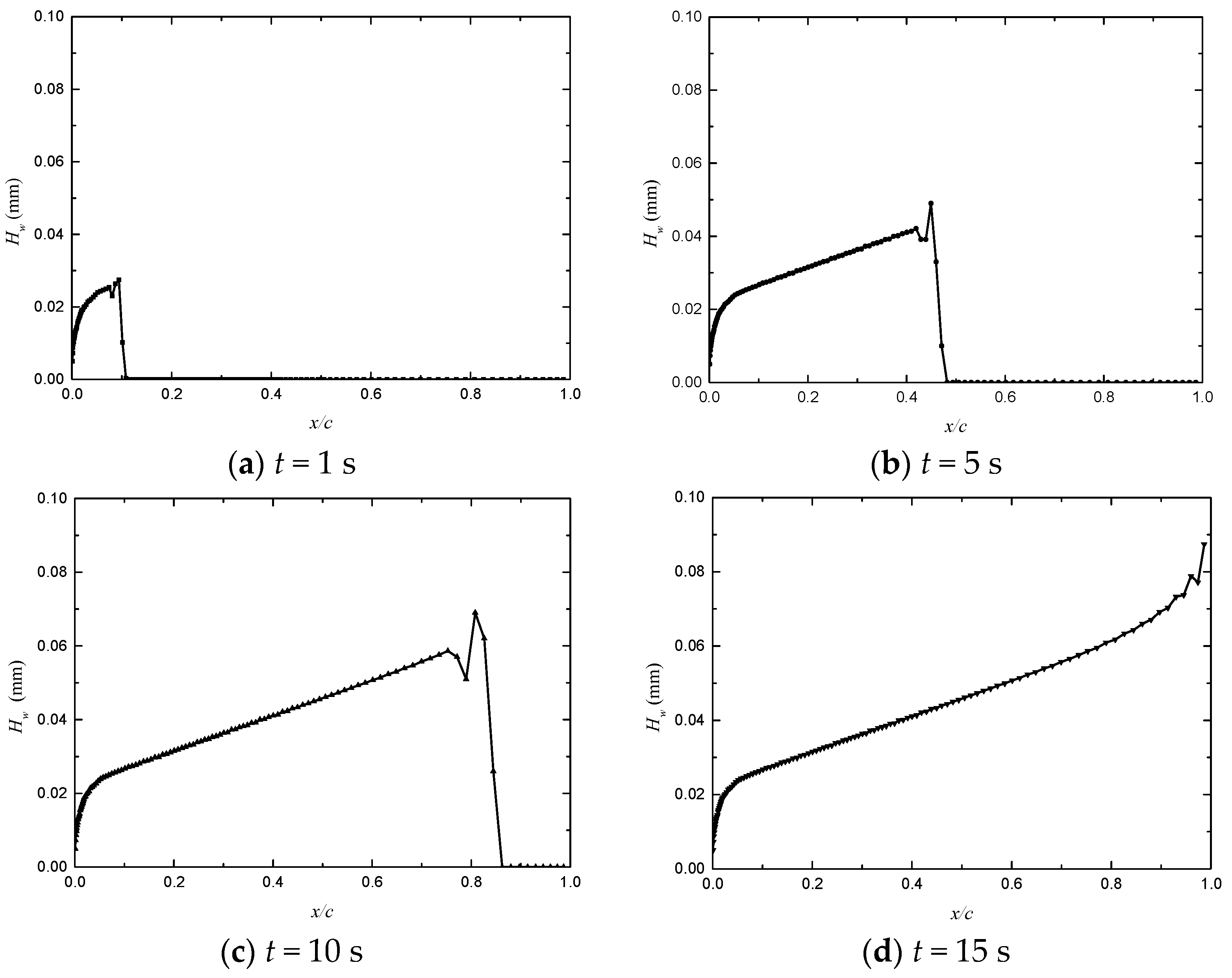
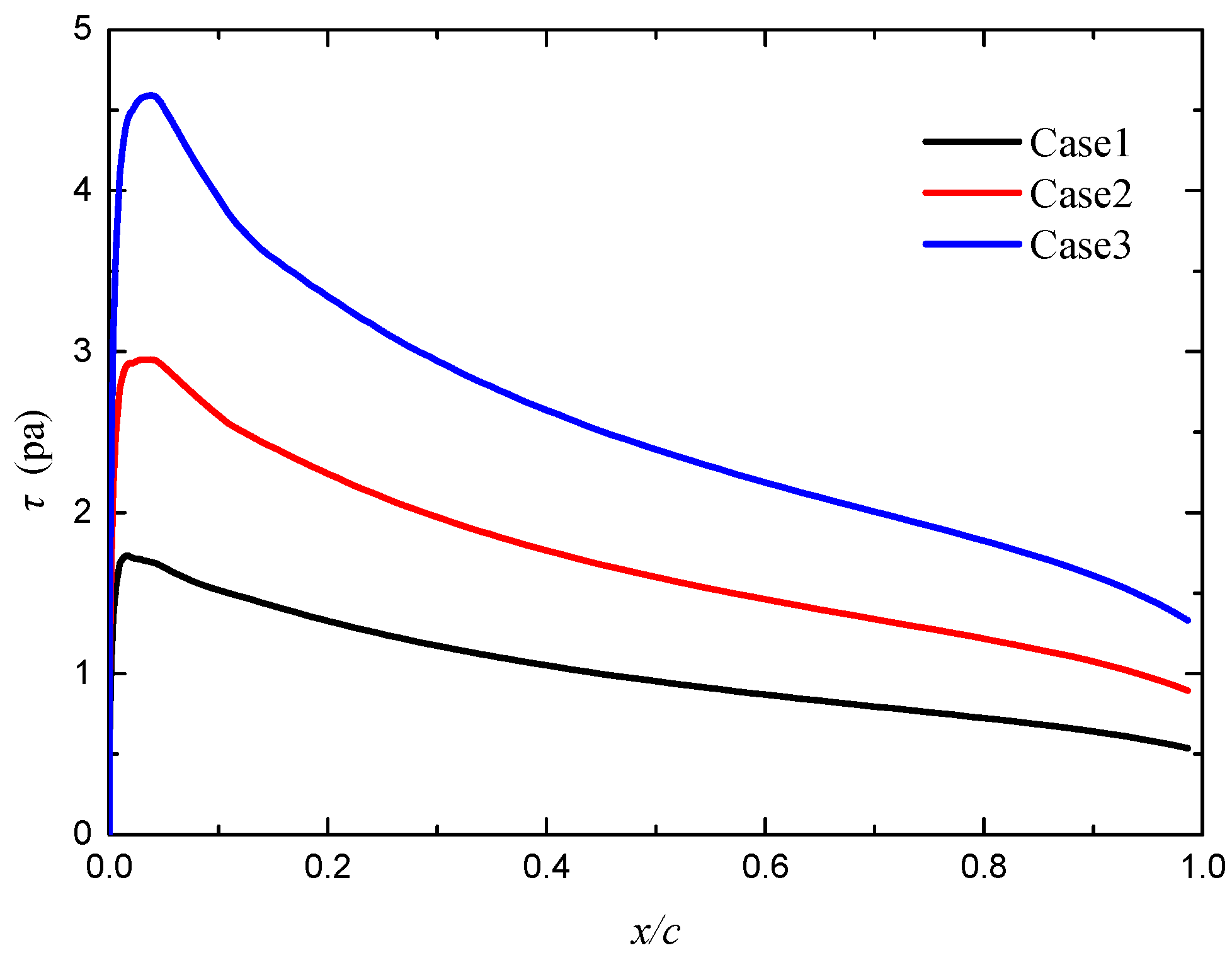
| Case | U∞ (m/s) | T∞ (K) | LWC (g/m3) | MVD (μm) | AOA (°) |
|---|---|---|---|---|---|
| 1 | 15 | 293.15 | 10 | 20 | 0 |
| 2 | 20 | ||||
| 3 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Liu, L.; Hu, Y.; Li, P. Numerical Simulation of Water Film Flow and Breakup on Anti-Icing Surface. Aerospace 2024, 11, 352. https://doi.org/10.3390/aerospace11050352
Zhang C, Liu L, Hu Y, Li P. Numerical Simulation of Water Film Flow and Breakup on Anti-Icing Surface. Aerospace. 2024; 11(5):352. https://doi.org/10.3390/aerospace11050352
Chicago/Turabian StyleZhang, Changxian, Lei Liu, Yaping Hu, and Pengfei Li. 2024. "Numerical Simulation of Water Film Flow and Breakup on Anti-Icing Surface" Aerospace 11, no. 5: 352. https://doi.org/10.3390/aerospace11050352
APA StyleZhang, C., Liu, L., Hu, Y., & Li, P. (2024). Numerical Simulation of Water Film Flow and Breakup on Anti-Icing Surface. Aerospace, 11(5), 352. https://doi.org/10.3390/aerospace11050352






