A Resilient Approach to a Test Rig Setup in the Qualification of a Tilt Rotor Carbon Fiber-Reinforced Polymer (CFRP) Wing

Abstract

The evolution of aircraft wing development has seen significant progress since the early days of aviation, with static testing emerging as a crucial aspect for ensuring safety and reliability. This study focused specifically on the engineering phase of static testing for the Clean Sky 2 T-WING project, which is dedicated to testing the innovative composite wing of the Next-Generation Civil Tiltrotor Technology Demonstrator. During the design phase, critical load cases were identified through shear force/bending moment (SFBM) and failure mode analyses. To qualify the wing, an engineering team designed a dedicated test rig equipped with hydraulic jacks to mirror the SFBM diagrams. Adhering to specifications and geometric constraints due to several factors, the jacks aimed to minimize the errors (within 5%) in replicating the diagrams. An effective algorithm, spanning five phases, was employed to pinpoint the optimal configuration. This involved analyzing significant components, conducting least square linear optimizations, selecting solutions that met the directional constraints, analyzing the Pareto front solutions, and evaluating the external jack forces. The outcome was a test rig setup with a viable set of hydraulic jack forces, achieving precise SFBM replication on the wing with minimal jacks and overall applied forces.

1. Introduction

In the early days of aviation, structural testing of aircraft wings was a relatively rudimentary process. The focus was on empirical methods, and designers relied heavily on material strength and construction principles rather than rigorous testing. As aircraft technology advanced, especially during and after World War II, there was a growing need for systematic static testing to ensure safety and reliability. The post-war era saw a shift toward more formalized testing procedures influenced by military and civil aviation standards [1]. Static testing became an integral part of airframe development, involving the application of loads to wings to simulate various flight conditions. Regulatory bodies like the Federal Aviation Administration (FAA) in the United States started establishing airworthiness standards, including requirements for static testing, to ensure the structural integrity of aircraft. After the 1980s, advances in materials science, particularly the use of composites, brought new challenges and opportunities for static testing. Traditional metallic wings were being replaced or supplemented with composite structures for their weight-saving benefits. Testing methodologies evolved, incorporating finite element analysis (FEA) and other computational tools to complement physical testing. Nowadays, static testing is an essential part of the aircraft certification process globally, ensuring compliance with airworthiness regulations. International organizations such as the International Civil Aviation Organization (ICAO) and regulatory bodies like the FAA, European Union Aviation Safety Agency (EASA), and others, set the standards for static testing as part of the broader certification process. The aviation industry has witnessed a significant shift toward composite materials for aircraft structures, including wings. Composite materials offer a high strength-to-weight ratio, corrosion resistance, and design flexibility. As aircraft manufacturers embraced composites, testing methodologies needed to adapt to the unique characteristics of these materials. The EASA, the European Union Aviation Safety Agency, plays a crucial role in setting safety and airworthiness standards for aircraft in Europe. AMC 20-29 [2] refers to the EASA’s Acceptable Means of Compliance and Guidance Material for Structural Testing of Composite Wings. Key aspects of the EASA’s AMC 20-29 include material characterization and guidelines for the planning and execution of static tests, ensuring representative loading conditions and addressing failure modes specific to composites. Testing composite wings introduces unique challenges, such as delamination, impact resistance, and anisotropic behavior, which need to be thoroughly addressed in the testing process. The building block approach outlined in the EASA’s AMC 20-29 is a systematic method for conducting static and fatigue testing of composite wings. This approach, which is incremental, is designed to ensure that the testing process is comprehensive, addressing the unique characteristics of composite materials. In this framework, ensuring representative loading conditions and placement of test loads is a key aspect that, if not properly managed, can lead to the failure of static testing [3]. Smith H. W. outlines in [4] the detailed process for conducting a static test on an ultralight airplane. The initial steps involved designing a steel reaction gantry, loading whiffletrees, and the necessary hydraulic and instrumentation systems. Extensive analyses, including loads and stress assessments, were performed on both the airplane and supporting structures. The test rig layout of a sub-component test like the P-3 Orion Wing Leading Edge is described in detail in [5]. In that specific case, tension was applied to the upper surface rubber pads using wire cables, employing pulley wheels in the lower part of the whiffle tree assembly to ensure the proper angular alignment of the loads while maintaining the majority of the structure in the vertical plane. Regarding the importance of the correct emulation of the boundary conditions, a test system was developed to perform static tests on the hyperstatic aero-engine pylon structure of an airliner [6], adhering to static structure testing standards. This involved tackling crucial challenges such as emulating the support stiffness of a hyperstatic engine pylon and reproducing the aero-engine loading conditions. Special emphasis was placed on designing a test rig structure that closely mimics the stiffness of the wing-to-fuselage mounting area and the nacelles mounting areas, with extensive utilization of finite element analysis to achieve the desired outcome. Besides the rig design, new techniques are approaching qualification tests: in [7], significant findings from a test campaign conducted on a very-light airplane (VLA) with a wet-laminate full-composite structure are reported, with a specific emphasis on validating innovative techniques, including digital image correlation (DIC), operational modal analysis (OMA), and taxing vibration test (TVT). With the advent of electrification in the aviation sector, the static tests contribute to validating and demonstrating the benefits that distributed electric propulsion (DEP) may yield for the future of aviation. This is the case for the NASA X-57, the testing of which was aimed at qualifying the wing and calibrating strain-gage instrumentation at the wing root. Calculating the qualification test pad load required careful consideration of the missing inertial loads and alignment with the design shear loads and bending moment envelope [8].

According to the literature review [4,5,7], conventional static test rig designs, which rely on cable-based loading systems, often feature tall gantries, presenting challenges in laboratories with limited space. Alternatively, in some scenarios [8], the use of actuators to directly apply loads to pads may require an excessive number of actuators, thus escalating the setup costs. This paper originates from the Clean Sky 2 T-WING project, dedicated to advancing an innovative composite wing for the Next-Generation Civil Tiltrotor Technology Demonstrator, a flagship endeavor within the Fast Rotorcraft Chapter of the Clean Sky 2 Program. The primary objective of this study is to develop a compact and cost-efficient rig with minimal actuators that is capable of accurately loading the wing structure while minimizing the discrepancies between the testing forces and the rig’s loading capacity. The essence of this research lies in the formulation of a numerical methodology aimed at optimizing the configuration of the actuators, representing a progression from conventional practices in static test rig design.

During the wing design phase, the critical load cases were identified by using the shear force/bending moment (SFBM) and failure modes. To qualify the wing, the engineering team must demonstrate its ability to endure forces, moments, and performance up to ultimate loads. Consequently, a dedicated test rig was designed to accurately reproduce the SFBM diagrams on the wing using hydraulic jacks and a test rig setup. The placement and orientation of the hydraulic jacks adhered to specified requirements, considering the maximum applied force, geometric constraints, and the need to replicate the SFBM diagrams with sustainable efforts and limited errors (within 5%). To achieve these objectives, an effective and robust algorithm has been implemented to determine the optimal configuration. This algorithm comprises five phases: firstly, identifying significant components by analyzing the independent components of the influence matrix (linking jacks forces to generated SFBMs); secondly, conducting least square linear optimizations without constraints to pinpoint suitable points for applying the jack forces (efficient components); thirdly, selecting and arranging solutions that satisfy the directional constraints based on the global error of the SFBMs’ and jack forces’ magnitude; fourthly, analyzing and optimizing the best solutions on the Pareto front (for more about the multi-objective optimization and Pareto front, see [9]) to meet all the constraints and choose a final solution; and finally, evaluating the external jack forces to replicate the reaction forces on the wing points attached to the supporting struts. The outcome of this process was a test rig setup configuration with a practical set of hydraulic jack forces capable of reproducing the SFBMs on the wing using a minimal number of hydraulic jacks and exerting minimal effort through the overall applied forces.

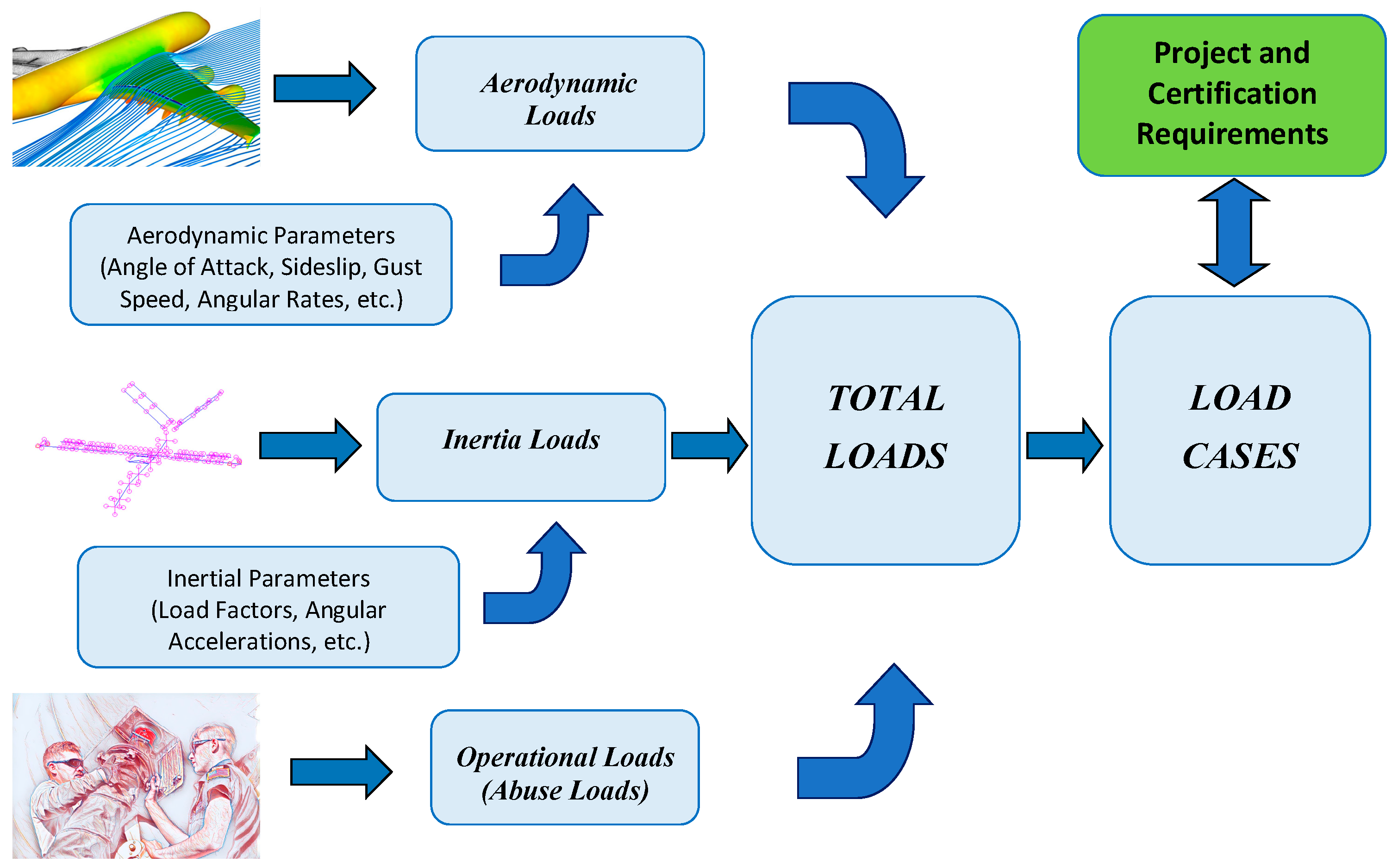
2. Loading Conditions

Aircraft are designed to withstand a variety of loads, as depicted in Figure 1 below and summarized in the following three points [10]:

• Aerodynamic loads, abbreviated as “airloads”, arise from forces and moments induced by the dynamic pressure acting on an aircraft. These loads encompass forces like the wing lift and drag, as well as moments such as the wing torsion and bending. Their intensity is influenced by the aircraft’s weight, load factor, geometry, and dynamic pressure. The overall magnitude adheres to requirements established by aviation authorities, exemplified by regulations like the 14 CFR Part 23 and 25. However, local values are contingent on the specific geometry.
• Inertia loads arise from the forces and moments experienced by aircraft components due to acceleration. Take the fuel or battery, for instance, which are not influenced by aerodynamic loads but require a support structure capable of withstanding the forces resulting from applied load factors. On the other hand, certain components, like a propeller engine, undergo both aerodynamic and inertia loads simultaneously.
• Operational loads encompass forces distinct from aerodynamics and inertia, arising from the inherent usage of the airplane. Examples of these loads include the forces on the door hinges and locks, floor loading, wing step-on forces, and similar factors.

Beyond the airframe’s primary function, the positioning and configuration of key load paths significantly influence the aircraft’s weight. From a certain perspective, it falls upon the structural engineer to devise a structure capable of supporting only the loads anticipated during operation. This is critical for the design’s success. An aircraft with strength surpassing its operational loads is essentially overdesigned; it possesses unnecessary strength and weight. Consequently, during each flight, it carries excess material that could otherwise contribute to the useful load. Moreover, the weight and positioning of components like the wings, stabilizing surfaces, engines, and landing gear play a substantial role in determining the aircraft’s center of gravity. This, in turn, may lead to loading challenges that necessitate the use of heavy ballast, further adding weight that could be part of the useful load [11].

All these loads, appropriately combined, determine the “loading conditions” or more simply “LCs”. For advanced aircraft like the Next-Generation Civil Tiltrotor Demonstrator, the number of load conditions exceeds 23,000 LC, without taking into account dynamic conditions such as continuous turbulence, discrete gusts, and dynamic landings. This is due to the need to consider a wide range of scenarios to ensure the safety and structural integrity of the aircraft under various operating conditions. All the loading conditions are taken into consideration during the design phases.

In general, the static test of an aeronautical structure represents the final step that ensures the validity of the project. In this paragraph, the guidelines followed for its implementation will be outlined. Since it is not possible to test all the load conditions, either through computer simulation or during the static test, a judicious selection of critical load conditions was necessary. By employing appropriate “cross plots” (convex hull algorithms [12,13]) of the shear forces and bending moments (SFBMs) diagrams, the number of conditions was significantly reduced. The following image depicts a typical cross plot and the selection made based on the criticality of three characteristic sections of the wing in the CFRP [14,15] (root, middle, and wing tip).

Figure 2 summarizes the optimization process followed. In this manner, only 57 critical load conditions were analyzed through computer simulation, from which important information about the wing structure was obtained.

Subsequently, as shown in Figure 3, it was possible to further reduce their number, resulting in 9 critical conditions, which represent the conditions to be subjected to static testing.

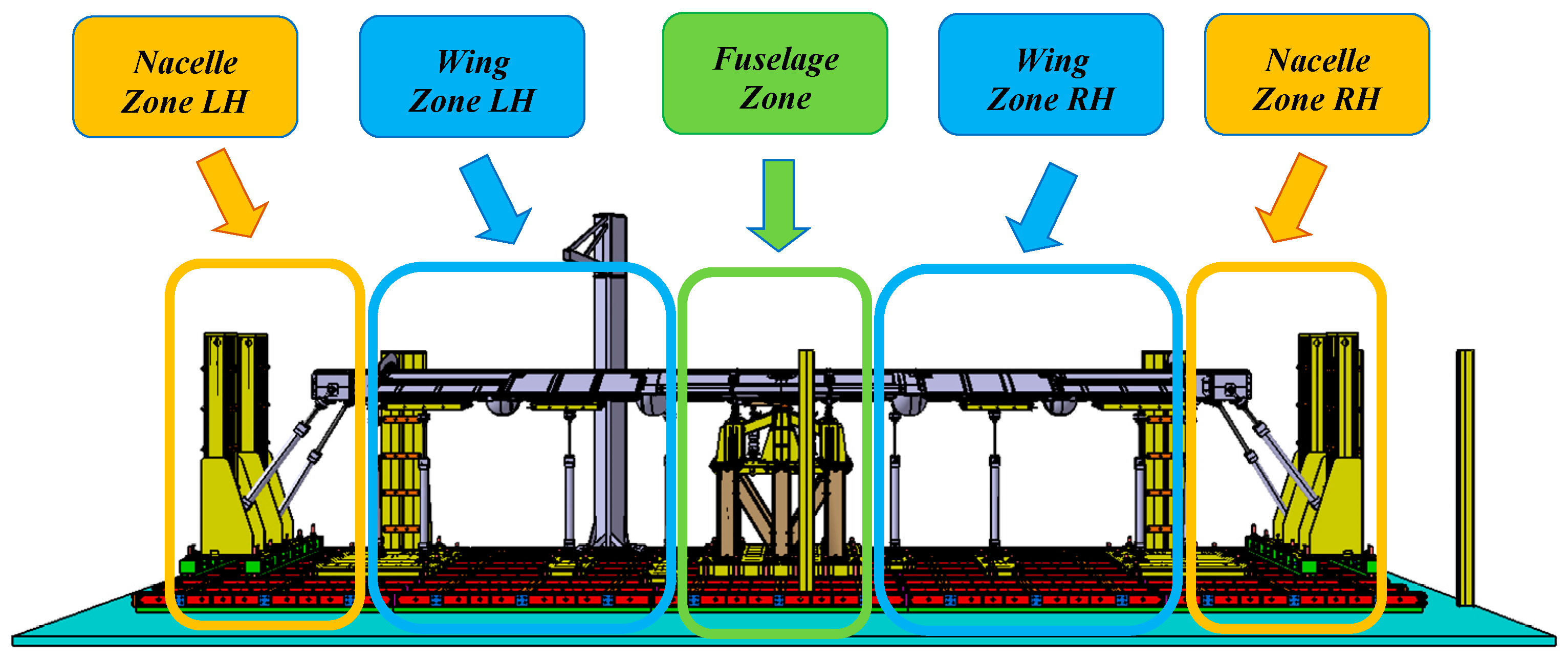
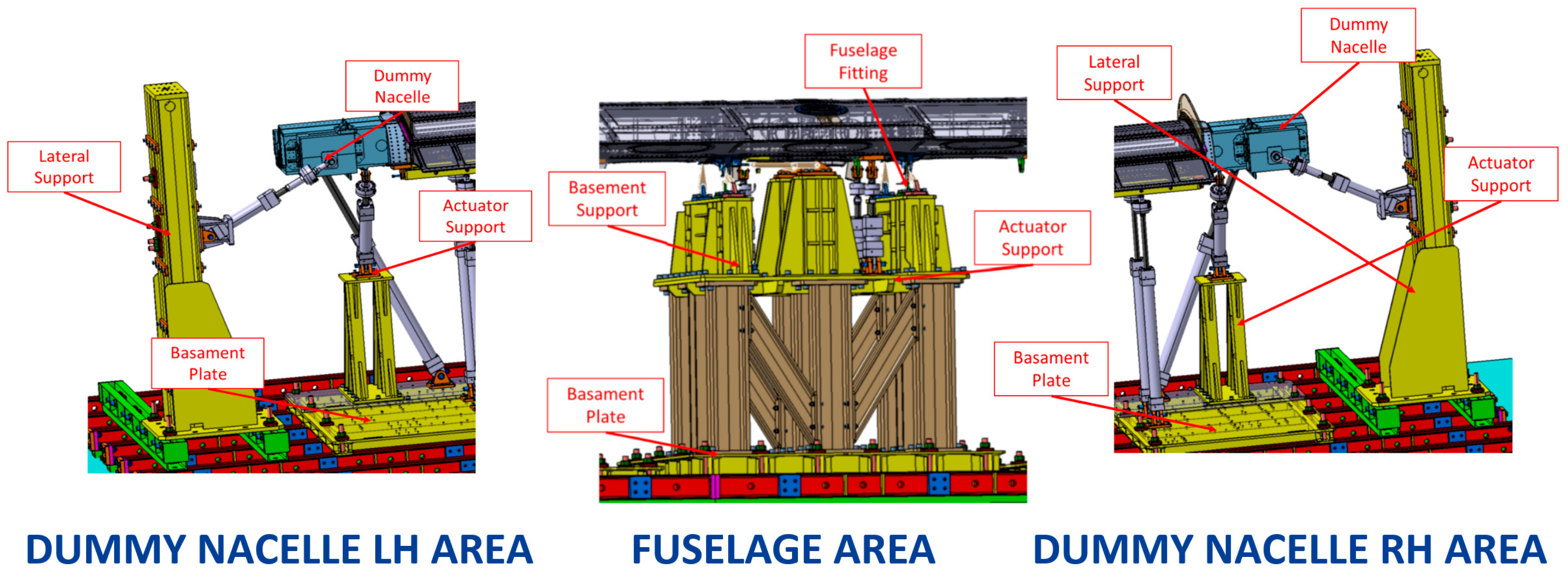
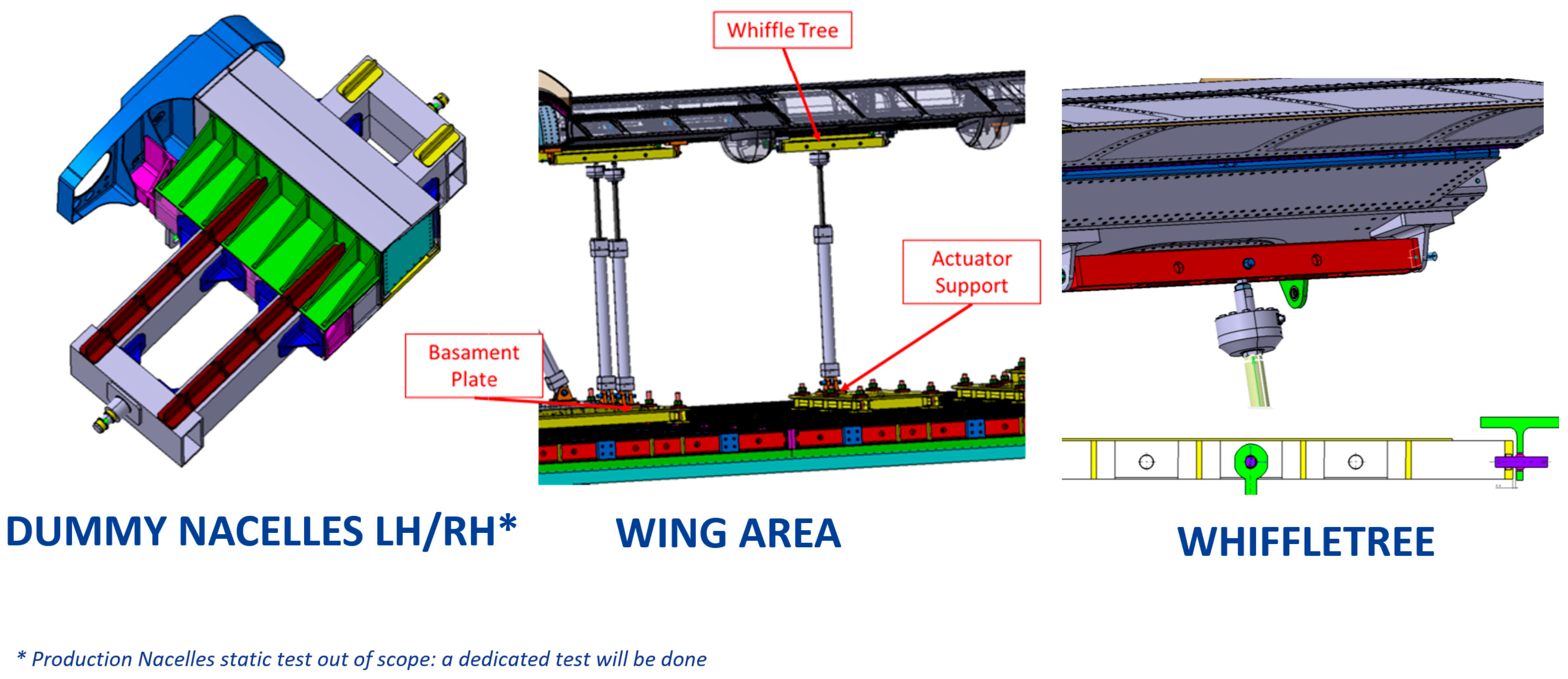
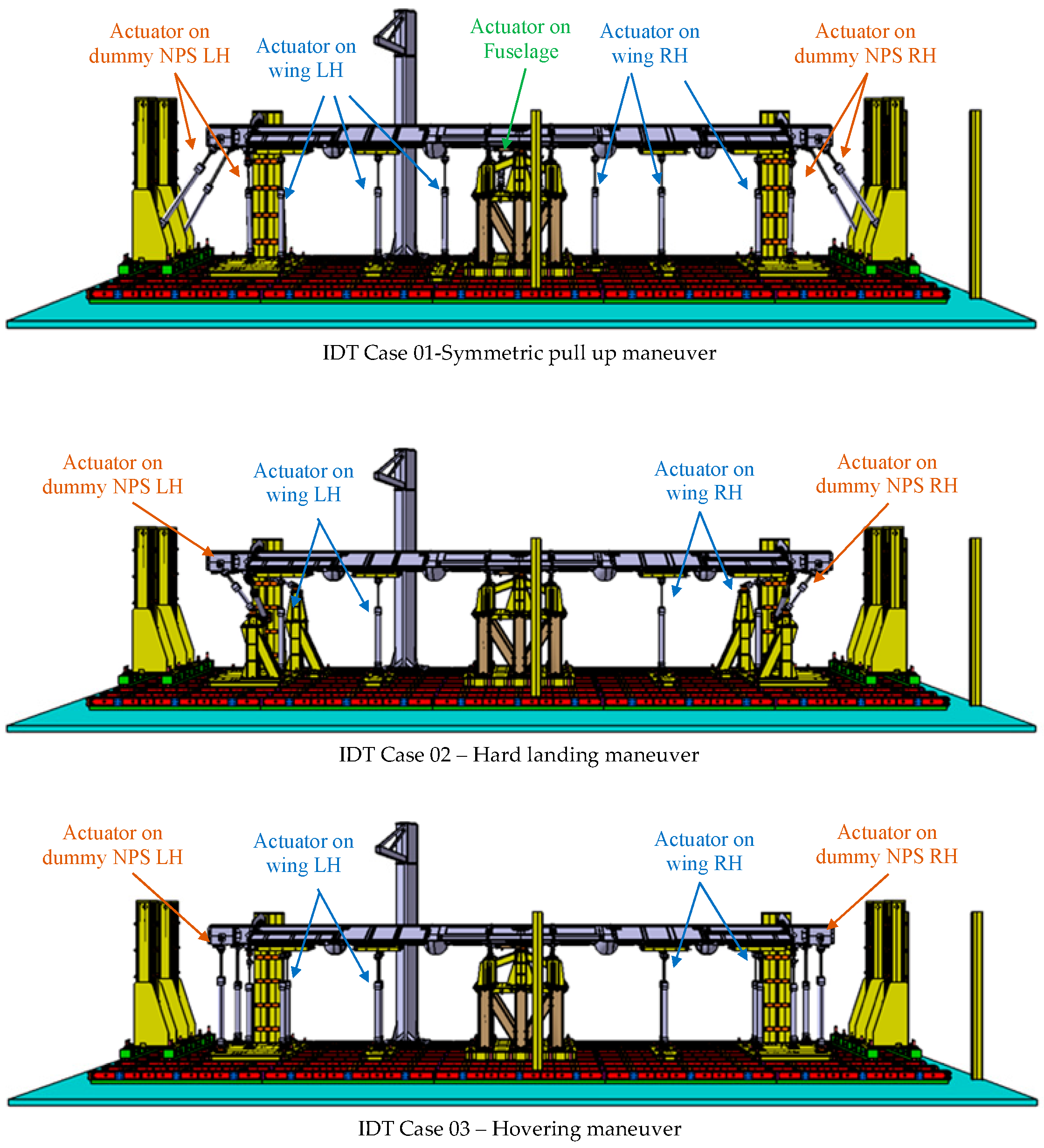
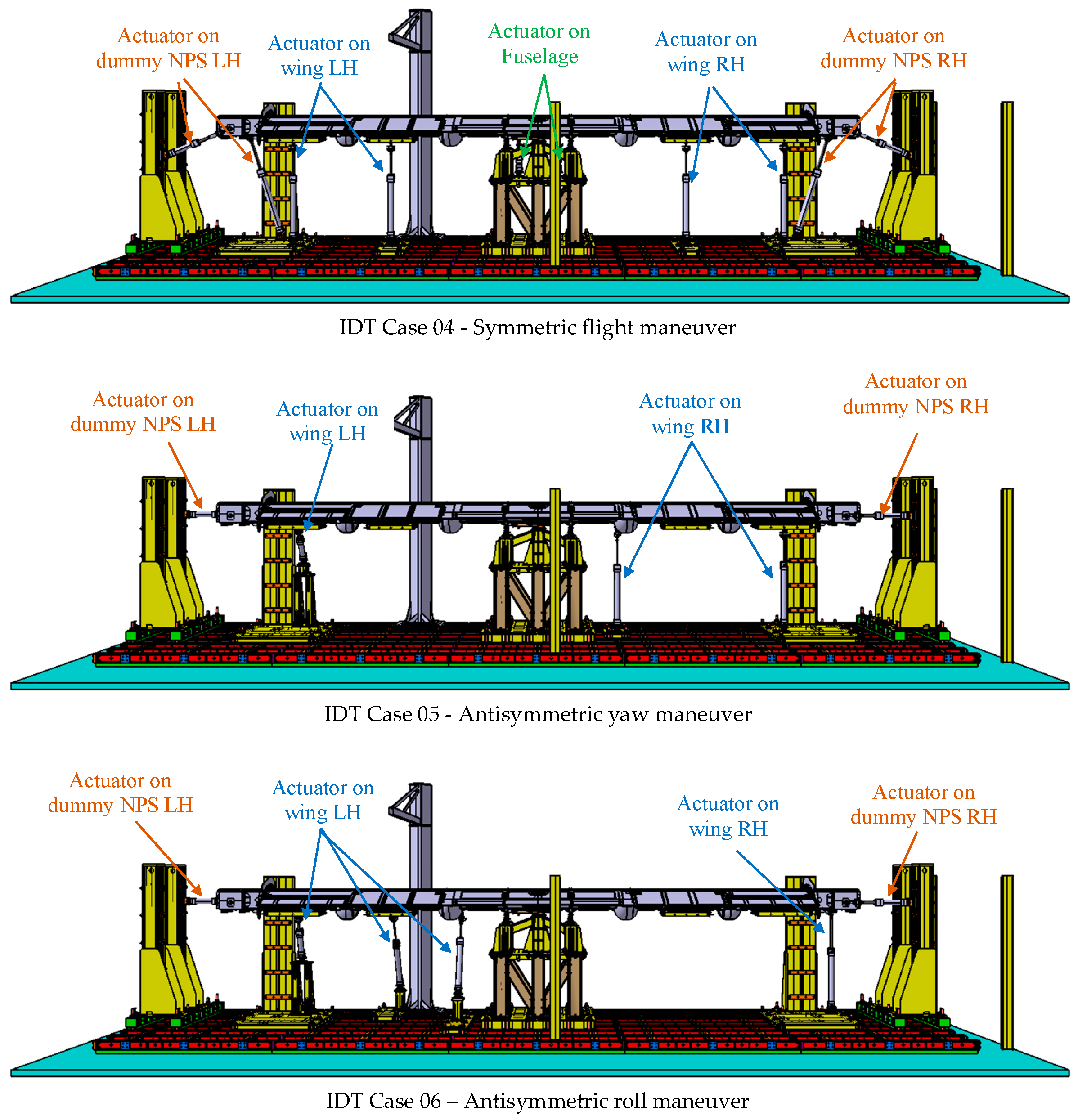
3. Geometrical Constraints

Static testing of wings is crucial for assessing the structural strength under simulated load conditions. This procedure, conducted on the ground, aims to replicate the stresses that wings undergo during operation. Numerical analysis, based on mathematical models such as finite element analysis, is employed to predict the structural behavior under various conditions. However, it is vital to validate these results through experimental analysis.

Experimental analysis involves physical tests on prototypes or components to verify numerical predictions. These tests take place on a dedicated test rig designed to simulate loads and stresses equivalent to those experienced in flight. It is essential that the test rig is stronger than the structure being tested, preventing any failures caused by the rig itself.

The key concept is that the validity of an aeronautical design is confirmed through the synergy between the numerical and experimental analyses. While numerical analysis provides predictions, physical testing ensures that the structure performs as designed in reality, contributing to the safety and reliability of wings in operational conditions.

Figure 4 depicts a classic design of a test rig for the static testing of a wing. It is evident that the structure is quite tall, and this forced choice is influenced by the utilization of a “whiffletree” for the optimal distribution of loads on the wing. The “whiffletree” is a device designed to ensure a uniform and balanced assignment of loads along the wing during static testing, guaranteeing a realistic distribution of aerodynamic and inertial loads. This approach enables an accurate simulation of the shear forces and bending moments that the wing would encounter during normal flight operations [16].

The constraints imposed by the laboratory, where the static test will be conducted, require a deep understanding of both the wing’s structural design and the test rig. The structural design of the components involves a careful examination of the geometry of the structures. Factors such as the load-bearing components (actuators and whiffletree), stress concentrations, and the overall configuration play a crucial role in guiding the selection of load application points.

The test rig for the static testing of the Clean Sky 2 T-WING wing can be divided into five zones where actuators will be installed to apply the load. As shown in Figure 5, the zones are:

• Nacelle Zone LH (left side of the aircraft)
• Wing Zone LH (left side of the aircraft
• Fuselage Zone
• Wing Zone RH (right side of the aircraft)
• Nacelle Zone RH (right side of the aircraft)

The main limitation imposed by the laboratory is on the height, which has required the use of a wing loading system different from the usual one. In fact, the wing will be loaded using actuators that operate from its underside, as shown in the Figure 6, where detailed views of the test rig are presented.

The structural design of the components involves a careful examination of the geometry of the structures. Factors such as the load-bearing components (actuators and whiffle-tree), stress concentrations, and the overall configuration play a crucial role in guiding the selection of load application points [9,17].

The selection of load application points is a crucial phase for the proper execution of the static test. At the core of this phase lies the strategic choice of where and how loads will be applied to the test structure. This selection is not arbitrary but is based on a profound understanding of the structural design and the expected load distribution patterns.

An in-depth understanding of the structural design is imperative during this selection process. It involves a close examination of the geometry and material composition of the structure under examination. Factors such as the load-bearing members, stress concentrations, and the overall configuration play a pivotal role in guiding the selection of load application points.

The test rig involves the use of 30 load application points to prevent stress concentrations on the wing structure, and in Figure 7 are shown the loading points, with their action lines highlighted in the right table.

When considering that each point can apply a load in three directions (X, Y, and Z), there are approximately 90 degrees of freedom (30 points x3 directions). However, not all of these degrees of freedom can be utilized due to the geometric constraints imposed by the feasibility of the test rig (see the table in Figure 7; “Work plane of the actuator” and “Max inclination”). Therefore, the table provides for the identification of the load application points and their respective degrees of freedom.

4. Optimization of Test Rig Setup

The test rig setup must reproduce in an accurate way the shear forces and bending moments (SFBMs) acting on the wing. The SFBMs can be reproduced through a discrete number of actuators acting on the wing, which can apply forces in only certain directions and up to a certain amount. The main task is to obtain a set of feasible forces for the actuators that do not overload the actuators themselves and are able to reproduce the SFBM diagrams of the most critical wing load conditions with a reasonable level of accuracy. To reach this goal, a multistep optimization procedure has been applied:

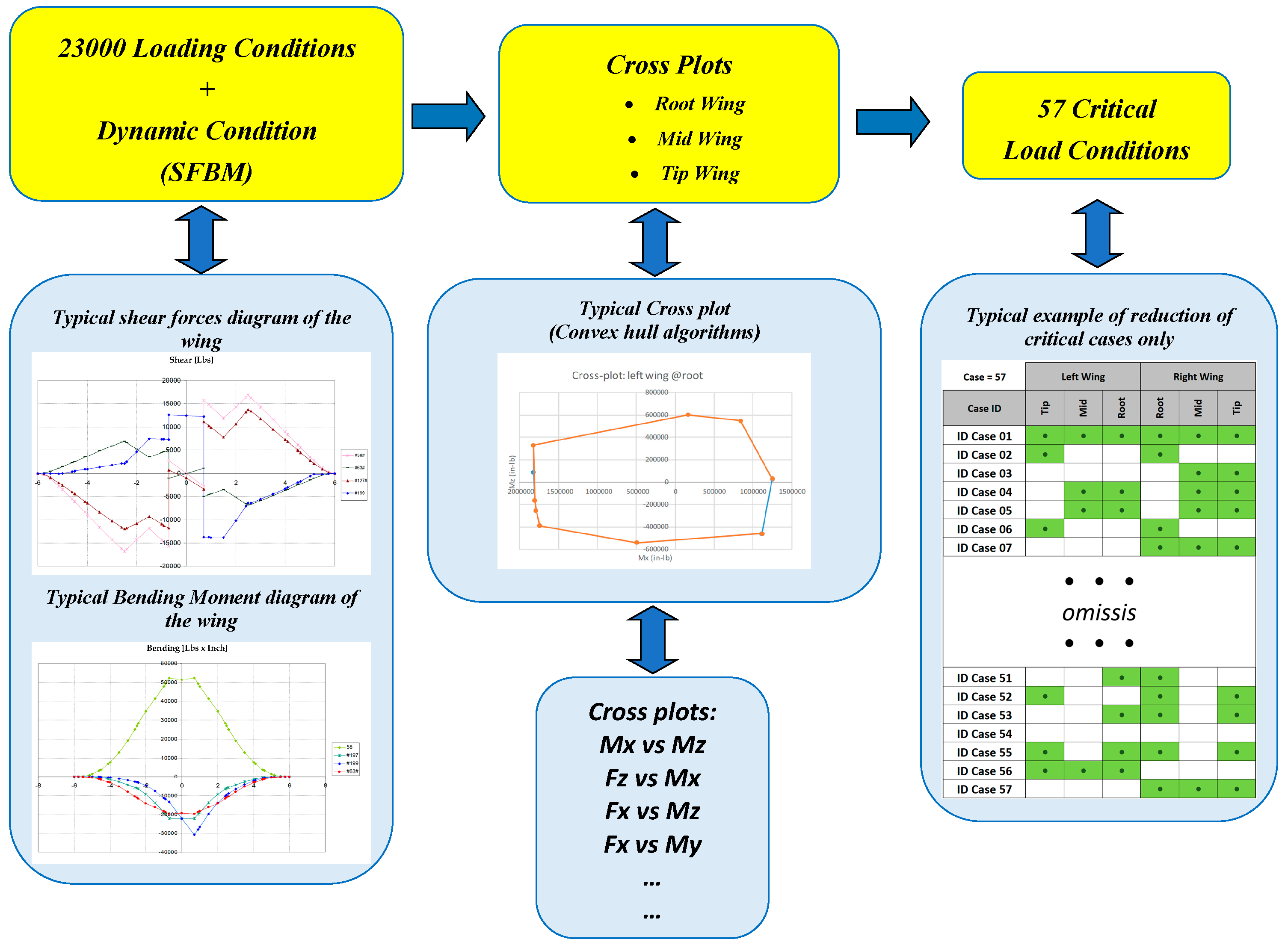
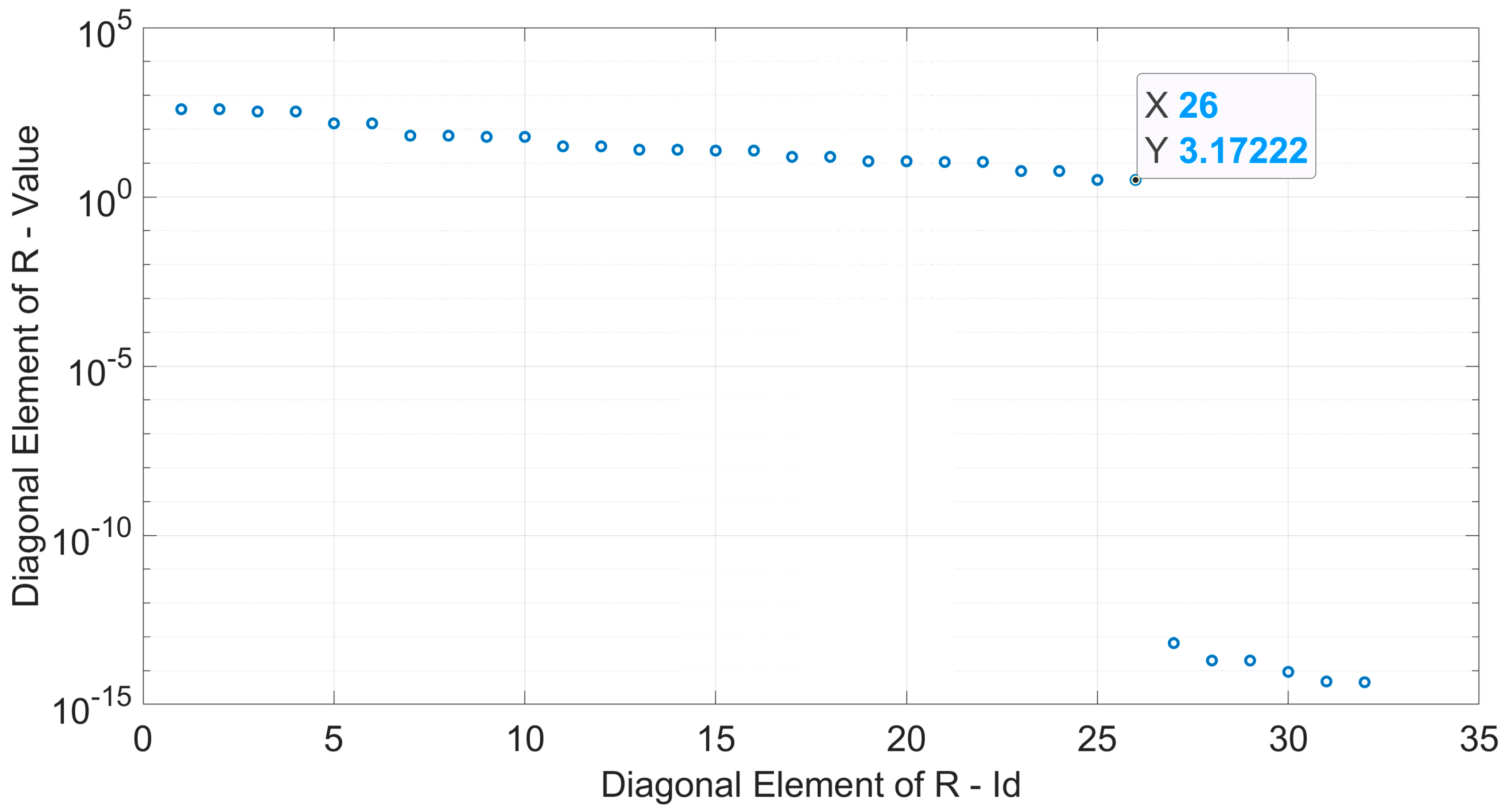
• Significant components determination (step 1): each actuator’s force component gives rise to a particular SFBM diagram. The global SFBM diagram is obtained as a linear combination of the SFBM diagram of each load component. Considering the constraints on the actuator force components (driven by the test rig implementation), only 32 actuator force components are “free” (actuators can be only placed respecting some relative positions between them and can mainly act along some preferential directions). To reduce the computational loads of the successive steps, a linear independence analysis of the SFBMs of these 32 load components has been performed by means of a QR decomposition—see [18,19]—of the SFBMs’ matrix (the matrix whose columns are the SFBMs on the control points generated by each load component). In Figure 8, the diagonal elements of the upper triangular matrix of the decomposition (calculated in Matlab, see [18]) are displayed: only 26 elements have values comparable between them and higher than the remaining 6, so only 26 load components are actually linear independent.

• Least square linear optimizations with only the actuator’s load direction constrained (step 2): a least square minimum norm unconstrained optimization has been launched for all the combinations (906,192). The number of combinations without repetition that can be formed taking k elements from a set made of n elements is given by the formula C(n,k) = n!/k!(n − k)! as 26 components among the 32 admissible actuators components (with the aim being to identify the best 26 independent load components between the 32 overall load components). For each combination, a minimum norm least square solution to the linear Equation (1) is calculated (where b—84 × 1 vector—is the SFBM diagram that must be replicated at the 14 control points—14 control points times 6 SFBM-, A—84 × 26—is the matrix whose columns are the SFBM generated by the 26 actuator force components retained and X—26 × 1—are the actuator force components retained).

$$AX=b$$

(1)

A least square minimum norm solution of system (1) is a solution of the overdetermined system (1) (in our case, 84 equations and only 26 unknowns) that minimizes the value of ‖A*X − b‖ (the norm of the vector, see [20,21]): the solution found is the one between all the least square solutions of the system that has a minimum norm, i.e., the actuator load components are the minimum possible.

To appreciate the difference between the least square solution and least square minimum norm solution, in the Figure 9 are shown the two solutions for the system:

$$X_2=-2/3X_1+8/3$$

(2)

To calculate the 906,192 minimum norm solutions (one for each combination of 26 load components) takes about 30 min on an Intel^® Core™ i7-8665U CPU with 4 cores. All the 906,192 optimal solutions have been plotted (see Figure 10) in terms of the sum of the SFBMs’ relative errors (calculated with respect to the max SFBMs values, i.e., for each SFBM the ratio of the maximum absolute difference on the control points between the target and reconstructed SFBM and the maximum absolute value of the target SFBM was calculated, and the six relative errors have then been added) versus the absolute sum of the actuator’s force components. The sum of the SFBMs’ relative errors is an indicator of how well the target SFBM is reconstructed. The absolute sum of the actuator’s force components is an indicator of the stress on the actuators themselves.

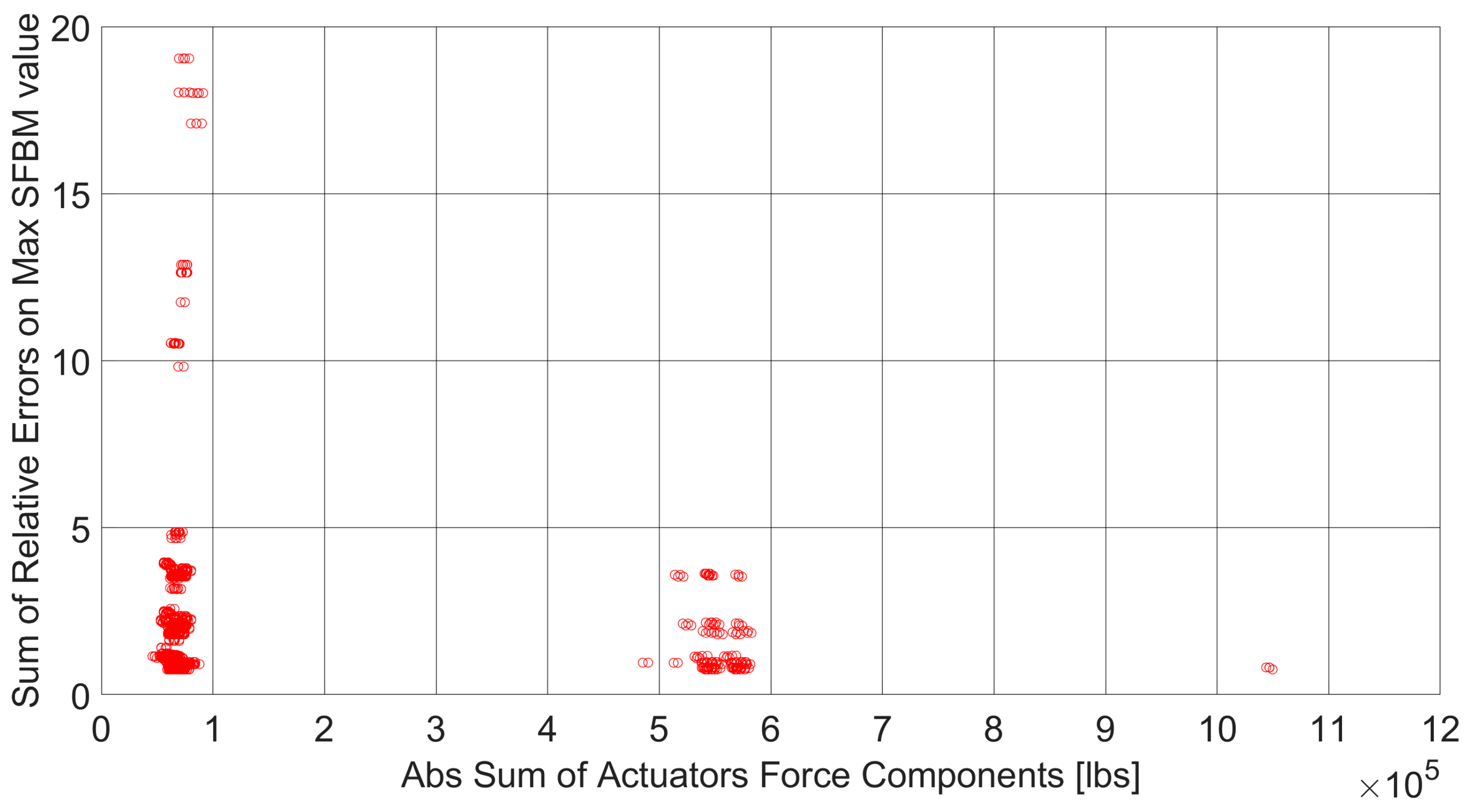
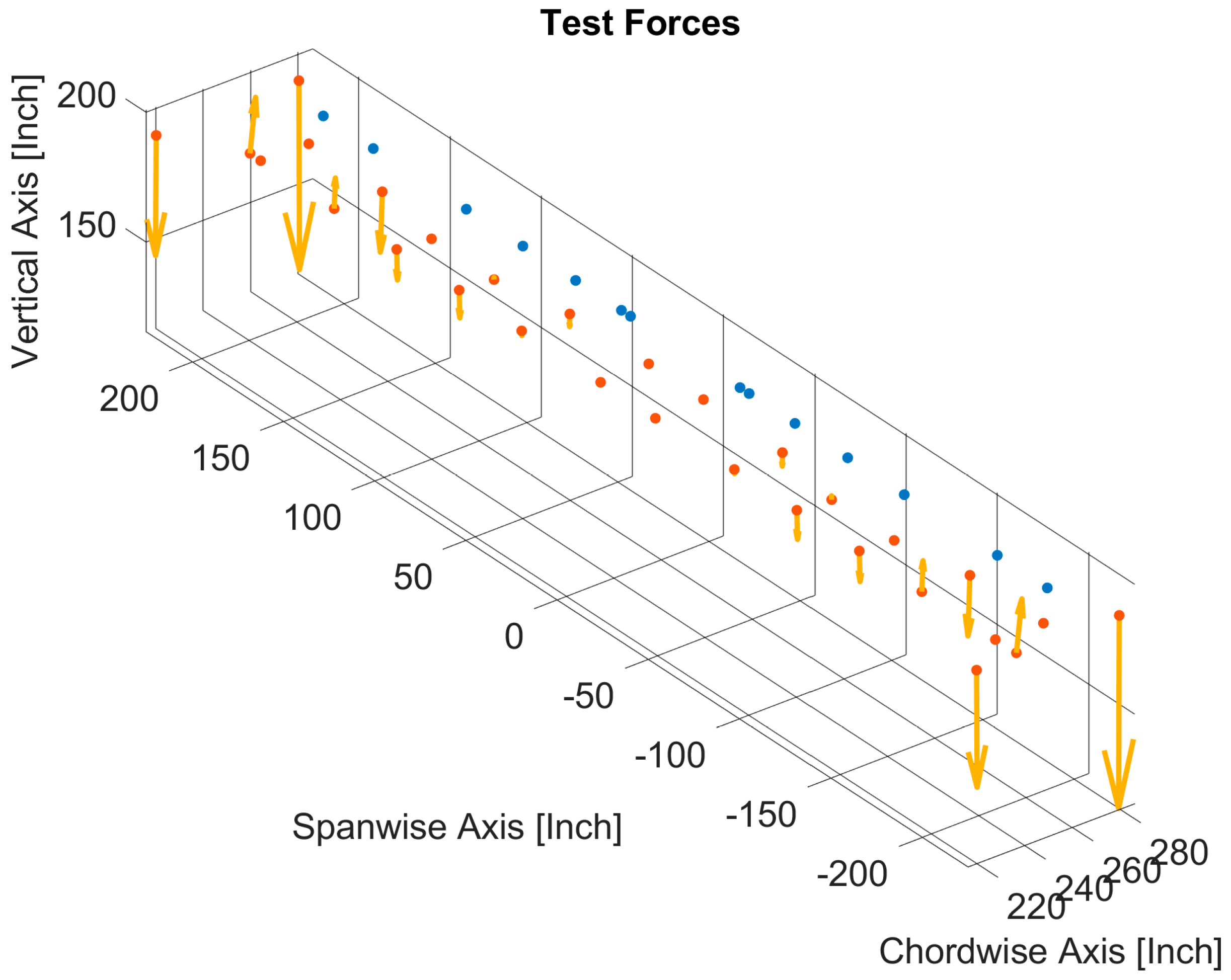
• Solution identification that satisfies the remaining test constraints (step 3): among the 906,192 optimized solutions, those solutions that verify all the other setup constraints (i.e., relative direction between actuators forces, maximum angle between load components of an actuator, see Section 4) have been identified and plotted (see Figure 11, where the red dots are a subset of the blue dots in Figure 10 that respect all the remaining setup constraints).

  Figure 11. Optimized solutions that verify all the test rig constraints.

  Figure 11. Optimized solutions that verify all the test rig constraints.

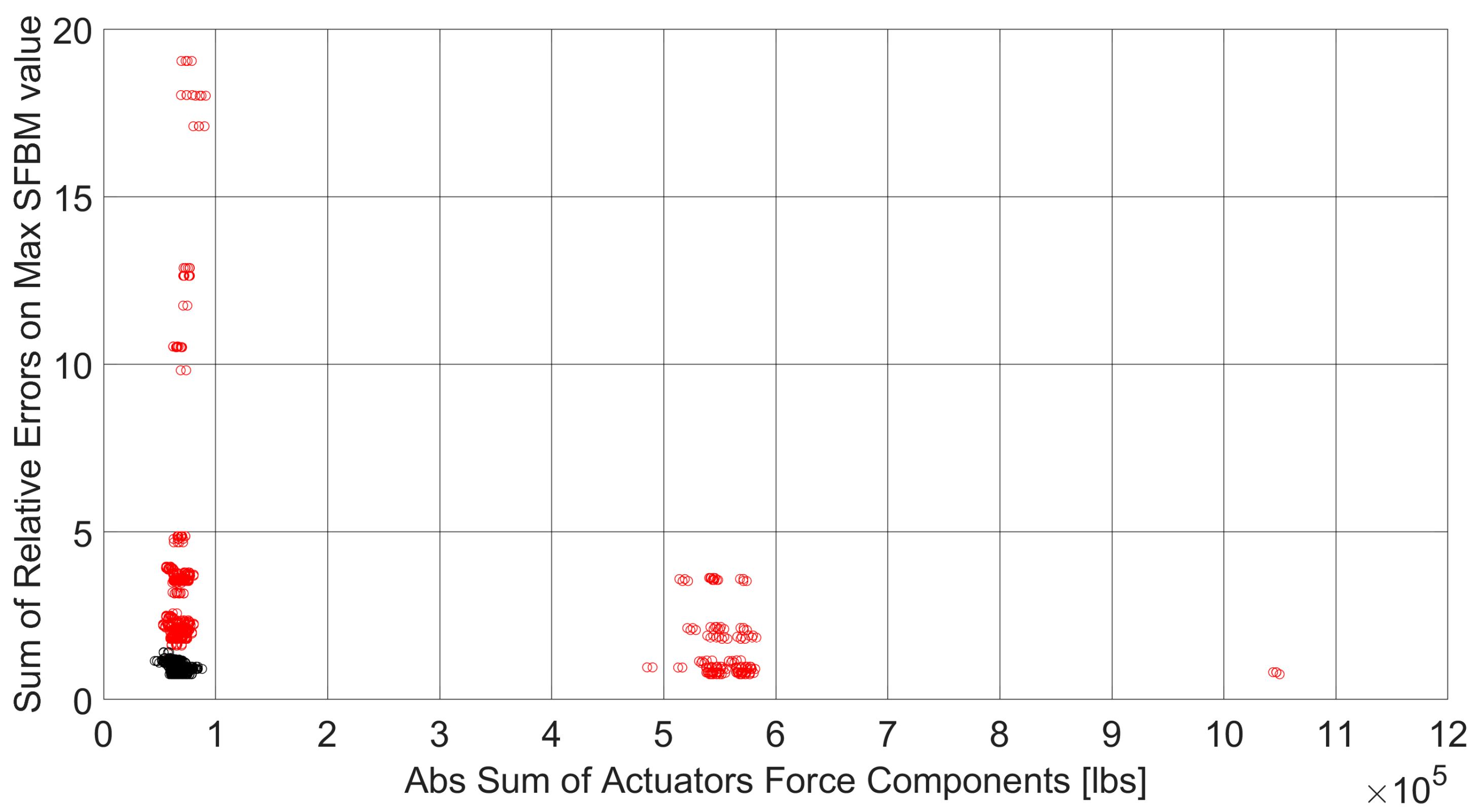
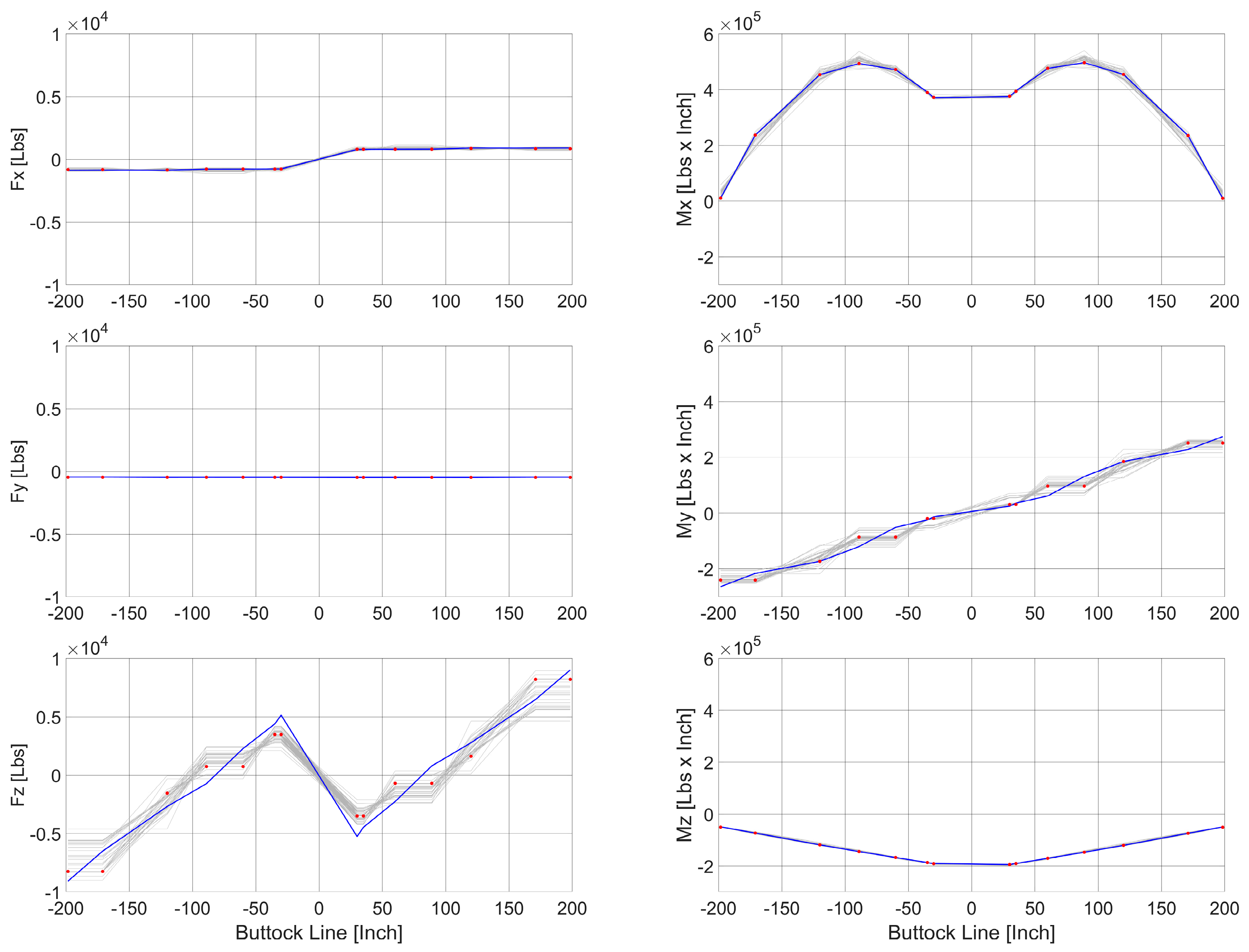
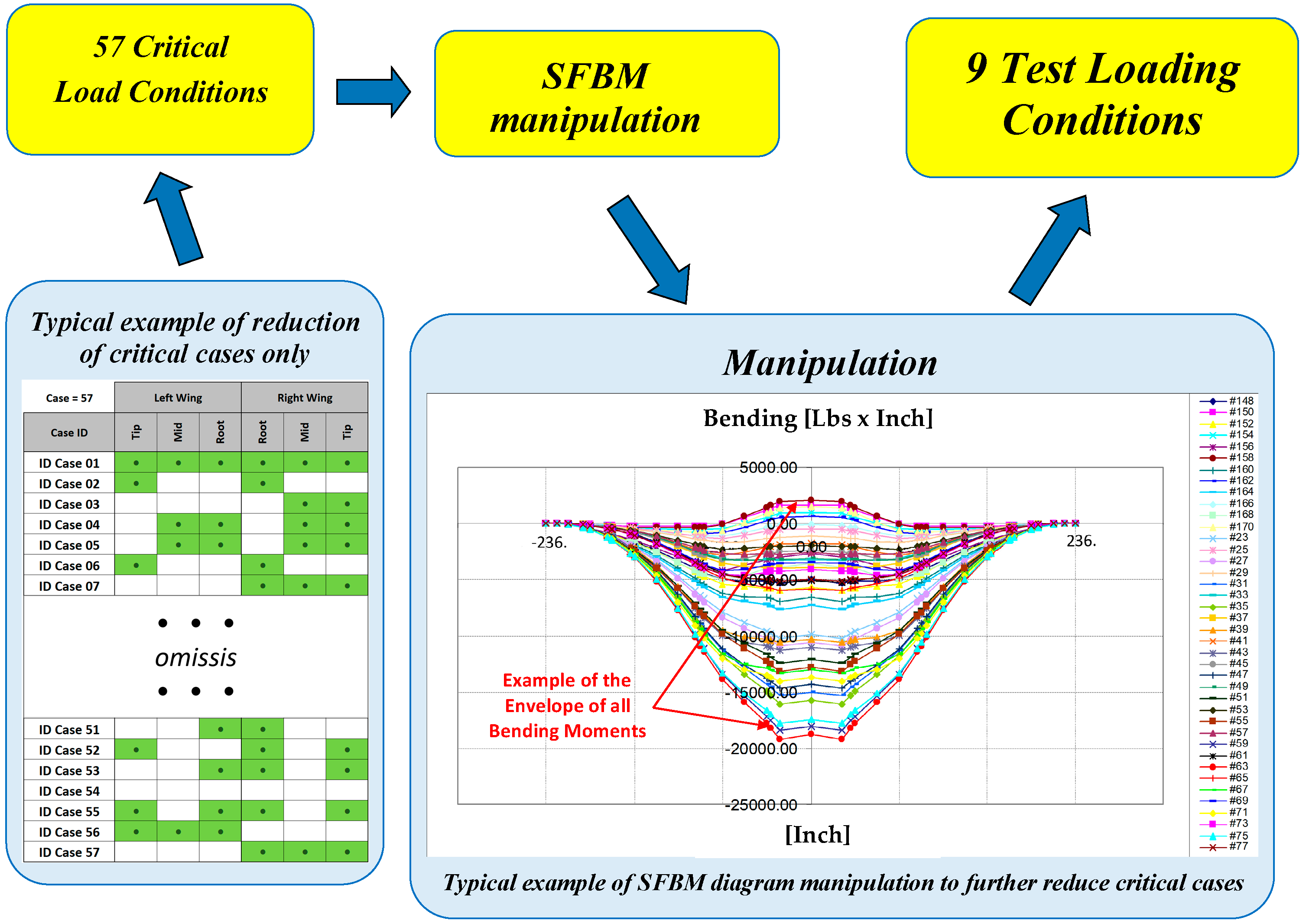
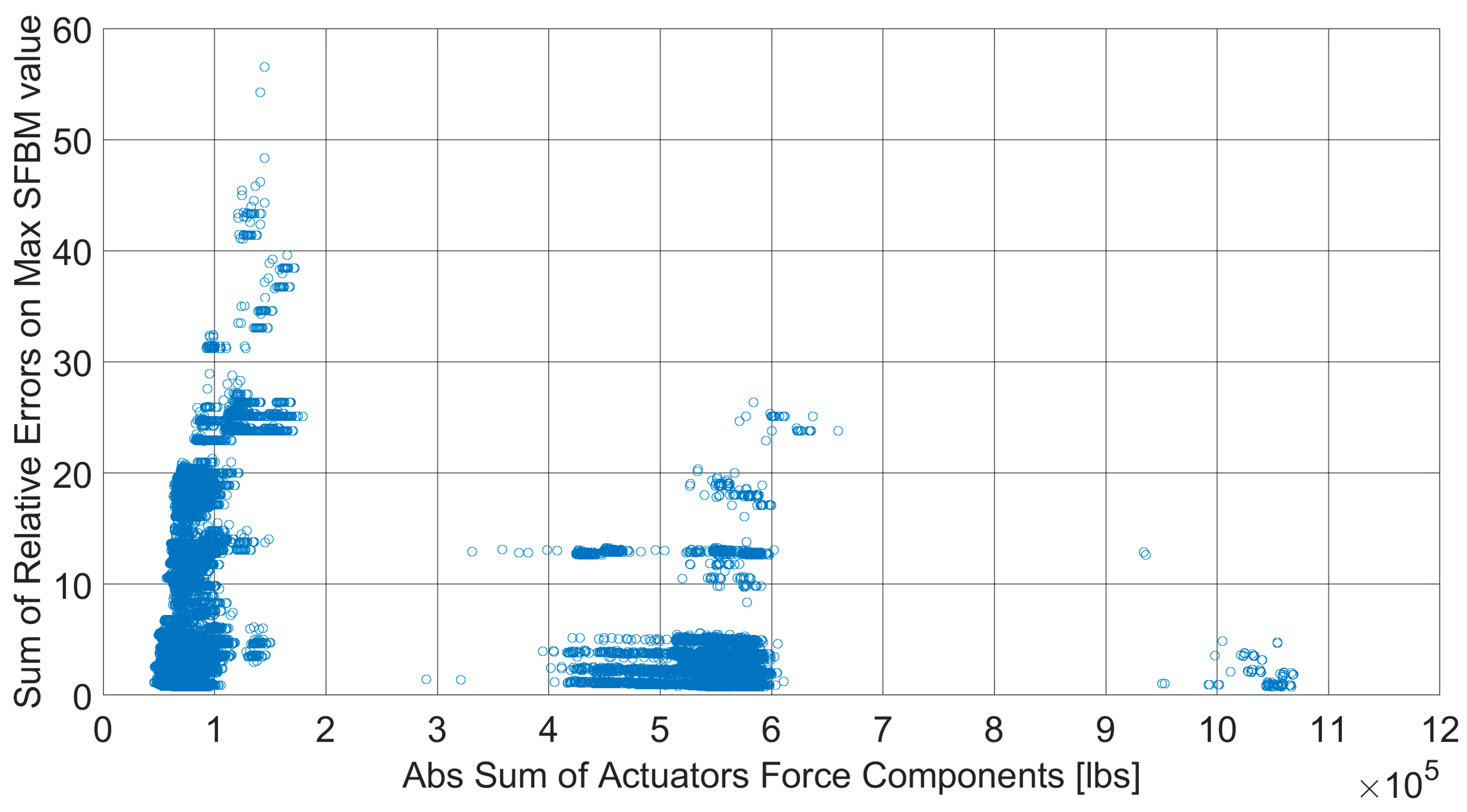
• Identification of a set of best solution constraints that comply (step 4): among the feasible solutions, those that have low values of actuation forces (low stress on the actuators) and SFBM errors (more accurate solutions) have been identified (black dot in Figure 12, those belonging to the lower-left part of the Pareto front). These solutions have been reviewed in detail in terms of SFBM plots (the differences in the target and reconstructed SFs and BMs have been calculated in the control points, raised to the fourth power and added, and the solution with the lowest errors both in SF and BM was then picked) to identify the best one between them (in Figure 13, all the “black dot” solutions of Figure 12 have been plotted in gray, the chosen one has been highlighted with red dots and compared with the target blue line).

  Figure 12. Best optimized solutions that verify all the test rig constraints (black dots).

  Figure 12. Best optimized solutions that verify all the test rig constraints (black dots).

  Figure 13. Comparison between the SFBMs target (blue), SFBMs of the optimized solutions (gray) and the selected one (red dots). Shear forces on the right (X–Y–Z from top to bottom) and bending moments on the left (X–Y–Z from top to bottom).

  Figure 13. Comparison between the SFBMs target (blue), SFBMs of the optimized solutions (gray) and the selected one (red dots). Shear forces on the right (X–Y–Z from top to bottom) and bending moments on the left (X–Y–Z from top to bottom).

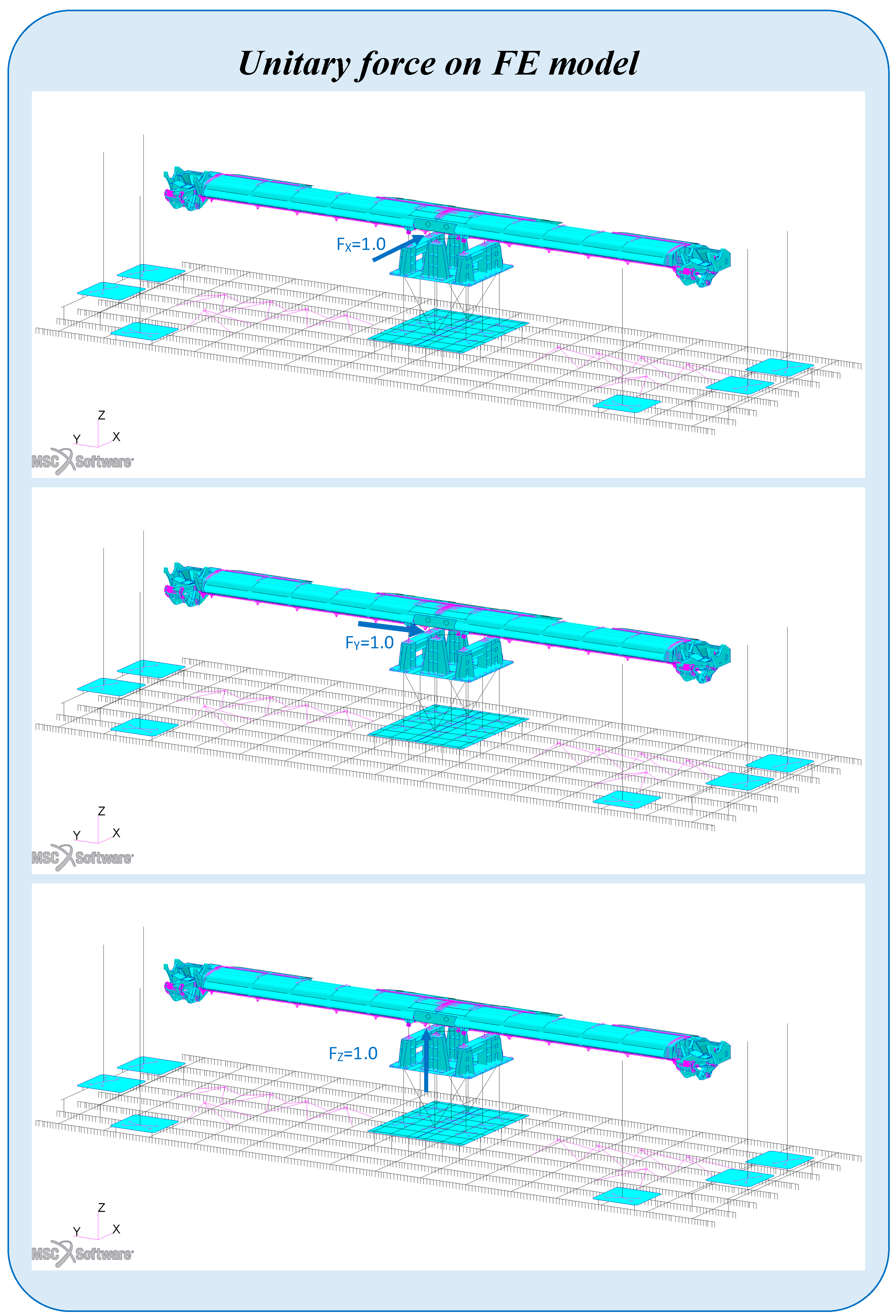
• Reaction forces matching (step 5): in the final step, a least square solution has been searched to match the forces at the interfaces through actuators placed at the wing root (actuators dedicated to this aim and not coincident with those used for the SFBMs reconstruction). An influence matrix C (forces at the interfaces generated by a unity force in each of the four additional internal actuators components) has been determined from the FEM model of the wing on the test rig. As depicted in the example in Figure 14, only the front right actuator is loaded with unit loads in all three directions. Subsequently, this procedure is repeated for all the loading points to obtain the influence matrix.

  Figure 14. Example of the FE model of the wing on the test rig subjected to unit loads in three directions to derive the influence matrix.

  Figure 14. Example of the FE model of the wing on the test rig subjected to unit loads in three directions to derive the influence matrix.

• A least squares solution for the system (2), where X represents the actuator forces and d represents the target interface forces, provides the solution.

$$CX=d$$

(3)

The target interface force components, those obtained through optimization and the differences between them are reported in Figure 15 for the interface force components different from zero.

5. Results

For the most demanding loads, the results are reported in terms of the matching between the SFBM diagrams, as in Figure 16. The blue lines represent the SFBMs target (those coming from the load analysis on the wing under test) and the red dots are the values obtained from the test rig configurations set up by the test department: the two matches with errors less than 5% (limit considered acceptable by the test department).

In more detail, the errors on the shear force and bending moment magnitude along the wing span are reported in the

Table 1. Errors on the shear force and bending moment magnitude along the wing span on the left side.

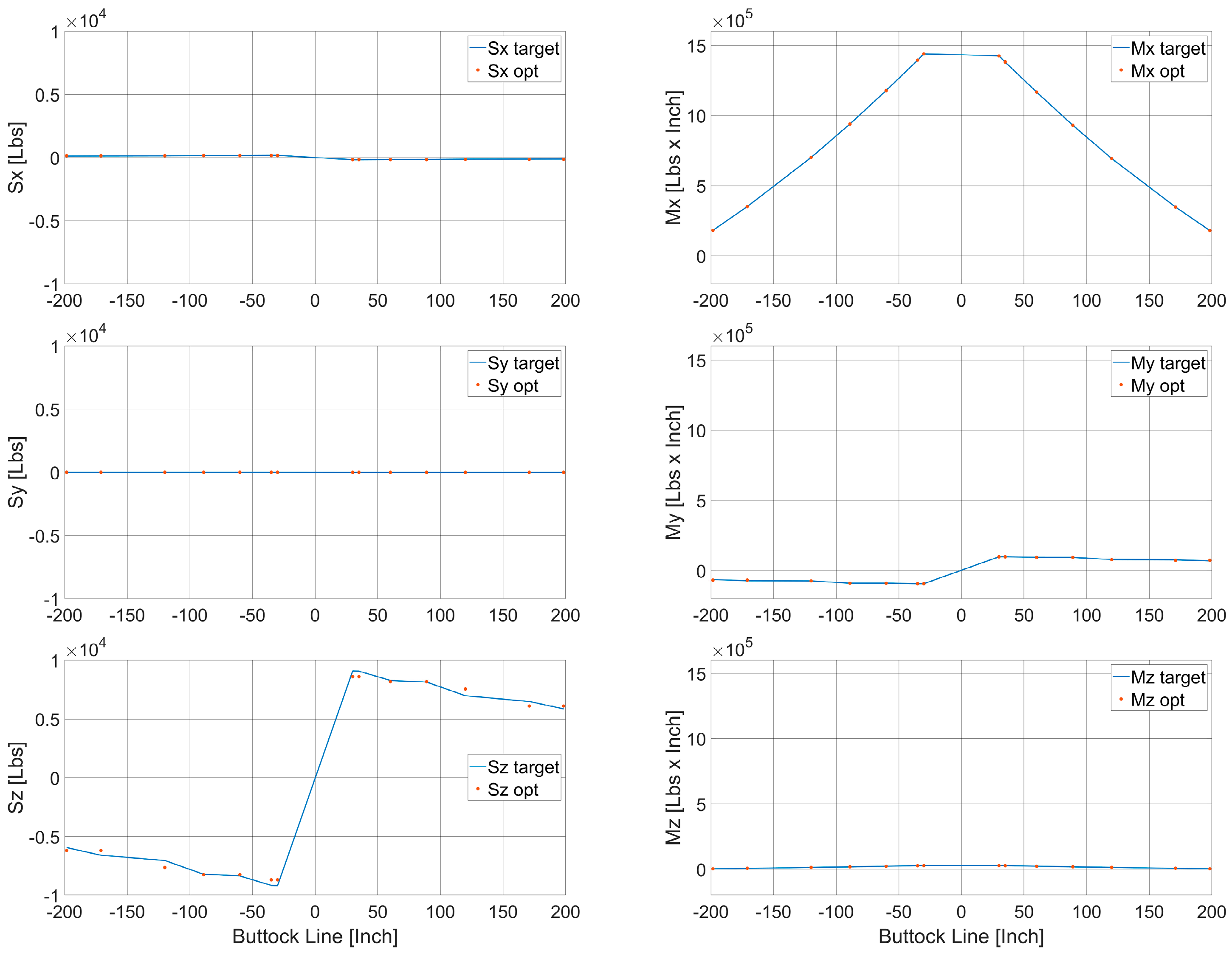
Spanwise Section (Left Side)	[Inch]	−198.4	−171	−120	−89	−60.1	−35	−30
	[mm]	−5039	−4343	−3048	−2261	−1527	−889	−762
Shear Force Magnitude	[Lbs]	6.19 × 103	6.19 × 103	7.63 × 103	8.25 × 103	8.25 × 103	8.68 × 103	8.68 × 103
	[N]	2.75 × 104	2.75 × 104	3.40 × 104	3.67 × 104	3.67 × 104	3.86 × 104	3.86 × 104
Shear Force Magnitude Relative Errors	[%]	−4.02%	6.49%	−7.78%	−0.42%	1.21%	5.57%	5.81%
Bending Moment Magnitude	[Lbs × Inch]	1.94 × 105	3.58 × 105	7.05 × 105	9.44 × 105	1.18 × 106	1.40 × 106	1.44 × 106
	[N × mm]	2.19 × 107	4.04 × 107	7.96 × 107	1.07 × 108	1.33 × 108	1.58 × 108	1.63 × 108
Bending Moment Relative Errors	[%]	−0.65%	0.20%	0.00%	0.00%	0.02%	−0.09%	0.07%

and

Table 2. Errors on the shear force and bending moment magnitude along the wing span on the right side.

Spanwise Section (Right Side)	[Inch]	30	35	60.1	89	120	171	198.4
	[mm]	762	889	1527	2261	3048	4343	5039
Shear Force Magnitude	[Lbs]	8.60 × 103	8.60 × 103	8.18 × 103	8.18 × 103	7.56 × 103	6.11 × 103	6.11 × 103
	[N]	3.83 × 104	3.83 × 104	3.64 × 104	3.64 × 104	3.36 × 104	2.72 × 104	2.72 × 104
Shear Force Magnitude Relative Errors	[%]	5.62%	5.50%	1.23%	−0.43%	−7.66%	6.27%	−4.04%
Bending Moment Magnitude	[Lbs × Inch]	1.43 × 106	1.39 × 106	1.17 × 106	9.35 × 105	6.98 × 105	3.55 × 105	1.95 × 105
	[N × mm]	1.61 × 108	1.57 × 108	1.32 × 108	1.06 × 108	7.89 × 107	4.02 × 107	2.20 × 107
Bending Moment Relative Errors	[%]	0.07%	−0.10%	0.02%	0.00%	0.00%	0.23%	−0.71%

respectively for the left and right side with a mean absolute error on the shear force equal to 4.43% and of 0.16% on bending moments.

The solution obtained by the outlined procedure also guarantees that the actual COTS actuators are able to deliver test loads to reproduce the SFBMs. As an example, a pictorial representation of the optimized solution in terms of the force vectors of the actuator loads is depicted in Figure 17 for one of the test conditions, namely IDT CASE 02 “Hard landing manoeuvre”.

The multi-level optimization process is repeated for all the loading conditions identified for the test, namely nine loading conditions, to qualify the wing structure. The pictures in “Figure 18, Figure 19 and Figure 20” depict the directions and positions of the actuators for each one of the nine qualification loading conditions.

By using such a rational approach that relies on optimization and on the deep understanding of both the rig and the test article behavior and mutual constraints, it can be argued that these results allow for fulfilling multiple objectives, such as the following:

• To minimize the actuator sizing and consequently to enhance safety of the test.
• To accommodate space constraints due to the overall rig size.
• To deliver to the lab personnel a suitable set of inputs on which to build and set up the test itself (e.g., actuator forces inputs to properly set up their activation, actuator positions in order to properly plan the change of setup between one test condition and the others)
• To minimize the overall time and costs connected to the whole qualification campaign.

The methodology presented in this paper can be easily applied to other types of rig and test articles, thus proving to be a powerful tool to ease and quicken the test rig deign and setup.

6. Conclusions

The optimized test rig setup plays a pivotal role in the qualification of aeronautical structures, particularly in the context of developing advanced composite wings for next-generation aircraft like the Civil Tiltrotor Demonstrator. By meticulously designing a test rig equipped with hydraulic jacks to accurately replicate critical load cases, the engineering team ensures the structural integrity and safety of the CFRP wing under various operating conditions.

The key achievements of this study lie in the meticulous identification of critical load cases through shear force/bending moment (SFBM) and failure mode analyses, the design and implementation of a dedicated test rig that minimizes the errors in diagram replication, and the utilization of an effective algorithm to optimize the test rig configuration. These achievements not only validate the structural performance of the CFRP wing but also contribute to advancing the field of aeronautical structure qualification.

The novelty of this research lies in the establishment of an optimization algorithm tailored to devise a test rig that addresses various constraints, including spatial limitations, actuator sizing, the quantity of actuators, and compliance with load applications. Consequently, this yields an effective and streamlined test rig design. Moreover, this methodology can be readily implemented for qualifying other structures, showcasing its efficacy in minimizing the workload during the definition phase of test setup.

In conclusion, the optimized test rig setup serves as a cornerstone in the qualification process of aeronautical structures, providing valuable insights into the behavior of composite wings and ensuring compliance with stringent airworthiness regulations. The meticulous design and implementation of the test rig underscores the commitment to safety, innovation, and excellence in aeronautical engineering. Moving forward, the lessons learned from this study can inform future research and development efforts in the aerospace industry, driving continuous improvement and resilience in aeronautical structure testing practices.