Precision Landing of Unmanned Aerial Vehicle under Wind Disturbance Using Derivative Sliding Mode Nonlinear Disturbance Observer-Based Control Method
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contribution
- We explored a nonlinear disturbance observer (NDOB) to design a DSMNDOBC. A derivative function is combined with the SMC to achieve dynamic and robust control. The derivative function can cancel out the overshoot effect, allowing the modeled system to achieve a satisfactory control performance. The SMC component has a fast dynamic response and immunity to changes in plant factors and provides an integration platform for estimated disturbance, such as random wind disturbance.
- The integrated NDOB has a low computational demand, with no need for supplementary sensors that can estimate and generate corrective control inputs for the annulment of random external disturbance effects.
- In numerical simulations, the proposed DSMNDOBC outperformed conventional proportional–derivative (PD) and SMC controllers with regard to altitude and attitude tracking.
1.4. Article Organization
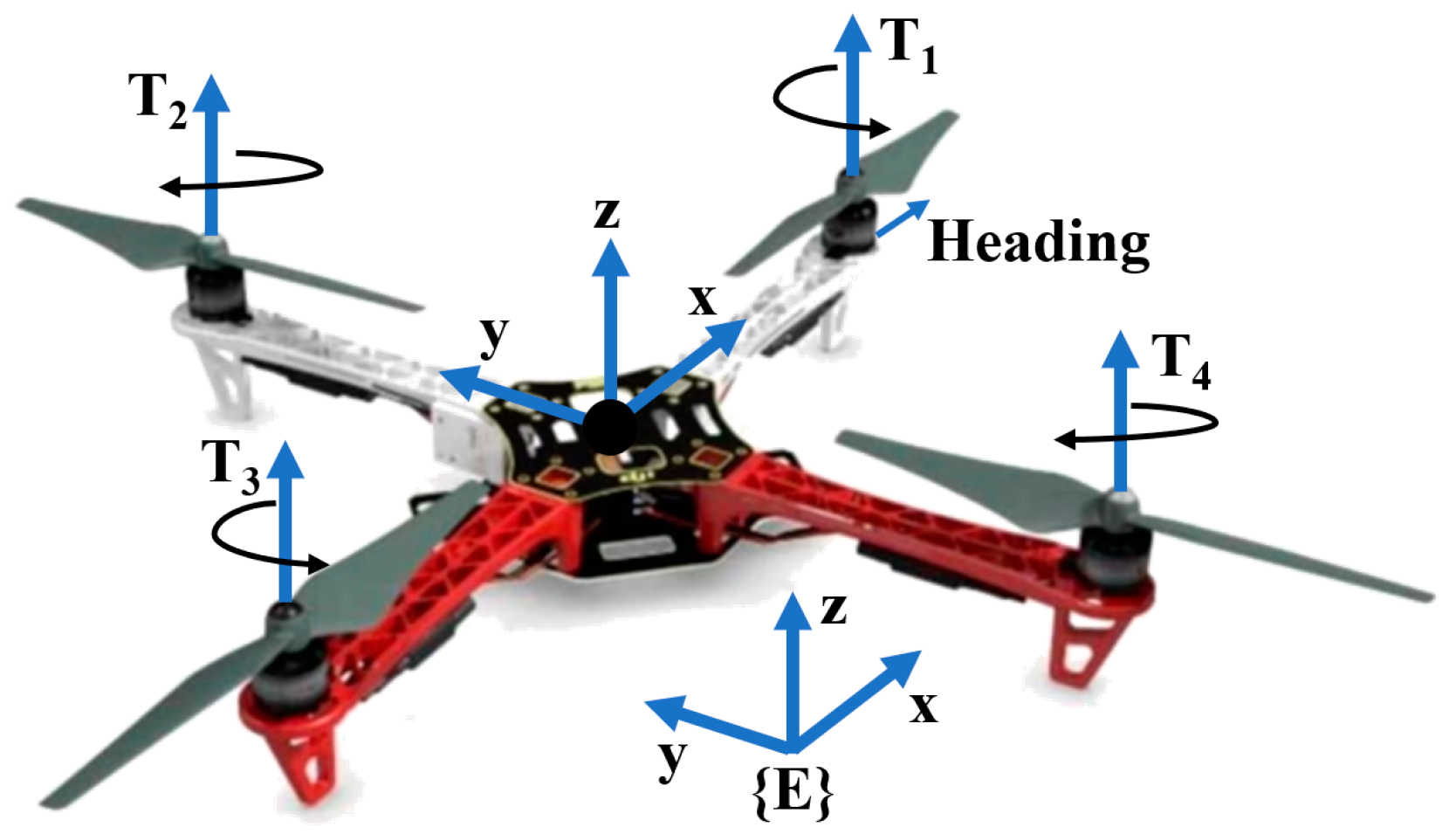
2. Quadrotor Dynamics
3. Precision Landing Control
- (1)
- A nonlinear composite controller centered on the SMC was designed to attain stability and satisfy additional performance requirements, with the hypothesis that the disturbance is quantifiable.
- (2)
- An NDOB was then built to estimate the disturbance.
- (3)
- The disturbance observer was integrated with a nonlinear controller by substituting the observer’s disturbance estimation into the control law.
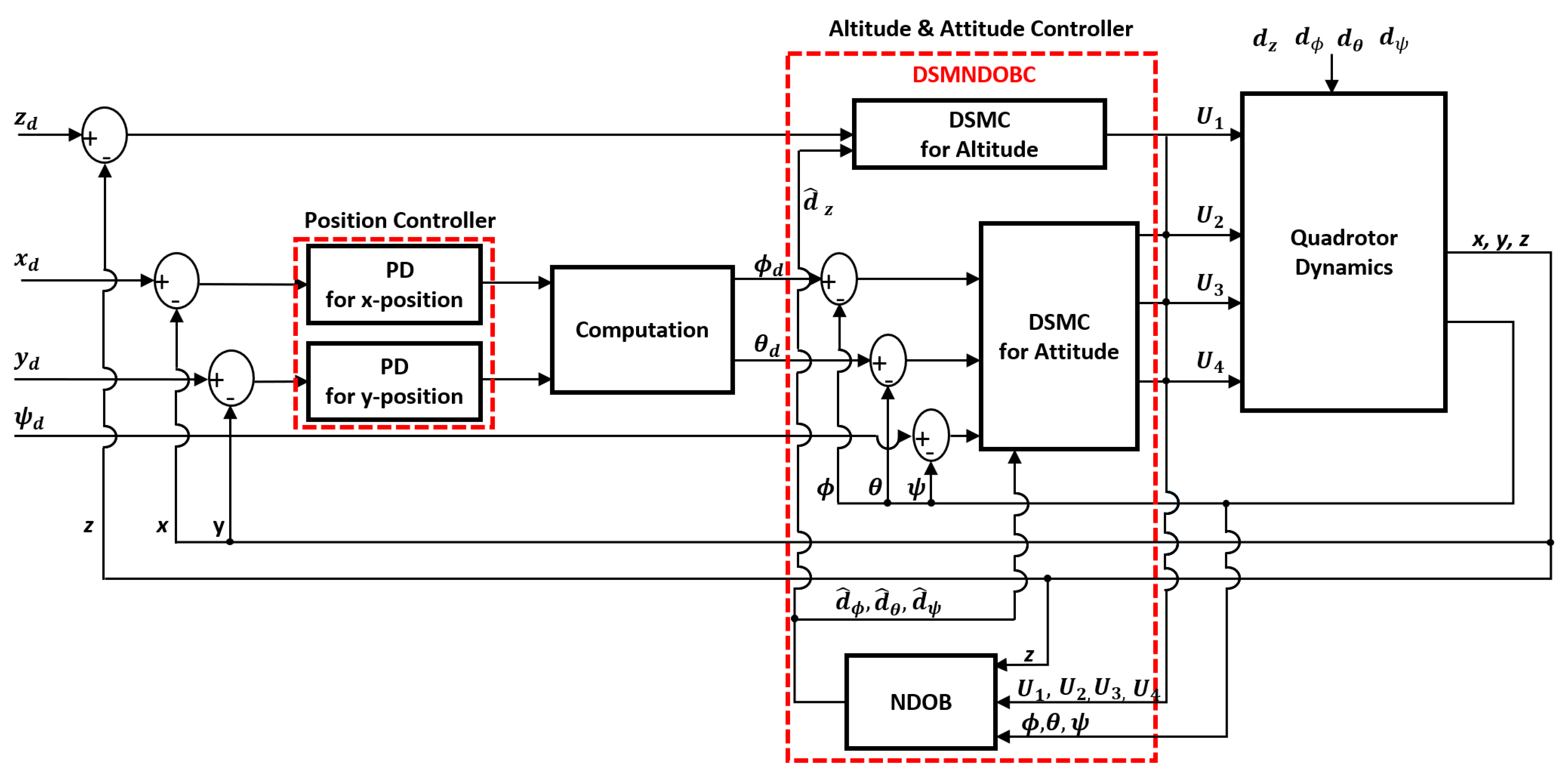
3.1. DSMNDOBC
- (1)
- NDOB
- (2)
- DSMC
3.2. PD Controller
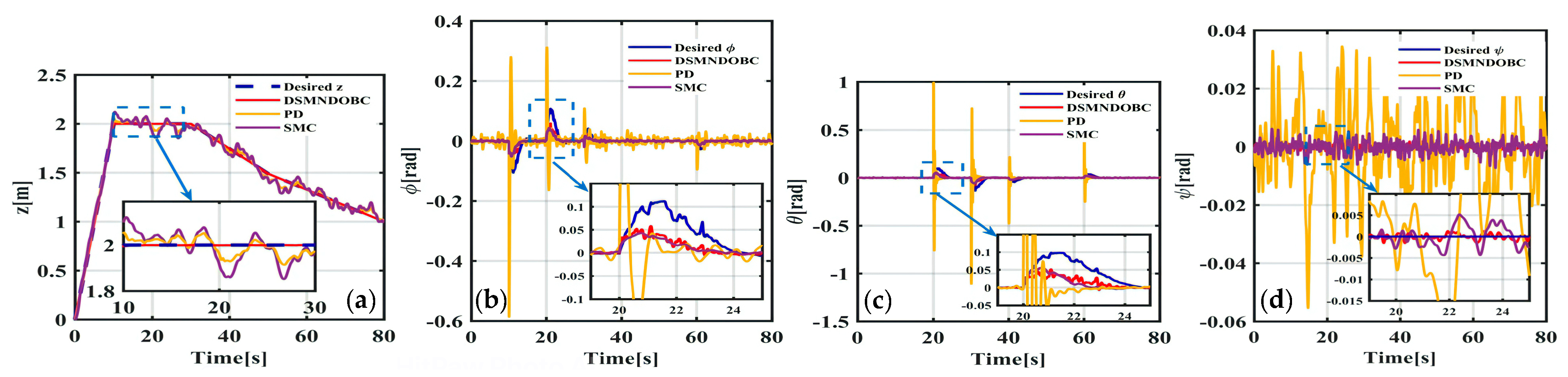
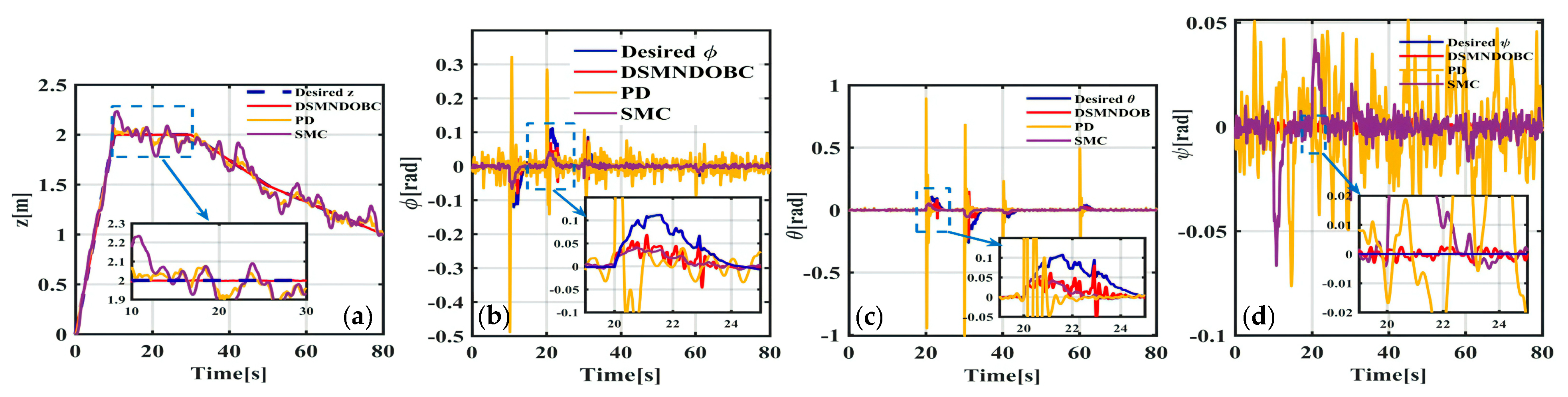
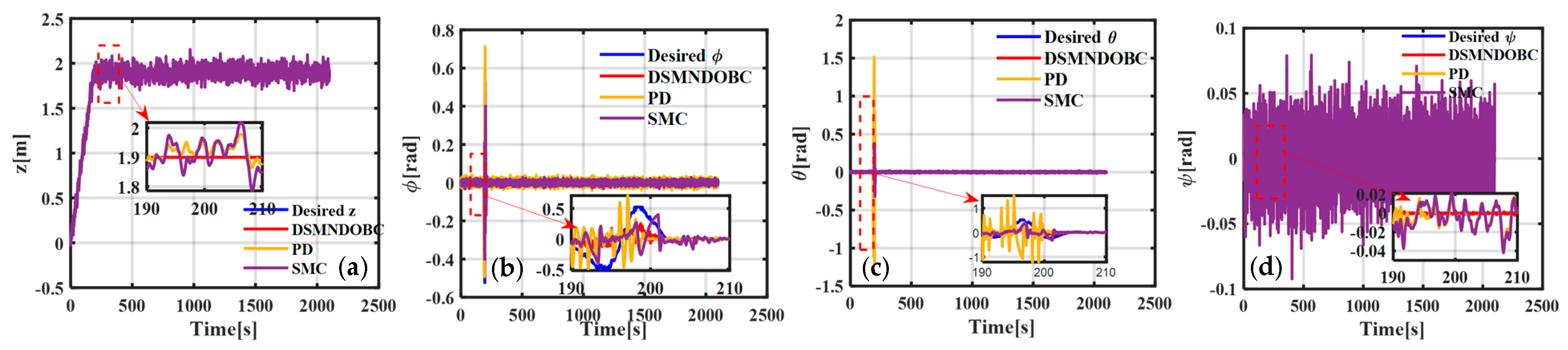
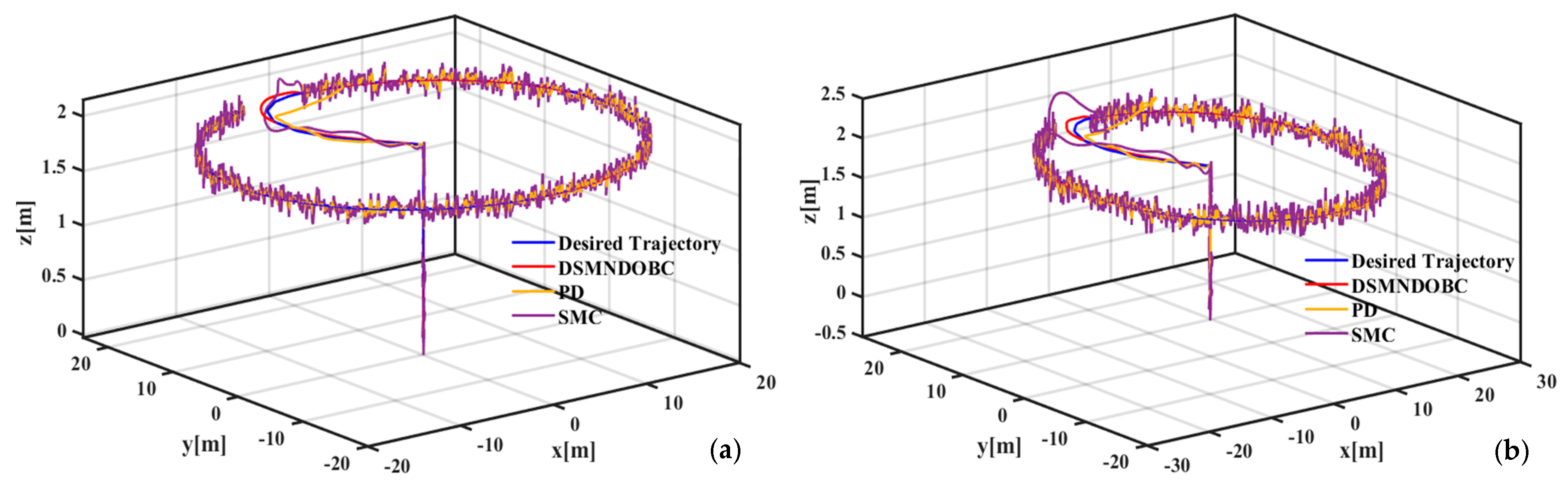
4. Simulation Results
4.1. Environmental Setup
4.2. Scenario
- (1)
- Scenario 1
- (2)
- Scenario 2
- (3)
- Scenario 3
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms
| DSMC | Derivative sliding mode control |
| DSMNDOBC | Derivative-sliding-mode nonlinear disturbance-observer-based control |
| GPS | Global positioning system |
| MPC | Model predictive control |
| NDOB | Nonlinear disturbance observer |
| NDOBC | Nonlinear disturbance-observer-based control |
| PD | Proportional derivative |
| PID | Proportional–integral–derivative |
| SMC | Sliding mode control |
| UAV | Unmanned aerial vehicle |
Nomenclature
| Force-to-moment coefficient | |||
| Horizontal distance between two opposite rotor axes | 0.32 | ||
| Vertical distance from the propeller surface to the ground | 0.65 | ||
| External wind disturbance | and | ||
| Disturbance observer estimation | |||
| Ground effects | |||
| Estimation error of NDOB | |||
| Smooth function | |||
| Smooth function | |||
| Smooth function | |||
| Smooth function | |||
| Gravitational acceleration | 9.81 | ||
| Inertial momentum | 0.0173, 0.0173, 0.0223 | ||
| Controller gain of DSMNDOBC | 5, 5, 5, 5 | ||
| Controller gain of DSMNDOBC | 30, 10, 10, 10 | ||
| Controller gain of DSMNDOBC | 50, 10, 10, 10 | ||
| Observer gain of DSMNDOBC | 30, 30, 30, 30 | ||
| Controller gain of PD | 4.0, 3.5 | ||
| Controller gain of PD | 3.5, 4.0 | ||
| Arm length | 0.225 | ||
| Quadrotor mass | 2.7 | ||
| Nonlinear function | |||
| Rotor radius | 0.127 | ||
| Time of arrival | |||
| Input vector | |||
| Frequency of the external wind disturbance | |||
| State vector | |||
| Output vector | |||
| Positions of the UAV in the inertial frame | |||
| Orientation of the UAV in the inertial frame | |||
| Desired positions of the UAV in the inertial frame | |||
| Desired orientation of the UAV in the inertial frame | |||
| Internal state variable of NDOB | |||
| Auxiliary variable of NDOB |
References
- Bashi, O.I.D.; Hasan, W.Z.W.; Azis, N.; Shafie, S.; Wagatsuma, H. Unmanned Aerial Vehicle Quadcopter: A Review. J. Comput. Theor. Nanosci. 2017, 14, 5663–5675. [Google Scholar] [CrossRef]
- Kangunde, V.; Jamisola, R.S.; Theophilus, E.K. A review on drones controlled in real-time. Int. J. Dyn. Control 2021, 9, 1832–1846. [Google Scholar] [CrossRef]
- Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Wang, S.; Polyakov, A.; Zheng, G. Quadrotor stabilization under time and space constraints using implicit PID controller. J. Frankl. Inst. 2022, 359, 1505–1530. [Google Scholar] [CrossRef]
- Koksal, N.; An, H.; Fidan, B. Backstepping-based adaptive control of a quadrotor UAV with guaranteed tracking performance. ISA Trans. 2020, 105, 98–110. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L.; Xie, X.; Iqbal, J. Theory and practice for autonomous formation flight of quadrotors via distributed robust sliding mode control protocol with fixed-time stability guarantee. Control Eng. Pract. 2022, 123, 105150. [Google Scholar] [CrossRef]
- Michel, N.; Bertrand, S.; Olaru, S.; Valmorbida, G.; Dumur, D. Design and flight experiments of a Tube-Based Model Predictive Controller for the AR.Drone 2.0 quadrotor. IFAC-PapersOnLine 2019, 52, 112–117. [Google Scholar] [CrossRef]
- Chandra, A.; Lal, P.P. Higher Order Sliding Mode Controller for a Quadrotor UAV with a Suspended Load. IFAC-PapersOnLine 2022, 55, 610–615. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.K.; Nguyen, N.P.; Ha, L.N.N.T.; Le, T.-L. Autonomous Quadcopter Precision Landing onto a Heaving Platform: New Method and Experiment. IEEE Access 2020, 8, 167192–167202. [Google Scholar] [CrossRef]
- Hordijk, B.J.P.; Scheper, K.Y.W.; de Croon, G.C.H.E. Vertical landing for micro air vehicles using event-based optical flow. J. Field Robot. 2017, 35, 69–90. [Google Scholar] [CrossRef]
- Goncalves, V.M.; McLaughlin, R.; Pereira, G.A.S. Precise Landing of Autonomous Aerial Vehicles Using Vector Fields. IEEE Robot. Autom. Lett. 2020, 5, 4337–4344. [Google Scholar] [CrossRef]
- Cabecinhas, D.; Naldi, R.; Silvestre, C.; Cunha, R.; Marconi, L. Robust Landing and Sliding Maneuver Hybrid Controller for a Quadrotor Vehicle. IEEE Trans. Control Syst. Technol. 2016, 24, 400–412. [Google Scholar] [CrossRef]
- Ho, H.W.; de Croon, G.C.H.E.; van Kampen, E.; Chu, Q.P.; Mulder, M. Adaptive Gain Control Strategy for Constant Optical Flow Divergence Landing. IEEE Trans. Robot. 2018, 34, 508–516. [Google Scholar] [CrossRef]
- Hu, B.; Lu, L.; Mishra, S. A Control Architecture for Time-Optimal Landing of a Quadrotor onto a Moving Platform. Asian J. Control 2018, 20, 1701–1712. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M. Autonomous Landing of a Quadrotor on a Moving Platform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1504–1519. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Sun, S.; Gupta, M.K.; Du, H.; Malekian, R.; Sotelo, M.A.; Li, W. Design a Novel Target to Improve Positioning Accuracy of Autonomous Vehicular Navigation System in GPS Denied Environments. IEEE Trans. Ind. Inform. 2021, 17, 7575–7588. [Google Scholar] [CrossRef]
- Hentschke, M.; de Freitas, E.P.; Hennig, C.H.; da Veiga, I.C.G. Evaluation of Altitude Sensors for a Crop Spraying Drone. Drones 2018, 2, 25. [Google Scholar] [CrossRef]
- Samir, M.; Assi, C.; Sharafeddine, S.; Ghrayeb, A. Online Altitude Control and Scheduling Policy for Minimizing AoI in UAV-assisted IoT Wireless Networks. IEEE Trans. Mob. Comput. 2022, 21, 2493–2505. [Google Scholar] [CrossRef]
- Yang, L.; Yao, H.; Wang, J.; Jiang, C.; Benslimane, A.; Liu, Y. Multi-UAV-Enabled Load-Balance Mobile-Edge Computing for IoT Networks. IEEE Internet Things J. 2020, 7, 6898–6908. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Ren, Y.; Han, Z.; Poor, H.V.; Hanzo, L. Age of Information in Energy Harvesting Aided Massive Multiple Access Networks. IEEE J. Sel. Areas Commun. 2022, 40, 1441–1456. [Google Scholar] [CrossRef]
- Jung, S.; Ariyur, K.B. Strategic Cattle Roundup using Multiple Quadrotor UAVs. Int. J. Aeronaut. Space Sci. 2017, 18, 315–326. [Google Scholar] [CrossRef]
- Chen, W.-H. Nonlinear Disturbance Observer Based Control for Nonlinear Systems with Harmonic Disturbances. IFAC Proc. Vol. 2001, 34, 329–334. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, X.; Zhang, L.; Tang, M. Disturbance rejection for nonlinear systems with mismatched disturbances based on disturbance observer. J. Frankl. Inst. 2017, 354, 4404–4424. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the Aerodynamic Ground Effect and Its Influence in Multirotor Control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications, 1st ed.; CRC Press—Taylor & Francis Group: New York, NY, USA, 2014; pp. 137–156. [Google Scholar]
- The Mathworks, Inc. Dryden Wind Turbulence Model (Continuous). Help Center. Available online: https://www.mathworks.com/help/aeroblks/drydenwindturbulencemodelcontinuous.html (accessed on 5 October 2023).
- Cahyadi, M.N.; Asfihani, T.; Mardiyanto, R.; Erfianti, R. Performance of GPS and IMU sensor fusion using unscented Kalman filter for precise i-Boat navigation in infinite wide waters. Geodesy Geodyn. 2023, 14, 265–274. [Google Scholar] [CrossRef]




| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| 10 | 0.0009 | 0.0345 | 0.0574 | |
| 0.0093 | 0.0397 | 0.0087 | ||
| 0.0150 | 0.0708 | 0.0159 | ||
| 0.0007 | 0.0149 | 0.0021 | ||
| 20 | 0.0011 | 0.0499 | 0.0932 | |
| 0.0163 | 0.0488 | 0.0171 | ||
| 0.0228 | 0.0752 | 0.0234 | ||
| 0.0014 | 0.0201 | 0.0033 |
| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| 10 | 0.0061 | 0.0913 | 0.1477 | |
| 0.0687 | 0.5862 | 0.0526 | ||
| 0.1158 | 1.0938 | 0.0807 | ||
| 0.0028 | 0.0554 | 0.0073 | ||
| 20 | 0.0065 | 0.1452 | 0.2361 | |
| 0.1122 | 0.4711 | 0.0941 | ||
| 0.3167 | 0.9928 | 0.2107 | ||
| 0.0056 | 0.0764 | 0.0119 |
| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| 0.0006 | 0.0374 | 0.0606 | ||
| 0.0215 | 0.0313 | 0.0490 | ||
| 0.0146 | 0.0408 | 0.0278 | ||
| 0.0007 | 0.0186 | 0.0209 | ||
| 0.0009 | 0.0541 | 0.0936 | ||
| 0.0235 | 0.0364 | 0.0609 | ||
| 0.0223 | 0.0465 | 0.0364 | ||
| 0.0013 | 0.0241 | 0.0265 |
| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| 0.0020 | 0.1283 | 0.2050 | ||
| 0.5311 | 0.4643 | 0.7864 | ||
| 0.4155 | 2.5710 | 0.6076 | ||
| 0.0029 | 0.0827 | 0.0923 | ||
| 0.0033 | 0.1949 | 0.3365 | ||
| 0.8845 | 1.4560 | 0.8014 | ||
| 2.8560 | 2.3060 | 0.7014 | ||
| 0.0057 | 0.1034 | 0.1150 |
| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| : +50% : +20% | 0.0011 | 0.0504 | 0.0905 | |
| 0.0154 | 0.0530 | 0.0163 | ||
| 0.0141 | 0.0810 | 0.0157 | ||
| 0.0014 | 0.0240 | 0.0033 | ||
| : −50% : −20% | 0.0011 | 0.0510 | 0.0905 | |
| 0.0152 | 0.0444 | 0.0162 | ||
| 0.0141 | 0.0681 | 0.0158 | ||
| 0.0014 | 0.0162 | 0.0033 |
| Condition | DSMNDOBC | PD | SMC | |
|---|---|---|---|---|
| : +50% : +20% | 0.0066 | 0.1483 | 0.2298 | |
| 0.1100 | 0.4707 | 0.0936 | ||
| 0.1691 | 1.0434 | 0.2513 | ||
| 0.0055 | 0.0913 | 0.0120 | ||
| : −50% : −20% | 0.0066 | 0.1477 | 0.2298 | |
| 0.1057 | 0.4837 | 0.1012 | ||
| 0.1690 | 1.1207 | 0.2513 | ||
| 0.0054 | 0.0614 | 0.0120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S. Precision Landing of Unmanned Aerial Vehicle under Wind Disturbance Using Derivative Sliding Mode Nonlinear Disturbance Observer-Based Control Method. Aerospace 2024, 11, 265. https://doi.org/10.3390/aerospace11040265
Jung S. Precision Landing of Unmanned Aerial Vehicle under Wind Disturbance Using Derivative Sliding Mode Nonlinear Disturbance Observer-Based Control Method. Aerospace. 2024; 11(4):265. https://doi.org/10.3390/aerospace11040265
Chicago/Turabian StyleJung, Sunghun. 2024. "Precision Landing of Unmanned Aerial Vehicle under Wind Disturbance Using Derivative Sliding Mode Nonlinear Disturbance Observer-Based Control Method" Aerospace 11, no. 4: 265. https://doi.org/10.3390/aerospace11040265
APA StyleJung, S. (2024). Precision Landing of Unmanned Aerial Vehicle under Wind Disturbance Using Derivative Sliding Mode Nonlinear Disturbance Observer-Based Control Method. Aerospace, 11(4), 265. https://doi.org/10.3390/aerospace11040265






