Lunar Rover Collaborated Path Planning with Artificial Potential Field-Based Heuristic on Deep Reinforcement Learning

Abstract

The International Lunar Research Station, to be established around 2030, will equip lunar rovers with robotic arms as constructors. Construction requires lunar soil and lunar rovers, for which rovers must go toward different waypoints without encountering obstacles in a limited time due to the short day, especially near the south pole. Traditional planning methods, such as uploading instructions from the ground, can hardly handle many rovers moving on the moon simultaneously with high efficiency. Therefore, we propose a new collaborative path-planning method based on deep reinforcement learning, where the heuristics are demonstrated by both the target and the obstacles in the artificial potential field. Environments have been randomly generated where small and large obstacles and different waypoints are created to collect resources, train the deep reinforcement learning agent to propose actions, and lead the rovers to move without obstacles, finish rovers’ tasks, and reach different targets. The artificial potential field created by obstacles and other rovers in every step affects the action choice of the rover. Information from the artificial potential field would be transformed into rewards in deep reinforcement learning that helps keep distance and safety. Experiments demonstrate that our method can guide rovers moving more safely without turning into nearby large obstacles or collision with other rovers as well as consuming less energy compared with the multi-agent A-Star path-planning algorithm with improved obstacle avoidance method.

1. Introduction

The International Lunar Research Station will be established after 2030 [1]. Initially, the construction of this station is facilitated by advanced lunar rovers outfitted with robotic arms. Traditional planning methods are mainly based on ground control by creating and verifying all human instructions [2]. However, this approach is inadequate given the dynamic lunar environment, particularly the partially observable lunar surface. Furthermore, the construction of the lunar station contains heavy tasks, such as carrying large cargo and collecting resources in a specific time, which cannot be completed with one single rover. Although collaborative planning among multiple rovers could address this challenge, it requires a considerable cadre of trained engineers and is inherently inefficient [3]. Consequently, there arises a critical need for automated path-planning methodologies that enable collaborative efforts among rovers, therefore enhancing the efficiency of lunar station construction.

An imperative challenge lies in devising a sequence of actions to guide rovers toward their targets within partially unknown environments. To address this, engineers have developed various planning systems tailored for spacecraft and rovers. Automated Scheduling and Planning Environment (ASPEN), formulated by NASA, generated activity sequences for one spacecraft with constraints on resources and operating rules [4]. The Japan Aerospace eXploration Agency (JAXA) has introduced a path-planning algorithm [5] that prioritizes decision-making considering the limitations of sunlight rather than simply avoiding obstacles. GPS-based path planning algorithm [6] is proposed for rovers to generate paths in difficult terrain. However, a mature positioning system for lunar environments has yet to be developed. The ant colony algorithm [7] is adapted for the global path planning of lunar rovers, but this approach necessitates waiting for convergence before generating the entire path.

In the dynamic path-planning environment for lunar rovers, actions may fail due to unforeseen situations, such as navigating at low speeds or traversing novel pathways, particularly in instances where rovers encounter restricted visibility. The planning systems mentioned above cannot react quickly to unforeseen situations on lunar rovers. However, recent studies in planning have emerged that leverage learning capacity. Prominent among these are reinforcement learning (RL) and deep reinforcement learning (DRL), which merge neural networks with traditional RL paradigms. These innovative approaches hold promise in enhancing the adaptability and responsiveness of lunar rover path-planning strategies.

Deep Reinforcement Learning (DRL) [8] is a general framework for adaptive decision-making, as it leverages the ability of an agent to autonomously interact with the environment and refine its decision-making processes to maximize cumulative rewards. It can explore complex and uncertain environments, relying on feedback mechanisms derived from a sequence of elemental reward signals rather than prescriptive human-designed rules. Minh et al. presented the deep Q network algorithm (DQN) model [9], which represents a milestone in the fusion of deep learning with reinforcement learning methodologies. The advent of the DQN model heralded a pivotal era in the evolution of reinforcement learning techniques.

Scholars across diverse disciplines have embraced the utilization of deep reinforcement learning. Fisac et al. [10] studied human motion safety models, analyzing the positions and velocities of humans and robots and treating human behavior deviations as contingencies. DRL was employed to facilitate swift adaptation to the environment, aiding in rapid path planning or collaboration with humans in aerial vehicles. Yu et al. [11] demonstrate the DRL application with safety constraints in end-to-end path planning on lunar rovers but without consideration of collaborative planning among rovers. Park et al. [12] apply the DRL on failure-safe motion planning for four-wheeled two-steering lunar rovers, although its efficacy in long-term planning remains questionable. Hu et al. [13] integrated the DRL with a long-short time memory(LSTM) network for obstacle avoidance, yet this approach was not extended to scenarios involving multiple rovers. Wei et al. [14] utilize multi-robots for environmental data collection, whose paths are generated by Independent Q-Learning. Results show that Independent Q-Learning performs better than Joint Action Q-Learning when there are more robots. Chen et al. [15] refined the Multi-Agent Proximal Policy Optimization method for three-dimensional path planning in unmanned aerial vehicles. Saqib et al. [16] implement Q-Learning alongside a Wall Follower algorithm to navigate mazes effectively.

Moreover, DRL planning may suffer from slow and long path planning, even low-security concerns [17]. To address these challenges, heuristics have been integrated into DRL frameworks to enhance search speed and circumvent local optima. Hu et al. proposed SP-ResNet [18], a methodology aimed at accelerating planning speeds relative to conventional search and sampling-based techniques. Within this framework, double branches of residual networks are employed to abstract global and local obstacles, therefore constraining the search space for the DRL agent and serving as a heuristic. Heuristically accelerated reinforcement learning [19] has also been developed and applied to contingency planning within complex dynamic environments, such as spacecraft traversing between planets. This heuristic aids in generating an initial estimate for a reference solution, a process traditionally reliant on human intuition, before subsequent numerical adjustments. Path planning around the lunar poles [20] employed heuristics to expedite search processes and reduce planning duration and resource consumption during transformations near lunar poles. Two tuning parameters in the heuristics balance solution quality with runtime when considering energy. The speed gains did not significantly sacrifice path quality. Artificial potential field (APF) is used in motion planning for safe autonomous vehicle overtaking [21] as the velocity difference potential field and acceleration difference potential field, which influence the path planning as heuristic. This approach enhances the feasibility and effectiveness of overtaking maneuvers in automated driving scenarios.

Although DRL has significantly been developed, most of the research in DRL does not perform well with obstacles or multiple rovers because rovers can be obstacles to each other. Path-planning methods must wait for convergence, which will not perform well when navigating uncharted lunar terrains. In response to these challenges, heuristic methods have emerged, primarily aimed at expediting training processes or reducing time and resource consumption. In our study, we propose an innovative approach that combines artificial potential fields with deep reinforcement learning as a heuristic, facilitating collaborative path planning for multiple rovers within a simulated lunar environment. Our novelty lies in two points: the first is the combination heuristic of small obstacles, large obstacles, the target, and other rovers, while the second is the design of rewards. This heuristic ensures that rovers maintain dynamic distances from large obstacles and other rovers while also optimizing paths to navigate small obstacles without significantly increasing path length. Additionally, we integrate heuristic information about the target destination into the DRL framework, providing dense rewards during target search periods. Second, we devise a methodology that combines path information derived from heuristics with task-related rewards obtained at the target destination. This hybrid approach ensures that rovers move safely while fulfilling their collection and delivery objectives.

The structure of the article is described below. Section 2 demonstrates the definition of the path-planning problem, the construction of lunar surface featuring various sizes of obstacles, places for mining, and the station to handle or blend the above materials. Furthermore, this section elucidates our methodology for representing the environment during Deep Reinforcement Learning (DRL) training. Section 3 mainly proposes the dissimilarity between multi-agent reinforcement learning and traditional single-agent reinforcement learning. We detail our approach to addressing the challenges posed by multi-agent scenarios, wherein the Artificial Potential Field (APF) method serves as a heuristic to enhance obstacle avoidance and rover navigation within the DRL framework. Additionally, this section discusses the planning agent’s capability to generate actions encompassing waiting, collection, and material processing beneath the blending apparatus, therefore serving as a task planner. In Section 4, comprehensive experiments of training and testing are proposed to show the adaptation of different obstacles out of view while finishing the task of collection and processing at the same time. Finally, the conclusions are provided in Section 5.

2. Modeling for the Lunar Environment

This section describes our consideration of the environment from the lunar surface, which is all designed as geometry points with extra flags or information.

2.1. Specification of the Lunar Environment

The lunar environment can be specified as follows. Suppose that there are N rovers, $N_m$ mining sites that contain $N_m^{\prime }$ types of materials to collect. The blender can accept $N_{rb}$ rovers once at a time, and $N_{mb}$ types of materials are about to be handled together, leading to cooperation. Please note that $N_{mb}\le N_{rb}$ is necessary, or our blender cannot handle this task. A rover will cost b power to move one distance with a constant speed v. If the rover i selects to collect resources at the j mining site, it will spend $D_{ij}$ distance and $t_{ij}$ time to arrive at the mining site. $D_k$ and $t_k$ will be used from the k-th mining site to the blender. The max power in the rover i is $B_i$. Therefore, the problem above can be expressed as follows:

$$\begin{array}{c}min{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^{N_m}}\left(D_{ij}+c_1{t}_{ij}\right)+{\displaystyle \sum _{k=1}^{N_m}}\left(D_k+c_2{t}_k\right)\hfill \\ s.t.\left\{\begin{array}{c}{N}_{mb}\le N_{rb}\\ {\displaystyle \prod _{i=1}^N}b{t}_i\le B_i=true\end{array}\right.\hfill \end{array}$$

(1)

Furthermore, rovers will depart from different points, but the time difference between arriving at the blender should be as short as possible. The entire environment can be represented as Figure 1.

There are variable types of obstacles on the moon’s surface: small rocks, large rocks, small craters, and large craters. For small rocks and small craters, lunar rovers can go across or step in and out easily, which only needs more energy. Therefore, they would not inhibit any action except consuming more energy for this kind of obstacle. In contrast, large rocks and large craters present significant challenges and hazards. Once rovers come across or come near, they may not move across, even fall off the craters, or must move backward because of the lack of power, which influences the function of the rovers. These two obstacles are about to be bypassed, as shown in Figure 2. When confronted with small obstacles, rovers may opt to maneuver around them or proceed directly through them, albeit at the expense of increased time and resource consumption. However, when encountering large obstacles, rovers must prioritize navigating around them to ensure a safe pass.

2.2. The Way of Simulating in the Deep Reinforcement Learning Environment

Since not all pieces of information can be expressed precisely in training, we have designed a framework to represent the environment in the simulated environment. This framework employs a grid-based system to delineate the environment, enabling the accurate recording of rovers, mining sites, blenders, and obstacles based on their respective coordinates and supplementary information. For example, points for mining sites and blenders will be marked as “mineX” and “mix” where X represents the number of the mining site. The positions of the rovers are indicated as ‘roverX’. Definitions of points are in

Table 1. Representation of different points.

Name	Mark or Value
Mining site	“mineX”
Blender	“mix”
Rover	“roverX”
Small obstacles	1
Large obstacles	2
Other accessible points	0

. Additionally, waypoints within the grid are categorized into three distinct types based on the presence and magnitude of obstacles: waypoints designated as 0 denote normal navigable points, allowing rover access without hindrance; those labeled as 1 denote waypoints obstructed by small obstacles, requiring additional energy expenditure for traversal; whereas waypoints marked as 2 denote locations obstructed by large obstacles, rendering them impassable to rovers. Each obstacle is represented by a cluster of adjacent waypoints, which may consist of one or multiple waypoints depending on the obstacle’s size and configuration. We consider the rover moving in four different directions, i.e., if the rover’s position is $(x,y)$, the next position without considering obstacles can be $(x+1,y),(x-1,y),(x,y-1),(x,y+1)$.

To simulate the uncertainty of our environment, two methods are set up to ensure that the DRL agent is adapted to the uncertain environment. First, obstacles are generated randomly, regardless of position or size, indicating that rovers may adapt to different situations or terrain. Second, to simulate the vision on the moon, the environment is restricted to each rover’s path planning, which indicates that rovers can only obtain the target waypoint and the status nearby (within several grids). It can be expressed as follows. For the rover i, the information the rover can obtain is $<W_t,W_n>$.

$$W_n=[W_1,W_2,...,W_{(2n+1)\times (2n+1)}]$$

(2)

The rover can obtain the grid n steps nearby, so the vision is considered to be a $(2n+1)\times (2n+1)$ square. In this way, the agent can guide the rover to complete the mining and mixing in a highly uncertain environment.

3. Multi-Agent Deep Reinforcement Learning with APF

This section will establish a heuristic adaptation based on the existing multi-agent deep reinforcement learning to guide and plan for rovers to mine and produce the materials.

3.1. Deep Reinforcement Learning Overview

For the timestep t that starts from 0, the environment provides the agent with an observation $S_t$, and the agent responds by selecting an action $A_t$. Then, the environment provides the next reward $R_{t+1}$ and state $S_{t+1}$, where the discount ${\gamma }_{t+1}$ is set as a hyper-parameter. This progress is the Markov Decision Process (MDP), represented by a tuple $<S,A,T,R,\gamma >$. S is a finite set of states, A is a finite set of actions, T in Equation (3) is the transition function or stochastic transition function.

$$T(s,a,s^{\prime })=P[S_{t+1}=s^{\prime }|s,a]$$

(3)

R in Equation (4) is the reward function of the current states and the next step action. $\gamma \in [0,1]$ is the discount factor.

$$R(s,a)=E\left[R_{t+1}\right|S_t=s,A_t=a]$$

(4)

The DQN algorithm is established based on MDP [9]. A neural network has been used to express the policy $\pi (s,a)$ from a replay memory buffer that holds the last certain number of transitions, i.e., $(S_t,A_t,R_{t+1},{\gamma }_{t+1},S_{t+1})$. The parameters of the neural network are optimized using stochastic gradient descent to minimize the loss

$${\left(R_{t+1}+{\gamma }_{t+1}\underset{a^{\prime }}{max}{q}_{\theta }^{\prime }\left(S_{t+1},a^{\prime }\right)-q_{\theta }\left(S_t,A_t\right)\right)}^2$$

(5)

where t is the time step, ${\theta }^{\prime }$ represents the neural network parameters or the network policy from the target network, $q_{\theta }^{\prime }$ is the Q value through policy ${\theta }^{\prime }$, and $\theta$ represents the ones from the online network, $q_{\theta }$ is the Q value through policy $\theta$, which is exactly the training and updating network.

3.2. Adaptation for Multi-Agent

The multi-agent reinforcement learning can be represented as a tuple

$$<X,U_1,...,U_n,T,R_1,...,R_n>$$

(6)

where n is the number of agents. X is the discrete set of environment states, $U_i,i=1,\dots ,n$ describe the discrete sets of actions available to the agents, which produces the joint action set $\mathbf{U}$.

$$\mathbf{U}=U_1\times ...\times U_n$$

(7)

T is the state transition probability function.

$$T:\mathbf{X}\times \mathbf{U}\times \mathbf{X}\to [0,1]$$

(8)

R are the reward functions of the agents.

$$R:\mathbf{X}\times \mathbf{U}\times \mathbf{X}\to \mathbb{R},i=1...n$$

(9)

However, T can be programmed in different ways. T can be trained and stored in one neural network, which is like the centralized policy, or in a separate neural network kept by each agent for one piece, which is like the decentralized policy.

Similarly, various approaches can be adopted to determine the action set $\mathbf{U}$. In the first approach, utilizing a single neural network, actions can be provided simultaneously. This entails the neural network generating an output vector with a length greater than one, encompassing multiple actions at once. Alternatively, actions can be decided cyclically, with each action being determined sequentially. This sequential decision-making process does not significantly impact time-sensitive environments, as it operates swiftly. There is another way that actions are decided only when necessary, such as when the former durative action is made. Even in decentralized scenarios, where decision-making may be distributed across multiple agents, these decision-making methods can still be applied. However, in decentralized settings, communication patterns may vary, particularly if communication costs are high. Differences between the list of the modes in

Table 2. Differences among the decision mode.

Policy Mode	Action Sequence Mode	Pros	Cons
Centralized	Simultaneous	Good for time-sensitive decision	Modify the neural network and cannot use ways in single agent
	Cycling	Easy to code and use	Cannot decide instantly
	Conditional	Flexible, can deal with complex problems	Hard to design the planning system
Decentralized	Simultaneous Cycling Conditional	Pressure of decision can be separated to multiple devices	Need time and bandwidth for communication

. We select the centralized and cycling decision mode in this article.

3.3. Improvements of the Multi-Agent Policy

In this work, we choose to use the centralized model with the decision to action the cycling because we do not design the time for each action, so the decision model the cycling is acceptable.

Usually, the observation of the environment will be designed separately for each rover. However, we compress the observation to minimize the data input by removing the repeated information from the rovers.

We define that the position of the i-th mining site is $P_m^i$, the position of the i-th rover is $P_r^i$, the position of the blender is $P_b$, and the positions of the 8 nearby points of the i-th rover are ${\mathbf{P}}_{ra}^i$.$C_i$ represents whether the collection of the i-th rover is prepared. The origin input ${\mathbf{O}}_{\mathbf{I}}$ of the centralized cycling way is:

$$o_i=<{\mathbf{P}}_{ra}^i,P_r^i,P_b,<P_m^1,...,P_m^{N_m}>,C_i>$$

(10)

$${\mathbf{O}}_I=[o_1,...,o_N]$$

(11)

Please note that the $P_b$ and $P_m^i$ are duplicated in all the $o_i$ so we can use one of these inputs because we use the centralized model, which becomes:

$${\mathbf{O}}_I=<{\mathbf{P}}_{ra},{\mathbf{P}}_r,P_b,{\mathbf{P}}_m,\mathbf{C}>$$

(12)

In this way, the representation of the environment will be largely compressed, and it will benefit training.

3.4. APF as Heuristic in DRL

Rovers can avoid obstacles while moving in the environment because the DRL agent has gained experience with different decisions in different situations. Nevertheless, while the agent prioritizes the shortest path, the resultant trajectory may not always ensure rover safety. There exists the risk of the path being in close proximity to large obstacles or leading to collisions with other rovers. To address this concern, we advocate for the integration of APF as a heuristic within the training process, guided by rewards. This heuristic aids in directing the search and training efforts, ensuring that the generated paths prioritize safety alongside efficiency.

The heuristic can be represented as:

$$\hslash ={\alpha }_l{\hslash }_l+{\alpha }_s{\hslash }_s+{\alpha }_r{\hslash }_r+{\alpha }_t{\hslash }_t$$

(13)

where $\alpha$ represents the rate of each heuristic. For a waypoint $P=(P_x,P_y)$, the heuristics ${\hslash }_l\left(P\right),{\hslash }_s\left(P\right),{\hslash }_r\left(P\right),{\hslash }_t\left(P\right)$ are as follows.

${\hslash }_l$ represents the heuristic of large obstacles, combined as a repulsive potential that influences a short distance but a large gradient. The purpose of ${\hslash }_l$ is to make rovers move away from the obstacles, especially when they become near enough. ${\hslash }_l$ is given by a repulsive artificial potential field $U_l\left(q_o\right)$ where $q_o$ is the distance between the rover and a large obstacle $o_l$ among all large obstacles $O_l$. $F_l$ is the force generated by the field $U_l$.

$$U_l\left(q^o\right)=\left\{\begin{array}{cc}\frac{1}{2}{K}_l{(\frac{1}{q_o}-\frac{1}{D_l})}^2& ,q_o\le D_l\\ 0& ,q_o>D_l\end{array}\right.$$

(14)

$${\hslash }_l=-\sum _{o\in O_l}{F}_l\left(q_o\right)=-\sum _{o\in O_l}-\nabla U_l\left(q_o\right)=\sum _{o\in O_l,q_o<D_l}{K}_l\left(\frac{1}{D_l}-\frac{1}{q_o}\right)\frac{1}{{\left(q_o\right)}^2}$$

(15)

${\hslash }_s$ represents the heuristic of small obstacles, combined as a repulsive potential that influences a long distance but a small gradient. The purpose of ${\hslash }_s$ is to make rovers move away from the obstacles. However, when rovers need to choose a long way to move around small obstacles, the energy of moving across the small obstacles may be lower than moving around. ${\hslash }_l$ is given by a smaller repulsive artificial potential field $U_s\left(q_o\right)$ where $q_o$ is the distance between the rover and a small obstacle $o_s$ among all small obstacles $O_s$.

$$U_s\left(q^o\right)=\left\{\begin{array}{cc}\frac{1}{2}{K}_s{(\frac{1}{q_o}-\frac{1}{D_s})}^2& ,q_o\le D_s\\ 0& ,q_o>D_s\end{array}\right.$$

(16)

$${\hslash }_s=-\sum _{o\in O_s}{F}_s\left(q_o\right)=-\sum _{o\in O_s}-\nabla U_s\left(q_o\right)=\sum _{o\in O_s,q_o<D_s}{K}_s\left(\frac{1}{D_s}-\frac{1}{q_o}\right)\frac{1}{{\left(q_o\right)}^2}$$

(17)

${\hslash }_r$ represents the heuristic of other rovers, combined as a repulsive potential that influences a short distance but a large gradient. The purpose of ${\hslash }_r$ is to keep the rovers away from each other. When rovers become next to each other in areas except collaboration areas, such as the mixture area, the ${\hslash }_r$ will be given in a short distance. ${\hslash }_r$ is provided by a small size large gradient repulsive artificial potential field $U_r\left(q_i\right)$ where $q_i$ is the distance between the i-th rover, $q_{\downarrow }$ is the minimum distance among all rovers.

$$U_r\left(q_i\right)=\left\{\begin{array}{cc}\frac{1}{2}{K}_r{(\frac{1}{q_i}-\frac{1}{D_r})}^2& ,q_i\le D_r\\ 0& ,q_i>D_r\end{array}\right.$$

(18)

$${\hslash }_r=-ma{x}_{i\in N}{F}_r\left(q_i\right)=ma{x}_{i\in N}\nabla U_r\left(q_i\right)=\left\{\begin{array}{cc}{K}_r\left(\frac{1}{D_r}-\frac{1}{q_{\downarrow }}\right)\frac{1}{q_{\downarrow }^2}& ,q_{\downarrow }\le D_r\\ 0& ,q_{\downarrow }>D_r\end{array}\right.$$

(19)

${\hslash }_t$ represents the current target heuristic, combined as an attractive potential. The purpose of ${\hslash }_t$ is to lead the rover to the target through a one-time given heuristic at different distances. ${\hslash }_r$ is provided by a quadratic curve and a linear artificial potential field $U_t\left(q_t\right)$ where $q_t$ is the distance between the rover and the current target.

$$U_t\left(q\right)=\left\{\begin{array}{cc}\frac{1}{2}{K}_t{q}_t^2& ,q_t\ge D_t\\ D_t{K}_t{q}_t-\frac{1}{2}{K}_t{D}_t^2& ,q_t<D_t\end{array}\right.$$

(20)

$${\hslash }_r=-F_r\left(q_t\right)=\nabla U_r\left(q_t\right)=\left\{\begin{array}{cc}{K}_t{q}_t& ,q_t\ge D_t\\ K_t{D}_t& ,q_t<D_t\end{array}\right.$$

(21)

3.5. Path-Planning Method Based on the Rainbow DQN

Our planning problem has discrete action and state spaces where DQN is widely used. We choose the most developed DQN algorithm, called Rainbow DQN [22], which combines several improved DQN algorithms into one algorithm and performs well in multiple environments. The basic framework of Rainbow DQN and the combination of heuristics of Section 3.4 are shown in Figure 3. The agent samples or predicts an action from the environment in which the state and the reward are generated and stored in the replay memory buffer with the action. Then the agent gains $<s,a,r,s^{\prime }>$ from the buffer and calculates the two Q-values through the network parameters ${\theta }_p$ and ${\theta }_t$, respectively, then the loss. Loss generates the gradient $\Delta {\theta }_p$ and updates the Q-Predict Net through back-propagating. Q-Predict Net and Q-Target Net share the same network structure so that Q-Predict Net can update itself through parameter copying. The heuristics are considered to be rewards in the training period, which leads rovers away from obstacles and each other while leading to the targets.

When the agent leads rovers to mining and blending, actions will be decided and recorded, which can be defined as action sequences. The action sequences are the solution to the planning problem, described as the actions transforming the environment from the initial states to the target states.

4. Experiments

This section simulates the methods proposed in this paper for lunar rovers collaborated operation with uncertainty through deep reinforcement learning. First, considering the real-world tasks for exploring lunar rovers, we establish the training and validating environment of the simulated DRL environment. Second, training and validation curves are provided to prove the effectiveness of training.

4.1. Environment Establishment

We establish an environment with two rovers and two mining sites, which contain different materials in each site. One blender and 80 obstacles where the ratio of small and large obstacles is 7/3. It means

$$N=2,N_m=N_m^{\prime }=N_{mb}=2,N_{rb}\ge 2$$

(22)

We select $N_{rb}=2$ here. One rover can only collect its material from the mining area and move near the blender together. If one rover moves to the target too early, it will wait for the other rover, during which a penalty reward will be given. The size of the map is $20\times 20$, and each rover can access the nearby 4 points information, which means the size of the input vision of each rover is ${(4\times 2+1)}^2=81$. The size of one rover is $1\times 1$ in the grid. The size of each obstacle is also $1\times 1$ in the grid, but they can be contiguous.

Our simulation code is written in Python 3.10 and benefits from Tianshou 0.4.9 and PyTorch 1.11 framework. The coding and running platform is a PC running Windows 10 with Intel Xeon Platinum [email protected] GHz, 32 GB RAM, and NVIDIA GeForce 3080ti. Parameters for training in Rainbow DQN modified through cycling action for multi-agents are shown in

Table 3. Hyper-parameters for Rainbow DQN training.

Name	Value
Epsilon	0.6
Buffer Size	80,000
Learning Rate	$3\times {10}^{-5}$
Discount Rate	0.9
Batch Size	64
Neural Network Size	[512, 256]
Target Update Freq	320

.

Table 4. Reward for each situation.

Name	Value
Small Obstacles	−3
Large Obstacles	−8
Crash	−10
Mining	100
Arrive to points	50
Put in blender	800
Wait	−2
Normal	−0.5

shows the reward values in different situations. Heuristics are also added to the rewards with the rate of $0.6$ for repulsive potential and 5 for attractive potential. Eight threads have been used for training. Training has been run $3.24\times {10}^7$ times. Although the sum of the target reward is $800+50\times 2+100\times 2=1100$, moving across small obstacles will gain rewards below 0, so we consider convergence as the sum of the reward exceeding 1000.

4.2. Multi-Agent Training

To train the agent to adapt to different terrains on the partially observed moon surface, we employ a strategy of generating a new environment at each epoch during the training phase. Obstacle points will be arranged in the new area randomly and separately to simulate the moon. Furthermore, 200 environments are created as validation to verify the training results and make a comparison with the A-Star algorithm. Comparisons among our RL method with APF, the state-of-the-art multi-agent path planning RL algorithm Multi-Agent Proximal Policy Optimization (MAPPO) [15], and the Rainbow DQN algorithm without heuristics are also proposed to demonstrate the efficiency of our method.

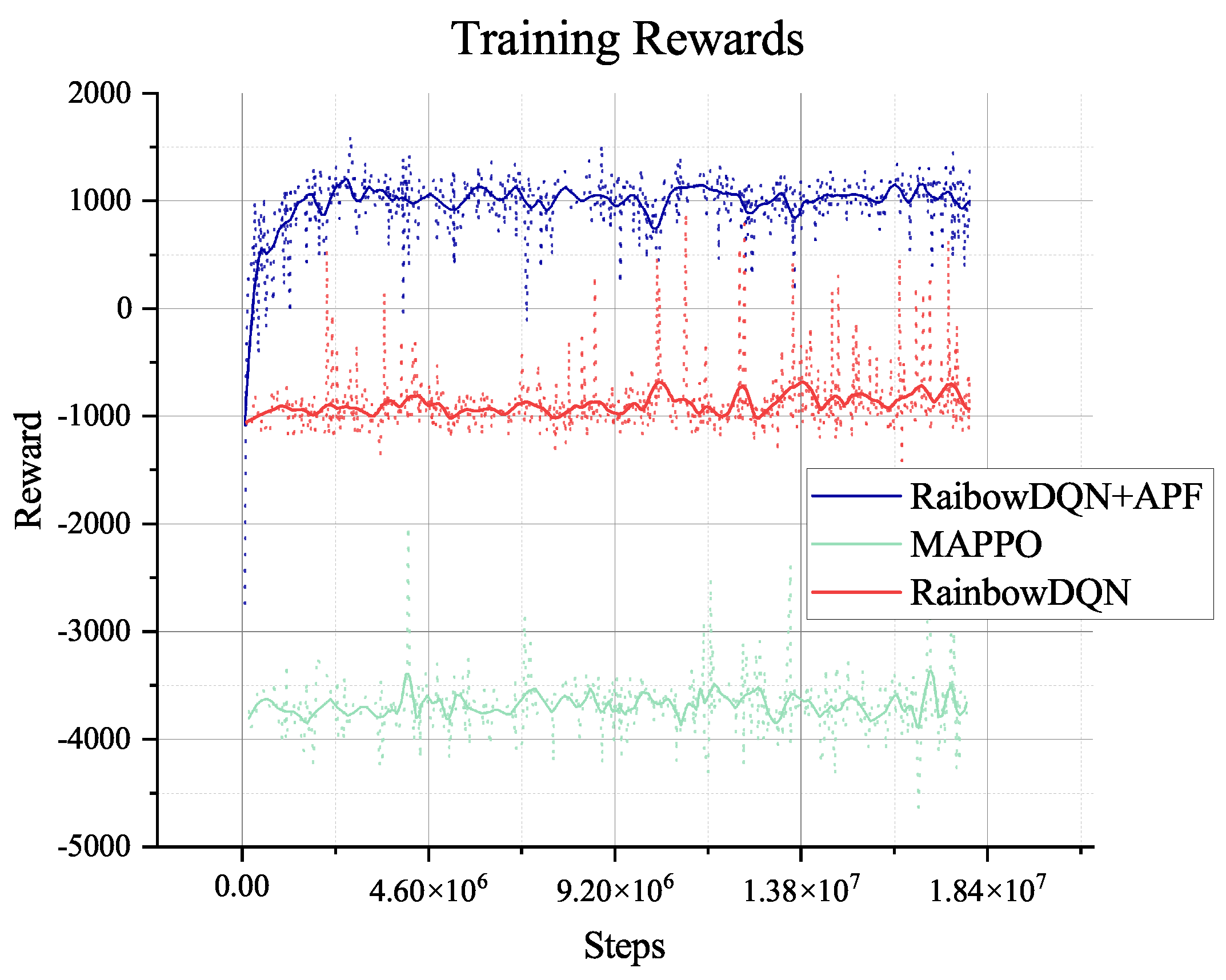
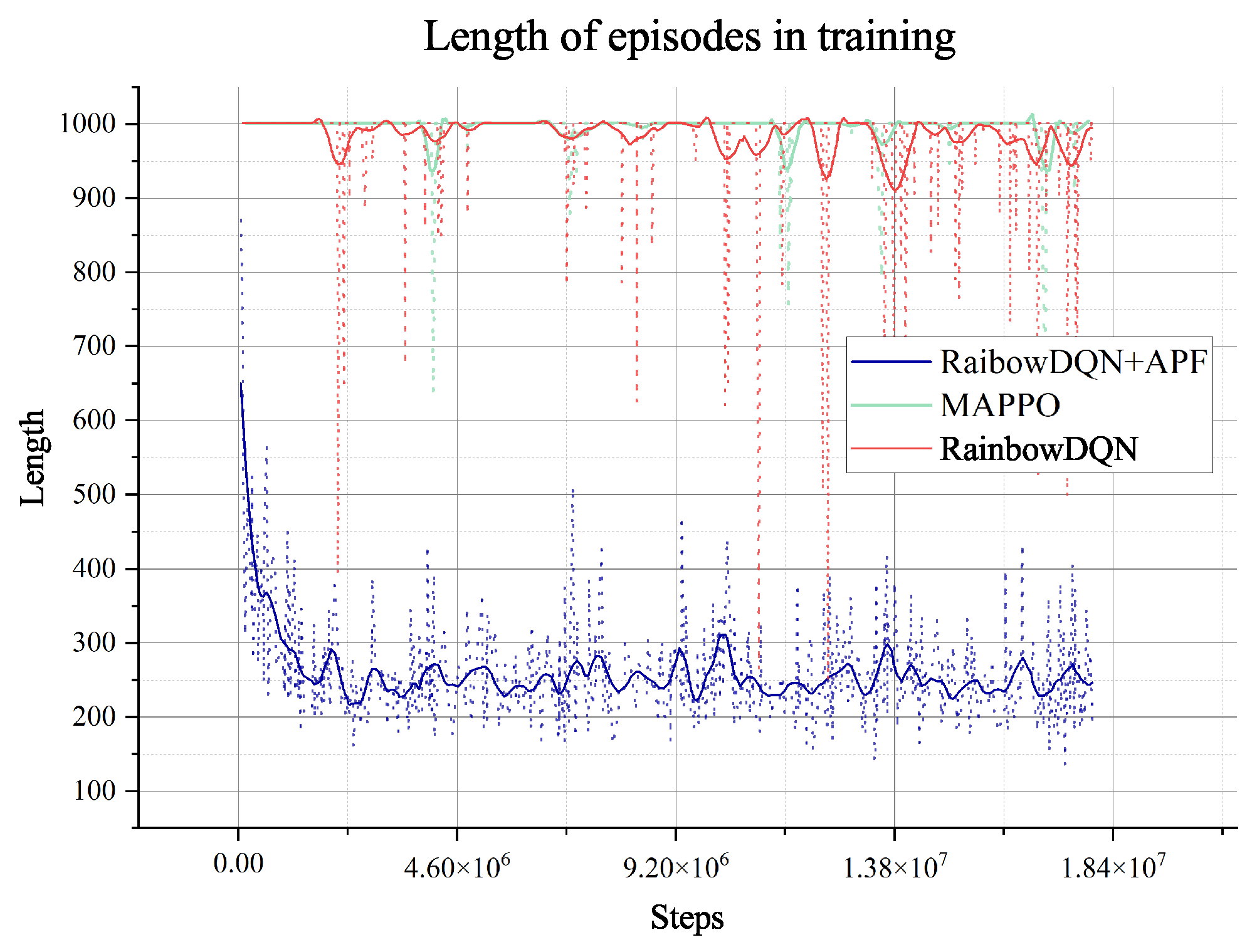
Figure 4, Figure 5, Figure 6 and Figure 7 show the agent’s response in the training process. The training figures show the convergence of the training from $4\times {10}^6$ steps. After that step, the agent explores the environment and obtains a much better path and solution to the planning problem, illustrated in Figure 5. The loss value decreases slightly after the $4\times {10}^6$ steps, which means that the agent has extensively explored the environment and becomes stable when faced with different data from other environments. Furthermore, the length of an episode decreases from the maximum of 650 to 250, which means that the trained agent can complete the task in about 250 steps. However, the training process involves random decisions that enhance the agent’s exploration. Even if there are random explorations, the agent can still complete the planning task during this training period.

The MAPPO algorithm converges to a local optimum during training, but such an agent is not enough to generate paths and plans for rovers, which is indicated in the training reward. Even when we change the hyper-parameter related to exploring, it shows no better result. So, we will not do any further tests on the algorithm. The pure Rainbow DQN algorithm with only the reward for collecting and terminal will also converge to a local optimum without the guidance of our proposed heuristic, which is treated as the dense reward in the Rainbow DQN. Like MAPPO, the agent in such optima cannot plan successfully either.

The two algorithms will only explore the epsilon-greedy policy, which is used in most RL algorithms. However, when it comes to the partially observable environment like the lunar surface environment we have used, it lacks global information and guidance and will only gain a positive reward when achieving the target of collection or mix. This cannot support the long-term searching, so even if we have adjusted the hyper-parameter of exploration (‘eps’ in figures), it does not show too much difference, as shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.

4.3. Comparison to the Multi-Agent A-Star Algorithm

This section presents a comparative analysis between our proposed algorithm and the multi-agent A-Star path planning algorithm [23] with small and large obstacle avoidance heuristics. Our DRL method can plan both the task and the path, during which the cooperative actions are added to decrease wasted time and collision between rovers, with the guide of 4 different kinds of heuristics through rewards. All the 200 randomly generated validation environments are chosen as the comparison. The A-Star algorithm plans paths by considering safety distances [24], accounting for the additional size of the rover and assessing multiple nodes concurrently. However, it is still applied to the whole environment rather than only the partially observed environment. In our comparison, the paths for two rovers are planned independently, from the mining site to the blender, as A-Star primarily serves as a path-planning method rather than a task-planning approach. In the visual representations of the planned paths, initial and target points are denoted by circles, while the direction of the paths is depicted by triangles. Both circles and triangles are color-coded to correspond with the trajectory of the rover. This visual aid facilitates the direction of the paths from the two algorithms.

Figure 16 shows the path lengths planned by RL and A-Star in a simulated area of size $20\times 20$. The agent in RL achieves a $91.5\%$ success rate in task planning and path planning in 200 validation environments. Most of the path lengths from A-Star are shorter than those from RL because the agent in RL has been trained for resource optimization by reducing the number of moves across small obstacles. The agent has also been designed to shorten the path, and the average RL length (50.58) is slightly lower than A-Star’s (55.26). This means that in the path planning part, the RL can plan an acceptable path compared to the path of A-Star.

Figure 17 shows the paths generated by the RL planning method and A-Star in the same environment. The A-Star path has longer turning times, making it more difficult for the control program on the rovers. Also, the path from the RL moves across the small obstacles less than the A-Star one because there is optimization in the DRL method, while A* can only move according to the given heuristics.

Table 5. Action sequences of rovers. The grey shows the two rovers have same action in different action order. The pink demonstrates there are waiting actions in planning to align the termination time. The yellow shows the rovers terminate at a similiar time.

NO.	Rover 0 Action Name	NO.	Rover 1 Action Name
6	Moving down	19	Moving right
7	Collect	20	Collect
8	Moving up	21	Moving left
...	...	...	...
37	Wait	36	Moving left
38	Moving up	37	Moving left
39	Moving up	38	Moving left
40	Moving up	39	Moving down
41	Mix	40	Mix

shows the action sequences for the rovers and the important actions after the path planning. The planning agent can generate both actions for moving, which indicates the path planning, and actions for executing, which means the task planning.

Figure 18 shows how often the rovers move across the small obstacles, indicating the quality of the path-planning solution. It appears that most of the solutions from the RL agent have fewer small-obstacle crossing times than the A-Star solution. The average time of the RL plan is also less than that of the A-Star plan. For validation environments, the RL agent performs better than the A-Star.

Figure 19 indicates the dangerous situations in which the algorithm leads the rovers. The number of RL agents that perform better is greater than the A-Star ones, and the average is better. In some of the validation environments, A-Star performs better because the RL agent only has partially observed information. Even if it can avoid large obstacles, sometimes it will still be near large obstacles.

Figure 20 shows the entire planning time and response time of the two methods. Here, we define the response time as the time until the agent can generate one action or path after the rovers complete tasks. The planning time of the RL agent also includes the planning time for collecting and delivering actions. The figure shows that even with the task planning time, the calculating time is still slightly lower than the A-Star, which only plans the paths. However, regarding the response time, the RL agent performs better than the A-Star method. Because the RL agent can generate one action according to the current state in the environment, the A-Star method needs to search till the target and then return the whole plan, which costs more time. Response time is valuable, especially in emergencies.

Table 6. Statistics of paths from RL and Multi-Agent A* with a format of Average (Standard derivation). Only successful plans are encountered here.

	RL	MA-A*
Path length	50.68 (15.46)	55.26 (14.05)
Moving across small-obstacle times	4.96 (2.71)	8.64 (3.59)
Being nearby large obstacle times	19.47 (10.54)	24.44 (16.47)
Calculating duration (ms)	14.08 (4.36)	6640.72 (812.75)
Responding duration (ms)	0.25 (0.006)	3435.64 (657.75)

illustrates the statistics of paths from the RL-trained agent and the multi-agent A* with improved obstacle avoidance. Our RL with APF training and planning method performs better than multi-agent A* from all aspects except the standard derivation of the path length. It performs better, especially with the calculation and responding duration. The multi-agent A* needs to plan separately, combine paths, and solve conflicts among paths, which costs more time than the direct decisions made by the RL agent.

We have identified two primary reasons for the occurrence of planning failures within the RL. First, the local optima in training. Most cases should have had a better planning result, but all of them terminate after several decisions when one rover starts to make an incorrect decision. For example, consider a scenario where two rovers approach each other closely. When they decide to move closer, If both rovers decide to move even closer, they will incur punishment rewards from the heuristic proposed in our methodology, signaling the undesirability of the action due to safety concerns. However, the rovers may persist in attempting to move closer, perpetually receiving penalization until the environmental step limit is reached. This should be blamed on the deficiencies in the training algorithm or shortcomings in the exploration period, leading to the local optima.

Second, another contributing factor to planning failures lies in the proposed heuristic’s inability to consistently fulfill the current target under all circumstances. When rovers move into an area encircled by large obstacles, a conflict emerges between the heuristic guiding obstacle avoidance and the heuristic directing movement toward the target. Consequently, the rovers persist in attempting to advance towards the large obstacles despite the impossibility of reaching them, resulting in gaining a punishment reward. Furthermore, it did not find a better solution because of the local optima in training. Some of the failure planning results are indicated in Figure 21.

4.4. Test in a Real Moon Topography from the Digital Elevation Model (DEM)

To further validate the efficacy of our task and path-planning methodology in a real lunar surface context, a map from Leibnitz beta plateau near the moon’s south pole sites is selected as the planning map of two rovers. The processing site for lunar materials is located within a flat region, while the rovers are tasked with collecting lunar soil or rocks from areas adjacent to small obstacles positioned at the periphery of the flat terrain. The agent trained with the randomly generated environments plans the action sequence of moving and collecting, and the paths for two rovers is shown in Figure 22. This visual representation serves to illustrate the planned trajectories of the rovers, affirming the effectiveness of our task and path-planning approach in real lunar surface scenarios.

Figure 22 and

Table 7. Plan statistics from RL for the DEM map.

Parameter Name	Value
Moving across small-obstacle times	0
Being nearby large obstacle times	2
Calculating duration	152.73 ms
Responding duration	0.38 ms

demonstrate the ability of the trained agent. It can complete the entire planning period even if it has not been trained in this area, indicating that the planning agent can generalize and plan in similar areas at an acceptable cost.

4.5. Training and Testing for More Rovers

The proposed method based on Rainbow DQN for task and path planning can also be adapted to more than two rovers. However, one single trained agent can only solve the planning problem of one certain number of rovers, which means solving three rovers’ planning problems requires additional training. So, we trained again for a three-rover task and path-planning problem with the proposed heuristics and randomly generated maps. Comparisons between two and three-rover training are demonstrated in Figure 23, Figure 24, Figure 25 and Figure 26.

Smooth training rewards converge until 500, and original training rewards reach above 1000 many times after steps $4.6\times {10}^6$, indicating convergence. Furthermore, the length of episodes in Figure 25 demonstrates that the average length of each training episode has reached 400 from the limitation length of 1000, indicating the agent has learned how to plan for three agents. However, when faced with three agents instead of two agents, Figure 23 illustrates that the agent needs to explore the environment and learn more times to understand the available planning experiences. It needs more steps to achieve convergence. Figure 27 is the path planned by the trained agent. All three agents can collect the resource from the mining point and reach the destination safely without accessing the large obstacles and moving across the less small ones.

5. Conclusions

We introduce a novel approach to task and path planning utilizing multi-agent deep reinforcement learning (DRL) in conjunction with artificial potential fields. The randomly generated obstacles are represented as points in the grid-simulated world with extra information. These obstacles are categorized into two types: small barriers, which impose increased energy costs but do not impede rover movement, and large barriers, which are impassable for rovers. To train our path-planning agent, we employ Rainbow DQN, a variant of the DRL methodology, to navigate the complex obstacle-laden environment and determine optimal paths to collect materials and deliver them to the blender. In our simulation setup, two rovers are deployed, operating collaboratively to handle materials efficiently. To augment the training process, we propose the incorporation of heuristic strategies based on repulsive potential fields for obstacle and rover avoidance, as well as attractive potential fields for continuous reward guidance towards the target. These heuristics serve to enhance the efficiency and effectiveness of our proposed path-planning methodology in training.

We also proposed a new way of representing the state of the environment and the rovers, aiming to reduce the complexity of the state space by consolidating observations and adopting a cyclical decision-making approach. Through experimental evaluations, we have demonstrated the effectiveness of our approach. Our findings illustrate that rovers can move, avoiding large barriers and reducing the number of small barriers that pass. The agent guides the rovers on a path and tries to avoid small obstacles while decreasing the waiting time near the blender to improve collaborative efficiency. The comparison between our method and the multi-agent A-Star path-planning algorithm with improved obstacle avoidance shows that our approach can plan a better path on which fewer small obstacles will be passed without largely increasing the paths’ length and guide the rovers through heuristics in training even if there are continuous targets while A-Star needs to pre-define targets. Our method can generate the path and the action sequence together faster than the multi-agent A-Star algorithm, which purely plans paths. This indicates that our method can solve certain jobs quickly and safely. Our method is also suitable for more rovers’ path planning, and it can also help them plan a safe path quickly on a real moon map from DEM.