A Ball-Contacting Dynamic Vibration Absorber with Adjustable Stiffness and Nonlinear Characteristics

Abstract

Structural vibration has always been a major concern in the engineering field. A dynamic vibration absorber in the form of contacts with adjustable stiffness (CDVA) offers effective vibration suppression and can improve conventional dynamic vibration absorbers with high sensitivity to frequency deviation and difficulty in adjusting the frequency. In this research, first, based on the theoretical model of the contact between a rubber ball and an inner cone, the feasibility of changing the axial contact state to change the structure’s natural frequency was verified using an ANSYS simulation. A theoretical model of the static contact stiffness between the ball and the inner cone was constructed using Hertzian contact theory and Hooke’s law, and a theoretical model of the cubic nonlinear elastic restoring force was used to characterize the stiffness properties of the rubber ball during compressive rebound. The steady-state frequency response equations of the main vibration structure were derived using the averaging method in conjunction with the two-degree-of-freedom dynamics model, and the stability of the solutions to the frequency response equations was obtained in conjunction with the stability determination criterion. Then, the impact of the CDVA’s design parameters on the nonlinear dynamic response of the primary vibration structure was simulated and analyzed. The resulting findings can serve as guidance for designing dynamic vibration absorber parameters. Based on the principles of ball-inner cone contact, a dynamic vibration absorber structure was proposed. A design test was conducted to verify the correctness of the contact stiffness model, and an experimental study was carried out to investigate the law of change in the dynamic stiffness and damping of the principle structure of CDVA under dynamic excitation conditions. Finally, the vibration test platform of the solidly supported beam structure was constructed, and vibration suppression tests of the CDVA in different compression states were conducted to investigate the tunability and feasibility of CDVA vibration suppression. The results showed that the dynamic vibration absorber had good vibration absorption characteristics and could be used for single-mode vibration suppression of multimodal main structures.

1. Introduction

The problem of mechanical vibration is progressively receiving attention and exploration as a result of ongoing advancements in science and technology, and the solution to several drawbacks resulting from vibration remains a popular research topic. Currently, dynamic vibration absorbers are an effective means of vibration suppression. By choosing the structural form of the substructure, the dynamic parameters, and the coupling relationship with the main vibration system, this technique attaches a substructure to the main vibration system and modifies its vibration system, reducing the forced vibration response of the main vibration system in the desired frequency band [1]. Traditional dynamic vibration absorbers [2,3] have a mass-damped-linear spring structure. However, despite this structure’s excellent capacity to reduce vibration, the dynamic vibration absorber’s parameters remain fixed, resulting in only single vibration frequency point suppression. The vibration reduction effect is severely constrained when dealing with the main vibration system that has a wide range of vibration bands. Additionally, when the dynamic vibration absorber deviates from the ideal design state due to changes in the damping ratio or natural frequency of the main vibration system, the performance of vibration control also declines. Therefore, multiple dynamic vibration absorbers [4,5,6,7,8] were developed, for which two or more dynamic vibration absorbers are utilized in parallel on the main vibration structure, to improve the robustness of dynamic vibration absorbers and accomplish multi-modal vibration suppression. Despite a slight increase in the dynamic vibration absorber’s vibration suppression frequency band due to this method, the band is still not particularly wide. Active adjustable dynamic vibration absorbers with feedback systems [9,10,11,12,13] have been extensively investigated to maximize the vibration suppression frequency band of a dynamic vibration absorber and to enhance self-adaptive capabilities. Using sensors to gather vibration data from the main vibration system and transmit it to the central controller, which then feeds back braking data to the actuator to control the variable structure of the dynamic vibration absorber in real-time, changing the absorber’s parameters, the active control of the dynamic vibration absorber is made possible. Although this technology effectively suppresses vibration, it is sophisticated and energy-intensive, making it unsuitable for environments where low energy consumption and high-reliability standards are required, such as in aerospace systems. To enhance the performance of the dynamic vibration absorber, nonlinear characteristics have been added to the construction [14,15,16,17]. The vibration suppression band of a nonlinear dynamic vibration absorber has been demonstrated to be twice as large as the corresponding linear vibration absorber when it is significantly nonlinear [18]. Additionally, nonlinear dynamic vibration absorbers have a higher frequency adaptability. There are still very few applications that supply nonlinear parameters in contact theory, and all current designs for nonlinear parametric structures are based on one-piece structures, such as nonlinear springs. Additionally, in earlier engineering applications, modifications to the contact states of a main system’s internal parts have led to more pronounced changes in the dynamics. For instance, in a rotating mechanism, modifications to the contact state between the bearing balls and the inner and outer raceways can cause the primary structure to exhibit more pronounced changes in the modal response [19]. Therefore, it is possible to construct variable stiffness dynamic vibration absorbers with vibration control utilizing the technique of indirectly modifying the stiffness of the main vibration system using changes in the contact conditions. In light of this, developing a dynamic vibration absorber with ball contact nonlinear stiffness adjustment is important.

This paper presents the development of a dynamic vibration absorber utilizing a rubber ball and inner cone contact. The feasibility of the absorber was verified through contact simulation, stiffness modeling, and applicability tests of the ball contact variable stiffness dynamic vibration absorber. Section 2 describes how a finite element model was constructed to analyze the law of natural frequency variation in the main structure with changing contact states. This was based on pre-stress modal simulations, which demonstrated the feasibility of using contact for dynamic absorber design. Section 3 presents a theoretical model for the static contact stiffness using Hertzian contact theory and Hooke’s law. The frequency response curve (FRC) of the main vibration structure was determined by introducing a three-time nonlinear elastic restoring force model for the rubber ball into a two-degree-of-freedom dynamics model. The nonlinear dynamic behaviors of the rubber ball, such as jumps and mutations, were analyzed. These behaviors were caused by the three-time nonlinearity of the elastic restoring force. Section 4 examines the impact of the CDVA design parameters on the nonlinear dynamics of the primary vibration structure through numerical simulation. This analysis can assist in designing CDVA. Section 5 describes the design of the application structure of the ball’s contact dynamic vibration absorber. Through the rubber ball’s contact dynamic and static stiffness test and the rubber ball damping test, the theoretical model of contact stiffness was verified, and the change rule of the dynamic stiffness and damping with the change of the excitation frequency was investigated. Section 6 presents an example of the application of a CDVA with a beam-supported platform as the main vibration structure to verify the vibration-damping effect of the CDVA. In Section 7, some conclusions are drawn and a brief vision of subsequent research is presented. The ball contact dynamic vibration absorber designed in this research used a passive adjustable method to change the stiffness, and the overall dynamic vibration absorber had no energy consumption, in contrast to conventional dynamic vibration absorbers, which have a fixed structure and vibration absorption parameters that cannot be changed. When specific contact forces are applied, rubber ball materials, which are frequently employed, may have their stiffness adjusted, making them very adaptable to loads and vibration frequencies. The dynamic mass and rubber ball can be changed to dampen vibrations across a larger frequency range. This is more interchangeable and eliminates the structural complexity and low dependability associated with active regulation. Considering the advantages exhibited by the application of nonlinear factors in dynamic vibration absorbers, this study investigates the influence of parameter variations in the utilization of the ball contact and rubber nonlinearities in dynamic vibration absorber applications using a combination of theoretical analysis and experimental approaches. Moreover, the performance of this type of dynamic vibration absorber in vibration reduction applications is evaluated. The findings of this research can serve as valuable references for the design of similar dynamic vibration absorbers in real-world engineering scenarios.

2. Simulation of Contact Variable Stiffness Principle

The variable stiffness principle structure consists of the host structure, the elastomeric rubber ball, and the mass elements. To prevent further concentrated forces brought on by slippage and loosening of the rubber balls, the rubber balls are installed in both the main structure and the inner tapered bore of the mass element. In the basic design, axial force is used to press the rubber ball against the inner cone’s wall, creating contact stiffness in the process. The rubber ball’s elastoplastic characteristics allow it to have both stiffness and damping. The principle structure of the contact stiffness is shown in Figure 1.

Pre-stress modal simulations of the contact principle structure were carried out using ANSYS to obtain the natural frequencies of the primary structure with various compression forces to investigate the impact of variations in the axial compression forces on the dynamic modal characteristics of the primary structure. The theoretical modal parameters are shown in

Table 1. Theoretical model parameters.

Components	Materials	Dimensions	Contact Angle
Housings	2A12	Diameter × Height 54 mm × 15 mm	45°
Ball	IIR	Diameter 35 mm	-

.

The boundary conditions for the simulation were as follows. The rubber ball was placed in contact with the inner cone of the main structure, a fixed constraint was applied in the lower plane of the main structure, a force was applied in the upper plane, and the direction of the force was perpendicular to the upper plane pointing toward the center of the rubber ball. The simulation results demonstrated that the compression forces had an impact on several major modes in the main structure, including the tension–compression mode, the sway mode, and the shear mode. The axial tension–compression mode was the primary emphasis of this work, and the pertinent axes for vibration suppression were all in the axial direction. The primary structure’s tensile-compression mode is shown in Figure 2.

Table 2. Natural frequencies of the primary structure with different compression forces.

Forces (N)	Natural Frequency (Hz)
10	110.61
50	126.26
100	135.37
300	146.42

presents the natural frequencies for the primary structure with various compression forces.

Table 2 shows that the primary structure’s natural frequency increased as the axial compression force increased, demonstrating that the stiffness change caused by the compression contact was somewhat sensitive to changes in the compression force. In terms of the trend of growth, the rate of change in the increase in the natural frequency of the primary structure trended lower in terms of growth. Therefore, it could be concluded that a continual increase in force value did not result in a significant increase in stiffness. The interaction between molecules might have been disrupted when the force value surpassed a particular value due to the elastoplasticity of rubber materials, which results in an abrupt shift in contact stiffness, according to experience. Based on the aforementioned study, the stiffness of the entire primary structure was determined by the rubber ball’s material, structural parameters, and the size of the compression force that was applied. If the stiffness of the contact-mounted dynamic vibration absorber structure could be predicted, then the parameters could be set according to the vibration characteristics of the main structure, and the dynamic vibration absorber could be applied to the main structure to achieve vibration control.

3. Theoretical Model of the CDVA

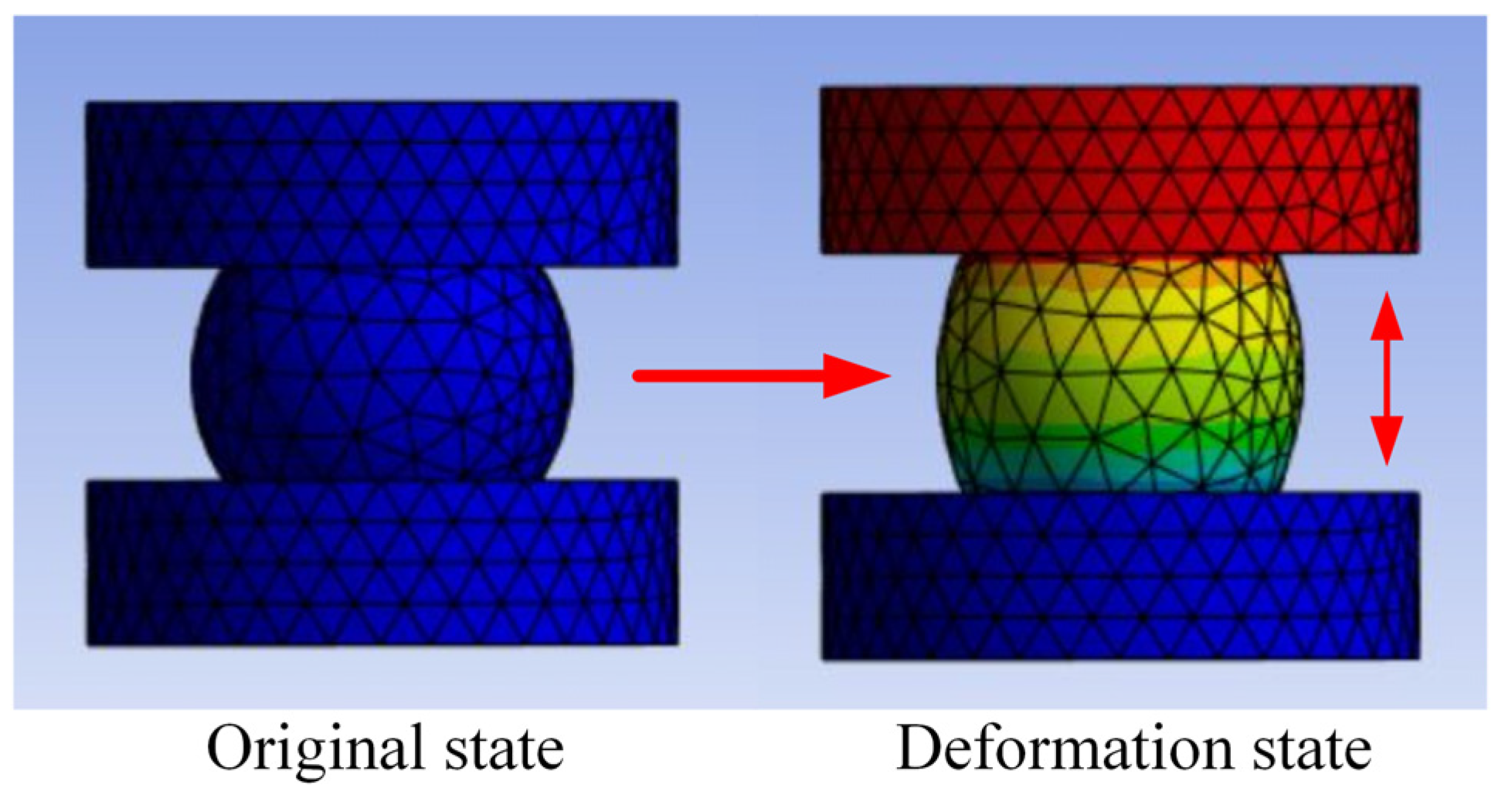
In practical applications, rubber ball compression exists in two compression states: static compression and dynamic compression. The overall structure exhibits dynamic stiffness and static stiffness. In the static state, there is no kinematic displacement difference between the moving mass of the CDVA and the main structure, and the contact state of the rubber ball does not change. The contact stiffness in this state is modeled and expressed by Hertzian contact theory. In the excited state, there is a displacement difference between the moving CDVA mass and the main structure, and this process breaks the compression state of the rubber ball in the static state, causing a change in the contact stiffness. The difference in displacement causes the rubber ball to produce an elastic recovery force in a static-to-dynamic transition over a period of time. During static compression, the rubber ball also generated a certain elastic restoring force due to its elastic–plastic properties, but the rubber ball was in equilibrium and the elastic restoring force was characterized by the contact stiffness. Therefore, to compensate for the excess of dynamic stiffness over static stiffness, the overall contact stiffness was corrected using a three-dimensional nonlinear elastic restoring force model for metal rubber materials.

3.1. Contact Stiffness

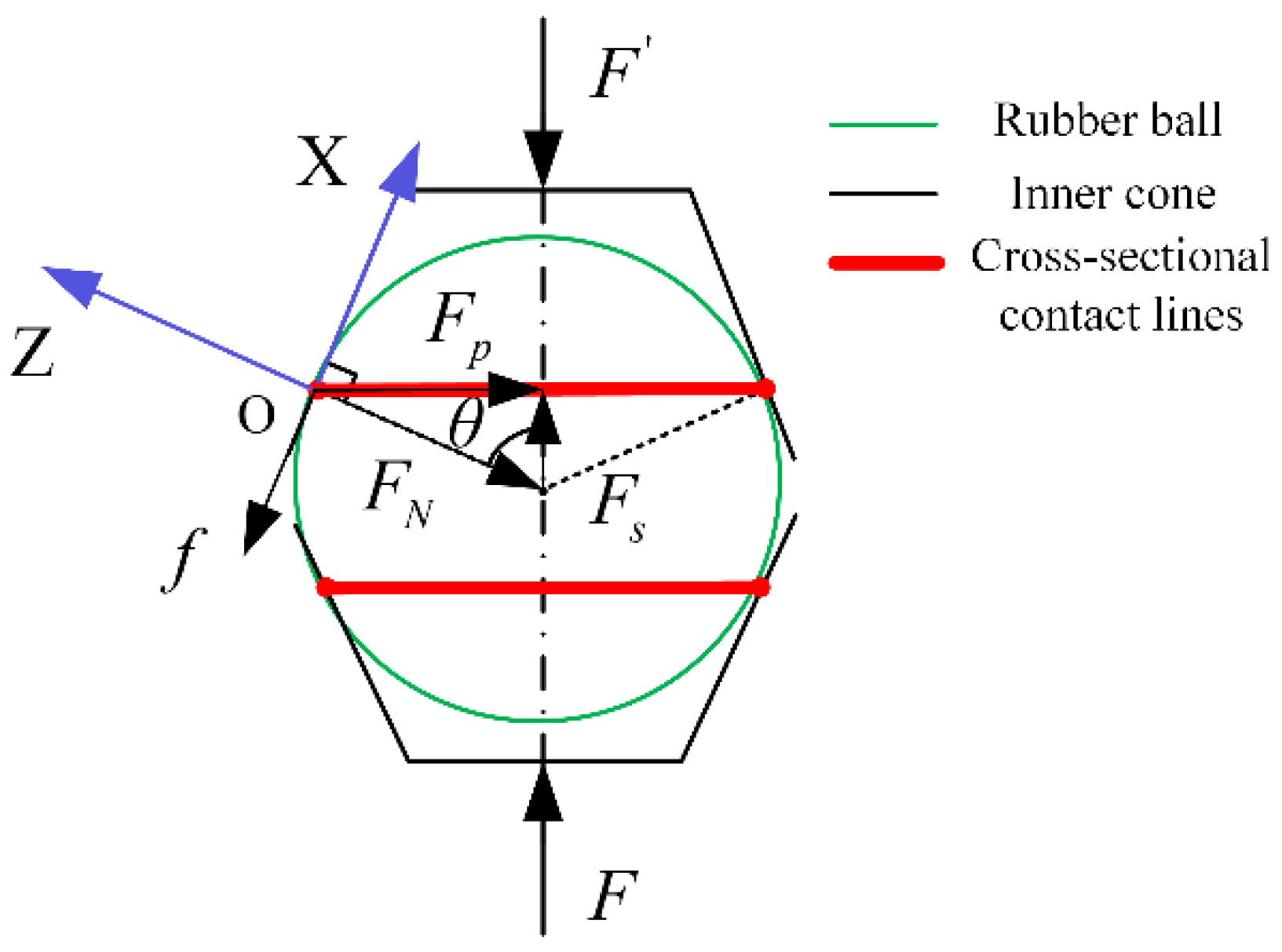
In this research, a theoretical model was developed based on contact mechanics and Hertz contact theory for the stiffness in the axial tension–compression mode produced by rubber ball contact. Some rubber ball modes can be excited to produce local resonance phenomena with the impact of high-frequency vibration, revealing a stiffness that is challenging to evaluate. Therefore, these higher-order modes were ignored. A diagram of the rubber ball in contact with the inner cone is shown in Figure 3.

$F$ represents for the applied axial force, $F^{\prime }$ is the reaction force, $F_N$ is the normal force (force per unit circle length) on the contact line between the supporting inner cone and the rubber ball sphere, and $\theta$ is the inner conical surface’s half-cone angle. The center of the contact area was used as the origin of the coordinates and the tangential and normal directions at the origin were used as the x and z axes, respectively, to establish a right-angle coordinate system. As the applied external force increased, the dynamic form of contact between the rubber ball and the inner conical surface changed from a linear contact to a conical ring with a surface. This was a non-coordinated contact mechanics problem. 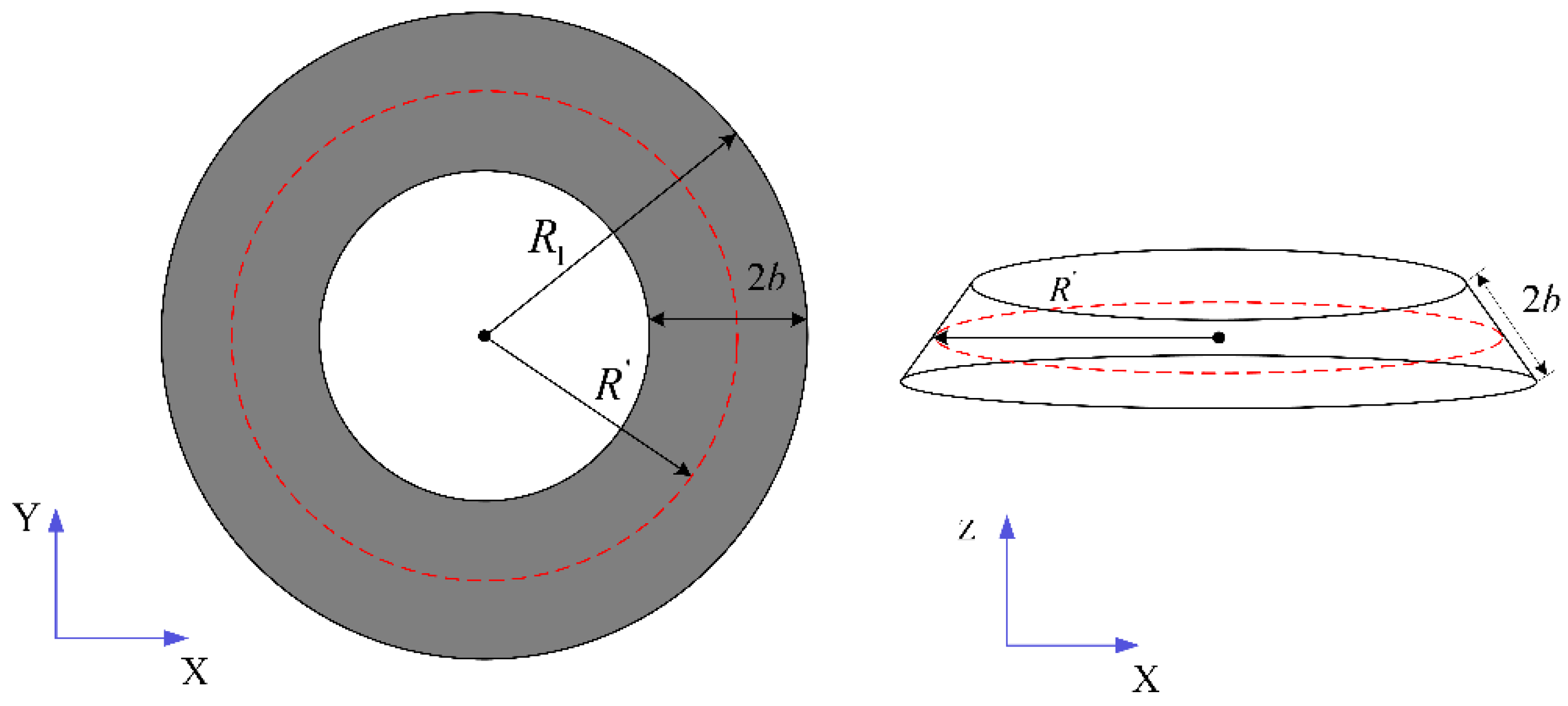The contact deformation is shown in Figure 4.

In Figure 4, $R_1$ is the radius of the rubber ball, $b$ is the contact half-width of the conical belt ring, and $R^{\prime }$ is the radius of the initial contact line.

Then, the relationship between $F$ and $F_N$ can be expressed as follows:

$$F=2\pi R^{\prime }{F}_s=2\pi R^{\prime }{F}_N\cos \theta$$

(1)

where $R^{\prime }=R_1\sin \theta$; then, we have

$$F_N=\frac{F}{2\pi R_1\sin \theta \cos \theta }$$

(2)

Letting the distribution function of the normal pressure on the contact surface be $p(x)$, based on the Hertzian contact theory [20,21], the normal pressure distribution function on the contact surface can be expressed as follows:

$$p(x)=p_0{(1-{(\frac{x}{b})}^2)}^{\frac{1}{2}}$$

(3)

$$p_0={(\frac{E^{*}{F}_N}{\pi R_1})}^{\frac{1}{2}}$$

(4)

where $E^{*}$ is the equivalent modulus of elasticity, $E^{*}=\frac{1-{\mu }_1^2}{E_1}+\frac{1-{\mu }_2^2}{E_2}$. $E_1$, ${\mu }_1$, $E_2$ and ${\mu }_2$ are the moduli of elasticity and Poisson’s ratios of the main structure and the rubber ball, respectively.

The contact half-width of the conical ring belt surface is given by

$$b={(\frac{4R_1{F}_N}{\pi E^{*}})}^{\frac{1}{2}}$$

(5)

The stress component generated by $p(x)$ at any point within the rubber ball is given by

$$\begin{array}{l}{\sigma }_x=-\frac{2z}{\pi }{\displaystyle {\int }_{-b}^b\frac{p(x)x^2}{{\left\{x^2+z^2\right\}}^2}dx}\\ {\sigma }_z=-\frac{2z^3}{\pi }{\displaystyle {\int }_{-b}^b\frac{p(x)}{{\left\{x^2+z^2\right\}}^2}dx}\\ {\tau }_{xz}=-\frac{2z^2}{\pi }{\displaystyle {\int }_{-b}^b\frac{p(x)x}{{\left\{x^2+z^2\right\}}^2}}dx\end{array}$$

(6)

In the contact mechanics formulation, Hooke’s law for plane strain for any contact surface pressure distribution yields the isotropic strain at any point in the entire rubber ball as

$$\left\{\begin{array}{l}{\epsilon }_x=\frac{1}{E}\left\{(1-{\nu }^2){\sigma }_x-\nu (1+\nu ){\sigma }_z\right\}\\ {\epsilon }_z=\frac{1}{E}\left\{(1-{\nu }^2){\sigma }_z-\nu (1+\nu ){\sigma }_x\right\}\\ {\gamma }_{xz}=\frac{1}{G}{\tau }_{xz}=\frac{2(1+\nu )}{E}{\tau }_{xz}\end{array}\right.$$

(7)

where $\nu ={\mu }_2$ and $E=E_2$. The normal strain in the contact area of the rubber ball is expressed as follows:

$$w^{\prime }={\displaystyle {\int }_0^{R_1}{\epsilon }_z}dz$$

(8)

The axial strain is given by

$$w=w^{\prime }\cos \theta$$

(9)

From Equations (1) to (9), the deflection–load relationship for the rubber ball can be derived without considering the effect of tangential friction. Differentiating this equation, the nonlinear stiffness produced by compression is given by

$$k_g={(\frac{\partial w}{\partial F})}^{-1}$$

(10)

The rubber ball has two contact forms at the top and bottom with the same structural shape, and their stiffnesses are in series. The equation for calculating the total stiffness resulting from contact is expressed as follows:

$${k_c}^{\prime }=\frac{k_g^2}{2k_g}=\frac{k_g}{2}$$

(11)

The relationship between the modulus of elasticity and the rubber’s hardness value can be expressed, as in Equation (12) [22], because hardness is frequently used to characterize the mechanical properties of rubber materials in engineering applications.

$$E_2=\frac{0.7554H_A+5.53}{100-H_A}$$

(12)

The contact stiffness can be obtained by combining Equations (1)–(12).

The effects of friction were omitted in the previously mentioned theoretical modeling, even though there was some friction present during application between the rubber and the structure’s contact surface. The value of the total contact stiffness would increase if the effect of friction was ignored. To decrease this margin of error, a stiffness correction factor $G_{\mathrm{factor}}$ is presented in this paper. Additionally, in a rubber ball contact in the actual installation process, there will be a rubber ball axis and upper and lower contact surface connection axial misalignment of the situation, and these factors will ultimately cause the contact stiffness error. In this research, these factors are not considered. The actual contact stiffness is expressed as follows:

$$k_c=G_{\mathrm{factor}}·{k_c}^{\prime }$$

(13)

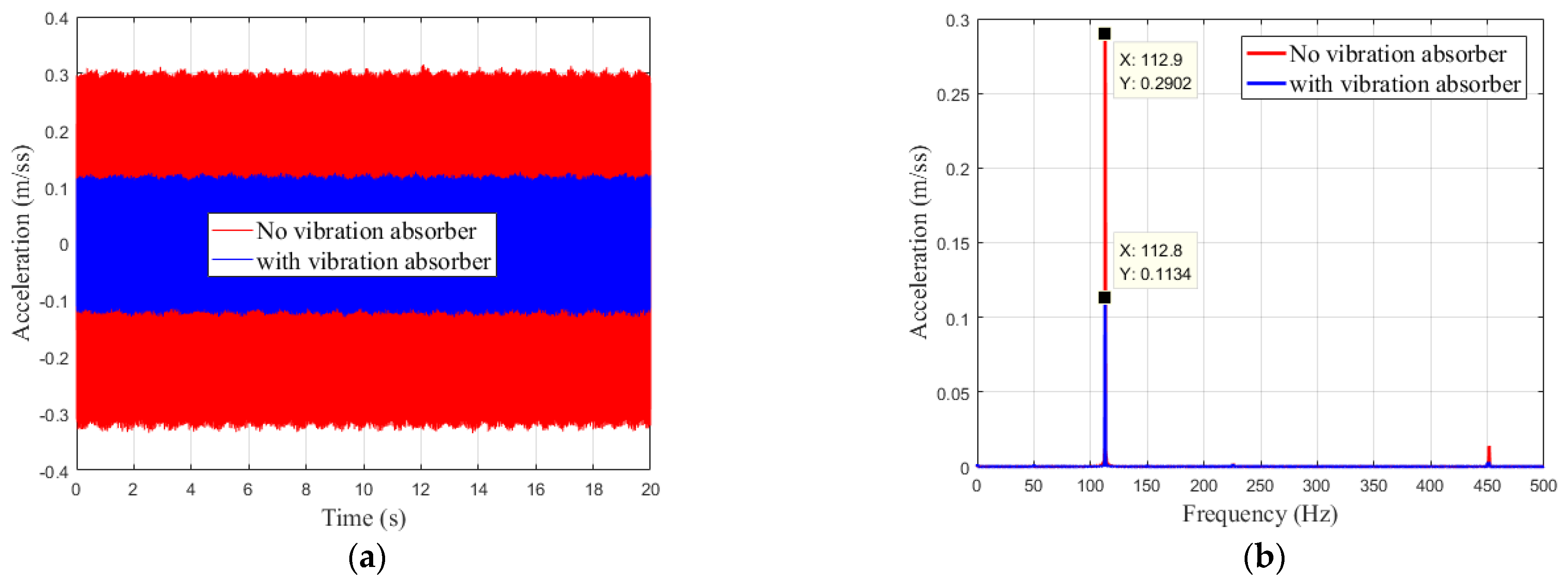
Figure 5 illustrates the contact stiffness variation curve obtained from a numerical simulation with each parameter adjustment.

In Figure 5, the contact stiffness curves resulting from each design factor exhibit nonlinear characteristics. As the compression force grew, as shown in Figure 5a, the contact stiffness also increased, but the growth rate slowed down. As can be seen, the starting point of the stiffness coordinates does not begin at zero because even though the displacement normal to the contact zone was incredibly small, a certain amount of contact stiffness was generated when the rubber ball first made contact with the structure. The rubber ball and the structure were connected by contact, and both the contact region and the rubber ball had stiffness characteristics. Figure 5b depicts a bifurcation in the rate of change in the contact stiffness with a variation in hardness, with a low rate of change in the stiffness in the hardness range of 0–80 and an exponential increase in stiffness in the 80–100 range. The overall stiffness fluctuated by large orders of magnitude, and the stiffness value was overly sensitive to changes in the hardness of the rubber ball in the 80–100 range. Furthermore, rubber ball hardness in actual engineering typically has a manufacturing variance of five hardness values, so it is not reasonable to use rubber ball hardness as an input for changes in stiffness. Similar to Figure 5b, the change in contact stiffness caused by a change in the rubber ball radius had a large magnitude and a “concave” peak at the beginning of the change, making it harder to predict the stiffness in this range of values and reducing the overall controllable range. The curve for the change in contact stiffness with a half-cone angle in Figure 5d roughly resembles a linear curve with an excellent degree of magnitude of variation. However, employing this value as an input to the stiffness variation would definitely result in multiple mechanical structural alterations to accommodate the variation in vibration, and would be less implementable. It is practical and logical to select the compression force as the input quantity for the stiffness change after considering the stability of the stiffness change generated by each parameter and the ease of implementation.

3.2. Elastic Restoring Force from Rubber Ball Contact

The elastic restoring force generated by the rubber ball contact is the source of the nonlinear nature of CDVA dynamics, and the contact part of the structure can be equated to a metal rubber-clad damping structure. It has been demonstrated that linear elastic forces, cubic nonlinear elastic forces, and first-order viscous damping make up the majority of the elastic restoring forces of rubber materials. Displacement derivatives of higher orders can be disregarded. The mathematical model of the elastic recovery force of a rubber material [23] can be described as follows:

$$F(x)=k_{a}x+k_b{x}^3+c_2\dot{x}$$

(14)

In the identification of the parameters of the actual rubber restoring force model, generally, based on the displacement and restoring force data obtained from simulation or testing, the hysteresis restoring force of the rubber material is fitted to a least squares cubic power polynomial based on the established total restoring force model of the rubber (Equation (14)), with the power function polynomial as

$$F(x)=a_0+k_{a}x+a_2{x}^2+k_b{x}^3$$

(15)

In the formulation of the literature [24], the rubber material has obvious hysteresis nonlinear characteristics, and the hysteresis return line of the rubber material can be decomposed into a non-energy-dissipating nonlinear elastic force and an energy-dissipating nonlinear damping force, and the dissipative damping provided by this nonlinear damping force is the damping characterized by the CDVA. From Equation (14), the damping force is expressed as

$$F_c=F-k_{a}x-k_b{x}^3$$

(16)

In practical calculations, the rubber ball compression force–displacement data are obtained from the tests, and the parameters related to the restoring force can be identified by the method of the literature [25].

Then, the dynamic equivalence provided by the contact part of the whole rubber ball is

$$F_{eq}=(k_c+k_a)x+k_b{x}^3+c_2\dot{x}$$

(17)

3.3. Two-Degree-of-Freedom Nonlinear Dynamics Model

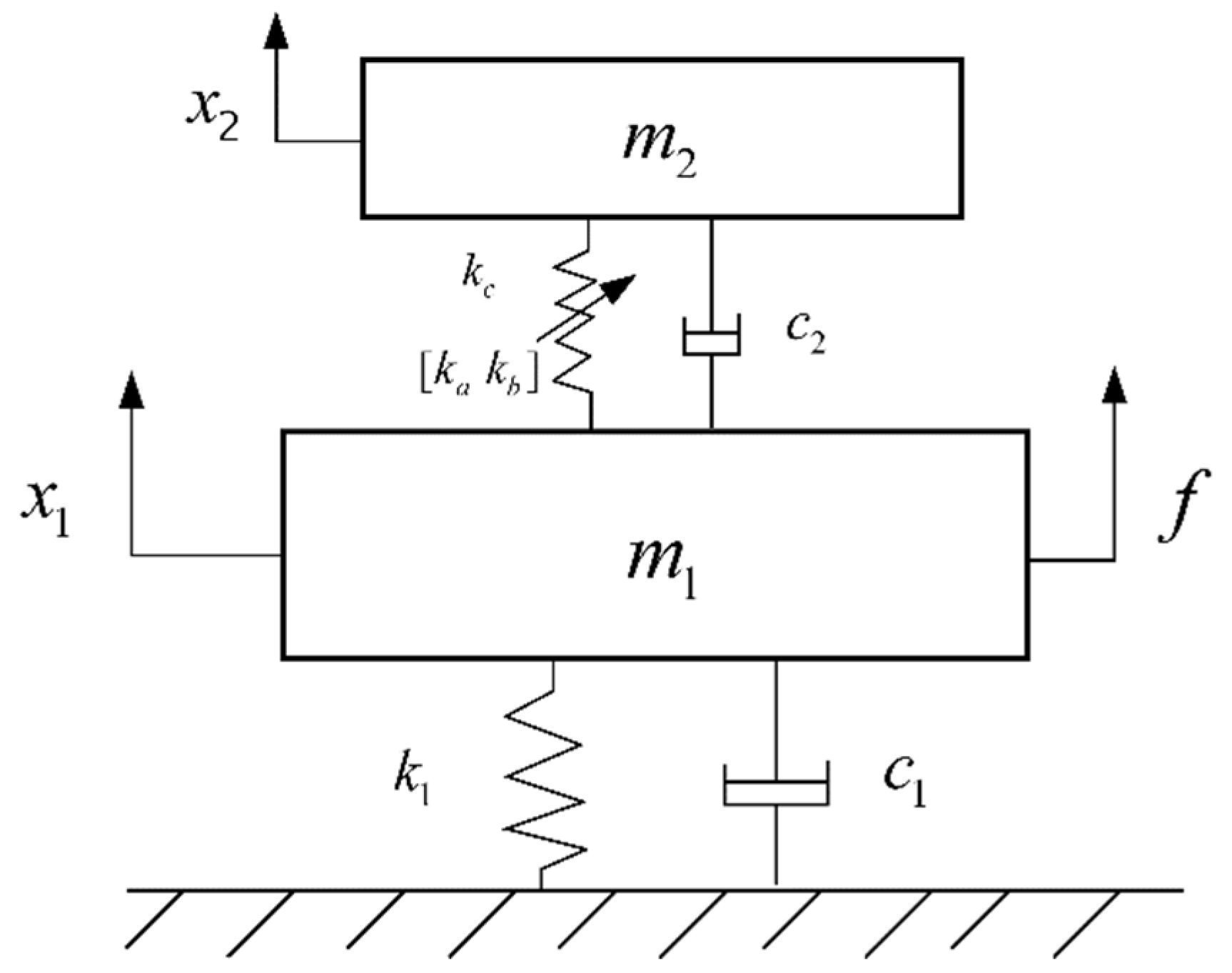
The equivalent dynamic model of the main vibration structure after the installation of the CDVA is shown in Figure 6.

In Figure 6, $m_1$ is the mass of the main vibration structure, $m_2$ is the mass of the dynamic vibration absorber, $k_c$ is the contact stiffness produced by the compression of the rubber ball, $k_a$ and $k_b$ are elastic restoring force stiffness correlation coefficients, $c_1$ is the damping of the main vibration structure, $c_2$ is the damping of the rubber ball, that is, damping in the contact state, and $f=F\cos \omega t$ is the disturbance to the main structure.

The kinetic equations of the overall system are as follows:

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1+c_1{\dot{x}}_1+k_1{x}_1+k_c(x_1-x_2)+k_a(x_1-x_2)+k_b(x_1-x_2{)}^3+c_2({\dot{x}}_1-{\dot{x}}_2)=f\\ m_2{\ddot{x}}_2+k_c(x_2-x_1)+k_a(x_2-x_1)+k_b(x_2-x_1{)}^3+c_2({\dot{x}}_2-{\dot{x}}_1)=0\end{array}\right.$$

(18)

Dimensionless quantities are introduced as follows:

$$\begin{array}{l}{x}_r=x_2-x_1,\hspace{0.33em}{x}_p=x_1,\hspace{0.33em}{X}_0=\frac{F}{k_1},\hspace{0.33em}A=\frac{x_1}{X_0},\hspace{0.33em}B=\frac{x_r}{X_0},\\ {\omega }_1=\sqrt{\frac{k_1}{m_1}},\hspace{0.33em}\hspace{0.33em}{\omega }_2=\sqrt{\frac{k_a+k_c}{m_2}},\hspace{0.33em}\hspace{0.33em}\mu =\frac{m_2}{m_1},\hspace{0.33em}\hspace{0.33em}{\zeta }_1=\frac{c_1}{2m_1{\omega }_1},\hspace{0.33em}\hspace{0.33em}{\zeta }_2=\frac{c_2}{2m_2{\omega }_2}\end{array}$$

Letting $\tau =\omega t$ be the new time measurement, then $\frac{D}{Dt}=\omega \frac{D}{D\tau },\hspace{0.33em}\frac{D^2}{D^{2}t}={\omega }^2\frac{D^2}{D^2\tau }$. Equation (18) can be simplified as follows:

$$\left\{\begin{array}{l}{\omega }^2\frac{1}{{\omega }_1^2}\ddot{A}+2{\xi }_1\omega {\omega }_1\frac{1}{{\omega }_1^2}\dot{A}+{\omega }_1^{2}A-\mu {\omega }_2^2\frac{1}{{\omega }_1^2}B-\frac{1}{{\omega }_1^2}\frac{k_b}{m_1}{X}_0^2{B}^3-\frac{1}{{\omega }_1^2}2\mu \omega {\xi }_2{\omega }_2\dot{B}=\frac{F}{k_1}\cos \omega t\\ {\omega }^2(\ddot{A}+\ddot{B})+{\omega }_2^{2}B+\frac{k_b}{m_2}{X}_0^2{B}^3+2\omega {\xi }_2{\omega }_2\dot{B}=0\end{array}\right.$$

(19)

Then, letting $\lambda =\frac{\omega }{{\omega }_1}$, $\alpha =\frac{{\omega }_2}{{\omega }_1}$, and $\kappa =\frac{k_b{X}_0^2}{k_1}$, substituting these into Equation (19), and simplifying yield

$$\left\{\begin{array}{l}{\lambda }^2(1+\mu )\ddot{A}+2\lambda {\xi }_1\dot{A}+A+\mu {\lambda }^2\ddot{B}=\cos \tau \\ {\lambda }^2(\ddot{A}+\ddot{B})+{\alpha }^{2}B+\frac{\kappa }{\mu }{B}^3+2{\xi }_2\lambda \alpha \dot{B}=0\end{array}\right.$$

(20)

The kinetic equation represented by Equation (20) is rewritten in matrix form as

$$M\ddot{X}+C\dot{X}+KX=F$$

(21)

where

$$\begin{array}{l}M=\left[\begin{array}{cc}{\lambda }^2(1+\mu )& \mu {\lambda }^2\\ {\lambda }^2& {\lambda }^2\end{array}\right],\hspace{0.33em}C=\left[\begin{array}{cc}2\lambda {\xi }_1& 0\\ 0& 2{\xi }_2\lambda \alpha \end{array}\right],\hspace{0.33em}K=\left[\begin{array}{cc}1& 0\\ 0& {\alpha }^2\end{array}\right],\hspace{0.33em}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}F=\left[\begin{array}{c}\cos \tau \\ -\frac{\kappa }{\mu }{B}^3\end{array}\right],\hspace{0.33em}X=\left[\begin{array}{c}A\\ B\end{array}\right]\end{array}$$

In the kinetic equations, the nonlinear factors are reflected in both the contact stiffness term and the restoring force correlation term. Because it is difficult to find the analytical solution for the contact stiffness, it is replaced by a numerical solution expressed as an integral function. In this research, we focus on the influence of the nonlinear factors caused by the elastic restoring force of the rubber ball on the overall vibration absorption characteristics. In Equation (21), for the nonlinear factor $\kappa =\frac{k_b{X}_0^2}{k_1}$, the substitution of $X_0=\frac{F}{k_1}$ can be expressed as

$$\kappa =\frac{k_b{F}^2}{k_1^3}$$

(22)

From Equation (22), it can be seen that the dynamic nonlinearity of the dynamic vibration absorber is related to the nonlinear term of the rubber ball’s restoring force stiffness, the excitation force applied to the main vibration structure and the stiffness of the main vibration structure. When the excitation amplitude of the main vibration structure is small or the stiffness of the main vibration structure is large, the overall dynamics show weak nonlinear characteristics. However, in practical engineering applications, the main vibration structure usually has a large structural stiffness, and the overall system exhibits excessively weak nonlinear characteristics. Therefore, the averaging method is used to solve the approximate response of the system dynamics.

The steady-state response of the main vibration structure after the installation of the CDVA is assumed to be

$$X(\tau )=u(\tau )\cos (\tau )+v(\tau )\sin (\tau )$$

(23)

With respect to the time-slowing parameter, $u(\tau )={\left[u_A\hspace{0.33em}{u}_B\right]}^T$, and $v(\tau )={\left[v_A\hspace{0.33em}{v}_B\right]}^T$. To satisfy the requirements of the Van der Pol transformation and to obtain a functional form of the velocity similar to the linear case, the derivation of Equation (24) yields

$$X^{\prime }(\tau )=-u\sin (\tau )+v\cos (\tau )$$

(24)

The slow-change assumption is

$$u^{\prime }(\tau )\cos (\tau )+v^{\prime }(\tau )\sin (\tau )=0$$

(25)

Substituting Equations (24) and (25) into Equation (21) yields

$$(M{v}^{\prime }-Mu+Cv+Ku)\cos (\tau )-(M{u}^{\prime }+Mv+Cu-Kv)\sin (\tau )=F(u,v,\tau )$$

(26)

Then, Equation (25) is multiplied by $M\cos (\tau )$, Equation (26) is multiplied by $-\sin (\tau )$, and the two resulting equations are added to obtain

$$M{u}^{\prime }=-(Mv+Cu-Kv){\sin }^2(\tau )+(-Mu+Cv+Ku)\sin (\tau )\cos (\tau )-\sin (\tau )F(u,v,\tau )$$

(27)

Assuming that $u$ and $v$ are constants, Equation (27) is integrated over the interval of 0—$2\pi$ and averaged, as follows:

$$M{u}^{\prime }=-\frac{1}{2}(M-K)v-\frac{1}{2}Cu-\left(\begin{array}{l}\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\sin \tau (\cos \tau )d\tau }\\ \frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\sin \tau ·(-\frac{\kappa }{\mu }{B}^3)d\tau }\end{array}\right)$$

(28)

The following substitutions are made: $A=a_A\cos (\tau -{\varphi }_A)$, $u_A=a_A\cos ({\varphi }_A)$,$v_A=a_A\sin ({\varphi }_A)$, $a_A^2=u_A^2+v_A^2$; $B=a_B\cos (\tau -{\varphi }_B)$, $u_B=a_B\cos ({\varphi }_B)$, $v_B=a_B\sin ({\varphi }_B)$, and $a_B^2=u_B^2+v_B^2$. From Equation (28), we have

$$M{u}^{\prime }=-\frac{1}{2}(M-K)v-\frac{1}{2}Cu-\frac{1}{2}\left(\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\\ -\frac{\kappa }{\mu }\frac{3}{4}{v}_B{a}_B^2\end{array}\right)$$

(29)

Similarly, Equation (25) is multiplied by $M\sin (\tau )$, Equation (26) is multiplied by $\cos (\tau )$, and the two resulting equations are added to obtain

$$M{v}^{\prime }=\frac{1}{2}(M-K)u-\frac{1}{2}Cv+\frac{1}{2}\left(\begin{array}{l}\hspace{0.33em}\hspace{0.33em}1\\ -\frac{\kappa }{\mu }\frac{3}{4}{u}_B{a}_B^2\end{array}\right)$$

(30)

To obtain the steady-state solution of the system, Equations (29) and (30) must satisfy $u^{\prime }=0,\hspace{0.33em}\hspace{0.33em}{v}^{\prime }=0$. Subsequent simplification by combining the two equations yields

$$\left\{\begin{array}{l}\left({\lambda }^2(1+\mu )-1\right)v_A+\mu {\lambda }^2{v}_B+2\lambda {\xi }_1{u}_A=0\\ {\lambda }^2{v}_A+({\lambda }^2-{\alpha }^2)v_B+2{\xi }_2\lambda \alpha u_B-\frac{\kappa }{\mu }\frac{3}{4}{a}_B^2{v}_B=0\\ \left({\lambda }^2(1+\mu )-1\right)u_A+\mu {\lambda }^2{u}_B-2\lambda {\xi }_1{v}_A+1=0\\ {\lambda }^2{u}_A+({\lambda }^2-{\alpha }^2)u_B-2{\xi }_2\lambda \alpha v_B-\frac{\kappa }{\mu }\frac{3}{4}{a}_B^2{u}_B=0\end{array}\right.$$

(31)

Equation (31) is a system of coupled nonlinear algebraic equations for $v_A$, $v_B$, $u_A$, and $u_B$, which can be solved numerically with respect to each parameter. There is then $a_A^2=u_A^2+v_A^2$ and $a_B^2=u_B^2+v_B^2$, and Equation (31) is simplified and substituted into the two equations. Through a series of complex simplifications, the main vibration system steady-state response equation can be obtained as follows:

$${\lambda }^4{a}_A^2={(2\alpha \lambda {\xi }_2{a}_B)}^2+{(({\alpha }^2-{\lambda }^2)a_B+\frac{3\kappa }{4\mu }{a}_B^3)}^2$$

(32)

$$\begin{array}{l}{\lambda }^4={\left(2{\xi }_2\lambda \alpha \left({\lambda }^2(1+\mu )-1\right)a_B-2{\xi }_1\lambda ({\alpha }^2-{\lambda }^2)a_B-\frac{3\kappa }{2\mu }{\xi }_1\lambda a_B^3\right)}^2+\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\left(4{\xi }_1{\xi }_2{\lambda }^2\alpha a_B+\mu {\lambda }^4{a}_B+\left({\lambda }^2(1+\mu )-1\right)({\alpha }^2-{\lambda }^2)a_B+\frac{3\kappa }{4\mu }\left({\lambda }^2(1+\mu )-1\right)a_B^3\right)}^2\end{array}$$

(33)

Equation (33) is a multiple algebraic equation solely for the steady-state response $a_B$ of the dynamic vibration absorber, and upon obtaining this equation, it can be substituted into Equation (32) to determine the steady-state response $a_A$ of the main vibration system. Since a single frequency of disturbance corresponds to multiple numerical solutions in nonlinear equations, it is essential to determine the amplitudes that can be achieved physically and to establish the stability of the solutions of the above nonlinear dynamic equation.

To analyze the stability of the solution, perturbation is carried out on Equations (29) and (30). The perturbed solution terms $\Delta u$ and $\Delta v$ are substituted into Equations (29) and (30), and the quadratic and higher-order terms are ignored. Then, the algebraic equation system that the amplitude and phase of the steady solution should satisfy can be obtained. The system of algebraic equations is transformed into the following form:

$$\left[\begin{array}{l}\Delta u^{\prime }\\ \Delta v^{\prime }\end{array}\right]=G\left[\begin{array}{l}\Delta u\\ \Delta v\end{array}\right]$$

(34)

where $G$ is the Jacobian matrix, given by

$$\begin{array}{l}G=\frac{1}{2}\left[\begin{array}{cc}{M}^{-1}& 0^{2\times 2}\\ 0^{2\times 2}& M^{-1}\end{array}\right]\times \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left[\begin{array}{cccc}-2{\xi }_1\lambda & 0& -{\lambda }^2(1+\mu )+1& -\mu {\lambda }^2\\ 0& -2{\xi }_2\lambda \alpha +\frac{3\kappa }{4\mu }{a}_B^2\sin 2{\varphi }_B& -{\lambda }^2& -({\lambda }^2-{\alpha }^2)+\frac{3\kappa }{4\mu }{a}_B^2(1+2{\sin }^2{\varphi }_B)\\ {\lambda }^2(1+\mu )-1& \mu {\lambda }^2& -2{\xi }_1\lambda & 0\\ {\lambda }^2& ({\lambda }^2-{\alpha }^2)-\frac{3\kappa }{4\mu }{a}_B^2(1+2{\cos }^2{\varphi }_B)& 0& -2{\xi }_2\lambda \alpha -\frac{3\kappa }{4\mu }{a}_B^2\sin 2{\varphi }_B\end{array}\right]\end{array}$$

(35)

Based on the stability determination criterion, the stability analysis of the solution can be carried out by judging the eigenvalues of the Jacobian matrix of the system, and all the eigenvalues of the real part of the eigenvalues are negative which indicates that the constant solution is asymptotically stable [26].

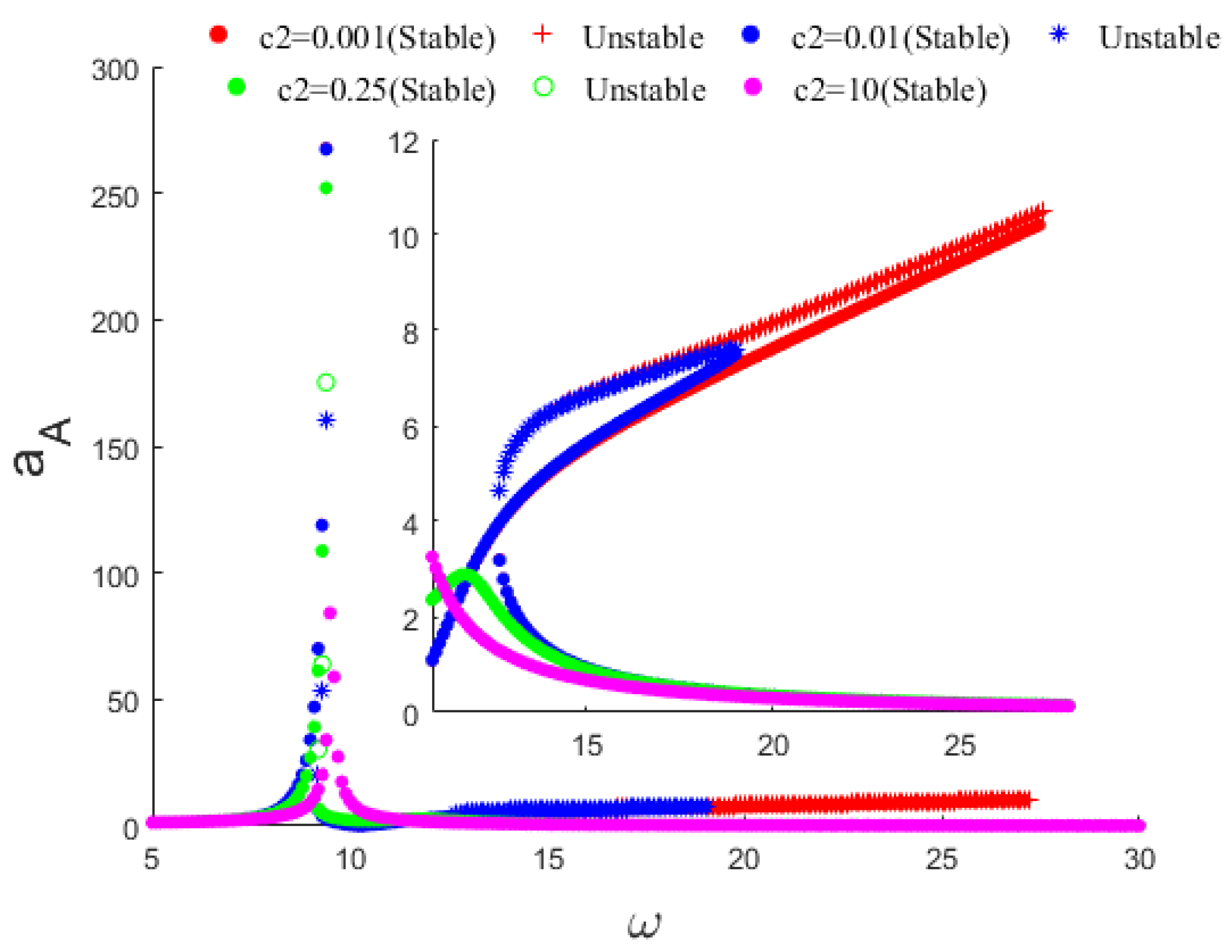
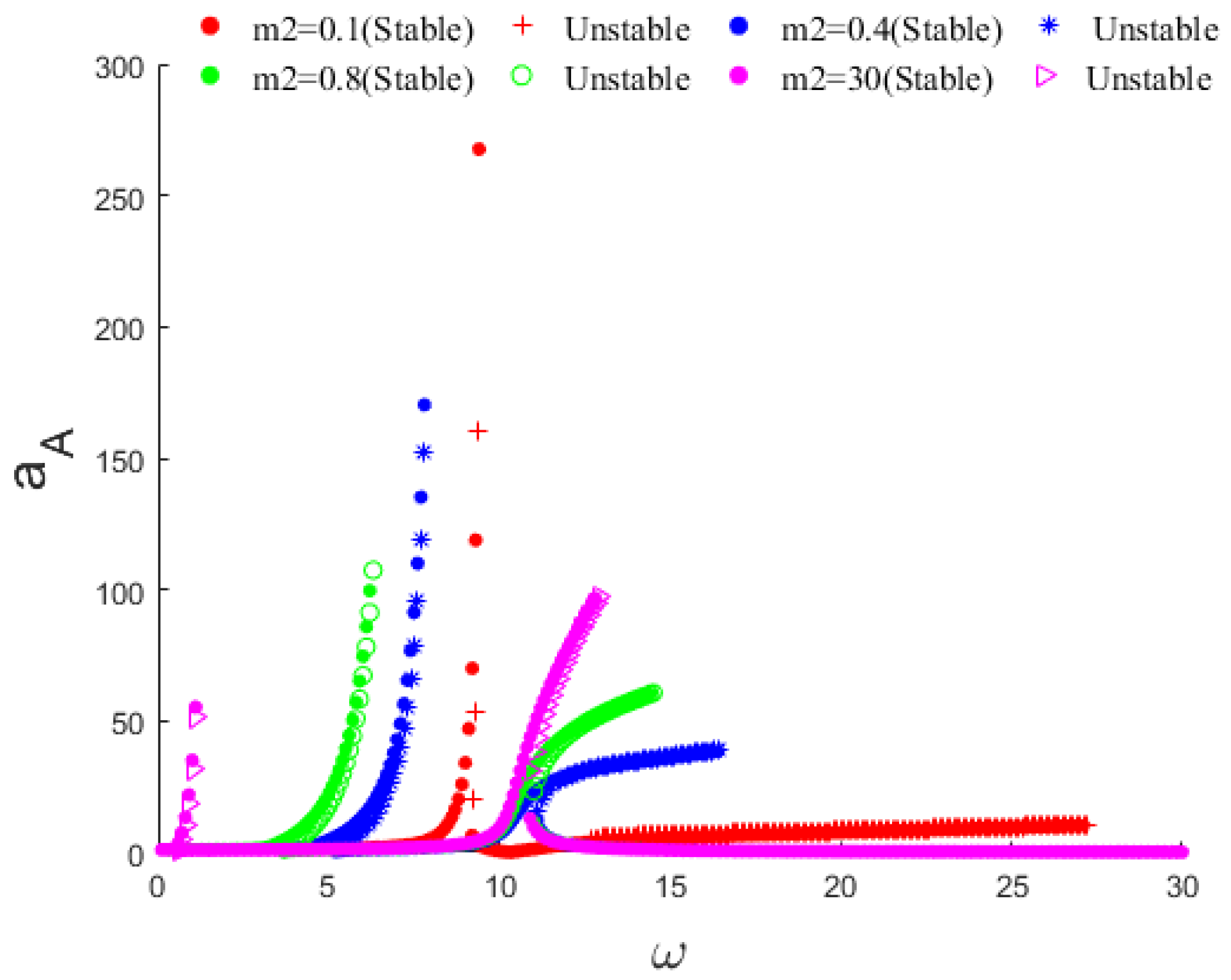
In this research, we used the vpasolve function in MATLAB to solve the dynamical equations of the coupled nonlinear system represented by Equations (32) and (33). The vpasolve function supports the numerical solution of polynomial functions and randomly selects initial values to obtain all numerical solutions within the prescribed range, making it a suitable technique for solving the coupled nonlinear system of equations in question. 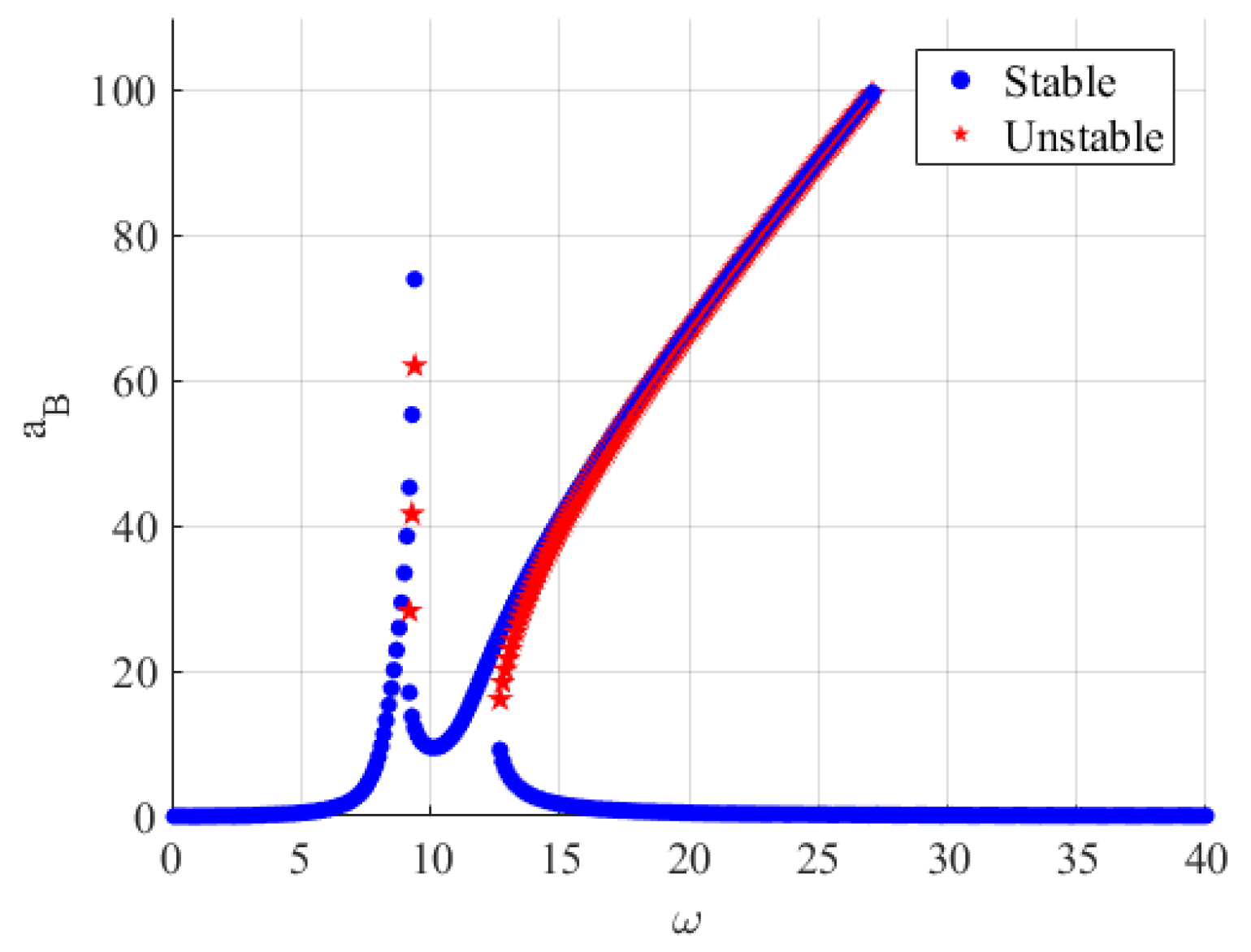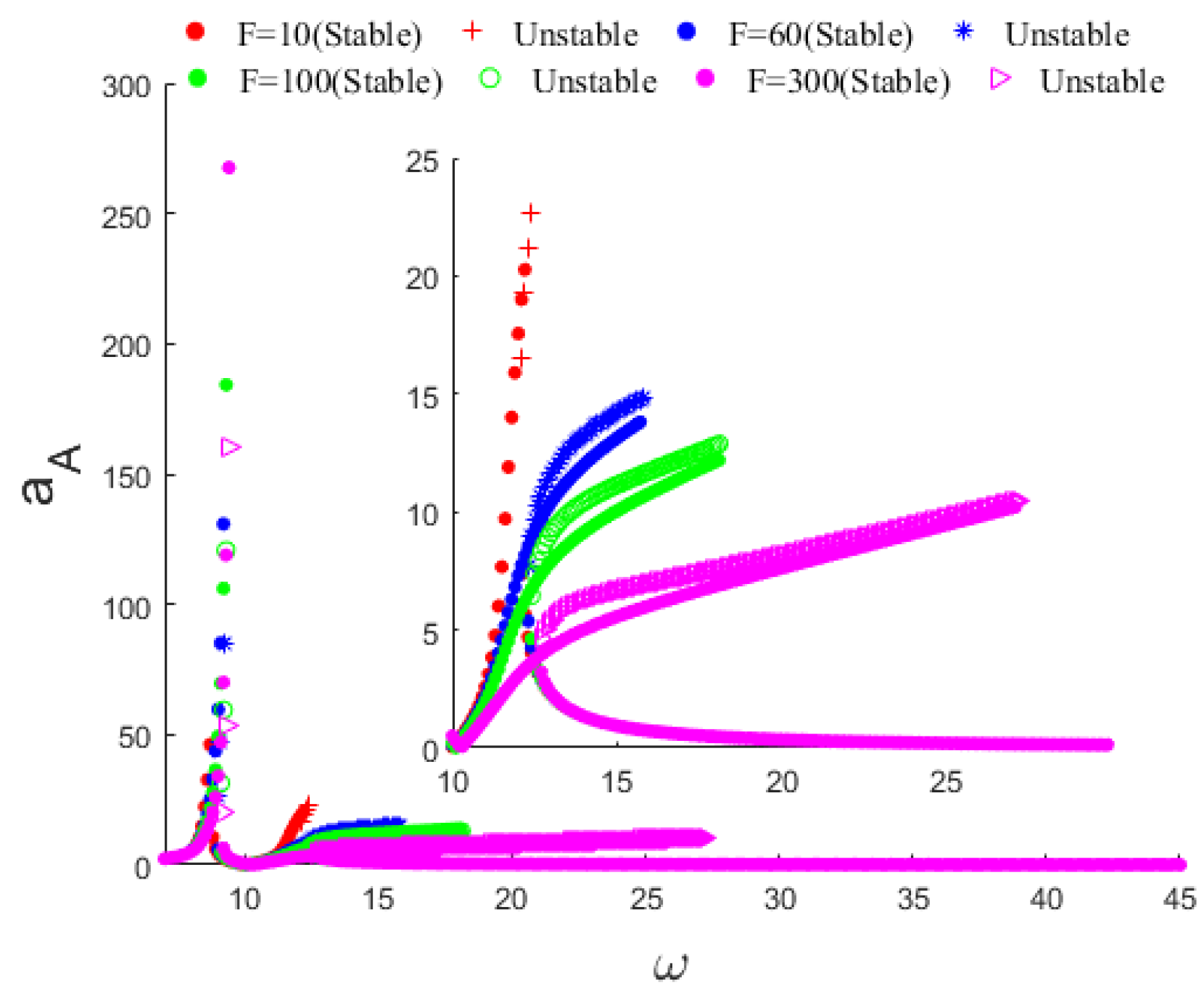The frequency response curves for both the main vibration structure and the dynamic vibration absorber are shown in Figure 7 and Figure 8, which depict the stable and unstable points of the response amplitude for the specified parameters, which can be found in

Table 3. Parameters for the main vibration structure and dynamic vibration absorber.

Parameters	${\mathit{m}}_1$ (kg)	${\mathit{c}}_1$ (N/(m/s))	${\mathit{k}}_1$ (N/m)	${\mathit{m}}_2$ (kg)	${\mathit{c}}_2$ (N/(m/s))	${\mathit{k}}_{\mathit{a}}$ (N/m)	${\mathit{k}}_{\mathit{b}}$ (N/m)	$\mathit{F}$ (N)	${\mathit{k}}_{\mathit{c}}$ (N/m)
Values	1	0.01	100	0.1	0.0033	0.0187	300	0.5	10

.

From the frequency response diagrams of the main vibration structure and the dynamic vibration absorber, it can be seen that for the vibration excitation, the first-order modal vibration frequency response exhibits a “soft” stiffness nonlinear characteristic, while the second-order modal vibration frequency response exhibits a “hard” stiffness nonlinear characteristic. The overall frequency response curve shows obvious amplitude jumps and an unstable response. Similar phenomena of nonlinear characterization can also be observed in the literature [27,28,29].

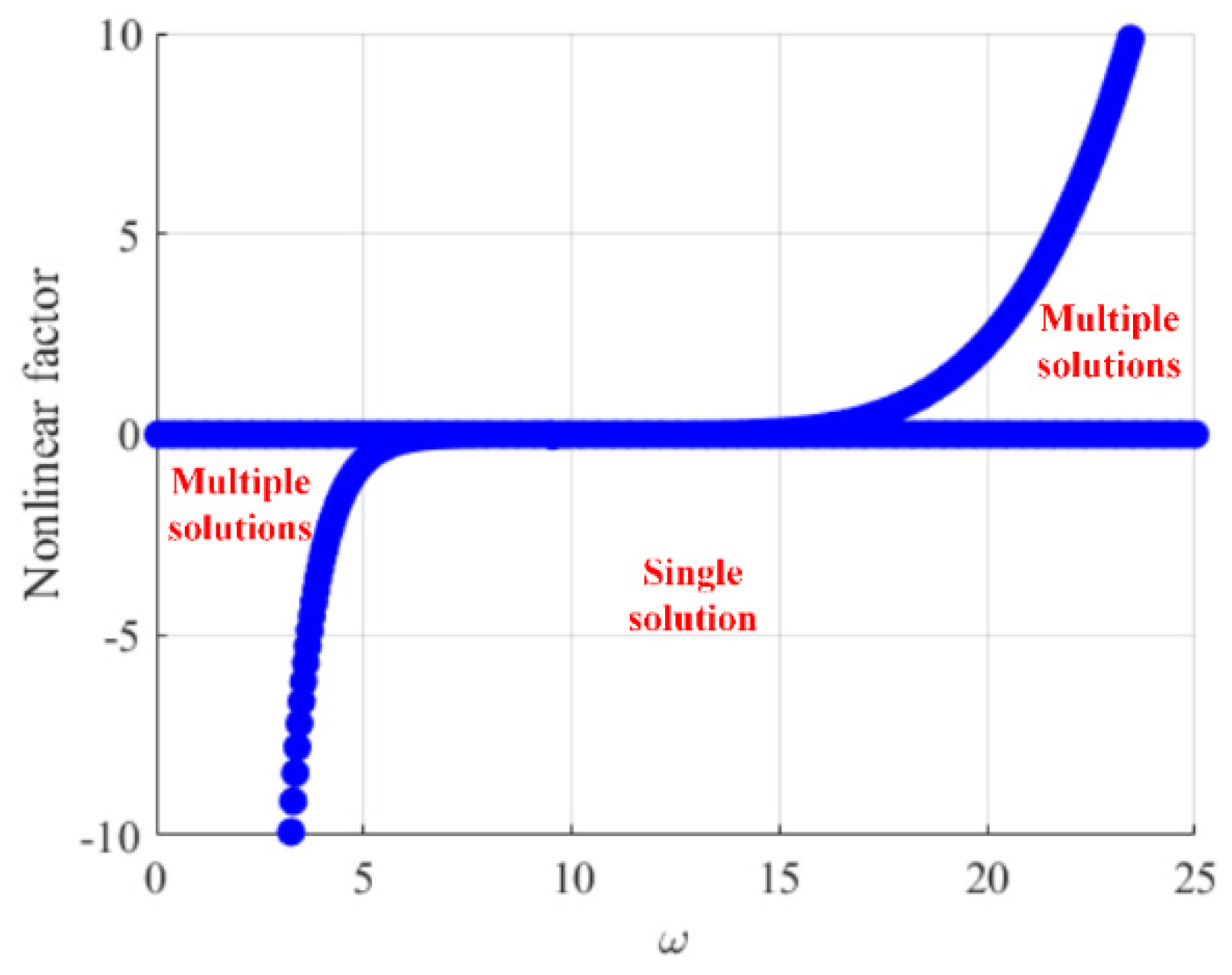
In the process of solving the system of nonlinear equations, we observed that there were both single and triple solutions for the vibration amplitude solution of the main vibration structure. This can also be seen in the above frequency response curves, indicating that the response of the main vibration system exhibited the saddle-knot bifurcation characteristic. The saddle-knot bifurcation diagram is shown in Figure 9. This diagram was used to analyze the stability, as well as the variability properties of the solution.

As shown in Figure 9, in the region of the curve encompassed by the excitation frequency and the corresponding nonlinear factor, there were three solutions for the displacement of the main vibration structure. In the other regions, there was only a single solution, which was consistent with the phenomenon shown in the frequency response curves. As the excitation frequency increased, the saddle-knot bifurcation condition was in the “single solution” region for the system’s own intrinsic property conditions, and the response of the main vibration structure continued to increase. When the amplitude solution of the main vibration structure reached the first saddle node, the structural response became unstable as a result of the bifurcation phenomenon. The saddle-node bifurcation condition then reached the “multi-solution” region, and the amplitude of the main vibration structure decreased sharply. Subsequently, the main vibration structure response “jumped” to the next stable region, representing the saddle-node bifurcation condition in the “single solution” region. As the frequency of excitation increased, the displacement response of the main vibration structure rose to its second peak after a brief decline. Subsequently, the entire system response reached the second saddle node. The structural response jumped to another unstable state and the saddle-node bifurcation condition came to another “multi-solution” region, where the system response amplitude jumped in the opposite direction (in the direction of decreasing frequency) to a stable point and thereafter ended at the second saddle node. Immediately after this, the response of the system during stabilization decreased in amplitude as the excitation frequency increased and eventually stabilized.

4. Numerical Analysis and Discussion

Nonlinear behavior broadens the frequency band of a dynamic vibration absorber to a certain extent, but the nonlinearity also gives rise to structural response instability and amplitude amplification problems [30,31]. The introduction of nonlinearities will cause nonlinear behaviors, such as response bouncing, bifurcation, and hysteresis in the main vibration structure, reducing the ability of the dynamic vibration absorber to suppress vibration [32]. This section analyzes the impact of parameter variations on the dynamic characteristics of the main vibration structure, considering relevant parameters that influence the nonlinearity of the dynamic vibration absorber. Furthermore, it explores the principles of vibration reduction from a parameter design perspective.

4.1. Damping

Damping, as an important parameter of the power absorber, has the effect of reducing the vibration amplitude of the main vibration system, as well as a certain frequency modulation property. The damping of the ball-contact dynamic vibration absorber studied in this research was provided by the damping of the rubber ball itself, and changes in damping will affect the dynamic behavior of the overall system. The parameters substituted for the numerical simulation are presented in Table 3, where the damping coefficients are $c_2=0.001,\hspace{0.33em}0.01,\hspace{0.33em}0.25,\hspace{0.33em}10$. The frequency response curves of the main vibration structure for different damping coefficients are shown in Figure 10.

As can be seen in Figure 10, during the damping change process, the main frame of the frequency response curve with the influence of nonlinear factors was basically the same, and the degree of inclination of the “hard” stiffness frequency response curve was unchanged. However, the region of unstable response exhibited at the second-order fundamental frequency of the main vibration structure decreased with increasing damping (the absorption frequency band was reduced). When the damping reached a specific value, the nonlinear effect at the second-order fundamental frequency disappeared entirely, and the frequency response curve became stable. At that moment, the amplitude of the frequency response was minimal. At the first-order fundamental frequency of the main vibration structure, with the increase in damping, the main resonance frequency point had a tendency to increase slightly, the main vibration frequency point was shifted to the right, the “soft” stiffness nonlinear effect decreased, and the amplitude of the response of the main vibration structure decreases first and then increases with the increase in damping. The aforementioned analysis demonstrated that the damping of the dynamic vibration absorber had an impact on the extent of the nonlinear effect region. A higher level of damping resulted in a smaller nonlinear effect area and enhanced the system stability. However, blindly increasing the damping of a dynamic vibration absorber is not advisable. While a certain level of damping can ensure system vibration stability, excessive damping will amplify the amplitude of first-order fundamental frequency vibrations in the main vibration system and diminish the overall vibration reduction effectiveness. Therefore, in the selection of damping parameters of a dynamic vibration absorber, appropriate damping values should be selected according to engineering requirements. Figure 11 shows the saddle-node bifurcation diagram in the damped condition $c_2=0.001,\hspace{0.33em}0.25$, which shows the process of the system’s multiple-solution versus single-solution region with damping, and explains the phenomenon of reduced nonlinear effects due to the reduction in the multiple-solution region.

4.2. Contact Stiffness

The contact stiffness of the rubber ball with initial compression also affects the nonlinear dynamic characteristics of the overall system. The influences of various factors on the contact stiffness and the overall growth trend with each factor’s increase were not individually considered in this research. Instead, the focus was placed on investigating the impact of the contact stiffness as an input parameter on the frequency response of the main vibration structure. Figure 12 shows the frequency response curves of the main vibration system when the contact stiffness values are $k_c=1,\hspace{0.33em}10\hspace{0.33em},100\hspace{0.33em},200$.

From Figure 12, it can be seen that at the second-order resonance frequency, the nonlinear frequency response curve of the main vibration system gradually becomes steeper as the contact stiffness increases; that is, the “hard” stiffness characteristic becomes more pronounced. In addition, the nonlinear frequency band decreases and the second-order nonlinear main resonance frequency shifts to the right, while the maximum response amplitude decreases. When the contact stiffness reached a certain value, the effect of nonlinear factors disappeared. The influence of nonlinear factors on the first-order principal vibration frequency diminished as the contact stiffness increased. The frequency response curve of the principal vibration structure exhibited a slight rightward shift, and the amplitude of the frequency response showed an oscillatory pattern characterized by an initial decrease followed by an increase with increasing contact stiffness and subsequently decreased. The above analyses show that an increase in the contact stiffness of the dynamic vibration absorber could reduce the degree of nonlinear influence, but this also had the disadvantage of reducing the vibration reduction effect, as well as shortening the absorption frequency band. Therefore, an appropriate increase in the contact stiffness value could increase the vibration reduction effect and improve the overall system stability.

4.3. Moving Mass

In the dynamic vibration absorption technique, the mass ratio is an important parameter that affects the vibration reduction effect. This paper focuses on the influence of the change in the dynamic mass of the dynamic vibration absorber on the dynamic response of the main vibration structure. The frequency response curves for the main vibration system with moving mass $m_2=0.1,\hspace{0.33em}0.4,\hspace{0.33em}0.8,\hspace{0.33em}30$ are shown in Figure 13.

Figure 13 shows an interesting phenomenon. In contrast to the effects of the contact stiffness and damping on the first-order frequency response of the main vibration system, the moving mass had a significant influence on both the resonance frequency and the amplitude of the first-order frequency response curve. With the increase in the dynamic mass, the second resonance frequency of the main vibration structure remained almost unchanged. However, the overall “hard” stiffness characteristics were boosted, resulting in a reduced nonlinear frequency band, and the maximum frequency response amplitude was gradually increased. The first-order resonant frequency response curve gradually shifted to the left as the moving mass increased, and the nonlinear frequency band decreased, representing the enhancement of “soft” stiffness characteristics. This suggested that an increase in the moving mass tuned the first-order resonance frequency point of the main oscillating structure to a lower frequency, contributing to the suppression of first-order low-frequency vibrations. However, when the moving mass increased, the nonlinear absorption frequency bandwidth was also lost, and the vibration reduction effect of the second-order resonance decreased.

4.4. Cubic Stiffness Term for Elastic Restoring Force

The cubic stiffness term $k_b$ of the elastic resilience is a parameter determined by the material properties of the rubber ball. As a parameter that can be selected from among nonlinear factors, it exhibited a positive correlation with the nonlinear factor $\kappa =\frac{k_b{F}^2}{k_1^3}$ and also influenced the nonlinear characteristics in dynamics. The frequency response curves of the main vibration structure at different $k_b$ values are shown in Figure 14.

At the second-order resonance frequency point, the various frequency response curves of the main vibration structure showed a certain degree of rightward shift as the coefficient of the cubic stiffness term increased, and the degree of nonlinearity exhibited an increase with the increase in the coefficient of the cubic stiffness term. The frequency response curve of the “soft” stiffness characteristics exhibited minimal changes at the first-order resonance frequency point, while the response amplitude of the main vibration structure increased with the increase in the coefficient of the cubic stiffness term. The effect of the cubic stiffness term on the first-order and second-order response amplitudes was exactly the opposite. Therefore, when selecting rubber ball materials, the response characteristics at the first-order and second-order resonance points should be weighed to select the value of the cubic stiffness term coefficient that optimizes the vibration reduction effect.

In this section, a list of parameters that influenced the nonlinear dynamic characteristics of the main vibration structure is provided. Generally, changes in relevant parameters alter the “soft” and “hard” stiffness characteristics, as well as the nonlinear frequency range to some extent. This could be attributed to variations in the occurrence of “a single solution” and “multiple solutions” generated by the nonlinear dynamic equation under different parameter conditions. When these parameter changes increased nonlinearity, there was a larger presence of “multiple solutions”, resulting in higher response instability within the main vibration structure. Although the decrease in the main vibration response amplitude might have varied, this also led to an expansion of the vibration absorption frequency band. Therefore, a reasonable selection of the parameters of the dynamic vibration absorber was the key to achieving the best vibration reduction effect. To compare the vibration reduction effects of a nonlinear dynamic vibration absorber and a linear dynamic vibration absorber, Figure 15 illustrates the frequency response curves of the main vibration structure under varying contact stiffness conditions, as well as the frequency response curves after linearization.

Figure 15 clearly illustrates the differences in the vibration suppression frequency range and amplitude between linear and nonlinear dynamic vibration absorbers. Disregarding stability requirements, it could be observed that the vibration suppression frequency range of the CDVA was wider than that of the linear dynamic vibration absorber. Additionally, the amplitude of the CDVA could be tuned to a reasonable level.

5. Structural Design and Experiments

5.1. Structure Design

The CDVA was built as a one-piece mounting structure based on a ball contact form to allow it to be attached and detached freely, as shown in Figure 16. The inner cone surfaces of the contact block and the moving mass held the rubber ball in place in the CDVA, creating stiffness with contact. The rubber ball’s own damping acted as the CDVA’s damping. The support sleeve was driven to apply a compression force to the rubber ball by screwing the nut into the threaded compression rod, and the compression force on the rubber ball could be adjusted by varying the depth of the nut. To ensure continuous vibration transmission and prevent unintended contact block wobbles in the support sleeve, the contact blocks were screwed into the sleeve. A threaded mounting rod on the upper support sleeve connected the entire CDVA to the main vibration structure. Denser metal materials were employed for the moving mass throughout the CDVA structure to increase the mass ratio and prevent the issue of excessive volume brought on by lighter materials. Additionally, an aluminum alloy with high strength and low-density properties was chosen for the support structure of the CDVA to reduce the additional mass of the main vibration structure induced by the CDVA. The structure material of the CDVA is shown in

Table 4. Structure material of the CDVA.

Components	Materials
Support sleeve	2A12
Threaded compression rod	2A12
Nut	2A12
Contact block	2A12
Moving mass	9Cr18Mo
Rubber ball	Nitrile

.

5.2. Experiments

5.2.1. Static Compression Stiffness Validation

Obtaining the displacement values of the rubber ball contact form for various compression forces and using differential calculations to obtain the stiffness values resulting from the contact were required to confirm the viability of the contact stiffness theoretical model. In this research, the force–displacement data were obtained using an Edelbrock HLD force tester with a range of 0–1000 N and a displacement accuracy of 0.01 mm. The rubber ball was positioned inside two contact blocks during the experiment, and the rubber ball-contact block served as the test structural component for the compression test. The micrometer on the manometer’s side measured the amount of deformation of the rubber ball, while the force transducer measured the applied force. The parameters of the overall structure are presented in

Table 5. Parameters of structural elements in compression tests.

Parameters	Values
Diameter of the rubber ball (mm)	35
The hardness of the rubber ball (Shore A)	50
Inner cone angle (°)	45

. The compression tests site view is shown in Figure 17.

Following the acquisition of the test data, the experimental data were subjected to displacement-force fitting and differential processing to provide the force-contact stiffness data. Figure 18 depicts the comparison diagram of the contact stiffness test and theory. Here, $G_{\mathrm{factor}}\approx 0.98$.

As shown in Figure 18, the theoretical model data for contact stiffness within 600 N agreed well with the test data in the comparison chart. However, above 600 N, the test data revealed a dramatic change in contact stiffness, indicating that the rubber was excessively stiff. The possible reason for this phenomenon was that the force between the molecules of the elastomeric material restricted the expansion in the radial direction, which made it difficult for the rubber ball to undergo further axial compression and caused it to exhibit a sharp increase in stiffness. In practice, the variable stiffness adjustment section of the dynamic vibration absorber needs to meet the requirements for controllability. Therefore, when changing the compression force of the dynamic vibration absorber, the situation of the rubber ball being over-compressed to form an overall structure that is excessively stiff should be avoided.

5.2.2. Dynamic Compressive Stiffness and Damping

The primary resonant structure of the CDVA was subjected to vibrational excitation in its operating environment, and variations in the initial contact state of the rubber ball, as well as changes in the excitation frequency, could affect the overall dynamic stiffness and damping. Previous studies have demonstrated that the dynamic response of elastic components is commonly influenced by various geometric and material properties. Additionally, it is well-known that the dynamic stiffness and damping characteristics of rubber materials exhibit a frequency-dependent behavior. To examine the variations in dynamic stiffness and damping characteristics of the contact principle structure between the rubber ball and the inner cone, resulting from different contact states and changes in excitation frequency, this study employed the loss factor as a measure of the overall damping characteristics. Experimental tests were conducted to investigate the dynamic stiffness and loss factor of the rubber ball contact at various excitation frequencies. The experimental setup for the testing of dynamic stiffness and loss factor involved the use of a Dynamic Mechanical Analyzer (DMA) capable of providing dynamic forces up to ±500 N and dynamic displacements within the range of ±6 mm. Sinusoidal excitation with lower frequencies was employed during the experiments to mitigate the influence of inertial forces within the vibrational system. Specifically, three excitation frequencies (5, 10, and 20 Hz) were utilized, with all excitation amplitudes set at 0.5 mm. The experimental specimens, composed of nitrile 50 rubber balls, were subjected to axial loads, and their corresponding deformations were measured for different contact states for three excitation frequencies. Hysteresis loops were then obtained for different initial compression force conditions, enabling the calculation of the dynamic stiffness and loss factors for each excitation frequency and contact state. The experimental setup is illustrated in Figure 19.

The variation in dynamic stiffness with different excitation frequencies and initial contact states is depicted in Figure 20.

It can be observed from the graph that the dynamic stiffness curves of the primary structure increased with an increase in the initial compression force for all three excitation frequencies. However, before 120 N, the dynamic stiffness did not exhibit significant frequency dependence for different excitation frequencies. After reaching 120 N, it was evident that the excitation frequencies of 10 Hz and 20 Hz had a more pronounced effect on the dynamic stiffness compared to 5 Hz, indicating a certain degree of frequency dependence. The overall dynamic stiffness increases as the excitation frequency was increased. The above analysis demonstrated that the designed contact principle structure exhibited a negligible influence from the excitation frequency within a certain frequency range. Furthermore, it was evident that the range of 0–120 N compression force represented the optimal adjustment stage, showing high stability in dynamic stiffness. The observed phenomenon might be attributed to the fact that the contact principle structure exhibited sufficient dynamic freedom of deformation for initial small-range compression. Because the compression force exceeded 120 N, it is possible that the deformation space decreased and the degree of stiffening increased, thereby enhancing the frequency dependence effect.

The variation in the loss factor of the contact principle structure with different initial contact forces at various excitation frequencies is shown in Figure 21.

In Figure 21, the loss factor of the contact principle structure demonstrates a significant frequency dependence for different compression states. At each excitation frequency, the loss factor increased to a certain extent with the increase in the initial compression force, and the magnitude of this increase was greater at higher excitation frequencies. Moreover, the overall magnitude of the loss factor increase became larger as the excitation frequency increased. This phenomenon was also observed in the structural damping, indicating that excessive excitation frequencies could lead to significant changes in the loss factor, potentially causing the tuned dynamic vibration absorber to deviate from its optimal absorption point. However, as analyzed in Section 4.1, it could be observed that increasing the damping of the CDVA can reduce the nonlinearity and stabilize the primary vibration system. Therefore, comprehensive consideration of stability and damping effectiveness is required in the design of dynamic vibration absorbers.

6. Application Test

A dynamic vibration reduction application test was performed to confirm the dynamic vibration absorber’s ability to absorb vibration. The majority of researchers [33,34] have chosen this kind of primary vibration structure for the performance assessment of dynamic vibration absorbers due to the simplicity of the two-end fixed support beam structure, which is typical of continuous systems. Therefore, this research also used a two-end fixed support beam to verify the vibration absorption effect. The constructed beam structure experimental platform is shown in Figure 22.

The adjustment frame was fastened to the beam structure, and the adjustment frame was attached to the vibration isolation platform with pressure blocks to lessen the impact of ambient vibrations on experimental data collection. The shaker was mounted underneath the beam, and it gave the beam a certain amount of vibration excitation in the middle position. The impedance collected the excitation signal, and the accelerometer acquired the vibration displacement acceleration of the beam during excitation. Random excitation was used to assess the platform’s dynamics, and modal identification of the vibration data, based on the least squares complex frequency domain method [35], was used to determine the natural frequencies of the beam. The material of the beam was 2A12. The structural parameters of the beam are presented in

Table 6. Structural parameters of the beam.

Parameters	Values
Dimensions (mm)	800 × 100 × 11
Elastic modulus (GPa)	70
Poisson’s ratio	0.3
Mass (kg)	2.39
First-order natural frequency (Hz)	126.1
Second-order natural frequency (Hz)	451.8

.

The amount of auxiliary materials used, how the rubber was vulcanized, and the rubber’s external dimensions all had an impact on the rubber’s damping value during the rubber production process. Because the damping values of customized rubber balls cannot be precisely controlled, extensive materials and testing are required to determine the damping values. In this research, the stiffness of the dynamic vibration absorber was adjusted by varying the compression force, and only the optimal homology was employed for the selection of parameters to produce the roughly necessary intrinsic frequency. To demonstrate the vibration reduction effect of the dynamic vibration absorber in various compression situations, the vibration amplitude–frequency curves of the primary vibration structure before and after vibration reduction were obtained. The parameters of the dynamic vibration absorber are shown in

Table 7. Parameters of the dynamic vibration absorber.

Parameters	Values
Mass (kg)	0.405
Damping	0.19
The hardness of the rubber ball (ShoreA)	50
Diameter (mm)	35
Half cone angle (°)	45

.

The dynamic vibration absorber was tuned to a certain compression condition. The description of excitation frequency is shown in

Table 8. Description of the excitation.

Type	Frequency (Hz)	Force (N)
Sinusoidal excitation	100	-

. The amplitude of the excitation force is not given due to the functional limitations of the signal generator. Figure 23 shows the comparison of the main vibration structure’s time domain and amplitude–frequency curves before and after vibration absorption when the compression state is close to the main frequency of the main vibration structure.

As shown in Figure 23, the dynamic vibration absorber exhibited a significant absorption effect when the excitation frequency was close to the natural frequency of the primary vibration system, as can be observed from the time-domain curves and the frequency-domain curves. The vibration attenuation ratio at the first order is 60.92%. In Figure 24, four sets of vibration amplitude–frequency curves of the primary vibration structure for various compression forces were obtained by adjusting the compression force of the rubber ball in the power absorber while maintaining the shaker’s excitation frequency. The vibration reduction performance would be significantly enhanced if the vibration absorber parameters were applied strictly according to the optimal design.

According to Figure 24, the dynamic vibration absorber demonstrated a specific capacity for vibration reduction at various compression forces, showing that the vibration reduction effect could be optimized by adjusting the dynamic vibration absorber’s frequency. The dynamic vibration absorber’s ability to reduce vibration grew as the compression force increased, but as the compression force increased further, the first-order mode vibration reduction effect no longer became better. This reverse growth phenomenon, which was in line with the conclusions of the theoretical analysis, indicated that the damping dissipation effect would be ineffective at that moment. The vibration reduction performance would be significantly enhanced if the vibration absorber parameters were applied strictly according to the optimal design. It is worth noting that the mass of the dynamic vibration absorber in this study is relatively high compared to the mass of the primary vibration system. Through comparative experiments, it was found that the increase in mass resulted in a vibration reduction percentage of approximately 10%, indicating that the designed dynamic absorber still has a good vibration reduction effect.

7. Conclusions

Based on contact variable stiffness characteristics, this research suggested a ball contact dynamic vibration absorber construction. The nonlinear dynamic behavior of the main vibration structure was simulated using the contact stiffness theory modeling and a two-degree-of-freedom nonlinear dynamic model. Additionally, the impact of the design parameters on the frequency response of the main vibration structure was examined. The stiffness theoretical model was validated through dynamic and static compression tests of the contact principle structures, enabling a study of the variations in the dynamic stiffness and damping characteristics of the contact for varying excitation frequencies. The ball contact dynamic vibration absorber was implemented on a fixed beam structure subjected to vibration excitation to assess its feasibility for reducing vibrations. The results indicated that the dynamic vibration absorber had a broad frequency band for vibration absorption and could be used effectively for vibration suppression of the first-order mode of the primary vibration structure. The entire structure could be used to reduce vibration in plate and beam constructions, and its basic structure could be miniaturized for use in reaction wheels and other aerospace structures that must adhere to rigorous volume, weight, and other requirements. Naturally, we also looked at the vibration reduction effect of the radial sway mode in the transverse direction during the experimental study of this dynamic vibration absorber, which was very impressive and served as our basis for the development of this dynamic vibration absorber into a multi-degree-of-freedom vibration reduction structure. Hence, the selection of contact parameters and the reasonable planning of rubber ball parameters will be the focus of multi-degree-of-freedom vibration suppression of a dynamic vibration absorber.