Research on Intelligent Design of Geometric Factor Encoding for Aircraft Engine Turbine Structures
Abstract
1. Introduction
2. Models
2.1. Geometric Coding Model for Turbine Rotor Structure
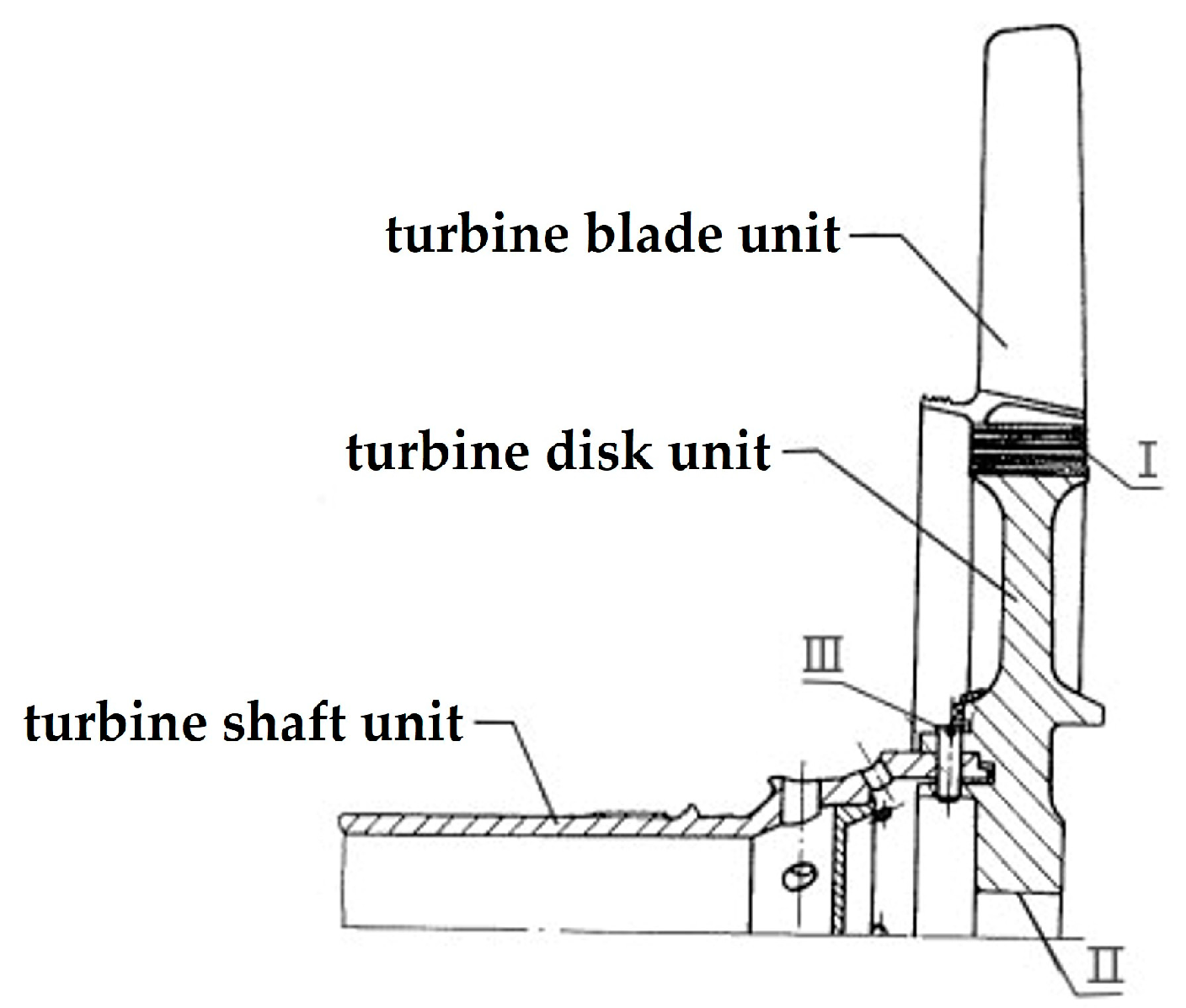
2.1.1. Turbine Rotor Structural Unit
2.1.2. Property Family of Turbine Rotor Structural Unit
2.2. Geometric Coding Model of Turbine Rotor Unit
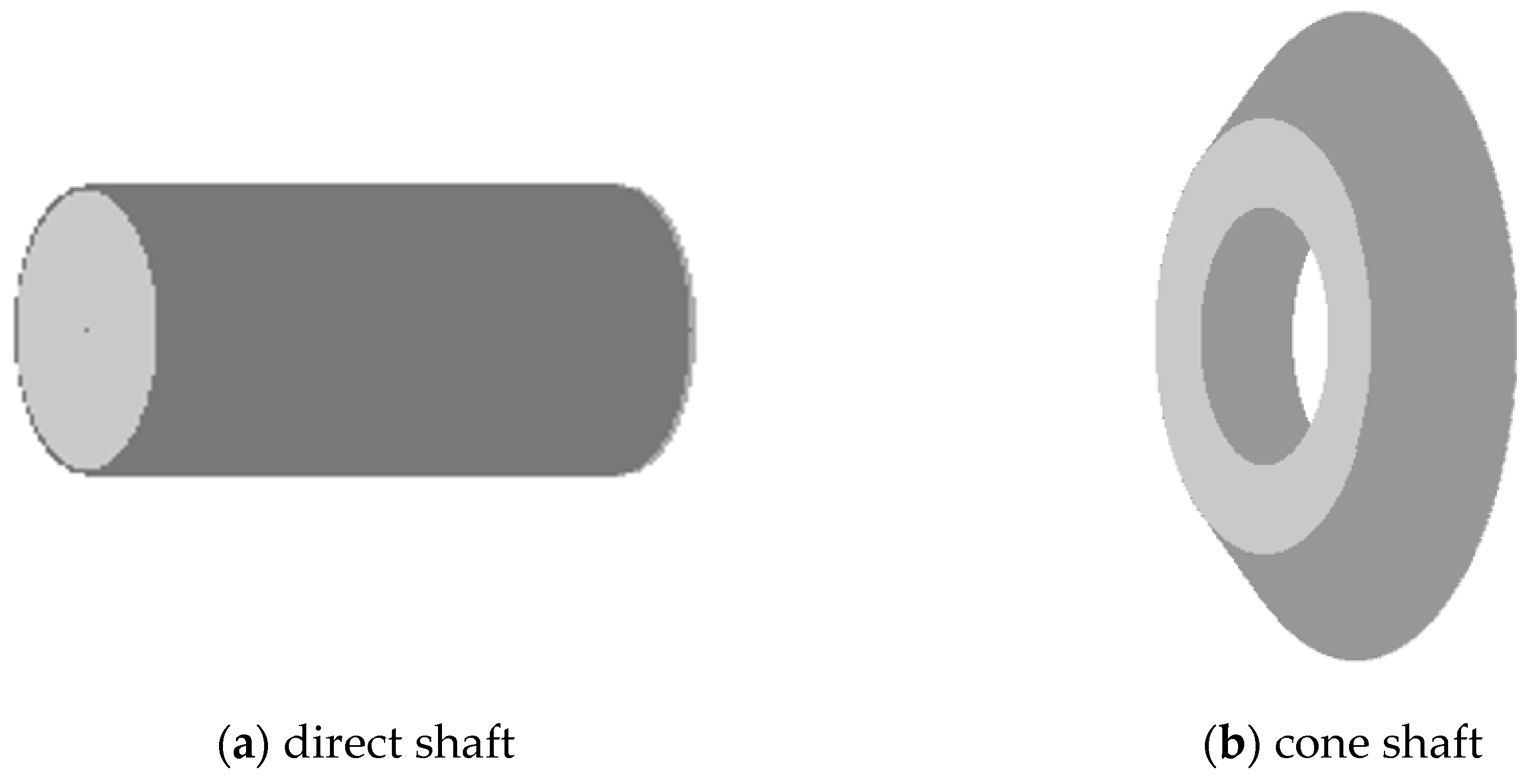
2.2.1. Geometric Encoding of Shaft Unit
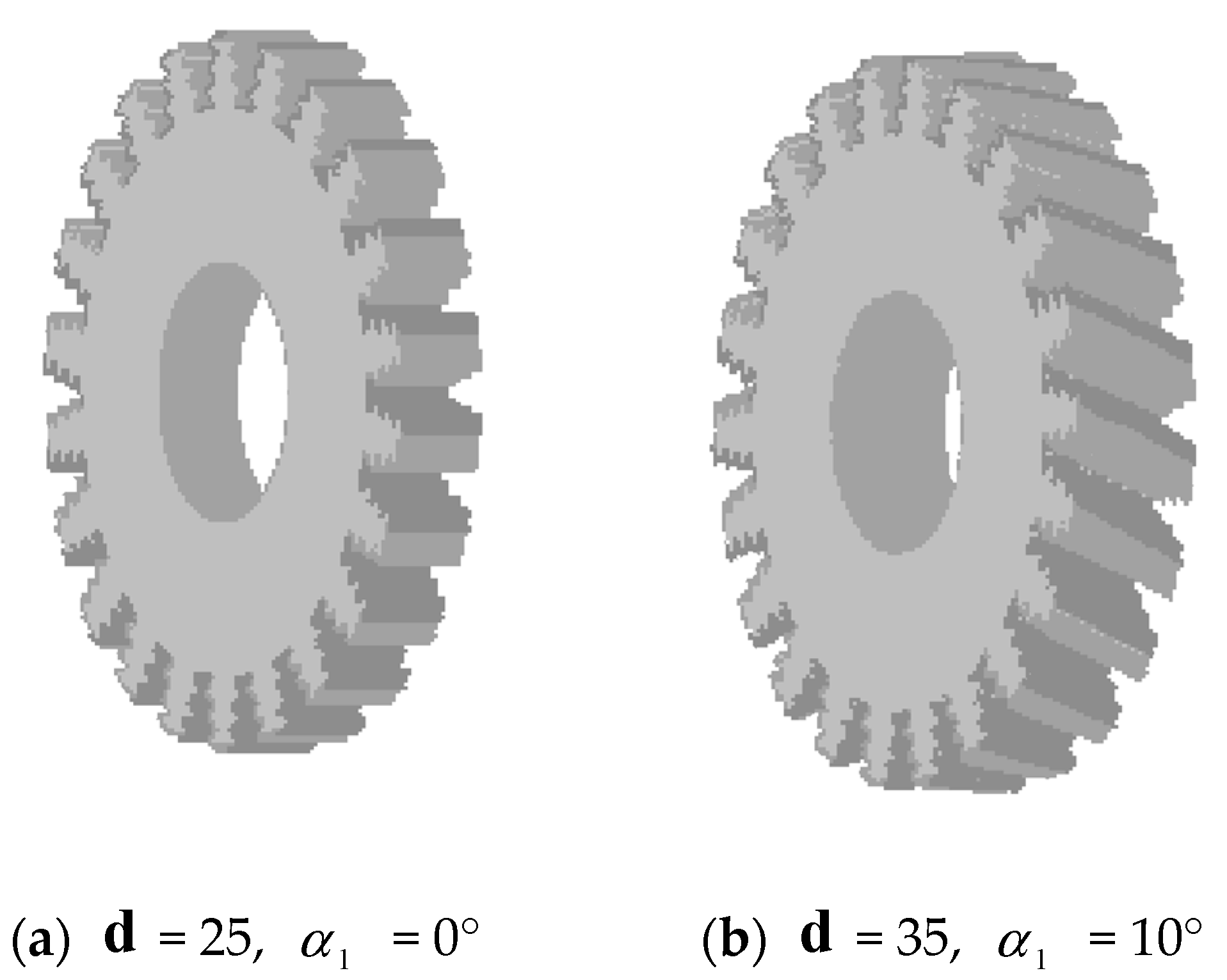
2.2.2. Geometric Encoding of Disk Unit
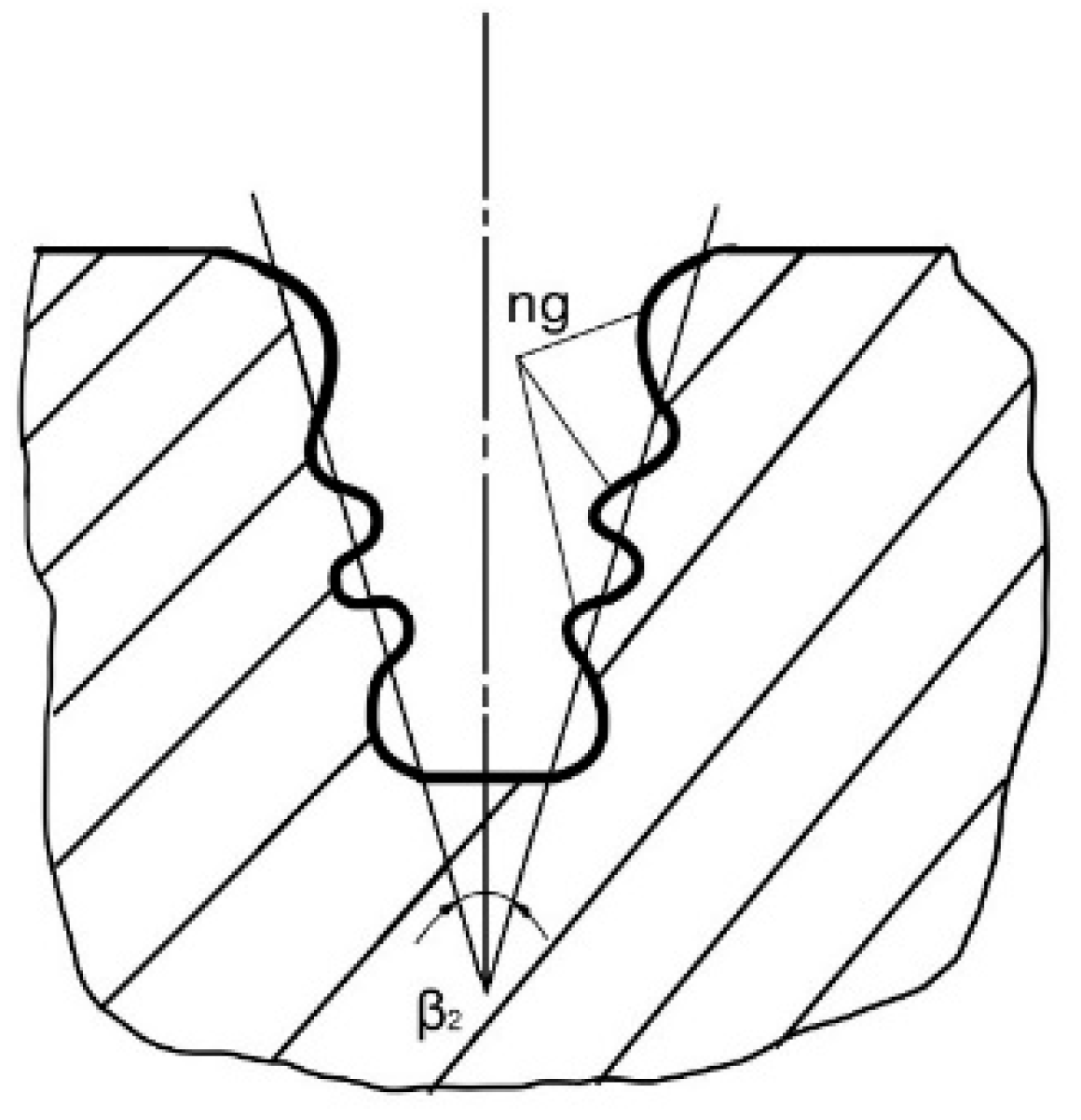
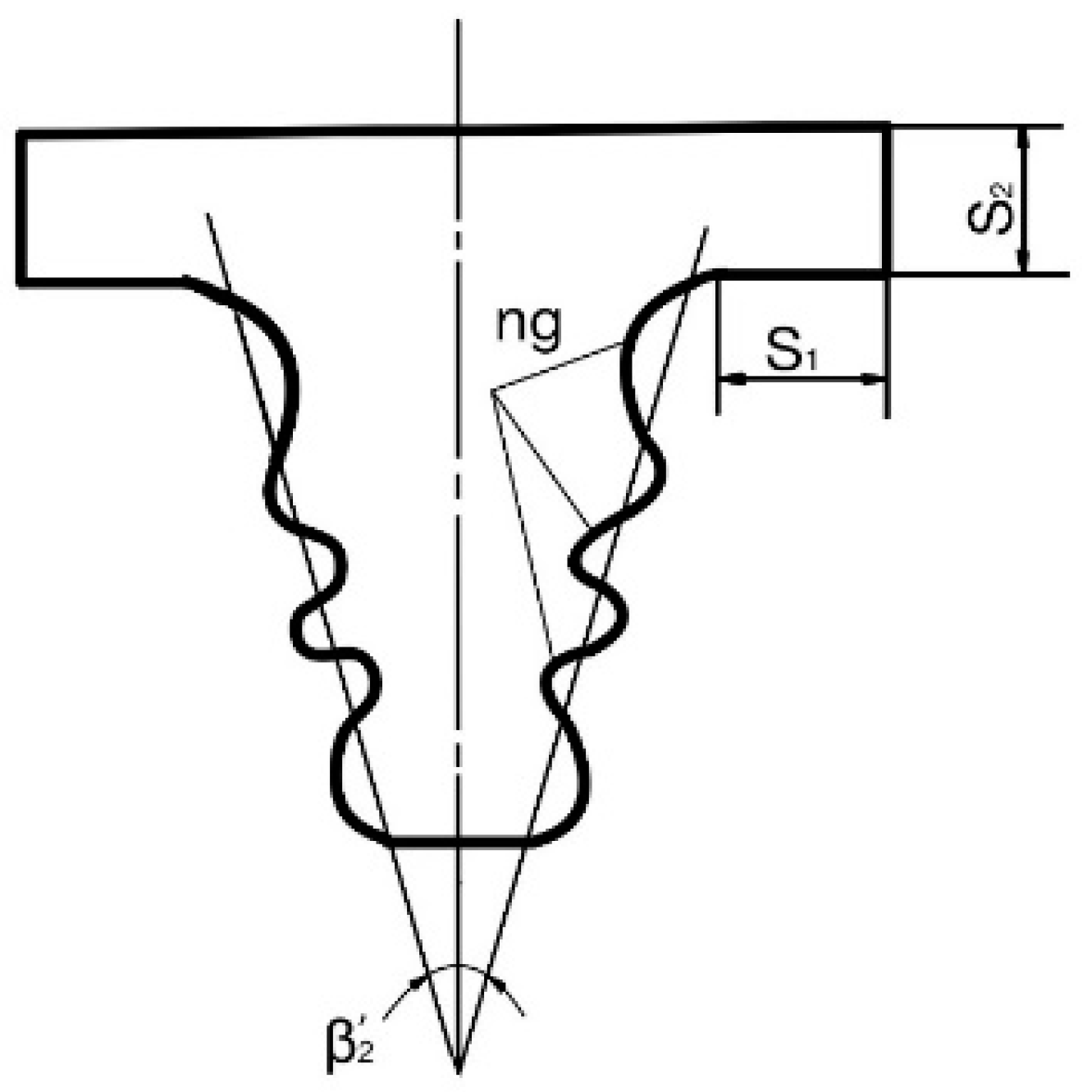
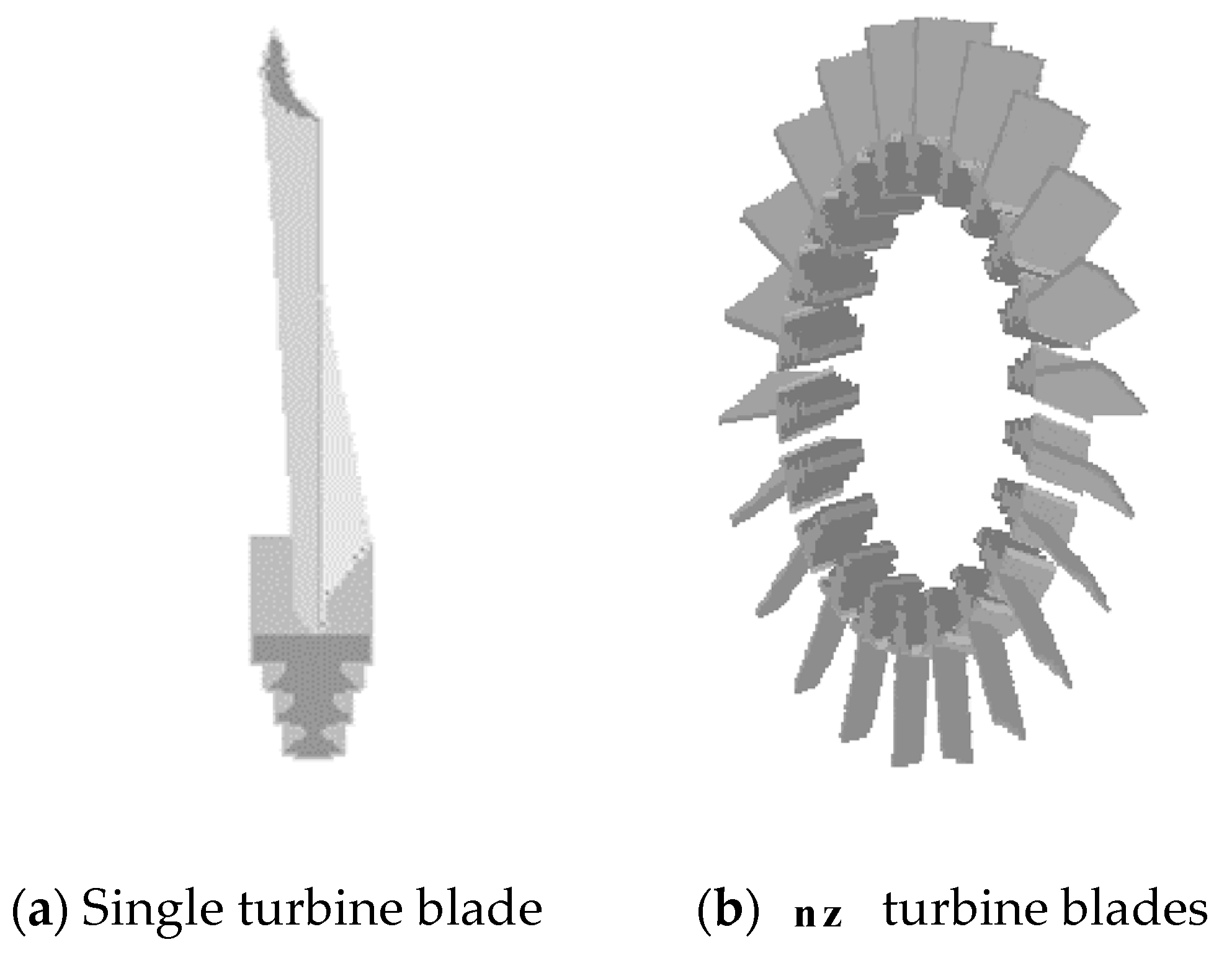
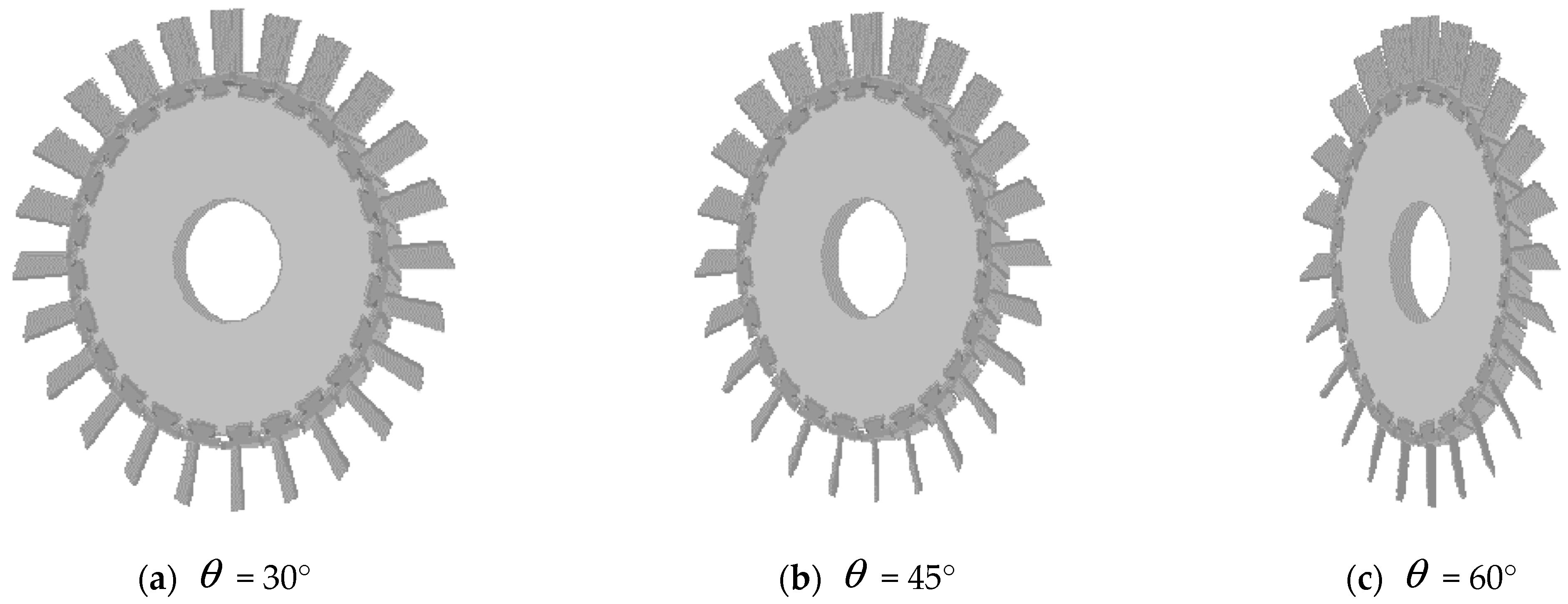
2.2.3. Geometric Encoding of Blade Unit
3. Methods
3.1. Modeling Algorithm for Rotor Shaft Unit Point Cloud Model
3.1.1. The Type Attribute Set of the Shaft
- 1.
- Two-dimensional point cloud modeling algorithm for shafts.
- 2.
- Three-dimensional point cloud modeling algorithm for shafts.
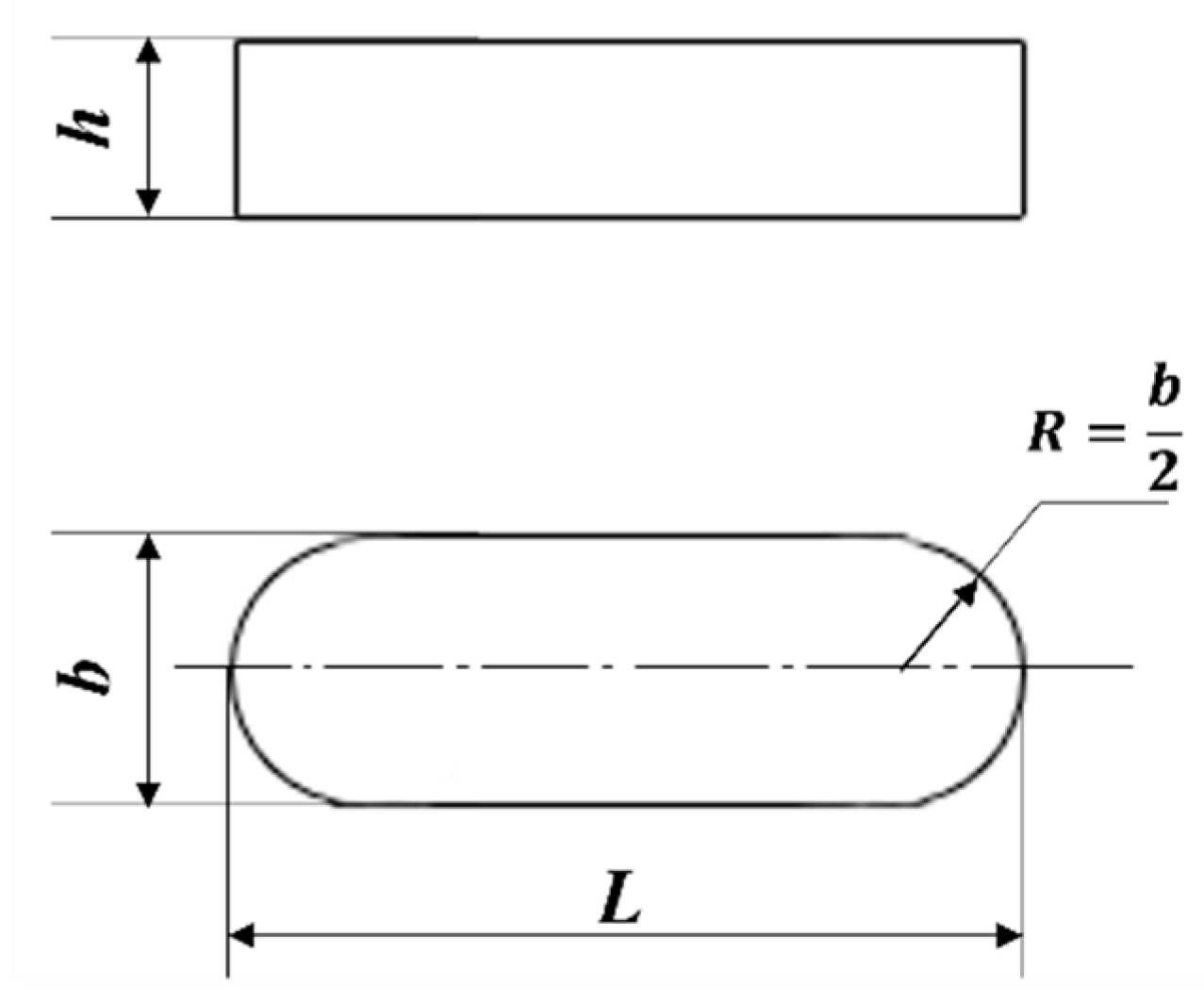
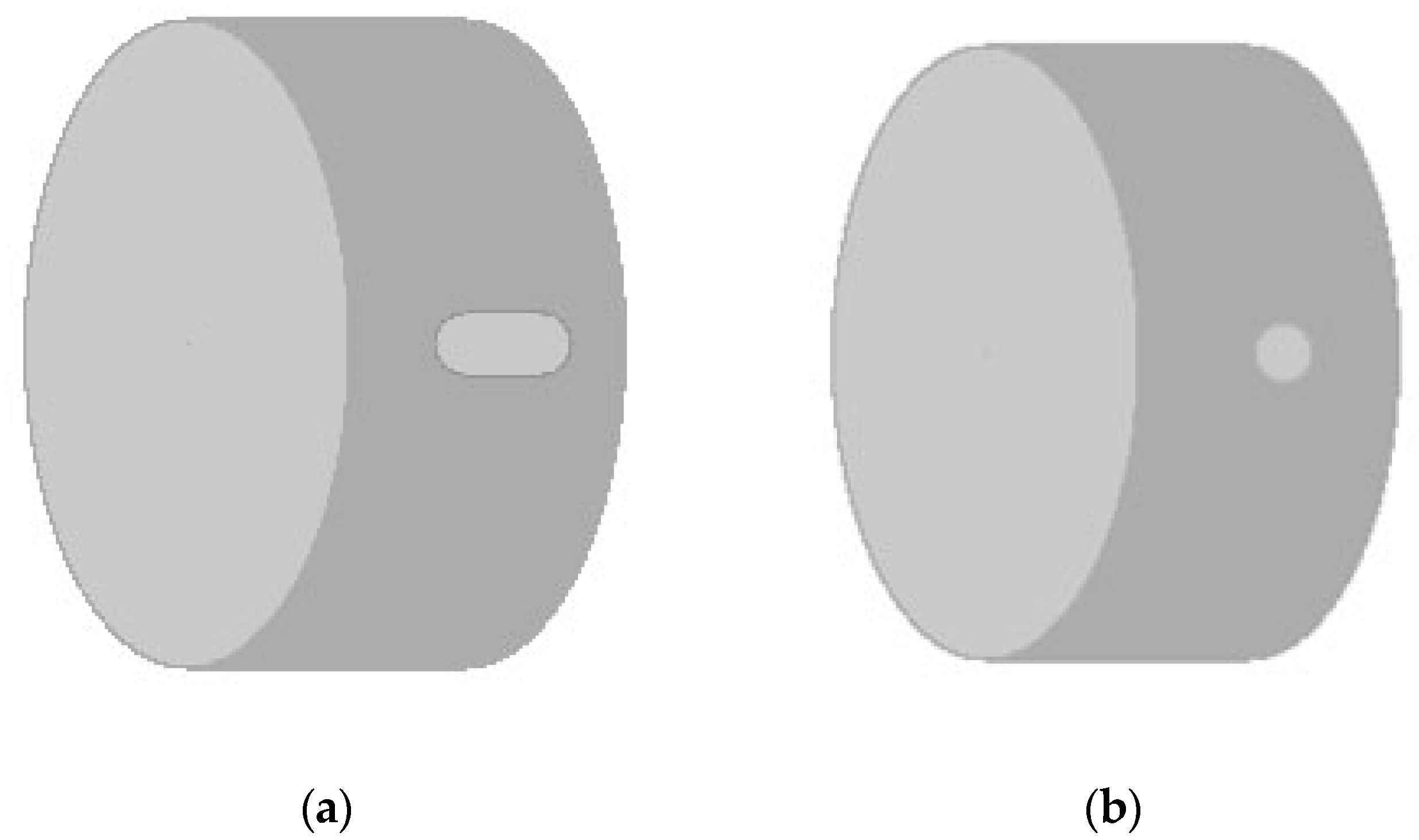
3.1.2. The Connection Attribute Set of the Shaft
- 3.
- Keyway generation.
- 4.
- Generation of pin holes.
3.1.3. The Material Attribute Set of the Shaft
3.2. Modeling Algorithm for Rotor Disk Unit Point Cloud Model
3.2.1. The Type Attribute Set of the Disk
- 5.
- 2D point cloud modeling algorithm for turbine disk;
- 6.
- 3D point cloud modeling algorithm for turbine disk;
3.2.2. The Connection Attribute Set of the Disk
- 7.
- Cooling hole point cloud modeling algorithm
- 8.
- Installation edge point cloud modeling algorithm for disks;
3.2.3. The Material Attribute Set of the Disk
3.3. Modeling Algorithm for Rotor Blade Unit Point Cloud Model
3.3.1. The Type Attribute Set of the Blade
- 9.
- Modeling algorithm for tenon point cloud model.
- 10.
- Modeling algorithm for blade body point cloud model.
3.3.2. The Connection Attribute Set of the Blade
3.3.3. The Material Attribute Set of the Blade
4. Results and Discussion
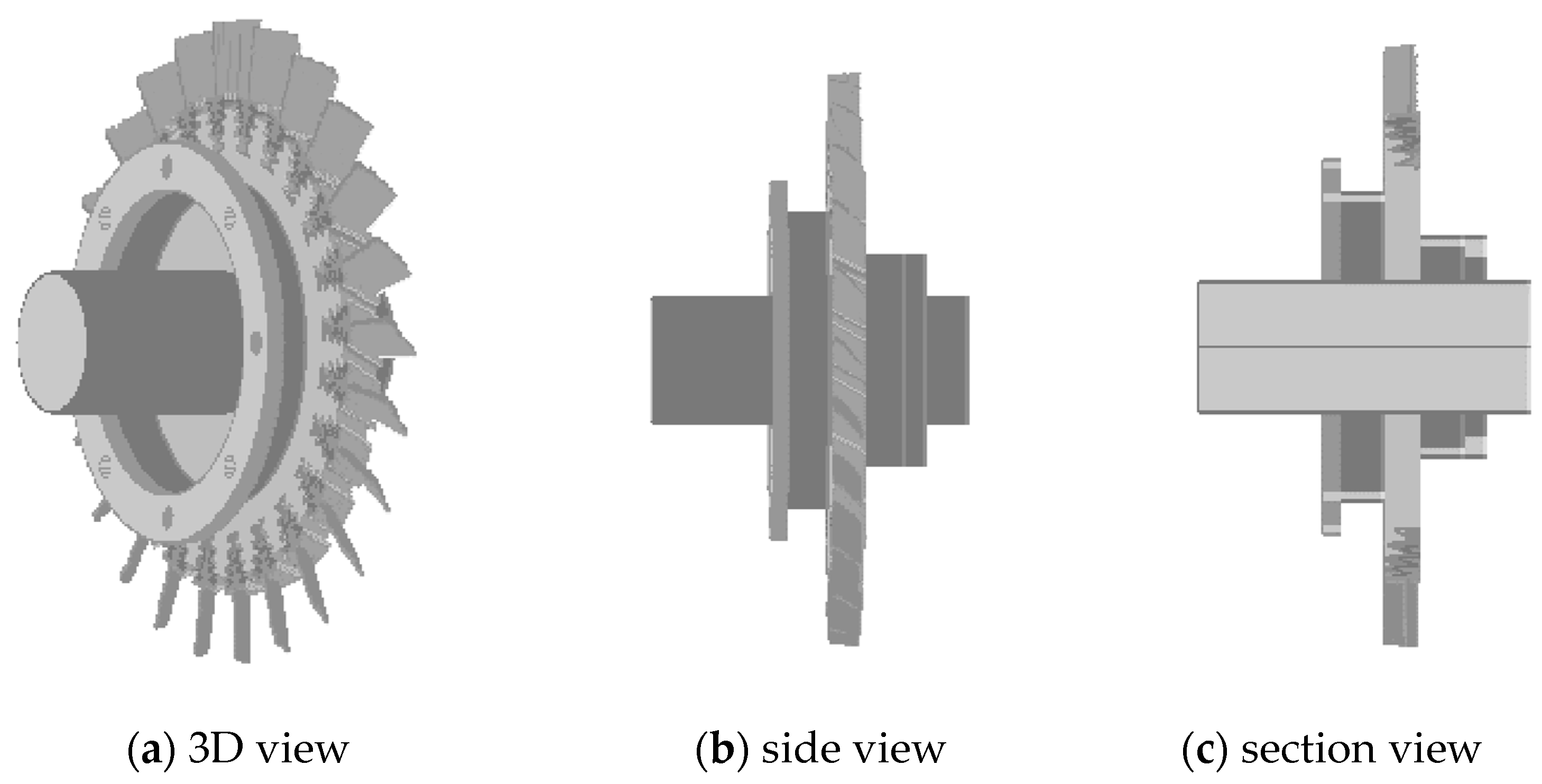
4.1. Display of 3D Point Cloud Model Data Results in MFC
4.2. Units Coordination Display
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y. Research on Intelligent CAD Innovation Design Based on Biological Genes. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2003. [Google Scholar]
- Li, N.; Bu, S.; Shang, B.; Li, Y.; Tang, Z.; Zhang, W. Vision and Key Issues of Intelligent Aircraft Design. J. Chin. J. Aeronaut. 2021, 42, 213–230. [Google Scholar]
- Behbahani, A.; Tulpule, B. Perspective for distributed intelligent engine controls of the future. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010; p. 6631. [Google Scholar]
- Rosenman, M.A. An exploration into evolutionary models for non-routine design. J. Artif. Intell. Eng. 1997, 11, 287–293. [Google Scholar] [CrossRef]
- Ming, D. Principles and Construction of Aviation Gas Turbine Engines; National Defence Industry Press: Beijing, China, 2008; pp. 2–3. [Google Scholar]
- Kraev, V.M.; Siluyanova, M.V.; Tikhonov, A.I. Assessment and improvement of rationality methods of modern aircraft engines design and technological solution. J. Phys. Conf. Ser. 2019, 1353, 012–033. [Google Scholar] [CrossRef]
- Wang, H. Parameterized Design, Analysis and Software Integration of Turbine Rotor Structure. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2005. [Google Scholar]
- Cao, J. Research on the Life Assessment Method of Aircraft Engine Turbine Rotors. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Collopy, P.D.; Hollingsworth, P.M. Value-driven design. J. Aircr. 2011, 48, 749–759. [Google Scholar] [CrossRef]
- Tammineni, S.V.; Rao, A.R.; Scanlan, J.P.; Reed, P.A.S.; Keane, A.J. A knowledge-based system for cost modelling of aircraft gas turbines. J. Eng. Des. 2009, 20, 289–305. [Google Scholar] [CrossRef]
- Curran, R.; Raghunathan, S.; Price, M. Review of aerospace engineering cost modelling: The genetic causal approach. J. Prog. Aerosp. Sci. 2004, 40, 487–534. [Google Scholar] [CrossRef]
- Weustink, I.F.; Ten Brinke, E.; Streppel, A.H.; Kals, H.J.J. A generic framework for cost estimation and cost control in product design. J. Mater. Process. Technol. 2000, 103, 141–148. [Google Scholar] [CrossRef]
- Xiao, R. Principles and Technologies of Intelligent Design; Science and Technology Press: Beijing, China, 2006; pp. 14–15. [Google Scholar]
- Reding, D.F.; Eaton, J. Science & Technology Trends 2020–2040. Exploring the S&T Edge; NATO Science & Technology Organization: La Spezia, Italy, 2020; pp. 71–73. [Google Scholar]
- Freeman, H. On the encoding of arbitrary geometric configurations. J. IRE Trans. Electron. Comput. 1961, 260–268. [Google Scholar] [CrossRef]
- Tianjue, G. Biochemistry; People’s Health Publishing House: Beijing, China, 2000; pp. 23–24. [Google Scholar]
- HB20082-2012; Aviation High-Temperature Alloy Shaft Forging Specification. People’s Republic of China Aviation Industry: Beijing, China, 2013.

| Material | Elastic Modulus (MPa) | Coefficient of Linear Expansion (/°C) | Density (kg/m3) |
|---|---|---|---|
| GH2901 | 198 | 15.5 | 8.21 |
| GH4169 | 207 | 12.9 | 8.19 |
| GH4500 | 217 | 12.9 | 8.05 |
| Material | Elastic Modulus (MPa) | Coefficient of Linear Expansion (/°C) | Density (kg/m3) |
|---|---|---|---|
| GH3030 | 210 | 13.2 | 8.40 |
| GH4169 | 207 | 12.9 | 8.19 |
| IN718 | 435 | 11.8 | 8.24 |
| Material | Elastic Modulus (MPa) | Coefficient of Linear Expansion (/°C) | Density (kg/m3) |
|---|---|---|---|
| N07750 | 214 | 7.0 | 8.28 |
| TC11 | 110 | 10.4 | 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Lu, H.; Zhao, L.; He, B. Research on Intelligent Design of Geometric Factor Encoding for Aircraft Engine Turbine Structures. Aerospace 2024, 11, 186. https://doi.org/10.3390/aerospace11030186
Xu W, Lu H, Zhao L, He B. Research on Intelligent Design of Geometric Factor Encoding for Aircraft Engine Turbine Structures. Aerospace. 2024; 11(3):186. https://doi.org/10.3390/aerospace11030186
Chicago/Turabian StyleXu, Wencong, Hongyi Lu, Lei Zhao, and Borui He. 2024. "Research on Intelligent Design of Geometric Factor Encoding for Aircraft Engine Turbine Structures" Aerospace 11, no. 3: 186. https://doi.org/10.3390/aerospace11030186
APA StyleXu, W., Lu, H., Zhao, L., & He, B. (2024). Research on Intelligent Design of Geometric Factor Encoding for Aircraft Engine Turbine Structures. Aerospace, 11(3), 186. https://doi.org/10.3390/aerospace11030186






