Abstract
Fuel burn during the actual route flown is an important indicator of aircraft operational efficiency. This study aims to assess and systematically evaluate the method for fuel consumed during flights using data from the automatic dependent surveillance–broadcast (ADS-B), European reanalysis (ERA5) meteorological dataset, and BADA 3 performance. A literature background and comprehensive methodology are provided for fuel estimation using track data. The airborne part of the trajectory was used to estimate the total trip fuel consumed during several flights of a commercial airliner. The calculated fuel burn is compared with measured fuel consumption from the flight data recorder (FDR). The results show that fuel consumption for the entire airborne part of the trajectory can be estimated with an average error of 1.2% and with a standard deviation of 1.3%. Detailed results of fuel burn for individual flight phases, from the initial climb to the approach, are also presented. In addition, this paper also discusses the sources of errors and the potential applications of the method for network operations and environmental monitoring.
1. Introduction
Accurate fuel burn estimation is essential for the evaluation of environmental impact. Fuel consumption directly affects the amount of greenhouse gases and other pollutants emitted into the atmosphere. In 2019, the average fuel inefficiency on flights within the Eurocontrol network manager area, from take-off to landing, was 8.6% to 11.2% [1]. Enhancing fuel efficiency is a critical aspect of addressing these environmental concerns.
Recently, SESAR 3 JU launched the campaign for European ATM Master Plan 2024 with an ambitious goal to establish Europe as the most efficient and environmentally friendly sky to fly in the world.
To increase flight efficiency, air traffic management (ATM) implements a number of initiatives, such as free route airspace, performance-based navigation, continuous climb and descent, and other solutions [2].
To assess flight efficiency, it is necessary to calculate fuel burn since airlines do not share these data. Without accurate fuel burn calculations, monitoring of flight efficiency or estimating the impact of ATM initiatives would be less reliable.
For operational monitoring and route evaluation purposes, fuel burn is calculated within the enhanced tactical flow management system (ETFMS) by Eurocontrol [3]. The ETFMS calculates fuel burn using meteorological data, flight profiles, and aircraft performance details extracted from the base of aircraft data (BADA) database. Real-time flight data updates, wind speed, and wind direction enrich these calculations. The ETFMS primarily deals with the in-flight segment of trajectories, excluding fuel consumption during take-off, landing, and taxiing (wheels up to wheels down) [3]. A comparative analysis of ETFMS predictions and actual airline data revealed a 10% disparity in fuel burn for the en-route part of the flight [3].
This paper focuses on data and methods for fuel consumption estimation using track data, specifically automatic dependent surveillance–broadcast (ADS-B) data. The significance of this methodology lies in its potential to serve as the basis for calculating advanced performance indicators based upon the real fuel burn data, which are instrumental in measuring flight efficiency and its environmental impact in real-time and during post-operational assessments [4].
ADS-B provides good coverage in many regions but may have limitations in remote or mountainous areas. The recent integration of real-time air traffic surveillance data from Aireon’s space-based ADS-B into the network manager operational system enables more accurate fuel burn algorithms due to better area coverage [5].
This research reviews existing literature on fuel flow estimation using surveillance data, highlighting various applied methodologies. Moreover, it presents an extensive and systematic approach for estimating fuel burn using track data. This approach refines the existing framework and can serve as a valuable resource for future research efforts.
The methodology employed in this study involves a detailed analysis of meteorological, ADS-B, and flight data recorder (FDR) data extracted from five distinct commercial flight instances of a single aircraft.
The main contribution of this research is the systematic validation of fuel burn estimation using surveillance data for the entire airborne trajectory (including part of trajectories with deployed configuration) and individual flight phases such as initial climb, climb, cruise, descent, and approach. FDR data are used for validation purposes. This approach yielded a wealth of data, offering meaningful insights regarding the accuracy of fuel burn estimation with BADA configuration scheduling, ADS-B, and available meteorological data currently missing in the available and published literature.
Advancements in fuel consumption estimation are pivotal for informed decisions regarding future airspace design. Policymakers and investors rely on these data to shape the industry’s environmental responsibilities and efficiencies.
This paper is organized in the following manner. Section 2 provides a comprehensive review of the existing literature on fuel consumption estimation using track data, highlighting the advantages and limitations of different methods and models. Section 3 includes a detailed description of the data sources, data processing, fuel estimation algorithm used in this study, and the validation procedure and performance indicators. Section 4 presents and analyzes the fuel estimation results for five commercial flights, comparing them with the FDR data and discussing the sources of error and uncertainty. The summary of the main findings, contributions, limitations, and implications of this study, as well as suggestions for future research, are given in concluding Section 5.
2. Background and Literature Review
The method of calculating fuel consumed from 4D track data (time, latitude, longitude, and altitude) was first introduced in the paper [6] by Oaks et al. The method used 4D radar track data, aircraft drag, and characteristics data from BADA v3.7. Weather information was extracted in the rapid update cycle (RUC) weather file from the Weather Service. The authors did not introduce a method for estimating initial weight since the weight was known from the available FDR of the aircraft used for validation. All data points from the 4D trajectory were used, and drag configuration was assumed to follow BADA flight phase altitude changes.
Chatterji et al. improved the method in [7] by deriving a fuel estimation procedure from nonlinear equations of motion with point-mass assumption instead of the approximations introduced in [6]. Accurately evaluating the fuel consumption rate requires knowing the aircraft’s initial weight. The method for estimating aircraft and wind states using proportional–integral–derivative (PID) filtering and the procedure of initial weight estimation is presented in [7]. Chatterji et al. [7] used Bombardier Global 5000, while Oaks et al. [6] used CRJ900 aircraft to validate the method using FDR data for a single flight. The paper by Chatterji et al. [7] used BADA flight phases to determine configuration changes. The authors managed to estimate fuel burn from a single flight with accurate initial mass with less than 1% estimation error after adjusting BADA drag coefficients to minimize the error.
The method from [6,7] was used to validate the possibility of fuel consumption calculation using track data in [8]. Dalmau et al. [8] used 2248 commercial flights of Airbus-type aircraft from top of descent (ToD) to 5000 ft above ground level (AGL) to avoid problems with unknown configurations. The configuration was assumed to be clean. The authors extracted 4D track and weather data from available FDR records. They also used radar tracks for the same flight to compare the algorithm’s accuracy with data of lower quality. The comparison was made to assess the accuracy of the algorithm and to see if any discrepancies could be attributed to data quality. The initial mass was used as known data. Dalmau et al. [8] also used the BADA performance model and the aircraft performance model obtained from the performance engineer’s program (PEP) made available by the aircraft manufacturer. The authors used data filtering techniques to lower the noise due to the numerical derivation of aircraft states. Results for fuel burn with a PEP-derived performance model gave a relative mean error of 4.8% using the FDR track. In contrast, with the BADA performance model, the estimated fuel burn was 18.7% different from the actual fuel burn.
A similar methodology to [8] was used by Harada et al. [9] with the purpose of accurate evaluation of the BADA model. Harada et al. [9] used FDR data to estimate fuel consumption in clean configuration flight phases, climb, cruise, and descent. They showed that fuel consumption during descent has reduced accuracy, even for clean configurations, due to the simplified idle thrust fuel flow defined in BADA 3. They showed that, based on fuel flow, the difference between the BADA model and flight data for clean configuration is within 5%. More recently, Sun et al. combined OpenSky’s ADS-B data with the open aircraft performance and emission model OpenAP [10] to perform a global study of different aviation emissions, including , , , and [11]. Additionally, they focused on business jet fuel emissions only in a separate study [12]. They used state vector data of each trajectory from the available OpenSky dataset. Due to a large amount of data, trajectories were down-sampled to one point per 30 s, and all calculations were based on the ground speed values, ignoring the effects of wind. A range of mass between 60% and 90% of the maximum take-off mass was used. Similar studies for global emission modeling from ADS-B are also studied in [13,14,15,16].
In papers by Filippone et al. [15,16], real-time ADS-B data from OpenSky network were integrated with flight performance computer program FLIGHT [17] to predict aviation emissions at altitude. They used ADS-B with Mode S to fly the route and calculate aircraft emissions based on the ability to calculate thrust.
Wickramasinghe et al. in [18] used BADA 4 and simulated data for continuous descent to estimate accurate fuel flow for clean and non-clean aircraft configurations with total fuel consumption being within ±6% of the actual value and descent fuel consumption within 10%. Table 1 provides specific details of the methodology, input data, and results of the most relevant research studies, including this paper’s research.

Table 1.
Detailed overview of key research studies with radar tracks or automatic dependent surveillance–broadcast (ADS-B) data in relation to our research framework and results.
Several methods have been suggested in the literature regarding the initial mass estimation [6,7,19,20,21]. Rohani et al. [20] used machine learning methods to estimate key performance data including the initial mass of aircraft using available flight data. Alligier et al. [21] used machine learning methods using millions of climbing segments from the OpenSky network to estimate the take-off mass and its uncertainty during the climb phase by fitting the observed power and energy rate to a point-mass model. Sun et al. [19] estimated the take-off mass using a total energy model at different flight phases, with validation experiments showing a mean absolute error of 4.3%. Some authors [6,7] used the iterative method to find take-off mass based on the assumption of 80% passenger load factor, maximum zero fuel mass (MZFM), and traveled distance. The iterative initial mass method is simple but sometimes erroneous since a short-haul flight can include more fuel than needed for the specific route. Longer-haul flights have a more successful approach to initial mass estimation than shorter ones using an iterative method [6].
Chati et al. [22] proposed a statistical approach based on Gaussian process regression to determine a mean estimate of the take-off mass (TOM) and the associated confidence interval using observed data from the take-off ground roll. More recently, Holzapfel et al. in [23] used Mode S data to estimate aircraft landing weight based on BADA descent speeds for the Airbus A320 family. The findings in [23] revealed a bias of approximately 1.6% and a standard deviation of 4.7% when the mass was restricted to 95% of the maximum landing mass (MLM), compared to the actual landing masses obtained from over 3328 flights involving various aircraft. The slightest deviation in landing mass was observed for data collected at altitudes below 1000 ft. However, the landing mass at higher altitudes deviated significantly due to air traffic control’s prescribed descent speeds, which often differed substantially from the BADA descent phase model airspeed due to varying wind and traffic conditions.
Despite extensive research, there is still a significant gap in the literature regarding fuel burn estimation using surveillance data. Current methodologies do not fully address accuracy across all flight phases, especially when combining ADS-B and ERA5 (European reanalysis) data with BADA configuration scheduling. Additionally, the influence of BADA 3 aircraft performance data and configuration scheduling on fuel consumption has not been adequately investigated. Furthermore, there is a lack of systematic validation of fuel burn estimation for the entire airborne trajectory. This study aims to fill these gaps by conducting a thorough evaluation of fuel burn estimation accuracy using the mentioned data sources and methodologies.
This research contributes to the existing body of knowledge by focusing on the accuracy of fuel flow estimation from ADS-B and ERA5 data using the highly reliable BADA 3 model for aircraft from the Airbus A320 family. It contributes to several key areas including the following:
- Verifying the reliability of ADS-B data by comparing them with FDR data.
- Demonstrating the accuracy of ERA5 wind and temperature data in calculating true airspeed.
- Providing an evaluation of the impact of BADA 3 aircraft performance data and configuration scheduling on fuel flow estimation precision.
- Conducting an examination of fuel flow accuracy throughout different flight phases.
This study used the actual flight data from FDR as reference points. The FDR data were obtained directly from one of the European airliners. ADS-B data for the same flights were also available from live tracking applications such as the OpenSky network. These data were used to calculate the fuel consumption of each flight.
Since ADS-B and radar track data do not provide information about aircraft configuration, this study also aims to investigate whether using BADA configuration scheduling can help estimate the aircraft fuel burn for the entire trajectory and, if so, how precise the estimates are.
This study is currently limited to five flights due to the complexities of acquiring a larger dataset. The findings should, therefore, be interpreted within this context, and any generalizations made from these results should be made cautiously due to the inherent limitations of this study. Additionally, initial mass uncertainty analysis was also evaluated.
3. Data and Methods
This section describes the data sources and methodologies used in the study. It details how ADS-B flight and weather data are collected, preprocessed, and used to estimate fuel consumption for five commercial flights of a single aircraft (Figure 1). This section also explains the use of the BADA performance model for fuel flow estimation, the point-mass model for representing the aircraft’s flight dynamics, and the data filtering techniques used to smooth and estimate the derivatives of altitude and ground speed measurements.
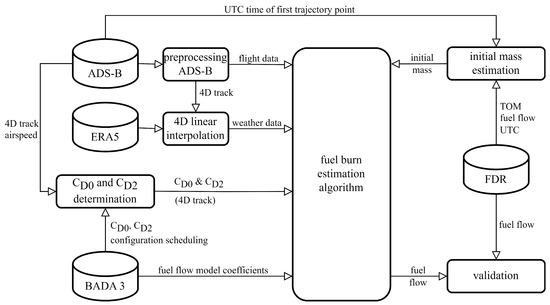
Figure 1.
Block diagram for validation of fuel burn algorithm using ADS-B and ERA5 data.
3.1. ADS-B Flight Data
ADS-B data are surveillance data that aircraft equipped with ADS-B Out transponders automatically broadcast. An ADS-B Out transponder emits a variety of information every second. This includes the timestamp, latitude, longitude, pressure altitude, ground speed, track angle, vertical speed, on-ground status, geometric altitude, and other data not used within this study (Table 2). Mode S is also sometimes available from the secondary surveillance radar for additional information, such as true airspeed and Mach number.

Table 2.
List of ADS-B data parameters, units, and data format.
ADS-B coverage of the OpenSky network differs globally, but the European Union (EU) is mostly covered at higher altitudes. At lower altitudes, coverage is sometimes inadequate due to obstacles between the receiver and the aircraft.
To estimate the fuel consumption of a particular aircraft during its entire flight, we analyzed FDR data from five flights that took place over two days in 2021. The Python traffic library [24] was utilized to search the historical dataset of the OpenSky network for the selected aircraft, using time records from the FDR and call signs for identification. All five flights were found, and data were analyzed for completeness of trajectory. Trajectory data were missing around one local airport where ADS-B coverage was poor for the period of interest, so part of the trajectory at lower altitudes was missing for three flights.
ADS-B data preprocessing was necessary since ADS-B data often display impossible altitudes, NaN, wrongly written data, and even missing data. Missing data between two consecutive points were interpolated using adjacent points, while NaN records were discarded. Altitudes were checked, and impossible altitude values were scaled to the proper values. The ’on ground’ status was used to filter out the part of the flight when the aircraft was airborne.
3.2. Weather Data
ADS-B data do not include wind and temperature data. To overcome this limitation, we utilized wind and temperature data from the ERA5 meteorological dataset of the European Centre for Medium-Range Weather Forecasts (ECMWF) [25]. The ERA5 dataset offers reanalyzed fields of wind and temperature values at 0.25° × 0.25° horizontally, with hourly temporal resolution, and at 37 pressure levels from 1000 hPa to 1 hPa with 25 hPa intervals (1000 hPa ≅ 0 m and 1 hPa ≅ 16,000 m in ISA).
The ERA5 weather data are provided in 4D coordinates with the following resolution:
- Longitude ;
- Latitude ;
- Altitude hPa;
- Time h.
Given that the resolution of our flight trajectory data is considerably higher than that of the available weather data, we employed multidimensional linear interpolation by time, longitude, latitude, and altitude to match weather data with trajectory points. At each 4D trajectory point, there are 16 4D weather points nearby. As we perform time interpolation, the number of weather points surrounding our trajectory point decreases to eight. Applying longitude interpolation on the remaining eight weather data points leaves us with four weather points that share the same time and longitude as our trajectory point. After applying the same linear interpolation process on latitude and altitude, we end up with a single weather point that matches the exact 4D coordinates of our trajectory point.
While our study primarily relies on ADS-B and ERA5 data, it is worth noting that alternative sources for meteorological data exist and could be considered. For instance, Mode S secondary surveillance radar technology allows air traffic controllers to access various information from aircraft, including airspeed, turn parameters, target altitudes, and meteorological conditions. Mode S enhanced surveillance (EHS) is a valuable feature for approximately 99% of Airbus- and Boeing-type aircraft [26]. In the EU, EHS is mandatory for all fixed-wing aircraft flying under instrument flight rules (IFR) within the general air traffic category. This requirement applies to aircraft with a maximum take-off weight exceeding 5700 kg or those with a maximum cruise true airspeed (TAS) higher than 250 kt [27]. Since the Mode S data are often incomplete [15] and not available for all aircraft flying under IFR, we considered ADS-B in combination with ERA5 data. Additionally, some aircraft transmit Mode S meteorological routine air report (MRAR) data. While MRAR data includes highly valuable information about wind and temperature, it is important to note that only a limited number of aircraft transmit these data [28]. Despite the potential of these alternative data sources, our study does not investigate these approaches in detail.
3.3. FDR Data
The FDR data from one European airline were taken as reference data. The FDR data were given in a comma-separated value (.csv) format with over 90 parameters recorded at various sampling rates ranging from one to eight samples per second. The data preprocessing in the first step included a selection of relevant parameters required for the fuel flow estimation method. The second step involved tedious data preprocessing tasks, encompassing raw data cleaning and formatting. This included converting string data to numerical values while ensuring accurate unit conversions and adherence to sign conventions. After preprocessing, data were used as an input file to the fuel flow estimation algorithm. The relevant FDR parameters used in the analysis are presented in Table 3 with units and available rates.

Table 3.
List of flight data recorder (FDR) parameters used for fuel estimation procedure validation.
The FDR data did not include the mass of the aircraft, but we were given the TOM for each flight from the mass and balance sheet. The fuel burnt was subtracted from TOM to obtain aircraft mass as a function of time.
Additionally, the FDR data did not directly provide the Mach number. Still, using the ground speed and available FDR wind heading and wind speed information, we calculated the true airspeed necessary for fuel flow estimation. The outside air temperature T is calculated from the energy equation for adiabatic flow (Equation (1)), using the measured total air temperature and calculated airspeed.
Since,
it follows that outside air temperature T is:
where J/kgK−1 and .
Track angle was not given in FDR, but heading , wind speed, wind direction, and drift angle were given. The north and east ground speed components and were calculated using heading and drift angle :
3.4. Flight Dynamics Model
In the field of aircraft performance modeling, a point-mass model is commonly employed. This model represents the aircraft as a single-point mass, with all forces at the center of gravity. It assumes zero sideslip and thrust is always aligned with the velocity vector. This model is described by seven state vectors: north and east positions x and y, pressure altitude h, true airspeed V, aerodynamic climb angle , heading , and aircraft mass m. These state vectors are governed by seven nonlinear differential equations, comprising three kinematic, three dynamic, and one equation representing mass decrease over time. For the point-mass aircraft model operating in a non-constant wind environment, specifically in an airmass-relative coordinate system with negligible vertical wind, the following set of equations is derived [29]:
In these equations, and represent the north and east wind components, is thrust, D is a drag, L is lift, is bank angle, g is the gravitational acceleration, and is fuel flow. The point-mass model, despite its simplifications, has a pivotal function in understanding and predicting aircraft performance in varying wind conditions and is a valuable tool in aviation research and analysis.
3.5. BADA Aircraft Performance and Fuel Flow Model
BADA, by Eurocontrol, serves as a comprehensive database widely employed by researchers in aviation. This invaluable resource offers a detailed repository of aircraft performance data, which is essential for conducting precise analyses. It is free of charge but requires a license agreement. BADA 3, used in the study, gives propulsion, aerodynamic, and fuel flow model specifications for nearly 100% of aircraft types in the European Civil Aviation Conference (ECAC) area. For each aircraft type, BADA specifies the model and engine used for modeling.
The aerodynamic model coefficients are modeled as a function of flight phase and landing gear configuration but do not include essential dependencies on Mach number. Using high-lift devices increases aerodynamic drag on the aircraft. This is primarily due to increased induced drag caused by changes in the lift distribution along the wing when flaps are extended and, to a lesser extent, due to parasite drag increase. Therefore, aircraft performance models usually specify different drag coefficient parameters for each high-lift device configuration. The aerodynamic drag D is computed using the drag coefficient from the following Equation.
where p is standard pressure at altitude h, T is the outside air temperature at aircraft position and altitude, V is true airspeed, and is wing reference area. Drag coefficient is given as the sum of parasite and induced drag where and depend on high-lift devices and landing gear position , ignoring compressibility effects or Reynolds number dependencies:
where
The drag model was employed using drag coefficients from BADA v3.16. Drag coefficients are given for take-off, initial climb, approach, cruise, and landing stage of the flight, plus extra drag due to extended landing gear. Each stage is associated with a typical aerodynamic configuration, which includes the positions of high-lift devices and landing gear. Climb, cruise, and descent are clean phases of flight, while take-off, initial climb, approach, and landing are associated with deploying high-lift devices and landing gear. There are several configurations of high-lift devices. Each configuration of high-lift devices, such as flaps and slats, has a designated speed and/or altitude range within which it can operate following the aircraft’s standard operating procedures (SOPs) as specified by BADA files.
Fuel flow is calculated using the BADA fuel flow model. Nominal fuel flow is a product of thrust-specific fuel consumption and thrust for turboprops and jets, while for piston engine aircraft, fuel flow is constant throughout all flight phases. For jets and turboprops, specific fuel consumption is a linear function of true airspeed V, and the fuel flow is:
BADA fuel flow for idle thrust conditions is:
BADA specifies , and coefficients in the operations performance file (OPF) for every aircraft type. is 1 for all phases except the cruise. The input V should be in knots, is kN and in ft, and fuel flow is provided in kg/min.
To avoid errors in the modeling fuel flow during descent when the configuration is used but not correctly recognized, fuel flow is set as max of nominal and idle fuel flow:
Finally, to estimate the fuel flow, we need, at every time recorded, the altitude, true airspeed, thrust, and whether the aircraft is in the cruise phase. Altitude is directly available from the ADS-B data, while all other data must be calculated.
3.6. Fuel Burn Estimation Method
From Equation (7), it follows that thrust is equal to
Two options are possible to estimate true airspeed V: looking for Mode S enhanced surveillance data available for some aircraft or using ground speed and wind data. Wind data can be obtained from a meteorological database such as the reanalyzed ERA5 wind speed. In this paper, we used ground speed and wind data from ERA5 in order to estimate the true airspeed V. Alternatively, ignoring winds and taking true airspeed equal to ground speed is also possible. This approach was used in studies such as [11,12,15]. If the V is determined using ground speed and wind data, the vertical wind is assumed to be zero, and only horizontal winds are considered. The true airspeed can then be estimated using Equation (17) derived from sum of Equations (4)–(6):
or and or can be calculated either from known latitude, longitude, and altitude data using ADS-B (Equation (18))
or directly from ground speed and track angle (Equation (19)).
Pressure data are derived from pressure altitude using the standard atmosphere pressure distribution model. Temperature data can be obtained from available weather data or assumed to match the standard atmosphere temperature at a given altitude. The density of the air is then calculated using the state equation for air.
Equation (20) becomes a simplified total energy equation if the wind rates are ignored:
The rate of true airspeed in the upper equations is calculated from the differentiation of Equation (17)
where:
And, finally:
To calculate , we need the lift, and lift is calculated using Equations (8) and (9). follows from Equation (8) and from Equation (9):
To calculate and , we need the rate of climb angle and the rate of heading angle . After differentiation of Equation (6), is available as:
since
The heading angle can be calculated from Equations (4) and (5)
and after differentiation of the upper expression, we obtain the rate of heading angle
Finally, the lift L and lift coefficient are calculated as:
Bank angle is then also possible to calculate as:
3.7. Data Filtering Methods
The second-order Savitzky–Golay (SG) filter [30], with a frame length of 25 data points, was employed to smooth altitude and ground speed measurements and estimate the first and second derivatives of altitude along with the first derivative of ground speed. These derivatives are important for calculating , , and derivatives. Alternative methods, including the PID state estimator [7], zero phases finite impulse response (FIR) low-pass filtering [9], and Kalman filtering, offer additional options for similar tasks, each with unique advantages. Before applying the SG filter, we utilized a low-pass infinite impulse response (IIR) filter designed using the Butterworth method.
The filter order for the IIR filter was set to 2, and the cutoff frequency was specified as 1/128 Hz relative to the original sampling rate. The procedure was implemented using the filtfilt function in Matlab, a dual-direction application that ensures zero-phase filtering. This process effectively attenuates higher frequency noise and fluctuations in the original signal, resulting in the smoothed data utilized for subsequent analysis. To maintain consistency and precision, we applied the same low-pass IIR filter configuration to preprocess the derivative of accurate airspeed data. This ensured a smoothed and noise-attenuated first derivative of true airspeed for further analysis.
3.8. Initial Mass Data
Understanding the aircraft’s mass is essential for accurate fuel flow estimation, yet it is often an unknown variable. In this analysis, we begin with the assumption of knowing the initial mass. This approach allows us to explore how various factors, including weather conditions, drag, and fuel flow model, influence the total fuel burn estimated from ADS-B data.
The initial mass is the aircraft mass at the first observed point of its trajectory. This value is determined from FDR data using a given TOM and fuel burn up to this first observed point.
First, we need to identify the coordinated universal time (UTC) at which the aircraft starts accelerating on the runway since this point reflects the given TOM. Using the recorded fuel flow data during this phase, we estimate the aircraft’s mass at each data point to reflect the fuel burn. Ensuring the time synchronization between FDR and ADS-B data is critical in this process. The synchronization procedure enables us to align specific data points from the ADS-B trajectory precisely with their corresponding mass values.
In cases where the ADS-B trajectory’s coverage is more limited than the actual trajectory, we use the calculated mass at a given time as the starting mass for ADS-B trajectory-based fuel estimation. It is important to note that, for fuel estimation, trajectory data are limited to the airborne phase. Take-off ground roll and landing roll are excluded from the current analysis.
This methodology ensures a reliable estimate of the aircraft’s initial mass, which is essential for subsequent fuel flow calculations.
4. Results and Discussion
Section 4 presents the results of the fuel burn estimation method applied to five commercial flights of a single Airbus aircraft. The results are compared with FDR data and the sources of error and uncertainty are discussed. The main points of this section are ADS-B and ERA5 data accuracy, fuel estimation algorithm accuracy, wind effects, initial mass sensitivity analysis, and configuration scheduling effects.
In Section 4.1, we compared and analyzed ADS-B and FDR data for identical flights to ascertain the reliability of ADS-B data. In Section 4.2, we performed a correlation study between ERA5 and FDR weather data for the same flight to establish the credibility of ERA5 weather data. In Section 4.3, we applied the fuel flow estimation algorithm to FDR data for validation purposes. In Section 4.4, we assessed the applicability of BADA scheduling procedures within the algorithm using FDR flight and weather data. Lastly, in Section 4.5, we carried out a validation process using ADS-B flight data, ERA5 weather data, and BADA scheduling within the fuel burn estimation algorithm.
4.1. Evaluation of Derived Variables—Comparing ADS-B with FDR Data
We compared ADS-B flight data with the FDR data to gain confidence in the ADS-B dataset. The results of those comparisons for pressure altitude, ground speed, and vertical speed are given. The pressure altitudes from ADS-B and FDR are plotted in Figure 2 against flight time with mean error (ME) and standard deviation mean error (SDME).
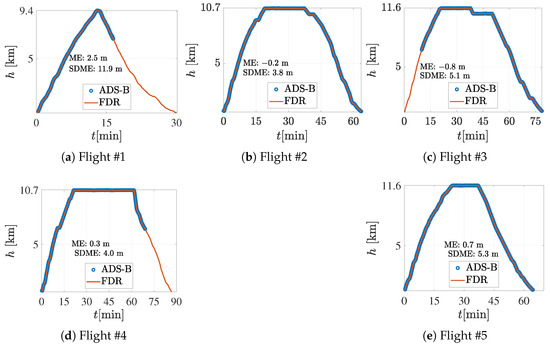
Figure 2.
The pressure altitude h from ADS-B and FDR plotted against flight time t with mean error (ME) and standard deviation mean error (SDME).
From Figure 2a,c,d, it is visible that part of ADS-B trajectories are incomplete due to missing ADS-B coverage at lower altitudes in some areas. The ME and SDME of altitude indicate minor discrepancies between FDR and ADS-B altitude data. We can conclude that pressure altitude from ADS-B is very accurate, with mean error variations from −0.8 m to 2.5 m, and SDME from 3.8 m to 11.9 m.
The ground speed data comparisons between ADS-B and FDR are plotted in Figure 3 against the same flight time following synchronization based on UTC. The FDR data are given with 8 Hz resolution, while ADS-B only provides one data point per second. To compare 8 Hz and 1 Hz data, the mean of these 8 data points for every second is compared against the exact second from ADS-B. Based on our statistical analysis of ME and SDME, it is evident that the ground speed data obtained from ADS-B sources exhibit high accuracy and consistency, showing only negligible deviations when compared to measurements. The same observation can be applied to the vertical speed plotted against flight time t in Figure 4.
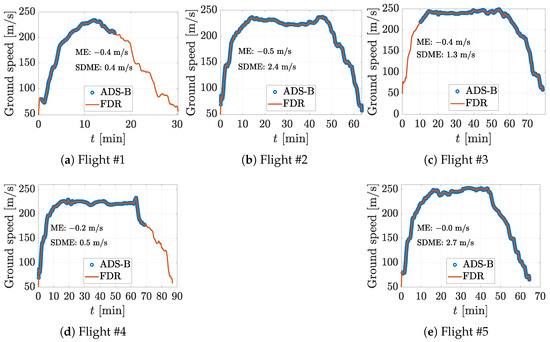
Figure 3.
The ground speed from ADS-B and FDR plotted against flight time t with ME and SDME.
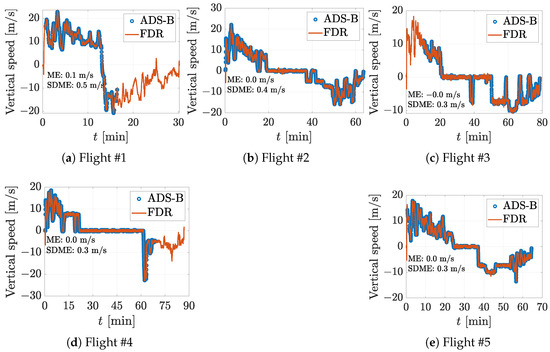
Figure 4.
The vertical speed from ADS-B and FDR plotted against time t with ME and SDME.
4.2. Evaluation of Weather Data—Comparing ERA5 with FDR Weather Data
Before comparing the precision of the fuel burn estimation algorithm executed on the ADS-B flight and ERA5 weather data with the actual fuel flow stated in the FDR records, it is important to evaluate the precision of ERA5 data.
The ERA5 wind heading is calculated from ERA5 north and eastward wind components. In Figure 5, wind headings from ERA5 and FDR records are plotted against time. The matching between ERA5 and FDR wind data enabled us to check the possibility of ERA5 data usage for true airspeed calculation. It can be observed that the wind heading MEs are relatively small, while standard deviations are from 15.3° to 32.6°.
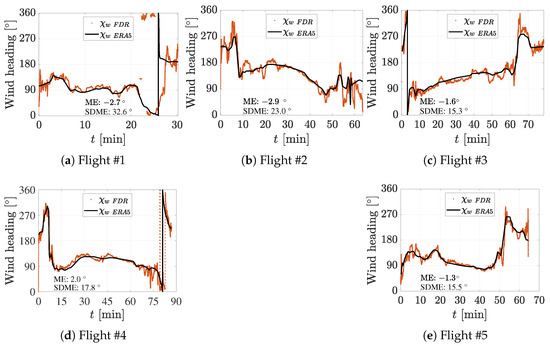
Figure 5.
The wind heading from ERA5 and FDR records plotted against time with ME and SDME.
The wind speed in Figure 6 calculated from extracted ERA5 and FDR-measured wind data are plotted against time for comparison. Although there is a significant variance and standard deviation in the wind speed, it will be shown in Section 4.5 that this difference does not significantly affect the accuracy of the calculated true airspeed. This is due to the small magnitude of the wind speed compared to the ground speed. We conclude that ERA5 wind speed is reasonably close to the actual values and should not introduce a substantial distortion or bias in the final results.
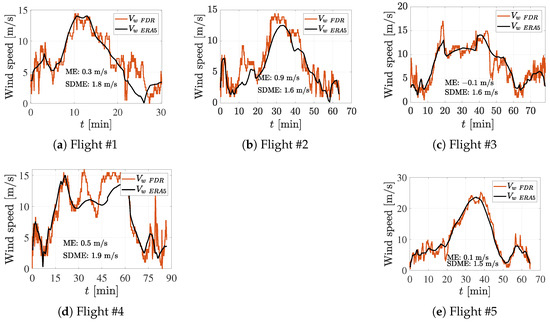
Figure 6.
The wind speed from ERA5 and FDR plotted against time t with ME and SDME.
The temperature is extracted from ERA5 and compared with FDR and ISA temperature (Figure 7). Examining the differences between air temperature from FDR and ERA5 shows that these two sources are consistent with high accuracy and precision, where ME is up to 0.9 K and SDME is up to 0.8 K.
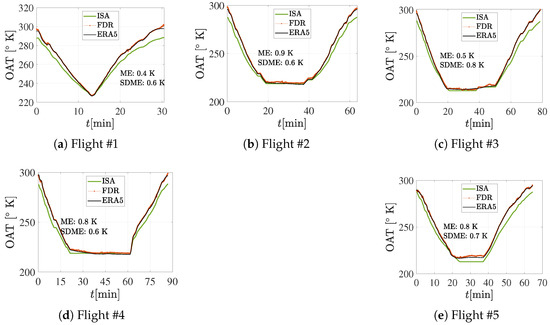
Figure 7.
ERA5, FDR, and ISA temperature plotted against time. ME and SDME of ERA5 temperature considering FDR temperature.
4.3. Evaluation of Fuel Estimation Algorithm Using Flight, Configuration, and Weather Data from FDR Records
The purpose of this section is to validate the presented fuel burn estimation algorithm by comparing the estimated fuel burn with the measured one from FDR records. The input data for the algorithm was obtained from FDR records with 8 Hz resolution. The goal was to emulate ADS-B and ERA5 data from the most accurate source so that errors in the results could be accounted for only by the algorithm’s features, not the input data. The input data from FDR records are initial mass, time, pressure altitude, latitude, longitude, vertical speed, ground speed, heading, drift angle, temperature, wind speed, and wind heading. The true airspeed was calculated using the FDR-measured wind records (Figure 8).
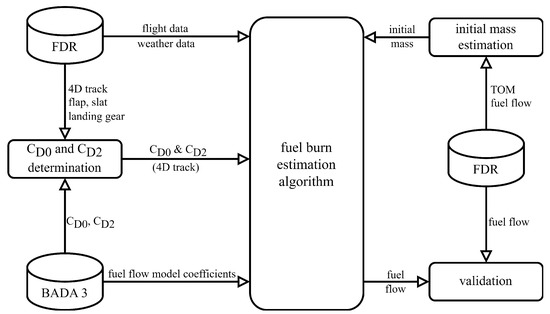
Figure 8.
Block diagram for validation of fuel estimation algorithm using flight, configuration, and weather data from FDR records.
The drag coefficients from BADA v3.16 were utilized in the drag model. BADA provides drag coefficients for take-off, initial climb, approach, cruise, and landing, along with extra drag due to extended landing gear. The configuration setup is taken as in actual flight. To estimate drag, we used the actual flap, slat, and landing gear schedules to apply drag coefficients for the time of configuration usage. However, drag coefficients do not dynamically adjust to changes in flap or slat angles during flight but use a set of predefined values given by BADA 3 at discrete flap and slat angles for specific configurations. The following rules were used regarding specific BADA coefficient applications:
- If in climb and with flap and/or slat extended, BADA initial climb coefficients and were applied.
- If in descent and with flap and/or slat extended, where the flap setting angle is less than 15°, BADA approach coefficients and were applied.
- If in descent and with flap and/or slat extended, while the flap setting angle was above 15°, the approach coefficient was supplemented with the additional term due to landing gear deployment.
The mass at a particular moment is calculated based on the initial mass for a specific flight and the fuel consumed until that moment.
The fuel was calculated for the entire trajectory (from lift-off to touch-down), the clean part of the trajectory, and during different flight phases: initial climb (includes part of take-off), climb, cruise, descent, and approach (includes part of landing). Initial climb and approach are part of the flight with extracted flaps, slats, or landing gear. Climb, cruise, and descent represent parts of the trajectory with clean configurations.
The calculated fuel burn was compared with the measured fuel burn, taken from FDR records. The discrepancies between the calculated and measured values are presented in Table 4. The fuel errors for the entire airborne trajectory vary from −0.2% to 3.5%.

Table 4.
Fuel burn error per flight phase in % and kg, and total fuel burn calculated (kg) using flight, configuration, and weather data from FDR records. The duration of the analyzed trajectory in minutes is given in the first column.
The most significant error of fuel burn is during flight phases with non-clean aerodynamic configuration, i.e., initial climb error is up to 12.7% and approach is up to −26.3%. These errors are due to mismatched drag coefficients, transient aircraft dynamics, and more emphasized noisy aircraft states because of the short flight phase.
The fuel burn error differs by less than 0.6% when comparing an entire and clean trajectory.
During clean phases of flight, the relative error is highest for descent, at up to 12.5% for flight #3. The relatively large errors during clean descent are primarily because of the BADA 3 modeling of idle fuel flow as a function of altitude only, outlined by Wickramasinghe et al. in [18]. During descent with a clean configuration, the calculated fuel burn is higher than the true one, which was also reported by Dalmau et al. in [8]. The mean error of fuel burn during clean descent in [8] was calculated from 2448 4D tracks from the FDR. The fuel burn ME was 18.7% when using performance data from BADA v3.6 and 4.8% when using PEP (Table 1).
In this research, the mean error during clean descent using ADS-B data emulated from FDR records is 2%. The smaller error may be explained by the direct availability of ground speed, which results in less numerical differentiation and less noisy aircraft states. Therefore, we could indicate that ADS-B data could improve fuel burn calculation during descent and overall. Nevertheless, this statement should be tested on more flights to verify it.
The BADA 4 idle fuel flow function is expected to enable even more accurate fuel flow during the clean descent.
In this research, we decided to apply exclusively BADA aircraft model coefficients since they have been developed for ATM purposes, and there is a database of more than one hundred different aircraft and their performance characteristics. The authors in [7,8,9] have shown that the fuel burn error can be minimized by correcting drag and fuel flow coefficients. The proprietary flight data records are not publicly available, and companies are often reluctant to share them. Therefore, it would be challenging to test hundreds of different aircraft types and look for their optimized coefficients since that would require access to their flight data records. Also, drag and fuel flow coefficients could differ due to manufacturing, operational wearing, and aging [31], even for the same aircraft model and type.
To demonstrate how the uncertainty of initial mass affects the total fuel burn, we calculated the fuel burn with a range of initial mass from 80% to 120% of actual mass provided by the airline company in Figure 9. From the initial mass sensitivity analysis, we conclude that an error in the initial mass estimation of up to 10% will result in up to 6% error in fuel burn for an entire trajectory. In tested examples, if the error of initial mass is 20%, the maximum error in total fuel burn is up to 10%.
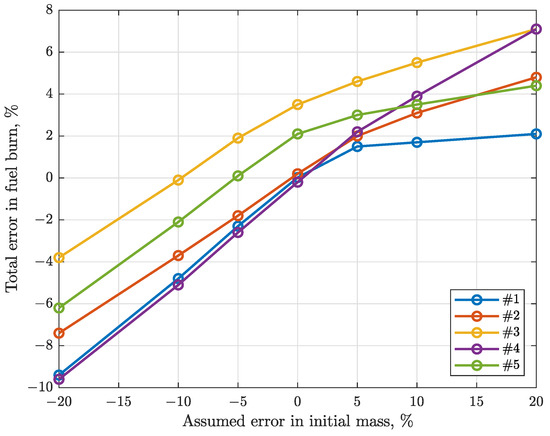
Figure 9.
Sensitivity of fuel burn error [%] for entire trajectory due to an error in initial mass.
4.4. Evaluation of BADA Configuration Scheduling Using Flight and Weather Data from FDR Records
While this study primarily relies on ADS-B and ERA5 data, it is worth noting that the ADS-B data do not contain information about aircraft configuration. In such cases, we can apply BADA assumptions regarding aerodynamic configuration scheduling. BADA configuration scheduling is based on speed and altitude limitations [32]. However, BADA scheduling utilized for configuration deployment may not always align perfectly with actual operational data, nor does it model aerodynamic coefficients as a function of flap and slat dynamics.
Given that the primary goal of this section is to evaluate the impact of BADA scheduling on fuel burn per flight phases and overall, we will apply BADA scheduling in combination with flight and weather data from FDR to estimate the fuel burn (Figure 10). Subsequently, we will compare the estimated fuel burn with the one measured from the FDR to determine the effect of BADA scheduling on fuel burn estimation.
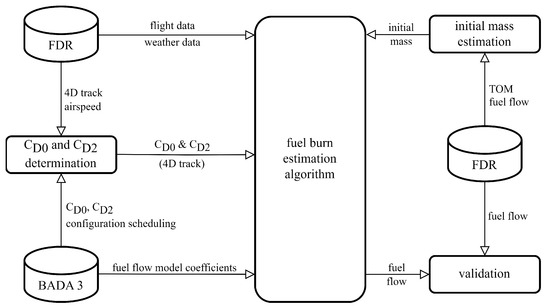
Figure 10.
Block diagram for validation of BADA configuration scheduling using flight and weather data from FDR records.
By analyzing the duration of the initial climb and approach phase for the actual configuration schedules, it is evident that the period of aircraft flight with deployed configuration ranges from 5.2 to 8.7 min. However, in the case of the BADA scheduling assumptions, these times are reduced to a range of 1.7 to 5 min.
The relative errors for fuel burn during the approach with BADA configuration applied are substantial, reaching up to −53.3% (flight #3 in Table 5). Regardless of this large relative error, the absolute error is 23.5 kg less than a measured fuel burn, which is 0.7% of total fuel consumed. This is mainly due to a brief flight time with extended configuration compared to the entire flight time.

Table 5.
Fuel burn error per flight phase in % and kg, and total fuel burn calculated (kg) using FDR flight, weather, and BADA configuration scheduling model. The duration of the analyzed trajectory is given in minutes.
In flights #1, #2, #3, and #5 from Table 5, we noticed a decrease in absolute fuel errors during the descent phase. This is attributed to the fact that a portion of the trajectory with extended configuration is included in the descent, as implied by reduced flight times with deployed configuration in the approach. The overestimated fuel flow during descent from Table 4 was compensated with negative fuel error from the approach.
Overall, the impact of large relative errors during the initial climb and approach phases was minimal on fuel burn for the entire trajectory (Table 5). The average error of total fuel burn for five flights with BADA configuration schedule is 0.5%, and with actual configuration is 1.1% (Figure 11a). The average error is smaller when using BADA scheduling, even with the less accurate knowledge of configuration. This is attributed to the low number of sample flights.
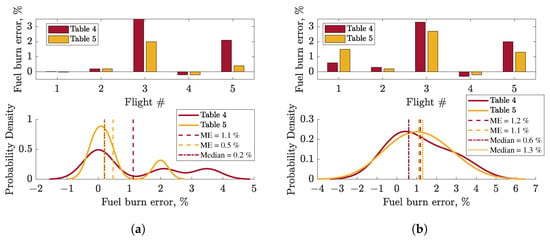
The evaluation of the clean phases also reveals discrepancies arising from the inherent mismatch between the clean trajectory segment defined by BADA configuration scheduling and the measured fuel flow data, which captures the actual (potentially differing) aircraft configuration during the same time window (Figure 11b).
Tests show minimal differences in fuel burn for the entire trajectory when actual and BADA scheduling aerodynamic configuration is applied. This suggests that BADA configuration scheduling is acceptable for detecting configurations when interested in overall trajectory fuel burn.
4.5. Evaluation of Fuel Burn Algorithm with ADS-B and ERA5 Data and BADA Scheduling Configuration
This section gives the final results of the algorithm precision with ADS-B flight and ERA5 weather data while using the BADA performance dataset and configuration scheduling (Figure 1). The results are compared with the measured fuel flow available from FDR data.
ADS-B available data trajectories are partially missing for three observed flights. If we compare the duration of ADS-B available data with FDR, it can be noted that ADS-B data covers the following proportions of the flights:
- #1 → 51.8%;
- #2 → 100%;
- #3 → 86.8%;
- #4 → 78.9%;
- #5 → 99% of total time.
For this reason, to observe the differences between fuel burn using FDR and ADS-B trajectory, all errors should be regarded only within the dataset and time frame for which both ADS-B and FDR data are available. Table 6 shows “NA” during the approach of flights #1 and #4 and the initial climb of flight #3 due to missing ADS-B data (also visible in Figure 12).

Table 6.
Fuel burn error per flight phase in % and kg, and total fuel burn calculated (kg) using ADS-B data, BADA configuration, and ERA 5 weather data. The duration of the analyzed trajectory is given in minutes.
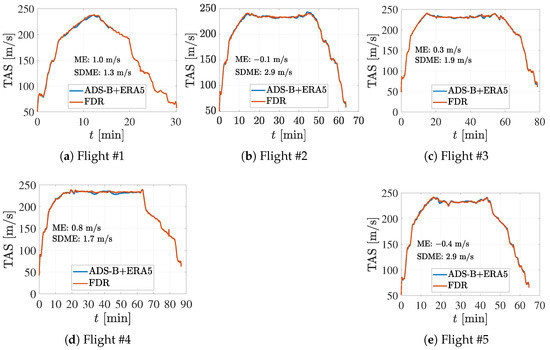
Figure 12.
Comparison of calculated TAS from ADS-B ground speed and ERA5 weather data with FDR TAS.
The true airspeed is calculated using ground speed from ADS-B and wind and temperature data from ERA5. The latter is compared with TAS derived from FDR and plotted against time in Figure 12. The ME for TAS is up to 1 m/s, while the SDME is up to 2.9 m/s. If the wind is not available, the TAS is usually set equal to ground speed as in [11,12,15]. Calculating TAS without wind would result in mean errors of TAS up to 8.6 m/s and SDME of up to 7.4 m/s. We can conclude that utilizing ERA5 wind data significantly improves the accuracy of true airspeed determination.
Table 6 gives calculated fuel burn results and errors for the available period of surveillance data for each trajectory. The fuel burn for the entire trajectory differs by up to 3.3% from the measured fuel burn and up to 2.9% for the clean part.
On average, five flights show a 1.2% error for the entire trajectory with a 1.3% standard deviation (Figure 13). The data exhibit a positively skewed distribution with heavier tails than the normal distribution, as visible from Figure 13a. This indicates that, for most flights, calculated fuel burn for the entire trajectory matches measured values. However, some flights, such as flight #1, with higher error values influence the distribution, contributing to skewness.
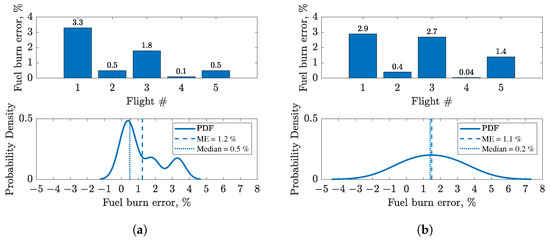
Figure 13b suggests the clean trajectory fuel burn error distribution resembles a normal distribution with a positive mean equal to 1.5% and a standard deviation of 1.3%. Notably, the entire trajectory mean error (1.2%) is lower than the mean error of clean trajectory due to negative fuel burn errors during the approach. Interestingly, median values for both clean and entire trajectory data are closer to zero (0.2%), suggesting a larger number of flight experience errors closer to zero than the average error. A larger flight sample would enable a more robust statistical analysis and confirm these observations.
The most significant differences in fuel flow and fuel burn are observable during non-clean phases of flight, i.e., initial climb and approach (Figure 14). This is primarily due to less accurate configuration scheduling, as explained in Section 4.4.
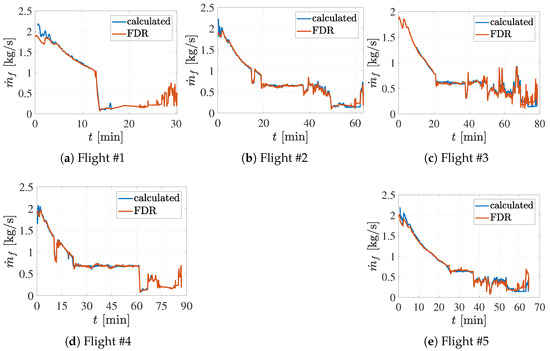
Figure 14.
The calculated fuel flow from ADS-B and ERA5 wind and temperature data compared to measured fuel flow from FDR.
The fuel burn during the approach phase was the least accurately calculated, reaching up to −53.5%. This discrepancy is attributed primarily to differences between actual and BADA configuration scheduling since fuel burn errors of up to −26.3% (Table 4) were observed during the approach with actual configuration scheduling. The underestimation of fuel burn during the approach with actual configuration can be mainly attributed to the drag approach coefficients not perfectly aligning with the true one and to the errors in dynamics modeling. Such differences could be reduced with aerodynamic coefficient optimization and better recognition of configuration scheduling.
For the initial climb phase, the errors were up to 17.2%. These opposite errors for the initial climb and approach counteract each other, resulting in low errors of burned fuel for an entire trajectory.
Most of the fuel is burned during the clean phase. Short phases of flight with extended configurations do not affect accuracy by more than 0.9% for an entire trajectory, e.g., flights #3 and #5 (Table 6). This is likely due to the short initial climbing time and low thrust during approach with lower flaps, slats, and gear-out time. We also observe small offsets of fuel consumed for the cruise phase for flight #5. This offset could be due to errors in initial mass or shorter cruise time compared with other flights. Also, differentiation errors are affected by the size of a dataset.
The most accurate fuel burn is calculated for climb and cruise phases with errors up to 2.8%, while descent errors are up to 6.9%.
To evaluate how the wind and ADS-B data affect the accuracy of fuel consumed, we studied the fuel errors for the most complete ADS-B trajectories. The fuel burns for the entire and clean flight segment are almost the same when comparing data from Table 5 (FDR weather and flight data) and data from Table 6 (ADS-B and ERA5 data), with a difference of less than 0.3%. This can be seen by comparing the relative errors of flights #2, #3, and #5 (Figure 15a). We can also observe that distributions for both data sources are positively skewed and that the same is valid for clean-phase fuel burn errors (Figure 15).
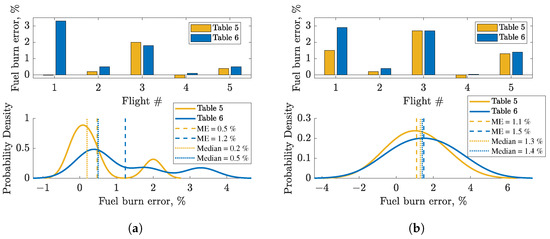
Overall, using ADS-B and ERA5 weather data and BADA 3 configuration scheduling provides a high level of accuracy in predicting aircraft fuel flow behavior for the clean-only and entire airborne flight trajectory within the limited flight data sample of the study.
5. Conclusions
Accurate information on fuel consumption based on aviation surveillance data is crucial for informed decision-making in airspace design and measuring the influence of emerging technologies, ATM effectiveness, and emission reduction. Policymakers and investors rely on these data to identify inefficiencies and make strategic decisions.
In this study, we have presented and tested a method to calculate fuel burn based on ADS-B data from the OpenSky network and weather data from the ERA5 dataset. The proposed method assumes a BADA 3 aircraft drag aerodynamic and configuration scheduling and a fuel consumption model of the engine installed on a single aircraft, which may not represent other aircraft of the same type. The aircraft is modeled as a point-mass model with non-constant wind. A linear interpolation of weather data from ERA5 was utilized to estimate wind and temperature data at specific 4D points for each flight. The algorithm was validated using a limited dataset of five flights for a complete set of 8 Hz FDR data. The available ADS-B data were compared with FDR data for the same UTC, and all data were found to be highly accurate and with acceptable precision:
- Pressure altitude up to ME of 2.5 m and SDME of 11.9 m;
- Ground speed up to ME of −0.5 m/s and SDME of 2.7 m/s;
- Vertical speed up to ME of 0.1 m/s and SDME of 0.5 m/s.
Also, weather data from ERA5 agree satisfactorily with the weather data from FDR:
- Wind heading up to ME of 2.9° and SDME of 32.6°;
- Wind speed up to ME of 0.9 m/s and SDME of 1.9 m/s;
- Temperature up to ME of 0.9 K and SDME of 0.8 K.
As a result, calculated true airspeed has a high accuracy along trajectories with ME up to 1 m/s and SDME up to 2.9 m/s.
Overall, the fuel burn estimation algorithm for the whole trajectory with the ADS-B flight, ERA5 weather data, and BADA configuration scheduling showed high accuracy with an average mean absolute error of 1.2%, standard deviation equal to 1.3%, and mean equal to 0.5%, indicating a positively skewed distribution. The results for the clean trajectory showed a slightly positively skewed distribution with ME = 1.1% and median being 0.2%, suggesting a slightly better accuracy. The accuracies of fuel consumption estimations during the initial climb, descent, and approach are still insufficient. Improving the accuracy of fuel burn estimations per phase is essential for enhancing flight efficiency and environmental performance indicators in the terminal maneuvering area.
The presented approach could contribute to optimizing flight paths by aligning with the industry’s objectives for operational efficiency and environmental responsibility. However, further research and validation are necessary to ensure its accuracy and robustness for diverse datasets and aircraft types, maximizing its impact on efficient route optimization through fuel burn calculation,
Future research could extend this approach to BADA 4 performance data and the implementation of methods for recognizing aerodynamic configuration from ADS-B data. Implementing a selected method for initial mass estimation is also a key focus in our ongoing research efforts.
Author Contributions
Conceptualization, K.K.N., P.P., D.N. and B.A.-F.; methodology, K.K.N., P.P. and D.N.; software, K.K.N., P.P. and D.N.; validation, K.K.N., P.P., D.N. and B.A.-F.; formal analysis, K.K.N., P.P. and D.N.; investigation, K.K.N., P.P., D.N. and B.A.-F.; data curation, K.K.N., P.P. and D.N.; writing—original draft preparation, K.K.N., P.P. and D.N.; writing—review and editing, K.K.N., D.N. and B.A.-F.; visualization, K.K.N., P.P. and D.N.; supervision, K.K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
OpenSky data are available at https://opensky-network.org (accessed on 17 July 2023). Other data are available upon reasonable request from the corresponding author.
Acknowledgments
This product/document has been created with or contains elements of Base of Aircraft Data (BADA) Family 3 Release 3.16 which has been made available by Eurocontrol to Faculty of Transport and Traffic Sciences. Eurocontrol has all relevant rights to BADA. ©2021 The European Organisation for the Safety of Air Navigation (Eurocontrol). All rights reserved. EUROCONTROL shall not be liable for any direct, indirect, incidental or consequential damages arising out of or in connection with this product or document, including with respect to the use of BADA. During the preparation of this work, the authors used OpenAI ChatGPT, Microsoft Bing, and Grammarly to improve clarity, readability, and language. After using this tool, the authors reviewed and edited the content as needed. They take full responsibility for the content of the publication.
Conflicts of Interest
Author Mr. Dario Nikolić was employed by the company Aerobit d.o.o. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADS-B | Automatic dependent surveillance–broadcast |
| AGL | Above ground level |
| ATM | Air traffic management |
| BADA | Base of aircraft data |
| ECAC | European civil aviation conference |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| EHS | Mode S enhanced surveillance |
| ERA5 | European reanalysis |
| ETFMS | Enhanced traffic flow management system |
| FDE | Flight dynamic equation |
| FDR | Flight data recorder |
| IFR | Instrument flight rules |
| IIR | Infinite impulse response |
| ISA | International standard atmosphere |
| KDE | Kernel density estimation |
| MLM | Maximum landing mass |
| MRAR | Meteorological routine air reports |
| MZFM | Maximum zero fuel mass |
| NaN | Not a number |
| NA | Not applicable |
| OPF | Operations performance file |
| PEP | Performance engineer’s program |
| Probability density function | |
| RUC | Rapid update cycle |
| SOP | Standard operating procedures |
| TAS | True airspeed |
| TOD | Take-off distance |
| TOM | Take-off mass |
References
- Eurocontrol. European ATM Network Fuel Inefficiency Study; Technical Report; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2020; Available online: https://www.eurocontrol.int/publication/environmental-assessment-european-atm-network-fuel-inefficiency-study (accessed on 25 August 2023).
- Eurocontrol. Master Plan Level 3 Implementation Plan 2023; Technical Report; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2023; Available online: https://www.eurocontrol.int/publication/european-atm-master-plan-implementation-plan-level-3 (accessed on 23 November 2023).
- Eurocontrol. Enhanced Tactical Flow Management System (ETFMS). 2023. Available online: https://www.eurocontrol.int/system/enhanced-tactical-flow-management-system (accessed on 17 October 2023).
- Eurocontrol. Critical Review of ATM/ANS Environmental Performance Measurements; Technical Report; European Organisation for the Safety of Air Navigation: Brussels, Belgium, 2023; Available online: https://www.easa.europa.eu/en/document-library/general-publications/easa-eurocontrol-critical-review-atmans-environmental (accessed on 1 February 2024).
- Eurocontrol. Space-Based ADS-B Data Now Integrated into EUROCONTROL’s Network Operations System. 2023. Available online: https://www.eurocontrol.int/news/space-based-ads-b-data-now-integrated-eurocontrols-network-operations-system (accessed on 1 January 2024).
- Oaks, R.; Ryan, H.; Paglione, M. Prototype implementation and concept validation of a 4-d trajectory fuel burn model application. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 8164. [Google Scholar] [CrossRef]
- Chatterji, G.B. Fuel burn estimation using real track data. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Including the AIAA Balloon Systems Conference and 19th AIAA Lighter-Than, Virginia Beach, VA, USA, 20–22 September 2011; p. 6881. [Google Scholar] [CrossRef]
- Dalmau, R.; Prats, X.; Ramonjoan, A.; Soley, S. Estimating fuel consumption from radar tracks: A validation exercise using FDR and radar tracks from descent trajectories. CEAS Aeronaut. J. 2020, 11, 355–365. [Google Scholar] [CrossRef]
- Harada, A.; Miyamoto, Y.; Miyazawa, Y.; Funabiki, K. Accuracy evaluation of an aircraft performance model with airliner flight data. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2013, 11, 79–85. [Google Scholar] [CrossRef][Green Version]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Sun, J.; Basora, L.; Olive, X.; Strohmeier, M.; Schäfer, M.; Martinovic, I.; Lenders, V. OpenSky Report 2022: Evaluating Aviation Emissions Using Crowdsourced Open Flight Data. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Sun, J.; Olive, X.; Strohmeier, M. Environmental Footprint of Private and Business Jets. Eng. Proc. 2022, 28, 13. [Google Scholar] [CrossRef]
- Quadros, F.D.A.; Snellen, M.; Sun, J.; Dedoussi, I.C. Global Civil Aviation Emissions Estimates for 2017–2020 Using ADS-B Data. J. Aircr. 2022, 59, 1394–1405. [Google Scholar] [CrossRef]
- Teoh, R.; Engberg, Z.; Shapiro, M.; Dray, L.; Stettler, M.E.J. The high-resolution Global Aviation emissions Inventory based on ADS-B (GAIA) for 2019–2021. Atmos. Chem. Phys. 2024, 24, 725–744. [Google Scholar] [CrossRef]
- Filippone, A.; Parkes, B.; Bojdo, N.; Kelly, T. Prediction of aircraft engine emissions using ADS-B flight data. Aeronaut. J. 2021, 125, 988–1012. [Google Scholar] [CrossRef]
- Filippone, A.; Bojdo, N.; Mehta, S.; Parkes, B. Using the OpenSky ADS-B Data to Estimate Aircraft Emissions. Eng. Proc. 2021, 13, 11. [Google Scholar] [CrossRef]
- Filippone, A. Flight Performance Software FLIGHT; Technical Report AERO-UNIMAN-2014-10; School of Mechanical, Aerospace and Civil Engineering, The University of Manchester: Manchester, UK, 2015. [Google Scholar]
- Wickramasinghe, N.K.; Toratani, D.; Fukushima, S.; Hirabayashi, H. A study on modeling techniques for fuel burn estimation based on flight simulator experiment data. In Proceedings of the 2017 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2566–2577. [Google Scholar] [CrossRef]
- Sun, J.; Ellerbroek, J.; Hoekstra, J.M. Aircraft initial mass estimation using Bayesian inference method. Transp. Res. Part C Emerg. Technol. 2018, 90, 59–73. [Google Scholar] [CrossRef]
- Rohani, A.S.; Puranik, T.G.; Kalyanam, K.M. Machine Learning Approach for Aircraft Performance Model Parameter Estimation for Trajectory Prediction Applications. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference, DASC, Barcelona, Spain, 1–5 October 2023. [Google Scholar] [CrossRef]
- Alligier, R. Predictive distribution of mass and speed profile to improve aircraft climb prediction. J. Air Transp. 2020, 28, 114–123. [Google Scholar] [CrossRef]
- Chati, Y.S.; Balakrishnan, H. Statistical Modeling of Aircraft Takeoff Weight. In Proceedings of the Twelfth USA/Europe Air Traffic Management Research and Development Seminar (ATM 2017), Seattle, DC, USA, 27–30 June 2017. [Google Scholar]
- Holzäpfel, F.; Rotshteyn, G. Estimating Aircraft Landing Weights from Mode S Data. J. Aircr. 2023, 60, 589–593. [Google Scholar] [CrossRef]
- Olive, X. Traffic, a toolbox for processing and analysing air traffic data. J. Open Source Softw. 2019, 4, 1518. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. 2023. Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 12 August 2023).
- Sun, J.; Vû, H.; Olive, X.; Hoekstra, J.M. Mode S Transponder Comm-B Capabilities in Current Operational Aircraft. Proceedings 2020, 59, 4. [Google Scholar] [CrossRef]
- European Union. Commission Implementing Regulation (EU) 2020/587. Off. J. Eur. Union 2020, L 138/1, 1–7. [Google Scholar]
- Strajnar, B. Validation of Mode-S Meteorological Routine Air Report aircraft observations. J. Geophys. Res. Atmos. 2012, 117, D23110. [Google Scholar] [CrossRef]
- Weitz, L.A. Derivation of a Point-Mass Aircraft Model used for Fast-Time Simulation; Technical Report MTR 150184; The MITRE Corporation: McLean, VA, USA, 2015. [Google Scholar]
- Savitzky, A.; Golay, M. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Krajček, K.; Nikolić, D.; Domitrović, A. Aircraft performance monitoring from flight data. Teh. Vjesn./Tech. Gaz. 2015, 22, 1337–1344. [Google Scholar] [CrossRef][Green Version]
- Mouillet, V. User Manual for the Base of Aircraft Data (BADA) Revision 3.16; EIH Technical/Scientific Report 22/05/12-45; EUROCONTROL Innovation Hub: Le Plessis-Pâté, France, 2022; Distribution: Public Restricted Confidential. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).