1. Introduction
In the last few decades, space debris, including inactive satellites, rocket bodies, and fragments of various sizes, has emerged as a global challenge for space agencies and institutions, thus becoming a major concern. The two orbit regions most densely populated by space objects are the low earth orbit (LEO) and the geostationary orbit (GEO). Notably, the majority of objects in orbit are space debris, while cooperative satellites make up only a small fraction [
1].
The presence of space debris poses a substantial threat to space operations. Potential collisions with space debris can result in a range of consequences, from gradual erosion of satellite surfaces to the complete destruction of active satellites. Such collisions can also lead to the creation of thousands of additional fragments, contributing to environmental problems and the risk of cascade effects [
2].
To ensure the safety of space operations, space agencies and organizations worldwide have implemented various strategies. Moreover, international cooperation is actively underway in the field of space surveillance and tracking (SST). In Europe, two noteworthy programs address this issue: the European Space Agency (ESA) Space Situational Awareness (SSA) Programme [
3] and the European Union Space Surveillance and Tracking (EUSST) Framework [
4]. EUSST is a collaborative consortium involving European national agencies and institutions, and it is responsible for providing essential services such as conjunction analysis [
5], fragmentation analysis [
6,
7], and re-entry prediction [
8]. These services rely on data collected from ground-based sensors, including optical telescopes (offering precise angular data) [
9], radars (providing both angles and range or Doppler shift measurements) [
10], and lasers (supplying exceptionally accurate range measurements) [
11]. In particular, survey radars play a critical role in characterizing the orbits of unidentified objects upon their initial detection [
12,
13,
14]. In addition to the above-mentioned services, a crucial role is played by maneuver detection [
15] and proximity operations monitoring [
16,
17]. The latter is expected to become more and more fundamental in the future for the active debris removal programs.
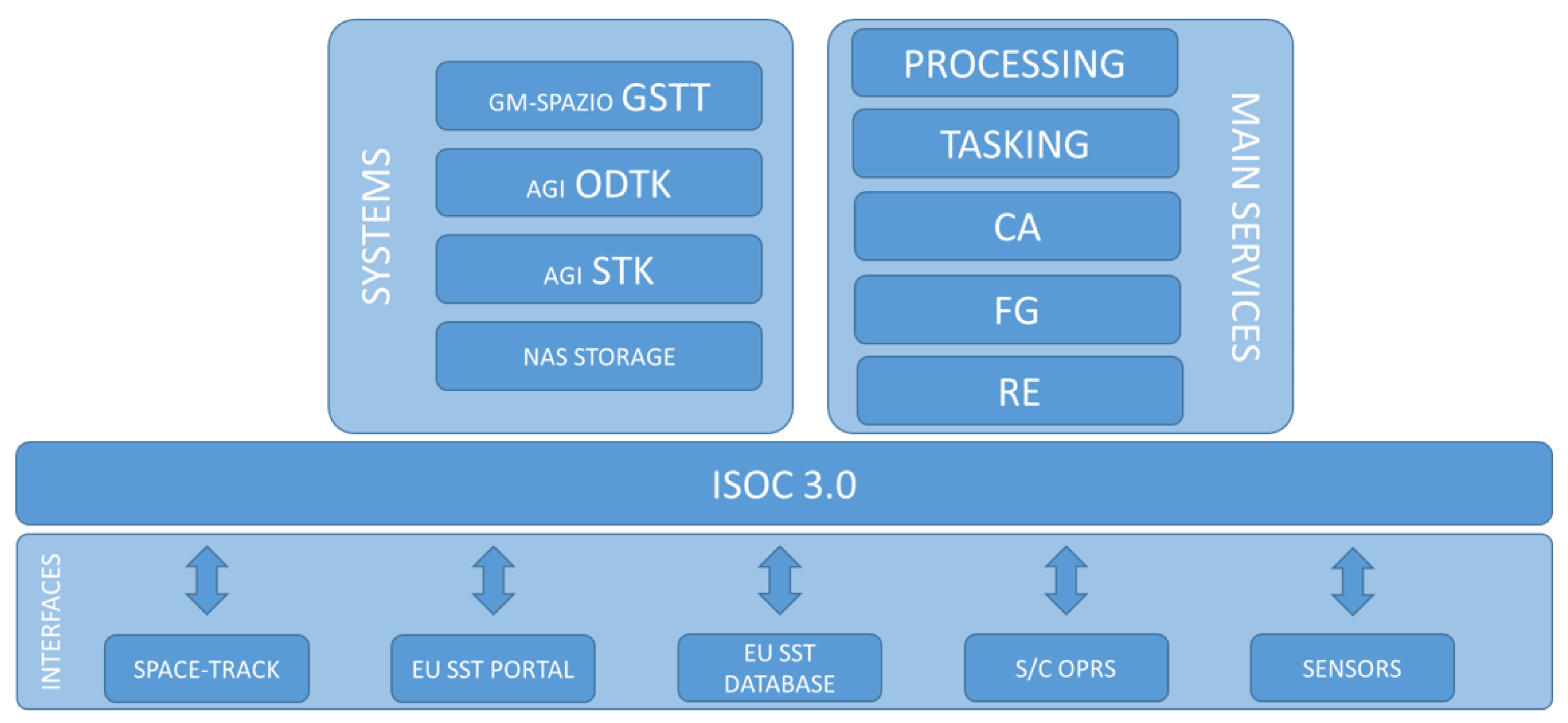
Italy’s participation in the EUSST program involves three entities: the Italian Space Agency (ASI), the Astrophysics National Institute (INAF), and the Italian Ministry Of Defence, with the Italian Air Force (AM) largely involved. Italy’s specific role within this program pertains to re-entry and fragmentation services. To effectively manage the vast amount of observational data, there is a need for the development of efficient and reliable tools. In this context, the Flight Test Department of the Italian Air Force is responsible for establishing a system architecture which collects and processes data to provide SSA services to both military and civilian users, as well as to the EUSST consortium. The system, named the ISOC Suite after the Italian SST Operational Centre (ISOC) of the Italian Air Force, has been meticulously designed with a web-based infrastructure, where space objects and associated data populate a catalog [
18]. The ISOC Suite provides SST services and functions which work in unison to enhance awareness of space events in Earth-centered orbits. The embedded software is the result of a collaborative effort with national industry and academia, designed and implemented with a focus on operational requirements.
As mentioned above, the collision avoidance service is crucial for space traffic management, and it is tasked with assessing potential conjunctions among cataloged objects. When a conjunction is detected, a conjunction data message (CDM) [
19] is generated, consolidating information about the involved satellites. Typically, these objects are categorized as primary (typically maneuverable satellites) and secondary (either operational or inactive satellites), composing a pair [
20]. The CDM includes information on the Cartesian state of these satellites, both in terms of mean and covariance, the time of closest approach (TCA), the associated miss distance (MD), representing the distance at the closest approach, and the probability of collision (PoC).
This work presents the prototype of the conjunction analysis tool developed for the ISOC Suite, a collaborative effort involving the Italian Air Force, Leonardo Company (Rome, Italy), and Politecnico di Milano. The development of this tool was conducted to meet the tailored requirements, satisfying very specific needs. The software architecture prioritizes optimal computational performance, and comprises three main modules, each dedicated to the precise identification and characterization of potential conjunction events. The initial module employs a filtering sequence to screen out pairs that fail to meet specific criteria, thus narrowing down the candidates. Subsequently, the remaining events are more meticulously characterized through the calculation of critical parameters (including the metrics mentioned above), and the user can choose to store information for relevant events and generate output files, such as the CDM, adhering to the standard format set by the Consultative Committee for Space Data Systems (CCSDS). In addition, based on the user requirements, the tool offers the possibility to compute a collision avoidance maneuver (CAM), providing operators with a potential means to avoid collisions. Overall, the tool can manage input files like the CDM, two-line elements (TLEs), Orbit Ephemeris Message (OEM), and Orbit Parameter Message (OPM).
The paper structure is as follows. The ISOC Suite and the PoC computation methodology are presented in
Section 2 and
Section 3, respectively. Then, the algorithmic flow is illustrated in
Section 4 and
Section 5. Subsequently, the tool validation is presented in
Section 6 and, finally, the algorithm performance is evaluated through real-case operational scenarios in
Section 7.
2. Italian SST Operations Centre
The ISOC was originally established in 2014 and operated by the military personnel of the Flight Test Department of the Italian Air Force. Currently, the operational activities are led by the the Space Situational Awareness Centre (C-SSA), whereas the Flight Test Department is responsible for research and development operations. The ISOC Suite is a complex system that was originally developed to support SST tasks, but it is currently evolving towards a broader awareness of the space scenario, to enhance the national security for both civil and military applications. The ISOC is also included in the EUSST framework, supporting the services listed below:
Re-entry (RE): primarily responsible for the analysis of uncontrolled re-entry into the low atmosphere for large and dangerous objects.
Fragmentation (FG): primarily responsible for the analysis of in-orbit fragmentation as a consequence of satellite break-ups or collisions.
Collision avoidance (CA): cold redundant operational center for the analysis of the collision probability and geometry for conjunction events.
The ISOC Suite is used to support the above-mentioned services, whose high level architecture is represented in
Figure 1. The main inputs of the suite are provided by national sensors, consortium observations, and the European observation catalog, along with available public sources. The inner part of the system is also able to use commercial off-the-shelf (COTS) and proprietary software. The system’s outputs are the services shown in the right part of
Figure 1. A functional part of the entire system is the collision avoidance service, that could be guaranteed by the suite described in this document.
3. Probability of Collision
To accurately deal with the uncertainty linked to the orbital state of a tracked satellite, it is crucial to determine the alert level in satellite conjunctions through a stochastic description. As a result, the PoC becomes a pivotal parameter in the operational management of the CA service. In the present suite, the PoC computation is conducted in the one-to-one analysis, as better discussed in
Section 4.2.
Let us consider the relative position between a primary and a secondary. Associating a diameter to the involved objects’ geometry, through the definition of and for the primary and the secondary objects, respectively, it is possible to define the hard body radius: . From a conceptual point of view, a collision occurs when and, to compute the associated PoC, two models exist, depending on the conjunction features:
The short-term encounter model [
21] is designed for conjunctions featuring a high relative velocity between the objects at the TCA. It is particularly well-suited for LEO encounters. This model operates under the assumption of constant position uncertainties during the conjunction and employs a deterministic approach for describing velocities [
20].
The long-term encounter model [
22] is designed for conjunctions with a minimal relative velocity between the involved objects. In these scenarios, the objects spend a substantial amount of time in close proximity, and the encounters may occur multiple times per orbit. This model is particularly applicable to GEO encounters, formation flying, and proximity operations.
In the present study, the focus is placed on the short-term encounter model due to its advanced state of development. This model assumptions facilitate the definition of an encounter frame, commonly referred to as the B-plane, at the TCA. The precise formulation of the B-plane may vary among authors, but it consistently exhibits two key characteristics: it is centered on the mean-position center of gravity of one of the two objects, and is oriented orthogonally to the direction of the relative velocity.
Based on the assumptions of the short-term model, it becomes feasible to simplify the problem into a two-dimensional space, thus obtaining the integral in Equation (
1), which is a compact version of the one in [
23].
This reduces the computation of the PoC to a multinormal law 2D integral over the random variable , which represents the two-dimensional position, and whose is the mean value, and where is the related covariance.
Therefore, the short-term encounter model enables the calculation of the PoC through a 2D integral. The problem can be solved using either numerical or analytical methods. In the tool, both approaches have been implemented for this purpose.
Concerning the numerical approaches, the algorithm presented in [
24] is selected and referred to as the “Patera” method in this work. It reformulates the 2D PoC as a one-dimensional integral by treating it as a path integral along the contour of the integration domain. To enhance the PoC’s numerical precision, a numerical scheme has been implemented in the suite to ensure convergence, and the accuracy of the PoC depends on the number of integration steps used. In addition to the numerical approach, two analytical methods have been incorporated: the algorithms described in [
21] and in [
25], referred to as the “Chan” and “LAAS” methods, respectively. Both methods exploit a series expansion of the PoC, and the accuracy of the results depends on the chosen expansion order. It is important to note that these analytical methods are computationally more efficient than the numerical methods. In addition, the “LAAS” method compensates numerical instabilities through the inclusion of a pre-conditioning term [
25].
In the context of the PoC computation, it is essential to highlight one more aspect. Since the PoC value relies on the covariance associated with the orbital states of the involved objects, underestimating or overestimating the uncertainty can have a significant impact on the results. This problem is usually referred to as probability dilution [
26], and it is experienced when an increase in the covariance that is used to compute the PoC leads to a decrease in this quantity. This seems to imply that lowering the data quality makes satellites safer, that makes no sense. Therefore, to face this issue, a sensitivity analysis can be conducted to determine the maximum PoC (referred to as max-PoC). As suggested in [
27], this analysis can be conducted adjusting the covariances of the involved objects by applying an inflating factor, typically within the range of 0.25 to 4, to assess the PoC sensitivity to these changes. From an operational perspective, within the algorithms implemented in the tool, a grid of N points ranging from 0.25 to 4 is defined, which are used as multiplicative factors to augment or reduce the covariance of the primary and the secondary, one at a time. For each augmented or reduced covariance the PoC is recomputed, finally obtaining a grid of values for this quantity that allows the max-PoC to be identified. The conjunction analysis suite developed for the ISOC Suite embeds the possibility to conduct this analysis as well.
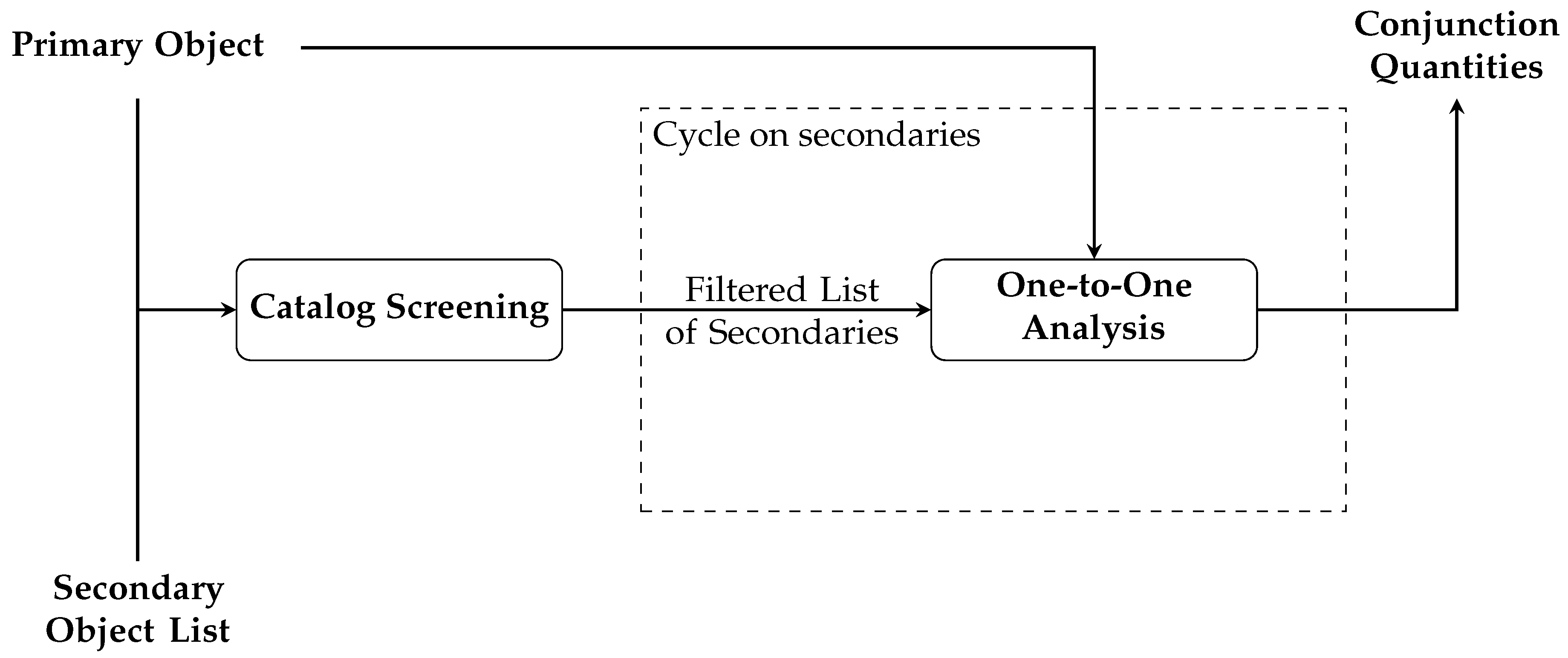
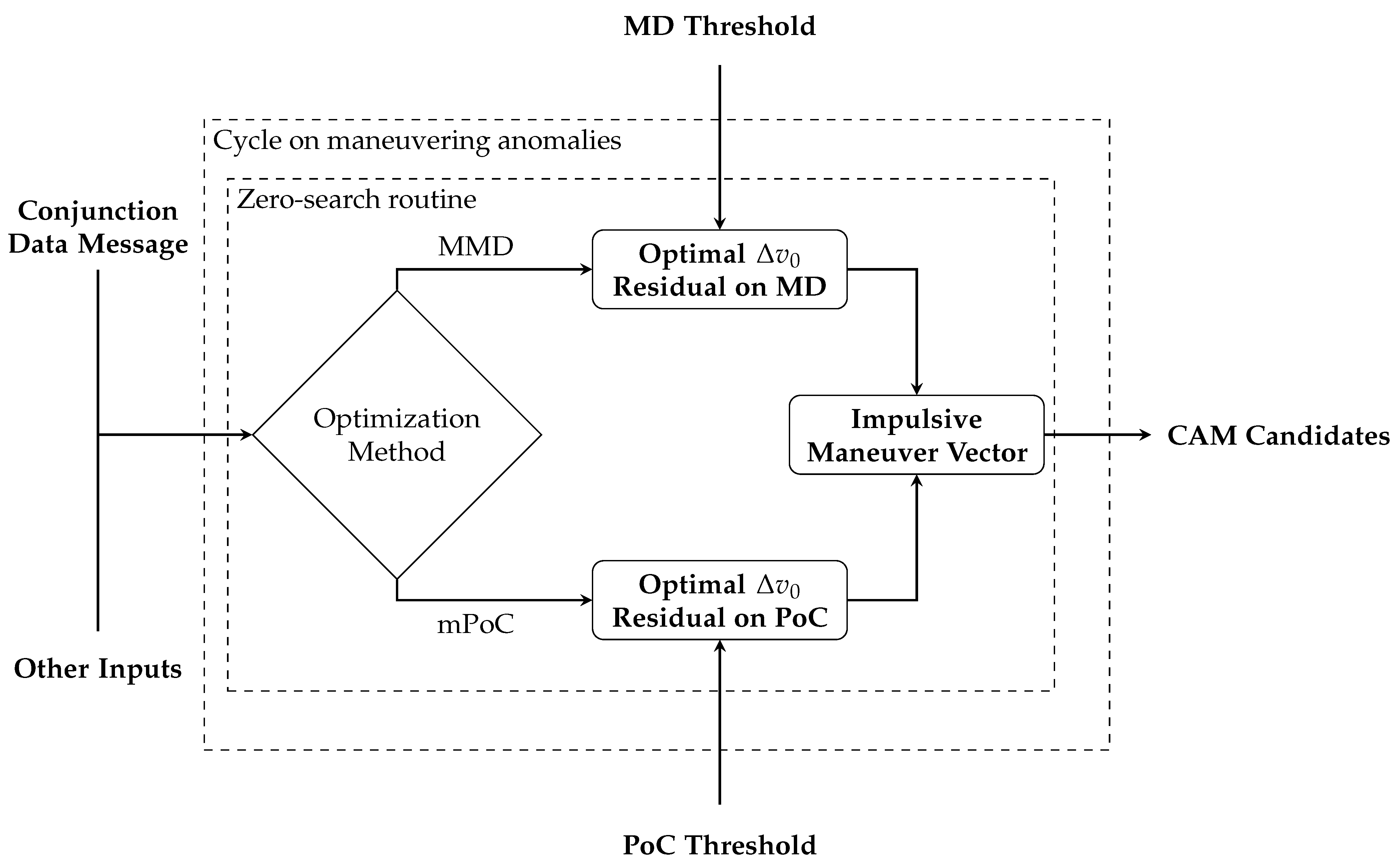
4. Conjunction Analysis Algorithm
The present section provides an insight into the algorithms included in the conjunction analysis software, except for the CAM planning module, which is described in more depth in
Section 5. First, a pre-processing phase is run to manage the input data before the conjunction analysis process begins. In particular, the objects’ ephemerides are evaluated at the starting epoch of the time interval of the analysis, which is set either by default or according to a specific request by the user. In addition, if no covariance is associated to an input object, this is attributed through the method presented in [
28]. Then, a catalog screening is conducted, which allows the overall computational demand to be reduced. Subsequently, a one-to-one analysis for the pairs passing the filters computes the essential conjunction parameters introduced in
Section 1. The overall process is represented in
Figure 2.
4.1. Catalog Screening
The catalog screening implements the filtering sequence outlined by Hoots et al. [
29]. It operates on the concept that primary and secondary objects may not be at risk of collision due to geometric considerations and the absence of overlapping time intervals. In particular, the apogee–perigee filter (AP filter) and the orbit path filter (OP filter) work to eliminate pairs when the orbits of the objects do not permit them to approach closely. Additionally, the time filter (T filter) considers the real-time positions of space objects on their orbits, removing pairs that do not cross a region of relative proximity simultaneously.
Based on the way the filters are implemented, they may require the user to define a duration of the analysis interval. About this, it is worth remarking that, according to what is highlighted in [
30], using simplified motion models in the filters may introduce errors which grow with longer analysis time windows. This issue is particularly relevant in the choice of the thresholds to be used within the criteria of the different filters, as the analysis interval length impacts the size needed to ensure precision in results. This problem can be partially attenuated by including the orbital perturbations.
Concerning the order of the filters within the catalog screening sequence, as stated in [
31], this choice is driven by the computational cost associated with their operations. Given the algorithms on which the filters are based, and after their numerical validation, the following choice of the order of the filters was taken. The result is a short-listed version of the original secondary object catalog, which then enters the one-to-one analysis, as described in
Section 4.2.
4.1.1. Apogee–Perigee Filter
The first filter in the series is the AP filter, as it is associated with the minimal computational requirements. It computes the apogee and perigee for each object. Subsequently, for each pair, it straightforwardly checks the following geometric criterion:
where
q represents the larger perigee,
Q denotes the smaller apogee, and
signifies a user-defined threshold distance. Alfano and Finkleman’s work [
31] investigated the use of different threshold values, finally suggesting a value close to 10 km, which should guarantee an effective trade-off. For this, and for all the filters in such a screening procedure, it is crucial to underline that the more precise the orbital data, the stricter the threshold setting can be. More details on this aspect are given in [
30].
The pairs satisfying Equation (
2) pass the AP filter and enter the T filter, which is described below.
4.1.2. Time Filter
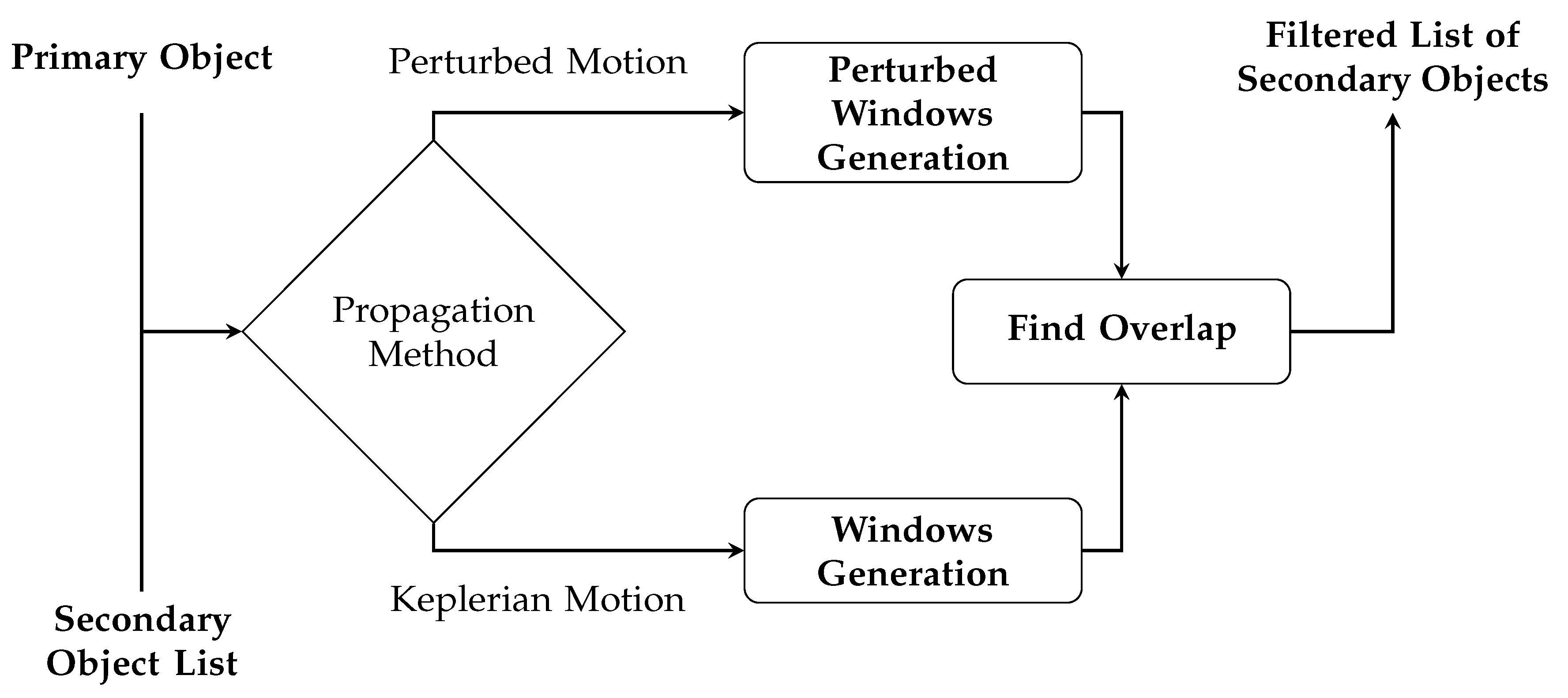
In the filtering process, it is vital to account for the real-time positions of both space objects on their respective orbits, extending beyond basic geometric factors. This criterion mandates that for a potential collision to be plausible, both primary and secondary objects must traverse a region of relative closeness at the same time.
The core concept of the T filter involves examining the alignment of time intervals determined by the transit of both the primary and secondary within these critical regions. Typically, two satellites can collide for a brief period before and after they cross the intersection line of the two orbital planes. To establish these periods, two orbital positions are selected around the line of nodes, and these positions are then converted into time intervals using the Kepler equation. For both the primary and secondary objects, a set of time windows is derived, which are spaced in time according to the orbital period. The subsequent step verifies possible overlapping time windows of the two objects to determine whether the pair will pass through the filter or not. In particular, multiple overlaps can be identified, that is, multiple conjunction time intervals for the same pair of objects.
In detail, the algorithm introduced by Hoots et al. [
29] is applied to calculate the time windows. However, this method proves ineffective in situations involving co-planar and nearly co-planar pairs. In such cases, an alternative approach is employed in the conjunction analysis suite, which leverages the rate of change in the relative position between the two objects to identify the region of closeness. This alternative method detects the change from negative to positive values in this rate of change, signifying a local minimum. It is worth to remark that the intersection line between the two orbital planes is not stationary and evolves over time. For this reason, it is possible for the user to select an accurate propagation method, to obtain a more accurate estimation across the analysis time window, as represented in
Figure 3. As mentioned above, the threshold setting of the T filter shall be selected in accordance to the length of the analysis time window.
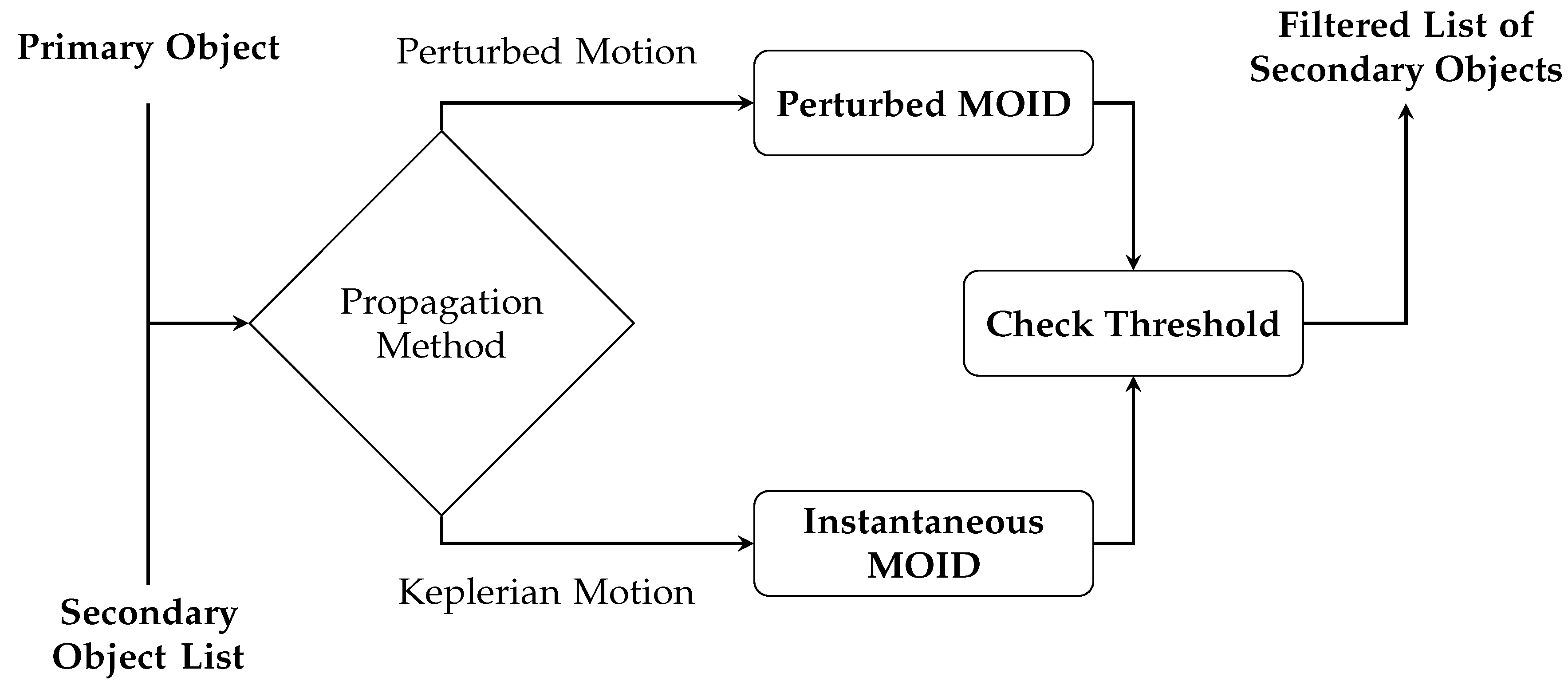
4.1.3. Orbit Path Filter
The OP filter takes as input the pairs which passed the T filter, each pair with possibly associated multiple conjunction time intervals. It relies on the determination of the minimum orbital intersection distance (MOID), which is computed for each conjunction epoch, and then compared to a threshold, based on the following criterion:
where
represents a user-selected threshold distance. Even for this filter, Alfano and Finkleman [
31] investigated the use of different threshold values, finally suggesting a value close to 90 km, which should guarantee an effective trade-off. If Equation (
3) is satisfied, the pair passes the filter and enters the one-to-one analysis described in
Section 4.2.
A focused discussion shall be devoted to the MOID computation, which is based on Gronchi’s algorithm [
32]. If a Keplerian propagation method is selected by the user, this approach is carried out using the orbital data available at that moment, without further refinement, and this results in a non-time-dependent MOID. However, when a more accurate propagation method is selected by the user, a specific procedure for MOID computation is activated. This latter procedure is presented in [
6], and is composed of the following steps:
Calculate the MOID and the corresponding true anomalies using the orbital elements of the primary and secondary objects as defined at the initial epoch of the analysis time window.
Determine the times of flight from the current positions to the true anomalies corresponding to the MOID.
Propagate the states of the primary and secondary objects for the times of flight computed in the previous step.
Convert the propagated states into orbital elements.
Recalculate the MOID and the corresponding true anomalies using the updated orbital elements of the primary and secondary.
Compute the times of flight from the updated positions to the updated true anomalies corresponding to the updated MOID.
Examine these times of flight, and if they exceed a predefined threshold, repeat the process.
The overall OP filter workflow is represented in
Figure 4. Given that it is the last filter of the sequence, and that the pairs passing it have already passed the T filter, temporal considerations can be made to extract useful information about the TCA. As also remarked by Hoots et al. [
29], the interval of interest in which to analyze the relative motion between the two objects may be shortened to those intervals identified by the T filter. In this regard, being that the time windows of the T filter have been generated around portions of the orbits close to the line of intersection, that is in proximity to the MOID, this allows the epoch of transit of one of the two objects through the MOID to be considered as a candidate TCA.
4.2. One-to-One Analysis
The pairs which pass the AP filter, the T filter, and the OP filter exit the catalog screening step and enter the one-to-one analysis, which implements more meticulous operations. To this end, the tool processes one primary object and one secondary object at a time, as follows.
To refine the TCA candidates computed in the OP filter, the states of both objects are propagated on the time intervals identified by the T filter, and their relative positions are computed. The TCAs are refined by using the time rate of change in the relative position, based on the method presented in [
29], which detects the presence of local minima. During this operation three cases can occur:
- 1.
The time rate of change in the relative position solely increases: this indicates that the two objects are moving away from each other, and the TCA is taken as the initial moment of the time interval.
- 2.
The time rate of change in the relative position exclusively decreases: in this case, the objects are approaching each other, but no local minimum is detected within the time window. Consequently, the TCA is assumed to be the final moment of the time interval.
- 3.
The time rate of change in the relative position undergoes a sign change from negative to positive: in this scenario, a local minimum exists within the time window, and the corresponding moment is selected as an initial estimate. This serves as a starting point for an optimization, which searches for the TCA as the epoch in which the relative position and the relative velocity between the two objects become orthogonal.
The MD is then computed as the norm of the relative position at the TCA. In the third case, it is possible to encounter multiple local minima in the relative position. If this occurs, the time corresponding to the minimum relative position norm is selected as the TCA, and the distance between the objects at that moment is recorded as the MD. In any case, the tool retains information about the other time points and their respective relative position norms for potential future use.
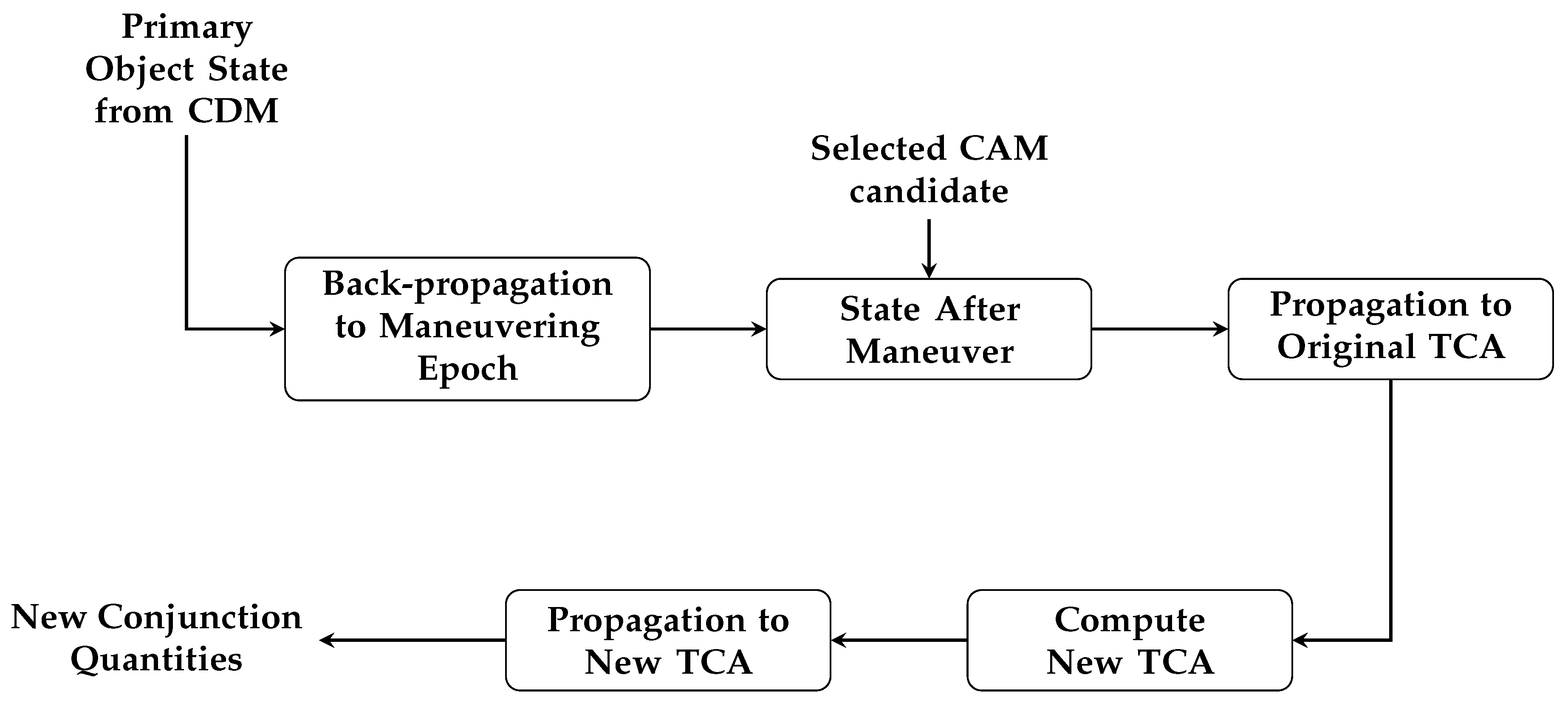
Following this stage, the state transition matrix, computed through the method presented in [
33], is applied to propagate the objects’ covariances (possibly associated during data pre-processing) to the TCAs. Subsequently, other conventional parameters associated with a conjunction event are computed, including the PoC, which is determined based on the user’s chosen method (i.e., Chan, Patera, LAAS) and can be then modified in the maximum PoC by applying the inflating factor to the covariances, as described in
Section 3Finally, the user can choose to create the CDM file for the one-to-one analysis carried out. If for the same object pair multiple conjunctions are identified, multiple CDMs can be written coherently.
8. Conclusions
This paper provides an in-depth overview of the conjunction analysis software for SST operations, which is integrated into the ISOC Suite. It facilitates the detection and detailed characterization of potential conjunction events between a selected catalog of primary objects and the comprehensive space catalog. The software can manage different formats of the input files and the settings of the parameters can be modified by the user, and this flexibility makes the tool versatile and accommodates different operator’s requirements.
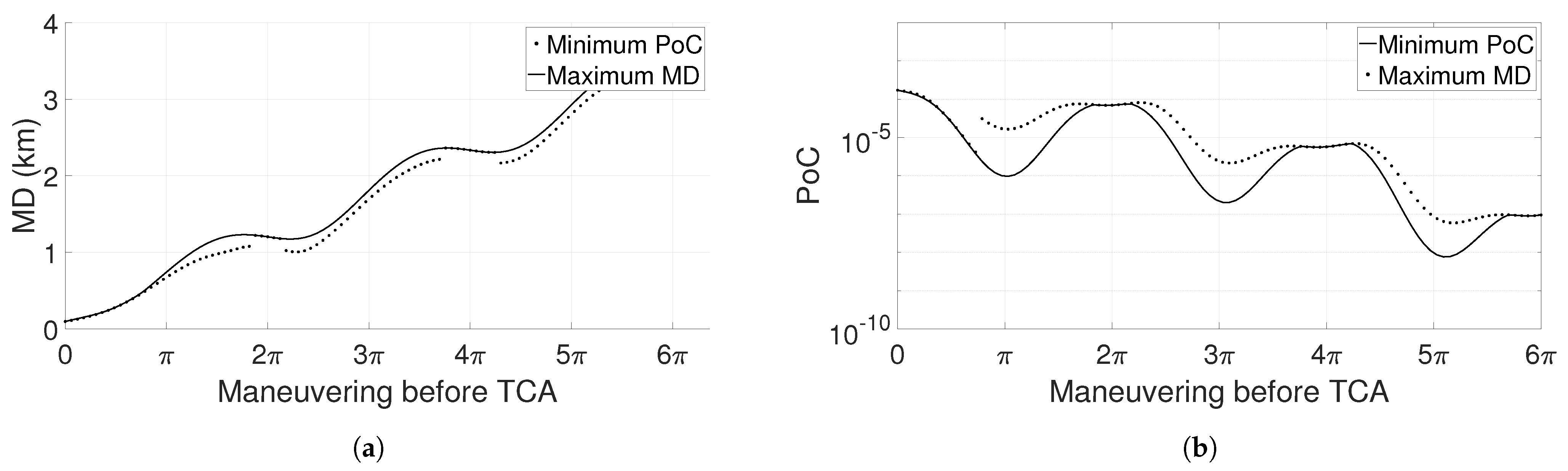
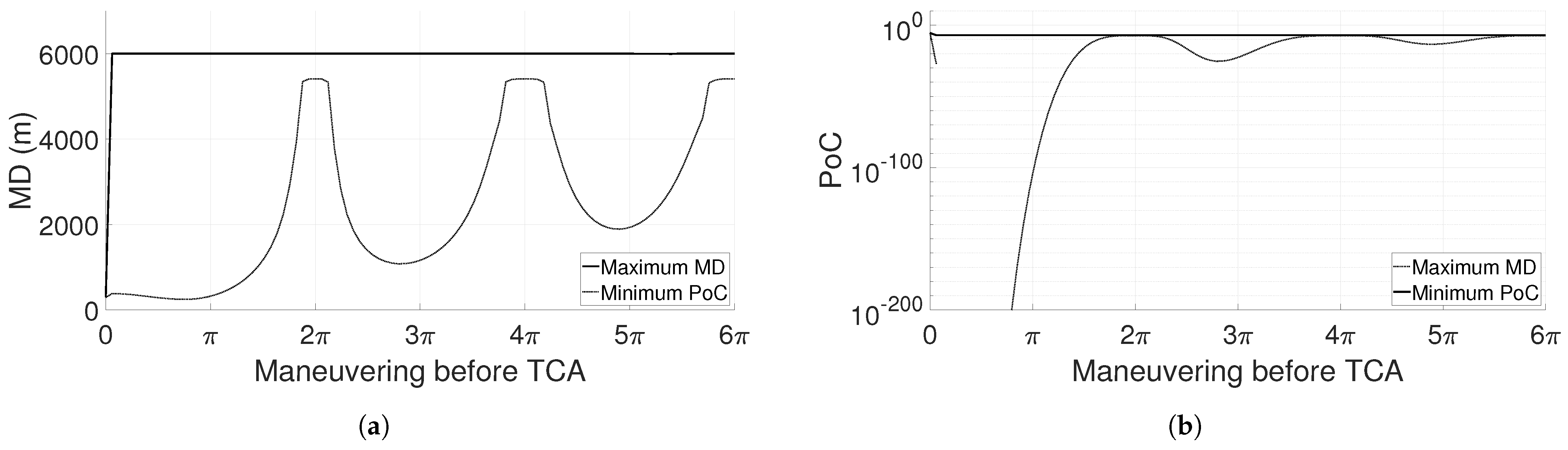
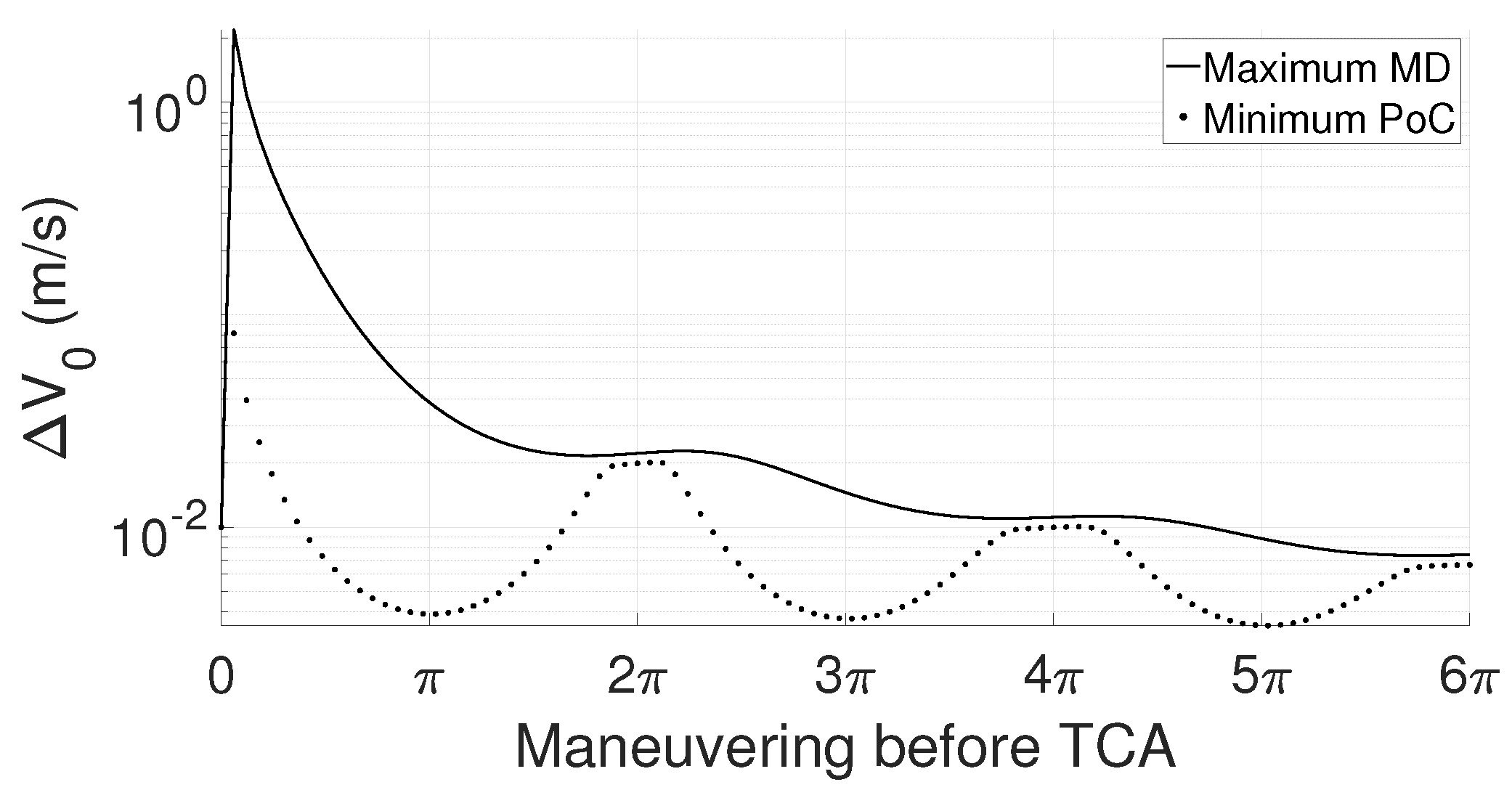
First, a catalog screening applies a filtering sequence to detect possible colliding pairs of space objects, and this short-listing allows a much faster computation in the one-to-one analysis, in which each conjunction is characterized in terms of TCA, MD, and PoC. In addition, once a potential colliding pair is identified, the tool offers the possibility to compute multiple candidate CAMs to match specific criteria in terms of the PoC and MD. From the range of output options, the user can select a candidate maneuver (typically the least expensive one) to verify whether the criteria are respected considering orbital perturbations, both at the original and at the new TCA.
The validation and the operational scenario analysis proved both the efficiency and the accuracy of the developed software. In the future, the ISOC Suite could be enriched with dedicated procedures to manage conjunctions which do not respect the short-term encounter model assumptions, through methods developed for the long-term case.