Transonic Buffet Suppression by Airfoil Optimization
Abstract
1. Introduction
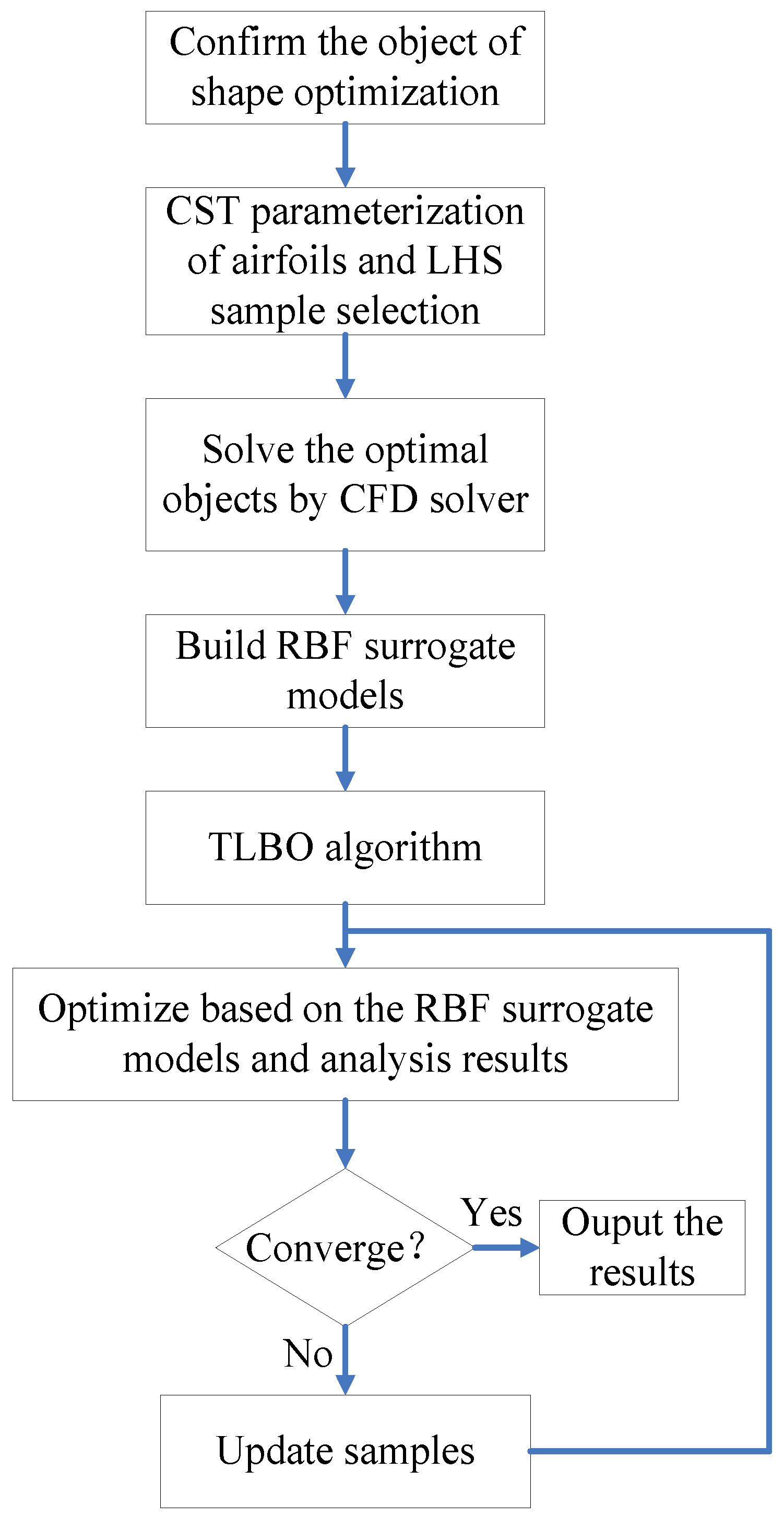
2. Optimization Framework
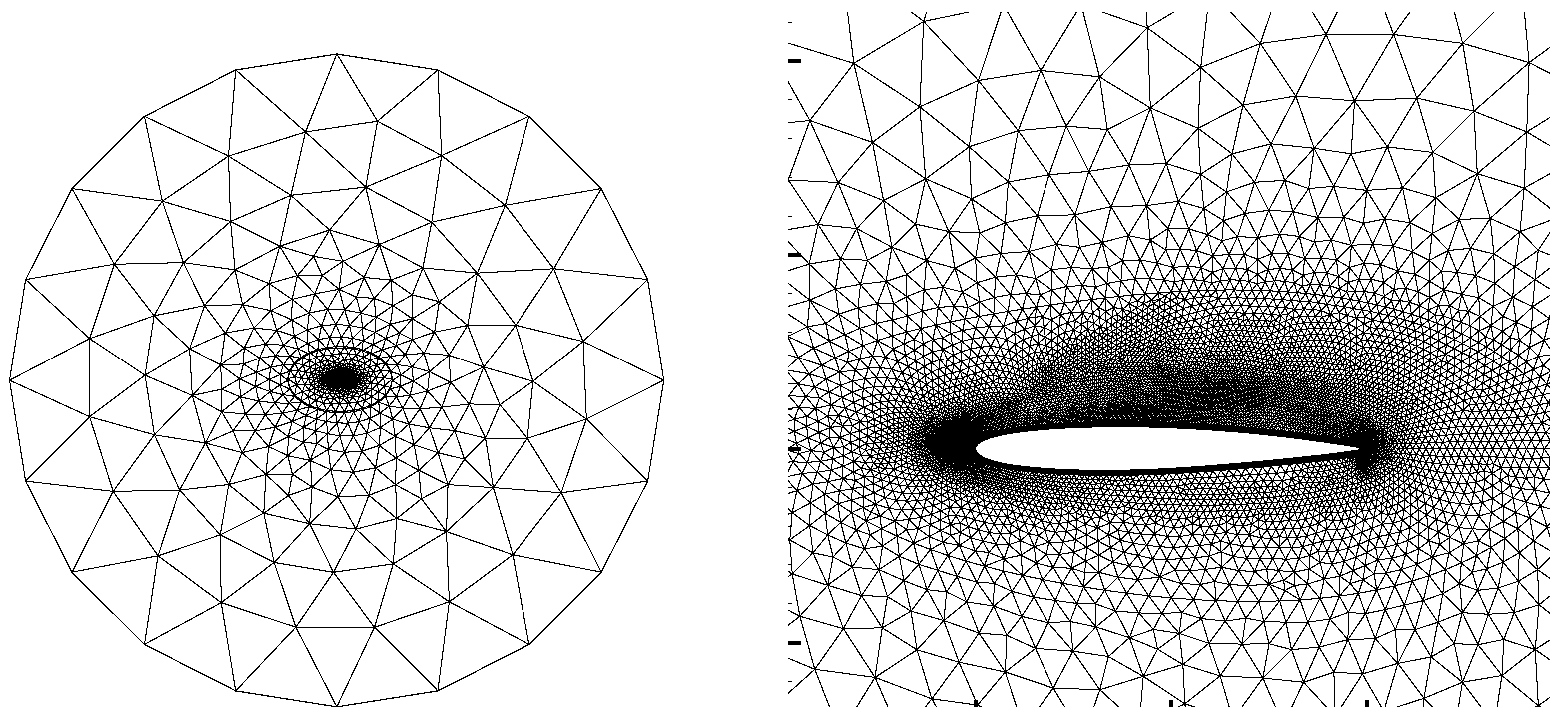
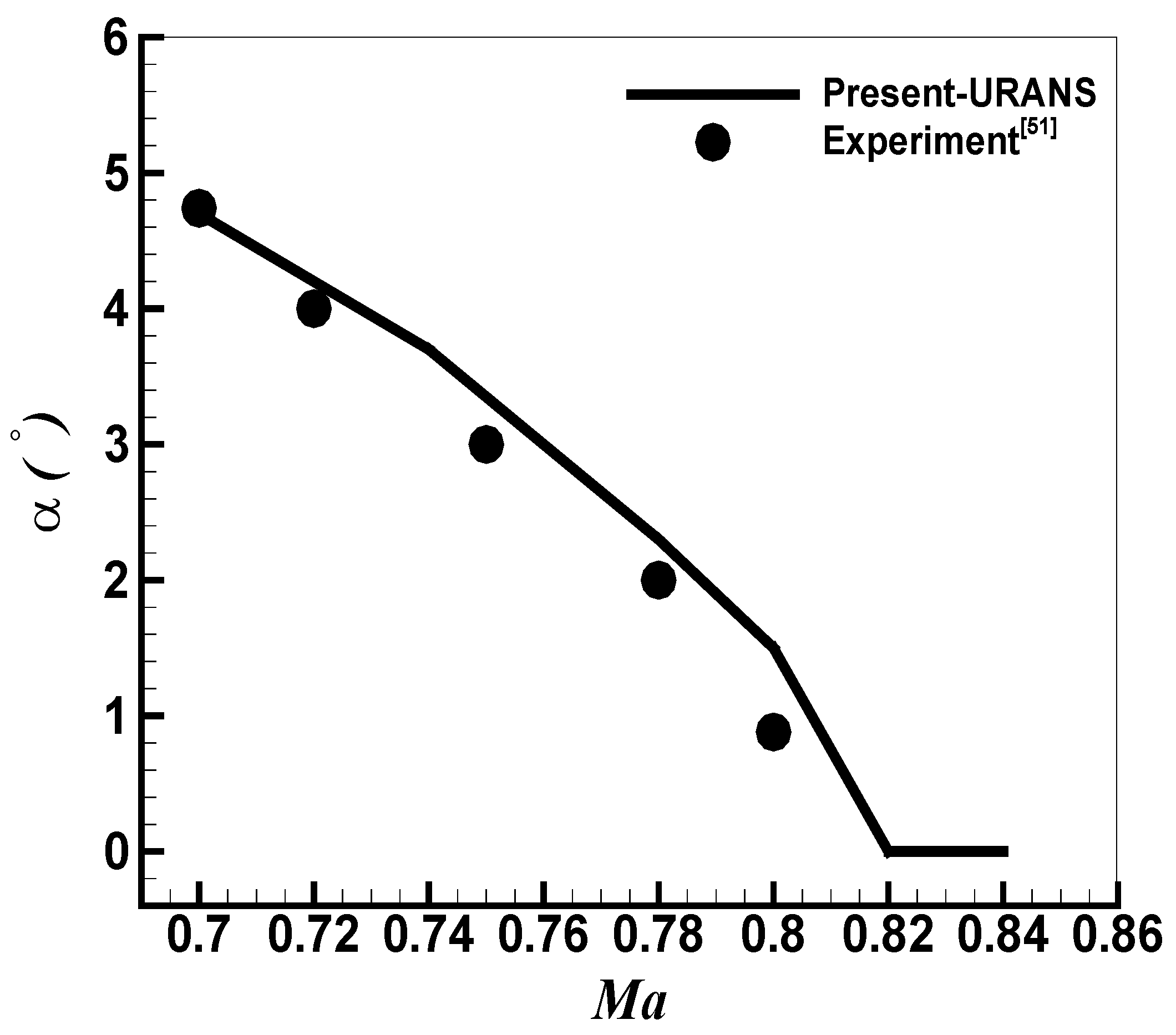
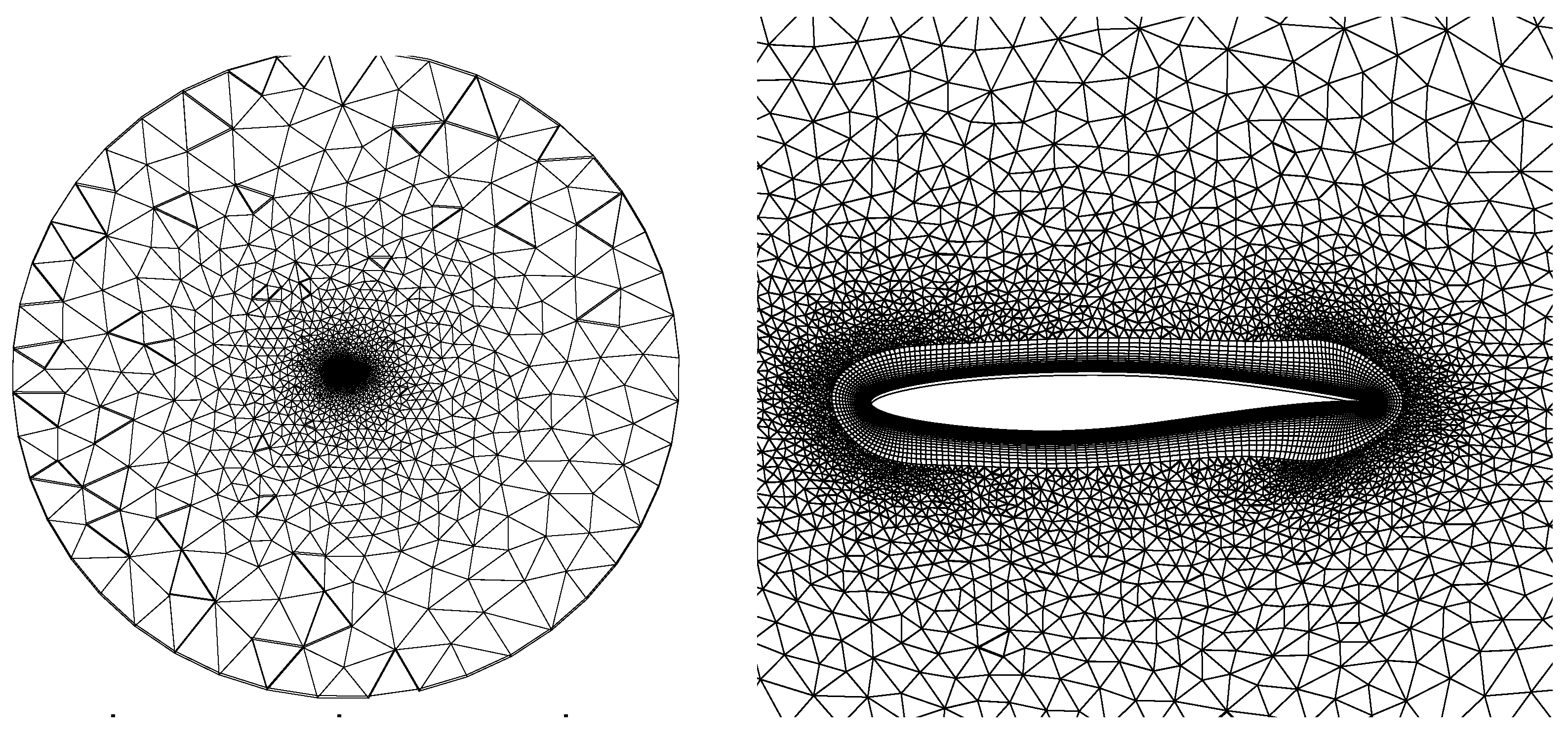
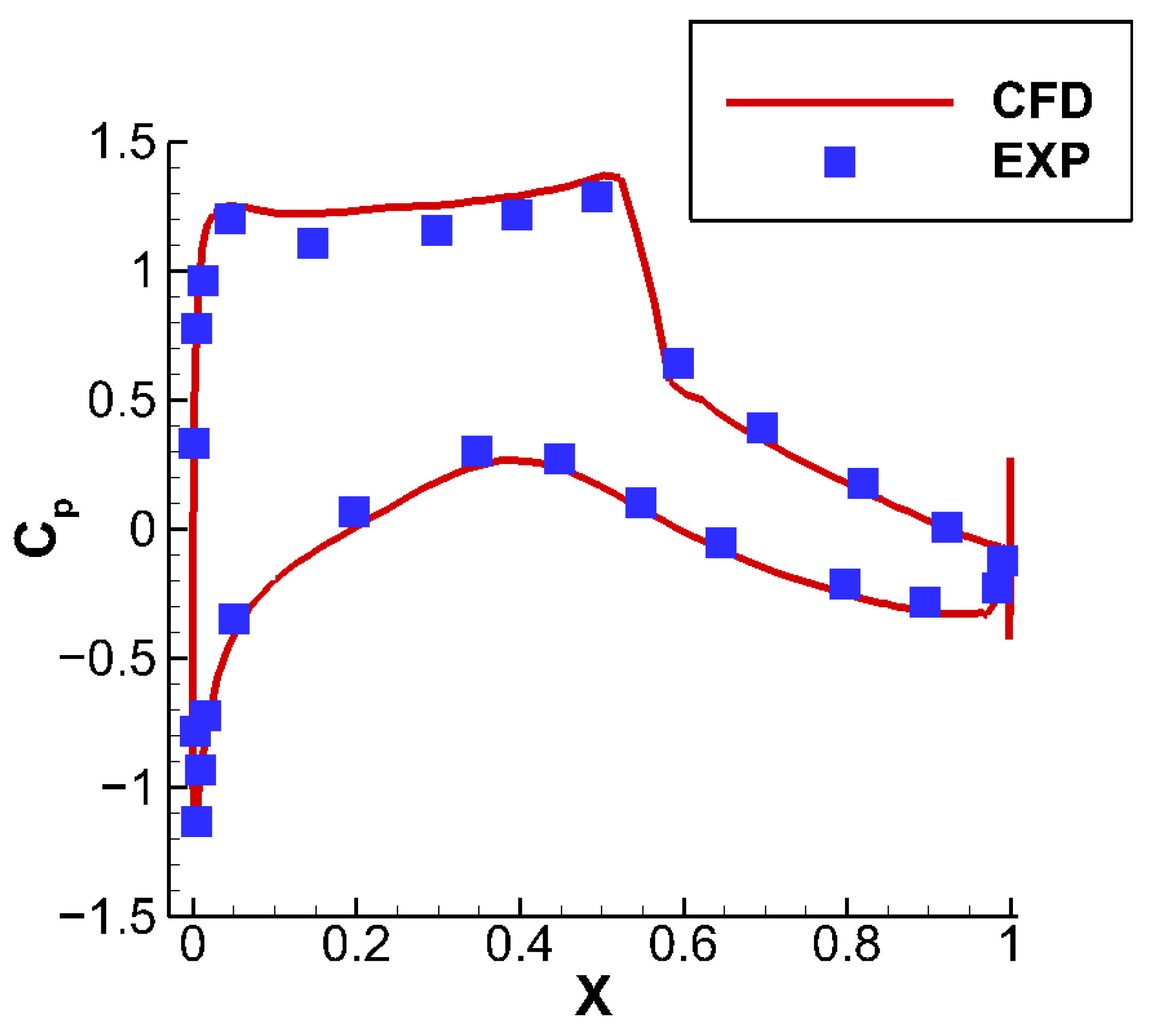
3. Numerical Method and Verification
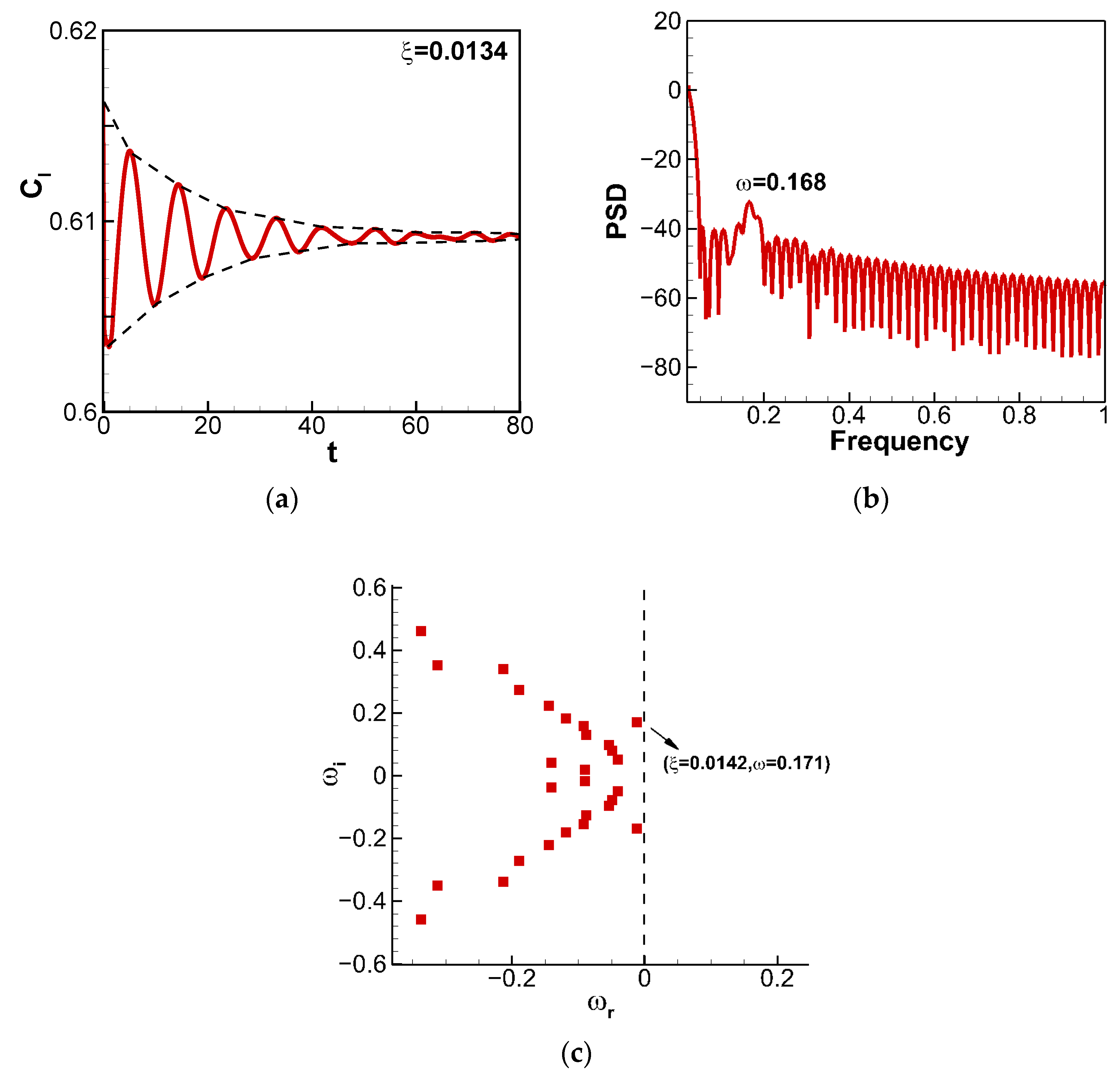
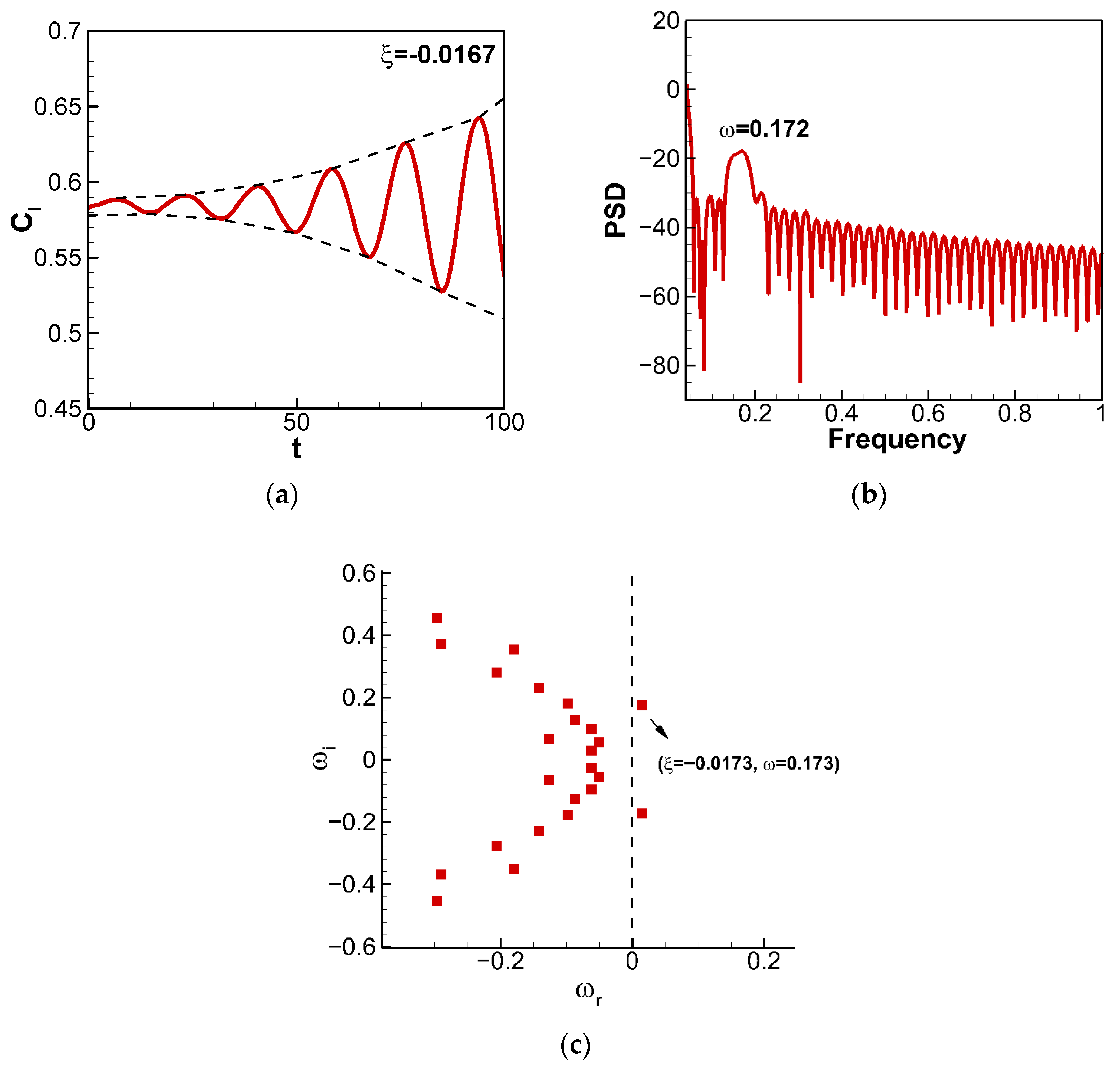
3.1. BiGlobal Stability Analysis
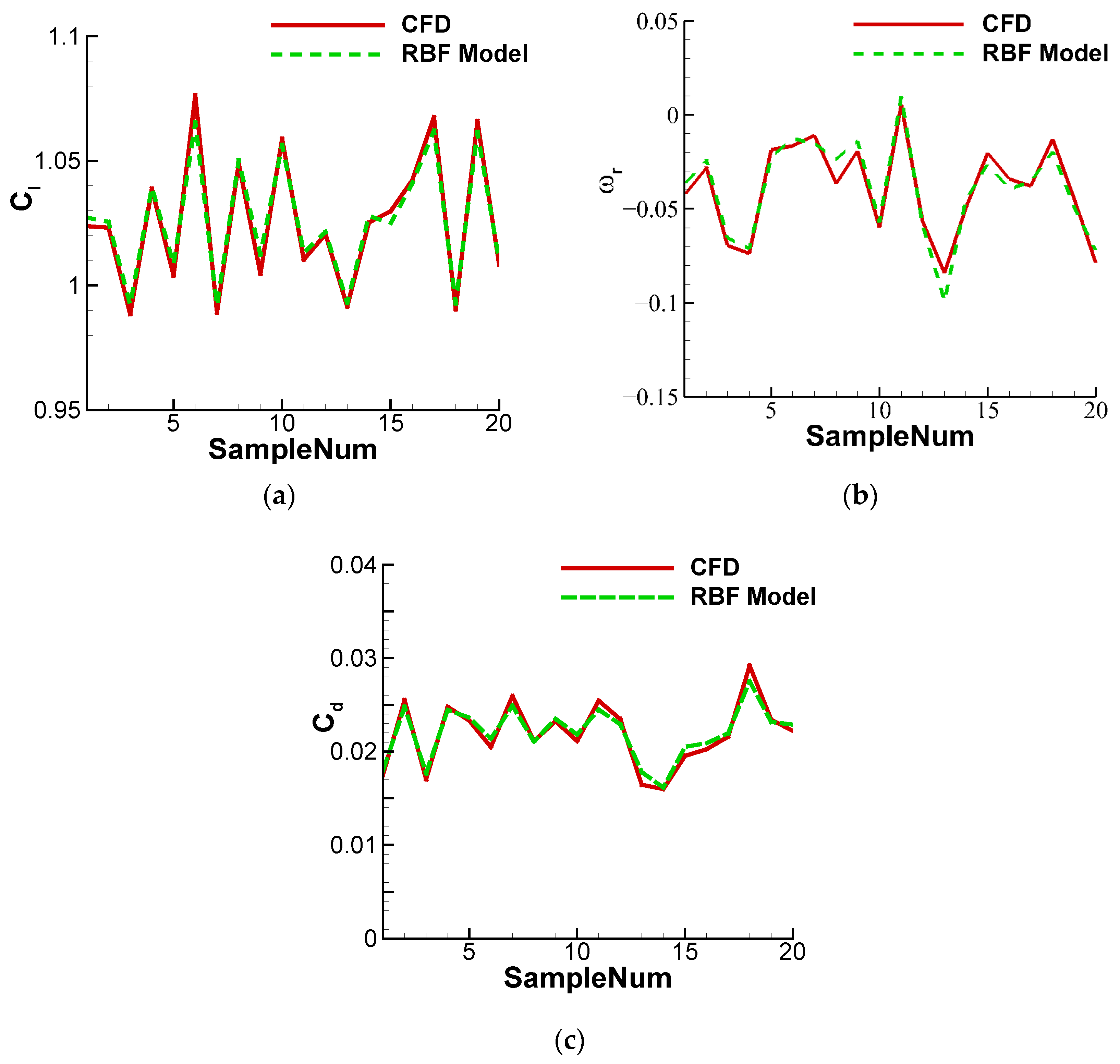
3.2. The Surrogate Model Based on the RBF Interpolation
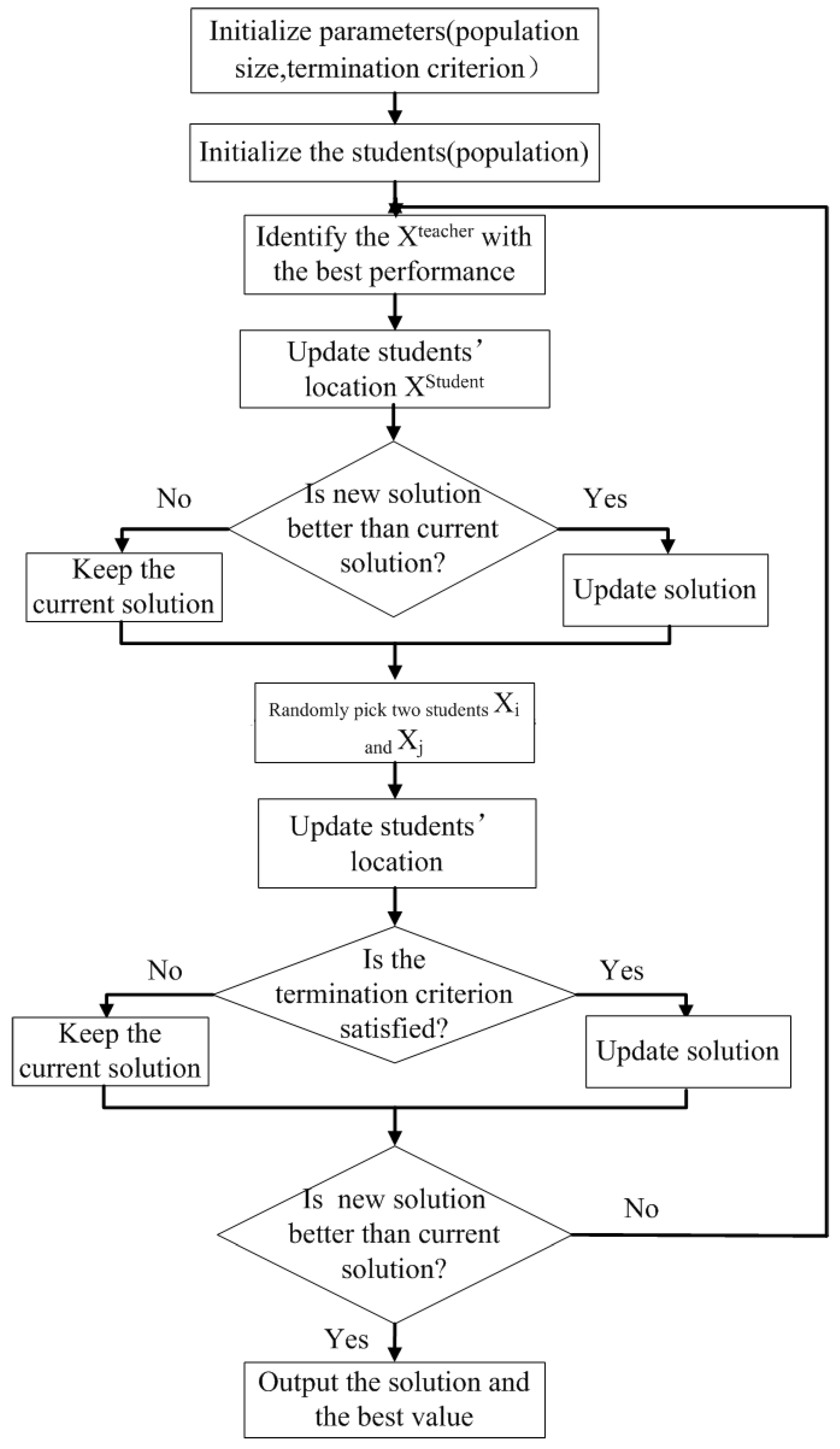
3.3. The Teaching- and Learning-Based Optimization
4. Airfoil Optimization
4.1. Optimization Description
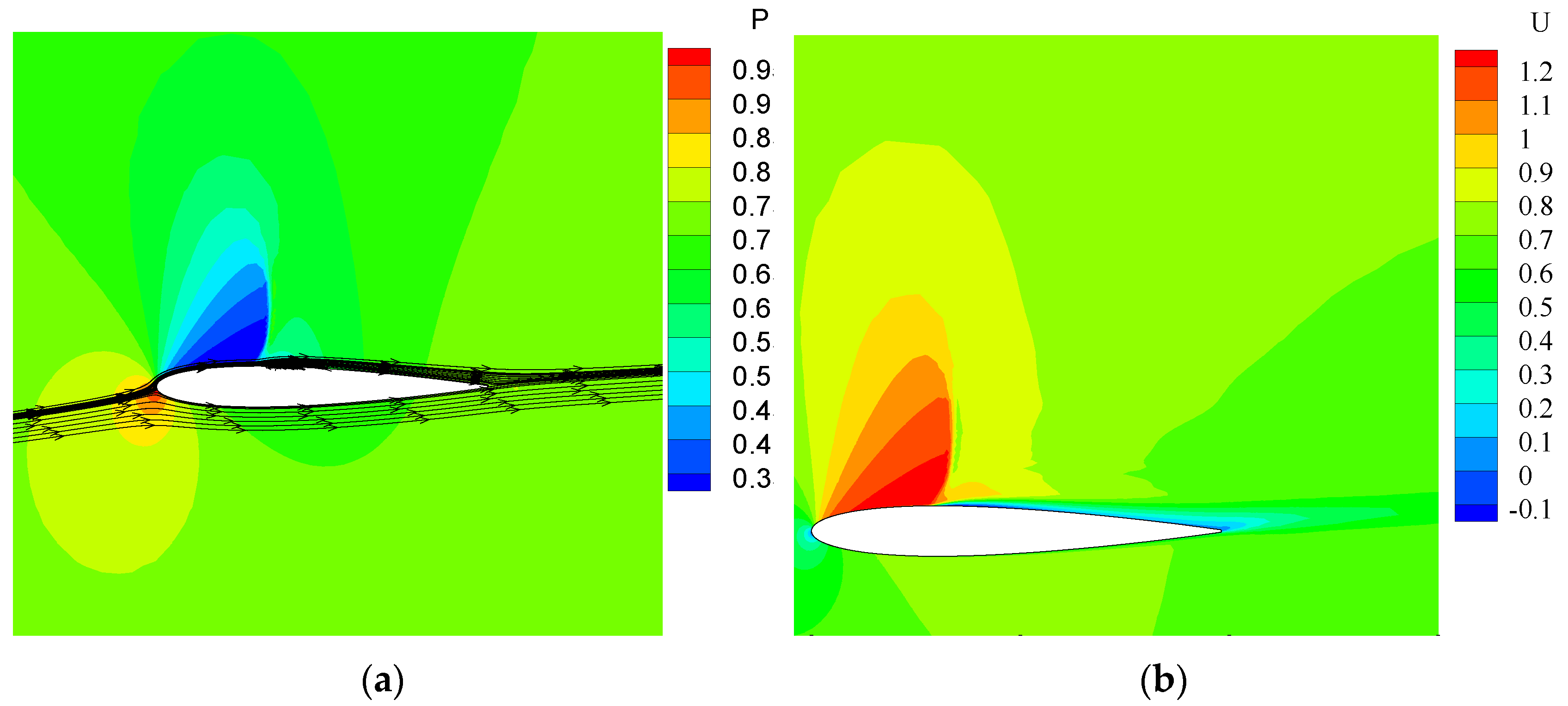
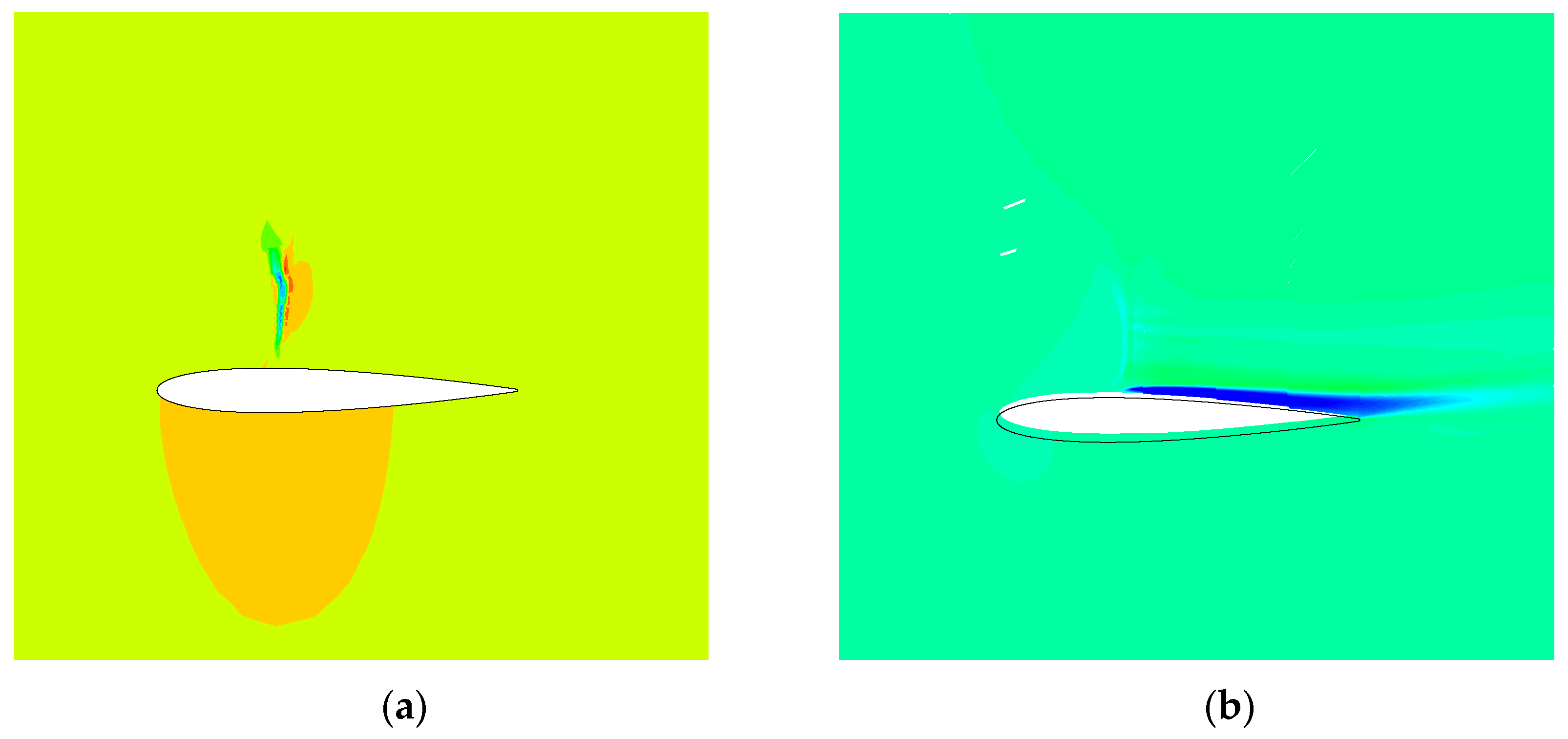
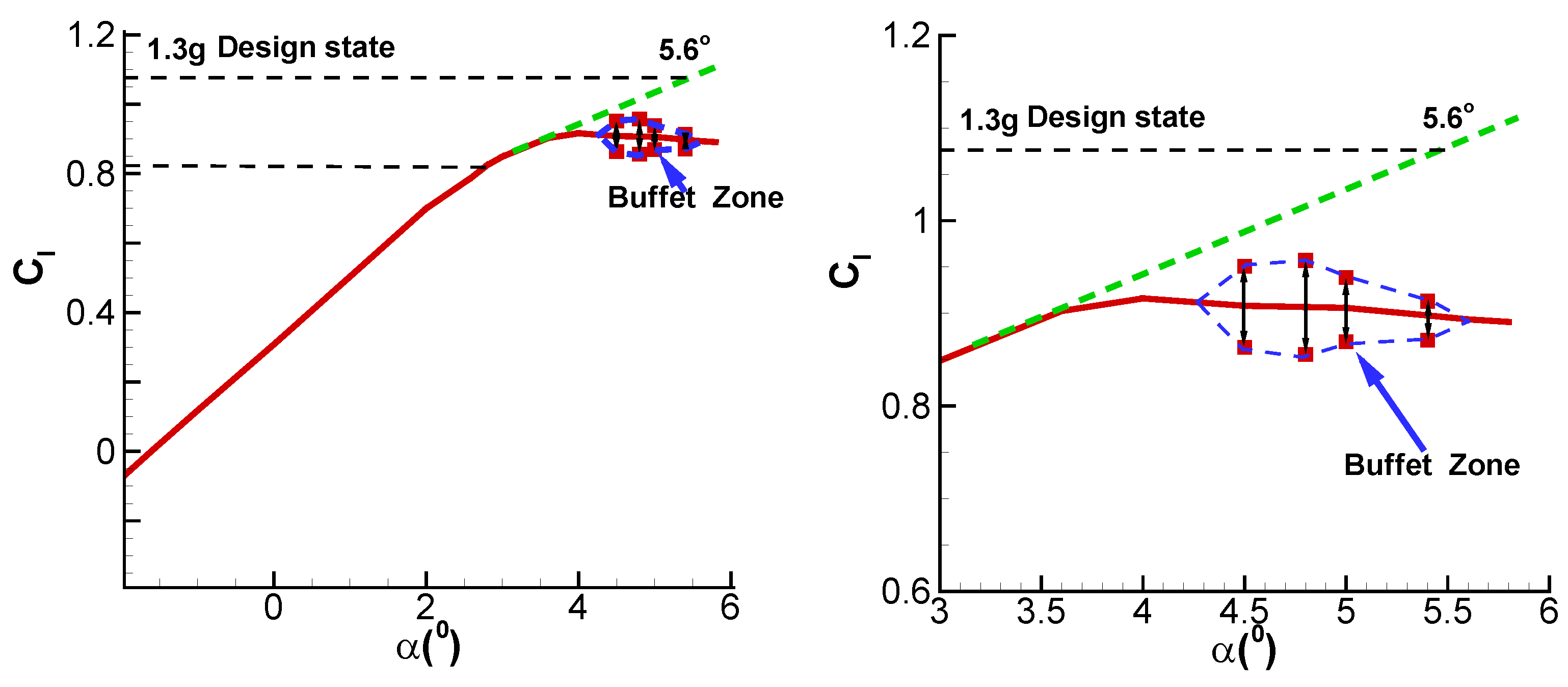
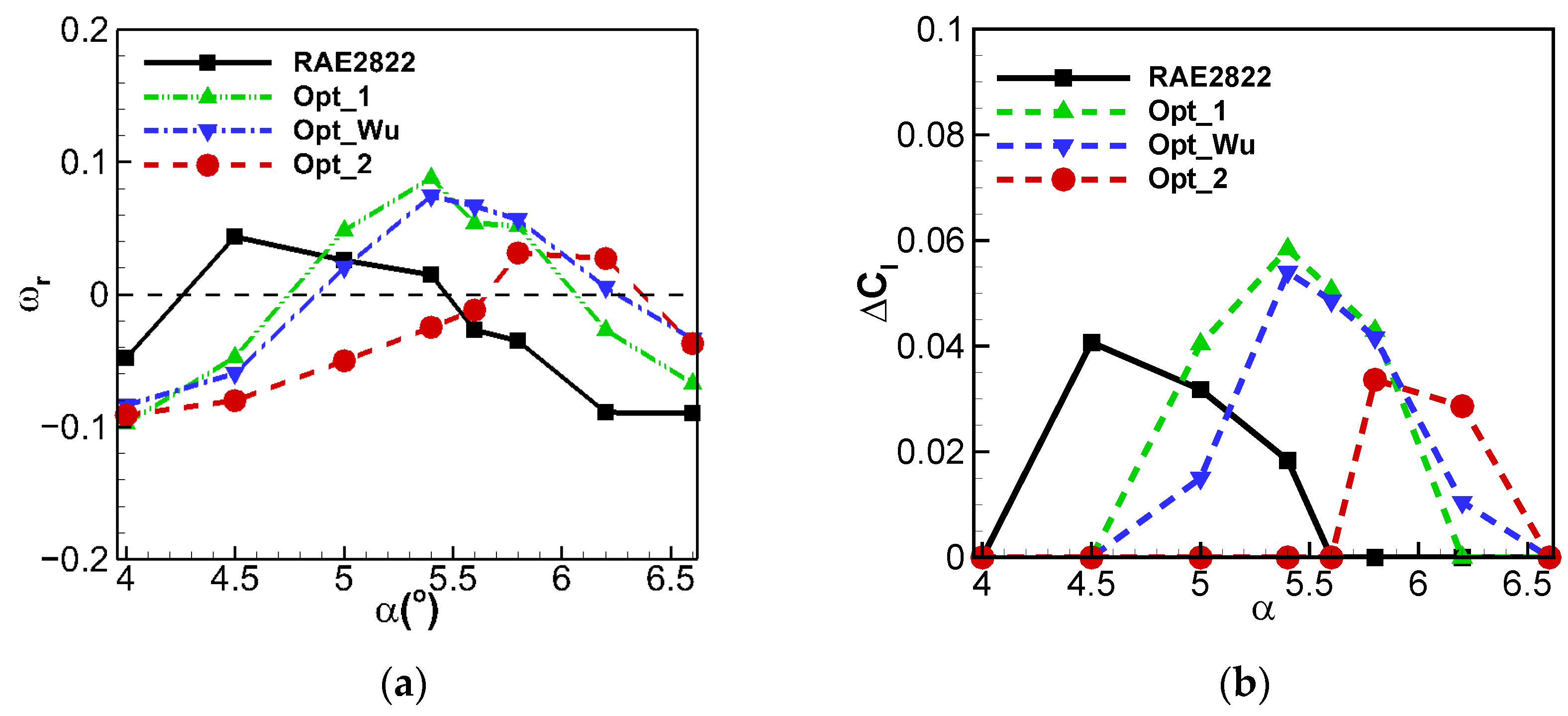
4.2. Optimization Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Jacobian matrix | |
| area of airfoil | |
| lift coefficient | |
| time-averaged lift coefficient | |
| drag coefficient | |
| pitch moment coefficient | |
| physical time step | |
| specific energy | |
| RBF interpolation function vector | |
| inviscid flux vector | |
| viscous flux vector | |
| Hessenberg matrix | |
| reduced frequency | |
| the weight coefficients of radial basis function | |
| Mach number | |
| cell face normal vector | |
| spatial residual vector | |
| pressure | |
| Reynolds number | |
| cell face area | |
| temperature | |
| time | |
| time interval | |
| conservative values | |
| time-averaged conservative values | |
| the perturbations of conservative values | |
| the amplitude of modes in frequency domain | |
| grid velocity | |
| control volume | |
| spatial position vector | |
| design parameter vector | |
| the lower bound of the design space | |
| the upper bound of the design space | |
| grid position | |
| angle of attack (°) | |
| radial basis function | |
| The matrix of radial basis function | |
| shape parameter of radial basis function | |
| virtual damping | |
| mass ratio | |
| density | |
| the eigenvalues in frequency domain | |
| the real part of | |
| the imaginary part of |
References
- Lee, B.H.K.; Murty, H.; Jiang, H. Role of Kutta waves on oscillatory shock motion on an airfoil. AIAA J. 1994, 32, 789–796. [Google Scholar] [CrossRef]
- Raghunathan, S.; Early, J.; Tulita, C. Periodic transonic flow and control. Aeronaut. J. 2008, 112, 1–16. [Google Scholar] [CrossRef]
- Ogawa, H.; Babinsky, H.; Pätzold, M.; Lutz, T. Shock-wave/boundary-layer interaction control using three-dimensional bumps for transonic wings. AIAA J. 2008, 46, 1442–1452. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, P.; Li, Z. Multi-objective optimization of shock control bump on a supercritical wing. Sci. China-Tech. Sci 2014, 57, 192–202. [Google Scholar] [CrossRef]
- Mayer, R.; Lutz, T.; Kramer, E. Control of transonic buffet by shock control bumps on wing-body configuration. J. Aircr. 2019, 56, 556–568. [Google Scholar] [CrossRef]
- Caruana, D.; Mignosi, A.; Corrège, M.; Le Pourhiet, A.; Rodde, A. Buffet and buffeting control in transonic flow. Aerosp. Sci. Technol. 2005, 9, 605–616. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Z.; Liu, P. Upper Trailing-Edge Flap for Transonic Buffet Control. J. Aircr. 2018, 55, 382–389. [Google Scholar] [CrossRef]
- Mabey, D.G. Oscillatory Flows from Shock Induced Separations on Biconvex Aerofoils of Varying Thickness in Ventilated Wind Tunnels, Boundary Layer Effects on Unsteady Airloads; Advisory Group for Aerospace Research and Development TR 296: Aix-en-Provence, France, 1981. [Google Scholar]
- Jiang, R.; Tian, Y.; Liu, P. Transonic buffet control by rearward buffet breather on supercritical airfoil and wing. Aerosp. Sci. Technol. 2019, 89, 204–219. [Google Scholar] [CrossRef]
- Zhou, H. Numerical analysis of effect of mini-TED on aerodynamic characteristic of airfoils in transonic flow. Acta Aeronaut. Astronaut. Sin. 2009, 30, 1367–1373. [Google Scholar]
- Sartor, F.; Minervino, M.; Wild, J.; Wallin, S.; Maseland, H.; Dandois, J. A CFD benchmark of active flow control for buffet prevention. CEAS Aeronaut. J. 2019, 11, 837–847. [Google Scholar] [CrossRef]
- Siauw, W.; Bonnet, J.-P.; Tensi, J.; Cordier, L.; Noack, B.; Cattafesta, L. Transient dynamics of the flow around a NACA 0015 airfoil using fluidic vortex generators. Int. J. Heat Fluid Flow 2010, 31, 450–459. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, W.; Ye, Z. Numerical study on closed-loop control of transonic buffet suppression by trailing edge flap. Comput. Fluids 2016, 132, 32–45. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Han, Z.-H.; Li, W.-J.; Song, W.-P. Bilevel adaptive weighted sum method for multidisciplinary multi-objective optimization. AIAA J. 2008, 46, 2611–2622. [Google Scholar] [CrossRef]
- Leifsson, L.; Koziel, S. Aerodynamic shape optimization by variable-fidelity computational fluid dynamics models: A review of recent progress. J. Comput. Sci. 2015, 10, 45–54. [Google Scholar] [CrossRef]
- Kenway, G.K.; Martins, J.R. Buffet-onset constraint formulation for aerodynamic shape optimization. AIAA J. 2017, 55, 1930–1947. [Google Scholar] [CrossRef]
- Thomas, J.P.; Dowell, E.H. Discrete adjoint design optimization approach for increasing transonic buffet onset angle-of-attack. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Thomas, J.P.; Dowell, E.H. Discrete adjoint constrained design optimization approach for unsteady transonic aeroelasticity and buffet. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual Event, 15–19 June 2020. [Google Scholar]
- Xu, Z.; Joseph, H.S.; Yang, V. Optimization of supercritical airfoil design with buffet effect. AIAA J. 2019, 57, 4343–4353. [Google Scholar] [CrossRef]
- Chen, H.; Gao, C.; Wu, J.; Ren, K.; Zhang, W. Study on optimization design of airfoil transonic buffet with reinforcement learning method. Aerospace 2023, 10, 486. [Google Scholar] [CrossRef]
- Chen, W.; Gao, C.; Zhang, W.; Gong, Y. Adjoint-based unsteady shape optimization to suppress transonic buffet. Aerosp. Sci. Technol. 2022, 127, 107668. [Google Scholar] [CrossRef]
- Iovnovich, M.; Raveh, D.E. Transonic unsteady aerodynamics in the vicinity of shock-buffet instability. J. Fluid Struct. 2012, 29, 131–142. [Google Scholar] [CrossRef]
- Deck, S. Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J. 2005, 43, 1556–1566. [Google Scholar] [CrossRef]
- Garnier, E.; Deck, S. Large-eddy simulation of transonic buffet over a supercritical airfoil. In Turbulence and Interactions; Springer: Berlin/Heidelberg, Germany, 2010; pp. 135–141. [Google Scholar]
- Sengupta, T.K.; Bhole, A.; Sreejith, N.A. Direct numerical simulation of 2D transonic flows around airfoils. Comput. Fluids 2013, 88, 19–37. [Google Scholar] [CrossRef]
- Li, Q.; Cao, X.L.; Liu, Y.; Wang, G. Numerical research on the transonic buffet loads of a supercritical airfoil. Tactical Missile Technol. 2018, 38, 44–51. [Google Scholar]
- Lipanov, A.M.; Karskanov, S.A. Direct numerical simulation of aerodynamic flows based on integration of the Navier—Stokes equations. Russ. J. Nonlinear Dyn. 2022, 18, 349–365. [Google Scholar] [CrossRef]
- Chen, R.; Tsay, R.S. Nonlinear additive ARX model. J. Am. Stat. Assoc. 1993, 88, 955–967. [Google Scholar] [CrossRef]
- Hall, K.C.; Dowell, E.H.; Thomas, J.P. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows. AIAA J. 2000, 38, 1852–1862. [Google Scholar] [CrossRef]
- Amsallem, D.; Farhat, C. Interepolation mthod for adapting reduced-order models and application to aeroelasticity. AIAA J. 2008, 46, 1803–1813. [Google Scholar] [CrossRef]
- He, G.; Wang, J.; Pan, C. Initial growth of a disturbance in a boundary layer influenced by a circular cylinder wake. J. Fluid Mech. 2013, 718, 116–130. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T.; Widnall, S.E. The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 1982, 114, 59–82. [Google Scholar] [CrossRef]
- Jackson, C. A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 1987, 182, 23–45. [Google Scholar] [CrossRef]
- Iorio, M.C.; Gonzalez, L.M.; Ferrer, E. Direct and adjoint global stability analysis of turbulent transonic flows over a NACA0012 profile. Int. J. Numer. Methods Fluids 2015, 76, 147–168. [Google Scholar] [CrossRef]
- Iorio, M.C.; Gonzalez, L.M.; Martínez-Cava, A. Global stability analysis of a compressible turbulent flow around a high-lift configuration. AIAA J. 2016, 54, 373–385. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D. Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 2007, 224, 924–940. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D.; Travin, A. Origin of transonic buffet on aerofoils. J. Fluid Mech. 2009, 628, 357–369. [Google Scholar] [CrossRef]
- Sartor, F.; Mettot, C.; Sipp, D. Stability, receptivity, and sensitivity analysis of buffet transonic flow over a profile. AIAA J. 2015, 53, 1980–1993. [Google Scholar] [CrossRef]
- Theofilis, V. Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 2003, 39, 249–315. [Google Scholar] [CrossRef]
- Theofilis, V. Global linear instability. Annu. Rev. Fluid Mech. 2011, 43, 319–352. [Google Scholar] [CrossRef]
- Gomez, F.; Gomez, R.; Theofilis, V. On three-dimensional global linear instability analysis of flows with standard aerodynamics codes. Aerosp. Sci. Technol. 2014, 32, 223–234. [Google Scholar] [CrossRef]
- Bagheri, S.; Schlatter, P.; Schmid, P.J.; Henningson, D.S. Global stability of a jet in crossflow. J. Fluid Mech. 2009, 624, 33–44. [Google Scholar] [CrossRef]
- Åkervik, E.; Brandt, L.; Henningson, D.S.; Hœpffner, J.; Marxen, O.; Schlatter, P. Steady solution of the Navier-Stokes equations by selective frequency damping. Phys. Fluids 2006, 18, 068102. [Google Scholar] [CrossRef]
- Illingworth, S.J.; Morgans, A.S.; Rowley, C.W. Feedback control of cavity flow oscillations using simple linear models. J. Fluid Mech. 2012, 709, 223–248. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Li, J. A simple strategy for capturing the unstable steady solution of an unsteady flow. Open J. Fluid Dyn. 2015, 5, 188–198. [Google Scholar] [CrossRef]
- Arnoldi, W. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Math. 1951, 9, 17–29. [Google Scholar] [CrossRef]
- Saad, Y. Variation of Arnoldi’s method for computing eigenelements of large unsymmetric matrices. Linear Algebra Appl. 1980, 34, 269–295. [Google Scholar] [CrossRef]
- Rivera, J.A., Jr.; Dansberry, B.; Bennett, R.; Durham, M.; Silva, W. NACA0012 benchmark model experimental flutter results with unsteady pressure distributions. In Proceedings of the 33rd Structures, Structural Dynamics and Materials Conference, Dallas, TX, USA, 13–15 April 1992; p. 107581. [Google Scholar]
- McDevitt, J.B.; Okuno, A.F. Static and Dynamic Pressure Measurements on a NACA0012 Airfoil in the Ames High Reynolds Number Facility; NASA TP-2485; National Aeronautics and Space Administration: Reston, VA, USA, 1985. [Google Scholar]
- Doerffer, P.; Hirsch, C.; Dussauge, J.P.; Babinsky, H.; Barakos, G.N.; Doerffer, P.; Hirsch, C.; Dussauge, J.P.; Babinsky, H.; Barakos, G.N. NACA0012 with aileron(Marianna Braza). In Unsteady Effects of Shock Wave Induced Separation; Springer: Berlin/Heidelberg, Germany, 2011; pp. 101–131. [Google Scholar]
- Soda, A.; Voss, R. Analysis of Transonic Aerodynamic Interference in the Wing-Nacelle Region for a Generic Transport Aircraft; IFASD: Munich, Germany, 2005. [Google Scholar]
- Tian, Y.; Gao, S.; Liu, P.; Wang, J. Transonic buffet control research with two types of shock control bump based on RAE2822 airfoil. Chin. J. Aeronaut. 2017, 30, 1681–1696. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems. Eng. Optim. 2012, 44, 1447–1462. [Google Scholar] [CrossRef]
- Lane, K.A.; Marshall, D.D. Inverse airfoil design utilizing CST parameterization. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 1228–1242. [Google Scholar]
- Leifsson, L.T.; Koziel, S.; Hosder, S. Aerodynamic design optimization: Physics-based surrogate approaches for airfoil and wing design. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Lee, C.; Koo, D.; Telidetzki, K.; Buckley, H.; Gagnon, H.; Zingg, D.W. Aerodynamic shape optimization of benchmark problems using Jetstream. In Proceedings of the 53rd Aerospace Science Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Wu, X.; Zhang, W.; Peng, X.; Wang, Z. Benchmark aerodynamic shape optimization with the POD-based CST airfoil parametric method. Aerosp. Sci. Technol. 2019, 84, 632–640. [Google Scholar] [CrossRef]


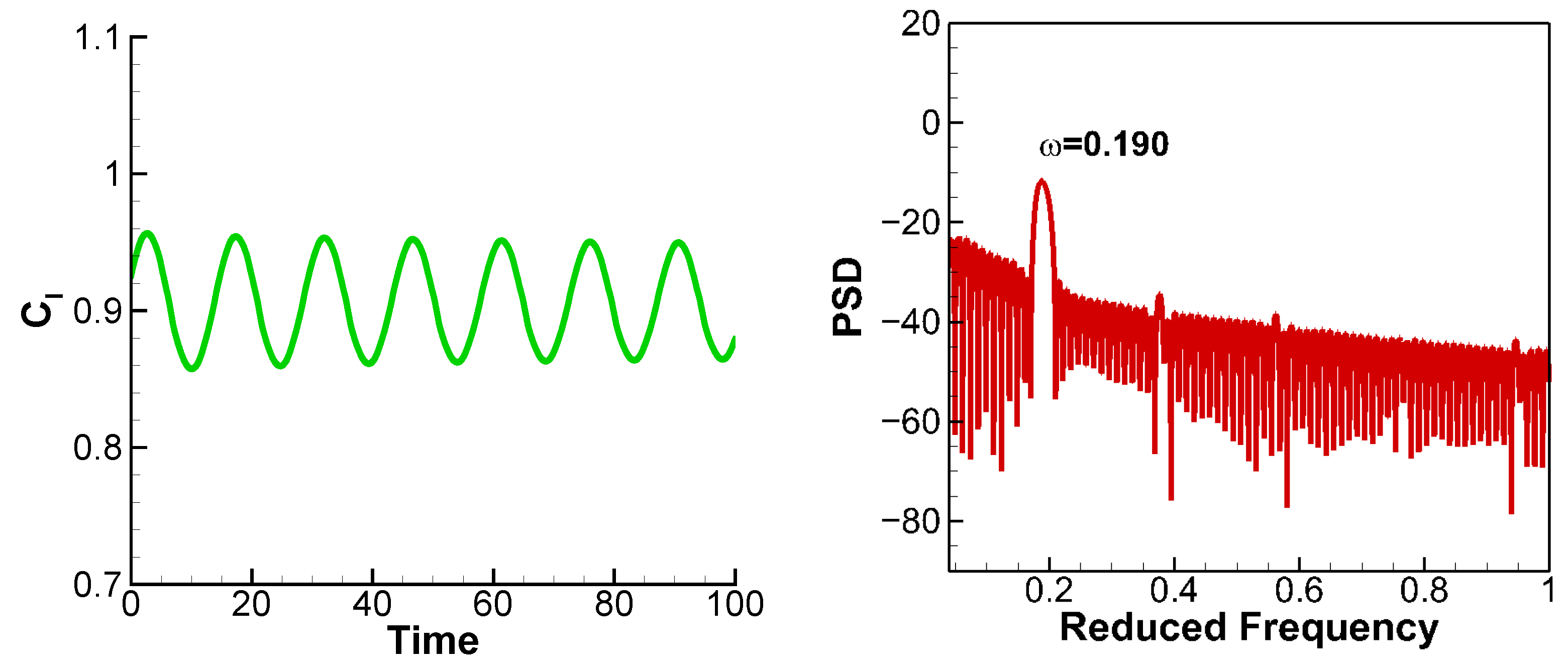
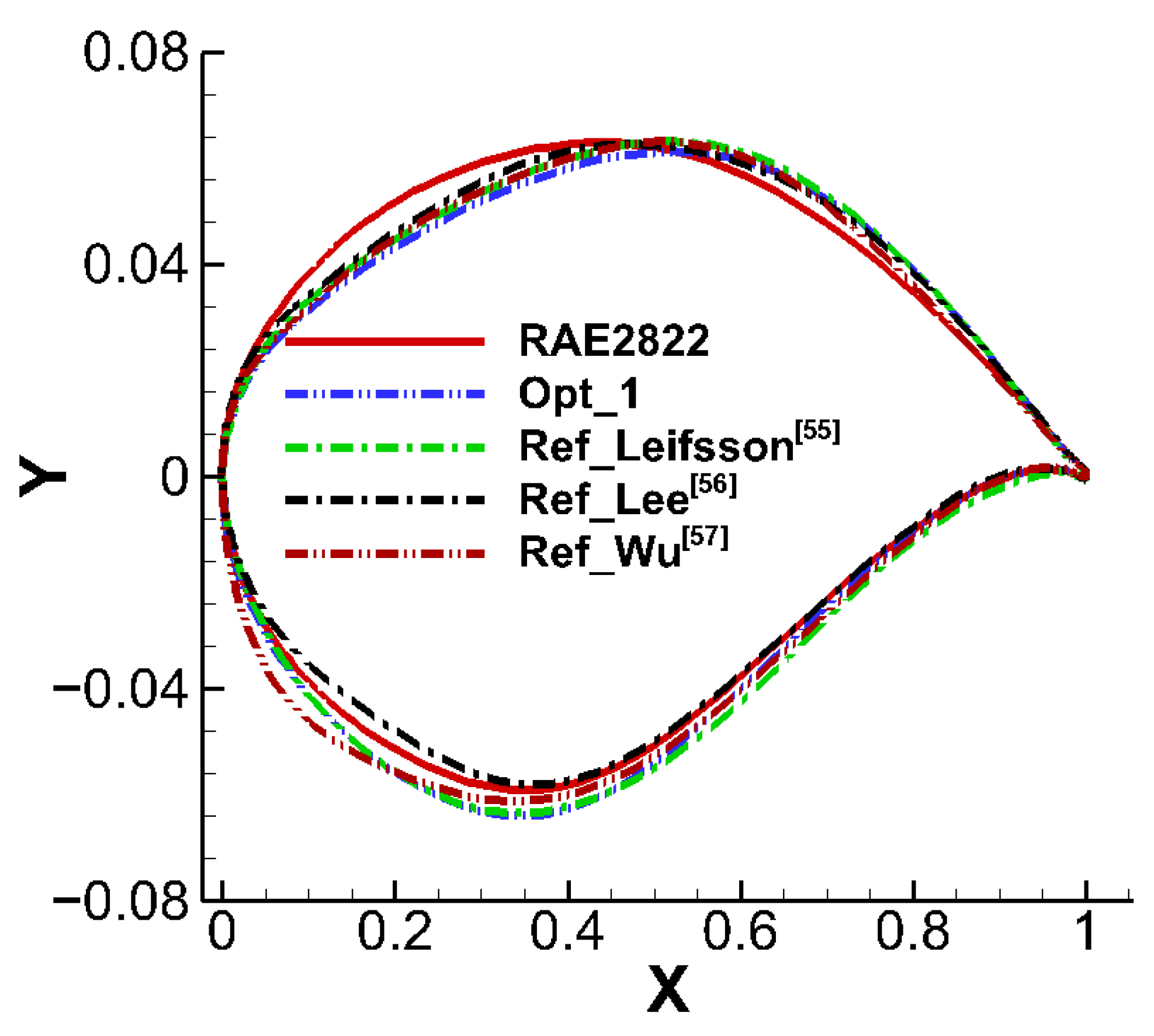

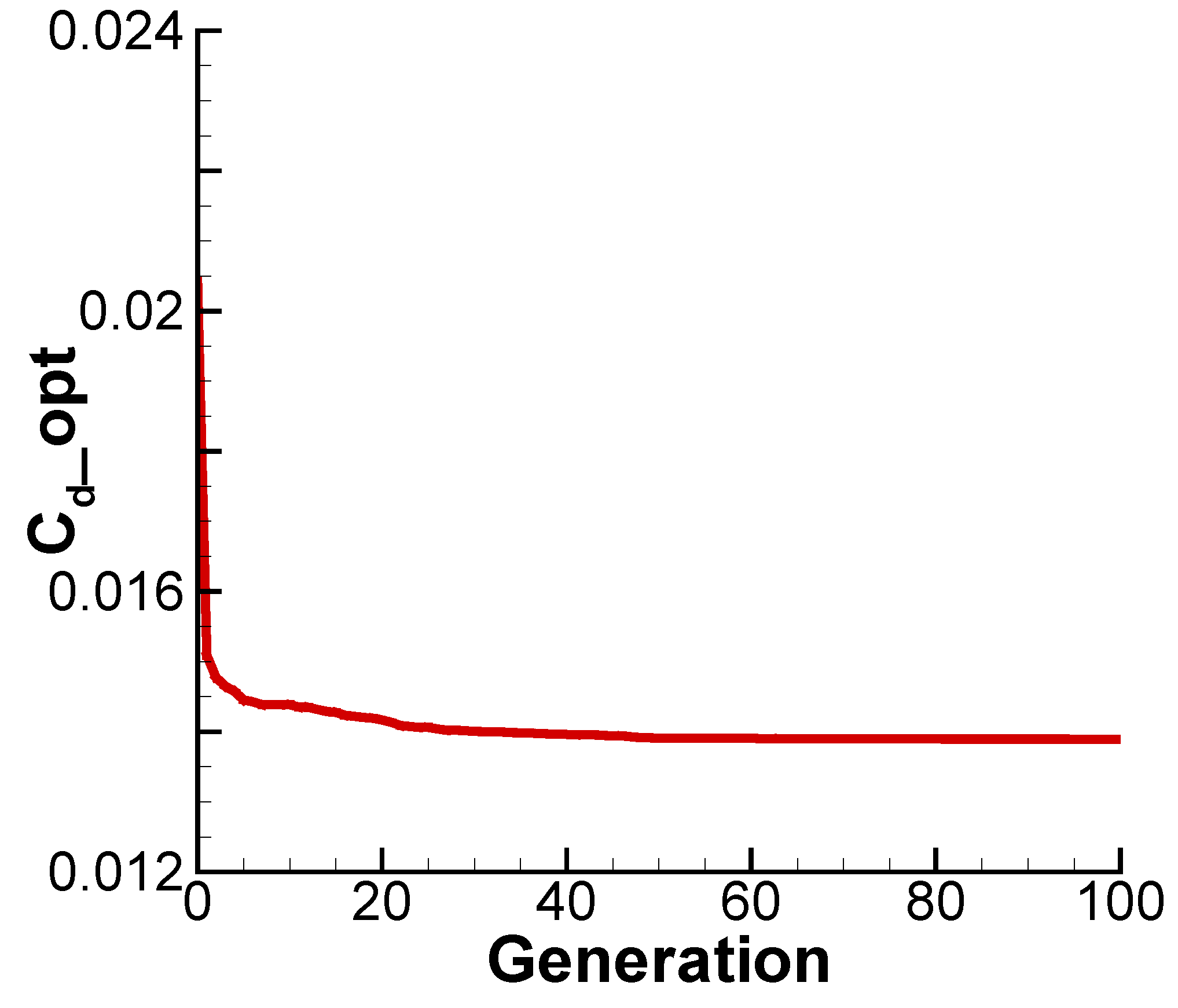
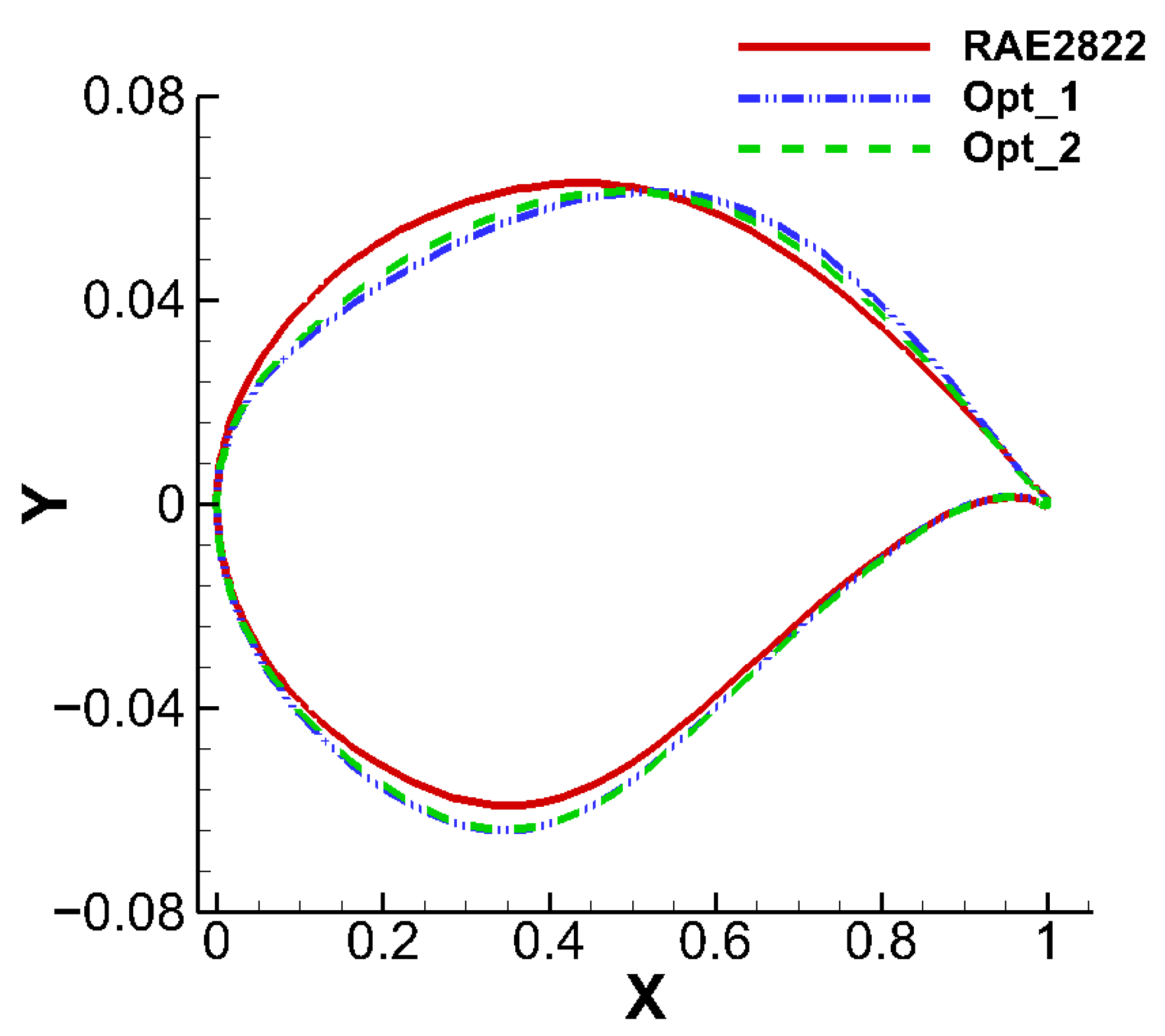
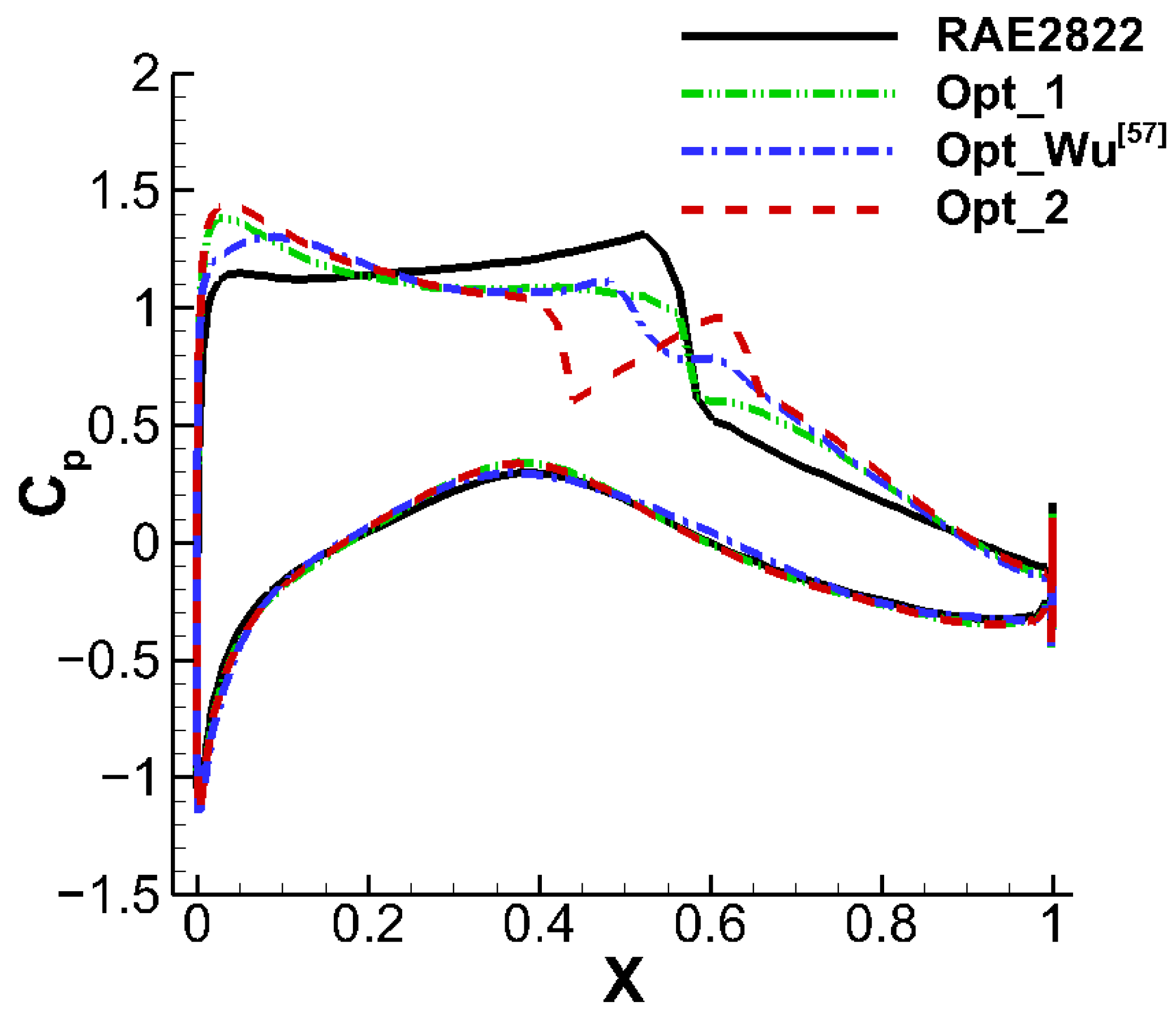

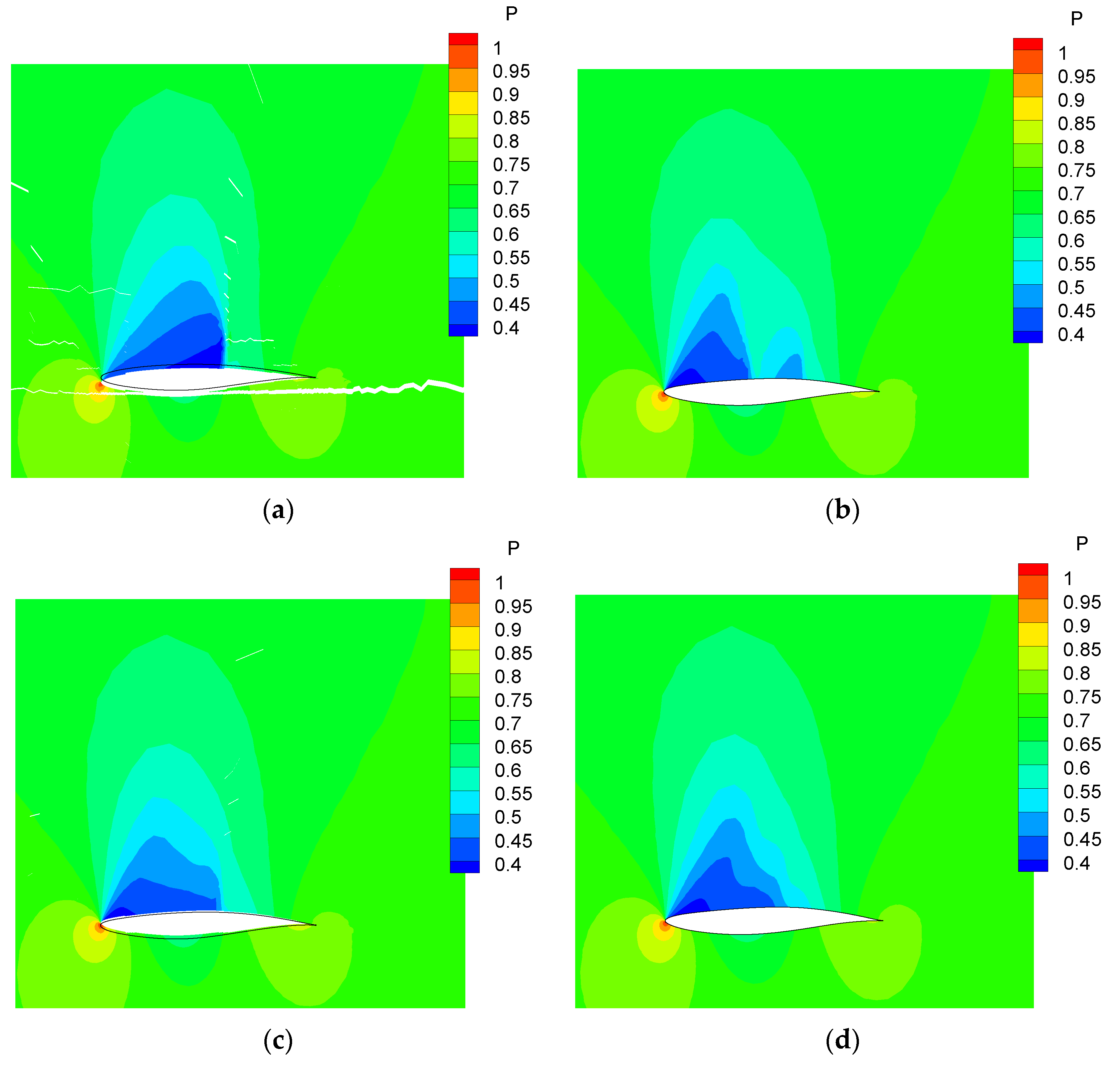
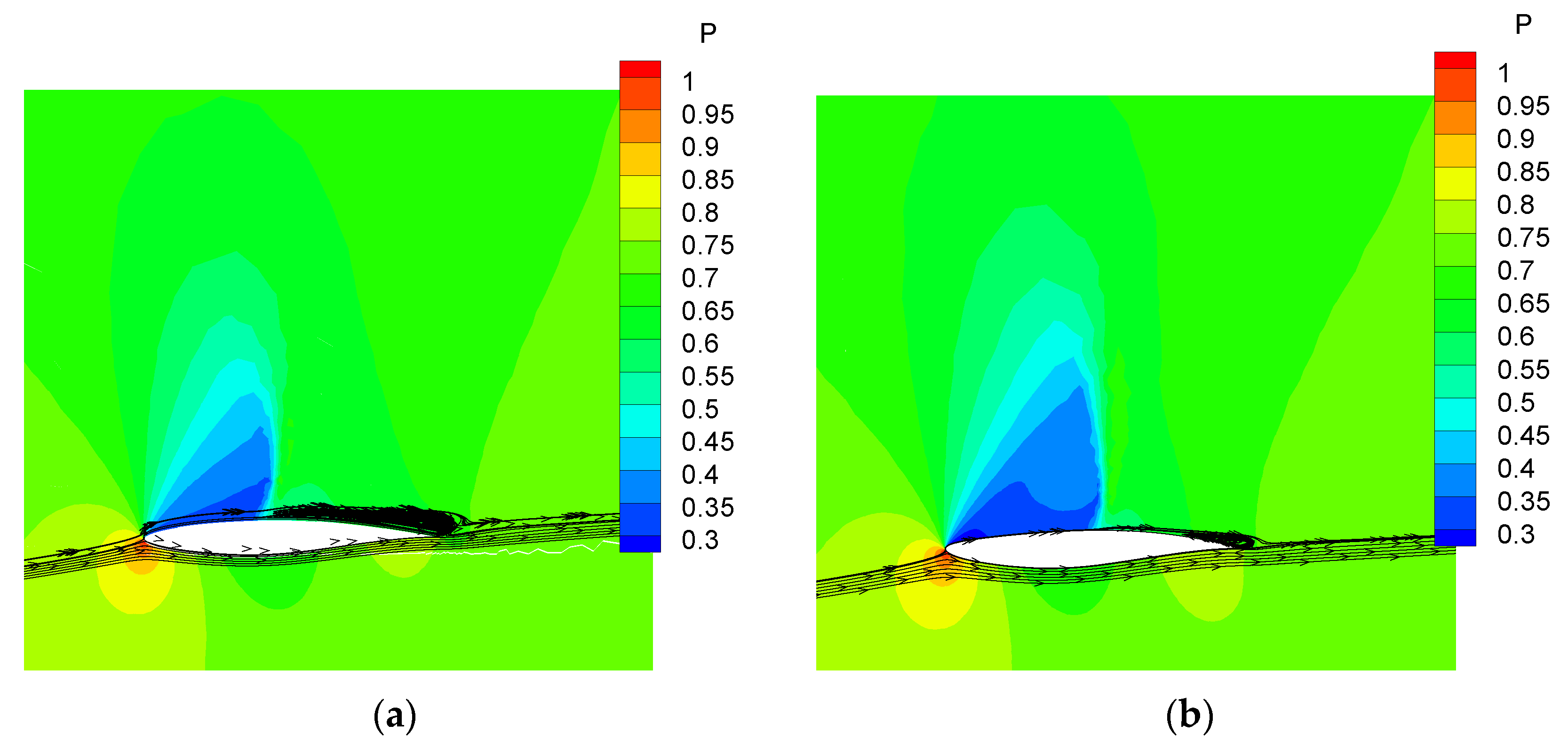

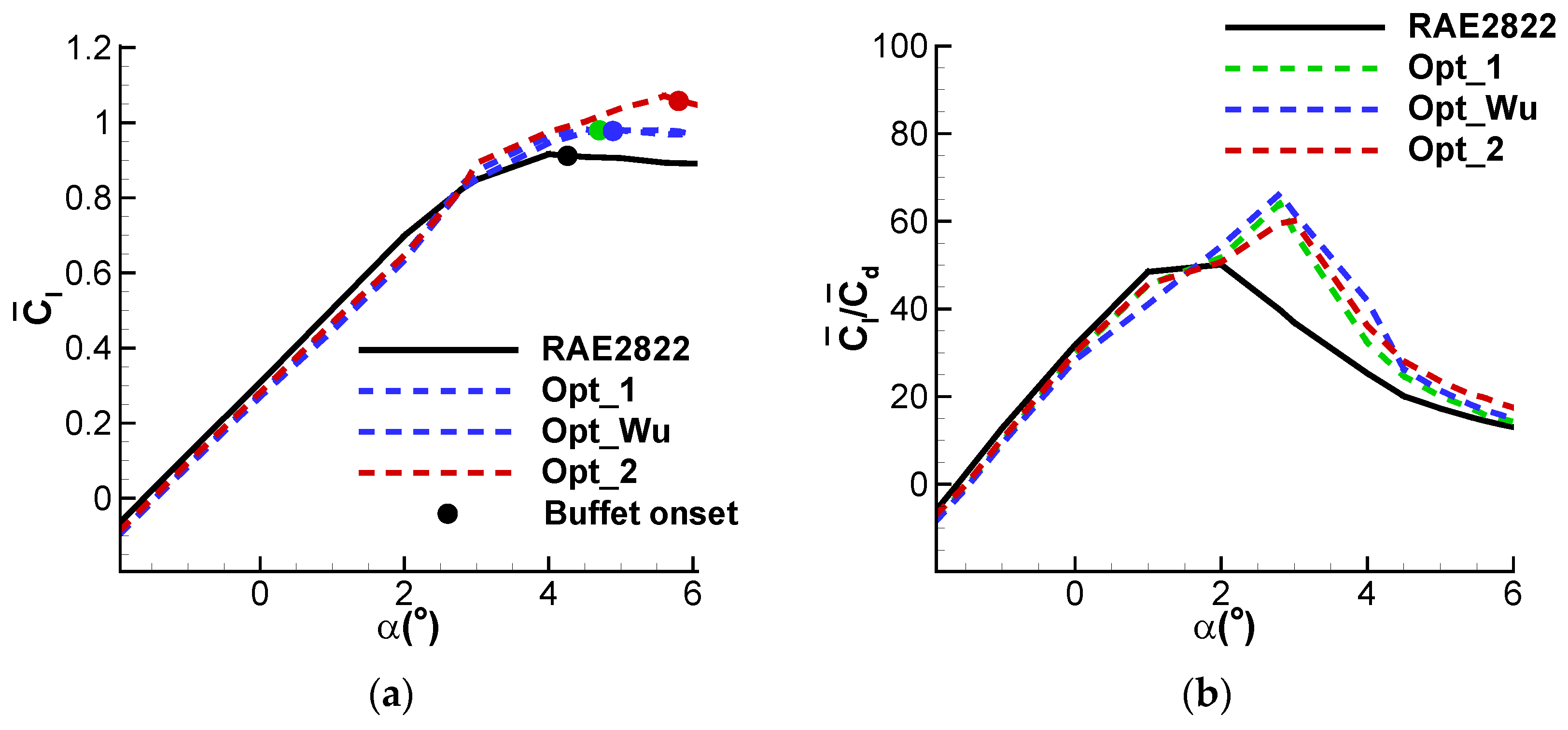

| Airfoil | |||||
|---|---|---|---|---|---|
| RAE2822 | 0.8247 | 0.02079 | 0.02079 | 0% | 39.75 |
| Optimize_1 | 0.8252 | 0.01306 | 0.02079 | −37% | 63.17 |
| Optimize_2 | 0.8248 | 0.01387 | 0.02079 | −33% | 59.46 |
| Ref_Leifsson [55] | 0.8246 | 0.01270 | 0.01652 | −23% | 64.93 |
| Ref_Lee [56] | 0.8239 | 0.01314 | 0.02340 | −44% | 62.70 |
| Ref_Wu [57] | 0.8241 | 0.01129 | 0.01953 | −42% | 72.98 |
| Airfoil | Cruise State | 1.3 g Cruise State | |||
|---|---|---|---|---|---|
| RAE2822 | 0.8247 | 0.02079 | 39.75 | 0.9152 | −0.02609 |
| Optimize_2 | 0.8248 | 0.01387 | 59.46 | 1.0714 | −0.01173 |
| Optimize_1 | 0.8252 | 0.01306 | 63.17 | 0.9784 | 0.03704 |
| Optimize_Wu | 0.8241 | 0.01245 | 66.19 | 0.9905 | 0.06714 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Gao, C.; Zhang, W. Transonic Buffet Suppression by Airfoil Optimization. Aerospace 2024, 11, 121. https://doi.org/10.3390/aerospace11020121
Gong Y, Gao C, Zhang W. Transonic Buffet Suppression by Airfoil Optimization. Aerospace. 2024; 11(2):121. https://doi.org/10.3390/aerospace11020121
Chicago/Turabian StyleGong, Yiming, Chuanqiang Gao, and Weiwei Zhang. 2024. "Transonic Buffet Suppression by Airfoil Optimization" Aerospace 11, no. 2: 121. https://doi.org/10.3390/aerospace11020121
APA StyleGong, Y., Gao, C., & Zhang, W. (2024). Transonic Buffet Suppression by Airfoil Optimization. Aerospace, 11(2), 121. https://doi.org/10.3390/aerospace11020121







