An Active Flow Control over the Ship Deck for Helicopter Shipboard Operations
Abstract
1. Introduction
2. Coupled Model of Helicopter Flight Dynamics and Ship Airwake
2.1. Helicopter Flight Dynamics Model
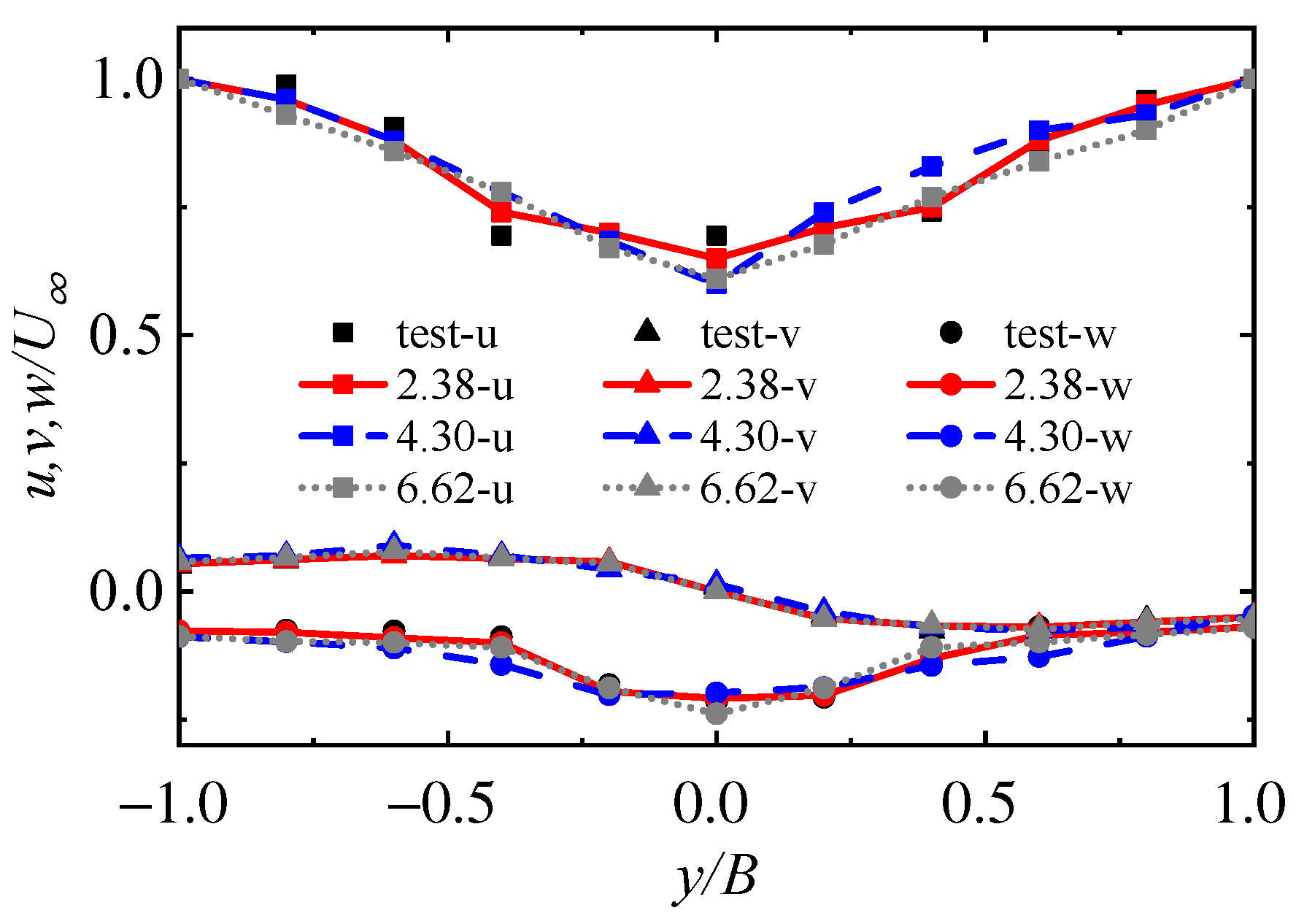
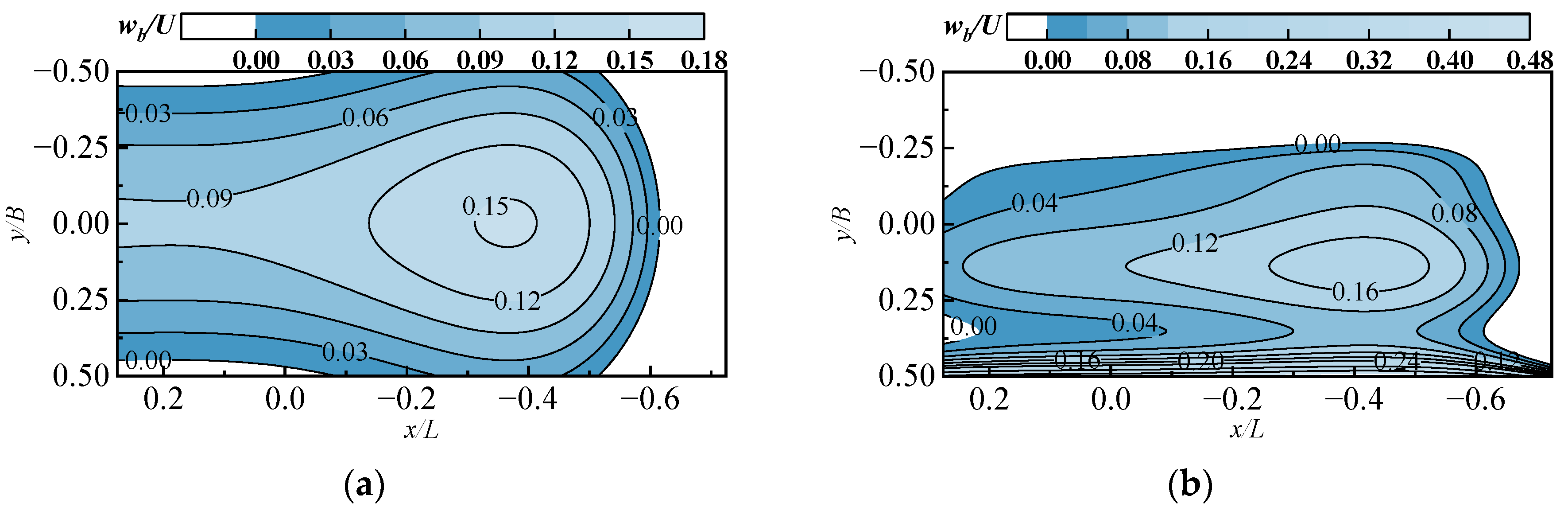
2.2. Ship Airwake Simulation
2.3. Helicopter Flight Dynamics Model Coupled with Ship Airwake
3. Influence of Ship Airwake on Helicopter Shipboard Operations
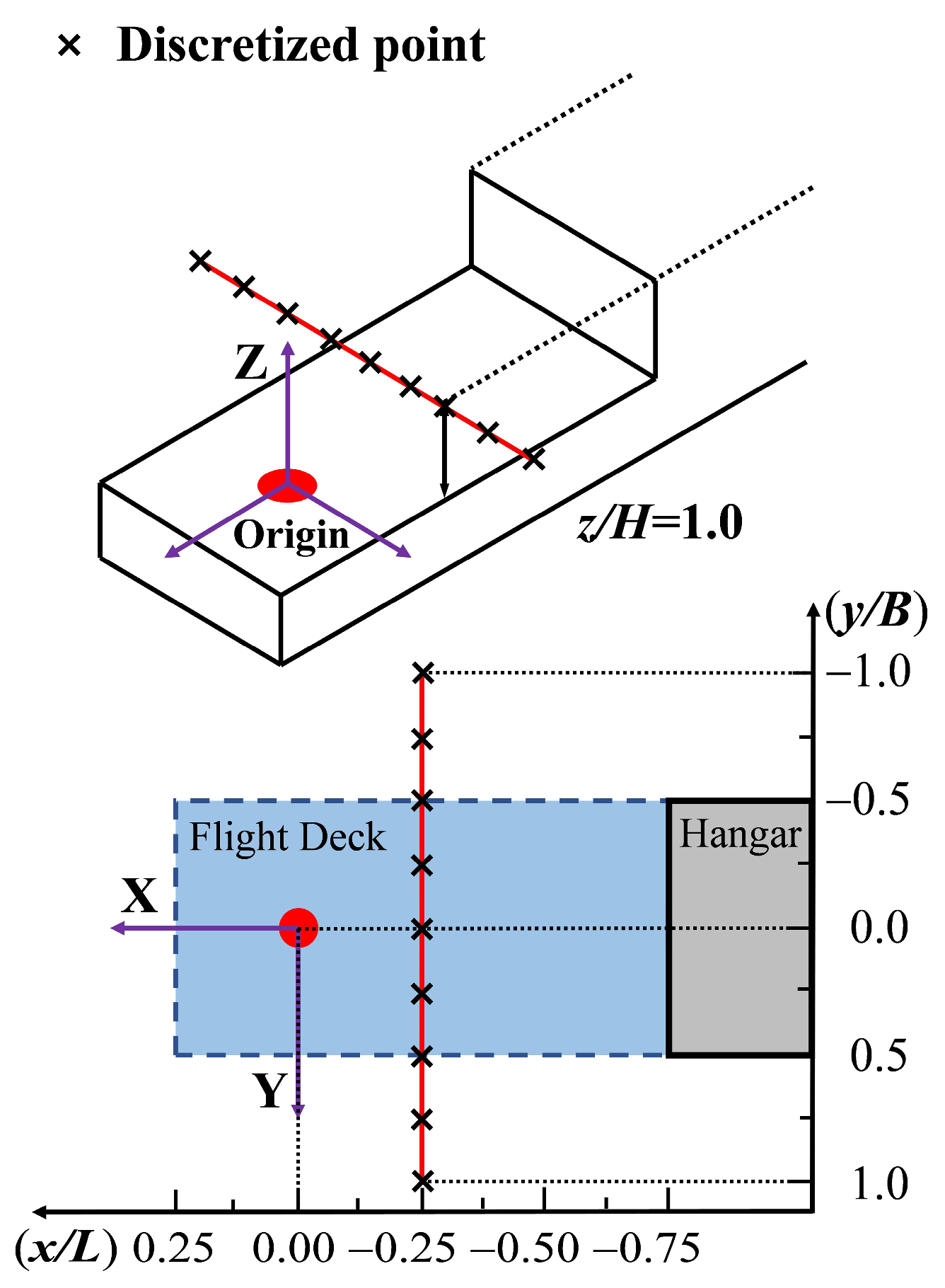
3.1. Definition of Shipboard Operations
- I.
- Approach and deck-sides hover;
- II.
- Lateral translation;
- III.
- Station keeping over the deck;
- IV.
- Vertical descent to the landing spot.
3.2. Influence on Flight Controls and Helicopter Attitudes in Shipboard Operations
4. Active Flow Control for Helicopter Shipboard Operations
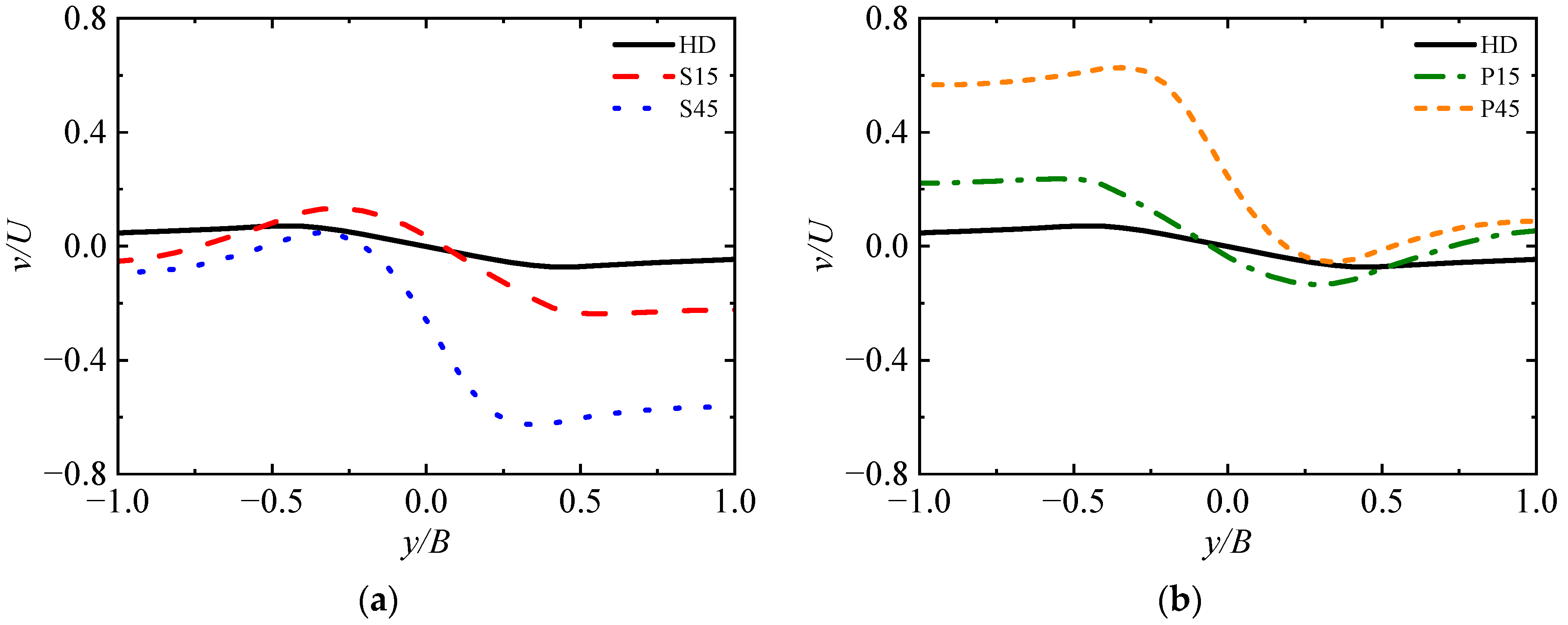
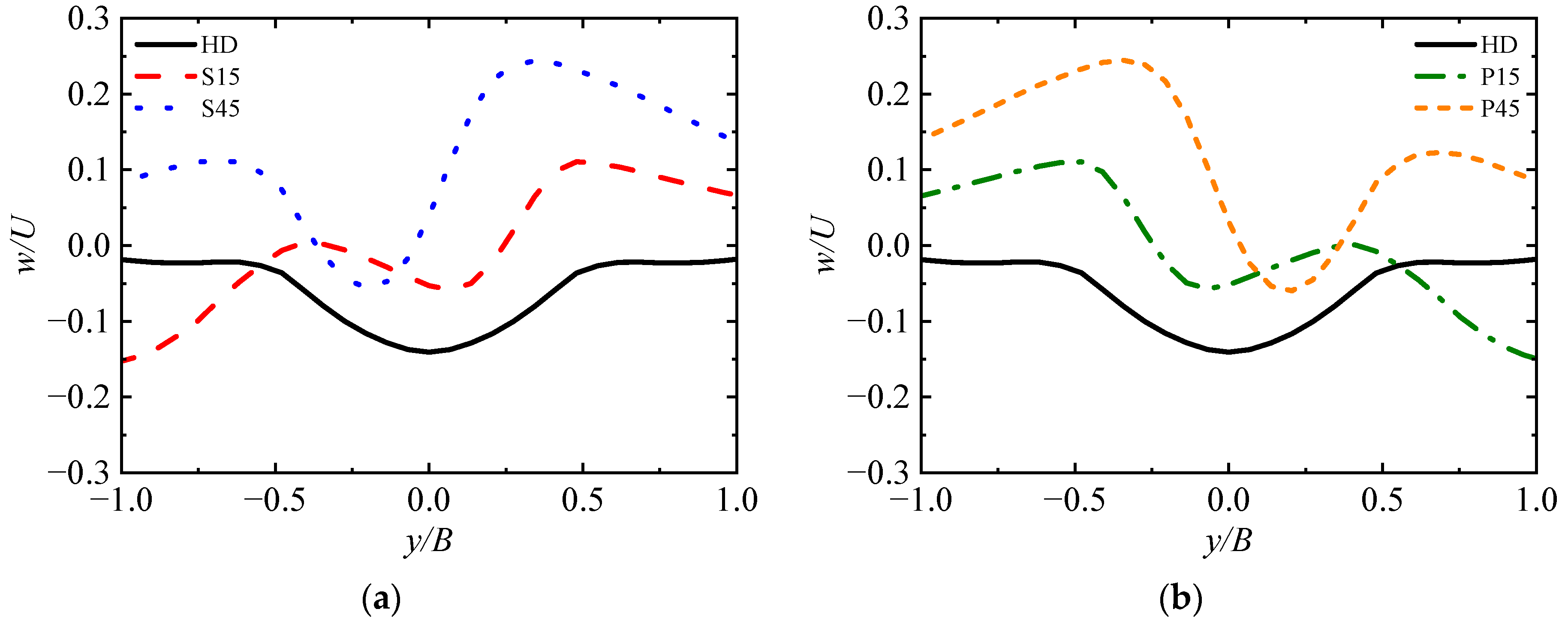
4.1. Design of Active Flow Control Strategy
- HD:
- S15:
- S45:
- P15:
- P45:
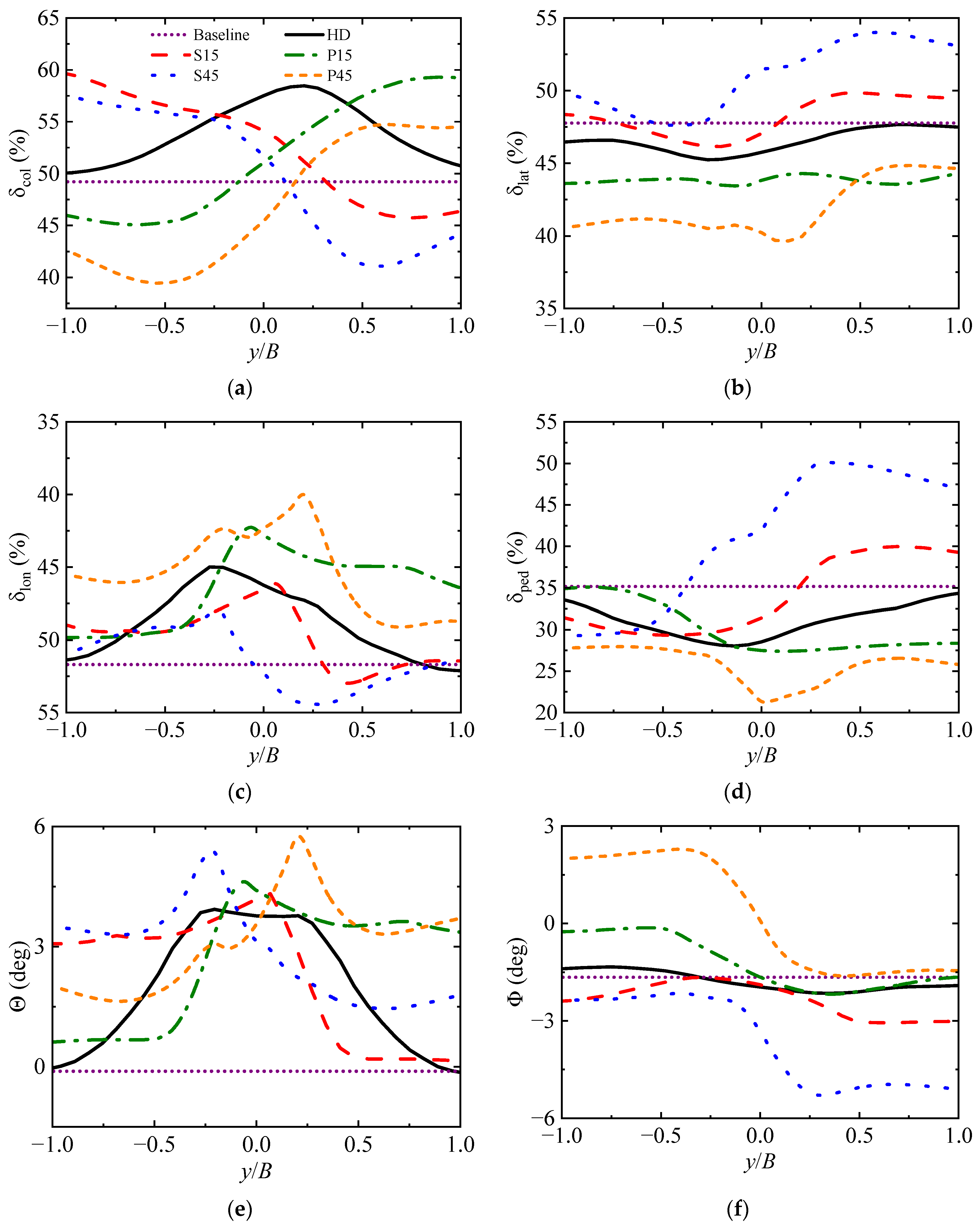
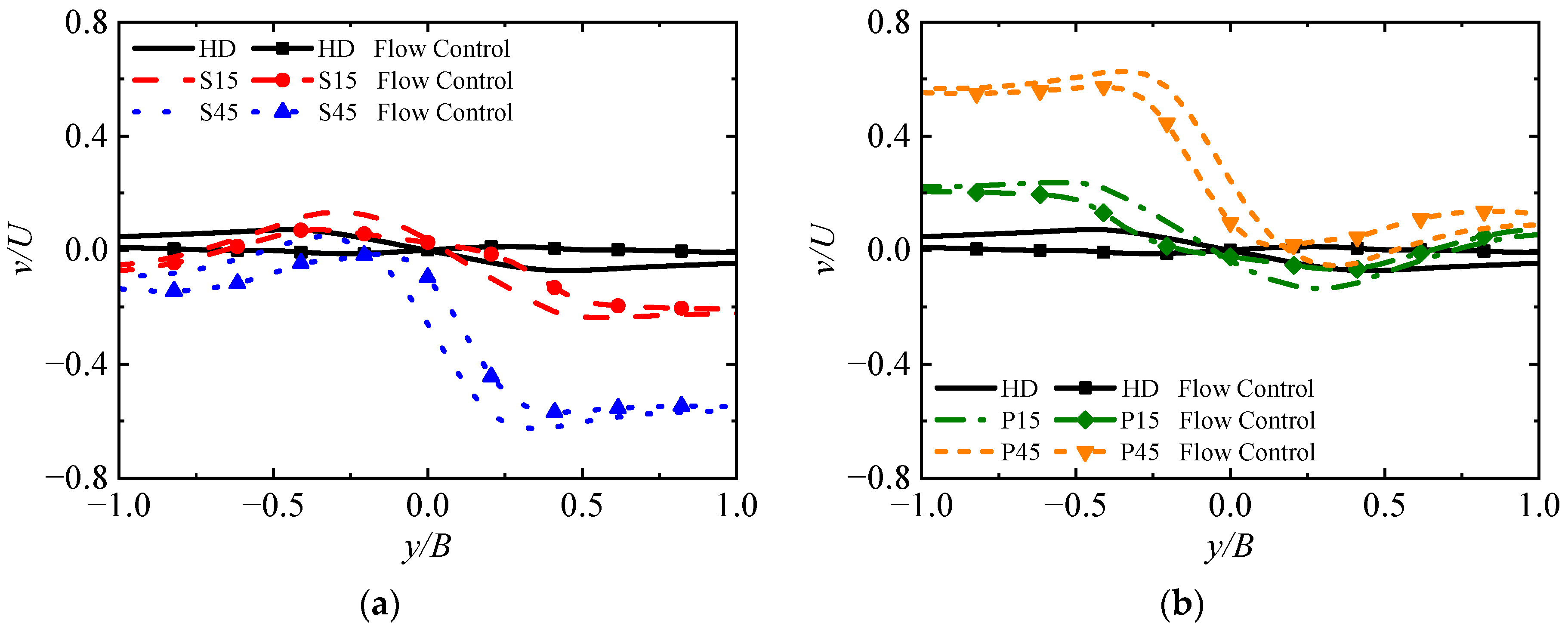
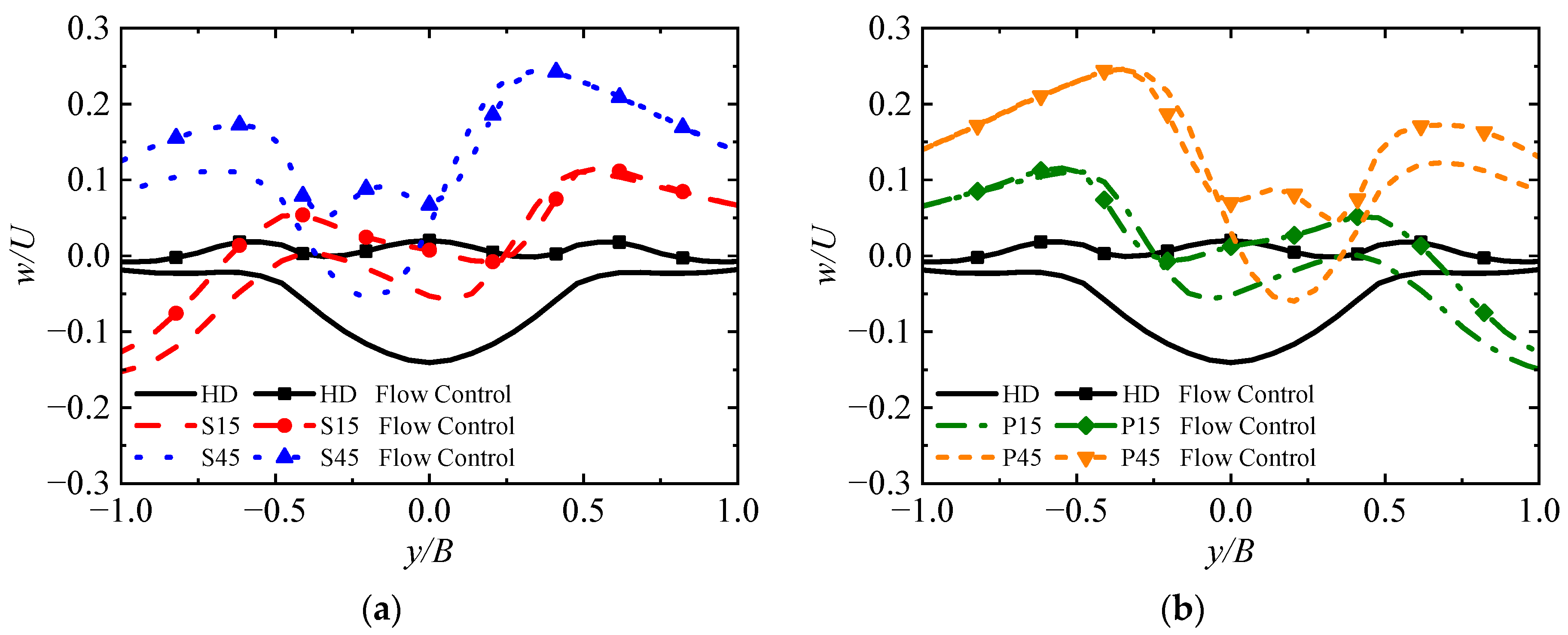
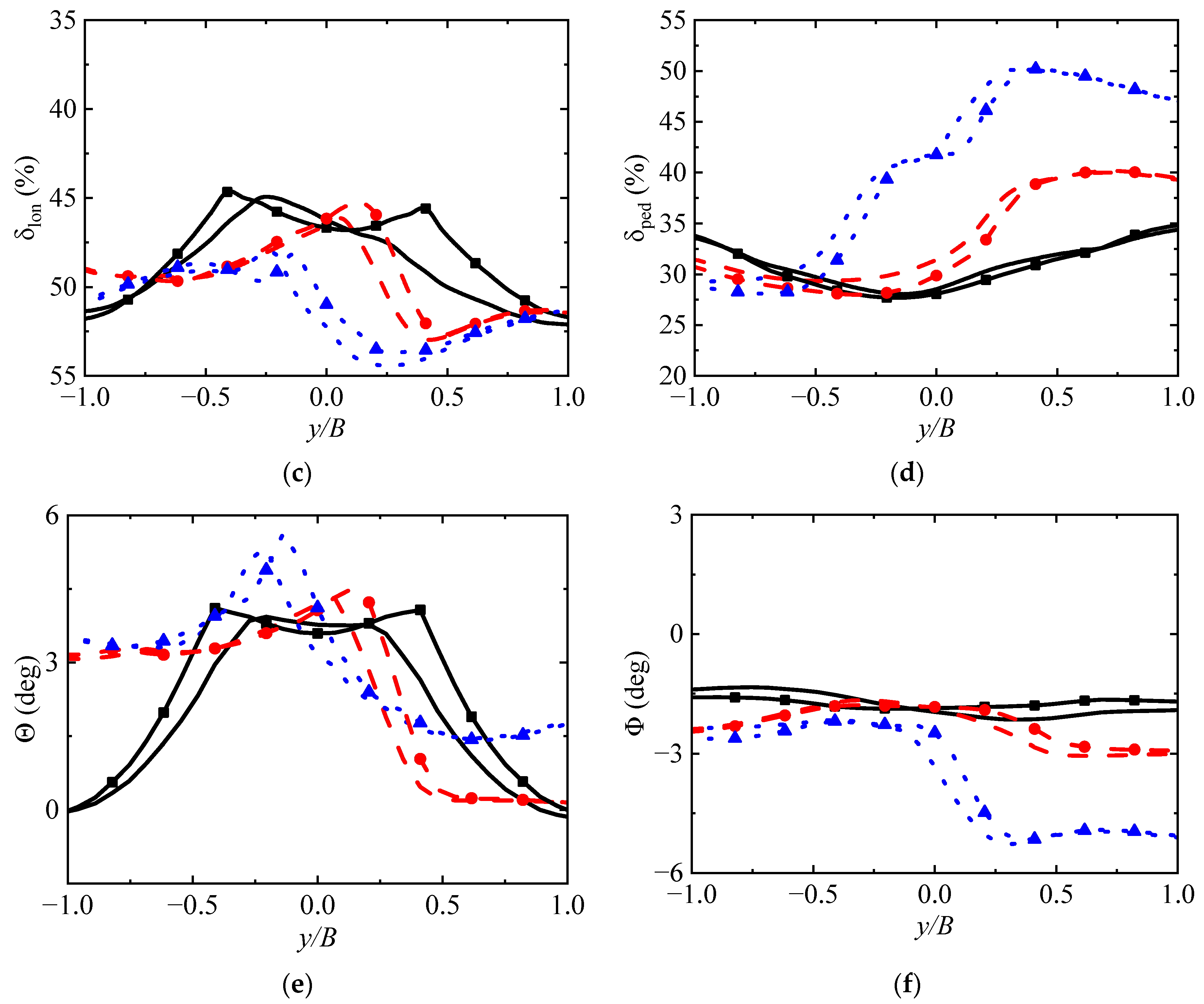
4.2. Influence on Flight Controls and Helicopter Attitudes
5. Conclusions
- The flow over the landing deck of a frigate is nonuniform and complex, which makes it more hazardous for helicopter shipboard operations than without airwake. The dilemma is made worse by the variation of the angles of WOD. By reducing control margins and increasing pilot workload, the airwake distribution brought on by large angles of WOD limits helicopter shipboard operations;
- Active flow control was applied by continuous nonuniform blowing on the deck. The control strategies matched the key flow characteristics, and the asymmetry of the sidewash distribution as well as the nonuniformity of the downwash distribution were weakened. In parallel, the majority of control margins were increased in the lateral translation task of helicopter shipboard operations, and the variations of flight control inputs and helicopter attitude angles were reduced, which contributes to improving the safety of shipboard operations. Nevertheless, under large angles of WOD, variations such as the helicopter pitch attitudes are beyond the control capability achieved by the active flow control strategy presented in this paper. How to effectively address the limitations of the control strategy is the next problem to be tackled;
- Based on the active flow control strategy presented in this paper, for the UH-60A helicopter, the landing approach can be conducted from the starboard to the landing spot when the direction of WOD is from the port side, while the landing approach is conducted from the port side to the landing spot if the direction of WOD is from the starboard.
6. Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reddy, K.R.; Toffoletto, R.; Jones, K.R.W. Numerical Simulation of Ship Airwake. Comput. Fluids 2000, 29, 451–465. [Google Scholar] [CrossRef]
- Polsky, S.; Bruner, C. Time-Accurate Computational Simulations of an LHA Ship Airwake. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000; American Institute of Aeronautics and Astronautics: Denver, CO, USA, 2000. AIAA 2000-4126. [Google Scholar]
- Forrest, J.S.; Owen, I. An Investigation of Ship Airwakes Using Detached-Eddy Simulation. Comput. Fluids 2010, 39, 656–673. [Google Scholar] [CrossRef]
- Polsky, S. A Computational Study of Unsteady Ship Airwake. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; American Institute of Aeronautics and Astronautics: Reno, NV, USA, 2002. AIAA 2002-1022. [Google Scholar]
- Polsky, S. CFD Prediction of Airwake Flowfields for Ships Experiencing Beam Winds. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2003. AIAA 2003-3657. [Google Scholar]
- Buonaccorso, J.A.; Widman, S.J.; Miklosovic, D.S. Pressure Field Mapping of a Modified YP Craft Flight Deck. In Proceedings of the AIAA Centennial of Naval Aviation Forum “100 Years of Achievement and Progress”, Virginia Beach, VA, USA, 21–22 September 2011; American Institute of Aeronautics and Astronautics: Virginia Beach, VA, USA, 2011. AIAA 2011-7044. [Google Scholar]
- Nacakli, Y.; Landman, D.; Doane, S. Investigation of Backward-Facing-Step Flow Field for Dynamic Interface Application. J. Am. Helicopter Soc. 2012, 57, 1–9. [Google Scholar] [CrossRef]
- Scott, P.; Kelly, M.F.; White, M.D.; Owen, I. Using Piloted Simulation to Measure Pilot Workload of Landing a Helicopter on a Smal Ship. In Proceedings of the 43rd European Rotorcraft Forum, Milan, Italy, 12–15 September 2017. [Google Scholar]
- Kääriä, C.H.; Forrest, J.S.; Owen, I. The Virtual AirDyn: A Simulation Technique for Evaluating the Aerodynamic Impact of Ship Superstructures on Helicopter Operations. Aeronaut. J. 2013, 117, 1233–1248. [Google Scholar] [CrossRef]
- Hoencamp, A.; Pavel, M.D. Concept of a Predictive Tool for Ship–Helicopter Operational Limitations of Various In-Service Conditions. J. Am. Helicopter Soc. 2012, 57, 1–9. [Google Scholar] [CrossRef]
- Forrest, J.S.; Owen, I.; Padfield, G.D.; Hodge, S.J. Ship-Helicopter Operating Limits Prediction Using Piloted Flight Simulation and Time-Accurate Airwakes. J. Aircr. 2012, 49, 1020–1031. [Google Scholar] [CrossRef]
- Findlay, D.; Ghee, T. Experimental Investigation of Ship Airwake Flow Control for a US Navy Flight II-A Class Destroyer (DDG). In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006; American Institute of Aeronautics and Astronautics: San Francisco, CA, USA, 2006. AIAA 2006-3501. [Google Scholar]
- Duy, T.N.; Hino, T.; Suzuki, K. Numerical Study on Stern Flow Fields of Ship Hulls with Different Transom Configurations. Ocean Eng. 2017, 129, 401–414. [Google Scholar] [CrossRef]
- Kaeaeriae, C.H.; Wang, Y.; White, M.D.; Owen, I. An Experimental Technique for Evaluating the Aerodynamic Impact of Ship Superstructures on Helicopter Operations. Ocean Eng. 2013, 61, 97–108. [Google Scholar] [CrossRef]
- Lasalle, N.R. Study of Passive Flow Control for Ship Air Wakes; USNA-TSPR-418; Defense Technical Information Center: Fort Belvoir, VA, USA, 2013.
- Shi, Y.; He, X.; Xu, Y.; Xu, G. Numerical Study on Flow Control of Ship Airwake and Rotor Airload during Helicopter Shipboard Landing. Chin. J. Aeronaut. 2019, 32, 324–336. [Google Scholar] [CrossRef]
- Forrest, J.S.; Kaaria, C.H.; Owen, I. Determining the Impact of HangarEdge Modifications on Ship-Helicopter Operations Using Offline and Piloted Helicopter Flight Simulation. In Proceedings of the American Helicopter Society 66th Annual Forum & Technology Display, VFS, Phoenix, AZ, USA, 11–13 May 2010. [Google Scholar]
- Shafer, D.; Ghee, T. Active and Passive Flow Control over the Flight Deck of Small Naval Vessels. In Proceedings of the 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, ON, Canada, 6–9 June 2005; American Institute of Aeronautics and Astronautics: Toronto, ON, Canada, 2005. AIAA 2005-5265. [Google Scholar]
- Shi, Y.; Su, D.; Xu, G. Numerical Investigation of the Influence of Passive/Active Flow Control on Ship/Helicopter Dynamic Interface. Aerosp. Sci. Technol. 2020, 106, 106205. [Google Scholar] [CrossRef]
- Matías-García, J.C.; Bardera, R.; Franchini, S.; Barderas, E.B. Experimental Comparison of Flow Control Techniques on Helicopter Flight Deck of Frigates. In Proceedings of the AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2023. AIAA 2023-4207. [Google Scholar]
- Matías-García, J.C.; Bardera, R.; Barroso, E.; Franchini, S. Improvement of Helicopter Operations on Frigates Using the Coanda Effect. J. Aircr. 2023, 60, 1626–1637. [Google Scholar] [CrossRef]
- Bardera-Mora, R.; Conesa, A.; Lozano, I. Simple Frigate Shape Plasma Flow Control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 2693–2699. [Google Scholar] [CrossRef]
- Howlett, J.J. UH-60A Black Hawk Engineering Simulation Program; NASA-CR-166309; NASA Ames Research Center: Moffett Field, CA, USA, 1981.
- Li, P.; Chen, R. A Mathematical Model for Helicopter Comprehensive Analysis. Chin. J. Aeronaut. 2010, 23, 320–326. [Google Scholar]
- Chen, R.; Yuan, Y.; Thomson, D. A Review of Mathematical Modelling Techniques for Advanced Rotorcraft Configurations. Prog. Aerosp. Sci. 2021, 120, 100681. [Google Scholar] [CrossRef]
- Yuan, Y.; Thomson, D.; Anderson, D. Aerodynamic Uncertainty Quantification for Tiltrotor Aircraft. Aerospace 2022, 9, 271. [Google Scholar] [CrossRef]
- Pitt, D.M.; Peters, D.A. Theoretical Prediction of Dynamic Inflow Derivatives. Vertica 1981, 5, 21–34. [Google Scholar]
- Peters, D.A.; Haquang, N. Dynamic Inflow for Practical Applications. J. Am. Helicopter Soc. 1988, 33, 64–68. [Google Scholar] [CrossRef]
- Bailey, F.J. A Simplified Theoretical Method of Determining the Characteristics of a Lifting Rotor in Forward Flight; NASA-TR-716; NACA Langley Memorial Aeronautical Laboratory: Langley Field, VA, USA, 1941. [Google Scholar]
- Ballin, M.G. Validation of a Real-Time Engineering Simulation of the UH-60A Helicopter; NASA-TM-88360; NASA Ames Research Center: Moffett Field, CA, USA, 1987.
- Syms, G.F. Numerical Simulation of Frigate Airwakes. Int. J. Comput. Fluid Dyn. 2004, 18, 199–207. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, H.; Ball, N. Numerical Simulation of Unsteady Flow over SFS 2 Ship Model. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2009. AIAA 2009-81. [Google Scholar]
- Ji, H.; Chen, R.; Li, P. Rotor-State Feedback Control to Alleviate Pilot Workload for Helicopter Shipboard Operations. J. Guid. Control Dyn. 2017, 40, 3088–3099. [Google Scholar] [CrossRef]
- Ji, H.; Chen, R.; Li, P. Real-Time Simulation Model for Helicopter Flight Task Analysis in Turbulent Atmospheric Environment. Aerosp. Sci. Technol. 2019, 92, 289–299. [Google Scholar] [CrossRef]
- Kang, S.; Choi, H. Suboptimal Feedback Control of Turbulent Flow over a Backward-Facing Step. J. Fluid Mech. 2002, 463, 201–227. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Chen, R.; Ji, H. An Active Flow Control over the Ship Deck for Helicopter Shipboard Operations. Aerospace 2024, 11, 119. https://doi.org/10.3390/aerospace11020119
Ye Y, Chen R, Ji H. An Active Flow Control over the Ship Deck for Helicopter Shipboard Operations. Aerospace. 2024; 11(2):119. https://doi.org/10.3390/aerospace11020119
Chicago/Turabian StyleYe, Yi, Renliang Chen, and Honglei Ji. 2024. "An Active Flow Control over the Ship Deck for Helicopter Shipboard Operations" Aerospace 11, no. 2: 119. https://doi.org/10.3390/aerospace11020119
APA StyleYe, Y., Chen, R., & Ji, H. (2024). An Active Flow Control over the Ship Deck for Helicopter Shipboard Operations. Aerospace, 11(2), 119. https://doi.org/10.3390/aerospace11020119




