Simulation and Analysis of Aerodynamic Characteristics during Parafoil Canopy Curving Process and Application by LBM
Abstract
1. Introduction
- (1)
- Accurate theory and modeling: The surface profile, sweep angle, span characteristics and other parameters of the 3D model are not available in the 2D model. In the flow phenomenon, effects such as wingtip vortices are generated, and the result is closer to the actual flight conditions.
- (2)
- Better optimization of the aerodynamic performance: By optimizing the aerodynamic shape under the 3D model of the parafoil, the aerodynamic efficiency and stability can be improved, and the test cost can be reduced.
- (3)
- Display & Rendering: Provide designers, engineers, customers and decision-makers with a visual display that provides a clearer understanding of the design intent and performance, facilitating communication and decision-making.
2. Method
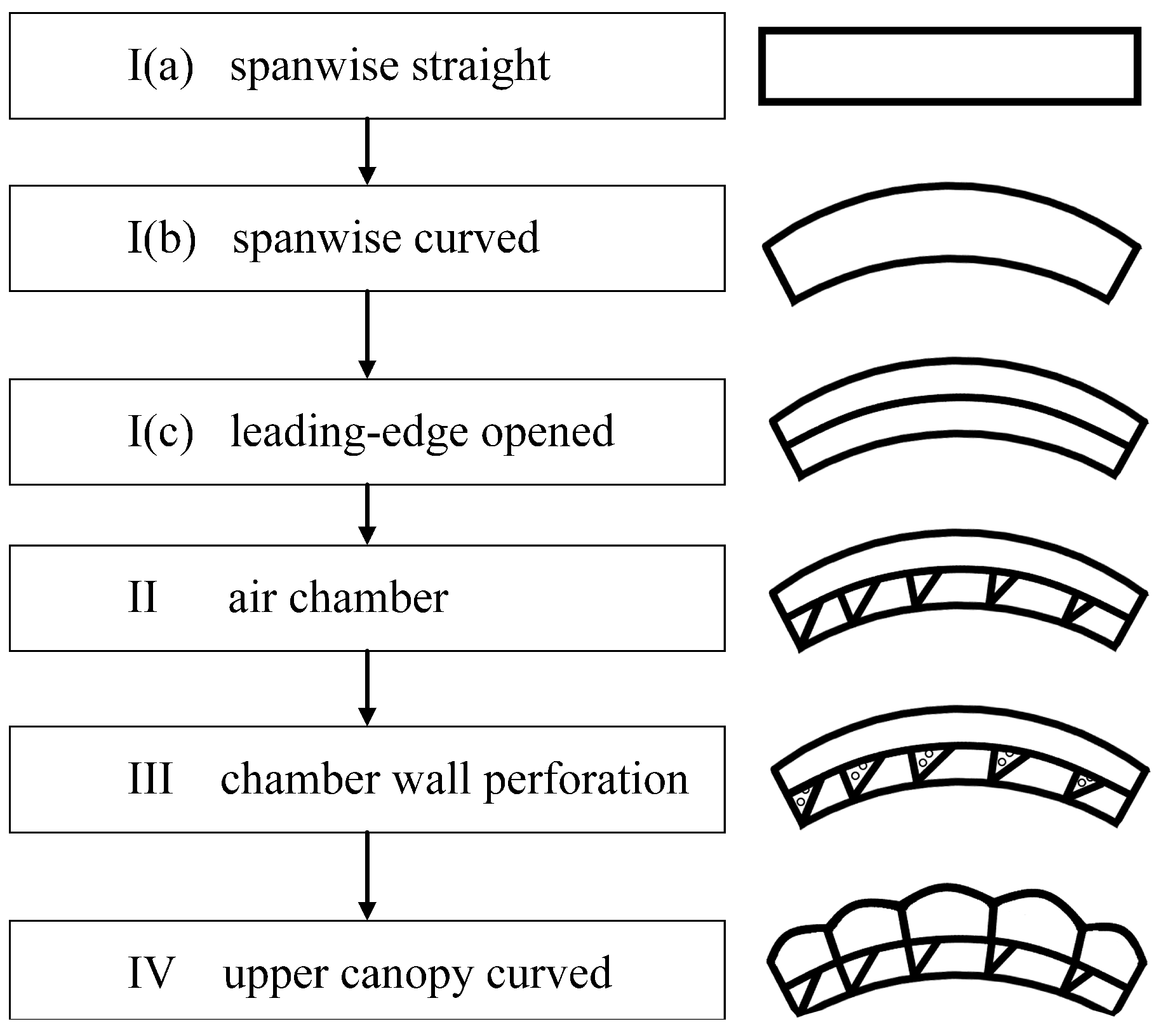
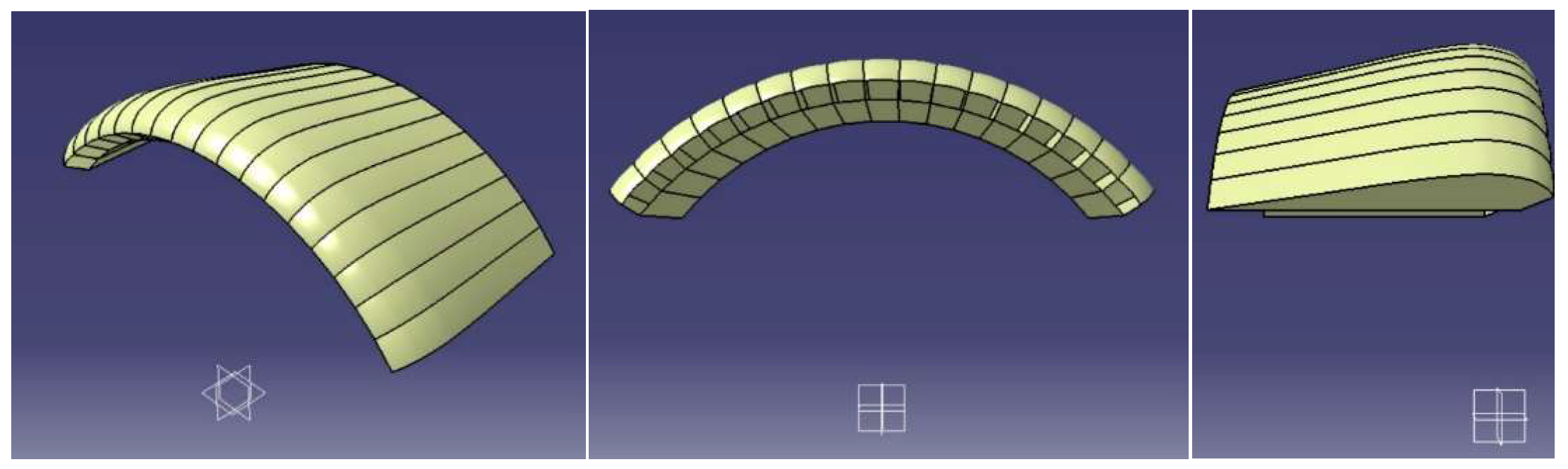
2.1. Research Object
2.2. Research Method
2.2.1. Lattice Boltzmann Method
2.2.2. Finite Volume Method
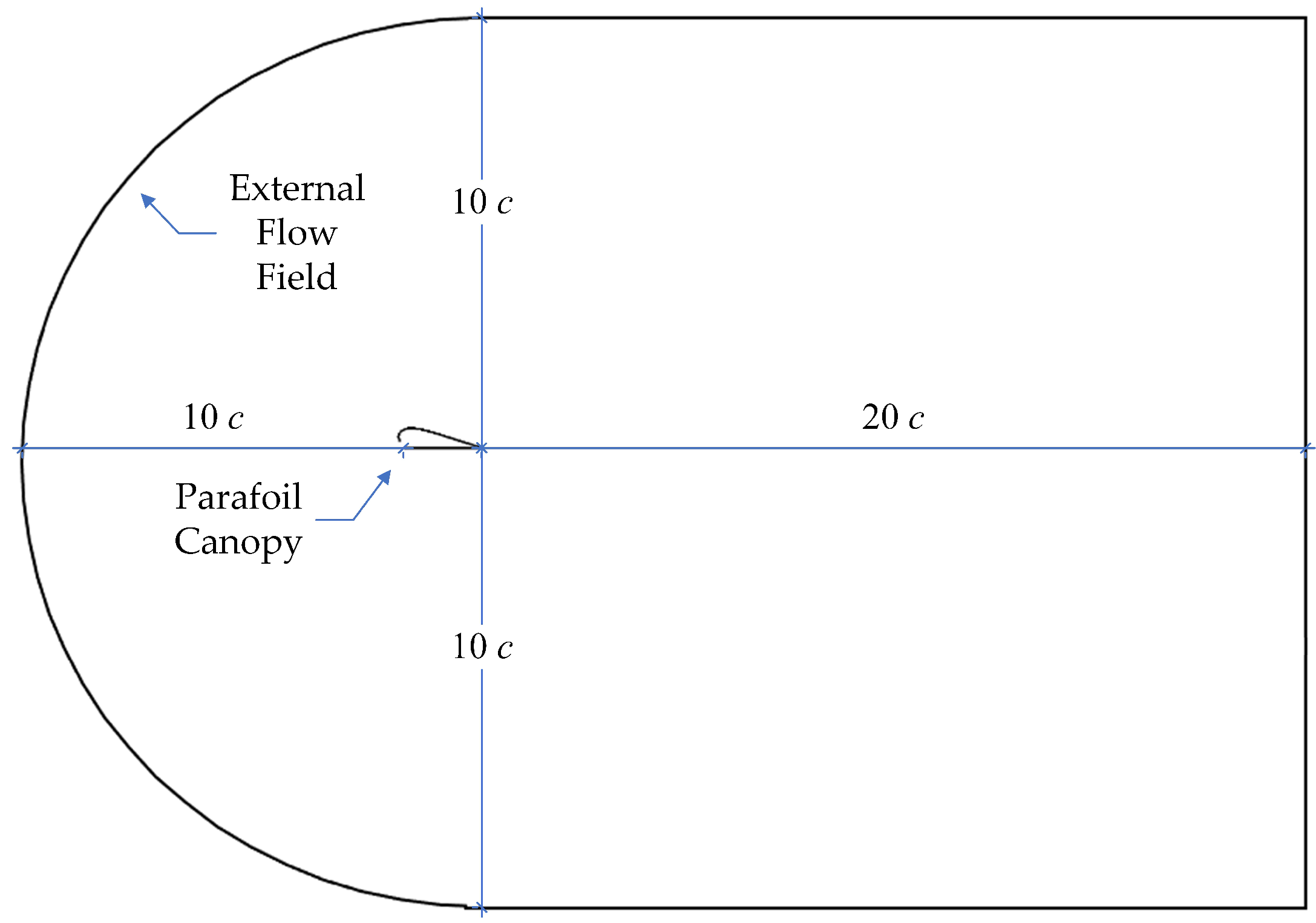
2.2.3. External Flow Field and Parameters
3. Results and Analysis
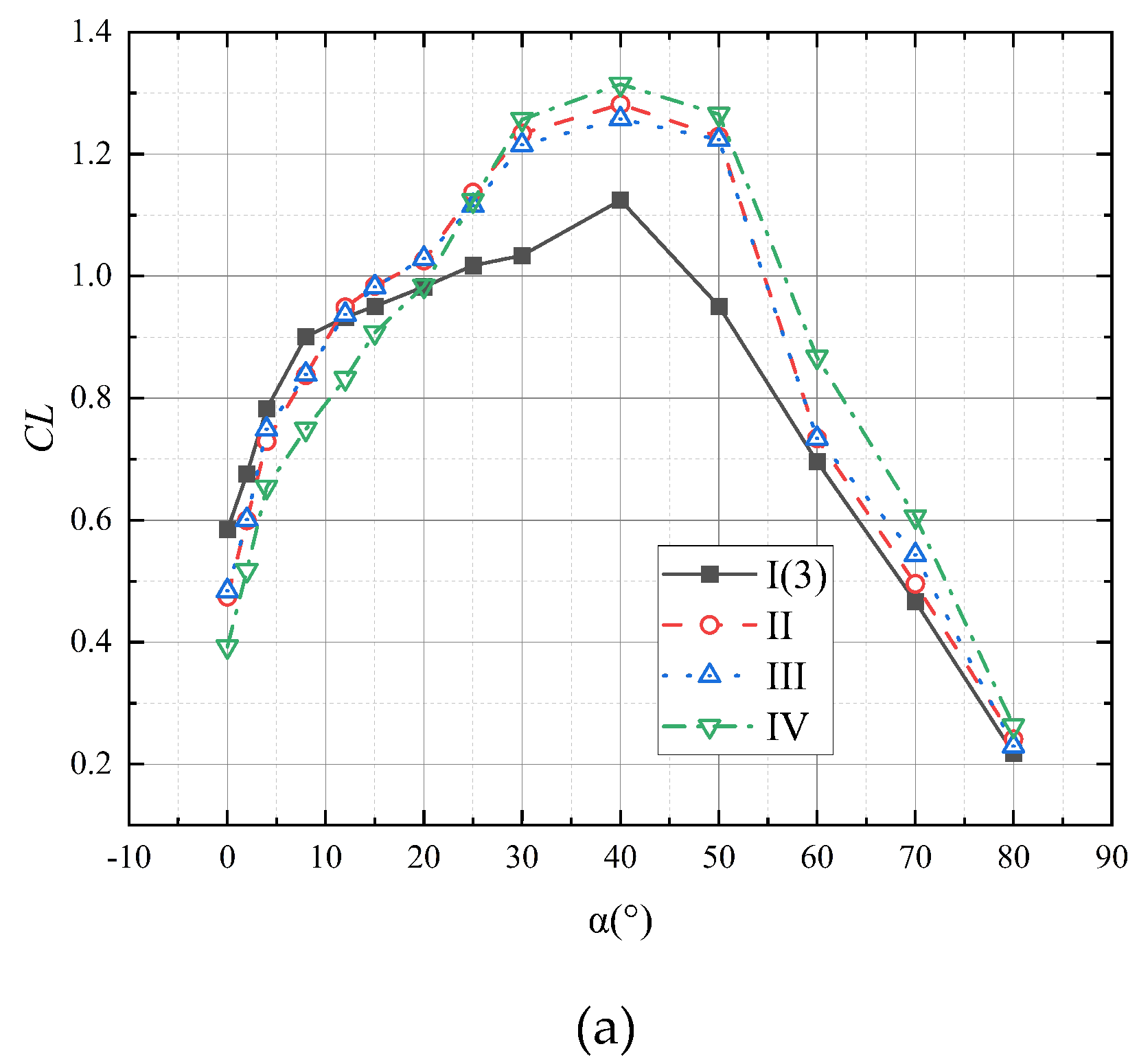
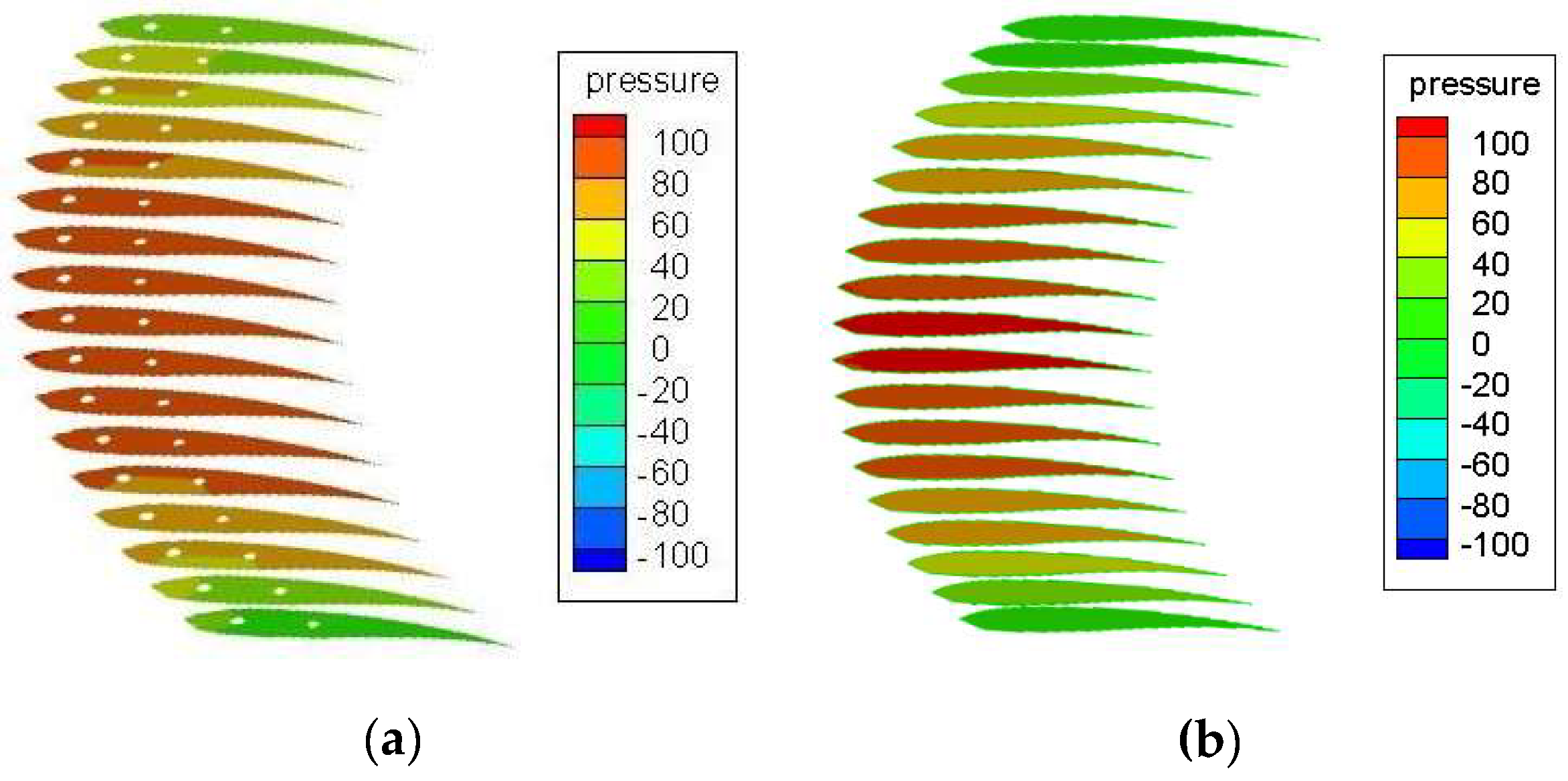
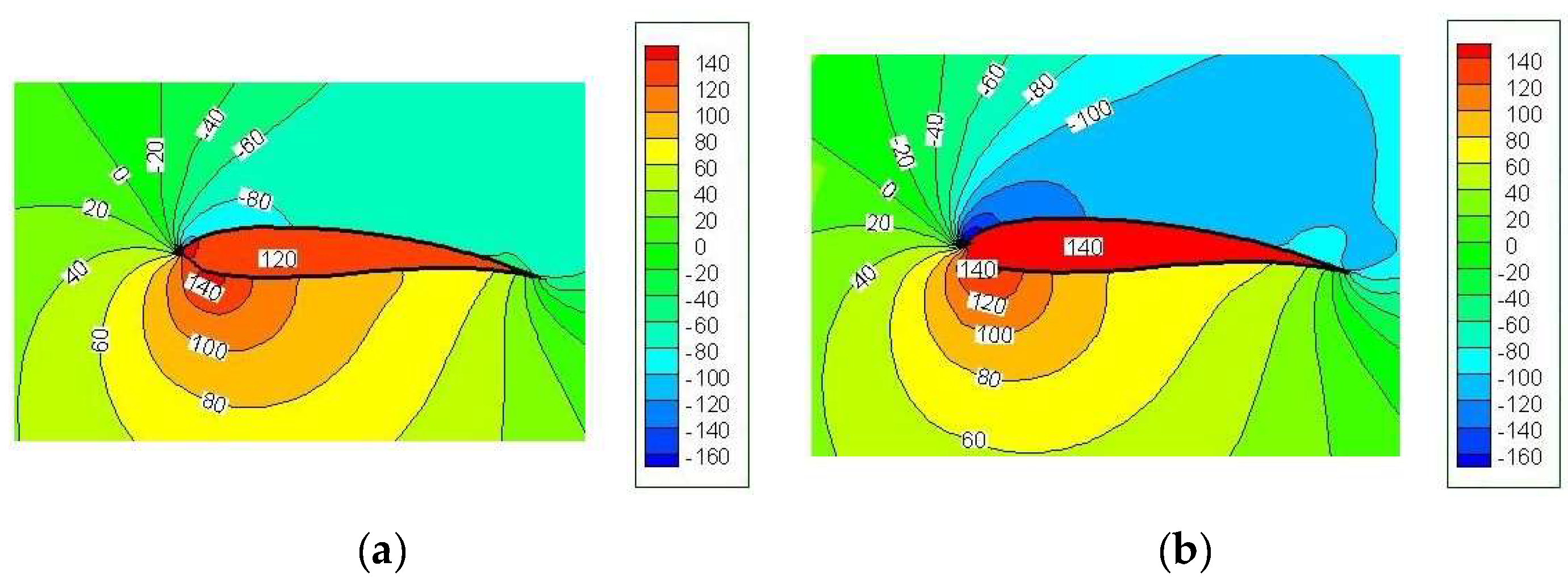
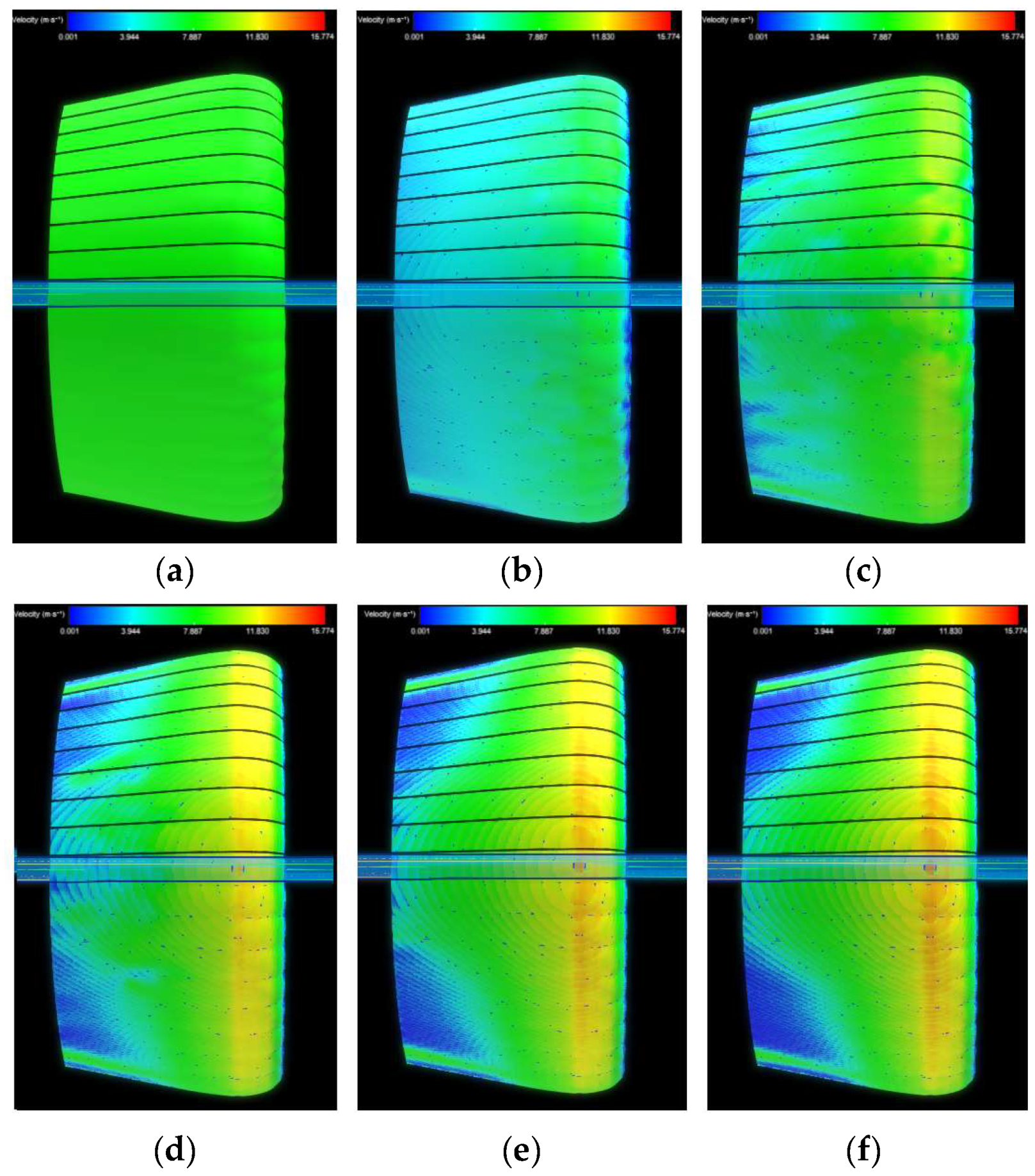
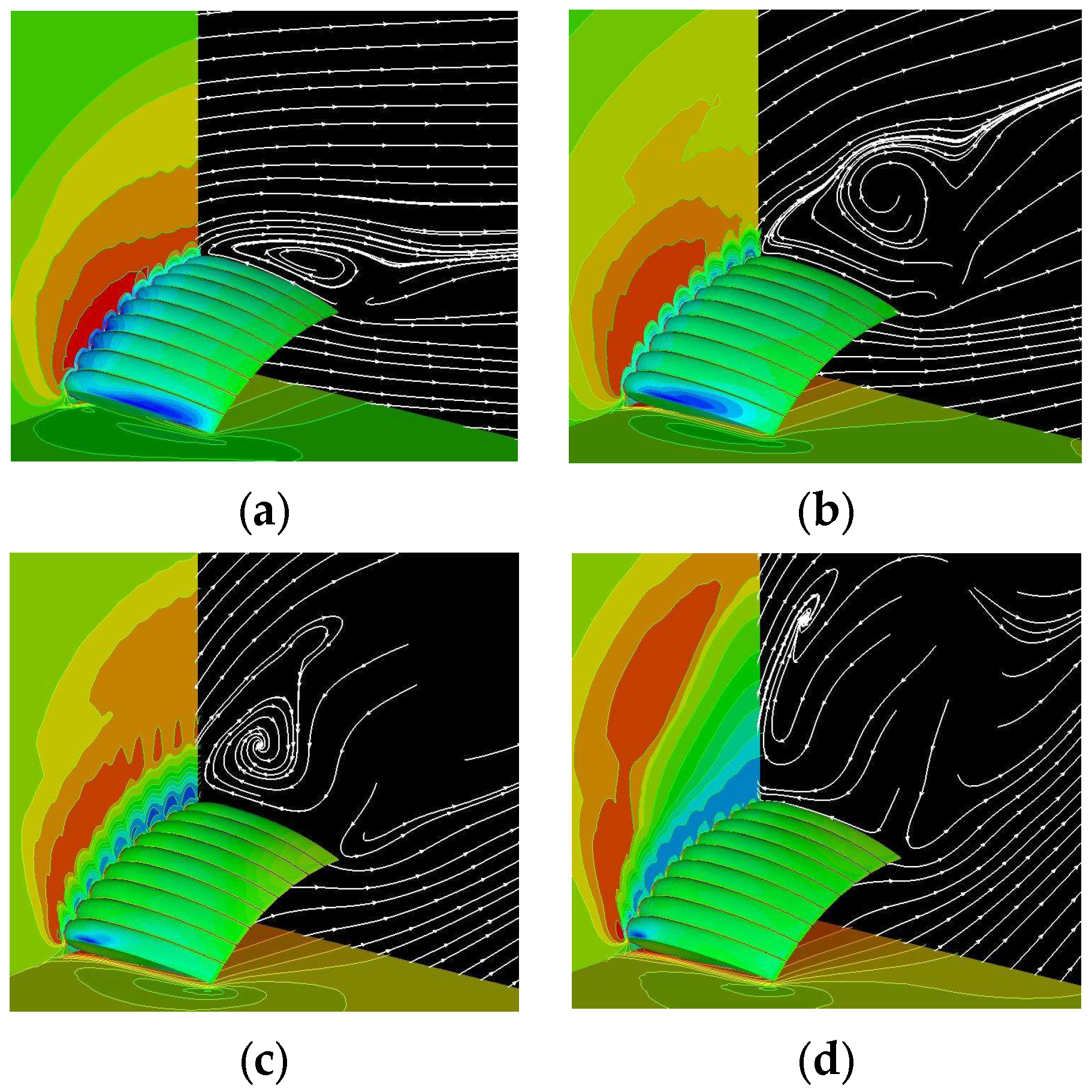
3.1. Aerodynamic and Flow Characteristics by LBM for Curving Stages and Air Chamber Structure
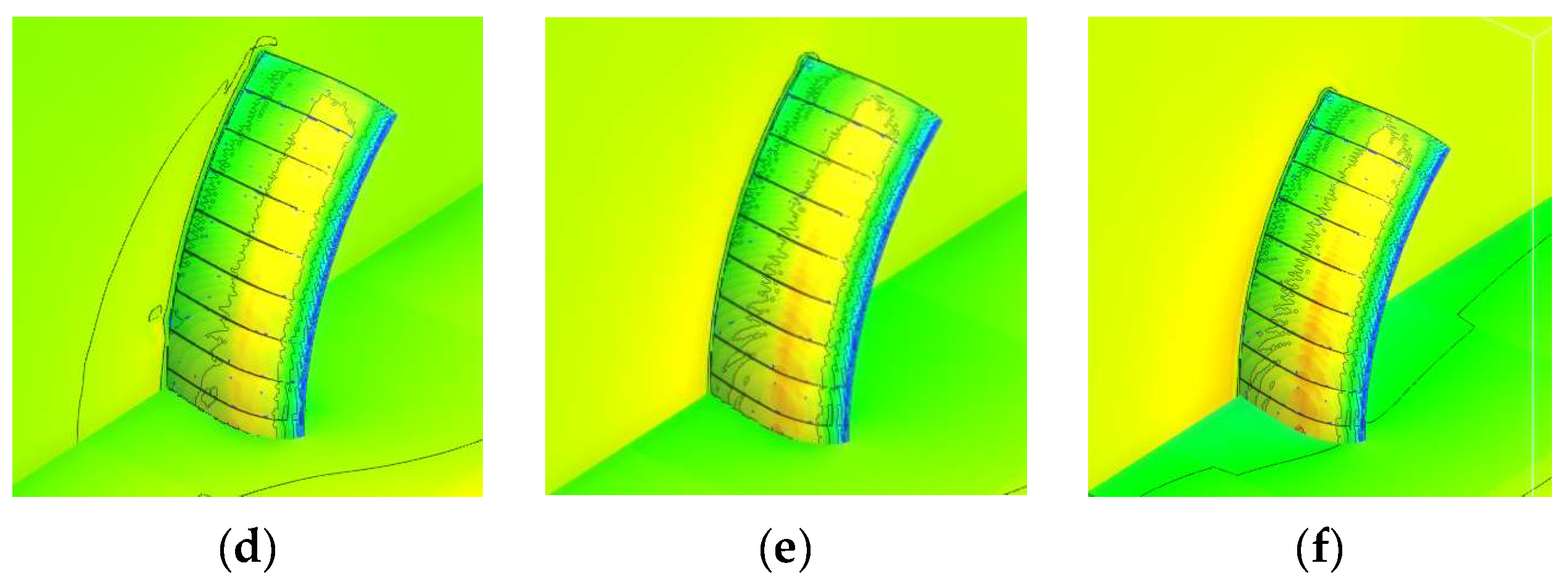
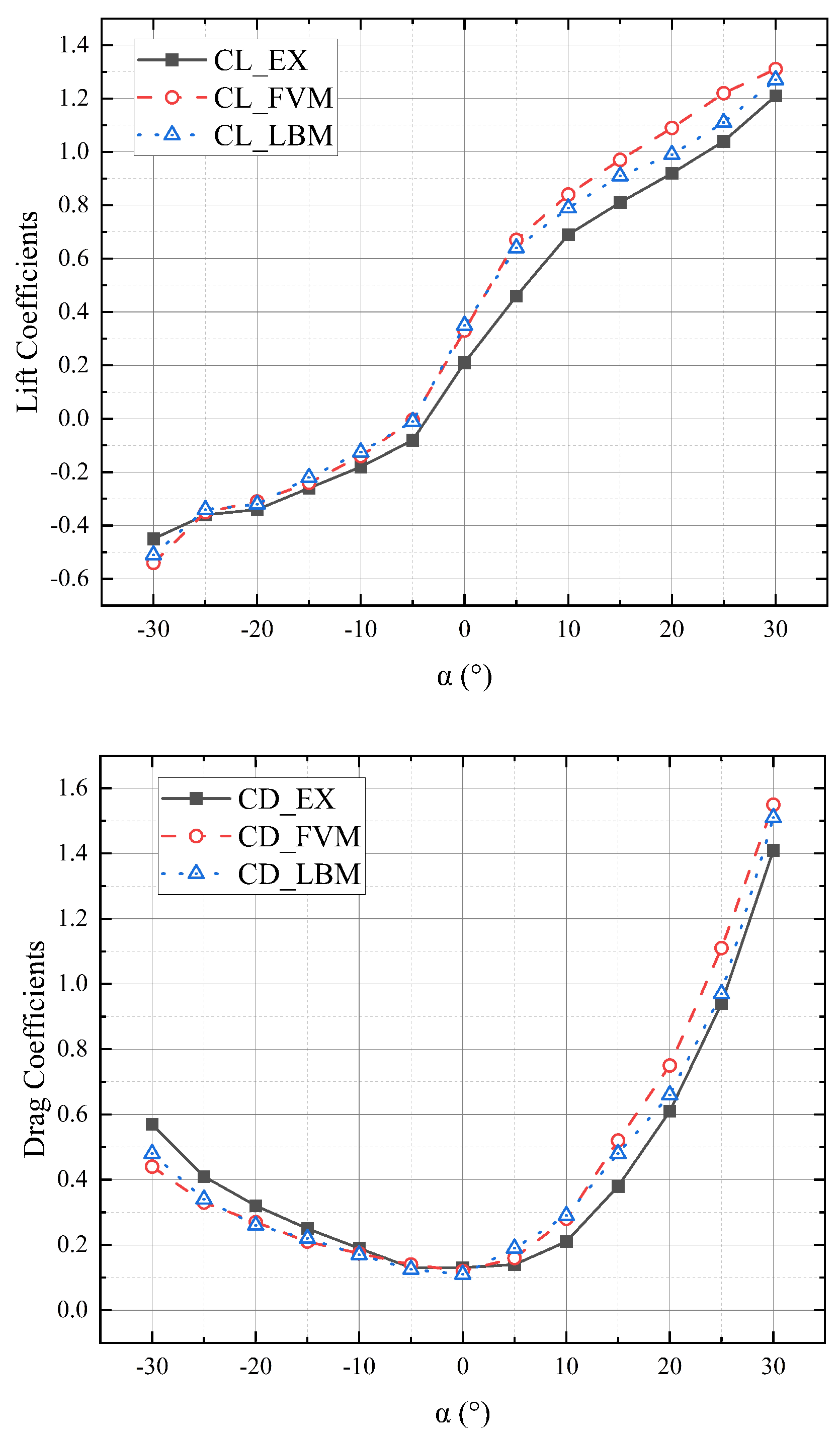
3.2. Stalling Phenomena Analysis and Validation by Finite Volume Method for Model IV
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, G.; Xi, H.; Duncan, C.; Chou, S.H. Finite volume scheme for the lattice Boltzmann method on unstructured meshes. Phys. Rev. E 1999, 59, 4675–4682. [Google Scholar] [CrossRef]
- Mylonas, D.; Sayer, P. The Hydrodynamic Flow around a Yacht Keel Based on LES and DES. Ocean Eng. 2012, 46, 18–32. [Google Scholar] [CrossRef]
- Constantinescu, G.S.; Squires, K.D. LES and DES Investigations of Turbulent Flow over a Sphere at Re = 10,000. Flow Turbul. Combust. 2003, 70, 267–298. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Rizzetta, D.P.; Fureby, C. Large-eddy Simulation: Current Capabilities Recommended Practices, and Future Research. AIAA J. 2010, 48, 1772–1784. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W.; Yu, D.; Luo, L.-S. Lattice Boltzmann Method for 3-D Flows with Curved Boundary. J. Comput. Phys. 2000, 161, 680–699. [Google Scholar] [CrossRef]
- Tsutahara, M.; Feng, S.D.; Kataoka, T. Simulation of the stratified flows using the two-component lattice Boltzmann method. Comput. Phys. Commun. 2000, 129, 131–137. [Google Scholar] [CrossRef]
- Satofukaa, N.; Sakai, T. Parallel Computation of Three-dimensional Two-phase Flows by the Lattice Boltzmann Method. Paral. Comput. Fluid Dynam 2000. preprint. [Google Scholar]
- Pan, A.C.; Luo, L.S.; Miller, C.T. An evaluation of lattice Boltzmann equation methods for simulating flow through porous media. Dev. Water Sci. 2004, 55, 95–106. [Google Scholar]
- Belov, E.B.; Lomov, S.V.; Verpoest, I.; Peters, T.; Roose, D.; Parnas, R.; Hoes, K.; Sol, H. Modelling of permeability of textile reinforcements: Lattice Boltzmann method. Compos. Sci. Technol. 2004, 64, 1069–1080. [Google Scholar] [CrossRef]
- Jiang, X.; Andreopoulos, Y.; Lee, T.; Wang, Z. Numerical investigations on the vortex-induced vibration of moving square cylinder by using incompressible lattice Boltzmann method. Comput. Fluids 2015, 124, 270–277. [Google Scholar] [CrossRef]
- An, B.; Bergadà, J.M.; Sang, W. A simplified new multigrid algorithm of lattice Boltzmann method for steady states. Comput. Math. Appl. 2023, 135, 102–110. [Google Scholar] [CrossRef]
- Bukreev, F.; Simonis, S.; Kummerlander, A.; Jeßberger, J.; Krause, M.J. Consistent lattice Boltzmann methods for the volume averaged Navier-Stokes equations. J. Comput. Phys. 2023, 490, 112301. [Google Scholar] [CrossRef]
- Dawid, S.; Maciej, M. Study of the convergence of the Meshless Lattice Boltzmann Method in Taylor–Green, annular channel and a porous medium flows. Comput. Fluids 2023, 269, 106122. [Google Scholar]
- Alamian, R.; Sawaf, M.; Stockinger, C.; Hadjadj, A.; Latt, J.; Shadloo, M. Modeling soot filter regeneration process through surface-reactive flow in porous media using iterative lattice Boltzmann method. Energy 2024, 298, 129980. [Google Scholar] [CrossRef]
- Yan, G.; As’ad Alizadeh; Rahmani, A.; Zarringhalam, M.; Shamsborhan, M.; Nasajpour-Esfahani, N.; Akrami, M. Natural convection of rectangular cavity enhanced by obstacle and fin to simulate phase change material melting process using Lattice Boltzmann method. Alex. Eng. J. 2023, 81, 319–336. [Google Scholar] [CrossRef]
- Emre, G.S.; Hakan, I.T. Numerical simulation of duct flow in the presence of participating media radiation with total energy based entropic lattice Boltzmann method. Int. J. Thermofluids 2023, 220, 100516. [Google Scholar]
- Tang, W.; Johari, H. Deformation of a ram-air canopy due to control line retraction. In Proceedings of the 24th AIAA Aerodynamic Decelerator Systems Technology Conference, Denver, CO, USA, 5–9 June 2017; AIAA: Reston, VA, USA, 2017; p. 3546. [Google Scholar]
- Takizawa, K.; Tezduyar, T.E.; Terahara, T. Ram-air parachute structural and fluid mechanics computations with the Space-Time Isogeometric Analysis (ST-IGA). Comput. Fluids 2016, 141, 191–200. [Google Scholar] [CrossRef]
- Fogell, N.A.; Iannucci, L.; Bergeron, K. Fluid-structure interaction simulations of the inflated shape and associated flowfield of the MC4/5 parafoil during steady gliding flight. In Proceedings of the 24th AIAA Aerodynamic Decelerator Systems Technology Conference, Denver, CO, USA, 5–9 June 2017; AIAA: Reston, VA, USA, 2017; p. 3543. [Google Scholar]
- Altmann, H. Fluid-structure interaction analysis of ram-air parafoil wings. In Proceedings of the 23rd AIAA Aerodynamic Decelerator Systems Technology Conference, Daytona Beach, FL, USA, 30 March–2 April 2015; AIAA: Reston, VA, USA, 2015; p. 2184. [Google Scholar]
- Zhang, S.; Yu, L.; Liu, X. Numerical simulation of parafoil inflation process based on fluid-structure interaction method. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1108–1115. (In Chinese) [Google Scholar] [CrossRef]
- Lingard, J.S. Ram-air parachute design. In Proceedings of the 13th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Clearwater Beach, FL, USA, 15–18 May 1995; pp. 10–23. [Google Scholar]
- Nie, S.; Cao, Y.H.; Wu, Z.L. Numerical simulation of parafoil inflation via a Robin-Neumann transmission-based approach. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 797–810. [Google Scholar] [CrossRef]
- Bergeron, K.; Seidel, J.; Ghoreyshi, M.; Jirasek, A.; Lofthouse, A.J.; Cummings, R.M. Numerical Study of Ram Air Airfoils and Upper Surface Bleed-Air Control. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Cao, Y.; Zhu, X. Effects of characteristic geometric parameters on parafoil lift and drag. Aircr. Eng. Aerosp. Technol. 2013, 85, 280–292. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.; Chen, Z.; He, Y. Dynamic Modeling of a Parafoil System Considering Flap Deflection. J. Southeast Univ. 2017, 33, 416–425. [Google Scholar]
- Gavrilovski, A.; Ward, M.; Costello, M. Parafoil Control Authority with Upper-Surface Canopy Spoilers. J. Aircr. 2015, 49, 1391–1397. [Google Scholar] [CrossRef]
- Bergeron, K.; Ward, M.; Costello, M.; Tavan, S. AG100 and Bleed-Air Actuator Airdrop Experimenting. In Proceedings of the AIAA Aerodynamic Decelerator Systems, Daytona Beach, FL, USA, 25–28 March 2013. [Google Scholar]
- Ke, P.; Yang, C.X.; Yang, X.S. Extraction Phase Simulation of Cargo Airdrop System. Chin. J. Aeronaut. 2006, 19, 315–321. [Google Scholar] [CrossRef]
- Succi, S.; Chen, H.; Orszag, S. Relaxation approximations and kinetic models of fluid turbulence. Phys. A Stat. Mech. Its Appl. 2006, 362, 1–5. [Google Scholar] [CrossRef]
- Burke, S.M.; Ware, G.M. Static Aerodynamic Characteristics of Three Ram-air Inflated Low Aspect Ratio Fabrics Wings; Langly Research Center, NASA WP 264; NTRS: Chicago, IL, USA, 1966. [Google Scholar]
- Bergeron, K.; Seidel, J.; Ghoreyshi, M.; Jirasek, A.; Lofthouse, A.J.; Cummings, R.M. Computational Fluid Dynamics for the Aerodynamic Design and Modeling of a Ram-Air Parachute with Bleed-Air Actuators. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Eslambolchi, A.; Johari, H. Simulation of Flowfield Around a Ram-Air Personnel Parachute Canopy. J. Aircr. 2013, 50, 1628–1636. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Polygon count | 10,468 |
| Point count | 5623 |
| Reference area(m2) | 137.087 |
| Reference volume(m3) | 31.2083 |
| Length of chord(m) | 4.84486 |
| Length of span(m) | 9.78134 |
| Height of arch | 2.84421 |
| Center of aerodynamic | Center of mass |
| Parameters | Value | ||
|---|---|---|---|
| Simulation Engine | Field types of analysis | External field | |
| Flow pattern | Single phase | ||
| Turbulence model | Auto | ||
| Thermal model | Isotherm | ||
| Simulation Environment | Global Feature | Scope type | Virtual wind tunnel |
| Extermal velocity field | X:0 Y:0 Z:9.8 m·s−2 | ||
| Initial velocity field | X:15 m/s Y:0 Z:0 | ||
| Initial pressure field(Pa) | 101,325 | ||
| Reference area | Front | ||
| Reference velocity | Local | ||
| Wind Tunnel characteristics | Location | (0,0,0) | |
| Dimensionality | (80,80,40) | ||
| Boundary layer model | Periodic | ||
| Boundary conditions | X:15 m/s Y:0 Z:0 | ||
| Angle-of-attack(°) | 0, ±5, ±10, ±15, ±20, ±25, ±30 | ||
| Parameters | Value |
|---|---|
| Molecular weight(u) | 28.996 |
| Temperature(K) | 288.15 |
| Dynamic viscosity(Pa·s) | 0.001 |
| Specific heat(J·(kg·K)−1) | 1006.43 |
| Reference density(kg·m3) | 1.225 |
| Viscosity model | Newtonian fluid |
| Thermal conductivity(W·(m·K)−1) | 0.0243 |
| Parameters | Value |
|---|---|
| Time frame(s) | 10 |
| Resolution | 0.04 (Flow field), 0.02 (Boundary) |
| Wall boundary condition | No-slip |
| Time step | Fixed automatically |
| Thinning algorithm | Near static walls |
| Parameters | Value |
|---|---|
| Number of blocks(million) | ≈0.54 |
| Type of grid | Structured grid for partition interconnection |
| Boundary conditions | Velocity inlet, pressure outlet |
| Flow speed(m/s) | 15 |
| Angle-of-attack(°) | 0°, 10°, 20°, 30°, 45°, 60° 3°, 6°, 9°, 12°, 15° and 18° |
| Relaxation factor λ | 0 |
| Wall boundary condition | No-slip |
| Turbulence model | [32] |
| Solver format | Implicit format for separating models [33] |
| Viscous term discrete | Central difference format |
| Convective term discrete | Second-order upwind format |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, C. Simulation and Analysis of Aerodynamic Characteristics during Parafoil Canopy Curving Process and Application by LBM. Aerospace 2024, 11, 118. https://doi.org/10.3390/aerospace11020118
Wang Y, Yang C. Simulation and Analysis of Aerodynamic Characteristics during Parafoil Canopy Curving Process and Application by LBM. Aerospace. 2024; 11(2):118. https://doi.org/10.3390/aerospace11020118
Chicago/Turabian StyleWang, Yi, and Chunxin Yang. 2024. "Simulation and Analysis of Aerodynamic Characteristics during Parafoil Canopy Curving Process and Application by LBM" Aerospace 11, no. 2: 118. https://doi.org/10.3390/aerospace11020118
APA StyleWang, Y., & Yang, C. (2024). Simulation and Analysis of Aerodynamic Characteristics during Parafoil Canopy Curving Process and Application by LBM. Aerospace, 11(2), 118. https://doi.org/10.3390/aerospace11020118






