Neural Field-Based Space Target 3D Reconstruction with Predicted Depth Priors

Abstract

As space technology advances, an increasing number of spacecrafts are being launched into space, making it essential to monitor and maintain satellites to ensure safe and stable operations. Acquiring 3D information of space targets enables the accurate assessment of their shape, size, and surface damage, providing critical support for on-orbit service activities. Existing 3D reconstruction techniques for space targets, which mainly rely on laser point cloud measurements or image sequences, cannot adapt to scenarios with limited observation data and viewpoints. We propose a novel method to achieve a high-quality 3D reconstruction of space targets. The proposed approach begins with a preliminary 3D reconstruction using the neural radiance field (NeRF) model, guided by observed optical images of the space target and depth priors extracted from a customized monocular depth estimation network (MDE). A NeRF is then employed to synthesize optical images from unobserved viewpoints. The corresponding depth information for these viewpoints, derived from the same depth estimation network, is integrated as a supervisory signal to iteratively refine the 3D reconstruction. By exploiting MDE and the NeRF, the proposed scheme iteratively optimizes the 3D reconstruction of spatial objects from seen viewpoints to unseen viewpoints. To minimize excessive noise from unseen viewpoints, we also incorporate a confident modeling mechanism with relative depth ranking loss functions. Experimental results demonstrate that the proposed method achieves superior 3D reconstruction quality under sparse input, outperforming traditional NeRF and DS-NeRF models in terms of perceptual quality and geometric accuracy.

1. Introduction

As space technology continues to advance, a variety of spacecrafts with different shapes and functions have been launched into space. Some satellites may malfunction or fail due to design, manufacturing, or environmental issues, becoming space debris. This not only results in the waste of orbital resources but also poses a threat to the safety of space activities. To ensure that human space activities can be conducted in a safe and controlled manner and to reduce resource wastage, on-orbit servicing technology can be employed to maintain spacecraft. One of the key steps in on-orbit servicing is obtaining information about the target spacecraft. The most direct, accurate, and complete way to describe a space target is by establishing its three-dimensional (3D) model. Acquiring 3D information of space targets can provide robust support for various space applications, including on-orbit servicing, collision avoidance, autonomous rendezvous, and satellite docking.

Currently, there are two main methods used for the 3D reconstruction of space targets. The first method is laser point cloud-based 3D reconstruction [1,2], which uses devices such as LiDAR to directly measure the target, obtaining depth information of the scene object. This depth information is then used to achieve 3D reconstruction. Su et al. [3] proposed a method for modeling the line array laser imaging of space targets by analyzing the motion state of space targets and the imaging mechanism of linear array LiDAR. Zhang et al. [4] introduced a 3D reconstruction method based on range scanning for SAL (synthetic aperture LiDAR) targets, using an overlapping imaging of adjacent image targets to achieve 3D reconstruction. Wang et al. [5] proposed an on-orbit LiDAR imaging simulation process for complex, unstable, and non-cooperative space targets, extracting the visible region point cloud from the target using an area-based method. While measurement devices such as LiDAR can directly obtain accurate 3D surface and dimensional information of a target, they cannot capture surface texture details, which complicates further applications such as determining target structures or identifying specific module functions. Additionally, LiDAR and similar equipment tend to have a large size, weight, and power consumption, and their performance is heavily dependent on the material properties of the target surface, limiting their application scenarios. The second method is image sequence-based 3D reconstruction. This method uses traditional cameras to capture overlapping multi-view image sequences of the target from multiple angles as the servicing spacecraft flies around and approaches the space target, which are then used to reconstruct a 3D model of the target. Chen et al. [6] studied a 3D reconstruction method based on sequential images, which can provide structural information for components such as solar panels and antennas. Yang et al. [7] proposed a multi-exposure image fusion method to handle a wide dynamic range for unstable and non-cooperative space targets, using fused images for 3D reconstruction. Li et al. [8] proposed a joint sparse prior constraint blind deconvolution algorithm based on sparse representation, which can better restore the edges and texture details of space target images. Image sequence-based 3D reconstruction methods are more flexible and practical, as they use traditional cameras with a low cost, small size, light weight, and low power consumption. These methods can directly capture the color and texture of the target and provide estimations of the relative position and attitude between the detector and the space target.

Despite the broader applicability of image sequence-based 3D reconstruction algorithms for space targets, existing methods still struggle to effectively reconstruct these targets due to the unique characteristics of both the space targets and the space environment. Traditional techniques require extracting feature points from the optical images of space targets and establishing correspondences between these feature points across adjacent images. However, common space targets, such as satellites, exhibit non-Lambertian characteristics under varying lighting conditions, leading to different radiative energy levels for the same point on the object’s surface when viewed from different angles, resulting in unsuccessful matches. Furthermore, the symmetric structures of artificial satellites often result in multiple groups of highly similar pixel blocks, making it difficult to distinguish them and causing errors in stereo matching. To address the issue of erroneous reconstruction caused by repetitive textures in space target images, Zhang et al. [9] proposed a novel strategy for recovering the 3D scene structure based on motion information. This approach utilizes the temporal order of sequential images acquired from the space target as prior information, incrementally incorporating new images for 3D reconstruction. Wang et al. [10] tackled the problems of incorrect or insufficient feature point matching caused by the structural symmetry of space targets and their non-Lambertian imaging characteristics by proposing a method based on the MVSNet deep learning network. This approach employs deep learning techniques to extract high-level semantic information from images, thereby improving the accuracy of 3D reconstruction for space targets.

Although existing 3D reconstruction methods for space targets have optimized feature matching steps by considering characteristics like repetitive textures and structural symmetry to improve reconstruction accuracy, they still do not fully account for the unique aspects of the space environment and the space targets. Recovering the 3D structure of a target from 2D images is an ill-posed problem, typically requiring a dense set of images from numerous perspectives as input. However, due to the irregular motion of space targets, safety concerns in space activities, and varying lighting conditions, obtaining these images can be challenging. In practice, we often rely on a limited number of images captured from sparse angles, which restricts feature point extraction. The significant differences in perspectives between adjacent images can hinder feature point matching, resulting in low reconstruction accuracy, incomplete models, and, in some cases, the inability to achieve successful 3D reconstruction.

To tackle the challenges of low reconstruction accuracy and incomplete structures in the 3D reconstruction of space targets from limited viewpoints, we introduce a novel NeRF-based 3D reconstruction technique tailored for space targets. The primary contributions of this work are as follows:

• New 3D reconstruction approach integrating monocular depth estimation with a NeRF: This method leverages a monocular depth estimation network to extract depth information from space target images captured from sparse viewpoints. The extracted depth information is used as prior knowledge to guide the NeRF-based 3D reconstruction process, significantly enhancing reconstruction quality under limited viewpoint conditions.
• Incorporation of unseen viewpoint depth information to improve reconstruction accuracy: Following the initial reconstruction, additional depth data from unseen viewpoints are incorporated using depth ranking loss and confidence modeling. This optimization reduces noise in the reconstruction process and substantially enhances geometric accuracy.
• High-quality reconstruction with minimal input data: Compared to the conventional NeRF and DS-NeRF methods, this technique sustains high reconstruction quality even with sparse viewpoints, demonstrating superior robustness and adaptability. This advantage is especially beneficial in scenarios with minimal input images, capturing both the detailed structure and geometric fidelity of space targets effectively.

The structure of this article is as follows: Section 2 introduces the monocular depth estimation network and the NeRF model involved in this study. Section 3 presents the proposed method and its implementation steps. Section 4 discusses the experimental results and provides an analysis.

2. Related Works

Our method utilizes a monocular depth estimation network to extract depth information from space target images and applies neural radiance field technology for 3D reconstruction. Below, we provide an overview of the depth estimation network and the NeRF framework.

2.1. Monocular Depth Estimation Network

Monocular depth estimation networks are a type of neural network model used to predict depth information from a single image. These networks can be categorized into two types, namely relative depth estimation networks and absolute depth estimation networks. Relative depth estimation networks [11,12,13] predict the relative position between pixel pairs in an image, offering good generalization performance. However, their effectiveness is limited in 3D reconstruction due to the lack of scale information [14]. On the other hand, absolute depth estimation networks [15,16,17] directly estimate the absolute distance between objects and the camera, making them more suitable for applications like 3D reconstruction. However, these networks exhibit weaker generalization across different environments and are less adaptable to diverse datasets, especially when there are significant variations in scene scale (e.g., between ground and space environments). A recent work, ZoeDepth [18], cleverly combines the strengths of both relative and absolute depth estimation. ZoeDepth first uses an encoder–decoder backbone to perform relative depth prediction and then adds the proposed metric bins module to the decoder to obtain an absolute depth prediction head. For each dataset, a separate head is added to estimate the absolute depth. Through this unique network design and training strategy, ZoeDepth maintains the robustness of relative depth estimation while achieving precise absolute depth estimation.

However, these models are primarily trained on datasets focused on terrestrial environments. Space target images often exhibit unique material reflections, non-Lambertian phenomena, and varying lighting conditions, which are uncommon in terrestrial datasets. These differences hinder existing networks from accurately estimating depth information in space target images. To improve the estimation accuracy of space targets, we conducted further research based on ZoeDepth.

2.2. Neural Radiance Fields (NeRF)

A neural radiance field (NeRF) [19] is an advanced technology that implicitly represents 3D scenes through neural networks. A NeRF models a 3D scene as a continuous mapping from 3D positions and 2D viewing directions to RGB colors and density values, using deep learning techniques to extract geometric shapes and the texture information of objects from images captured from multiple viewpoints. This information is then utilized to generate a continuous 3D radiance field, allowing the 3D model to be rendered from any angle and distance. The 3D models generated by a NeRF exhibit higher quality and realism, displaying true surface and texture details at any angle and distance. Building on the NeRF, the GRAF [20] generates high-fidelity multi-view consistent images from unposed 2D images by using neural radiance fields, addressing the limitations of voxel-based methods, such as memory inefficiency and discretization artifacts. Instant neural graphics primitives (NGPs) [21] further enhance NeRF-based techniques by introducing a multiresolution hash encoding, which accelerates neural network training across various tasks, achieving high-quality results in mere seconds using a single GPU. Meanwhile, D-NeRF [22] extends the NeRF framework to handle dynamic scenes, enabling a novel view synthesis of objects undergoing both rigid and non-rigid deformations using only monocular input without requiring ground truth geometry or multi-view images.

In recent years, some researchers have begun exploring the application of NeRFs in the context of space targets. Anne et al. [23] investigated the use of NeRF and GRAF models to generate 3D models of spacecraft from 2D images, comparing their performance in generating novel viewpoints and reconstructing 3D shapes, particularly in the context of aerospace missions. Their study found that the NeRF outperformed in image accuracy, while the GRAF could generate precise views and details without requiring pose information. Bu et al. [24] proposed a new method based on the NeRF for reconstructing 3D models of space targets from wide baseline optical image sequences, addressing the limitations of traditional methods when dealing with poorly textured images and large viewpoint discrepancies. Caruso et al. [25] further explored the application effects of NeRF, instant NeRF, and D-NeRF algorithms in the high-fidelity 3D reconstruction of non-cooperative space targets.

However, these studies have only provided preliminary evaluations of the effectiveness of neural radiance field technology for space target reconstruction, with a heavy reliance on a large number of densely captured images from multiple viewpoints. To overcome this limitation, we further investigate NeRF-based 3D reconstruction methods for space targets, focusing on achieving high-quality reconstructions even with sparse or limited viewpoint coverage.

3. Method

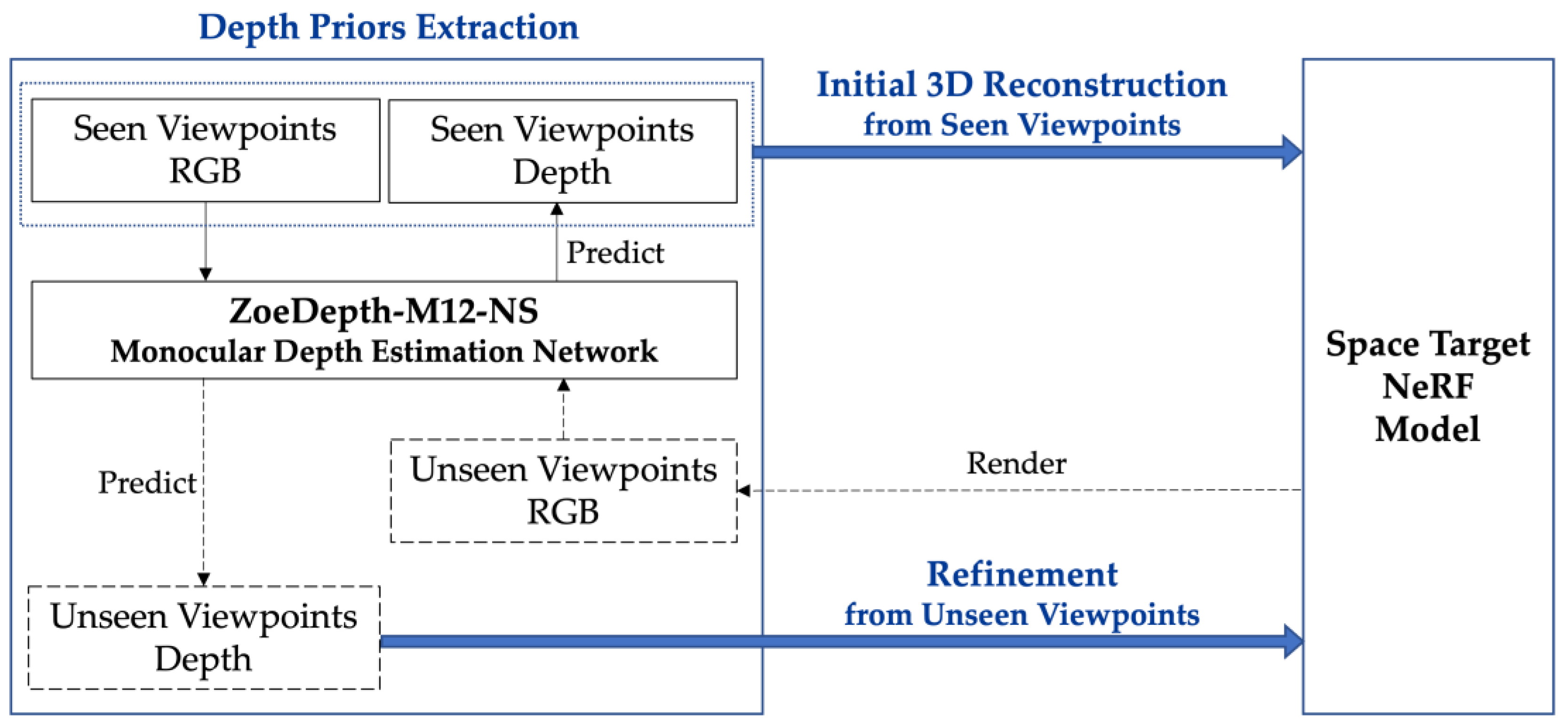
This article aims to combine monocular depth estimation with neural radiance fields by introducing depth information from seen viewpoint images of space targets and depth information from NeRF-rendered images at unseen viewpoints. The NeRF model is optimized using depth supervision, enabling a high-quality 3D reconstruction of space targets under few-shot conditions. The technical workflow is shown in Figure 1.

The method proposed in this article is summarized as follows: First, we constructed a space target dataset and customized a depth estimation module specifically designed for space targets based on the ZoeDepth model. This resulted in the creation of a monocular depth estimation network named ZoeDepth-M12-NS, which enabled a more accurate extraction of depth information from space target images. During the 3D reconstruction process of space targets, we initially used ZoeDepth-M12-NS to process optical images from seen viewpoints to obtain the corresponding depth information. Using these images and depth data, we performed a preliminary 3D reconstruction based on the neural radiance field framework. Then, we rendered optical images of the space target from unseen viewpoints using the neural radiance field and then employed ZoeDepth-M12-NS to obtain depth information from these new viewpoints. Subsequently, we used the depth information from these unseen viewpoints as supervision to further optimize the 3D reconstruction results of the space target, ultimately achieving high-precision 3D reconstruction in sparse-viewpoint scenarios.

3.1. Depth Prior Extraction by ZoeDepth-M12-NS

In this study, to more accurately extract depth information from space targets, we first constructed a monocular depth estimation dataset specifically designed for space targets. Based on this dataset, we optimized the absolute depth estimation head of the ZoeDepth model, aiming to effectively extract both relative and absolute depth information from the images.

Existing depth estimation models are normally trained on datasets of common ground scenes and perform poorly when handling the unique characteristics of space targets, such as complex lighting conditions, non-Lambertian reflection properties, and symmetrical structures. To address this, we used Blender (Version 3.6.0) to create a monocular depth estimation dataset specifically designed for space targets. This dataset includes 50 different spacecraft models sourced from NASA’s 3D Resources, covering a range of shapes, materials, and structures, including satellites, space station modules, and other spacecraft components. To further improve the fidelity of the simulations, we added Gaussian noise to the simulated images, representing sensor-related disturbances, such as thermal and read-out noise and Poisson noise, which simulates photon noise caused by statistical fluctuations in photon arrivals under low-light conditions. To ensure the diversity of the dataset and prevent overfitting, we preprocessed all models by randomly scaling them to sizes ranging from 100 mm to 1000 mm and assigned them different material properties, such as diffuse reflection, specular reflection, and metallic surfaces, to realistically simulate the surface characteristics of space targets. During the simulation process, the camera was randomly moved within a radius of 1500 mm ± 500 mm from the target, with its focus always pointed toward the space target. This setup ensured the collection of rich image data from multiple viewpoints. Each model generated 200 pairs of sequential images, including RGB images and corresponding depth maps. Through this multi-view, multi-material, and varied lighting simulation setup, we created a diverse and high-quality dataset specifically for the depth estimation task. The simulation scene is shown in Figure 2, and examples from the generated dataset are shown in Figure 3.

We further optimized the ZoeDepth-M12-N model for the absolute depth estimation of space targets. ZoeDepth-M12-N is a robust baseline model that integrates an encoder–decoder backbone, pre-trained on 12 diverse datasets (M12) for relative depth estimation, with an absolute depth prediction head fine-tuned on the NYU Depth v2 dataset for metric depth prediction in indoor scenes. Built upon a MiDaS-based architecture, it leverages advanced transformer backbones like BEiT384-L and a metric bins module with adaptive binning, enabling state-of-the-art performance in depth estimation tasks. However, the absolute depth prediction head was primarily trained for terrestrial and indoor environments, which differ significantly from the unique depth distributions and environmental conditions characteristic of space targets.

To address these challenges, we enhanced the ZoeDepth-M12-N model by introducing an additional absolute depth estimation head, inspired by the original ZoeDepth design, to better capture the unique depth distribution characteristics of space targets. The head of ZoeDepth utilizes a metric bins module based on adaptive binning, which can dynamically adjust the range and precision of depth estimation, making it better suited to the depth distribution characteristics of space targets. This improves the accuracy of depth prediction under complex lighting conditions and varied geometries. Specifically, the metric bins module is capable of adaptively dividing the depth range into bins based on the features of the input image, then estimating absolute depth values according to these bins. This approach allows the model to flexibly adjust the granularity of depth estimation based on the actual depth distribution of the space target, avoiding estimation errors caused by a fixed depth range.

We conducted end-to-end fine-tuning of the model to better accommodate the depth estimation needs specific to space targets. In the subsequent steps, we used this optimized ZoeDepth model (referred to as ZoeDepth-M12-NS or ${ZD}_{st}\left(·\right)$) to process the space target images to obtain absolute depth information.

3.2. Initial 3D Reconstruction by NeRF-SD

We first used information from seen viewpoints to perform an initial 3D reconstruction of the space target based on neural radiance fields.

NeRFs use a multi-layer perceptron (MLP) neural network $F_{\mathsf{\Theta }}$ to describe the radiance $\mathit{c}=\left(r,g,b\right)$ emitted from each point $\mathit{x}=\left(x,y,z\right)$ in the scene in each direction $\mathit{d}=\left(\theta ,\mathrm{\varnothing }\right)$, along with the volume density $\sigma$ at each point, expressed as

$$F_{\mathsf{\Theta }}\left(\gamma \left(\mathit{x}\right),\gamma \left(\mathit{d}\right)\right)\to \left(\mathit{c},\sigma \right)$$

(1)

Here, $\gamma \left(\mathit{x}\right)$ and $\gamma \left(\mathit{d}\right)$ are positional encodings used to enhance the network’s ability to represent high-frequency details. When rendering a novel view, the NeRF samples along every ray cast from the camera into the scene and computes the color and depth of each ray using volumetric rendering methods.

For a ray ${\mathit{r}}_{\mathit{p}}\left(t\right)=\mathit{o}+t{\mathit{d}}_{\mathit{p}}$, points are sampled along the ray between the near and far boundaries, accumulating the volume density $\sigma$ and color $\mathit{c}$. The corresponding color $\widehat{I}\left(\mathit{p}\right)$ and depth $\widehat{D}\left(\mathbf{p}\right)$ for that ray can be calculated using the following formulas:

$$\widehat{I}\left(\mathit{p}\right)={\int }_{t_1}^{t_2}\sigma \left({\mathit{r}}_{\mathit{p}}\left(t\right)\right)·c\left({\mathit{r}}_{\mathit{p}}\left(t\right),\mathit{d}\right)·T\left(t\right)·dt$$

(2)

$$\widehat{D}\left(\mathbf{p}\right)={\int }_{t_1}^{t_2}T\left(t\right)·\sigma \left({\mathit{r}}_{\mathit{p}}\left(t\right)\right)·t·dt$$

(3)

where $T\left(t\right)=\exp \left(-{\int }_{t_1}^t\sigma \left({\mathit{r}}_{\mathit{p}}\left(u\right)\right)·du\right)$ represents the accumulated transmittance along the ray from $t_1$ to $t_2$.

During training, the NeRF adjusts the MLP parameters by minimizing the difference between the rendered images $\widehat{I}\left(\mathit{p}\right)$ from the NeRF and the ground truth images $I\left(\mathit{p}\right)$ using the following loss function:

$$L_{color}=\sum _{I_i\in S}\sum _{p\in R}{ \left|\left|I_i\left(\mathbf{p}\right)-{\widehat{I}}_i\left(\mathbf{p}\right)\right|\right|}_2^2$$

(4)

where $S$ represents the set of input views used during training and $R$ is the set of ray pixels for training.

Under few-shot conditions, neural radiance fields (NeRFs) are prone to inaccurate geometric reconstructions and texture artifacts. To improve the accuracy of 3D reconstruction for space targets, we incorporated the absolute depth information obtained from ZoeDepth as pseudo-prior information and introduced a depth loss function [26] to constrain NeRF training, enabling it to more accurately represent the geometric structure of the space target. We named this method NeRF-SD.

For each input image $I_i$ from a seen viewpoint, the optimized ZoeDepth model ${ZD}_{st}\left(·\right)$ was used to obtain the pseudo-absolute depth prior, denoted as $D_i={ZD}_{st}\left(I_i\right)$. During training, NeRF parameters were further optimized by minimizing the error between the NeRF-rendered depth $\widehat{D}$ and the pseudo-depth prior $D_i$. The depth loss function used is expressed as follows:

$${\mathcal{L}}_{\mathrm{depth}}=\sum _{I_i\in \mathrm{S}}\sum _{p\in P}||D_i\left(\mathit{p}\right)-{\widehat{D}}_i\left(\mathbf{p}\right)||$$

(5)

where $P$ represents the set of all pixels in the image and $\mathit{p}$ denotes a pixel in the image. This loss function helps ensure that the NeRF accurately captures the geometric structure of the space target.

By combining the depth loss with the color loss, we perform end-to-end optimization of the entire neural radiance field. The final loss function is as follows:

$${\mathcal{L}}_{\mathrm{seen}}=L_{color}\left(\mathbf{p}\right)+\lambda {\mathcal{L}}_{\mathrm{depth}}\left(\mathbf{p}\right)$$

(6)

where $\lambda$ is the weight coefficient of the depth loss. In our experiments, we set $\lambda =0.2$. Through this joint optimization, the NeRF can more accurately reconstruct the geometric structure of the target object under few-shot conditions.

3.3. Progressive Refinement by NeRF-SD-UD

Following the preliminary reconstruction, we introduced depth information from unseen viewpoints of the space target to constrain NeRF training, thereby further optimizing the 3D reconstruction results.

The depth maps for unseen viewpoints were obtained by processing RGB images rendered by the NeRF through the ZoeDepth model. This indirect estimation approach can introduce cumulative errors and uncertainties, which become more pronounced, especially with significant viewpoint changes. To prevent these uncertainties from introducing excessive noise and destabilizing the optimization process, we introduced a confidence mechanism [27] to validate the accuracy and reliability of each ray before distillation.

For an unseen viewpoint $l$, we first render the corresponding RGB image ${\widehat{I}}_l^{\mathrm{*}}$ and depth map ${\widehat{D}}_l^{\mathrm{*}}$ through NeRF. Next, we process the rendered optical image ${\widehat{I}}_l^{\mathrm{*}}$ with ZoeDepth to obtain the estimated depth map ${\widehat{D}}_l={ZD}_{st}\left({\widehat{I}}_l^{\mathrm{*}}\right)$. We then project ta pixel $\mathit{p}$ from the unseen viewpoint $l$ to the corresponding pixel ${\mathit{p}}_{l\to i}$ in the seen viewpoint $i$ using the following projection formula:

$${\mathit{p}}_{l\to i}~ K{R}_{l\to i}{\widehat{D}}_l\left(\mathit{p}\right)K^{-1}\mathit{p}$$

(7)

where $K$ is the camera’s intrinsic parameter matrix, and $R_{l\to i}$ is the transformation matrix from the unseen viewpoint $l$ to the seen viewpoint $i$.

Next, we determine the confidence $M_l\left(\mathit{p}\right)$ for the ray passing through pixel $\mathit{p}$ at the unseen viewpoint $l$ by checking whether the difference between the estimated depth ${\widehat{D}}_l\left(\mathit{p}\right)$ and the corresponding pixel’s estimated depth ${\widehat{D}}_i\left({\mathit{p}}_{l\to i}\right)$ at the seen viewpoint $i$ is within an acceptable range:

$$M_l\left(\mathit{p}\right)=[ {\left|\right|\widehat{D}}_l\left(\mathit{p}\right)-{\widehat{D}}_i\left({\mathit{p}}_{l\to i}\right)||<\tau ]$$

(8)

where $\tau$ is the threshold parameter for confidence and [•] indicates whether the condition is met (1 if true, 0 if false).

Through this process, we can effectively filter out geometrically inconsistent regions, avoiding excessive noise when incorporating depth information from new viewpoints, thereby enhancing the reconstruction quality and stability.

To further reduce noise when incorporating depth information from unseen viewpoints to constrain NeRF training, we relaxed the depth supervision by adopting a more robust depth ranking loss function [28] ${\mathcal{L}}_{\mathrm{rank}}$ for the unseen viewpoint. This function supervises the consistency of relative depth between two points rather than enforcing absolute depth values, which is formulated as follows:

$${{\mathcal{L}}_{\mathrm{unseen}}=\mathcal{L}}_{\mathrm{rank}}=\sum _{{\widehat{I}}_l^{*}\in \mathrm{U}}{M}_l\left(\mathit{p}\right) \sum _{{\widehat{D}}_l\left(\mathit{p}1\right)\le {\widehat{D}}_l\left(\mathit{p}2\right)}\max \left({\widehat{D}}_l^{*}\left(\mathit{p}1\right)-{\widehat{D}}_l^{*}\left(\mathit{p}2\right)+m, 0\right)$$

(9)

where two depth pixels are randomly sampled from ${\widehat{D}}_l$, denoted as ${\widehat{D}}_l\left(\mathit{p}1\right)$ and ${\widehat{D}}_l\left(\mathit{p}2\right)$, and ${\widehat{D}}_l\left(\mathit{p}1\right)\le {\widehat{D}}_l\left(\mathit{p}2\right)$. If the depth ranking in ${\widehat{D}}_l^{\mathrm{*}}$ contradicts this, i.e., ${\widehat{D}}_l^{\mathrm{*}}\left(\mathit{p}1\right)>{\widehat{D}}_l^{\mathrm{*}}\left(\mathit{p}2\right)$ while ${\widehat{D}}_l\left(\mathit{p}1\right)\le {\widehat{D}}_l\left(\mathit{p}2\right)$, we penalize the NeRF. This ensures that the NeRF’s rendered depth ordering fits the depth ordering obtained from ZoeDepth-M12-NS. Here, $U$ represents the set of images from unseen viewpoints and $m$ is the allowable depth ranking error, which is set to $m=1.0\times {10}^{-4}$ in our experiments.

We then combine the losses from seen and unseen viewpoints to continue optimizing the entire neural radiance field end-to-end. The final loss function is as follows:

$${\mathcal{L}}_{\mathrm{refinement}}={{\mathcal{L}}_{\mathrm{seen}}+\mu \mathcal{L}}_{\mathrm{unseen}}$$

(10)

where $\mu$ is the weight coefficient for the unseen viewpoint loss. In our experiments, we set $\mu =0.02$.

4. Experiments and Results

We validated our method by selecting a representative real-world task, namely the 3D reconstruction of non-cooperative defunct satellites. Before clearing large space debris, such as defunct rockets or satellites, it is often necessary to capture images of the target through fly-around maneuvers, followed by 3D reconstruction of the space object. This reconstruction provides critical information for subsequent missions, such as capturing the target and removing it from low Earth orbit. However, satellites in low Earth orbit typically travel at speeds of 7 to 8 km per second. At such high velocities, the tasks of locating, approaching, and flying around non-cooperative defunct satellites to collect data become highly challenging. In practice, due to uncertainties in the motion of space objects and strict safety requirements in space activities, only a limited number of sparse-view images of defunct satellites can usually be captured. This limitation significantly hampers the 3D reconstruction process, often resulting in incomplete or low-quality 3D models of the defunct satellites or even failure to reconstruct them at all. By conducting experiments in this real-world scenario, our proposed model could demonstrate its ability to overcome these challenges and achieve high-quality 3D reconstruction from sparse views under such demanding conditions.

This section details the experimental setup, the process of depth prior extraction, performance comparisons with other models, and an ablation analysis of how core components affect reconstruction quality.

4.1. Experimental Setup

4.1.1. Experimental Materials

We selected a Beidou satellite model as the simulated space target. The Beidou satellite includes typical components of space targets, such as a roughly cubical main body, parabolic antennas, and solar panels. The model was constructed at a 1:35 scale with rich textures and detailed features, making it well suited for evaluating reconstruction performance.

We built an imaging platform to simulate fly-around imaging of a space target in the experiments, which is shown in Figure 4a. The platform features a fly-around turntable with a central platform, a rotating arm, and imaging equipment. The Beidou satellite model is placed on the central platform, while the imaging equipment, mounted on the rotating arm, moves around the target to mimic fly-around observations. To simulate a space environment, the turntable is enclosed in a 4 m × 4 m × 2 m steel frame covered with low-reflectivity black fabric. Lighting was provided by a Sidande LED panel set to a 5600 K color temperature and a brightness of 3000 lumens.

All experiments were performed on a computational setup comprising PyTorch 2.0.0 as the deep learning framework, Python 3.8 running on Ubuntu 20.04, and CUDA 11.8 for GPU acceleration. The hardware included an NVIDIA GeForce RTX 2080 Ti GPU with 11 GB of memory (NVIDIA, Santa Clara, CA, USA), a 12-core Intel^® Xeon^® Platinum 8255C CPU clocked at 2.50 GHz (Intel Corporation, Santa Clara, CA, USA), and 40 GB of RAM (Samsung, Suwon, South Korea).

4.1.2. Datasets

To train and evaluate the performance of our method for space target reconstruction in sparse-viewpoint scenarios, we created four datasets. All datasets were captured using our custom-built space target simulation imaging platform. As shown in Figure 4, we selected the Beidou navigation satellite model as the simulated space target, placing it at the center of the imaging platform. Using the main camera and LiDAR scanner of an iPhone 14 Pro Max, which enable the simultaneous capture of optical images and depth information, we performed 360° circular shooting at a radius of 1000 ± 50 mm from the target. The main camera of the iPhone 14 Pro Max features a 48-megapixel sensor with a 24 mm focal length and an ƒ/1.78 aperture, ensuring high-resolution optical image capture. The LiDAR scanner was used to obtain depth maps from observed viewpoints solely for evaluating the performance of the proposed monocular depth estimation network. It was not utilized as input data for the 3D reconstruction of space targets. The distance corresponds to a scaled-down equivalent of the typical fly-around distance of 25 to 50 m for real space targets, given the 1:35 scale of the model. The Polycam app (version 3.5.2 for iOS) was used to capture and export raw data, including optical images, depth maps, and camera parameters from the recorded viewpoints. All images were preprocessed by scaling them to a resolution of 640 × 480 and setting the background to black to better simulate the space environment.

The four datasets differ only in the number of captured viewpoints; images were taken at intervals of 10°, 20°, and 40°, creating training and validation sets with 36, 18, and 9 images, respectively, named 36-v, 18-v, and 9-v. Additionally, we created a test set by capturing images at 5° intervals, consisting of 72 images from different viewpoints than those used in the training and validation sets. Figure 4 shows examples of images from the dataset.

4.1.3. Implementation Details

Our method was implemented based on the official NeRF Studio framework [29] and utilized the Adam optimizer [30] for training. To ensure effective model convergence, we employed an exponential decay strategy, gradually reducing the learning rate from $5\times {10}^{-3}$ to $5\times {10}^{-5}$. During training, the batch size was set to 2048. For each scene, we performed up to 10,000 iterations of training.

4.1.4. Evaluation Metrics

For evaluating the accuracy of depth prior estimations of space targets, we computed the relative error (REL), root mean squared error (RMSE), and ${log}_{10}$error between the estimated depth and the ground truth depth. Lower values of REL, RMSE, and log10 error indicate better accuracy in depth prior estimations. The formulas for these metrics are as follows:

$$REL={\displaystyle \frac{1}{M}}\sum _{i=1}^M{\displaystyle \frac{{|d}_i-{\widehat{d}}_i| }{d_i}}$$

(11)

$$RMSE=\sqrt{{\displaystyle \frac{1}{M}}\sum _{i=1}^M{\left(d_i-{\widehat{d}}_i\right)}^2}$$

(12)

$$log10 error={\displaystyle \frac{1}{M}}\sum _{i=1}^M\left|{log}_{10}{d}_i-{log}_{10}{\widehat{d}}_i\right|$$

(13)

where $d_i$ and ${\widehat{d}}_i$ are the ground truth depth and predicted depth of the $i$-th pixel, respectively, and $M$ is the total number of pixels in the image.

In terms of the reconstruction accuracy for space targets, we evaluated the 3D reconstruction performance in sparse scenarios from two aspects, namely texture geometry reconstruction accuracy and structural geometry reconstruction accuracy.

For texture reconstruction accuracy, the evaluation was based on the quality of the rendered images. We used three image quality assessment metrics, the PSNR, SSIM, and LPIPS. The PSNR (peak signal-to-noise ratio) measures the difference between the reconstructed image and the reference image by calculating the mean squared error (MSE) between pixels—a higher PSNR value indicates better image quality. The SSIM (structural similarity index) evaluates the similarity between images in terms of luminance, contrast, and structure—a higher SSIM value indicates that the reconstructed image is closer to the reference image in perceived quality. The LPIPS (learned perceptual image patch similarity) is a deep learning-based perceptual similarity metric—a lower LPIPS value indicates that the reconstructed image is more visually similar to the reference image.

For structural geometry reconstruction accuracy, we use Chamfer distance (CD) to measure the geometric differences between the NeRF-generated point cloud and the target point cloud. CD calculates the distance from each point in one point cloud to the nearest point in another point cloud—a lower CD value indicates that the point cloud geometries are more similar, reflecting better performance in geometric reconstruction.

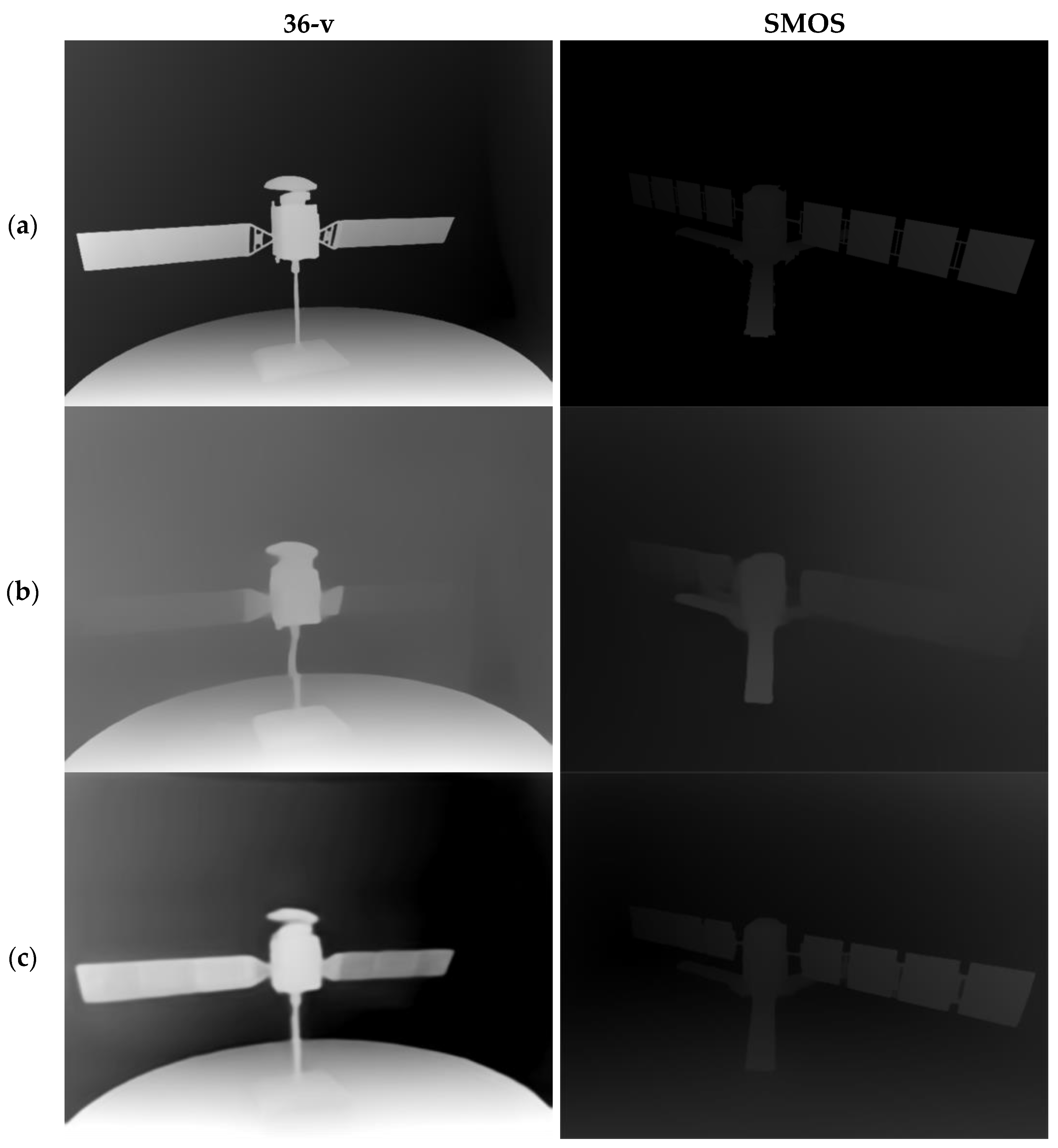
4.2. Depth Prior Extraction

We conducted comparative experiments between our fine-tuned ZoeDepth-M12-NS model, which includes an absolute depth estimation head for space targets, and the baseline model, ZoeDepth-M12-N [18], on the 36-v dataset and a publicly available dataset provided by Anne [23], which includes optical images and corresponding depth maps of two satellites (SMOS and CUBESAT). The experimental results are shown in

Table 1. Accuracy of estimated depth priors.

Method	$\mathbf{REL} \downarrow$		$\mathbf{RMSE} \downarrow$		$\mathbf{log}10 \mathbf{Error} \downarrow$
	36-v	SMOS	36-v	SMOS	36-v	SMOS
ZoeDepth-M12-N	0.127	0.137	0.562	0.573	0.054	0.055
ZoeDepth-M12-NS	0.109	0.117	0.438	0.509	0.047	0.048

and Figure 5.

As shown in Table 1, in the comparison experiment on the 36-v dataset, the REL (relative error) of the ZoeDepth-M12-NS model decreased by 14.2%, the RMSE (root mean squared error) was reduced by 22%, and the log10 error dropped by 13%. Similarly, on the SMOS dataset, the ZoeDepth-M12-NS model achieved an REL reduction of 14.6%, an RMSE reduction of 11.1%, and a log10 error reduction of 12.7%. These results indicate that ZoeDepth-M12-NS significantly outperformed the untuned ZoeDepth-M12-N model in estimating the depth prior for space targets.

More accurate depth prior estimation results provide a more reliable foundation for the subsequent 3D reconstruction of space targets. The higher the precision of the depth prior, the more accurately the geometric structure of the object’s surface can be reconstructed, effectively reducing reconstruction errors and improving the final quality of the 3D model. This is particularly critical when performing the 3D reconstruction of space targets under few-shot viewpoints, where high-quality depth priors can significantly enhance the reconstruction results, better capturing and restoring the model’s details. In Section 4.4, we further validate the contribution of ZoeDepth-M12-NS to the final 3D reconstruction of space targets through ablation experiments.

4.3. Space Target Reconstruction

In this section, we compare our method with the NeRF [14] and DS-NeRF [23], which also incorporates depth supervision in the NeRF. In the experiments, both our method and the DS-NeRF use the depth information estimated by ZoeDepth-M12-NS as depth priors. We evaluate the texture reconstruction results of space targets using the PSNR, SSIM, LPIPS, and rendered images from test viewpoints. The geometric structure reconstruction results of space targets are evaluated using Chamfer distance (CD) and visualized point clouds.

Table 2. Experimental results of texture reconstruction for space targets.

Method	$\mathbf{PSNR} \uparrow$			$\mathbf{SSIM} \uparrow$			$\mathbf{LPIPS} \downarrow$
	36-v	18-v	9-v	36-v	18-v	9-v	36-v	18-v	9-v
NeRF	21.913	19.259	15.694	0.843	0.833	0.579	0.331	0.664	0.74
DS-NeRF	23.819	22.545	19.787	0.857	0.88	0.82	0.274	0.308	0.645
Our Methods	25.141	24.229	21.394	0.918	0.858	0.823	0.175	0.23	0.395

and Figure 6 present the results of texture reconstruction for space targets. As shown in Table 2, our method significantly outperforms both the NeRF and DS-NeRF under different numbers of input viewpoints (36, 18, and 9 images), maintaining high-quality 3D reconstruction even in sparse-viewpoint scenarios, demonstrating a clear advantage. For example, with only nine input viewpoints, our method achieves a PSNR of 21.394 and an SSIM of 0.823, which is almost equivalent to the NeRF’s performance with 36 input viewpoints (PSNR = 21.913, SSIM = 0.843). This result indicates that our method can effectively capture and reconstruct the geometric and texture details of space targets even with sparse input viewpoints, delivering reconstruction quality comparable to that achieved with more viewpoints.

A further comparison of the robustness of different methods as the number of input viewpoints decreases reveals that the reconstruction quality of the NeRF and DS-NeRF significantly deteriorates under sparse-viewpoint conditions, whereas our method demonstrates stronger robustness when input viewpoints are reduced. For example, when the number of input viewpoints is reduced from 36 to 9, the NeRF’s PSNR drops sharply from 21.913 to 15.694, a decrease of 28.36%. Similarly, the DS-NeRF’s PSNR decreases from 23.819 to 19.787, a 16.93% reduction. In contrast, our method’s PSNR only decreases from 25.141 to 21.394, a reduction of 14.90%. This demonstrates that our method maintains more stable reconstruction accuracy in sparse-viewpoint scenarios.

Figure 6 visualizes the experimental results of the 9-v dataset, showing that with nine input images, our method significantly outperforms the NeRF and DS-NeRF. The NeRF’s rendering results are blurry, with severe color distortion and object contour blurring, particularly at the edges and detailed areas of the object. The DS-NeRF improves the reconstruction to some extent but still suffers from noticeable noise and blurriness, especially in the rendering of object surfaces and details. In contrast, our method produces results that are much closer to the real scene, with sharper edges and more accurate color reproduction. This improvement is attributed to the integration of absolute depth information, relative depth ranking loss, and confidence modeling in our approach, allowing the model to maintain high reconstruction quality and detail accuracy even with sparse input viewpoints.

Table 3. Experiment results of geometric structure reconstruction for space targets.

Method	$\mathbf{CD} ({\times 10}^{-3}$$) \downarrow$
	36-v	18-v	9-v
NeRF	5.93	53.887	269.234
DS-NeRF	2.742	23.186	69.328
Our Methods	1.545	8.968	25.419

and Figure 7 present the results of the geometric structure reconstruction of space targets. As shown in Table 3, our method achieves favorable results in reconstructing the geometric structure of space targets even under sparse-viewpoint conditions. With 18 input viewpoints, our method’s Chamfer distance (CD) value is 8.968 × 10⁻³, which is close to the performance of the NeRF with 36 input viewpoints (CD = 5.93 × 10⁻³). With nine input viewpoints, our method’s CD value is 25.419 × 10⁻³, comparable to the performance of the DS-NeRF with 18 input viewpoints (CD =23.186 × 10⁻³), demonstrating that our method maintains high geometric reconstruction accuracy even with reduced inputs, showcasing its advantage in handling sparse-viewpoint scenarios.

Additionally, our method exhibits better robustness as the number of viewpoints gradually decreases. As the number of viewpoints is reduced, the Chamfer distance (CD) values for the NeRF and DS-NeRF increase rapidly. Specifically, when the number of viewpoints decreases from 36 to 9, the NeRF’s CD value increases by approximately 44 times and the DS-NeRF’s CD value increases by about 24 times. In contrast, the CD value of our method only increases by 15 times. This relatively smooth change in CD values under the same conditions highlights that our method demonstrates stronger adaptability and stability when dealing with sparse viewpoint inputs.

Figure 7 provides a visual comparison of the point cloud output from the experiments on the 9-v dataset. From the figure, it is evident that with only nine input images, our method significantly outperforms the NeRF and DS-NeRF in 3D reconstruction. The NeRF’s reconstruction results are the most blurry and incomplete, with low point cloud density and many regions that are not clearly discernible. This reflects the NeRF’s poor performance when using only sparse viewpoint inputs due to insufficient depth constraints and a lack of multi-view information, resulting in issues such as the loss of target structure and blurred details. While the DS-NeRF shows some improvement over the NeRF in reconstruction quality, it still has many blurry and incomplete areas, particularly around the edges and certain detailed regions of the target object. This may be because the DS-NeRF, when handling sparse-viewpoint scenarios, only introduces depth information from the input viewpoints as supervision and does not fully utilize multi-view information to optimize the reconstruction.

Our reconstruction results are superior to those of the NeRF and DS-NeRF in both structural completeness and detail. The point cloud density is higher, the object edges are clearer, and the geometric shape is more complete, showing a better reconstruction effect for space targets. Especially in the left and right areas of the object, our method significantly reduces blurriness and incompleteness in the reconstruction, capturing the complex geometric features of space targets more accurately. This indicates that our method, by incorporating absolute depth information, relative depth ranking loss, and confidence modeling, effectively enhances the quality and reliability of 3D reconstruction under sparse-viewpoint conditions.

4.4. Ablation Study

4.4.1. Ablation on Depth Prior Extraction

To further validate the effectiveness of our improved monocular depth estimation network for space targets in the 3D reconstruction process, we conducted ablation experiments. In our proposed 3D reconstruction method, we utilized both ZoeDepth-M12-N and the enhanced ZoeDepth-M2-NS for extracting 3D priors. The experimental results under the 18-v dataset are presented in

Table 4. Results of ablation experiments on depth prior extraction.

Method	$\mathbf{PSNR} \uparrow$	$\mathbf{SSIM} \uparrow$	$\mathbf{LPIPS} \downarrow$	$\mathbf{CD} ({\times 10}^{-3}$$) \downarrow$
Our Methods_ZDM12-N	23.248	0.842	0.275	11.111
Our Methods_ZDM12-NS	24.229	0.858	0.23	8.968

. The results indicate that the depth information extracted by the improved ZoeDepth-M2-NS provides significantly stronger support for the 3D reconstruction of space targets compared to the original ZoeDepth-M12-N, achieving higher reconstruction accuracy.

4.4.2. Ablation on Core Components

We conducted ablation experiments on the 18-v dataset to verify the effectiveness of each component in our method. The experimental results are shown in

Table 5. Results of ablation experiments on core components.

Method		$\mathbf{PSNR} \uparrow$	SSIM ↑	$\mathbf{LPIPS} \downarrow$	$\mathbf{CD} ({\times 10}^{-3}$$) \downarrow$
(a)	Baseline	19.259	0.833	0.664	53.887
(b)	NeRF-SD	23.098	0.841	0.331	30.536
(c)	NeRF-SD-UD	24.229	0.858	0.23	8.968

. The results demonstrate that the reconstruction quality improves significantly with the gradual introduction of depth prior information. From the baseline method (a) to the inclusion of seen viewpoint depth priors (b), the PSNR increased from 19.259 to 23.098 and the CD value decreased from 53.887 × 10⁻³ to 53.887 × 10⁻³. Further introducing unseen viewpoint depth priors (c) resulted in a PSNR increase to 24.229 and a CD value reduction to 8.968 × 10⁻³. This indicates that adding depth prior information, whether from seen or unseen viewpoints, has a significant positive impact on the 3D reconstruction results.

5. Conclusions

We propose a novel method for the 3D reconstruction of space targets under sparse-viewpoint conditions by integrating monocular depth estimation with neural radiance fields (NeRFs). By introducing depth priors from both seen and unseen viewpoints, our approach enhances the reconstruction process, significantly improving perceptual quality and geometric accuracy over the traditional NeRF and DS-NeRF models with limited input viewpoints. Ablation studies confirm the effectiveness of using depth priors from multiple viewpoints, resulting in robust reconstruction even with fewer viewpoints, as validated by performance metrics (PSNR, SSIM, LPIPS, and CD) and visual results.

In summary, this method offers a viewpoint-robust solution for 3D reconstruction in sparse scenarios, demonstrating high-quality performance even with minimal observations. However, the method’s reliance on camera parameters for seen viewpoints could limit practical applications. Future research may focus on reducing this dependency to enable precise 3D reconstructions under even more challenging conditions.