Dynamics Model and Its Verification of Aerospace Three-Ring Gear Reducer
Abstract
1. Introduction
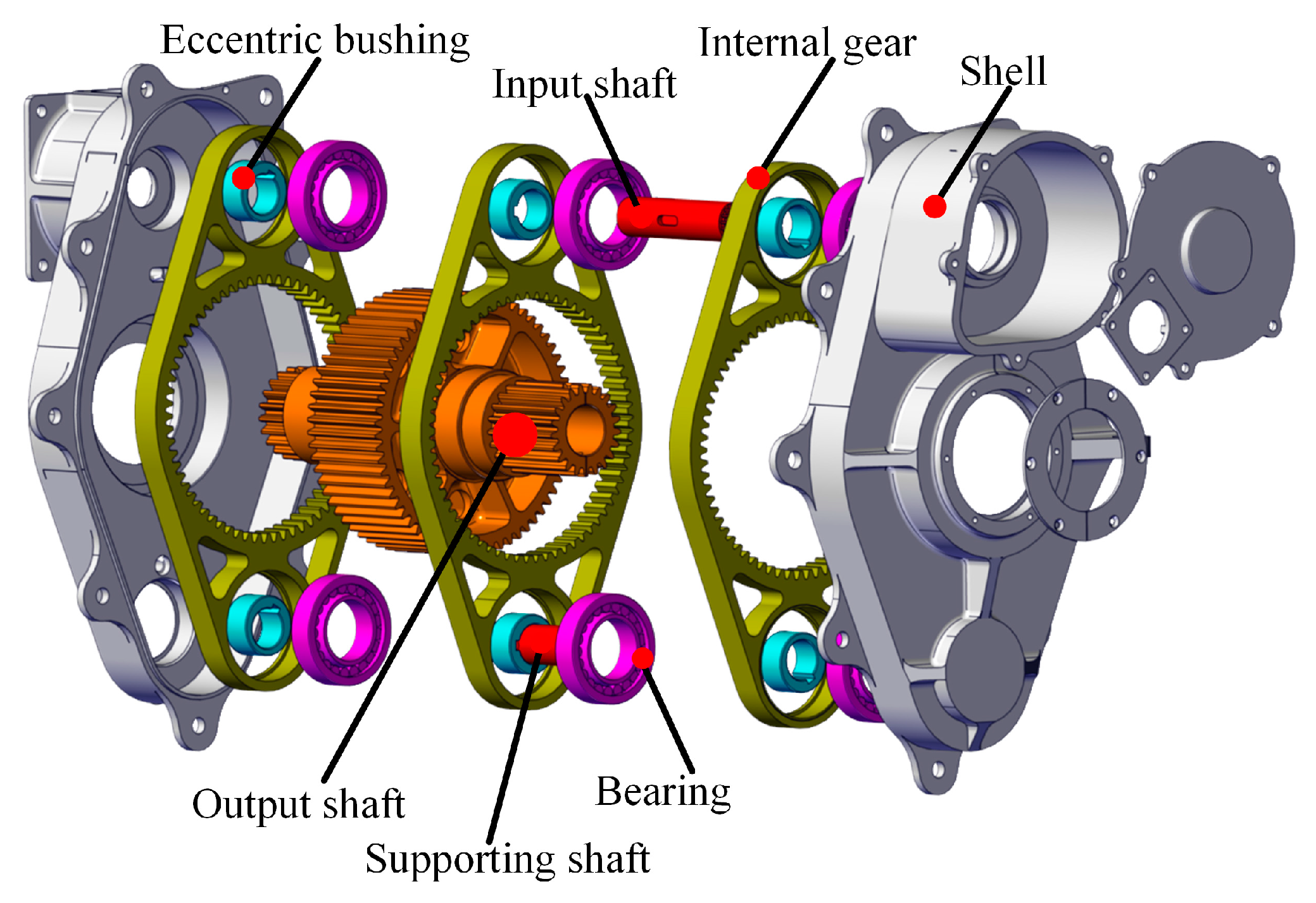
2. Parameter Calculation and Dynamic Model Establishment of Aerospace Three-Ring Reducer
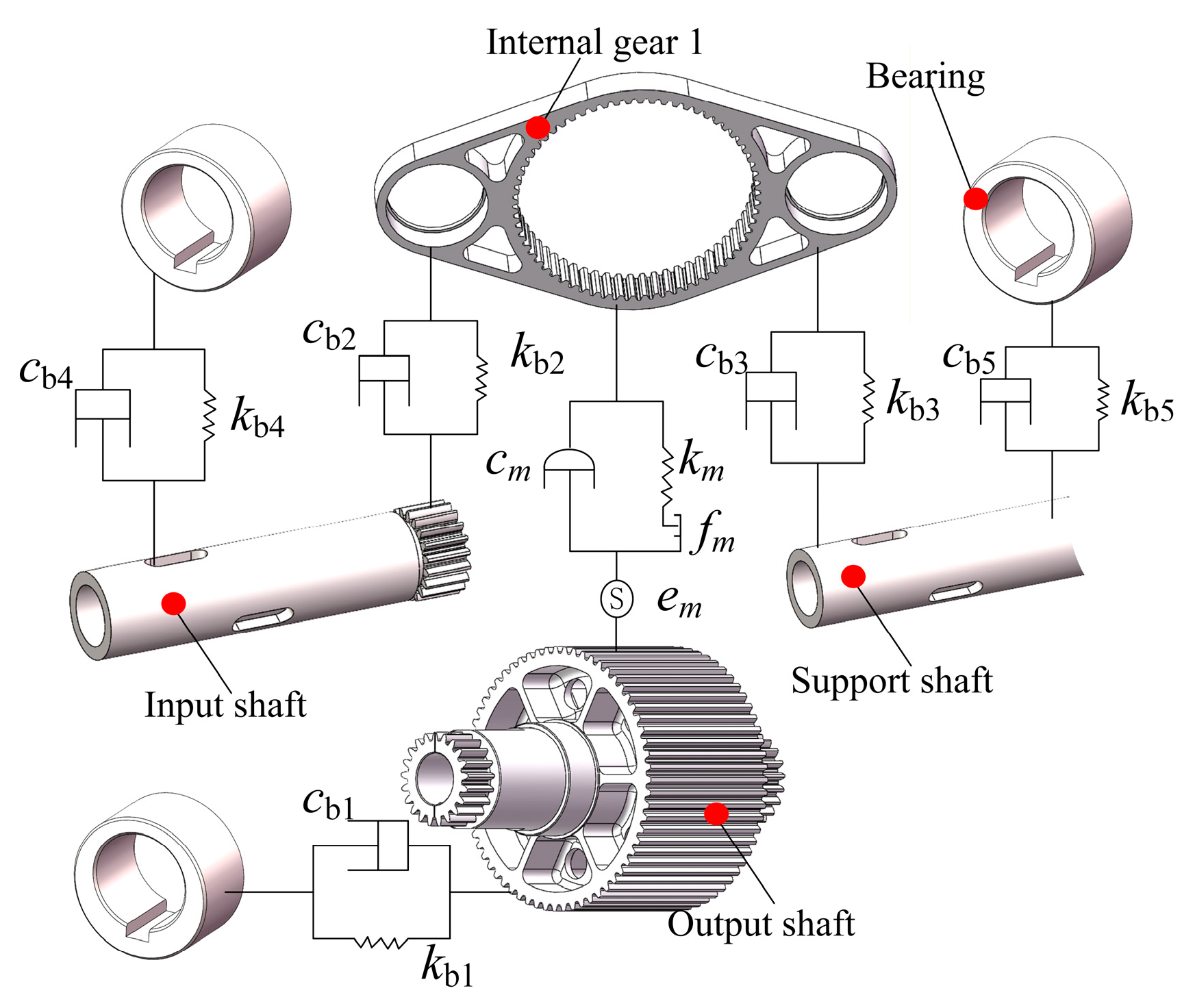
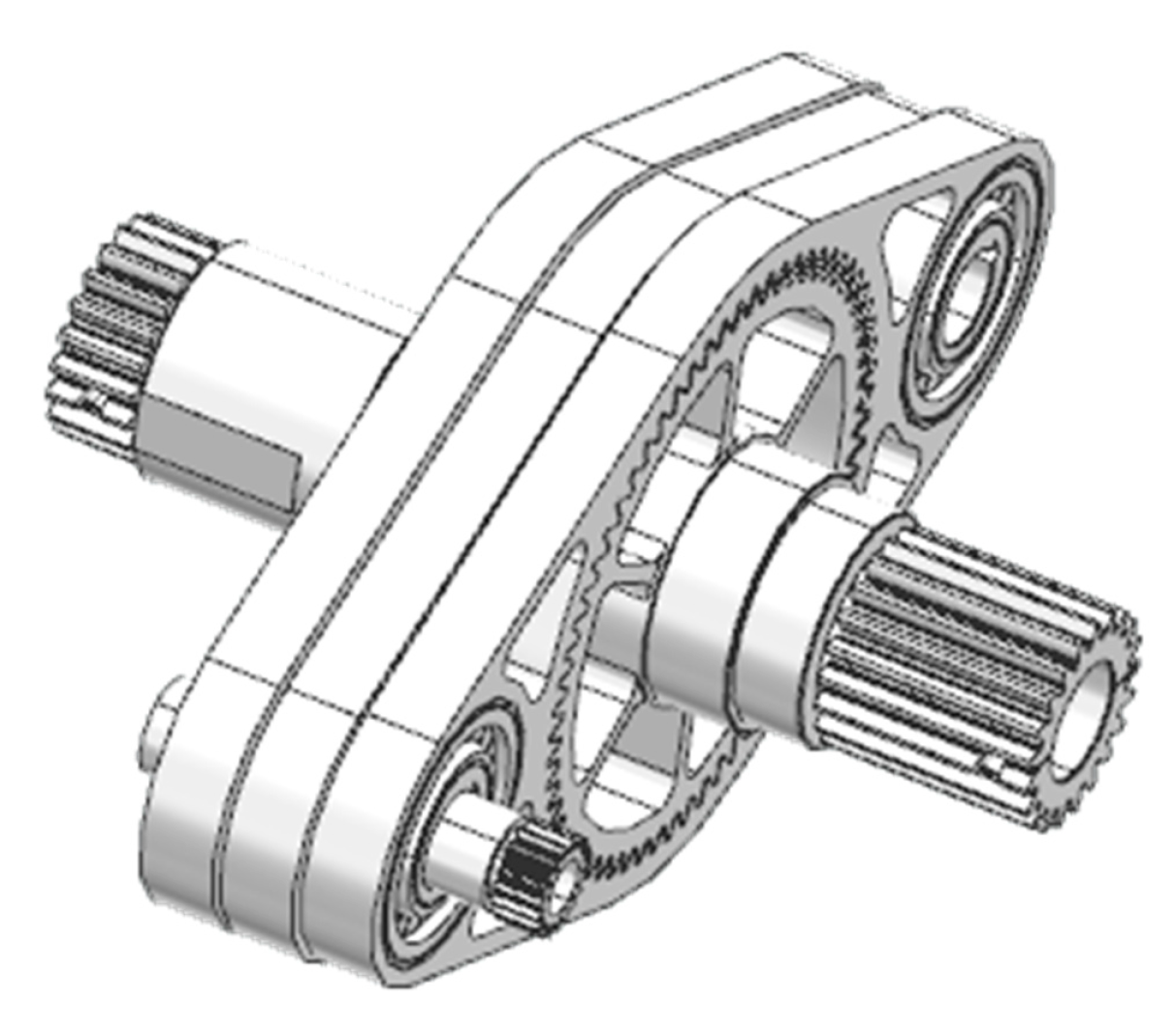
2.1. Dynamic Model of Aerospace Three-Ring Reducer
2.2. Calculation of Dynamic Parameters
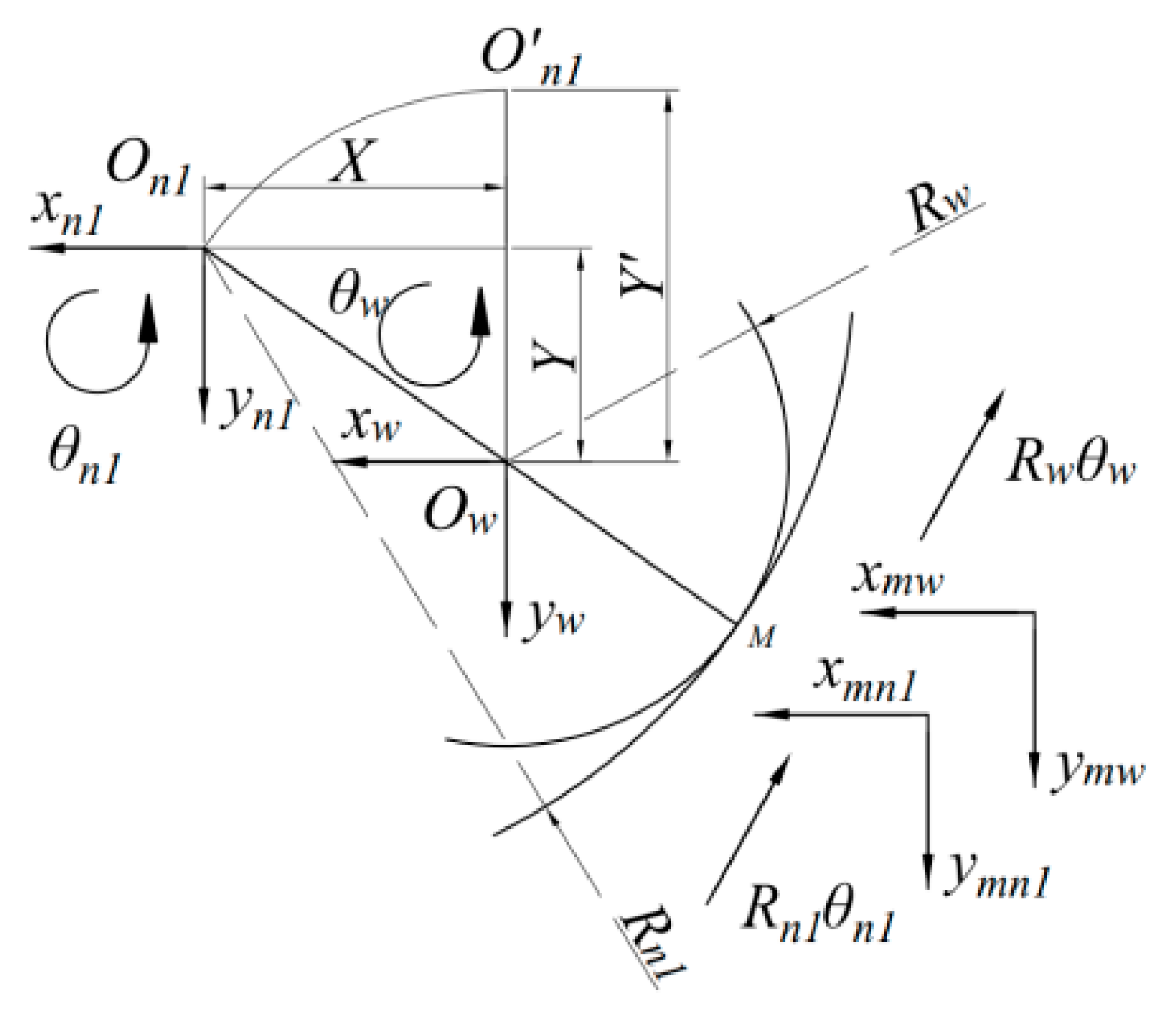
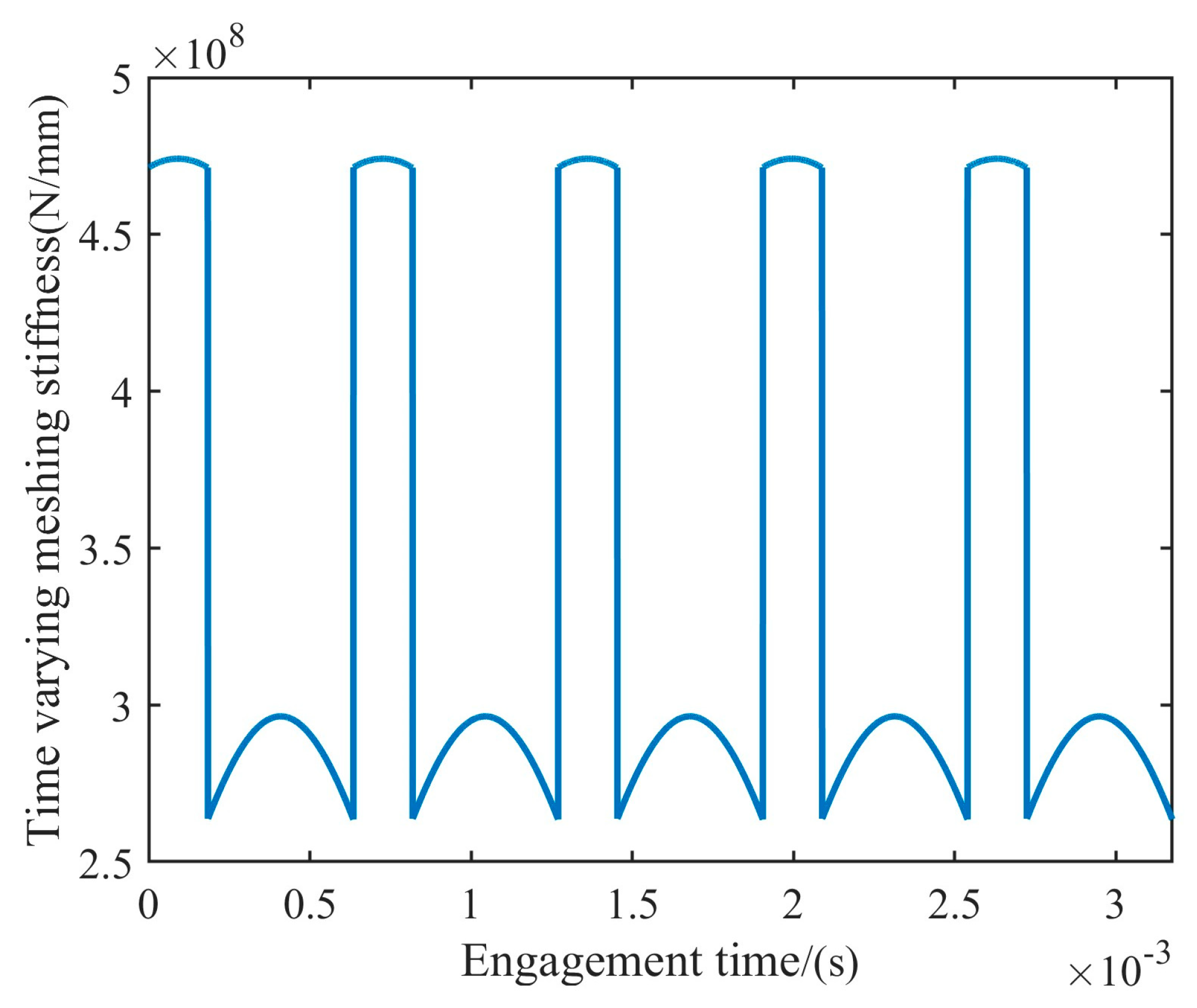
2.2.1. Meshing Stiffness
2.2.2. Meshing Damping
3. Validation of the Correctness of the Dynamic Model
3.1. Modal Frequency Solution of Dynamic Equation
3.2. Modal Frequency Solution of Finite Element Method
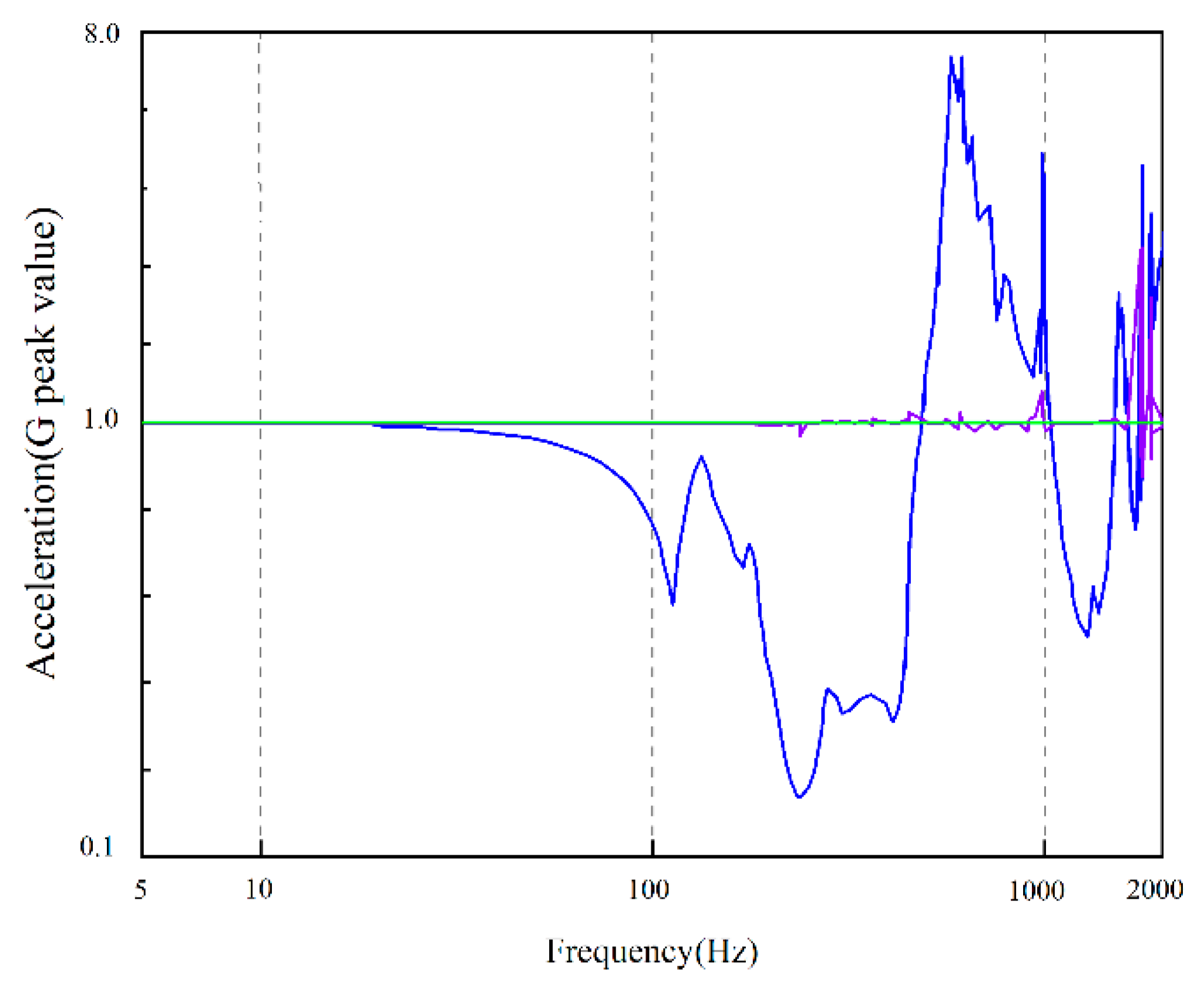
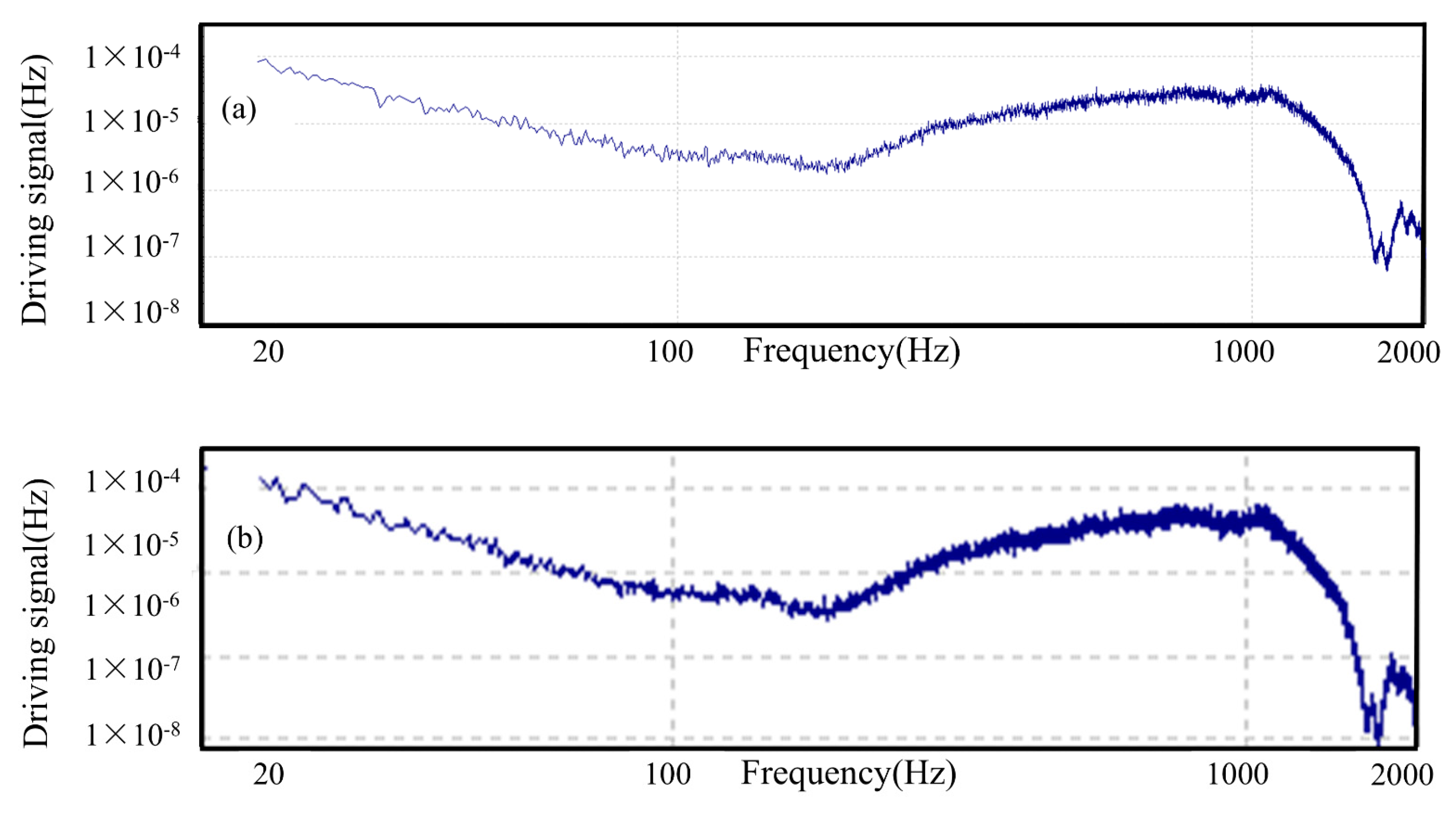
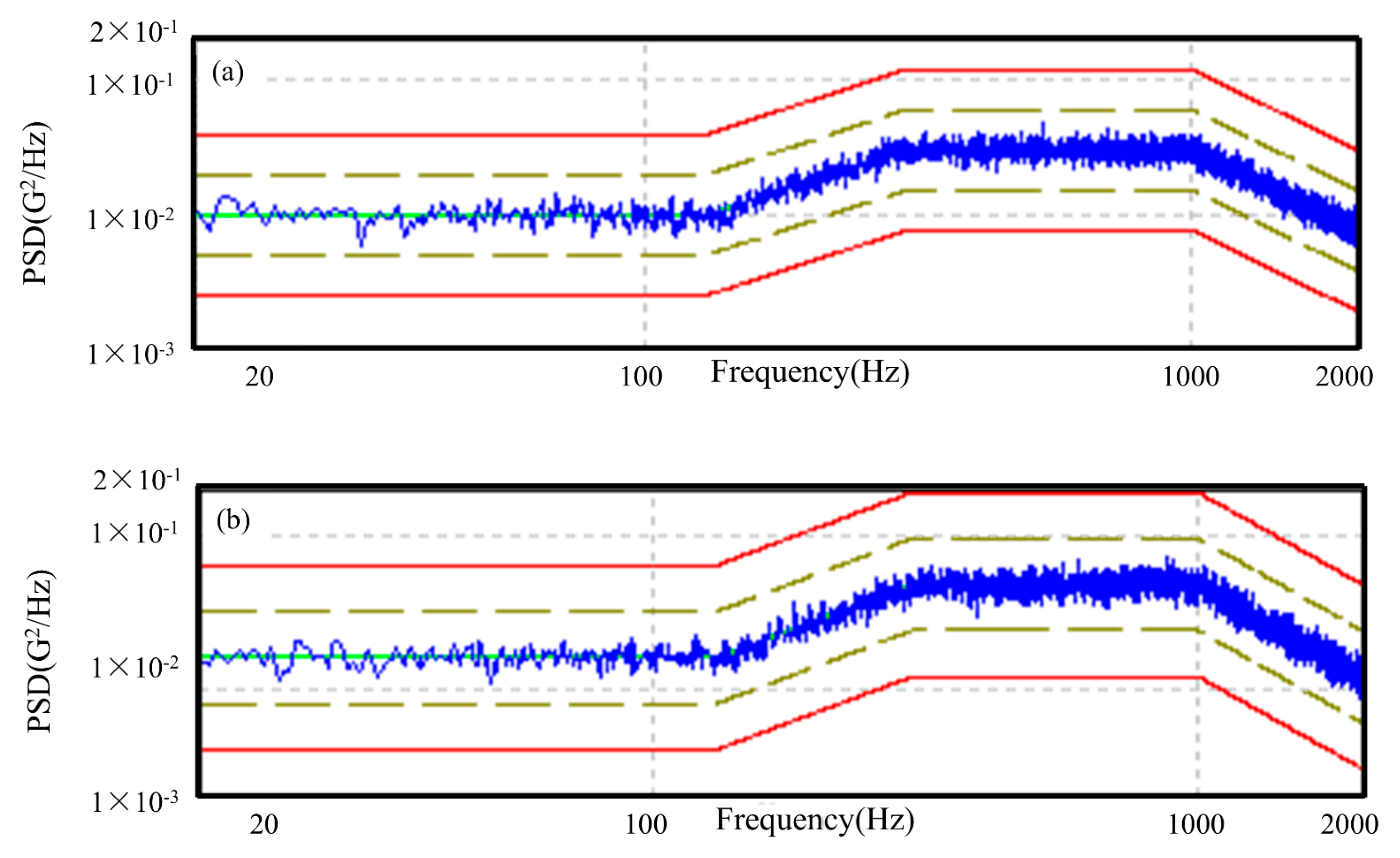
3.3. Experimental Method of Modal Frequency Solving
4. Analysis of Dynamic Model Results and Validation by ADAMS-Based Simulation Analysis
4.1. The Solution Method and Result Analysis of Nonlinear Vibration Equation
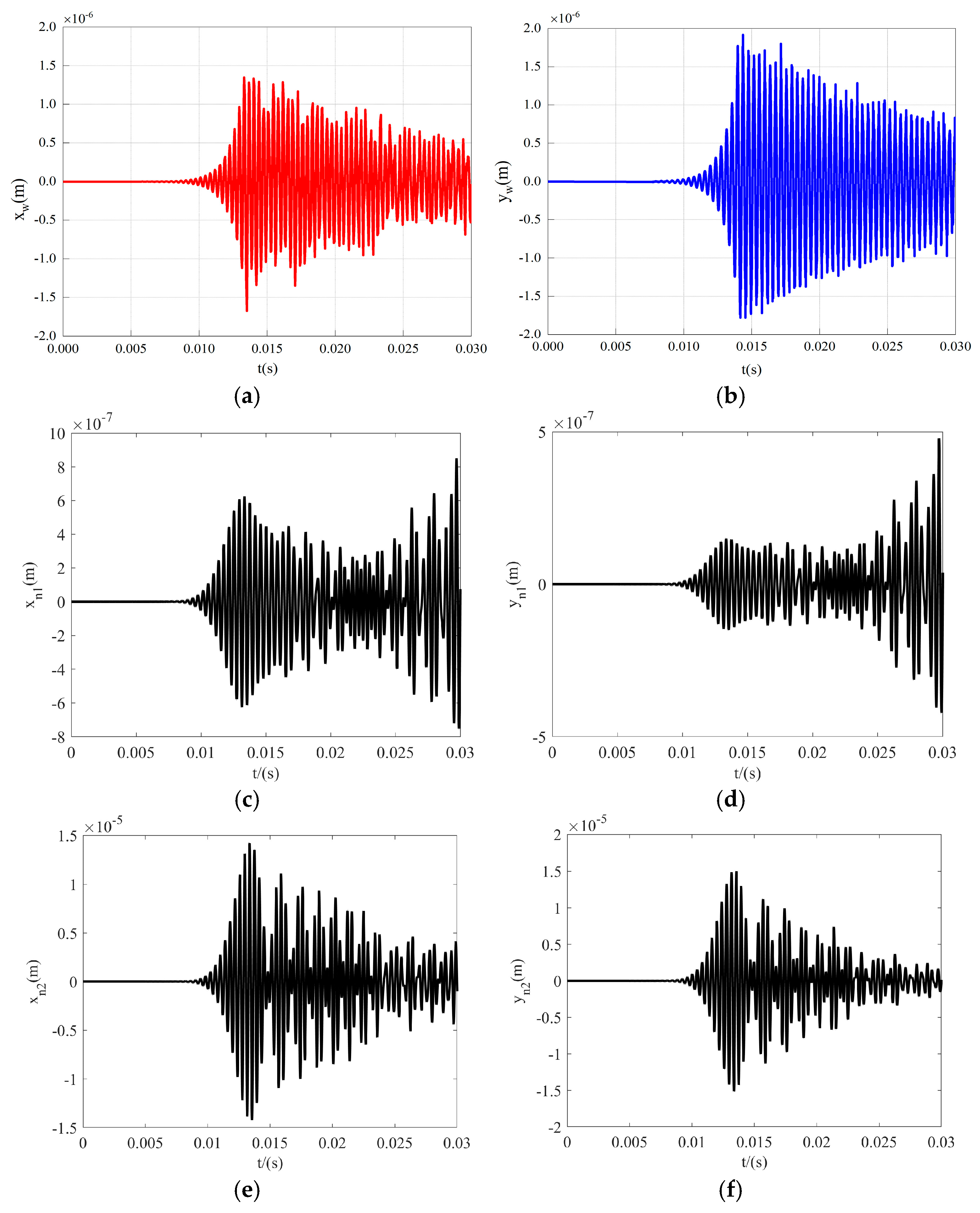
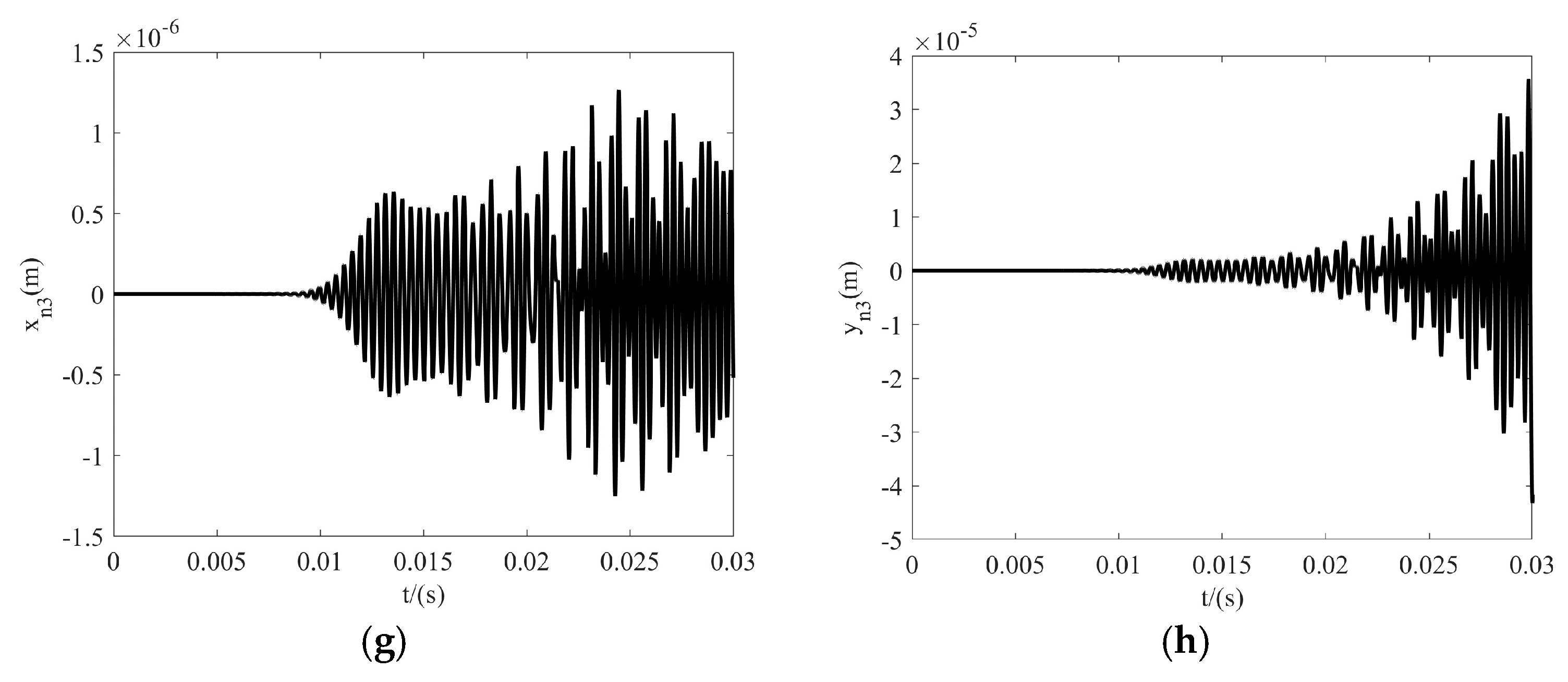
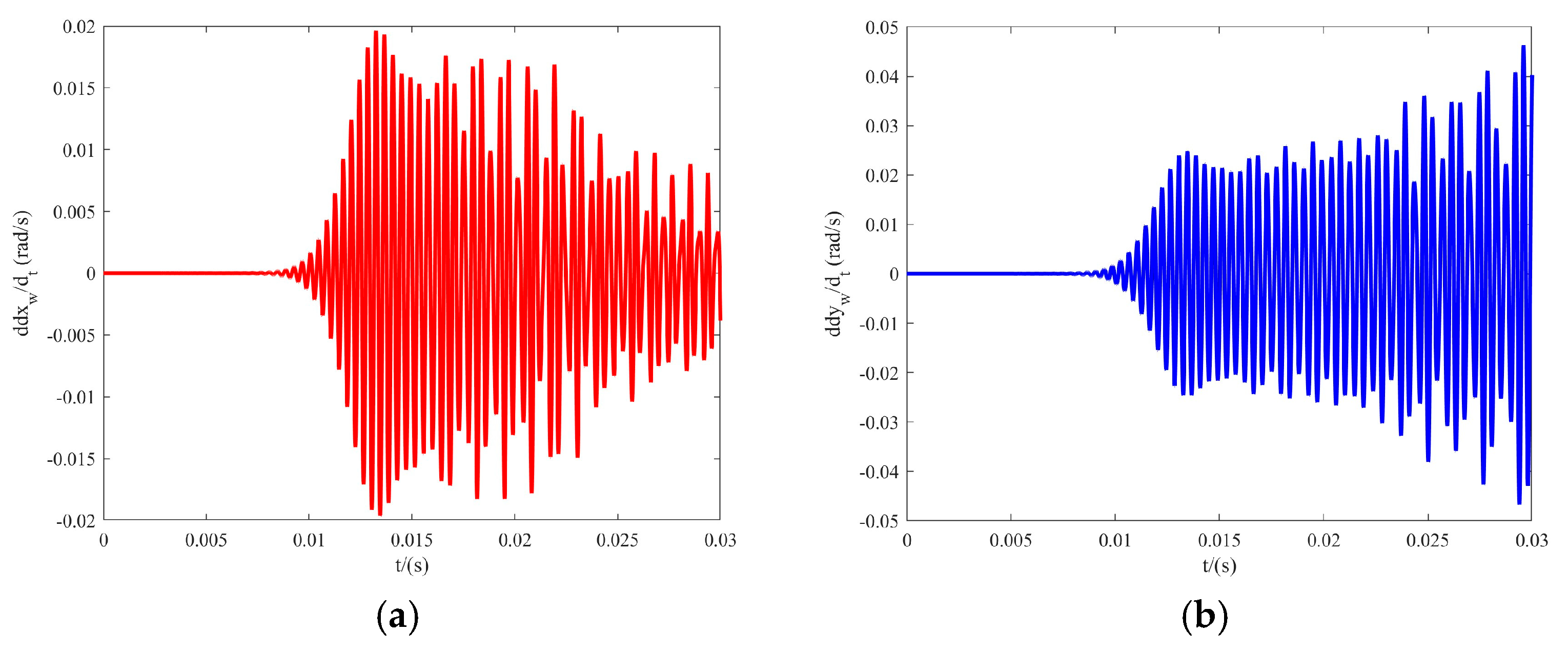
4.2. Vibration Response Analysis
4.3. ADAMS Simulation Condition Parameter Setting
4.4. ADAMS Simulation Analysis Results
5. Conclusions
- (1)
- In this paper, the 12-degree-of-freedom nonlinear dynamic equations of the aerospace three-ring reducer gear train were derived and experimentally investigated. By comparing the modal frequencies obtained from the experimental values, finite element values, and dynamical equations (Table 1), it is evident that the finite element values within 2000 Hz align with the modal frequencies obtained from experiments, with the error remaining within the permissible range. This indicates that the dynamic model established in this paper is accurate and effectively reflects the vibration characteristics of the aerospace three-ring reducer gear.
- (2)
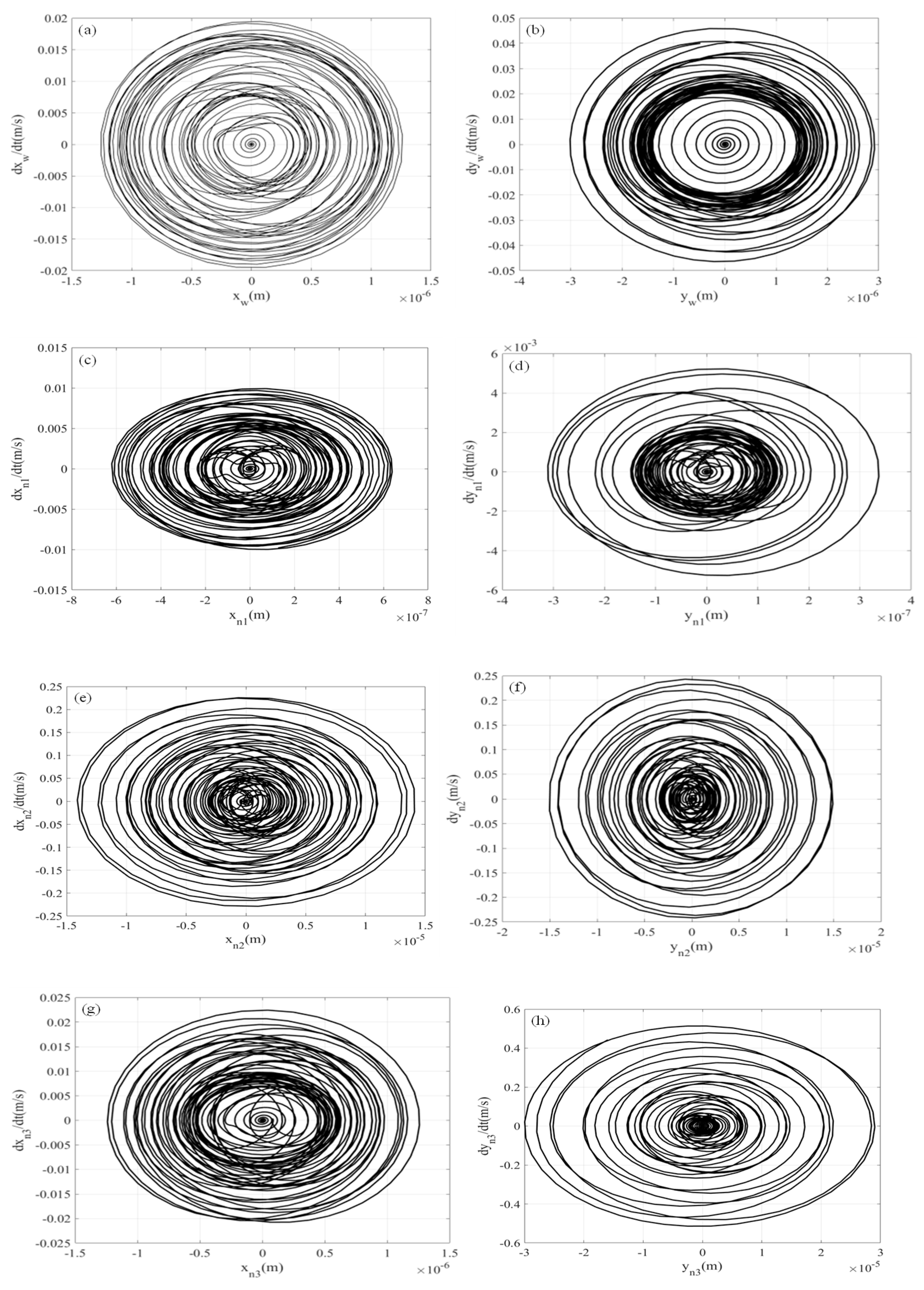
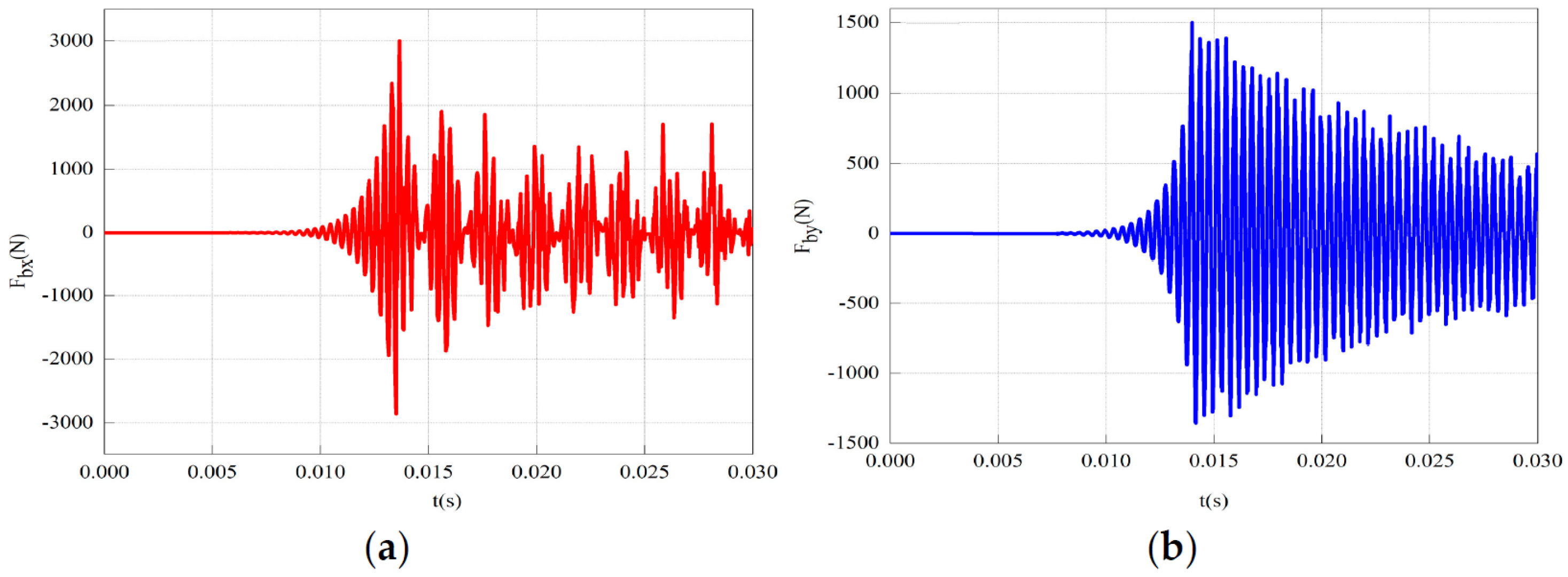
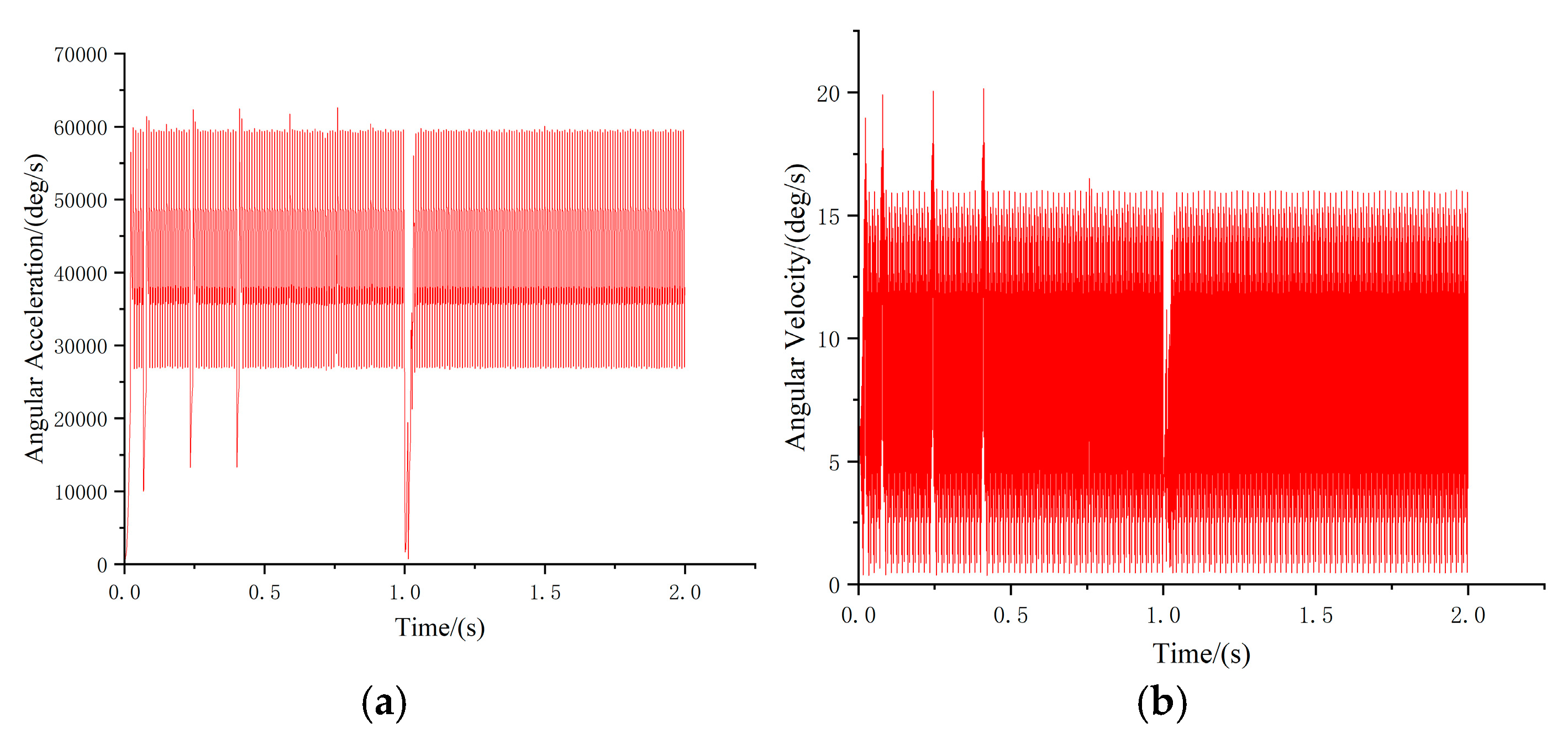
- The vibration displacement amplitude and angular velocity amplitude of the output gear in all directions are relatively small compared to the inner gear plate. The vibration gradually increases to its maximum value after being excited, then decreases and stabilizes. The displacement–velocity phase diagrams of each gear–rotor component exhibit repeated closed curves, while the vibration phase diagrams of the output outer gear in the x- and y-directions are notably more regular, confirming the relative stability of the output outer gear’s vibration in the three-ring gearbox from the side. Coupled with the ADAMS simulation results, the speed and acceleration curves of the output external gear exhibit both stability and fluctuations, while the force curves on the three internal gear plates also reveal stability and fluctuations. However, in both instances, the duration of the stable period exceeds that of the fluctuating period. This shows that the vibration of the aerospace three-ring reducer is small, can bear large loads, and is suitable for high-speed and heavy-duty occasions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, Z. Multi-Variable Coupling Nonlinear Dynamic Characteristics Research on A Planetary Reducer with Small Tooth Number Difference. Master’s Thesis, Chongqing University, Chongqing, China, 2015. (In Chinese). [Google Scholar]
- Wang, J.; Li, Q.; Xiao, K.; Shi, Z. Research on nonlinear coupled vibration of planet reducer with fewer tooth difference. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 44, 40–46. (In Chinese) [Google Scholar]
- Yang, H. Analysis of Transmission Precision of Reducing Mechanism for Actuator with Small Tooth Number Difference. Master’s Thesis, Chongqing University, Chongqing, China, 2018. (In Chinese). [Google Scholar]
- Zhang, J. Research on Dynamic Characteristics of NN Planetary Gear Servo Drive System with Small Tooth Difference. Master’s Thesis, Chongqing University, Chongqing, China, 2016. (In Chinese). [Google Scholar]
- Fakhfakh, H.; Bruyère, J.; Velex, P.; Becquerelle, S. A torsional model of multistage gears influence of external excitations and tooth shape modifications. Mech. Ind. 2016, 17, 413–420. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhu, R.P. Nonlinear torsional dynamics of star gearing transmission system of GTF gearbox. Shock Vib. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Zhao, M.M.; Ji, J.C. Nonlinear torsional vibrations of a wind turbine gearbox. Appl. Math. Model. 2015, 39, 4928–4950. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, C.; Qin, D. Elastic dynamics analysis of three-ring reducer. J. Mech. Eng. 2010, 54–58. [Google Scholar]
- Wang, J.; Li, Q.; Xiao, K.; Shi, Z. Study on nonlinear coupled vibration of planetary reducer with small tooth difference. Huazhong Univ. Sci. Technol. J. 2016, 44, 40–46. [Google Scholar]
- Zhou, W.; Zhu, R.; Liu, W.; Shang, Y. An Improved Dynamic Transmission Error Model Applied on Coupling Analysis of Gear Dynamics and Electrohydrodynamic Lubrication. J. Tribol. 2022, 144, 051601. [Google Scholar] [CrossRef]
- Wang, Y.; Hood, A.A.; Cooley, C.G. Finite element/contact mechanics analysis of spur gear pairs with tooth root cracks. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2021; Volume 10, p. V010T10A024. [Google Scholar]
- Kumar, R.; Roy, S.K. Model-based diagnostic tool for detection of gear tooth crack in a wind turbine gearbox under constant load. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 1666–1687. [Google Scholar] [CrossRef]
- Zhai, H.; Zhu, C.; Song, C.; Liu, H.; Bai, H. Influences of carrier assembly errors on the dynamic characteristics for wind turbine gearbox. Mech. Mach. Theory 2016, 103, 138–147. [Google Scholar] [CrossRef]
- Sanjib, C.; Rama, K. Vibration of high-speed helical geared shaft systems mounted on rigid bearings. Int. J. Mech. Sci. 2018, 142–143, 176–190. [Google Scholar]
- Zhang, H. Design of New Type Involute Planetary Gear Reducer of Small Tooth Number Difference. Adv. Mater. Res. 2012, 490, 2076–2080. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.X.; Xiao, K.; Li, M.; Li, J.Y. Dynamic characteristics analysis and experimental research on a new type planetary gear apparatus with small tooth number difference. J. Mech. Sci. Technol. 2013, 27, 1233–1244. [Google Scholar] [CrossRef]
- Huang, C.; Huang, B.; Zhang, Y.; Xiao, K. Modal analysis and experimental research on a planetary reducer with small tooth number difference. Trans. Can. Soc. Mech. Eng. 2019, 44, 202–212. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, Y.; Chen, Z.; Zuo, M.J. Transient meshing performance of gears with different modification coefficients and helical angles using explicit dynamic FEA. Mech. Syst. Signal Process. 2011, 25, 1786–1802. [Google Scholar] [CrossRef]
- Wang, P.Y.; Cai, X.L. Vibrational analysis of planetary gear trains by finite element method. Appl. Mech. Mater. 2013, 284–287, 1012–1017. [Google Scholar] [CrossRef]
- Tristan, M.E.; Robert, G.P. Planetary gear modal vibration experiments and correlation against lumped-parameter and finite element models. J. Sound Vib. 2013, 332, 2350–2375. [Google Scholar]
- Huang, Q.B.; Li, X. Modal Analysis on Tooth Ring Plate of Three-Ring Gear Reducer. Appl. Mech. Mater. 2013, 345, 124–127. [Google Scholar] [CrossRef]
- Liu, Y.K.; Wei, Y.L. The Performance Study of Three-Ring Gear Reducer. Adv. Mater. Res. 2013, 605, 1261–1264. [Google Scholar] [CrossRef]
- Yang, H.B.; Wang, Q. Three-ring gear reducer Internal tooth plate processing method in the research and analysis. Appl. Mech. Mater. 2014, 472, 312–315. [Google Scholar] [CrossRef]
- Tong, Y. Research on Multi Body Dynamics of Three-ring Reducer with Small Tooth Difference for Aero Electromechanical Actuator. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2021. (In Chinese). [Google Scholar]
- Du, W. Study on Dynamic Analysis and Simulation of Three-Ring Reducer Based on Dynamic Balance. Northeast Petroleum University: Daqing, China, 2020. (In Chinese) [Google Scholar]
- Zhou, Y. Research on Mechanical Properties and Optimization of Structure Parameters for Three-ring Gear Reducer. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2016. (In Chinese). [Google Scholar]
- Wen, F.; Pang, Y.; Chen, J.; Liu, W. Study on the Dynamics Characteristic of Three-ring Gear Reducer with Thermo-elastic Coupling. J. Mech. Transm. 2015, 39, 22–25. (In Chinese) [Google Scholar]
- Zhao, Z. The Dynamics Analysis and Simulation Investigation of the Three-ring Gear Reducer Based on Virtual Prototyping Technology. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2016. (In Chinese). [Google Scholar]
- Liu, G.; Lu, Z.R.; Wang, L.; Liu, J.K. A new semi-analytical technique for nonlinear systems based on response sensitivity analysis. Nonlinear Dyn. 2021, 103, 1529–1551. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.K.; Wang, L.; Lu, Z.R. A new semi-analytical approach for quasi-periodic vibrations of nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105999. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.K.; Wang, L.; Lu, Z.R. Time-domain minimum residual method combined with energy balance for nonlinear conservative systems. Mech. Syst. Signal Process. 2022, 170, 108818. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.K.; Lu, Z.R. High-precision semi-analytical solution for the quasi-periodic nanobeam system based on the weight time-domain minimum residual method. Compos. Struct. 2023, 323, 117457. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Dong, J. Load sharing characteristics of multistate planetary gear train using analytical and finite element mode. Int. J. Comput. Appl. Technol. 2016, 53, 107–120. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Y.; Wu, J. Contact finite element analysis of the influence of manufacturing error on gear pair meshing. Vib. Shock 2015, 34, 43–50. [Google Scholar]

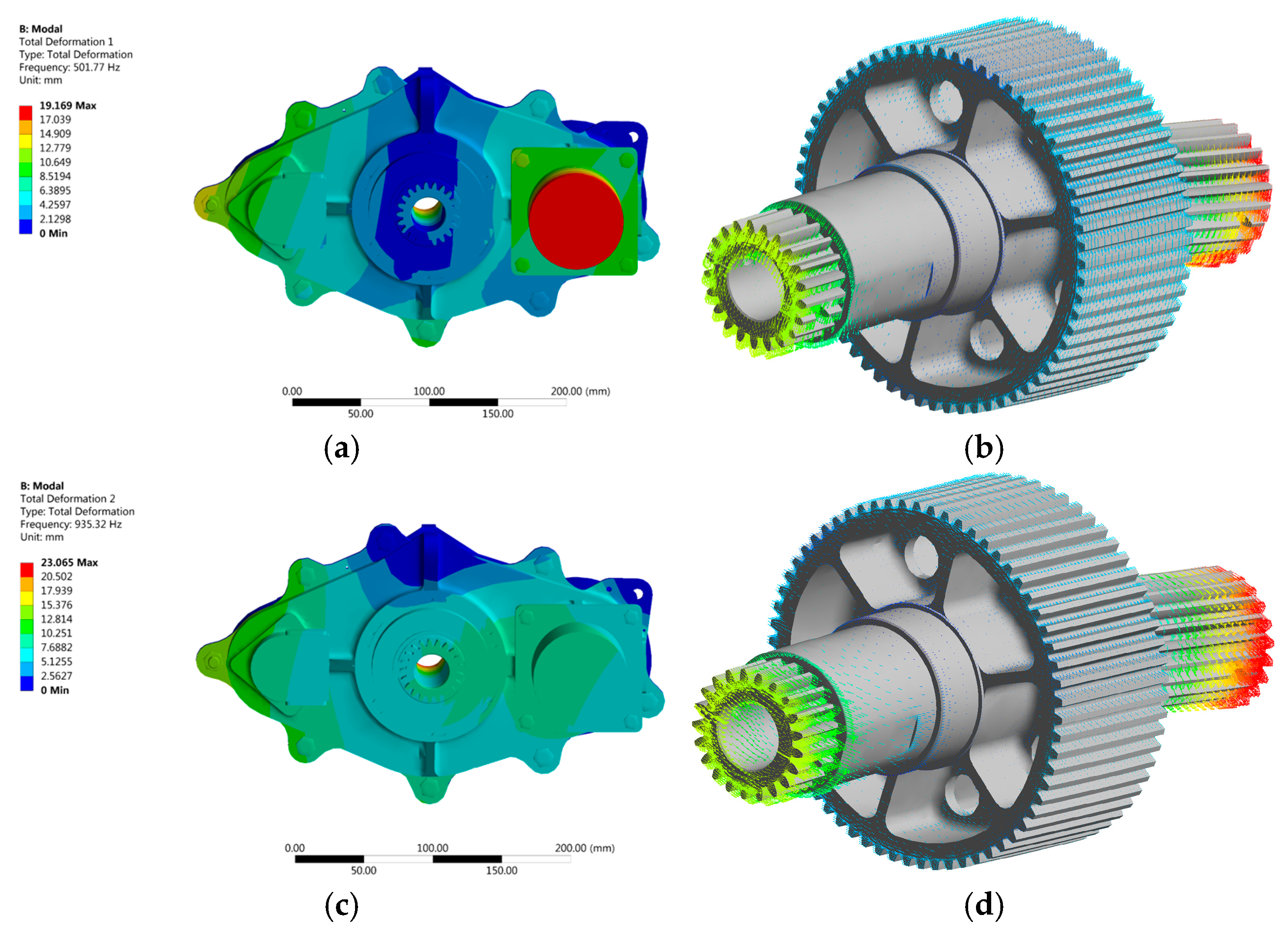
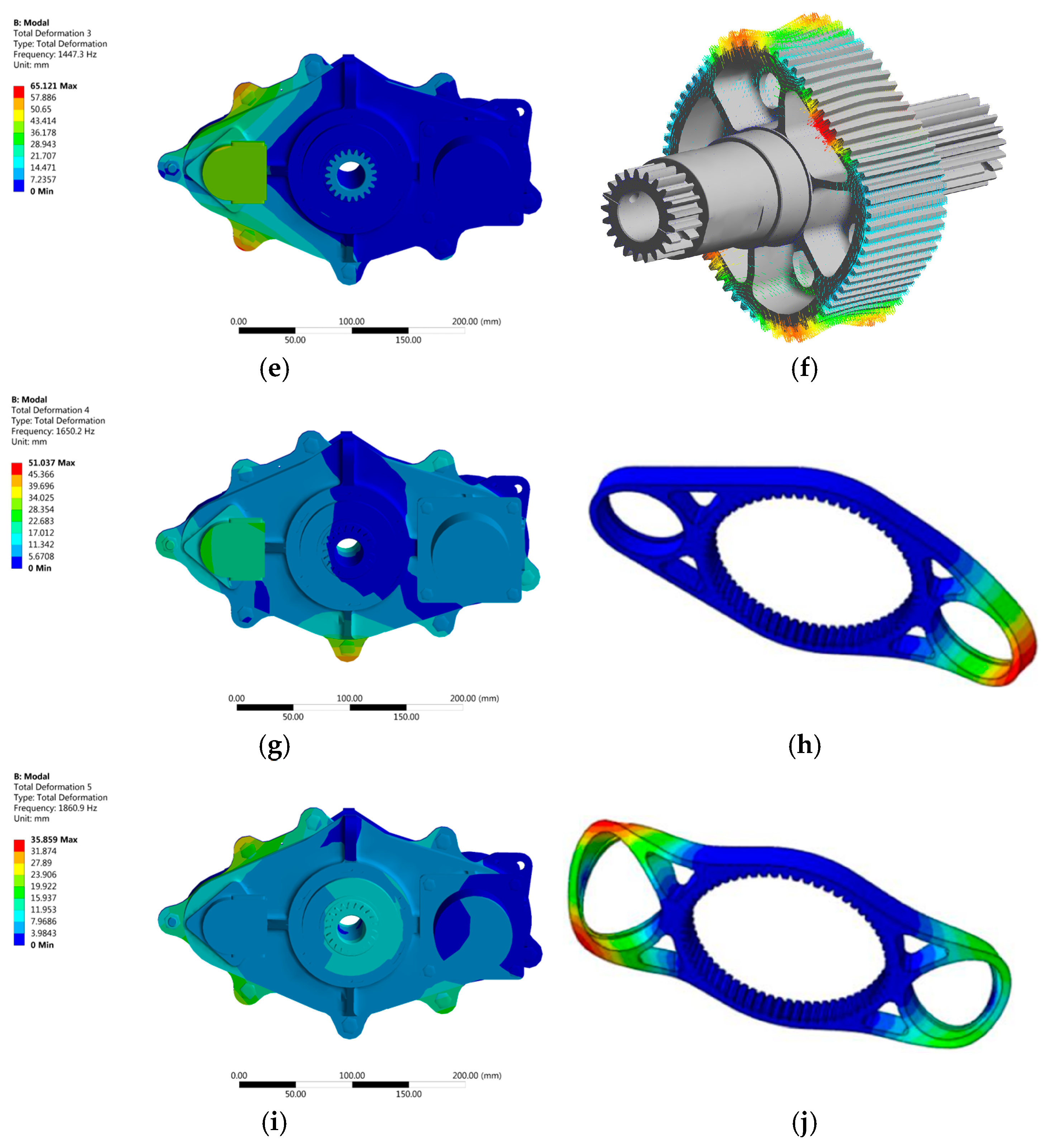



| Order | Vibration Characteristic Equation (Hz) | Finite Element (Hz) | Experimental Method (Hz) |
|---|---|---|---|
| 1 | 529.83 | 501.77 | 582 |
| 2 | 976.51 | 935.32 | 977 |
| 3 | 1487.14 | 1447.3 | 1487 |
| 4 | 1727.93 | 1650.2 | 1747 |
| 5 | 1862.31 | 1860.9 | 1839 |
| Design Parameters | External Gear W | Internal Gear Plate n1, n2, and n3 |
|---|---|---|
| m (mm) | 2 | 2 |
| Z | 63 | 64 |
| X | −0.1 | 0.25 |
| ha* | 0.7 | 0.7 |
| c* | 0.25 | 0.2 |
| m0 (kg) | 4.125 | 0.961 |
| I0 (kg∙m2) | 0.006 | 0.007 |
| lb (mm) | 107 | |
| R (mm) | 1.51 | |
| kb/(108 N/m−1) | 1.5 | 4.4 |
| cb/(105 N/s/m−1) | 2.1 | 2.3 |
| km/(108 N/m−1) | 3.5854 | 3.9547 |
| cm/(N/s/m−1) | 566.1293 | 687.1411 |
| Components | Constraint Type | |
|---|---|---|
| Input Shaft | Ground | Revolute Pair |
| Supporting Shaft | Ground | Revolute Pair |
| Gear Shaft | Ground | Revolute Pair |
| Input Shaft | Internal Gear | Revolute Pair |
| Supporting Shaft | Internal Gear | Revolute Pair |
| Gear shaft | Internal Gear | Contact |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, J.; Luo, L.; Luo, G.; Chao, S. Dynamics Model and Its Verification of Aerospace Three-Ring Gear Reducer. Aerospace 2024, 11, 1049. https://doi.org/10.3390/aerospace11121049
Lai J, Luo L, Luo G, Chao S. Dynamics Model and Its Verification of Aerospace Three-Ring Gear Reducer. Aerospace. 2024; 11(12):1049. https://doi.org/10.3390/aerospace11121049
Chicago/Turabian StyleLai, Jinyong, Lan Luo, Guangzhao Luo, and Shiyuan Chao. 2024. "Dynamics Model and Its Verification of Aerospace Three-Ring Gear Reducer" Aerospace 11, no. 12: 1049. https://doi.org/10.3390/aerospace11121049
APA StyleLai, J., Luo, L., Luo, G., & Chao, S. (2024). Dynamics Model and Its Verification of Aerospace Three-Ring Gear Reducer. Aerospace, 11(12), 1049. https://doi.org/10.3390/aerospace11121049






