Pose Estimation for Cross-Domain Non-Cooperative Spacecraft Based on Spatial-Aware Keypoints Regression

Abstract

Reliable pose estimation for non-cooperative spacecraft is a key technology for in-orbit service and active debris removal missions. Utilizing deep learning techniques for processing monocular camera images is effective and is a hotspot of current research. To reduce errors and improve model generalization, researchers often design multi-head loss functions or use generative models to achieve complex data augmentation, which makes the task complex and time-consuming. We propose a pyramid vision transformer spatial-aware keypoints regression network and a stereo-aware augmentation strategy to achieve robust prediction. Specifically, we primarily use the eight vertices of a cuboid satellite body as landmarks and the observable surfaces can be transformed by, respectively, using the pose labels. The experimental results on the SPEED+ dataset show that by using the existing EPNP algorithm and pseudo-label self-training method, we can achieve high-precision pose estimation for target cross-domains. Compared to other existing methods, our model and strategy are more straightforward. The entire process does not require the generation of new images, which significantly reduces the storage requirements and time costs. Combined with a Kalman filter, the robust and continuous output of the target position and attitude is verified by the SHIRT dataset. This work realizes deployment on mobile devices and provides strong technical support for the application of an automatic visual navigation system in orbit.

1. Introduction

With the deepening of human space exploration, the frequency of spacecraft launches has increased rapidly, resulting in an increasingly crowded orbital environment. According to the European Space Agency’s Annual Space Environment Report published in July 2024, the number of recorded objects in space in Earth orbit has exceeded 34,000, including a number of defunct satellite platforms and payloads that have become non-cooperative targets, taking up valuable orbital resources [1]. Monitoring and tracking of these objects, on the one hand, can prevent space debris from deviating from the original orbit and posing a threat to other space vehicles and astronauts, and on the other hand, carrying out inspections or maintenance work on retired satellites can extend their service life or achieve recycling.

When estimating the pose of the target satellite and stabilizing its tracking to approach a plane perpendicular to the axis of free rotation, achieving relative stationary motion with respect to the target star is a crucial prerequisite for subsequent autonomous capture or docking, fuel replenishment, maintenance services, and debris removal operations. Consequently, photoelectric image-sensitive detectors are essential devices for enabling close-range relative navigation of non-cooperative, unstable space targets. Compared to active sensing and imaging measurement devices and multi-vision structural strategies, monocular cameras are low in size, weight, power, and cost (SWaP-C) sensors. They are particularly well suited for the limited onboard capacity of small satellites, such as CubeSats [2]. In addition, monocular camera imaging has the advantages of being less susceptible to interference in the space environment and covering a larger working range. However, historically, matching algorithms that utilize hand-engineered feature descriptors such as SIFT, FAST, SURF, and ORB are susceptible to degradation in performance due to the low signal-to-noise ratios and high contrast resulting from the variable lighting conditions in space. Crucially, non-cooperative spacecraft often lack pre-designed visual docking markers, which complicates the design of handcrafted visual matching operators.

In recent years, the rapid advancements in computer vision and artificial intelligence have led to significant breakthroughs in monocular real-time 6D pose estimation technology for various objects in daily life, particularly for standardized industrial parts, utilizing monocular cameras. Some existing works have demonstrated that the application of deep learning techniques to spacecraft imaging has markedly enhanced the precision and quality of image feature extraction, establishing it as a mainstream approach for addressing such challenges. In summary, the pose estimation method of a space-based monocular camera based on deep learning is suitable for addressing various future mission concepts related to the sustainability of near-Earth space development.

Deep-learning-based approaches still rely heavily on data, and since in-orbit images with accurate annotations are rarely available and difficult to obtain, researchers have begun using computer image rendering technology to obtain large amounts of synthetic images. While synthetic data generation and laboratory data acquisition have been identified as the most tractable ways to train and test such algorithms, the model performance degrades significantly when testing real in-orbit images [3,4]. This issue is also termed the domain adaptation problem [5]. For this subject, the European Space Agency’s Advanced Concepts Team (ACT) and Stanford University’s Space Rendezvous Laboratory (SLAB) co-organized the Satellite Pose Estimation Challenge (SPEC2021). Recently, the AI4Space workshop and the Interdisciplinary Centre for Security, Reliability and Trust (SnT) at the University of Luxembourg issued the SPARK 2024 trajectory estimation challenge [6].

In order to obtain better results, researchers have widely used multi-stage and multi-task prediction methods [2,7,8,9,10] to excavate cross-domain invariant characteristics and generated adversarial networks or “Render-and-Compare” methods to achieve style transition from source domain images to target domain images [11,12,13] to alleviate inter-domain differences. Although some methods have yielded remarkable results, employing additional neural networks for tasks such as object detection, instance segmentation, and style transfer has led to a significant increase in model parameters, making both training and inference more time-consuming. In the direct regression of the object position and attitude, the absence of interpretable image features complicates the network’s ability to swiftly learn accurate mapping relationships. Consequently, many researchers [8,9,11,14,15,16] have adopted approaches that combine keypoints detection with existing Perspective-n-Point (PnP) pose estimation solvers. This strategy employs the PnP algorithm to establish correspondences between the true 3D keypoints’ positions of the target and the predicted keypoints’ projection coordinates in the image. The mechanism for automatically selecting inliers within a customized error range mitigates the issue of prediction errors arising from blurred features in certain regions of the target due to poor image quality. Using this approach as a baseline, combined with designed 2D–3D structure losses and the pseudo-labels self-training method, Perez-Villar et al.’s [8] VPU achieved the best average score in the SPEC2021 Challenge. In order to accurately return the coordinates of keypoints, they adopted the heatmap-based method, which makes the generation of multiple heatmaps occupy a lot of time and storage space in the self-training process. Wang et al. [11] designed a CNN network to predict keypoint heatmaps and segmentation masks for spacecraft targets, and they added geometric constraints during the pseudo-label generation process. Leveraging the use of a CycleGAN network to adapt the style of the source domain images to the target domain images, they won first place in the sunlamp domain. Huang et al. [16] employed a pose regression subnetwork in place of the PnP solver, achieving superior results. However, they did not provide details on how they addressed the cross-domain issue. As the sponsor and dataset producer of SPEC2021, Park et al. [2] proposed SPNv2 as a new baseline for this task. This model simultaneously performs object detection, direct pose regression, keypoint prediction, and binary segmentation of satellite foreground masks. It also achieved commendable results after online domain refinement.

In this work, we aim to maintain high precision in the measurements while keeping the model’s structural size compact, and to improve the efficiency of the cross-domain self-training. To this end, we propose a monocular pyramid vision transformer spatial-aware keypoints regression network (PVSAR) and use OpenCV’s USAC_MAGSAC [17] to estimate spacecraft position and attitude. Under the model architecture of Encoder–Decoder, PVTv2 [18] is used as the backbone to obtain the output patches of the compressed pyramid vision transformer feature, and the keypoint feature graphs with the same size as the input are obtained through multi-layer deconvolution. Finally, by referring to the spatial-aware regression for keypoint localization (SAR) [19] proposed by Wang and Zhang, the 2D coordinates of 11 customized keypoints in the image are directly obtained. As a network directly regresses keypoint coordinates, there is no need to generate heatmaps of the Gaussian distribution as labels. This greatly saves the storage space and the time of pseudo-tag generation during self-training. The proposed PVSAR integrates seamlessly with Kalman filtering, enabling a complete vision-based autonomous navigation pipeline. We validated our method on the Spacecraft Pose Estimation Dataset (SPEED+) and the Satellite Hardware-In-the-loop Rendezvous Trajectory (SHIRT) dataset. Experimental results demonstrate that our approach achieves high precision and exhibits strong generalization capability. Our solution is available at https://github.com/indigo1973/PVSAR, accessed on 1 November 2024.

Our main contributions can be summarized as follows:

1.

By integrating PVT and SAR, we propose a novel network for monocular camera space non-cooperative target keypoints detection. This network is well suited for combining with PnP methods to obtain the target pose and for rapidly adapting to new domains through self-training techniques.

2.

We propose a local data augmentation strategy for stereoscopic perception established through keypoints and target geometric structures, which effectively enhances the generalization capability of the source domain training model.

3.

We achieved promising results on the SPEED+ and SHIRT datasets and successfully deployed the method on a mobile device. In the lightbox domain, which is a focal point of the research, our method achieves a 37.7% improvement over the baseline method SPNv2. Compared with the VPU using a heatmap for keypoint detection, a 24.7% performance improvement is obtained.

2. Methods

2.1. Overview

For a target spacecraft, our goal is to estimate its 6D pose $[R|\mathit{t}]\in SE\left(3\right)$, where R and t denote the rotation matrix and translation vector, respectively. Directly regressing the position and attitude of a spacecraft is a complex task. Moreover, the absence of strict constraints in direct regression as pseudo-label filtering criteria hinders the application of self-training techniques during the cross-domain adaptation process [20]. Benefiting from existing PnP solvers, we choose to reformulate the pose estimation problem as a keypoints coordinates regression task. In the PnP algorithm, the confidence, the range of reprojection errors and the number of inliers obtained from the solution can naturally serve as criteria for evaluating the quality of the pseudo-labels. The target spacecraft has a large movable range within the camera’s field of view, resulting in inconsistencies in the imaging quality. Researchers have previously utilized target size normalization based on bounding boxes in images for regression, and they have employed heatmap-based methods to enable the network to locate keypoints more swiftly and accurately. However, the former approach often results in erroneous pose outputs due to deviations in the target detection, while the latter is limited by the inherent challenges of heatmap-based methods in accurately locating points outside the image. We used the method of direct regression, and the flowchart of the whole method is shown in Figure 1.

We first completed the dataset preprocessing. For the Tango satellite target in the SPEED+ dataset, we selected the 11 keypoints provided by the official sources. In the training set, we computed the projection coordinates of the keypoints in the image using the provided pose labels, camera intrinsic matrix, and camera distortion coefficients. Considering that the target satellite body is a rectangular, we identified which surfaces of the spacecraft target can be observed in the image based on the keypoint closest to the origin of the camera coordinate system during the projection coordinate calculation. After resizing, data augmentation, and normalization of the input images, we proceeded to train the designed PVSAR network. Our network can output the pixel coordinates of each keypoint in the original image, and we can obtain the corresponding pose estimation results using the existing marginalizing sample consensus (MAGSAC) PnP solver. Finally, we used the number of inliers from the PnP results as a criterion to generate new small sample datasets online, thereby achieving a cross-domain self-training loop.

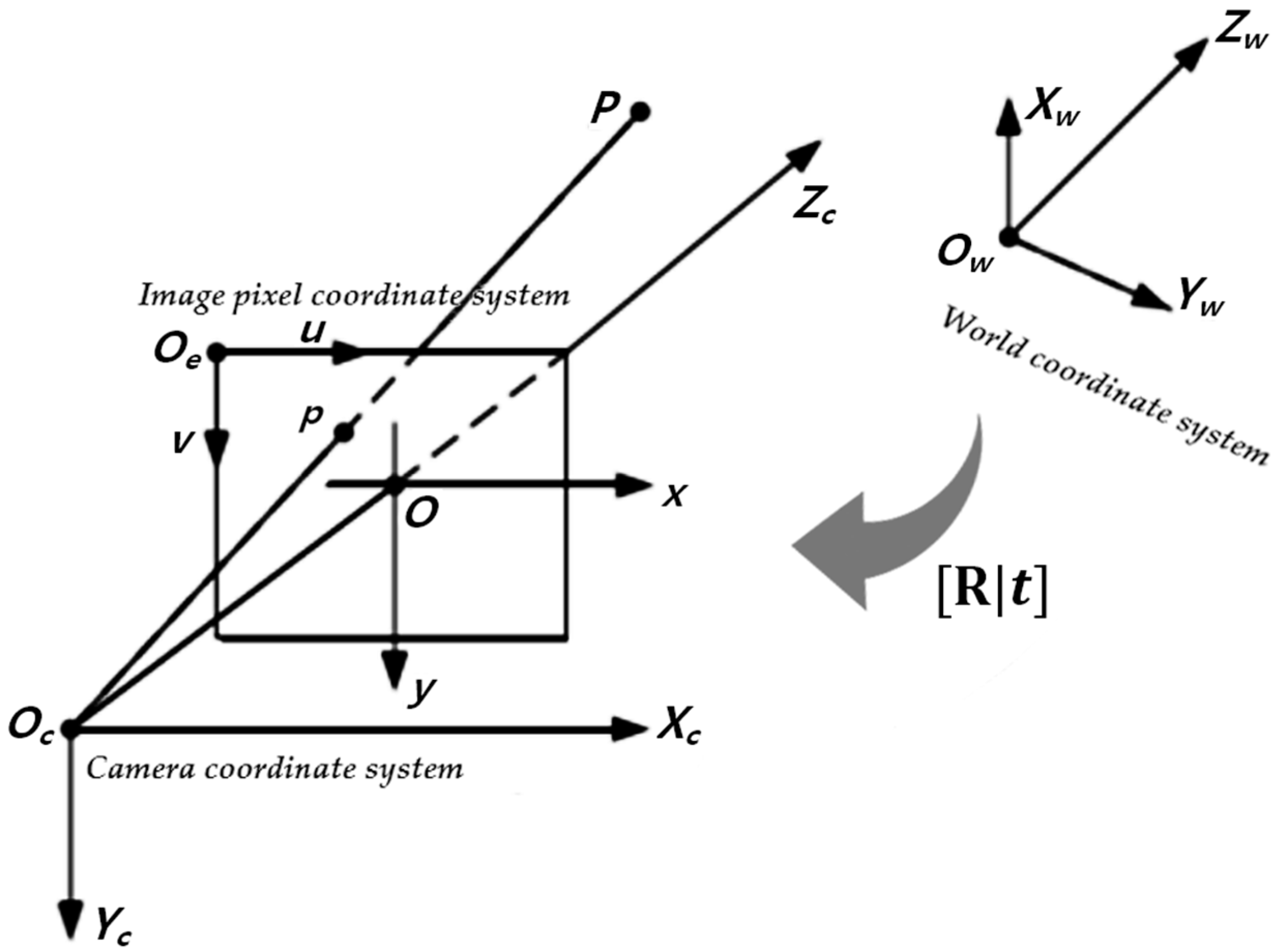
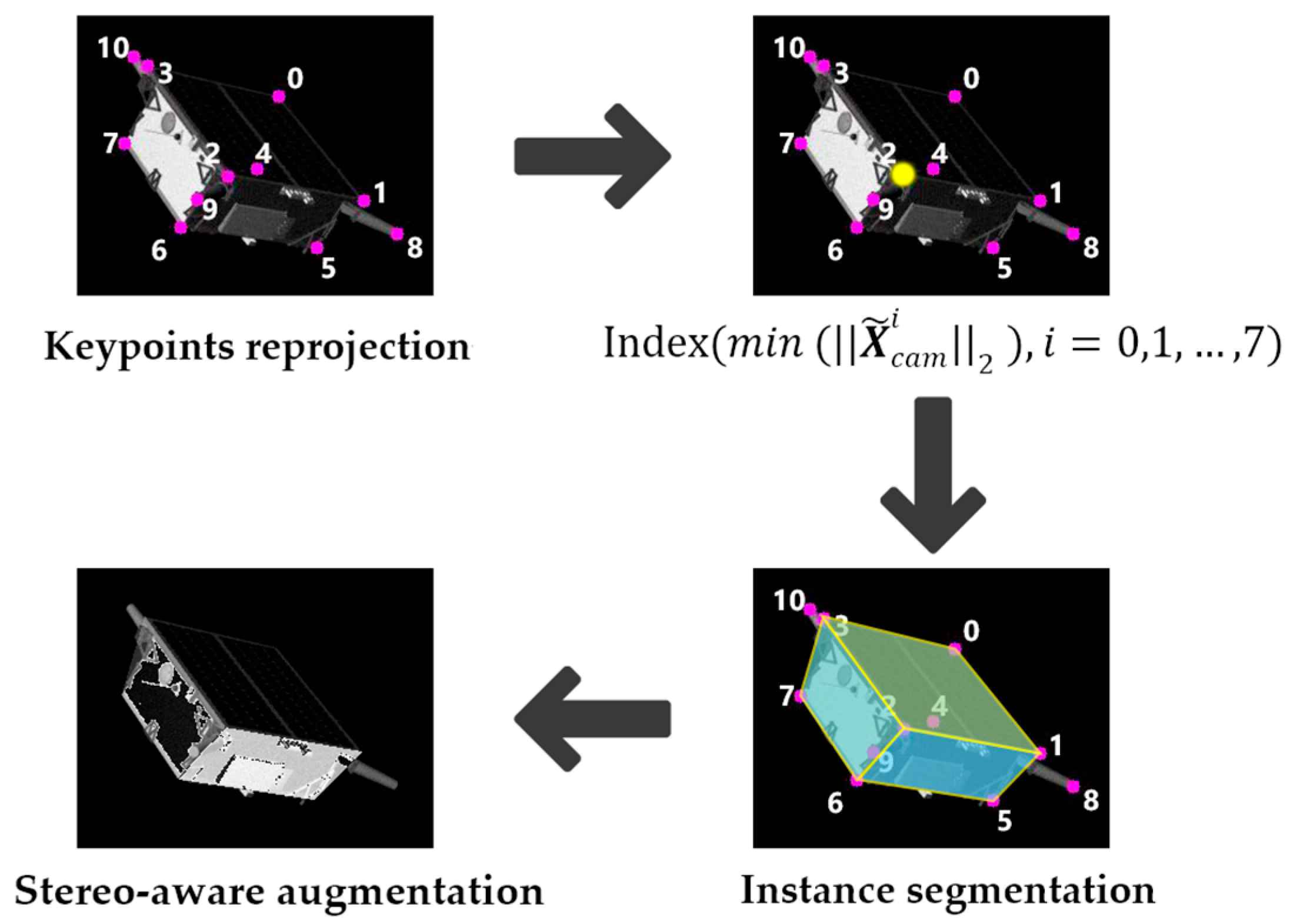
2.2. Three-Dimensional Reconstruction and Reprojection

The monocular camera projects the 3D world objects onto the 2D imaging plane of the camera through its imaging lens, with the 3D spatial coordinates and 2D pixel coordinates related by a homography matrix. Based on the known information about the target, we can solve the spatial information of the 3D object corresponding to the 2D pixel coordinate location of the feature points by extracting and matching the keypoint features from the captured images. To calculate the relative pose relationship between the target and the camera in 3D space, it is crucial to define the transformation relationships among the various coordinate systems. The spacecraft pose estimation task can directly merge the target coordinate system with the world coordinate system, allowing for the determination of the translation and rotation of the target coordinate system relative to the camera coordinate system on the servicing spacecraft. This perspective projection transformation relationship between the camera image pixel coordinate system and the 3D space is shown in Figure 2. The transformation from the world coordinate system to the camera coordinate system can be expressed in homogeneous coordinates as in Equation (1).

$${\mathit{X}}_{cam}=\left[\begin{array}{cc}R& -R\tilde{\mathit{C}}\\ {\mathbf{0}}^T& 1\end{array}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)=\left[\begin{array}{cc}R& -R\tilde{\mathit{C}}\\ {\mathbf{0}}^T& 1\end{array}\right]\mathit{X}$$

(1)

where $\mathit{X}$ is a four-dimensional homogeneous vector of the coordinates of a point in the world coordinate system, ${\mathit{X}}_{cam}$ is the representation of the same point in the camera coordinate system, $\tilde{\mathit{C}}$ refers the 3 × 1 inhomogeneous vector of the coordinates of the camera center in the world coordinate system, and $R$ is a 3 × 3 rotation matrix representing the orientation of the camera coordinate system. The $-R\tilde{\mathit{C}}$ in the above equation is the translation vector t to be evaluated. According to the principle of pinhole imaging, by introducing the camera intrinsic parameter matrix K, the projection coordinates vector $\mathit{x}$ of this point in the image pixel coordinate system can be obtained through Equation (2). Here, $u$ and $v$ represent the coordinate positions in the pixel coordinate system, and $I$ denotes a 3 × 3 identity matrix. To achieve more accurate results, it is also necessary to apply radial correction using the lens distortion coefficients.

$$\mathit{x}=\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=K[R\left|\mathit{t}\left]\mathit{X}=KR\right[I\right|-\tilde{\mathit{C}}]\mathit{X}$$

(2)

At this point, we were able to accurately compute the 2D coordinates of the 11 keypoints using the officially provided 3D coordinates and pose labels. Compared to manually annotating a large number of images in the training set, this method is not only faster and more precise but also capable of identifying the occluded keypoints of rigid objects. In the absence of known 3D keypoint coordinates, the three-dimensional reconstruction of spacecraft targets can be achieved using the principles of multi-view geometry in computer vision, followed by the selection of keypoints. The images in the training set, along with the camera’s external parameters (pose labels), can be directly used as input for triangulation. Existing software such as COLMAP v3.11 [21,22] can be utilized to complete the 3D reconstruction. The keypoints need to be defined according to the 3D object model. In general, we choose the vertices of the target wireframe model as keypoints. Using keypoints scattered on the surface of the target object can make the subsequent PnP algorithm more stable. For example, the farthest point sampling (FPS) algorithm is used to select keypoints in PVNet [23]. In the case of the same number of keypoints, selecting non-coplanar points generally leads to the higher accuracy of pose estimation [24]. To implement the stereo-aware enhancement method, we selected the vertices of each plane of the object as keypoints.

2.3. Data Augmentation

Data augmentation is often the only strategy to improve the generalization ability of a model without exploiting the test set images. On the one hand, diversifying the training samples can effectively alleviate model overfitting in the source domain; on the other hand, appropriate image transformations can help align the feature representations of the training domain images with those of the test domain images. Although researchers have employed neural-network-based methods such as CycleGAN and style augmentation to achieve the enhancement of spacecraft styles and textures in synthetic domain images, significantly improving the generalization ability of pose estimation models, these approaches necessitate an additional model inference process to obtain the transformed images and require extra storage space to save them. We followed the strategy in SPNv2, using random brightness contrast, random solar flare, blur, and noise from the Albumentations library, but abandoning the random erase because we believe that Random Sun Flare has achieved random occlusion of the spacecraft target, while coarse dropout destroys the target structure characteristics and surface texture. Building on this, we consider that the solar reflectance varies significantly among different materials on the satellite’s surface, particularly with multi-layer insulating materials, which tend to exhibit strong specular reflections. Through the simulations and experimental results conducted by Wang et al. [25], it is evident that under varying lighting conditions, the bidirectional reflectance distribution function (BRDF) values of thermal control multilayer materials are significantly greater than those of solar panels. However, in the synthetic data, the illumination effects are predominantly represented as diffuse reflections. We believe that this constitutes the largest discrepancy between the synthetic domain and real-world imaging, aside from the surface texture of the target.

Based on this analysis, we designed a stereo-aware local data augmentation method. Specifically, since the target satellite body has a structure that approximates a rectangular cuboid, we selected the eight vertices of the cuboid as the keypoints. After calculating the coordinates of the eight vertices in the camera coordinate system using Equation (1), the closest vertex to the camera origin can be identified by evaluating the Euclidean distances. Based on the structural characteristics of the rectangular cuboid, we can further determine which surfaces are visible while the remaining ones are in a state of self-occlusion. By obtaining the vertex indices of the visible surfaces, we can identify their corresponding coordinates in the image. Connecting these points in order allows us to distinguish these surfaces in the image, thus achieving a simple form of instance segmentation. For more accurate segmentation results, the official target foreground mask can be used in conjunction with the surface obtained by this method through a bitwise AND operation; however, this will require additional storge space. According to the set probabilities, we sequentially add a random number to the grayscale values of these surfaces to simulate complex and variable lighting conditions. The whole process is shown in Figure 3.

We also experimented with random brightness and contrast transformations, but the former yielded better results. We believe that this approach preserves the texture characteristics of the target surfaces to a greater extent and, due to the effects of the color inversion after overflow, produces some instances that are more closely aligned with the real-world imaging outcomes. Figure 4 presents a visualization of the data augmentation using img000005 from the training set. The first image in the top-left corner is the original image, while the two adjacent images show the results of the stereo-aware augmentation. For each type of data augmentation, we maintained the implementation probability of 0.5, as set in SPNv2.

2.4. PVSAR Network

The main architecture of the PVSAR network is illustrated in Figure 5. In this framework, we employ a PVTv2 backbone with pre-trained weights to extract features. Subsequently, we apply five sequences of deconvolution operation, along with batch normalization and rectified linear unit (ReLU) activation, to generate the keypoints’ feature maps with the same size as the input image.

Considering the varying relative distances between the spacecraft and the camera, the target sizes in the images differ significantly. For the spacecraft pose estimation task, the input image size is significantly larger than that of the object classification task. Meanwhile, in order to facilitate subsequent deployment on mobile devices, we selected the PVTv2-B1 version, which has a smaller number of parameters. Compared to ResNet18 of a similar size, PVTv2 has demonstrated significantly better performance across tasks such as image classification, object detection, and semantic segmentation. Additionally, PVTv2 can process images of any size, showcasing computational efficiency even with high-resolution inputs [18]. PVTv2 uses a pyramid vision transformer architecture to extract rich multi-scale features, and we use the last-level features.

When training with the SAR [19] method, it is necessary to integrate spatial positional priors into the regression. To enhance the localization performance, we aimed for the output feature map of the final layer to be consistent in size with the input image, enabling a direct correspondence between the two image coordinate systems. We employed a layer-by-layer deconvolution method, which not only expands the feature map size but also increases the network depth. A single deconvolution layer can be represented by Equation (3).

$$F_{n+1}=ReLU\left(BatchNorm2d\left(ConvTranspose2d(F_n\right)\right))$$

(3)

After obtaining the feature maps of the original size, through two independent convolution operations, the keypoint features and logit features are generated. At this stage, we can integrate the spatial positional priors into the regression process, similar to the SAR methodology, which can be represented as follows:

$$K_t=\mathcal{R}\left(f_t\right)+p_t$$

(4)

where $\mathcal{R}\left(f_t\right)$ represents the regression on the visual feature corresponding to the t-th grid, and $p_t$ is its location prior. $K_t$ is the regressed output by the t-th grid. $f_t$ is obtained by directly taking the feature value at the corresponding location of keypoint feature map $F_{kpt}$ in Figure 5. Our goal is to optimize $K_t$ so that it approximates the true value $K^{\ast }$, computing the regression quality score $r_t$ for each grid using the Laplacian kernel. λ is a tunable hyperparameter and defaults to 16.

$$r_t=e^{-\lambda \cdot \left|K_t-K^{\ast }\right|}$$

(5)

The logit features in Figure 5 are utilized as confidence scores, and the corresponding regression weight values $w_t$ are obtained through the SoftMax function. We further obtain a unified loss function, as represented as Equation (6), which aims to maximize the overall regression quality score weighted by the regression confidence.

$$\mathcal{L}=-\log \sum w_t\cdot r_t$$

(6)

In the inference phase, it only needs to find the $K_{top}$ corresponding to the index with the maximum confidence value as the keypoint coordinate position output.

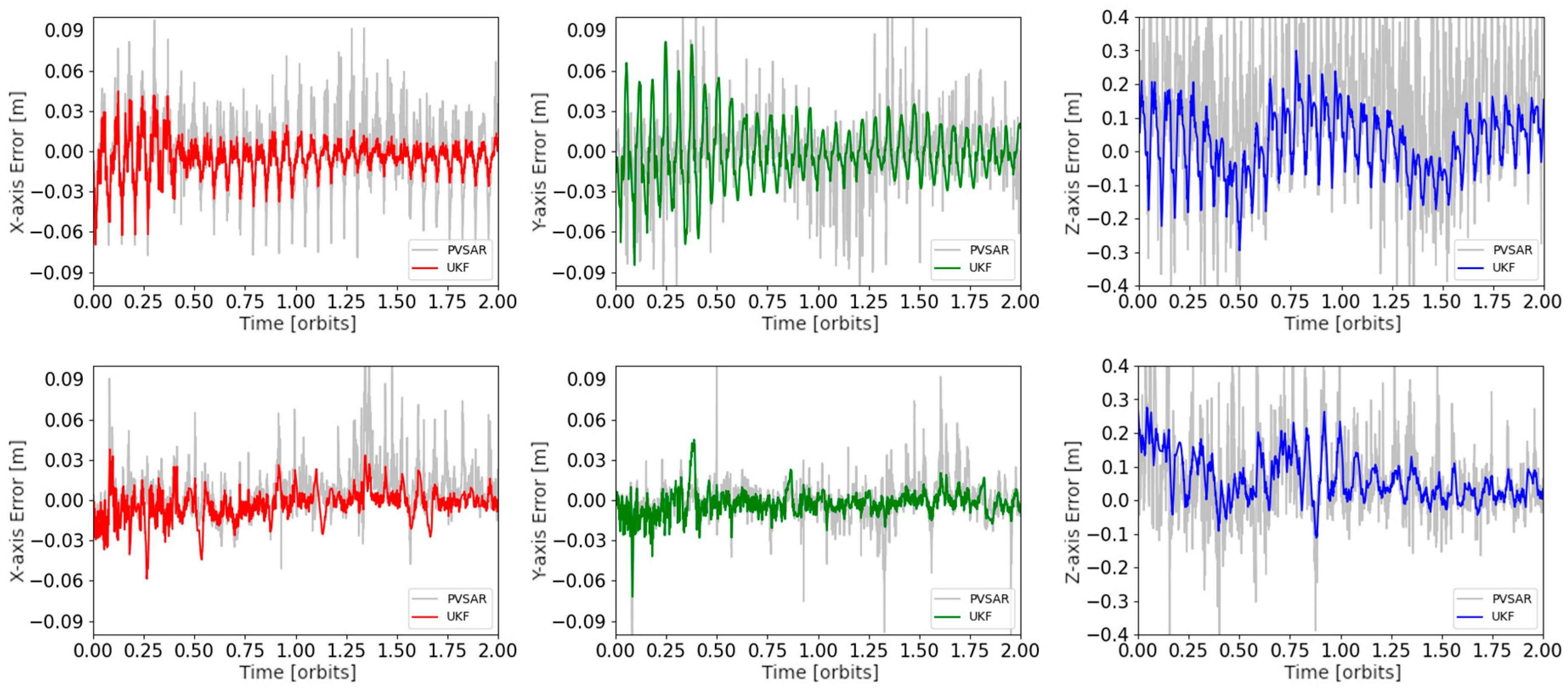
2.5. PnP and Online Self-Training

After obtaining the estimated values of the key two-dimensional projection positions, we utilize the PnP algorithm to solve the nonlinear equations, resulting in the pose matrix represented in Equation (3). Unlike the RANSAC_EPnP commonly used in the past, we have opted for MAGSAC [17]. Random sample consensus (RANSAC) employs a fixed threshold to classify inliers and outliers, whereas MAGSAC adapts this threshold based on the data, thereby enhancing the robustness under varying conditions. MAGSAC typically converges faster than RANSAC because it can optimize estimates more effectively, making it suitable for larger datasets and yielding more accurate results. Using the USAC_MAGSAC method provided by OpenCV, no infinite or non-numeric outputs were observed during testing. To ensure the robustness, we output the initial pose in cases where the PnP solver has no result to prevent program interruption. At this point, we have realized the whole process of spacecraft pose estimation. To address any cross-domain adaptation issues, we utilized an online self-training method, with the pseudo-label generation process illustrated in Figure 6.

The selected keypoints consist of the eight vertices of the satellite’s rectangular body and three antenna vertices, which can be difficult to distinguish from each other in some observation cases. This ambiguity can lead to some incorrect keypoint predictions achieving high confidence scores. Therefore, we chose to use the number of inliers returned by the PnP solver, rather than confidence scores, as the constraint to determine whether the current pose output can be further utilized to create pseudo-labels. The method for generating pseudo-labels is the same as the reprojection approach introduced in Section 2.2. Thanks to our use of direct regression, we only need to save the reprojection coordinate positions, without the need to produce a large number of heatmap labels. When generating pseudo-labels, we set a smaller reprojection error threshold for determining inliers compared to the inference stage in order to mitigate the forgetting problem. However, since the nature of online pseudo-label self-training involves learning from labels that contain errors, noise is inevitably introduced throughout the iterative process, making model forgetting almost unavoidable. Gradually relaxing the constraints on the number of inliers during the self-training loop is expected to yield better average scores on the test set, although this may result in shifts in the defined 3D keypoint positions.

3. Experiments

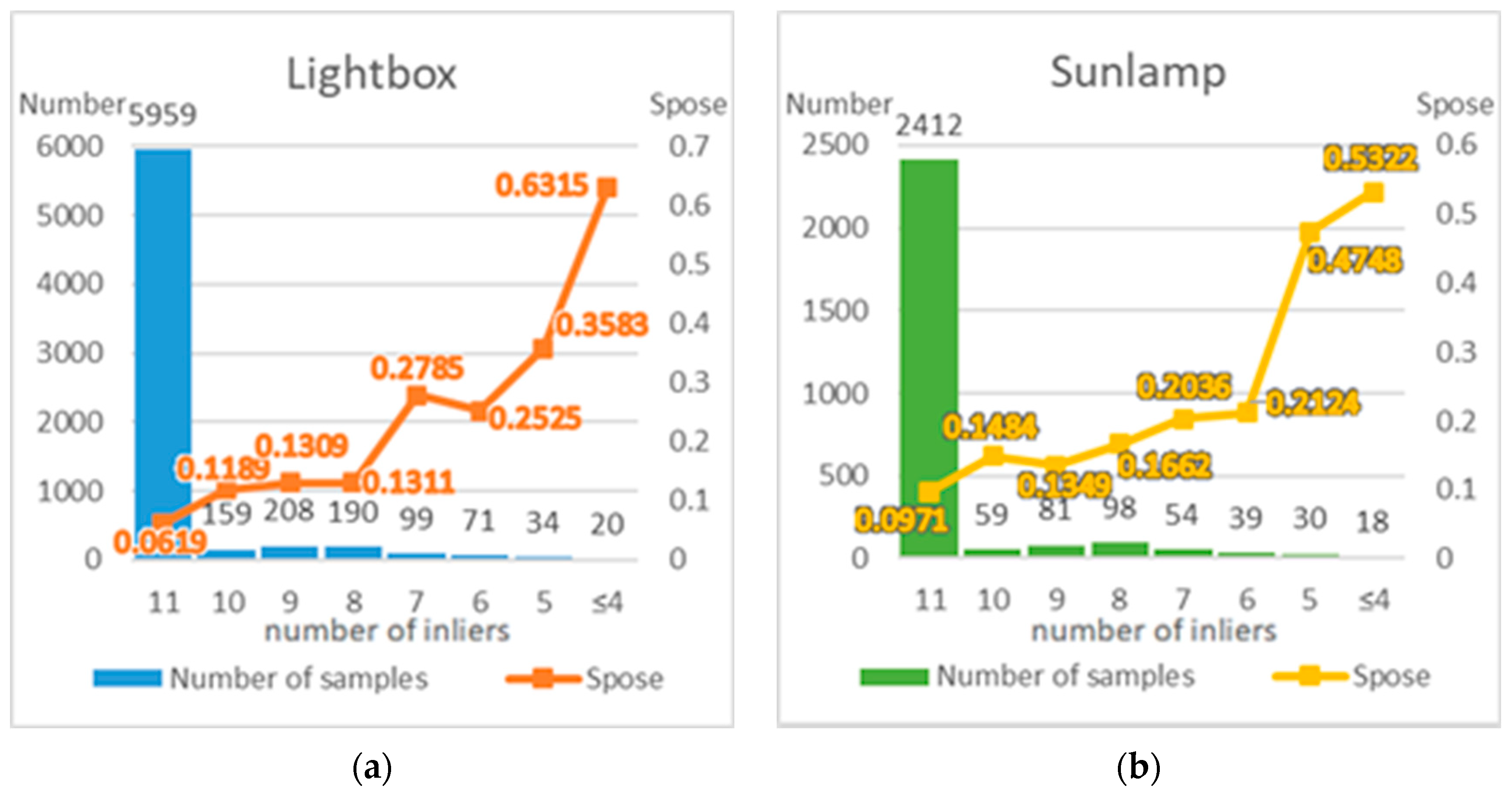
3.1. Dataset Analysis

To address the issue of pose estimation for spacecraft using monocular cameras cross-domain, SPEC2021 released the SPEED+ dataset, which focuses on the Tango spacecraft of the PRISMA mission. The Tango spacecraft model is shaped like a frustum and can be roughly simplified to an 80 cm × 80 cm × 30 cm cuboid. In addition to the 59,960 synthetic images generated through the OpenGL rendering pipeline, which are divided into training and validation sets in a 4:1 ratio, the SPEED+ dataset includes 9533 images of physical models captured using the Rendezvous and Optical Navigation (TRON) test platform [26], featuring diverse pose distributions and high-fidelity lighting configurations. The lightbox and sunlamp represent the results of two different lighting setups: the lightbox simulates diffuse illumination using reflectance lamps that mimic the Earth’s albedo, while the sunlamp utilizes metal halide lamps to simulate the direct, high-intensity, uniform sunlight typically encountered in Earth orbit. Both of them use the same pinhole camera model as the synthetic data and are employed as cross-domain test data in the SPEC2021 competition. The test images of SPEED+ expand the three-dimensional space and distance up to 10 m, providing a unique and unprecedented quantity and quality of spacecraft model images. In addition to providing pose labels for synthetic domain images in terms of three-axis translation and rotation quaternion in the camera’s Euclidean coordinate system, along with the new baseline SPNv2, the dataset creators also offered the 3D ground truth coordinates for the body vertices and antenna vertices, as well as binary segmentation masks for the target satellite foreground. Building upon the SPEED+ dataset, Park et al. [27] released the new Satellite Hardware-In-the-loop Rendezvous Trajectories (SHIRT) dataset, which simulates sequences of images of target physical satellites during rendezvous trajectories. The SHIRT dataset provides two representative in-orbit rendezvous docking scenarios, each containing sequences of images from both the synthetic and lightbox domains under the same pose labels. Although the synthetic and lightbox domain images of the same trajectory have geometric and lighting consistency, there are still noticeable visual differences. The lightbox trajectory images in SHIRT can be used for quantitative analysis of the performance of the designed pose estimation model and the navigation filter across domain gaps. Examples of images from the different domains in the dataset are shown in Figure 7.

3.2. Evaluation Metrics and Implementation Details

To facilitate comparison with other methods, we utilized the evaluation standards provided by the ESA to define the estimation errors for the translation, rotation, and 6D pose. The rotation quantity is represented by the unit rotation quaternion q, and the translation quantity is represented by the 3D translation vector T. In SPEC2021, taking into account the precision of hardware devices, translation errors below 2.173 mm/m and rotation errors below 0.169° can be considered negligible, respectively. The specific calculation formula is given in Equation (7), and the final score S_pose is the average of the scores of all the samples.

$$\left\{\begin{array}{c}{S}_{pose}^{\left(i\right)}=S_R^{\left(i\right)}+S_t^{\left(i\right)}, \hfill \\ S_R^{\left(i\right)}=2arccos\left(\left|\langle {\mathit{q}}_{est}^{\left(i\right)},{\mathit{q}}_{gt}^{\left(i\right)}\rangle \right|\right),S_R^{\left(i\right)}=0 if{S}_R^{\left(i\right)}<0.00295\hfill \\ \Delta t^{\left(i\right)}={\Vert {\mathit{T}}_{gt}^{\left(i\right)}-{\mathit{T}}_{est}^{\left(i\right)}\Vert }_2\hfill \\ S_t^{\left(i\right)}={\displaystyle \frac{\Delta t^{\left(i\right)}}{{\Vert {\mathit{T}}_{gt}^{\left(i\right)}\Vert }_2}}, S_t^{\left(i\right)}=0 if S_t^{\left(i\right)}<0.002173\hfill \end{array}\right.$$

(7)

Our model is trained on an NVIDIA GeForce RTX4090D GPU and implemented by PyTorch. The AdamW optimizer is used with a start learning rate of 0.0001 and a batch size of 8. The learning rate is decremented from the 5th epoch, set to 0.00002 from the 30th epoch, and 0.000001 from the 40th epoch, with a total of 50 epochs trained. The input image is resized from 1920 × 1200 to 768 × 480. In accordance with the competition setup, we used only 47,966 samples from the synthetic data as the training set, while the remaining 11,994 samples served as the validation set. The lightbox and sunlamp data were specified as the test sets.

During the online pseudo-labeling self-training phase, the use of true labels or manually annotated data is not permitted. The learning rate is set to 0.00001, with an inner point quantity threshold successively set to 9, 8, and 7, training for 10 epochs each, totaling 30 epochs. During inference testing, the PnP solver’s confidence is set to 0.99 and the reprojection error is set to 20.0.

3.3. Results and Discussion

3.3.1. Offline Training Results

First, PVSAR is trained on the synthetic domain dataset accompanied by a series of data augmentation.

Table 1. Ablation experiments for data augmentation. Bold numbers indicate best performances.

Data Augmentation Methods	Synthetic			Lightbox			Sunlamp
	St	SR	Spose	St	SR	Spose	St	SR	Spose
Only Normalize	0.0024	0.0105	0.0129	0.2412	0.5629	0.8041	0.1997	0.7185	0.9183
+Sun Flare, Noise, etc.	0.0037	0.0141	0.0178	0.0423	0.151	0.1933	0.1398	0.4678	0.6076
+Stereo-aware Aug.	0.0037	0.0144	0.0182	0.0344	0.1087	0.1431	0.1471	0.4206	0.5677

presents the results of the ablation study conducted on the employed data augmentation methods.

It can be seen that the proposed stereo-aware augmentation effectively enhances the model’s generalization capability. The offline-trained model performs poorly in the sunlamp domain, which does not imply that our keypoint regression model has not learned adequately. As shown in Figure 7, the sunlamp domain includes images that capture metal halide lamps, which possess certain characteristics similar to those of the target spacecraft. Errors in the keypoint regression can significantly affect the pose estimation results from PnP calculations, but the online pseudo-label self-training phase can gradually correct these errors. During the self-training phase, we use the number of inliers from the PnP calculations as a constraint. Therefore, we conduct inference testing on the model obtained from offline training, analyzing the sample count and the estimation errors of 6D poses under varying inlier thresholds. In order to set strict constraints in the self-training process, the reprojection error of the PnP is set to 5, and the results are shown in Figure 8.

Consistent with our expectations, samples with a greater number of inliers generally exhibit smaller pose estimation errors. The results from the lightbox domain consistently outperform those from the sunlamp domain, which is logical, as subjective observations suggest that lightbox is more closely aligned with the synthetic data used for training. In other words, the data distribution in the sunlamp domain shows a greater deviation.

3.3.2. Self-Training Results

We use SPNv2 as the baseline and compare our method with results from several known high-performing methods. Some of these methods achieve impressive results, but their parameters cannot be quantified as they are not open source. The highest-scoring method currently is a dense matching approach proposed by Ulmer et al. [12], which, as we understand, is significantly more complex than keypoint-based sparse matching. Additionally, their model has at least 88 M parameters based on the backbone they used.

Compared to the current state-of-the-art methods, we do not require additional network models for object detection and data augmentation, nor have we designed multi-head predictions. Our network architecture is simpler and more direct, resulting in fewer parameters. Coupled with efficient pseudo-label self-training techniques, our method clearly outperforms the baseline and demonstrates competitive performance. The results are shown in

Table 2. Comparison with the top ten state-of-the-art methods.

Methods	Additional Model	Num. of Param.	Lightbox			Sunlamp
			St	SR	Spose	St	SR	Spose
EagerNet [12]	-	>88 M	0.009	0.031	0.039	0.013	0.046	0.059
haoranhuang_njust [16]	-	-	0.014	0.051	0.065	0.011	0.048	0.059
TangoUnchained [4]	Object detection	-	0.017	0.056	0.073	0.015	0.075	0.090
Legrand et al. [13]	NeRF	-	0.021	0.064	0.085	0.033	0.136	0.169
VPU [8]	/	190.1 M	0.021	0.080	0.101	0.012	0.049	0.061
PVSPE [10]	/	-	0.017	0.084	0.101	0.022	0.156	0.178
prow	-	-	0.019	0.094	0.114	0.013	0.084	0.097
SPNv2 [2]	Style Aug.	52.5 M	0.025	0.097	0.122	0.027	0.170	0.197
Liu et al. [28]	Object detection	-	0.03	0.12	0.15	0.03	0.10	0.13
lava1302 [11]	NeuS, CycleGAN	-	0.046	0.116	0.163	0.007	0.048	0.055
Ours	/	30.6 M	0.018	0.057	0.076	0.023	0.089	0.112

.

By visualizing the inference results, we further analyze the performance of our model. Figure 9 and Figure 10 illustrate the model inference results before and after pseudo-label self-training in the lightbox and sunlamp domains, respectively. The predicted object coordinate system is represented by RGB arrows, while the predicted target satellite bodies and their corresponding ground truth are delineated using cyan and yellow wireframes.

It can be seen that the use of pseudo-label self-training significantly enhances the cross-domain accuracy of our pose estimation outputs without exhibiting any model degradation. Particularly in the sunlamp domain, the model has successfully distinguished between metal halide lamps and target spacecraft through online self-learning, in the absence of manual annotations. We also plotted histograms of the final model inference results, showing the sample counts and 6D pose estimation errors at different inlier threshold values, as seen in Figure 11. Compared to Figure 8, it is clear that our pseudo-label self-training method enables the model to effectively learn features from new domains, resulting in improved pose outputs. Our model also achieves correct results after being deployed on an NVIDIA AGX Xavier mobile device.

At last, we focus on some of the worst-performing samples in the two domains, as shown in Figure 12. In the lightbox domain, certain images suffer from suboptimal lighting conditions or improper camera exposure settings, making it difficult to observe the target spacecraft. In the sunlamp domain, harsh lighting obscures the spacecraft and additional background noise further complicates detection. These challenging scenarios can lead to ambiguity in keypoint detection, resulting in the misidentification of the current keypoint as belonging to another keypoint. Notably, when calculating the score S_pose, the rotation error is not normalized like the translation error, generally resulting in a larger impact. Errors in the keypoint identification can cause the output pose to exhibit a flipped relationship with the ground truth, thereby maximizing the rotation error. In real space rendezvous scenarios, the input image sequences are continuous, and employing filtering techniques holds promise for addressing the pose estimation errors induced by such ambiguities.

3.3.3. Validation on SHIRT

The SHIRT dataset contains two image sequences simulating accompanying flight and approach operations in a typical low Earth orbit (LEO) rendezvous scenario, respectively. In sequence 1, the server maintains a relatively constant position, while in sequence 2, it executes a spiral approach trajectory toward the target. We directly tested the model on the lightbox domain of the SHIRT dataset and found that sequence 2 achieved the same score as on the SPEED+ dataset, while the first sequence’s score dropped to 0.175. This phenomenon is consistent with the experimental results of SPNv2. Upon examining sequence 1, we observed that the target was far away and, due to the suboptimal lighting conditions, tended to blend into the background. This easily led to the keypoint ambiguities described in Figure 12. By introducing a simple filtering mechanism that outputs the pose of the previous frame when the pose error S_pose between the current frame and the previous frame exceeds 2.0, we were able to improve the score for sequence 1 to 0.135. To fully leverage the temporal continuity of the image sequences, we used a navigation filter based on an unscented Kalman filter and low-pass filter to further refine the output pose. Directly applying the Kalman filter to the rotated quaternion is complicated, so we converted it to the r6d [29] representation and used the Euler angle representation when computing the error. This also meets the criteria for pitch, yaw, and roll angles commonly used for displays in the guidance, navigation, and control (GNC) systems. Figure 13 and Figure 14 show the effect of the navigation filter, where the rotation error at the degree level and the translation error at the centimeter level can be achieved in a steady state. The average error is less than 5° or 5 cm. In these figures, the gray part is the result of direct inference by the model, and the colored part is the filtered result.

4. Conclusions

This paper presents PVSAR, a keypoint position regression network based on a vision transformer (ViT), for the task of monocular camera-based non-cooperative spacecraft pose estimation. A spatial-aware local augmentation method is proposed to effectively enhance the model’s generalization capability during the offline training phase. We further employ pseudo-label self-training technology and Kalman filters to establish a vision-based autonomous navigation pipeline. The proposed method has been validated on the latest SPEED+ and SHIRT datasets, and the experimental results demonstrate that our method effectively handles cross-domain issues and can be applied as a visual navigation solution in the GNC subsystems of service spacecraft. In the future, we will further improve the tracking pose navigation filter and mine the best performance of the current method. The lightweight version of the current network architecture will be investigated to reduce the amount of computation and improve the reasoning speed on mobile devices.