A Study on the Aerodynamic Impact of Rotors on Fixed Wings During the Transition Phase in Compound-Wing UAVs
Abstract
:1. Introduction
2. Models and Methods
2.1. Numerrical Simulation Methods
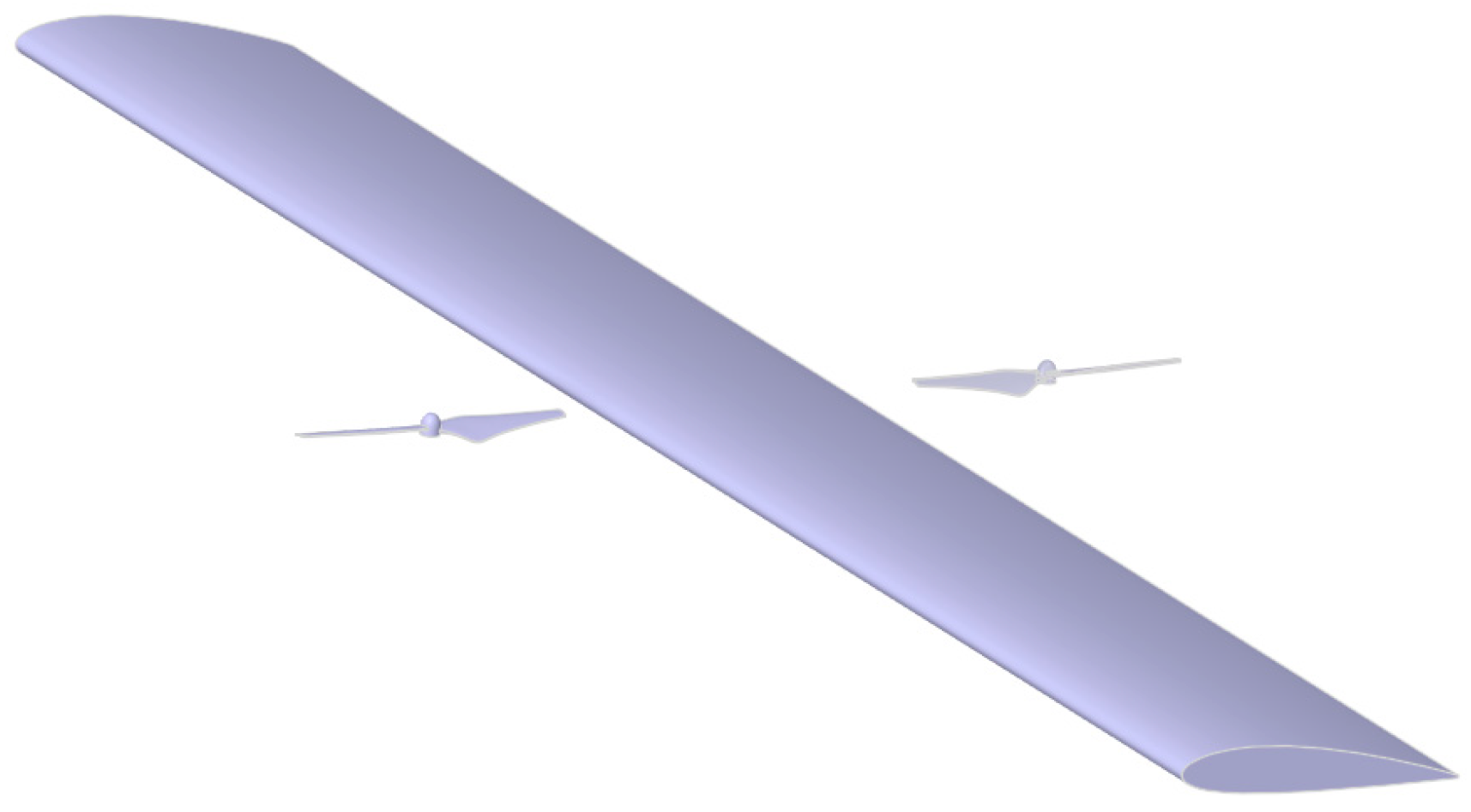
2.2. Computational Model
2.3. Computational Domain
2.4. Mesh Generation
2.5. Solver Settings
2.6. Validation of Numerical Method
2.7. Mesh Independence Study
3. Results and Discussion
3.1. Setting of Rotor Position
3.2. Effect of Rotor Position on Magnitude of Fixed-Wing Lift and Drag
3.3. Fluctuating Effects of Rotor on Lift and Drag in Fixed Wing
3.4. Discusstion
4. Conclusions
- (1)
- The fixed wing’s lift and drag decreased with the decreasing distance of the front rotor; the fixed wing’s lift and drag increased with the decreasing distance of the rear rotor.
- (2)
- During the rotation of the rotor, the lift and drag fluctuations of the fixed wing changed periodically due to the influence of the rotor wake, and the fixed wing’s lift and drag fluctuations decreased as the distance between the front and rear rotors and the fixed wing increased.
- (3)
- During the design of the compound-wing UAV, the front and rear rotor mounting positions should be set as R/L1 = 0.25 and R/L2 = 0.25. With these values, it is possible to mitigate the lift and drag fluctuations of the fixed wing due to the rotor wake, while the total lift and total drag are only slightly changed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alsamhi, S.H.; Ma, O.; Ansari, M.S.; Almalki, F.A. Survey on Collaborative Smart Drones and Internet of Things for Improving Smartness of Smart Cities. IEEE Access 2019, 7, 128125–128152. [Google Scholar] [CrossRef]
- Rejeb, A.; Abdollahi, A.; Rejeb, K.; Zailani, S.; Treiblmaier, H. Drones in agriculture: A review and bibliometric analysis. Comput. Electron. Agric. 2022, 198, 107017. [Google Scholar] [CrossRef]
- Ghali, R.; Akhloufi, M.A. Deep learning approaches for wildland fires remote sensing: Classification, detection, and segmentation. Remote Sens. 2023, 15, 1821. [Google Scholar] [CrossRef]
- Kinaneva, D.; Hristov, G.; Raychev, J.; Gadzhev, V. Early forest fire detection using drones and artificial intelligence. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 1060–1065. [Google Scholar]
- Sungheetha, A.; Sharma, R. Real-time monitoring and fire detection using internet of things and cloud-based drones. J. Soft Comput. Paradigm 2020, 2, 168–174. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Shvetsov, A.V.; Kumar, S.; Ansari, M.S.; Rajput, N.S.; Baker, T. UAV computing-assisted search and rescue mission framework for disaster and harsh environment mitigation. Drones 2022, 6, 154. [Google Scholar] [CrossRef]
- Amukele, T. Current state of drones in healthcare: Challenges and opportunities. J. Appl. Lab. Med. 2019, 4, 296–298. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.T.; Lee, S.; Son, H.C.; Jeong, H.; Mohaisen, A. Survey on anti-drone systems: Components, designs, and challenges. IEEE Access 2021, 9, 42635–42659. [Google Scholar] [CrossRef]
- Gregory, D. From a view to a kill: Drones and late modern war. Theory Cult. Soc. 2011, 28, 188–215. [Google Scholar] [CrossRef]
- Yaacoub, J.P.; Noura, H.; Salman, O.; Chehab, A. Security analysis of drones systems: Attacks, limitations, and recommendations. Internet Things 2020, 11, 100218. [Google Scholar] [CrossRef]
- Kai, J.M. Full-envelope flight control for compound vertical takeoff and landing aircraft. J. Guid. Control Dyn. 2024, 47, 1–17. [Google Scholar] [CrossRef]
- Misra, A.; Jayachandran, S.; Kenche, S.; Sharma, M. A review on vertical take-off and landing (VTOL) tilt-rotor and tilt wing unmanned aerial vehicles (UAVs). J. Eng. 2022, 2022, 1803638. [Google Scholar] [CrossRef]
- Sembiring, J.; Sasongko, R.A.; Bastian, E.I.; Hidayat, S. A deep learning approach for trajectory control of tilt-rotor UAV. Aerospace 2024, 11, 96. [Google Scholar] [CrossRef]
- Anderson, R.B.; Marshall, J.A.; L’Afflitto, A. Constrained robust model reference adaptive control of a tilt-rotor quadcopter pulling an unmodeled cart. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 39–54. [Google Scholar] [CrossRef]
- Filippone, A. Flight Performance of Fixed and Rotary Wing Aircraft; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Liu, Y. Vertical Takeoff and Landing Fixed-Wing UAV Design, Control, and Test. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- He, X.; Li, Y.; Zhu, F.; Yu, L. Development status and design and manufacturing key technology of foreign vertical take-off and landing unmanned aircraft. Fly. Missile 2016, 6, 22–27. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, C.; Wang, Q. Development of new vertical takeoff and landing unmanned aircraft. In Proceedings of the 2014 (Fifth) China UAV Conference; China Aeronautical Society: Beijing, China; Chinese People’s Liberation Army Air Force Equipment Department: Beijing, China; Chinese People’s Liberation Army Navy Aerospace Technology Department: Beijing, China; Aviation Industry Corporation of China: Beijing, China; Beijing University of Aeronautics and Astronautics: Beijing, China, 2014; p. 7. [Google Scholar]
- Wei, Z.; Liu, F.; Yang, S. Development status and technical points of vertical take-off and landing fixed-wing UAV. Aircraft Design 2024, 44, 5–13. [Google Scholar] [CrossRef]
- Garcia, A.J.; Barakos, G.N. Numerical simulations on the ERICA tiltrotor. Aerosp. Sci. Technol. 2017, 64, 171–191. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Q.; Wang, Z.; Wang, B. Highly-efficient CFD method for predicting aerodynamic force of tiltrotor in conversion mode. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 189–197. [Google Scholar]
- Dong, D.; Yang, W. Transient response analysis of rotor/wing coupled during tiltrotor transition flight. J. Nanjing Univ. Aeronaut. Astronaut. 2006, 38, 361–366. [Google Scholar]
- Hadytama, M.R.; Sasongko, R. Dynamics simulation and analysis of transition stage of tilt-rotor aircraft. Appl. Mech. Mater. 2016, 842, 251–258. [Google Scholar]
- Wu, Z.; Li, C.; Cao, Y. Numerical simulation of rotor–Wing transient interaction for a tiltrotor in the transition mode. Mathematics 2019, 7, 116. [Google Scholar] [CrossRef]
- Lin, K.; Qi, J.; Wu, C.; Tang, X. Control system design of a vertical take-off and landing unmanned aerial vehicle. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6750–6755. [Google Scholar]
- Gunarathna, J.; Munasinghe, R. Simultaneous execution of quad and plane flight modes for efficient take-off of quad-plane unmanned aerial vehicles. Appl. Sci. 2021, 1. [Google Scholar] [CrossRef]
- Hangxuan, H.E.; Haibin, D. A multi-strategy pigeon-inspired optimization approach to active disturbance rejection control parameters tuning for vertical take-off and landing fixed wing UAV. Chin. J. Aeronaut. 2022, 35, 19–30. [Google Scholar]
- Hernández-García, R.G.; Rodríguez-Cortés, H. Transition flight control of a cyclic tiltrotor UAV based on the Gain-Scheduling strategy. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 951–956. [Google Scholar] [CrossRef]
- Tang, S.; Liu, Z.; Zhou, Y.; Li, Z.; Guo, J. Investigation on aerodynamic performance of tandem wing UAV with rear wing dihedral. Trans. Beijing Inst. Technol. 2015, 35, 1211–1216. [Google Scholar]
- Haci Sogukpinar, I.; Bozkurt, I. Implementation of different turbulence models to find the proper model to estimate aerodynamic properties of airfoils. AIP Conf. Proc. 2018, 1935, 020003. [Google Scholar]
- Park, Y.M.; Jee, S. Numerical study on interactional aerodynamics of a quadcopter in hover with overset mesh in OpenFOAM. Phys. Fluids 2023, 35, 8. [Google Scholar]
- Kenneth, E.; Pinkerton, R.M. The Characteristics of 78 Related Airfoil Sections from Tests in the Variable-Density Wind Tunnel; Report No. 460; National Advisory Committee for Aeronautics: Washington, DC, USA, 1933; p. 14.
- Yang, L.; Wang, S.; Quan, B. Correlation analysis between key simulation parameters and numerical accuracy of subsonic outflow field. J. Mianyang Norm. Coll. 2024, 43, 16–24. [Google Scholar]



















| UAV Model | Photo | Dimensions/Performance |
|---|---|---|
| CW-20 [16] |  | Wingspan 3.2 m, cruise speed 90 m/s, max take-off weight 24.8 kg. |
| AV-2 Pelican HTOL/VTOL Aircraft [17] |  | Max take-off weight 15 kg, endurance 12 h. |
| Chachihu M8 [18] |  | Wingspan 2.5 m, cruising speed 90 km/h, max take-off weight 6.5 kg. |
| Arcturus Jump-15 [19] |  | Endurance 20 h, range 185 km. |
| Model | Wing Lift (N) | Total Lift (N) |
|---|---|---|
| (a) | 2.815 | 18.874 |
| (b) | 2.384 | 18.511 |
| (c) | 2.145 | 18.161 |
| (d) | 3.377 | 18.632 |
| (e) | 2.683 | 18.197 |
| (f) | 2.292 | 18.021 |
| (g) | 3.874 | 19.384 |
| (h) | 2.976 | 18.887 |
| (i) | 2.613 | 18.086 |
| Model | Drag Lift (N) | Total Drag (N) |
|---|---|---|
| (a) | 0.201 | 0.649 |
| (b) | 0.114 | 0.562 |
| (c) | 0.095 | 0.566 |
| (d) | 0.241 | 0.627 |
| (e) | 0.135 | 0.563 |
| (f) | 0.102 | 0.561 |
| (g) | 0.261 | 0.622 |
| (h) | 0.216 | 0.676 |
| (i) | 0.159 | 0.631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, L.; Xia, H.; Yang, J.; He, Y.; Tang, W.; Fan, M.; Xiang, J. A Study on the Aerodynamic Impact of Rotors on Fixed Wings During the Transition Phase in Compound-Wing UAVs. Aerospace 2024, 11, 945. https://doi.org/10.3390/aerospace11110945
Ai L, Xia H, Yang J, He Y, Tang W, Fan M, Xiang J. A Study on the Aerodynamic Impact of Rotors on Fixed Wings During the Transition Phase in Compound-Wing UAVs. Aerospace. 2024; 11(11):945. https://doi.org/10.3390/aerospace11110945
Chicago/Turabian StyleAi, Longjin, Haiting Xia, Jianting Yang, Ying He, Weibo Tang, Minglong Fan, and Jinwu Xiang. 2024. "A Study on the Aerodynamic Impact of Rotors on Fixed Wings During the Transition Phase in Compound-Wing UAVs" Aerospace 11, no. 11: 945. https://doi.org/10.3390/aerospace11110945
APA StyleAi, L., Xia, H., Yang, J., He, Y., Tang, W., Fan, M., & Xiang, J. (2024). A Study on the Aerodynamic Impact of Rotors on Fixed Wings During the Transition Phase in Compound-Wing UAVs. Aerospace, 11(11), 945. https://doi.org/10.3390/aerospace11110945






