Three-Dimensional Flutter Numerical Simulation of Wings in Heavy Gas and Transonic Flutter Similarity Law Correction Method
Abstract
1. Introduction
2. Goland Wing Numerical Calculation Method
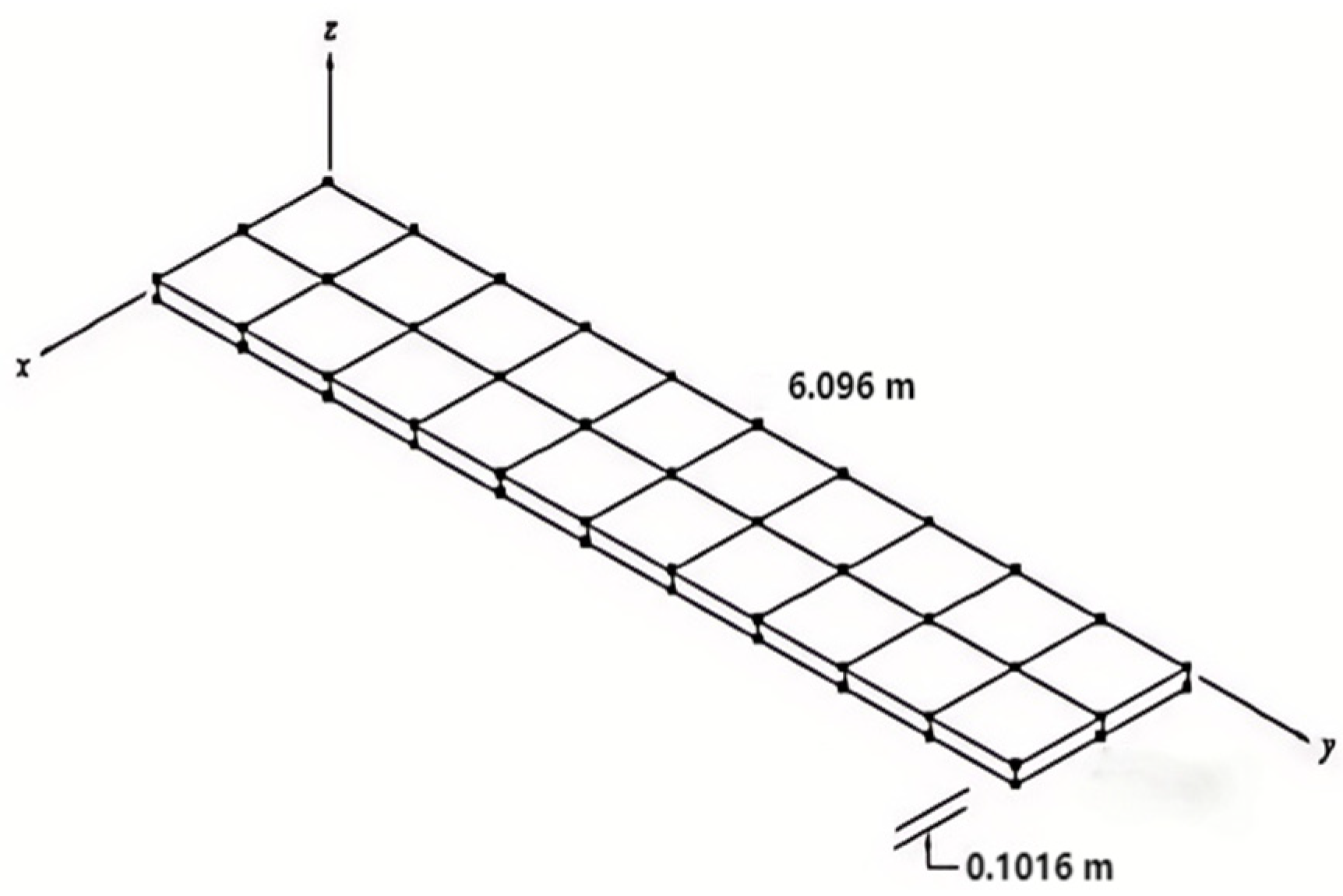
2.1. Structural
2.2. Fluid and FSI
- (1)
- The finite element model of the structure is established, and Nastran obtains the vibration mode and frequency information.
- (2)
- The structural information at time tn is interpolated from the structural grid to the aerodynamic grid by RBF interpolation method.
- (3)
- Using dynamic mesh technology to update the pneumatic mesh, performing pseudo-time iteration until convergence.
- (4)
- The aerodynamic information at time tn+1 is calculated and interpolated into the structural grid. The generalized and actual displacement on the structural grid at time tn+1 are obtained by solving the structural Equation.
- (5)
- Determine whether the requirements for the end of calculation are met; if not, return to step 1 and repeat the iterative calculation.
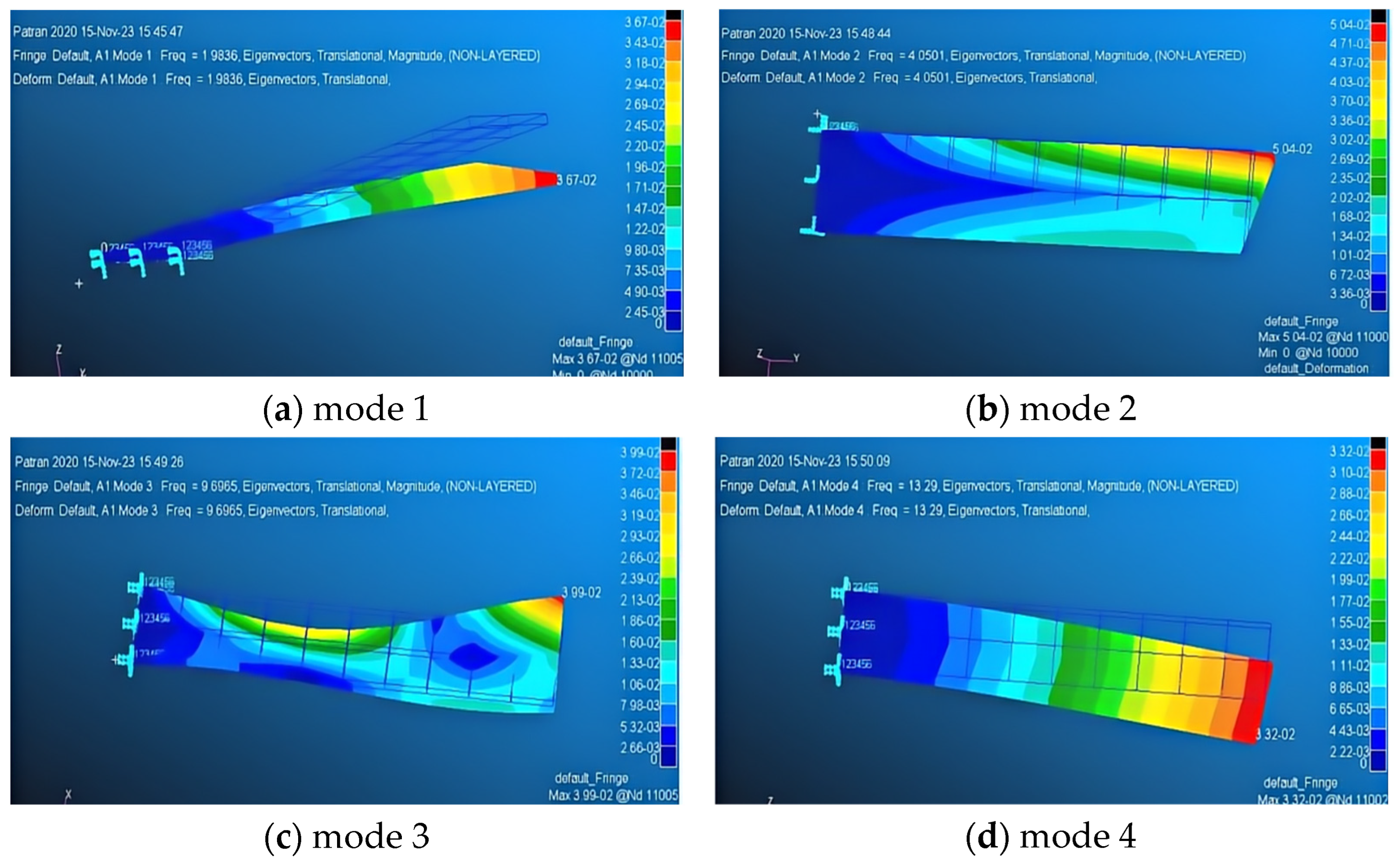
2.3. Verification of Algorithms
3. Flutter of Goland Wing in Heavy Gas
4. Similarity Law for Transonic Flutter in Heavy Gases
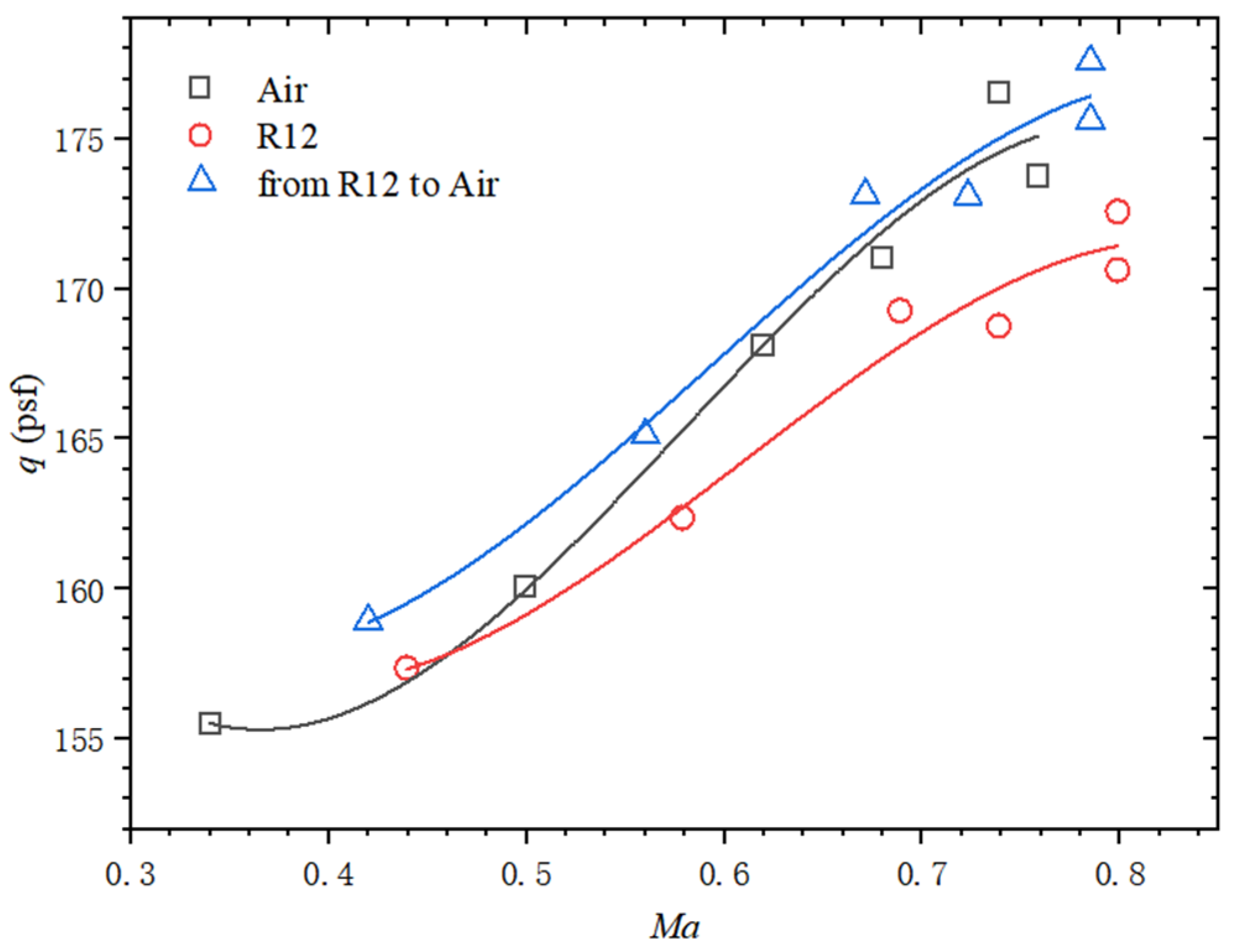
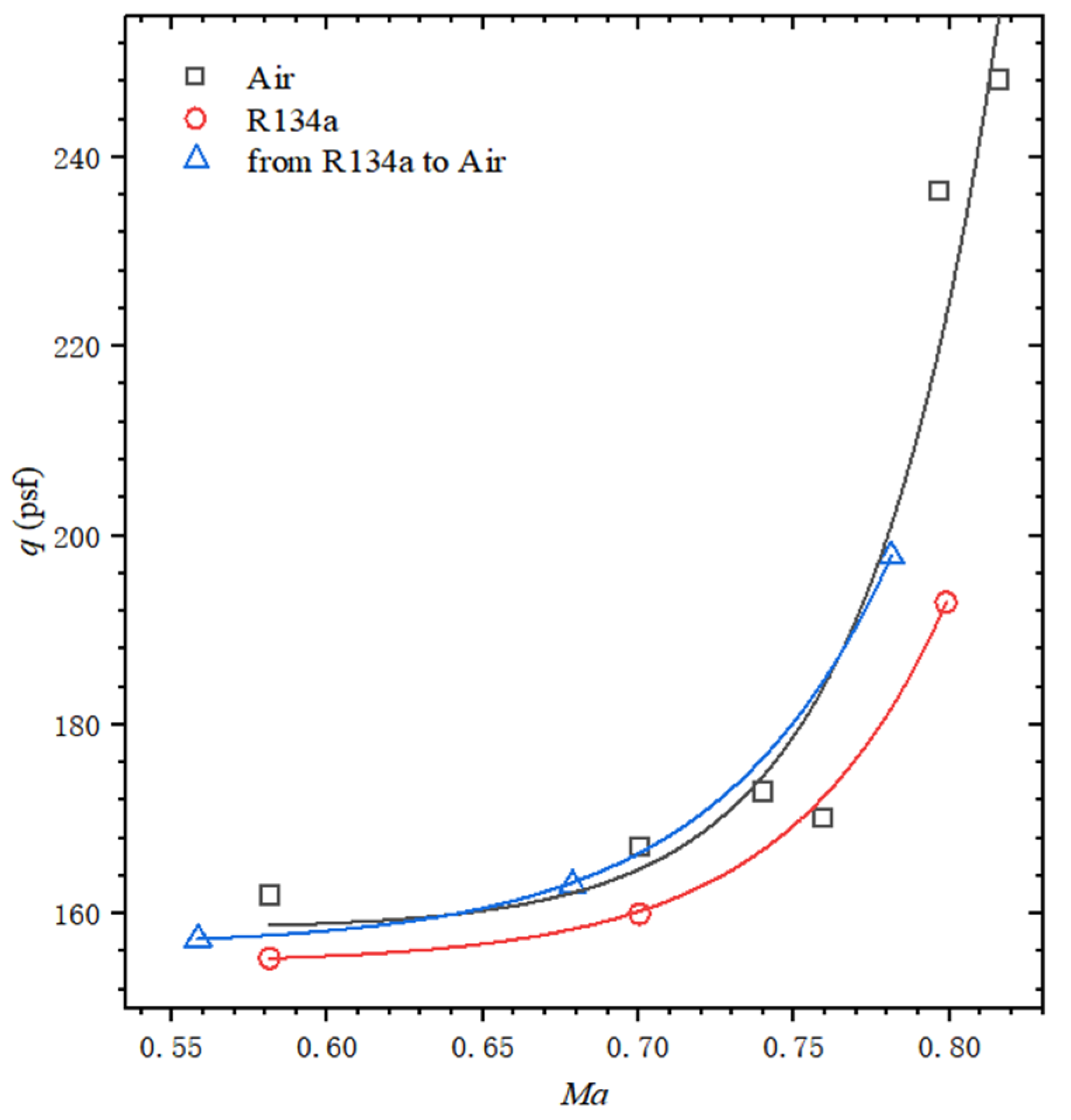
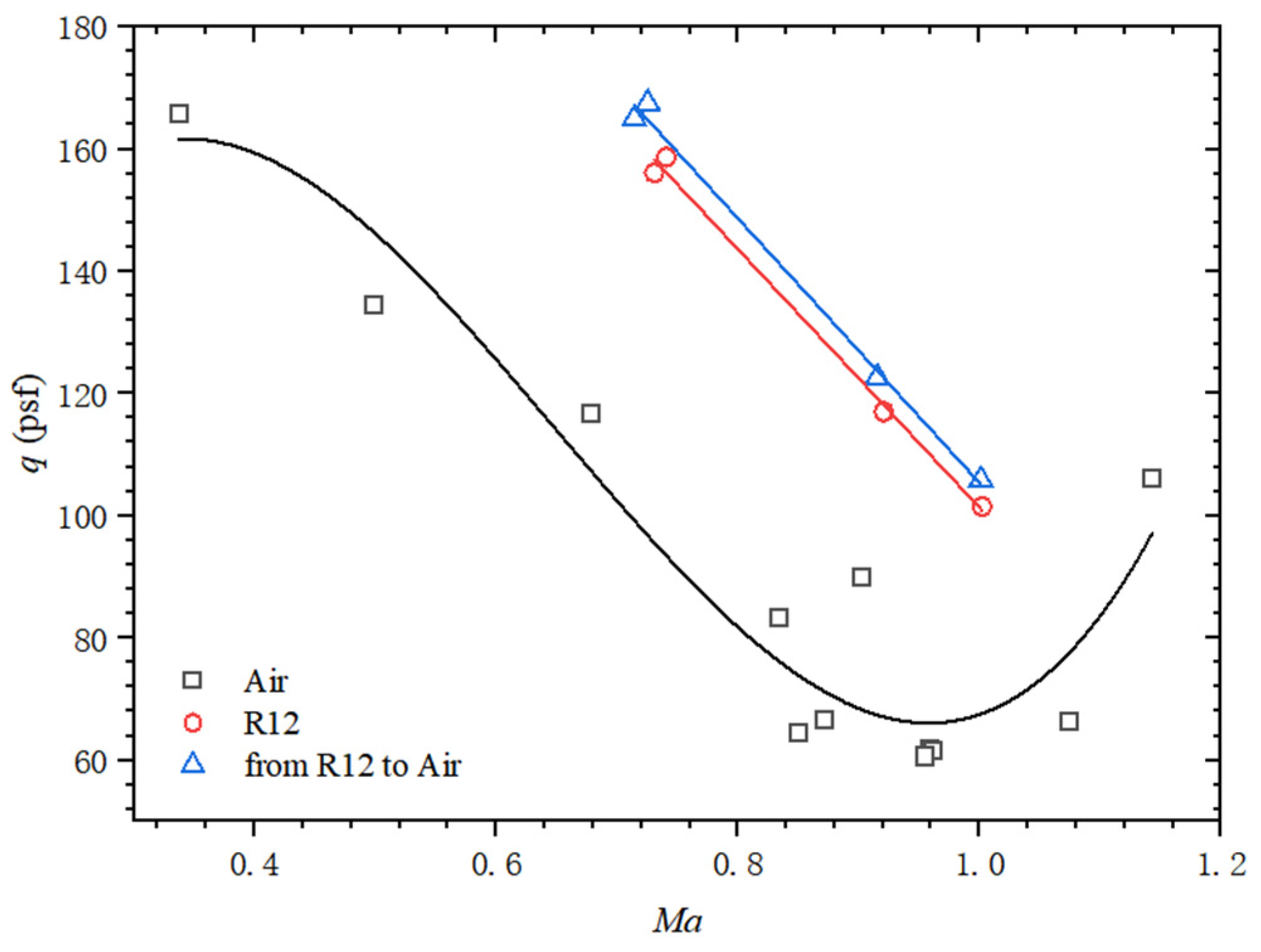
5. Correction of Flutter Data for Heavy Gas
5.1. BSCW
5.2. A 45° Sweptback Wing (NACA65A004)
5.3. Goland Wing
- (1)
- Compared with the binary rigid model, the flexible wing has more combined flutter modes. Due to the difference in mass ratio and reduced frequency, the dynamic characteristics of the model are different in air and heavy gas, and the flutter boundary has an opposite trend.
- (2)
- The transonic flutter similarity law is derived under quasi-steady conditions, neglecting the effects of unsteady aerodynamic derivatives. This approach is similar to the subsonic Theodorsen–Garrick theory and remains valid only at very low reduced frequencies and high mass ratios. Consequently, this may result in the inadequacy of the transonic flutter similarity law when applied to scenarios with high reduced frequencies and low mass ratios.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Q.Y.; Yin, Y.P. Discussion on flutter of aircraft and bridge. Mech. Eng. 2023, 45, 721–727. [Google Scholar]
- Robert, V.; Doggett. A Bibliography of Transonic Dynamics Tunnel (TDT) Publications; NASA Langley Research Center: Hampton, VA, USA, 2016. [Google Scholar]
- Shi, G.H.; Wu, W.H.; Tao, R.; Luo, J.; Lin, H.; Li, Q.; Sun, Q. Application Requirement Analysis of Additive Manufacturing Technology in Aircraft Structure. J. Mech. Eng. 2024, 60, 74–84. [Google Scholar]
- Corrado, G.; Ntourmas, G.; Sferza, M.; Traiforos, N.; Arteiro, A.; Brown, L.; Chronopoulos, D.; Daoud, F.; Glock, F.; Ninic, J.; et al. Recent progress, challenges and outlook for multidisciplinary structural optimization of aircraft and aerial vehicles. Prog. Aerosp. Sci. 2022, 135, 100861. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, K.; Xia, L.; Gao, Z. A multi-disciplinary global/local optimization method for flying-wing airfoils design. Acta Aerodyn. Sin. 2021, 39, 37–52. [Google Scholar]
- Perry, B.; Thomas, E.N. Activities in Aeroelasticity at NASA Langley Research Center. NASA Langley Res. Cent. 1997, 53, 77–88. [Google Scholar]
- Yeager, J.W.T.; Kvaternik, R.G. Contributions of the Langley Transonic Dynamics Tunnel to Rotorcraft Technology and Development. In Proceedings of the AIAA Dynamics Specialists Conference, Atlanta, GA, USA, 5–6 April 2000; p. 1771. [Google Scholar]
- Yeager, J.W.T. A Historical Overview of Aeroelasticity Branch and Transonic Dynamics Tunnel Contributions to Rotorcraft Technology and Development; NASA: Washington, WA, USA, 2001; TM-2001-211054. [Google Scholar]
- Cole, S.; Keller, D.; Piatak, D. Contributions of the NASA Langley Transonic Dynamics Tunnel to launch vehicle and spacecraft development. In Proceedings of the AIAA Dynamics Specialists Conference, Atlanta, GA, USA, 5–6 April 2000; p. 1772. [Google Scholar]
- Perr, B.; Noll, T.; Scott, R. Contributions of the Transonic Dynamics Tunnel to the testing of active control of aeroelastic response. In Proceedings of the AIAA Dynamics Specialists Conference, Atlanta, GA, USA, 5–6 April 2000; p. 1769. [Google Scholar]
- Schuster, D.M.; Liu, D.D.; Huttsell, L.J. Computational aeroelasticity: Success, progress, challenge. J. Aircr. 2003, 40, 843–856. [Google Scholar] [CrossRef]
- Fu, Q.; Zhang, X.; Zhao, M.; Zhang, C.H.; He, W. Research progress on the wind tunnel experiment of a bionic flapping-wing aerial vehicle. Chin. J. Eng. 2022, 44, 767–779. [Google Scholar]
- Anders, J.B.; Anderson, W.K.; Murthy, A.V. Transonic similarity theory applied to a supercritical airfoil in heavy gas. J. Aircr. 1999, 36, 957–964. [Google Scholar] [CrossRef]
- Liu, Y.P.; Kou, X.P.; Zha, J.; Yu, L.; Lu, B. The isentropic flow characteristics of heavy gas medium. J. Aerosp. Power 2023.
- Zha, J.; Zeng, K.C.; Kou, X.P.; Yang, X.; Zhang, H. Transonic flow characteristics of supercritical airfoil in heavy gas medium. J. Aerosp. Power. 2021, 36, 1894–1905. [Google Scholar]
- Liu, Y.P.; Zha, J.; Hu, Z.; Kou, X.P.; Yu, L.; Lu, B. Correction of Aerodynamic Characteristics in Heavy Gas Medium. J. Aerosp. Power, 2024; accepted. [Google Scholar]
- Bendiksen, O.O. Transonic Similarity Rules for Flutter and Divergence. In Proceedings of the 39th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Long Beach, CA, USA, 20–23 April 1998; p. 1726. [Google Scholar]
- Bendiksen, O.O. Improved similarity rules for transonic flutter. In Proceedings of the 40th Structures, Structural Dynamics, and Materials Conference and Exhibit, St. Louis, MO, USA, 12–15 April 1999; p. 1350. [Google Scholar]
- Goland, M. The Flutter of a Uniform Cantilever Wing. J. Appl. Mech. 1945, 12, 197–208. [Google Scholar] [CrossRef]
- Liu, N. Investigation of Transonic Nonlinear Flutter and Efficient Analysis Approach; Northwestern Polytechnical University: Xi’an, China, 2016; pp. 73–74. [Google Scholar]
- Sarma, R.; Dwight, R.P. Uncertainty Reduction in Aeroelastic Systems with Time-Domain Reduced-Order Models. AIAA J. 2017, 55, 2437–2449. [Google Scholar] [CrossRef]
- Goland, M.; Luke, Y.L. The flutter of a uniform wing with tip weights. J. Appl. Mech. 1948, 15, 13–20. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H.; Cesnik, C.E. Nonlinear aeroelastic analysis of complete aircraft in subsonic flow. J. Aircr. 2000, 37, 753–760. [Google Scholar] [CrossRef]
- Carmelo, R.V.; Giuseppe, M.; Antonio, E.; Orlando, C.; Alaimo, A. An aeroelastic beam finite element for time domain preliminary aeroelastic analysis. Mech. Adv. Mater. 2023, 30, 1064–1072. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; The McGRAW-Hill Companies: New York, NY, USA, 2001; Volume 5. [Google Scholar]
- Liu, Y.P.; Xia, H.Y.; Zha, J.; Yu, L.; Lu, B. A Survey of the Test Data Correction Method in Heavy Gas Wind Tunnel. J. Aerosp. Power, 2024; accepted. [Google Scholar]
- Bryan, E.; Dansberry, M.H.; Robert, M. Experimental unsteady pressures at flutter on the Supercritical Wing Benchmark Model. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993; p. 1592. [Google Scholar]
- Jirasek, A.; Seidel, J. Study of Benchmark Super Critical Wing at Mach 0.8. In Proceedings of the AIAA SciTech Forum and Exposition, San Diego, CA, USA, 3–7 January 2022; p. 175. [Google Scholar]
- Foughner, J.T., Jr.; Land, N.S.; Yates, E.C., Jr. Measured and Calculated Subsonic and Transonic Flutter Characteristics of a 45 Deg Sweptback Wing Planform in Air and in Freon-12 in the Langley Transonic Dynamics Tunnel; NASA: Washington, WA, USA, 1963; NASA-TN-D-1616.



| Title 1 | Air | R12 | R134a | SF6 |
|---|---|---|---|---|
| Eelative molecular mass | 29 | 121 | 102 | 146 |
| Standard status density/(kg/m3) | 1.29 | 5.40 | 4.55 | 6.52 |
| Specific heat ratio γ | 1.40 | 1.14 | 1.13 | 1.095 |
| Viscosity coefficient | 38.6 | 31.3 | 28.6 | 32.6 |
| Speed of sound/(m/s) | 340 | 154 | 165 | 134 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Young’s modulus E | 2.307 × 10³ (GPa) | Shear modulus | 8.65 × 102 (GPa) |
| Skin thickness of upper and lower surfaces (kg/m3) | 4.7244 × 10−3 (m) | Thickness of front and rear edge spar | 1.8288 × 10−4 (m) |
| Center spar thickness | 2.7097 × 10−2 (m) | Thickness of wing ribs | 1.0577 × 10−2 (m) |
| The area of the transition area | 7.4322 × 10−5 (m2) | The area of the top area of the front and rear edge spar | 3.8648 × 10−3 (m2) |
| The area of the top area of the center spar | 1.3898 × 10−2 (m2) | The area of the top area of the wing rib | 3.9205 × 10−3 (m2) |
| This Paper | Liu Nan [20] | Rakesh Sarma [21] | |
|---|---|---|---|
| mode 1 | 1.9836 | 1.98 | 1.98 |
| mode 2 | 4.0501 | 4.05 | 4.04 |
| mode 3 | 9.6965 | 9.69 | 9.68 |
| mode 4 | 13.29 | 13.29 | 13.28 |
| Referencerefer | Modeling Approach | Flutter Velocity (m/s) |
|---|---|---|
| Goland and Luke | Analytical | 137.25 |
| Patil | Intrinsic beam + strip theory | 135.25 |
| This paper | Wingbox + RANS | 142.92 |
| Carmelo | Wingbox + 2-D unsteady aerodynamics | 137.40 |
| Mach number/M | 0.421 | 0.550 | 0.650 | 0.750 | 0.880 |
| Density/ρ (kg/m3) | 6.962 | 3.641 | 2.439 | 1.696 | 1.049 |
| flutter boundary/U (m/s) | 66.8 | 88.0 | 104.3 | 120.6 | 141.7 |
| Dynamic pressure/q (kpa) | 15.533 | 14.098 | 13.266 | 12.334 | 10.531 |
| speed of sound/a (m/s) | 156.98 | 159.15 | 159.93 | 160.41 | 160.83 |
| specific heat ratio/γ | 1.132 | 1.122 | 1.118 | 1.115 | 1.114 |
| Reynolds number/Re | 4.07 × 107 | 2.80 × 107 | 2.22 × 107 | 1.79 × 107 | 1.30 × 107 |
| Mach number/M | 0.421 | 0.550 | 0.650 | 0.750 | 0.825 | 0.880 |
| Density/ρ (kg/m3) | 1.225 | 0.719 | 0.467 | 0.334 | 0.244 | 0.184 |
| flutter boundary/U (m/s) | 143.3 | 187.2 | 221.2 | 255.2 | 280.7 | 299.5 |
| Dynamic pressure/q (kpa) | 12.577 | 12.598 | 11.425 | 10.876 | 9.613 | 8.252 |
| speed of sound/a (m/s) | 340.40 | 340.37 | 340.35 | 340.34 | 340.34 | 340.33 |
| specific heat ratio/γ | 1.402 | 1.401 | 1.401 | 1.400 | 1.400 | 1.400 |
| Reynolds number/Re | 9.77 × 106 | 7.49 × 106 | 5.75 × 106 | 4.74 × 106 | 3.82 × 106 | 3.07 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Lu, B.; Liu, Y.; Yu, L.; Kou, X.; Zha, J. Three-Dimensional Flutter Numerical Simulation of Wings in Heavy Gas and Transonic Flutter Similarity Law Correction Method. Aerospace 2024, 11, 932. https://doi.org/10.3390/aerospace11110932
Hu Z, Lu B, Liu Y, Yu L, Kou X, Zha J. Three-Dimensional Flutter Numerical Simulation of Wings in Heavy Gas and Transonic Flutter Similarity Law Correction Method. Aerospace. 2024; 11(11):932. https://doi.org/10.3390/aerospace11110932
Chicago/Turabian StyleHu, Zhe, Bo Lu, Yongping Liu, Li Yu, Xiping Kou, and Jun Zha. 2024. "Three-Dimensional Flutter Numerical Simulation of Wings in Heavy Gas and Transonic Flutter Similarity Law Correction Method" Aerospace 11, no. 11: 932. https://doi.org/10.3390/aerospace11110932
APA StyleHu, Z., Lu, B., Liu, Y., Yu, L., Kou, X., & Zha, J. (2024). Three-Dimensional Flutter Numerical Simulation of Wings in Heavy Gas and Transonic Flutter Similarity Law Correction Method. Aerospace, 11(11), 932. https://doi.org/10.3390/aerospace11110932





