Effects of the Uncertainty of Wall Distance on the Simulation of Turbulence/Transition Phenomena
Abstract
1. Introduction
2. Materials and Methods
2.1. Introduction of Turbulence Model
2.2. Computational Code
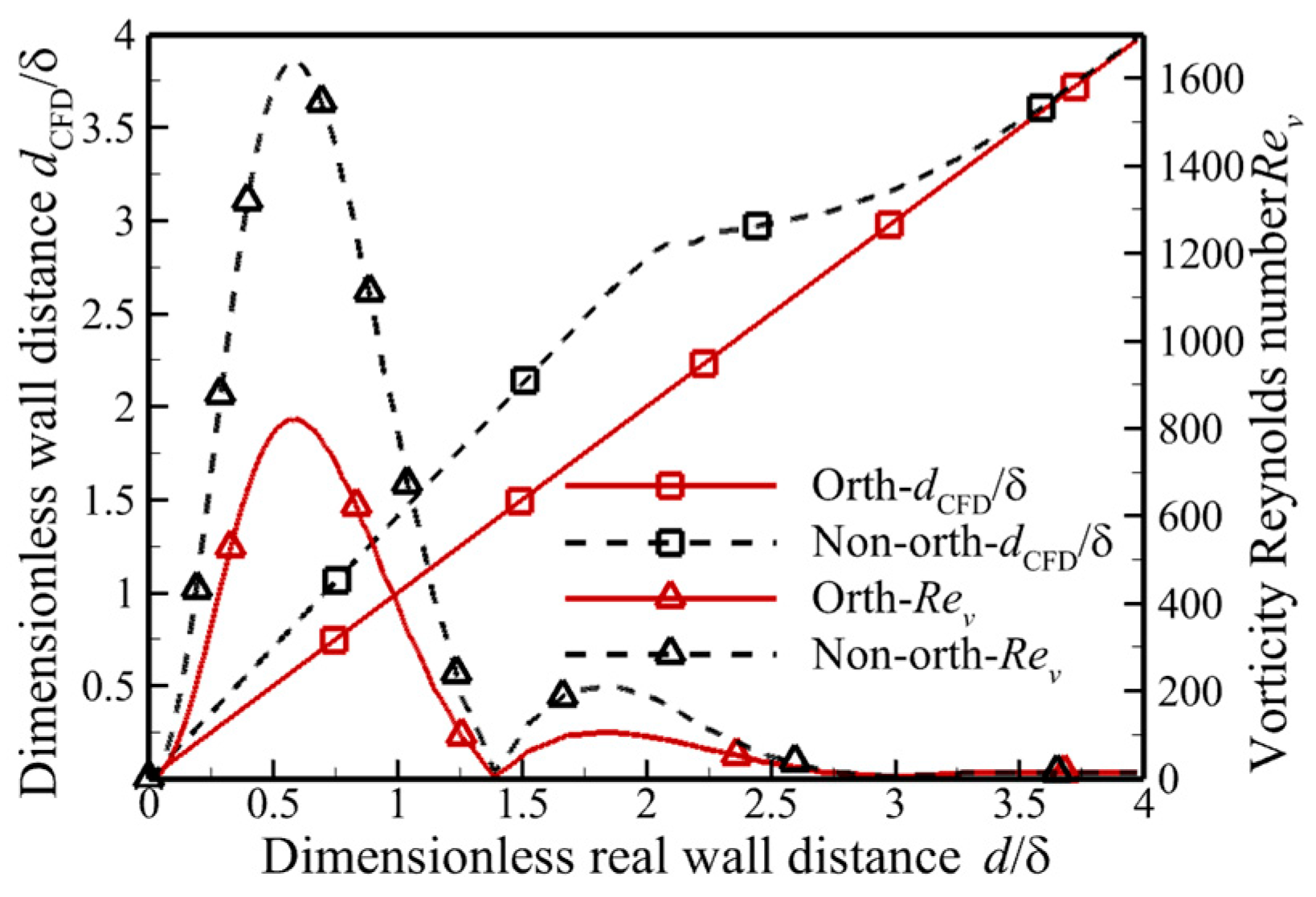
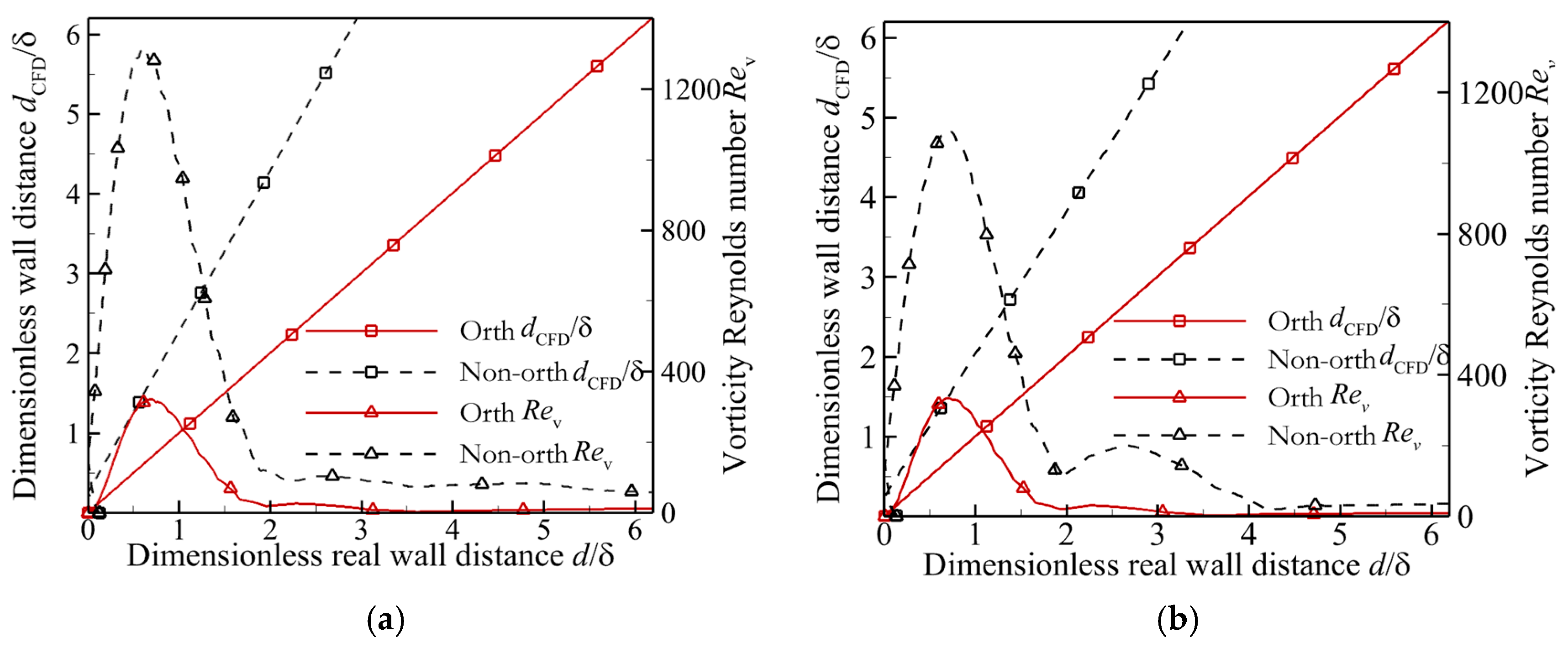
2.3. The Analysis of the Relationship Between Wall Distance and Mesh
3. Results
3.1. The Flat Plate with ZPG
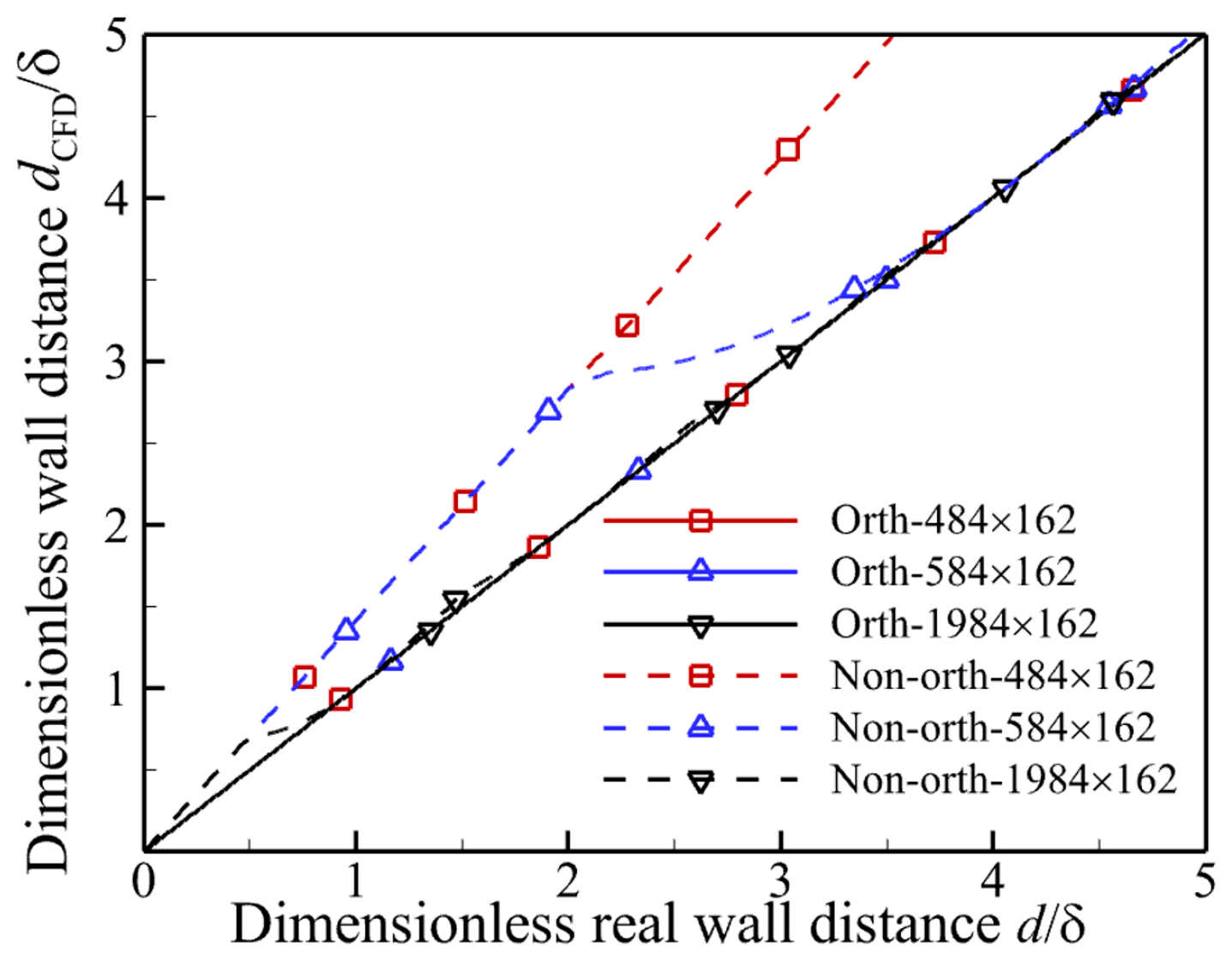
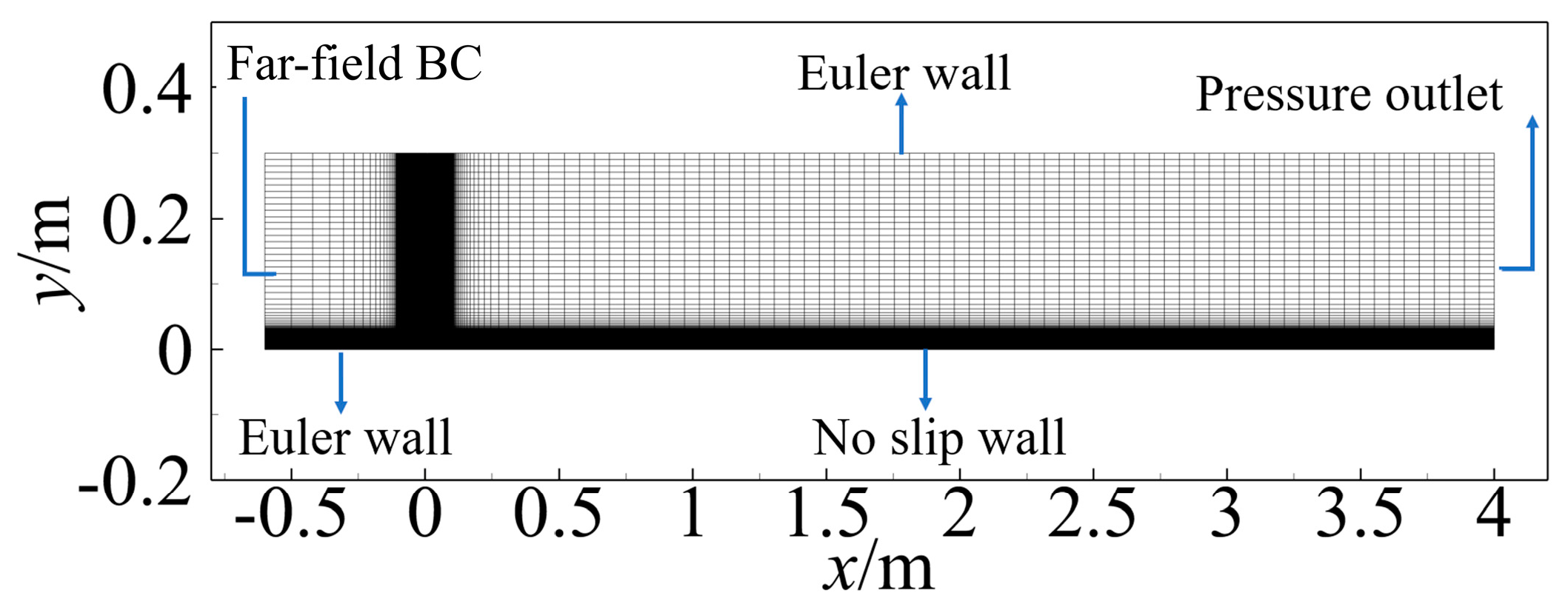
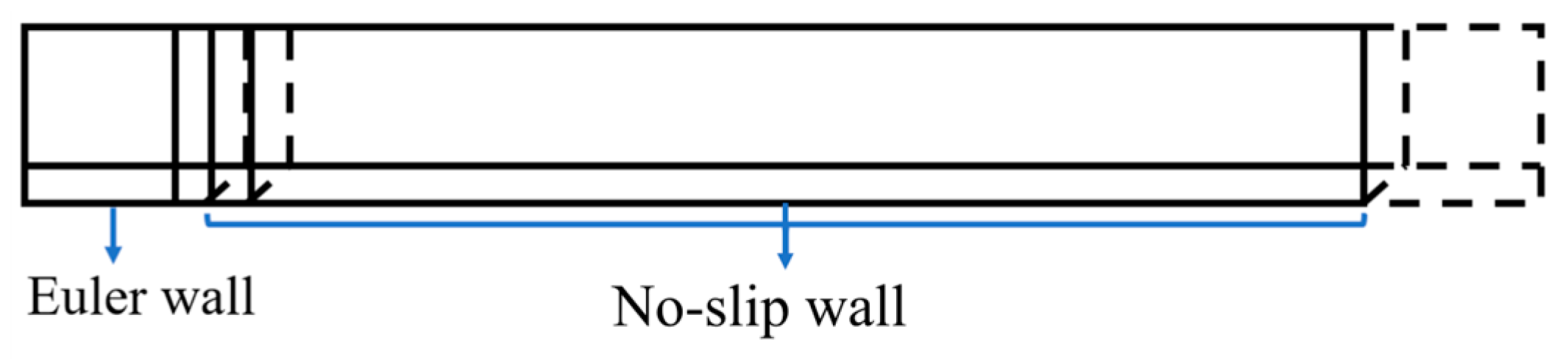
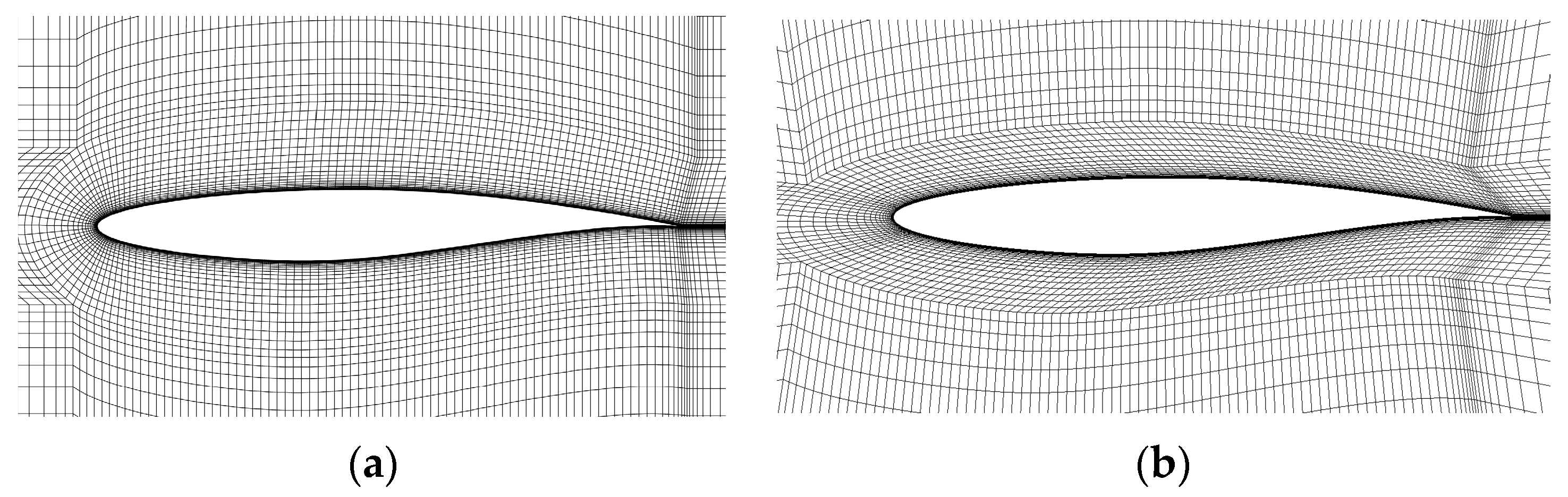
3.1.1. Mesh and Boundary Condition
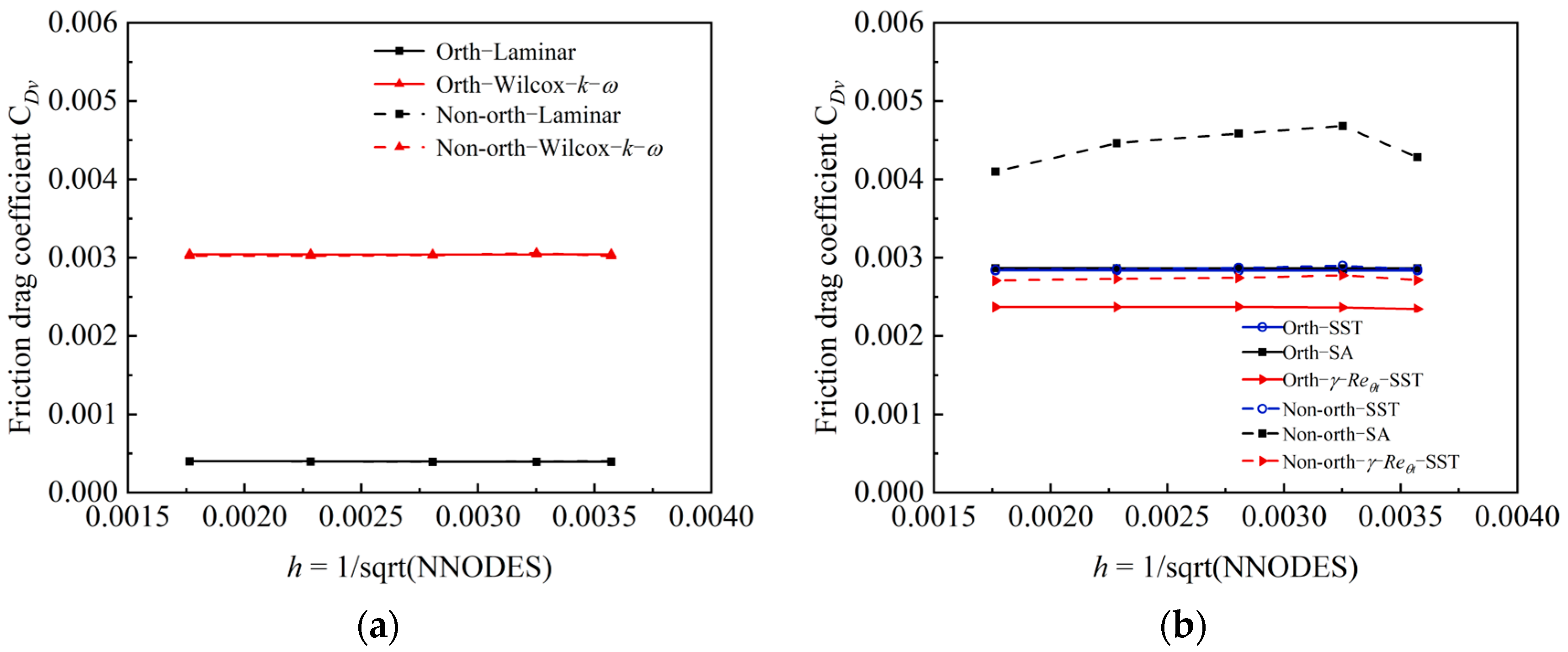
3.1.2. Mesh Convergence Analysis for All Models
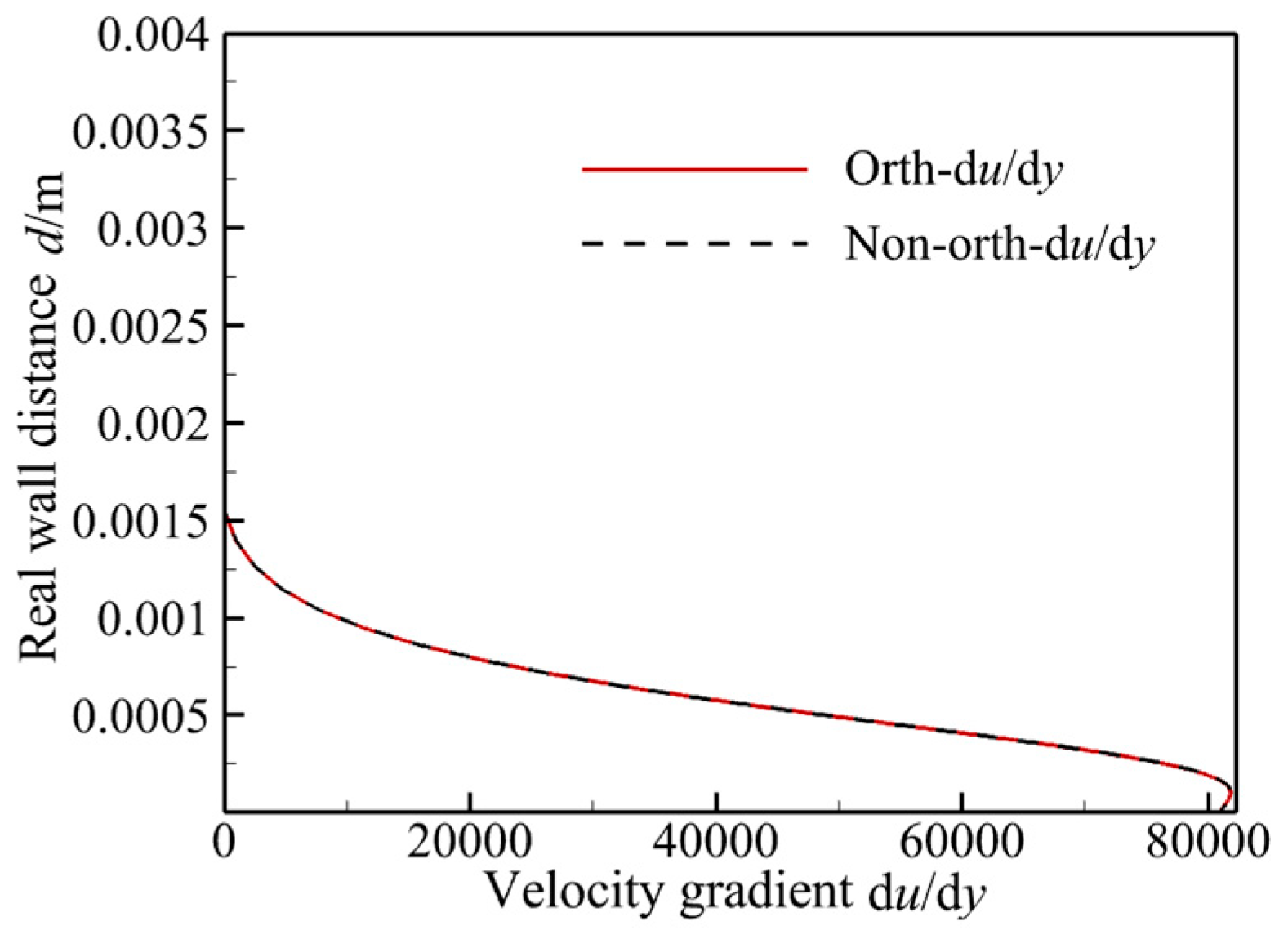
3.1.3. The Analysis of the Effects of Mesh Oblique Degree on the SA, SST and γ-Reθt-SST Models
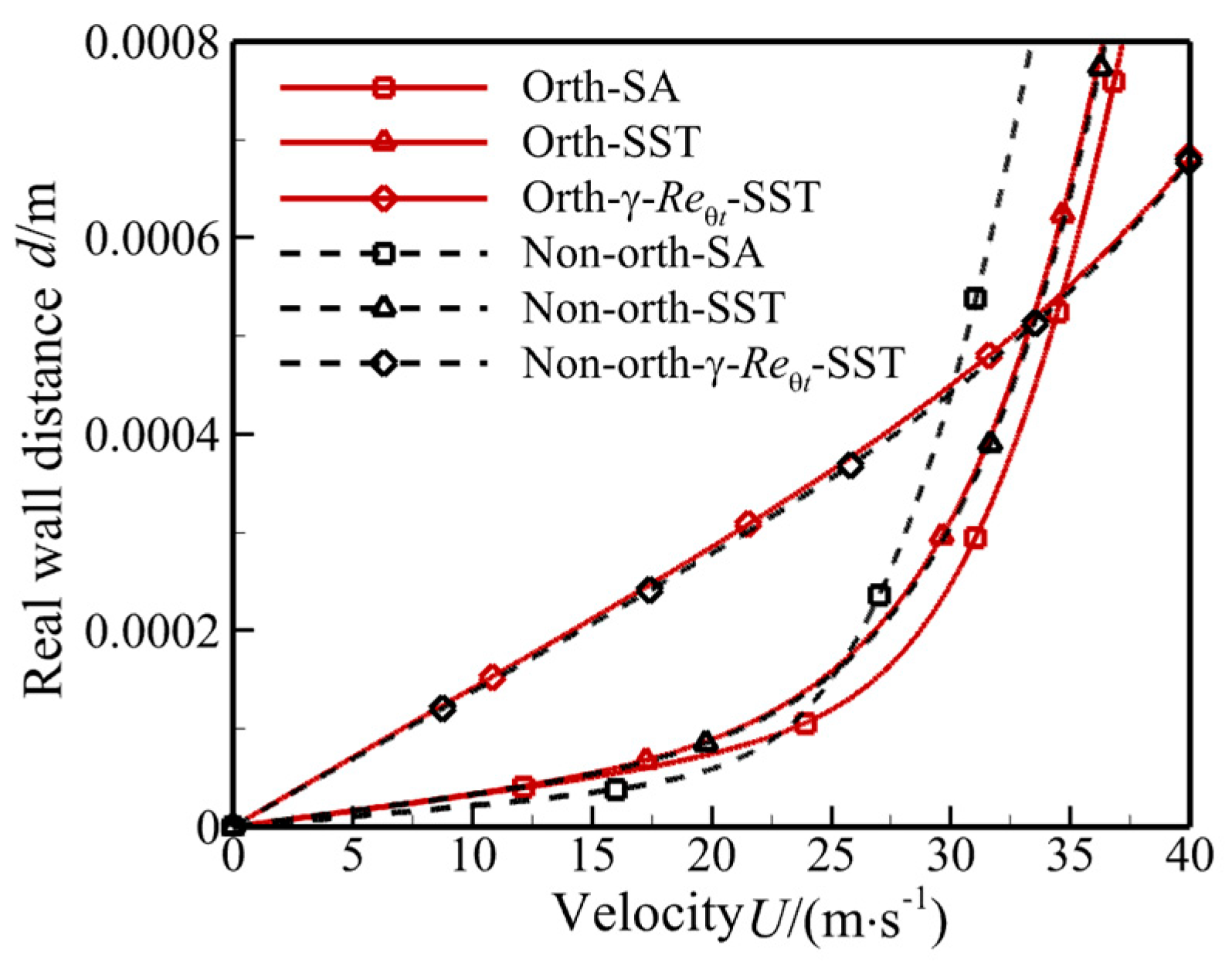
3.1.4. The Effects of Wall Distance Uncertainty on Transition Model
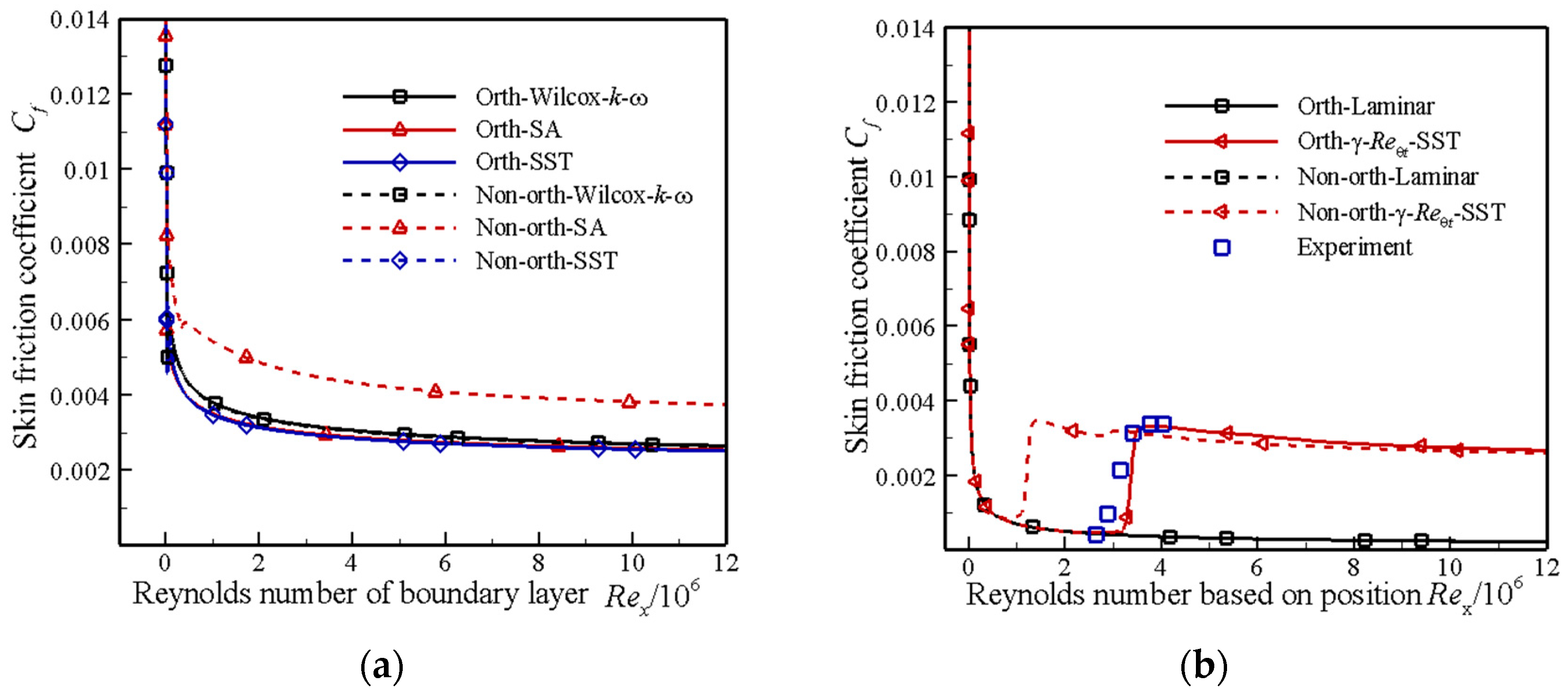
3.1.5. The Comparison Analysis of the Accuracy of the Turbulence Model
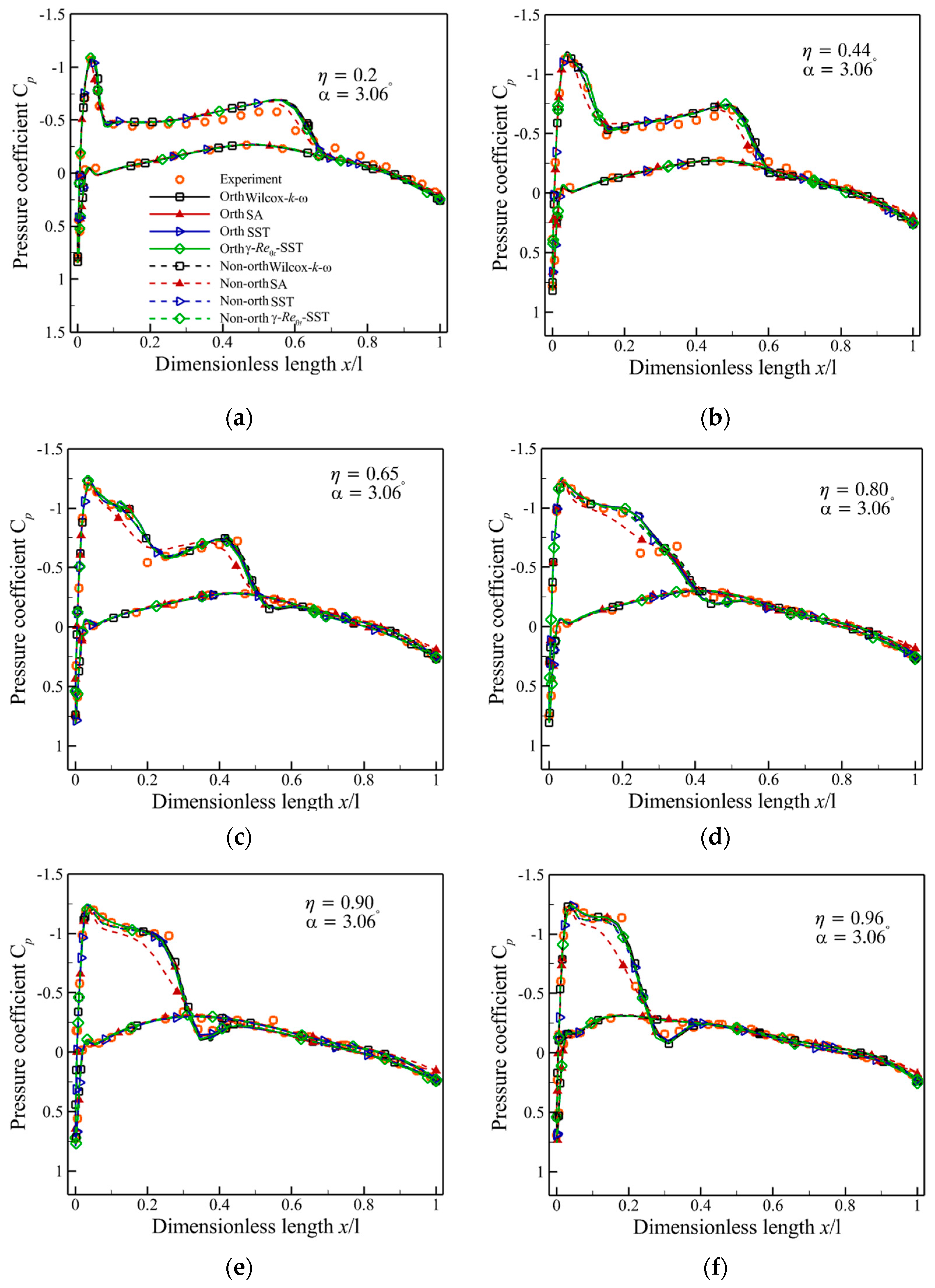
3.2. RAE2822 Airfoil
3.2.1. Mesh and Boundary Condition
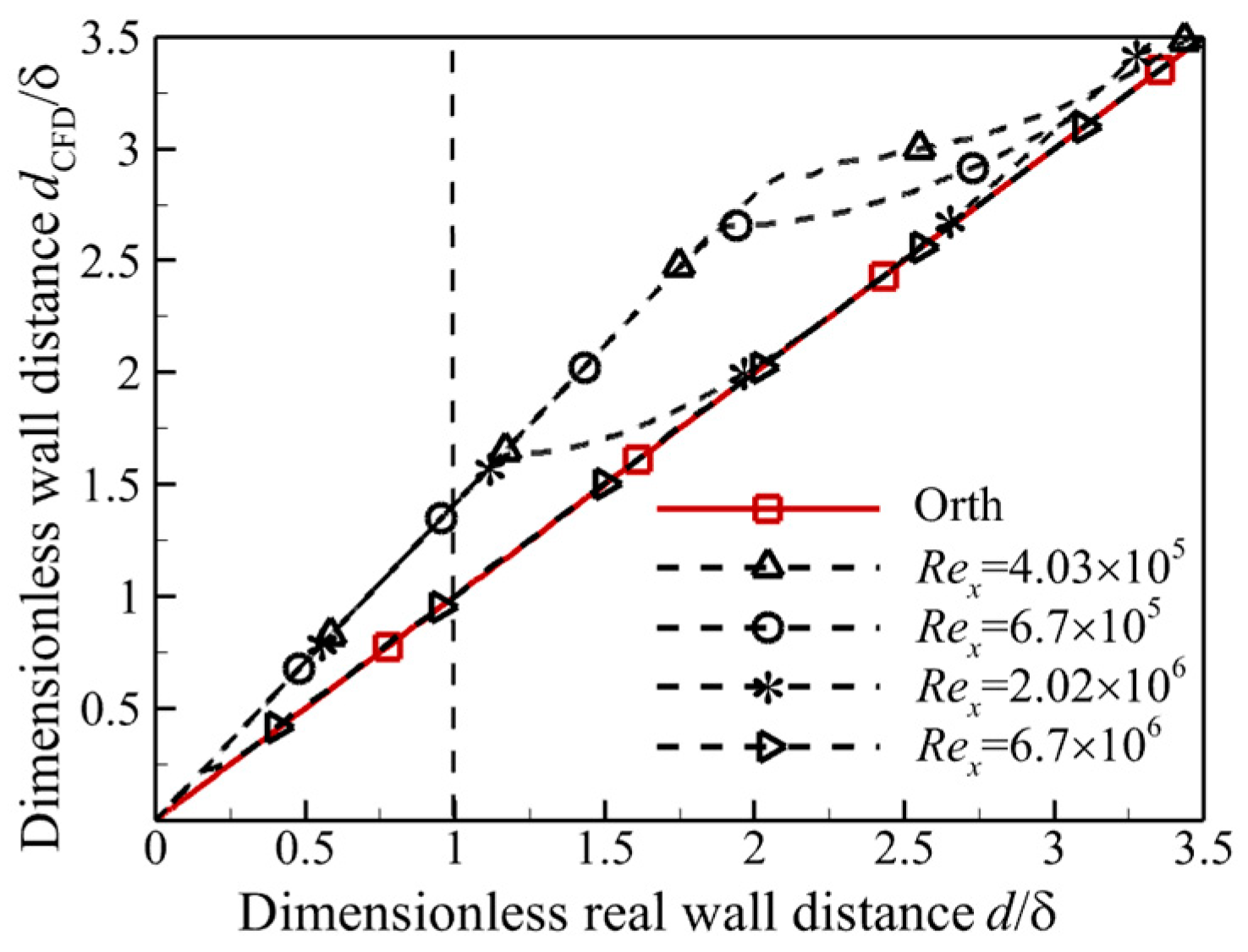
3.2.2. Mesh Convergence Analysis
3.2.3. The Effects of the Uncertainty of Wall Distance on the Transition Model
3.2.4. The Comparison of the Accuracy of the Turbulence Model
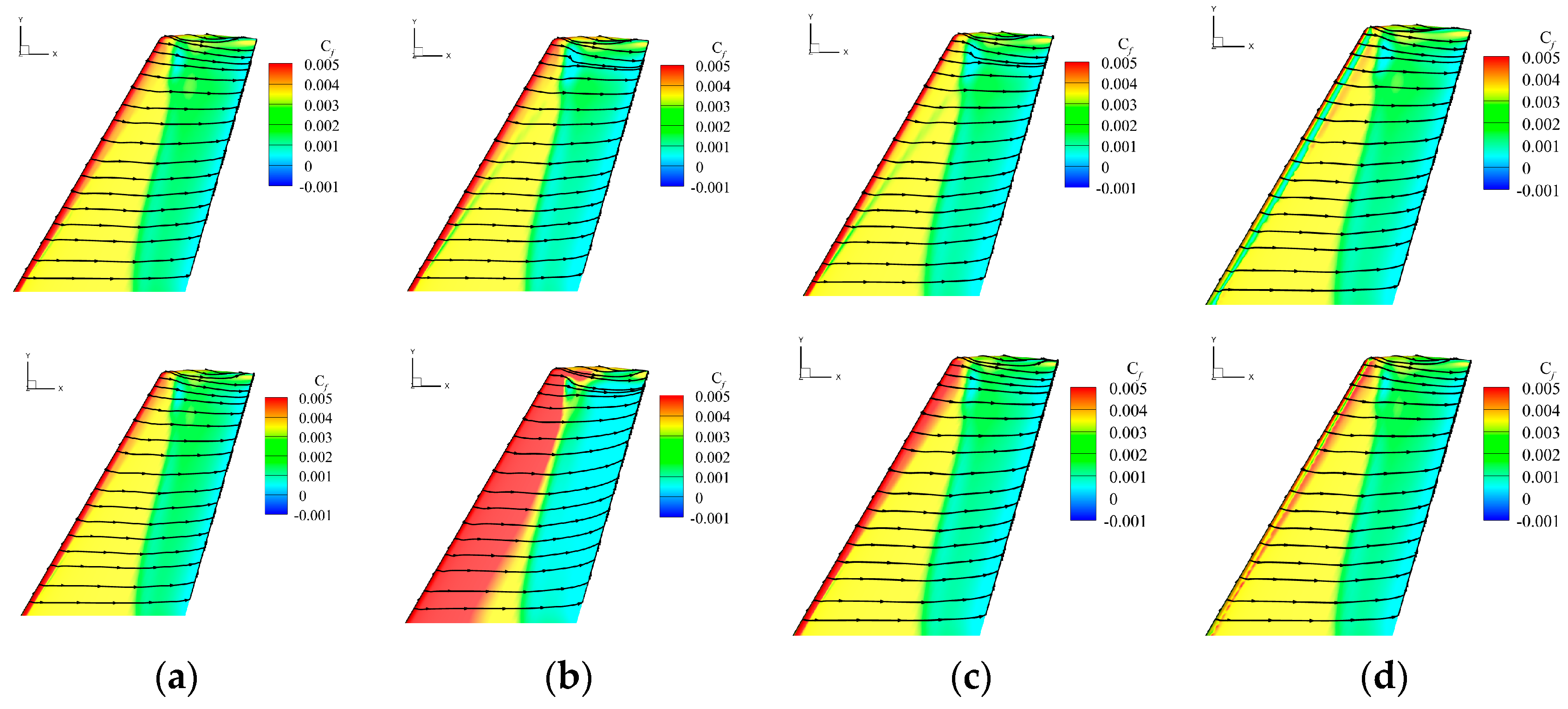
3.3. ONERA M6 Airfoil
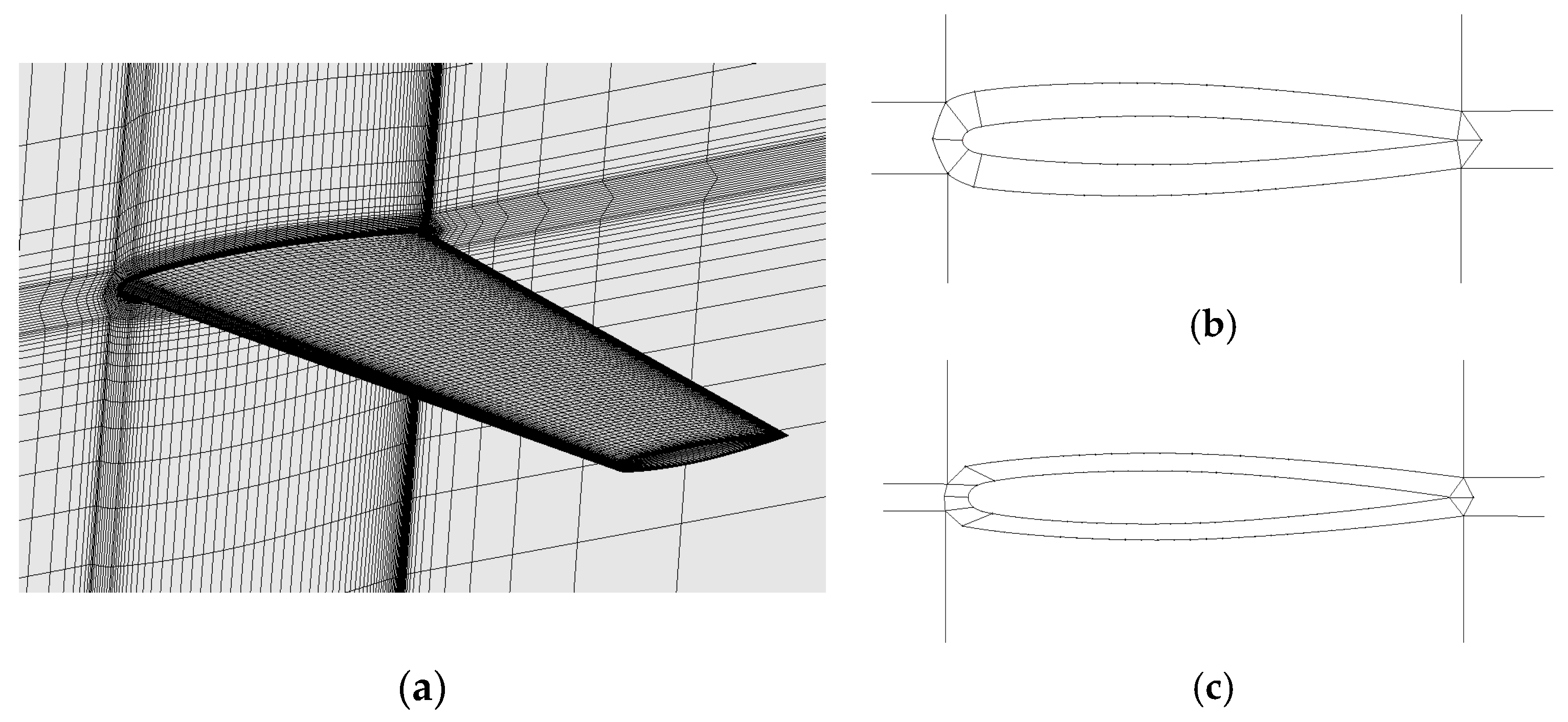
3.3.1. Mesh and Boundary Condition
3.3.2. The Effects of Wall Distance Uncertainty on the Transition Model
3.3.3. The Comparison of the Uncertainties of the Turbulence Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences: NASA/CR-20414-218178; NASA: Washington, DC, USA, 2014.
- Yan, C.; Qu, F.; Zhao, Y.T.; Yu, J.; Wu, C.H.; Zhang, S.H. Review of development and challenges for physical modeling and numerical scheme of CFD in aeronautics and astronautics. Acta Aerodyn. Sin. 2020, 38, 829–857. (In Chinese) [Google Scholar]
- Cary, A.W.; Chawner, J.R.; Duque, E.P.N.; Gropp, W.; Kleb, W.L.; Kolonay, R.M.; Nielsen, E.; Smith, B. CFD vision 2030 roadmap: Progress and perspectives. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2021. [Google Scholar]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Yang, Z.Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar]
- Moser, R.D.; Haering, S.W.; Yalla, G.R. Statistical properties of subgrid-scale turbulence models. Annu. Rev. Fluid Mech. 2021, 53, 255–286. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2008, 41, 181–202. [Google Scholar] [CrossRef]
- Durbin, P.A. Some recent developments in turbulence closure modeling. Annu. Rev. Fluid Mech. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- He, X.; Zhao, F.; Vahdati, M. Detached eddy simulation: Recent development and application to compressor tip leakage flow. J. Turbomach. 2021, 144, 011009. [Google Scholar] [CrossRef]
- Zhang, K.L.; Li, S.Y.; Duan, Y.; Yan, C. Uncertainty quantification of parameters in SST turbulence model for inlet simulation. Acta Aeronaut. Astronaut. Sin. 2023, 44, 729429. (In Chinese) [Google Scholar]
- Chen, J.T.; Zhang, C.; Wu, X.J.; Zhao, W. Quantification of turbulence model-selection uncertainties considering discretization errors. Acta Aeronaut. Astronaut. Sin. 2021, 42, 625741. (In Chinese) [Google Scholar]
- Zhao, Y.T.; Liu, H.K.; Zhou, Q.; Yan, C. Quantification of parametric uncertainty in k–ω–γ transition model for hypersonic flow heat transfer. Aerosp. Sci. Technol. 2020, 96, 105553. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Yan, C.; Liu, H.K.; Zhang, K. Uncertainty and sensitivity analysis of flow parameters for transition models on hypersonic flows. Int. J. Heat Mass Transf. 2019, 135, 1286–1299. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of model uncertainty in RANS simulations: A review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reston, NV, USA, 6–9 January 1992; AIAA: Reston, VI, USA, 1992. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Tucker, P.G.; Rumsey, C.L.; Spalart, P.R.; Bartels, R.E.; Biedron, R.T. Computations of wall distances based on differential equations. AIAA J. 2005, 43, 539–549. [Google Scholar] [CrossRef]
- Xu, J.L.; Yan, C.; Fan, J.J. Computations of wall distances by solving a transport equation. Appl. Math. Mech. 2011, 32, 135–143. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G.; Zeng, Z.; Ye, Z.Y. An efficient search algorithm for calculating minimum wall distance of unstructured mesh. Northwestern Polytech. Univ. 2014, 32, 511–516. (In Chinese) [Google Scholar]
- Zhao, H.Y.; He, X.Z.; Le, J.L. Recursive box method for wall distance computation. Chin. J. Comput. Phys. 2008, 25, 427–430. (In Chinese) [Google Scholar]
- Meng, S.; Zhou, D.; Li, X.L.; Bi, L. Accurate and efficient wall distance calculation method for Cartesian grids. Acta Aerodyn. Sin. 2023, 41, 93–101. (In Chinese) [Google Scholar]
- Zhao, Z.; He, L.; Zhang, J.; Xu, Q.; Zhang, L. MPI/OpenMP hybrid parallel computation of wall distance for turbulence flow simulations. Acta Aerodyn. Sin. 2019, 37, 883–892. (In Chinese) [Google Scholar]
- Rumsey, C. The Splart-Allmaras Turbulence Model [EB/OL]. Available online: https://turbmodels.larc.nasa.gov/spalart.html (accessed on 23 July 2023).
- Rumsey, C. Turbulence Modeling Resource [EB/OL]. Available online: https://turbmodels.larc.nasa.gov/ (accessed on 23 July 2023).
- Nie, S.Y.; Wang, Y.; Liu, Z.Q.; Jin, P.; Jiao, J. Numerical inverstigation and discussion on CHN-T1 benchmark model using Spalart-Allmaras model and SSG/LRR-w model. Acta Aerodyn. Sin. 2019, 37, 310–319, 328. (In Chinese) [Google Scholar]
- Schubauer, G.B.; Klebanoff, P.S. Contributions on the mechanics of boundary-layer transition. Tech. Rep. Arch. Image Libr. 1956, 39, 411–415. [Google Scholar]
- He, S.T.; Lan, W.; Hu, X.J. Numerical simulation of flow pattern structure in boundary layer on flat plate surfaces. J. South China Univ. Technol. (Nat. Sci. Ed.) 2021, 49, 9–18. (In Chinese) [Google Scholar]
- Spalart, P.R.; Rumsey, C.L. Effective inflow conditions for turbulence models in aerodynamic calculations. AIAA J. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Bai, J.Q.; Hua, J.; Yang, T.H. Transition prediction based on amplification factor and Spalart-Allmaras turbulence model. J. Aerosp. Power 2015, 30, 1670–1677. (In Chinese) [Google Scholar]
- Cook, P.H.; Mcdonald, M.A.; Firmin, M.C.P. Aerofoil RAE2822-pressure distributions, and boundary layer and wake measurements. In Experimental Data Base for Computer Program Assessment; AGARD AR-138; 1979; Available online: https://www.sto.nato.int/publications/AGARD/AGARD-AR-138/AGARD-AR-138.pdf (accessed on 22 October 2024).
- Bai, W. Analyses of wind-tunnel test data of the transonic airfoil RAE2822. Acta Aerodyn. Sin. 2023, 41, 55–70. (In Chinese) [Google Scholar]
- Dervieux, A.; Braza, M.; Dussauge, J.P. Computation and Comparison of Efficient Turbulence Models for Aeronautics—European Research Project ETMA; Notes on Numerical Fluid Mechanics; Vieweg: Wiesbaden, Germany, 1998. [Google Scholar]
- Schmitt, V.; Charpin, F. Pressure Distributions on the ONERA M6-Wing at Transonic Mach Numbers. AGARD AR-138. 1979. Available online: https://www.semanticscholar.org/paper/Pressure-distributions-on-the-ONERA-M6-wing-at-Mach-Schmitt-Charpin/6498e2b6c38d7da95a07fe539bbf8525eba8f730 (accessed on 9 November 2023).








| Mesh | Total Point Number | Number on Surface | Normal Point Number |
|---|---|---|---|
| coarse | 19,964 | 183 | 41 |
| basic | 41,400 | 271 | 61 |
| fine | 97,704 | 415 | 93 |
| mildly finer | 228,760 | 639 | 141 |
| finer | 524,468 | 979 | 213 |
| finest | 909,812 | 1495 | 321 |
| Model | Orthogonal Mesh | Non-Orthogonal Mesh | ||
|---|---|---|---|---|
| CD | CDv | CD | CDv | |
| Wilcox-k-w | 0.0183 | 0.0062 | 0.0185 | 0.0062 |
| SST | 0.0160 | 0.0056 | 0.0164 | 0.0060 |
| SA | 0.0175 | 0.0058 | 0.0233 | 0.0112 |
| γ-Reθt-SST | 0.0155 | 0.0028 | 0.0156 | 0.0052 |
| Model | Orthogonal Mesh | Non-Orthogonal Mesh | ||
|---|---|---|---|---|
| CD | CDv | CD | CDv | |
| Wilcox-k-ω | 0.0177 | 0.0057 | 0.0177 | 0.0056 |
| SST | 0.0170 | 0.0052 | 0.0174 | 0.0055 |
| SA | 0.0175 | 0.0055 | 0.0231 | 0.0099 |
| γ-Reθt-SST | 0.0155 | 0.0044 | 0.0173 | 0.0054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, W.; Zhang, H.; Wang, L.; Nie, S.; Jiao, J.; Zuo, Y. Effects of the Uncertainty of Wall Distance on the Simulation of Turbulence/Transition Phenomena. Aerospace 2024, 11, 898. https://doi.org/10.3390/aerospace11110898
Tan W, Zhang H, Wang L, Nie S, Jiao J, Zuo Y. Effects of the Uncertainty of Wall Distance on the Simulation of Turbulence/Transition Phenomena. Aerospace. 2024; 11(11):898. https://doi.org/10.3390/aerospace11110898
Chicago/Turabian StyleTan, Weiwei, Heran Zhang, Lan Wang, Shengyang Nie, Jin Jiao, and Yingtao Zuo. 2024. "Effects of the Uncertainty of Wall Distance on the Simulation of Turbulence/Transition Phenomena" Aerospace 11, no. 11: 898. https://doi.org/10.3390/aerospace11110898
APA StyleTan, W., Zhang, H., Wang, L., Nie, S., Jiao, J., & Zuo, Y. (2024). Effects of the Uncertainty of Wall Distance on the Simulation of Turbulence/Transition Phenomena. Aerospace, 11(11), 898. https://doi.org/10.3390/aerospace11110898





