Abstract
The aerospace industry faces the challenge of maintaining product excellence amidst intricate processes and demands for cost and time efficiency. Mathematical modeling emerges as a valuable tool for optimizing the engineering process and enhancing quality, with potential applications extending beyond aerospace to other sectors with high quality and safety standards. This study develops and validates a mathematical model specific to the aerospace industry, aiming to assess the impact of human resource expertise on product quality. Through a case study within an aerospace organization, an IDEF0-methodology-based mathematical model, coupled with weighted averages, was constructed to depict the comprehensive engineering process and quantify knowledge’s impact on deliverable quality. Simulation data, gathered through human resource knowledge assessments and non-conformity analyses, revealed a direct correlation between technical knowledge levels and deliverable quality, consequently impacting final product quality. The proposed model serves as a tool for estimating potential deliverable error rates and pinpointing critical areas within the process that necessitate refinement. The research underscores the significance of knowledge investment and effective knowledge management strategies in upholding quality and competitiveness across industries with stringent quality requirements.
1. Introduction
In the context of the ongoing transition from the fourth industrial revolution (Industry 4.0) towards the fifth (Industry 5.0), industrial organizations are experiencing an unprecedented digital transformation. While Industry 4.0 laid the foundation for digitalization and automation, Industry 5.0 further emphasizes the collaboration between humans and machines, recognizing the central role of human skills and knowledge in advanced manufacturing environments. This shift brings with it a massive flow of information and increased process complexity. The challenge lies not only in effectively managing this volume of data but also in adapting engineering processes to leverage human expertise alongside technology, to meet the complex and changing customer requirements in an environment characterized by fierce competition and constant pressure for innovation.
The aerospace industry stands out for its exceptional demands in terms of quality and safety. Each component of an aircraft must meet stringent standards, and any error can have catastrophic consequences. At the same time, the industry is facing pressure to reduce costs and production time to remain competitive in an ever-expanding global market.
In this complex and dynamic context, mathematical modeling emerges as an essential tool for optimizing the global engineering process in the aerospace industry. By mathematically representing processes, a structured and quantitative perspective can be obtained, facilitating the understanding of interactions between different stages and the identification of critical factors that influence product quality.
Mathematical modeling allows for the simulation and analysis of various scenarios, contributing to informed decision making and process optimization to improve quality, reduce non-conformities, and increase efficiency. In the aerospace industry, where every detail matters, mathematical modeling can make the difference between success and failure.
This paper aims to develop a comprehensive mathematical model for the global engineering process in the aerospace industry, with the goal of assessing the impact of technical knowledge on product quality. Through this model, the way in which the level of knowledge of the human resources involved in the process influences product compliance with quality requirements will be investigated.
The main contributions of the paper include:
- -
- The proposal of an original mathematical model, based on a systemic approach and the use of the weighted average, to represent the global engineering process and quantify the impact of knowledge on quality.
- -
- The presentation of a structured methodology for evaluating the technical knowledge of human resources involved in the process, using questionnaires and non-conformity analysis.
- -
- The demonstration, through the simulation of the mathematical model, of how it can be used to identify critical areas in the process and implement measures to improve product quality.
This paper aims to make a significant contribution to the development of more efficient and safer engineering practices in the aerospace industry by highlighting the important role of technical knowledge in ensuring product quality.
2. Literature Review
In the aerospace industry, the overall engineering process refers to the entire lifecycle of a product, from the early concept and design phase, through production and testing, to final delivery and subsequent maintenance. Each step in this complex process generates a series of deliverables (technical documentation, 3D models, prototypes, finished products, etc.) that must meet rigorous quality standards. This holistic perspective on the engineering process is also emphasized by other authors, such as [1,2,3,4], who emphasize the importance of integrated quality management throughout the product lifecycle.
Mathematical modeling is a scientific approach that builds an abstract and simplified representation of a real system or process using mathematical language. In an engineering context, mathematical modeling allows the simulation and analysis of system behavior under different conditions, facilitating decision making and process optimization. This approach is supported by numerous studies, such as those of [5,6,7,8], which demonstrate the usefulness of modeling in assessing the linearity and partitioning of variables in industrial processes. In the present work, mathematical modeling is used to assess and predict the quality level of the deliverables in the engineering process, according to the quality requirements and the technical knowledge involved.
Quality in the aviation industry is not just about compliance with technical specifications. It also encompasses aspects such as product safety, reliability and performance, which are essential for mission success and human life. Quality standards in the aviation industry are extremely rigorous and any deviation can have serious consequences. This perspective is reinforced by work such as that of [9,10,11,12], which emphasizes the importance of quality management systems in the aerospace industry to ensure compliance with these high standards.
While the literature contains studies addressing various facets of mathematical modeling and quality management in engineering, particularly within the aerospace industry, the specific model proposed in this paper represents a novel contribution. This model, grounded in IDEF0 methodology and employing weighted averages to quantify the impact of human resource expertise on product quality, has not been previously utilized in this manner. Our research distinguishes itself by its unique focus on the role of human resource knowledge, the integration of IDEF0 for detailed process representation, and the quantification of knowledge’s impact on deliverable and final product quality. Developed and validated specifically for the aerospace industry, this model offers a practical and innovative tool for organizations seeking to optimize their engineering processes and enhance quality performance.
Numerous studies have focused on the development of mathematical models to represent and analyze manufacturing and engineering processes. For example, studies [13,14,15,16,17,18,19] explore the use of modeling techniques such as IDEF and UML to describe and optimize industrial processes. Other relevant works in this context include those by [20,21,22], who investigate the influence of additive manufacturing technologies on the machinability of titanium parts, and [23,24,25], who propose a hybrid approach for multi-response optimization of micro-milling parameters.
Another important direction in the literature is quality management in the aeronautics industry. Ref. [26], for example, analyzes quality management systems specific to this field and emphasizes the importance of integrating quality requirements at all stages of the engineering process. Other significant contributions in this area come from authors such as [27,28,29], who discuss trends in the development of digital quality management systems in the aerospace industry, and [30,31,32,33], who propose improvements to the Design for Manufacturing and Assembly (DFMA) guidelines for aerospace applications.
Although there are numerous studies on process modeling and quality management, there is still a gap in understanding and quantifying the direct impact of technical knowledge on product quality. This observation is also supported by work such as that of [34,35,36,37], which emphasizes the importance of applying a systems approach to engineering projects to ensure quality. The present work aims to address this gap by developing a mathematical model that explicitly links the knowledge level of human resources to the quality of deliverables in the engineering process.
The concept of Industry 5.0, which emphasizes human–machine collaboration and the central role of humans in the production process, has gained ground in recent years. This vision emphasizes the importance of human knowledge and skills in the context of advanced technologies. Work such as that of [38,39,40,41,42,43] explores the mechanical properties and machinability of additively manufactured titanium alloys, highlighting the need to adapt technical knowledge to new technologies.
In addition, it is important to note that international quality management standards, such as AS9100D, provide a general framework for implementing and improving quality management systems, including in the aviation industry, and can be adapted to meet the specific requirements of this sector [44].
In conclusion, this research is based on a solid theoretical foundation, capitalizing on existing knowledge in the field of mathematical modeling and quality management, and aims to make an original contribution by investigating the relationship between technical knowledge and product quality in the specific context of the aerospace industry.
The aerospace industry’s stringent quality and safety requirements necessitate a comprehensive understanding of factors influencing product quality. While existing literature explores mathematical modeling and quality management, there remains a gap in quantifying the direct impact of technical knowledge on product quality, especially within the context of Industry 5.0’s emphasis on human–machine collaboration. This research aims to bridge this gap by developing a mathematical model that explicitly links human resource knowledge levels to the quality of deliverables in the engineering process, offering a practical tool for organizations to evaluate and optimize their processes, not only in aerospace but also in other industries with high quality and safety demands.
3. Research Methodology
3.1. Description of the Mathematical Model
The mathematical model developed in this research is based on a systems approach, in which the overall engineering process is viewed as a sequence of interdependent sub-processes, each contributing to the transformation of product quality requirements into concrete deliverables.
Figure 1 illustrates how the mathematical model has been built based on a functional graphical model using the IDEF0 methodology. This methodology allows for a clear visual representation of the process, facilitating the understanding of the relationships between the different sub-processes and the flow of information and materials.
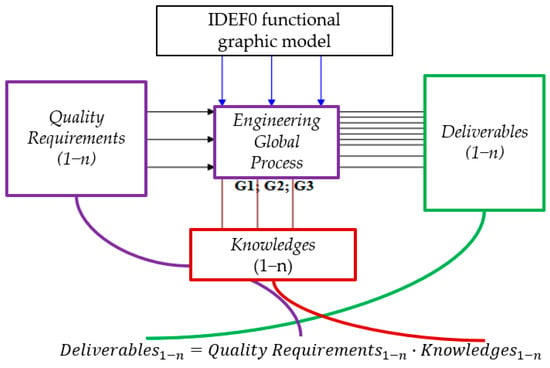
Figure 1.
Building the mathematical model based on the functional graphical model.
The model transformation function, described by relation (1), expresses mathematically how the deliverables of the overall engineering process are generated by the interaction between the quality requirements of the products and the technical knowledge involved in the process:
In this equation, “Deliverables 1−n” is the set of all deliverables generated by the engineering process, “Quality Requirements 1−n” are the specific requirements imposed on the product, and “Knowledge 1−n” reflects the level of technical knowledge of the human resources involved in the process.
3.2. Using Weighted Averaging
Since both quality requirements and technical knowledge may vary over time and depending on the specifics of each product and sub-process, the use of weighted averaging in mathematical modeling was chosen. This approach allows for a more realistic estimation of the quality level of the deliverables, considering the relative importance of each quality requirement and each type of knowledge.
3.3. Mathematical Modeling of Deliverables
Each deliverable of the overall engineering process has been individually mathematically modeled, considering specific inputs and influencing factors, in particular technical knowledge. This research presents in detail the mathematical modeling for the deliverable “G1.1.1.L1-technical product documentation registered in PLM”, using relations (2)–(19).
The sub-process addressed is G1.1.1.1-receiving and registering documentation, whose deliverable is G1.1.1.L1 or the technical product documentation registered in PLM. We can thus consider the deliverable as a transformation function of product quality requirements through the component activities of sub-process (2):
where:
is the sum of the component activities of the sub-process G1.1.1.
To find the degree of influence of the activities on the deliverable, we can express the mathematical relationship of this accumulation of activities by establishing the weights of influence of the knowledge of each activity using the mathematical relationship of the weighted average, as follows:
where:
G1.1.1.A1 is the activity “accessing the product technical documentation in the customer’s system”;
G1.1.1.A2 is the activity “download files and save to the appropriate location on the internal network”;
G1.1.1.A3 is the activity “registration of technical documentation in the internal PLM application and sorting of documents by document type”;
G1.1.1.A4 is the activity “communicating confirmation of registration of technical documents in the PLM system”;
is the number weights of the values of the terms in the mathematical relation (3) where .
Since each activity is performed based on the knowledge involved in it, we can consider the activity expressed by a mathematical relationship as the percentage product of the knowledge involved.
For activity G1.1.1.1.A1, the mathematical relation can be considered as the weighted average of the weighted averages of the categories of knowledge involved in the realization of the activity, as expressed in the following mathematical relation (4):
where:
| —the sum of technical knowledge involved in activity G1.1.1.A1; | |
| —the sum of the knowledge of the processes within the SMC involved in activity G1.1.1.A1; | |
| —cumulative knowledge of software involved in activity G1.1.1.A1; | |
| —cumulative communication knowledge involved in activity G1.1.1.1.A1; | |
| —the number weights of the term values in the mathematical relation (4), where . |
For activity G1.1.1.1.A1, the product of the knowledge involved leads to the percentage level of knowledge available at a given time and can be expressed by the following mathematical relations:
where:
| —knowledge of aerospace product identification; | |
| —knowledge of the identification of technical documentation designed for aerospace products; | |
| —knowledge of the approval steps of the designed technical documentation; | |
| —knowledge on the identification of the type of product (technical specification, semi-manufacture, landmark, sub-assembly, assembly, standard item); | |
| —knowledge of internal document control procedures; | |
| —knowledge of internal procedures concerning the confidentiality of technical aerospace data; | |
| —knowledge of customer procedures for access to technical documentation; | |
| —knowledge of internal procedures relating to data security and confidentiality within the organization; | |
| —knowledge of internal procedures for aerospace product type identification | |
| —knowledge of WEB applications and the use of an operating system; | |
| —knowledge of secure file transfer applications; | |
| —knowledge of communicating information in the official aerospace language (English); | |
| —knowledge of how to communicate technical information relating to the contractual products; | |
| —the number weights of the values of the terms in the mathematical relations (5)–(8), where . |
For activity G1.1.1.A2, the mathematical relationship can be considered as the weighted average of the weighted averages of the categories of knowledge involved in the realization of the activity, as expressed in the following mathematical relationship (9):
where:
| —the sum of the knowledge of the processes in the SMC involved in activity G1.1.1.A2; | |
| —the accumulation of software knowledge involved in activity G1.1.1.1.A2; | |
| —the number weights of the values of the terms in the mathematical relation (9) where . |
For activity G1.1.1.1.A2, the product of the knowledge involved leads to the percentage level of knowledge available at a given time and can be expressed by the following mathematical relations:
where:
| —knowledge of internal file management procedures in the internal system; | |
| —knowledge of web applications and the use of an operating system. |
For activity G1.1.1.A3, the mathematical relationship can be considered as the weighted average of the weighted averages of the categories of knowledge involved in the realization of the activity, as expressed in the following mathematical relationship (12):
where:
| —the sum of technical knowledge involved in activity G1.1.1.A3; | |
| —the sum of the knowledge of processes within the SMC involved in activity G1.1.1.A3; | |
| —the sum of software knowledge involved in activity G1.1.1.1.A3; | |
| —the number weights of the values of the terms in the mathematical relation (13) where . |
For activity G1.1.1.1.A3, the product of the knowledge involved results in the percentage level of knowledge available at a given point in time and can be expressed by the following relations:
where:
| —knowledge of how to organize product items in a tree structure; | |
| —knowledge of the identification of the type of technical documents specific to the aerospace field; | |
| —knowledge of grouping technical documents by customer (product) item; | |
| —knowledge of extracting structured item information required in production processes; | |
| —knowledge of the internal procedures for registration in the PLM application; | |
| —knowledge of how to use PLM application; | |
| —the number weights of the term values in the mathematical relation (13), where . |
For the activity G1.1.1.A4, the mathematical relationship can be considered as the weighted average of the weighted averages of the categories of knowledge involved in the realization of the activity, as expressed in the following mathematical relationship (16):
where:
| —the combined knowledge of the MSC processes involved in activity G1.1.1.A4; | |
| —the sum of software knowledge involved in activity G1.1.1.1.A4; | |
| —the sum of the communication knowledge involved in activity G1.1.1.1.A4; | |
| —the number weights of the values of the terms in the mathematical relation (16) where . |
For activity G1.1.1.1.A4, the product of the knowledge involved leads to the percentage level of knowledge available at a given time and can be expressed by the following mathematical relations:
where:
| —knowledge of internal procedures for managing the transfer of technical documentation from the customer to the organization; | |
| —knowledge of the use of Microsoft 365 applications (Excel, Outlook, PowerPoint); | |
| —knowledge of communicating technical information within the organization. |
This detailed approach allows a granular analysis of how technical knowledge influences the quality of each deliverable. By assessing the level of knowledge and applying the appropriate mathematical relationships, it is possible to estimate the level of compliance of each deliverable with the required quality requirements.
Overall, the research methodology proposed in this paper combines functional graphical modeling with mathematical modeling, using weighted averaging to account for the variation influencing factors. This approach allows a quantitative assessment of the impact of technical knowledge on product quality in the engineering process, providing a valuable tool for process optimization and quality improvement in the aerospace industry.
3.4. Justification of Methods
Integration Definition for Function Modeling (IDEF0): The choice of IDEF0 for functional graphical modeling of the overall engineering process is justified by its ability to represent in a clear and structured way both the activities and their relationships, the information and material flows, and the constraints and resources involved. In the context of the aerospace industry, where processes are complex and interdependent, IDEF0 provides a comprehensive visualization of the system, facilitating the understanding and communication of relevant information to all parties involved. This methodology also allows a hierarchical decomposition of the process into sub-processes and activities, which facilitates detailed analysis and identification of critical points.
Weighted average: The use of weighted averaging in mathematical modeling was motivated by the need to account for the inherent variation in quality requirements and level of technical knowledge. In the aircraft industry, quality requirements may differ significantly from one product to another, and the technical knowledge of human resources may evolve over time. Weighted averaging allows different weights to be assigned to each requirement and each type of knowledge, reflecting their relative importance in the engineering process. This approach leads to a more accurate and realistic estimation of the impact of knowledge on the quality of deliverables.
4. Case Study
The simulation of the mathematical model was carried out in an aerospace industrial organization specialized in the manufacturing of metallic structural components for aircraft. This industry is characterized by a high level of product and process complexity as well as stringent quality and safety requirements.
Data used for the simulation were collected by two main methods:
- -
- Knowledge assessment by questionnaires: The human resources involved in the sub-process “3D model preparation” were assessed in relation to the basic and specific knowledge needed to understand and interpret the quality requirements. The results of this assessment are presented in Table 1 and Table 2.
- -
- Analysis of non-conformities: The non-conformities recorded in the organization were analyzed, identifying those cases where the primary cause was related to the interpretation or omission of quality requirements. These data were used to validate and complement the results obtained through questionnaires.

Table 1.
Results of the assessment of the resources involved in the sub-process “3D model preparation” on the quality requirements of a beam product used in aircraft flooring.
Table 1.
Results of the assessment of the resources involved in the sub-process “3D model preparation” on the quality requirements of a beam product used in aircraft flooring.
| No. | Product Quality Requirements | Requirement Weight in Evaluation [%] | Weighted Average [%] | Res.1 [%] | Res.2 [%] | Res.3 [%] | Res.4 [%] | Res.5 [%] | Res.6 [%] | Res.7 [%] | Res.8 [%] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Compliance with all dimensions | 5.88 | 98.4 | 95.6 | 95.8 | 100 | 99.0 | 99.0 | 99.0 | 99.0 | 100 |
| 2 | Respecting the relative position of all geometrical characteristics of the part | 5.88 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 |
| 3 | Realization of all designed characteristics | 5.88 | 96.0 | 96.7 | 94.0 | 94.0 | 94.0 | 95.0 | 94.0 | 100 | 100 |
| 4 | Chemical composition | 5.88 | 94.9 | 92.3 | 96.4 | 94.3 | 95.4 | 90.0 | 91.0 | 100 | 100 |
| 5 | Mechanical properties | 5.88 | 96.6 | 97.0 | 95.2 | 99.0 | 95.2 | 95.0 | 96.4 | 96.8 | 98.0 |
| 6 | Material certification considering the production process | 5.88 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 | 95.0 |
| 7 | Production tolerances | 5.88 | 91.3 | 85.0 | 92.0 | 90.0 | 85.0 | 90.0 | 93.2 | 96.0 | 99.0 |
| 8 | Assembly tolerances | 5.88 | 93.1 | 87.0 | 98.0 | 97.5 | 85.0 | 89.0 | 93.0 | 96.0 | 99.0 |
| 9 | Functional deviations in the final product | 5.88 | 93.3 | 88.0 | 97.0 | 97.0 | 90.0 | 86.0 | 93.6 | 96.0 | 99.0 |
| 10 | Surface corrosion protection | 5.88 | 95.2 | 91.0 | 98.0 | 91.0 | 92.0 | 93.0 | 97.8 | 99.0 | 99.6 |
| 11 | Traceability | 5.88 | 99.0 | 99.0 | 99.0 | 99.0 | 99.0 | 99.0 | 100 | 99.0 | 99.0 |
| 12 | Technical documentation drawn to scale drawings | 5.88 | 95.4 | 94.0 | 94.2 | 95.0 | 93.8 | 94.0 | 95.0 | 98.0 | 99.0 |
| 13 | Digital technical documentation | 5.88 | 93.6 | 92.2 | 93.5 | 94.1 | 91.8 | 91.7 | 92.3 | 94.5 | 99.0 |
| 14 | Different inspection levels depending on the safety class of the product | 5.88 | 98.3 | 92.0 | 100 | 97.5 | 100 | 98.9 | 99.0 | 100 | 99.0 |
| 15 | Preparation of product control documentation | 5.88 | 96.2 | 94.0 | 97.2 | 98.6 | 96.1 | 94.3 | 94.8 | 96.2 | 98.7 |
| 16 | Quality management system certification requirements | 5.88 | 94.5 | 95.4 | 94.2 | 94.1 | 93.7 | 92.8 | 93.9 | 92.1 | 100 |
| 17 | Control of design data | 5.88 | 94.0 | 94.0 | 94.0 | 94.0 | 94.0 | 94.0 | 94.0 | 94.0 | 94.0 |
| Requirement weight in evaluation | 93.1% | 95.8% | 95.6% | 94.1% | 93.6% | 95.1% | 96.9% | 98.4% | |||

Table 2.
Results of the knowledge assessment involved in the sub-process.
Table 2.
Results of the knowledge assessment involved in the sub-process.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
[%] | 96.1 | 98.4 | 96.0 | 94.9 | 96.6 | 99 | 95.4 | 93.6 | 98.3 | 96.2 | 94.5 | 94 | |||||
[%] | 95.7 | 96.0 | 96.6 | 99 | 95.4 | 93.6 | 96.2 | 94.5 | 94 | ||||||||
[%] | 95.9 | 96.0 | 99 | 95.4 | 93.6 | 98.3 | 96.2 | 94.5 | 94 | ||||||||
[%] | 95.6 | 98.4 | 96.0 | 94.9 | 96.6 | 91.3 | 93.1 | 93.3 | 95.2 | 99 | 98.3 | ||||||
[%] | 95.6 | 98.4 | 96.0 | 94.9 | 96.6 | 91.3 | 93.1 | 93.3 | 95.2 | 99 | 98.3 | ||||||
[%] | 95.0 | 98.4 | 96.0 | 91.3 | 93.1 | 93.3 | 99 | 95.4 | 93.6 | 96.2 | 94 | ||||||
[%] | 95.9 | 99 | 95.4 | 93.6 | 98.3 | 96.2 | 94.5 | 94 | |||||||||
[%] | 95.8 | 94.9 | 96.6 | 95.2 | 99 | 95.4 | 93.6 | 98.3 | 96.2 | 94.5 | 94 | ||||||
[%] | 95.0 | 98.4 | 95.0 | 96.0 | 91.3 | 93.1 | 93.3 | 99 | 95.4 | 93.6 | 96.2 | 94.5 | 94 | ||||
[%] | 95.5 | 99 | 95.4 | 93.6 | 96.2 | 94.5 | 94 | ||||||||||
[%] | 95.5 | 99 | 95.4 | 93.6 | 96.2 | 94.5 | 94 | ||||||||||
[%] | 95.1 | 98.4 | 96.0 | 94.9 | 96.6 | 91.3 | 93.1 | 93.3 | 95.2 | 99 | 95.4 | 93.6 | 96.2 | 94.5 | 94 | ||
[%] | 95.5 | 99 | 93.6 | 96.2 | 94.5 | 94 | |||||||||||
[%] | 95.5 | 99 | 93.6 | 96.2 | 94.5 | 94 | |||||||||||
[%] | 95.1 | 98.4 | 96.0 | 94.9 | 96.6 | 91.3 | 93.1 | 93.3 | 95.2 | 99 | 93.6 | 96.2 | 94.5 | 94 | |||
[%] | 95.3 | 98.4 | 96.0 | 94.9 | 96.6 | 91.3 | 93.1 | 93.3 | 95.2 | 99 | 95.4 | 93.6 | 98.3 | 96.2 | 94.5 | 94 |
Table Legend: 1—Weighted average. 2—Respecting all dimensions. 3—Respecting the relative position of all geometrical characteristics of the part. 4—Realization of all designed features. 5—Chemical composition. 6—Mechanical properties. 7—Production tolerances. 8—Mounting tolerances. 9—Functional deviations in the final product. 10—Surface corrosion protection. 11—Respecting traceability. 12—Technical documentation drawn to scale drawings. 13—Digital technical documentation. 14—Different inspection levels depending on the safety class of the product. 15—Preparation of product control documentation. 16—Quality management system certification requirements. 17—Design data control. Knowledge Code: Description of type of knowledge. —Knowledge of aerospace product identification. —Knowledge of the stages of approval of designed technical documentation. —Knowledge on identification of the type of technical documents, specific to the aerospace domain. —Knowledge of how to interpret technical drawings, 3D models, and symbols specific to aerospace. —Knowledge of how to interpret written requirements (texts) on shape, deviations, tolerances, characteristics of aerospace products. —Knowledge of the general standards for realization of geometries in 3D model (transitions from one plane to another using standard radii, criteria for realization of unfolded, bent, etc.). —Knowledge to identify the type of product (technical specification, semi-manufactured part, landmark, sub-assembly, assembly, standard element). —Knowledge of grouping technical documents by customer item (product). —Knowledge of 3D modeling of products according to aerospace customer standards. —Knowledge of internal aerospace product type identification procedures. —Knowledge of internal file management procedures in the internal system. —Knowledge of internal procedures for checking and creating internal 3D models of products. —Knowledge on the use of PLM application. —Knowledge of using ERP application. —Knowledge of the use of CAD applications (Catia V5). —Knowledge of communicating technical information within organizations.
Table 1 presents the results of the evaluation of human resources in relation to different quality requirements of the product, such as dimensional compliance, tolerances, chemical composition, etc.
In Table 1, the abbreviation “Res.” refers to “Resource”. Each column labeled “Res.1” through “Res.8” represents an individual human resource involved in the “3D model preparation” sub-process. The values in these columns indicate the percentage scores obtained by each resource in relation to the specific quality requirements of the product. The weighted average presented in Table 1 was derived under the premise of equal significance for all 17 quality requirements, thereby assigning an approximate weight of 5.88% to each individual requirement. This weighted average serves as a comprehensive indicator of the overall average score. To enhance clarity and precision, Table 1 explicitly includes the weight assigned to each quality requirement, along with the corresponding weighted average value utilized in the final computation.
Table 2 details the assessment of the specific technical knowledge involved in the sub-process under analysis such as knowledge on the interpretation of technical drawings, 3D modeling standards, use of software applications, etc.
These data were used to feed the mathematical model and simulate the impact of the technical knowledge on the quality of the deliverable “G1.3.1.L1-3D Model”. The results of this simulation will be presented and discussed in the next section.
5. Results and Discussion
5.1. Results
The simulation of the mathematical model for the deliverable “G1.3.1.L1-3D Model” has led to several relevant results, detailed below.
Figure 2 details how the product quality requirements are correlated with the deliverable of sub-process G1.3.1, i.e., the 3D model. This figure emphasizes that each quality requirement, such as dimensional compliance, tolerances, or chemical composition, must be accurately reflected in the 3D model to ensure the final product quality.
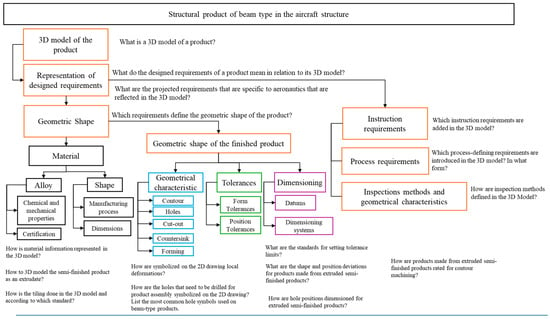
Figure 2.
Detailing product quality requirements in relation to sub-process deliverables.
Figure 3, Figure 4, Figure 5 and Figure 6 illustrate the distribution of the levels of technical, process, software, and communication knowledge involved in each of the four activities of sub-process G1.3.1. These figures show that, in general, technical knowledge plays an important role in all activities, underlining its significant role in 3D model quality assurance. However, a relevant contribution of other types of knowledge is also observed, especially at certain stages of the process. There is also a variation in the level of knowledge between the different human resources involved, which underlines the importance of an individualized approach to knowledge development and management.
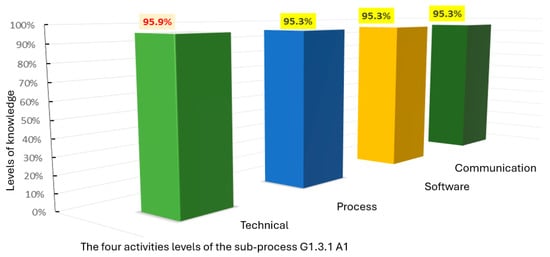
Figure 3.
Distribution of knowledge levels involved in activity G1.3.1.A1.
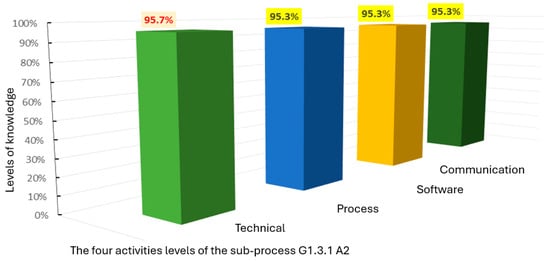
Figure 4.
Distribution of knowledge levels involved in activity G1.3.1.A2.
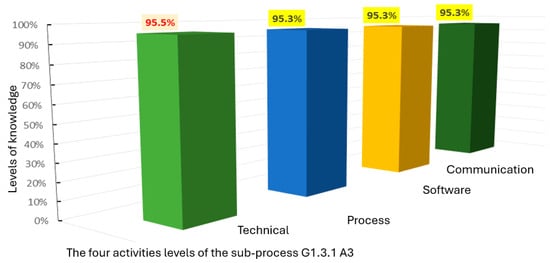
Figure 5.
Distribution of knowledge levels involved in activity G1.3.1.A3.
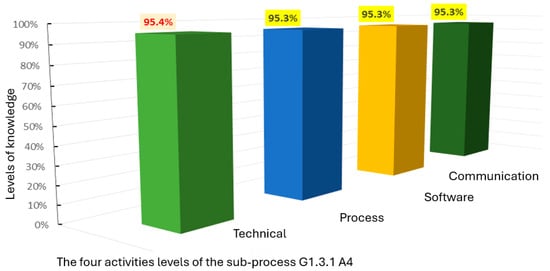
Figure 6.
Distribution of knowledge levels involved in activity G1.3.1.A4.
Figure 7 shows the graphical representation of the result of deliverable function G1.3.1.L1. This figure shows that, under simulation conditions, with a knowledge level of about 95.4%, there is a probability of about 4.5% of obtaining a non-conforming 3D model. This value can be interpreted as a potential error rate of the deliverable, which can be used to estimate the number of possibly non-conforming 3D models in a production batch.
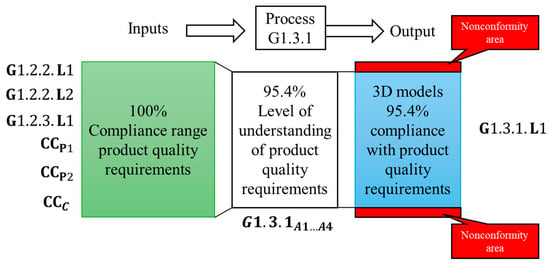
Figure 7.
Graphical representation of the result of deliverable function G1.3.1.L1.
5.2. Discussion
The simulation results demonstrate the direct and significant impact of technical knowledge on the quality of the 3D model, which in turn influences the final product quality. In the context of the aerospace industry, where any error can have serious consequences, these results emphasize the critical importance of continuously evaluating and developing the technical knowledge of the human resources involved in the engineering process.
Organizations in this sector should invest in training and professional development programs to ensure that their employees possess the necessary knowledge and skills to meet rigorous quality requirements. It is also essential to create a work environment that encourages knowledge sharing and collaboration between the various departments and teams involved in the engineering process.
The mathematical model proposed in this paper provides a valuable tool for evaluating the impact of knowledge on quality and for identifying critical areas in the process that require improvement. However, the model also has some limitations. For example, it is based on a series of simplifying assumptions and does not consider all the factors that can influence the quality of the products.
To overcome these limitations, future research is needed to explore and integrate other relevant factors into the model, such as employee experience, product complexity, or technologies used. It would also be useful to extend the model to cover the entire overall engineering process, not just the 3D model preparation sub-process.
In conclusion, the results of this research emphasize the importance of technical knowledge in assuring product quality in the aerospace industry, while highlighting the complementary role of other types of knowledge, such as process, software, and communication. The proposed mathematical model, although perfectible, provides a practical training for the evaluation and optimization of engineering processes, contributing to a better understanding of the complex relationship between knowledge and quality in this demanding field.
6. Conclusions
This paper explored the complex relationship between technical knowledge and product quality in the context of the global engineering process in the aerospace industry. Through the development and simulation of an innovative mathematical model, it has been shown that the knowledge level of human resources has a direct and significant impact on the quality of the deliverables and, implicitly, on the final quality of the products.
The case study carried out highlighted the fact that, even in the case of a specific sub-process such as the preparation of the 3D model, variations in the level of knowledge can lead to a significant probability of non-conformities. This finding underscores the critical importance of the continuous assessment and development of technical knowledge within aerospace organizations.
The paper makes several original contributions to the field of quality management and aerospace engineering:
- -
- Development of a mathematical model: A mathematical model based on the weighted average was proposed, which allows quantifying the impact of technical knowledge on the quality of deliverables from the engineering process. This model can be used to estimate the potential error rate of deliverables and to identify critical areas in the process that require improvement.
- -
- A knowledge assessment method: The paper presents a structured methodology for assessing technical knowledge, using questionnaires and non-conformity analysis. This method can be adapted and applied in various industrial contexts to assess the training level of human resources and identify training needs.
- -
- A quality optimization tool: By simulating the mathematical model, it has been shown that it can be used as a practical tool for optimizing the engineering process and improving product quality. Organizations can use this model to assess the impact of different scenarios and make informed decisions to increase quality and efficiency.
Although this work has made a significant contribution to the field, there are still many future research directions that can be explored:
- -
- Application of the model in other contexts: The proposed mathematical model can be extended and applied in other stages of the global engineering process or in other organizations in the aerospace industry to assess the impact of knowledge on quality in a wider range of activities and products.
- -
- Development of more sophisticated knowledge assessment methods: Knowledge assessment methodology can be improved by using more advanced techniques, such as competency analysis or cognitive modeling, to obtain a more accurate and detailed picture of the level of training of human resources.
- -
- Integrating the model with other tools: The mathematical model can be integrated with other process optimization tools, such as discrete simulation or risk analysis, to obtain an even more complete insight into the factors influencing product quality and to identify the most effective strategies for improvement.
In conclusion, this paper demonstrated the importance of technical knowledge in product quality assurance in the aerospace industry. By developing an innovative mathematical model and knowledge assessment methodology, the way to a more systematic and effective approach to quality management in this complex and demanding field has been opened. Future research will be able to deepen and extend these results, contributing to the development of better-performing and safer engineering practices in the aerospace industry.
Author Contributions
Conceptualization, G.I.P. and A.M.T.; methodology, G.I.P. and A.M.T.; software, G.I.P.; validation, G.I.P., formal analysis, A.B.P.; investigation, G.I.P.; resources, G.I.P.; data curation, G.I.P. and A.M.T.; writing—original draft preparation, G.I.P. and A.M.T.; writing—review and editing, A.B.P.; visualization, G.I.P. and A.M.T.; supervision, G.I.P. and A.M.T.; project administration, G.I.P.; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Gheorghe Ioan Pop was employed by the company S.C. Universal Alloy Corporation Europe S.R.L. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Pop, G.I.; Titu, A.M. Contributions Regarding the Specific Approach on the Management of the Global Engineering Process in Aerospace Organization. Strategica, 1031. Available online: https://strategica-conference.ro/wp-content/uploads/2022/04/78-1.pdf (accessed on 9 September 2024).
- Pop, G.I.; Titu, A.M.; Pop, A.B. Requirements versus Knowledge in the Quality Management of the Global Engineering Process within an Organization in the Aerospace Industry. Aerospace 2022, 9, 817. [Google Scholar] [CrossRef]
- Ţîţu, A.M.; Pop, G.I. Modeling the global engineering process in an aerospace organization. Int. J. Mechatron. Appl. Mech. 2021, 9, 217–224. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N.; Manohar, K.; Aravkin, A.Y.; Morgansen, K.; Klemisch, J.; Goebel, N.; Buttrick, J.; Poskin, J.; Blom-Schieber, A.W.; et al. Data-driven aerospace engineering: Reframing the industry with machine learning. AIAA J. 2021, 59, 2820–2847. [Google Scholar] [CrossRef]
- Li, O.; Feng, P.; Zeng, L.; Xu, C.; Zhang, J. Path planning method for on-machine inspection of aerospace structures based on adjacent feature graph. Robot. Comput.-Integr. Manuf. 2018, 54, 17–34. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.; Sun, R.; Yue, X. Optimal path planning for automated dimensional inspection of free-form surfaces. J. Manuf. Syst. 2020, 56, 84–92. [Google Scholar] [CrossRef]
- Deng, T.; Li, Y.; Chen, J.; Liu, X.; Wang, L. Informed machine learning-based machining parameter planning for aircraft structural parts. Int. J. Adv. Manuf. Technol. 2021, 117, 3563–3575. [Google Scholar] [CrossRef]
- Chen, X. UAV patrol path planning based on machine vision and multi-sensor fusion. Open Comput. Sci. 2023, 13, 20220276. [Google Scholar] [CrossRef]
- Tomić, B.; Brkić, V.S.; Klarin, M. Quality Management System for the Aerospace Industry. J. Eng. Manag. Compet. 2011, 2, 11–15. [Google Scholar]
- Khorasani, M.; Ghasemi, A.; Rolfe, B.; Gibson, I. Additive manufacturing a powerful tool for the aerospace industry. Rapid Prototyp. J. 2022, 28, 87–100. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving aircraft performance using machine learning: A review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Zonnenshain, A.; Kenett, R.S. Quality 4.0—The challenging future of quality engineering. Qual. Eng. 2020, 32, 614–626. [Google Scholar] [CrossRef]
- Li, W.; Zhao, C.; Gao, F. Linearity Evaluation and Variable Subset Partition Based Hierarchical Process Modeling and Monitoring. IEEE Trans. Ind. Electron. 2018, 65, 2683–2692. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, C. Linear and nonlinear hierarchical multivariate time delay analytics for dynamic modeling and process monitoring. J. Process Control 2021, 107, 83–93. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, J.; Wu, D.; Huang, K.; Gui, W. Variable partition based parallel dictionary learning for linearity and nonlinearity coexisting dynamic process monitoring. Control Eng. Pract. 2024, 142, 105750. [Google Scholar] [CrossRef]
- Fu, M.; Wang, D.; Wang, J.; Li, M. Modeling Method of Operational Task Combined with IDEF and UML. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 1443–1447. [Google Scholar] [CrossRef]
- Yun, W.; Zhang, X.; Li, Z.; Liu, H.; Han, M. Knowledge modeling: A survey of processes and techniques. Int. J. Intell. Syst. 2021, 36, 1686–1720. [Google Scholar] [CrossRef]
- Ullmann, T.A.; Scalice, R.K. A unified method for functional modeling of mechatronic products. J. Eng. Des. 2021, 32, 115–139. [Google Scholar] [CrossRef]
- Makarov, A.; Shabunin, A. Unified Design Methodology for State Information Systems. In Proceedings of the MIP Computing-V 2022: V International Scientific Workshop on Modeling, Information Processing and Computing, Krasnoyarsk, Russia, 25 January 2022. [Google Scholar]
- Alonso, U.; Veiga, F.; Suárez, A.; Artaza, T. Experimental Investigation of the Influence of Wire Arc Additive Manufacturing on the Machinability of Titanium Parts. Metals 2020, 1, 24. [Google Scholar] [CrossRef]
- Naksuk, N.; Poolperm, P.; Nakngoenthong, J.; Printrakoon, W.; Yuttawiriya, R. Experimental investigation of hot-wire laser deposition for the additive manufacturing of titanium parts. Mater. Res. Express 2022, 9, 056515. [Google Scholar] [CrossRef]
- Veiga, F.; Gil Del Val, A.; Suárez, A.; Alonso, U. Analysis of the machining process of titanium Ti6Al-4V parts manufactured by wire arc additive manufacturing (WAAM). Materials 2020, 13, 766. [Google Scholar] [CrossRef] [PubMed]
- Brahmeswara Rao, D.; Venkata Rao, K.; Gopala Krishna, A. A hybrid approach to multi response optimization of micro milling process parameters using Taguchi method based graph theory and matrix approach (GTMA) and utility concept. Measurement 2018, 120, 43–51. [Google Scholar] [CrossRef]
- Vookoti, U.S.V.P.; Rao, V.; Kumar, S. Optimization of machining characteristics during helical milling of AISI D2 steel considering chip geometry. Indep. J. Manag. Prod. 2022, 13, 750–770. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chakraborty, S. A scoping review on the applications of MCDM techniques for parametric optimization of machining processes. Arch. Comput. Methods Eng. 2022, 29, 4165–4186. [Google Scholar] [CrossRef]
- Țîțu, A.M.; Pop, G.I. Regarding Quality Management System in Aerospace Industry Organizations. Mater. Sci. Forum 2019, 957, 221–230. [Google Scholar] [CrossRef]
- Kovrigin, E.; Vasiliev, V. Trends in the development of a digital quality management system in the aerospace industry. IOP Conf. Ser. Mater. Sci. Eng. 2020, 868, 012011. [Google Scholar] [CrossRef]
- Li, L.; Aslam, S.; Wileman, A.; Perinpanayagam, S. Digital twin in aerospace industry: A gentle introduction. IEEE Access 2021, 10, 9543–9562. [Google Scholar] [CrossRef]
- Dutta, G.; Kumar, R.; Sindhwani, R.; Singh, R.K. Digitalization priorities of quality control processes for SMEs: A conceptual study in perspective of Industry 4.0 adoption. J. Intell. Manuf. 2021, 32, 1679–1698. [Google Scholar] [CrossRef]
- Rajamani, M.; Punna, E. Enhancement of Design for Manufacturing and Assembly Guidelines for Effective Application in Aerospace Part and Process Design. SAE Tech. Pap. 2020, 1, 6001. [Google Scholar] [CrossRef]
- Gradl, P.; Tinker, D.C.; Park, A.; Mireles, O.R.; Garcia, M.; Wilkerson, R.; Mckinney, C. Robust metal additive manufacturing process selection and development for aerospace components. J. Mater. Eng. Perform. 2022, 31, 6013–6044. [Google Scholar] [CrossRef]
- Tepylo, N.; Huang, X.; Patnaik, P.C. Laser-based additive manufacturing technologies for aerospace applications. Adv. Eng. Mater. 2019, 21, 1900617. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Alblawi, A.; Nawab, M.; Alsyaari, A. Application of systems engineering approach in senior design projects. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Santa Cruz de Tenerife, Canary Islands, Spain, 17–20 April 2018; pp. 1151–1160. [Google Scholar] [CrossRef]
- Kossiakoff, A.; Biemer, S.M.; Seymour, S.J.; Flanigan, D.A. Systems Engineering Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Buede, D.M.; Miller, W.D. The Engineering Design of Systems: Models and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Martin, J.N. Systems Engineering Guidebook: A Process for Developing Systems and Products; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Shunmugavel, M.; Polishetty, A.; Goldberg, M.; Singh, R.; Littlefair, G. A comparative study of mechanical properties and machinability of wrought and additive manufactured (selective laser melting) titanium alloy–Ti-6Al-4V. Rapid Prototyp. J. 2017, 23, 1051–1056. [Google Scholar] [CrossRef]
- Ren, X.P.; Li, H.Q.; Guo, H.; Shen, F.L.; Qin, C.X.; Zhao, E.T.; Fang, X.Y. A comparative study on mechanical properties of Ti–6Al–4V alloy processed by additive manufacturing vs. traditional processing. Mater. Sci. Eng. A 2021, 817, 141384. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Pramanik, A.; Basak, A.; Dong, Y.; Prakash, C.; Debnath, S.; Shankar, S.; Jawahir, I.; Dixit, S.; Buddhi, D. A critical review on additive manufacturing of Ti-6Al-4V alloy: Microstructure and mechanical properties. J. Mater. Res. Technol. 2022, 18, 4641–4661. [Google Scholar] [CrossRef]
- Tambare, P.; Meshram, C.; Lee, C.C.; Ramteke, R.J.; Imoize, A.L. Performance measurement system and quality management in data-driven Industry 4.0: A review. Sensors 2021, 22, 224. [Google Scholar] [CrossRef] [PubMed]
- Filz, M.A.; Bosse, J.P.; Herrmann, C. Digitalization platform for data-driven quality management in multi-stage manufacturing systems. J. Intell. Manuf. 2024, 35, 2699–2718. [Google Scholar] [CrossRef]
- Czvetkó, T.; Kummer, A.; Ruppert, T.; Abonyi, J. Data-driven business process management-based development of Industry 4.0 solutions. CIRP J. Manuf. Sci. Technol. 2022, 36, 117–132. [Google Scholar] [CrossRef]
- AS9100D; Quality Management Systems-Requirements for Aviation, Space and Defense Organizations. SAE International: Warrendale, PA, USA, 2016.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).