Probabilistic Air Traffic Complexity Analysis Considering Prediction Uncertainties in Traffic Scenarios

Abstract

This article presents a methodology for analyzing probabilistic air traffic complexity by integrating prediction uncertainties in convective weather scenarios. With the Performance Review Unit (PRU) model as a base, this method modifies the original framework by incorporating a weather-related complexity indicator. The approach was tested in Austrian airspace using ensemble weather forecasts and historical flight plan data. The results demonstrated that a probabilistic model effectively assesses traffic complexity and captures trends in complexity over time, providing greater reliability in high-complexity sectors. Validation revealed a strong alignment between simulator complexity values and probabilistic complexity, especially in sectors characterized by dense data distributions. In contrast, sectors with more elongated distributions tended to overestimate complexity. Quantitative analysis indicated that the error between the probabilistic mean complexity and the simulator complexity values ranged from 12% to 23%, with higher errors in sectors with lower complexity. This validation confirmed the model’s ability to predict complexity trends, thereby assisting flow manager positions (FMPs) in traffic flow and airspace management. Overall, this study demonstrated that probabilistic complexity assessment provides a deeper understanding of traffic behaviour, facilitating more effective air traffic flow management in uncertain and dynamic conditions.

1. Introduction

Air traffic complexity, a metric used to assess current and anticipated traffic scenarios, provides information on how difficult it is to manage and perform mandatory tasks in a given traffic situation for air traffic controllers (ATCOs) [1]. Sector capacity refers to the maximum number of aircrafts that can be present at the same time within a sector, serving as a critical operational parameter. In addition, traffic demand should match capacity limitations, allowing for only minor deviations. However, an imbalance between capacity and demand often occurs. A traffic demand that exceeds capacity results in traffic congestion and increases the workload for ATCOs. Traffic complexity provides insights into traffic characteristics and their relationship to other aircraft within a specified time frame. Typically, traffic complexity is a deterministic value available to flow manager positions (FMPs). FMPs rely on this metric to determine sector configurations, activate air traffic control (ATC) sectors, develop strategies to reduce ATCO workload, and implement appropriate measures to match traffic demand with sector capacity. Depending on the phase of air traffic flow management (ATFM) in which an imbalance is recognized, different measures can be implemented [2]. These measures affect both sector capacity and traffic demand, which in turn influence traffic complexity. With an accurate prediction of traffic complexity, the implementation of these measures is expected to be optimized.

When faced with convective weather characterized by high vertical propagation and an elongated squall line, traffic often exhibits an unpredictable behaviour. Pilots often deviate from their originally planned routes to avoid adverse weather conditions, which introduces additional uncertainty in trajectory prediction. Various research efforts tackled this issue by trying to identify which weather parameters pilots usually avoid [3,4], which routes are optimal in dynamic weather conditions [5,6], or how and which weather products have a greater impact on prediction and could be used to improve trajectory prediction [7,8,9,10]. The authors in [11] highlight the importance of accurate trajectory prediction in future ATM systems, identifying weather uncertainties as a major source of prediction errors. To address this issue, they developed a trajectory predictor using a Bayesian deep learning (BDL) approach, which more effectively accounts for these uncertainties. Compared to traditional deterministic models, the BDL model significantly reduces prediction variance, particularly in convective weather conditions. Given that weather is one of the most significant factors influencing trajectory prediction models, it is essential to explore various methods for integrating weather forecasts. A novel approach to incorporating weather forecasts is presented in the SESAR Horizon 2020 project FMP-Met, which utilizes ensemble weather forecasting (EWF) to obtain accurate meteorological information [12].

The dynamic characteristics and unpredictability of the weather indicate that the occurrence of convection directly impacts the workload of ATCOs [13]. The impact of convective weather on traffic complexity, however, remains uncertain. The authors in [14,15] demonstrated that workload and complexity are closely related terms, where an increase in one leads to an increase in the other. Therefore, if convective weather influences the workload of ATCOs, it will also impact traffic complexity.

A comprehensive assessment of current complexity calculation methods is presented in [16], where the authors provide an in-depth explanation of relevant complexity calculation methods together with existing issues limiting the accuracy and applicability of each method. The complexity calculation presented in this paper is based on the model developed by the Performance Review Unit (PRU). The PRU model assesses complexity by examining the interactions between traffic and traffic density, using four indicators: horizontal interaction, vertical interaction, speed interaction, and adjusted density [17]. Given that the effects of convective weather are not directly considered in these indicators, this study proposes a concept in which the weather-related indicator is integrated into the complexity calculation. Previous studies [18,19] demonstrated how a probabilistic approach was employed to predict sector capacity and traffic demand during convective weather conditions. A shift from a deterministic approach has been made to incorporate a probabilistic dimension into the assessment of traffic scenarios. This approach involves the use of various traffic scenarios that incorporate prediction uncertainties, thereby providing a more comprehensive understanding of sector capacity and traffic demand. Another approach described in [20] employs supervised machine learning to predict entry count, regulated entry count, and active weather regulations. The study finds that model performance varies significantly based on the predictive algorithms employed, with the random forest algorithm appearing to be the most effective for predicting entry counts and weather regulations. Overall, the application of machine learning shows significant potential for improving ATFM during convective weather conditions.

This paper presents the adaptation of the PRU model to convective weather conditions and introduces a methodology for calculating probabilistic complexity. Unlike common single-value complexity assessments, this research adopts a probabilistic distribution-range complexity assessment. This approach takes into account the impact of prediction uncertainties on calculated complexity values. Complexity analysis includes two different approaches: airspace-based complexity analysis and sector-based complexity analysis. A case study is conducted to assess the applicability of the proposed methodology, and a simulation environment is developed to validate the proposed method. Section 2 explains the characteristics of the study, Section 3 elaborates on methodology, Section 4 presents the results of complexity prediction and validation, and Section 5 and Section 6 discuss the results and give an overall conclusion of the presented study.

2. Characteristics of the Study

To evaluate the performance of the probabilistic air traffic complexity model, a case study was conducted in the Austrian airspace under the control of the Wien Area Control Centre (Wien ACC). The objective was to select a day with recorded deep convection in that area and analyze the traffic for that day. Consequently, the 12th of June 2018 was chosen. Deep convection is characterized by sudden increases in wind speed, a drop in air temperature, downdrafts, and violent gusts of wind [21]. Complexity prediction began at 12:00 and covered a period of up to 8 h ahead. The duration of the prediction was conditioned by the characteristics of the European Weather Forecast (EWF), which was the weather product used for this case study. The following subsections outline the characteristics of the case study.

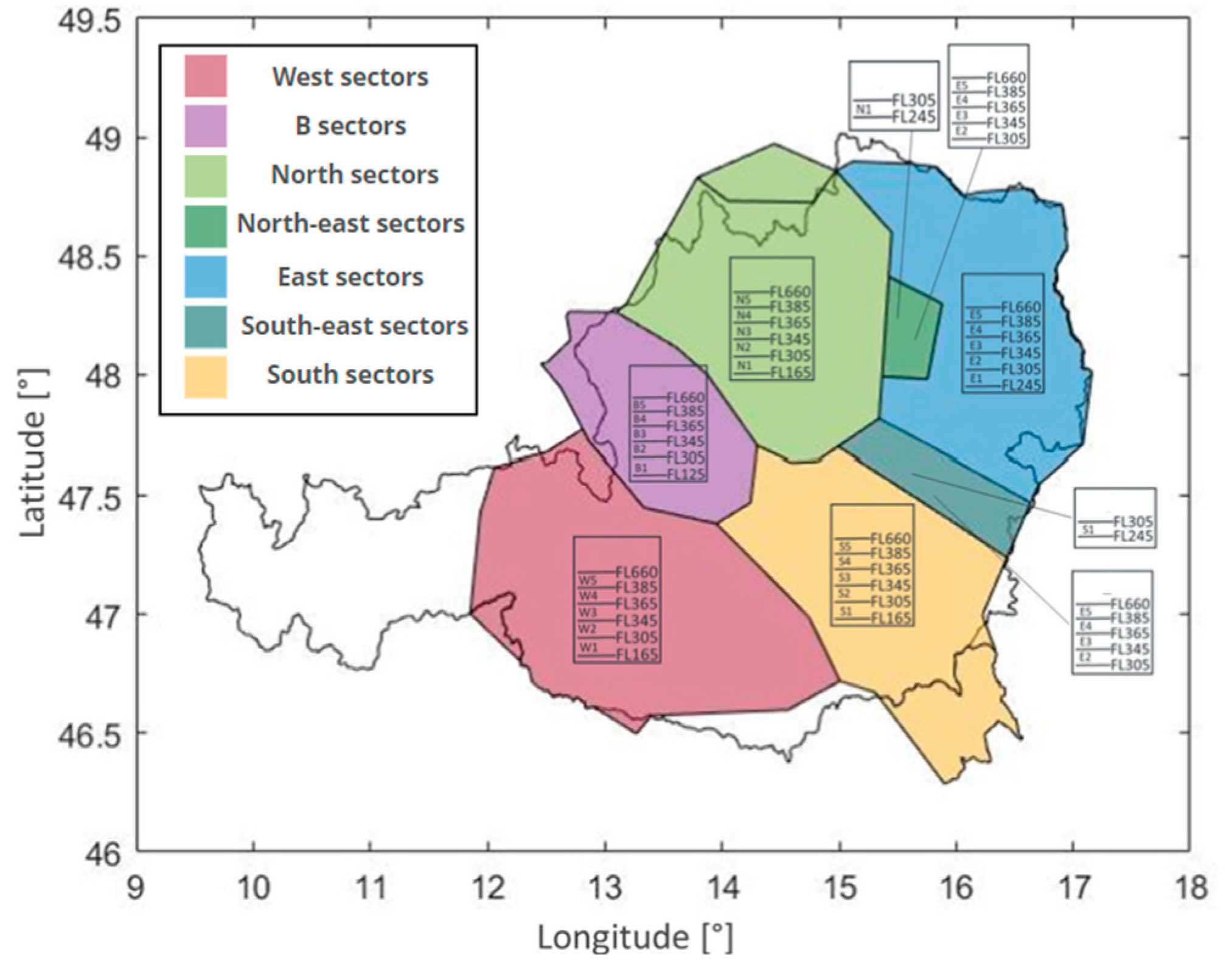
2.1. Airspace

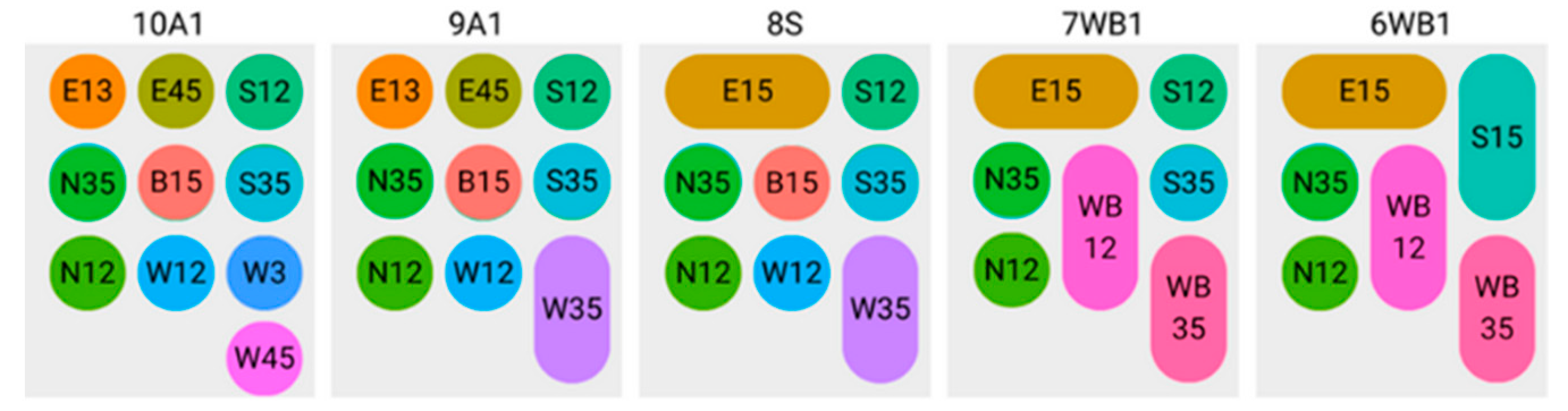
The Austrian airspace under the control of the Wien ACC is divided into five geographical regions (B, E, N, S, and W), each further subdivided into five vertical layers. Figure 1 illustrates the layout of ACC Wien. In total, ACC Wien contains 60 distinct ATC sectors and 190 potential sector configurations.

At the initial prediction time, ten sectors were active, constructing configuration 10A1. As the traffic situation evolved, various airspace configurations were used. If demand fell below sector capacity, two sectors could merge. Conversely, a sector could split into two when demand consistently exceeded the sector capacity. Traffic complexity was calculated for each sector and the entire Wien ACC airspace.

2.2. Weather Product

For predictions up to 8 h in advance, three weather products were used: the ensemble nowcast, the global ensemble prediction system, and the local EPS. Ensemble nowcast consisted of 15 statistically independent members that identified convective cells and provided forecasts every 15 min, one hour in advance. Global and local EPSs were used to generate probabilistic forecasts ranging from 1 to 8 h in advance. The global EPS consisted of 20 independent members, each with a resolution of 20 km. The local EPS more accurately identified convective areas with a resolution of 2 km. The main disadvantage of the local EPS was that its coverage was restricted to the Iberian Peninsula and Central Europe. Both global and local EPS forecasts were updated hourly. Additionally, an optical flow method was implemented to interpolate weather values between the available forecasts, enabling ensemble nowcast updates every 5 min and EPS forecasts every 15 min [22].

2.3. Traffic Data

The traffic data used in this study were sourced from EUROCONTROL’s R&D Data Archive, which employed historical planned flight plan data. It is important to note that the case study relied on flight plan data instead of actual flight data. The analysis focused on airborne traffic at 12:00 and the flights planned to take off or cross the area under the control of ACC Wien (area of interest) within the following 8 h. A 50 nm buffer around the area of interest was considered to account for traffic that may enter the area while initiating avoiding actions in neighbouring sectors. In total, 2542 flights met these criteria.

3. Methodology

In this section, the methodology is presented through four steps: PRU model adjustment, scenario sampling, determination of a sufficient number of traffic scenarios, and the calculation of traffic complexity. Additionally, to validate the complexity results, they are compared with complexity values obtained from the simulation environment rather than radar data, as elaborated upon later in this section.

3.1. PRU Model Adjustment

The EUROCONTROL PRU model, as previously mentioned, relies on the interaction between traffic and traffic density to calculate complexity scores. To calculate complexity, four complexity dimensions need to be considered: traffic density, traffic in evolution, traffic structure, and traffic mix [17]. These dimensions are calculated within predefined cells, each measuring 20 NM × 20 NM × 3000 ft in spatial dimensions and 60 min in temporal dimensions. Within each spatio-temporal cell, complexity values are calculated based on indicators derived from complexity dimensions. Complexity indicators represent potential interactions rather than actual interactions. Specifically, when two aircraft occupy the same spatio-temporal cell, they are considered to be vertically interacting if either aircraft changes altitude. This accounts for the interaction between both aircraft, with each interaction being counted twice—once for each aircraft involved. Therefore, the presence of multiple aircraft within the same cell increases traffic complexity, particularly when the aircraft do not share the same track, altitude, or performance capabilities. The PRU model produces a complexity score that summarizes the impact of various indicators and the adjusted density, resulting in a single complexity metric. To reduce the negative effect of the cell boundary, the cell is shifted horizontally four times by 10 nautical miles in each of the four directions and vertically by 1000 ft. This process generates a total of 12 different cells. The calculated results are presented as the average value obtained from the calculations performed across these 12 cells.

In addition to the previously mentioned PRU indicators, this paper introduces an additional complexity indicator designed to connect convective weather with traffic complexity [23]. This indicator aims to quantify the increased workload coming from communication, coordination, and aircraft separation tasks when convective weather is present within a sector. In this method, an aircraft is considered to be interacting with the weather if it is located within a cell occupied by convective weather or bordering convective weather.

The weather interaction indicator operates on the same principle as the indicators presented in the PRU method. The weather interaction time is determined by multiplying the flight time of an aircraft within a cell by the duration of its interaction with the weather. The original PRU complexity indicators, as described in the preceding sections, assume bidirectional interactions between aircraft. In other words, if Aircraft A interacts with Aircraft B, it is also considered that Aircraft B interacts with Aircraft A, resulting in a double count of all aircraft interactions. To preserve the dimensionality and scale of the original indicators, the new weather interactions indicator will be considered bidirectional. This means that all interactions will be considered both weather-to-aircraft interactions and aircraft-to-weather interactions. The duration of a weather interaction is calculated as the square of the aircraft’s flight hours within that cell, as expressed in Equation (1):

$$T{X}_{k_i}={t_{i_k}}^2$$

(1)

where

$T{X}_{k_i}—$duration of the interactions of aircraft i within time interval k in the cell;

${t_{i_k}}^2—$flight time of aircraft i within time interval k in the cell.

The impact of the weather interaction indicator is incorporated with other interaction-based indicators to calculate the overall complexity score.

The author in [23] examined the impact of a weather interaction indicator on complexity scores across 23 traffic scenarios, using the traffic complexity of the most complex sector as a reference point. Simulations were initially conducted under nominal conditions, excluding convective weather. Subsequently, weather inputs were incorporated, and the complexity was evaluated for both standard and modified PRU models over a duration of 20 min. The results are presented in

Table 1. Complexity scores for nominal, standard, and modified PRU models in 20 min intervals.

No. of Traffic Scenarios	Nominal (Nom)	Standard PRU Model						Modified PRU Model
		Mean	Mean/Nom	Min	Min/Nom	Max	Max/Nom	Mean	Mean/Nom	Min	Min/Nom	Max	Max/Nom
23	6.73	6.88	102%	6.48	96%	8.21	122%	6.94	103%	6.50	97%	8.61	128%

. Focusing solely on the mean values might hide the full impact of the modified PRU model; however, analyzing both the maximum and minimum values reveals that both the standard and modified models effectively capture the increased complexity caused by convective weather. Notably, the modified model highlights this effect more strongly. Despite the expectation that convective weather would invariably increase complexity, the underlying traffic structures explain why this is not always the case. Frequently, the most complex sector is not the one affected by convective clouds, a matter which diminishes the clarity of the weather interaction indicator’s true impact. Overall, the modified PRU model amplifies the effect of convective weather on traffic complexity. Interestingly, in certain instances, this effect may also lead to a decrease in traffic complexity, with reductions of 96% for the standard PRU and 97% for the modified PRU.

Another adaptation of the PRU model involves reducing the temporal dimension from 60 to 20 min, which better aligns with the characteristics of convective weather. Convective weather typically develops, shifts, and dissipates over a shorter time frame, making a one-hour period less effective for representing traffic complexity. To verify this, the same traffic sample used to assess the impact of the weather interaction indicator was analyzed over a one-hour time frame. The results are presented in

Table 2. Complexity score for nominal, standard, and modified PRU models in one-hour intervals.

No. of Traffic Scenarios	Nominal (Nom)	Standard PRU Model						Modified PRU Model
		Mean	Mean/Nom	Min	Min/Nom	Max	Max/Nom	Mean	Mean/Nom	Min	Min/Nom	Max	Max/Nom
23	10.66	10.76	101%	10.54	99%	11.35	106%	10.87	102%	10.61	100%	11.78	111%

. Overall, the complexity scores for both nominal and PRU model values are higher when considering the one-hour temporal dimension. However, this extended time frame fails to capture peak complexity instances, with Max/Nom ratios of only 106% for the standard PRU and 111% for the modified PRU. Therefore, the 20 min temporal dimension more accurately identifies complexity peaks associated with convective weather.

3.2. Scenario Sampling

The second step to obtain a probabilistic traffic complexity analysis is to generate aircraft trajectories. A comprehensive overview of the trajectory prediction (TP) algorithm can be found in [18]. Two types of TP products are available: nowcast-based TP and EPS-based TP. Given that the TP algorithm also uses a probabilistic approach, a product of nowcast-based TP consists of an ensemble of possible trajectories that consider take-off, safety margins, and weather uncertainties. For instance, an aircraft scheduled for take-off at 12:30 may have up to 10 different potential take-off times, 15 members of the ensemble weather forecast, and five safety margins considered by the TP algorithm. Consequently, the nowcast-based trajectory prediction (TP) generates 750 distinct trajectories for a single aircraft. The EPS-based TP follows a similar approach; each aircraft has 20 different weather scenarios and 10 take-off times, resulting in a total of 200 possible trajectories per aircraft. With this example, it is clear that the probabilistic approach generates a wide range of possible traffic scenarios.

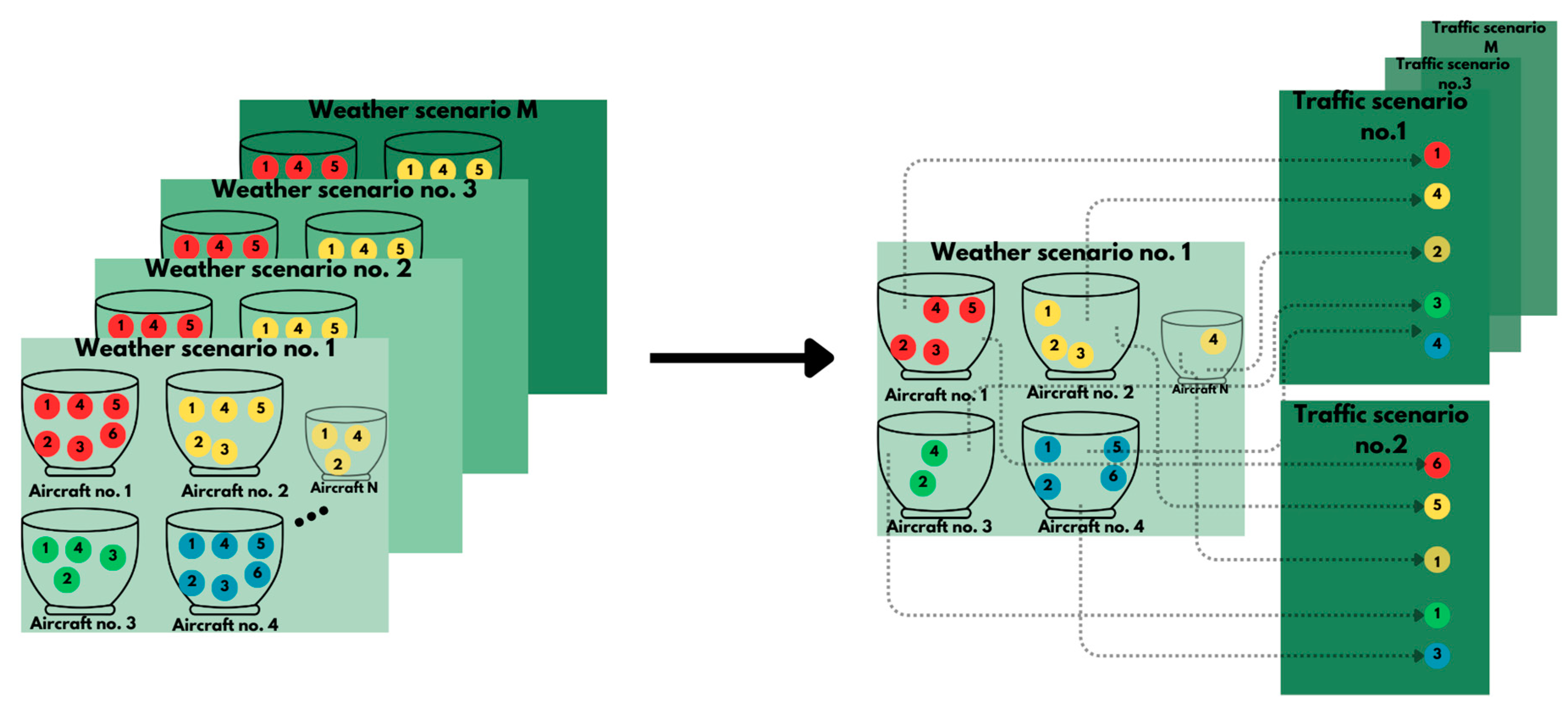
Since each trajectory is independent of the others within a given weather scenario, they can be combined in various ways. Consequently, efforts were made to explore options for reducing the computational time, as traffic complexity could be calculated for each possible traffic scenario. One of the options considered was scenario sampling. Semi-random sampling without replacement was introduced. The sampling algorithm is illustrated in Figure 2, first extracting all aircraft trajectories within a specific weather scenario. Each aircraft has a unique pool of potential trajectories generated through nowcast-based and EPS-based TP. Afterward, a single trajectory is selected from each aircraft pool, removed from the pool, and assigned to a traffic scenario. The aircraft pool is reset once it has been depleted. This random selection and assignment process is repeated until a sufficient number of traffic scenarios have been generated. Through this sampling method, traffic scenarios are generated randomly, ensuring an equal use of all trajectories.

3.3. Determination of a Sufficient Number of Scenarios

As the probabilistic approach generates a vast number of traffic scenarios, it is essential to determine a sufficient number of these scenarios to ensure reliable complexity results while maintaining a manageable computational time. Otherwise, calculating the complexity for the entire dataset would make the computational time unmanageable. For the initial robustness assessment, 1500 nowcast-based TP traffic scenarios and 1000 EPS-based TP traffic scenarios were selected empirically. The purpose of a robustness analysis is to determine the number of traffic scenarios that produce stable results. Stable results are defined as those that, with an increasing number of traffic scenarios, exhibit a minimal impact on both the standard deviation and the mean of complexity.

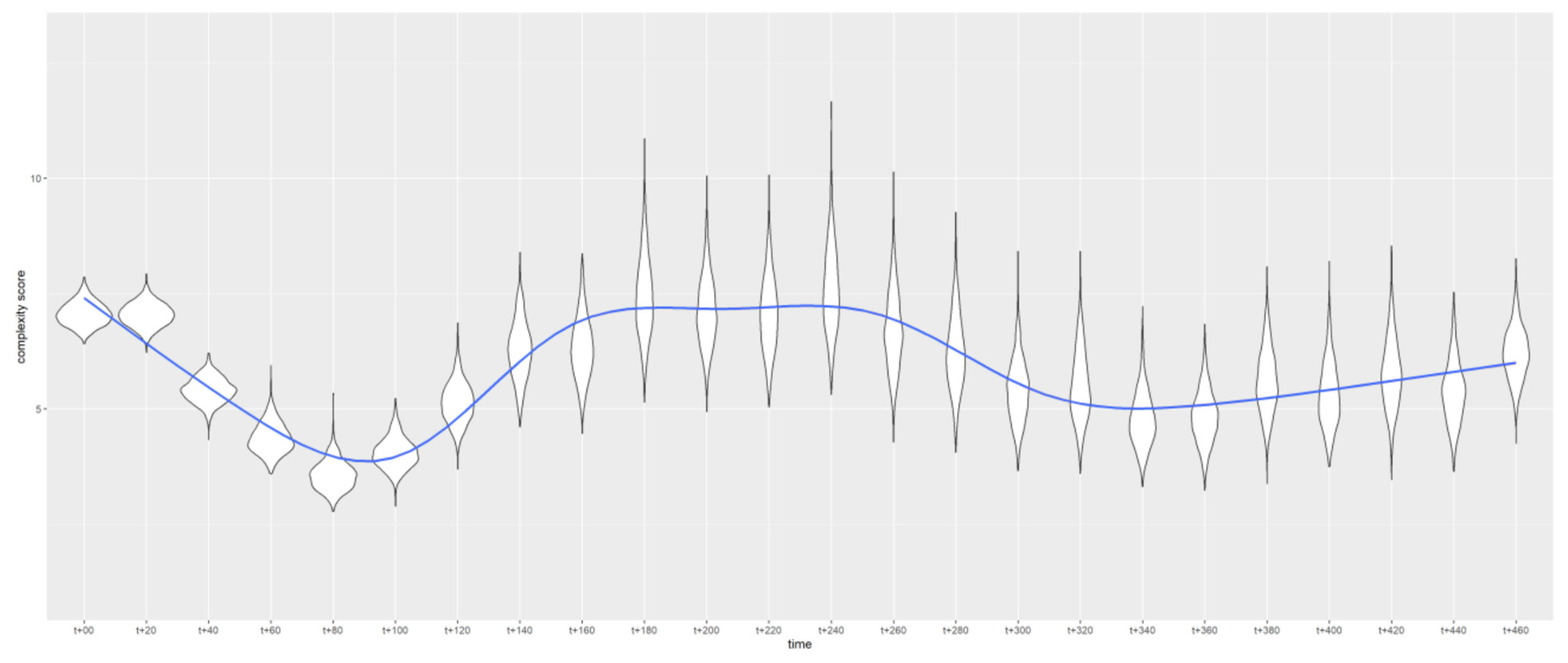
Firstly, the mean and standard deviations were calculated for the entire initial dataset. Afterward, the dataset was reduced to one-half, one-third, one-fourth, and one-tenth of the initial data size, which is also referred to as the baseline set. Figure 3 presents the complexity results, illustrating the means and standard deviations of complexity over a duration of 460 min. The results revealed that, as the data size decreases, the standard deviation increases and the mean diverges further from the baseline dataset. However, the maximum difference between the baseline mean and the means of the reduced datasets (half, one-third, one-fourth, and one-tenth of the data size) does not exceed 2%, while the difference in standard deviations can reach up to 13%, depending on the sample size.

The determination of the sample size should be influenced by the acceptable levels of variation in the mean and standard deviation, which can be established by users according to their priorities for system performance, whether they prefer greater precision or faster computation. In this research, because the baseline data size was selected empirically and the mean of the entire dataset could not be calculated, we prioritized greater precision as long as the computational time remained manageable.

The analysis revealed that using half of the data resulted in a standard deviation difference of up to 3% when compared to the full dataset. When the data were further reduced to one-third, the mean changed by less than 1%. This indicated that a sample size of 500 to 1500—approximately one-third of the baseline set—was adequate for this application.

Although the baseline dataset was selected empirically, a further analysis demonstrated that this sample size was adequate, as the complexity results showed minimal deviation after a certain number of samples. This analysis presents a method for determining the appropriate sample size through a bottom–up approach, in which the size of the dataset is defined not by the number of traffic scenarios but by the required precision of the output data.

3.4. Complexity Calculation

After sampling and determining a sufficient number of scenarios through a robust analysis, it is possible to calculate traffic complexity. Using the PRU method described in Section 3.1, complexity was calculated by considering convective weather, aircraft interactions, and dynamic density. The results of this calculation were complexity scores that were classified as low, medium, or high. Each cell within the airspace was assigned a specific value, which contributed to the overall complexity of both the sector and the entire airspace. The probabilistic complexity calculation allowed for the calculation of complexity by providing a mean value and a standard deviation over a specified period.

3.5. Simulation Environment

Traffic management at a tactical level can significantly change traffic characteristics, disabling the ability to validate predicted values with reliable data. Additionally, ATCO interventions, such as direct routing, can affect traffic flow and, consequently, complexity values. To address this, a simulation environment was developed that utilized actual weather observations alongside flight plans to generate aircraft trajectories and calculate complexity. The complexity calculated within this simulation environment was compared to the predictions generated by the model proposed in this paper. This comparison was presented both graphically and through the absolute error between the simulation and predicted data. The purpose of this validation was to assess the accuracy of the results and identify potential areas for further improvement.

NAVSIM is a simulation platform utilized for generating flight trajectories. It serves as an air traffic ATM simulation tool, capable of functioning as either a real-time or fast-time simulator. NAVSIM incorporates navigation data and accounts for aircraft performance throughout all phases of flight. In the MET4LOWW project, NAVSIM was modified to conduct simulations that take into account adverse weather conditions [24]. This adaptation has since been validated, demonstrating a strong correlation between the simulated trajectories and the actual flight paths, proving the simulator’s highly realistic behaviour.

4. Results

This section presents the results of traffic complexity predictions, which refer to the case study outlined in Section 2. It also validates the complexity prediction results by comparing them to the complexity derived from the simulation environment.

4.1. Complexity Predictions

The results of the complexity predictions will be presented using violin plots, which are particularly effective for illustrating the distribution and density of data. The width of each curve corresponds to the approximate frequency of data points within the respective region; thus, a wider violin plot indicates a higher probability of an event occurring. In the context of complexity computations, the vertical axis of the plot represents the range of complexity scores. The width of the violin reflects the total number of traffic scenarios with similar complexity scores. The total area within the plot always amounts to 1. “Short” violin plots indicate a smaller standard deviation, while wider violins suggest a larger standard deviation. The analysis will be conducted for the entire Wien ACC area, as well as for each active sector during selected time intervals.

4.1.1. Complexity of the Wien ACC Airspace

Results from the analysis of the complexity of the Wien ACC airspace (airspace-based analysis) are presented in Figure 4. Complexity is calculated every 20 min from 12:00 to 20:00, resulting in 24 violin plots. The blue line represents the complexity trend, which helps in understanding the behaviour of complexity over time and drawing conclusions based on its pattern. Until t+120, the violin plots were short and thick, indicating a trend of a decreasing complexity. After t+120, the scores became more dispersed, suggesting less reliable results.

4.1.2. Complexity of an Individual Sector

As the previous section presented the results of the airspace-based complexity analysis, an individual complexity calculation for each sector (sector-based analysis) is necessary to obtain more accurate results. This section uses sector S35 as an example, as it has been in use for the entire duration of the complexity analysis. Figure 5 displays the complexity scores for the sector between 12:00 and 20:00, represented by violin plots. Similar to the results for the Wien ACC airspace, the violin plots are thick and short up until t+120. Beyond this point, the violin plots become elongated. The data distribution reveals a consistent pattern in both Figure 4 and Figure 5, with the exception of t+20, where the complexity scores exceed a value of 10, which is higher than that observed for the Wien ACC airspace.

4.2. Validation of Complexity Prediction Results

The probabilistic complexity analysis, obtained through the method presented in Section 2, is compared with the complexity calculated based on the simulated traffic environment. The simulator approach did not include a probabilistic complexity analysis; instead, a single complexity score was calculated every 20 min for the entire Wien ACC airspace (Section 4.2.1) and for each active sector (Section 4.2.2).

4.2.1. Validation of Airspace-Based Complexity Analysis

In Figure 6, a comparison of the complexity values from the airspace-based complexity analysis is presented using violin plots. The blue line represents the trend of the predicted probabilistic complexity, while the red line represents the deterministic complexity score calculated within the simulation environment. Both the simulator and the predicted complexities are computed using the same PRU method to enable comparison.

4.2.2. Validation of Sector-Based Complexity Analysis

The sector-based complexity analysis provides insights into how complexity scores fluctuate throughout the day, depending on the active configuration opening scheme. The opening scheme includes the following configurations: 10A1 (12:00–14:30), 9A1 (14:30–17:00), 8S (17:00–18:00), 7WB1 (18:00–19:30), and 6WB1 (19:30–20:00). A list of configurations along with their corresponding ATC sectors is presented in Figure 7, which illustrates the sectors that are merged after each configuration change. Figure 8 demonstrates the complexity distribution across the five sector configurations. The simulator’s complexity is compared with the predicted complexity values derived from probabilistic trajectory predictions.

In addition to the graphical analysis,

Table 3. Maximum value of simulator complexity score and non-dimensional Mean Absolute Error for complexity scores for each active sector.

Sector	Simulator_Max	MAE/Simulator_Max
B15	10.8	18%
E13	8.9	16%
E15	6.5	16%
E45	10.6	12%
N12	7.5	16%
N35	10.7	15%
S12	8.1	15%
S15	5.7	27%
S35	10.7	20%
W12	7.5	21%
W3	21.7	20%
W35	10.2	19%
W45	17.3	18%
WB12	4.9	23%
WB35	7.5	30%

offers a quantitative comparison by calculating the non-dimensional Mean Absolute Errors (MAEs). The MAE is determined by taking the absolute difference between the forecast median and the simulator complexity and then dividing this difference by a reference value that corresponds to the maximum simulator complexity over various periods (referred to as Simulator_max).

5. Discussion

5.1. Airspace-Based and Sector-Based Complexity

From the complexity values presented in Figure 4, it is evident how the violin plots evolve over time. The initial plots around t+00 are characterized as short and wide, indicating the early stages during which the weather and predicted trajectories have not yet significantly diverged. Up until t+120, the violin plots maintain a thick and recognizable shape, with a small standard deviation in the complexity scores ranging from 6 to 7.5, alongside a downward trend in the overall complexity. As the x-axis values increase, the complexity score begins to rise again, reaching its peak at t+240. During this period, the violin plots become elongated and narrow, reflecting a greater standard deviation in the data. Several factors contribute to this shift. First, a change in the weather product and trajectory prediction model at t+100 may explain the alteration in the shapes of the violin plots. Additionally, as traffic interacts with convective weather, the trajectories become more dispersed, and traffic interactions vary from one scenario to another. At t+240, complexity reaches its peak, with scores distributed between 5.5 and 11.5. Toward the end of the prediction window, the complexity values show less variation, as indicated by denser violin plots and a decline in the complexity trend. This suggests that, as the overall complexity decreases and weather disruptions lessen, the traffic characteristics tend to yield more consistent complexity values across different traffic scenarios.

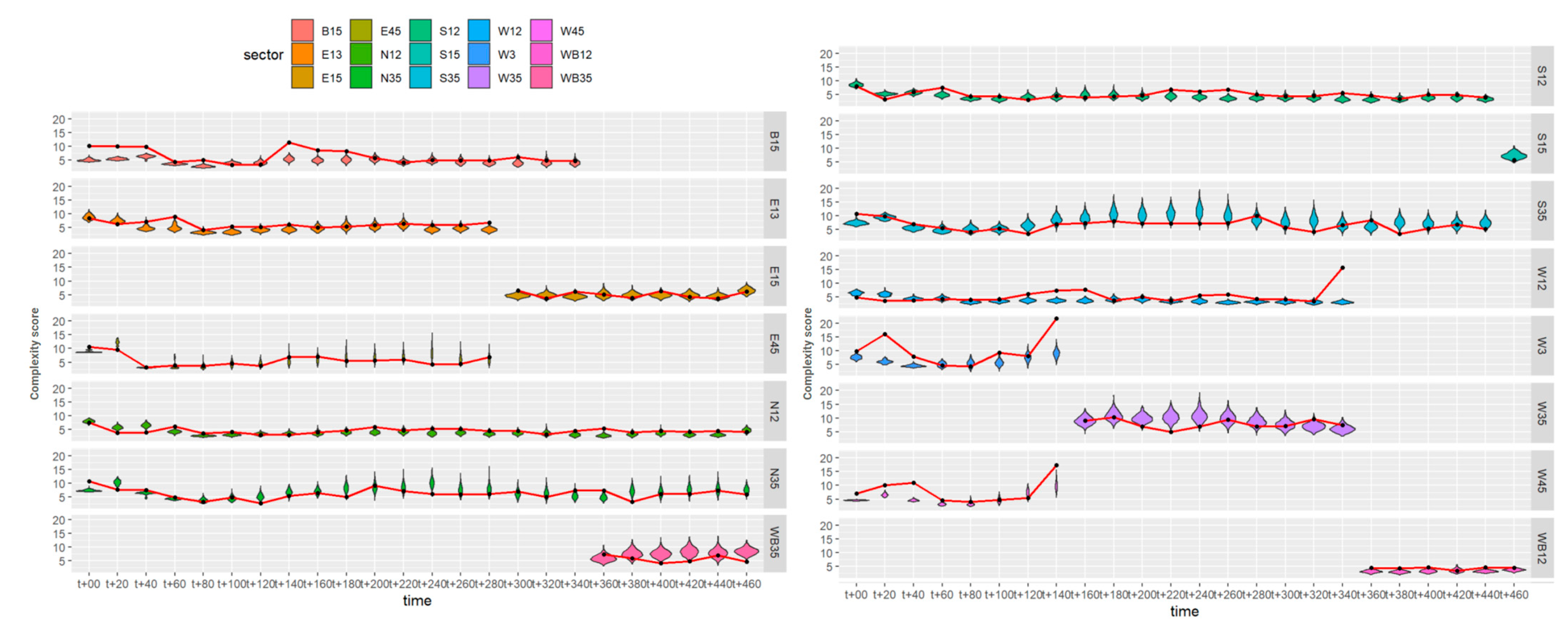
The sector-based complexity analysis mirrors the trends observed in the airspace-based analysis, as illustrated by the comparison of Figure 4 and Figure 5. The violin plots indicate that the complexity scores derived from the nowcast-generated and EPS-generated trajectories do not exhibit significant or noticeable differences. The transition from one weather product to another is, in this context, seamless. As observed in the airspace-based analysis, significant changes in the shape of the violin plots occur after t+120, potentially influenced by the different weather products utilized. During the first two hours, the complexity distribution is represented by thick violin plots, indicating a dense data distribution. Between t+140 and t+260, the complexity becomes more dispersed, peaking at t+240, with values ranging from 5 to 20. The most elongated violin plot is observed at this time as well. As the prediction time increases, a greater variety of potential traffic scenarios with differing complexities develops. This increasing variability not only results in greater data dispersion but also leads to a higher mean complexity, which is influenced by convective weather conditions as well. Consistent with the airspace-based analysis, higher complexity values are associated with a wider data distribution. By the end of the simulation, the violin plots become thicker, with the mean complexity values dropping below 10, further supporting the earlier observations.

The primary distinction in the sector-based complexity analysis is the increase in the complexity score at t+20, along with a generally higher maximum complexity value. Additionally, at t+240, when the complexity peak is identified, the airspace-based complexity analysis records maximum values of approximately 13 during the same time frame. This suggests that sector-based complexity analysis is more responsive to higher complexity scores, assigning greater significance to them compared to the airspace-based approach. In contrast, the airspace-based complexity analysis takes into account the complexity scores of all cells, including a considerable number of cells with lower complexity, which ultimately diminishes the overall complexity of the selected area.

5.2. Validation of Airspace-Based and Sector-Based Complexity

Figure 6 presents information regarding the predicted probabilistic complexity and the simulated complexity. The comparison indicates that the values of simulator complexity generally follow the trend in the probabilistic complexity prediction, with slight variations. The initial reduction in complexity values from t+00 to t+80 is consistent for both values, followed by a minor increase and a period of stagnation in complexity until t+260. Beyond this point, the complexity values exhibit instability. By time t+380, the complexity value stabilizes and continues to increase. When comparing the complexity values to the trend line (in blue), it becomes evident that the simulator trajectories exhibit higher complexity than predicted up until time t+120. At t+120, the simulator complexity aligns with the blue trend line, but, by t+280, it falls below the predicted values while remaining within the expected range. At t+280, the simulator complexity once again matches the trend line, followed by instances of both overestimation and underestimation of the predicted complexity. By t+380, the simulator complexity is lower than the predicted values but maintains the same upward trend. These oscillations are not easily attributed to a single factor. When making shorter-term predictions, the estimated probabilistic complexity tends to underestimate the simulator complexity. However, after the time point t+120, the simulator complexity drops below the predicted trend line and approaches the lower quartile of the violin plots. Towards the end of the prediction period (t+380), both the predicted and simulator complexities stabilize and follow the same trend. This analysis reveals that, when the violin plots indicate a greater data distribution, the simulator complexity tends to align with the lower quartile. Conversely, shorter and denser plots suggest a more irregular and inconsistent correlation between the simulator and predicted complexity scores.

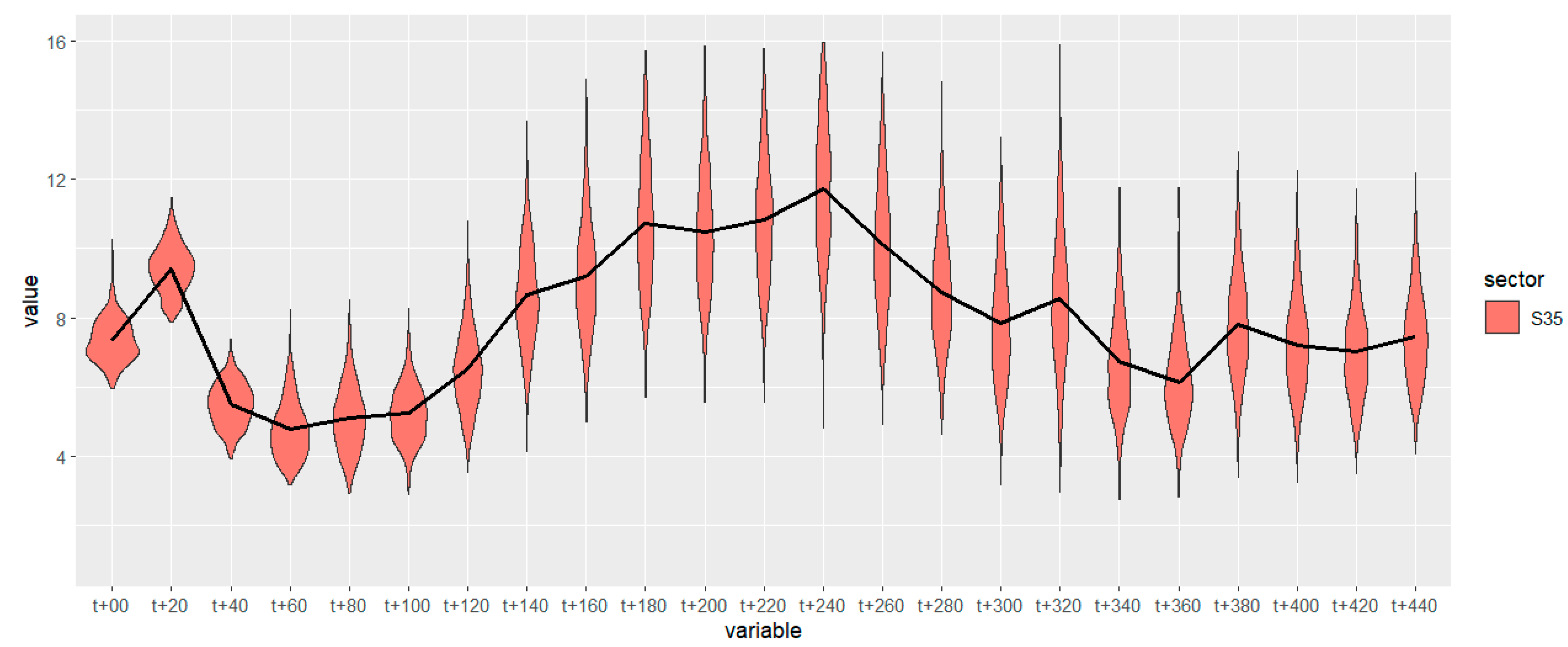
Examining the sector-based complexity, most simulator complexity values match the predicted complexity distribution. Sectors characterized by dense and wide distributions with small standard deviations, such as N12 and S12, show a close correspondence between the predicted and simulator complexity results. In these sectors, simulator complexity tends to be near or slightly above the mean. In contrast, sectors with elongated distributions and higher standard deviations, such as sector S35 from t+160 to t+260 and sector N35 from t+180 to t+280, exhibit an overestimation of complexity compared to the simulator results. There are only a few instances where the simulator complexity falls below the complexity distribution predicted by the probabilistic model, such as in sector W3 at t+20 and W12 at t+340. Furthermore, in the airspace-based analysis, elongated plots are associated with a simulator complexity that is close to the lower quartile. Additionally, sectors like W3 and W45 contain elongated plots before being merged into a larger sector. This indicates that, when the demand is lower than the capacity, allowing for the merging of sectors, the distribution of complexity increases. Larger sectors, particularly those formed by the combination of two collapsed sectors, are characterized by shorter and wider plots, suggesting more stable complexity predictions.

The quantitative analysis of MAE supports the trend illustrated in Figure 8. With the exception of sectors S15 and WB35, the MAE falls within the range of 12% to 23%. A lower percentage indicates a closer similarity between the predicted and simulated values. Sector S15 was active for only a short period, so the actual trend in the predicted complexity could not develop. Sector WB35 is characterized by low maximum simulator complexity values; consequently, the ratio of MAE to Simulator_max is higher than that of other sectors. To minimize the overall error, it is essential to examine the simulator platform’s environment, the methods used for trajectory generation, and the system’s behaviour during convective weather. This issue arises from the fact that the simulator uses a different model for trajectory generation compared to the probabilistic model. Nonetheless, we believe that the traffic scenario produced by the simulator is accounted for within the probabilistic model; however, based on the error percentage, it is considered less likely than other scenarios. Consequently, it can be concluded that sectors with a low overall complexity and those that are only active for a short duration may produce greater errors in predictions than other sectors.

6. Conclusions

This paper introduces a methodology for probabilistic complexity analysis that accounts for prediction uncertainties. It modifies the interaction-based PRU model to include the effects of convective weather, which the original model does not consider.

The proposed probabilistic method was used to evaluate traffic complexity at the airspace and sector level. A significant challenge of this approach is the vast number of possible traffic scenarios. To address this issue, a sampling technique was introduced, and an appropriate sample size was determined based on the desired precision of the results. Herein are the key findings from the complexity analysis:

• The probabilistic air traffic complexity model can calculate the distribution of complexity data while considering prediction uncertainties.
• Convective weather has a significant impact on aircraft trajectories, resulting in an increased variability in complexity calculations across different scenarios.
• It is possible to determine the level of uncertainty in complexity predictions, which improves decision making, especially in sectors with low standard deviations.
• Some sectors remain unaffected by the weather, maintaining a low complexity. This information helps FMPs make more informed decisions regarding which sectors to merge, where an increase in complexity is anticipated, and the overall possibility of such changes.
• A greater distribution of complexity results is associated with a higher mean complexity and an extended prediction time.

The probabilistic methodology was validated using a simulation platform. Herein are the key outcomes from the validation:

• The validation results support the applicability of the method.
• The validation clarified how complexity changes before and after sectors are merged, with a greater data distribution prior to merging and a denser data distribution appearing post merge.
• Validation indicated that the complexity values of the simulator closely matched the probabilistic predictions, particularly in sectors characterized by dense data distributions. In contrast, sectors with more elongated distributions tended to overestimate complexity.
• Shorter and denser plots indicate a more irregular and inconsistent relationship between the simulator and predicted complexity.
• The Mean Absolute Error (MAE) between the predicted and simulated complexity values typically ranges from 12% to 23%. However, sectors that are active for shorter periods or exhibit low complexity levels tend to demonstrate higher error rates.

Future work will focus on validating probabilistic complexity assessments using actual operational data instead of simulations. Furthermore, since an increased complexity indicates a mismatch between sector capacity and traffic demand, applying a probabilistic method to identify complexity reduction measures could enhance traffic flow and improve decision making regarding demand–capacity balancing.