Optimization Design of Honeycomb Absorbing Structure and Its Application in Aircraft Inlet Stealth
Abstract
1. Introduction
2. Theoretical Calculation Model and Methods
2.1. Theoretical Model
2.2. Equivalent Electromagnetic Properties of Honeycomb Cores
2.3. Reflectivity of Multi-Layer Structure
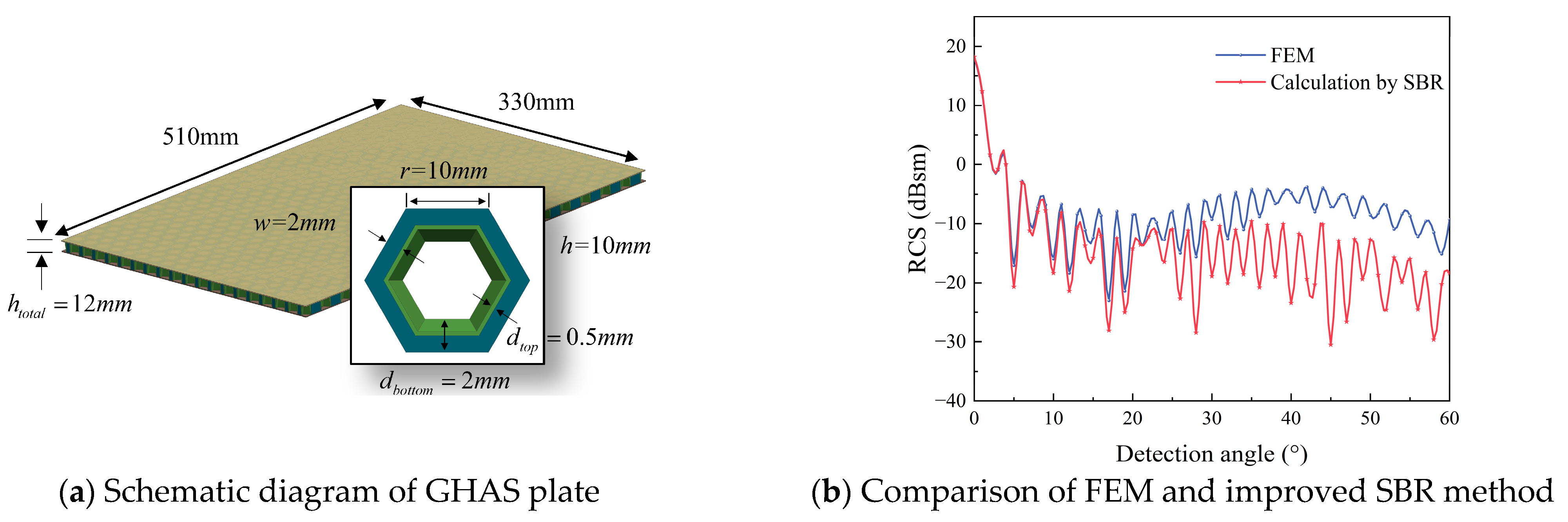
2.4. Verification of Proposed Method
2.5. Optimization Model
3. Results and Discussion
3.1. Single-Layer Honeycomb Absorbing Structure
3.2. Optimization of Multi-Layer Gradient Honeycomb Absorbing Structure
3.3. Application of Honeycomb Absorbing Structure on Aircraft Inlet
4. Conclusions
- (1)
- The homogenization method is applied to study the EM wave absorption characteristics of an NHAS and a GHAS at various bandwidths and angles. The impact patterns and mechanisms of gradient design in impregnation materials are analyzed. An MGHAS is proposed; it primarily comprises a top skin, middle honeycomb cores, bonding layers, and a bottom reflective layer. The impact of the selection and sequence of impregnated materials within the honeycomb core is investigated. Research has demonstrated that using an impregnated material with a smaller electromagnetic loss tangent near the top skin allows this layer to act as a transmission medium, thereby enhancing the impedance matching between the honeycomb absorber structure and free space. Incorporating an impregnated material with a higher dielectric loss tangent near the bottom reflective layer significantly enhances the dissipation of electromagnetic waves, thereby maximizing EM wave absorption. An improved PSO algorithm is employed to optimize the electromagnetic absorption performance of the MGHAS. The results indicate that the reflectivity of the optimized MGHAS is below −10 dB in the frequency range of 2–18 GHz, demonstrating that the proposed MGHAS structure exhibits effective electromagnetic wave absorption properties.
- (2)
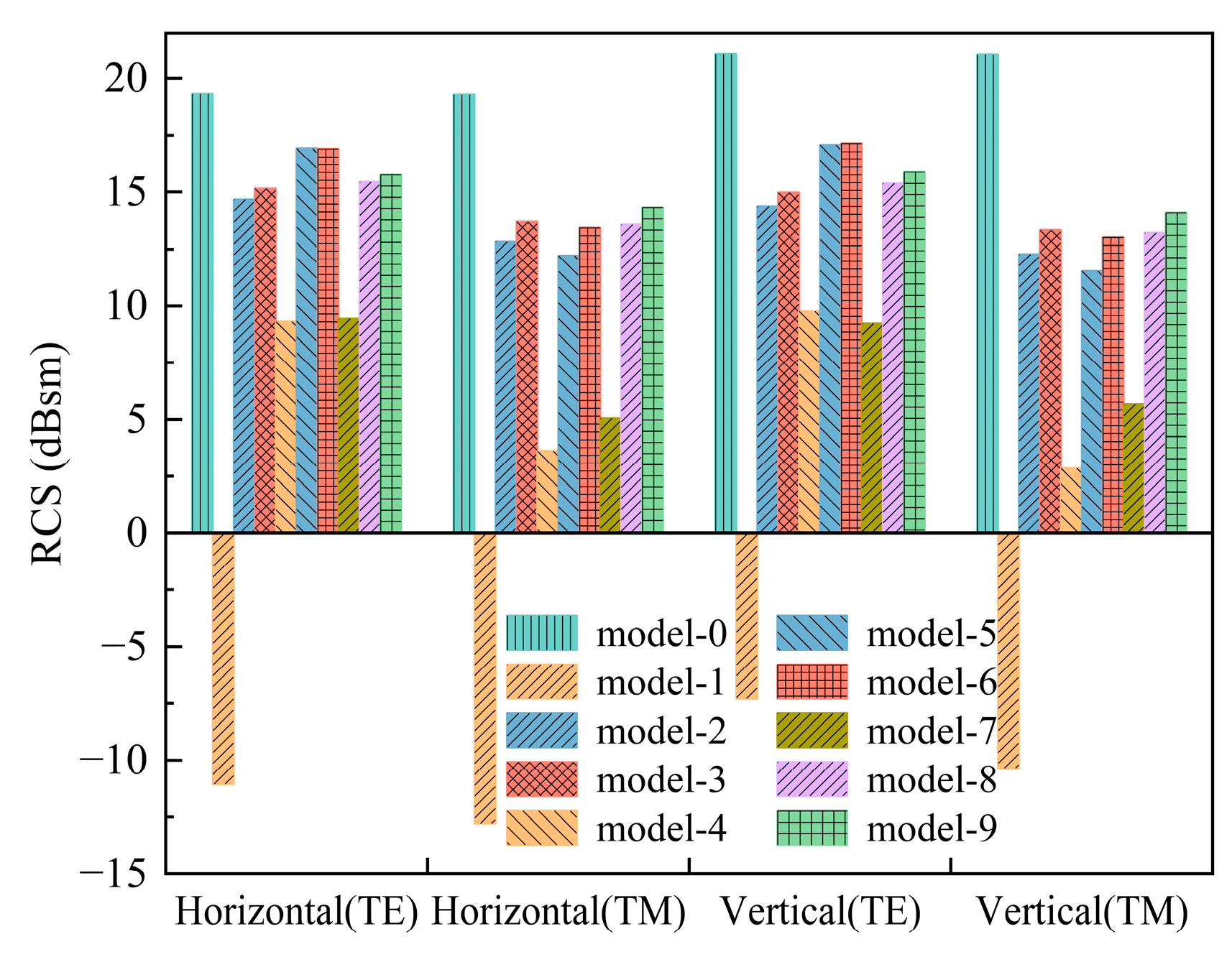
- Both the application of the MGHAS and the coating-type absorbing materials reduce the RCS of the aircraft inlet. However, the RCS reduction achieved with the MGHAS is more substantial than that achieved with the coating-type absorbing material. The scheme of applying an MGHAS to the inlet end face and adjacent surface reduces the RCS of the inlet at the 0° detection angle and 10 GHz frequency, achieving reductions of 99.74% (TM; horizontal plane) and 99.76% (TE; vertical plane) compared with an inlet without stealth technologies. The mean RCS of the inlet equipped with the MGHAS approaches −20 dBsm. In contrast, the mean RCS of the inlet without stealth technologies is approximately 10 dBsm, and the mean RCS of the inlet with the coating-type material also exceeds −10 dBsm. Furthermore, due to the anisotropic properties of the honeycomb absorber structure, the optimal placement of the structure is closely related to the angle of incidence of the EM waves. It is advisable to align the principal axis of the honeycomb structure as closely as possible with the direction of the incident waves.
- (3)
- Given that HASs typically need to withstand mechanical loads when applied to aircraft, it is essential to comprehensively consider both their electromagnetic absorbing and mechanical properties. This comprehensive analysis will be the focus of our subsequent research work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sang, J.H. Low-Observable Technologies of Aircraft, 1st ed.; Aviation Industry Press: Beijing, China, 2013; pp. 8–10. ISBN 978-7-5165-0135-1. [Google Scholar]
- Ruiz-Perez, F.; López-Estrada, S.M.; Tolentino-Hernández, R.V.; Caballero-Briones, F. Carbon-based radar absorbing materials: A critical review. J. Sci. Adv. Mater. Devices 2022, 7, 100454. [Google Scholar] [CrossRef]
- Fante, R.L.; McCormack, M.T. Reflection properties of the Salisbury screen. IEEE Trans. Antennas Propag. 1988, 36, 1443–1454. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 2012, 24, 98–120. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.L.; Meng, F.H.; Yang, W. Mechanical Behaviors and Bending Effects of Carbon Fiber Reinforced Lattice Materials. Arch. Appl. Mech. 2006, 75, 635–647. [Google Scholar] [CrossRef]
- Fan, H.L.; Yang, W.; Chao, Z.M. Microwave absorbing composite lattice grids. Compos. Sci. Technol. 2007, 67, 3472–3479. [Google Scholar] [CrossRef]
- Li, W.; Xu, L.; Zhang, X.; Gong, Y.; Ying, Y.; Yu, J.; Zheng, J.W.; Qiao, L.; Che, S.L. Investigating the effect of honeycomb structure composite on microwave absorption properties. Compos. Commun. 2020, 19, 182–188. [Google Scholar] [CrossRef]
- Baimova, J.A.; Shcherbinin, S.A. Strength and Deformation Behavior of Graphene Aerogel of Different Morphologies. Materials 2023, 16, 7388. [Google Scholar] [CrossRef]
- Laur, V.; Maalouf, A.; Chevalier, A.; Comblet, F. Three-Dimensional Printing of Honeycomb Microwave Absorbers: Feasibility and Innovative Multiscale Topologies. IEEE Trans. Electromagn. Compat. 2021, 63, 390–397. [Google Scholar] [CrossRef]
- Smith, F.C.; Scarpa, F.; Chambers, B. The electromagnetic properties of re-entrant dielectric honeycombs. IEEE Microw. Guid. Wave Lett. 2000, 10, 451–453. [Google Scholar]
- Gao, Z.P.; Luo, Q. Reflection Characteristic of Impregnated Absorbent Honeycomb under Normal Incidence of Plane Wave. J. Univ. Electron. Sci. Technol. China 2023, 32, 389–394. [Google Scholar]
- Wu, L.; Wang, Q.; Tang, Z. Absorbing properties of three dimensional honeycomb-structured absorbing materials. In Proceedings of the 2012 6th Asia-Pacific Conference on Environmental Electromagnetics, Shanghai, China, 6–9 November 2012. [Google Scholar]
- Ghosh, S.; Lim, S. Perforated Lightweight Broadband Metamaterial Absorber Based on 3-D Printed Honeycomb. Antennas Wirel. Propag. Lett. 2018, 17, 2379–2383. [Google Scholar] [CrossRef]
- Mei, C.C.; Auriault, J.L.; Ng, C.O. Some Applications of the Homogenization Theory. Adv. Appl. Mech. 1996, 32, 277–348. [Google Scholar]
- Johansson, M.; Holloway, C.L.; Kuester, E.F. Effective electromagnetic properties of honeycomb composites, and hollow-pyramidal and alternating-wedge absorbers. IEEE Trans. Antennas Propag. 2005, 53, 728–736. [Google Scholar] [CrossRef]
- Ouchetto, O.; Jai-Andaloussi, S.; Sekkaki, A.; Zaamoun, S. Analytical Effective Parameters of Artificial Structures. In Proceedings of the 19th International Radar Symposium, Bonn, Germany, 20–22 June 2018. [Google Scholar]
- Chen, H.; Shen, R.; Han, L.; Zhou, Y.; Li, F.X.; Lu, H.P.; Weng, X.L.; Xie, J.L.; Li, X.Q.; Deng, L.J. Closed-form representation for equivalent electromagnetic parameters of biaxial anisotropic honeycomb absorbing materials. Mater. Res. Express 2019, 6, 085804. [Google Scholar] [CrossRef]
- Zhao, Y.C. Study on the Extraction Theory and Applications of Equivalent Electromagnetic Parameters of Radar Absorbing Structure. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2014. [Google Scholar]
- Choy, T.C. Effective Medium Theory: Principles and Applications, 2nd ed.; Oxford University Press: Oxford, UK, 2015; pp. 25–28. ISBN 978-0-19-870509-3. [Google Scholar]
- Zhu, H.; Gao, J.; Zhao, J.; Wang, T.T.; Feng, X.G.; Liang, F.C.; Wang, Y.S.; Chen, X. Effective medium theory applied to frequency selective surfaces on periodic substrates. Chin. Opt. Lett. 2010, 8, 1175–1177. [Google Scholar] [CrossRef]
- Stogryn, A. The bilocal approximation for the electric field in strong fluctuation theory. IEEE Trans. Antennas Propag. 1983, 31, 985–986. [Google Scholar] [CrossRef]
- Stogryn, A. Strong fluctuation theory equations for electric field second moments in anisotropic media. IEEE Trans. Antennas Propag. 1990, 38, 1099–1101. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A. Scattering of electromagnetic waves from random media with strong permittivity fluctuations. Radio Sci. 1981, 16, 303–320. [Google Scholar] [CrossRef]
- He, Y.F.; Gong, R.Z.; Wang, X.; Zhao, Q. Study on Equivalent Electromagnetic Parameters and Absorbing properties of honeycomb-structured absorbing materials. Acta. Phys. Sin. 2008, 57, 5261–5266. [Google Scholar]
- Zhao, P.; Xu, Y.G.; Wei, F.M.; Liu, T.; Su, D.L. Electromagnetic property of a novel gradient honeycomb composite fabricated by 3D forming. J. Magn. Magn. Mater. 2020, 493, 165742. [Google Scholar]
- Zhou, P.H.; Huang, L.R.; Xie, J.L.; Liang, D.F.; Lu, H.P.; Deng, L.J. Prediction of Microwave Absorption Behavior of Grading Honeycomb Composites Based on Effective Permittivity Formulas. IEEE Trans. Antennas Propag. 2015, 63, 3496–3501. [Google Scholar] [CrossRef]
- Zhao, Y.C.; Ren, F.; He, L.; Zhang, J.S.; Yuan, Y.N.; Xi, X.L. Design of graded honeycomb radar absorbing structure with wide-band and wide-angle properties. Int. J. Microw. Wirel. Technol. 2019, 11, 143–150. [Google Scholar] [CrossRef]
- Khurram, A.A.; Ali, N.; Rakha, S.A.; Zhou, P.H.; Munir, A. Optimization of the carbon coating of honeycomb cores for broadband microwave absorption. IEEE Trans. Electromagn. Compat. 2014, 56, 1061–1066. [Google Scholar] [CrossRef]
- He, F.; Zhao, Y.; Si, K.X.; Zha, D.C.; Li, R.; Dong, J.X.; Bie, S.W.; Jiang, J.J. Multisection step-impedance modeling and analysis of broadband microwave honeycomb absorbing structures. J. Phys. D Appl. Phys. 2020, 54, 015501. [Google Scholar] [CrossRef]
- Choi, J.H.; Jang, M.S.; Jang, W.H.; Kim, C.G. Investigation on microwave absorption characteristics of conductive-coated honeycomb absorber. Compos. Struct. 2020, 242, 112129. [Google Scholar] [CrossRef]
- Shen, R.B. Modeling and Application Research of Electromagnetic Parameters of Honeycomb Absorbing Structure. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2020. [Google Scholar]
- Li, B.; Zhang, F.; Jin, P. Multi-objective optimization of composites sandwich containing multi-layer honeycomb considering load-bearing capacities and EM absorbing characteristics. Mech. Adv. Mater. Struct. 2023, 31, 4246–4253. [Google Scholar] [CrossRef]
- Sun, P.C.; Wang, L.M.; Wang, T.; Huang, J.; Shao, S.W.; Chen, W. Structural Optimization of the Design of a Double-layer Absorbing Honeycomb Composite. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2019, 46, 58–64. [Google Scholar]
- Zhang, X.H.; Sun, Q.; Xu, S.F. Optimal Design of Multi-Layer Absorbent Honeycomb Cellular Composite Material Structure. Key Eng. Mater. 2017, 723, 335–343. [Google Scholar]
- Yakovenko, O.; Matzui, L.; Danylova, G.; Zadorozhnii, V.; Vovchenko, L.; Perets, Y.; Lazarenko, O. Electrical Properties of Composite Materials with Electric Field-Assisted Alignment of Nanocarbon Fillers. Nanoscale Res. Lett. 2017, 12, 471. [Google Scholar] [CrossRef]
- Yakovenko, O.S.; Matzui, L.Y.; Vovchenko, L.L.; Oliynyk, V.V.; Zagorodnii, V.V.; Trukhanov, S.V.; Trukhanov, A.V. Electromagnetic Properties of Carbon Nanotube/BaFe12−xGaxO19/Epoxy Composites with Random and Oriented Filler Distributions. Nanomaterials 2021, 11, 2873. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Zhao, Z.S.; Wu, M.Z.; He, H.H. The Reflection of Obliquely Incident Electromagnetic Wave to Radar Absorbing Material. J. Huazhong Univ. Sci. Technol. 1998, 26, 36–38. [Google Scholar]
- Chen, H.Y.; Shen, R.B.; Li, F.X.; He, Q.T.; Li, G.Y.; Lu, H.P.; Weng, X.L.; Xie, J.L.; Zhang, G.R.; Deng, L.J. Equivalent electromagnetic parameters extraction method for graded honeycomb absorbing materials. Appl. Phys. B Lasers Opt. 2021, 127, 84. [Google Scholar] [CrossRef]
- He, Y.B.; Yang, Q.Z.; Gao, X. Comprehensive optimization design of aerodynamic and electromagnetic scattering characteristics of serpentine nozzle. Chin. J. Aeronaut. 2021, 34, 118–128. [Google Scholar] [CrossRef]
- Ananth, P.B.; Abhiram, N.; Krishna, K.H.; Nisha, M.S. Synthesis of radar absorption material for stealth application. Mater. Today Proc. 2021, 47, 4872–4878. [Google Scholar] [CrossRef]
- Yao, J.J. Evaluation of Scattering from Electrically Large and Complex PEC Target Coated with Anisotropic Material and Its Software Realization. Ph.D. Thesis, Wuhan University, Wuhan, China, 2013. [Google Scholar]
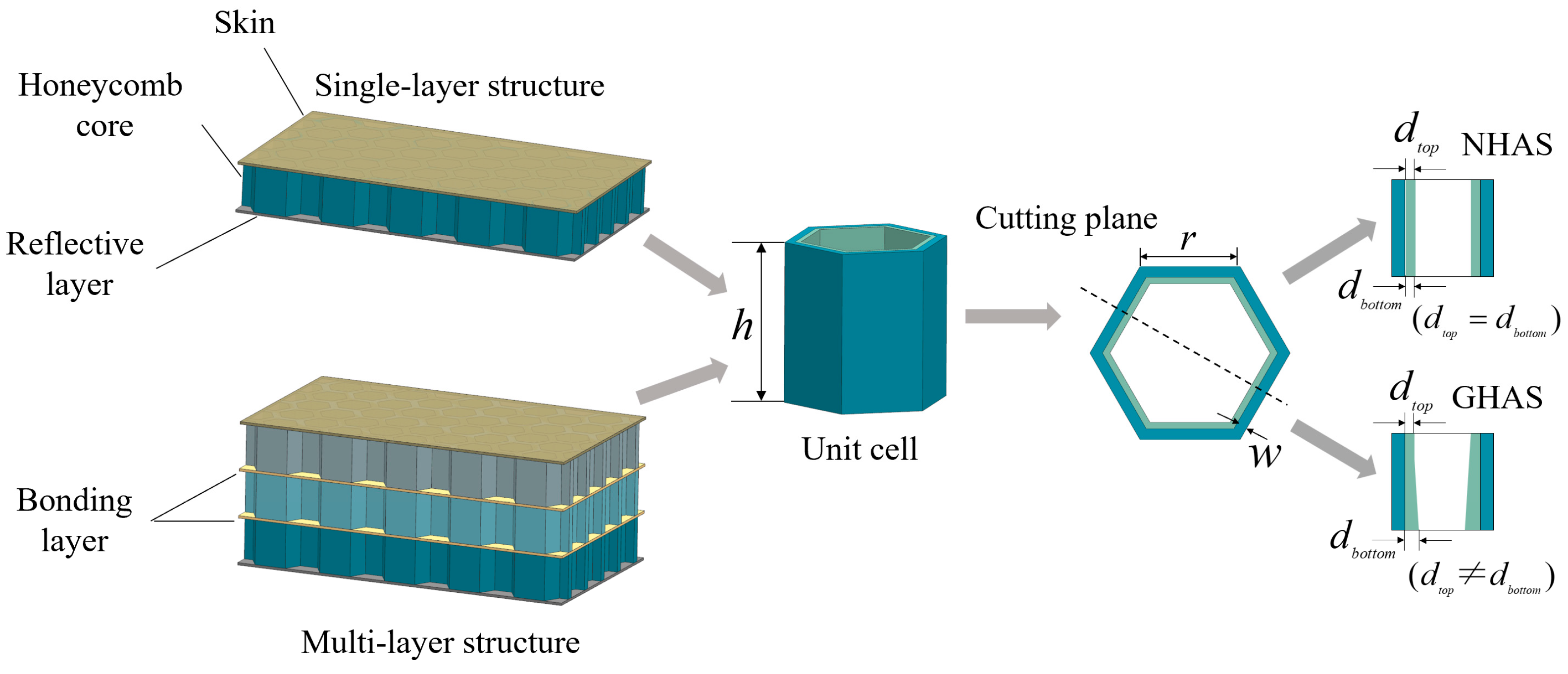
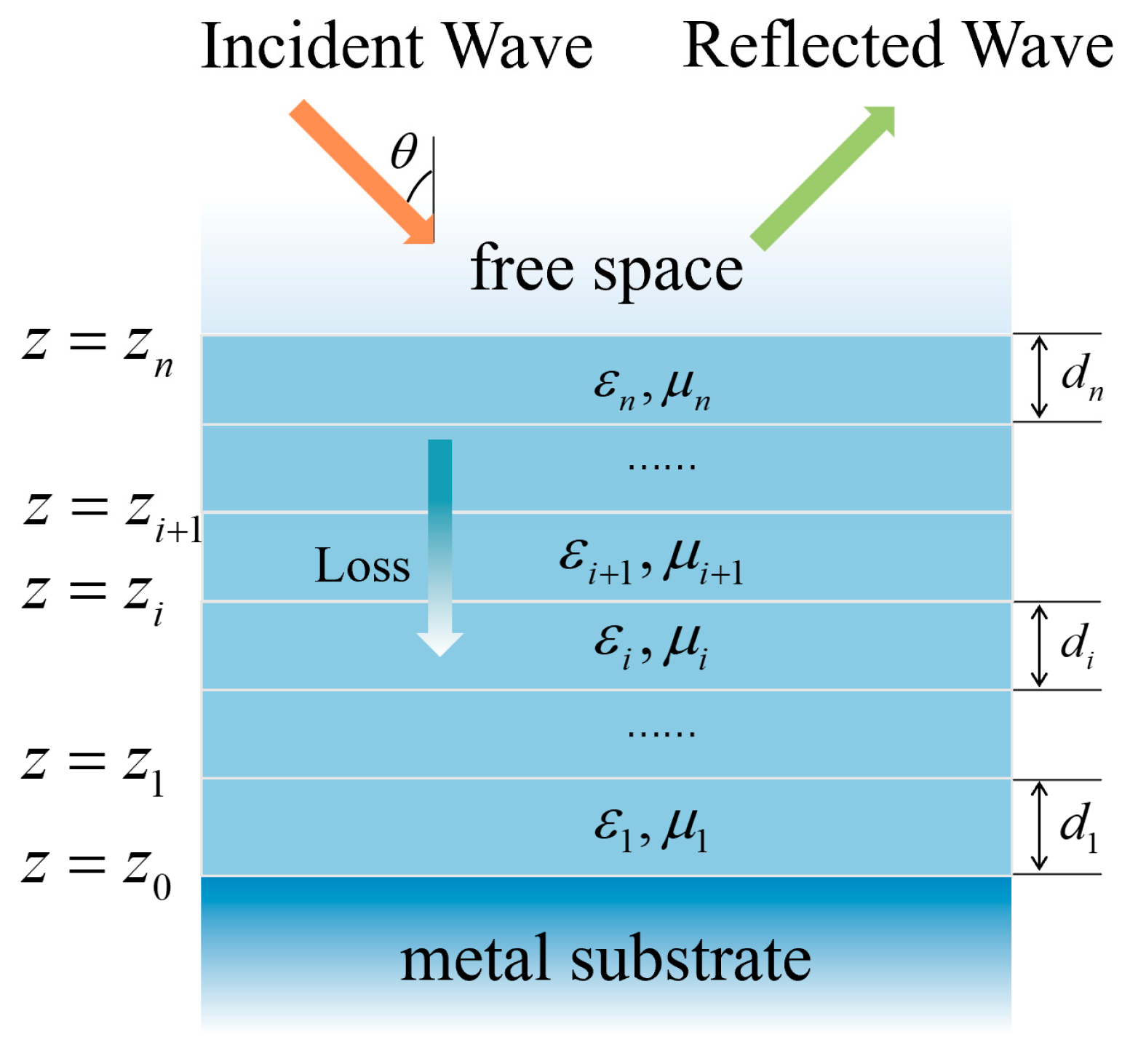

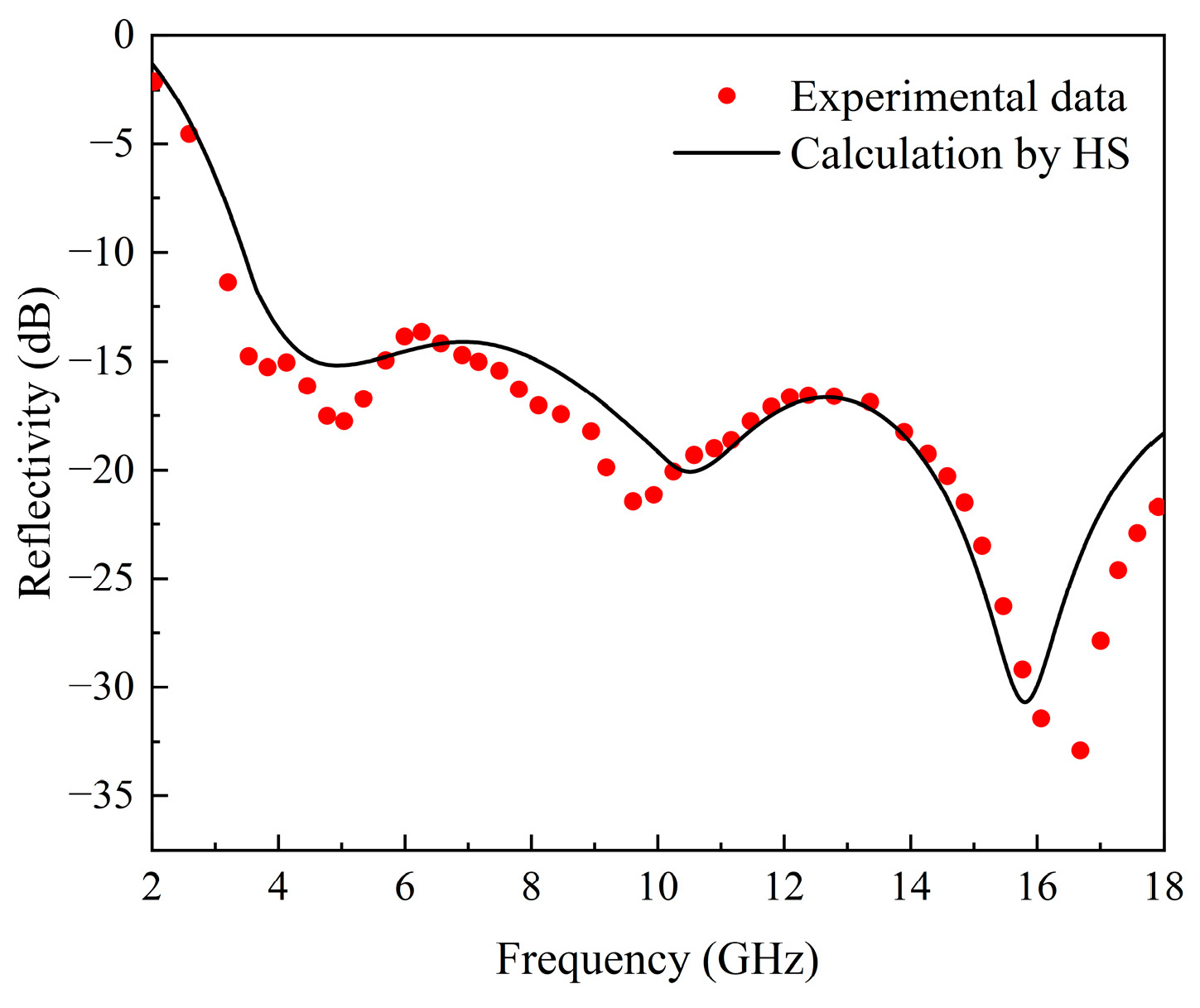
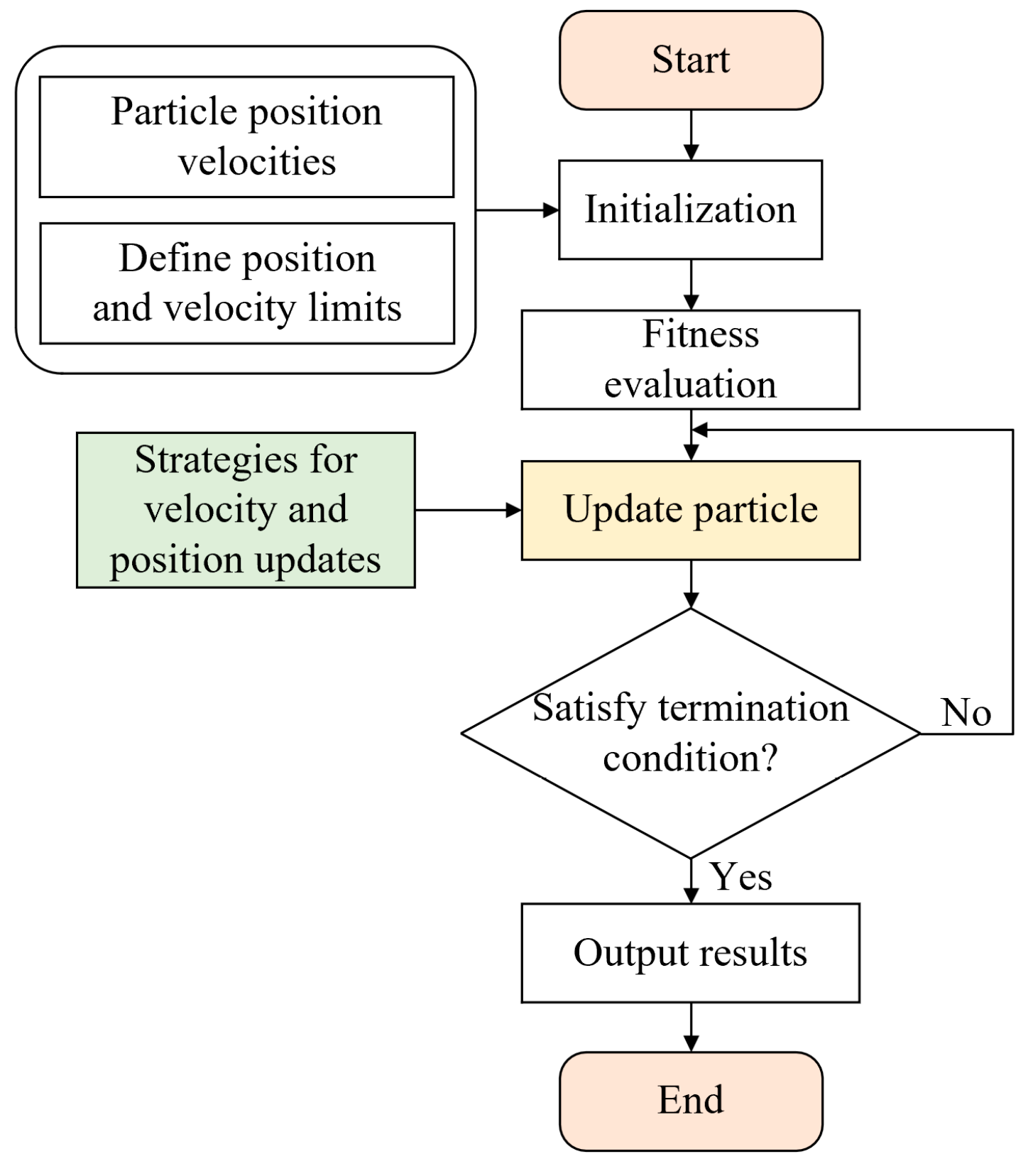


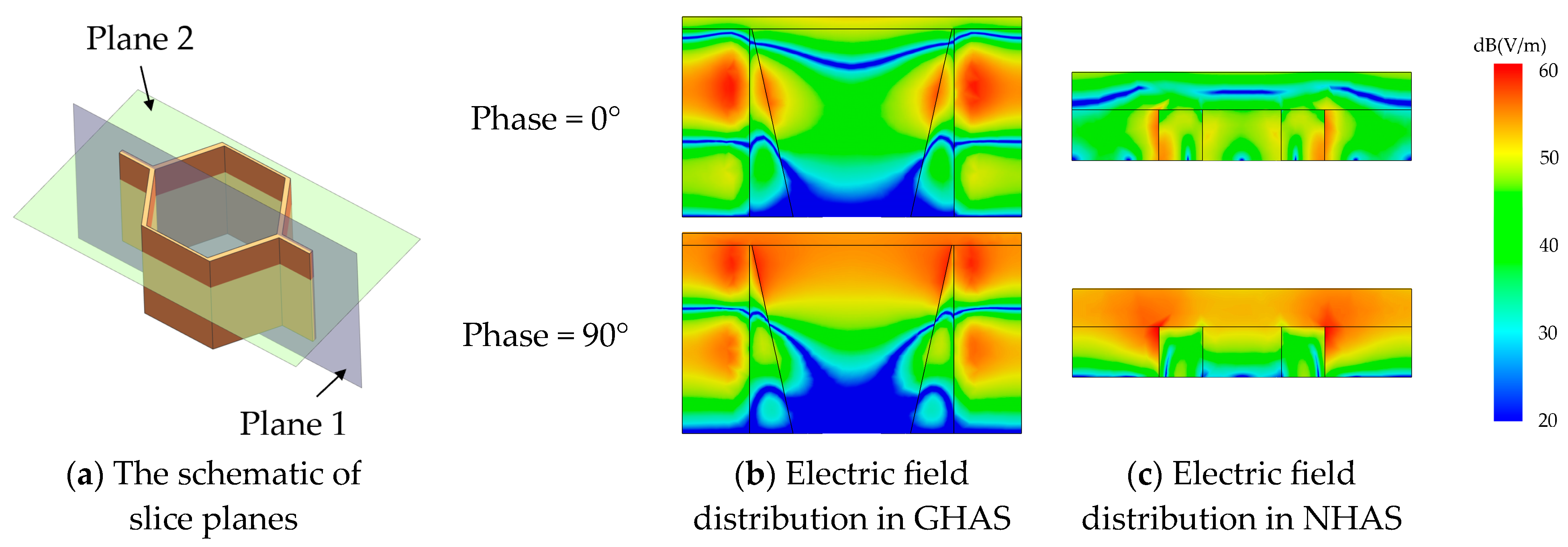
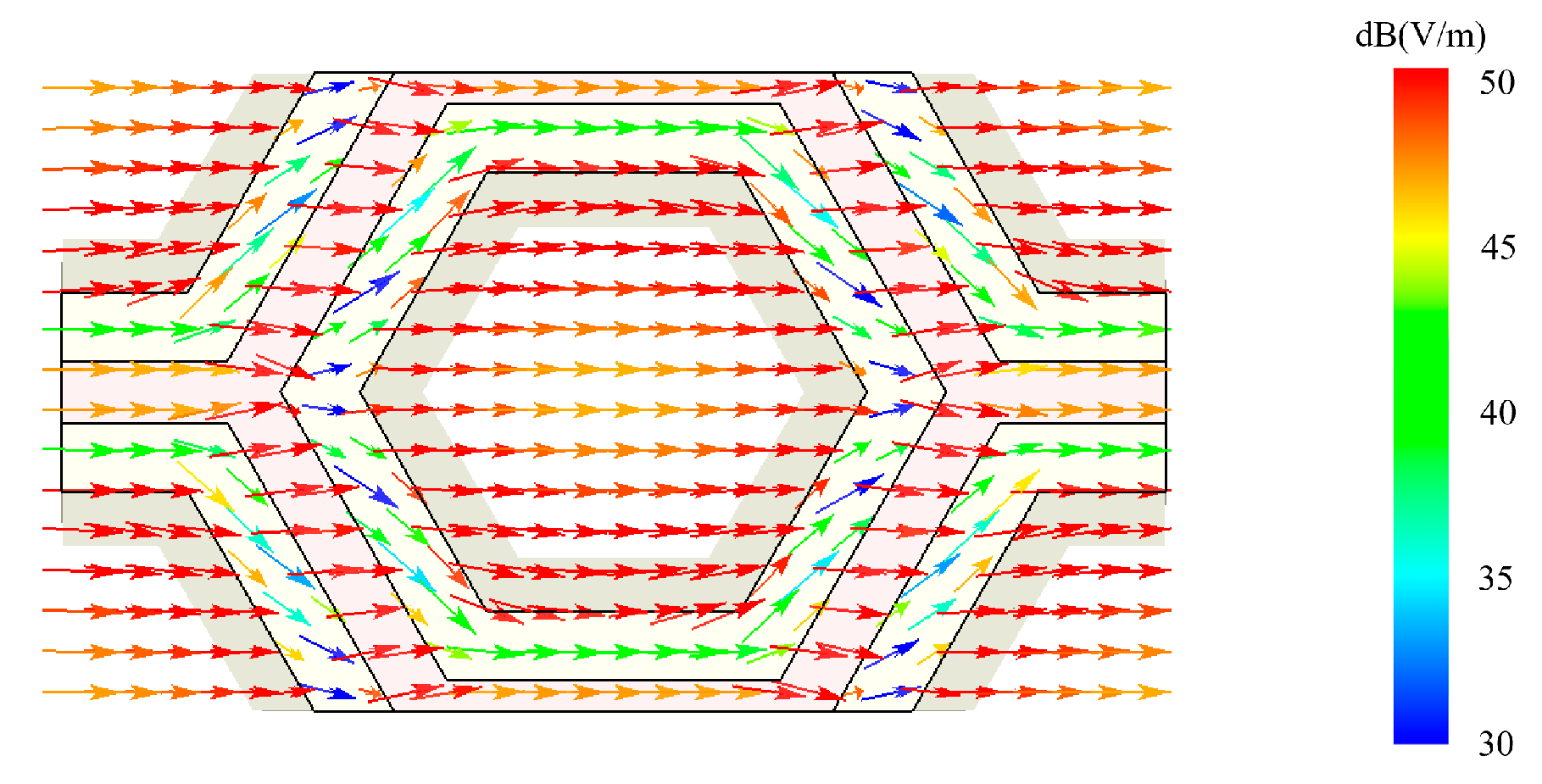
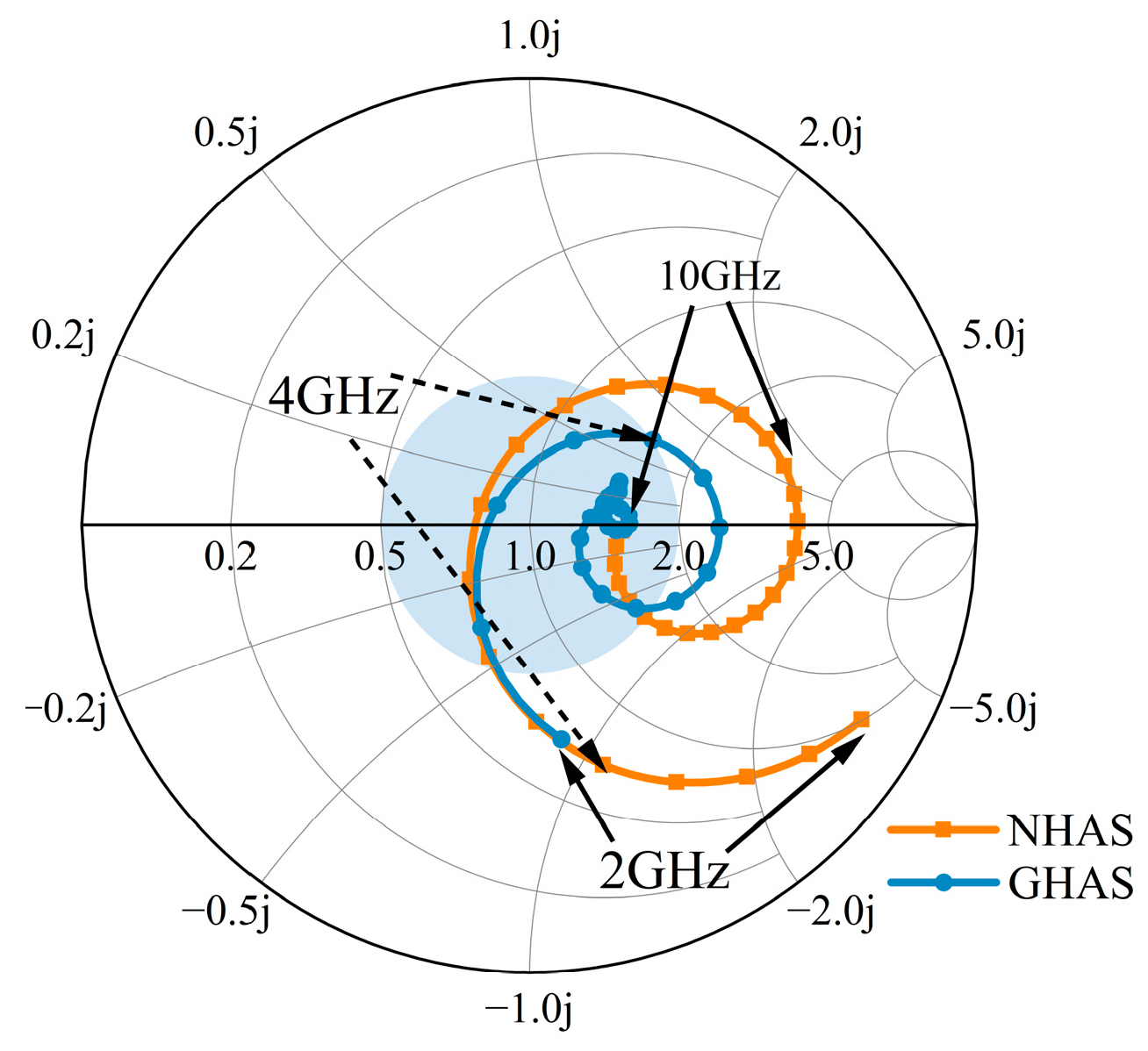



| Material | |||||
|---|---|---|---|---|---|
| Honeycomb Framework | 2.4 | 0 | 1 | 0 | |
| Coating medium | RAM1 | 22.68 | 6.58 | 2.23 | 1.94 |
| RAM2 | 11.46 | 1.5 | 1.12 | 0.17 | |
| RAM3 | 20.18 | 18.25 | 3.1 | 2.79 | |
| Skin | 4.2 | 0.3 | 1 | 0 | |
| Bonding layer | 2.9 | 0.008 | 1 | 0 | |
| h | dtop | dbottom | r | w | Material | |
|---|---|---|---|---|---|---|
| Honeycomb core | 10 | 0.4 | 0.8 | 2 | 0.2 | Honeycomb framework + RAM2 |
| Skin | 1 | — | — | — | — | Skin medium |
| Target | Honeycomb Framework | Coating Medium | Skin | |||
|---|---|---|---|---|---|---|
| Parameter | r | w | h | dtop | dbottom | dskin |
| Value range (mm) | 6 | 0.5~2 | 1~10 | 0.1~2 | 0.1~2 | 0.5~2 |
| NHAS | GHAS | |
|---|---|---|
| 1.39 | 0.5 | |
| 2.69 | 10 | |
| 2 | 0.1 | |
| 2 | 2 | |
| 2 | 0.63 | |
| Objective function value | 0.83 | 0.56 |
| NHAS | GHAS | |||
|---|---|---|---|---|
| −10 dB Bandwidths (GHz) | Fractional Bandwidths | −10 dB Bandwidths (GHz) | Fractional Bandwidths | |
| 0° | 4.7 | 36.07% (5–7.2 GHz) 13.65% (15.7–18 GHz) | 13.3 | 47.62% (2.4–3.9 GHz) 95.08% (6.4–18 GHz) |
| 30° TE | 3.9 | 34.15% (5.1–7.2 GHz) 9.3% (16.4–18 GHz) | 12.7 | 45.16% (2.4–3.8 GHz) 89.16% (6.9–18 GHz) |
| 30° TM | 4.9 | 35.48% (5.1–7.3 GHz) 14.93% (15.5–18 GHz) | 13.7 | 48.49% (2.5–4.1 GHz) 98.76% (6.1–18 GHz) |
| 60° TE | 1.9 | 29.03% (5.3–7.1 GHz) | 0.6 | 16.39% (2.8–3.3 GHz) |
| 60° TM | 4.6 | 28.57% (13.5–18 GHz) | 14.6 | 134.88% (3.5–18 GHz) |
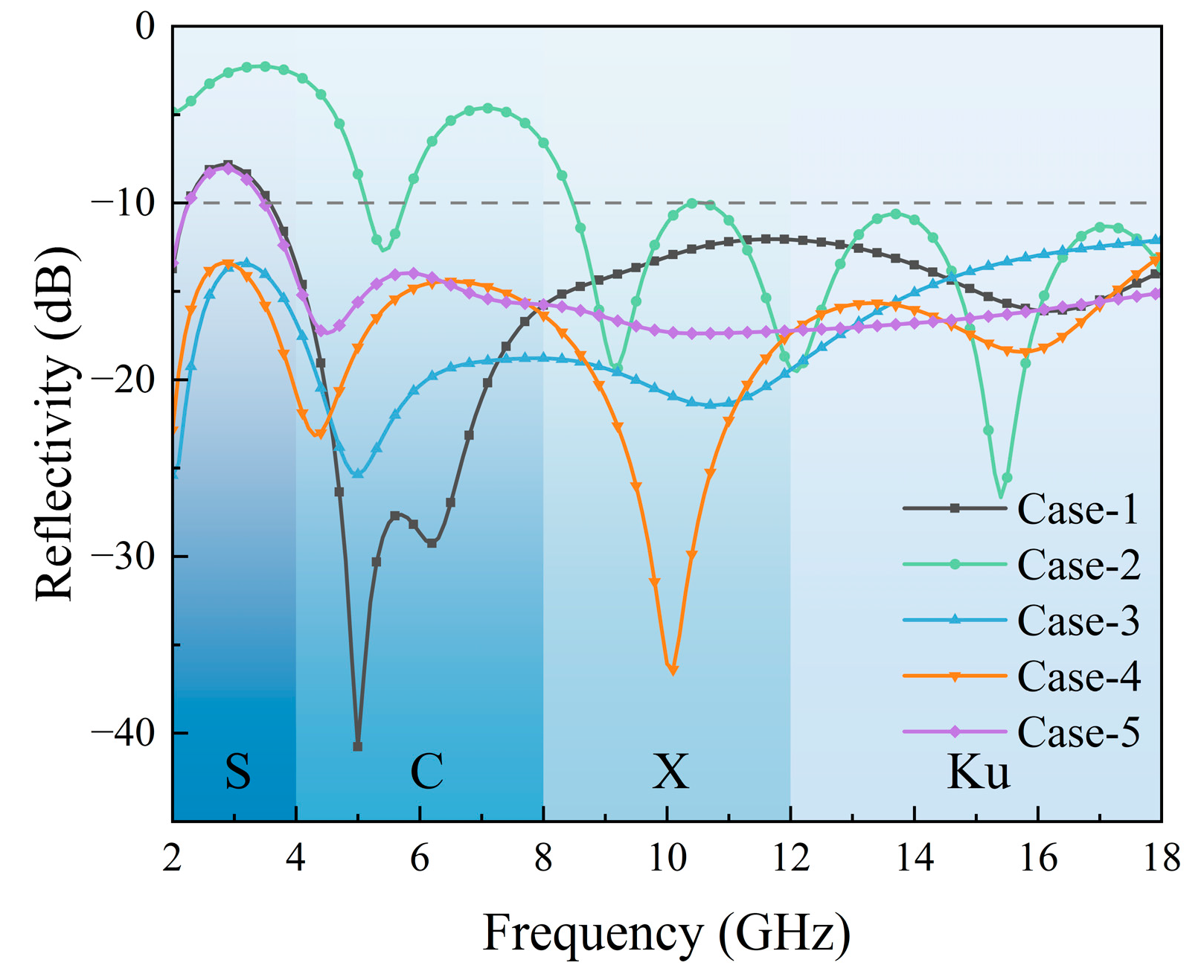
| Samples | 1st Layer Material | 2nd Layer Material | 3rd Layer Material |
|---|---|---|---|
| Case-1 | RAM1 | RAM1 | RAM1 |
| Case-2 | RAM2 | RAM2 | RAM2 |
| Case-3 | RAM3 | RAM3 | RAM3 |
| Case-4 | RAM3 | RAM1 | RAM2 |
| Case-5 | RAM2 | RAM1 | RAM3 |
| Case-1 | Case-2 | Case-3 | Case-4 | Case-5 | ||
|---|---|---|---|---|---|---|
| Objective function value | 0.43 | 0.63 | 0.34 | 0.32 | 0.48 | |
| 19.08 | 19.37 | 17.43 | 19.24 | 19.04 | ||
| d | 2 | 2 | 1.31 | 2 | 1.08 | |
| 2 | 2 | 2 | 1.88 | 2 | ||
| 0.78 | 1.79 | 0.10 | 0.12 | 2 | ||
| 2 | 2 | 0.50 | 0.63 | 1.49 | ||
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| 0.26 | 2 | 0.1 | 0.1 | 1.14 | ||
| h | h1 | 7.89 | 9.41 | 7.30 | 7.02 | 1.31 |
| h2 | 2.59 | 2.72 | 4.69 | 8.16 | 6.73 | |
| h3 | 7.61 | 6.24 | 4.44 | 3.06 | 10 |
| L | W | H | β | |
|---|---|---|---|---|
| Parameter | 1500 mm | 400 mm | 400 mm | 60° |
| Number of Cores | Number of Meshes | Required Time | |
|---|---|---|---|
| FEM | 12 | 1.81 million | 23.58 h |
| SBR | 12 | 3844 | 91 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, H.; Shi, Y.; Yang, Q.; Wang, X.; He, Y. Optimization Design of Honeycomb Absorbing Structure and Its Application in Aircraft Inlet Stealth. Aerospace 2024, 11, 796. https://doi.org/10.3390/aerospace11100796
Xiang H, Shi Y, Yang Q, Wang X, He Y. Optimization Design of Honeycomb Absorbing Structure and Its Application in Aircraft Inlet Stealth. Aerospace. 2024; 11(10):796. https://doi.org/10.3390/aerospace11100796
Chicago/Turabian StyleXiang, Huimin, Yongqiang Shi, Qingzhen Yang, Xufei Wang, and Yubo He. 2024. "Optimization Design of Honeycomb Absorbing Structure and Its Application in Aircraft Inlet Stealth" Aerospace 11, no. 10: 796. https://doi.org/10.3390/aerospace11100796
APA StyleXiang, H., Shi, Y., Yang, Q., Wang, X., & He, Y. (2024). Optimization Design of Honeycomb Absorbing Structure and Its Application in Aircraft Inlet Stealth. Aerospace, 11(10), 796. https://doi.org/10.3390/aerospace11100796






