EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development
Abstract
1. Introduction
2. Simulator Design
2.1. The DARTS Multibody
2.1.1. URDF Representation
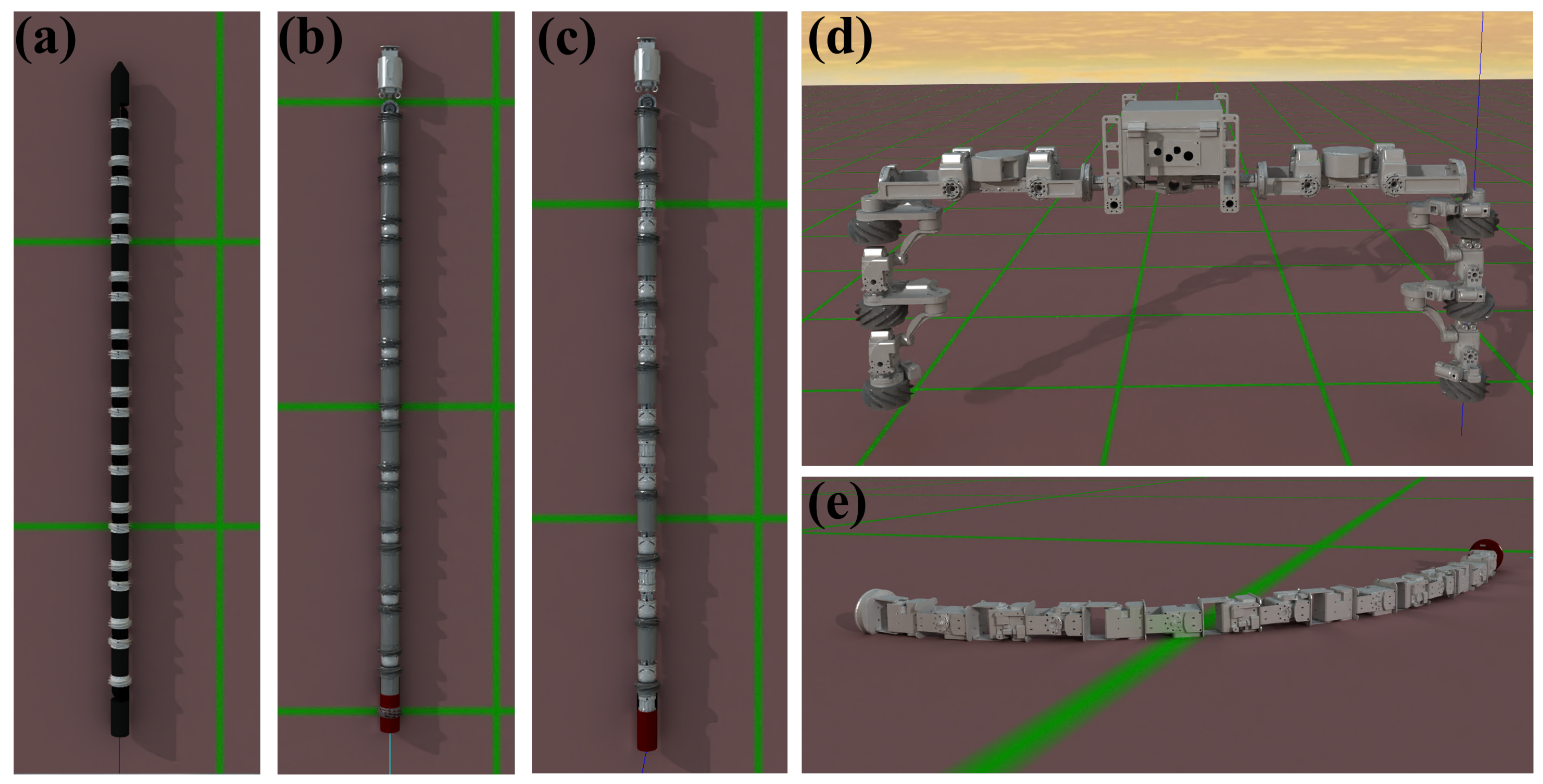
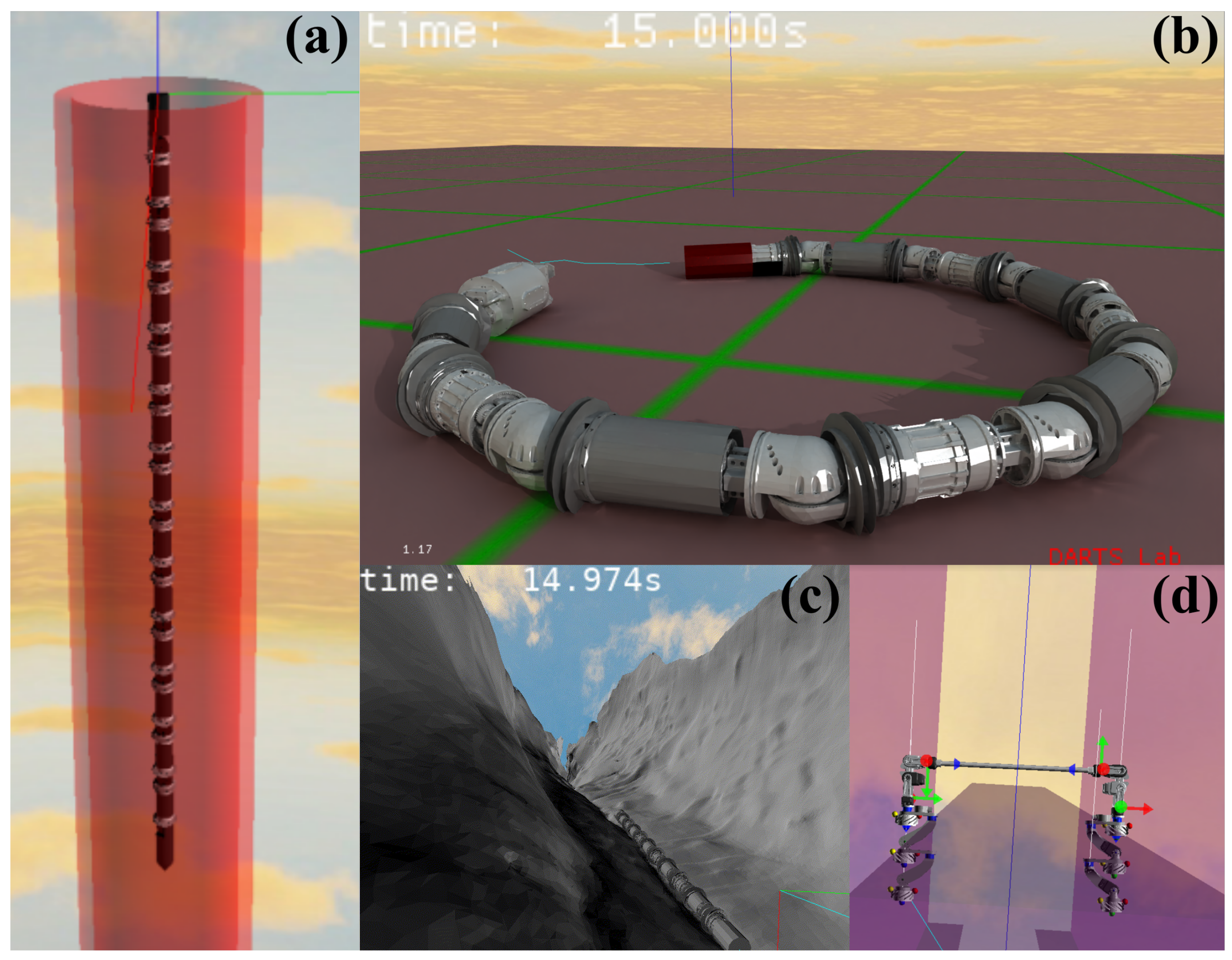
2.1.2. EELS Robot Models
- EELS—An early EELS design concept with two counter-rotating screws per module. See Figure 3a.
- EELS 1.0, alternating—Version 1.0 EELS hardware. A robot built with 10 modules and an optional perception head. Used for surface traversal and perception experiments. The alternating variant has two counter-rotating screws per module. See Figure 3b.
- EELS 1.0, front only—The “front only” variant removed the rear screw for each module resulting in one screw per module. See Figure 3c.
- EELS 1.5—Version 1.5 EELS hardware. A low-cost EELS robot built with off-the-shelf components. Designed exclusively for subsurface experiments, EELS 1.5 features a cross bar in the middle of the robot with an avionics box. See Figure 3d.
- Mini EELS 1.0—Smaller, low-cost robot with only bend joints and no screws, suitable for tasks such as climbing up small pipes. Primarily used as a test bed for reinforcement learning-based locomotion gaits. See Figure 3e.
2.1.3. Constraint Embedding for Counter-Rotating Screws
2.1.4. Multibody Optimization
2.1.5. Configuring the Robot Definition at Launch Time
2.2. Component Models
2.2.1. Terrain
2.2.2. Collision Detection and Contact Models
2.2.3. Graphics and Perception Models
2.2.4. Force-Torque Sensor Models
2.2.5. Joint Control
2.2.6. Robot Initialization and Placement
3. Using the Simulator
3.1. Command Line Interface
- Sim—select robot to use, toggle interactive command-line mode, etc.
- Integrator—select integrator type, tolerances, step size, etc.
- Graphics—select graphics back-end to use, path-tracing options, skybox settings, etc.
- Contact—select contact model to use, set parameters for contact models.
- Terrain—select terrain to use.
- Perception—enable/disable cameras and lidar, set parameters for perception models.
- Joints—enable/disable spring–damper models for joints, set spring–damper parameters.
- ROS—enable/disable ROS interface, set ROS topic publishing rate.
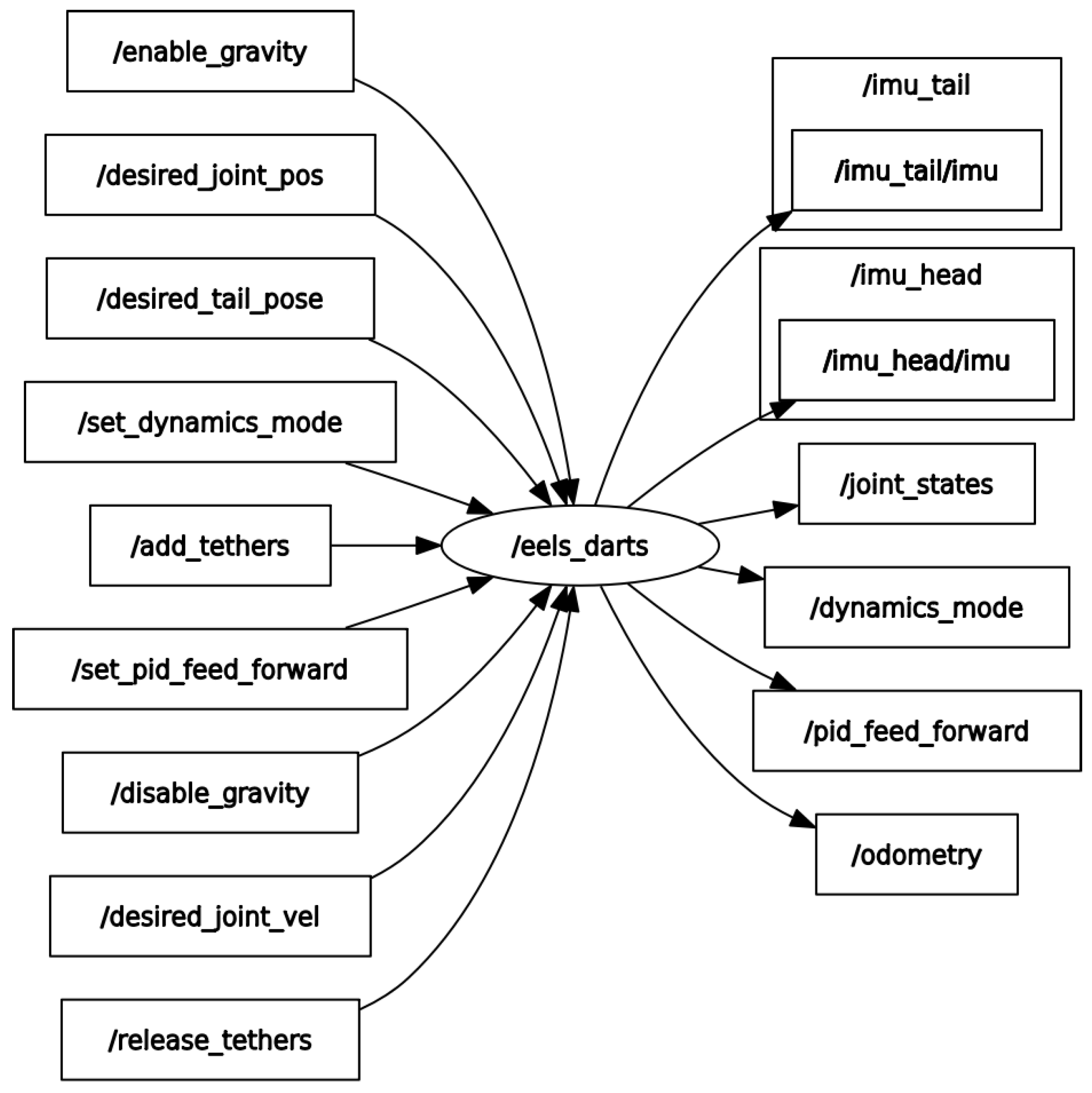
3.2. ROS Interface
4. Results
4.1. Example Uses of the EELS-DARTS Simulator
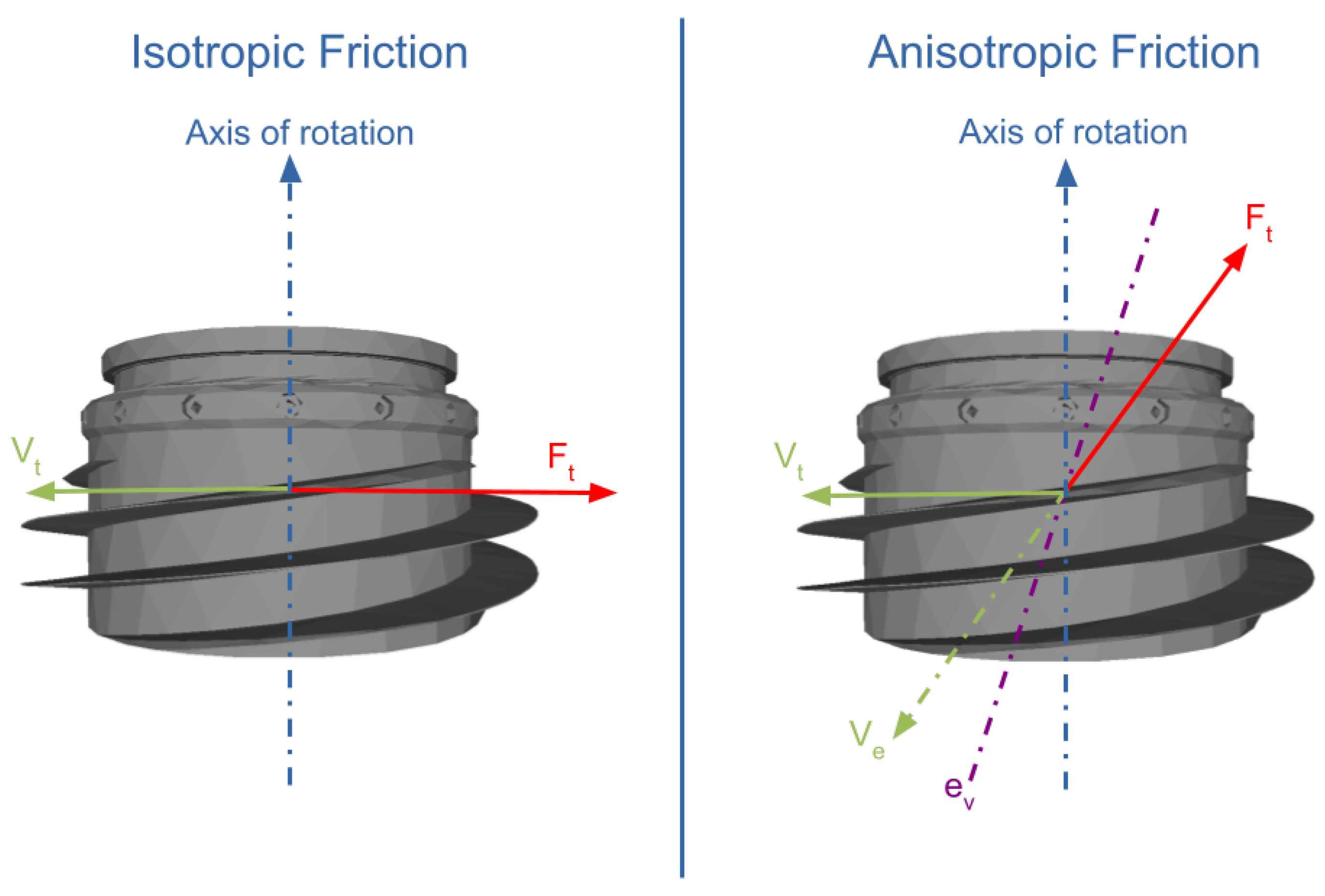
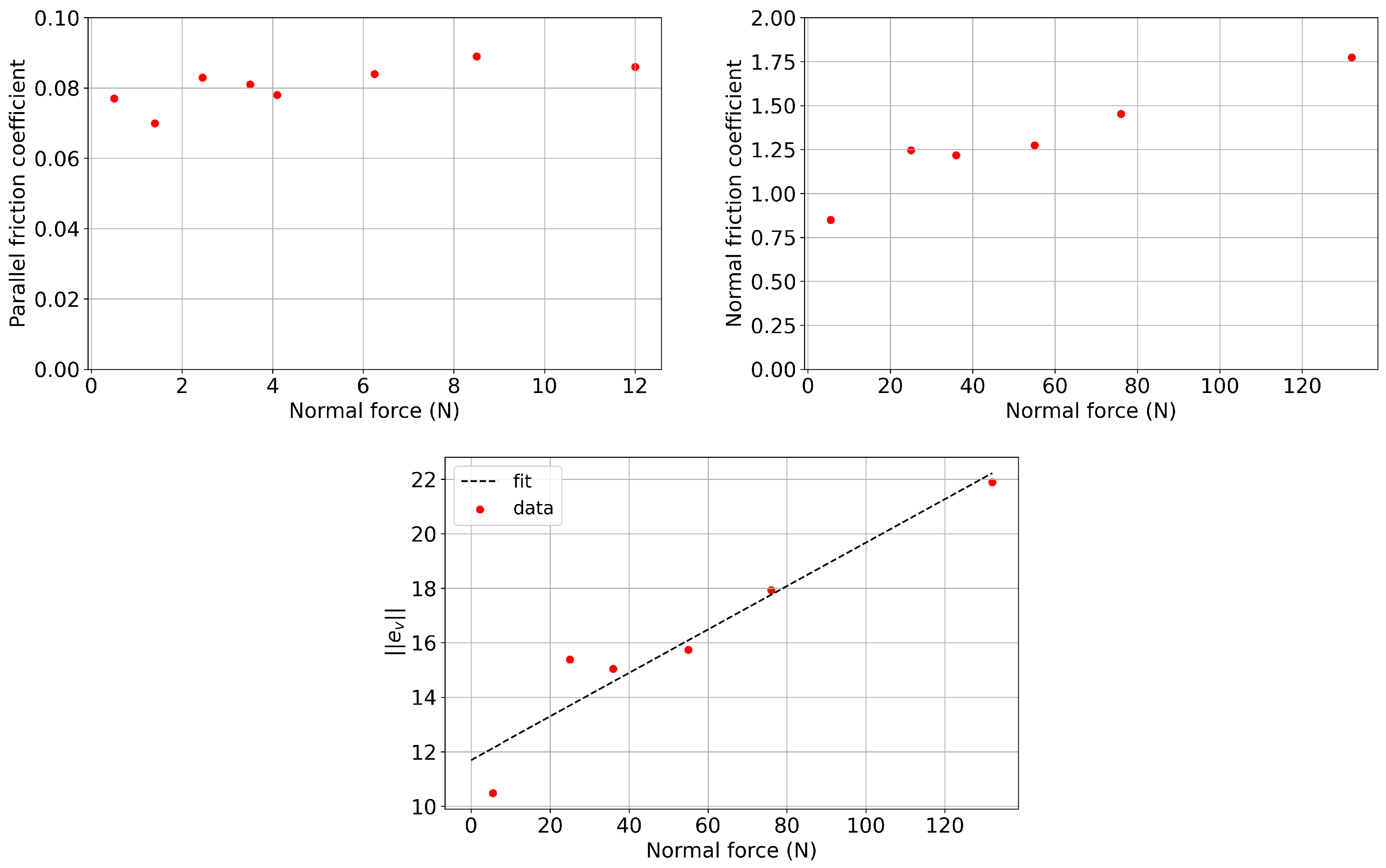
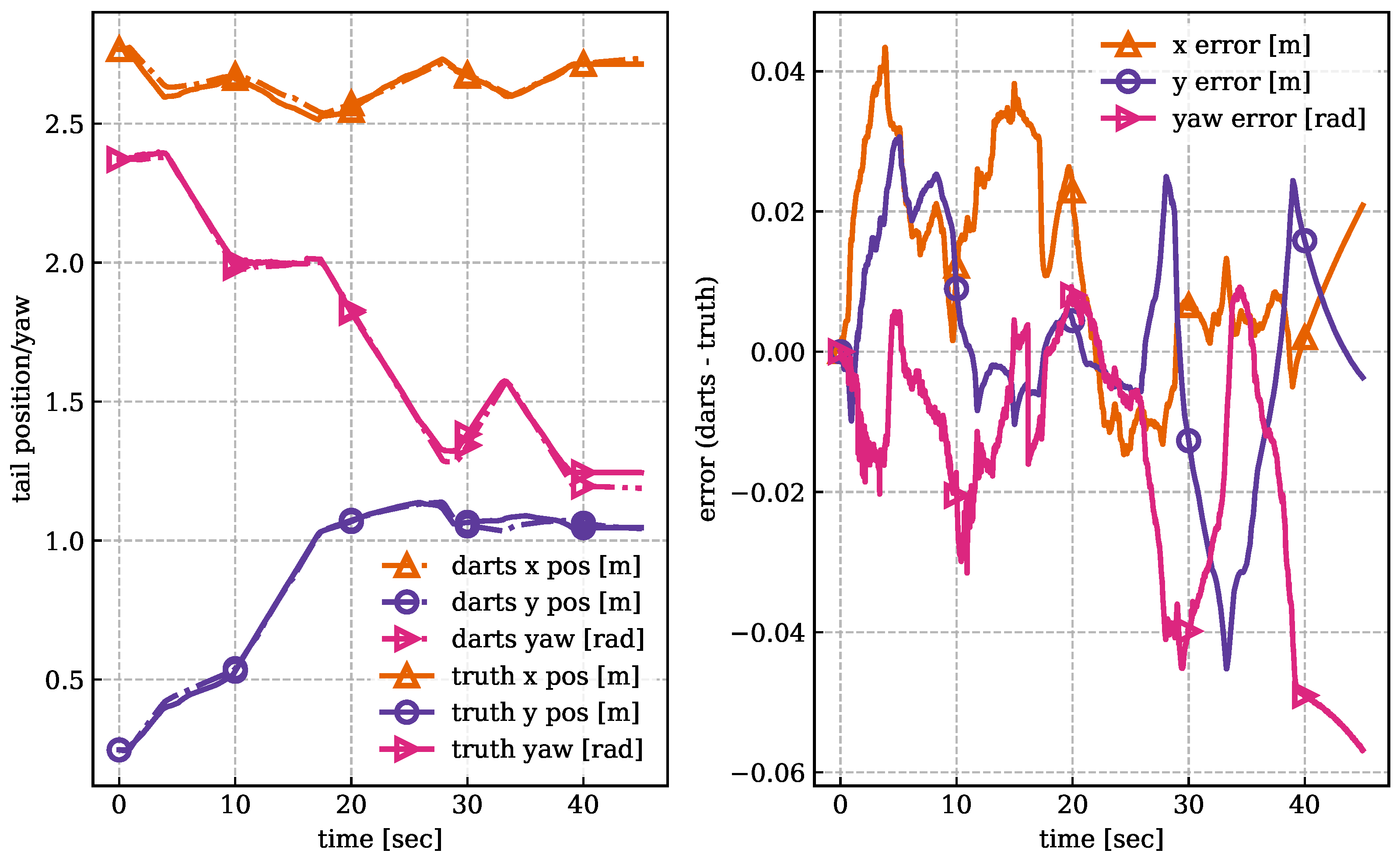
4.2. Contact Model Validation
4.3. Athabasca Glacier Field Test
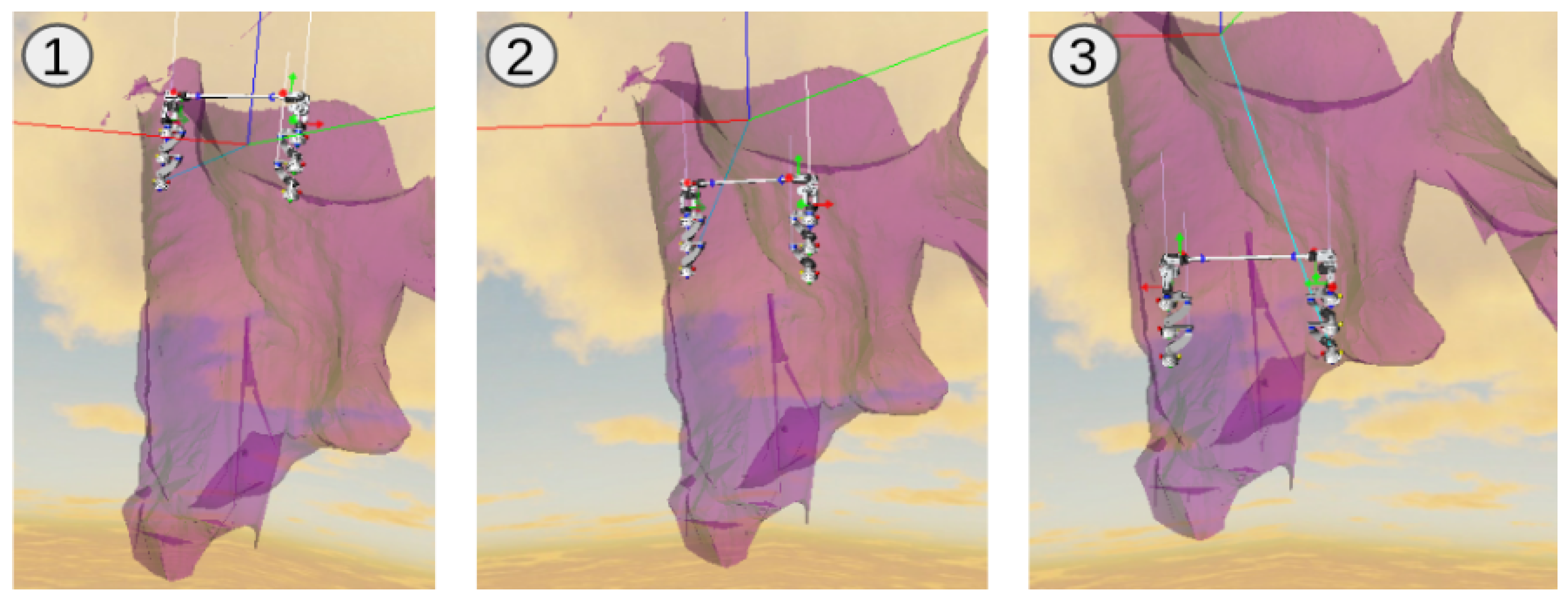
4.3.1. Simulation Testing for Field Test Scenarios
4.3.2. Challenges
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLI | Command-line interface |
| DARTS | Dynamics Algorithms for Real-Time Simulation |
| DEM | Digital elevation model |
| DOF | Degree of freedom |
| EDL | Entry, descent, and landing |
| EELS | Exobiology extant life surveyor |
| FSW | Flight software |
| FTS | Force torque sensor |
| GNC | Guidance, navigation, and control |
| GPU | Graphics processing unit |
| IK | Inverse kinematics |
| IMU | Inertial measurement unit |
| JPL | Jet Propulsion Laboratory |
| MDPI | Multidisciplinary Digital Publishing Institute |
| ML | Machine learning |
| NASA | National Aeronautics and Space Administration |
| PID | Proportional–integral–derivative |
| ROS | Robot operating system |
| SDF | Signed distance field |
| SOA | Spatial operator algebra |
| URDF | Universal robotic description format |
References
- Ono, M.; Thakker, R.; Georgiev, N.; Gavrilov, P.; Archanian, A.; Drevinskas, T.; Daddi, G.; Paton, M.; Strub, M.; Melikyan, H.; et al. To Boldly Go Where No Robots Have Gone Before—Part 1: EELS Robot to Spearhead a New One-Shot Exploration Paradigm with In-situ Adaptation. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Carpenter, K.; Cable, M.L.; Choukroun, M.N.; Ono, H.; Thakker, R.A.; Ingham, M.D.; McGarey, P.; Barchowsky, A.; Iacoponi, S.; Bowkett, J.; et al. Venture Deep, the Path of Least Resistance: Crevasse-Based Ocean Access without the Need to Dig or Drill. Bull. Am. Astron. Soc. 2021, 53, 356. [Google Scholar]
- Exobiology Extant Life Surveyor Website. Available online: https://www.jpl.nasa.gov/robotics-at-jpl/eels (accessed on 25 June 2024).
- Thakker, R.; Paton, M.; Jones, B.; Daddi, G.; Royce, R.; Swan, M.; Strub, M.; Aghli, S.; Zade, H.; Nakka, Y.; et al. To Boldly Go Where No Robots Have Gone Before—Part 4: NEO Autonomy for Robustly Exploring Unknown, Extreme Environments with Versatile Robots. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Vaquero, T.S.; Daddi, G.; Thakker, R.; Paton, M.; Jasour, A.; Strub, M.P.; Swan, R.M.; Royce, R.; Gildner, M.; Tosi, P.; et al. EELS: Autonomous snake-like robot with task and motion planning capabilities for ice world exploration. Sci. Robot. 2024, 9, eadh8332. [Google Scholar] [CrossRef]
- Talbot, W.; Nash, J.; Paton, M.; Ambrose, E.; Metz, B.; Thakker, R.; Etheredge, R.; Ono, M.; Ila, V. Principled ICP Covariance Modelling in Perceptually Degraded Environments for the EELS Mission Concept. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 10763–10770. [Google Scholar] [CrossRef]
- Marvi, H.; Gong, C.; Gravish, N.; Astley, H.; Travers, M.; Hatton, R.L.; Mendelson, J.R.; Choset, H.; Hu, D.L.; Goldman, D.I. Sidewinding with minimal slip: Snake and robot ascent of sandy slopes. Science 2014, 346, 224–229. [Google Scholar] [CrossRef]
- Tesch, M.; Lipkin, K.; Brown, I.; Hatton, R.; Peck, A.; Rembisz, J.; Choset, H. Parameterized and Scripted Gaits for Modular Snake Robots. Adv. Robot. 2009, 23, 1131–1158. [Google Scholar] [CrossRef]
- Marteau, E.; Tosi, L.P.; Veismann, M.; Gavrilov, P.; Peticco, M.; Hockman, B.; Ono, M.; Khanum, M.; Abdelrahim, M.; Marvi, H. To Boldly Go Where No Robots Have Gone Before—Part 3: The Screw Mobility System of EELS for Robust Surface and Subsurface Mobility on Highly Unknown Terrains. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Thakker, R.; Paton, M.; Strub, M.; Swan, M.; Daddi, G.; Royce, R.; Tosi, P.; Gildner, M.; Vaquero, T.; Veismann, M.; et al. EELS: Towards Autonomous Mobility in Extreme Terrain with a Versatile Snake Robot with Resilience to Exteroception Failures. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023. [Google Scholar]
- Vadlamannati, A.; Beknalkar, S.; Best, D.; Bryant, M.; Mazzoleni, A. Design, Prototyping, and Experiments Using Small-Scale Helical Drive Rover for Multi-Terrain Exploration. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, FL, USA, 29 October–2 November 2023. Volume 6: Dynamics, Vibration, and Control. [Google Scholar] [CrossRef]
- Beknalkar, S.; Bryant, M.; Mazzoleni, A. Algorithm for Locomotion Mode Selection, Energy Estimation and Path Planning for a Multi-terrain Screw-Propelled Vehicle for Arctic Exploration. In Proceedings of the 2024 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–19 July 2024; pp. 1462–1467. [Google Scholar] [CrossRef]
- Hasseler, T.D.; Leake, C.; Gaut, A.; Elmquist, A.; Swan, R.M.; Royce, R.; Jones, B.; Hockman, B.; Paton, M.; Daddi, G.; et al. EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development. In Proceedings of the 7th International Conference on Multibody System Dynamics, Madison, WI, USA, 9–13 June 2024. [Google Scholar]
- Wan, Z.; Sun, Y.; Qin, Y.; Skorina, E.H.; Gasoto, R.; Luo, M.; Fu, J.; Onal, C.D. Design, Analysis, and Real-Time Simulation of a 3D Soft Robotic Snake. Soft Robot. 2023, 10, 258–268. [Google Scholar] [CrossRef]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y. 3-D Snake Robot Motion: Nonsmooth Modeling, Simulations, and Experiments. IEEE Trans. Robot. 2008, 24, 361–376. [Google Scholar] [CrossRef][Green Version]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y.; Liljeback, P. Snake Robot Obstacle-Aided Locomotion: Modeling, Simulations, and Experiments. IEEE Trans. Robot. 2008, 24, 88–104. [Google Scholar] [CrossRef]
- Monsalve, J.; Leon, J.; Melo, K. Modular snake robot oriented open simulation software. In Proceedings of the 4th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, Hong Kong, China, 4–7 June 2014; pp. 546–550. [Google Scholar] [CrossRef]
- Sibilska-Mroziewicz, A.; Hameed, A.; Możaryn, J.; Ordys, A. Virtual Reality Simulations of the Snake Robot. In Proceedings of the Digital Interaction and Machine Intelligence, Warsaw, Poland, 12–15 December 2022; Biele, C., Kacprzyk, J., Kopeć, W., Owsiński, J.W., Romanowski, A., Sikorski, M., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 307–313. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3. [Google Scholar]
- Jain, A. DARTS—Multibody Modeling, Simulation and Analysis Software. In Proceedings of the Multibody Dynamics 2019 (ECCOMAS 2019), COMPUTMETHODS Conference, Duisburg, Germany, 15–18 July 2019; Kecskemethy, A., Geu Flores, F., Eds.; Springer Nature: Cham, Switzerland, 2019; Volume 53, pp. 433–441. [Google Scholar]
- Jain, A. Robot and Multibody Dynamics: Analysis and Algorithms; Springer: New York, NY, USA, 2010. [Google Scholar]
- Dynamics Algorithms for Real-Time Simulation (DARTS) Lab Website. Available online: https://dartslab.jpl.nasa.gov (accessed on 25 June 2024).
- Cameron, J.; Balaram, J.; Jain, A.; Kuo, C.; Lim, C.; Myint, S. Next Generation Simulation Framework for Robotic and Human Space Missions. In Proceedings of the AIAA SPACE Conference and Exposition, Pasadena, CA, USA, 11–13 September 2012. [Google Scholar]
- Jain, A.; Cameron, J.; Lim, C.; Guineau, J. SimScape Terrain Modeling Toolkit. In Proceedings of the Second IEEE International Conference on Space Mission Challenges for Information Technology (SMC-IT), Pasadena, CA, USA, 17–20 July 2006. [Google Scholar]
- Myint, S.; Jain, A.; Cameron, J.; Lim, C. Large Terrain Modeling and Visualization for Planets. In Proceedings of the Fourth IEEE International Conference on Space Mission Challenges for Information Technology (SMC-IT), Palo Alto, CA, USA, 2–4 August 2011. [Google Scholar]
- Aiazzi, C.; Gaut, A.; Young, A.; Elmquist, A.; Jain, A. IRIS: High-fidelity Perception Sensor Modeling for Closed-Loop Planetary Simulations. In Proceedings of the AIAA Scitech Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Ryan, R.R. ADAMS—Multibody System Analysis Software. In Multibody Systems Handbook; Schiehlen, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 361–402. [Google Scholar] [CrossRef]
- Mittal, M.; Yu, C.; Yu, Q.; Liu, J.; Rudin, N.; Hoeller, D.; Yuan, J.L.; Singh, R.; Guo, Y.; Mazhar, H.; et al. Orbit: A Unified Simulation Framework for Interactive Robot Learning Environments. IEEE Robot. Autom. Lett. 2023, 8, 3740–3747. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and Use Paradigms for Gazebo, An Open-Source Multi-Robot Simulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 2149–2154. [Google Scholar]
- Paton, M.; Rieber, R.; Cruz, S.; Gildner, M.; Abma, C.; Abma, K.; Aghli, S.; Ambrose, E.; Archanian, A.; Bagshaw, E.A.; et al. 2023 EELS Field Tests at Athabasca Glacier as an Icy Moon Analogue Environment. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024; pp. 1–18. [Google Scholar] [CrossRef]
- Jain, A. Computing Inter-Body Constraint Forces in Recursive Multibody Dynamics. In Proceedings of the 5th Joint International Conference on Multibody System Dynamics, Lisboa, Portugal, 24–28 June 2018. [Google Scholar]
- Leake, C.; Jain, A. FModal: A Flexible Body Dynamics Modeling Pipeline for Guidance and Control. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023. [Google Scholar]
- Jain, A.; Rodriguez, G. Recursive Flexible Multibody System Dynamics Using Spatial Operators. J. Guid. Control Dyn. 1992, 15, 1453–1466. [Google Scholar] [CrossRef]
- Coumans, E.; Bai, Y. PyBullet, a Python Module for Physics Simulation for Games, Robotics and Machine Learning. 2016–2021. Available online: http://pybullet.org (accessed on 6 August 2024).
- Parker, S.G.; Bigler, J.; Dietrich, A.; Friedrich, H.; Hoberock, J.; Luebke, D.; McAllister, D.; McGuire, M.; Morley, K.; Robison, A.; et al. OptiX: A General Purpose Ray Tracing Engine. ACM Trans. Graph. 2010, 29, 66. [Google Scholar] [CrossRef]
- Madison, R.; Pomerantz, M.; Jain, A. Camera Response Simulation for Planetary Exploration. In Proceedings of the i-SAIRAS Conference, Munich, Germany, 5–8 September 2005. [Google Scholar]
- Nagaoka, K.; Otsuki, M.; Kubota, T.; Tanaka, S. Terramechanics-based propulsive characteristics of mobile robot driven by Archimedean screw mechanism on soft soil. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4946–4951. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasseler, T.D.; Leake, C.; Gaut, A.; Elmquist, A.; Swan, R.M.; Royce, R.; Jones, B.; Hockman, B.; Paton, M.; Daddi, G.; et al. EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development. Aerospace 2024, 11, 795. https://doi.org/10.3390/aerospace11100795
Hasseler TD, Leake C, Gaut A, Elmquist A, Swan RM, Royce R, Jones B, Hockman B, Paton M, Daddi G, et al. EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development. Aerospace. 2024; 11(10):795. https://doi.org/10.3390/aerospace11100795
Chicago/Turabian StyleHasseler, Tristan D., Carl Leake, Aaron Gaut, Asher Elmquist, Robert Michael Swan, Rob Royce, Bryson Jones, Ben Hockman, Michael Paton, Guglielmo Daddi, and et al. 2024. "EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development" Aerospace 11, no. 10: 795. https://doi.org/10.3390/aerospace11100795
APA StyleHasseler, T. D., Leake, C., Gaut, A., Elmquist, A., Swan, R. M., Royce, R., Jones, B., Hockman, B., Paton, M., Daddi, G., Ono, M., Thakker, R., & Jain, A. (2024). EELS-DARTS: A Planetary Snake Robot Simulator for Closed-Loop Autonomy Development. Aerospace, 11(10), 795. https://doi.org/10.3390/aerospace11100795





