Cruise Range Optimization of a Propeller-Driven Light Aircraft Using a Direct Transcription Method with a Regularization Term
Abstract
1. Introduction
2. Cruise Conditions and Propulsion System
2.1. Flight Dynamics
2.2. Propulsion System Characterization
Control Function
2.3. Optimal Control Problem for Cruise Maximum Range
3. Reciprocating Engine Light Aircraft: Piper Cherokee PA-28 Full and Simplified Models
- Mission parameters (M): These define the requirements of the level flight, such as the altitude, the amount of fuel, the mixture conditions, and the rotational speed. So, it is necessary to specify h, , , and . For the sake of simplicity, we assume that the flight takes place under ISA conditions, which allows us to obtain the pressure, density, and temperature from h (if needed).
- Aircraft and propulsion system constants (AP): These are related to geometry, aerodynamics, structural masses, and the operational limits of both the airframe and the propulsion system. The involved quantities are S, , K, , , , , and .
- Propulsion system performance functional model (PFM): This describes the performance of the reciprocating engine and the propeller by providing the functions , , and .
3.1. Piper Cherokee PA-28 and Level Flight Conditions
3.2. Reciprocating Engine Model
3.3. Propeller Model
3.4. Simplified Models
3.4.1. Von Mises Model
3.4.2. Pargett and Ardema Model
4. Numerical Solution Method
4.1. Direct Transcription Method
4.2. Regularization Term
5. Results
5.1. Setup of the Numerical Method
5.2. The Von Mises Model: Validation of the Numerical Solution
5.2.1. Results and Discussion
5.2.2. Effect of the Regularization Term
5.3. Cruise Maximum Range for the Piper Cherokee PA-28: Comparison of Von Mises, PA, and Full Models
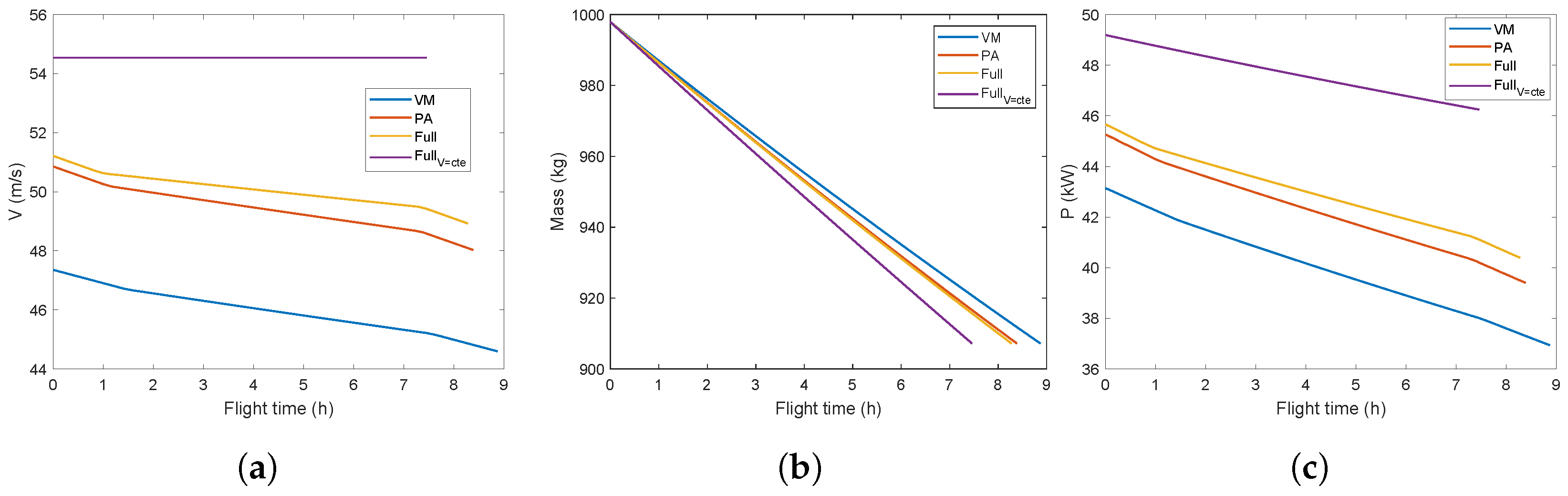
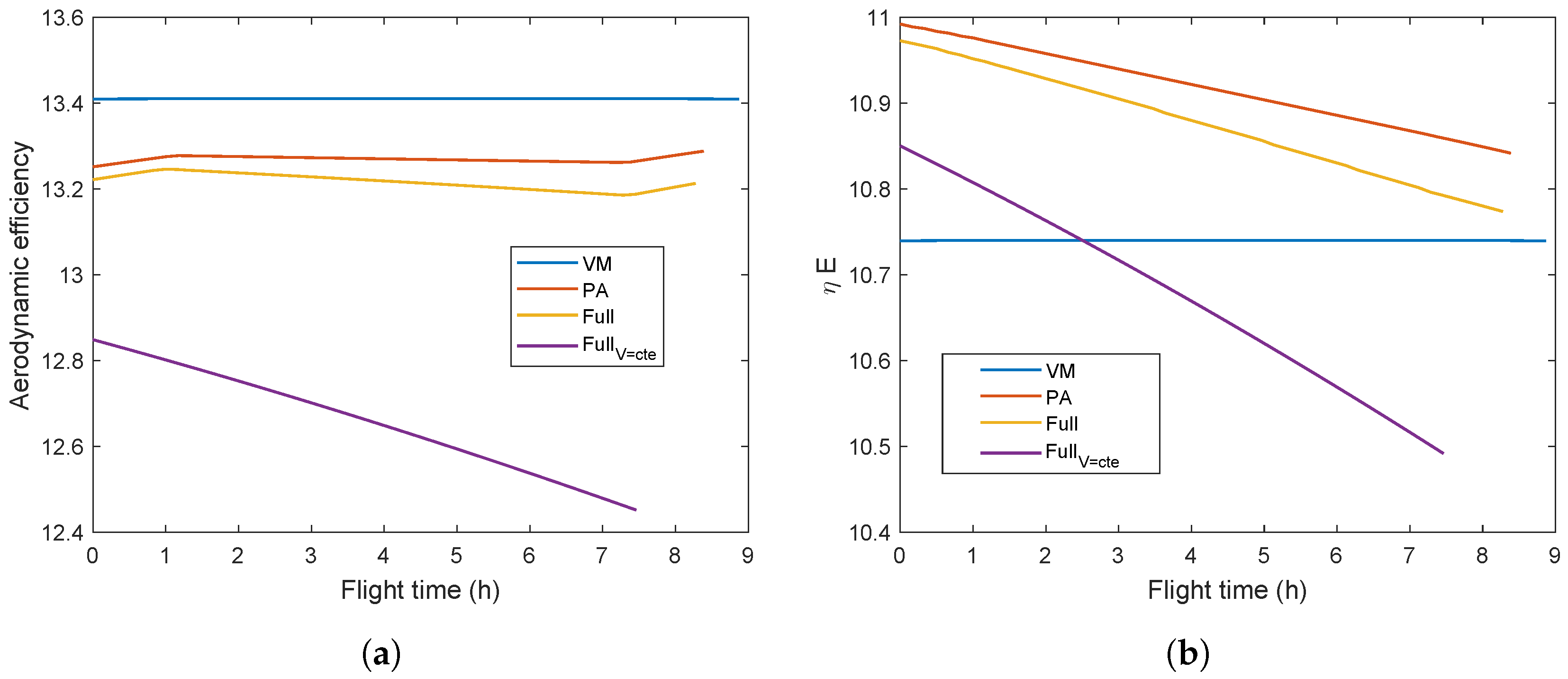
5.3.1. Results and Discussion
5.3.2. PA and Full Models Comparisons
5.3.3. Characteristics of Optimal Flights
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| V | velocity |
| m | mass |
| available power | |
| required power | |
| T | thrust |
| D | drag force |
| L | lift force |
| fuel flow rate | |
| g | gravitational acceleration |
| ISA | International Standard Atmosphere |
| air density | |
| S | reference area of the airplane |
| zero-lift drag coefficient | |
| K | induced drag coefficient |
| range | |
| initial time | |
| final time | |
| initial mass | |
| final mass | |
| mass of fuel | |
| mass of the aircraft fully equipped plus the payload (and the reserve fuel) | |
| propulsive efficiency | |
| P | shaft brake power |
| rotational speed of the propeller | |
| diameter of the propeller | |
| dimensionless thrust coefficient | |
| dimensionless power coefficient | |
| rpm | revolutions per minute |
| blade angle | |
| blade angle at 75% of the radial distance | |
| J | advance ratio |
| the throttle power parameter | |
| n | rotational speed of the engine |
| C | specific fuel consumption |
| maximum aerodynamic efficiency | |
| reference velocity | |
| reference available power | |
| reference thrust | |
| VM | Von Mises |
| PA | Parget and Ardema |
| N | number of subintervals |
| defects | |
| regularization term | |
| UAV | unmanned air vehicles |
References
- Miele, A. Flight Mechanics. Volume 1: Theory of Flight Paths; Addison-Wesley: Boston, MA, USA, 1962. [Google Scholar]
- Hale, F.J. Introduction to Aircraft Performance, Selection, and Design; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Anderson, J.D. Aircraft Performance and Design; WCB/McGraw-Hill: Boston, MA, USA, 1999; Volume 1. [Google Scholar]
- Bryson, A.E. Optimal control-1950 to 1985. IEEE Control Syst. Mag. 1996, 16, 26–33. [Google Scholar] [CrossRef]
- Saucier, A.; Maazoun, W.; Soumis, F. Optimal speed-profile determination for aircraft trajectories. Aerosp. Sci. Technol. 2017, 67, 327–342. [Google Scholar] [CrossRef]
- Hargraves, C.; Paris, S. Direct trajectory optimization using nonlinear programming and collocation. J. Guid. Control Dyn. 1987, 10, 338–342. [Google Scholar] [CrossRef]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528. [Google Scholar]
- Conway, B.A. A survey of methods available for the numerical optimization of continuous dynamic systems. J. Optim. Theory Appl. 2012, 152, 271–306. [Google Scholar] [CrossRef]
- Mai, T.; Mortari, D. Theory of functional connections applied to quadratic and nonlinear programming under equality constraints. J. Comput. Appl. Math. 2022, 406, 113912. [Google Scholar] [CrossRef]
- Leake, C.; Johnson, H.; Mortari, D. The Theory of Functional Connections: A Functional Interpolation Framework with Applications; Lulu Press, Inc.: Morrisville, NC, USA, 2022. [Google Scholar]
- Betts, J.T.; Cramer, E.J. Application of Direct Transcription to Commercial Aircraft Trajectory Optimization. J. Guid. Control Dyn. 1995, 18, 151–159. [Google Scholar] [CrossRef]
- González-Arribas, D.; Soler, M.; Sanjurjo-Rivo, M.; Kamgarpour, M.; Simarro, J. Robust aircraft trajectory planning under uncertain convective environments with optimal control and rapidly developing thunderstorms. Aerosp. Sci. Technol. 2019, 89, 445–459. [Google Scholar] [CrossRef]
- Menon, P.K.A. Study of aircraft cruise. J. Guid. Control Dyn. 1989, 12, 631–639. [Google Scholar] [CrossRef]
- Bell, D.J.; Jacobson, D.H. Singular Optimal Control Problems; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Pargett, D.M.; Ardema, M.D. Flight Path Optimization at Constant Altitude. J. Guid. Control Dyn. 2007, 30, 1197–1201. [Google Scholar] [CrossRef]
- Kelley, H.; Kopp, R.; Moyer, H.G. 3 singular extremals. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1967; Volume 31, pp. 63–101. [Google Scholar] [CrossRef]
- Rivas, D.; Valenzuela, A. Compressibility Effects on Maximum Range Cruise at Constant Altitude. J. Guid. Control Dyn. 2009, 32, 1654–1658. [Google Scholar] [CrossRef]
- Franco, A.; Rivas, D. Minimum-Cost Cruise at Constant Altitude of Commercial Aircraft Including Wind Effects. J. Guid. Control Dyn. 2011, 34, 1253–1260. [Google Scholar] [CrossRef]
- Ardema, M.D.; Asuncion, B.C. Flight path optimization at constant altitude. In Variational Analysis and Aerospace Engineering; Springer: New York, NY, USA, 2009; pp. 21–32. [Google Scholar] [CrossRef]
- Von Mises, R. Theory of Flight; McGraw-Hill: New York, NY, USA, 1945. [Google Scholar]
- Cavcar, M.; Cavcar, A. Optimum Range and Endurance of a Piston Propeller Aircraft with Cambered Wing. J. Aircr. 2005, 42, 212–217. [Google Scholar] [CrossRef]
- Lowry, J. Performance of Light Aircraft; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999. [Google Scholar]
- Tulapurkara, E.; Ananth, S.; Kulkarni, T.M. Performance Analysis of a Piston Engined Airplane-Piper Cherokee PA-28-180; Technical Report REPORT NO: AE TR 2007-1; Department of Aerospace Engineering, IIT Madras: Chennai, India, 2007. [Google Scholar]
- Donateo, T.; Totaro, R. Hybridization of training aircraft with real world flight profiles. Aircr. Eng. Aerosp. Technol. 2019, 91, 353–365. [Google Scholar] [CrossRef]
- Rostami, M.; Chung, J.; Neufeld, D. Vertical tail sizing of propeller-driven aircraft considering the asymmetric blade effect. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. SAGE Publ. 2021, 236, 1184–1195. [Google Scholar] [CrossRef]
- Bergmann, D.; Denzel, J.; Pfeifle, O.; Notter, S.; Fichter, W.; Strohmayer, A. In-flight Lift and Drag Estimation of an Unmanned Propeller-Driven Aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. SAGE Publ. 2021, 8, 43. [Google Scholar] [CrossRef]
- Bravo, G.; Praliyev, N.; Veress, Á. Performance analysis of hybrid electric and distributed propulsion system applied on a light aircraft. Energy 2021, 6, 1184–1195. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Zheng, X.; Xia, F.; Lin, D.; Jin, T.; Su, W.; He, S. Constrained Parameterized Differential Dynamic Programming for Waypoint-Trajectory Optimization. Aerospace 2024, 11, 420. [Google Scholar] [CrossRef]
- Li, R.; Yang, Z.; Yan, G.; Jian, L.; Li, G.; Li, Z. Robust Approximate Optimal Trajectory Tracking Control for Quadrotors. Aerospace 2024, 11, 149. [Google Scholar] [CrossRef]
- Ruijgrok, G. Elements of Airplane Performance; VSSD Pub: Delft, The Netherlands, 2009. [Google Scholar]
- Torenbeek, E. Synthesis of Subsonic Airplane Design; Springer: New York, NY, USA, 1982. [Google Scholar]
- Lycoming. Operator’s Manual: O-360, HO-360, IO-360, AIO-360, HIO-360 & TIO-360 Series; Technical Report; Lycoming: Williamsport, PA, USA, 2005. [Google Scholar]
- Piper Aircraft. A Brief History of Piper Aircraft; Piper Aircraft. 2022. Available online: https://www.piper.com/blog/piper-history/ (accessed on 18 September 2024).
- Corporation, P.A. Cherokee 180, PA-28-180. In Owner’s Handbook (761-513); Technical Report; Piper Aircraft Corporation: Vero Beach, FL, USA, 1973. [Google Scholar]
- Federal Aviation Administration. Type Certyficate Data Sheet No. 2A13; Technical Report; U.S. Department of Transportation: Washington, DC, USA, 2009.
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics; John Wiley and Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Abbott, I.H.; Von Doenhoff, A.E.; Stivers, L., Jr. Summary of Airfoil Data; Technical Report NACA Report 824; NASA Technical Reports Server; The National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1945.
- Cavcar, M. Bréguet Range Equation? J. Aircr. 2006, 43, 1542–1544. [Google Scholar] [CrossRef]
- Schwartz, A.L. Theory and Implementation of Numerical Methods Based on Runge-Kutta Integration for Solving Optimal Control Problems; University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Jacobson, D.; Gershwin, S.; Lele, M. Computation of optimal singular controls. IEEE Trans. Autom. Control 1970, 15, 67–73. [Google Scholar] [CrossRef]
- Pager, E.R.; Rao, A.V. Method for solving bang-bang and singular optimal control problems using adaptive Radau collocation. Comput. Optim. Appl. 2022, 81, 857–887. [Google Scholar] [CrossRef]
- Dadebo, S.; McAuley, K.; McLellan, P. On the computation of optimal singular and bang–bang controls. Optim. Control Appl. Methods 1998, 19, 287–297. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A.; Wong, E. User’s guide for SQOPT Version 7.7: Software for large-scale linear and quadratic programming. In Center for Computational Mathematics Report CCoM 19-01; University of California: San Diego, CA, USA, 2019. [Google Scholar]
- Silva, C.; Trelat, E. Smooth Regularization of Bang-Bang Optimal Control Problems. IEEE Trans. Autom. Control 2010, 55, 2488–2499. [Google Scholar] [CrossRef]
- Zelikin, M.I.; Borisov, V. Theory of Chattering Control; Birkhäuser: Boston, MA, USA, 1994. [Google Scholar] [CrossRef]
- Lavezzi, G.; Guye, K.; Cichella, V.; Ciarcià, M. Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning. Drones 2023, 7, 487. [Google Scholar] [CrossRef]
- Boucher, O.; Bellouin, N.; Clark, H.; Gryspeerdt, E.; Karadayi, J. Comparison of Actual and Time-Optimized Flight Trajectories in the Context of the In-Service Aircraft for a Global Observing System (IAGOS) Programme. Aerospace 2023, 10, 744. [Google Scholar] [CrossRef]

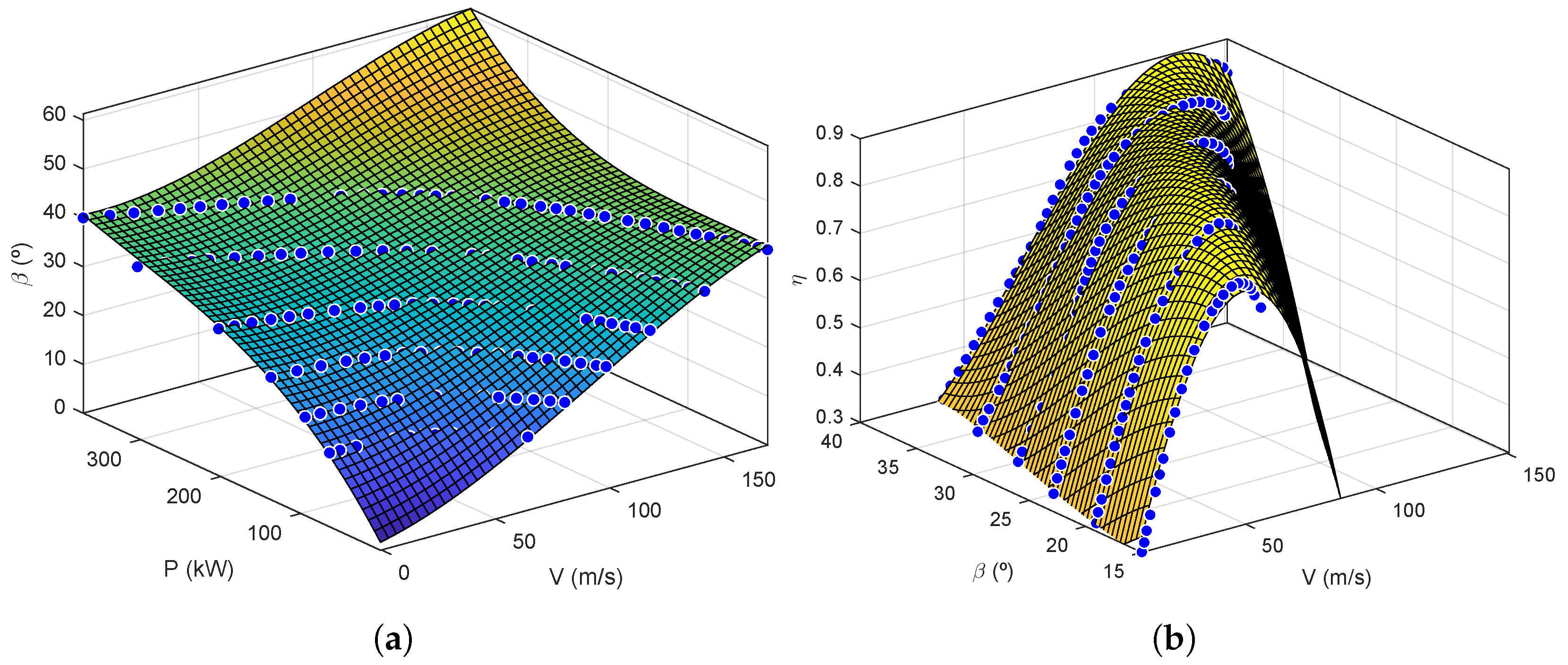
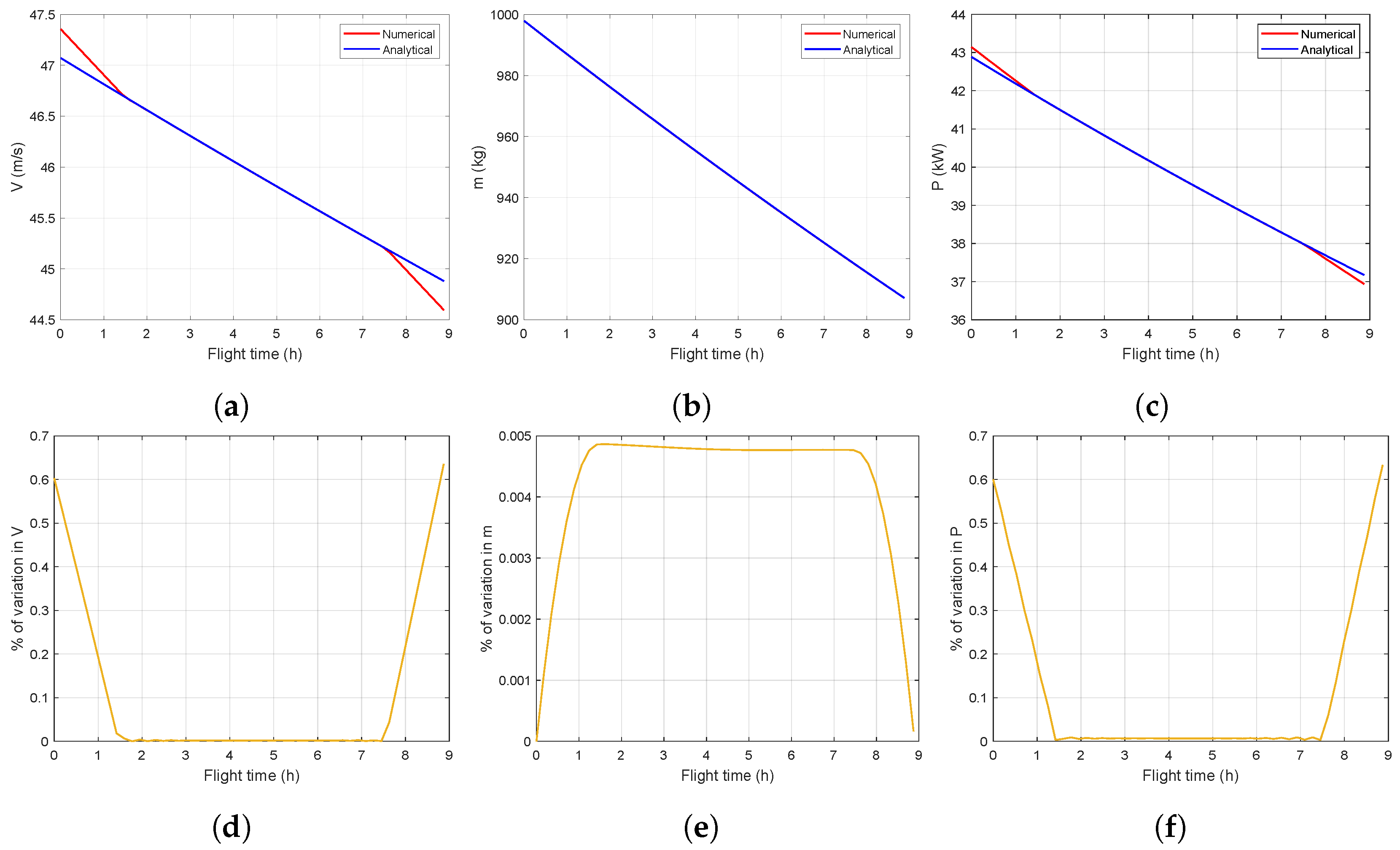


| Parameter | Value | Unit | Group |
|---|---|---|---|
| h | 2133.60 | m | M (equivalent to 7000 ft) |
| 0.9930 | kg/m3 | M (derived at ISA conditions) | |
| 90.72 | kg | M ([37,38]) | |
| 2400 | rpm | M ([37,38]) | |
| 102.25 | kW | AP (estimated from [35] at given h) | |
| S | 15.79 | m2 | AP ([37,38]) |
| 907.18 | kg | AP ([37,38]) | |
| 1.88 | m | AP ([39]) | |
| 69.43 | m/s | AP ([37,38]) | |
| 33.75 | m/s | AP ([37,38]) | |
| 0.021 | – | AP (estimated from [37,38,40]) | |
| K | 0.0662 | – | AP (estimated from [37,38,40]) |
| A | 0.1646 | kg/m | M & AP (computed from Equation (3)) |
| B | 0.0084 | m/kg | M & AP (computed from Equation (3)) |
| Case | Type | Speed | Power | Range | Time | Aer. Effic. | Prop. Effic. |
|---|---|---|---|---|---|---|---|
| (m/s) | (kW) | (km) | (h) | (adim) | (adim) | ||
| Von Mises | M, O | 44.60–47.36 | 36.94–43.14 | 1467.91 (−1.5%) | 8.87 (+7.1%) | 13.41–13.41 | 0.8009–0.8009 |
| PA | M, O | 48.03–50.86 | 39.40–45.26 | 1492.34 (+0.1%) | 8.39 (+1.3%) | 13.25–13.29 | 0.8159–0.8295 |
| Full | M, O | 48.93–51.21 | 40.39–45.66 | 1491.52 | 8.28 | 13.21–13.22 | 0.8154–0.8299 |
| FullV=cte | P, NO | 54.54 | 46.25–49.19 | 1464.82 (−1.8%) | 7.46 (−9.9%) | 12.45–12.85 | 0.8426–0.8445 |
| Full | PA | Von Mises | Breguet | FullV=cte | |
|---|---|---|---|---|---|
| Accuracy | Very high | High | Moderate | Moderate | High |
| Optimal flight | Complete | Differences <5% | Differences <10% | Differences <10% | Differences of about 10% |
| Evolution of the variables | Most realistic scenario | Very similar results | Similar trends | Similar trends | Different behavior, specific of the program non-optimal flight |
| Efficiency | Computation of several seconds | Computation of several seconds | Computation of few seconds | Computation almost instantaneous (analytical solution) | Computation of few seconds |
| Propulsive system | Data to build the model | Data to build the model | Estimating constant values | Estimating constant values | Data to build the model |
| Application | Precise analysis considering all the dependences | Provides good physical insight | Initial estimations | Initial estimations | Trade-off between range and flight time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, A.; Rubio, C.; Domínguez, D.; Escapa, A. Cruise Range Optimization of a Propeller-Driven Light Aircraft Using a Direct Transcription Method with a Regularization Term. Aerospace 2024, 11, 794. https://doi.org/10.3390/aerospace11100794
Delgado A, Rubio C, Domínguez D, Escapa A. Cruise Range Optimization of a Propeller-Driven Light Aircraft Using a Direct Transcription Method with a Regularization Term. Aerospace. 2024; 11(10):794. https://doi.org/10.3390/aerospace11100794
Chicago/Turabian StyleDelgado, Adrián, Carlos Rubio, Diego Domínguez, and Alberto Escapa. 2024. "Cruise Range Optimization of a Propeller-Driven Light Aircraft Using a Direct Transcription Method with a Regularization Term" Aerospace 11, no. 10: 794. https://doi.org/10.3390/aerospace11100794
APA StyleDelgado, A., Rubio, C., Domínguez, D., & Escapa, A. (2024). Cruise Range Optimization of a Propeller-Driven Light Aircraft Using a Direct Transcription Method with a Regularization Term. Aerospace, 11(10), 794. https://doi.org/10.3390/aerospace11100794






