A Review of Multi-Satellite Imaging Mission Planning Based on Surrogate Model Expensive Multi-Objective Evolutionary Algorithms: The Latest Developments and Future Trends

Abstract

Multi-satellite imaging mission planning (MSIMP) is an important focus in the field of satellite application. MSIMP involves a variety of coupled constraints and optimization objectives, which often require extensive simulation and evaluation when solving, leading to high computational costs and slow response times for traditional algorithms. Surrogate model expensive multi-objective evolutionary algorithms (SM-EMOEAs), which are computationally efficient and converge quickly, are effective methods for the solution of MSIMP. However, the recent advances in this field have not been comprehensively summarized; therefore, this work provides a comprehensive overview of this subject. Firstly, the basic classification of MSIMP and its different fields of application are introduced, and the constraints of MSIMP are comprehensively analyzed. Secondly, the MSIMP problem is described to clarify the application scenarios of traditional optimization algorithms in MSIMP and their properties. Thirdly, the process of MSIMP and the classical expensive multi-objective evolutionary algorithms are reviewed to explore the surrogate model and the expensive multi-objective evolutionary algorithms based on MSIMP. Fourthly, improved SM-EMOEAs for MSIMP are analyzed in depth in terms of improved surrogate models, adaptive strategies, and diversity maintenance and quality assessment of the solutions. Finally, SM-EMOEAs and SM-EMOEA-based MSIMP are analyzed in terms of the existing literature, and future trends and directions are summarized.

1. Introduction

Satellite imaging mission planning (SIMP) refers to the appropriate scheduling of a single satellite to effectively complete an Earth observation mission. During the planning process, it is necessary to not only consider the coverage of satellites for multiple observation targets but also address the potential failure or delay of the observation mission. The efficiency and reliability of the entire mission could potentially be impacted by unforeseen circumstances, such as malfunctions in individual satellite equipment [1,2]. In contrast, multi-satellite imaging mission planning (MSIMP) can achieve the efficient and coordinated execution of Earth observation missions through rational scheduling and optimal allocation of multiple satellite resources (including multiple satellites with different orbits, imaging capabilities, and observational coverage), thus improving imaging coverage and accuracy. By reducing repeated observations and optimizing the time window of the imaging mission, MSIMP can effectively shorten the observation time required for the whole mission, avoid unnecessary resource occupation and waste, and further enhance the flexibility and response speed of the system when facing dynamic tasks. Thus far, MSIMP has been widely used in many fields, such as environmental monitoring, agricultural management, urban planning, and so on, and has become a focal area of research [3,4].

However, the MSIMP based on traditional optimization algorithms faces additional challenges stemming from three main factors: the continuous increase in the number of satellites in orbit, the explosive growth in the demand for observation targets, and the numerous uncertainties encountered by satellites during mission execution. Specifically, MSIMP involves a variety of coupled constraints and optimization objectives, such as visible time windows, satellite energy limitations, remote sensor tuning time, and so on, as well as maximizing the imaging coverage while minimizing the imaging time [5,6]. This means that determining the optimal MSIMP approach requires a high-dimensional and complex solution space. Simultaneously, the MSIMP solution usually requires extensive simulations and evaluations to determine the optimal path, imaging time, and mission assignment scheme for each satellite. However, each evaluation is computationally expensive, which not only reduces the responsiveness of the satellite planning system but also increases the delay rate of the planning system [7]. Therefore, there is an urgent need to find a method that reduces the solution space and drastically reduces the number of actual evaluations to improve the overall efficiency of the system.

The proposed surrogate model expensive multi-objective evolutionary algorithms (SM-EMOEAs) provide an effective approach to overcome the above challenges. First, the SM-EMOEAs exploit the natural selection and genetic mechanisms of evolutionary algorithms to continuously explore and optimize the solution space, aiming to find the Pareto optimal solution set that can satisfy multiple optimization objectives simultaneously. Second, the SM-EMOEAs use surrogate models to approximate the objective function and reduce the direct assessment of the objective function. In this case, the surrogate model is also well suited to addressing the impacts of dynamic factors on MSIMP, and can better predict and respond to changes in the planning environment through the collection of and training on historical and current data [8,9,10,11,12]. These advantages make SM-EMOEAs a key approach to the MSIMP challenge. To date, to the best of our knowledge, no researchers have systematically summarized this subject. Therefore, this work focuses on the application of surrogate model expensive multi-objective evolutionary algorithms based on the MSIMP problem. The main contributions are as follows.

• MSIMP is classified in detail from the dimensions of time, space, and task planning and management; in addition, the specific applications of MSIMP in the four phases of pre-processing, task planning, execution, and feedback replanning, considering the related disciplines and various application areas, are introduced in detail. A specific example of forest fire monitoring is used for concrete description. Then, research on MSIMP based on SM-EMOEAs is analyzed in terms of both MSIMP modeling and optimization algorithms.
• The mathematical model of MSIMP is introduced from four aspects: the target mission set, satellite resource set, time window set, and evaluation set. In addition, the currently most commonly used traditional optimization algorithms are classified into two categories—deterministic algorithms and heuristic algorithms—to provide a detailed overview of the traditional optimization algorithms based on MSIMP. We also discuss the strengths and weaknesses of traditional optimization algorithms in solving the MSIMP problem.
• A detailed overview of the classical expensive multi-objective evolutionary algorithms (EMOEAs) and a discussion of the process of EMOEA-based MSIMP are provided. We summarize the main ideas, advantages, and disadvantages of the most commonly used surrogate models from three categories: statistical models, function approximation models, and machine learning models. Then, the surrogate model is selected according to the actual situation in the MSIMP problem, and the EMOEA framework based on the surrogate model is further explored.
• The improved SM-EMOEAs for MSIMP are discussed in terms of surrogate model improvement, adaptive strategy improvement, and the diversity maintenance and quality assessment of the solutions. The improvements provided by four types of surrogate models—namely, the global surrogate model, local surrogate model, bi-layer surrogate model, and aggregation model—are summarized. Then, the improved adaptive strategies, such as the adaptive sampling strategy, multi-group co-evolutionary strategy, and domain knowledge strategy, are further summarized. Finally, the solution diversity maintenance methods and solution quality assessment are discussed.

The remainder of this paper is organized as follows. Section 2 introduces the basics of MSIMP and analyzes the MSIMP constraints. Section 3 describes the MSIMP problem and introduces MSIMP based on traditional optimization algorithms. Section 4 presents the flowcharts of the expensive multi-objective evolutionary algorithms based on MSIMP and the surrogate model used to assist the EMOEAs, and explores the expensive multi-objective evolutionary algorithms based on the surrogate model. Section 5 describes the MSIMP method based on the improved SM-EMOEAs in detail, in terms of the improved surrogate model, the improved adaptive strategy, and the diversity maintenance and quality assessment of the solutions. Section 6 discusses the SM-EMOEAs and SM-EMOEA-based MSIMP literature and concludes this work by providing future research directions.

2. Related Work

In this section, the basic classification of MSIMP is first introduced, followed by the applications of MSIMP in different fields. Finally, the constraints of MSIMP are analyzed.

2.1. Basic Classification of MSIMP

MSIMP can be classified into multi-satellite static mission planning and dynamic mission planning according to the mode of operation. MSIMP aims to obtain the optimal planning scheme that meets the satellite resource constraints and mission constraints through an optimization algorithm before mission planning is executed [13]. Multi-satellite static mission planning has poor anti-interference abilities and is not able to address emergency mission requirements and unexpected operating environments. Comparatively speaking, multi-satellite dynamic mission planning can be adjusted according to real-time environment changes and the mission requirements, providing a timely response and dynamic adjustment to the target mission [14]. Multi-satellite dynamic mission planning is more adaptable to complex mission environments and real-time changing requirements, thus enhancing the flexibility of MSIMP mission execution.

MSIMP can be divided into area coverage task planning, target identification task planning, and event task planning, according to the spatial dimension. Area coverage task planning focuses on covering a specific geographical area and is suitable for application scenarios such as land resource assessment and environmental monitoring [15]. Target identification task planning focuses on locating specific targets within a broad coverage area and is particularly suited for detecting targets at various spatial locations with high precision [16]. Event task planning, on the other hand, prioritizes the allocation of resources to observe the region when an anomaly occurs [17]. This classification method helps to clarify the core requirements of different tasks and optimize the imaging strategy and resource allocation, thus enhancing the overall efficiency of MSIMP.

MSIMP can also be divided into centralized mission planning, distributed mission planning, and autonomous mission planning, according to the decision-making method. Centralized mission planning consists of a central node that manages all mission information and satellite resources in a unified manner, and a ground control center maximizes the coordination of each satellite mission based on global information [18]. Distributed mission planning employs a decentralized management strategy, distributing mission and satellite resource data across multiple nodes. These nodes share information and coordinate tasks through communication and collaboration, offering enhanced flexibility and fault tolerance [19]. Autonomous mission planning integrates the advantages and disadvantages of centralized and distributed mission planning and empowers satellites with autonomous planning capabilities, where each satellite reasonably evaluates its own resources and mission requirements, with high autonomy and real-time responsiveness [20]. This classification method helps to systematically investigate different planning methods for multi-satellite imaging missions to better meet the needs of different application scenarios and improve the autonomy of MSIMP mission execution.

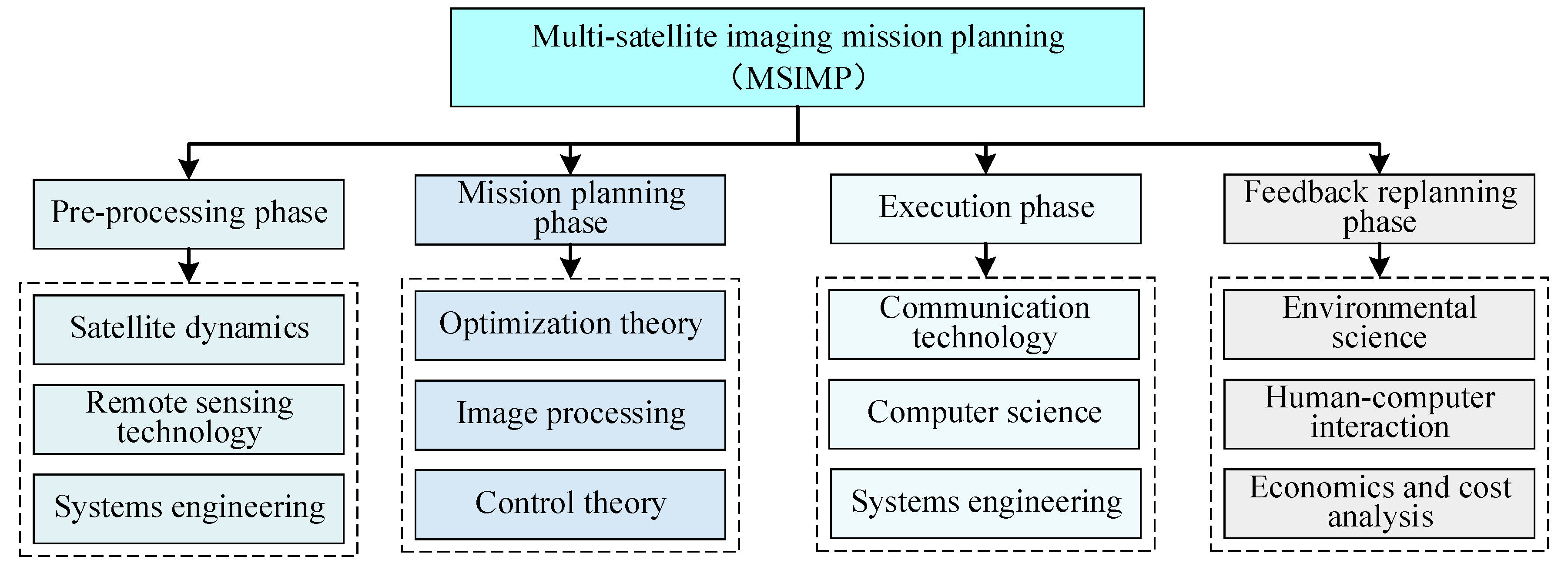
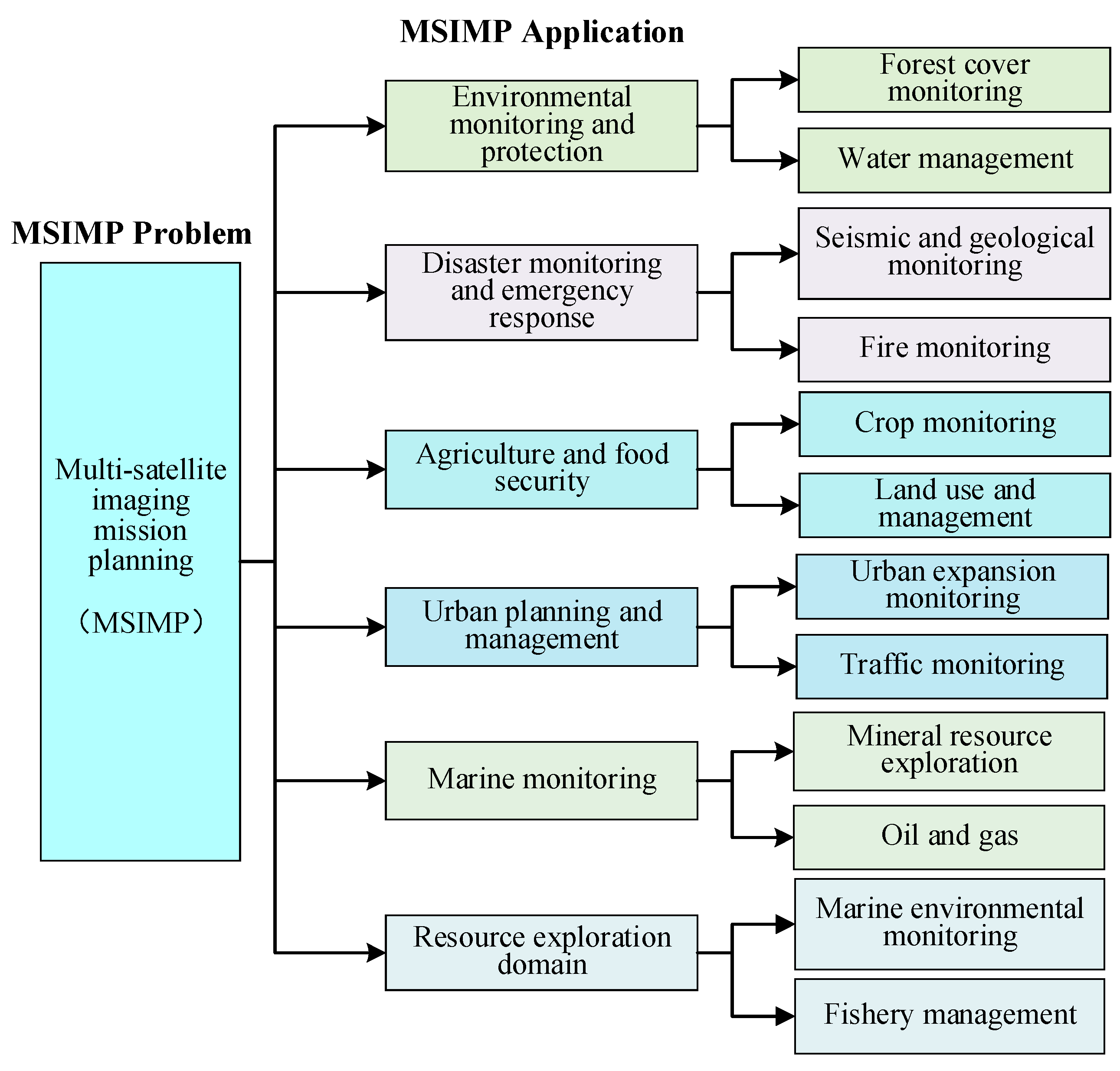
2.2. MSIMP Applications in Different Areas

MSIMP involves multiple areas of expertise. Figure 1 describes the relevant knowledge involved in MSIMP according to the pre-processing phase, mission planning phase, execution phase, and feedback replanning phase. Figure 2 describes the MSIMP application in various fields in detail.

• The pre-processing phase involves satellite dynamics, remote sensing technology, and systems engineering, which are the key areas of knowledge required to provide basic support for the calculation of the initial satellite orbit parameters, the performance of satellite imaging to meet the mission resolution requirements, and the development of the MSIMP system architecture. Knowledge of satellite dynamics ensures the position and attitude control of the satellites during mission execution by accurately calculating their orbital parameters. Remote sensing technology is not only used to ensure that the imaging equipment meets the resolution requirements of a specific mission but also includes the enhancement of geo-positioning accuracy, data acquisition speed, and environmental adaptability to ensure reliable performance under different observation conditions. System engineering comprehensively considers the architectural design and realization of the whole MSIMP process, ensuring the coordinated and efficient operation of the subsystems [21].
• The mission planning phase involves optimization theory, image processing, and control theory. Optimization theory determines the satellite’s imaging mission sequence, which refers to the prioritized order of observation tasks, and the time window, defined as the period during which the satellite can perform a specific imaging task. Various optimization algorithms are used to maximize mission efficiency and resource utilization by optimally scheduling both factors. Image-processing techniques are employed to analyze and process surface observation images captured by satellites during mission execution. These techniques assist in determining the optimal imaging paths and target areas by identifying key regions, analyzing geographic features, and evaluating environmental factors. The goal is to detect spatial distributions, boundaries, and changes in target characteristics, enabling the optimization of satellite flight paths to maximize coverage of the mission area [22].
• The execution phase involves communication technology, computer science, and systems engineering. Communication technology is used to ensure coordinated communication between multiple satellites for the efficient transmission and sharing of data and instructions. Computer science enables the real-time processing, analysis, and storage of imaging data to ensure data availability. Systems engineering is responsible for coordinating the stable operation of the subsystems within the MSIMP system, ensuring the seamless and efficient operation of the different stages of the mission execution process [23].
• The feedback replanning phase involves environmental science, human–computer interaction, and economics and cost analysis. Environmental science techniques are employed to monitor real-time environmental conditions, such as weather changes and light intensity, providing crucial data to the MSIMP. Based on these real-time data, MSIMP dynamically adjusts the satellite observation plan or flight path to mitigate the impact of environmental factors, ensuring that the mission is completed on time and achieves the desired outcomes. Using environmental data, multiple satellites can also adjust parameters such as imaging angle and resolution, optimizing both image quality and overall mission effectiveness. The human–computer interaction system helps the satellite controllers to intuitively and easily make adjustments to the target mission and improve decision making efficiency and accuracy. In addition, economics and cost analysis optimize satellite resource allocation through weighing the costs and benefits of mission replanning to ensure the maximum mission benefits and resource utilization under the premise of controllable costs [24].

MSIMP has a wide range of application areas. In the field of environmental monitoring and protection, MSIMP is applied to monitor forest cover and track water resources like lakes and rivers [25]. In disaster monitoring and emergency response, MSIMP is used to track geological disasters like earthquakes and mudslides and to provide prompt early warnings and assessments of forest and urban fires [26]. In the field of agriculture and food security, MSIMP is used to monitor crop growth and land use [27]. In the field of urban planning and management, MSIMP is often used as a tool to control the urban traffic flow [28]. In the field of resource exploration, the superior imaging technology of MSIMP is used to monitor the distribution of surface minerals [29]. This section describes the execution process of MSIMP using forest fire monitoring as a concrete instance, as shown in Figure 3.

In the pre-processing phase, suitable orbital parameters are designed through satellite dynamics to ensure comprehensive coverage of the global forest area. Remote sensing technology is used to select and calibrate high-resolution satellite imaging sensors, while system engineering is responsible for defining the mission requirements and developing the system architecture to ensure the orderly integration of all aspects of the mission. In the mission planning stage, optimization algorithms prioritize satellite observation areas based on fire risk assessment data, allocating satellite resources to high-risk regions to focus on monitoring potential fire hotspots. Image-processing technology is then used to plan the satellite’s imaging path, ensuring the spatial continuity and temporal consistency of the data. Additionally, control theory is applied to design and optimize the satellite’s trajectory, ensuring accurate tracking of the designated imaging path. In addition, the MSIMP system has reserved a spare fault-tolerant window to cope with system failures, mission delays, or other unforeseen events beyond the time period between the satellite and the ground target that satisfies, for example, the resolution, sunlight, etc., so as to ensure that the mission can be carried out smoothly. Entering the executive phase, the satellite monitors the forest area in real time as planned, and once the sensors detect fire smoke, the observation data will be rapidly transmitted via communication technology to the ground station, which uses image-processing technology to quickly identify the fire area and notify the emergency response authorities of the information. According to the development of the fire, the system dynamically adjusts the imaging mission and trajectory to ensure continuous monitoring and assessment. In the feedback replanning phase, the MSIMP system dynamically adjusts to the actual monitored fire data, replans the imaging mission and satellite trajectory to ensure that the system can flexibly respond to changes in the environment, updates the observation mission in real time, and maintains long-term monitoring of fires to ensure that the mission can be successfully completed and provide continuous data support for emergency response. Through collaborative work at all stages, the MSIMP system detects fires in a timely manner, assesses impacts, and provides critical data support for emergency response in forest fire monitoring [30].

2.3. Limitations of MSIMP

MSIMP is affected by a variety of constraints, such as the complexity of orbit design, the diversity of multi-star and multi-mission requirements, the dynamics of environmental changes, and the complexity of high-dimensional data processing. These create multiple challenges for MSIMP modeling.

2.3.1. Complexity of Mathematical Models

The complexity of MSIMP modeling stems from the collaboration between satellites, the precise description of the imaging process, and the highly dynamic and multivariate execution environment. First, the MSIMP model needs to consider the motion states and imaging capabilities of multiple satellites working together. The model must ensure that satellites operate without interference and cooperate seamlessly in complex tasks, while the need for the real-time communication and synchronization of motion states and imaging capabilities poses significant challenges for the MSIMP model [31]. Second, the precise description of the satellite imaging process further exacerbates the difficulty of modeling, as the satellite’s moment-to-moment position, the velocity and geometrical changes of the orbit, the satellite sensor’s field-of-view angle, the satellite’s fuel consumption, attitude adjustments, and many other factors require the model to have an extremely high level of mathematical descriptive capabilities [32]. Finally, the satellite in-orbit operation process is affected by a variety of uncertainties, such as the weather conditions and changes in the observation requirements of the imaging satellites. This requires the MSIMP model to have the ability to make real-time adjustments and optimizations to the scheme in order to ensure the efficient and continuous execution of MSIMP [33].

2.3.2. Limitations of Optimization Algorithms

The limitations of MSIMP’s optimization algorithms are mainly related to the dramatic growth of the computational dimensions, the inherent conflict in multi-objective optimization, and the real-time adaptability to dynamic environments. These limitations mean that MSIMP consumes a large amount of time and computational resources [34]. Specifically, MSIMP involves the multi-satellite, multi-mission, and real-time computation of the satellites’ orbital parameters and attitude, which requires extensive simulation and evaluation of the optimal MSIMP methodology to determine the optimal paths, imaging times, and mission assignment schemes for each satellite. In addition, MSIMP needs to simultaneously optimize multiple mutually constraining objective functions, such as the task revenue, response time, area coverage, and so on, making it challenging to achieve global and local optimization trade-offs [35]. Finally, the rapid changes in the space environment and ground targets require the optimal MSIMP algorithms to have fast and dynamic response capabilities and the ability to adjust the planning strategy in real time to ensure the continuous execution and effectiveness of the task. However, traditional optimization algorithms suffer from response delays and computational inefficiency when dealing with such problems [36]. These limitations indicate that there is an urgent need for optimization algorithms that can effectively cope with the high-dimensional complexity, multi-objective conflicts, dynamic changes, and high-cost evaluations of MSIMP in practical applications.

3. Description of MSIMP

This section first describes the MSIMP problem, detailing the mathematical model of MSMIP and its constraints. Then, the traditional algorithms currently used for the MSIMP problem are summarized.

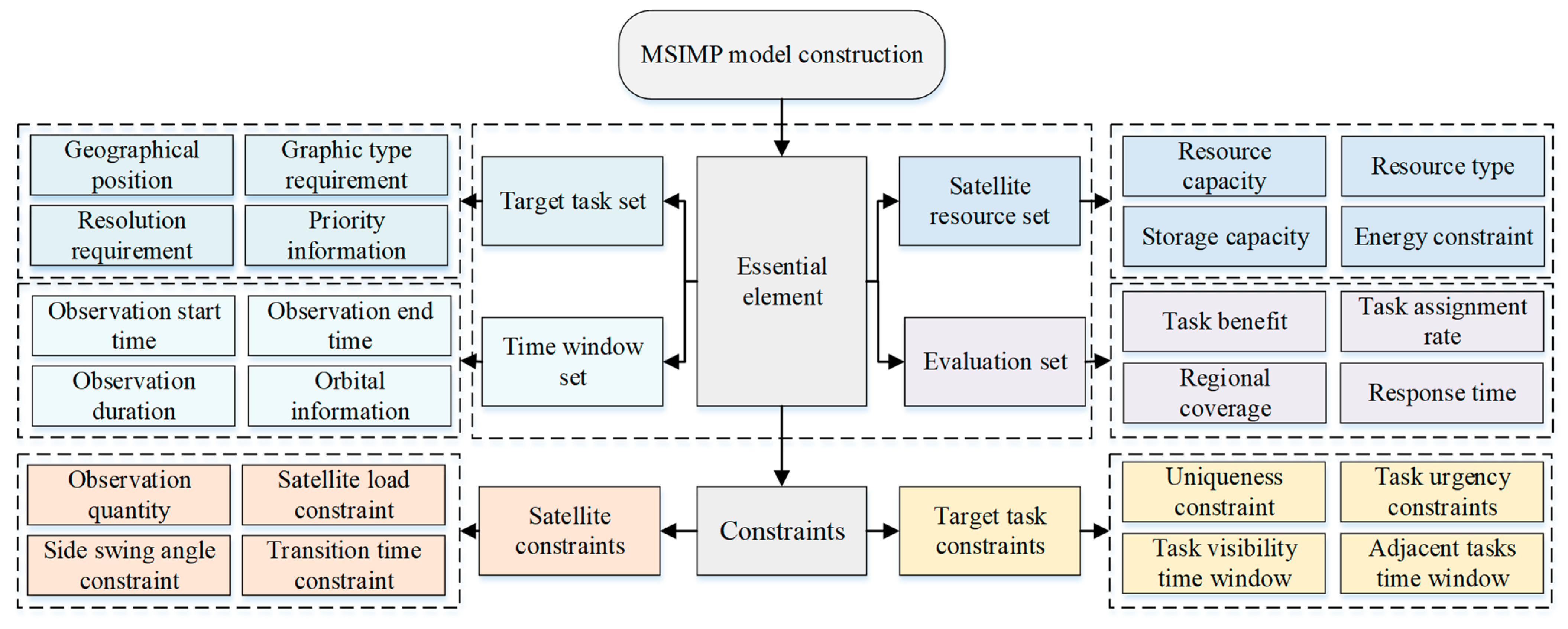
3.1. MSIMP Mathematical Modeling

MSIMP defines the optimal allocation sequences and visible time window allocation schemes between multiple satellites and the target mission using precise mathematical descriptions. MSIMP models often adopt objective functions and constraints to satisfy the user’s mission requirements, as well as multiple environmental requirements [36]. The objective function may involve maximizing the mission benefits, maximizing the mission allocation rate, minimizing resource consumption, minimizing the response time, and so on. The considered constraints include environmental factors, mission conflicts, imaging visible time windows, fuel consumption, and so on [37]. Common MSIMP models include integer planning models [38], constraint satisfaction models [39], dynamic planning models [40], Markov decision models [41], and so on. Figure 4 shows the main factors affecting the MSIMP model, including the target mission set, the satellite resource set, the time window set, and the evaluation set. Figure 4 is a schematic diagram describing the key factors affecting the MSIMP model and the related constraints. The main factors include the target task set, satellite resource set, time window set, and evaluation set, while the constraints involve satellite limitations and target task restrictions. The specific details are as follows:

The target task set is critical in MSIMP modeling, representing a collection of imaging or observation tasks to be carried out by multiple satellites. These tasks typically involve precise imaging of ground areas or objects. The target task set includes several key attributes, such as the geographic location of the tasks, image requirements, image resolution, and priority information. These attributes directly influence the imaging location, sensor type, and image resolution settings for the satellites. Priority information is used to distinguish the importance and urgency of the tasks, helping to determine the order in which tasks should be executed. These task attributes not only define the complexity and demands of the mission but also impose strict constraints on the optimal scheduling of satellite resources, ensuring that imaging tasks are completed with maximum quality and efficiency within the limits of available satellite resources [42,43].

The satellite resource set is a crucial element in MSIMP modeling and solution, representing the collection of satellites and all their available resources used to carry out tasks. This set plays a decisive role in the formulation and execution of the MSIMP plan. Key components of the satellite resource set include resource capacity, resource types, storage capabilities, and energy constraints. Resource capacity and energy constraints determine the number of tasks that each satellite can perform and the duration of its operation. Resource types ensure that the satellites can meet the diverse needs of different target tasks, while storage capacity directly impacts the efficiency of data storage and transmission during missions. By optimally allocating the satellite resource set, satellite controllers can maximize resource utilization under limited conditions, improving the success rate and efficiency of mission planning and execution [44,45].

The time window set is a critical component of MSIMP, referring to the collection of time periods during which satellites can image ground targets. These windows are determined by the start time, end time, and duration of target task observations, along with satellite orbital information. Additionally, precise calculation of time windows must consider factors such as sunlight conditions and weather in the target area to ensure imaging quality and the successful execution of the mission. By effectively scheduling time windows, satellite resources can be maximized, resource waste minimized, and the overall success rate of mission planning improved [46,47].

The evaluation set is a key component in MSIMP for assessing the quality of mission planning schemes. It establishes a series of evaluation metrics to measure the effectiveness of mission execution, providing a comprehensive assessment of the feasibility and stability of the MSIMP model. Key metrics include task benefit, task allocation rate, area coverage, and response time. Task benefit evaluates the value and effectiveness of each mission, while task allocation rate reflects the rationality and balance in the distribution of satellite resources across tasks. Area coverage assesses the completeness and accuracy of imaging over the target area, and response time measures the efficiency from the submission of task requests to the completion of the mission. These evaluation indicators assist in optimizing the mission planning scheme, ensuring efficient resource utilization while meeting user requirements [48,49,50,51].

The constraints in MSIMP are divided into two categories: satellite constraints and target task constraints. Satellite constraints include limits on observation quantity, payload capacity, side swing angle, and transition time, ensuring the stability of satellite operations and the efficiency of mission execution. Target task constraints involve uniqueness, task urgency, visible time window, and adjacent task time window constraints, ensuring a reasonable prioritization and sequence of task execution. These constraints guarantee the operability and rationality of the satellite mission planning process, enabling the effective implementation of multi-satellite imaging mission plans in complex real-world environments.

3.2. MSIMP Based on Traditional Optimization Algorithms

MSIMP based on traditional optimization algorithms is mainly used to solve problems such as maximizing the task benefit, maximizing the task assignment rate, and minimizing the response time. The traditional optimization algorithms commonly used at present can be divided into two categories: deterministic algorithms and heuristic algorithms. Deterministic algorithms mainly include linear programming [52], integer programming [53], mixed integer programming [54], dynamic programming [55], the branch and bound method [56], and the column generation method [57]. Heuristic algorithms mainly include the simulated annealing algorithm [58], genetic algorithm [59], particle swarm algorithm [60], ant colony algorithm [61], forbidden search [62], and differential evolutionary algorithm [63]. The application scenarios for each algorithm are specifically detailed in

Table 1. Applications of MSIMP based on traditional optimization algorithms.

Algorithm Type	Algorithm	Computation Costs /Response Time	Application Scenario/Algorithm Feature
Deterministic algorithm	Linear programming (LP)	Low/Fast	It solves optimization problems under linear constraints, such as maximizing imaging coverage and minimizing imaging time.
	Integer programming (IP)	Moderate/Moderate	It solves task allocation problems that require integer solutions and ensures the rationality of task and resource allocation.
	Mixed integer programming (MIP)	High/Slow	It is used to solve complex programming problems with both continuous and discrete variables.
	Dynamic programming (DP)	High/Slow	It is used for phased decision problems to ensure that the optimal decision at each stage can find the global optimal solution.
	Branch and bound (B&B)	High/Moderate	It is used for integer and combinatorial optimization problems to find the optimal solution by systematically dividing search space.
	Column generation (CG)	Moderate/Fast	It is used for large-scale integer programming and mixed integer programming, optimized by decomposing the problem and gradually generating solution columns.
Heuristic algorithm	Simulated annealing algorithm (SA)	Moderate/Moderate	It solves global optimization in search space and achieves optimization from global to local by gradually reducing randomness.
	Genetic algorithm (GA)	High/Slow	It is used to search for the approximate optimal solution in the large-scale space for global search by simulating natural selection genetic variation.
	Particle swarm optimization (PSO)	Moderate/Fast	It is used for optimization in continuous search space to search for optimal solutions through group behavior simulation.
	Ant colony algorithm (ACO)	High/Moderate	It is used in discrete optimization problems to find the optimal task assignment method by simulating ant foraging behavior.
	Tabu search (TS)	Moderate/Moderate	It is used for global optimization to avoid falling into local optimality by recording and prohibiting certain solutions.
	Differential evolution algorithm (DE)	Moderate/Fast	It is used for global optimization, and the optimal solution is found through the difference and recombination between individuals suitable for continuous optimization problems.

.

The above traditional optimization algorithms have many advantages, such as strong global search capabilities, the wide coverage area of the solution space, and so on, and can effectively deal with a variety of optimization objective functions and constraints. From the perspective of the objective task requirements, LP, IP, and MIP are suitable for solving optimal MSIMP problems with linear and discrete objective tasks; CG, SA, GA, PSO, and ACO are suitable for solving optimal MSIMP problems with large-scale objective tasks; and DP, B&B, TS, and DE are suitable for optimal MSIMP problems with complex temporal and integer constraints. In terms of the convergence speed of the optimization algorithms used to solve the MSIMP model and the quality of the mission planning scheme, LP, IP, MIP, DP, B&B, and DE converge faster and are able to solve higher-quality MSIMP schemes, while SA, GA, PSO, ACO, CG, and TS converge slower but are able to solve MSIMP schemes in complex situations.

However, there are some limitations in solving MSIMP based on traditional optimization algorithms. SA, GA, PSO, ACO, TS, and other methods need to adjust the algorithmic parameters during the optimization search process and present high computational complexity when dealing with large-scale and complex problems, especially complex multi-peak optimization problems; thus, they can easily fall into local optimal solutions. In addition, algorithms such as LP, IP, MIP, B&B, CG, and DP fail to adapt to changes in dynamic environments, making it difficult to meet the demands of highly dynamic and intelligent MSIMP. Therefore, although the traditional optimization algorithms for MSIMP have a certain degree of effectiveness, they still exhibit problems such as difficulty of parameter adjustment, high computational complexity, and easily falling into local optima. Thus, there is an urgent need to enhance the optimization algorithms to improve their efficiency in solving the MSIMP problem.

4. MSIMP Based on EMOEAs

This section first provides a detailed overview of the classical literature on EMOEAs and then introduces an MSIMP flowchart based on expensive multi-objective evolutionary algorithms and the surrogate model used to assist the EMOEAs. Finally, an expensive multi-objective evolutionary algorithm based on the surrogate model is explored.

4.1. Traditional EMOEAs

EMOEAs are a class of multi-objective evolutionary algorithms that solve for three or more optimization objective functions and are expensive to evaluate, where “expensive” refers to the large amount of computational resources and time consumed for each evaluation of the objective functions [64,65]. In the field of satellite planning, MSIMP often considers multiple optimization objectives, and the calculation of the fitness values of potential mission planning schemes consumes large amounts of resources. EMOEAs can provide an effective solution for MSIMP via complex multi-objective optimization through their powerful optimization and search capabilities.

Table 2. Classical EMOEAs.

Algorithm	Proposed/Published	Computation Costs /Response Time	Main Ideas
Evaluating the Epsilon-Domination-Based Multi-Objective Evolutionary Algorithm (EEMOEA) [66]	Kalyanmoy Deb/2005	Moderate/Moderate	The application of a distribution metric in an expensive multi-objective evolutionary algorithm is emphasized in the ε-MOEA, which is realized by an ε-dominating metric.
Surrogate-Assisted Evolutionary Algorithm (SAEA) [67]	Keane/2006	Low/Fast	The target value of the candidate solution is predicted by the Gaussian process and radial basis function to reduce the expensive calculation cost.
Kriging-Based Optimization (KO) [68]	Kleijnen/2009	Moderate/Slow	The optimization method based on the Kriging model provides the prediction of fitness value and variance and effectively realizes the global optimization.
Adaptive Surrogate-Model-Based Optimization (ASMO) [69]	Zhou/2012	Moderate/Moderate	The sampling method is used to optimize and update the proxy model and gradually approach the global optimal, which has strong adaptability.
Ensemble of Surrogates-Assisted Evolutionary Algorithm (ESEA) [70]	Chugh/2016	Low/Fast	A Gaussian process, neural network, and decision tree are used to complement each other in prediction and evaluation to reduce the calculation cost.
Trust Region-Based Multi-Objective Evolutionary Algorithm (TR-MOEA) [71]	Cai, Jianping/2018	Moderate/Moderate	By combining the trust region and evolutionary algorithm, the optimization search is limited to a potential region by updating and iterating the trust region to improve search efficiency.
Efficient Global Optimization (EGO) [72]	Letham, Benjamin/2019	Low/Fast	A Gaussian process is used as the cost model, and the expected improvement in the acquisition function is used to guide the selection of sampling points, which promotes the fast convergence of the algorithm.
Ensemble of Surrogates-Assisted Evolutionary Algorithm (ESAEA) [73]	Zhao, Rui/2020	Low/Fast	A variety of surrogate models are combined to approximate the expensive objective function, and the surrogate model is used to improve the prediction accuracy and search efficiency.
Surrogate-Assisted Covariance Matrix Adaptation Evolution Strategy (SA-CMA-ES) [74]	Ulmer, Hannah/2021	Moderate/Moderate	The surrogate model is combined with the covariance matrix adaptive evolution strategy to effectively explore and develop the search space.

provides a detailed list of classical EMOEAs.

A detailed review of Table 2 reveals that classical EMOEAs are designed to address multi-objective optimization problems with high computational costs. These algorithms reduce the computational burden of objective function evaluations by applying surrogate models (such as Gaussian processes and Kriging models) and optimization strategies (such as trust-region methods and expected improvement functions). For instance, EEMOEA [66] emphasizes the use of ε-dominance measures to maintain solution diversity, with a moderate computational cost and response time. Both the SAEA [67] and KO [68] utilize surrogate models (such as Gaussian processes and Kriging models) to predict objective values, whereas the SAEA is characterized by a low computational cost and fast response while KO has a moderate computational cost and slower response. The SAEA significantly reduces the computational cost of objective function evaluations. ASMO [69] and the ESEA [70] integrate multiple surrogate models (such as Gaussian processes, neural networks, and decision trees), resulting in a moderate computational cost with moderate response time and low computational cost with fast response, respectively. The TR-MOEA [71], EGO [72], and ESAEA [73] improve search efficiency, with the TR-MOEA and EGO offering a moderate computational cost/moderate response time and low computational cost/fast response, respectively, while the ESAEA enhances search efficiency and prediction accuracy through a combination of multiple surrogate models. The SA-CMA-ES [74] leverages a covariance matrix adaptation strategy to explore the search space, achieving a moderate computational cost and response time, and excels in complex search spaces. By analyzing these classical EMOEAs, valuable insights can be gained, particularly in the application of surrogate models, integration of optimization strategies, and enhancement of search efficiency. These insights can be applied to design more efficient SA-EMOEAs, providing more effective solutions to high-computational-cost multi-objective optimization problems.

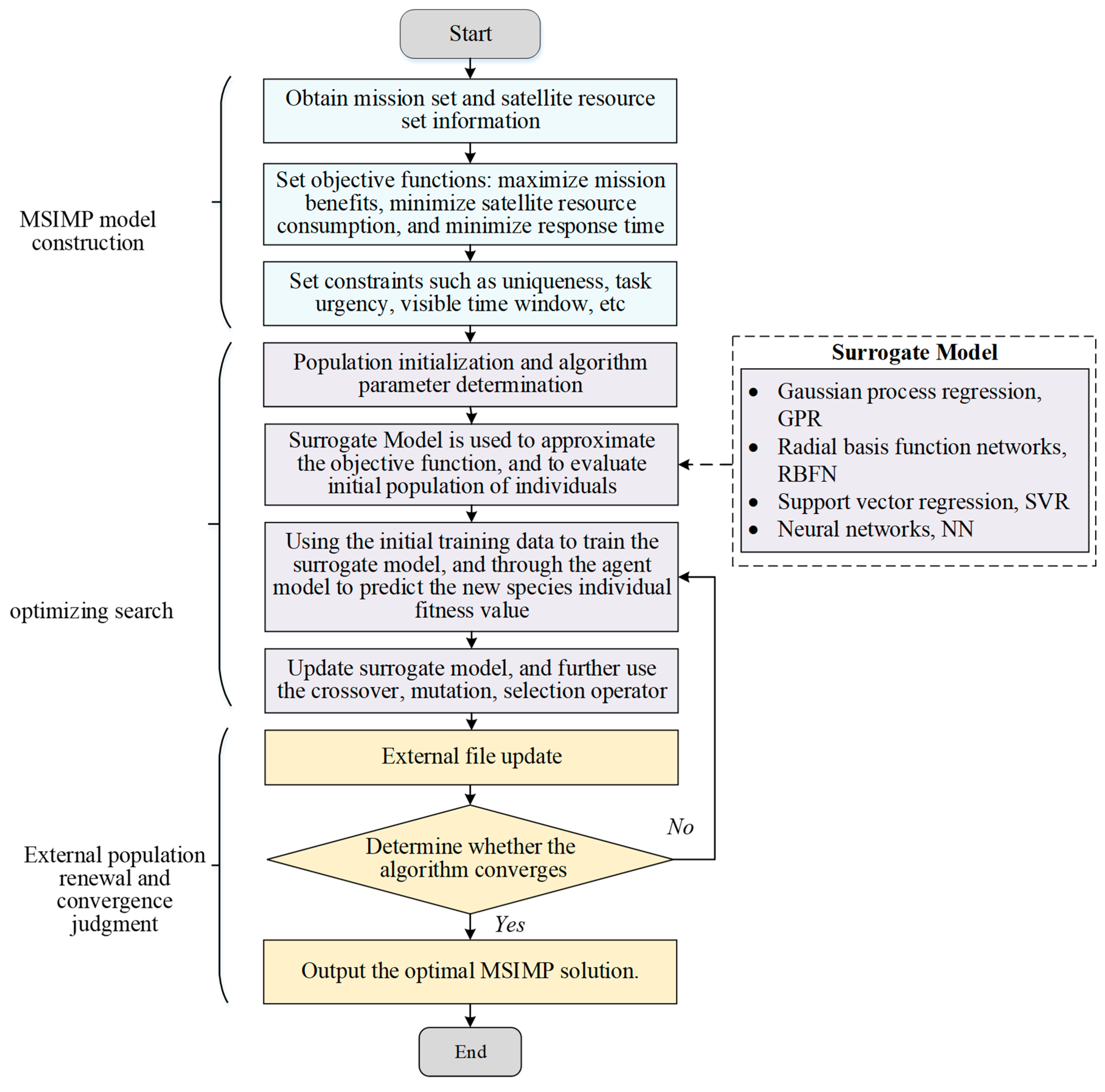
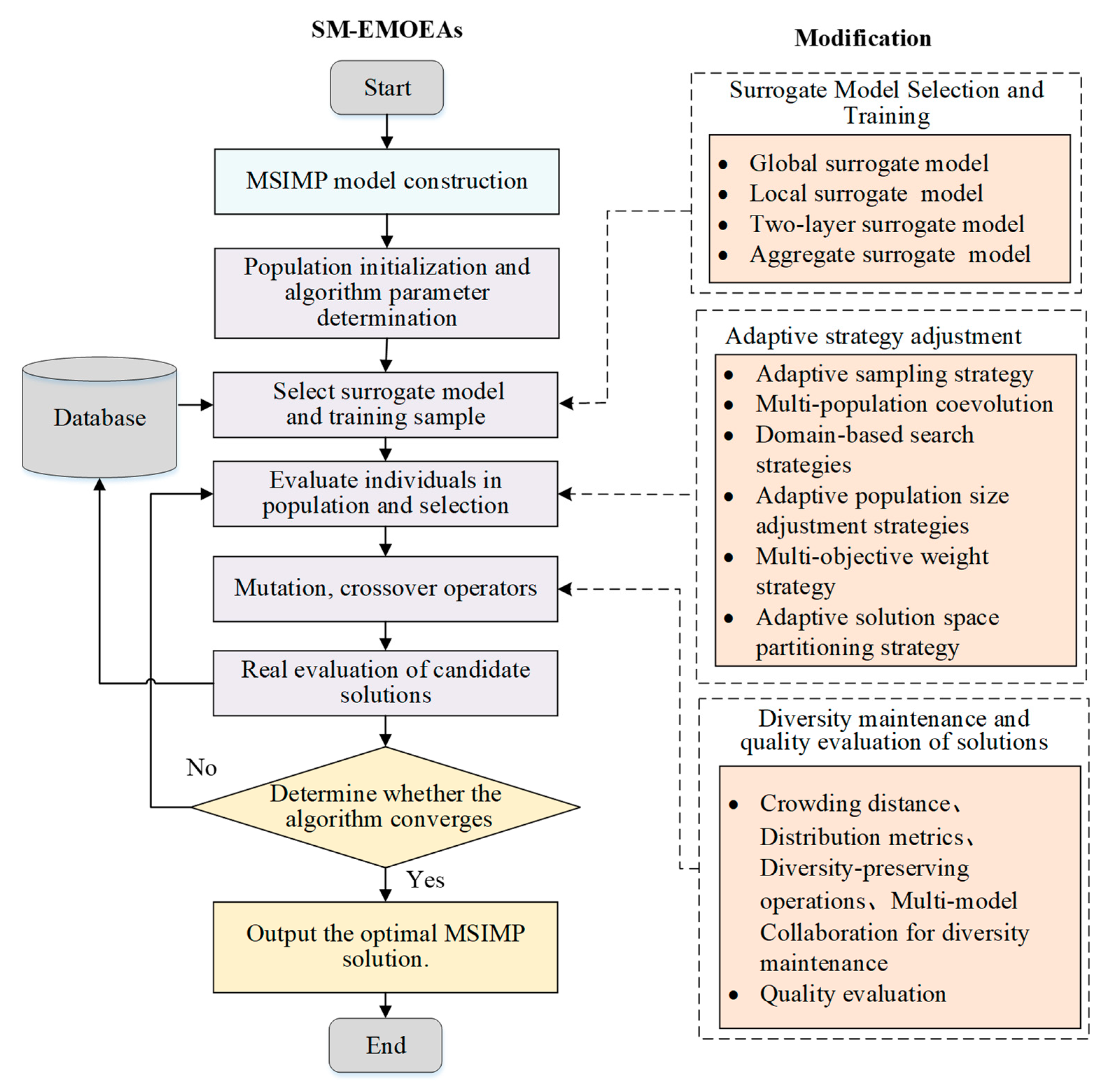
4.2. Flowchart of MSIMP Based on EMOEAs

Classical expensive multi-objective evolutionary algorithms based on EMOEAs are used to solve the MSIMP problem. The flowchart of MSIMP based on EMOEAs is shown in Figure 5, which mainly includes MSIMP problem modeling, an optimal search, external population updating, and convergence judgment [75,76,77,78,79,80,81,82].

• In the modeling of the MSIMP problem, information about the mission set and satellite resource set is obtained according to the application scenario. The objective functions, including the maximum mission benefit, minimum satellite resource consumption, and minimum response time, are constructed following the user’s requirements. Moreover, the constraints, such as the mission uniqueness constraint, mission urgency constraint, and visible time window constraint, are set.
• In the optimization search, a set of individuals is randomly generated to form the initial population, and the algorithm’s parameters are configured. The fitness of each individual in the initial population is evaluated based on the objective function. High-quality individuals are selected through processes like crossover, mutation, and selection, which are then used to produce the next generation of the population.
• In the external update and convergence evaluation steps, non-dominated solutions from the new population are stored in an external population, which is updated to preserve population diversity. Once the maximum number of iterations is reached, the final set of non-dominated solutions is produced as the optimal MSIMP scheme for the selected satellite control task [83].

However, as the MSIMP scheme involves a large-scale task set and complex satellite resource allocation, tens of thousands of evaluations are required to find a high-quality task planning scheme. This leads to high computational complexity and consumes large amounts of computational resources. In addition, EMOEAs are prone to falling into local optimal solutions when facing complex multi-peak optimization problems, resulting in the algorithms not being able to effectively explore the global optimal solution space. In particular, in the context of the dynamically changing mission requirements and satellite resource state changes faced by MSIMP in complex environments, the response-ability is limited, making it difficult to solve the mission planning scheme in real scenarios [84].

To solve the above problems, a surrogate model is introduced in the optimization search part of the algorithm. The surrogate model is a simplified mathematical model used to replace the high-dimensional objective function with constraints in the optimization search process, which helps to achieve rapid evaluation of the solution through approximating the real objective function and can identify a high-quality solution with a limited number of evaluations. It applies to complex optimization problems with large computational resource requirements or tight time constraints. Surrogate models include Gaussian process regression (GPR) [85], radial basis function networks (RBFNs) [86], support vector regression (SVR) [87], and neural networks (NNs) [88].

4.3. Surrogate Models

The surrogate model approximates the original expensive objective function by collecting and analyzing real data to improve the efficiency and feasibility of the EMOEAs in solving the MSIMP problem. At present, the most commonly used surrogate models can be categorized into statistical models, function approximation models, and machine learning models. Statistical models, which aim to use statistical methods as surrogate models to filter out poor candidate solutions to achieve the goal of reducing the computational cost, include Kriging [89], support vector regression (SVR) [90], and Bayesian optimization [91]. Function approximation models are mathematical functions that approximate the true fitness value of the objective function, thus reducing the number of evaluations, which include the response surface methodology (RSM) [92], radial basis functions (RBFs) [93], and polynomial regression [94]. Machine learning models are analyzed via training on historical data to predict candidate solutions and include artificial neural networks (ANNs) [95], deep learning [96], and decision tree regression [97]. The main ideas, advantages, and disadvantages of the three types of surrogate models are summarized in

Table 3. The main ideas, advantages, and disadvantages of the three types of surrogate models.

Types	Surrogate Model	Main Ideas	Advantages and Disadvantages
Statistical Model	Kriging	Assuming that the value of the objective function follows the multivariable normal distribution, the candidate solution is predicted by historical data.	Advantages: it can provide the prediction and variance of the objective function value, and is suitable for dealing with highly nonlinear problems. Disadvantages: it has high computational complexity for large-scale data sets.
	Support Vector Regression	To minimize the error, a hyperplane is found in the higher-dimensional space by classification and analysis.	Advantages: it performs well in high-dimensional space and has good generalization ability. Disadvantages: the selection kernel function and parameter tuning are complex.
	Bayesian Optimization	Bayesian statistics and surrogate models are used to approximate the objective function, and the acquisition function is used to select new evaluation points.	Advantages: it effectively handles expensive black-box function optimization problems, balancing exploration and development. Disadvantages: it is very sensitive to the quality and quantity of initial data, and improper selection of initial samples may lead to a poor performance of proxy models.
Function approximation model	Response Surface Methodology	Lower-order polynomial functions, such as linear polynomials, are often used to approximate objective functions and optimize stochastic processes.	Advantages: the calculation is simple and suitable for linear or low-order nonlinear problems. Disadvantages: for complex systems, the model is overly sensitive to training data, which can lead to overfitting and affect generalization ability.
	Radial Basis Function	The influence of each sample point is expressed as a function of distance, and the objective function is approximated and fitted.	Advantages: it is suitable for processing multidimensional nonlinear problems with high flexibility. Disadvantages: it has low computational efficiency for processing large-scale data sets.
	Polynomial Regression	The objective function is fitted using polynomial functions.	Advantages: it is suitable for low-dimensional problems and the calculation is simple. Disadvantages: it is not effective for high-dimensional nonlinear problems.
Machine learning models	ANN	Complex objective functions are fitted through multiple hidden layers and nonlinear activation functions.	Advantages: it can deal with highly complex and nonlinear problems and has strong adaptability. Disadvantages: it requires a large amount of data for training and complex parameter adjustment.
	Deep Learning	By increasing the depth of the network, it is able to handle more complex pattern recognition and prediction tasks.	Advantages: it adjusts the network architecture and loss function to adapt to different types of optimization problems. Disadvantages: it has high data requirements and a need to label the data before training.
	Decision Tree Regression	By constructing a decision tree, the dataset is split into regions and a simple regression is performed within each region.	Advantages: it has a good processing effect on nonlinear and complex data sets and is suitable for processing large-scale data. Disadvantages: Making local decisions at each node cannot capture the global optimization solution.

.

According to Table 3, the three types of surrogate models differ in their scope of application and ability to handle data. Among them, statistical models require a medium-sized dataset to train the surrogate model and are suitable for complex, high-dimensional, and highly nonlinear problems. Function approximation models, on the other hand, require fewer data to train and are suitable for low-dimensional, linear, and low-order nonlinear problems. Machine learning models are more data-demanding, especially for big data and complex tasks requiring large amounts of data for training, and are suitable for complex and high-dimensional problems. The MSIMP problem can be solved in practice through choosing an appropriate surrogate model according to the specific user requirements in order to improve the efficiency and quality of problem solving. The use of surrogate models will be further discussed hereafter.

4.4. Surrogate Model for EMOEAs

In recent years, researchers at home and abroad have proposed a variety of surrogate model expensive multi-objective evolutionary algorithms, including EMOEAs based on multi-surrogate co-optimization models, transfer learning surrogate models, parallel surrogate models, and multi-objective Bayesian optimization, which have shown better performance in solving optimal MSIMP problems.

Table 4. Various surrogate model for EMOEAs.

Categories	Main Ideas	Advantages and Disadvantages
Cooperative Surrogate Models for Multi-Objective Optimization [98]	Multiple surrogate models are combined for collaborative optimization, and the optimization effect is improved by weighted average prediction results. According to the feedback of the optimization process, the model weight and combination strategy are dynamically adjusted to meet the optimization needs of different stages.	Advantages: The synthesis of different surrogate models makes the advantages of each model complementary, reduces the possible bias of a single model, and improves the data generalization ability of the algorithm. Disadvantages: The training and evaluation of multiple surrogate models greatly increases computational complexity and resource consumption.
Transfer Learning for Surrogate-Assisted Multi-Objective Optimization [99]	The similarities and differences between the source and target domains are analyzed, effective knowledge migration methods are designed to migrate the surrogate models trained on the source domain to the target domain, and the adaptability of the surrogate models to new tasks is improved.	Advantages: Using historical knowledge to construct more accurate initial prediction models and transferring knowledge from the source domain to the target domain to speed up the convergence of EMOEAs. Disadvantages: The similarity and difference judgments between different tasks are complex and highly dependent on the quality of historical data.
Parallel Surrogate Models for Multi-Objective Optimization [100]	Multiple surrogate models are trained in parallel, the fitness value of each objective function is estimated separately, and an incremental sampling strategy is designed to increase the sample points in the optimal search process chapter foot to accelerate the training process of surrogate models using parallel computing resources.	Advantages: Accelerates model training and evaluation through parallel computing, capable of handling large-scale datasets and high-dimensional problems, and greatly reduces surrogate model training time. Disadvantages: The implementation of parallel computing requires high-computational resources and needs to solve the problems of data synchronization and load balancing.
Multi-Objective Bayesian Optimization [101]	Different approximate objective functions of the surrogate model are selected for each objective function, acquisition functions suitable for multi-objective optimization are designed to select new evaluation points, and the surrogate model is updated according to the new evaluation points to ensure its applicability and robustness in different scenarios.	Advantages: Effectively balancing exploration and exploitation through Bayesian modeling and acquisition functions enables optimization problems with high dimensionality and complex constraints to be handled with less unnecessary evaluation. Disadvantages: Bayesian model optimization consumes a large amount of computational resources and is ineffective for optimization with insufficient data.

summarizes the main ideas, advantages, and disadvantages of various surrogate model expensive multi-objective evolutionary algorithms.

Surrogate model expensive multi-objective evolutionary algorithms (SM-EMOEAs) have the following advantages with regard to solving the MSIMP problem.

• They reduce the computational cost and improve the optimization efficiency: The surrogate model replaces the real objective function for evaluation and predicts the objective value of the candidate solution, allowing the evolutionary algorithm to efficiently generate and assess new individuals in each generation. This enables the algorithm to carry out more evaluations and optimizations, substantially reducing the large computational overhead within the limited time and resource constraints, thus accelerating the speed of convergence. The model maintains high computational efficiency when dealing with high-dimensional and complex problems, overcoming the computational bottlenecks of traditional optimization methods when dealing with high-dimensional optimal MSIMP problems.
• They enhance the diversity and quality of the solutions: Through efficient predictions and uncertainty steering provided by surrogate models, the algorithm can effectively balance exploration and exploitation during the evaluation process based on prediction uncertainty. The algorithm tends to prioritize exploring candidate solution areas with higher uncertainty, preventing premature convergence to local optima. For areas with lower uncertainty, the focus shifts to exploitation, further refining the existing solutions. The uncertainty steering encourages the generation of more diverse candidate solutions, thereby promoting population diversity. Additionally, multi-satellite imaging mission planning often involves multiple conflicting objectives, such as imaging coverage, image quality, and task completion time. By incorporating surrogate models with uncertainty guidance, the algorithm achieves balanced optimization across multiple objective functions, thereby improving solution quality.
• They enhance the adaptability of the algorithm: Through continuously updating the surrogate model to cope with dynamic changes in the environment, such as changes in the target area, changes in the mission requirements, and so on, the algorithm can maintain efficient optimization capabilities in the face of dynamic problems. In MSIMP, this adaptability enables the system to cope with changes and uncertainties in the task requirements and ensures the smooth execution of the task.

5. Improved SM-EMOEAs for MSIMP

The SM-EMOEA has shown significant advantages in MSIMP problem solving; however, SM-EMOEAs still suffer from several problems, such as high computational costs, the poor generalization of surrogate models, poor adaptation to dynamic environments, and poor solution quality [102,103]. To overcome these serious problems, further improvements to SM-EMOEAs are needed. First, the generalization ability of the surrogate model can be optimized to reduce the computational cost [104]. Second, it is necessary to design effective adaptive strategies that enable the algorithm to quickly adapt to dynamic environmental changes [105]. Finally, it is crucial to ensure that the population retains sufficient diversity to output a high-quality MSIMP scheme for task planning [106]. In this section, we focus on the surrogate model’s improvement, adaptive strategy improvement, and diversity maintenance and quality assessment of the solutions, and the specific improvement ideas are shown in Figure 6.

5.1. Surrogate Model Improvement

Regarding the improved SM-EMOEAs for MSIMP, improved surrogate models are crucial to ensure the efficiency and accuracy of the solution of the MSIMP scheme, and suitable improved surrogate models can enable SM-EMOEAs to better adapt to MSIMP problems in different scenarios. They also improve the adaptability of the algorithms to dynamic problems [107,108,109]. The improvement of the surrogate model depends on the MSIMP problem’s characteristics. For example, for MSIMP problems applied to environmental monitoring and weather forecasting in large-scale scenarios, it is required to plan satellites and target missions globally and as a whole. The introduction of a global surrogate model can assist the algorithm in searching the distribution characteristics of the candidate solutions in the solution space and thus quickly identifying high-quality task planning solutions. Figure 7 summarizes the methods used to improve the surrogate model in MSIMP-oriented SM-EMOEAs, including the global surrogate model, local surrogate model, two-layer surrogate model, and aggregation surrogate model.

• The global surrogate model aims to cover the global characteristics of all satellites and missions by modeling the whole MSIMP problem, mainly by using Gaussian process regression, radial basis functions, support vector regression, and so on. Through collecting global data to train the model, the global surrogate model can capture global trends for optimization to find an excellent solution for overall mission planning. It is suitable for mission planning scenarios that require global coverage, such as the monitoring of the global forest cover, through SM-EMOEAs based on global surrogate models. The global multi-satellite coverage area target task is optimized to search and capture the global trends of the forest cover so as to find an excellent overall mission planning solution [110,111,112].
• The local surrogate model focuses on the optimization properties of a specific region, divides the optimal MSIMP problem into several sub-problems, and performs the fine optimization of a specific region by collecting data from this region for training so as to improve the quality of the local solution. Common local surrogate models include local weighted regression, local Gaussian processes, and local radial basis function networks. They are applicable to high-frequency imaging missions in a specific area that requires delicate tuning. For example, after a natural disaster, SM-EMOEAs using local surrogate models are applied to divide the MSIMP into multiple sub-problems for focused local-scale observation. Frequent high-resolution imaging of the affected city is conducted to enhance observation efficiency, monitor the disaster’s impact, and track recovery progress [113,114].
• The two-layer surrogate model first uses the global surrogate model for the initial optimization of the MSIMP problem. It then selects specific regions for local optimization, stores global and local data for the training of the global and local surrogate models, and uses them for different levels of optimization. The two-layer surrogate model mainly includes a two-layer Gaussian process, a hierarchical radial basis function network, and hierarchical support vector regression. It is suitable for complex tasks that require both global and local optimization. For example, in an agricultural monitoring project, multiple satellites are required to monitor crop growth in different agricultural zones. The global surrogate model is used in the initial stage to globally optimize the imaging tasks for the whole agricultural area, and then the local surrogate model is used to assign high-resolution imaging tasks to specific areas. This achieves fast and accurate agricultural monitoring imaging, task assignment, and execution [115,116].
• An aggregate surrogate model involves the integration of artificial neural networks, deep learning, decision tree regression, and other surrogate models. It aims to collect comprehensive data to support multi-model training based on global, local, and uncertainty searches. It aggregates the prediction results of multiple surrogate models through integration techniques to enhance the accuracy and robustness of the overall prediction, thus improving the quality of the overall planning scheme. It is suitable for complex MSIMP scenarios involving many different types of imaging tasks. In practical applications, such as urban planning tasks, the aggregated model can achieve the monitoring and optimization of various aspects, such as urban expansion, traffic flows, green space coverage, and so on, and provide accurate and reliable overall planning solutions [117,118].

5.2. Adaptive Strategy Improvement

Adaptive strategy improvement is a key aspect in improving EMOEAs. Through the optimal and dynamic adjustment of the search strategies and parameters, the efficiency and adaptability of the algorithms can be significantly improved. There are various ways to improve the adaptive strategies in the improved SM-EMOEAs of MSIMP, which include the adaptive sampling strategy, multiple-population co-evolution strategy, domain knowledge strategy, adaptive population size adjustment strategy, multi-objective weighting strategy, and adaptive solution space division strategy.

Table 5. Improved adaptive strategies based on EMOEAs.

Improvement Strategy	Specific Improvement Methods	Year	Main Ideas
Adaptive sampling strategy	Probabilistic sampling strategy	2023	The probability improvement criterion is used to adjust the sampling, the probability guidance algorithm is used to sample the candidate solution successfully, and the region with a high fitness value is sampled emphatically.
	Dynamic sampling adjustment strategy	2023	The radial basis function (RBF) network model for denoising is established according to the real-time feedback noise level in the process of evolution, and dynamic adjustment of data sampling density is carried out.
Multi-population co-evolutionary strategy	Adaptive variable grouping strategy	2022	The Bayesian Gaussian process latent variable model is combined with adaptive sampling to iteratively select new partially observable training sample points.
	Hierarchical co-evolution strategy	2022	In the stage of model training, a multi-classification model is constructed to divide the whole population into several classes to ensure diversity. In the evolutionary phase, a coevolutionary framework is used to guide evolution according to the new selection criteria.
Domain knowledge strategy	Domain knowledge adaptive strategy	2024	The schema layer is built based on domain knowledge, the query sentence is used to extract knowledge, and the knowledge graph is established to extract and reuse domain knowledge adaptively.
	Domain knowledge extraction strategy	2023	A variable fidelity proxy model is established to obtain the low-fidelity undominated solution. A K-means clustering algorithm is used to extract knowledge from the low-fidelity undominated solution to search space.
Adaptive population size adjustment strategies	Population size adjustment strategy	2024	The spatial determination mechanism and population size reduction strategy are implemented by improving the dimension between the test vector and the target vector.
	External file resource allocation strategy	2022	An external archive is constructed to periodically add vectors from external archives to the population in the iterative process to achieve adaptive population size adjustment.
Multi-objective weight strategy	Inverse distance weighting strategy	2024	Inverse distance weighting and radial basis function strategies are established to provide prediction target values and uncertainty, and an improved lower confidence boundary filling criterion is proposed.
	Weighted prediction variance strategy	2023	The output fitting uncertainty index is calculated based on the weighted prediction variance strategy, and the uncertainty of sample dispersion and surrogate model fitting is taken into account.
Adaptive solution space partitioning strategy	Spatial hierarchical decomposition strategy	2019	The object space is divided into multiple subspaces, and the best individual of adjacent estimates in each subspace is selected.
	Adaptive interval decomposition strategy	2024	The objective space is divided into a series of optimization subproblems, and a feasible solution of each subspace is saved to a feasible solution set of a partition. Once a subspace has a feasible solution, the search strategy is changed from a constrained search to unconstrained search.

summarizes the specific improvements of the adaptive strategies.

• The adaptive sampling strategy improves the accuracy of surrogate model evaluation by dynamically adjusting the density of sampling. In the early stage of the optimized search, coarse sampling is used to cover the search space quickly. Meanwhile, in the middle and late stages of the optimized search, the sampling density is gradually increased to improve the local accuracy of the surrogate model. The adaptive sampling strategy ensures that the sampling density is adaptively adjusted at different stages of the optimal search, thus balancing the needs of the global search and local fine search. Common approaches include the dynamic sampling adjustment strategy [119] and the probabilistic sampling strategy [120].
• The multi-population co-evolution strategy divides the population into multiple sub-populations that are co-evolving; each sub-population independently evolves to explore different solution spaces and exchanges information at the appropriate time, improving the diversity and adaptability of the algorithms through co-evolution and enhancing the overall planning effect. Common approaches include adaptive variable grouping strategies [121] and hierarchical co-evolutionary strategies [122].
• The domain knowledge strategy adaptively selects the knowledge transfer strategy by calculating the difference between the current domain knowledge and the historical knowledge. When the similarity between the two types of knowledge is high, the direct transfer method is used to directly invoke the historical knowledge. The knowledge is adjusted and corrected when the similarity between the two types of knowledge is low, thus helping the algorithm to identify and exploit the properties of the problem during the optimization process and to quickly locate the area covered by the high-quality solution. Common approaches include domain knowledge adaptive strategies [123] and domain knowledge extraction strategies [124].
• The adaptive population size adjustment strategy dynamically adjusts the population size according to the problem convergence speed and complexity to ensure that the algorithm maintains efficient search capabilities at different optimization stages. If the algorithm converges too quickly, it indicates that the algorithm may be trapped in a local optimum and that it is necessary to adaptively increase the population size to increase the diversity of the search space. If the convergence of the algorithm stagnates, the population size needs to be reduced to improve the optimization efficiency. Common methods include the population size adjustment strategy [125] and external file resource allocation strategy [126].
• The multi-objective weighting strategy adjusts the weights of multiple objective functions according to the real-time feedback information obtained during the optimization process. If the prediction error of the surrogate model of the objective function is large, its weight can be temporarily reduced to avoid misleading the optimization. If the prediction error of the surrogate model of the objective function is small, its weight can be increased to effectively advance the optimization process. Commonly used methods include the inverse distance weighting strategy [127] and weighted prediction variance strategy [128].
• The adaptive solution space division strategy dynamically divides the solution space based on the feedback information from the optimal search process, constantly monitors the quality of the candidate solutions and their distribution in the space, and achieves a trade-off between the exploration of new regions and the refinement of the known regions by conducting local and global searches in different solution space regions. Commonly used methods include the spatial hierarchical decomposition strategy [129] and adaptive interval decomposition strategy [130].

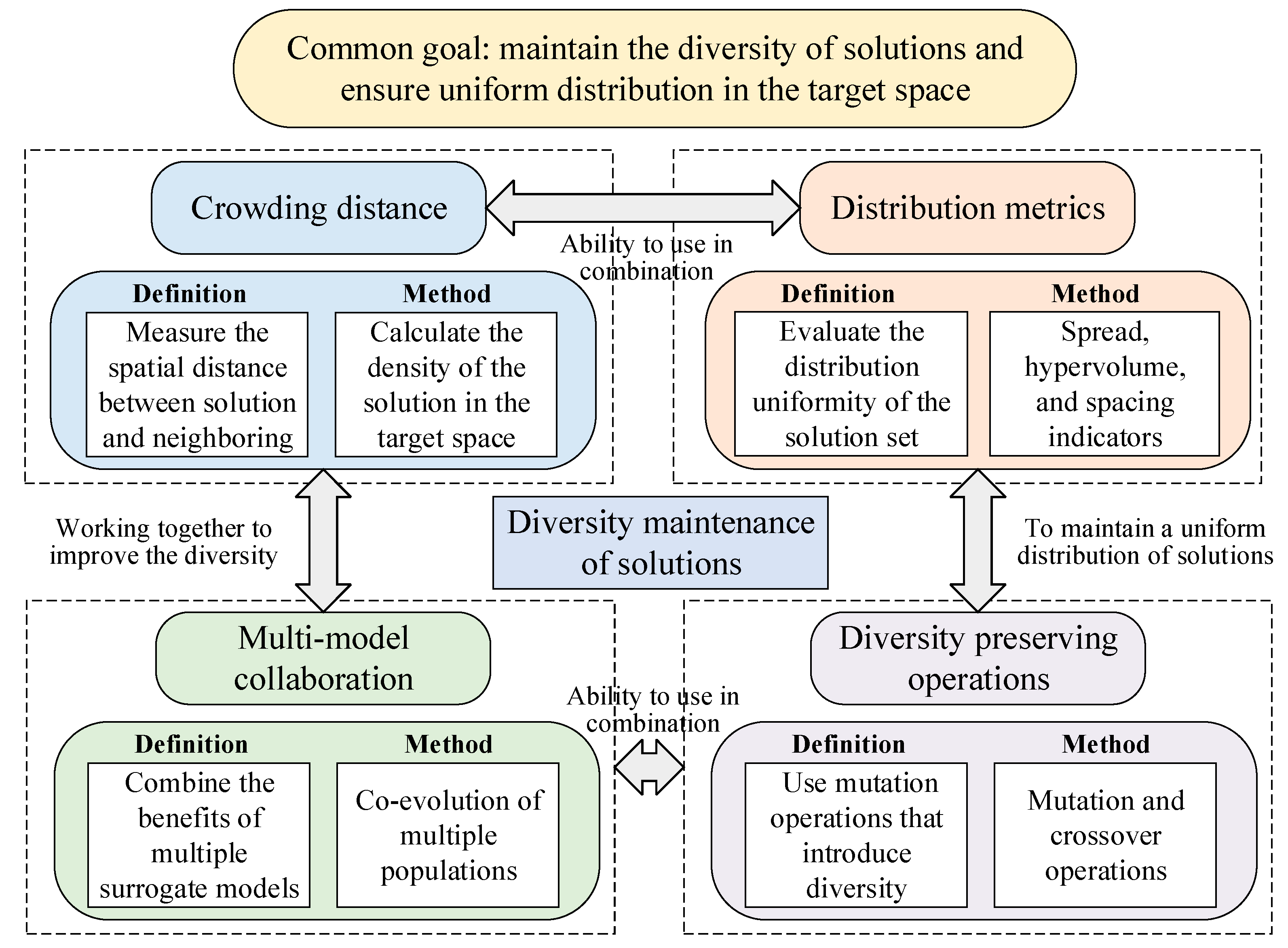
5.3. Diversity Maintenance and Quality Assessment of Solutions

The diversity maintenance and quality assessment of solutions are important processes when evaluating the performance of SM-EMOEAs [131,132]. The diversity maintenance of solutions aims to improve the prediction accuracy of the surrogate model by providing richer and more diverse training data for the model through a diverse solution set. Diversity maintenance ensures that the solutions are uniformly distributed across the whole target space, preventing the algorithm from focusing on certain regions too early and thus preventing it from falling into a local optimal solution. The diversity solution enables broader coverage of the solution space, helping the surrogate model to capture global problem characteristics. This facilitates the model in finding reasonable near-optimal solutions more quickly during the evolutionary process, preventing the algorithm from getting trapped in local optima and accelerating the optimization process [133]. Solution quality refers to the superiority of candidate solutions in multi-objective optimization, typically assessed by how closely they approach the global optimal region in the solution space. It reflects the performance of SA-EMOEAs in balancing multiple optimization objectives, such as task benefits and response time, while evaluating the algorithm’s search efficiency. High-quality solutions indicate that candidate solutions not only achieve high objective values but also demonstrate strong stability and diversity in both the global exploration and local exploitation of the solution space [134]. In addition, the consistent occurrence of high-quality solutions indicates that the surrogate model can approximate the true objective function more accurately, thus effectively guiding the optimization search process [135].

At present, diversity maintenance methods for solutions include computing the crowding distance, using distribution metrics, performing multi-model collaboration, and implementing diversity-preserving operations, as shown in Figure 8.

• The crowding distance is used to measure the distance between the current solution and its neighboring solutions in the target space. The candidate solutions are ranked based on their fitness values for the objective functions, followed by calculating the crowding distance for each solution. A larger crowding distance indicates that the solution is located in a sparsely populated region of the objective space, where there are fewer neighboring solutions. Conversely, a smaller crowding distance suggests that the solution is in a densely populated region with more neighboring solutions in the objective space. A larger crowding distance indicates that there are fewer solutions in the current region while a smaller crowding distance indicates that there are more solutions in the current region. Through calculating the crowding distance, the density of each solution in the target space can be effectively evaluated, thus providing a reference for the selection of the next generation of solutions and ensuring the uniform distribution of the solutions in the target space [136,137].
• Distribution metrics are used to assess the uniformity of distribution and the coverage of a solution set in the target space. The specific method is to cluster the solutions using a clustering algorithm, where each cluster centroid represents a subset of the solutions, reflecting the characteristics of each subset in the solution space. The clustering centroids are preferentially selected as part of the next generation of solutions to ensure the uniform distribution of the solutions. Distribution metrics can be used in conjunction with the crowding distance to jointly maintain the solution diversity through different metrics [138,139].
• Diversity-preserving operations aim to introduce and maintain diversity in the population during the optimization search process to prevent the algorithm from falling into a local optimum. The diversity preservation of solutions in the population is achieved by improving the mutation and crossover operations, setting up an external archive to preserve non-dominated solutions, and periodically introducing randomly generated new individuals [140,141].
• Multi-model collaboration combines the advantages of multiple surrogate models through dynamically selecting and updating different surrogate models, guiding the search process to explore the target space more comprehensively by evaluating and exploiting the prediction uncertainty at different stages of the optimization search, and prioritizing the solutions with higher prediction uncertainty for evaluation to maintain the diversity of the solutions [142,143].

The SM-EMOEA ensures the uniform distribution and comprehensive coverage of the solution in the objective space through the above four methods, which provide richer training data for the surrogate model and improves the overall optimization performance of the algorithm.

The assessment of the quality of the solutions in the improved SM-EMOEAs for MSIMP includes both the performance metrics of MSIMP and the performance metrics of the improved SM-EMOEA. The performance measures of MSIMP include maximizing the mission benefit [144], maximizing the task allocation rate [145], maximizing satellite resource utilization [146], minimizing motion disturbances [147], and minimizing the response time [148]. The performance measures of the improved SM-EMOEA include Pareto frontier approximation [149], hypervolume metrics [150], the surrogate model prediction error [151], the average fitness value [152], the maximum fitness value [153], and the minimum fitness value [154].

In the performance metrics of the improved SA-EMOEAs, the Pareto frontier proximity is used to evaluate the distance between the solution set and the Pareto frontier. The Pareto frontier represents the set of non-dominated solutions in the objective space. Smaller proximity to the Pareto frontier indicates that the solution set is closer to the optimal solutions in the objective space, reflecting better algorithm convergence. The hypervolume metric measures the coverage of the solution set in the objective space by calculating the volume formed between the solution set and a reference point. A larger hypervolume value indicates that the solution set covers a wider range in the objective space, demonstrating higher diversity and better solution quality. The surrogate model prediction error is used to assess the accuracy of the surrogate model’s approximation of the actual objective function: the smaller the error, the better the performance of the surrogate model. In the improved SA-EMOEAs for MSIMP, fitness values represent the objective function values, such as task benefit and task completion, and are used to assess the quality of the solution set and the performance of the algorithm. Specifically, the average fitness value reflects the overall fitness level of the population, indicating the general quality of the solutions. The maximum fitness value represents the fitness of the best solution in the current population and is used to evaluate the quality of the current optimal solution. The minimum fitness value indicates the fitness of the worst solution in the population, helping to determine whether the population has fallen into a local optimum.

6. Discussion

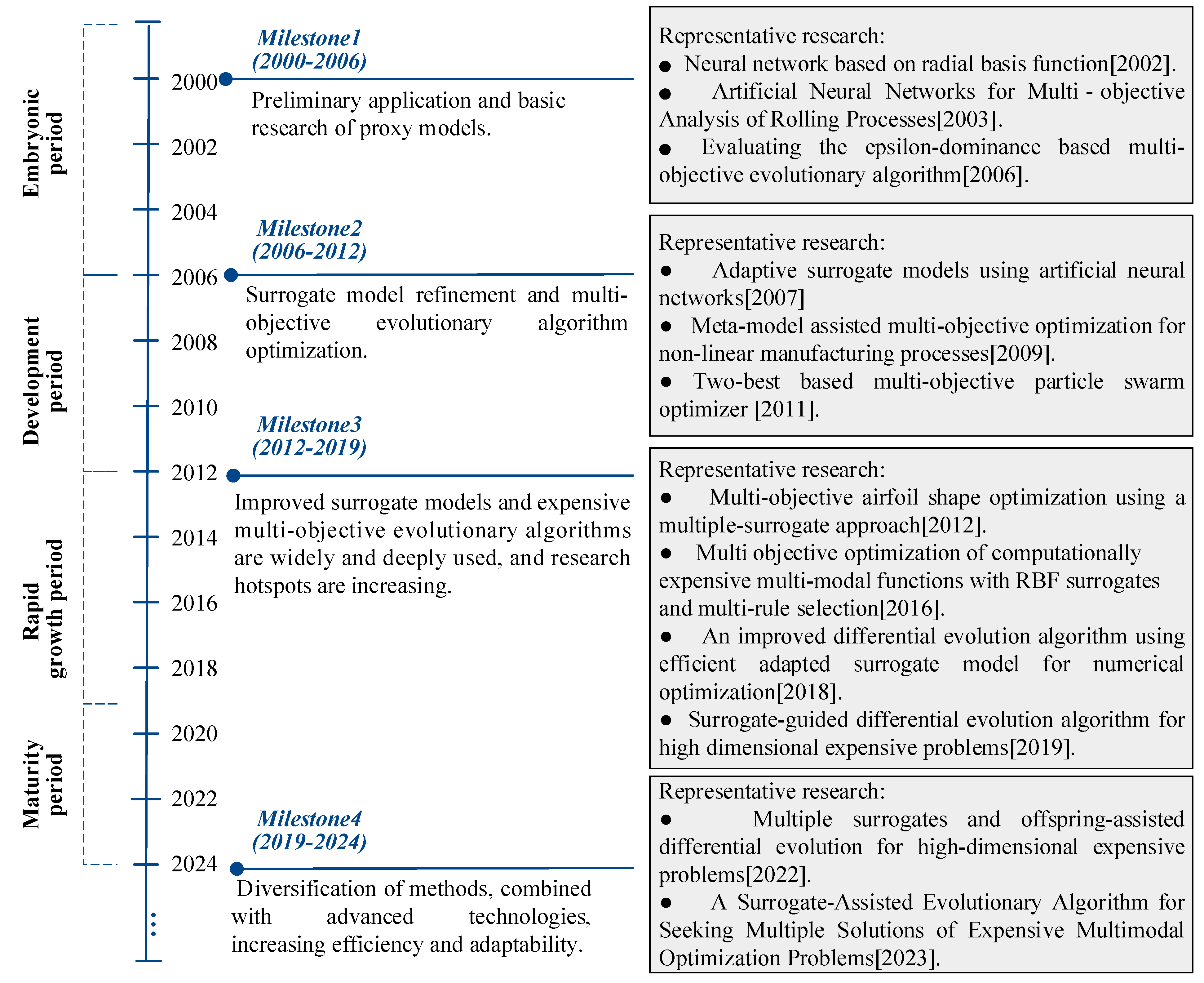
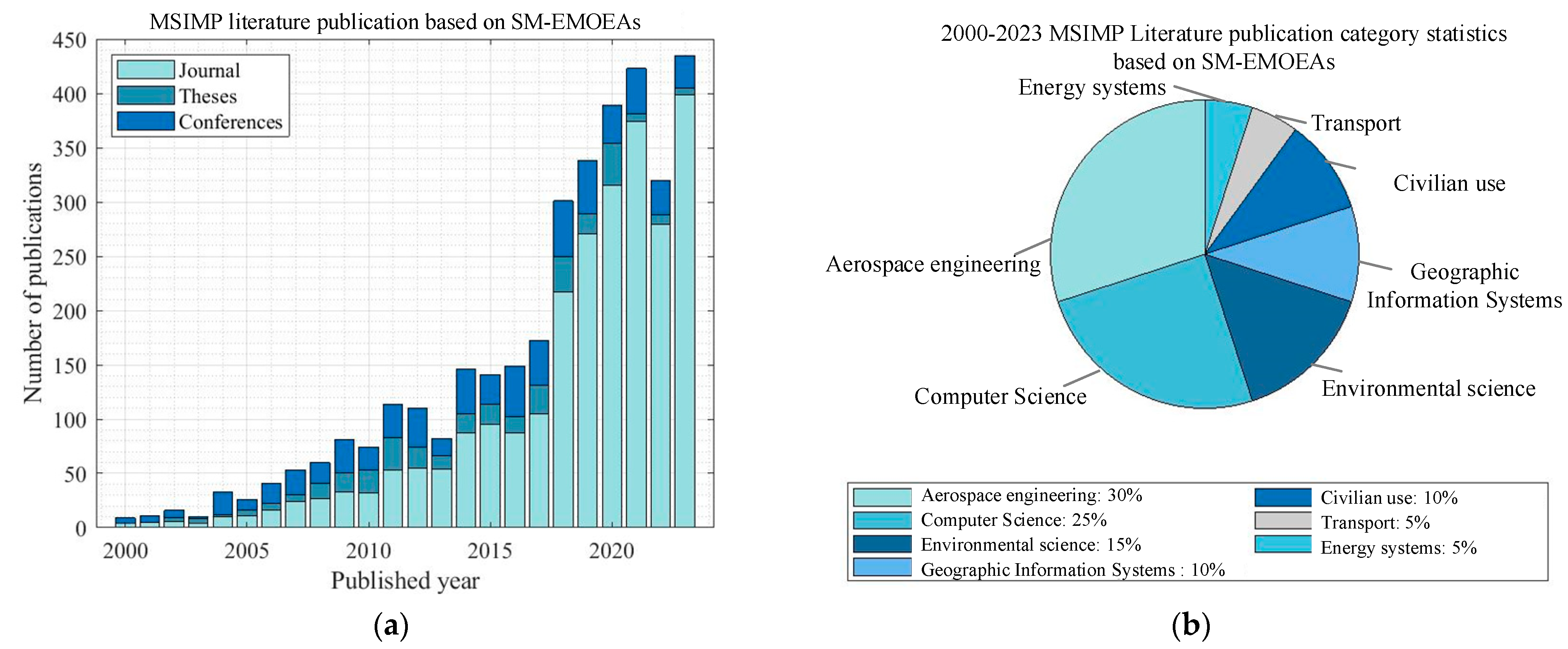
6.1. Publication of Literature on SM-EMOEAs and MSIMP Based on SM-EMOEAs

In this work, we searched through databases such as the Science Citation Index (SCI), Scopus Literature Index, and EI Engineering Index (EI); conducted literature research on SM-EMOEAs; and classified the development of SM-EMOEAs into four stages as follows.

• Embryonic period (2000–2005): preliminary application and basic research of surrogate models [155,156,157].
• Development period (2006–2012): improvement of surrogate models and optimization of expensive multi-objective evolutionary algorithms [158,159,160].
• Rapid growth period (2012–2019): improvement of surrogate models and application of expensive multi-objective evolutionary algorithms [161,162,163].
• Maturity period (2019–2024): combination of advanced technology leads to methodologically diverse SM-EMOEAs, improving their efficiency and adaptability [164].

The specifics regarding the development of SM-EMOEAs are shown in Figure 9.

In Figure 10, the publication of journal papers, conferences, and dissertations involving SM-EMOEAs from 2000 to 2023 is summarized. Figure 10a demonstrates the publication numbers of these three types of papers, and the results show that the research interest and attention of domestic and foreign researchers regarding SM-EMOEAs have been increasing, especially in 2015, which showed significant growth. Figure 10b shows the statistics of the literature publication categories based on SM-EMOEAs, in which the three categories of technology, science, and computer science occupy the main share, indicating that SM-EMOEAs have a wide range of application scenarios in these fields.

In addition, the literature on MSIMP based on SM-EMOEAs was analyzed. The publication of MSIMP studies based on SM-EMOEAs between 2000 and 2023 is shown in Figure 11. Figure 11a shows that the number of MSIMP studies based on SM-EMOEAs exhibited a significant increase between 2000 and 2023. Figure 11b reflects that MSIMP based on SM-EMOEAs provides strong technical support and a good algorithmic foundation in technical fields such as aerospace and computer science.

6.2. Future Research Trends

MSIMP based on SM-EMOEAs has significant advantages in effectively dealing with high-dimensional complexity, multi-objective conflicts, and dynamic changes. However, MSIMP based on SM-EMOEAs still faces many challenges, so it is important to discuss the future directions and trends of this field.

• Distributed parallel computing combined with MSIMP based on SM-EMOEAs. There has recently been a sharp increase in the demand for observation data for multi-satellite imaging missions, and the training process of surrogate models in SM-EMOEAs involves a large amount of computational data. However, a single node has limited computational capabilities, which makes it difficult to satisfy the huge demand for data processing in a short time. Distributed parallel computing is capable of training surrogate models in a multi-node parallel environment, accelerating agent model training using a distributed deep learning framework and realizing the parallelized evaluation of MSIMP schemes. Thus, it can significantly improve the computational efficiency and processing power of SM-EMOEAs. Therefore, the investigation of efficient and robust distributed parallel computing is of great significance for the future development of MSIMP based on SM-EMOEAs.
• Data-driven and big data analysis combined with MSIMP based on SM-EMOEAs. MSIMP involves mission requirements in a complex environment with multiple objectives, constraints, and dynamic variables, and there is a large number of uncertainties, such as weather variations and satellite orbital drift, in the implementation of the MSIMP scheme. In addition, SM-EMOEAs rely on high-precision surrogate models to evaluate the real objective function, which involves a large amount of observation data. Data-driven and big data analytics enable real-time MSIMP observation and the analysis of historical data, respond to the changing needs of MSIMP in complex environments, and improve the prediction accuracy and generalization of surrogate models. Therefore, the investigation of efficient and intelligent data-driven approaches and big data analysis are crucial for the future development of MSIMP based on SM-EMOEAs.
• Integrating deep and reinforcement learning techniques with MSIMP based on SM-EMOEAs. Optimal MSIMP involves complex decision-making scenarios, such as disaster monitoring and emergency response, crop growth monitoring, urban traffic flows, and so on, and traditional optimization methods have limitations in dealing with high-dimensional complexity. Integrating deep learning with reinforcement learning can improve the optimization accuracy and efficiency through enabling the processing of high-dimensional data through deep neural networks and the capture of complex relationships in mission planning. In addition, an end-to-end learning framework that integrates deep learning with reinforcement learning can extract key features from satellite sensor data to guide MSIMP task allocation. Therefore, the integration of deep learning and reinforcement learning techniques with MSIMP based on SM-EMOEAs can provide powerful technical support and optimization capabilities for MSIMP.
• Augmented reality (AR) and virtual reality (VR)-assisted decision-making combined with MSIMP based on SM-EMOEAs. MSIMP involves high-dimensional data and complex decision-making processes, and traditional decision support systems are limited in terms of interface interaction. AR and VR technologies provide immersive and interactive environments that enable the real-time visualization of the mission progress and satellite status, enabling users to intuitively manipulate and analyze mission planning data in a virtual space. Therefore, investigating the combination of AR- and VR-assisted decision making with MSIMP based on SM-EMOEAs will significantly advance the development of MSIMP visualization.

6.3. Conclusions

In this work, we first classified MSIMP according to the time dimension, space dimension, and task planning and management; introduced the related disciplines and application areas regarding MSIMP in the pre-processing phase, task planning phase, execution phase, and feedback re-planning phase; and analyzed the constraints of MSIMP. Second, the mathematical model of MSIMP was introduced from four aspects—namely, the target mission set, satellite resource set, time window set, and evaluation set—and the application scenarios and characteristics of traditional optimization algorithms for MSIMP were analyzed in detail. Then, the MSIMP process was discussed to provide a comprehensive overview of the classical EMOEAs. Three types of commonly used surrogate models—namely, statistical models, function approximation models, and machine-learning-based models—were summarized and analyzed to explore surrogate-model-based algorithms for EMOEAs. Finally, improved SM-EMOEAs for MSIMP were discussed in terms of improved surrogate models, improved adaptive strategies, and solution diversity maintenance and quality assessment. Moreover, we summarized the improvement methods, such as the global surrogate model, local surrogate model, two-layer surrogate model, and aggregated surrogate model. We also summarized the adaptive improvement strategies, including the adaptive sampling strategy, multiple-population co-evolutionary strategy, and domain knowledge strategy, as well as the diversity maintenance and quality assessment methods, to enable broad comprehension.