Continuum Modeling and Boundary Control of a Satellite with a Large Space Truss Structure

Abstract

Due to its advantages of easy deployment and high stiffness-to-mass ratio, the utilization of truss structures for constructing large satellites presents an appealing solution for modern space missions, including Earth observation and astronomy. However, the dimensions of the traditional finite element model for a satellite with a large space truss structure become exceedingly large as the structure’s size increases. The control system design process based on the finite element model is complex and time-consuming. This paper employs the continuum modeling method to represent the truss structure as a continuous entity. The bending vibrations of the truss structure are encapsulated by a simplified partial differential equation (PDE), as opposed to the more intricate traditional finite element model. Simultaneously, the satellite’s attitude motion is characterized by an ordinary differential equation (ODE). Building upon this coupled PDE-ODE model, a boundary control law that only requires sensors/actuators at the boundary is formulated to effectively mitigate structural vibrations and regulate the satellite’s attitude. The exponential stability of this closed-loop system is scrutinized using Lyapunov’s direct method. The simulation results affirm that the continuum modeling method is indeed well-suited for satellites endowed with substantial truss structures, and the proposed boundary law proves to be highly effective in both attitude tracking and vibration suppression.

1. Introduction

Large space truss structures have found extensive applications in modern space missions, including Earth observation [1,2,3], deep space exploration [4,5], and astronomy observation [6], owing to their attributes of easy deployment and high stiffness-to-mass ratios. However, due to launch capacity limitations, these structures tend to be highly flexible with low and dense natural frequencies, presenting significant challenges in control system design.

Smart materials have been widely used for the active vibration control of flexible structures [7,8,9]. In recent years, several researchers have explored the use of smart materials to actively suppress vibrations in large space structures. In a previous study [10], a pair of parallel-mounted piezoelectric actuators were deployed at one end of the antenna to mitigate first-order bending vibrations in the hoop truss structure. The author proposed a Mamdani-type fuzzy logic controller and verified its effectiveness through experiments. Additionally, in another study [11], a hybrid controller integrating PD and fuzzy logic control was devised, where the control gains of the PD controller were adaptively adjusted by a fuzzy logic controller in response to varying vibration amplitudes. This resulted in an enhanced damping of the closed-loop system, demonstrating superior performance in vibration suppression compared to the traditional PD controller. Furthermore, in ref. [12], a gravity compensation system was designed, affirming that a controller based on the PD algorithm and fuzzy algorithm effectively dampens vibrations in the hoop truss structure within a weightless environment.

Conversely, distributed control strategies employing sensors and actuators strategically mounted on large space structures have also been investigated for active vibration suppression. Ref. [13] introduced a linear–quadratic–Gaussian (LQG) controller for truss structures, optimizing actuator placement via a genetic algorithm to enhance quadratic performance indices, thereby achieving superior performance in structural vibration suppression. In ref. [14], an online learning algorithm was introduced to autonomously update the rule base of the fuzzy controller based on the structural response, eliminating the need for human expertise in rule base designs. Ref. [15] tried to use adaptive piezoelectric vibration absorbers to dampen the vibrations in the truss structure and conducted experiments to validate the effectiveness of the absorbers. Additionally, in ref. [16], a velocity feedback control strategy was utilized to attenuate vibrations induced by attitude maneuvers and orbital perturbations. Genetic algorithms and reinforcement learning were employed to optimize the velocity feedback gain, minimizing actuator power consumption. Ref. [17] proposed an integrated control scheme combining distributed control for flexible truss and centralized control for the platform. Sensors and actuators were mounted on the truss structure for vibration control, with optimized placement using Gramian-based techniques. PD and PID control laws were applied for attitude control and vibration suppression, respectively. The authors assessed controller performance during attitude maneuvers through numerical simulations. Furthermore, in ref. [18], the author considered uncertainties in the dynamical model and developed an attitude robust controller based on the μ-synthesis theory. Ref. [19] developed a disturbance observer-based integral terminal sliding-mode controller to constrict the vibration of truss structures under unknown disturbances. In ref. [20], a distributed adaptive neural network control approach was proposed to reduce the dependence of controller designs on dynamic models. Lastly, in ref. [21], the control of dynamic vibration and quasi-static deformation of space truss structures induced by thermal loads was studied. An integrated controller comprising a positive position feedback compensator for quasi-static deformation and a positive acceleration feedback compensator for dynamic vibration was developed. Cable actuators were used in ref. [22] to suppress vibrations in the antenna structure. Moreover, unilateral and saturation constraints on the inputs were also considered in the design of the control law. The work in ref. [23] focused on suppressing high-frequency vibrations in truss structures by regulating power flow transmission, demonstrating its effectiveness.

In prior studies, finite element models were employed for control system designs. However, the dimensions of these models become exceedingly large as the structure’s size increases. Additionally, obtaining a suitable reduced-order model to accurately depict the dynamic behavior of large space truss structures characterized by low natural frequencies and dense frequency distribution proves to be complex and time-consuming.

To tackle this issue, some scholars have explored the utilization of the continuum modeling method to represent large truss structures [24,25,26,27,28]. Truss structures, being periodic and composed of numerous fundamental elements, can be equivalently represented as continua through an energy-equivalence homogenization approach. This modeling technique has demonstrated effectiveness, particularly for large-scale structures. In ref. [29], the equivalent continuum modeling method was employed to characterize beam-like truss structures with repeated patterns. The experimental results substantiate that the derived continuum model accurately predicts the natural frequencies of these structures. Subsequently, in ref. [30], continuum modeling was applied to hoop truss structures that are commonly utilized in space missions. The natural frequencies and mode shapes obtained from the continuum model closely matched those obtained from the full-scale finite element model. Building upon the continuum model, vibration control for large truss structures was further investigated in ref. [31]. The author strategically placed three actuators within the structure and devised a linear quadratic regulator (LQR) controller to suppress structural vibrations. The efficacy of the LQR vibration controller was assessed through numerical simulations. The works in ref. [32] discretized the continuum model using the Galerkin method and limited consideration to the first three bending modes in LQR controller design. Both refs. [31,32] involved the discretization of the continuum model and distributed actuators were used for vibration control. In this present work, we delve into the boundary controller design of a satellite featuring a large truss structure, exclusively relying on the continuum model without any discretization or reduction. The control system design process is much simpler. Moreover, the proposed boundary controller only uses actuators at the central hub to ensure that the system is exponentially stable, which is easy to implement in real applications.

The organization of this paper is structured as follows: Section 2 employs the continuum modeling method to formulate the equations of motion for the satellite equipped with a large truss structure. Subsequently, in Section 3, a boundary control law that only requires sensors/actuators at the central hub is crafted to achieve both attitude tracking and vibration suppression for the flexible satellite. Finally, Section 4 conducts numerical simulations to evaluate the effectiveness of the proposed boundary control law.

2. Dynamic Modeling

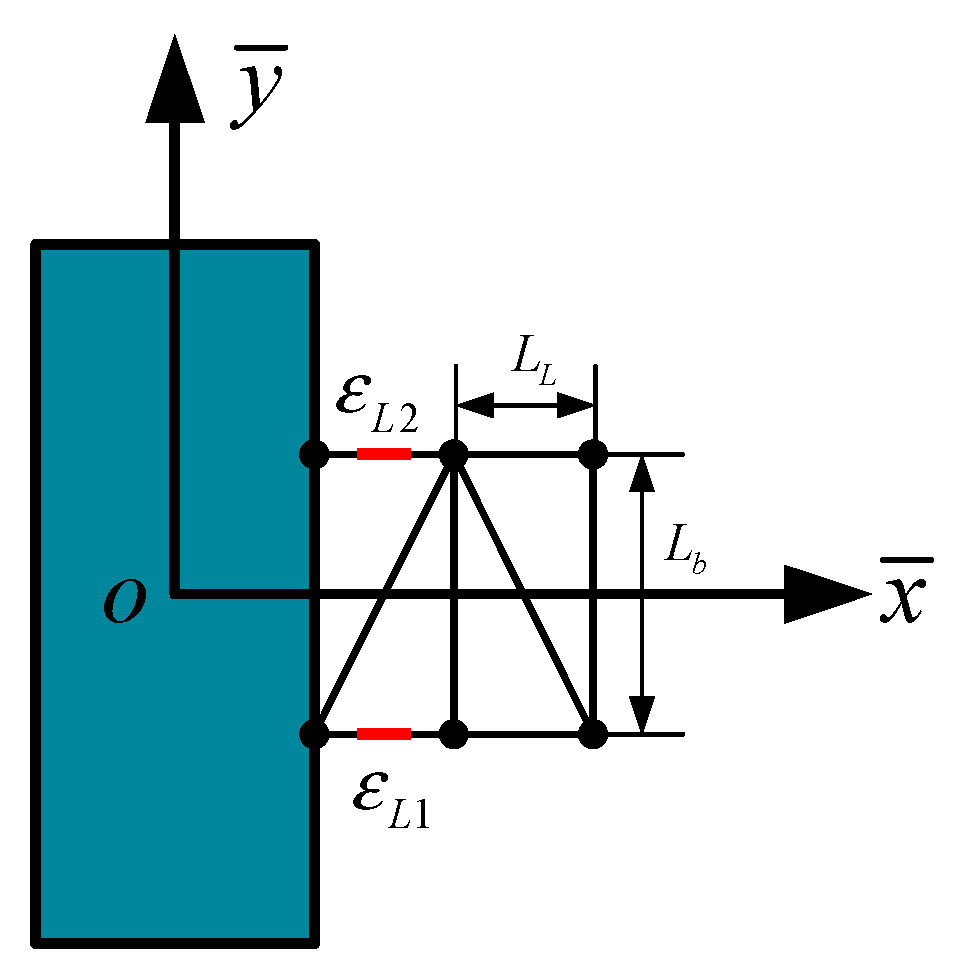
The satellite under investigation, illustrated in Figure 1, comprises a central hub and a symmetric truss structure. In this configuration, the attitude motion of the central hub is interlinked with the bending vibration of the truss structure. Ref. [24] asserts that the bending vibration of the symmetric truss can be decoupled in distinct motion coordinates. Consequently, this study exclusively addresses the motion of the flexible satellite in the plane xoy.

Truss structures, prevalent in space applications, exhibit a repetitive pattern and consist of numerous elemental components, as depicted in Figure 1. Leveraging this characteristic, a continuum modeling approach is employed to represent the truss structure. This technique assumes that the energy of an elemental component equates to that of a continuum segment of equivalent length, rendering the truss equivalent to a continuum. Consequently, the vibration of the truss structure can be succinctly delineated through simple partial differential equations. Before modeling the flexible satellite, the following assumptions are established:

(1)

The truss structure is characterized by pin connections, allowing the members to be modeled as bar elements.

(2)

Transverse deformation in the truss structure is negligible, enabling the dismissal of geometric and material nonlinearity.

(3)

The nonlinear coupling effect between attitude motion and structural vibration is deemed insignificant and thus disregarded.

To represent the attitude motion and structural vibration of the satellite, three coordinate systems are defined: an inertial coordinate system xoy, a body coordinate system $\overline{x}o\overline{y}$, and a local coordinate system for continuum modeling of the truss structure, as illustrated in Figure 2.

Within the continuum modeling framework, it is posited that the strain energy of the elemental component matches that of a continuum under the same displacement field. Adhering to the linear assumption adopted in ref. [25], the displacement field is defined as follows:

$$\begin{array}{l}{u}_1(\widehat{x},\widehat{y})=-\widehat{y}\frac{\partial u_{20}(\widehat{x})}{\partial \widehat{x}}\\ u_2(\widehat{x},\widehat{y})=u_{20}(\widehat{x})+\widehat{y}{\epsilon }_{\widehat{y}}(\widehat{x})\end{array}$$

(1)

where $u_{20}(\widehat{x})$ represents transverse displacement at the centerline, and $\partial u_{20}(\widehat{x})/\partial \widehat{x}$ represents the slope of the transverse displacement. In this study, we assumed that the rotation component ${\phi }_0(\widehat{x})$ is equal to $\partial u_{20}(\widehat{x})/\partial \widehat{x}$. Hence, ${\epsilon }_{\widehat{y}}(\widehat{x})$ is the strain in the y direction.

Taking derivatives of Equation (1) with respect to $\widehat{x}$ and $\widehat{y}$, the strain field expression can be written as

$$\begin{array}{l}{\epsilon }_{\widehat{x}}(\widehat{x},\widehat{y})=\frac{\partial u_1(\widehat{x},\widehat{y})}{\partial \widehat{x}}=-\widehat{y}\frac{{\partial }^2{u}_{20}(\widehat{x})}{\partial {\widehat{x}}^2}\\ {\epsilon }_{\widehat{y}}(\widehat{x},\widehat{y})=\frac{\partial u_2(\widehat{x},\widehat{y})}{\partial \widehat{y}}={\epsilon }_{\widehat{y}}(\widehat{x})\\ {\epsilon }_{\widehat{x}\widehat{y}}(\widehat{x},\widehat{y})=\frac{1}{2}\left(\frac{\partial u_1(\widehat{x},\widehat{y})}{\partial \widehat{y}}+\frac{\partial u_2(\widehat{x},\widehat{y})}{\partial \widehat{x}}\right)=\widehat{y}\frac{\partial {\epsilon }_{\widehat{y}}(\widehat{x})}{\partial \widehat{x}}\end{array}$$

(2)

According to Equation (2), the strain energy of the fundamental element can be written as

$$U_f=\frac{1}{2}{\displaystyle \sum _{i=1}^9{E}^{(i)}{A}^{(i)}{L}^{(i)}{\left({\epsilon }^{(i)}\right)}^2}$$

(3)

where $E^{(i)}$ is the elastic modulus of member $i$, $A^{(i)}$ is its cross-sectional area, and $L^{(i)}$ is its length. Members 1 and 2 are shared with the adjacent fundamental elements; hence, $A^{(1)}$ and $A^{(2)}$ should be halved. ${\epsilon }^{(i)}$ is the axial strain of member $k$ evaluated at the center and can be determined by the expression

$${\epsilon }^{(i)}=l_x^2{\epsilon }_{\widehat{x}}(\widehat{x},\widehat{y})+l_y^2{\epsilon }_{\widehat{y}}(\widehat{x},\widehat{y})+2l_x{l}_y{\epsilon }_{\widehat{x}\widehat{y}}(\widehat{x},\widehat{y})$$

(4)

where $l_x$ and $l_y$ represent the directional cosine of member $i$.

From Equation (2), it can be determined that the strain components are related to $\widehat{x}$ in an implicit form. To solve this problem, the strain components given in Equation (2) are approximated by Taylor’s series expansions as follows:

$$\begin{array}{l}{\epsilon }_{\widehat{x}}(\widehat{x},\widehat{y})=-\widehat{y}\frac{{\partial }^2{u}_{20}({\widehat{x}}_0)}{\partial {\widehat{x}}^2}-\widehat{x}\widehat{y}\frac{{\partial }^3{u}_{20}({\widehat{x}}_0)}{\partial {\widehat{x}}^3}\\ {\epsilon }_{\widehat{y}}(\widehat{x},\widehat{y})=\frac{\partial u_2(\widehat{x},\widehat{y})}{\partial \widehat{y}}={\epsilon }_{\widehat{y}}({\widehat{x}}_0)+\widehat{x}\frac{\partial {\epsilon }_{\widehat{y}}({\widehat{x}}_0)}{\partial \widehat{x}}+\frac{1}{2}{\widehat{x}}^2\frac{{\partial }^2{\epsilon }_{\widehat{y}}({\widehat{x}}_0)}{\partial {\widehat{x}}^2}\\ {\epsilon }_{\widehat{x}\widehat{y}}(\widehat{x},\widehat{y})=\frac{1}{2}\left(\frac{\partial u_1(\widehat{x},\widehat{y})}{\partial \widehat{y}}+\frac{\partial u_2(\widehat{x},\widehat{y})}{\partial \widehat{x}}\right)=\widehat{y}\frac{\partial {\epsilon }_{\widehat{y}}({\widehat{x}}_0)}{\partial \widehat{x}}+\widehat{y}\widehat{x}\frac{{\partial }^2{\epsilon }_{\widehat{y}}({\widehat{x}}_0)}{\partial {\widehat{x}}^2}\end{array}$$

(5)

where ${\widehat{x}}_0$ is the coordinate at the center of the fundamental element.

Substituting Equation (5) into Equations (3) and (4), the strain energy of the fundamental element can be determined. Following the assumption of local free deformation, beam theory, and compatibility condition used in ref. [18], we have

$$\frac{\partial U_f}{{\partial }^3{u}_{20}({\widehat{x}}_0)/\partial {\widehat{x}}^3}=0,\frac{\partial U_f}{{\partial }^2{\epsilon }_{\widehat{y}}({\widehat{x}}_0)/\partial {\widehat{x}}^2}=0,\frac{\partial U_f}{\partial {\epsilon }_{\widehat{y}}({\widehat{x}}_0)/\partial \widehat{x}}=0,\frac{\partial U_f}{\partial {\epsilon }_{\widehat{y}}({\widehat{x}}_0)}=0.$$

(6)

Utilizing Equation (6), the strain energy of the fundamental element can be condensed as

$$U_f=\frac{1}{2}{E}_L{A}_L{L}_L{L}_b^2{\left(\frac{{\partial }^2{u}_{20}({\widehat{x}}_0)}{\partial {\widehat{x}}^2}\right)}^2$$

(7)

where subscripts $L,b$ denote longeron and batten members, respectively.

Based on the assumption of energy equivalence, the strain energy density of the continuum can be obtained by dividing Equation (7) by the length of the fundamental element

$${\overline{U}}_f=\frac{1}{4}{E}_L{A}_L{L}_b^2{\left(\frac{{\partial }^2{u}_{20}({\widehat{x}}_0)}{\partial {\widehat{x}}^2}\right)}^2.$$

(8)

Integrating Equation (8) over the entire structure in the body coordinate system, the strain energy of the system can be found using the expression

$$U=\frac{1}{4}{\displaystyle {\int }_0^L{E}_L{A}_L{L}_b^2{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}=\frac{1}{2}{\displaystyle {\int }_0^L{C}_1{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}.$$

(9)

The kinetic energy of the truss structure contains angular kinetic energy and vibrational kinetic energy. The position of the truss structure in the inertial coordinate system can be expressed as

$$r\left(x,y\right)=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{r}_{0x}+u_1\\ r_{0y}+u_2\end{array}\right]$$

(10)

where $\left(r_{0x},r_{0y}\right)$ is defined in the body coordinate system and refers to the position of the point $\left(x,y\right)$ in the undeformed state. $u\left(x,y\right)=\left(u_1,u_2\right)$ refers to the displacement of the point $\left(x,y\right)$ in the body coordinate system. $\theta$ is the angle of rotation of the central body.

Taking derivatives of Equation (10) with respect to time and neglecting nonlinear coupling terms, we have

$$\dot{r}=\left[\begin{array}{c}{\dot{r}}_x\\ {\dot{r}}_y\end{array}\right]=\left[\begin{array}{cc}-\sin \theta & -\cos \theta \\ \cos \theta & -\sin \theta \end{array}\right]\left[\begin{array}{c}{r}_{0x}\dot{\theta }\\ r_{0y}\dot{\theta }\end{array}\right]+\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{\dot{u}}_1\\ {\dot{u}}_2\end{array}\right].$$

(11)

The kinetic energy of a fundamental element can be expressed as

$$T_f=\frac{1}{6}{\displaystyle \sum _{i=1}^9{\rho }^{(i)}{A}^{(i)}{L}^{(i)}\left[{\left({\dot{r}}_{x,1}^{(i)}\right)}^2+{\left({\dot{r}}_{y,1}^{(i)}\right)}^2+{\left({\dot{r}}_{x,2}^{(i)}\right)}^2+{\left({\dot{r}}_{y,2}^{(i)}\right)}^2+{\dot{r}}_{x,1}^{(i)}{\dot{r}}_{x,2}^{(i)}+{\dot{r}}_{y,1}^{(i)}{\dot{r}}_{y,2}^{(i)}\right]}+\frac{1}{2}{\displaystyle \sum _{k=1}^6{m}^{(k)}\left[{\left({\dot{r}}_x^{(k)}\right)}^2+{\left({\dot{r}}_y^{(k)}\right)}^2\right]}$$

(12)

where ${\rho }^{(i)}$ denotes the density of member $i$. Subscripts 1 and 2 denote nodes 1 and 2 of the members, respectively. $m^{(k)}$ is the mass of joint $k$. Since the truss structure exhibits a repetitive pattern, we assumed that all joints have equal mass in this study. The mass of the joint is $m_j$.

The displacement field $\left(u_1,u_2\right)$ is the same as that given in Equation (1). Substituting Equation (11) into Equation (12) and neglecting the effects of strain components on kinetic energy, the kinetic energy of a fundamental element can be rewritten as

$$\begin{array}{ll}{T}_f=& \frac{1}{6}{\rho }_L{A}_L{L}_L\left[12{\left(r_{0x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+4L_L^2{\dot{\theta }}^2+12{\left(\frac{L_b}{2}\dot{\theta }\right)}^2\right]+\frac{1}{6}{\rho }_d{A}_d{L}_d\left[6{\left(r_{0x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+2L_L^2{\dot{\theta }}^2+2{\left(\frac{L_b}{2}\dot{\theta }\right)}^2\right]\\ & +\frac{1}{6}{\rho }_b{A}_b{L}_b\left[6{\left(r_{0x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+3L_L^2{\dot{\theta }}^2+2{\left(\frac{L_b}{2}\dot{\theta }\right)}^2\right]+m_j\left[2{\left(r_{0x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+L_L^2{\dot{\theta }}^2+2{\left(\frac{L_b}{2}\dot{\theta }\right)}^2\right]\end{array}$$

(13)

where the subscript $d$ denotes diagonal members.

According to Equation (13), the kinetic energy for a continuum of the same length can be written as

$$T_f=\frac{1}{2}{\displaystyle \underset{r_{0x}-L_L}{\overset{r_{0x}+L_L}{\int }}\left[m_0{\left(\overline{x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+m_1{\dot{\theta }}^2\right]d\overline{x}}$$

(14)

in which

$$\begin{array}{l}{m}_0=2{\rho }_L{A}_L+{\rho }_d{A}_d\frac{L_d}{L_L}+{\rho }_b{A}_b\frac{L_b}{L_L}+\frac{2m_j}{L_L}\\ m_1=\left[\frac{{\rho }_L{A}_L}{2}+{\rho }_d{A}_d\frac{L_d}{12L_L}+{\rho }_b{A}_b\frac{L_b}{12L_L}+\frac{m_j}{2L_L}+{\rho }_b{A}_b\frac{L_b}{6L_L}\frac{L_L^2}{L_b^2}+\frac{m_j}{3L_L}\frac{L_L^2}{L_b^2}\right]L_b^2\end{array}$$

(15)

Adding the kinetic energy of the central body and integrating Equation (14) over the entire structure, the kinetic energy of the system can be expressed as

$$T=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}\left[m_0{\left(\overline{x}\dot{\theta }+{\dot{u}}_{20}\right)}^2+m_1{\dot{\theta }}^2\right]d\overline{x}+\frac{1}{2}}J{\dot{\theta }}^2.$$

(16)

The virtual work carried out by the control force can be written as

$$\delta W=\tau \left(t\right)\delta \theta .$$

(17)

Combining Equations (9), (14), and (17) and using Hamilton’s principle, the equations of motion of the system can be obtained as

$$m_0{\ddot{u}}_{20}\left(\overline{x},t\right)+m_0\overline{x}\ddot{\theta }\left(t\right)+C_1\frac{{\partial }^4{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^4}=0$$

(18)

$$J\ddot{\theta }\left(t\right)+{\displaystyle \underset{0}{\overset{L}{\int }}{m}_0\overline{x}\left[x\ddot{\theta }\left(t\right)+{\ddot{u}}_{20}\left(\overline{x},t\right)\right]d\overline{x}}+{\displaystyle \underset{0}{\overset{L}{\int }}{m}_1\ddot{\theta }\left(t\right)d\overline{x}}=\tau \left(t\right),$$

(19)

with the following boundary conditions

$$u_{20}\left(0,t\right)=0,\frac{\partial u_{20}\left(0,t\right)}{\partial \overline{x}}=0,\frac{{\partial }^2{u}_{20}\left(L,t\right)}{\partial {\overline{x}}^2}=0,\frac{{\partial }^3{u}_{20}\left(L,t\right)}{\partial {\overline{x}}^3}=0.$$

(20)

Substituting Equation (18) into Equation (19) and using boundary conditions expressed in Equation (20), Equation (19) can be rewritten as

$$J\ddot{\theta }\left(t\right)+{\displaystyle \underset{0}{\overset{L}{\int }}{m}_1\ddot{\theta }\left(t\right)d\overline{x}}=C_1\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}+\tau \left(t\right).$$

(21)

Partial differential Equation (18) represents the motion of bending vibration of the truss structure. Equation (21) represents the attitude motion of the central body. The attitude motion of the central body is coupled with the bending vibration of the truss.

3. Control Design

The primary objective of this study is to formulate a boundary control law that can effectively regulate the attitude of the central body while concurrently suppressing truss vibration. Boundary control, recognized for its applicability in distributed parameter systems, has demonstrated successful implementation in various domains, including robot control [33] and cable elevator control [34], among others. This section is dedicated to the development of a boundary control law tailored for the flexible satellite, utilizing the coupled ODE-PDE model delineated in Equations (18) and (21). The stability of the resultant closed-loop system is assessed via Lyapunov’s direct method.

For ease of stability analysis, the following lemmas are introduced:

Lemma 1.

For any continuously differentiable function, $\kappa \left(x\right)$, defined on $(x,t)\in \left[0,L\right]\times \left[0,\infty \right)$, we have [35]

$${\displaystyle \underset{0}{\overset{L}{\int }}\kappa {\left(x,t\right)}^{2}dx}\le 2L\kappa {\left(0,t\right)}^2+4L^2{{\displaystyle \underset{0}{\overset{L}{\int }}\left[\frac{\partial \kappa \left(x,t\right)}{\partial x}\right]}}^{2}dx.$$

(22)

Lemma 2.

For any continuous functions, ${\kappa }_1$ and ${\kappa }_2$, we have [35]

$${\displaystyle \underset{0}{\overset{L}{\int }}{\kappa }_1{\kappa }_{2}dx}\le \frac{\gamma }{2}{\displaystyle \underset{0}{\overset{L}{\int }}{\left[{\kappa }_1\right]}^2}dx+\frac{1}{2\gamma }{\displaystyle \underset{0}{\overset{L}{\int }}{\left[{\kappa }_2\right]}^2}dx.$$

(23)

To stabilize the flexible satellite, the following boundary control law is proposed:

$$\tau \left(t\right)=-C_1\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}+\frac{{\lambda }_2}{{\chi }_3}\left({\chi }_3\dot{\theta }-{\chi }_2\left({\chi }_1{\theta }_e-\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}\right)\right)-\left(\frac{J_A{\chi }_1{\chi }_2}{{\chi }_3}+\frac{C_1}{{\chi }_2{\chi }_3}\right) \dot{\theta }(t)+\frac{J_A{\chi }_2}{{\chi }_3}\frac{{\partial }^2{\dot{u}}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}-{\lambda }_{1}S(t).$$

(24)

where $S(t)={\chi }_3\dot{\theta }+{\chi }_2[{\chi }_1{\theta }_e-{\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2]$ and $J_A=J+{\displaystyle \underset{0}{\overset{L}{\int }}{m}_{1}d\overline{x}}$. In ${\theta }_e=\theta -{\theta }_d$, ${\theta }_d$ is the desired attitude angle.

As seen in Equation (24), the proposed boundary control law requires $\dot{\theta }(t),\theta (t),{\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2$, and ${\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2$. ${\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2,{\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ are used for vibration suppression, and $\dot{\theta }(t),\theta (t)$ are used for attitude control. As described in Section 2, the strain field of the truss structure can be expressed by Equation (2). Therefore, ${\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ can be measured by strain gauges configured, as shown in Figure 3. By using Equations (2) and (4), ${\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ can be easily obtained with

$$\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}=\frac{\left({\epsilon }_{L1}-{\epsilon }_{L2}\right)}{L_b}.$$

(25)

Remark 1.

The control inputs $\tau \left(t\right)$ requires $\dot{\theta }(t),\theta (t),{\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ and ${\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2$. ${\partial }^2{u}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ can be obtained from Equation (25), where ${\epsilon }_{L1},{\epsilon }_{L2}$ can be measured by strain gauges. ${\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2$ can be further obtained using the numerical difference method. $\dot{\theta }(t)$ and $\theta (t)$ can be measured using a gyroscope and a star sensor mounted onto the central body.

Theorem 1.

For the dynamical system described by governing Equations (18) and (21) and boundary condition (20), the closed-loop system will be exponentially stable under the proposed boundary control law (24).

Proof. 

To perform an analysis of the stability of the closed-loop system, the following Lyapunov function is defined as

$$V\left(t\right)=E_k\left(t\right)+E_s\left(t\right)+{\eta }_1{E}_1\left(t\right)+{\eta }_2{E}_2\left(t\right)+\frac{1}{2}{J}_{A}S{(t)}^2+\frac{1}{2}{\chi }_1{C}_1{\theta }_e^2$$

(26)

where

$$E_k\left(t\right)=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}\left[m_0{\left(\overline{x}\dot{\theta }+{\dot{u}}_{20}\right)}^2\right]d\overline{x}},$$

(27)

$$E_s\left(t\right)=\frac{1}{2}{\displaystyle {\int }_0^L{C}_1{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}},$$

(28)

$$E_1\left(t\right)={\displaystyle {\int }_0^L\left[\overline{x}-L\right]\left(\frac{\partial u_{20}(\overline{x},t)}{\partial \overline{x}}\right)\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]d\overline{x}},$$

(29)

$$E_2\left(t\right)={\displaystyle {\int }_0^L\left[\overline{x}{\theta }_e(t)+u_{20}(\overline{x},t)\right]\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]d\overline{x}}.$$

(30)

Using Lemmas 1 and 2, the bounds for $E_1\left(t\right)$ and $E_2\left(t\right)$ can be found using

$$\begin{array}{ll}\left|E_1\left(t\right)\right|& \le \frac{L}{2}{\displaystyle {\int }_0^L{\left(\frac{\partial u_{20}(\overline{x},t)}{\partial \overline{x}}\right)}^{2}d\overline{x}}+\frac{L}{2}{\displaystyle {\int }_0^L{\left(\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right)}^{2}d\overline{x}}\\ & \le 2L^3{\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}+\frac{L}{2}{\displaystyle {\int }_0^L{\left(\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right)}^{2}d\overline{x}}\end{array},$$

(31)

$$\begin{array}{ll}\left|E_2\left(t\right)\right|& \le \frac{1}{2}{\displaystyle {\int }_0^L{\left(\overline{x}{\theta }_e(t)+u_{20}(\overline{x},t)\right)}^{2}d\overline{x}}+\frac{1}{2}{\displaystyle {\int }_0^L{\left(\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right)}^{2}d\overline{x}}\\ & \le 4L^3{\left[{\theta }_e(t)\right]}^2+8L^4{\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}+\frac{1}{2}{\displaystyle {\int }_0^L{\left(\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right)}^{2}d\overline{x}}\end{array}.$$

(32)

Substituting Equations (31) and (32) in Equation (24), the lower bound of the Lyapunov function can be obtained as

$$\begin{array}{ll}V\left(t\right)& \ge \left[\frac{1}{2}{m}_0-\frac{L}{2}{\eta }_1-\frac{1}{2}{\eta }_2\right]{\displaystyle {\int }_0^L{\left(\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right)}^{2}d\overline{x}}\\ & +\left[\frac{1}{2}{C}_1-2{\eta }_1{L}^3-8{\eta }_2{L}^4\right]{\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}\\ & +\left[\frac{1}{2}{\chi }_1{C}_1-4{\eta }_2{L}^3\right]{\left[{\theta }_e(t)\right]}^2+\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}\left[m_1{\dot{\theta }}^2\right]d\overline{x}}+\frac{1}{2}S{(t)}^2\end{array}.$$

(33)

Then, using Lemma 2, the upper bound of the Lyapunov function is expressed as

$$\begin{array}{ll}V\left(t\right)& \le \left[m_0+L{\eta }_1+{\eta }_2\right]{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}\\ & +\left[m_0{L}^3+{\eta }_1{L}^4+{\eta }_2{L}^3+\frac{1}{2}{m}_{1}L\right]{\dot{\theta }}^2(t)\\ & +\left[\frac{1}{2}{C}_1+2{\eta }_1{L}^3+8{\eta }_2{L}^4\right]{\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}\\ & +\left[\frac{1}{2}{\chi }_1{C}_1+4{\eta }_2{L}^3\right]{\left[{\theta }_e(t)\right]}^2+\frac{1}{2}S{(t)}^2\end{array}.$$

(34)

To ensure that the Lyapunov function is positive and definite, the following inequalities should hold true:

$$\left[\frac{1}{2}{m}_0-\frac{L}{2}{\eta }_1-\frac{1}{2}{\eta }_2\right]\ge 0,$$

(35)

$$\left[\frac{1}{2}{C}_1-2{\eta }_1{L}^3-8{\eta }_2{L}^4\right]\ge 0,$$

(36)

$$\left[\frac{1}{2}{\chi }_1{C}_1-4{\eta }_2{L}^3\right]\ge 0.$$

(37)

Taking the derivatives of Equation (24) with respect to time yields

$$\dot{V}\left(t\right)={\dot{E}}_k\left(t\right)+{\dot{E}}_s\left(t\right)+{\eta }_1{\dot{E}}_1\left(t\right)+{\eta }_2{\dot{E}}_2\left(t\right)+S(t)\dot{S}(t)+{\chi }_1{C}_1{\theta }_e\dot{\theta }.$$

(38)

Substituting the equations of motion of the system into ${\dot{E}}_k\left(t\right)$ and using integration by parts twice lead to

$$\begin{array}{ll}{\dot{E}}_k\left(t\right)& =-{\displaystyle \underset{0}{\overset{L}{\int }}\left[C_1\frac{{\partial }^4{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^4}\left(\overline{x}\dot{\theta }+{\dot{u}}_{20}\right)\right]d\overline{x}}\\ & =-C_1\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}\dot{\theta }-{\displaystyle \underset{0}{\overset{L}{\int }}\left[C_1\frac{{\partial }^2{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^2}\frac{{\partial }^2{\dot{u}}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^2}\right]d\overline{x}}\end{array}.$$

(39)

Differentiating $E_s\left(t\right)$, we have

$${\dot{E}}_s\left(t\right)={\displaystyle {\int }_0^L{C}_1\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\frac{{\partial }^2{\dot{u}}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)d\overline{x}}.$$

(40)

Similar to the process for ${\dot{E}}_k\left(t\right)$, the derivative of $E_1\left(t\right)$ can be expanded as

$$\begin{array}{ll}{\dot{E}}_1\left(t\right)& ={\displaystyle {\int }_0^L\left[\overline{x}-L\right]\left(\frac{\partial {\dot{u}}_{20}(\overline{x},t)}{\partial \overline{x}}\right)\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]d\overline{x}}+{\displaystyle {\int }_0^L\left[\overline{x}-L\right]\left(\frac{\partial u_{20}(\overline{x},t)}{\partial \overline{x}}\right)\left[\overline{x}\ddot{\theta }(t)+{\ddot{u}}_{20}(\overline{x},t)\right]d\overline{x}}\\ & ={\displaystyle {\int }_0^L\left[\overline{x}-L\right]\left(\frac{\partial {\dot{u}}_{20}(\overline{x},t)}{\partial \overline{x}}\right)\left[\left(\overline{x}\dot{\theta }(t)\right)+\left({\dot{u}}_{20}(\overline{x},t)\right)\right]d\overline{x}}-{\displaystyle {\int }_0^L\left[\overline{x}-L\right]\left(\frac{\partial u_{20}(\overline{x},t)}{\partial \overline{x}}\right)\left[\frac{C_1}{m_0}\frac{{\partial }^4{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^4}\right]d\overline{x}}\\ & ={\displaystyle {\int }_0^L\left[2\overline{x}-L\right]{\dot{u}}_{20}(\overline{x},t)\dot{\theta }(t)d\overline{x}}-\frac{1}{2}{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}-\frac{3}{2}\frac{C_1}{m_0}{\displaystyle {\int }_0^L{\left[\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right]}^{2}d\overline{x}+}\frac{1}{2}\frac{C_1}{m_0}L{\left[\frac{{\partial }^2{u}_{20}(0,t)}{\partial {\overline{x}}^2}\right]}^2\end{array}.$$

(41)

Substituting Equation (18) into the derivative of $E_2\left(t\right)$ and integrating by parts, we have

$$\begin{array}{ll}{\dot{E}}_2\left(t\right)& ={\displaystyle {\int }_0^L\left[\overline{x}{\theta }_e(t)+u_{20}(\overline{x},t)\right]\left[\overline{x}\ddot{\theta }(t)+{\ddot{u}}_{20}(\overline{x},t)\right]d\overline{x}}+{\displaystyle {\int }_0^L{\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}\\ & =-{\displaystyle {\int }_0^L\left[\overline{x}{\theta }_e(t)+u_{20}(\overline{x},t)\right]\left[\frac{C_1}{m_0}\frac{{\partial }^4{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^4}\right]d\overline{x}}+{\displaystyle {\int }_0^L{\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}\\ & =-\frac{C_1}{m_0}{\displaystyle {\int }_0^L{\left[\frac{{\partial }^2{u}_{20}\left(\overline{x},t\right)}{\partial {\overline{x}}^2}\right]}^{2}d\overline{x}}-\frac{C_1}{m_0}\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}{\theta }_e(t)+{\displaystyle {\int }_0^L{\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}\end{array}.$$

(42)

Differentiating $S(t)$ and substituting the proposed boundary law into $\dot{S}(t)$, we have

$$\begin{array}{ll}{J}_A\dot{S}(t)& ={\chi }_3{J}_A\ddot{\theta }+{\chi }_2{J}_A[{\chi }_1\dot{\theta }-{\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2]\\ & ={\chi }_3\left[C_1\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}+\tau \left(t\right)\right]+{\chi }_2{J}_A[{\chi }_1\dot{\theta }-{\partial }^2{\dot{u}}_{20}\left(0,t\right)/\partial {\overline{x}}^2]\\ & ={\lambda }_2\left[{\chi }_3\dot{\theta }-{\chi }_2[{\chi }_1{\theta }_e-\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}]\right]-(\frac{C_1}{{\chi }_2})\dot{\theta }(t)-{\lambda }_1{\chi }_{3}S(t)\end{array}.$$

(43)

$J_A\dot{S}(t)S(t)$ can be adjusted by designing the structure of $\tau \left(t\right)$ so that the derivative of the Lyapunov function is negative.

Combining Equations (39)–(49), the derivative of Lyapunov function can be rewritten as

$$\begin{array}{ll}\dot{V}\left(t\right)=& -\left[\frac{1}{2}{\eta }_1\right]{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}+{\eta }_2{\displaystyle {\int }_0^L{\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}+{\eta }_1{\displaystyle {\int }_0^L\left[2\overline{x}-L\right]{\dot{u}}_{20}(\overline{x},t)\dot{\theta }(t)d\overline{x}}\\ & -\left[\frac{3}{2}\frac{{\eta }_1{C}_1}{m_0}+\frac{{\eta }_2{C}_1}{m_0}\right]{\displaystyle {\int }_0^L{\left[\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right]}^{2}d\overline{x}}+\left[\frac{1}{2}\frac{{\eta }_1{C}_1}{m_0}L-{\lambda }_2{\chi }_2^2\right]{\left[\frac{{\partial }^2{u}_{20}(0,t)}{\partial {\overline{x}}^2}\right]}^2\\ & -\left[\frac{{\chi }_3{C}_1}{{\chi }_2}-{\lambda }_2{\chi }_3^2\right] {\dot{\theta }}^2(t)-{\lambda }_1{\chi }_3{S}^2(t)-{\lambda }_2{\chi }_2^2{\chi }_1^2{\theta }_e^2+\left[2{\lambda }_2{\chi }_2^2{\chi }_1-\frac{{\eta }_2{C}_1}{m_0}\right]\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}{\theta }_e(t)\end{array}.$$

(44)

Utilizing Lemma 2, the bounds of the second and third terms in the right hand of Equation (44) can be found using the following expression:

$${\eta }_1{\displaystyle {\int }_0^L\left[2\overline{x}-L\right]{\dot{u}}_{20}(\overline{x},t)\dot{\theta }(t)d\overline{x}}\le \frac{{\eta }_1}{2{\delta }_1}{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}+\frac{{\delta }_1}{2}{\eta }_1{L}^3{\dot{\theta }}^2(t),$$

(45)

$${\eta }_2{\displaystyle {\int }_0^L{\left[\overline{x}\dot{\theta }(t)+{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}\le \frac{2}{3}{\eta }_2{L}^3{\dot{\theta }}^2(t)+2{\eta }_2{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}.$$

(46)

Substituting Inequalities (45) and (46) into Equation (44), the upper bound of $\dot{V}\left(t\right)$ is expressed as

$$\begin{array}{ll}\dot{V}\left(t\right)\le & -\left[\frac{1}{2}{\eta }_1-\frac{{\eta }_1}{2{\delta }_1}-2{\eta }_2\right]{\displaystyle {\int }_0^L{\left[{\dot{u}}_{20}(\overline{x},t)\right]}^{2}d\overline{x}}-\left[\frac{3}{2}\frac{{\eta }_1{C}_1}{m_0}+\frac{{\eta }_2{C}_1}{m_0}\right]{\displaystyle {\int }_0^L{\left[\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right]}^{2}d\overline{x}}\\ & +\left[\frac{1}{2}\frac{{\eta }_1{C}_1}{m_0}L-{\lambda }_2{\chi }_2^2\right]{\left[\frac{{\partial }^2{u}_{20}(0,t)}{\partial {\overline{x}}^2}\right]}^2-\left[\frac{{\chi }_3{C}_1}{{\chi }_2}-{\lambda }_2{\chi }_3^2-\frac{{\delta }_1}{2}{\eta }_1{L}^3-\frac{2}{3}{\eta }_2{L}^3\right] {\dot{\theta }}^2(t)\\ & -{\lambda }_1{\chi }_3{S}^2(t)-{\lambda }_2{\chi }_2^2{\chi }_1^2{\theta }_e^2+\left[2{\lambda }_2{\chi }_2^2{\chi }_1-\frac{{\eta }_2{C}_1}{m_0}\right]\frac{{\partial }^2{u}_{20}\left(0,t\right)}{\partial {\overline{x}}^2}{\theta }_e(t)\end{array}.$$

(47)

If the control coefficients ${\lambda }_1,{\lambda }_2,{\chi }_1,{\chi }_2,{\chi }_3$ are chosen to make the following relationships hold,

$$\left[\frac{1}{2}{\eta }_1-\frac{{\eta }_1}{2{\delta }_1}-2{\eta }_2\right]>0,$$

(48)

$$\left[\frac{1}{2}\frac{{\eta }_1{C}_1}{m_0}L-{\lambda }_2{\chi }_2^2\right]\le 0,$$

(49)

$$\left[\frac{{\chi }_3{C}_1}{{\chi }_2}-{\lambda }_2{\chi }_3^2-\frac{{\delta }_1}{2}{\eta }_1{L}^3-\frac{2}{3}{\eta }_2{L}^3\right] >0,$$

(50)

$$\left[2{\lambda }_2{\chi }_2^2{\chi }_1-\frac{{\eta }_2{C}_1}{m_0}\right]=0,$$

(51)

$${\lambda }_1>0,{\lambda }_2>0,{\chi }_1>0,{\chi }_2>0,{\chi }_3>0,$$

(52)

then utilizing the upper bound of the Lyapunov function given in (34), we have

$$\dot{V}\left(t\right)\le -\lambda V\left(t\right)$$

(53)

where $\lambda ={\lambda }_n/{\lambda }_x$, and

$${\lambda }_x=\max \left\{\begin{array}{l}\left[m_0+L{\eta }_1+{\eta }_2\right],\left[m_0{L}^3+{\eta }_1{L}^4+{\eta }_2{L}^3+\frac{1}{2}{m}_{1}L\right],\\ \left[\frac{1}{2}{C}_1+2{\eta }_{1}L+8{\eta }_2{L}^4\right],\left[\frac{1}{2}{\chi }_1{C}_1+4{\eta }_2{L}^3\right],\frac{1}{2}\end{array}\right\},$$

$${\lambda }_n=\min \left\{\begin{array}{l}\left[\frac{1}{2}{\eta }_1-\frac{{\eta }_1}{2{\delta }_1}-2{\eta }_2\right],\left[\frac{3}{2}\frac{{\eta }_1{C}_1}{m_0}+\frac{{\eta }_2{C}_1}{m_0}\right],{\lambda }_1{\chi }_3,\\ \left[\frac{{\chi }_3{C}_1}{{\chi }_2}-{\lambda }_2{\chi }_3^2-\frac{{\delta }_1}{2}{\eta }_1{L}^3-\frac{2}{3}{\eta }_2{L}^3\right],{\lambda }_2{\chi }_2^2{\chi }_1^2\end{array}\right\}.$$

From Inequality (53), we have the following relationship for $V\left(t\right)$:

$$V\left(t\right)\le V\left(0\right)e^{-\lambda t}.$$

(54)

Based on Inequality (54), it can be concluded that the Lyapunov function converges exponentially. Utilizing the lower bound of the Lyapunov function and Inequality (54), we have

$$\begin{array}{l}{\left[{\theta }_e(t)\right]}^2\le \frac{2}{\left[{\chi }_1{C}_1-8{\eta }_2{L}^3\right]}V\left(t\right)\le \frac{2}{\left[{\chi }_1{C}_1-8{\eta }_2{L}^3\right]}V\left(0\right)e^{-\lambda t}\\ {\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}\le \frac{2}{\left[C_1-4{\eta }_{1}L-16{\eta }_2{L}^4\right]}V\left(t\right)\le \frac{2}{\left[C_1-4{\eta }_{1}L-16{\eta }_2{L}^4\right]}V\left(0\right)e^{-\lambda t}\end{array}.$$

(55)

Using Lemma 2 twice yields

$${\displaystyle {\int }_0^L{\left[u_{20}(\overline{x},t)\right]}^{2}d\overline{x}\le \frac{1}{16L^4}}{\displaystyle {\int }_0^L{\left(\frac{{\partial }^2{u}_{20}(\overline{x},t)}{\partial {\overline{x}}^2}\right)}^{2}d\overline{x}}\le \frac{1}{8L^4\left[C_1-4{\eta }_{1}L-16{\eta }_2{L}^4\right]}V\left(0\right)e^{-\lambda t}.$$

(56)

Inequalities (55) and (56) indicate that the vibration of the truss structure and the attitude tracking error of the central body converge to zero exponentially. The results of this analysis prove that the closed-loop system is exponentially stable under the proposed boundary control law when the relationships expressed in (35)–(37) and (48)–(52) hold true.

According to the aforementioned constraints, the control coefficients ${\lambda }_1,{\lambda }_2,{\chi }_1,{\chi }_2,{\chi }_3$ can be determined using the following procedure.

First, Inequality (49) holds when

$${\eta }_1=\frac{2m_0}{C_{1}L}{\lambda }_2{\chi }_2^2.$$

(57)

Then, ${\eta }_2$ can be determined using Equation (51)

$${\eta }_2=\frac{2m_0}{C_1}{\lambda }_2{\chi }_2^2{\chi }_1.$$

(58)

Substituting Equations (57) and (58) into Inequality (48), the upper bound of ${\chi }_1$ can be found using the expression

$${\chi }_1<\frac{1}{4L}\left(1-\frac{1}{{\delta }_1}\right),\hspace{1em}{\delta }_1>1.$$

(59)

Similarly, to make Inequality (50) hold, the coefficient ${\lambda }_2$ should satisfy

$${\lambda }_2<\frac{{\chi }_3{C}_1}{{\chi }_2\left[{\chi }_3^2+\frac{m_0{\delta }_1}{C_1}{\chi }_2^2{L}^2+\frac{4m_0}{3C_1}{\chi }_2^2{\chi }_1{L}^3\right]}.$$

(60)

Utilizing Inequalities (35)–(37), we have

$${\lambda }_2\le \frac{C_1}{2{\chi }_2^2+2{\chi }_2^2{\chi }_1},$$

(61)

$${\lambda }_2\le \frac{C_1^2}{8m_0{\chi }_2^2{L}^2+32m_0{\chi }_2^2{\chi }_1{L}^4},$$

(62)

$${\lambda }_2\le \frac{C_1^2}{16m_0{\chi }_2^2{L}^3}.$$

(63)

Finally, combining Inequalities (60)–(63), the upper bound of coefficient ${\lambda }_2$ can be obtained

$${\lambda }_2\le \min \left\{\begin{array}{l}\frac{{\chi }_3{C}_1}{{\chi }_2\left[{\chi }_3^2+\frac{m_0{\delta }_1}{C_1}{\chi }_2^2{L}^2+\frac{4m_0}{3C_1}{\chi }_2^2{\chi }_1{L}^3\right]},\frac{C_1}{2{\chi }_2^2+2{\chi }_2^2{\chi }_1},\\ \frac{C_1^2}{8m_0{\chi }_2^2{L}^2+32m_0{\chi }_2^2{\chi }_1{L}^4},\frac{C_1^2}{16m_0{\chi }_2^2{L}^3}\end{array}\right\}.$$

(64)

The other control coefficients ${\lambda }_1,{\chi }_2,{\chi }_3$ are arbitrary. For a satellite with given structural parameters, the control coefficients can be determined to make the equality and inequalities given in (35)–(37) and (48)–(52) hold. Thus, the closed-loop system is exponentially stable. This completes the proof. □

Remark 2.

Equations (35)–(37) and (48)–(52) are sufficient conditions for the exponential stability of the closed-loop system. Equations (35)–(37) and (48)–(52) include 11 inequalities and 1 equality. Although there are only eight coefficients, ${\lambda }_1,{\lambda }_2,{\chi }_1,{\chi }_2,{\chi }_3,{\eta }_1,{\eta }_2,{\delta }_1$, we have proved that the control coefficients ${\lambda }_1,{\chi }_2,{\chi }_3$ in boundary control law (24) can be any positive numbers. In practical applications, one can adjust the coefficients ${\lambda }_1,{\chi }_2,{\chi }_3$ carefully to obtain better control performance.

4. Simulation

In this section, the efficacy of the boundary control law, developed based on the continuum model for the satellite featuring a symmetric truss structure, is substantiated through numerical simulations. The material and geometrical attributes of the satellite, utilized in the simulations, are enumerated in

Table 1. Material and geometrical properties of the satellite.

Parameter	Value
Moment of inertia of the rigid hub, $J$	1000 kgm2
Length of the longeron, $L_L$	1 m
Length of the batten, $L_b$	1 m
Cross-sectional area of the truss member, $A_L,A_b,A_d$	2 × 10−5 m2
Density of the truss member, ${\rho }_L,{\rho }_b,{\rho }_d$	1800 kg/m3
Elastic modulus of the truss member, $E_L,E_b,E_d$	70 GPa
Mass of the joint, mj	0.2 Kg
Total length of the truss structure, $L$	50 m

. The dynamic response of the flexible satellite is computed employing a dynamic model [16], which relies on the finite element method coupled with modal decomposition. In this work, the truss members are modeled using bar elements. Using modal decomposition technique, the position of the truss structure in the body coordinate system can be expressed as

$$\overline{r}\left(\overline{x},\overline{y}\right)={\overline{r}}_0\left(\overline{x},\overline{y}\right)+{\displaystyle \sum _{i=1}^N{q}_i\left(t\right){\phi }_i\left(\overline{x},\overline{y}\right)}.$$

(65)

${\overline{r}}_0\left(\overline{x},\overline{y}\right)$ refers to the position of the point $\left(\overline{x},\overline{y}\right)$ in the undeformed state. $q_i$ refers to the generalized coordinate. ${\phi }_i\left(\overline{x},\overline{y}\right)$ is the mode shape of the truss structure, which can be obtained from the finite element model. $N$ represents the number of modes used to approximate the deformation of the truss. Following the modeling approach in ref. [16], the dynamic model can be written as

$$\left\{\begin{array}{l}J\ddot{\theta }\left(t\right)+{\displaystyle \sum _{i=1}^N{B}_{ri}{\ddot{q}}_i}=\tau \left(t\right)\\ {\ddot{q}}_i+{\omega }_i^2{q}_i+B_{ri}\ddot{\theta }\left(t\right)=0,i=1,\dots ,N\end{array}\right..$$

(66)

where $B_{ri}={\displaystyle {\int }_{Vtruss}\rho \left(\overline{x},\overline{y}\right){\overline{\mathbf{r}}}_0\left(\overline{x},\overline{y}\right)\times {\mathbf{\phi }}_i\left(\overline{x},\overline{y}\right)dV}$ is the rotational coupling coefficient. ${\omega }_i$ represents the natural frequency of the ith mode.

In this work, the first ten mode shapes are employed to represent the deformation of the truss structure. Equation (66) is solved using the fourth order Runge–Kutta method, and the time step is set to 0.001 s.

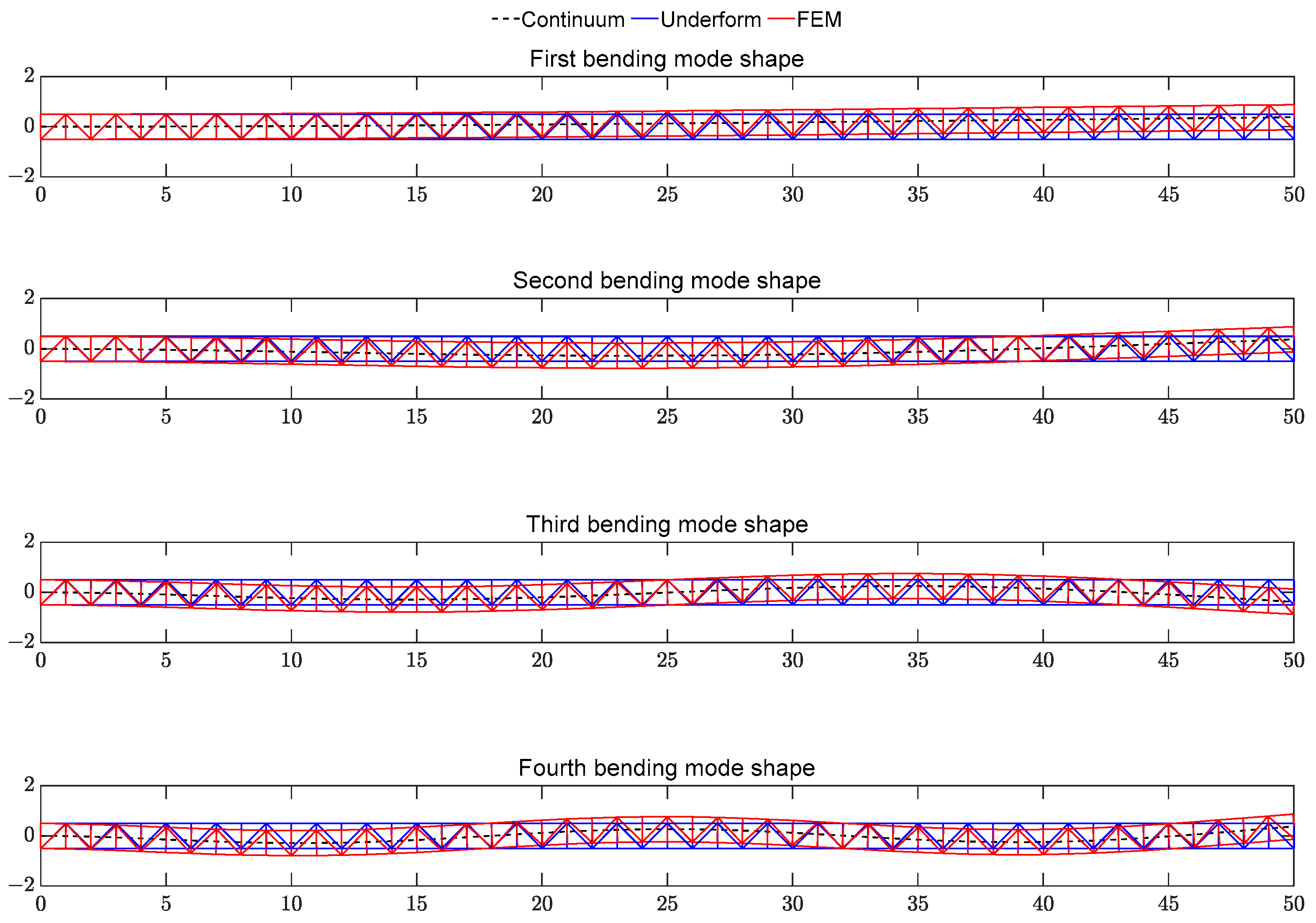
Initially, the precision of the continuum model is confirmed by comparing the natural frequencies derived from the continuum model against those obtained from the finite element model. Given that one end of the truss connected to the rigid hub is fixed while the other end is free, the natural frequencies of the truss structures are determined, as presented in

Table 2. First four natural frequencies for bending modes.

Mode	Natural Frequency, Hz		Error, %
	Continuum	FEM
1	0.2505	0.2504	0.040
2	1.5699	1.5532	1.075
3	4.3956	4.2815	2.665
4	8.6137	8.2092	4.927

. It is evident that the maximum frequency error for the first four bending modes is only 4.927%, attesting to the accuracy of the continuum model. Moreover, Figure 4 showcases the first four bending mode shapes of the truss structure, with the mode shapes obtained from the continuum model closely aligning with those obtained from the finite element model.

To validate the effectiveness of the proposed boundary control law, the following three cases are examined.

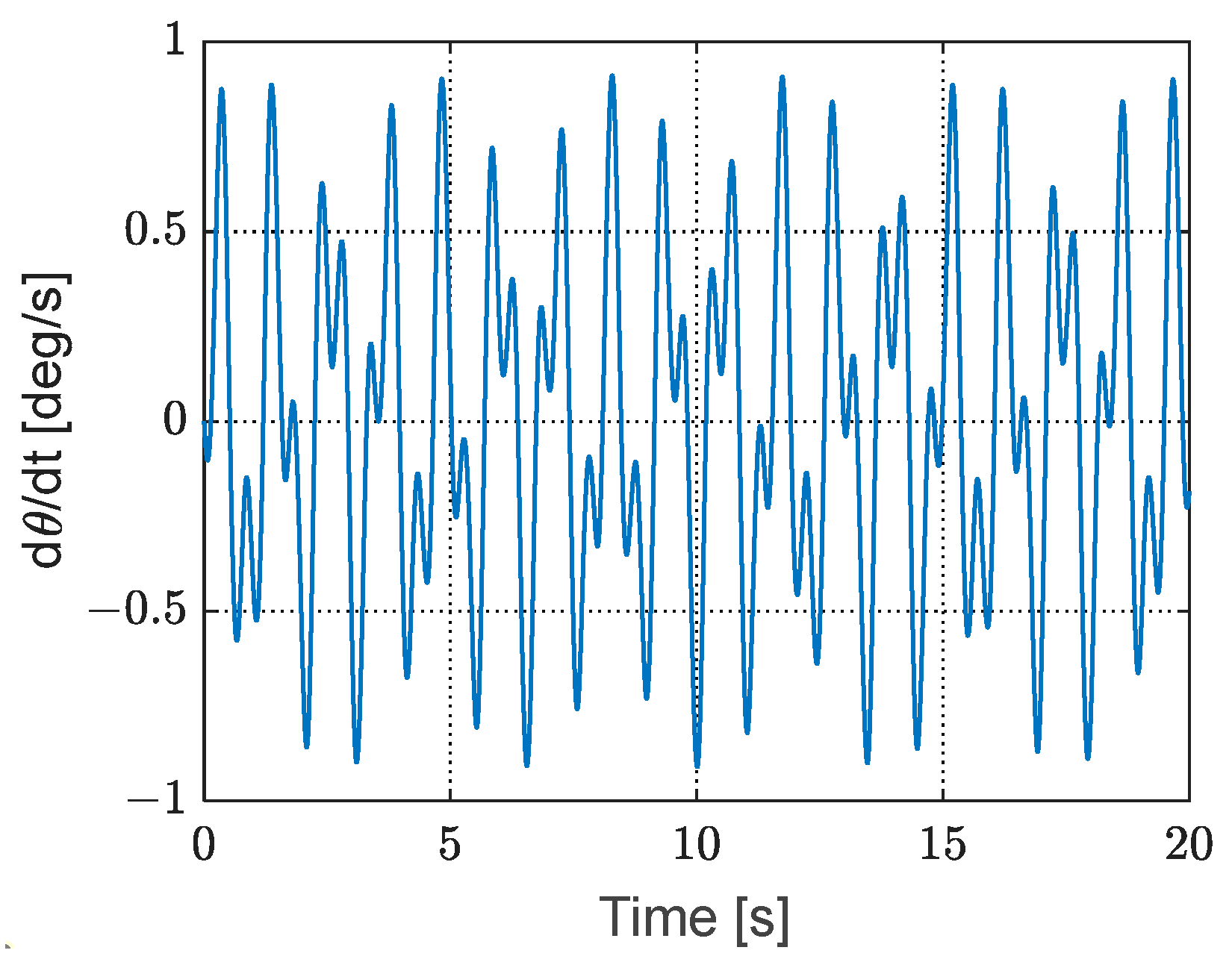
Case 1: Assuming an initial displacement of the truss structure as $u\left(x,y\right)=0.2{\phi }_1+0.05{\phi }_2$ and an initial velocity of the truss structure as 0. ${\phi }_1$ and ${\phi }_2$ represent the first two mass-normalized mode shapes of the truss structure, as illustrated in Figure 4. The initial angle of the satellite is 0. With no applied control force, the dynamic response of the flexible satellite is simulated in this instance. 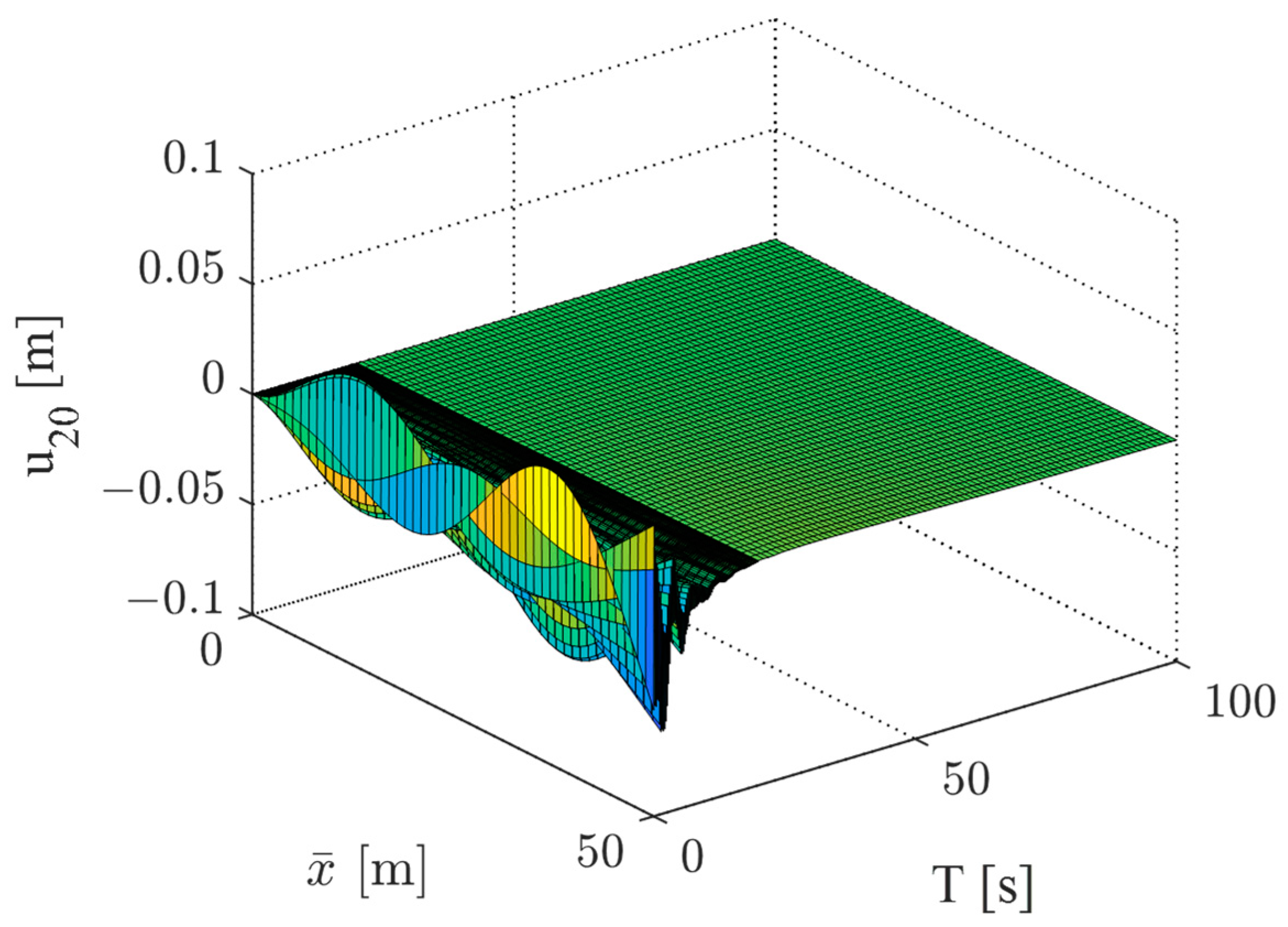Figure 5 illustrates the time history of generalized coordinates of the truss structure. The displacement at the centerline of the truss structure is depicted in Figure 6, which can be calculated using Equation (1). It is discernible that the truss structure experiences vibrations due to the initial deformation, resulting in an oscillation in attitude, as demonstrated in Figure 7 and Figure 8. This, in turn, induces vibrations in the structure at higher frequencies.

Case 2: In this instance, the boundary control law, as proposed in this study, is applied to the satellite. Following the procedure outlined in

Table 3. Coefficients of the proposed boundary control law.

Step	Inequality	Coefficient	Value
1	Arbitrary	${\chi }_3$	100
2	Arbitrary	${\chi }_2$	700
3	Arbitrary	${\lambda }_1$	1
4	Inequality (59)	${\delta }_1$	50
5	Inequality (59)	${\chi }_1$	0.0049
6	Inequality (64)	${\lambda }_2$	0.6

, the control coefficients are selected as ${\lambda }_1=1,{\lambda }_2=0.6,{\chi }_1=0.0049,{\chi }_2=700,{\chi }_3=100$. The initial displacement of the truss is $u\left(x,y\right)=0.2{\phi }_1+0.05{\phi }_2$, which remains unchanged from Case 1. The initial and desired angles of the satellite are set at 0° and 20°, respectively.

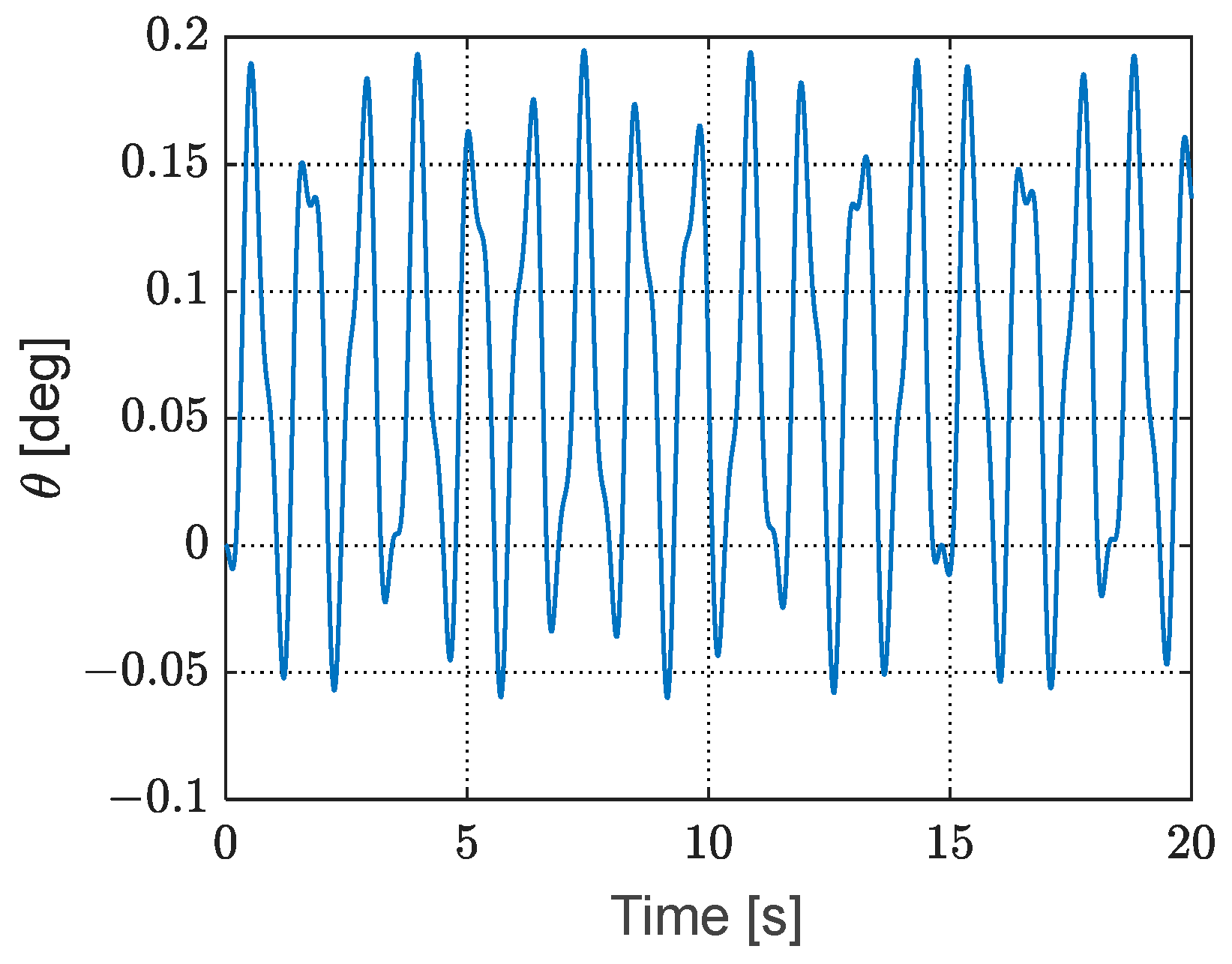
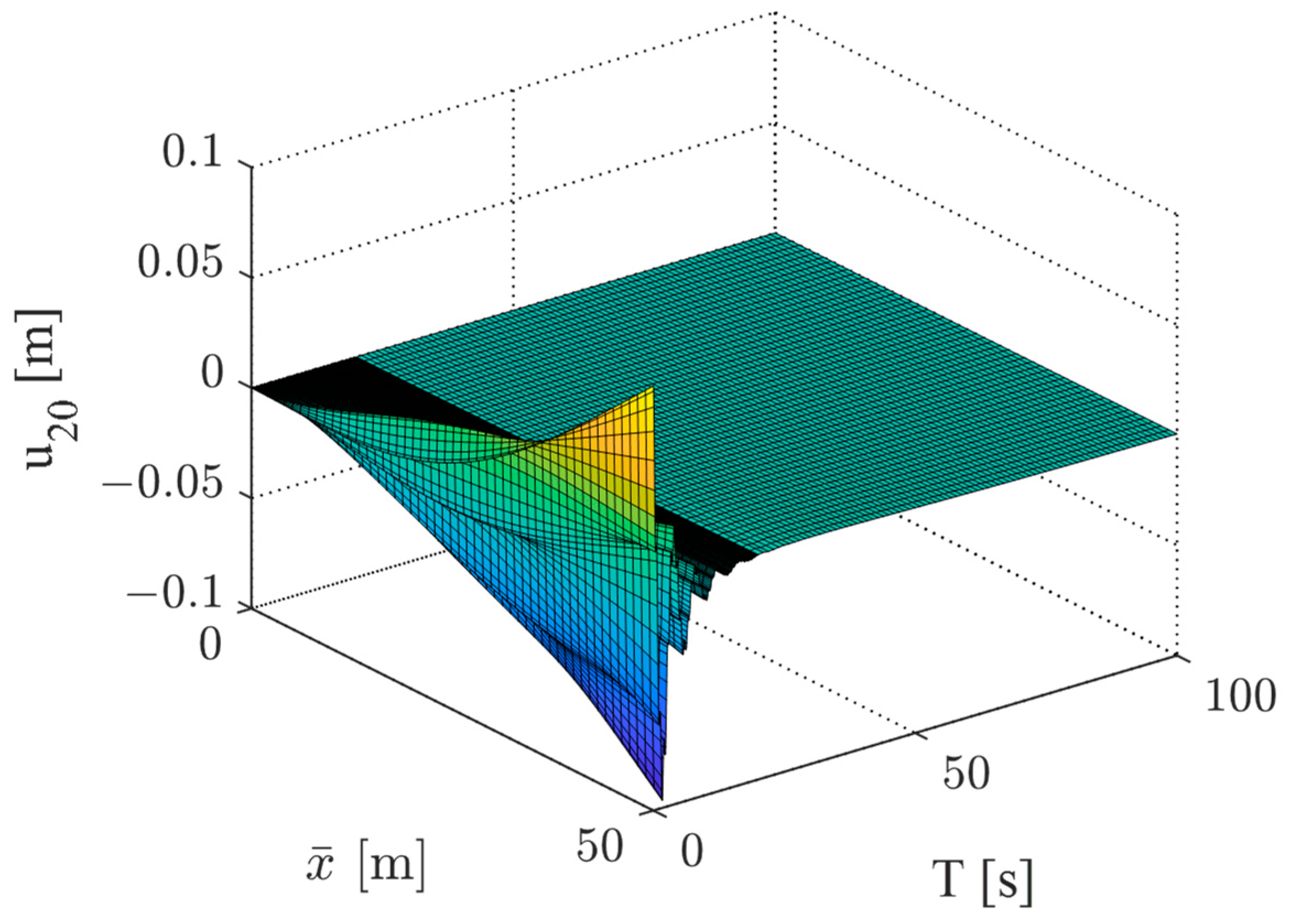
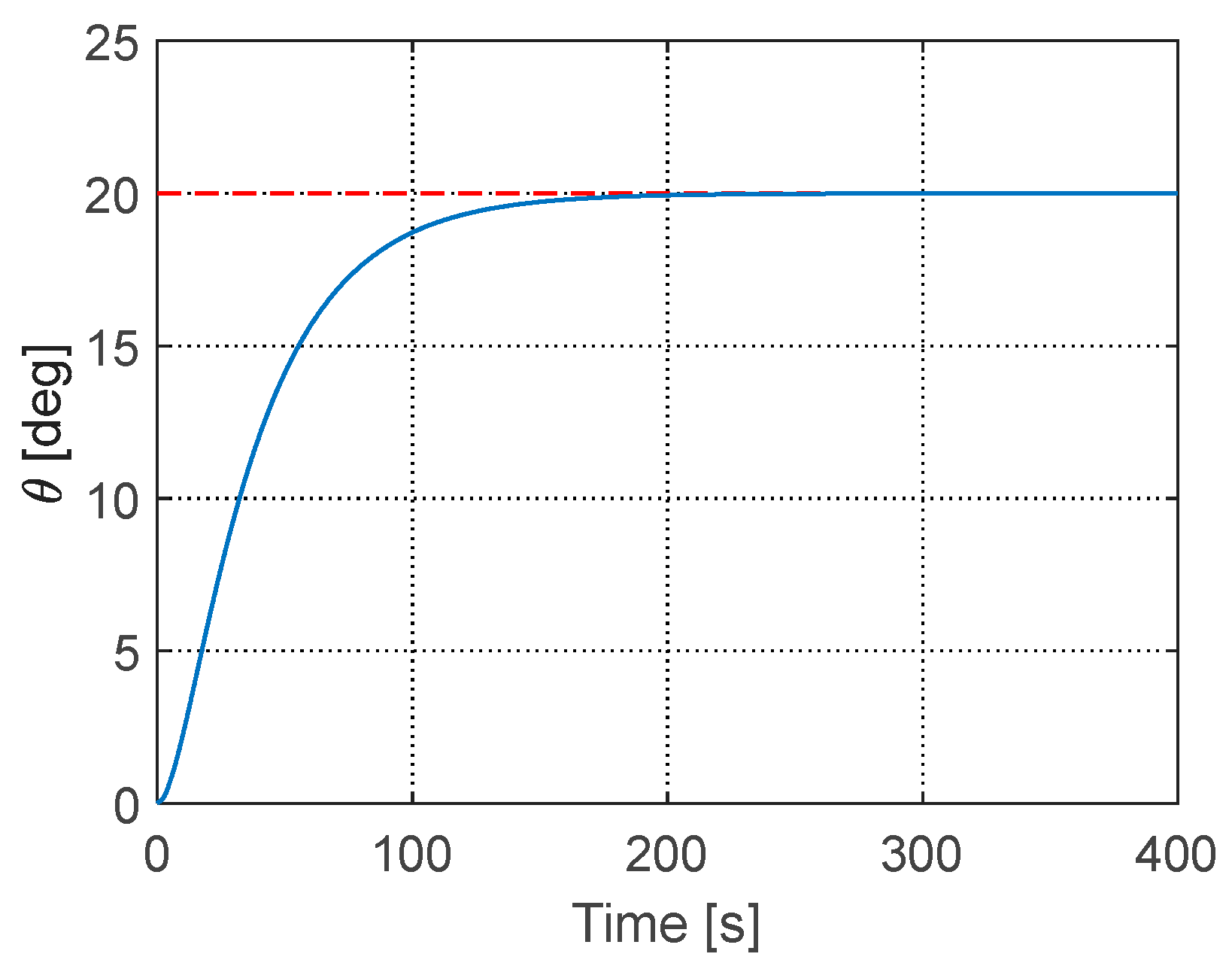
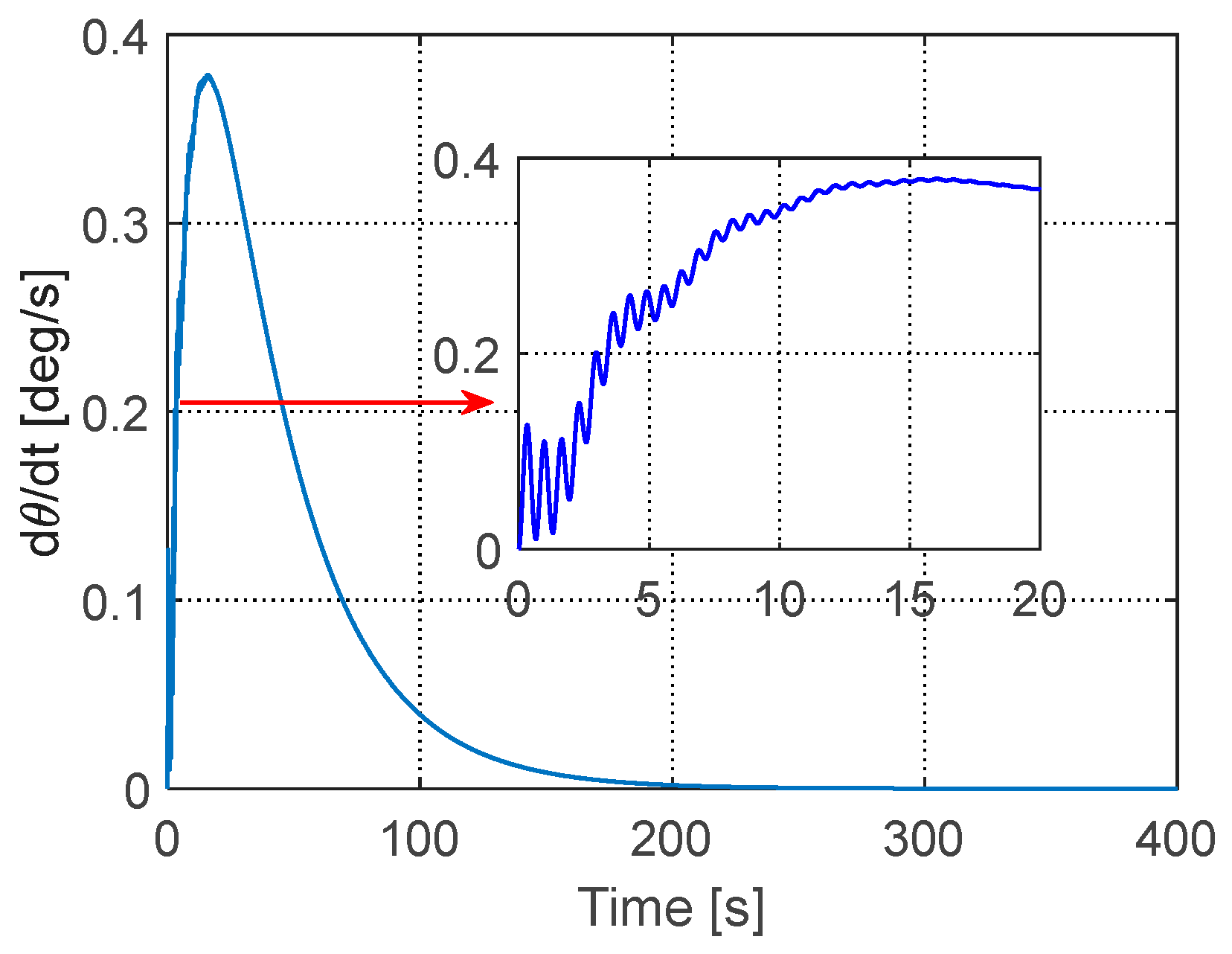
The dynamic response of the truss structure under boundary control is depicted in Figure 9. It is evident that the vibration amplitude gradually diminishes to zero. As illustrated in Figure 10, the vibration of the truss structure is effectively suppressed within 40 s. The attitude angle and angular velocity of the satellite are presented in Figure 11 and Figure 12, respectively. Due to the initial vibration of the truss structure, the angular velocity exhibits fluctuations initially. As the vibration is suppressed, the angular velocity smoothens, and the satellite’s angle gradually converges to the desired value. This demonstrates the effectiveness of the proposed boundary control law in both attitude tracking and vibration suppression. The time history of the control input is provided in Figure 13.

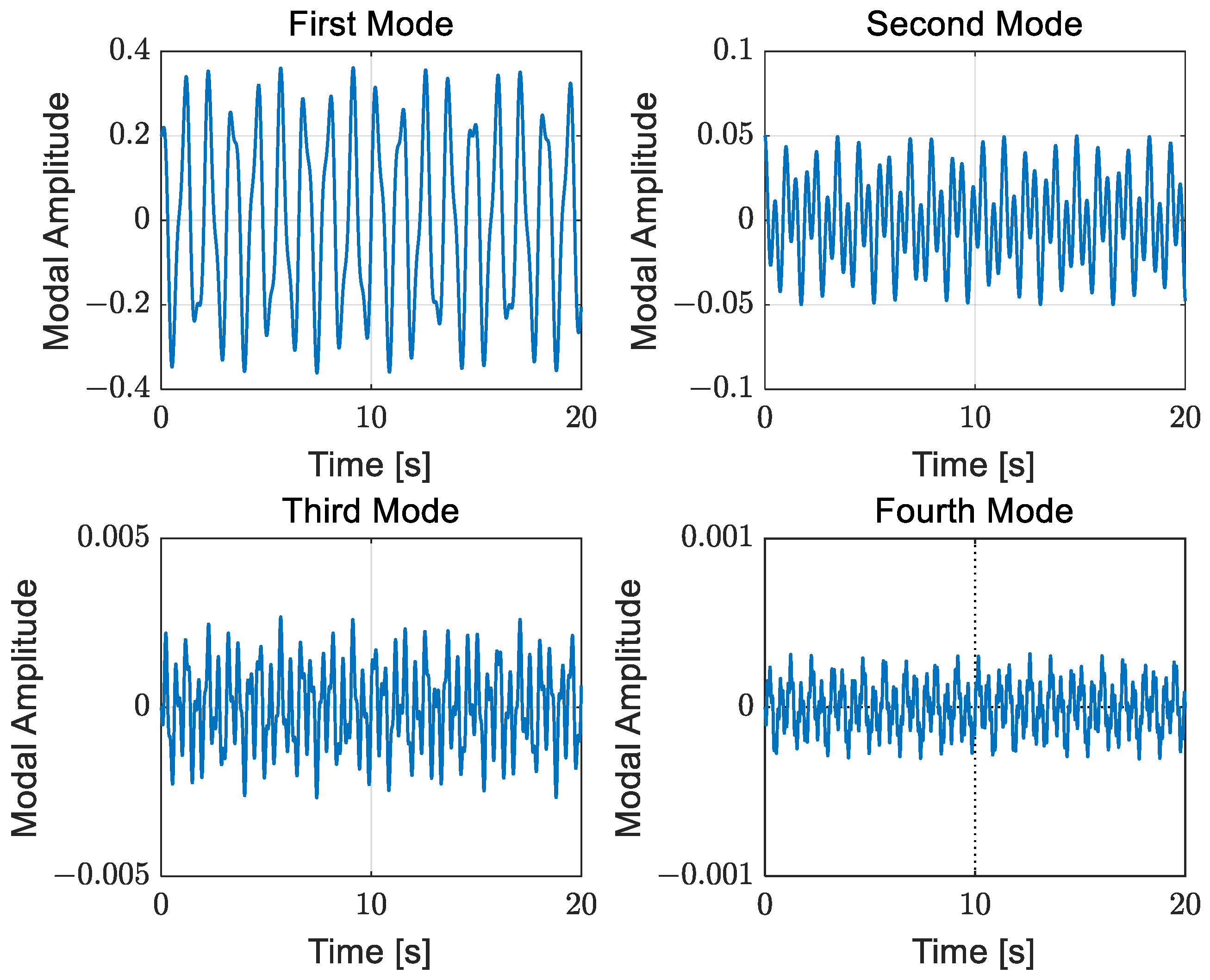
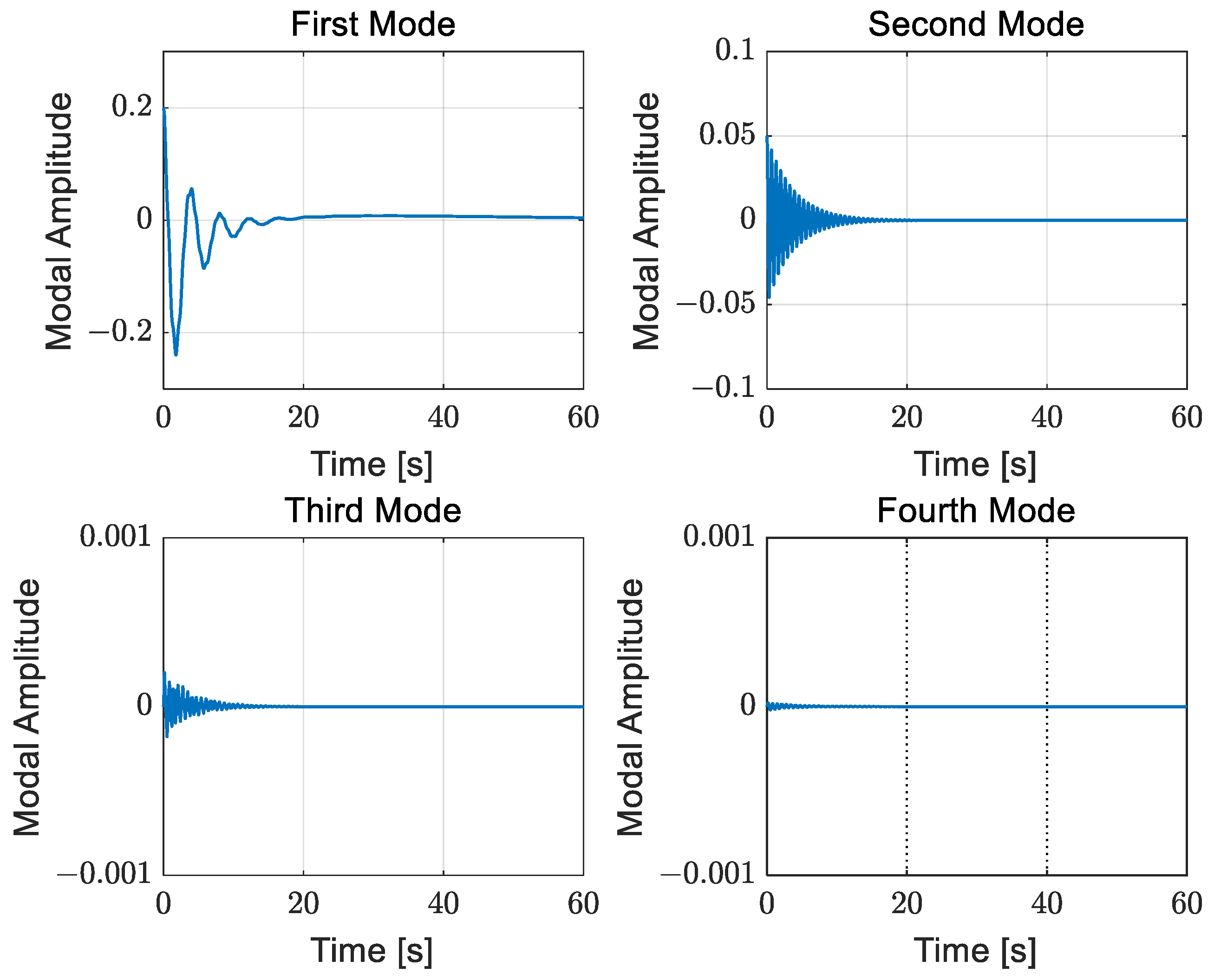
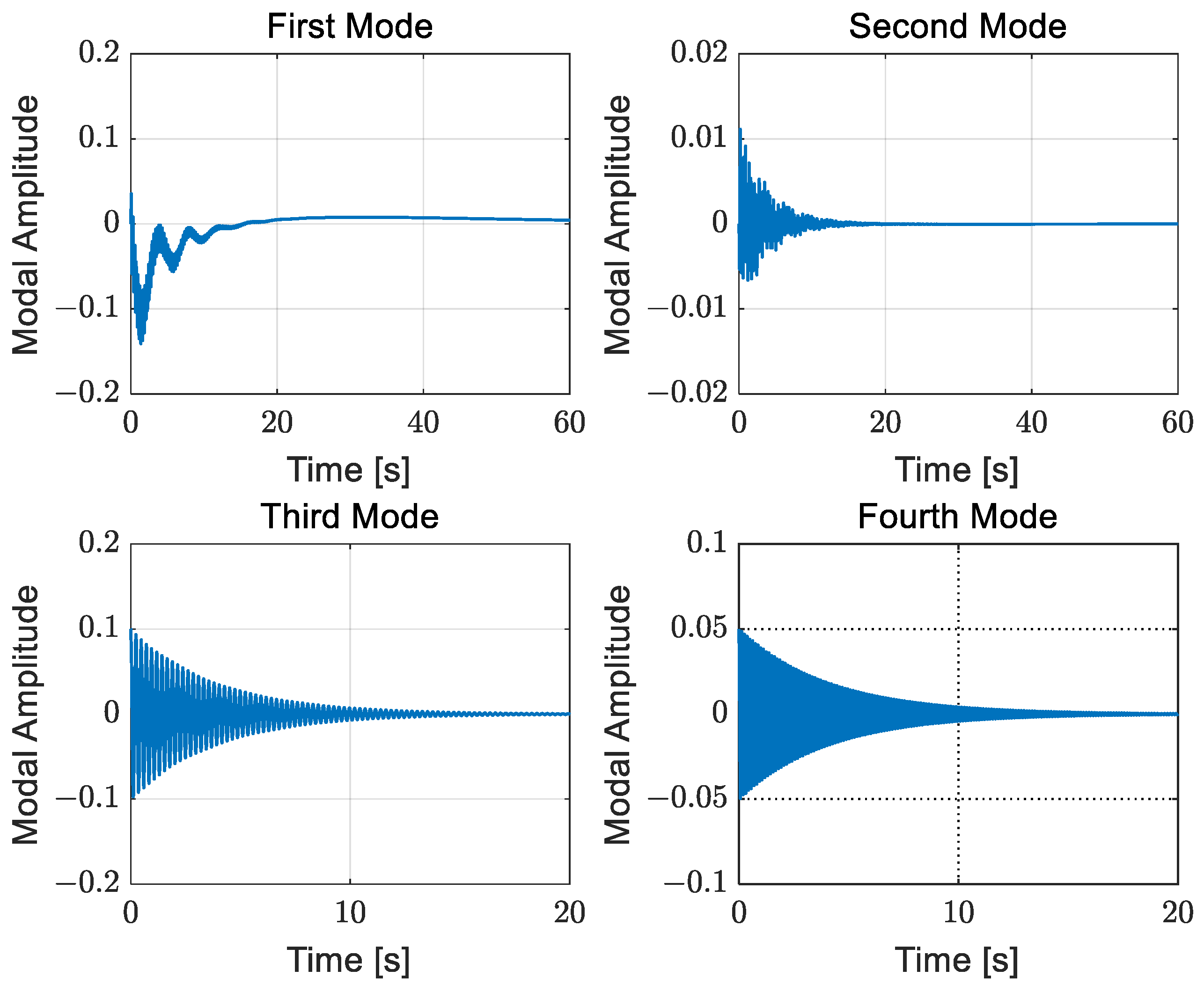
Case 3: In contrast to Case 2, this case assumes an initial deformation of the truss structure as $u\left(x,y\right)=0.1{\phi }_3+0.05{\phi }_4$. ${\phi }_3,{\phi }_4$ represent the third and fourth mass-normalized mode shapes of the truss structure, respectively. The control coefficients are set to be the same as those in Case 2. The dynamic response of the truss is displayed in Figure 14, demonstrating effective vibration suppression. As depicted in Figure 15, the amplitudes of the first four modal coordinates quickly converge to zero. Simultaneously, the attitude angle and angular velocity of the satellite are regulated to the desired values. As indicated in Table 2, the frequency error between the continuum model and finite element model is larger for the third and fourth modes. However, the simulation results confirm that the proposed boundary law performs well in this case. This underscores that the proposed boundary law exhibits robustness to frequency deviation, a valuable trait for practical applications.

5. Conclusions

This study addresses the continuum modeling and boundary control of a satellite equipped with a large truss structure. The dimensions of the traditional finite element model for a satellite with a large space truss structure will become exceedingly large as the structure’s size increases. Thus, the control system design process based on the finite element model is complex and time-consuming. In this work, relying on the principle of energy equivalence, the truss structure is equated to a continuum, resulting in a partial differential equation governing the bending vibration, coupled with the ordinary differential equation governing the attitude motion of the satellite. Subsequently, a boundary control law is formulated to regulate both the attitude and vibration of the flexible satellite based on the coupled PDE-ODE model. The closed-loop system’s exponential stability is established using Lyapunov’s direct method. The proposed boundary controller only uses actuators at the central hub, which is easy to implement in real-life applications. The numerical simulations validate the continuum model’s ability to accurately predict the dynamic behavior of the large truss structure, with a maximum frequency error of only 4.927% for the first four bending modes. The proposed boundary law successfully suppresses the vibration of the truss structure while regulating the satellite’s attitude.

The control system design for three-axis attitude maneuver and vibration suppression of the satellite with a large truss structure based on the continuum model will be further studied in future works.