Coupled Aerodynamics–Structure Analysis and Wind Tunnel Experiments on Passive Hinge Oscillation of Wing-Tip-Chained Airplanes
Abstract
1. Introduction
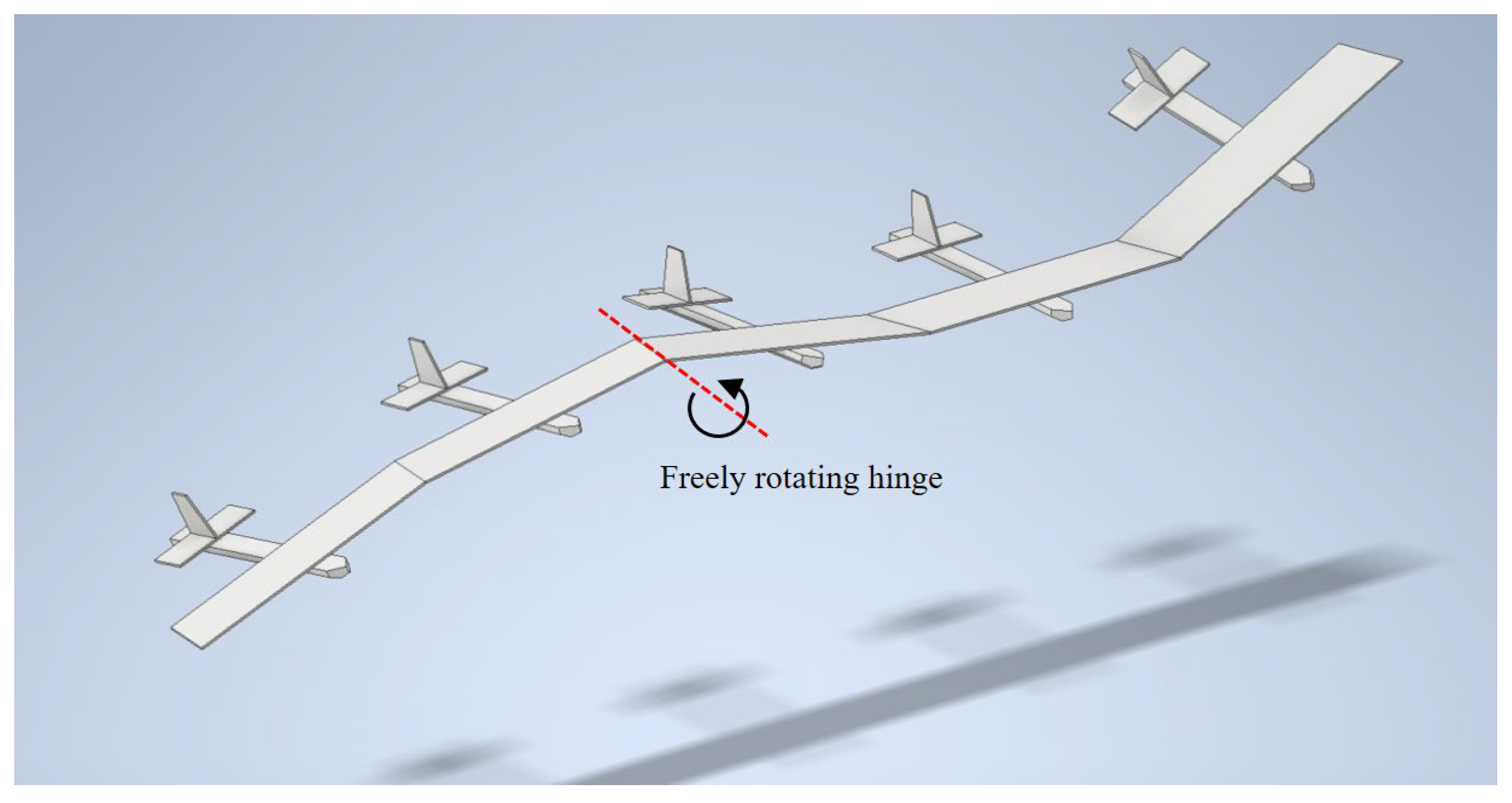
- The possibility of attaining passive attitude resilience, namely oscillation stability around the hinge joints, with three or more wings chained.
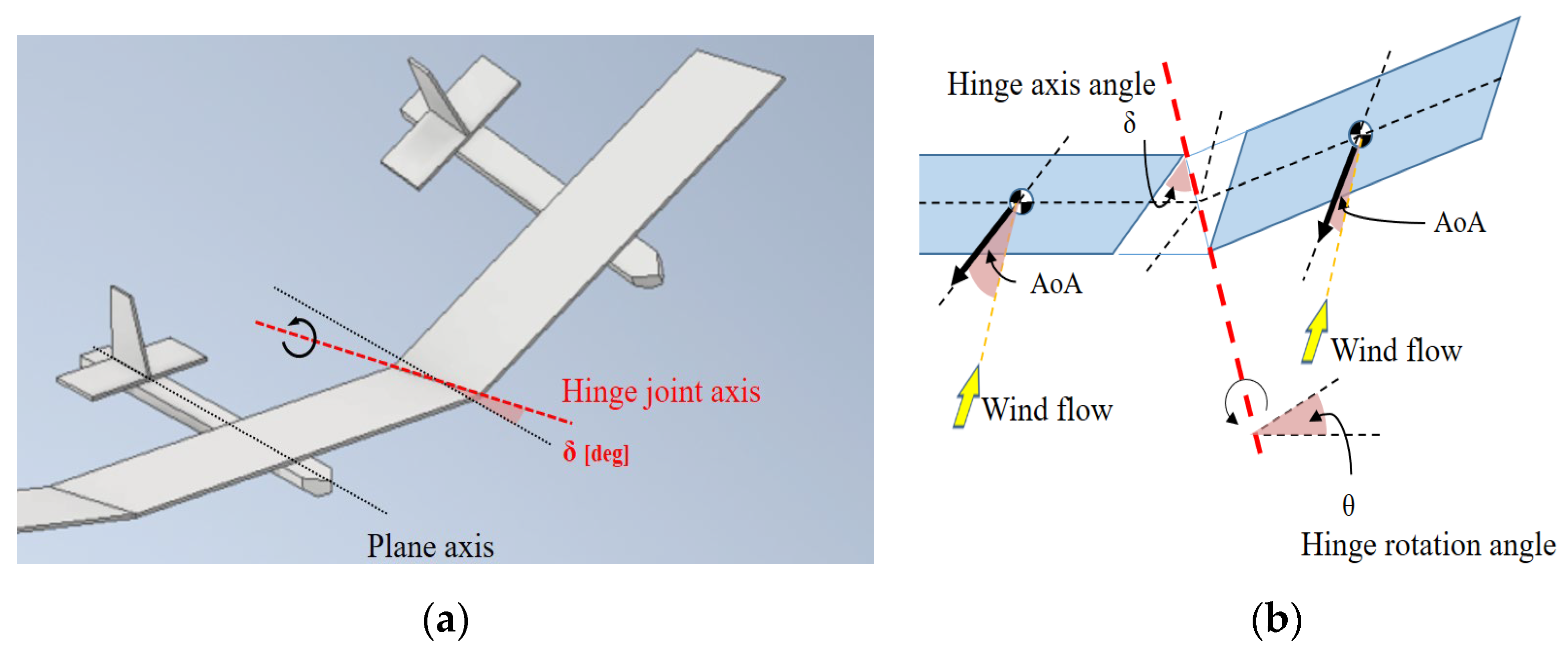
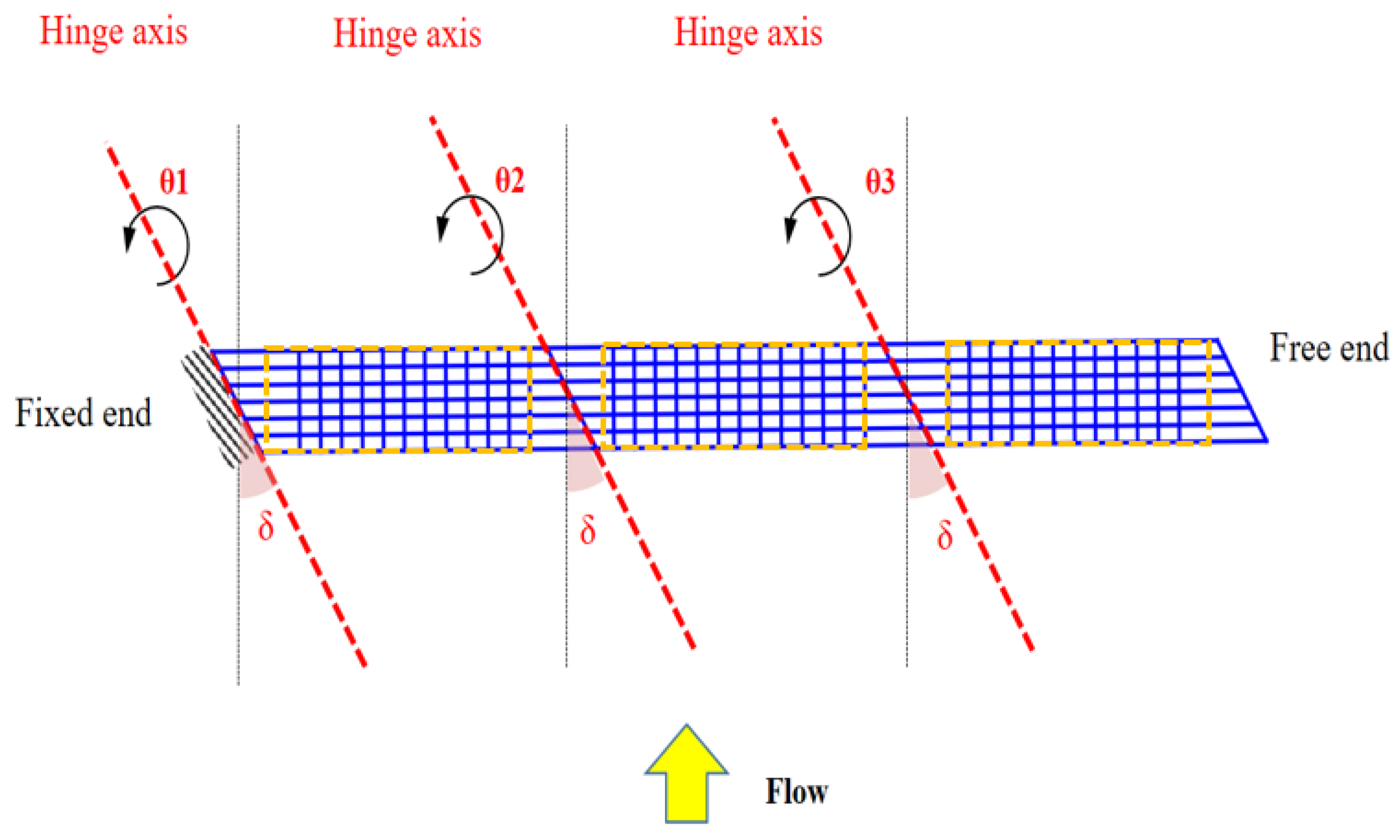
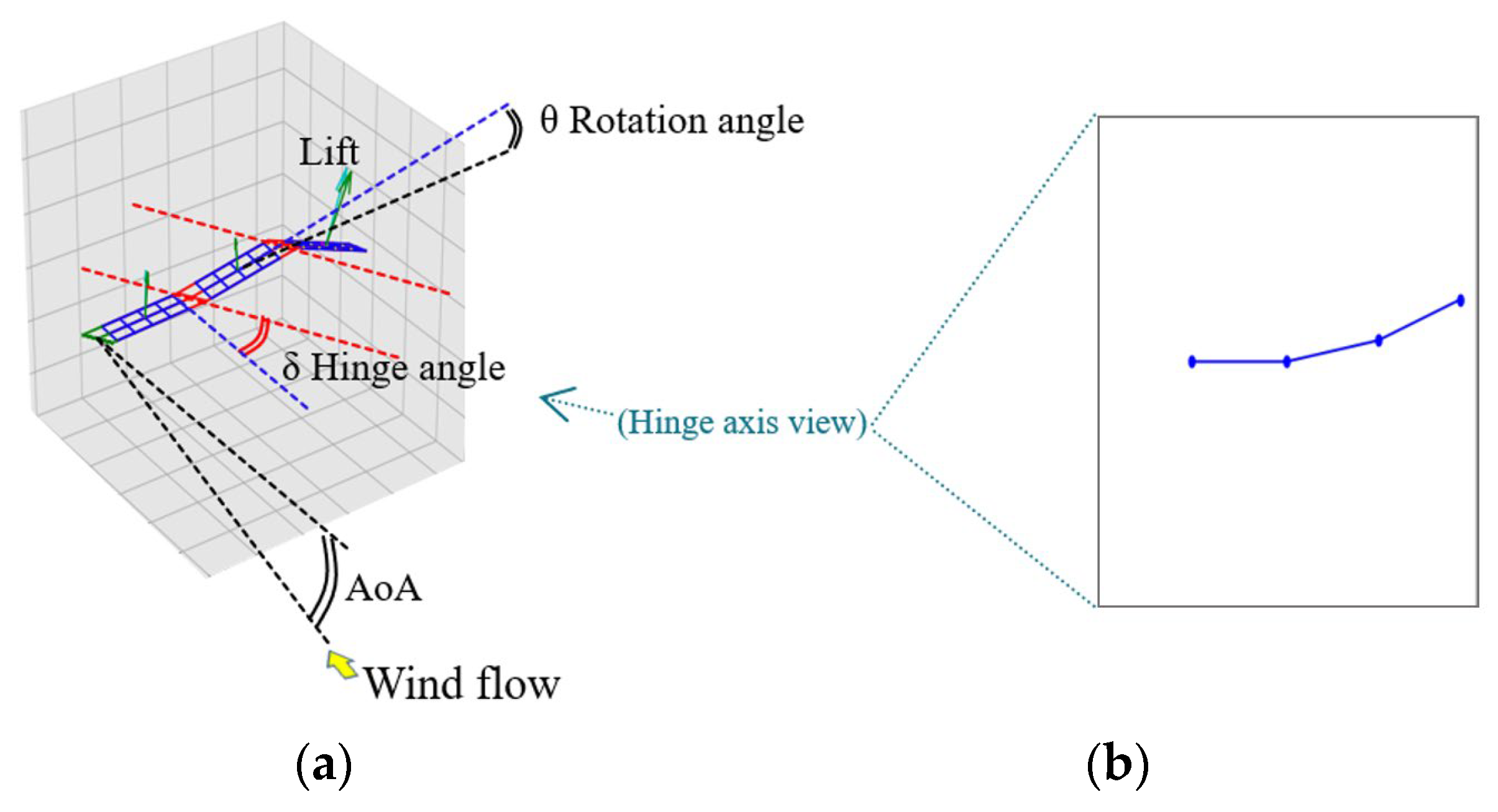
- Investigation of the effects of the angle of attack (AoA) and chained-hinge axis angle (δ) on the passive oscillation stability around multiple chained wings in wind flow and the assessment of these values.
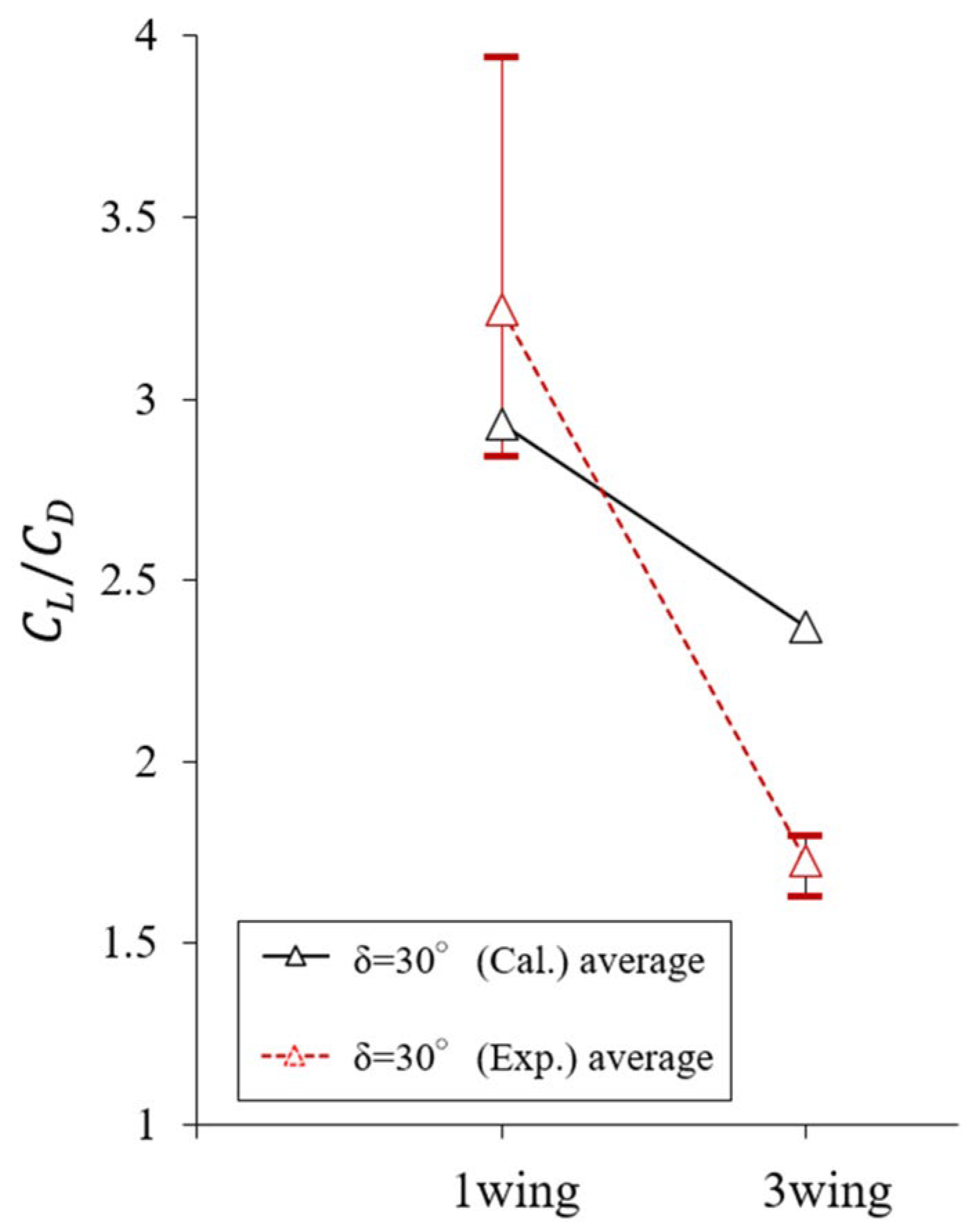
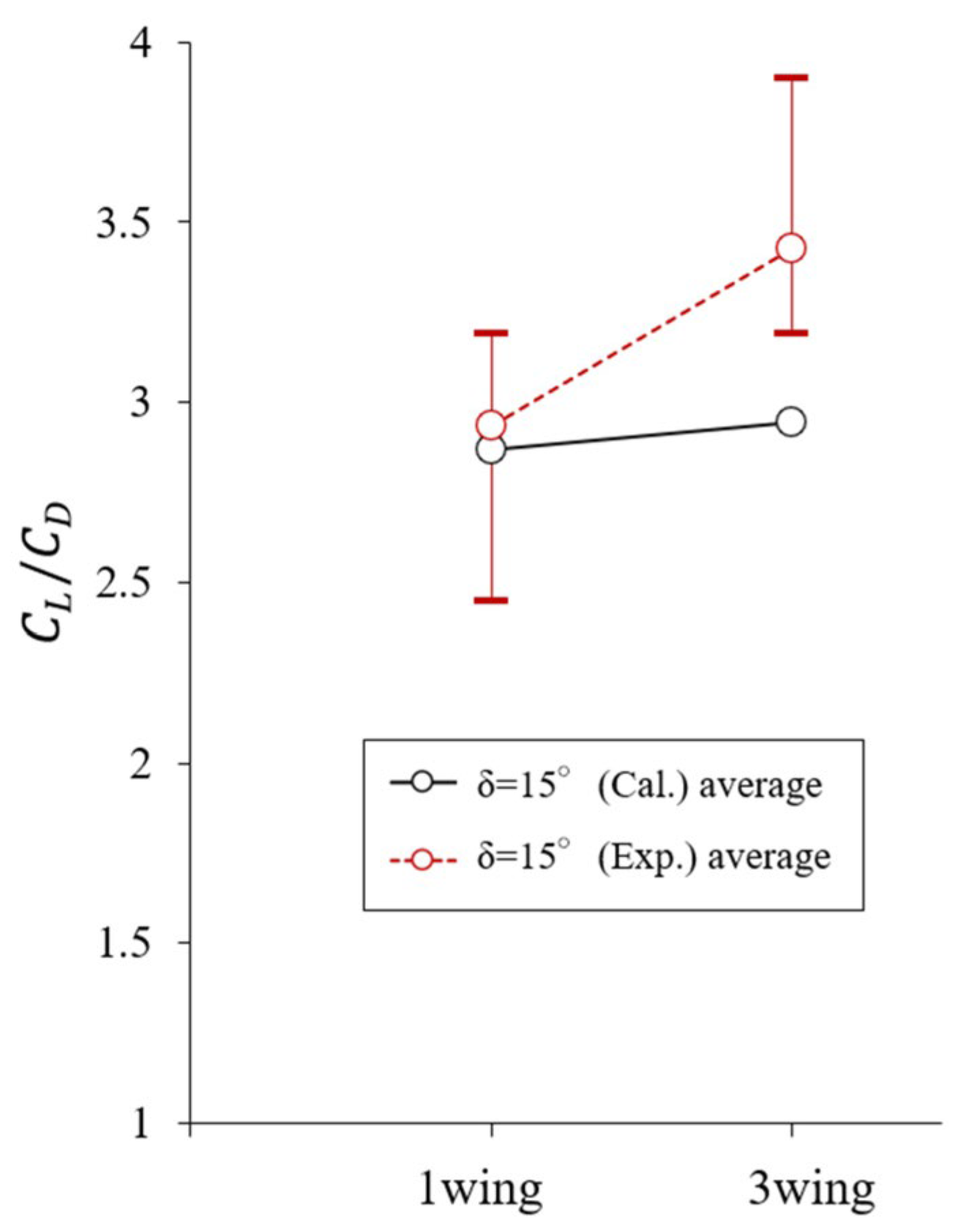
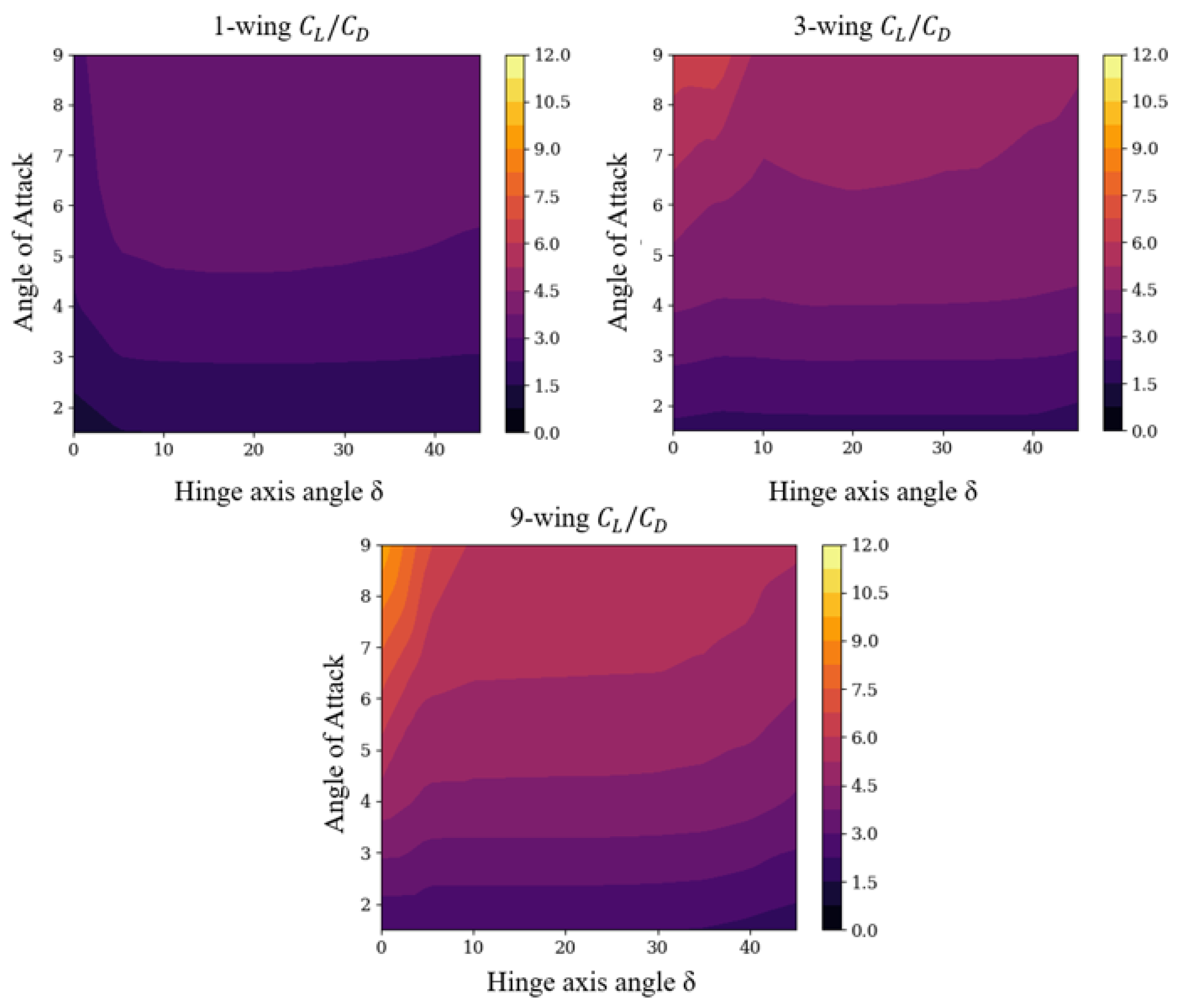
- Feasibility of increased lift to drag (L/D or ) with multiple wings chained via freely rotating hinges.
- The authors designed a novel general calculation model for the aerial force and performed a body movement analysis of a chained wing with a sufficient balance between accuracy and calculation cost, while accounting for the relative aerodynamic effect and the hinge axis angle of each wing section using robust analytical derivations and a numerical aerodynamic calculation method, for a high number of chained wings.
- The authors compared and validated the calculation model utilizing small-scale wind tunnel tests.
2. Mathematical Modeling of Chained Aircraft
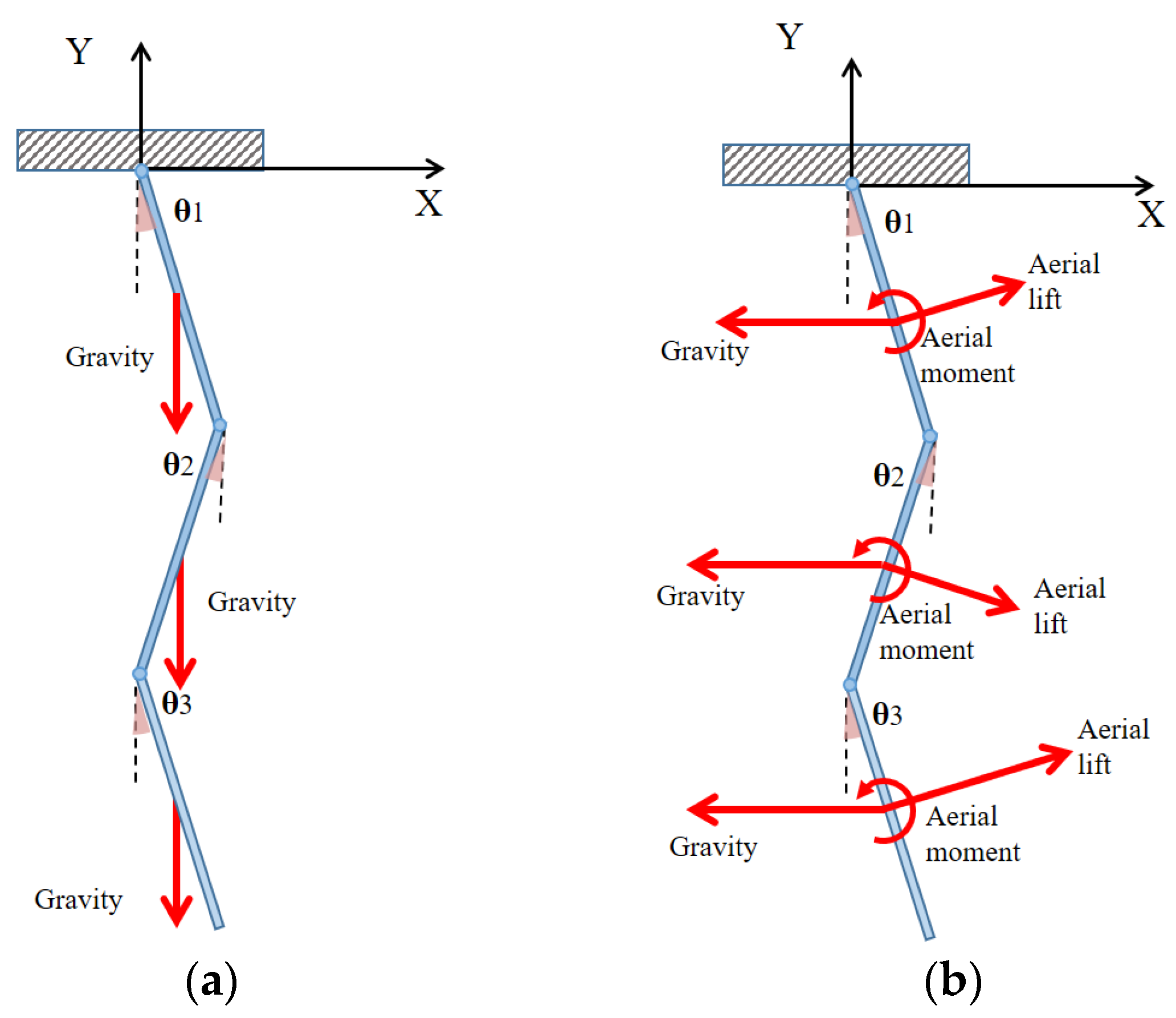
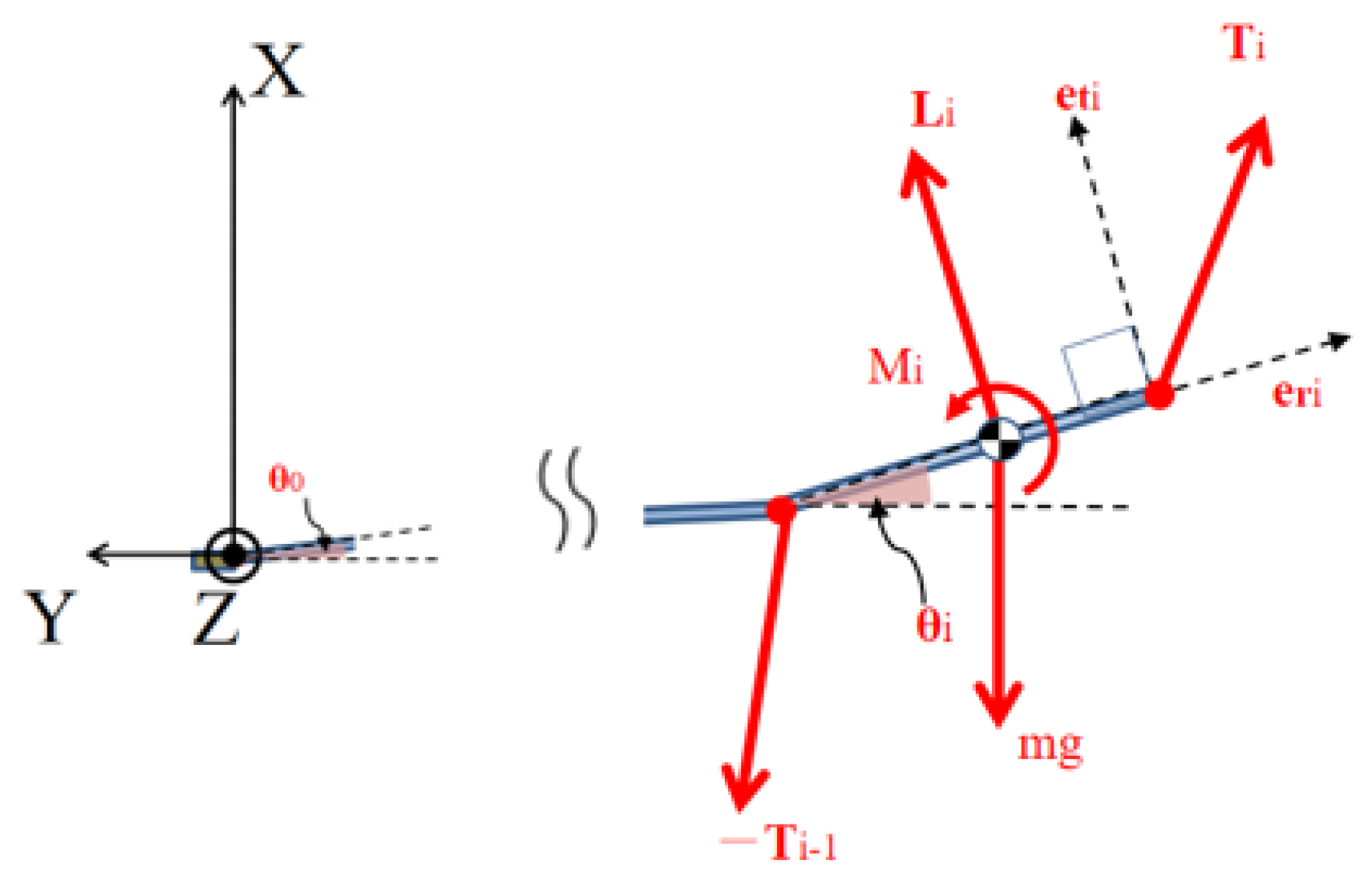
2.1. Equation of Motion for a Multi-Link Rigid Pendulum
2.2. Vortex Lattice Method
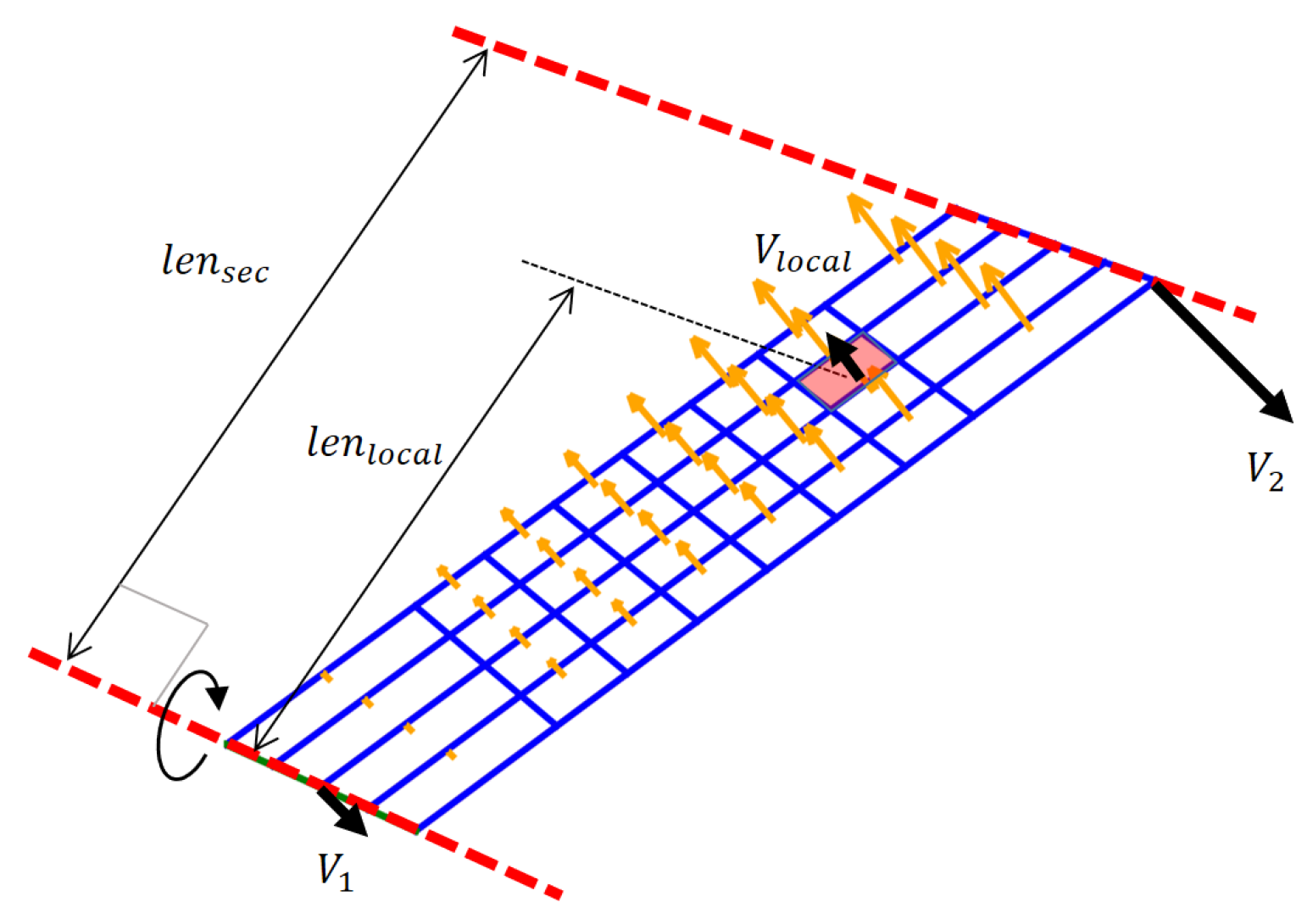
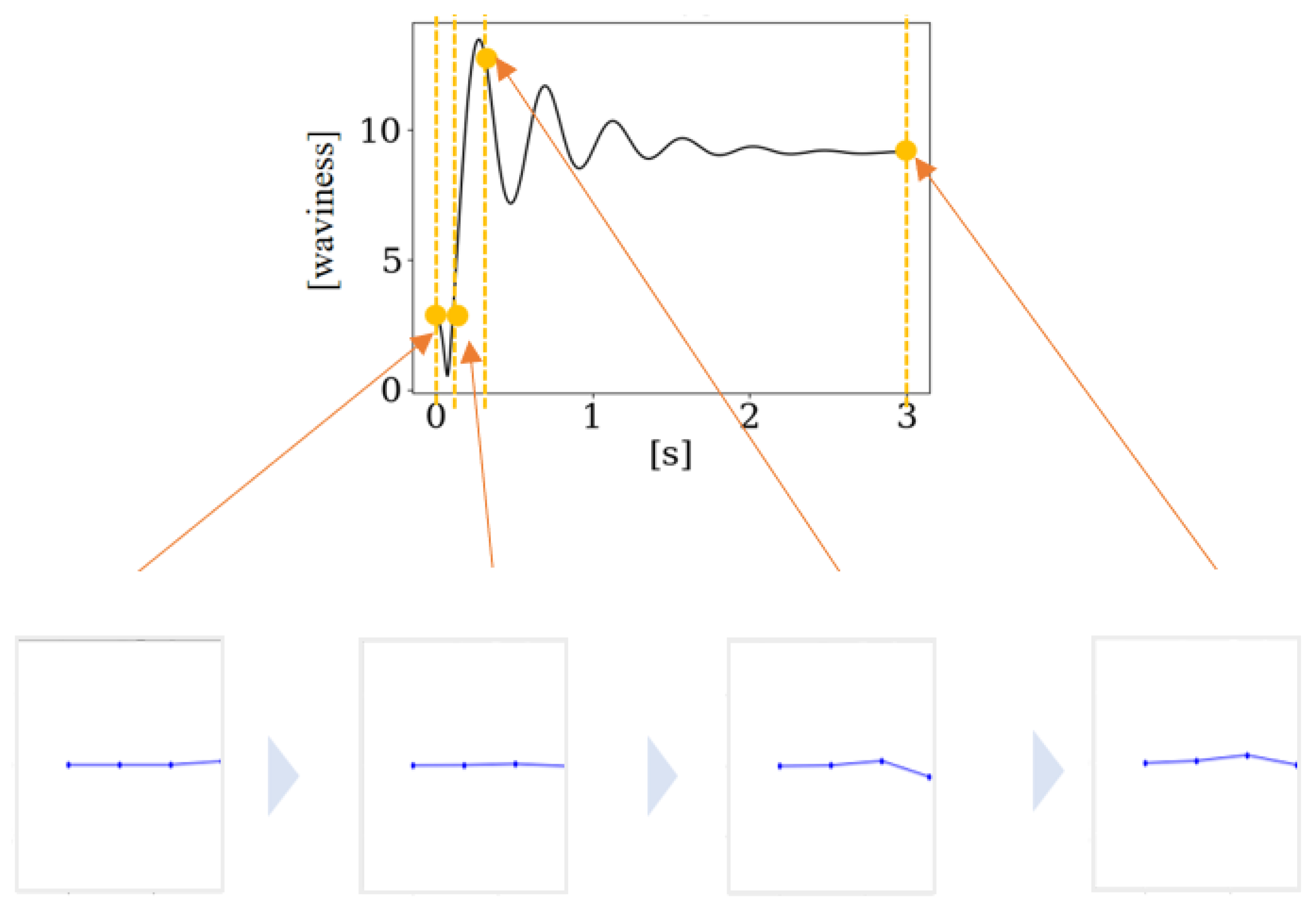
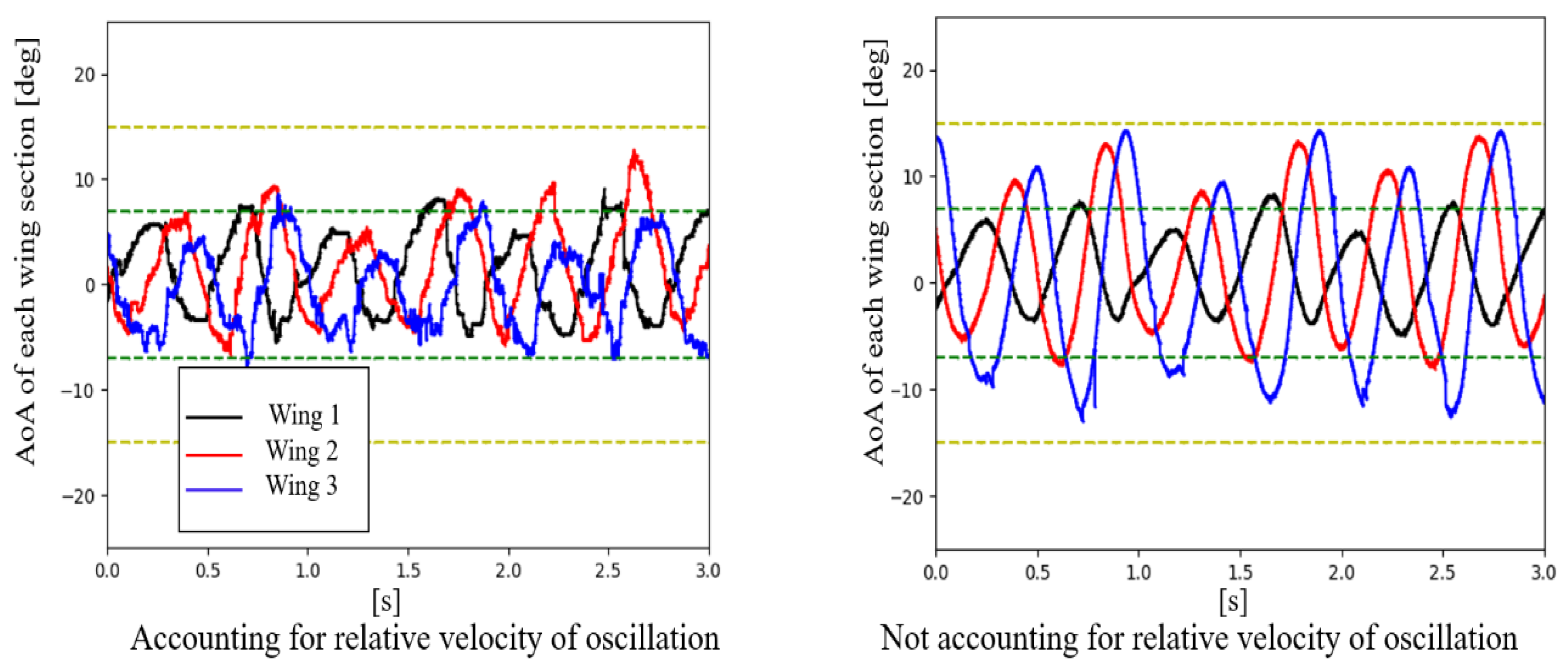
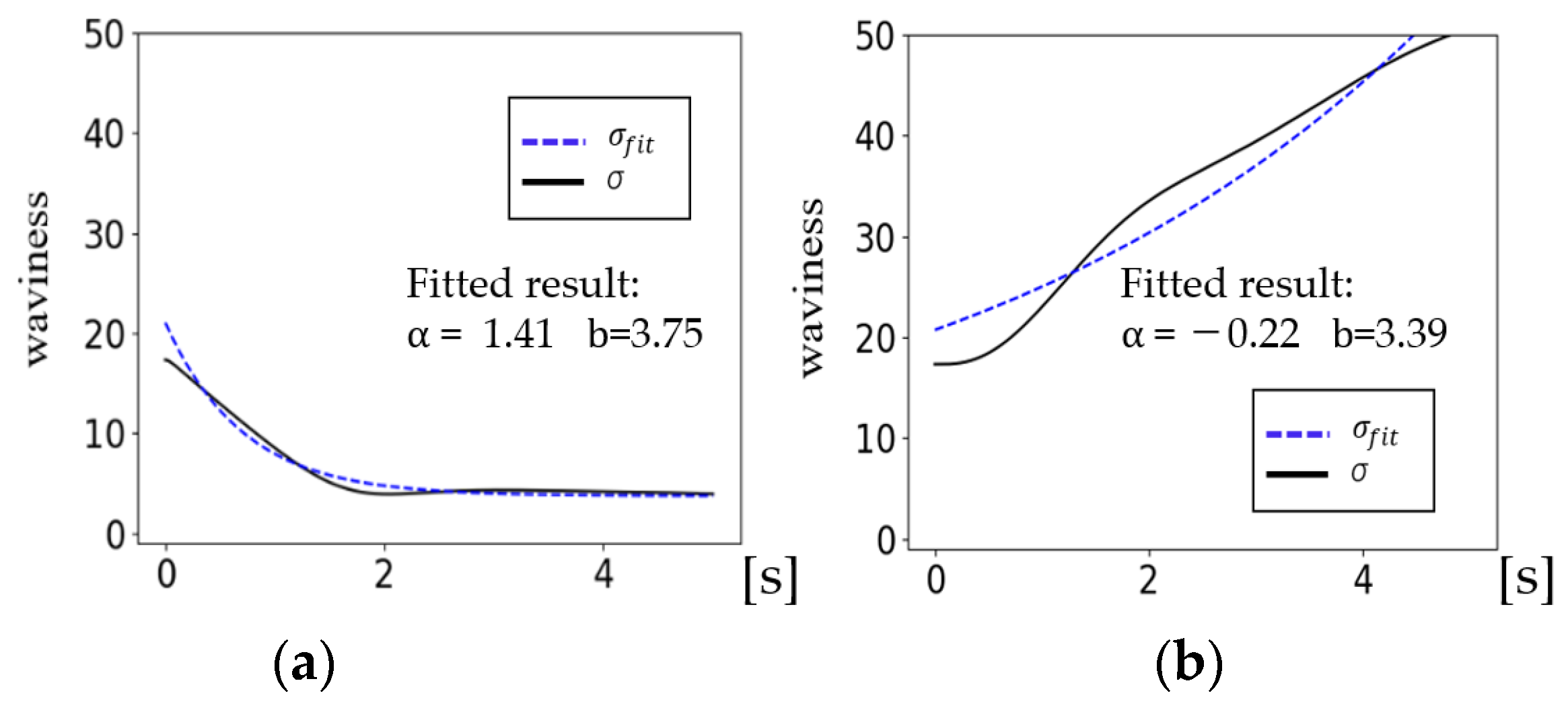
2.3. Coupled Calculation Setup and Waviness
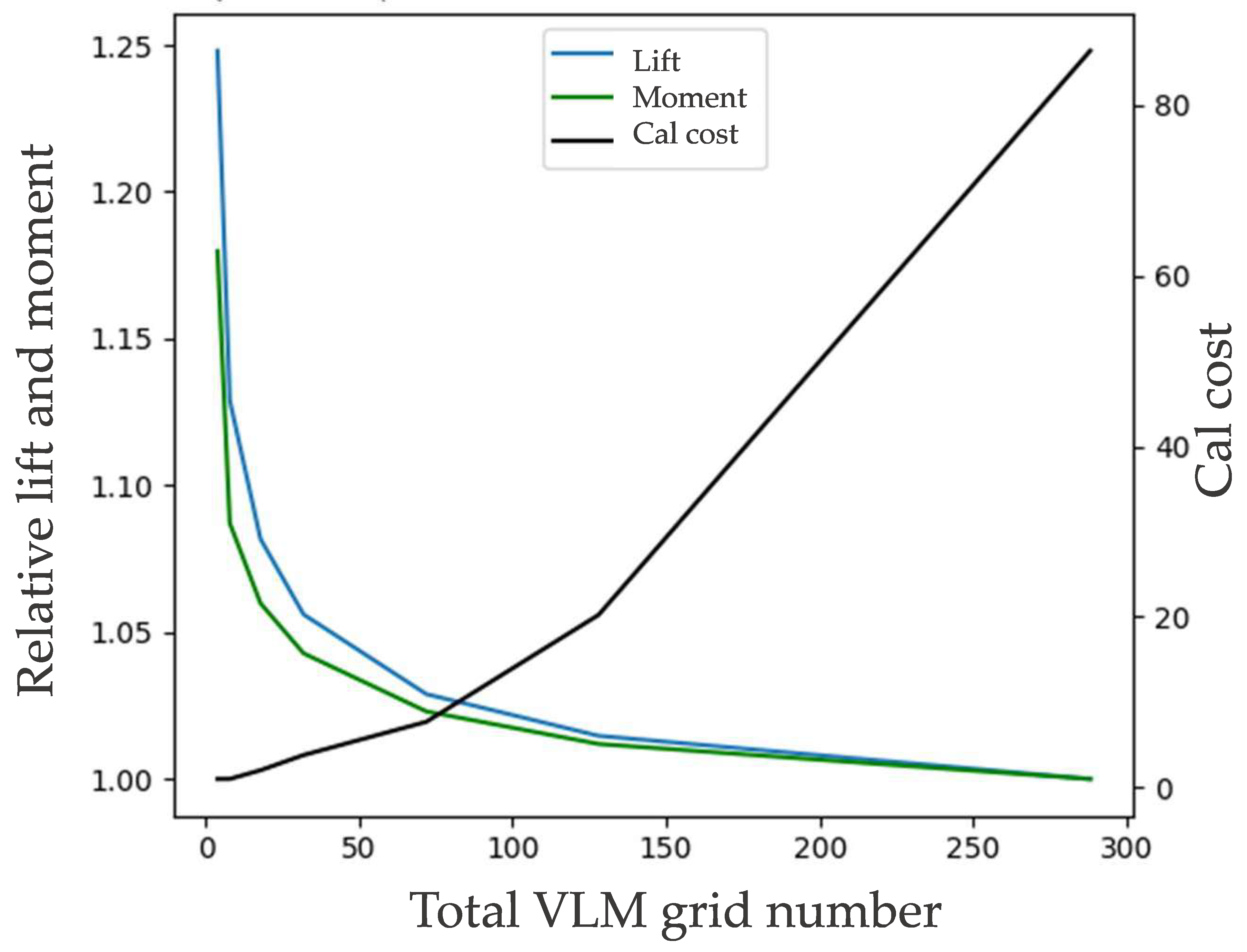
2.4. Grid Convergence
3. Experiments
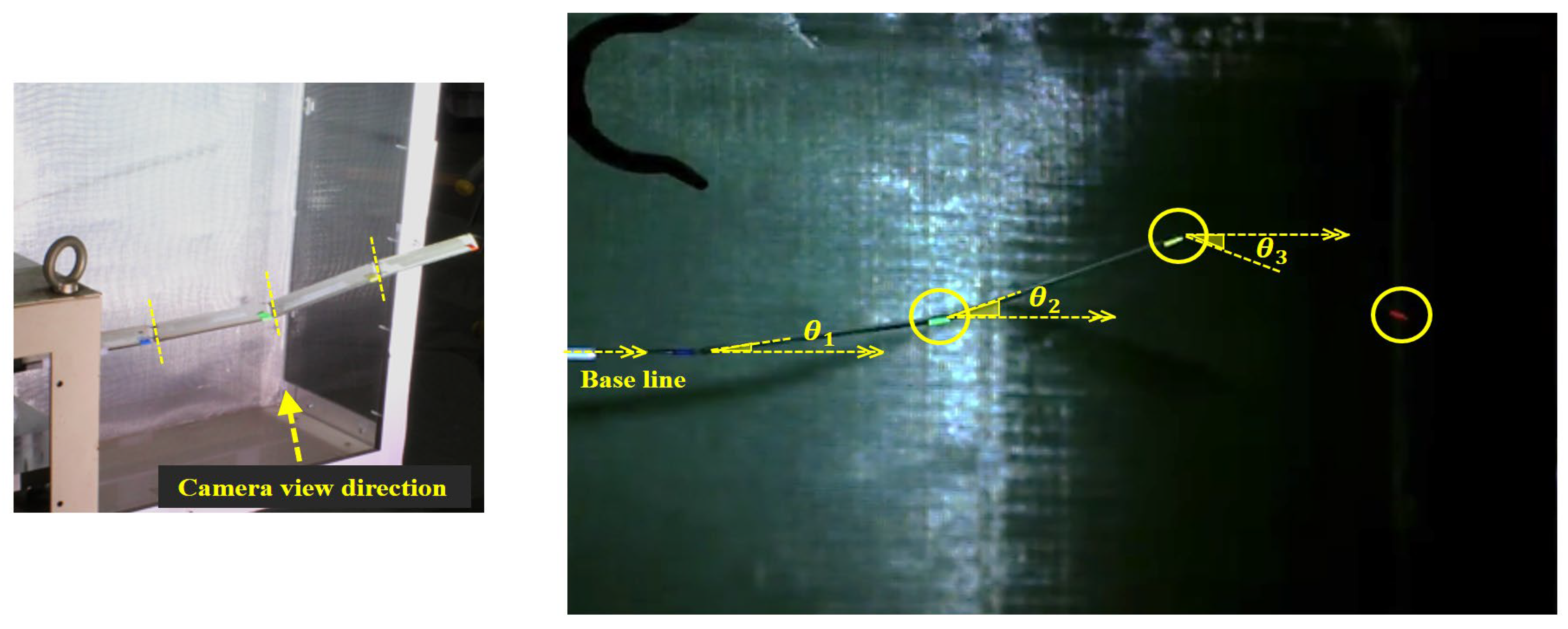
3.1. Small-Scale Low-Speed Wind Tunnel
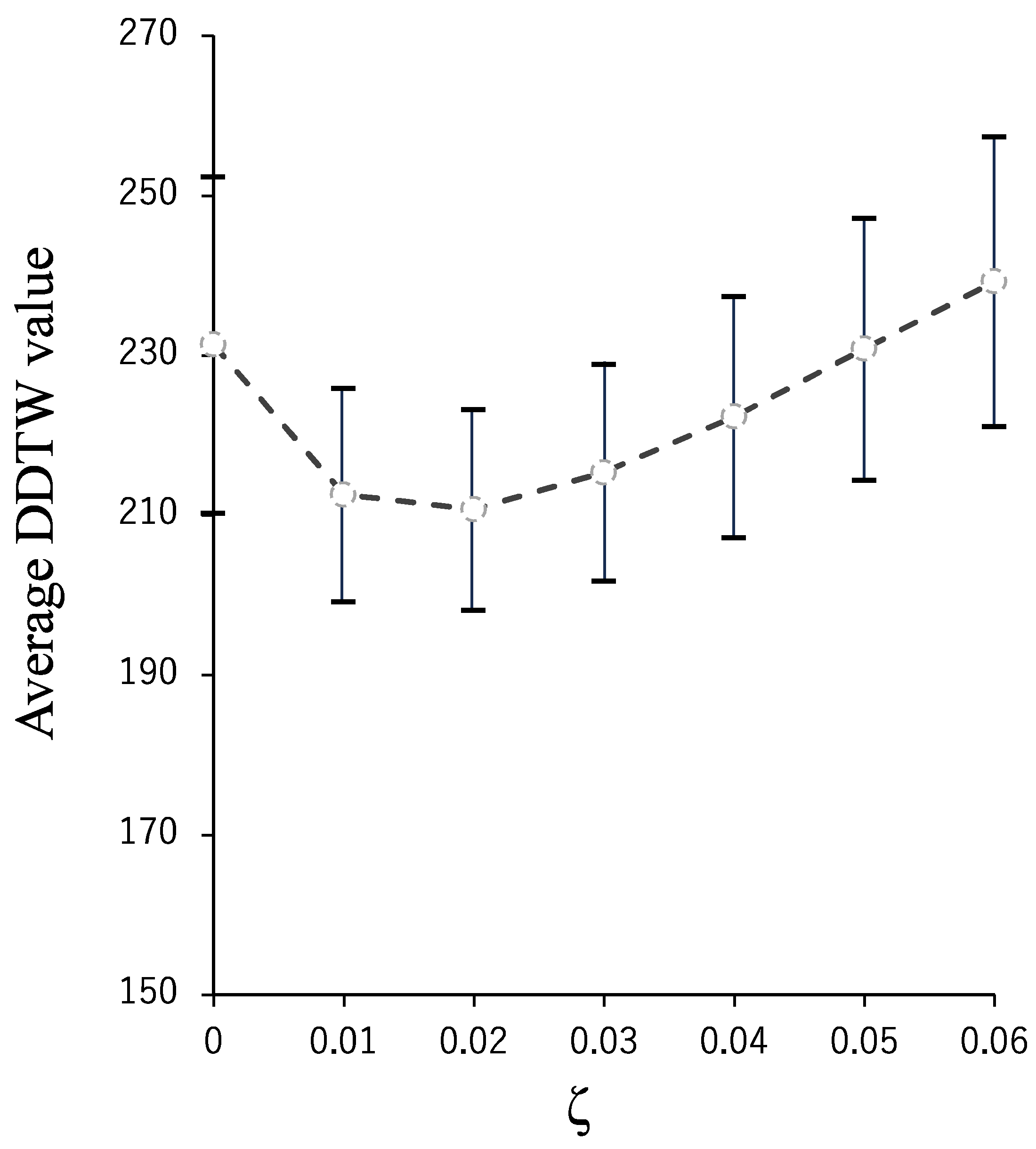
3.2. Structural Hinge Damping Coefficient
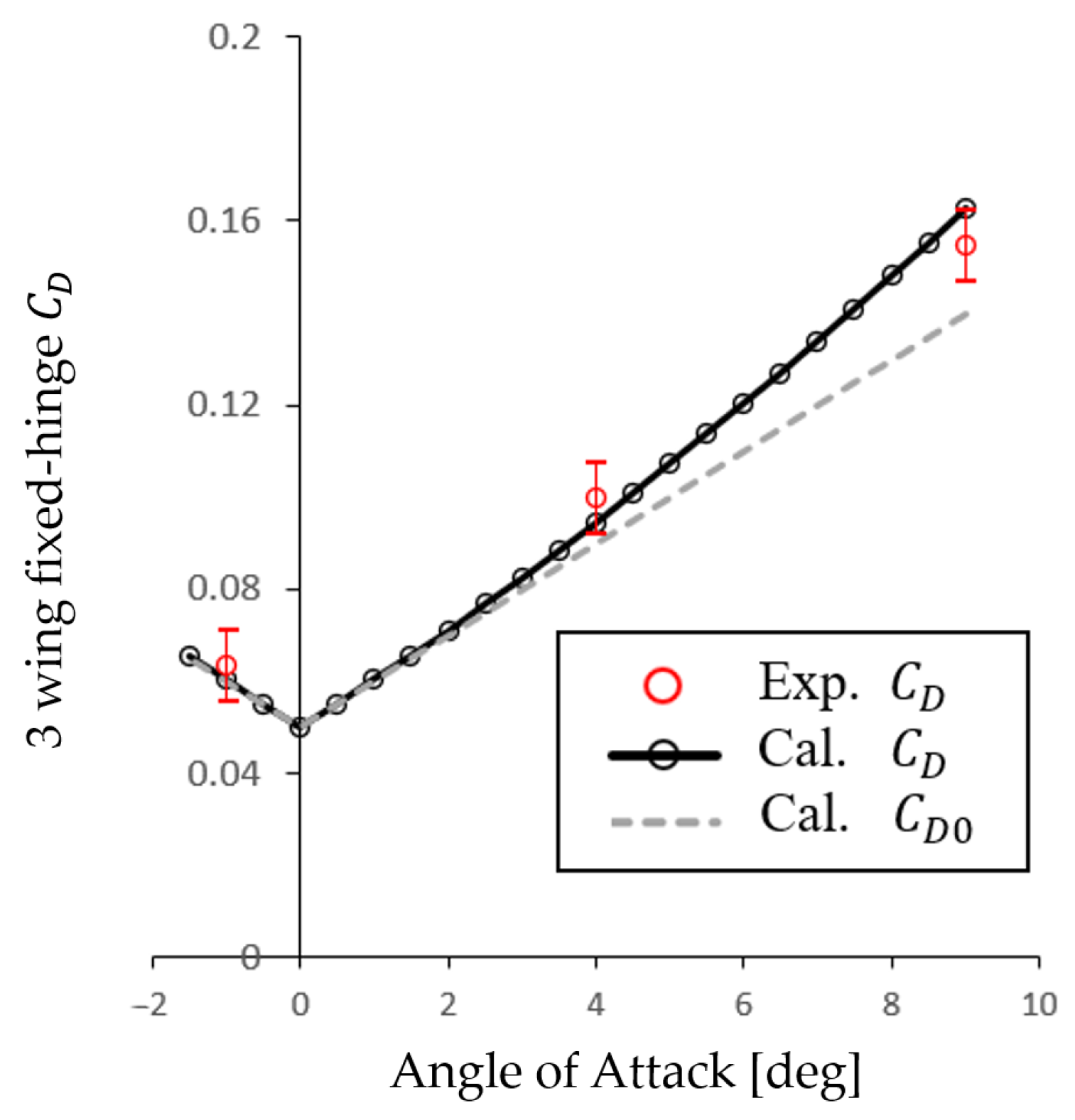
3.3. Derivation of Parasite Drag Coefficient to Use with VLM
3.4. Reference Experiment with Hinge-Axis Angle δ = 0°
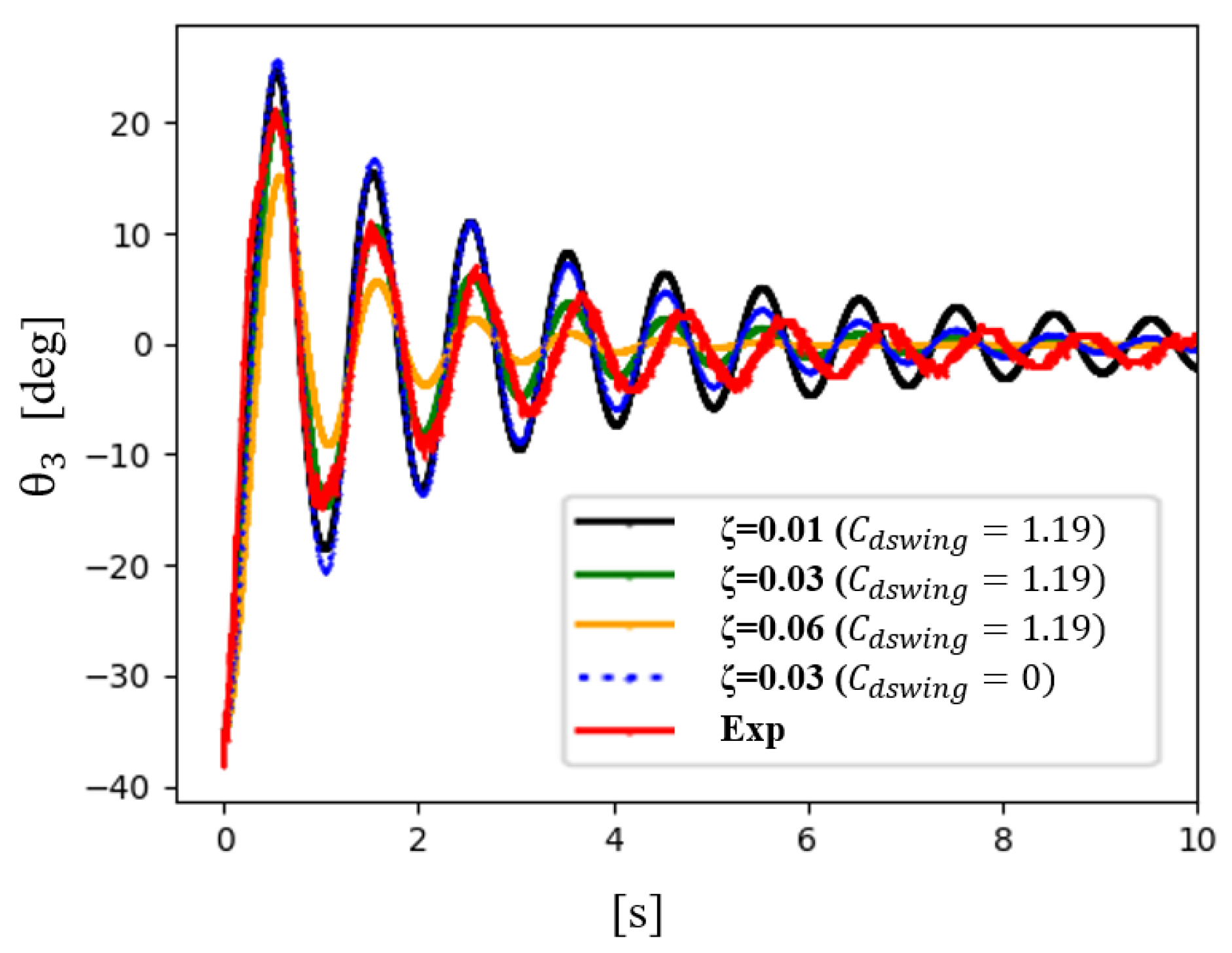
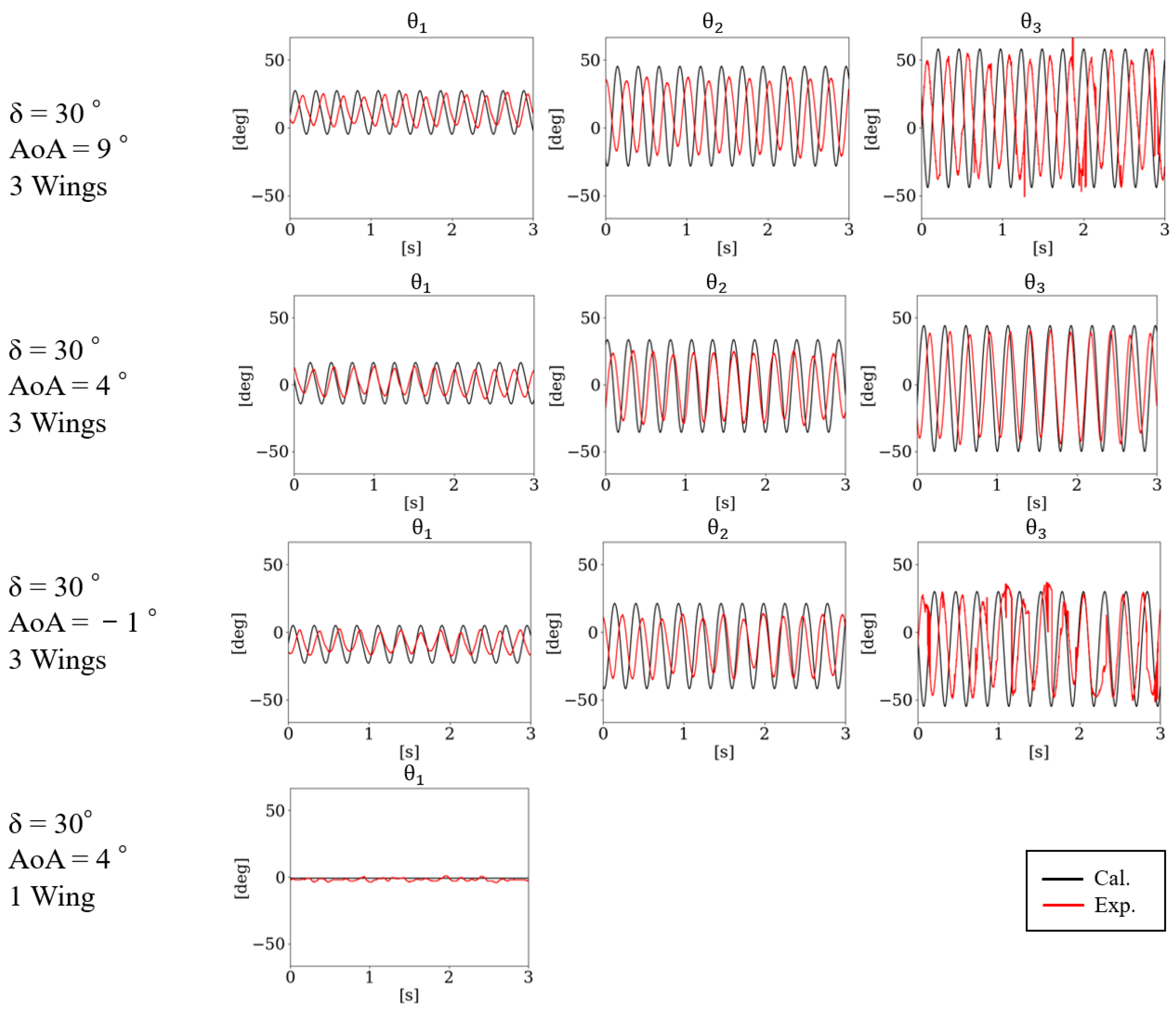
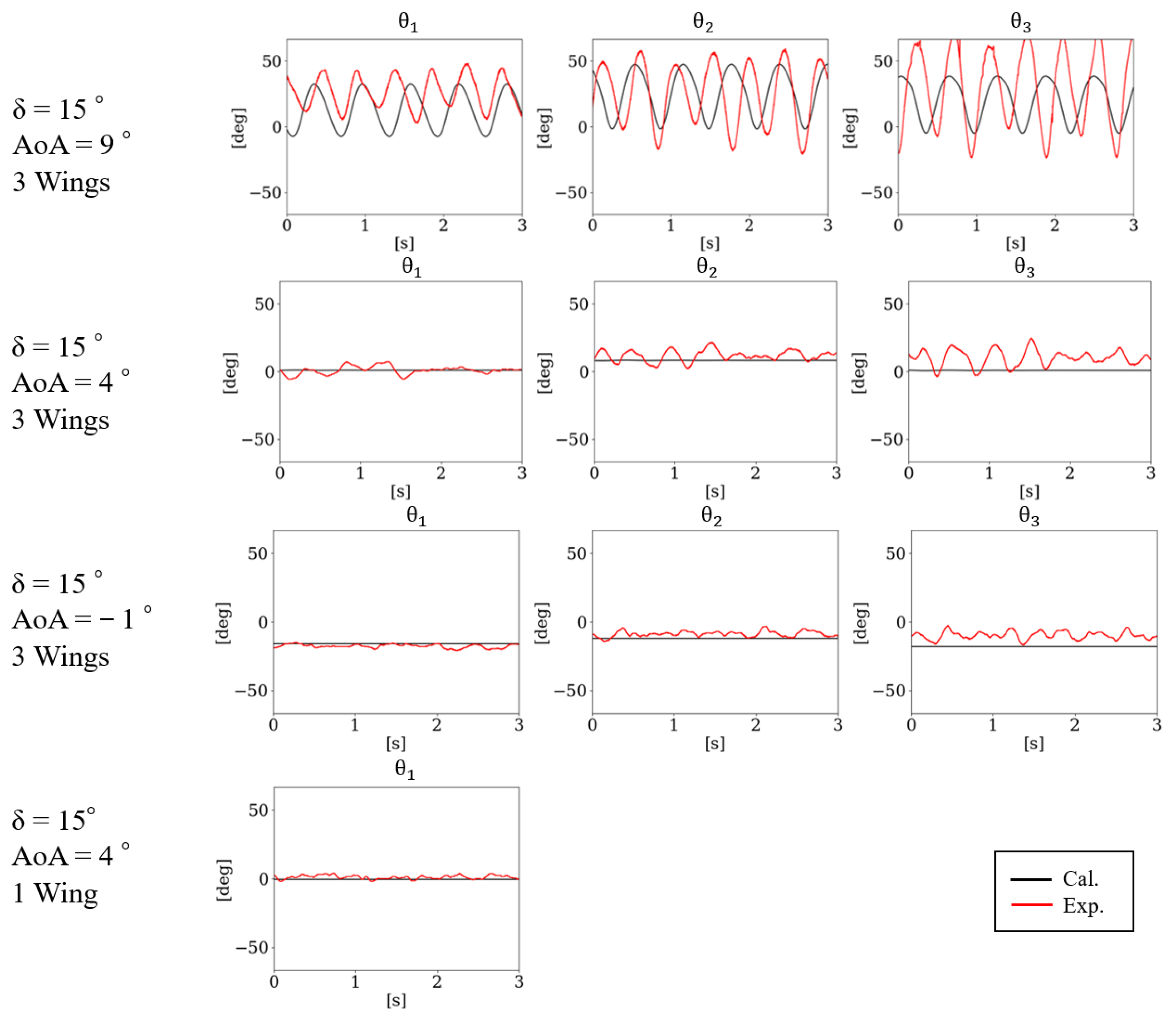
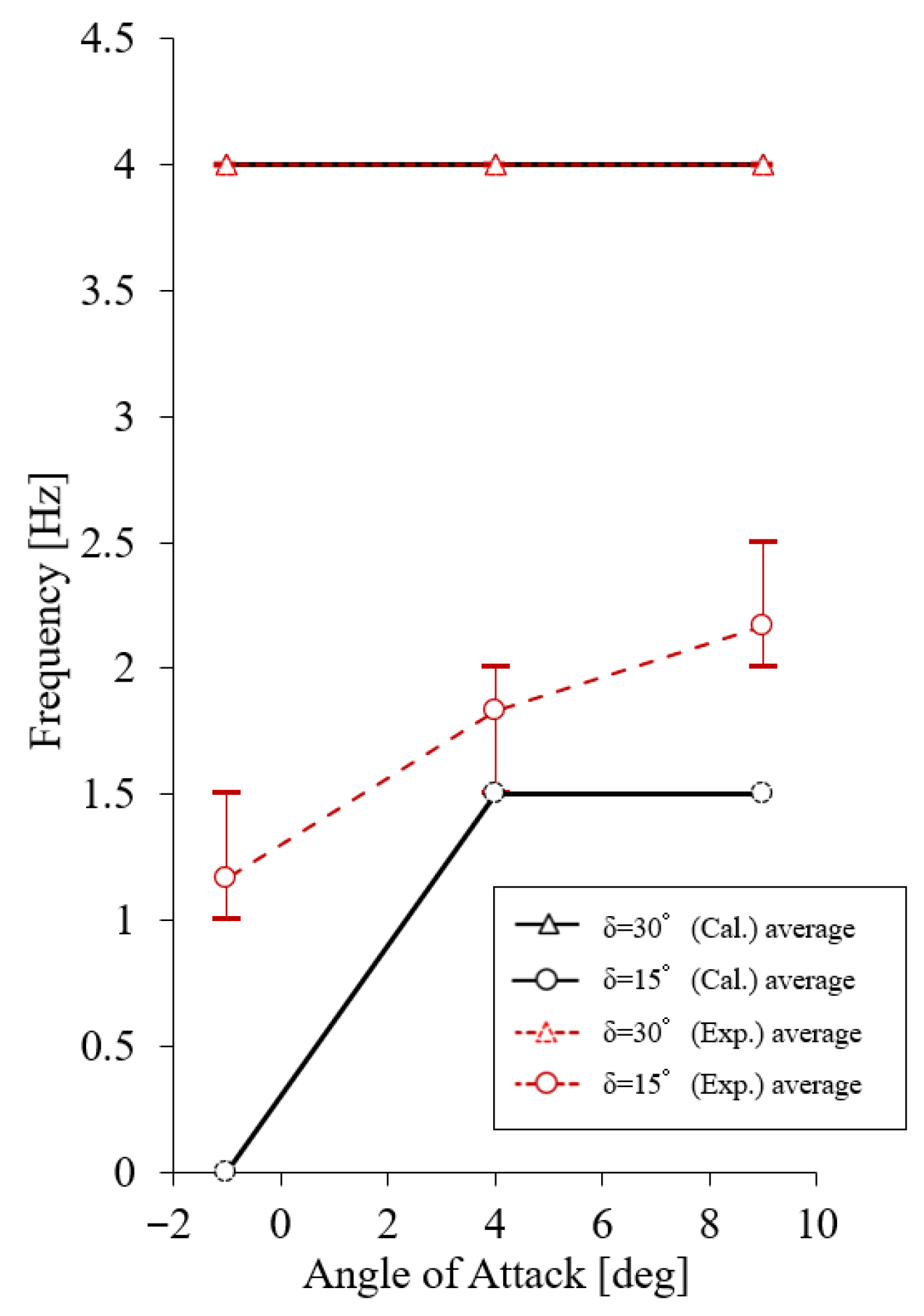
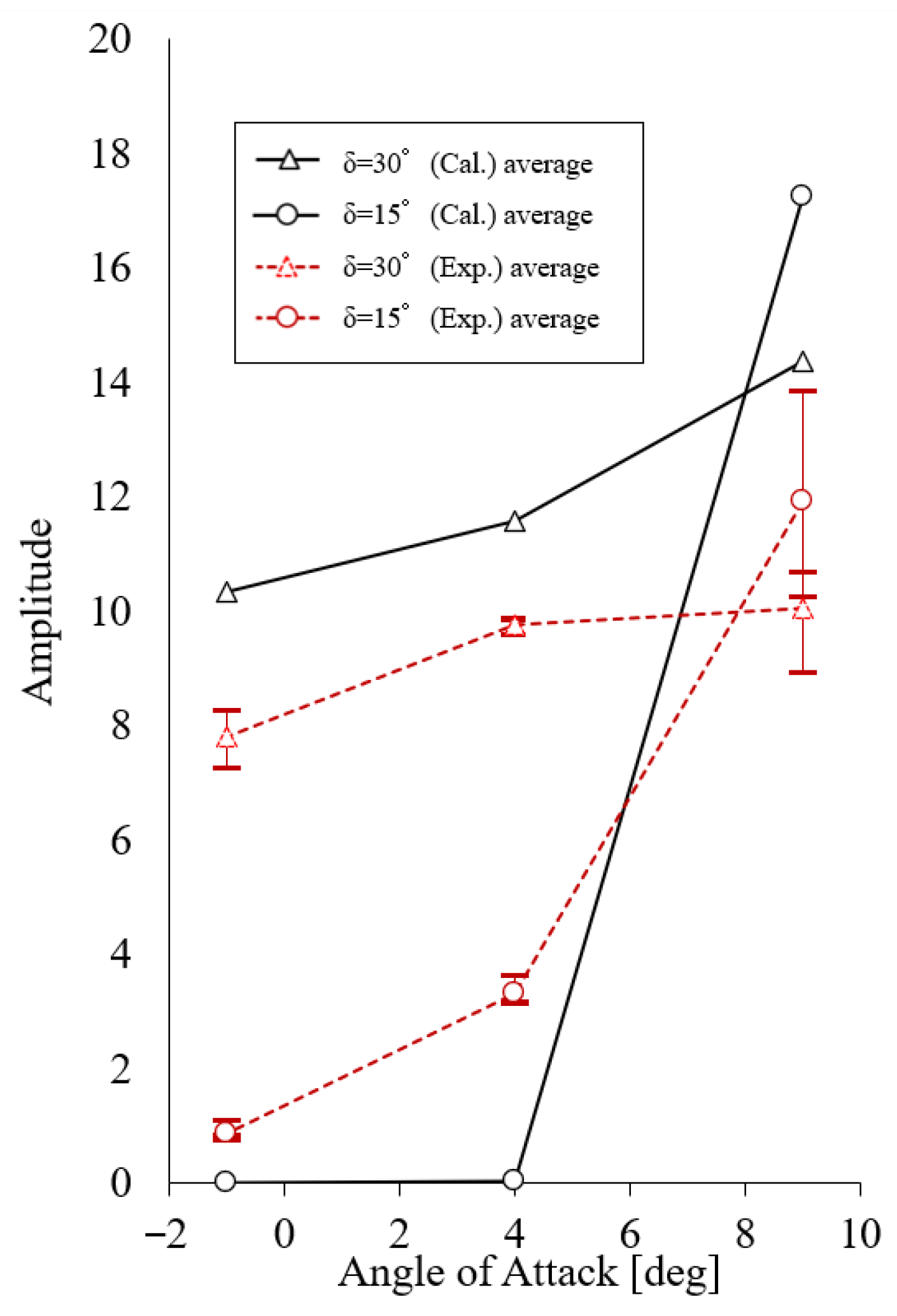
3.5. Hinge Oscillation Comparison of Experimental Results for Stable Flight Condition
3.6. Comparison of Experimental Results for Stable Wind Flow
4. Theoretical Calculation with No Structurally Induced Hinge Damping
4.1. Comparison of Hinge Axis Angle and AoA with no Structurally Induced Hinge Damping
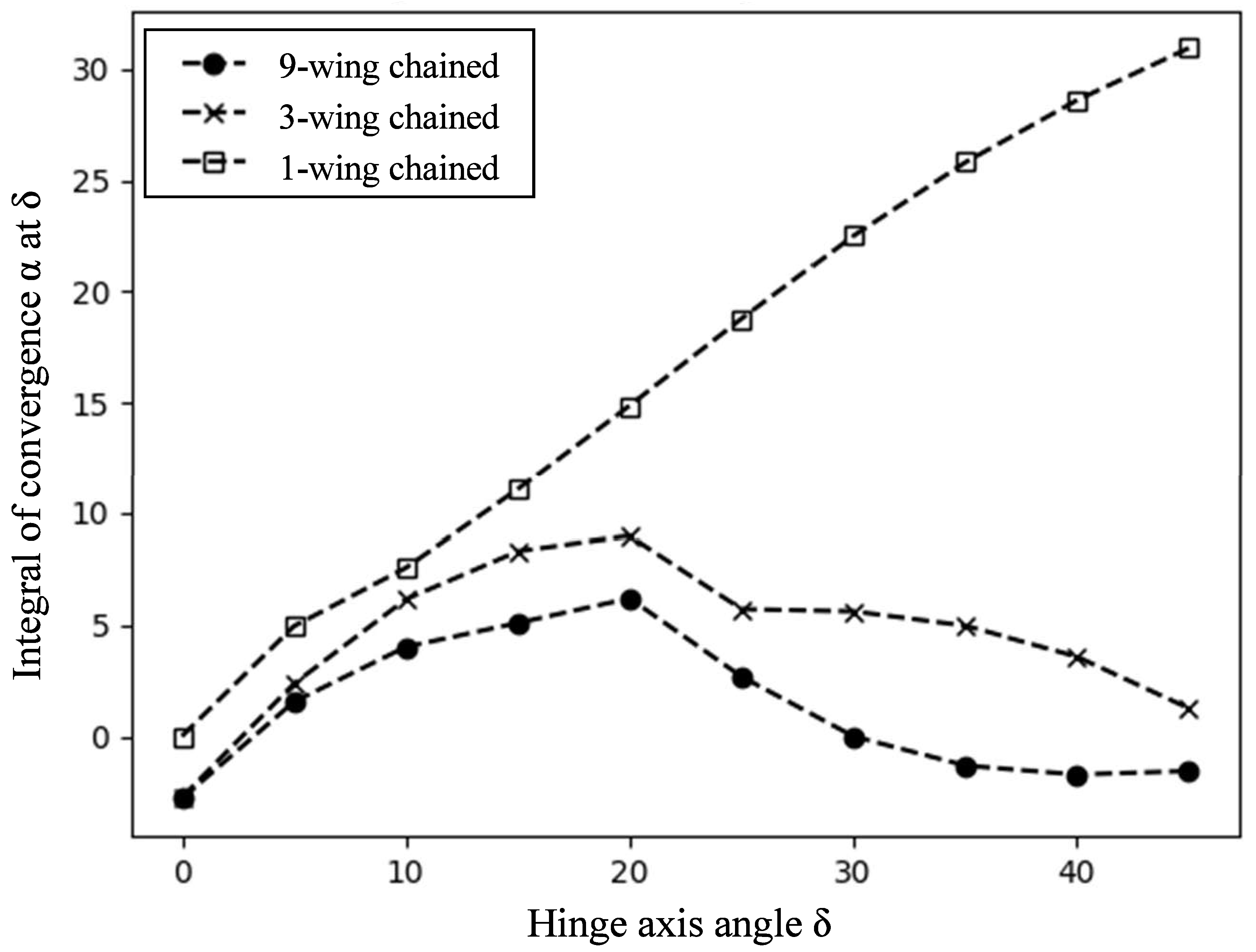
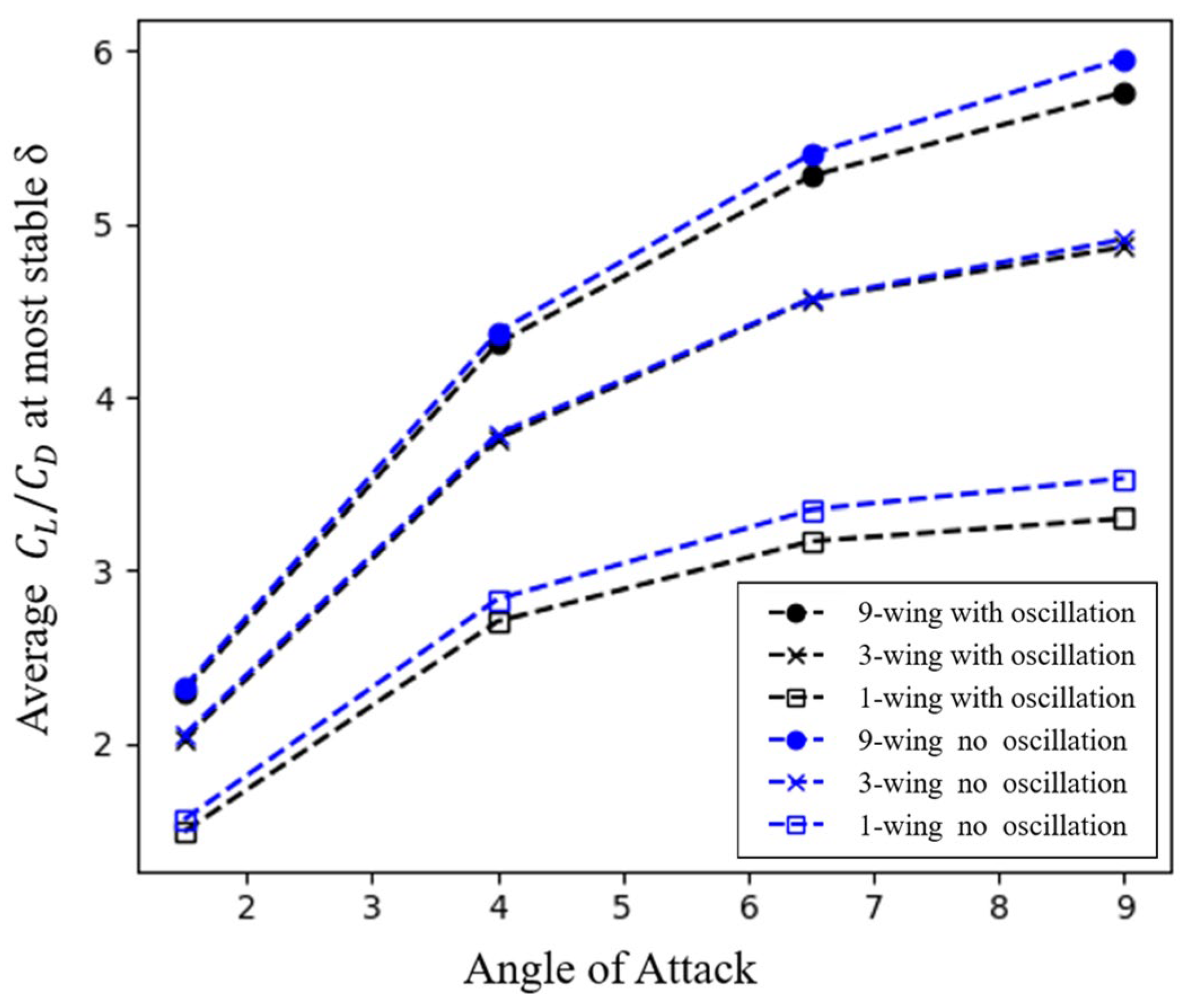
4.2. Passive Oscillation Stability and under 1-, 3- and 9-Chained Wing Flight Configurations
5. Conclusions
- Experiments and calculations confirmed that an increase in could be achieved, even without complete convergence of the oscillation of the chained wings if the oscillation was sufficiently maintained passively.
- Calculations showed that even if the rotational hinges had no structural damping ζ with an ideal smooth freely rotating hinge joint, passive oscillation convergence could still be achieved just by aerodynamic force for different numbers of chained wings with the appropriate selection of AoA and hinge-axis angle δ and without any active control.
- There is a lower and upper limit to the hinge-axis angle δ that would enable the oscillation to converge completely passively. The lower limit changed only slightly as the chained number increased, but the upper limit changed drastically and decreased with an increase in the chained-wing number.
- In the unmanned airplane case of each wing section span including the joints of the joint airplane being 2 m in length and 1.5 kg in weight, the hinge-axis angles δ that would provide the best passive convergence for the 1-wing, 3-wing, and 9-wing chains were δ = 45°, 20°, and 20°, respectively.
- Under stable wind flow, if the hinge-axis angle was δ = 0°, there would be no convergence, and the oscillations of the chained wings would diverge, but with a higher hinge axis angle, in a certain range, passive convergence or a stable limit cycle oscillation (LCO) could be achieved without diversion.
- A higher AoA leads to a higher oscillation frequency and amplitude and a lower likelihood of achieving passive oscillation convergence.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |||
| δ | joint hinge axis angle to plane direction | aerial calculation coefficients | |
| θ | rotation angle of wing around hinge axis | structural damping coefficient | |
| σ | “waviness” calculated from all the θ | α | “convergence” for passive oscillation stability |
| m | mass of each joint wing or rigid beam | r | coordinates for the center of rigid beam |
| g | gravitational acceleration | e | unit vector |
| D | aerial drag | a | coefficient defined during calculation |
| L | aerial lift | b | coefficient defined during calculation |
| M | aerial moment | W | downwash velocity for drag calculation |
| T | translational force from adjoining beam | Γ | vortex density of horseshoe vortex |
| n | number of total panels(or: unit vector perpendicular to panel) | ρ | air density (or: rigid beam density per length) |
| V | velocity at a certain panel | ||
| I | moment of inertia of rigid beam | U | velocity at wing section during swinging test |
| S | Surface area of each wing section | l | length of distance between hinge axes |
| t | time | ||
| Subscripts | |||
| i | joint airplane number/panel number | r | direction parallel to the beam |
| j | joint airplane number/panel number | t | direction perpendicular to the beam |
| k | joint airplane number | L | lift |
| local | relative flow speed due to motion | D | total drag |
| pend | for motion of pendulum calculation | D0 | parasite drag |
| vlm | coefficients related to VLM calculation | Dind | induced drag |
| fit | fitted curve | dswing | drag for flat plate perpendicular to flow |
| ini | initial | ||
References
- Makino, M. Fundamentals of Aerodynamics, 3rd ed.; Sangyotosho: Tokyo, Japan; pp. 153 and 264. (In Japanese)
- Shearer, C.M.; Cesnik, C.E.S. Non-linear flight dynamics of very flexible aircraft. J. Aircr. 2007, 44, 1528–1545. [Google Scholar] [CrossRef]
- Hasan, J.Y.; Roeser, S.M.; Hepperle, M.; Niemann, S.; Voß, A.; Handojo, V. Flight mechanical analysis of a solar-powered high-altitude platform. CEAS Aeronaut. J. 2023, 14, 201–223. [Google Scholar] [CrossRef]
- Carre, D.A.; Teixeira, P.; Palacios, R.; Cesnik, C.E.S. Non-linear response of a very flexible aircraft under lateral gust. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics 2019, IFASD 2019, Savannah, GA, USA, 10–13 June 2019. [Google Scholar]
- Gonzales, A.A.; Corpus, C.J.; Hall, D.W.; Parks, R.W. Development of a useful mars airplane exploration concept at NASA/ames research center. In Proceedings of the 6th Mars Society Conference, League City, TX, USA, 14–17 August 2003. [Google Scholar]
- Karpovich, E.; Kombaev, T.; Gueraiche, D.; Evdokimova, D.; Alexandrov, K. Long-Endurance Mars Exploration Flying Vehicle: A Project Brief. Aerospace 2023, 10, 965. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned Aerial Vehicles for Search and Rescue: A Survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Suenaga, Y.; Suzuki, K. Study on Mars exploration utilizing many wing-tip-chained airplanes. In Proceedings of the 64th Space Sciences and Technology Conference, 3K04, Online, 27–30 October 2020. (In Japanese). [Google Scholar]
- Suenaga, Y.; Suzuki, K. Preliminary analysis of the aerodynamic characteristics and flight dynamics of wing-tip-chained airplanes. JAXA-Sp. 2020, 19-007, 113. (In Japanese) [Google Scholar]
- Otsuka, K.; Makihara, K. Parametric Studies for the Aeroelastic Analysis of Multibody Wings. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2016, 14, Pc_33–Pc_42. [Google Scholar] [CrossRef] [PubMed]
- Wilson, T.; Azabal, A.; Castrichini, A.; Cooper, J.; Ajaj, R.; Herring, M. Aeroelastic behaviour of hinged wing tips. In Proceedings of the 5th Aircraft Structural Design Conference, Royal Aeronautical Society, Manchester, UK, 4–6 October 2016. 15p. [Google Scholar]
- Castrichini, A.; Wilson, T.; Cooper, J. On the dynamic release of the semi aeroelastic wing-tip hinge device. In Proceedings of the 6th Aircraft Structural Design Conference, Bristol, UK, 9–11 October 2018. [Google Scholar]
- Suenaga, Y.; Suzuki, K. Aerodynamic characteristics analysis and wind tunnel experiment of WITCH type long span airplanes. In Proceedings of the Fluid Dynamics Conference, 1B10, Online, 30 June–2 July 2021. (In Japanese). [Google Scholar]
- Suenaga, Y.; Suzuki, K. Preliminary study on aerodynamic design of wing-tip-chained airplanes for Mars exploration. In APISAT 2019: Asia Pacific International Symposium on Aerospace Technology, Gold Coast, Australia, 4–6 December 2019; Engineers Australia: Gold Coast, Australia, 2019; pp. 2048–2055. ISBN 978-1-925627-40-4. [Google Scholar]
- Padfield, D.G. Helicopter Flight Dynamics: Including a Treatment of Tiltrotor Aircraft, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; p. 121. [Google Scholar]
- Wilde, E.; Bramwell, A.R.S.; Summerscales, R. The Flapping Behaviour of a Helicopter Rotor at High Tip-Speed Ratios; Aeronautical Research Council Current Papers; Ministry of Aviation: London, UK, 1966; p. 877.
- Chen, R.T.N. Flap-lag equations of motion of rigid, articulated rotor blades with three hinge sequences. In NASA Technical Memorandum; NASA: Moffett Field, CA, USA, 1987; p. 100023. [Google Scholar]
- Castillo-Rivera, S.; Tomas-Rodriguez, M. Description of a dynamical framework to analyse the helicopter tail rotor. Dynamics 2021, 1, 171–180. [Google Scholar] [CrossRef]
- Johnson Aeronautics. CAMRAD II Software Description. Available online: http://johnson-aeronautics.com/CAMRADII.html (accessed on 18 September 2023).
- Fujita, K.; Nagai, H.; Oyama, A. Effect of yaw-tilted hinge axis on deployment robustness of mars airplane. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences, ICAS, Daejeon, Republic of Korea, 25–30 September 2016. [Google Scholar]
- Fujita, K.; Nagai, H.; Motoda, T. Dynamic behaviour of mars airplane with folded-wing deployment. Trans Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2014, 12, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Pitt, D. Static and dynamic aeroelastic analysis of structural wing fold hinges that are employed as an aeroelastic tailoring tool. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar]
- AIRBUS. AlbatrossONE A Revolutionary Approach to Aircraft Wing Design. Available online: https://www.airbus.com/en/innovation/disruptive-concepts/biomimicry/wings/albatrossone (accessed on 18 September 2023).
- Wilson, T.; Castrichini, A.; Paterson, J.; Arribas Ardura, R. Non-linear aeroelastic behaviour of hinged wing tips. In Proceedings of the 6th Aircraft Structural Design Conference, We The Curious, Bristol, UK, 9–11 October 2018. [Google Scholar] [CrossRef]
- Balatti, D.; Khodaparast, H.H.; Friswell, M.I. Experimental and numerical investigation of an aircraft wing with hinged wingtip for gust load alleviation. J. Fluids Struct. 2023, 119, 103892. [Google Scholar] [CrossRef]
- Youtube. Ran D. St. Clair Flex 9 Flight. Available online: https://www.youtube.com/watch?v=mrJgoQz5wSU (accessed on 9 March 2022).
- Youtube. Ran D. St. Clair Flex 9 Explainer. Available online: https://www.youtube.com/watch?v=GWGqs3zqttA&t=1s (accessed on 18 September 2023).
- Gabor, O.Ş.; Koreaschi, A.; Botez, R.M.; Mamou, M.; Mebarki, Y. Analysis of the aerodynamic performance of a morphing wing-tip demonstrator using a novel nonlinear vortex lattice method. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics Inc., AIAA: Reston, VA, USA. [Google Scholar] [CrossRef][Green Version]
- Suenaga, Y.; Suzuki, K. Aerodynamic characteristics of multiple wing-tip-chained airplanes (WITCH) for Mars exploration. In Proceedings of the Fluid Dynamics Conference, 3A07, Online, 28–30 September 2020. (In Japanese). [Google Scholar]
- Suenaga, Y.; Suzuki, K. Effect of joint angle on stability of flight configuration and aerodynamic characteristics of wing-tip-chained airplane. In Proceedings of the APISAT-2022, S43-3, Niigata, Japan, 12–13 October 2022. (In Japanese). [Google Scholar]
- Takeno, S. Equation of Motion for Multi-Rigid-Pendulum. Available online: http://takeno.iee.niit.ac.jp/~shige/math/lecture/misc/data/pendulum1.pdf (accessed on 9 March 2022). (In Japanese).
- Kier, T.M. Comparison of Unsteady Aerodynamic Modelling Methodologies with Respect to Flight Loads Analysis; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013; pp. 1–14. [Google Scholar]
- Gutierrez-Castillo, P.; Aguilar-Cabello, J.; Alcalde-Morales, S.; Parras, L.; del Pino, C. On the lift curve slope for rectangular flat plate wings at moderate Reynolds number. J. Wind Eng. Ind. Aerodyn. 2021, 208, 104459. [Google Scholar] [CrossRef]
- Flandro, G.A.; McMahon, H.M.; Roach, R.L. Incompressible Flow about Wings of Finite Span, Basic Aerodynamics: Incompressible Flow; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2011; pp. 254–260. [Google Scholar]
- Beitz, W.; Wei, Z.; Küttner, K.-H. DUBBEL—Handbook of Mechanical Engineering (Chinesisch): Volume 1: Fundamentals; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Keogh, E.; Michael, J.; Pazzani, J. Derivative dynamic time warping. In Proceedings of the 2001 SIAM International Conference on Data Mining, Society for Industrial and Applied Mathematics, Chicago, IL, USA, 5–7 April 2001. [Google Scholar]
- Okamoto, M.; Fukatsu, S.; Sasaki, D. Measurement of unsteady aerodynamic characteristics of a heaving wing in a low reynolds number flow. Trans. Jpn. Soc. Aeronaut. Space Sci. 2021, 64, 147–155. [Google Scholar] [CrossRef]
- Okamoto, M.; Azuma, A. Experimental study on aerodynamic characteristics of unsteady wings at low Reynolds number. AIAA J. 2005, 43, 2526–2536. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suenaga, Y.; Suzuki, K. Coupled Aerodynamics–Structure Analysis and Wind Tunnel Experiments on Passive Hinge Oscillation of Wing-Tip-Chained Airplanes. Aerospace 2024, 11, 53. https://doi.org/10.3390/aerospace11010053
Suenaga Y, Suzuki K. Coupled Aerodynamics–Structure Analysis and Wind Tunnel Experiments on Passive Hinge Oscillation of Wing-Tip-Chained Airplanes. Aerospace. 2024; 11(1):53. https://doi.org/10.3390/aerospace11010053
Chicago/Turabian StyleSuenaga, Yoichi, and Kojiro Suzuki. 2024. "Coupled Aerodynamics–Structure Analysis and Wind Tunnel Experiments on Passive Hinge Oscillation of Wing-Tip-Chained Airplanes" Aerospace 11, no. 1: 53. https://doi.org/10.3390/aerospace11010053
APA StyleSuenaga, Y., & Suzuki, K. (2024). Coupled Aerodynamics–Structure Analysis and Wind Tunnel Experiments on Passive Hinge Oscillation of Wing-Tip-Chained Airplanes. Aerospace, 11(1), 53. https://doi.org/10.3390/aerospace11010053






