Abstract
The submerged inlet exhibits good stealth characteristics and lower drag, but it has a low total pressure recovery coefficient and high distortion rate, which limits its widespread application. This paper proposes a vortex diverter aimed at enhancing the performance of the submerged inlet and investigates the aerodynamic coupling mechanism between the vortex diverter and the submerged inlet in detail. Firstly, based on the flow field characteristics of the submerged inlet, the design principles of the vortex diverter are proposed. Then, the impact of the vortex diverter on the flow field of the submerged inlet is analyzed using the numerical method. Finally, the matching design between the vortex diverter and the submerged inlet is explored. The results show that the vortex diverter improves the average total pressure of the airflow inside the inlet by exhausting the low-energy flow from the larger radius side of the inlet, thereby suppressing flow separation and enhancing flow field uniformity. The vortex diverter improves the intake performance of the submerged inlet under different incoming flow Mach numbers, inlet exit Mach numbers, angles of attack, and small sideslip angles. The maximum increase in the total pressure recovery coefficient is 3.1099%, and the maximum reduction in the circumferential total pressure distortion is 49.5207%. Among the design parameters, the horizontal distance between the leading edge of the vortex diverter and the inlet lip has the greatest influence on the intake performance, and the best control effect is achieved when the vortex diverter is installed at the throat position. Furthermore, after installing the vortex diverter, reducing the side-edge angle of the entrance appropriately can effectively reduce the intensity of the secondary flow, thereby improving the total pressure recovery at the exit and reducing the distortion rate.
1. Introduction
In future wars dominated by beyond-visual-range operations, the stealth performance of aircraft is particularly important [1]. Relevant research has shown that, within the ±30° frontal range of a fighter aircraft, the inlet and lip of the aircraft contribute approximately 40% to radar cross-section scattering [2,3,4]. Therefore, in addition to focusing on the stealth of the aircraft body, the stealth design of the inlet is also crucial. Compared to traditional inlets, submerged inlets integrate into the fuselage and offer many advantages. In addition to being geometrically compact and lightweight, they effectively reduce radar cross-section and minimize drag. The emergence of the unmanned aerial refueler MQ-25 in 2019 further demonstrates the application potential of submerged inlets in future military aircraft.
As early as 1945, Frick of the National Advisory Committee for Aeronautics proposed a submerged inlet, which uses a long inclined plate with a small inclination angle (about 7°) to guide the airflow into the inlet, a design commonly seen in the AGM-84 anti-ship missile (nicknamed Harpoon) [5]. Subsequently, a lot of research has been conducted on the design and optimization of the submerged inlet: Taylor et al. compared the total pressure recovery coefficient and external drag of the baseline configuration and the optimized configuration of the submerged inlet in the transonic range [6]. Hall et al. investigated the effects of the angle of attack, installation position, and boundary layer thickness on the total pressure recovery coefficient within the Mach number range of 0.3 to 0.9 [7,8]. Mossman et al. studied the effects of inlet width-to-depth ratio, ramp–wall divergence, and ramp angle on inlet efficiency [9,10]. Anderson et al. explored the performance of the submerged inlet at supersonic Mach numbers [11]. The above studies not only provide a design methodology for the submerged inlet but also investigate its applicable range and the effects of different parameters on air intake efficiency. The research results show that the submerged inlet has the advantages of low drag and simple structure. It not only is practical in different angles of attack and Mach number ranges but also has the disadvantages of low air intake and total pressure recovery coefficient. In 2005, Sun proposed a rectangular-shaped-entrance submerged inlet, then analyzed the internal flow field structure and the effect of the missile body’s boundary layer on the aerodynamic performance of the inlet system [12]. Subsequently, in 2007, three important parameters of the submerged inlet, namely, the side-edge angle, the ramp angle, and the characteristic parameter of the aft lip, were introduced, and the effects of these parameters on flow characteristics were investigated. The results show that the side-edge angle determines the strength of the entrained vortex, the ramp angle determines the pressure gradient perpendicular to the incoming flow at the front lip, and the characteristic parameter of the aft lip has a certain regulating effect on the total pressure distribution of the outlet cross-section [13]. In 2016, Wang proposed a method for constructing the lip surface of a submerged inlet. This method involves the construction of important curves, such as inner and outer contour curves and ridge lines, to define the shape of the lip [14]. Combined with the above research, it can be seen that the main factor restricting the performance of the submerged inlet is that the entrance is located on the surface of the missile body, which can not make full use of the stamping intake of the incoming flow, so the capture flow is relatively low. Moreover, the inability to install a boundary layer diverter results in the inhalation of a significant amount of low-energy airflow from the boundary layer. Therefore, the intake efficiency of the submerged inlet is not high, which seriously restricts the wide application of the submerged inlet. Consequently, researchers shifted their research focus from inlet design to inlet flow control.
With the development and practical application of flow control technology, various flow control methods have been tried in the improvement of the submerged inlet flow field. Flow control technology can be divided into active flow control and passive flow control, depending on whether additional momentum or energy injection is required [15]. Active flow control mainly includes boundary layer blowing, suction, and jetting. Neal compared and analyzed the layout forms of microjets, including the circumferential layout, the bottom plate axial layout, and the bottom plate V-shaped layout. The research results showed that all the layout forms of microjets effectively reduced the distortion index of the inlet, and the circumferential layout and bottom plate V-shaped layout had better control effects [16]. Yadav studied the Y-shaped dual inlet and compared the effect of slotted synthetic jets and a row of four circular synthetic jets on improving the internal flow characteristics of the inlet. The research results showed that slotted synthetic jets, due to the vortices generated, were more easily mixed with the mainstream, thus having better control effects [17]. Cheng installed blowing and suction devices upstream of the inlet to remove low-energy airflow from the boundary layer. The research results showed that the control scheme based on blowing and suction on the surface of the body could improve the inlet performance to a certain extent [18]. However, active flow control requires additional devices such as controllers, power supplies, and air pumps, and the overall benefits still need to be improved. Therefore, various passive flow control methods with stronger applicability have also been developed. Passive flow control includes various vortex generators and deflectors. According to the mechanism of improving internal flow characteristics, passive flow control can be subdivided into the following three categories:
- Install flow control devices near the entrance to displace the local boundary layer and prevent low-energy airflow from entering the intake duct. For example, Pérez installed a triangular wing vortex generator upstream of the entrance to reduce the boundary layer thickness, resulting in a 20% increase in the mass flow rate in the intake duct [19]. Sun placed a Bump-type vortex generator on the upstream surface, which effectively displaced the low-energy flow in the upstream boundary layer, improving the inlet flow quality. Under cruise conditions, the total pressure recovery coefficient at the exit increased by 3.7% [20]. Xie designed a boundary layer splitter that improved the quality of airflow inside the intake duct by displacing the low-energy flow in the boundary layer. The study results showed an improvement of 3.3% in the total pressure recovery coefficient of the intake duct and a 28.2% reduction in circumferential distortion DC60 [21]. Saheby designed a ridge-type vortex generator near the entrance, which can divert the boundary layer at the intake entrance. The total pressure recovery coefficient increased by 0.97%, 2.17%, and 4.33% at Mach numbers of 0.3, 0.5, and 0.8, respectively [22].
- Install flow control devices to promote the local beneficial mixing of airflow within the intake duct and facilitate energy exchange between the flows, thereby delaying flow separation. For example, Jirasek installed two sets of 64 micro-vane vortex generators inside the intake duct. The best control effect was achieved when the height of the vortex generators was approximately 50% of the local boundary layer thickness. This arrangement resulted in a 2% increase in the total pressure recovery coefficient and a nearly 50% reduction in the distortion index [23]. Micro-vane vortex generators are typically small in size and are proportionally related to the local boundary layer thickness. Each micro-vane vortex generator generates a small streamwise vortex, so an array of these generators is commonly used for flow control. Gissen studied the array configuration of micro-vane vortex generators and established a mapping relationship between the array parameters and the performance parameters of the intake duct using the response surface methodology. The results showed that the optimal control effect was achieved when the vane height was approximately 30% of the boundary layer thickness and the vane had a relative flow angle deviation of 13° [24].
- Direct the low energy flows within the intake duct to migrate towards designated locations and divert vortices and low energy flows out of the intake duct. For example, Cheng arranged a pair of vortex-excising slots on the sidewall of the intake duct. The exits of these slots led to the exterior surface of the body, resulting in two channels that could release vortices and low energy flows. After vortex discharged, the total pressure recovery coefficient increased by 2.8%, and the distortion index decreased by 51.0% [25]. Xie proposed a flow control method that combines boundary layer bleeding and ramp side-edge vortex diverting. During cruise flight, the total pressure recovery coefficient of the intake duct increased by 3.06%, and the DC60 value decreased by 72.57% [26].
Overall, the current passive flow control methods for submerged inlets have a wide variety, but their practicality is not high. In fact, they may even lead to noticeable increases in structural weight and additional drag, resulting in lower overall benefits for aircraft and inlet systems. Duran-Matuute and Akkermans carried out a large number of experimental and numerical simulation studies on the dipolar vortex in a shallow fluid layer. The research results show that there is a complex three-dimensional flow in the shallow fluid layer. Only when the Reynolds number and the aspect ratio reach a certain range can the flow in the shallow fluid be considered to be quasi-two-dimensional [27,28,29], considering the strong three-dimensional effect of the vortex in the submerged inlet and the negative influence of the vortex on the intake performance. In this paper, a simple idea of installing a vortex diverter on the side of the larger curvature radius of the duct is proposed. The low-energy airflow inside the submerged inlet is discharged through the vortex diverter, thereby suppressing the flow separation inside. The proposed vortex diverter structure in this paper is simpler and more efficient compared to other passive control methods. It is expected to be widely used in cruise missiles.
2. Baseline Configuration of Submerged Inlet and Numerical Simulation Method
2.1. Baseline Configuration of Submerged Inlet
Figure 1 illustrates the baseline configuration of the submerged inlet and the missile body. In order to facilitate the description, the baseline configuration of the submerged inlet is referred to as the baseline configuration. In Figure 1a, the main parameters of the baseline configuration and the missile body are presented. The entrance section of the baseline configuration is trapezoidal, with a side-edge angle () of 4°. The exit section of the baseline configuration is circular, with a diameter of D = 65 mm. The length of the inlet measures 5.45 D, with an offset of 0.88 D from the center line. Figure 1b depicts a three-dimensional view of the baseline configuration, shown in half-mode. The cross-sectional shape of the missile body is that of a rectangle with rounded corners. The submerged inlet is located on the lower abdomen plane of the missile body. To facilitate easy observation, the subsequent figures display the upper and lower surfaces of the missile body in an inverted manner.
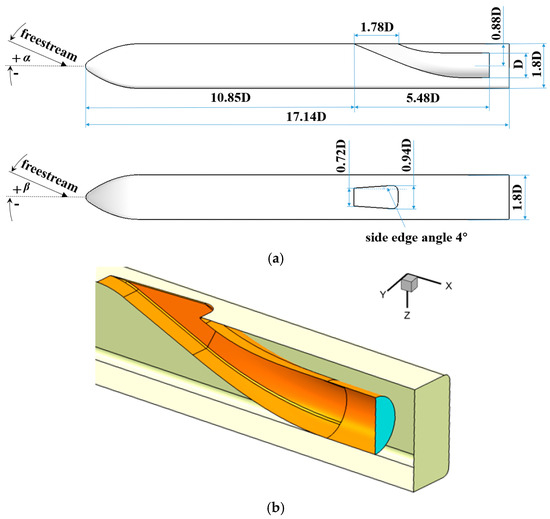
Figure 1.
Baseline configuration and missile body. (a) The main parameters of baseline configuration and missile body; (b) three-dimensional view (half-mode) of baseline configuration.
In this paper, the performance of the submerged inlet is quantitatively evaluated using the total pressure recovery coefficient, as indicated by Formula (1). Furthermore, to comprehensively assess the uniformity of the airflow on the exit section of the submerged inlet, the circumferential total pressure distortion index is employed, providing a quantitative depiction of the distortion characteristics of the outlet section of the inlet, as expressed by Formula (2):
where is the total pressure recovery coefficient; PAIP is the average total pressure (mass-averaged) of the AIP section; and P0 is the total pressure of the freestream flow;
where is the circumferential total pressure distortion; and is the total pressure recovery coefficient of the low-pressure region on the measuring surface (when there are multiple low-pressure regions, the minimum value of the low-pressure region is taken). It should be noted that the low-pressure region here refers to the region where the total pressure is lower than the average total pressure at the AIP. However, the low-pressure region in the following text mostly refers to the region with relatively static pressure/total pressure in the figure.
2.2. Numerical Simulation Method Validation
2.2.1. Calculation Method and Calculation Grid
Numerical simulation was performed using FLUENT (2021R2) software. In this paper, the Reynolds-averaged Navier–Stokes equation (RANS equation) is solved based on the finite volume method. The convection term was treated using a second-order upwind scheme, while the diffusion term was discretized using a central differencing scheme. The coupled method is employed for the pressure-velocity coupling. In the three-dimensional rectangular co-ordinate system, the differential form of the Reynolds-averaged Navier–Stokes equation is:
where Q is a conserved variable, E, F, and G are inviscid flux, and , and are viscous flux. The calculation formula and values of these parameters can be referred to [30], which is not described here.
In this study, the Spalart–Allmaras turbulence model was primarily employed for the numerical simulations. This turbulence model is a one-equation model that can directly solve for the modified turbulent viscosity. The solution variable of the Spalart–Allmaras model is , which characterizes the viscosity coefficient of turbulent motion outside the near-wall (viscosity effect) region. The transport equation is:
where is the turbulent viscosity generation term; is due to the reduction of turbulent viscosity caused by wall blocking and viscous damping; and are constants; and is the molecular viscosity coefficient. The calculation formula and values of these parameters can be referred to [31], which is not described here. Due to its high accuracy and relatively low computational cost, it has been widely applied in the field of aviation. With its ability to accurately simulate flow details such as boundary layer transition, turbulence separation, and turbulence intensity, the Spalart–Allmaras turbulence model was the ideal choice for the flow scenarios in this research [19].
The flow field exhibits symmetry in the absence of sideslip, and using half-model grids can reduce the number of grids required. However, previous studies have shown that imposing symmetry boundary conditions can guide the flow and prevent the formation of a complete three-dimensional flow structure within the inlet duct [32]. Therefore, in this research, full-model grids were used for the computations. The grid for the far-field and symmetry plane of the computational domain are shown in Figure 2. The computational domain is a rectangular prism with dimensions of 30 m in length, 10 m in width, and 10 m in height. The maximum grid size in the far-field region is 500 mm, while the maximum grid size on the missile body surface and inlet duct surface is 3 mm, and the minimum grid size is 0.5 mm. Two grid refinement zones were arranged around the missile body and the inlet duct. In order to accurately capture the flow features near the missile and inlet duct, an enhanced wall treatment (EWT) technique was employed in this study. This technique requires a very dense grid close to the wall, with a y+ value close to 1. However, excessively fine boundary layer grids can result in low grid quality and reduced computational accuracy. Therefore, it was necessary to appropriately adjust the boundary layer grid to maintain the accuracy of the simulation. The final boundary layer settings were 10 layers, with a first grid height of 0.01 mm and a growth rate of 1.2. The total number of volume grids for the baseline configuration of the submerged inlet was approximately 1.3 million, which is sufficient to accurately capture flow features and turbulence characteristics.

Figure 2.
Computational grid. (a) Grid of far field; (b) grid on the symmetric plane.
In order to simulate the free flow at infinity, the far field of the computational domain is set to the pressure-far-field boundary condition, and the free flow direction, Mach number, and static conditions are specified. To effectively approximate true infinite-extent conditions, the pressure-far-field boundary must be placed far enough from the object. This boundary condition is often used in the aerodynamic calculation of the aircraft. For example, the cruise missile in this paper is at an altitude of 5000 m when cruising, with the free stream Mach number M0 = 0.7, the angle of attack = 0°, and the sideslip angle = 0°. The static conditions at this time are set according to the unperturbed atmospheric parameters at 5000 m, and the free flow direction and Mach number are set according to the corresponding flight conditions. The exit of the inlet is set as the pressure outlet boundary condition and the static pressure at the outlet is given. The setting of the outlet static pressure is related to the running state of the engine. For example, when the cruise missile in this paper is cruising, the static pressure at the outlet of the inlet should be set to the corresponding static pressure of Me = 0.4. The wall boundary condition is used to constrain the fluid and solid regions, so the missile body and the wall of the inlet are set as the wall boundary condition. The shear stress between the fluid and wall are computed based on the flow details in the local flow field. The boundary condition settings employed in the inlet numerical calculations in this study have been widely recognized [20].
2.2.2. Grid Independence Analysis
In order to minimize the influence of the grid on the accuracy of the flow field simulation, the nodal density of the surface grid was adjusted to obtain four sets of grid schemes. The number of volume grids for the four schemes were 0.9 million, 1.3 million, 1.8 million, and 5 million, respectively. The results of the four grid schemes are shown in Table 1. Compared to the reference case with 5 million grids, the errors in the results of the 0.9 million, 1.3 million, and 1.8 million grid schemes were all less than 0.2%, meeting the accuracy requirements. In order to save computational time and ensure the accuracy of the results, the nodal density of grid scheme 2 was chosen for the calculations.

Table 1.
Grid scheme.
2.3. Example Verification
To validate the accuracy of the numerical simulation method proposed in this paper, the aforementioned simulation method and grid partition method were employed to numerically simulate the flow field of the submerged inlet discussed in reference [12]. The simulated results were then compared with the relevant experimental data. The baseline configuration of submerged inlet in this study was derived from the lip-smoothed inlet of reference [12], resulting in consistent variations of the centerline and the distribution of the cross-sectional area along the centerline.
The computational conditions were set according to the experimental conditions described in reference [12]. Table 2 presents a comparison of the total pressure recovery coefficients for different Me. The relative errors between the numerical simulation results and the experimental results were all within 1%. Figure 3 illustrates the distribution of total pressure at the exit of the inlet submerged for Me = 0.4, which also shows good agreement with the experimental results. Therefore, the accuracy of the numerical simulation method proposed in this paper has been validated.

Table 2.
Comparison of total pressure recovery coefficients at AIP.

Figure 3.
Total pressure distribution at AIP.
3. Simulation Analysis of Aerodynamic Characteristics of Baseline Configuration of Submerged Inlet
The static pressure distribution on the symmetry plane of the baseline configuration is illustrated in Figure 4. As the airflow passes through the inlet lip, the cross-sectional area of the flow passage increases, leading to an expansion of the airflow and a decrease in pressure. Consequently, a distinct low-pressure region can be observed at the inlet lip. In this process, a pressure gradient perpendicular to the incoming flow direction is formed. This pressure gradient is one of the significant factors that induce the airflow into the inlet.

Figure 4.
The static pressure distribution on the symmetry plane.
Apart from the pressure gradient at the lip of submerged inlet, the entrained vortex generated at the side edge of the submerged inlet entrance also plays a significant role in inducing the airflow into the inlet. The distribution of the total pressure recovery coefficient on the cross-section (x = −30 mm) is shown in Figure 5. From the figure, it can be seen that the entrained vortex generated at the side edge drives the external airflow into the interior of the inlet, significantly increasing the flow capture area of the submerged inlet. The zoomed-in diagram on the left shows the structure of the side-edge vortex, where a small secondary vortex is generated above the main vortex core.

Figure 5.
Total pressure recovery coefficient distribution on the cross-section (x = −30 mm).
Figure 6 demonstrates the distribution of the total pressure recovery coefficient along the flow direction. From the figure, it can be observed that the entrained vortex generated at the side edge also entrains a small amount of low-energy airflow from the boundary layer near the missile body into the inlet when inducing the external airflow into the inlet. As the entrained vortex progresses, its position gradually shifts from the sides of the cross-section towards the center, ultimately leading to the formation of a prominent low-pressure region on the side with a smaller curvature radius. The total pressure recovery coefficient in this region of low pressure is approximately 0.85.

Figure 6.
Distribution of total pressure recovery coefficient along the flow direction.
A substantial amount of low-energy airflow from the leading edge of the boundary layer enters the inlet and gradually forms large-scale separation vortices. Ultimately, a prominent low-pressure region is formed on the side of the inlet exit section with a larger curvature radius. The total pressure recovery coefficient in this region of low pressure is less than 0.82.
At the exit section of the baseline configuration, two low-pressure zones can be observed. The low-pressure zone resulting from boundary layer accumulation surpasses the low-pressure zone caused by side-edge entrained vortices in terms of coverage and pressure loss. The calculation formula for circumferential total pressure distortion (Equation (2)) reveals that the distortion characteristics are influenced by both the pressure distribution in the low-pressure region and the average total pressure recovery coefficient in the low-pressure zones. Therefore, the main reason that affects the intake efficiency and distortion characteristics of the baseline configuration is that the entrance of inlet is always submerged in the boundary layer near the fuselage, and the low-energy airflow in the boundary layer inevitably flows into the inlet. An obvious low-pressure region is formed on the side with a larger curvature radius, which may be accompanied by large-scale flow separation.
The baseline configuration exhibits two low-pressure regions at the exit section, among which the low-pressure region generated by boundary layer accumulation shows a significantly larger coverage and pressure loss compared to the one caused by the entrained vortex at the side edge. According to the calculation formula (Equation (2)) for circumferential total pressure distortion, the distortion characteristics are influenced by the average total pressure and total pressure distribution of the low-pressure region with greater pressure loss when multiple low-pressure regions are present. Therefore, to improve distortion characteristics, it is essential to address the low-pressure region generated by boundary layer accumulation in the first place.
4. Vortex Diverter Design Method for Improving the Performance of Submerged Inlet
4.1. Design Principle
Due to the constraints imposed by the internal structure of the aircraft, the space available for the arrangement of the inlet duct is limited. The key to maximizing the inlet efficiency in this limited space lies in: (1) reducing or eliminating the negative impact of low-energy airflow from the boundary layer near the entrance on the inlet duct, and (2) increasing the energy of the airflow within the inlet duct or organizing the migration of low-energy fluid within the duct to avoid the accumulation of large-scale separation vortices caused by low-energy airflow. One solution is to install vortex generators upstream of the inlet duct entrance [33]. However, installing vortex generators at the entrance of the inlet duct can introduce additional drag to the aircraft and increase its radar cross-sectional area. Based on the analysis of the baseline configuration, it is evident that the ingestion of a substantial amount of low-energy airflow from the boundary layer is the main cause of low total pressure recovery coefficient and significant total pressure distortion.
Figure 7a depicts a schematic diagram of a submerged inlet with the installation of a vortex diverter. The green segment in the figure represents the vortex diverter. The design requirements for the vortex diverter include: 1. effectively handling the low-energy airflow inside the inlet and improving the airflow quality; 2. not changing the air intake mechanism of the submerged inlet; and 3. not increasing the resistance and radar wave scattering area of the aircraft. In order to facilitate the description, the submerged inlet with a vortex diverter is referred to as the control configuration.

Figure 7.
Submerged inlet with the installation of a vortex diverter. (a) Three-dimensional view of control configuration; (b) vortex diverter to improve the intake performance schematic diagram.
Figure 7b depicts the vortex diverter to improve the intake performance schematic. A significant amount of low-energy airflow enters the inlet duct from the leading edge, and, if left untreated, it is prone to the formation of large-scale separation vortices under the influence of the pressure gradient generated by the wall curvature. To address this issue, the vortex diverter is installed on the side of the submerged inlet with a larger curvature radius. A large amount of low-energy airflow is expelled from the submerged inlet through the vortex diverter. This approach not only improves the average total pressure of the airflow within the inlet duct but also suppresses flow separation, thus enhancing the inlet quality of the submerged inlet.
Based on the previous analysis of the flow characteristics of the baseline configuration and the design requirements for the vortex diverter, the vortex diverter should primarily expel the low-energy airflow from the side of the inlet duct with a larger curvature radius, while not affecting the higher energy airflow within the inlet duct. The three key design parameters of the vortex diverter are presented in Figure 8: the distance L from the leading edge of the vortex diverter to the front lip of the inlet, the angle between the vortex diverter and the wall with a larger curvature radius of the inlet on the symmetry plane, and the thickness b of the vortex diverter. The original structure is modified to a certain extent by installing a vortex diverter. The structural integrity of the missile body and the duct is a well-discussed topic. The structural strength and structural reliability are important for designers, but the analysis of structural integrity is not within the scope of this paper.

Figure 8.
The main design parameters of vortex diverter.
The calculation grid of the control configuration is shown in Figure 9. The grid form, grid size setting, and boundary condition setting are exactly the same as those of the baseline configuration.

Figure 9.
The grids of the control configuration on the symmetry plane.
4.2. The Improvement Mechanism of Vortex Diverter on Submerged Inlet Performance
In this section, we analyze the flow fields of the baseline configuration and the control configuration and discuss the effects of the vortex diverter on the inlet performance and the mechanisms of performance improvement from the perspectives of total pressure distribution, Mach number distribution, and the development of the streamwise vortices.
4.2.1. Distribution of Total Pressure Recovery Coefficient
- (1)
- Distribution of the total pressure recovery coefficient on the symmetry plane
Figure 10 presents the total pressure recovery coefficient distribution on the symmetry plane. In Figure 10a, the total pressure recovery coefficient distribution of the baseline configuration is demonstrated. It is evident that the low-energy airflow directly enters submerged inlet from its leading edge. This part of the low-energy airflow is relatively easy to produce flow separation. With the development of the flow, a large-scale separation is gradually formed, and an obvious low total pressure zone is formed on the side with a larger curvature radius. At the exit section of the submerged inlet, the thickness of the low-energy airflow on the side with a larger radius of curvature accounts for about a quarter of the exit diameter.

Figure 10.
The distribution of total pressure recovery coefficient on the symmetry plane. (a) Baseline configuration; (b) control configuration.
Figure 10b presents the distribution of the total pressure recovery coefficient for the control configuration. It is evident from the figure that, despite the low-energy airflow entering the submerged inlet from its leading edge, this part of the low-energy airflow does not generate a large-scale separation vortex that would impact the uniformity of the airflow within the inlet. The majority of the low-energy airflow is expelled via the vortex diverter. The size of the low total pressure region on the side with a larger radius of curvature is considerably smaller compared to the baseline configuration. At the exit section of submerged inlet, the thickness of the low-energy airflow on the side with a larger radius of curvature accounts for about one-tenth of the exit diameter.
The vortex diverter expels the low-energy airflow from the side of the inlet duct with a larger curvature radius, resulting in an increase in the average total pressure of the airflow inside the inlet duct. This improves the intake quality of the submerged inlet and reduces total pressure distortion.
- (2)
- Distribution of total pressure recovery coefficient on monitoring surface
Inside the inlet duct, there are five monitoring surfaces that are arranged along the direction of airflow, as illustrated in Figure 11. These monitoring surfaces are located at x-co-ordinates of 0 mm, 60 mm, 120 mm, 180 mm, and 240 mm, respectively. Notably, the fifth monitoring surface corresponds to the exit of the submerged inlet.
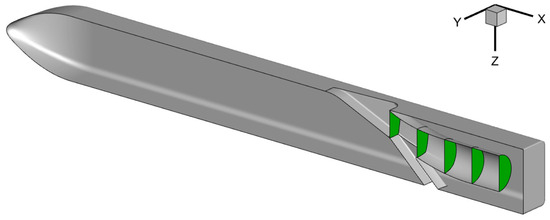
Figure 11.
Monitoring surface inside the inlet.
The distribution of the total pressure recovery coefficient with streamline on the monitoring surface of the baseline configuration is shown in Figure 12a. The cross-sections in the figure are perpendicular to the x-axis, so the streamlines in the figure only consider the velocity in the y direction and the velocity in the z direction. Observing the monitoring surfaces at x = 60 mm, x = 120 mm, and x = 180 mm, it can be seen that, as the airflow further develops, the range of influence of the separation vortex on both sides of the cross-section near the top gradually expands. The vortex cores converge from both sides towards the center, ultimately forming a pair of separation vortices at the top of the intake duct. After the low-energy airflow from the upstream enters the intake duct, it forms a distinct low-pressure area on the side with a larger radius of curvature in the intake duct. By observing the monitoring surfaces at x = 0 mm, x = 60 mm, x = 120 mm, and x = 180 mm, it can be observed that the area occupied by low-energy airflow gradually increases. This is due to the lateral pressure difference generated by the curvature of the intake duct walls, as well as the effects of wall friction and the interaction with large-scale flow separation. After the airflow passes through the cross-section at x = 180 mm and enters the straight section of the intake duct, the area occupied by low-energy airflow decreases to some extent. By observing the streamline plots on the cross-section, it can be seen that the bottom of the cross-section is covered by low-energy airflow, indicating weaker resistance to flow separation, as flow separation occurs at x = 60 mm. As the airflow further develops, the scale of the separation vortex gradually increases. The formation of large-scale separation vortices disrupts the stability of the internal airflow in the intake duct and increases the total pressure loss.

Figure 12.
Distribution of total pressure recovery coefficient with streamlines on the monitoring surface. (a) Baseline configuration; (b) control configuration.
The distribution of the total pressure recovery coefficient with streamline on the monitoring surface of the control configuration is shown in Figure 12b. At x = 0 mm position, the total pressure distribution on the cross-section of the control configuration is generally consistent with that of the baseline configuration. After x = 60 mm position (passing through the vortex diverter), the development pattern of the low-pressure region at the top caused by the entrained vortex is similar to that of the baseline configuration, but the flow conditions at the bottom of the intake duct are completely different. By observing the monitoring surfaces at x = 60 mm, x = 120 mm, x = 180 mm, and x = 240 mm, it can be observed that the area of the low-pressure region at the bottom significantly decreases, and the position where the separation vortex forms is noticeably delayed compared to the baseline configuration, delayed by approximately 120 mm. Additionally, there are distinct differences in the vortex patterns on the side with a larger radius of curvature between the two configurations. In the baseline configuration, the streamlines on the side with a larger radius of curvature do not form a uniformly distributed helical pattern, making it difficult to observe a prominent rotation center. Eventually, they converge to form a single line on the cross-section. This indicates that the prominent motion characteristic of the separation vortex at the bottom of the baseline configuration is the rotational movement around the vortex core along the flow direction. On the other hand, in the control configuration, the streamlines at the bottom are relatively evenly distributed, and, when vortices are present, a distinct rotation center can be observed. The main reason for these differences is the significant disparity in the intensity and scale of the separation vortices. For the baseline configuration, the formation of the separation vortex at the bottom is primarily due to the lower kinetic energy carried by the bottom airflow, resulting in weaker resistance to separation. Under the influence of the pressure gradient generated by the bending and wall surface friction, a large-scale separation vortex forms along the flow direction. In contrast, for the control configuration, the lower-energy airflow is expelled from the intake duct through the vortex diverter, resulting in a higher kinetic energy carried by the airflow inside the duct, leading to stronger resistance to separation. Therefore, when influenced by the pressure gradient and wall surface friction caused by the curvature of the intake duct, only a secondary flow is generated in the cross-section perpendicular to the mainstream direction, without the formation of large-scale separation vortices along the flow direction.
4.2.2. Mach Number Distribution
The Mach number distribution with streamlines on the symmetry plane is shown in Figure 13. Figure 13a illustrates the Mach number distribution of the baseline configuration, where it can be observed that a large-scale separation vortex gradually forms on the side with a larger radius of curvature as a result of the accumulation of low-energy airflow in the intake duct. The vortex structure and location of the vortex core can be clearly observed from the streamline distribution on the symmetry plane, which is consistent with the analysis in the previous section. This separation vortex intensifies the mutual interference of nearby airflow, resulting in mixing losses. Ultimately, this may lead to airflow blockage, further reducing the actual flow area of the inlet duct.

Figure 13.
Mach number distribution with streamlines on the symmetry plane. (a) Baseline configuration; (b) control configuration.
Figure 13b presents the Mach number distribution of the control configuration, where it can be observed that, on the side with a larger radius of curvature of the intake duct, the low-energy airflow is expelled from the intake duct through the vortex diverter. the local flow energy of control configuration is significantly higher than that of the baseline configuration, and no apparent separation phenomenon is observed.
4.3. Study on the Adaptability of Vortex Diverter Design
In order to evaluate the applicability of the control configuration under different flight conditions, the intake efficiency of the control configuration (L = 115.7 mm, b = 17.43 mm, and = 20°) was calculated under different freestream Mach numbers (M0), exit Mach numbers (Me), angles of attack (), and angles of sideslip (β). Figure 14, Figure 15, Figure 16 and Figure 17 provide the calculated results of the total pressure recovery coefficient and circumferential total pressure distortion at the exit of the intake duct for different freestream Mach numbers (M0), exit Mach numbers (Me), angles of attack (), and sideslip angle (). The calculation results demonstrate that the vortex diverter has a significant improvement effect on the intake efficiency of the submerged inlet for various freestream Mach numbers (M0), exit Mach numbers (Me), and angles of attack (). Under cruising conditions ( = 0°, = 0°, M0 = 0.7, Me = 0.4), compared to the baseline configuration, the control configuration shows a 1.01% improvement in the total pressure recovery coefficient and a 32.77% reduction in the circumferential total pressure distortion. Under low engine speed conditions ( = 0°, = 0°, M0 = 0.7, Me = 0.33), compared to the baseline configuration, the control configuration shows a 3.11% improvement in the total pressure recovery coefficient and a 49.52% reduction in the circumferential total pressure distortion.

Figure 14.
Comparison of inlet performance at different incoming Mach numbers. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.
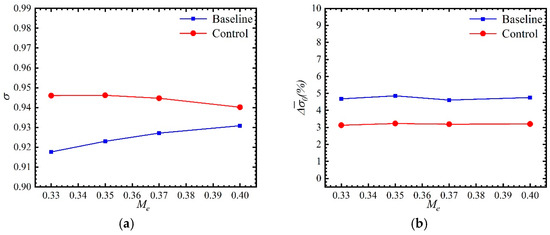
Figure 15.
Comparison of inlet performance at different exit Mach numbers. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.

Figure 16.
Comparison of inlet performance at different angles of attack. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.

Figure 17.
Comparison of inlet performance at different sideslip angles. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.
However, the vortex diverter is sensitive to changes in the sideslip angle, and, as the sideslip angle increases, the improvement effect of the vortex diverter on the performance of the submerged inlet gradually decreases. Additionally, in our previous study [34], it was found that, regardless of whether it is under low subsonic or high subsonic conditions, the effect of the sideslip angle on the internal flow structure of the submerged inlet is greater than that of the angle of attack. Therefore, the focus of this research is to investigate the influence of the sideslip angle on both configurations.
Six monitoring planes were arranged along the flow direction, and the distribution of total pressure on these planes is shown in Figure 18. The x-co-ordinates of the six monitoring planes are −140 mm, −65 mm, 0 mm, 80 mm, 160 mm, and 240 mm (from left to right). In order to facilitate the observation of high-pressure regions in the contour plots, the portion of the total pressure recovery coefficient distribution exceeding 0.999 is truncated. The left side shows the distribution of the total pressure recovery coefficient near the baseline configuration and the missile body, while the right side shows the distribution near the control configuration and the missile body.

Figure 18.
Total pressure distribution on the monitoring surface. (a) = 0°; (b) = 4°; (c) = 8°.
From the distribution of the total pressure recovery coefficient on the monitoring planes depicted in Figure 18, it can be observed that, as the sideslip angle increases, the low-pressure region inside the intake duct gradually shifts from the bottom wall to the sidewall. During this process, the efficiency of the vortex diverter in expelling low-energy airflow decreases gradually. When = 8°, the internal total pressure distribution of the intake duct becomes highly asymmetrical. Observing the cross-section at x = 0 mm reveals that there is almost no low-pressure region on the left side of the bottom, while a large amount of low-energy airflow accumulates on the right side. At this point, the vortex diverter will inevitably expel a portion of higher-energy airflow, resulting in a slightly lower total pressure recovery coefficient at the exit compared to the baseline configuration.
Considering the small variation in sideslip angle during the cruise of subsonic cruise missiles, it can be concluded that the vortex diverter exhibits good adaptability. Furthermore, since the vortex diverter is embedded inside the missile body without increasing the frontal area, it adds almost no additional drag. Therefore, this flow control technology has high practicality in engineering applications.
4.4. The Influence of Vortex Diverter Design Parameters on the Performance of the Submerged Inlet
To further elucidate the influence of the design parameters of the vortex diverter on the performance of the intake duct, the design parameters were modified based on L = 115.7 mm, b = 17.43 mm, and φ = 20°. The values for each design parameter are presented in Table 3.

Table 3.
Design parameter values.
Figure 19, Figure 20 and Figure 21 show the influence of the design parameters L, b, and of the vortex diverter on the intake performance. It can be seen from the figure that the intake performance of all control configurations is improved compared to the baseline configuration. This indicates that the vortex diverter has a strong stability for the improvement of the intake performance of the submerged inlet. At the same time, the vortex diverter has a high fault tolerance rate in design and use.

Figure 19.
The influence of design parameter L on the performance of the inlet. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.

Figure 20.
The influence of design parameter b on the performance of the inlet. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.

Figure 21.
Effect of design parameter on inlet performance. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.
Figure 22, Figure 23 and Figure 24 show the influence of the design parameters L, b, and of the vortex diverter on the total pressure distribution at the exit of the inlet. It can be seen from Figure 22 that, with the increase of L, the area of the bottom low-pressure region decreases gradually. This phenomenon occurs because, when the vortex diverter is positioned closer to the exit, the low-energy airflow at the bottom does not have enough time to fully develop. Additionally, the mixing of low-energy airflow with high-energy airflow in the intake duct results in mixing losses, and expelling the low-energy airflow earlier is advantageous for enhancing the uniformity of airflow within the intake duct. Therefore, when the vortex diverter is farther away from the exit, the extent of the low-pressure region at the top is smaller. In addition, combined with the transformation law of the cross-sectional area of the duct, it can be seen that, since the cross-sectional area at the throat is the smallest, the efficiency of improving the intake performance is higher when the vortex diverter is installed near the throat.

Figure 22.
Influence of design parameter L on total pressure distribution. (a) L = 116 mm; (b) L = 146 mm; (c) L = 176 mm; (d) L = 206 mm; (e) L = 236 mm.
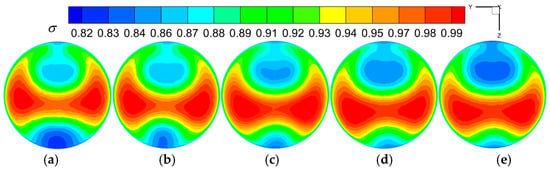
Figure 23.
Influence of design parameter b on total pressure distribution. (a) b = 3.8 mm; (b) b = 7.7 mm; (c) b = 11.7 mm; (d) b = 15.8 mm; (e) b = 20.1 mm.

Figure 24.
Effect of design parameter on total pressure distribution. (a) = 10°; (b) = 15°; (c) = 20°; (d) = 25°; (e) = 30°.
It can be seen from Figure 23 that, with b increasing, the area of the low-pressure region at the bottom gradually decreases, while the extent of the low-pressure region at the top increases. This is because the thickness (b) of the vortex diverter determines its maximum exhaust capacity. When the exhaust capacity is too low, low-energy airflow cannot be fully discharged from the intake duct. Conversely, when the exhaust capacity is too high, high-energy airflow will also be discharged from the intake duct. Therefore, both excessively large and small values of b result in inferior improvements in intake efficiency.
The parameter determines the pressure gradient at the leading edge of the vortex diverter. It can be seen from Figure 24 that, with increasing, the pressure gradient at the leading edge of the vortex diverter intensifies, making it easier to expel low-energy airflow. Consequently, the low-pressure region at the bottom gradually decreases, while the extent of the low-pressure region at the top increases. However, when becomes excessively large, the airflow at the leading edge of the vortex diverter tends to separate under the influence of the pressure gradient. This results in a decrease in the efficiency of the vortex diverter for expelling low-energy airflow. Therefore, both excessively large and small values of result in inferior improvements in intake efficiency.
4.5. The Matching Design of Vortex Diverter and Submerged Inlet
According to the research results from reference [13], the side-edge angle of the submerged inlet entrance determines the intensity of the entrained vortex generated. However, in the previous study on the baseline configuration, we have already known that there are two distinct low-pressure regions at the exit of the intake duct. The low-pressure zone is generated by the entrained vortex from the side edge and the accumulation of the boundary layer. The low-pressure zone generated by the accumulation of the boundary layer has been significantly reduced by the vortex diverter. In this section, we will explore the adjustment effect of the side-edge angle on the performance of the control configuration while keeping the entrance area of the intake duct unchanged.
Figure 25 illustrates the influence of the variation in the side-edge angle on the intake performance. As c increases, the total pressure recovery coefficient decreases gradually, and the circumferential total pressure distortion increases.

Figure 25.
Influence of on intake performance. (a) Total pressure recovery coefficient; (b) the circumferential total pressure distortion.
To explore the reasons for the decrease in intake efficiency of the control configuration with increasing side-edge angle (), six monitoring planes were arranged along the direction of flow, and the distribution of total pressure on these planes is shown in Figure 26. The x-co-ordinates of the six monitoring planes are −140 mm, −70 mm, 0 mm, 80 mm, 160 mm, and 240 mm (from left to right). To facilitate the observation of high-pressure regions in the contour plot, the portion of the total pressure recovery coefficient distribution exceeding 0.999 is truncated.

Figure 26.
Total pressure distribution on the monitoring surface. (a) = −2°; (b) = 2°; (c) = 6°.
As c increases, it can be observed from Figure 26 that the area of the low-pressure region caused by the entrained vortex from the side edge gradually increases on the monitoring surface. This is because the strength of the entrained vortex gradually increases with the increase in the side-edge angle (). While the entrained vortex promotes airflow into the intake duct, it also causes the low-energy airflow near the missile body to enter the intake. Observing the total pressure distribution, it can be noted that the low-energy airflow begins to accumulate near the side edge and gradually converges towards the top of the intake along the flow direction from both sides of the wall. Additionally, with the side-edge angle increasing, there is a noticeable change in the distribution of the low-pressure region at the bottom. When the side-edge angle is small, the low-energy airflow adheres to the bottom surface in a flattened distribution. However, as the side-edge angle increases, the low-energy airflow converges towards the symmetry plane, resulting in a convex shape at the bottom.
Figure 27 shows a two-dimensional vector distribution on the exit section of the intake duct. It can be clearly observed that there is a pair of counter-rotating vortices generated by the side edge at the top of the section. These counter-rotating vortices induce downward velocity near the symmetry plane and upward velocity near the two side walls. This is also one of the reasons why the low-pressure region generated by the entrained vortices from the side edge gradually converges from both sides of the wall towards the top of the intake duct along the flow direction, and then moves downward.

Figure 27.
The two-dimensional vector distribution on the exit section of the intake duct under different side-edge angles. (a) = −2°; (b) = 2°; (c) = 6°.
As the side-edge angle increases, the strength of the entrained vortices generated by the side edge also increases. Consequently, the strength of the counter-rotating vortices at the top of the exit section gradually increases. When the strength reaches a certain level, a pair of counter-rotating vortices formed by the secondary flow appears at the bottom of the section. These vortices induce upward velocity near the symmetry plane and a pair of velocities pointing towards the symmetry plane at the bottom. This explains why, as the side-edge angle increases, the low-pressure region at the bottom gradually changes from a flattened distribution adhering to the wall to a convex shape converging towards the symmetry plane.
5. Conclusions
Based on the flow characteristics of a submerged inlet, this paper proposes a flow control method to improve the intake performance of submerged inlets by installing a vortex diverter on the side of the larger curvature radius of the inlet duct. A comparison and analysis were conducted using numerical simulation methods on the baseline configuration and control configuration under different operating conditions. Furthermore, the parameters of the vortex diverter and matching design with the submerged inlet were investigated. The research findings indicate the following:
- (1)
- The vortex diverter exhausts the low-energy airflow on the side of the larger curvature radius of the inlet duct. As a result, the average kinetic energy of the airflow inside the inlet duct increases, the ability to resist separation strengthens, and the formation of separation vortices on the side of the larger curvature radius of the inlet duct is suppressed. This improves the airflow quality inside the submerged inlet and reduces the total pressure distortion. The maximum increase in the total pressure recovery coefficient is 3.1099%, and the maximum reduction in the circumferential total pressure distortion is 49.5207%.
- (2)
- The vortex diverter can enhance the intake performance of the submerged inlet under different flow Mach numbers, exit Mach numbers, and angles of attack, demonstrating its wide adaptability. However, when the sideslip angle is relatively large (greater than 8°), the performance of the control configuration is slightly inferior to that of the baseline configuration. This is because when the sideslip angle is too large, the low-energy airflow within the inlet is transferred from the bottom to the sidewalls of the duct. As a result, the efficiency of the vortex diverter in expelling low-energy airflow is reduced. However, considering that the sideslip angle variation is relatively small during the cruising of supersonic cruise missiles, it can be concluded that the vortex diverter exhibits good adaptability.
- (3)
- The vortex diverter has a relatively stable effect on improving the inlet performance of the submerged inlet. Among the key parameters of the vortex diverter: the distance L between the leading edge of the vortex diverter and the leading edge of the inlet determines the exhaust location of the vortex diverter; the thickness b of the vortex diverter determines the maximum exhaust flow rate of the vortex diverter; and the angle between the vortex diverter and the sidewall of the larger radius of curvature of the inlet determines the pressure gradient at the leading edge of the vortex diverter. Among these parameters, the distance L is the most influential on performance. The calculation results indicate that the installation of the vortex diverter near the throat region yields the optimal improvement in inlet performance.
- (4)
- The computational results indicate the presence of two distinct low-pressure regions at the exit of the baseline configuration. These low-pressure regions are caused by the accumulation of the boundary layer and the entrained vortices generated by the side edges. The vortex diverter can effectively expel the low-energy airflow from the accumulation of the boundary layer. Furthermore, by installing the vortex diverter and appropriately decreasing the side-edge angle at the entrance of the inlet, the intensity of the entrained vortices generated by the side edges can be significantly reduced, thereby improving the total pressure distribution at the exit of the inlet. Therefore, combining the installation of the vortex diverter with adjustments to the side-edge angle provides a more effective approach to enhancing the inlet performance.
Author Contributions
Conceptualization, J.Z.; methodology, J.Z.; software, J.Z.; validation, J.Z. and B.M.; formal analysis, J.Z. and H.Z.; investigation, J.Z. and B.M.; resources, H.Z. and B.M.; data curation, J.Z. and H.Z.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z., B.M. and H.Z.; visualization, J.Z.; supervision, B.M.; project administration, B.M.; funding acquisition, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was made possible with the support of the National Natural Science Foundation of China under Grant No. 12202363, the Fundamental Research Funds for the Central Universities under Grant No. G2020KY05115, and the Natural Science Basic Research Program of Shaanxi under Program No. 2021JQ-084.
Acknowledgments
This work was made possible with the support of the National Natural Science Foundation of China under Grant No. 12202363, the Fundamental Research Funds for the Central Universities under Grant No. G2020KY05115, and the Natural Science Basic Research Program of Shaanxi under Program No. 2021JQ-084.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| AIP | aerodynamic interface plane |
| b | the thickness of the vortex diverter, mm |
| D | exit diameter of inlet duct, mm |
| L | the distance from the leading edge of the vortex diverter to the front lip of the inlet, mm |
| M0 | freestream Mach number |
| Me | Mach number at the exit |
| P0 | the total pressure of the freestream flow, Pa |
| PAIP | mass-averaged total pressure over the aerodynamic interface plane, Pa |
| angle of attack, ° | |
| angle of sideslip, ° | |
| angle of side edge, ° | |
| total pressure recovery coefficient | |
| the total pressure recovery coefficient of the low-pressure region | |
| the circumferential total pressure distortion | |
| the angle between the vortex diverter and the wall with a larger curvature radius of the inlet on the symmetry plane, ° |
References
- Jia, G.W.; Yin, P.; Shao, S.; Wang, J. Review of RCS measurement and imaging methods of stealth aircraft. J. Natl. Univ. Def. Technol. 2022, 44, 93–103. [Google Scholar]
- Zheng, R.S.; Qi, K.N.; Zhang, Q.B.; Xiao, Z.; Liu, H.J. Integrated Investigation of Aerodynamic Shape and Stealth Performance for Supersonic Vehicle with “X” Sawtooth Lip Inlet. J. Propuls. Technol. 2017, 38, 9. [Google Scholar] [CrossRef]
- Yu, X.H.; Zhao, Y.M. A Study on Stealth Technology in UAV Inlet Design. Flight Dyn. 2007, 4, 69–72. [Google Scholar]
- Shi, L.; Guo, R. Electromagnetic Scattering of a Submerged Inlet. Acta Aeronaut. Astronaut. Sin. 2008, 29, 1098–1104. [Google Scholar]
- Frick, C.W.; Davis, W.F.; Randall, L.M.; Mossman, E.A. An Experimental Investigation of NACA Submerged Duct Entrances; Technical Report Archive & Image Library: Washington, DC, USA, 1945. [Google Scholar]
- Taylor, R.A. Some Effects of Side-Wall Modifications on the Drag and Pressure Recovery of an NACA Submerged Inlet at Transonic Speeds; Technical Report Archive & Image Library: Washington, DC, USA, 1952. [Google Scholar]
- Hall, C.F.; Frank, J.L. Ram-Recovery Characteristics of NACA Submerged Inlets at High Subsonic Speeds; Technical Report Archive & Image Library: Washington, DC, USA, 1948. [Google Scholar]
- Axelson, J.A.; Taylor, R.A. Preliminary Investigation of the Transonic Characteristics of an NACA Submerged Inlet; Technical Report Archive & Image Library: Washington, DC, USA, 1950. [Google Scholar]
- Mossman, E.A.; Randall, L.M. An Experimental Investigation of the Design Variables for NACA Submerged Duct Entrances; Technical Report Archive & Image Library: Washington, DC, USA, 1948. [Google Scholar] [CrossRef]
- Frank, J.L. Pressure-Distribution and Ram-Recovery Characteristics of NACA Submerged Inlets at High Subsonic Speeds; Technical Report Archive & Image Library: Washington, DC, USA, 1950. [Google Scholar]
- Anderson, W.E.; Frazer, A.C. Investigation of an NACA Submerged Inlet at Mach Numbers from 1.17 to 1.99; Technical Report Archive & Image Library: Washington, DC, USA, 1952. [Google Scholar]
- Sun, S.; Guo, R.R. Numerical Analysis and Experimental Validation of a Submerged Inlet on the Plane Surface. Chin. J. Aeronaut. 2005, 18, 199–205. [Google Scholar] [CrossRef]
- Sun, S.; Guo, R.R.; Wu, Y.Z. Characterization and Performance Enhancement of Submerged Inlet with Flush-Mounted Planar Side Entrance. J. Propuls. Power 1971, 23, 987–995. [Google Scholar] [CrossRef]
- Wang, Y.G.; Wang, C.H.; Xiao, Y.C.; Chen, B.; Zhou, S.; Guo, J.; Sun, M. Construction methodology for lip surface of a submerged inlet. Aerosp. Sci. Technol. 2016, 54, 340–352. [Google Scholar] [CrossRef]
- Huang, H.X. Recent Progress in Subsonic S-Shaped Inlets. J. Propuls. Technol. 2020, 41, 2641. [Google Scholar] [CrossRef]
- Harrison, N.A.; Anderson, J.; Fleming, J.L.; Ng, W.F. Active Flow Control of a Boundary Layer-Ingesting Serpentine Inlet Diffuser. J. Aircr. 2013, 50, 262–271. [Google Scholar] [CrossRef]
- Yadav, K.R.; Paul, A.R.; Hegde, N.; Jain, A. A Comparison of Circular and Slotted Synthetic Jets for Flow Control in a Twin Air Intake. Def. Sci. J. 2020, 70, 113–121. [Google Scholar] [CrossRef]
- Cheng, D.S.; Sun, S.; Wen, Y.F.; Tan, H.J. Submerged inlet performance improvement with blowing on fuselage. J. Aerosp. Power 2012, 27, 1131–1138. [Google Scholar]
- Perez, C.C.; Ferreira, S.B.; Silva, L.F.F.D.; Jesus, A.B.D.; Oliveira, G.L. Computational Study of Submerged Air Inlet Performance Improvement Using Vortex Generators. J. Aircr. 2007, 44, 1574–1587. [Google Scholar] [CrossRef]
- Sun, S.; Tan, H.-J.; Wang, C.-X. Submerged Inlet Performance Enhancement Using a Unique Bump-Shaped Vortex Generator. J. Propuls. Power 2016. [Google Scholar] [CrossRef]
- Xie, W.Z.; Yang, S.Z.; Zeng, C.; Guo, S. Effects of forebody boundary layer on the performance of a submerged inlet. Aeronaut. J. 2021, 125, 1260–1281. [Google Scholar] [CrossRef]
- Saheby, E.B.; Shen, X.; Huang, G.; Hays, A.P. Flow structure of the ridge integrated submerged inlet. Aerosp. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Jirasek, A. Design of Vortex Generator Flow Control in Inlets. J. Aircr. 2006, 43, 1886–1892. [Google Scholar] [CrossRef]
- Gissen, A.N.; Vukasinovic, B.; Mcmillan, M.L.; Glezer, A. Distortion Management in a Boundary Layer Ingestion Inlet Diffuser Using Hybrid Flow Control. J. Propuls. Power 2014, 30, 834–844. [Google Scholar] [CrossRef]
- Cheng, D.S.; Tan, H.J.; Sun, S.; Tong, Y. Computational Study of a High-Performance Submerged Inlet with Bleeding Vortex. J. Aircr. 2012, 49, 852–860. [Google Scholar] [CrossRef]
- Xie, W.Z.; Zeng, C.; Wang, Z.Z.; Guo, S.M. Flow Control for a Submerged Inlet. J. Fluids Eng. 2022, 144, 121202. [Google Scholar] [CrossRef]
- Akkermans, R.A.D.; Cieslik, A.R.; Kamp, L.P.J.; Trieling, R.R.; Clercx, H.J.H.; van-Heijst, G.J.F. The three-dimensional structure of an electromagnetically generated dipolar vortex in a shallow fluid layer. J. Phys. Fluids 2008, 20, 116601. [Google Scholar] [CrossRef]
- Duran-matute, M.; Kamp, L.P.J.; Trieling, R.R.; van-Heijst, G.J.F. Scaling of decaying shallow axisymmetric swirl flows. J. Fluid Mech. 2010, 648, 471. [Google Scholar] [CrossRef]
- Duran-Matute, M.; Albagnac, J.; Kamp, L.P.J.; van-Heijst, G.J.F. Dynamics and structure of decaying shallow dipolar vortices. J. Phys. Fluids 2010, 22, 116606. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-Averaged Navier–Stokes Equations for Turbulence Modeling. Appl Mech. Rev. 2009, 62, 933–944. [Google Scholar] [CrossRef]
- Deck, S.; Duveau, P.L.; D’Espiney, P. Development and application of Spalart—Allmaras one equation turbulence model to three-dimensional supersonic complex configurations. Aerosp. Sci. Technol. 2002, 6, 171–183. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhan, H.; Mi, B.G. Study on Aerodynamic Design of the Front Auxiliary Inlet. Aerospace 2023, 10, 700. [Google Scholar] [CrossRef]
- Bai, X.; Mi, B.G. Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet. Aerospace 2023, 10, 649. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Mi, B.G. Internal Aerodynamic Performance Enhancement for Aircraft with High Maneuver by Designing a Distributed Submerged Inlet. Appl. Sci. 2023, 13, 1459. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).