Abstract
A fan is part of the core equipment of a super-pressure balloon altitude control system, and high-performance fans have a significant impact on the altitude control capability and flight safety of super-pressure balloons. This paper proposes a mixed-flow MIX-140 fan for use with super-pressure balloons. Changes in the fan’s operating characteristics at various flight altitudes of a super-pressure balloon were investigated. First, the performance of the fan at ground level was obtained through numerical simulation and compared with measured data of the prototype to verify the accuracy of the simulation analysis. On this basis, the influences of changes in the atmospheric pressure, temperature, and fan speed on fan performance were investigated through numerical simulation. Furthermore, the MIX-140 fan was compared with an existing fan, and the variation of two parameters, namely, the ratio of inflation volume per unit time and the ratio of inflation volume per unit power, were investigated at different altitudes. Finally, the changes in the operating characteristics of the fan under different high-altitude environments were investigated through actual testing. The results reveal that changes in altitude can lead to significant changes in fan performance, and changes in the atmospheric pressure, temperature, and fan speed affect the fan’s working characteristics. Compared with the existing fan, the MIX-140 fan achieves an average increase of 295.8% in the inflation volume per unit of time, and 14.6% in the inflation volume per unit of power at altitudes of 16–20 km. The performance variation characteristics and testing methods of this proposed super-pressure balloon fan can provide a foundation and reference for the design of a super-pressure balloon control system.
1. Introduction
As an important platform for conducting near-space research and exploration, a super-pressure balloon has significant advantages such as long residence time, high flight altitude, cost effectiveness, and rapid response [1,2,3]. Compared with aeronautical and astronautical platforms, a super-pressure balloon has significant advantages in terms of temporal and spatial resolution [4]. Researchers in many countries, including the United States, Japan, and China [5,6,7,8], have conducted multiple experiments on super-pressure balloons.
The vertical motion of a super-pressure balloon in the stratosphere is achieved by changing the buoyancy–weight balance of a super-pressure balloon through techniques such as the throwing solid ballast [9], air ballast height-adjustment technology [10], and connecting multiple balloon systems in series [11]. The horizontal motion is determined by the speed and direction of the wind at the balloon location. By utilizing the variation of wind speed and direction in different wind layers, it is possible to achieve the regional residence or flight trajectory planning of a super-pressure balloon in the stratosphere, thus achieving specific trajectory control objectives. Owing to the uncertainty of high-altitude wind field changes, the height control capability and control accuracy of a super-pressure balloon determine the success or failure of the balloon mission. In extreme cases, it may take several weeks of circling flight to recover from control errors [12]. Air ballast height-adjustment technology uses air as a ballast and changes the weight of air in the airbag of a super-pressure balloon by controlling the fan inflation and deflation to adjust the net buoyancy of the balloon system, making the balloon reach buoyancy–weight balance again at a new height, and thus achieve height adjustment. The effectiveness of this technology has been verified by the Loon super-pressure balloon project [13,14] and super-pressure balloon project of the Chinese Academy of Sciences Honghu pilot project [15].
A fan is part of the core equipment in the altitude control system. A fan with superior performance can endow a super-pressure balloon with better altitude adjustment capabilities, and lower energy consumption can allow more energy for the payload. Owing to the particular environment in the stratosphere, the development of a super-pressure balloon fan is extremely challenging and manifests as follows: (a) harsh operating conditions: a super-pressure balloon fan operates both in ground and high-altitude environments, and the external environment varies greatly; therefore, a fan must avoid getting too cold and overheating; (b) power consumption limitation: the energy source of a super-pressure balloon comes from the onboard lithium battery and solar array [16], and the energy supply is limited; therefore, the power consumption of a fan is limited; (c) high-reliability requirements: owing to the irreversibility of a super-pressure balloon mission, when the fan fails to operate during the flight process, this will result in the loss of the active altitude adjustment capability of a super-pressure balloon, which will affect the success or failure of the mission; and (d) high-performance requirements: in the low-temperature and low-pressure environment of the stratosphere, a fan must have sufficient pressure head and flow, while being highly efficient to minimize energy consumption.
With the increasing progress of super-pressure balloon technology, the volume of a super-pressure balloon is continuously increasing, and the pressure resistance is continuously improving; the task requirements of multisphere networking, rapid response, and prolonged air presence are increasingly gaining prominence, and the requirements for the height control ability and steering ability of a super-pressure balloon are continuously increasing. The fan currently used in super balloons has gradually become unable to satisfy the height adjustment requirements, owing to its inability to overcome the problems of the internal pressure inflation of the sphere, slow inflation speed, and single control method [17]. Therefore, it is necessary to carry out relevant design modifications and research on the airbag fan of a super-pressure balloon.
Domestic and overseas studies have conducted relevant research in this field. Sun et al. [18] proposed a fan for stratospheric airships and analyzed the impacts of different geometric parameters on the fan’s efficiency. Wei et al. [19] proposed a method for selecting centrifugal fans for aerostats. Zhao et al. [20] considered the changes in air density, pressure, and temperature in high-altitude environments, proposed a numerical method for predicting the performance of centrifugal compressors, and investigated the impact of changes in key parameters on compressor performance. Yang et al. [21] investigated the flow field characteristics of large-flow axial fans in a 20 km environment using computational fluid dynamics (CFD) methods; their results revealed that the selection of the fans’ vanes and diffusers significantly affected the fan’s efficiency. Zhang et al. [22] proposed a method for using super-pressure balloon fans in series, which can compensate for the impact of an insufficient fan capacity to a certain extent. Qu et al. [17] proposed an optimization method for mixed-flow fans applicable to stratospheric airships.
The above-mentioned studies on the fan for stratospheric aerostats is typically based on the research background of the aerostat’s altitude. The high-altitude control results in a super-pressure balloon being greatly affected by external factors, such as temperature and pressure, and wide parameter variation. If the fan is still operated within its rated working state, it may experience an overpower operation or overspeed operation [20]. Therefore, to ensure the safe operation and efficient altitude control of a super-pressure balloon, it is necessary to analyze and investigate the fan’s working characteristics in environments corresponding to varying altitudes.
This study considered the MIX-140 fan for a super-pressure balloon as the research object and we conducted a simulation analysis and experimental testing to investigate the impacts of pressure, temperature, and speed changes on the fan’s performance on the ground and in high-altitude environments. Moreover, the fan was compared with the existing fan for super-pressure balloons, and the comparison results were analyzed to verify the high efficiency of the MIX-140 fan in high-altitude environments.
The rest of this paper is organized as follows: Section 2 presents the simulation of the MIX-140 fan’s performance in the ground environment using CFD software and compares it with measured data to validate the simulation analysis. Section 3 discusses the influences of speed, pressure, and temperature changes on the performance of the MIX-140 fan through a simulation analysis. Furthermore, the performance differences between the MIX-140 fan and existing fans at different altitudes are compared through two parameters: the ratio of air volume per unit time and the ratio of air volume per unit power. Section 4 discusses the working performance of the fan under different ambient pressure through actual testing. Section 5 summarizes the findings and suggests directions of future work.
2. Physical Models and Numerical Methods
2.1. Physical Model and Analytical Model
In super-pressure balloons and other aerostats with air bags, fans are used in conjunction with valves. The research object of this study, namely, the mixed-flow MIX-140 fan [23], and the valve are shown in Figure 1a; the core component of the fan, the impeller, is shown in Figure 1b. The specific design parameters are shown in Table 1. This fan and valve are designed and manufactured by the Chinese Academy of Sciences Aerospace Information Research Institute, who possess the relevant intellectual property rights.

Figure 1.
(a) MIX-140 fan and valve. (b) MIX-140 fan impeller.

Table 1.
Design parameters of MIX-140 fan.
Owing to the installation location of the valve at the inlet of the fan, the valve has a certain impact on the flow area of the fan’s inlet. Therefore, the impact of the valve must be considered during the analysis process. Based on the structure of the MIX-140 fan, the fluid domain of the fan was extracted as shown in Figure 2. The fluid domain includes the inlet pipe, impeller, and diffuser.
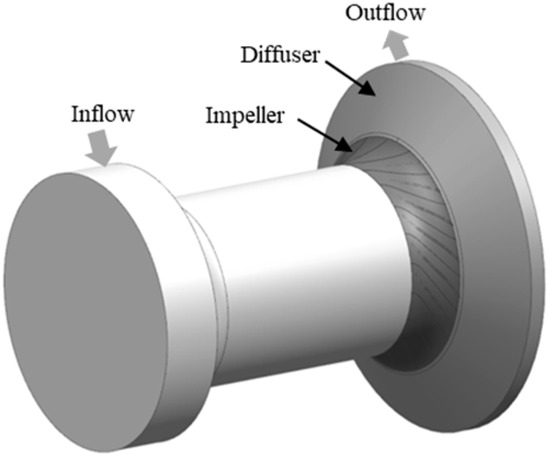
Figure 2.
Fluid domain of MIX-140 fan.
2.2. Numerical Methods and Boundary Conditions
This study used CFX 18.0 (ANSYS, Pittsburgh, PA, USA) fluid dynamics analysis software to perform numerical analysis on the fan’s fluid characteristics. Owing to the complex turbulent flow inside the fan, a suitable turbulence solution method must be selected to simulate the air flow inside the fan with satisfactory accuracy [24]. According to existing research, the shear stress transport model (SST) is more suitable for analysis under high-altitude and low-Reynolds-number conditions [25]. Therefore, the SST model was selected to solve the three-dimensional time-averaged Navier–Stokes equation.
Considering the symmetrical characteristics of the fan flow channel structure, to reduce the computational burden during numerical analysis, a 1/20 flow channel was used for analysis by setting circular symmetrical boundaries, as shown in Figure 3.
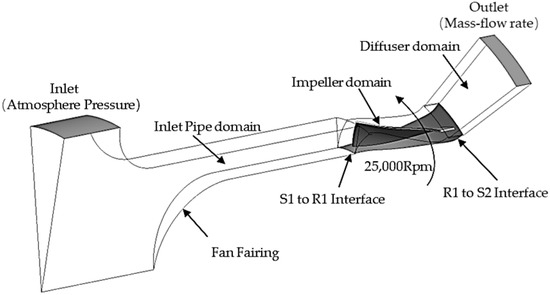
Figure 3.
Computational domain.
Among these components, the impeller part was set as a rotating region at a given speed, and the inlet tube and diffuser parts were set as stationary regions. The transition between the rotating and stationary interfaces was connected using a “mixed plane” technique, which averages the parameters of the previous-stage component interface axially and transfers them to the interface of the next-stage component [26]. All wall surfaces were assumed to be slip-free. In steady-state computation, the calculation was considered convergent when the root mean square residual was less than 10−5.
The boundary conditions for the simulation analysis of the MIX-140 fan must be consistent with the actual environment. The specific values are related to the flight height of a super-pressure balloon. Atmospheric temperature, pressure, and density at high altitudes can be calculated based on the International Standard Atmosphere (ISA) model [27], as presented below.
In Equations (1)–(3), T is the external atmospheric temperature in kelvin, h is the altitude about sea level in meters, P is the atmospheric pressure in pascal, and is the air density in Kg*m−3.
According to Equations (1)–(3), the external atmospheric temperature, atmospheric pressure, and air density can be calculated when a super-pressure balloon is flying at any height up to 32 km about sea level.
2.3. Meshing and Independence
In this study, ANSYS Mechanic was used to mesh the inlet duct and diffuser of the fan, generating a hexahedral mesh. The mesh structure of the fan impeller was generated using ANSYS Turbo Mesh. As shown in Figure 4, all meshes were hexahedral meshes.
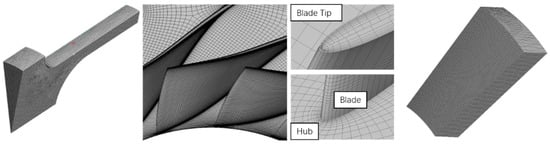
Figure 4.
Computational mesh.
The number of meshes directly affects the accuracy of the simulation results, and selecting a reasonable number of meshes can reduce the computational burden. Therefore, it is important to perform mesh independence checks. This study selected six different mesh number sets for mesh independence testing.
The mesh distribution and independence check results are presented in Table 2. PRi represents the fan’s static pressure ratio at different mesh numbers, and ηi represents the fan’s efficiency at different mesh numbers.

Table 2.
Mesh independence check.
The analysis results reveal that when the inlet pipe mesh number reached 26,900, the impeller mesh number reached 400,000, and the diffuser mesh number reached 50,000; the change rate of the fan’s efficiency and static pressure ratio was relatively small. Therefore, it was decided that the total mesh number should be controlled at 500,000 in subsequent calculations and analyses.
The fan performance was tested to verify the accuracy of the results obtained by numerical methods. Because the design point of the MIX-140 fan considers high-altitude, low-temperature, and low-pressure conditions, if the fan is tested under normal temperature and pressure conditions on the ground, it will encounter overpower problems when operated at full speed under high-altitude conditions. Therefore, the testing speed must be reduced to ensure that the fan power is consistent with high-altitude conditions. Typically, the principle of similarity is used to carry out performance conversion for fans under different conditions [28,29]. The principle of similarity for fans is expressed by Equations (4)–(6).
Here, , , , , and are the flow rate, pressure, power, speed, and medium density of the fan under the design point environment, respectively, and , , , , and are the operating values of the fan under other conditions.
The performance test of the MIX-140 fan was conducted on a fan test bench that complies with AMCA (Air Movement and Control Association) specifications, as shown in Figure 5. The test bench was used to measure and record the performance curve of the fan. The test was conducted at the ambient temperature of 25 °C, ambient pressure of 101,312 Pa, and a relative humidity of 50%.

Figure 5.
Fan performance test bench.
The performance curve of the fan in the ground environment was obtained through the test bench test and the simulation method described in Section 2, as shown in Figure 6. As the fan’s flow rate increased, the pressure difference of the fan gradually decreased. In the entire process, the maximum pressure difference of the fan was 2045 Pa, and the maximum flow rate was 547 m3/h. By comparing the measured data curve with the simulation data curve, it can be seen that the two curves have a good agreement. When the flow rate was less than 400 m3/h, the difference between the simulation data and the measured data was small, and the error was approximately 3%.
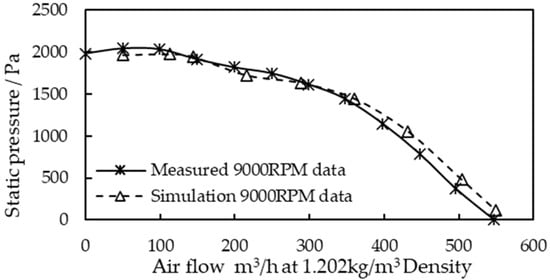
Figure 6.
Ground performance curve of fan.
During the test, to verify the compliance of the similarity law, the performance curves of the fan at three different speeds were tested, as shown in Figure 7. The three curves in the figure are the performance curves of the fan at 9000 RPM, 8000 RPM, and 7000 RPM. As can be seen, the three curves exhibit a consistent trend and are parabolic. As the fan speed decreased, the maximum pressure and maximum flow decreased correspondingly. Considering the 9000 RPM data as the standard, the flow and pressure of the fan at 8000 RPM and 7000 RPM were converted using Equations (4) and (5), as indicated by the triangular and circular points in the figure. As can be seen, both of them are in good agreement with the actual test curve. The average error is approximately 1%, demonstrating that the similarity law can accurately convert the fan performance curves at different speeds under the same working conditions.
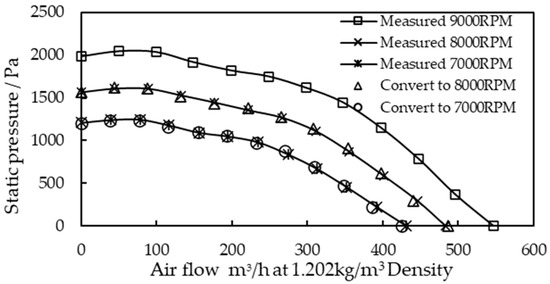
Figure 7.
Performance curves of fan at various speeds.
3. Analysis of Fan Operating Characteristics
3.1. Rated Working Conditions
When a super-pressure balloon leaves the ground and gradually rises, it reaches a float altitude when the buoyancy and weight reach a balance. The rated operating point of the MIX-140 fan is designed based on the ambient air pressure and temperature at the altitude of a super-pressure balloon. Table 3 presents the setting of the boundary conditions in the fan simulation analysis under the rated working conditions.

Table 3.
Boundary conditions for numerical analysis of MIX-140 fan.
Owing to the complexity of the upper atmosphere, during the flight of a super-pressure balloon, the actual atmospheric parameters, such as the temperature and air pressure, will deviate from those obtained by the theoretical formula. Therefore, it is of great practical importance to investigate the influence of parameter deviation on the fan characteristics. In this section, based on the float height of a super-pressure balloon, the investigated parameters include the air pressure, temperature, and fan speed. Assuming that the deviation of these parameters is ±10%, the output pressure, power consumption, and fan efficiency were checked with different flow rates.
3.1.1. Influence of Speed Change
Speed adjustment is an important method for controlling a super-pressure balloon airbag fan. By changing the speed, the power, air volume, air pressure, and other important fan parameters can be controlled to achieve efficient height control. The total pressure and temperature at the fan inlet are kept unchanged, and the fan speed changes by ±10%. The method described in Section 2 was used to calculate the change in the fan’s performance under the flow rate of 0.4 Q–1.6 Q.
As shown in Figure 8a, the increase (decrease) in the fan speed will lead to a corresponding increase (decrease) in the total pressure at the fan outlet, and the total pressure change rate caused by the fan speed change of ±10% is approximately ±20%. As shown in Figure 8b, the power change trend caused by the change in the fan speed is the same as the total pressure change curve, and the power change rate caused by the fan speed change of ±10% is approximately ±30%. As shown in Figure 8c, the change in fan efficiency caused by the speed change is small. As the speed increases, the maximum efficiency point shifts to the right; as the speed decreases, the maximum efficiency point shifts to the left. In both cases, however, the maximum efficiency value does not change significantly. By comparing Figure 8b, c, it can be found that the maximum power consumption point of the fan corresponds to the optimal efficiency point. Therefore, the outlet pressure of the fan and optimal efficiency point can be effectively controlled by changing the speed. However, attention must be paid to the power consumption increase brought about by the speed increase.
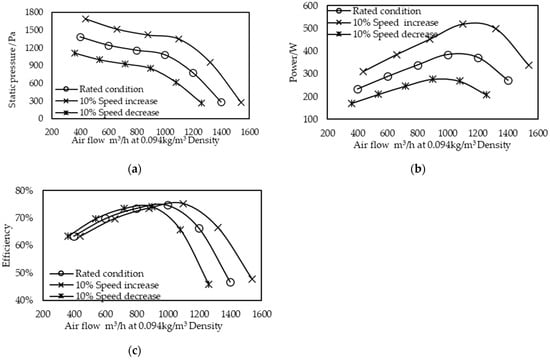
Figure 8.
Effect of speed variation on performance curve: (a) flow-pressure curve; (b) flow-power curve; (c) flow-efficiency curve.
3.1.2. Influence of Pressure Change
With the fan speed and fan inlet temperature unchanged, and a fan inlet pressure deviation of ±10%, the calculation method described in Section 2 was used to analyze the performance, power consumption, and efficiency changes of the fan under the flow rate of 0.4 Q–1.6 Q.
As shown in Figure 9a, the increase (decrease) in the inlet pressure of the fan will lead to the corresponding increase (decrease) in the fan’s outlet pressure. Under the same speed condition, the increase (decrease) in the air pressure at the fan inlet will cause the working range of the fan to become wider (narrower). In Figure 9b, the change trend of the fan power consumption is the same as that shown in Figure 9a. When the flow rate was within the range of 0.4 Q–1 Q, the change in power consumption caused by the pressure change was ±4%; when the flow rate was greater than 1 Q, the change in power consumption increased significantly, and the power consumption increase caused by a 10% increase in pressure was approximately 16%. A 10% reduction in air pressure reduced the power consumption by 24%. The effect of the air pressure change on the fan efficiency is shown in Figure 9c. Unlike Figure 9a,b, when the flow rate was less than 0.8 Q, the change in fan efficiency caused by the air pressure change was 5%, and the decrease (increase) in inlet pressure led to the increase (decrease) in fan efficiency. When the flow rate was greater than 1 Q, the fan efficiency significantly decreased. However, the rate of decline was different. Generally, in the fan’s flow-efficiency diagram, the increase (decrease) in the inlet pressure will result in the fan’s optimal efficiency point shifting to the right (left).
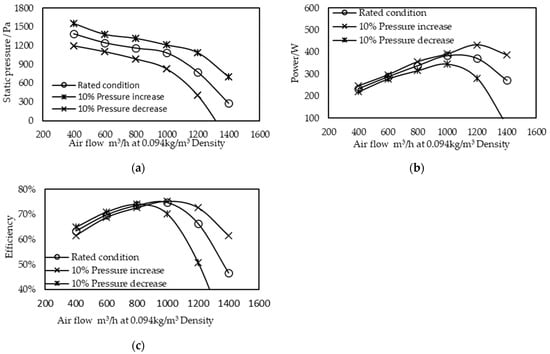
Figure 9.
Effect of inlet pressure variation on performance curve: (a) flow-pressure curve; (b) flow-power curve; (c) flow-efficiency curve.
3.1.3. Influence of Temperature Change
During the flight of a super-pressure balloon, the ambient temperature fluctuates and the temperature difference between day and night can reach 22 K [30]. The temperature change will have a certain impact on the fan’s performance. In this study, the fan speed and fan inlet pressure were kept unchanged, the fan inlet temperature was varied by ±10%, and the method described in Section 2 was used to calculate the fan’s performance under the flow rate of 0.4 Q–1.6 Q.
As shown in Figure 10a, the increase (decrease) in the fan inlet temperature led to the corresponding decrease (increase) in the fan outlet pressure. Under the same speed condition, the increase (decrease) in the fan inlet temperature led to the narrowing (widening) of the fan’s working range. The pressure loss can be compensated by appropriately increasing the fan’s rotating speed. As shown in Figure 10b, the decrease (increase) in temperature led to a certain increase (decrease) in the fan’s power consumption. When the flow rate was within the range of 0.4 Q–1 Q, the change in power consumption caused by the temperature change was 15%, and the change in power consumption increased significantly as the air volume increased. The effect of the temperature change on the fan’s efficiency is shown in Figure 10c. When the flow rate was less than 0.8 Q, the increase (decrease) in temperature increased (decreased) the fan’s efficiency by approximately 2%. However, as the flow rate increases, the temperature increase will have an adverse impact on the fan’s efficiency. Generally, in the fan’s flow-efficiency diagram, the increase (decrease) in the inlet temperature will result in the optimal efficiency point of the fan shifting to the left (right).
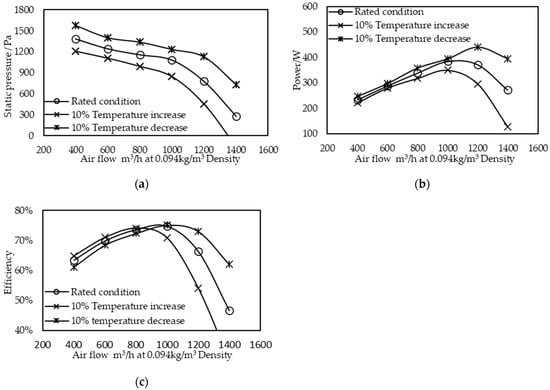
Figure 10.
Effect of inlet temperature variation on performance curve: (a) flow-pressure curve; (b) flow-power curve; (c) flow-efficiency curve.
3.2. Analysis and Comparison of Variable-Height Operating Characteristics
As a super-pressure balloon takes off from the release point, the external atmospheric environment gradually changes with the flight height. In this process, the working characteristics of the airbag fan will also change. The fan’s working characteristics cover various factors. This subsection analyzes the influence of altitude change on the working characteristics of the fan from three perspectives, namely, the unit time charging capacity, unit power charging capacity, and effective work of inflation, starting from the application requirements of a super-pressure balloon’s fan.
The unit time inflation volume of the fan refers to the volume of air in a super-pressure balloon that the fan can fill in a unit time, and its definition is expressed by Equation (7). As the unit time inflation volume increases, the inflation efficiency of the fan becomes higher.
Here, QPT is the unit time inflation volume, Q is the inflation volume, and t is the unit time.
However, the fan must use electricity to do work. A super-pressure balloon flight process relies on solar energy to provide energy across the day and night cycle. Because solar energy input is limited for a super-pressure balloon system, the unit time inflation volume for measuring the fan’s performance is not comprehensive; therefore, the unit power of the fan is also an important indicator.
The unit power inflation of the fan refers to the volume of air that the fan can fill into a super-pressure balloon under unit electric power consumption, and its definition is expressed by Equation (8). As the air inflation per unit power increases, the fan’s power consumption decreases, and the efficiency improves.
Here, QPW is the unit power inflation volume, Q is the inflation volume, and W is the average power.
To analyze the working characteristics of the MIX-140 fan more closely to the actual use situation, a fan (defined as fan B) that has been used several times was selected for a comparative evaluation. In the following analysis, the MIX-140 fan is defined as fan A.
Fan B is an axial fan with a fixed speed, and its flow-pressure curve and power-pressure curve are shown in Figure 11.
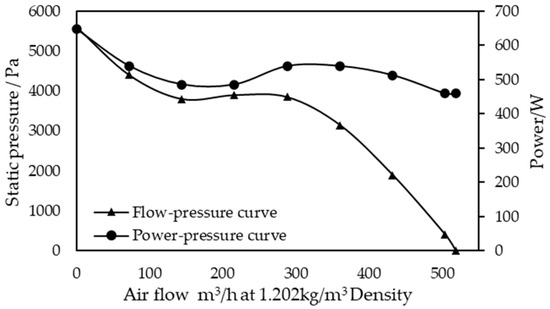
Figure 11.
Performance curve of fan B.
To facilitate the comparative analysis of fan A and fan B, two parameters are further defined: the unit time inflation ratio TR and unit power inflation ratio WR. The details are described below.
In Equation (9), and represent the unit time air inflation of fan A and fan B, respectively. In Equation (5), and represent the air inflation per unit power of fan A and fan B, respectively.
Here, TR and WR are dimensionless numbers, expressed as percentages; positive values indicate that fan A is better, and negative values indicate that fan B is better.
3.2.1. Ground Performance Comparison
By fitting the performance curve data of fan A and fan B at 0 km (Figure 6 measured 9000 RPM data curve and Figure 11 flow-pressure curve) to a multistage function, the relationship between the fan flow and pressure difference can be obtained. On this basis, the fan’s TR and WR under different pressure differences can be calculated by Equations (9) and (10).
As shown in Figure 12a, the TR value of the fan varies with the pressure difference in the ground environment. As can be seen in Figure 12b, the WR value of the fan also varies with the pressure difference at zero altitude as described. By combining the two figures, it can be seen that at zero altitude, the inflation unit charge ratio curve and inflation unit power ratio curve of fan A both exhibit a downward trend. When the pressure difference is less than 800 Pa, fan A has obvious advantages in terms of its inflation efficiency and energy consumption. However, when the pressure is higher than 800 Pa, fan A is limited by the upper limit of the output power. The maximum speed of the design cannot be reached, and the advantages of its inflation efficiency and power consumption are gradually lost compared with fan B.
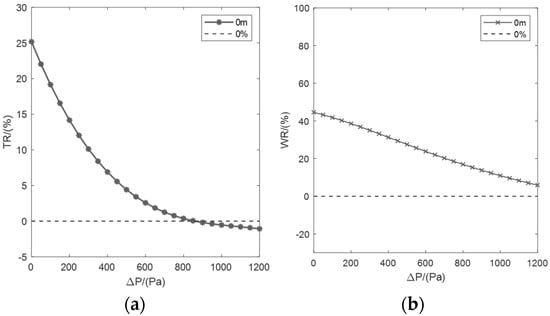
Figure 12.
Comparison of ground performance. (a) TR% curve; (b) WR% curve.
3.2.2. Comparison of High−Altitude Performance
- A.
- Fan performance curve cluster
Based on Equations (1)–(3), the atmospheric pressure, temperature, and density at different altitudes can be obtained. Based on Equations (4)–(6), the performance curves of the fan at different altitudes can be converted. Figure 13 shows the performance curve cluster of fan A and fan B from 0 to 20 km.
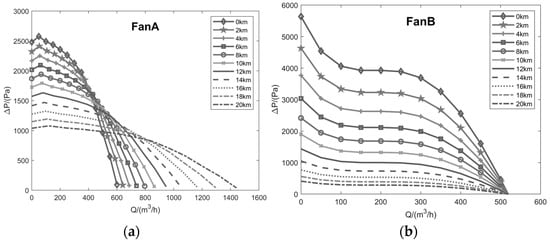
Figure 13.
(a) Performance curve cluster of fan A; (b) performance curve cluster of fan B.
Owing to the constant power control mode of fan A, the fan can compensate for the power decline caused by the decrease in air density by increasing the speed. As shown in Figure 13a, as the altitude and speed increased, the maximum flow rate of fan A continued to increase, from 600 Pa at 0 km to 1450 Pa, marking an increase of over 240%. The maximum static pressure was also decreased by the reduction in air density from the initial altitude of 2500 Pa at 0 km to 1000 Pa at 20 km, marking a reduction of approximately 60%.
As shown in Figure 13b, because the rotational speed of fan B is constant, the maximum flow rate of fan B does not change as the altitude increases, and the maximum static pressure difference keeps decreasing from 5500 Pa at the initial altitude of 0 km to 500 Pa at the altitude of 20 km, marking a decrease of approximately 90%. This also means that when the internal pressure of a super-pressure balloon is higher than 500 Pa at about 20 km, fan B will not be able to compress air into the balloon.
By comparing performance curve clusters of fan A and fan B, it can be seen that performance curve clusters of fans with constant speeds and fans with variable speeds are different in the high-altitude environment. By constantly increasing the working speed, the flow rate and pressure of fans in a high-altitude environment can be effectively improved.
- B.
- Comparative analysis of unit time inflation
Corresponding to the normal float height of a super-pressure balloon at an altitude of 16–20 km, the fan’s working characteristics will change to some extent. By fitting the performance curve data of fan A and fan B at 16–20 km (Figure 13a,b) to a multistage function, the relationship between the flow and pressure difference of fans at different altitudes can be obtained. On this basis, Equation (4) can be used to calculate the unit time air charging ratio (TR) values of fan A and fan B under different pressure differences.
In the high-altitude environment, as the pressure difference of a super-pressure balloon increases, it gradually exceeds the maximum pressure difference that fan B can achieve, and then, the actual flow rate of the fan approaches zero, or even has negative flow rate. In this case, fan B has lost its function; therefore, the difference between fan B and fan A is only compared when fan B is available.
The TR values obtained from the calculation are listed in Table 4. A positive TR value indicates that fan A has the advantage of a higher air capacity. Among them, TR-average refers to the arithmetic average of all TR values in the common pressure range of 0–400 Pa of a super-pressure balloon at a certain altitude, which reflects the fan’s average performance characteristics at a certain altitude.

Table 4.
TR values at different heights.
The data in the Table 4 are plotted in Figure 14a, which illustrates TR curves in different high-altitude environments. As shown in Figure 14a, under the same pressure difference, the TR value increased with the altitude, indicating that when a super-pressure balloon maintains the same pressure, the inflation efficiency of fan A will be higher than that of fan B as the float height increases. A further comparison reveals that at the same altitude, if the pressure of a super-pressure balloon increases continuously compared with using fan B, the inflation efficiency will further improve as the pressure increases. As shown in Figure 14b, the average TR value changes with the altitude. As can be seen, the TR average value exhibits an obvious increasing trend as the altitude increases.
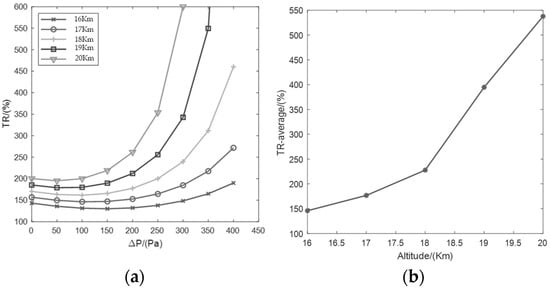
Figure 14.
(a) TR% curve at different heights; (b) TR−avg% curve at different heights.
As can be seen, in a high-altitude environment, fan A outperforms fan B significantly in terms of inflation efficiency, owing to the variable speed mode of fan A. At the height of 16−20 km and pressure range of 0−400 Pa, fan A can increase the unit time air capacity by 295.8% when averaged over the entire altitude range.
- C.
- Comparative analysis of unit power inflating
Similar to unit time inflation, the fan’s unit power inflation will also change to a certain extent at high altitudes.
Based on Equations (8) and (10), the fan’s WR value was calculated as presented in Table 5. A positive WR indicates that fan A has a distinct power consumption advantage; the WR-average refers to the arithmetic average of all WR values within the common pressure range of 0–400 Pa of a super-pressure balloon at a certain altitude. This value reflects the fan’s average performance characteristics at a certain altitude.

Table 5.
WR values at different heights.
The data in the Table 5 are plotted in Figure 15a, which illustrates the WR curves in different high-altitude environments. As can be seen, under the same pressure difference, the WR value increased with the altitude, indicating that when a super-pressure balloon maintained the same pressure as the float height increased, the adoption of fan A to inflate the balloon consumed the same electric energy and filled more air compared with using fan B. The variation curve of the average WR value with the altitude is shown in Figure 15b. As can be seen, the average WR switches from negative to positive at about 18 km and exhibits an obvious increasing trend as the altitude increases.
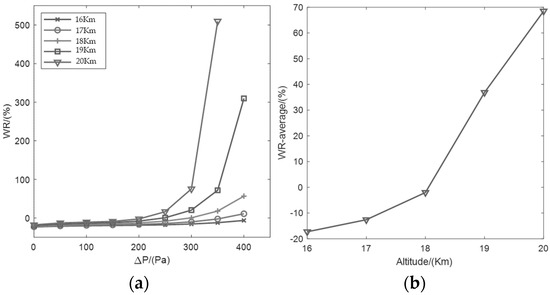
Figure 15.
(a) WR% curve at different heights; (b) WR−avg% curve at different heights.
Therefore, at a height of 16−20 km and pressure range of 0−400 Pa, fan A is superior to fan B in terms of its unit power charging capacity, and fan A can increase the unit power charging capacity by 14.6% when averaged over the entire altitude range.
4. Test and Analysis
4.1. Test Bench and Test Scope
Because it is expensive to carry out super-pressure balloon flight testing to obtain a fan’s working characteristics, it is more common to verify a fan’s working characteristics using a ground test bench. To this end, a compressed super-pressure balloon test bench was built as shown in Figure 16. Through this test platform, static pressure characteristics of a fan in all working environment conditions can be obtained. The test platform consisted of an environmental test chamber, scaled balloon, pressure measuring device, temperature measuring device, data acquisition computer, and fan to be measured.

Figure 16.
Scaled super-pressure balloon test bench.
The environmental test chamber was used to simulate the external environment when a fan was operating in a high-altitude environment, because it can achieve specific temperatures and air pressures. The chamber volume is about 2 m3.
Scaled balloon: The actual super-pressure balloon was scaled down for the simulation. The sac had good air tightness.
Fan being tested: The inlet part of the fan was connected to the environmental simulation box, and the outlet part of a fan was connected to the balloon. When a fan operated, the air in the environmental simulation box was compressed into the balloon, and the fan was controlled by a computer located outside of the environmental test box.
Temperature measurement: Numerous temperature measurement points were arranged on the fan surface and in the environmental test chamber for temperature measurements.
Air pressure measurement: An air pressure sampling hose was installed to pass through the sealed sac.
Data acquisition instrument: This instrument measured the pressure in the balloon, ambient pressure, and temperature, and transmitted the data to a computer outside the test chamber.
During the test, the fan speed was increased step by step, and the difference between the balloon pressure and pressure of the external environment was recorded to verify the fan’s performance under different ambient pressures.
4.2. Results and Discussion
The environmental test chamber was set to ambient pressure and the temperature corresponded to the altitudes of 21 km, 18 km, 16 km, and 14 km, respectively, and the maximum static pressure value that the fan could achieve at different speeds was tested. To verify the accuracy of the test results, the numerical simulation method in Section 2 was used to calculate the fan’s maximum static pressure under the same environmental conditions.
Figure 17 shows the relationship between the fan speed and sac pressure difference under different environmental pressures. The black curve in the figure indicates the fan’s running speed, the green curve indicates the measured pressure difference value of the sac, and the red dot indicates the value in simulation.
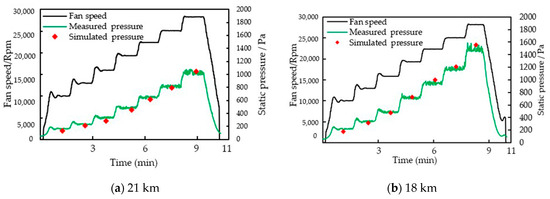
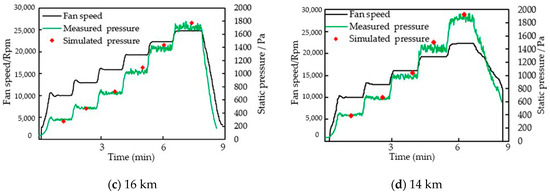
Figure 17.
Relationship between fan speed and pressure: (a) 21 km environment; (b) 18 km environment; (c) 16 km environment; (d) 14 km environment.
As shown in Figure 17a, under the ambient pressure and temperature of the 21 km environment, the fan’s maximum speed reached 28,300 RPM, and the maximum pressure difference reached 1022 Pa without exceeding the upper power limit. In this case, the maximum numerical simulation pressure was 1047 Pa, and the error between the two pressure values was 2.5%.
As shown in Figure 17b, under the ambient pressure and temperature of 18 km, the fan’s maximum speed reached 28,000 RPM, and the maximum pressure difference reached 1485 Pa without exceeding the upper power limit. In this case, the maximum numerical simulation result was 1047 Pa, and the error between the two values was 4.6%.
As shown in Figure 17c, under the ambient pressure and temperature of the 16 km environment, the fan’s maximum speed reached 24,800 RPM, and the maximum pressure difference reached 1700 Pa without exceeding the upper power limit. At this time, the maximum numerical simulation pressure was 1047 Pa, and the error between the two pressure values was 4.4%.
As shown in Figure 17d, under the ambient pressure and temperature of 14 km, the fan’s maximum speed reached 22,300 RPM, and the maximum pressure difference reached 1867 Pa without exceeding the upper power limit. At this time, the maximum numerical simulation pressure was 1047 Pa. The error between the two pressure values is 3.4%.
By comprehensively analyzing Figure 17a–d, it can be seen that the values obtained from the simulation are in good agreement with the measured values, and the errors are within the allowable range. As the altitude increased, the air density decreased, and the fan’s air load decreased. Therefore, the fan can constantly increase the speed to increase the power capacity when the total power consumption is unchanged. The fan’s maximum pressure difference is positively correlated with the fan speed. Different pressure difference values can be obtained by adjusting the fan speed. The test data provide an effective reference for the fan speed and sac pressure control in an actual super-pressure balloon flight.
5. Conclusions
This study investigated the working characteristics of the MIX-140 fan as the height of a super-pressure balloon’s flight varied. The effects of air pressure, temperature, and fan speed on the fan’s operating characteristics were analyzed. Compared with the existing fan, the variations in unit time and unit power with altitude and pressure of balloon were investigated. Finally, the variation of the fan’s working characteristics under different altitude environments was analyzed through experimental testing.
The conclusions drawn from this study are summarized as follows:
- An average error of 3% between the performance curve of the MIX-140 fan on the ground working conditions was obtained through testing and numerical calculation, demonstrating that the CFD method and experimental approach used in this study can obtain the performance curve of the mixed-flow fan with high accuracy.
- Changes in the atmospheric temperature and air pressure affect a fan’s working characteristics. By adjusting the fan speed, the fan pressure and power consumption can be effectively controlled, and the optimal efficiency point can be adjusted to mitigate the impact of atmospheric temperature and air pressure changes.
- In the altitude environment of 16–20 km, compared with the existing constant-speed fan, the MIX-140 fan with adjustable speed can increase the unit time charging capacity by 295.8% on average and the unit power charging capacity by 14.6%, demonstrating the superiority of the MIX-140 fan design.
- A fan’s working characteristics in different environments can be effectively tested using a scaled balloon test bench. By adjusting the fan speed, different pressure difference values can be obtained, providing an effective reference for controlling the fan speed and controlling balloon pressure in actual super-pressure balloon flights.
Author Contributions
Conceptualization, W.Q. and Q.Z.; methodology, W.Q.; software, W.Q. and Q.Z.; validation, Y.Q. and J.M.; investigation, Z.H. and Y.Y.; data curation, W.Q. and Q.Z.; writing—original draft preparation, W.Q., Q.Z. and Z.H.; writing—review and editing, Y.Q., Y.Y. and J.M.; visualization, Y.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the CAS science and disruptive technology research pilot fund, “Research on Key Technologies for Hydrogen Replacement in Near Space aerostatics”, E3Z220020F.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank Jiangsu Jiu Gao Tech Co., Ltd. for providing testing support for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jing, Y.; Wu, Y.; Tang, J.; Zhou, P.; Duan, D. Receding horizon trajectory generation of stratospheric airship in low-altitude return phase. Aerospace 2022, 9, 670. [Google Scholar] [CrossRef]
- Jiang, Y.; Lv, M.; Li, J. Station-keeping control design of double balloon system based on horizontal region constraints. Aerosp. Sci. Technol. 2020, 100, 105792. [Google Scholar] [CrossRef]
- Agrawal, R.; Buchanan, W.P.; Arora, A.; Girija, A.P.; De Jong, M.; Seager, S.; Petkowski, J.J.; Saikia, S.J.; Carr, C.E.; Grinspoon, D.H.; et al. Mission Architecture to Characterize Habitability of Venus Cloud Layers via an Aerial Platform. Aerospace 2022, 9, 359. [Google Scholar] [CrossRef]
- Deng, X.; Yang, X.; Zhu, B. Simulation research and key technologies analysis of intelligent stratospheric aerostat Loon. Acta Aeronaut. Astronaut. Sin. 2023, 44, 28–44. [Google Scholar]
- Sirks, E.L.; Massey, R.; Gill, A.S.; Anderson, J.; Benton, S.J.; Brown, A.M.; Clark, P.; English, J.; Everett, S.W.; Fraisse, A.A.; et al. Data Downloaded via Parachute from a NASA Super-Pressure Balloon. Aerospace 2023, 10, 960. [Google Scholar] [CrossRef]
- Koseki, K.; Matsuo, T.; Arikawa, S. Measurement of Super-Pressure Balloon Deformation with Simplified Digital Image Correlation. Appl. Sci. 2018, 8, 2009. [Google Scholar] [CrossRef]
- Du, H.; Lv, M.; Li, J.; Zhu, W.; Zhang, L.; Wu, Y. Station-keeping performance analysis for high altitude balloon with altitude control system. Aerosp. Sci. Technol. 2019, 92, 644–652. [Google Scholar] [CrossRef]
- Hoffmann, L.; Hertzog, A.; Rössler, T.; Stein, O.; Wu, X. Intercomparison of meteorological analyses and trajectories in the Antarctic lower stratosphere with Concordiasi super-pressure balloon observations. Atmos. Chem. Phys. 2017, 17, 8045–8061. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, W.; Lin, J.; Niu, S.; Li, Z. Maneuverability Analysis of Active Phase Change Adjustment Airbag to Stationary Altitude and Differential Pressure of Super-pressure Balloon. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 230–235. [Google Scholar]
- Lin, K.; Zheng, Z.; Wu, Z.; Wang, Q. Path following of a stratospheric satellite by the aid of wind currents. Proceedings of the Institution of Mechanical Engineers, J. Aerosp. Eng. 2018, 233, 3983–4003. [Google Scholar] [CrossRef]
- Saito, Y.; Akita, D.; Fuke, H.; Izutsu, N. Properties of tandem balloon connected by extendable suspension wires. Adv. Space Res. 2010, 45, 482–489. [Google Scholar] [CrossRef]
- Bellemare, M.G.; Candido, S.; Castro, P.S.; Gong, J.; Machado, M.C.; Moitra, S.; Ponda, S.S.; Wang, Z. Autonomous navigation of stratospheric balloon using reinforcement learning. Nature 2020, 588, 77–82. [Google Scholar] [CrossRef]
- Schoeberl, M.R.; Jensen, E.H.; Podglajen, A.; Coy, L.; Lodha, C.; Candido, S.; Carver, R.L. Gravity wave spectra in the lower stratosphere diagnosed from Project Loon balloon trajectories. J. Geophys. Res. Atmos. 2017, 122, 8517–8524. [Google Scholar] [CrossRef]
- Friedrich, L.S.; McDonald, A.J.; Bodeker, G.E.; Cooper, K.E.; Lewis, J.; Paterson, A.J. A comparison of Loon balloon observations and stratospheric reanalysis products. Atmos. Chem. Phys. 2016, 17, 855–866. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, S.; Yang, Y.; Liu, Q. Analysis of day-night thermal properties of super-pressure balloon during cruising flight. Comput. Simul. 2020, 37, 54–59. [Google Scholar]
- Gao, Y.; Xu, G.; Wang, S.; Li, Z.; Cai, R. Modeling and small signal stability analysis of stratospheric airship energy system. Acta Energiae Solaris Sin. 2022, 43, 50–57. [Google Scholar]
- Qu, W.; Gong, W.; Chen, C.; Zhang, T.; He, Z. Optimization Design and Experimental Verification for the Mixed-Flow Fan of a Stratospheric Airship. Aerospace 2023, 10, 107. [Google Scholar] [CrossRef]
- Sun, P.; Wang, X.; Xie, W. Centrifugal blower of stratospheric airship. IEEE Access 2018, 6, 10520–10529. [Google Scholar] [CrossRef]
- Wei, K.; Wu, Q.; Zhang, Y.; Li, X. Aerodynamic performance calculation of centrifugal compressors for pressurized balloon based on similarity theory. J. Xi’an Aeronaut. Univ. 2019, 3, 28–32. [Google Scholar]
- Zhao, D.; Hua, Z.; Dou, M.; Huang, F. Control oriented modeling and analysis of centrifugal compressor working characteristic at variable altitude. Aerosp. Sci. Technol. 2018, 72, 174–182. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Z.; Zhang, S.; Song, C. Aerodynamic design of key components of the large-discharge axial fan at high altitude. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, 14 September 2018. [Google Scholar]
- Zhang, Q.; Miao, J.; Li, J.; Zhao, C.; Li, R. Characteristics Research of Fans in Series and Parallel on Super-Pressure Balloon; Aerospace Information Research Institute, CAS: Beijing, China, 2022. [Google Scholar]
- Aerospace Information Research Institute. Patent Search and Analysis. Available online: https://pss-system.cponline.cnipa.gov.cn/documents/detail?prevPageTit=changgui (accessed on 28 November 2023).
- Wang, S. Design of Helium Centrifugal Compressor and Optimization of High-Pressure Ratio. Master’s Thesis, Harbin Engineering University, Harbin, China, 2021. [Google Scholar]
- Niu, Z. Effects and Mechanisms of Low Reynolds Number on Compressors’ Flow Stability. Master’s Thesis, Tsinghua University, Beijing, China, 2021. [Google Scholar]
- Wang, S.; Liu, B.; Yue, G.; Jiang, Y. Research on high pressor ratio design of helium centrifugal compressor. J. Eng. Therm. Energy Power 2021, 36, 147–154. [Google Scholar]
- Zhang, J.; Yang, X.; Deng, X.; Guo, Z.; Zhai, J. Altitude control of stratospheric aerostat based on deep reinforcement learning. J. Beijing Univ. Aeronaut. Astronaut. 2021, 49, 2062–2070. [Google Scholar] [CrossRef]
- Xie, H.; Zhang, S.; Yang, B. Research on the application of similarity principle on the centrifugal compressor. J. Eng. Thermophys. 2021, 36, 147–154. [Google Scholar]
- Wang, L.; Gu, B.; Wang, T. Fast calculation model of fan performance based on similarity theory. Fluid Mach. 2012, 7, 24–28. [Google Scholar]
- Zhu, R.; Wang, S.; Yang, Y. Simulation and analysis of thermal and dynamic properties of super-pressure balloon during ascent. J. Natl. Univ. Def. Technol. 2020, 42, 151–158. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).