Multi-Phase Vertical Take-Off and Landing Trajectory Optimization with Feasible Initial Guesses
Abstract
:1. Introduction
- A comprehensive analysis of operational constraints critical to VTOL trajectory optimization, coupled with the formulation of multi-phase take-off and landing trajectories to address unique constraints in each phase of VTOL operations.
- A “divide and conquer” approach proposed to generate feasible initial guesses for multi-phase problems, effectively leveraging the INDI controller.
- Computation of high-fidelity, energy-minimum take-off and landing trajectories for a tilt-wing eVTOL aircraft, revealing its unique flight characteristics.
2. Operational Constraints on VTOL Trajectories
2.1. Airworthiness Requirements
2.2. Flight Dynamics Constraints
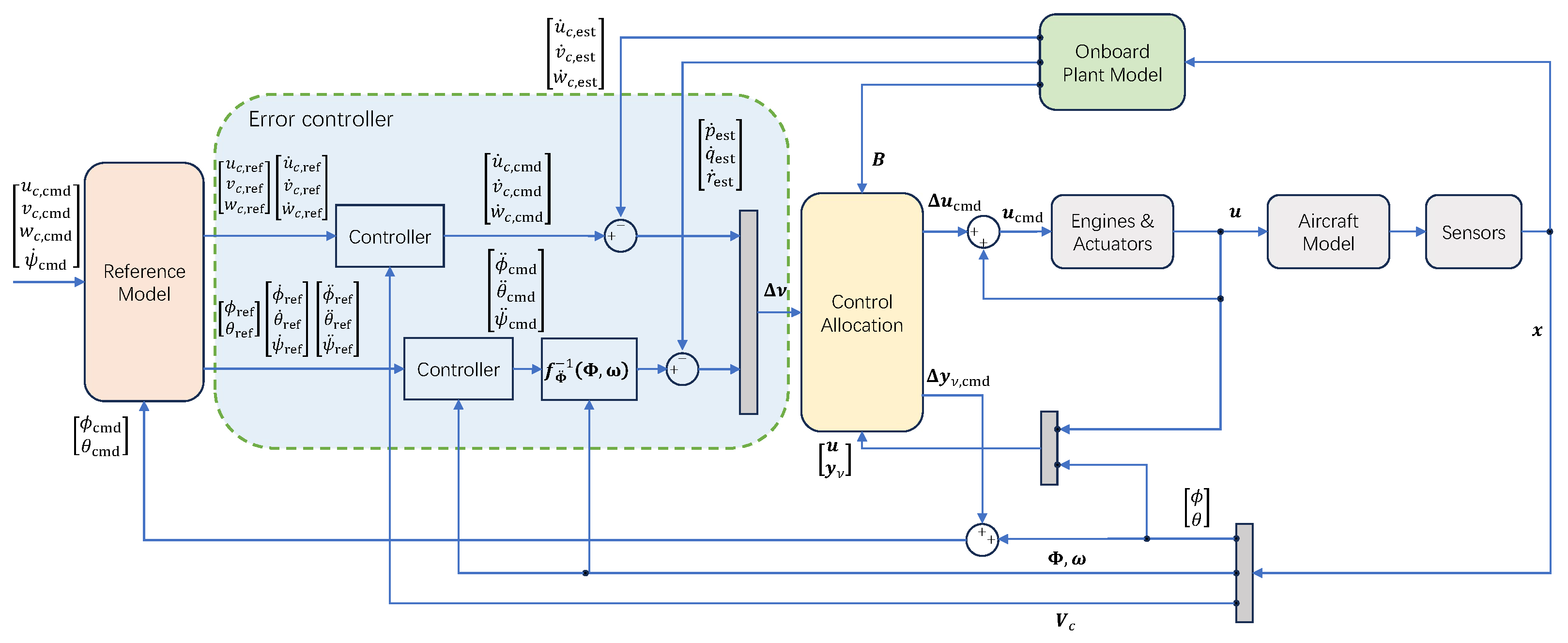
3. Six-DOF Dynamics Model and Controller
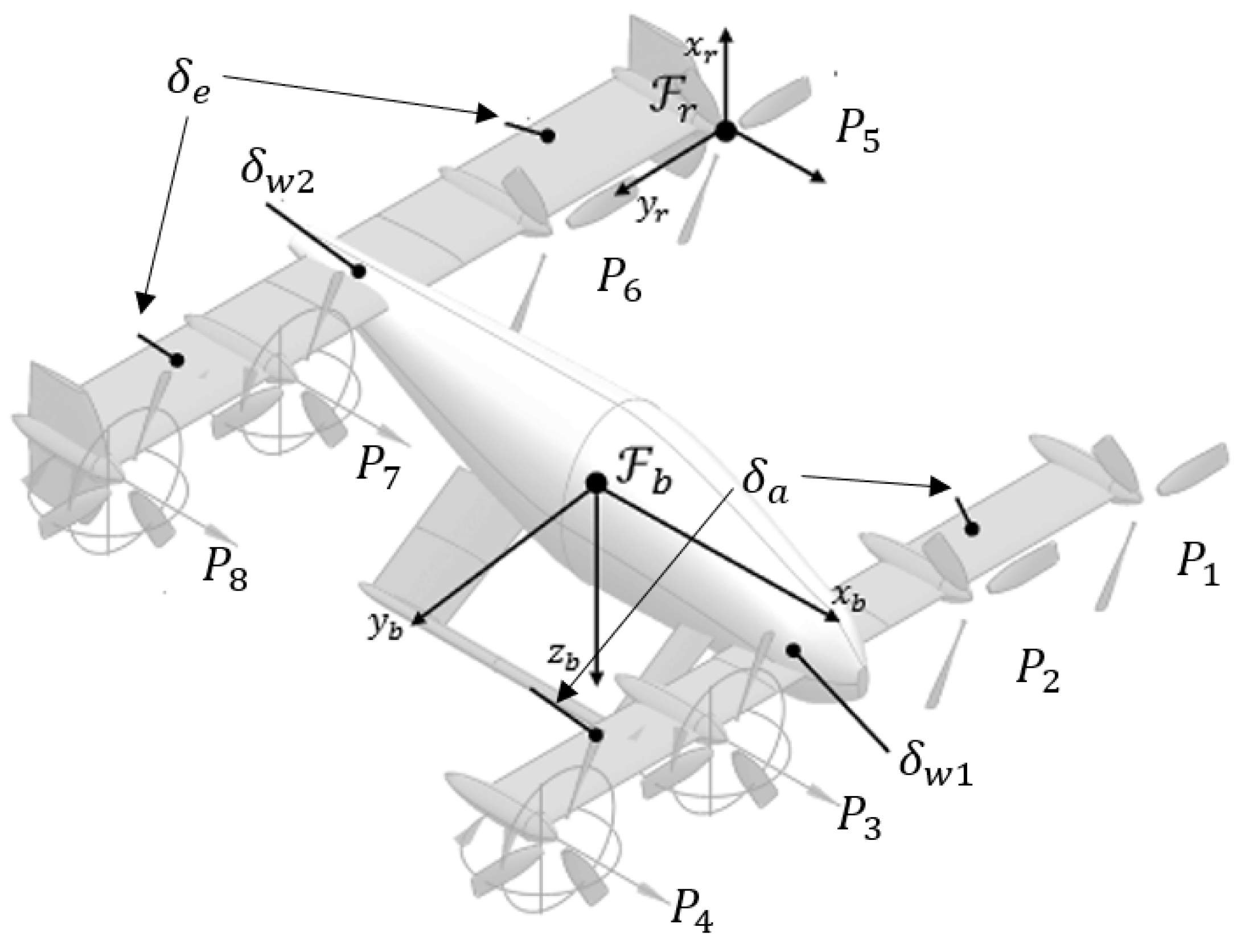
3.1. Configuration Parameters
3.2. Flight Dynamics Model
3.3. Incremental Nonlinear Dynamic Inversion Controller
4. Vertical Take-Off Trajectory Optimization
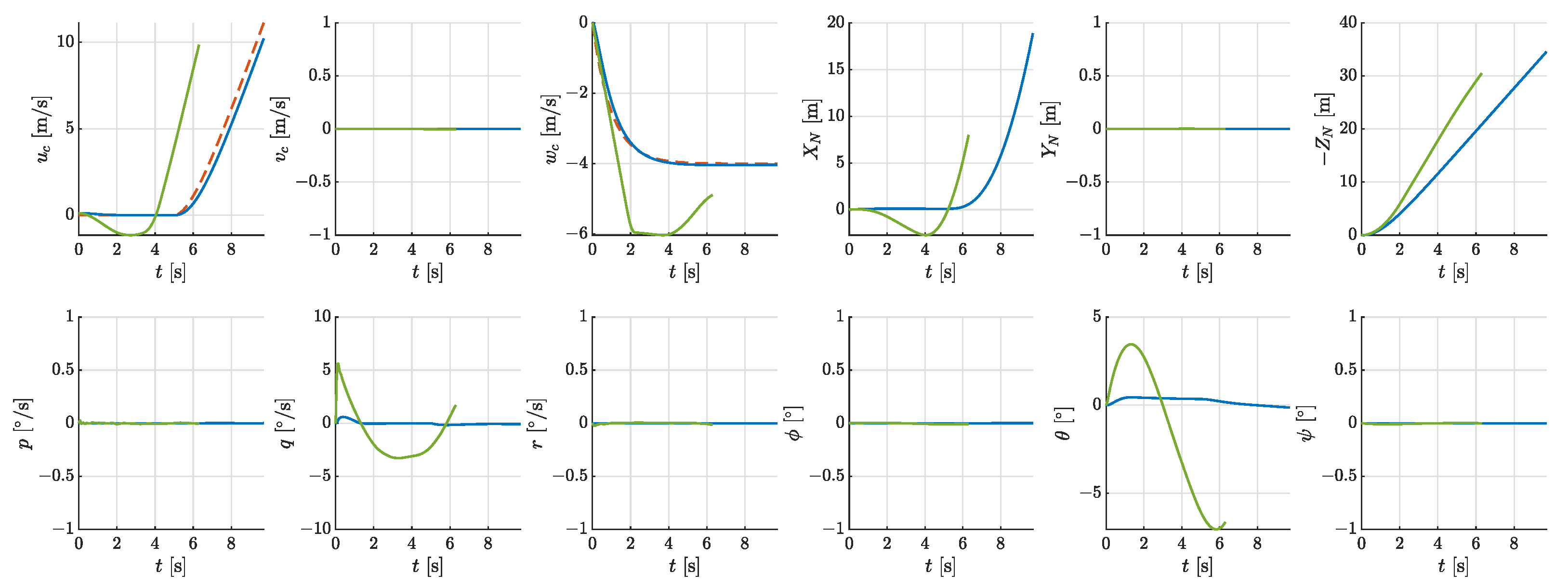
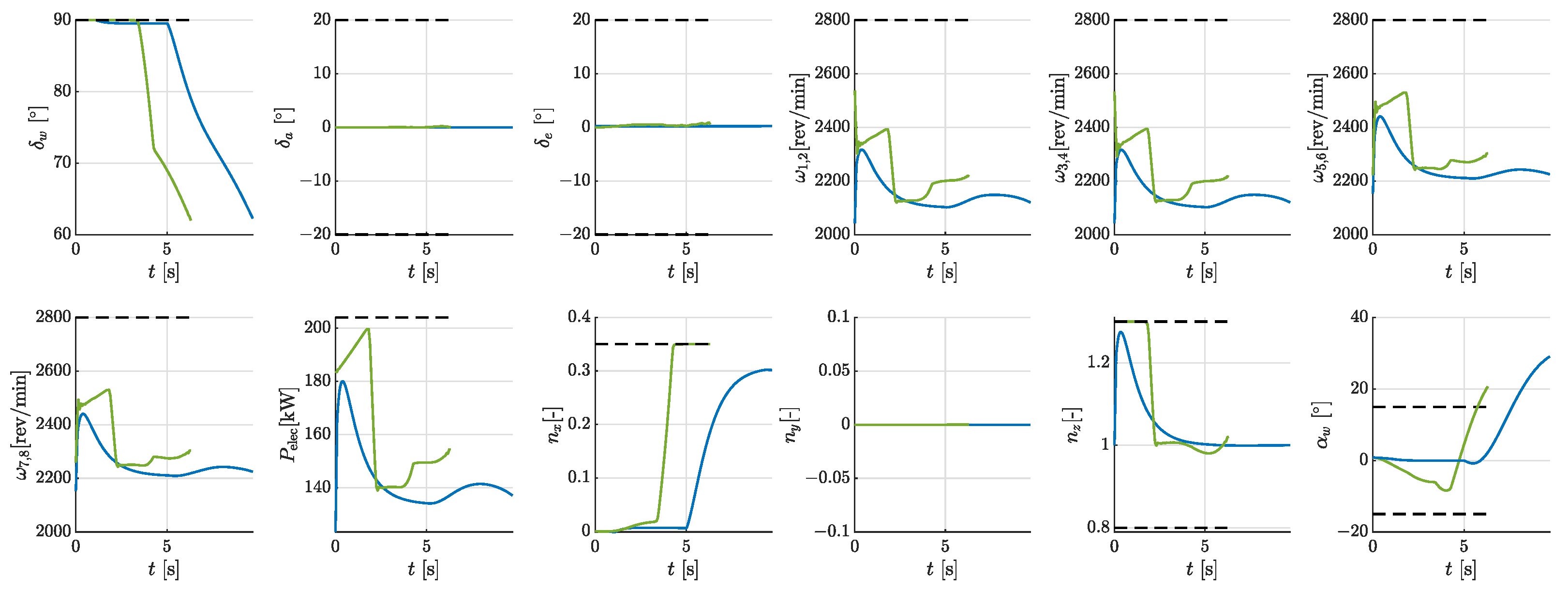
4.1. Phase 1—Initial Take-Off
4.2. Phase 2—First Climb Segment
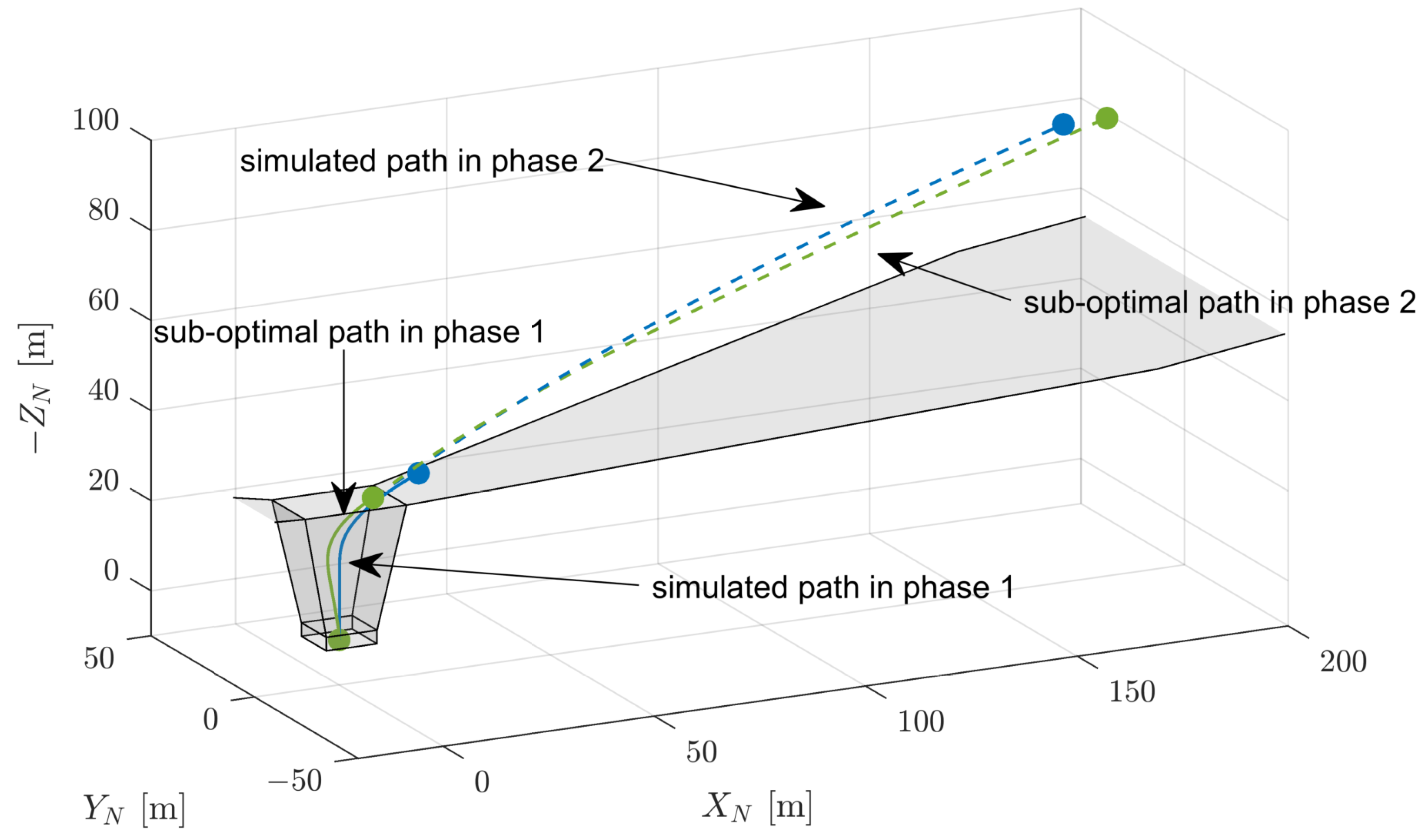
4.3. Phase 3—Second Climb Segment and Phase 4—Turning
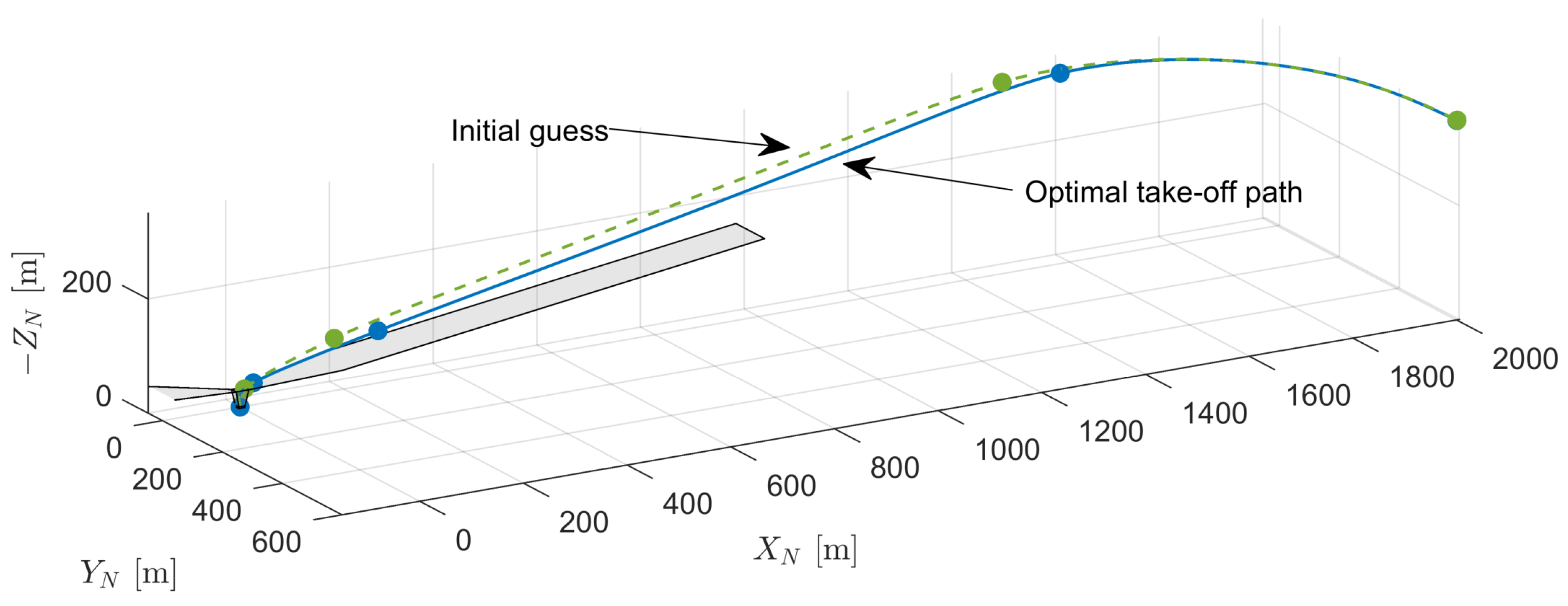
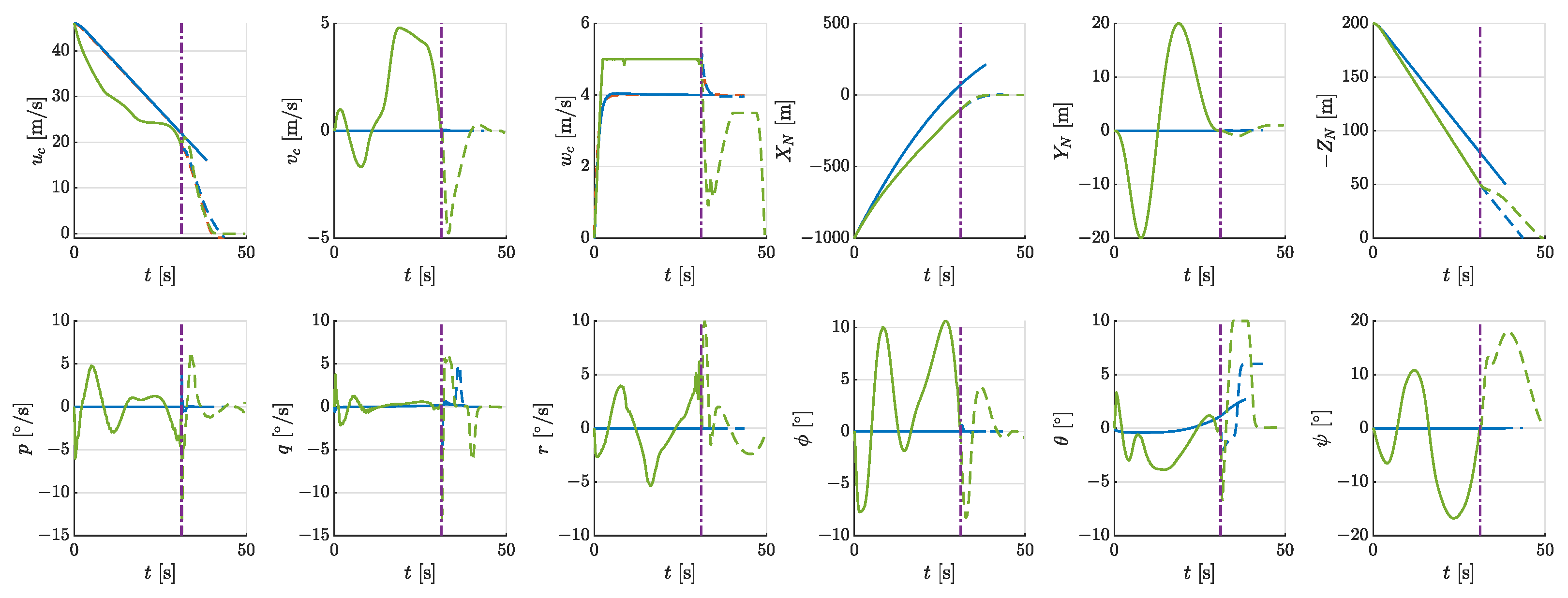
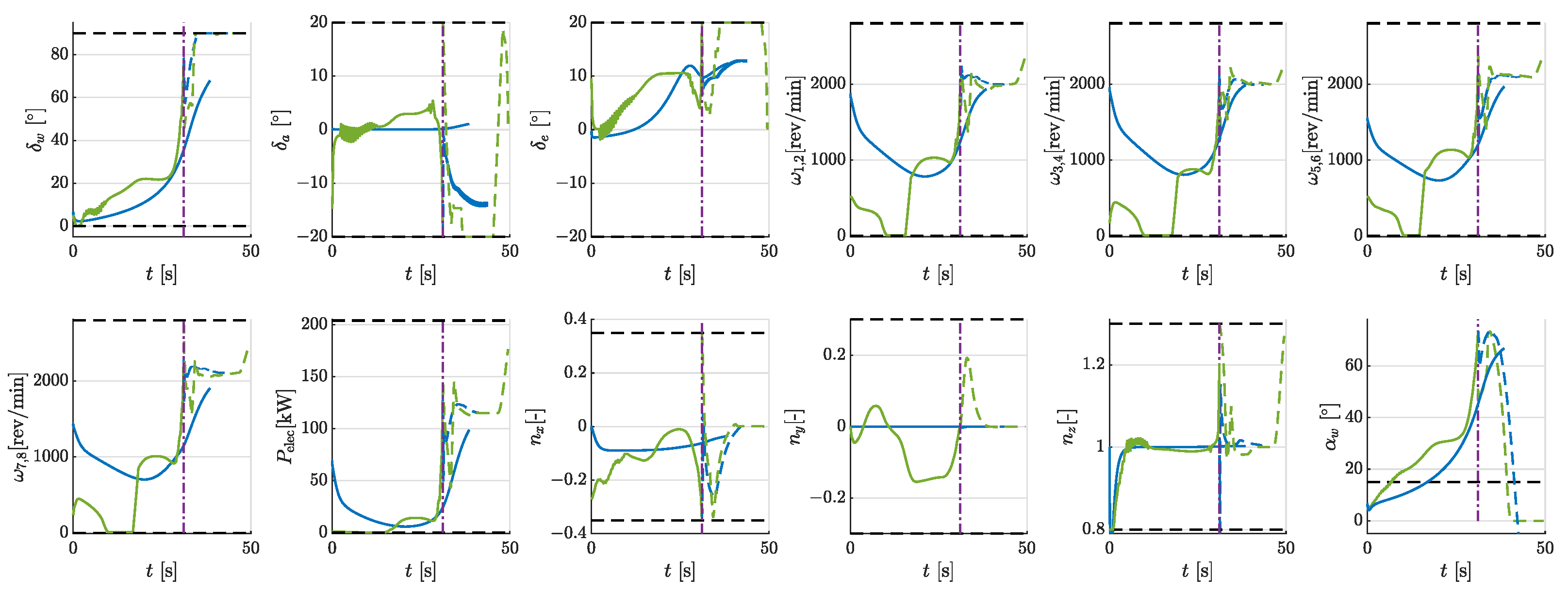
4.4. Multi-Phase Take-Off Trajectory
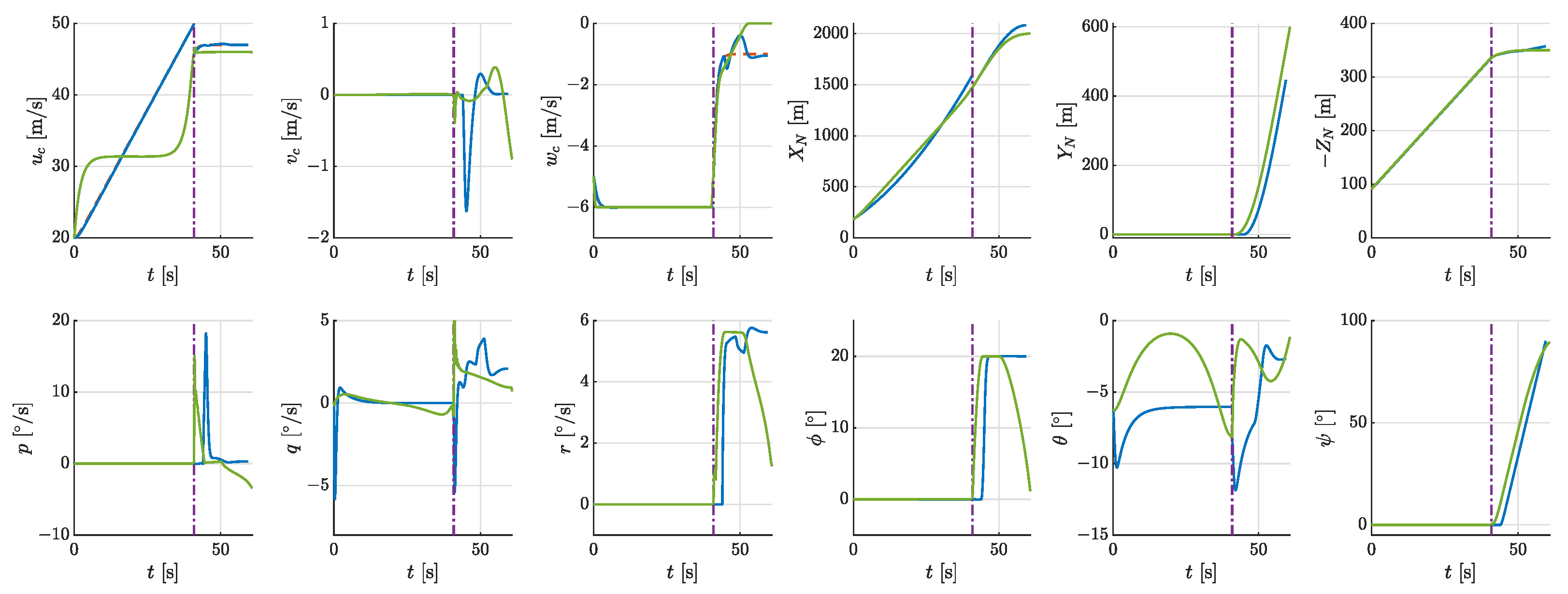
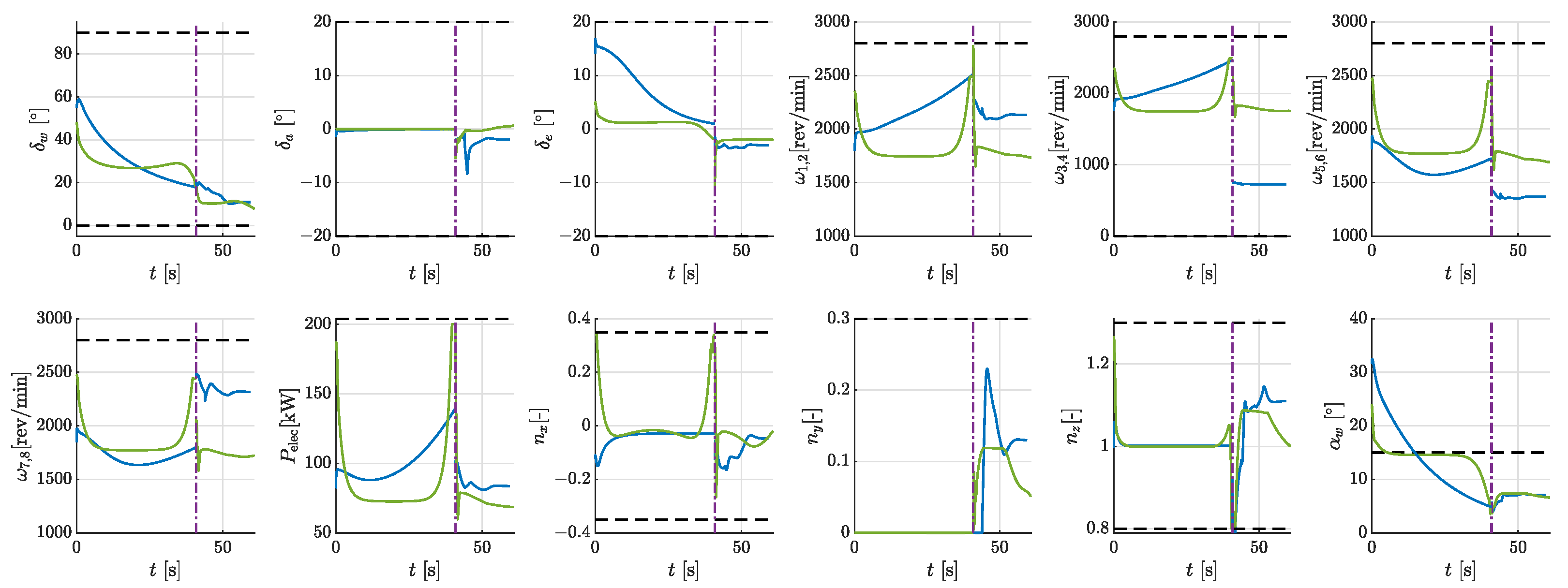
- Phase 1 (0–7.41 s): The aircraft pitched downward and decreased the wing-tilt angle from 90 to 52, climbing and accelerating with almost the maximum power. The energy consumption was 0.34 kWh, and the average power was 167 kW.
- Phase 2 (7.41 s–16.31 s): The tilt angle decreased to 32. The aircraft further accelerated to near stall speed, with the power reduced to 40% of the maximum power. The energy consumption was 0.25 kWh, and the average power was 101 kW.
- Phase 3 (16.31 s–57.02 s): The wings stop tilting forward. The aircraft maintained a climb near the stall speed. Toward the end of this phase, it accelerated to at maximum power. The energy consumption was 0.93 kWh, and the average power was 83 kW.
- Phase 4 (57.02 s–74.59 s): The aircraft operated at its lowest power, making a 90-degree turn with a roll angle of 20 degrees and a turning rate of approximately . The energy consumption was 0.36 kWh, and the average power was 74 kW.
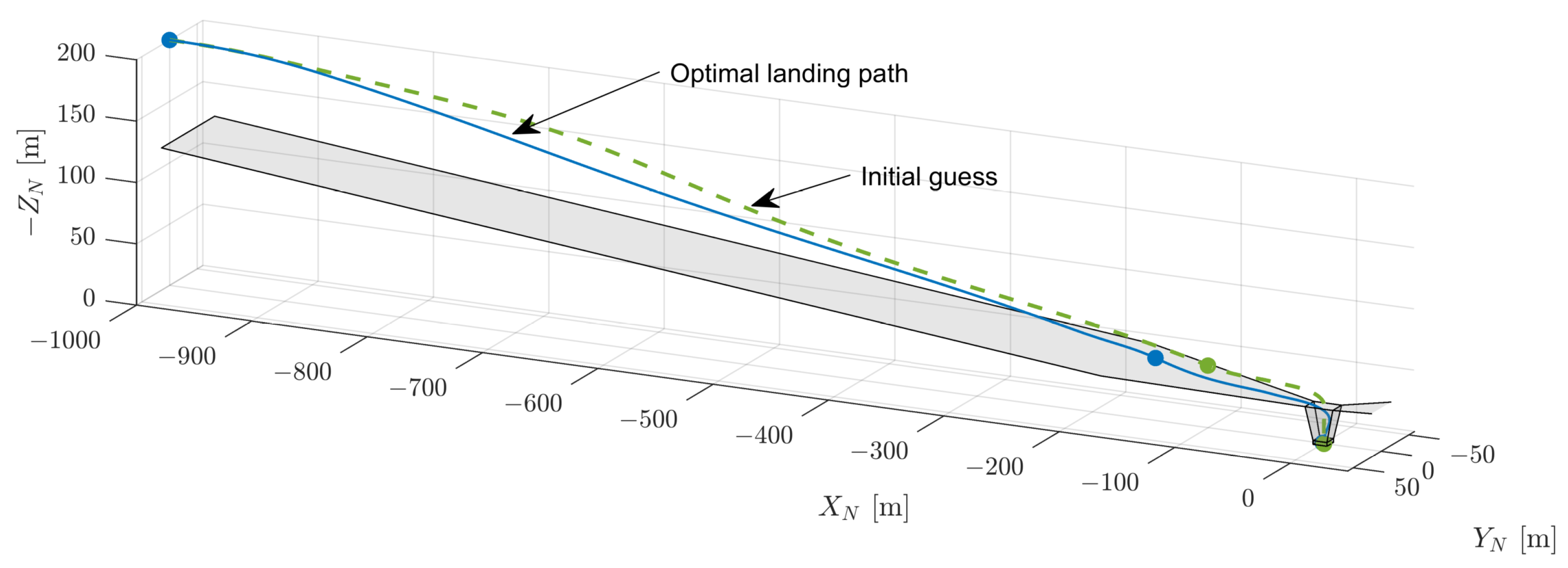
5. Vertical Landing Trajectory Optimization
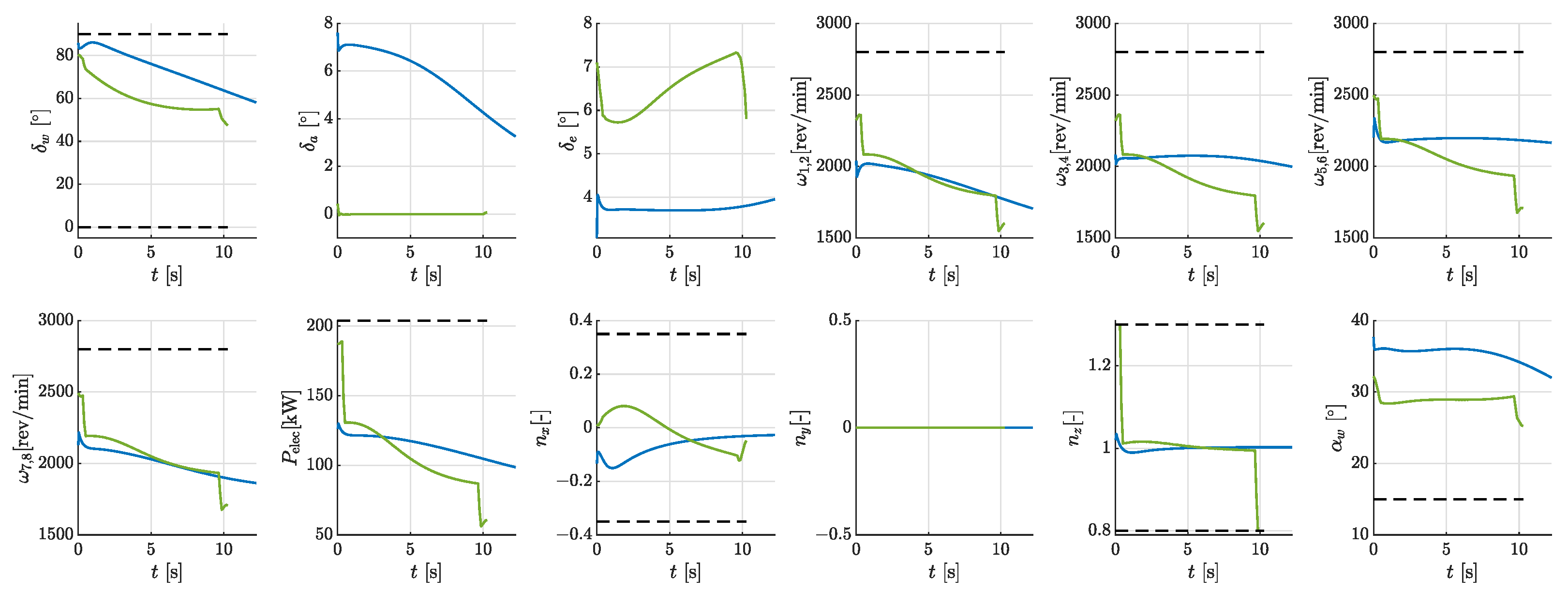
5.1. Individual Phases
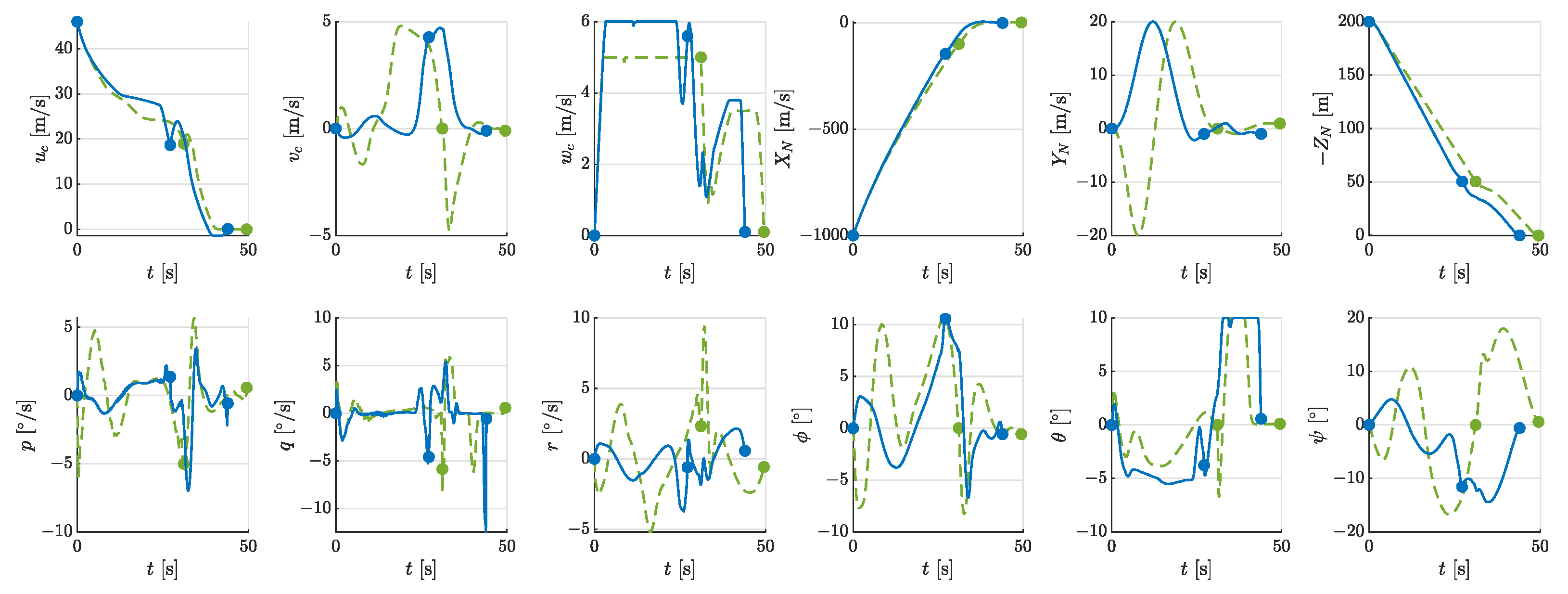
5.2. Multi-Phase Landing Trajectory
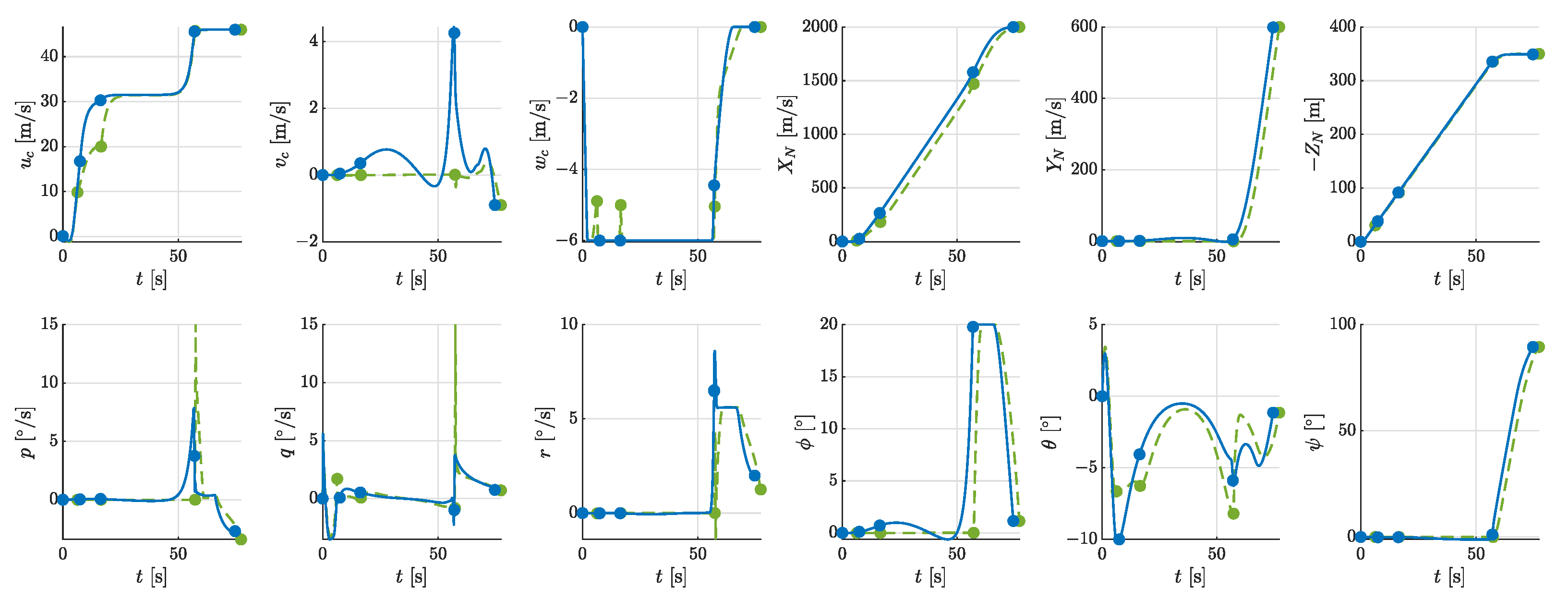
- Phase 1 (0–27.17 s): Characterized by minimal propeller rotational speeds, this phase exhibited negligible total power. The aircraft decelerated to the landing reference speed by increasing the tilt angle, resulting in almost zero energy consumption.
- Phase 2 (27.17 s–43.98 s): The tilt angle rapidly increased to 90, and the propellers produced sufficient lift to counteract gravity. Meanwhile, the aircraft pitched upward to further decelerate its forward speed. This phase involved coordinated position, velocity, and attitude adjustment to achieve zero values at touchdown. The energy consumption was 0.48 kWh, with an average power of 104 kW.
6. Conclusions
- The flight trajectory is segmented into multiple phases, each tailored to unique constraints, considering vertical take-off and landing complexities and airworthiness requirements.
- Integrating 6DOF dynamics in the multi-phase problem results in a large-scale NLP that necessitates a good initial guess. The INDI control simplifies vehicle operation. Simulated trajectories exhibit dynamic feasibility and provide viable initial guesses for generating sub-optimal trajectories within individual phases. Concatenating these sub-optimal trajectories forms a feasible initial guess for the original multi-phase problem.
- Successful computation of energy-minimum take-off and landing trajectories for a tilt-wing eVTOL is demonstrated. In take-off, the hover flight demands the highest power, while the transition flight consumes the most energy, over 60%. To save energy, the eVTOL aircraft maintains a favorable forward speed at about 32 m/s for a long duration, accelerating to the final take-off speed primarily toward the end of the transition. In landing, the bulk of energy consumption transpires in the final landing, with total energy in landing being about 26% of that in take-off.
- The tilt-wings’ angle of attack manifests large values during take-off and landing, suggesting that enforcing the stall angle as a strict constraint in low-speed VTOL operations may not be necessary.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boeing Wisk. Concept of Operations for Uncrewed Urban Air Mobility; The Boeing Company: Arlington, VA, USA, 2022; Available online: www.boeing.com/innovation/con-ops (accessed on 1 November 2023).
- European Union Aviation Safety Agency. Special Condition for Small-Category VTOL Aircraft; European Union Aviation Safety Agency: Cologne, Germany, 2019. Available online: www.easa.europa.eu/en/downloads/99957/en (accessed on 1 November 2023).
- European Union Aviation Safety Agency. Second Publication of Proposed Means of Compliance with the Special Condition VTOL; European Union Aviation Safety Agency: Cologne, Germany, 2022. Available online: www.easa.europa.eu/en/downloads/137443/en (accessed on 1 November 2023).
- European Union Aviation Safety Agency. Vertiports Prototype Technical Specifications for the Design of VFR Vertiports for Operation with Manned VTOL-Capable Aircraft Certified in the Enhanced Category; European Union Aviation Safety Agency: Cologne, Germany, 2022. Available online: www.easa.europa.eu/en/downloads/136259/en (accessed on 1 November 2023).
- Civil Aviation Administration of China. Special Conditions for EHang EH216-S Unmanned Aircraft System: SC-21-002; Civil Aviation Administration of China: Beijing, China, 2022; (In Chinese). Available online: www.caac.gov.cn/XXGK/XXGK/BZGF/ZYTJHHM/202202/t20220222_211914.html (accessed on 1 November 2023).
- Federal Aviation Administration. Airworthiness Criteria: Special Class Airworthiness Criteria for the Joby Aero, Inc. Model JAS4-1 Powered-Lift: FAA-2021-0638; Federal Aviation Administration: Washington, DC, USA, 2022. Available online: www.federalregister.gov/documents/2022/11/08/2022-23962/airworthiness-criteria-special-class-airworthiness-criteria-forthe-joby-aero-inc-model-jas4-1 (accessed on 1 November 2023).
- Federal Aviation Administration. Airworthiness Criteria: Special Class Airworthiness Criteria for the Archer Aviation Inc. Model M001 Powered-Lift: FAA-2022-1548; Federal Aviation Administration: Washington, DC, USA, 2022. Available online: www.federalregister.gov/documents/2022/12/20/2022-27445/airworthiness-criteria-special-class-airworthiness-criteria-forthe-archer-aviation-inc-model-m001 (accessed on 1 November 2023).
- Federal Aviation Administration. Engineering Brief No. 105, Vertiport Design: EB No. 105; Federal Aviation Administration: Washington, DC, USA, 2022. Available online: www.faa.gov/airports/engineering/engineering_briefs/engineering_brief_105_vertiport_design (accessed on 1 November 2023).
- Pradeep, P.; Wei, P. Energy-efficient arrival with rta constraint for multirotor evtol in urban air mobility. J. Aerosp. Inf. Syst. 2019, 16, 263–277. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Martins, J.R. Tilt-wing eVTOL takeoff trajectory optimization. J. Aircr. 2020, 57, 93–112. [Google Scholar] [CrossRef]
- Doff-Sotta, M.; Cannon, M.; Bacic, M. Fast optimal trajectory generation for a tiltwing VTOL aircraft with application to urban air mobility. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 4036–4041. [Google Scholar]
- Lu, Z.; Li, H.; He, R.; Holzapfel, F. Energy-Efficient Incremental Control Allocation for Transition Flight via Quadratic Programming. In Proceedings of the International Conference on Guidance, Navigation and Control, Harbin, China, 5–7 August 2022; Springer: Singapore, 2022; pp. 4940–4951. [Google Scholar]
- Piprek, P.; Holzapfel, F. Robust Trajectory Optimization of VTOL Transition Maneuver Using Bi-Level Optimal Control. In Proceedings of the 31st Congress of the International Council of the Aeronautica Science, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Wang, M.; Diepolder, J.; Zhang, S.; Söpper, M.; Holzapfel, F. Trajectory optimization-based maneuverability assessment of eVTOL aircraft. Aerosp. Sci. Technol. 2021, 117, 106903. [Google Scholar] [CrossRef]
- Krammer, C.; Schweighofer, F.; Gierszewski, D.; Scherer, S.; Akman, T.; Hong, H.; Holzapfel, F. Requirements-based Generation of Optimal Vertical Takeoff and Landing Trajectories for Electric Aircraft. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences (ICAS), Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- Lu, Z.; Hong, H.; Diepolder, J.; Holzapfel, F. Maneuverability Set Estimation and Trajectory Feasibility Evaluation for eVTOL Aircraft. J. Guid. Control. Dyn. 2023, 46, 1184–1196. [Google Scholar] [CrossRef]
- Akman, T.; Schweighofer, F.; Afonso, R.; Ben-Asher, J.; Holzapfel, F. Robust eVTOL trajectory optimization under uncertainties–Challenges and approaches. Proc. J. Phys. Conf. Ser. 2023, 2514, 012002. [Google Scholar] [CrossRef]
- Fisch, F. Development of a Framework for the Solution of High-Fidelity Trajectory Optimization Problems and Bilevel Optimal Control Problems. Ph.D. Thesis, Technische Universität München, München, Germany, 2011. [Google Scholar]
- Bittner, M.; Fisch, F.; Holzapfel, F. A multi-model gauss pseudospectral optimization method for aircraft trajectories. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4728. [Google Scholar]
- Lu, Z.; Hong, H.; Gerdts, M.; Holzapfel, F. Flight Envelope Prediction via Optimal Control-Based Reachability Analysis. J. Guid. Control. Dyn. 2022, 45, 185–195. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Flight Test Guide for Certification of Transport Category Airplanes, AC No: 25-7D; Federal Aviation Administration: Washington, DC, USA, 2018. Available online: https://www.faa.gov/documentLibrary/media/Advisory_Circular/AC_25-7D.pdf (accessed on 1 November 2023).
- May, M.S.; Milz, D.; Looye, G. Dynamic modeling and analysis of tilt-wing electric vertical take-off and landing vehicles. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0263. [Google Scholar]
- Holzapfel, F. Nichtlineare Adaptive Regelung eines Unbemannten Fluggerätes. Ph.D. Thesis, Technische Universität München, München, Germany, 2004. [Google Scholar]
- Sieberling, S.; Chu, Q.; Mulder, J. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. J. Guid. Control. Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Harris, J.J. F-35 flight control law design, development and verification. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3516. [Google Scholar]
- Lu, Z.; Tang, P.; Zhang, S. Incremental nonlinear dynamic inversion based control allocation approach for a BWB UAV. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Li, H.; Myschik, S.; Holzapfel, F. Null-Space-Excitation-Based Adaptive Control for an Overactuated Hexacopter Model. J. Guid. Control. Dyn. 2023, 46, 483–498. [Google Scholar] [CrossRef]
- Raab, S.A.; Zhang, J.; Bhardwaj, P.; Holzapfel, F. Proposal of a unified control strategy for vertical take-off and landing transition aircraft configurations. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3478. [Google Scholar]
- Lombaerts, T.; Kaneshige, J.; Schuet, S.; Hardy, G.; Aponso, B.L.; Shish, K.H. Nonlinear dynamic inversion based attitude control for a hovering quad tiltrotor eVTOL vehicle. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0134. [Google Scholar]
- Zhang, J.; Bhardwaj, P.; Raab, S.A.; Saboo, S.; Holzapfel, F. Control allocation framework for a tilt-rotor vertical take-off and landing transition aircraft configuration. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3480. [Google Scholar]
- Rieck, M.; Bittner, M.; Grüter, B.; Diepolder, J.; Piprek, P.; Göttlicher, C.; Schwaiger, F.; Hosseini, B.; Schweighofer, F.; Akman, T.; et al. FALCON.m User Guide; Institute of Flight System Dynamics, Technical University of Munich: München, Germany, 2023. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
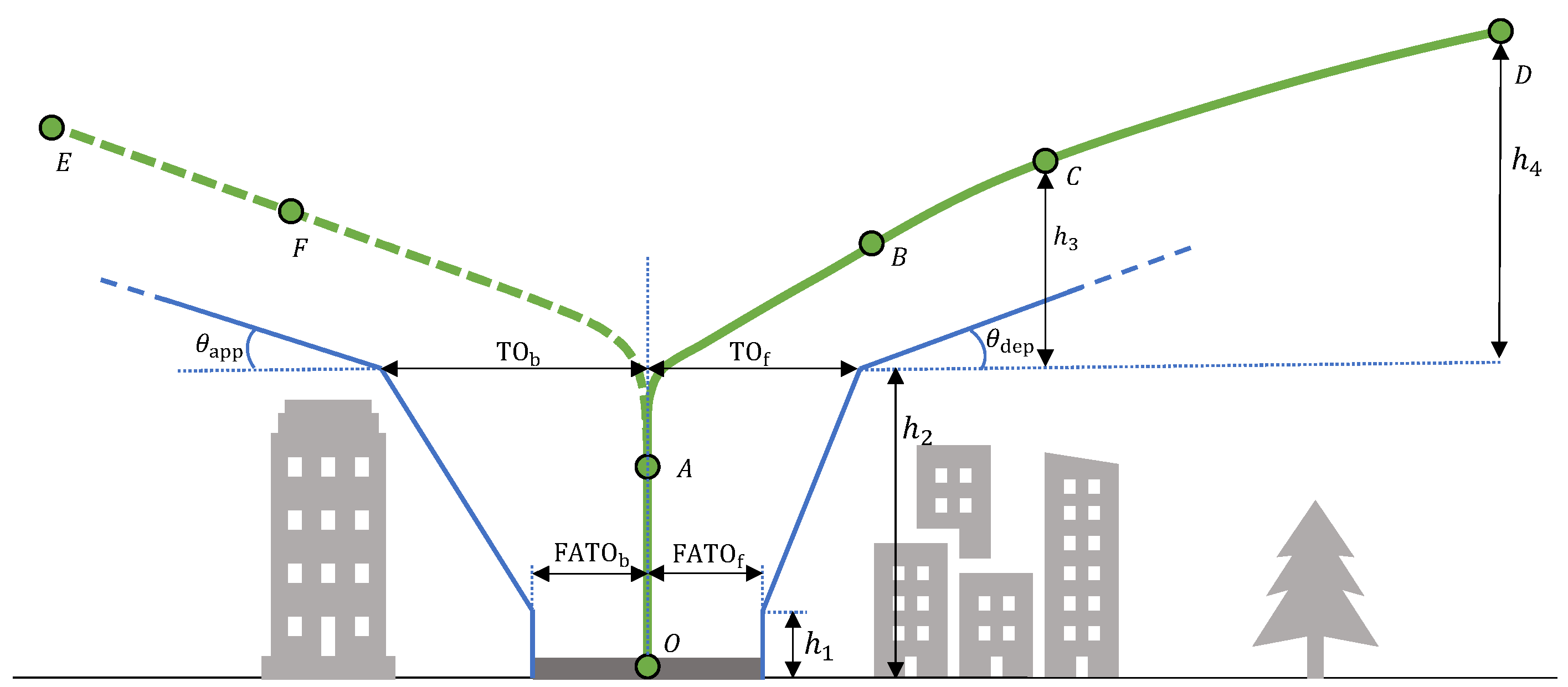
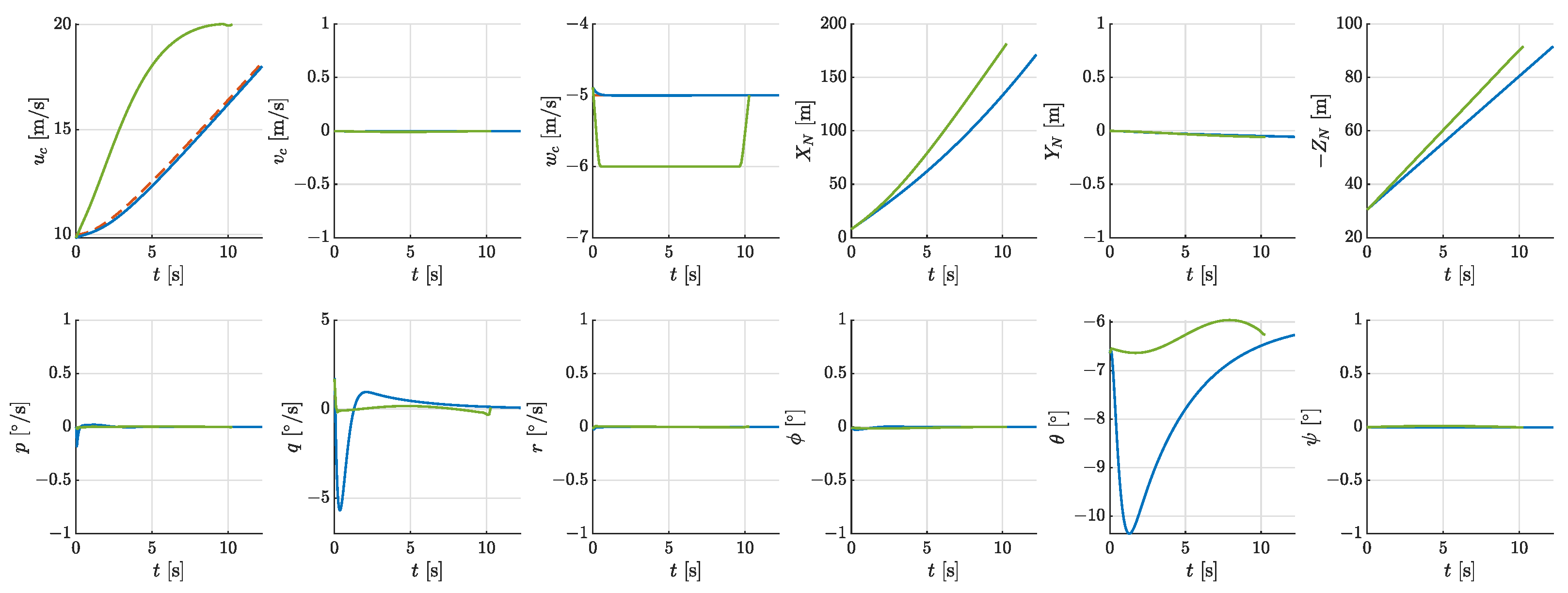


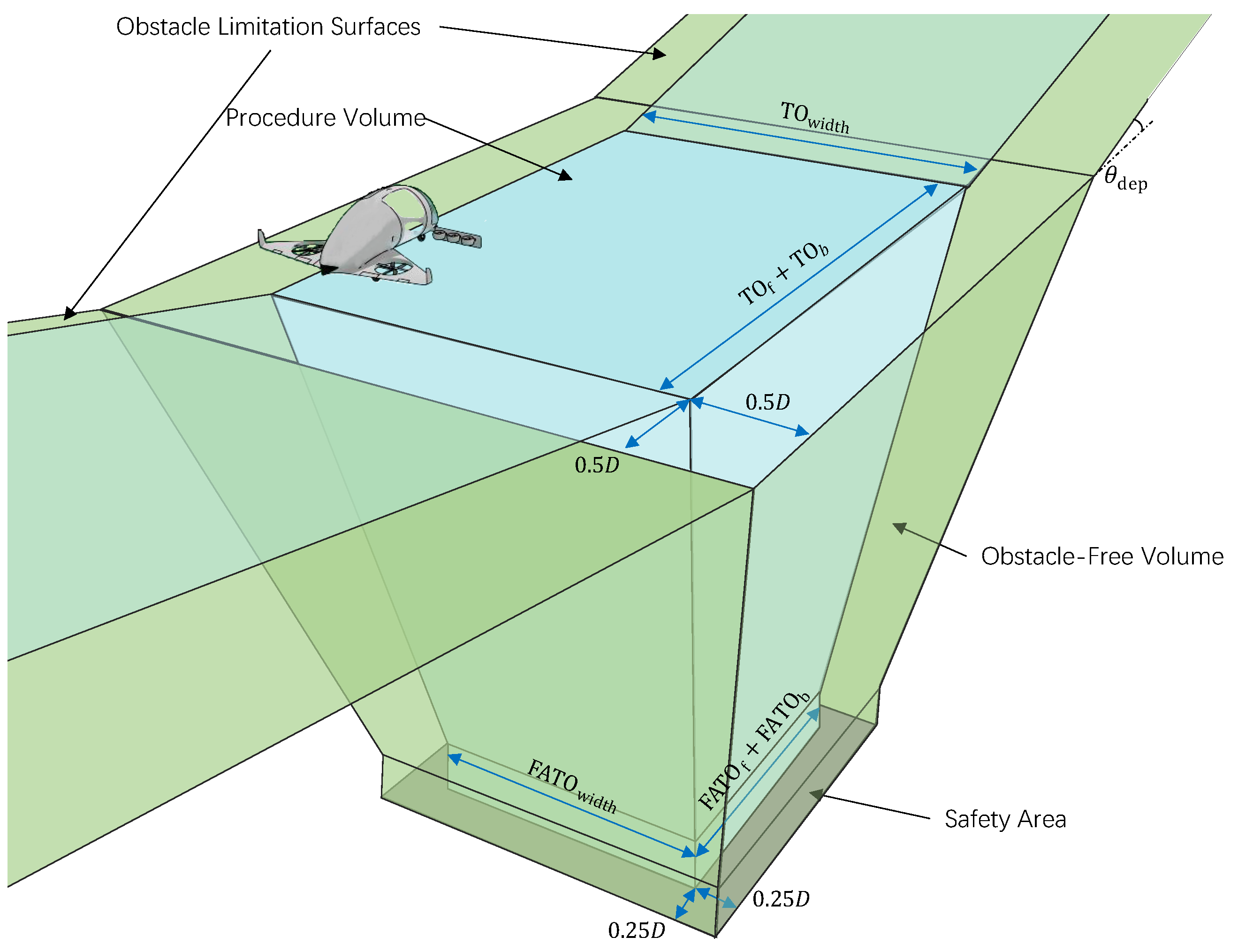
| Nr. | Requirement | |
|---|---|---|
| Take-off | 1 | The aircraft should reach while clearing any surface by 4.6 m |
| 2 | should be reached at or before 10.7 m (35 ft) above | |
| 3 | In the first climb segment, the minimum climb gradient is and the speed is no less than | |
| 4 | In the second climb segment, the minimum climb gradient is 2.5% | |
| 5 | The aircraft should be accelerated to at a height over 305 m (1000 ft) | |
| 6 | After reaching , the aircraft should be capable of a directional trajectory change with at least 3/s and no descent | |
| Landing | 1 | LDP should be reached at a speed equal or lower to the reference speed |
| 2 | The speed, position, and attitude of the aircraft when it touches the ground are within certain ranges | |
| Symbol | Meaning | Range | Recommanded Value |
|---|---|---|---|
| Low hover height | - | 3 m | |
| High hover height | ≥ | 30.5 m | |
| Width at | ≤ | ||
| Front distance at | ≤ | ||
| Back distance at | ≤ | ||
| Width of the FATO | ≥ | ||
| Front distance on FATO | ≥ | ||
| Back distance on FATO | ≥ | ||
| Slope of approach surface | ≥ | 12.5% | |
| Slope of departure surface | ≥ | 12.5% |
| Parameter | Value | Unit |
|---|---|---|
| Mass m | 575 | kg |
| Wing span b | 6 | m |
| Wing mean chord length c | 0.67 | m |
| Wing reference area | 8.04 | |
| Wing stall angle | 15 | |
| Diameter of propeller | 1.5 | m |
| VTOL dimension D | 8 | m |
| Stall speed | 35 | m/s |
| Take-off safety speed | 11 | m/s |
| Final take-off speed | 46 | m/s |
| Landing reference speed | 20 | m/s |
| Variable | Constraint |
|---|---|
| Forward velocity in the body-frame | m/s m/s |
| Side velocity in the body-frame | m/s m/s |
| Vertical velocity in the body-frame | m/s m/s |
| Roll rate in the body-frame | |
| Pitch rate in the body-frame | |
| Yaw rate in the body-frame | |
| Roll angle | |
| Pitch angle | |
| Forward load factor | |
| Side load factor | |
| Vertical load factor |
| Variable | Constraint |
|---|---|
| Wing-tilt angle | /s |
| Deflection angle of ailerons | /s |
| Deflection angle of elevators | /s |
| Rotational speed of propellers | 2800 r/min, rad/s |
| Variable | Constraint |
|---|---|
| Torque of a single propeller | ≤ |
| Output power of a single propeller | ≤ |
| Output power of all propellers | ≤ |
| Phase | Initial Condition | Final Condition | Path Constraints |
|---|---|---|---|
| 1 | Obstacle-free volume | ||
| 2 | Final state of the first take-off phase solution | m | Obstacle limitation surface |
| 3 | Final state of the second take-off phase solution | ||
| 4 | Final state of the third take-off phase solution | , |
| Phase | Initial Condition | Final Condition | Path Constraints |
|---|---|---|---|
| 1 | Obstacle limitation surface | ||
| 2 | Final state of the first landing phase solution | Obstacle limitation surface Obstacle-free volume |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Hong, H.; Holzapfel, F. Multi-Phase Vertical Take-Off and Landing Trajectory Optimization with Feasible Initial Guesses. Aerospace 2024, 11, 39. https://doi.org/10.3390/aerospace11010039
Lu Z, Hong H, Holzapfel F. Multi-Phase Vertical Take-Off and Landing Trajectory Optimization with Feasible Initial Guesses. Aerospace. 2024; 11(1):39. https://doi.org/10.3390/aerospace11010039
Chicago/Turabian StyleLu, Zhidong, Haichao Hong, and Florian Holzapfel. 2024. "Multi-Phase Vertical Take-Off and Landing Trajectory Optimization with Feasible Initial Guesses" Aerospace 11, no. 1: 39. https://doi.org/10.3390/aerospace11010039
APA StyleLu, Z., Hong, H., & Holzapfel, F. (2024). Multi-Phase Vertical Take-Off and Landing Trajectory Optimization with Feasible Initial Guesses. Aerospace, 11(1), 39. https://doi.org/10.3390/aerospace11010039