Accuracy Investigations of Dynamic Characteristic Predictions of Tip Leakage Flow Using Detached Eddy Simulation
Abstract
:1. Introduction
2. Computational Model and Numerical Method
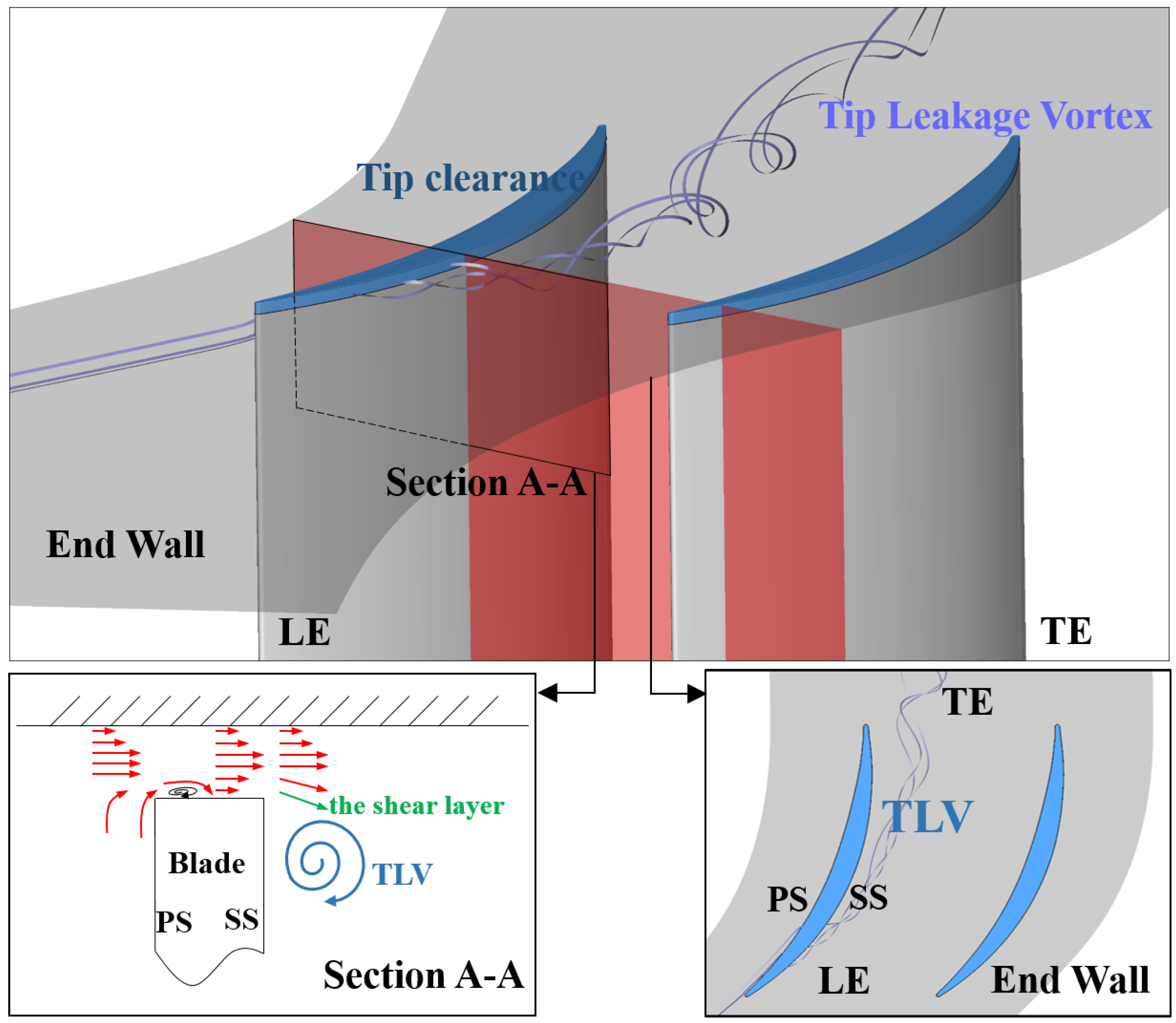
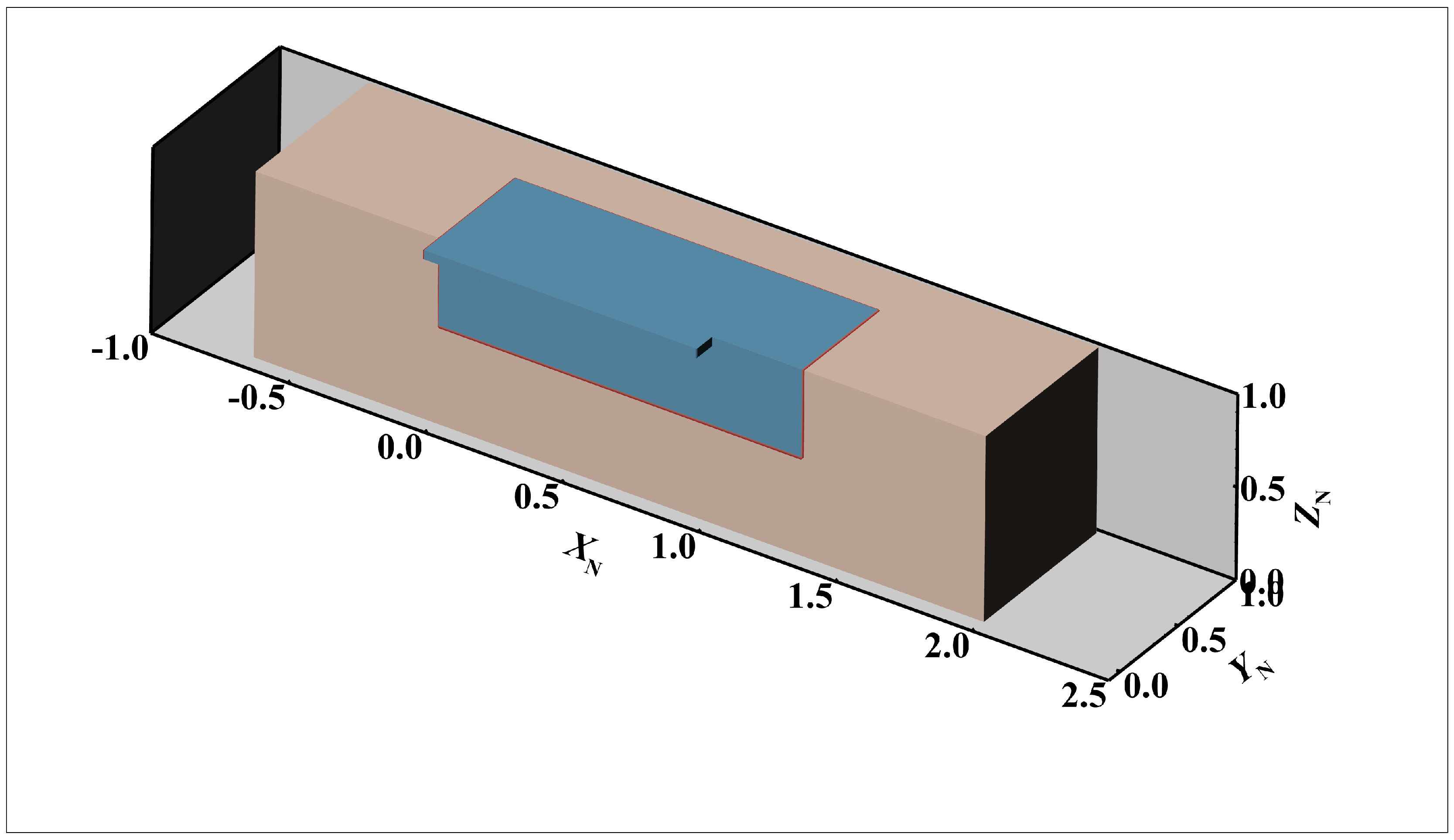
2.1. Simplified Model of the Tip Clearance
2.1.1. Geometry and Flow Characteristics of Compressor Tip Clearance
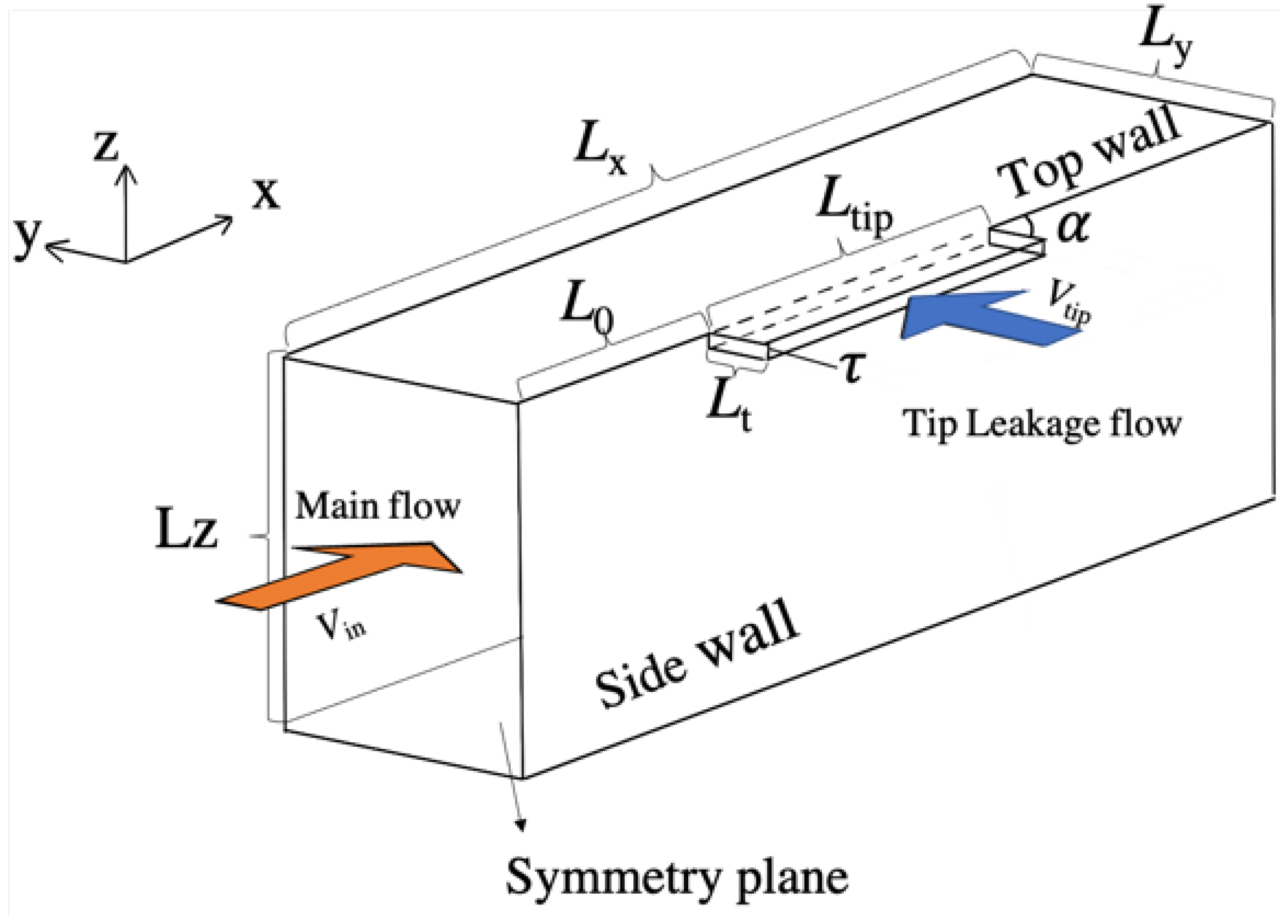
2.1.2. Simplified Model of the Tip Leakage Flow
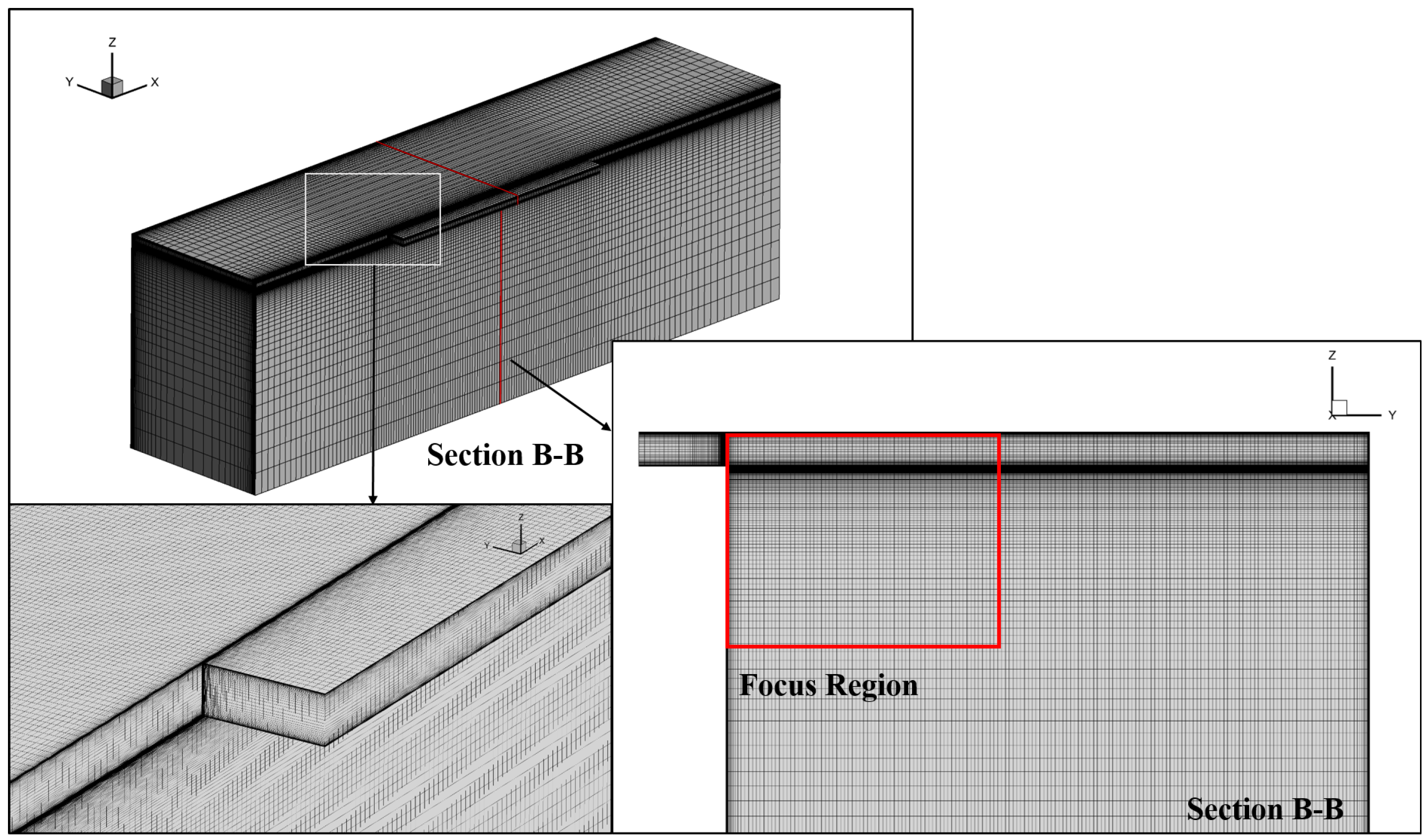
2.2. Numerical Methods
- is the constant 0.61 in the DES method,
- k is the turbulent kinetic energy,
- is the turbulent dissipation rate,
- is a constant 0.09,
- d is the distance from the grid center to the nearest wall,
- is the kinematic viscosity,
- is the maximum value of a grid-scale in the x, y, z directions.
2.3. Data Processing Methods
2.3.1. Time Average of the Unsteady Flow Field
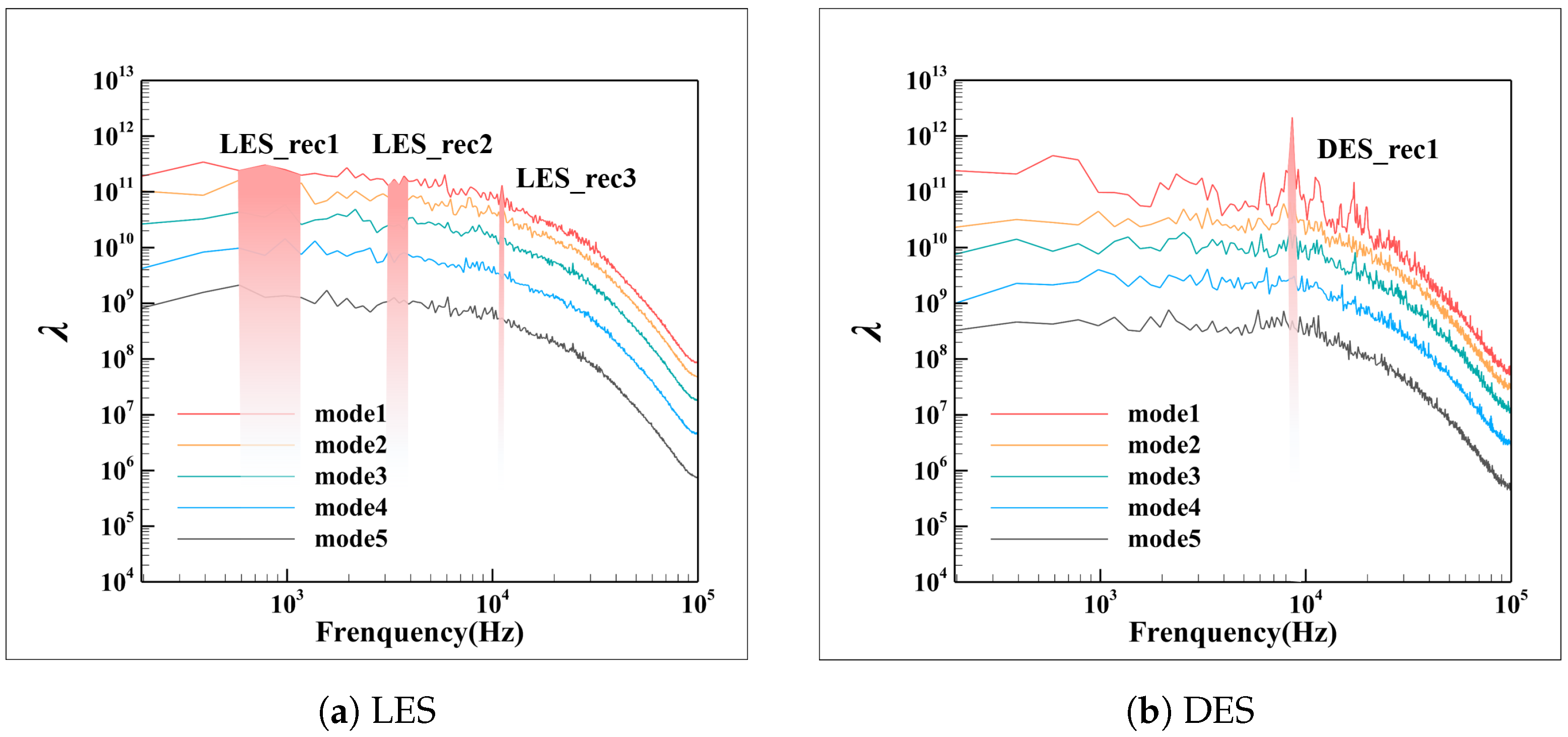
2.3.2. Spectral Proper Orthogonal Decomposition (SPOD)
3. Results and Analysis
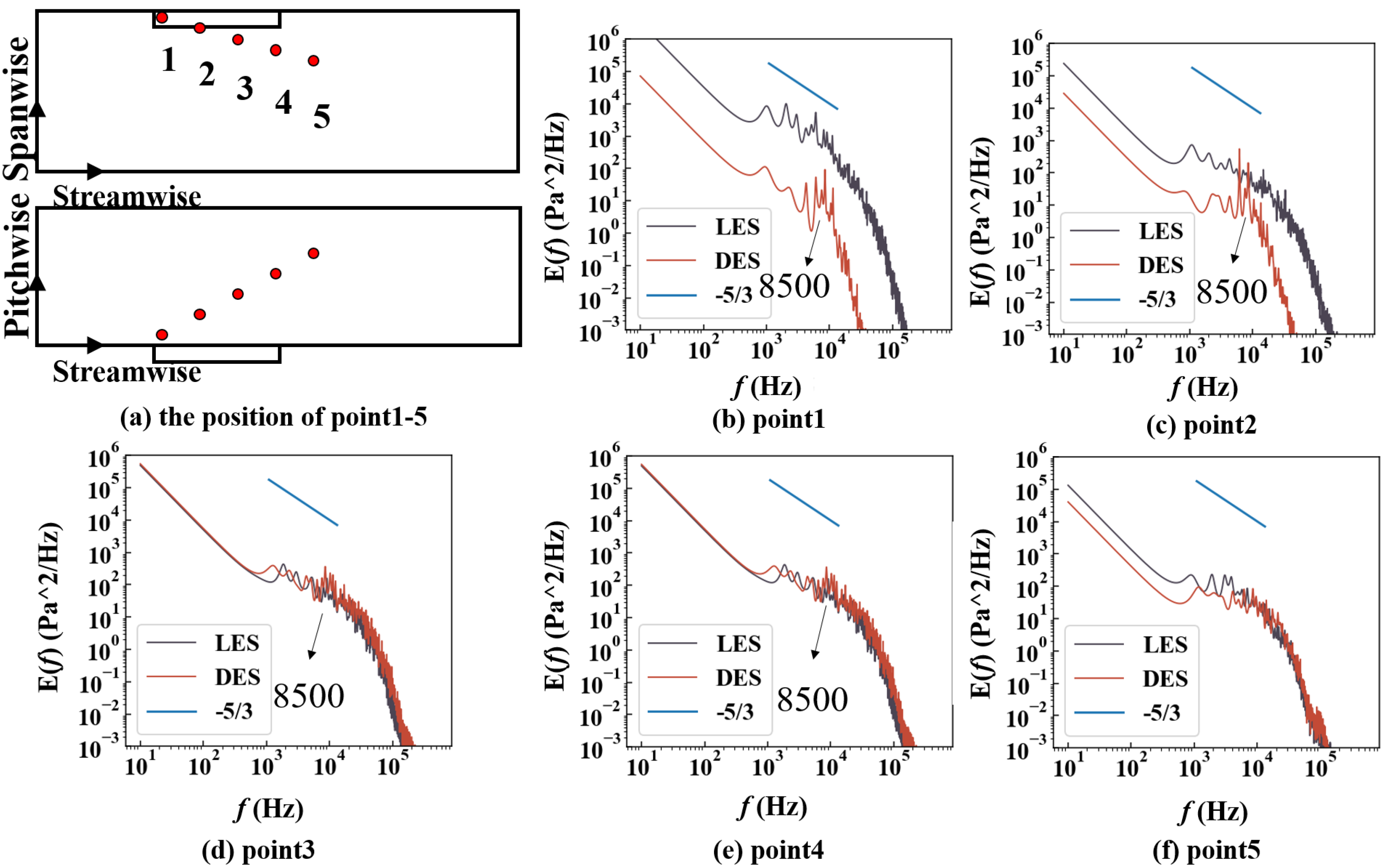
3.1. The Resolution of the DES Method for Tip Leakage Flow
3.2. The Prediction of the Critical Time-Averaged Parameters
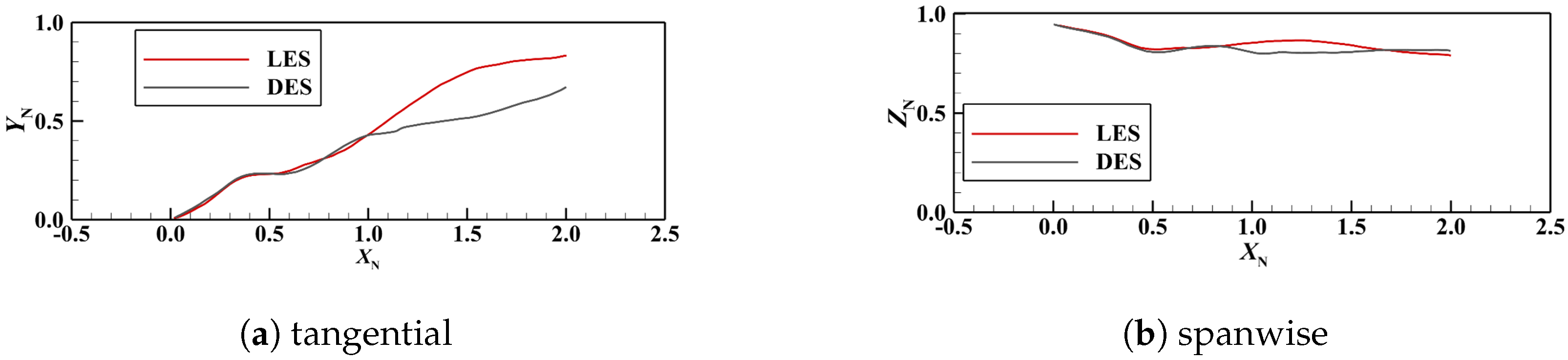
3.2.1. Trajectory of Tip Leakage Vortex
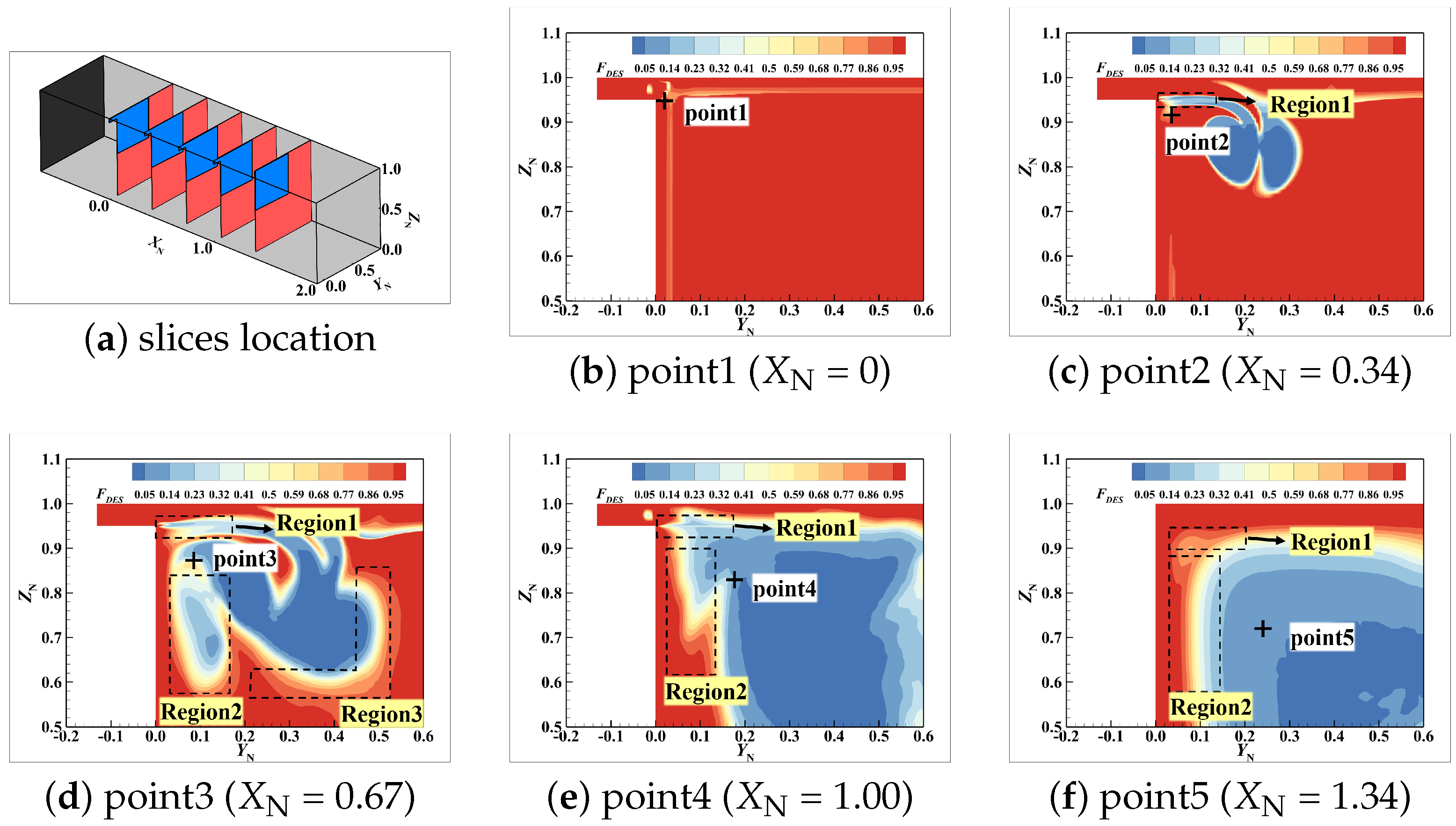
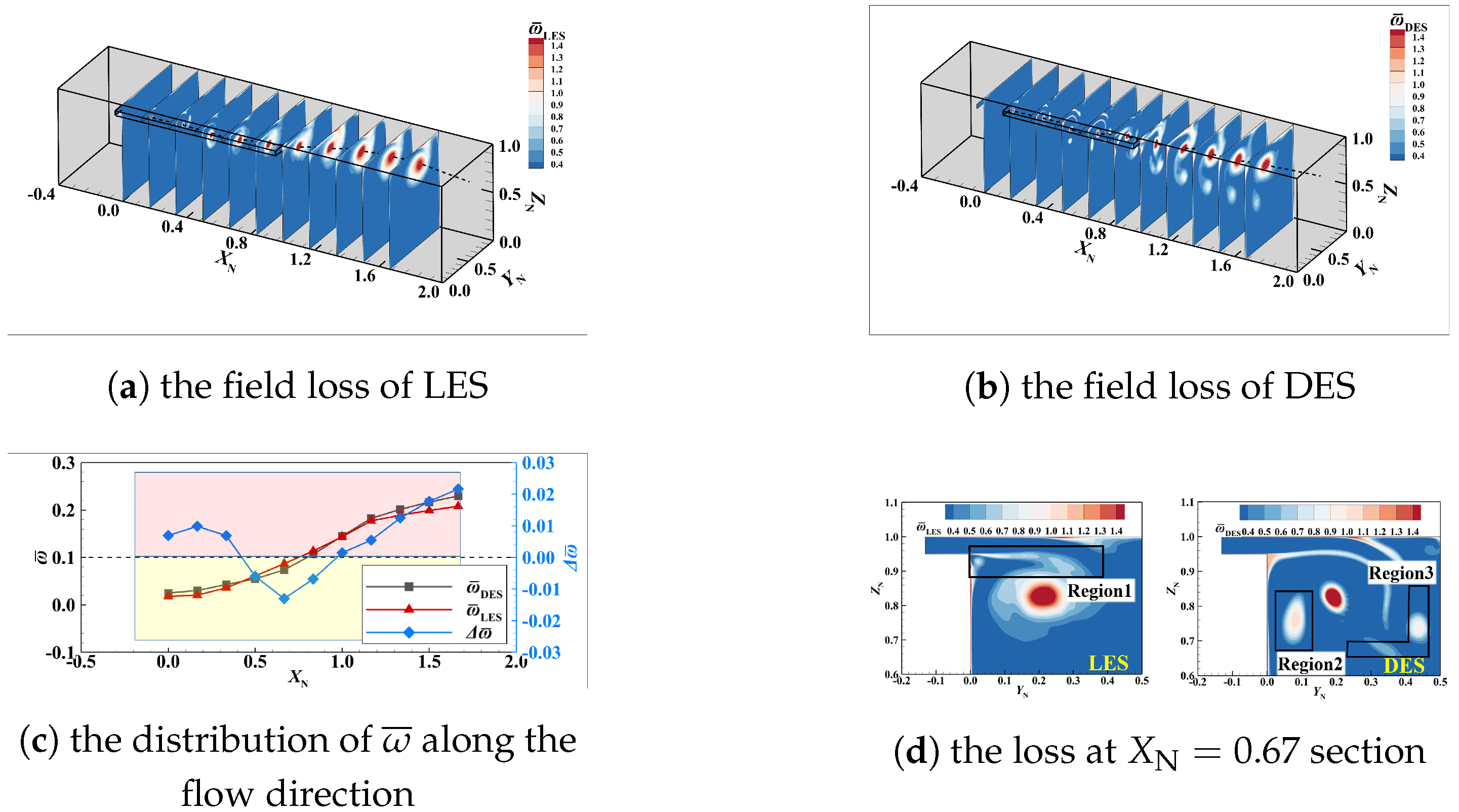
3.2.2. Flow Field Loss
3.3. Mechanism Analysis of the Time-Averaged Parameters Difference Based on Detailed Flow Structures
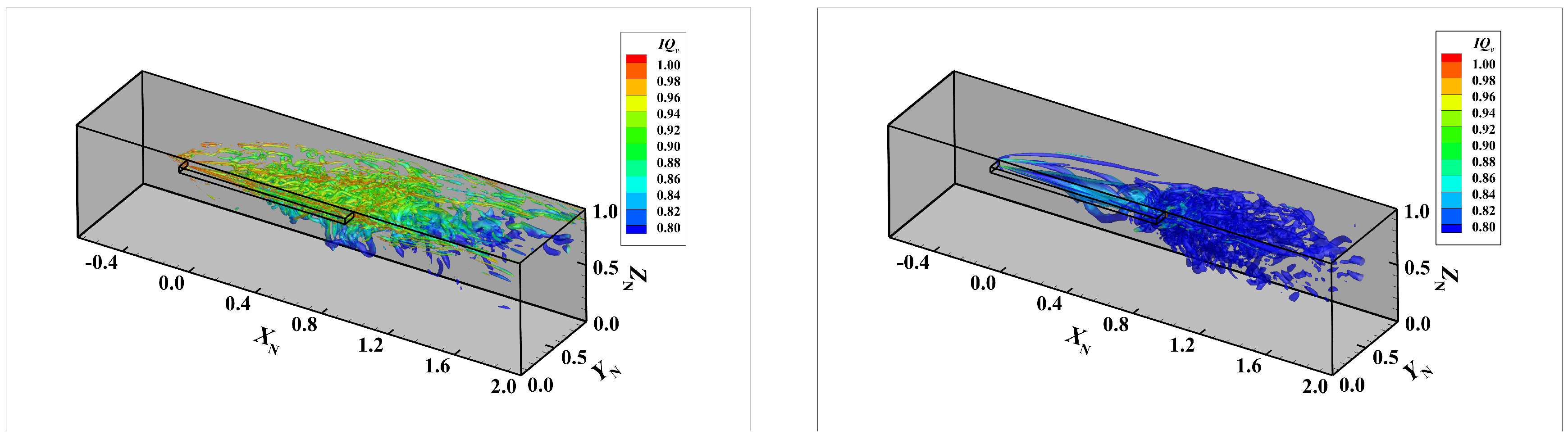
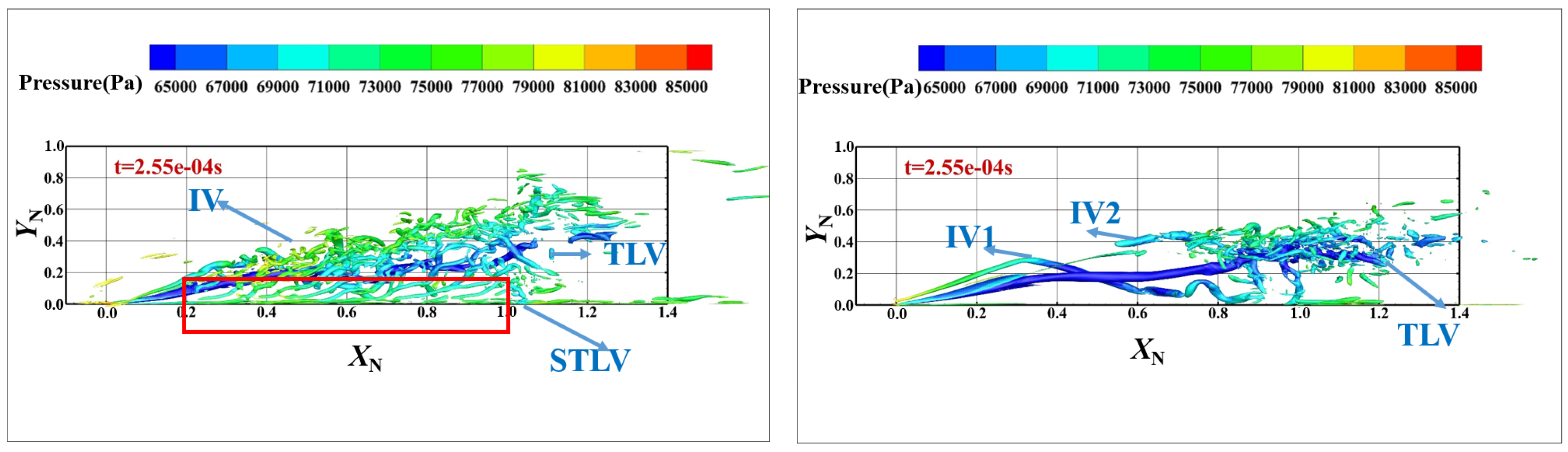
3.3.1. Detailed Structure of Tip Leakage Flow
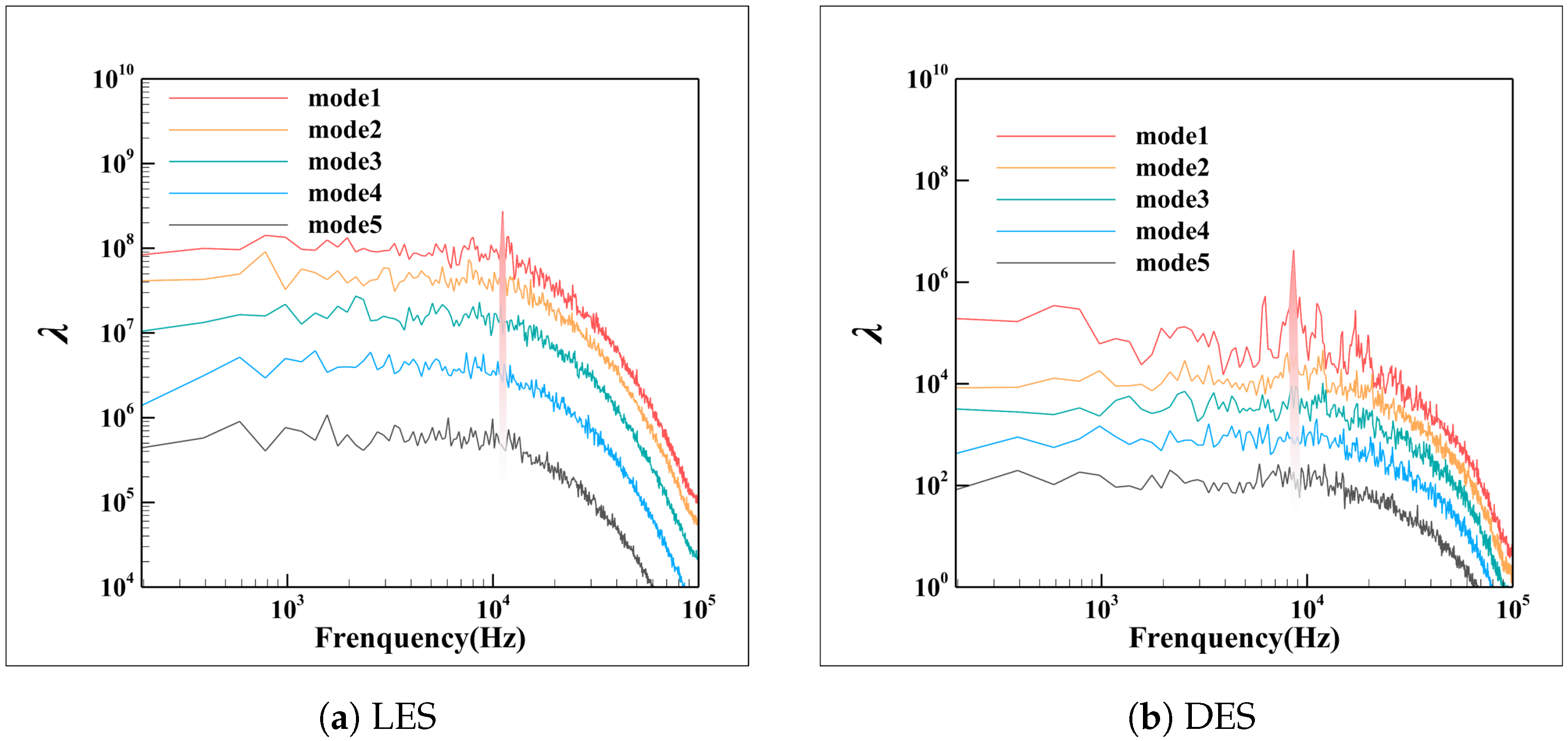
3.3.2. The Dominant Flow Structures in the Tip Leakage Flow Field
3.3.3. Impact of Dominant Flow Structures on Time-Averaged Parameters
- (1)
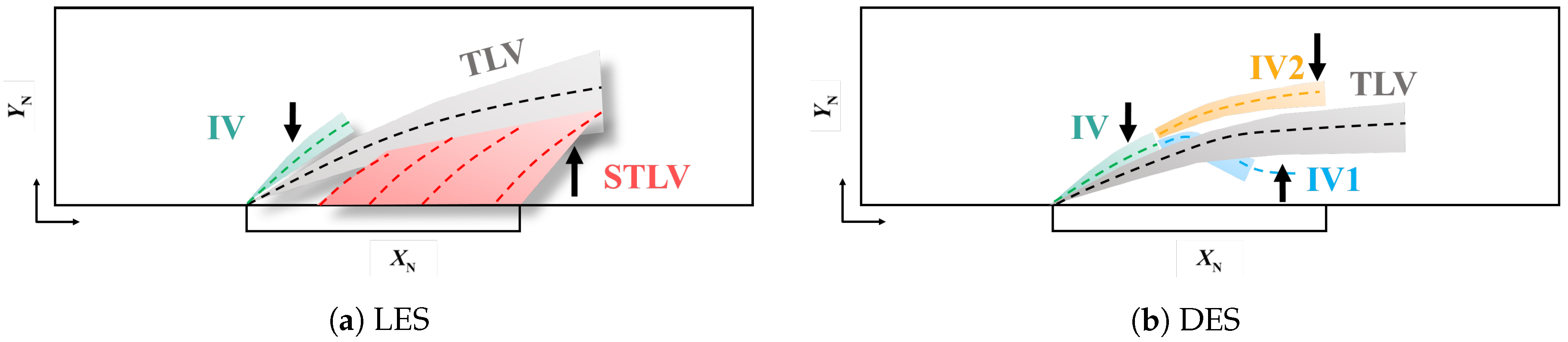
- Reasons for the differences in tip leakage flow trajectory
- (2)
- Reasons for the differences in flow loss
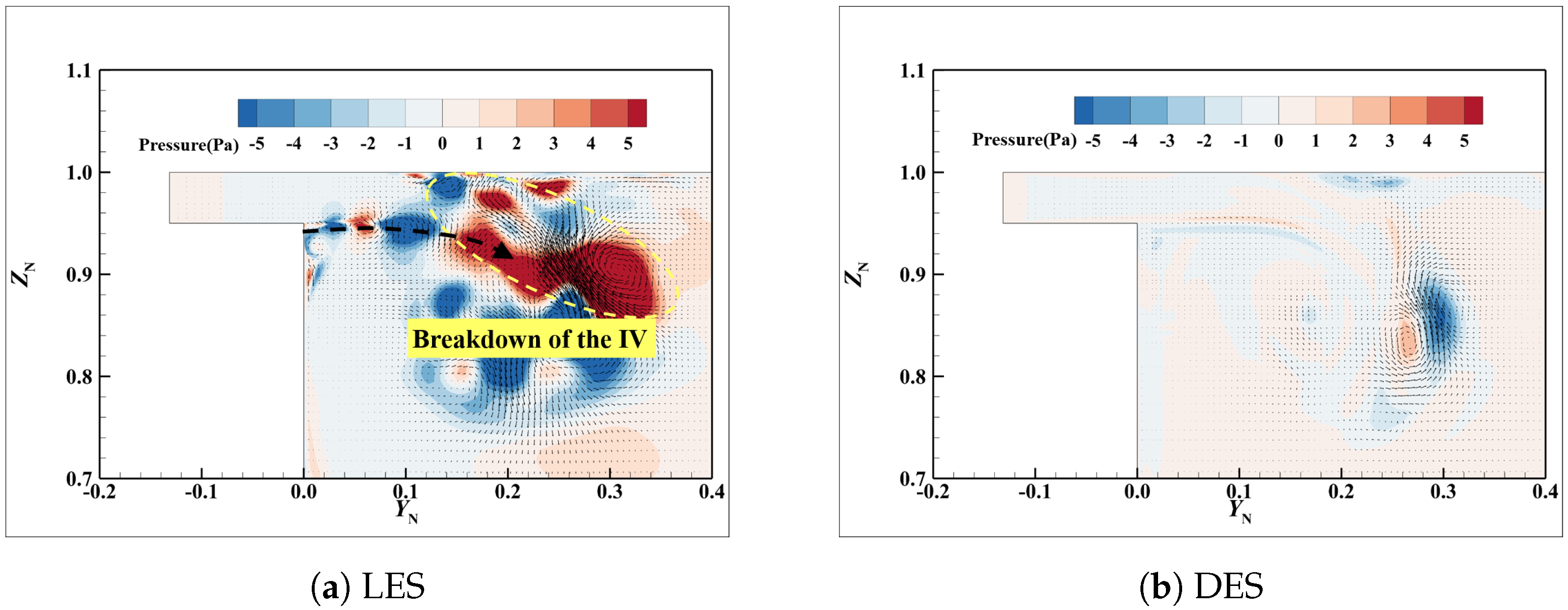
3.3.4. The Reason for Inaccurate Prediction in Detailed Structures
4. Conclusions
- (1)
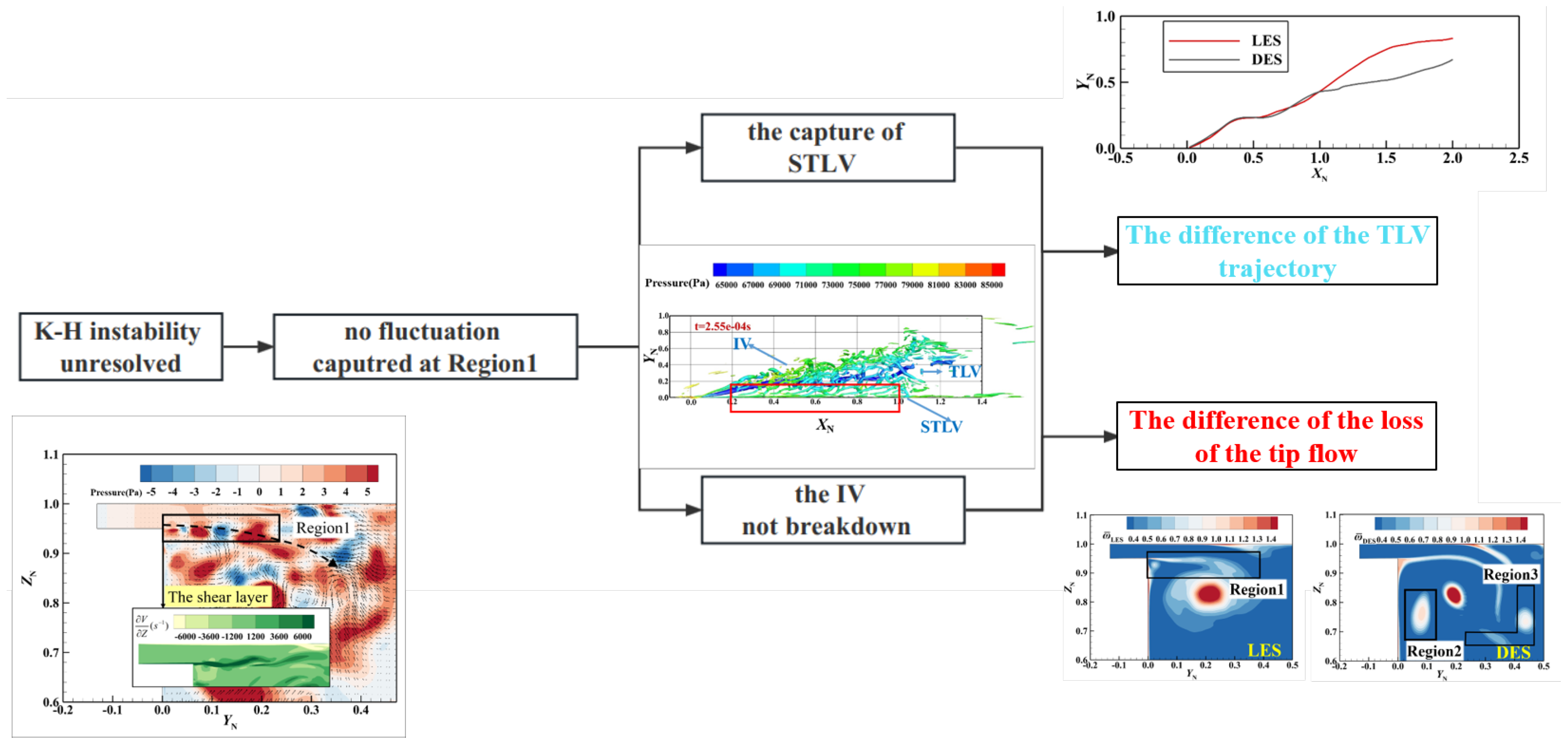
- Differences between the DES and LES results during the simulation of time-averaged parameters and detailed structures: Regarding the time-averaged parameters, compared with the LES results, the DES-captured TLV trajectories are close inside the passage and different outside of it, both in spanwise and tangential directions. Meanwhile, the value and spatial distribution of the flow field loss captured by the DES are different from the LES results. Furthermore, the loss predicted by DES is larger from the beginning to the middle part and outside of the passage, and smaller from the middle to the end part of the passage. As for detailed flow structures, the DES method could not capture the generation of the STLV and the breakdown of the IV.
- (2)
- The correlation between the difference in detailed structures and the deviation of time-averaged parameters: due to the inaccurate capture of STLV and IV, the force on the TLV core is different, leading to inaccurate TLV trajectory predictions in the spanwise and tangential directions. For the total pressure loss, the diversity of IV development leads to the different predictions of the main fluctuation sources in the flow field, which leads to inaccurate prediction of the loss position and value.
- (3)
- The influence mechanism of the “gray area” on detailed structures: In the flow field prediction of tip clearance leakage flow by the DES method, the gray area mainly exists in the shear layer Region 1 formed by the leakage jet and mainstream, Region 2 near the side wall (), downstream of the leakage, and Region 3 in the middle of the passage. Due to the slow transition from the RANS to the LES in Region 1, the K-H instability, which should have been resolved was suppressed, causing the STLV to not successfully be captured. Consequently, the IV development is correctly resolved because the fluctuation injection of STLV is not captured, resulting in incorrect simulation results of IV development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DES | Detached eddy simulation |
| DDES | Delay detached eddy simulation |
| EDDES | Enhanced detached eddy simulation |
| GIS | Grid induced separation |
| IV | Induced vortex |
| IV1 | Induced vortex branch 1 |
| IV2 | Induced vortex branch 2 |
| LES | Large eddy simulation |
| SLD | Slow LES development |
| SPOD | Spectral proper orthogonal decomposition |
| STLV | Secondary tip leakage vortex |
| TKE | Turbulence kinetic energy |
| TLV | Tip leakage vortex |
| ZDES | Zonal detached eddy simulation |
References
- Wisler, D.C. Loss reduction in axial-flow compressors through low-speed model testing. J. Eng. Gas Turbines Power 1985, 107, 354–363. [Google Scholar] [CrossRef]
- Yamada, K.; Kikuta, H.; Furukawa, M.; Gunjishima, S.; Hara, Y. Effects of tip clearance on the stall inception process in an axial compressor Rotor. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, San Antonio, TX, USA, 3–7 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Fukano, T.; Jang, C.M. Tip clearance noise of axial flow fans operating at design and off-design condition. J. Sound Vib. 2004, 275, 1027–1050. [Google Scholar] [CrossRef]
- Wilke, I.; Kau, H.P. A Numerical Investigation of the flow mechanisms in a high pressure compressor front stage with axial slots. J. Turbomach. 2004, 126, 339–349. [Google Scholar] [CrossRef]
- Mao, X.; Liu, B.; Tang, T.F. Control of Tip Leakage Flow in Axial Flow Compressor Cascade by Suction on the Blade Tip. J. Appl. Fluid Mech. 2018, 11, 137–149. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Nie, C.; Zhang, H. Review of tip air injection to improve stall margin in axial compressors. Prog. Aerosp. Sci. 2019, 106, 15–31. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Li, Y.; Yu, X.; Liu, B. Control of compressor tip leakage flow using plasma actuation. Aerosp. Sci. Technol. 2019, 86, 244–255. [Google Scholar] [CrossRef]
- Inoue, M.; Kuroumaru, M.; Fukuhara, M. Behavior of Tip Leakage Flow Behind an Axial Compressor Rotor J. Eng. Gas Turbines Power 1997, 108, 7–14. [Google Scholar] [CrossRef]
- Kang, S.; Hirsch, C. Experimental study on the three-dimensional flow within a compressor cascade with tip clearance: Part II–The tip leakage vortex. J. Turbomach. 1992, 115, 444–450. [Google Scholar] [CrossRef]
- Kang, S.; Hirsch, C. Tip Leakage Flow in Linear Compressor Cascade. J. Turbomach. 1994, 116, 657–664. [Google Scholar] [CrossRef]
- Garnier, V.H. Rotating waves as a stall inception indication in axial compressors. J. Turbomach. 1991, 113, 1098–1102. [Google Scholar] [CrossRef]
- Day, I.J. Stall inception in an axial flow compressor. J. Turbomach. 1993, 115, 1–9. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, L.; Lu, L. Comparison of DDES and URANS for Unsteady Tip Leakage Flow in an Axial Compressor Rotor. J. Fluids Eng. 2019, 141, 121405. [Google Scholar] [CrossRef]
- Geng, S.; Zhang, H.; Chen, J.; Huang, W. Numerical Study on the Response of Tip Leakage Flow Unsteadiness to Micro Tip Injection in a Low-Speed Isolated Compressor Rotor. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Zhang, H.; Deng, X.; Chen, J.; Huang, W. Unsteady Tip leakage Flow in an Isolated Axial Compressor Rotor. J. Therm. Sci. 2005, 14, 211–219. [Google Scholar] [CrossRef]
- You, D.; Wang, M.; Moin, P. Large-eddy simulation analysis of mechanisms for viscous losses in a turbomachinery tip-clearance flow. J. Fluid Mech. 2007, 586, 177–204. [Google Scholar] [CrossRef]
- Tucker, P.G. Computation of Unsteady Turbomachinery Flows: Part 2—LES and Hybrids. Prog. Aerosp. Sci. 2011, 47, 546–569. [Google Scholar] [CrossRef]
- Jagadeesh, M.; Dimitrios, P.; Stéphane, H. Assessment of Wall Modelling for Large Eddy Simulations of Turbomachinery. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Spalart, P.R. Comments on the feasibility of les for wings, and on a hybrid rans/les approach. In Proceedings of the First Afosr International Conference on Dns/Les, Greden Press 1997. pp. 137–147. Available online: https://www.researchgate.net/publication/236888805_Comments_on_the_Feasibility_of_LES_for_Wings_and_on_a_Hybrid_RANSLES_Approach (accessed on 20 November 2023).
- Li, R.; Gao, L.; Ma, C.; Lin, S.; Zhao, L. Corner separation dynamics in a high-speed compressor cascade based on detached-eddy simulation. Aerosp. Sci. Technol. 2020, 99, 105730. [Google Scholar] [CrossRef]
- Li, R.; Gao, L.; Zhao, L. Dominating unsteadiness flow structures in corner separation under high mach number. AIAA J. 2019, 57, 2923–2932. [Google Scholar]
- Ma, W.; Ottavy, X.; Lu, L. Intermittent corner separation in a linear compressor cascade. Exp. Fluids 2013, 54, 1546. [Google Scholar]
- Yan, H.; Liu, Y.; Lu, L. Turbulence anisotropy analysis in a highly loaded linear compressor cascade. Aerosp. Sci. Technol. 2019, 91, 241–254. [Google Scholar] [CrossRef]
- Yamada, Y.; Furukawa, M.; Nakakido, S. Large-scale des analysis of unsteady flow field in a multi-stage axial flow. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montréal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M. Adaptation of eddy-viscosity turbulence models to unsteady separated flow behind vehicles. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains; Springer: Berlin, Germany, 2004; pp. 339–352. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. An enhanced version of DES with rapid transition from RANS to LES in separated flows. Flow Turbul. Combust. 2015, 95, 709–737. [Google Scholar] [CrossRef]
- Biollo, R.; Benini, E. Shock/Boundary-Layer/Tip-Clearance Interaction in a Transonic Rotor Blade. J. Propuls. Power 2009, 25, 668–677. [Google Scholar] [CrossRef]
- Fang, J.; Gao, Y.; Liu, Y.; Lu, L.; Yao, Y.; Le Ribault, C. Direct numerical simulation of a tip-leakage flow in a planar duct with a longitudinal slit. Phys. Fluids 2019, 31, 125108. [Google Scholar] [CrossRef]
- Deck, S. Recent improvements in the Zonal Detached eddy simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 2012, 26, 523–550. [Google Scholar] [CrossRef]
- Su, X.; Ren, X.; Li, X.; Gu, C. Unsteadiness of tip leakage flow in the detached-eddy simulation on a transonic rotor with vortex breakdown phenomenon. Energies 2019, 12, 954. [Google Scholar] [CrossRef]
- Wu, J. Improved delayed detached eddy simulation of compressor cascade tip leakage flow. Int. J. Aeronaut. Space Sci. 2020, 22, 17–32. [Google Scholar] [CrossRef]
- Riéra, W.; Marty, J.; Castillon, L.; Deck, S. Zonal detached-eddy simulation applied to the tip-clearance flow in an axial compressor. AIAA J. 2016, 54, 2377–2391. [Google Scholar] [CrossRef]
- He, X.; Zhao, F.; Vahdati, M. Detached Eddy Simulation: Recent Development and Application to Compressor Tip Leakage Flow. J. Turbomach. 2022, 144, 011009. [Google Scholar] [CrossRef]
- Gao, L.; Lin, S.; Li, R.; Zhao, L. Research on the Vortex Structure Near the Tip Clearance in a Highly Loaded Compressor Cascade Based on Oil Flow Pattern. J. Aerosp. Power 2023, 38, 2473–2482. [Google Scholar]
- Yu, X.; Liu, B.; Jiang, H. Three-Dimensional Flows Near Rotor Tip in an Axial Compressor I—Experimental and Theoretical Studies. Acta Astronaut. Astronaut. Sin. 2010, 31, 48–57. [Google Scholar]
- Yu, X.; Liu, B.; Jiang, H. Three-Dimensional Flows Near Rotor Tip in an Axial Compressor II—Numerical Simulation Study. Acta Astronaut. Astronaut. Sin. 2010, 31, 58–69. [Google Scholar]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Schmidt, O.T.; Colonius, T. Guide to Spectral Proper Orthogonal Decomposition. AIAA J. 2020, 58, 1023–1033. [Google Scholar] [CrossRef]
- He, X.; Fang, Z.; Rigas, G.; Vahdati, M. Spectral Proper Orthogonal Decomposition of Compressor Tip Leakage Flow. Phys. Fluids 2021, 33, 105105. [Google Scholar] [CrossRef]
- Heinzel, G.; Rüdiger, A.; Schilling, R. Spectrum and Spectral Density Estimation by the Discrete Fourier Transform (DFT), Including a Comprehensive List of Window Functions and Some New At-Top Windows. 2002. Available online: https://www.researchgate.net/publication/267956210_Spectrum_and_spectral_density_estimation_by_the_Discrete_Fourier_transform_DFT_including_a_comprehensive_list_of_window_functions_and_some_new_flat-top_windows (accessed on 20 November 2023).
- Nekkanti, A.; Schmidt, O.T. Frequency-time Analysis, Low-rank Reconstruction and Denoising of Turbulent Flows using SPOD. J. Fluid Mech. 2021, 926, A26. [Google Scholar] [CrossRef]
- Kay, S.M.; Marple, S.L. Spectrum Analysis—A Modern Perspective. Proc. IEEE 1981, 69, 1380–1419. [Google Scholar] [CrossRef]
- Liu, C. Liutex and Third Generation of Vortex Identification Methods. In Liutex and Third Generation of Vortex Definition and Identification; Liu, C., Wang, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 3–36. [Google Scholar]
- Wang, Y.; Gao, Y.; Liu, C. Letter: Galilean Invariance of Rortex. Phys. Fluids 2018, 30, 111701. [Google Scholar] [CrossRef]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of Resolution Quality for Large Eddy Simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Hoying, A.; Tan, C.S.; Vo, H.D.; Greitzer, E.M. Role of Blade Passage Flow Structures in Axial Compressor Rotating Stall Inception. J. Turbomach. 1999, 121, 735–742. [Google Scholar] [CrossRef]
- Furukawa, M.; Inoue, M.; Saiki, K.; Yamada, K. The role of tip leakage vortex breakdown in compressor rotor aerodynamics. J. Turbomach. 1999, 121, 469–480. [Google Scholar] [CrossRef]
- Tan, D.; Li, Y.; Wilkes, I.; Miorini, R.L.; Katz, J. Visualization and Time-Resolved Particle Image Velocimetry Measurements of the Flow in the Tip Region of a Subsonic Compressor Rotor. J. Turbomach. 2015, 137, 041007. [Google Scholar] [CrossRef]
- Mailach, R.; Lehmann, I.; Vogeler, K. Rotating Instabilities in an Axial Compressor Originating From the Fluctuating Blade Tip Vortex. J. Turbomach. 2001, 123, 453–460. [Google Scholar] [CrossRef]
- Chu, B.T. On the Energy Transfer to Small Disturbances in Fluid Flow (Part I). Acta Mech. 1965, 1, 215–234. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| h | |
| h | |
| LES | DES | ||
|---|---|---|---|
| LES_rec1 | LES_rec2 | LES_rec3 | DES_rec4 |
| 700–1000 Hz | 2000–3000 Hz | 10,500–11,500 Hz | 8000–9000 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Li, R.; Gao, L.; Ge, N. Accuracy Investigations of Dynamic Characteristic Predictions of Tip Leakage Flow Using Detached Eddy Simulation. Aerospace 2024, 11, 29. https://doi.org/10.3390/aerospace11010029
Lin S, Li R, Gao L, Ge N. Accuracy Investigations of Dynamic Characteristic Predictions of Tip Leakage Flow Using Detached Eddy Simulation. Aerospace. 2024; 11(1):29. https://doi.org/10.3390/aerospace11010029
Chicago/Turabian StyleLin, Shiyan, Ruiyu Li, Limin Gao, and Ning Ge. 2024. "Accuracy Investigations of Dynamic Characteristic Predictions of Tip Leakage Flow Using Detached Eddy Simulation" Aerospace 11, no. 1: 29. https://doi.org/10.3390/aerospace11010029
APA StyleLin, S., Li, R., Gao, L., & Ge, N. (2024). Accuracy Investigations of Dynamic Characteristic Predictions of Tip Leakage Flow Using Detached Eddy Simulation. Aerospace, 11(1), 29. https://doi.org/10.3390/aerospace11010029






