Large Eddy Simulation of Pulsed Film Cooling with a Dielectric Barrier Discharge Plasma Actuator
Abstract
:1. Introduction
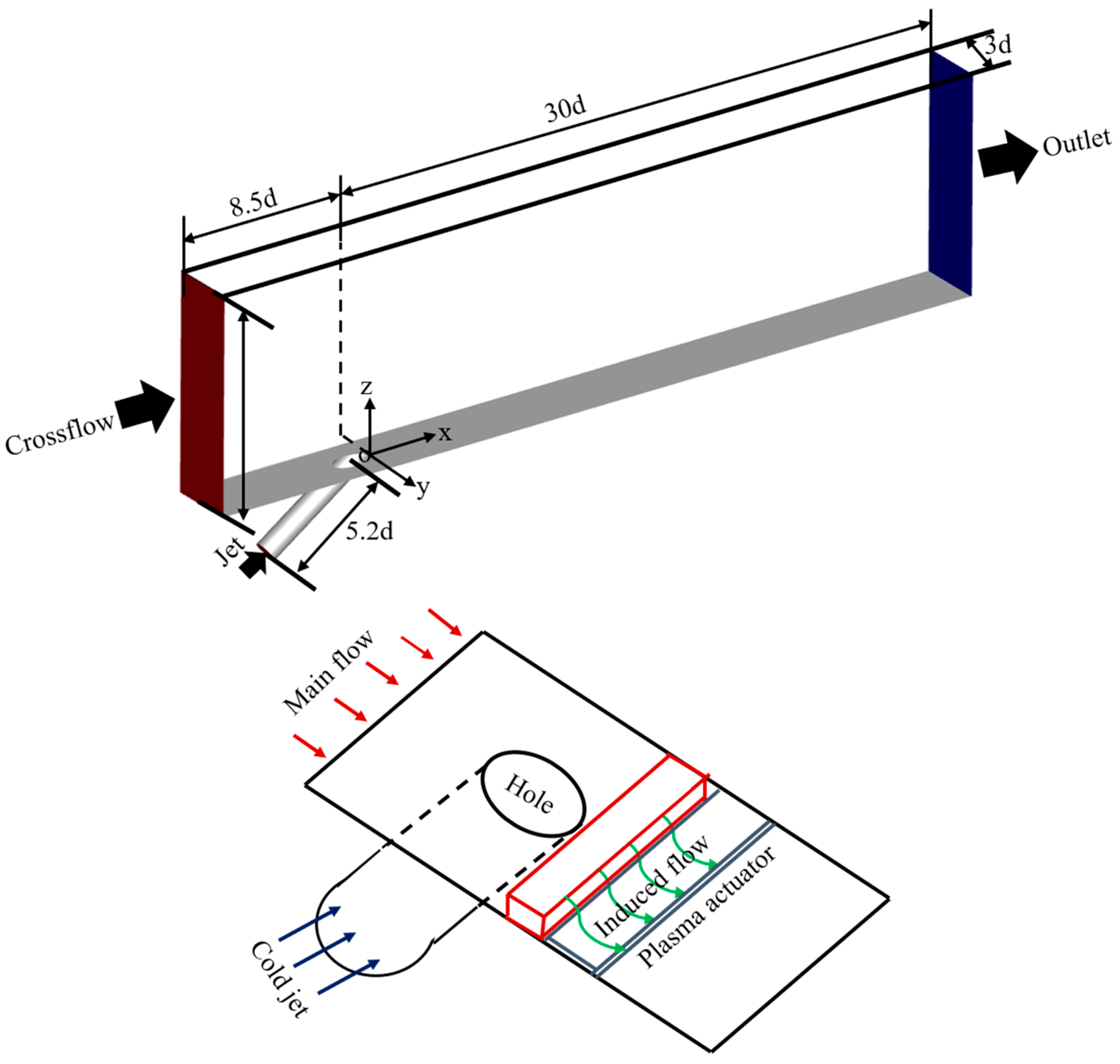
2. Computational Domain and Boundary Conditions (BCs)
3. Governing Equations and Phenomenological Plasma Model
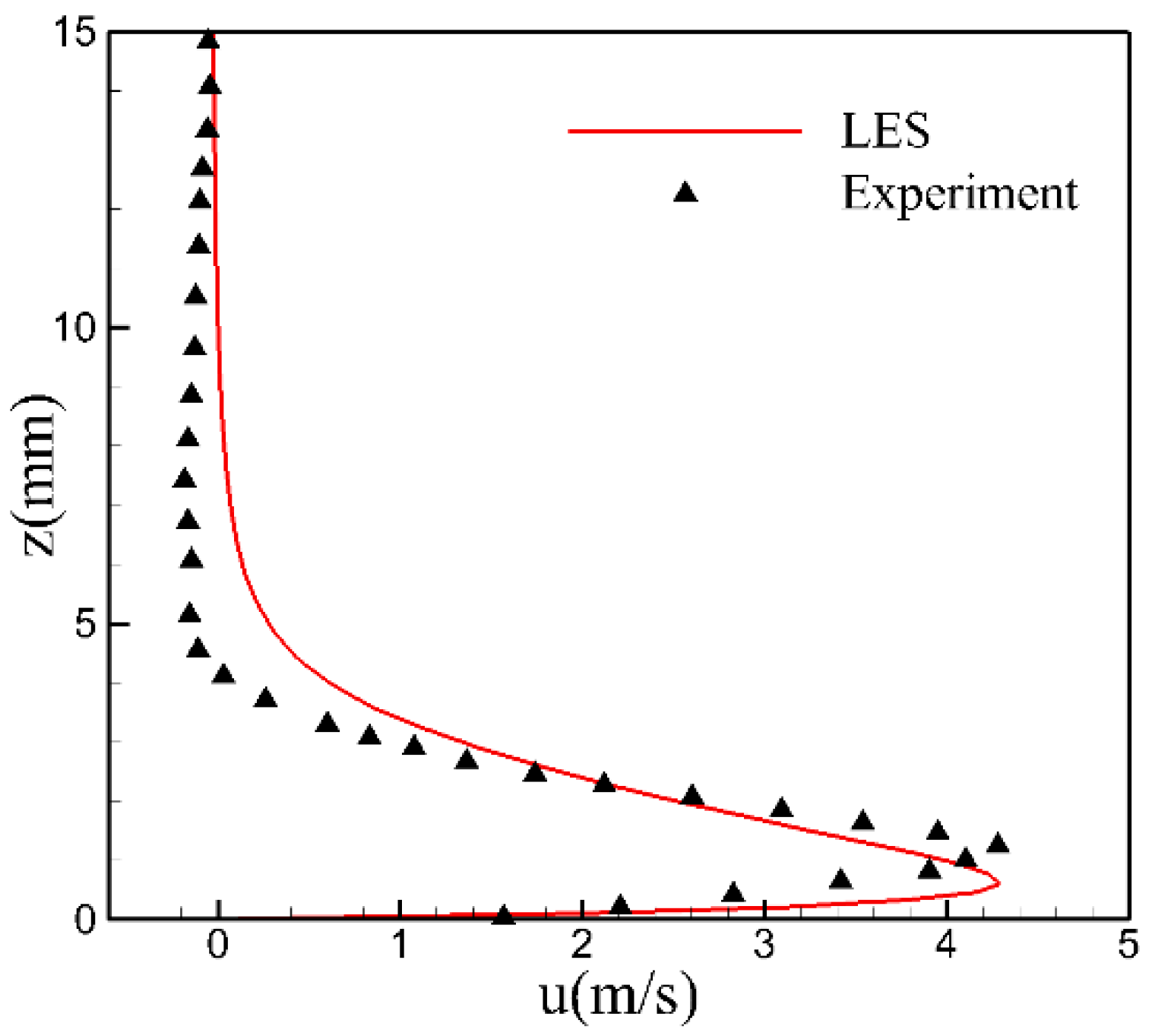
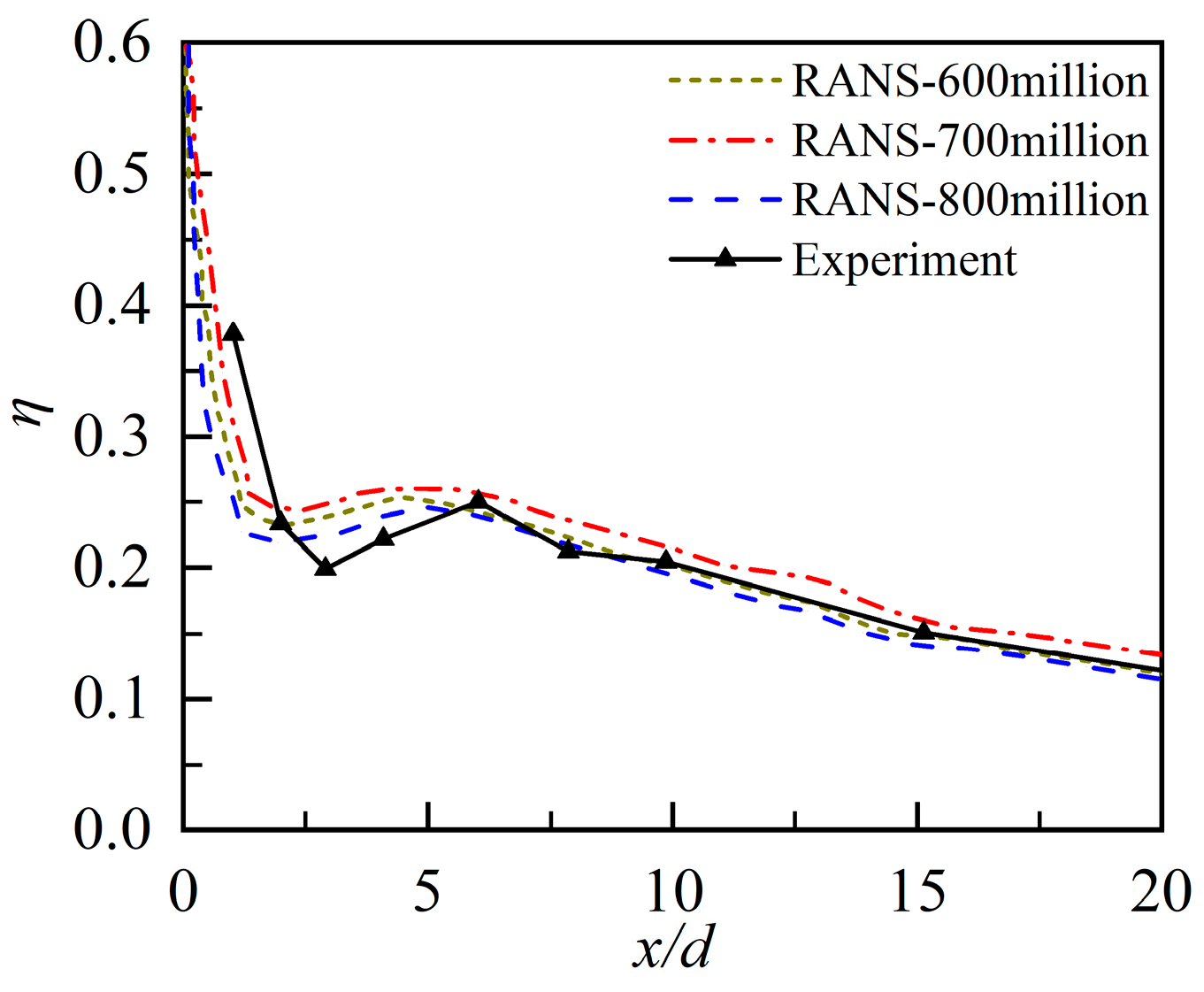
4. Model Validation
5. Results and Discussion
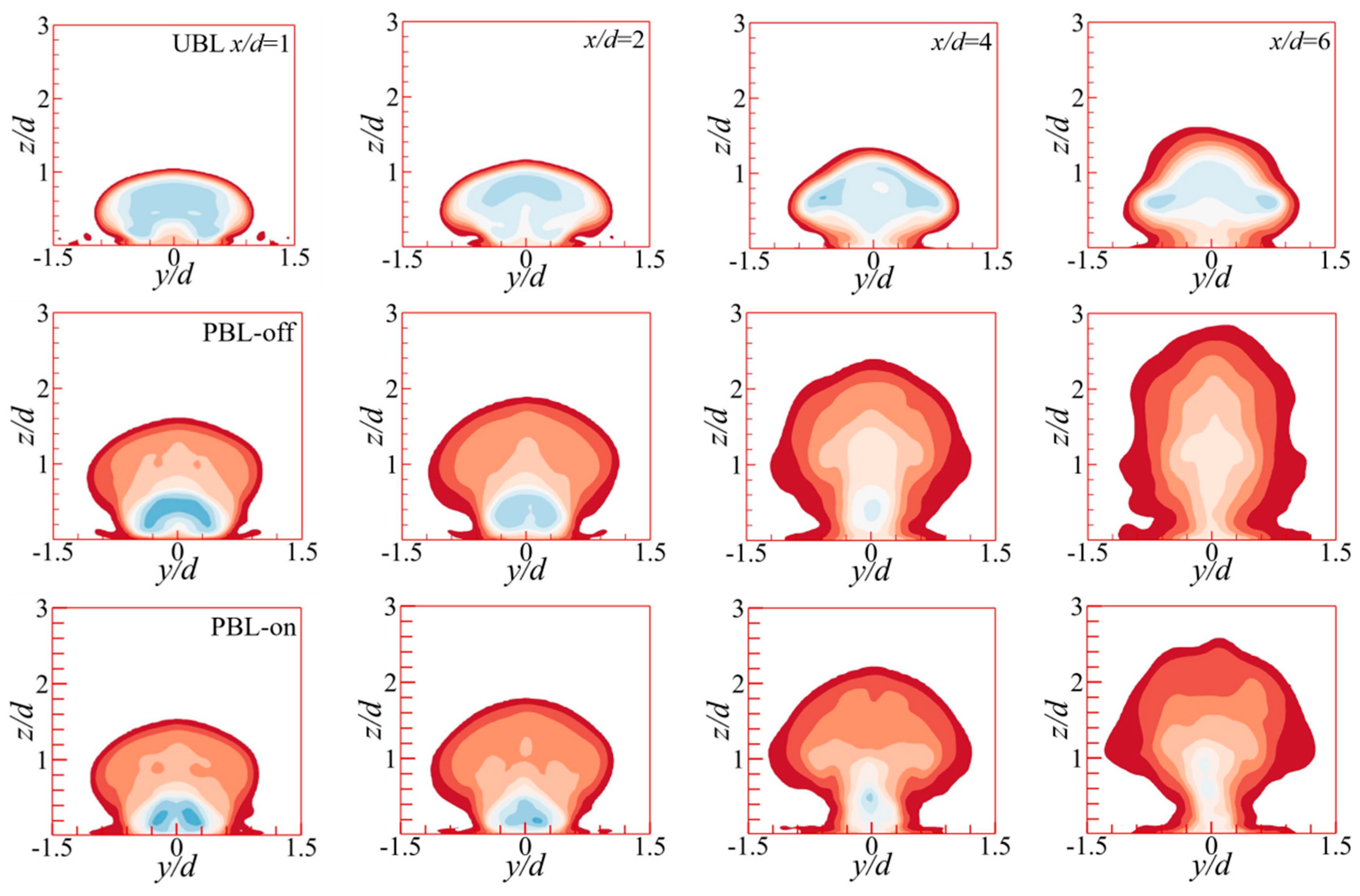
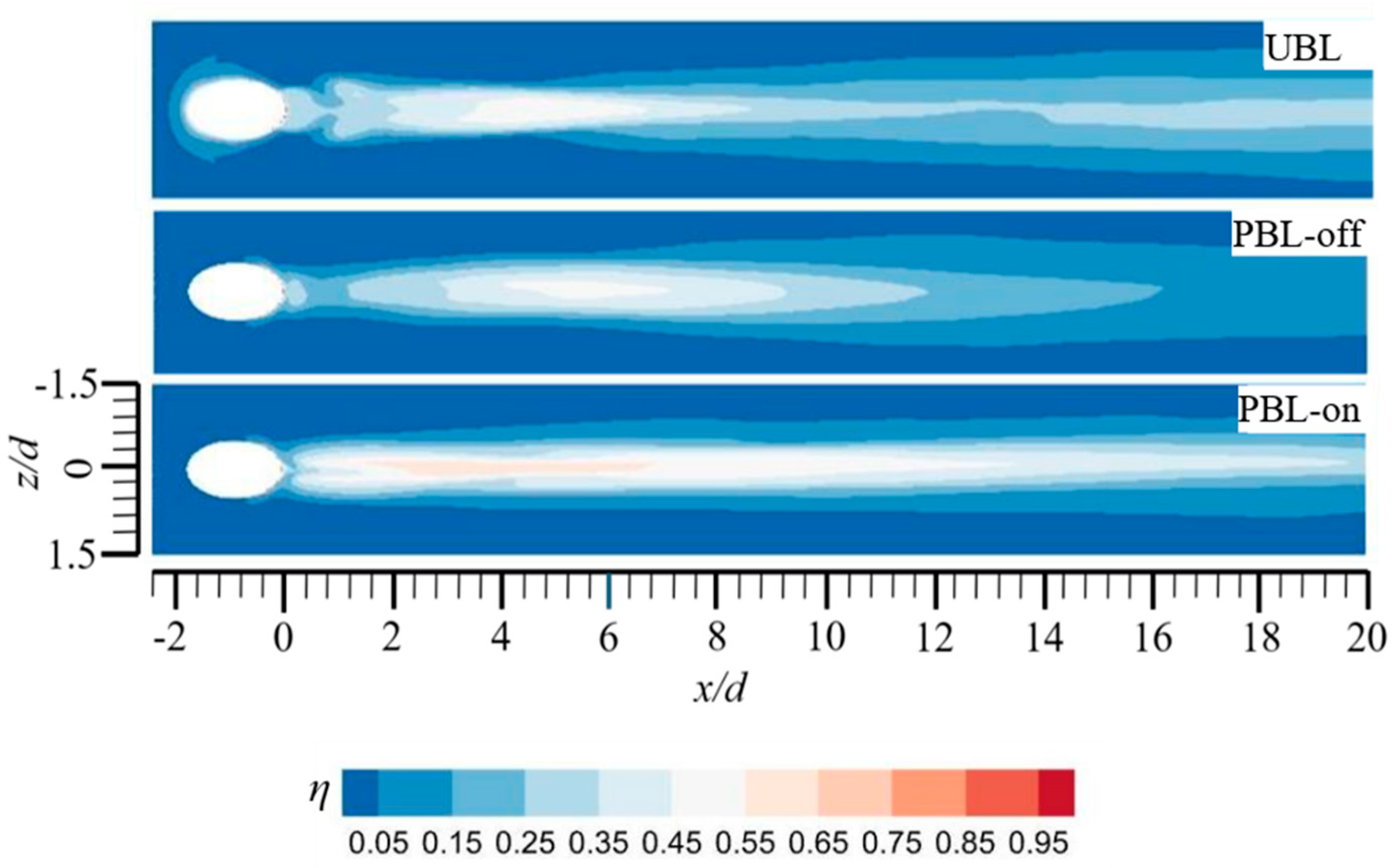
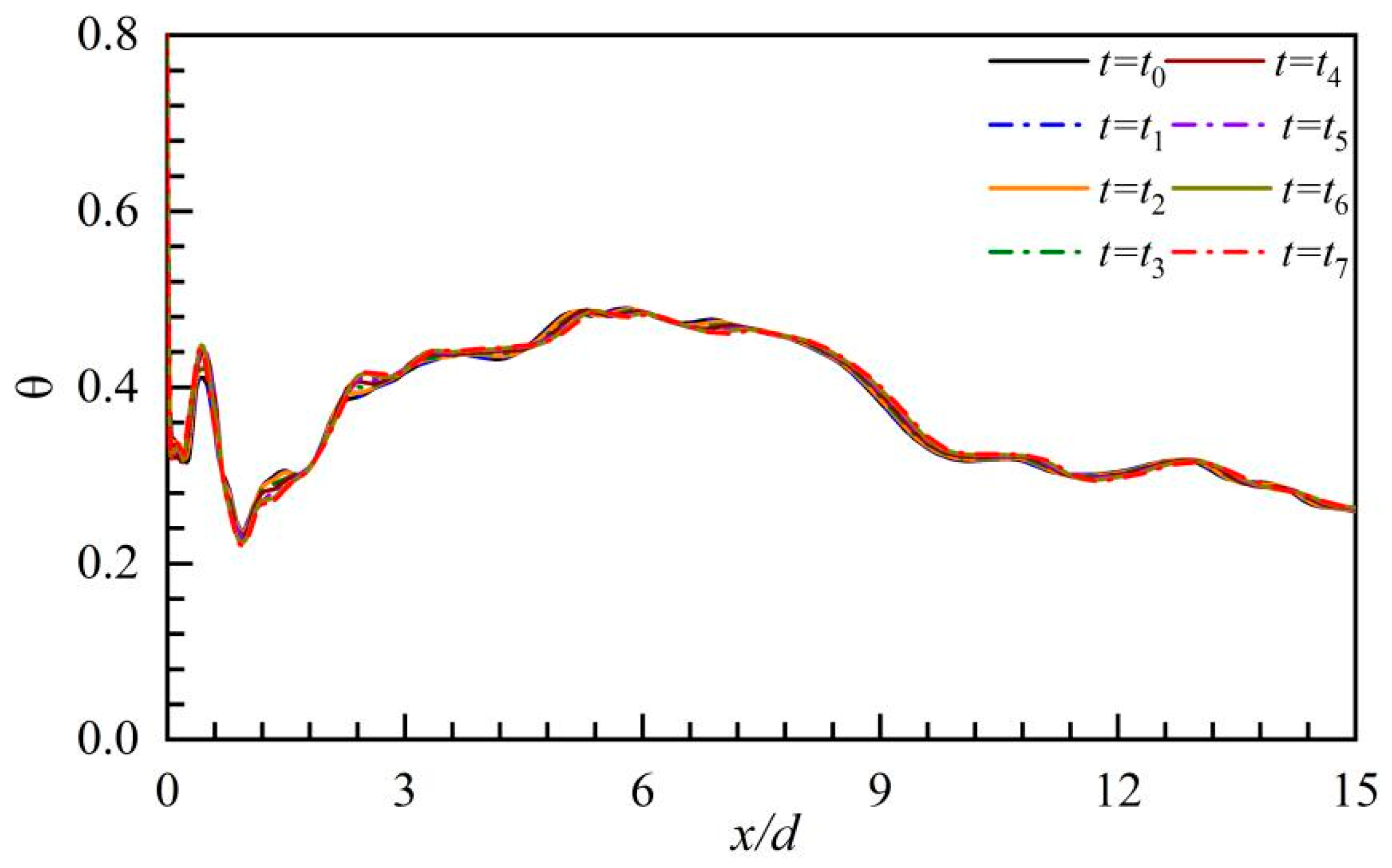
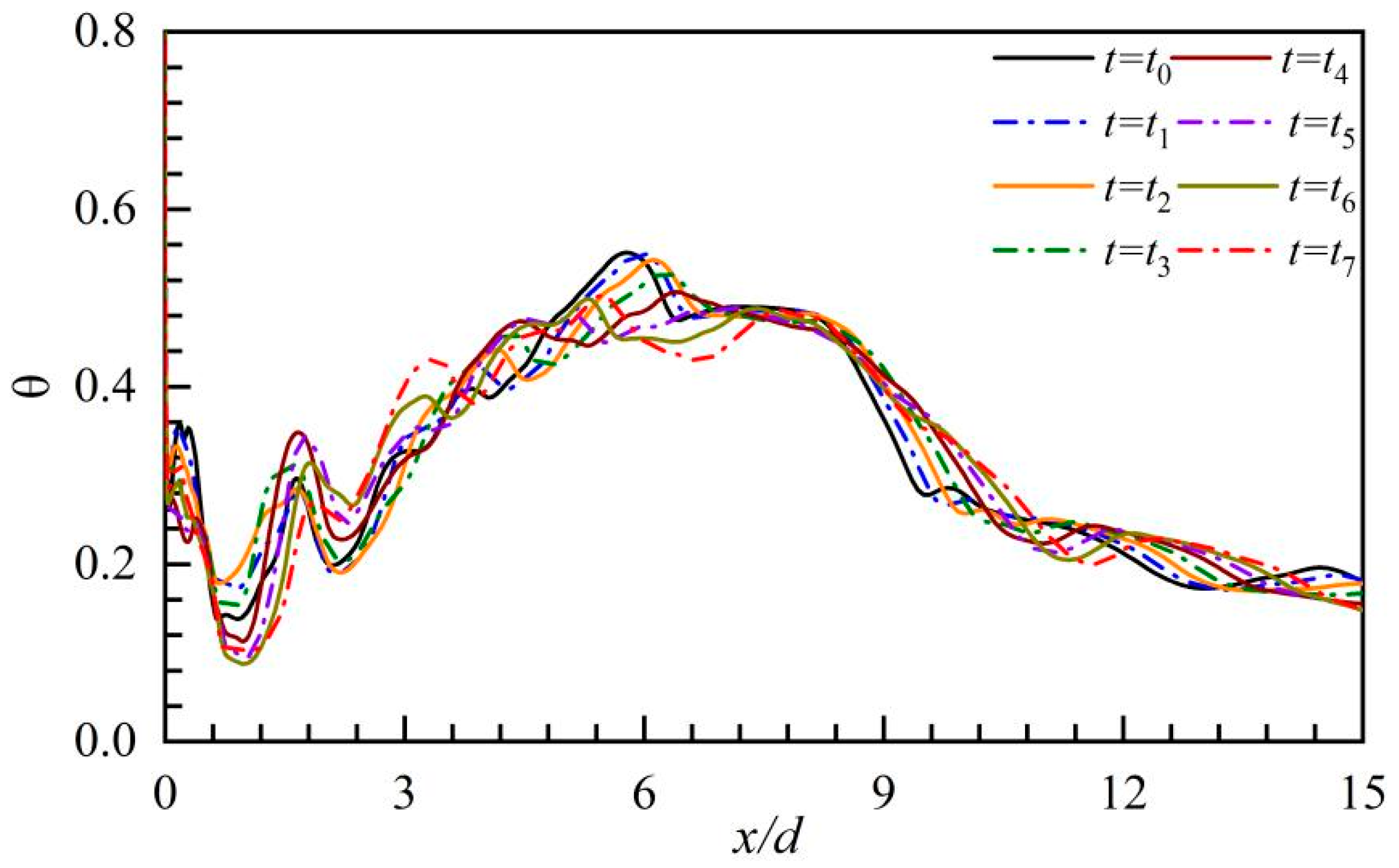
5.1. Time-Averaged Flow Fields
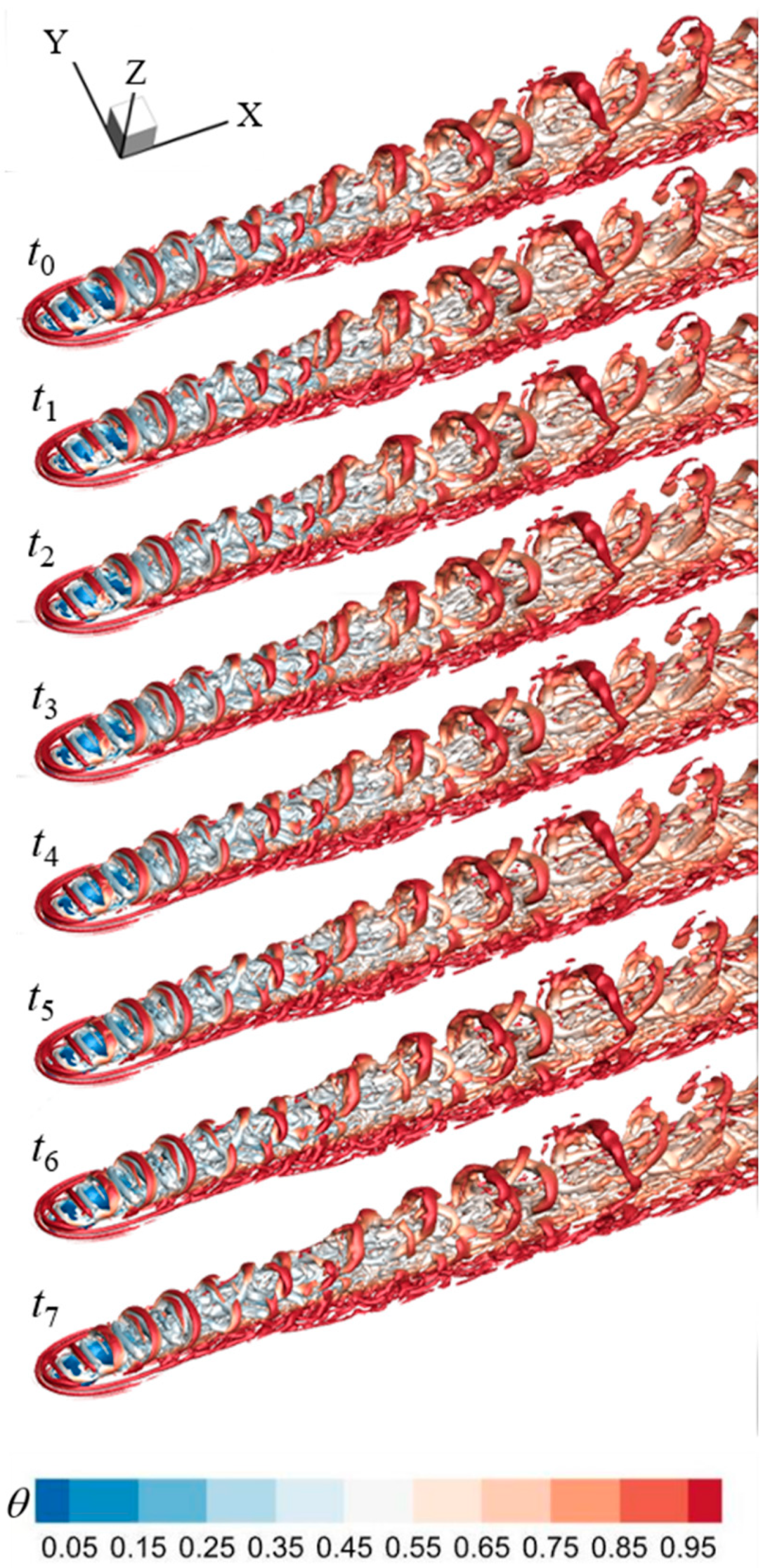
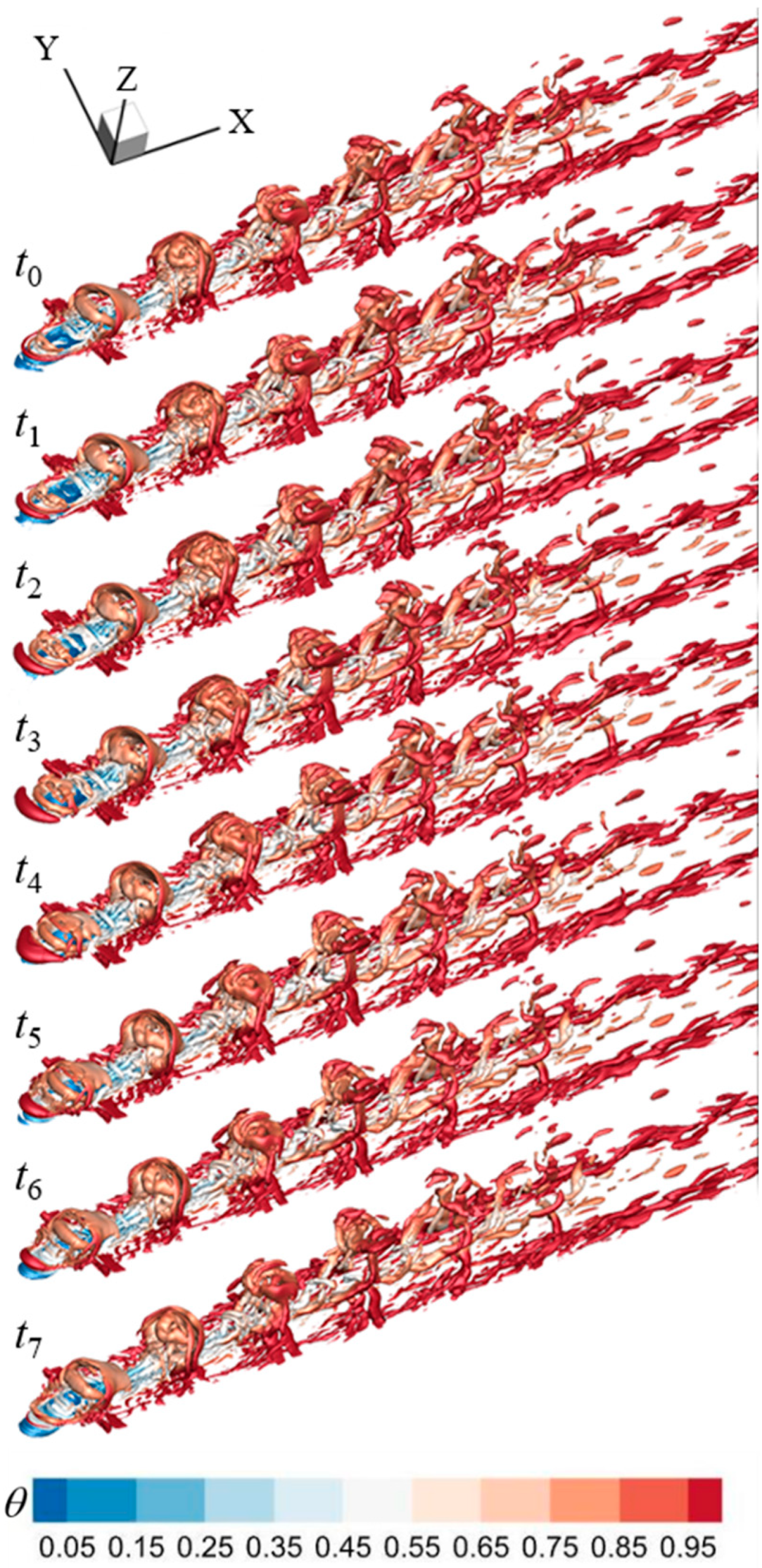
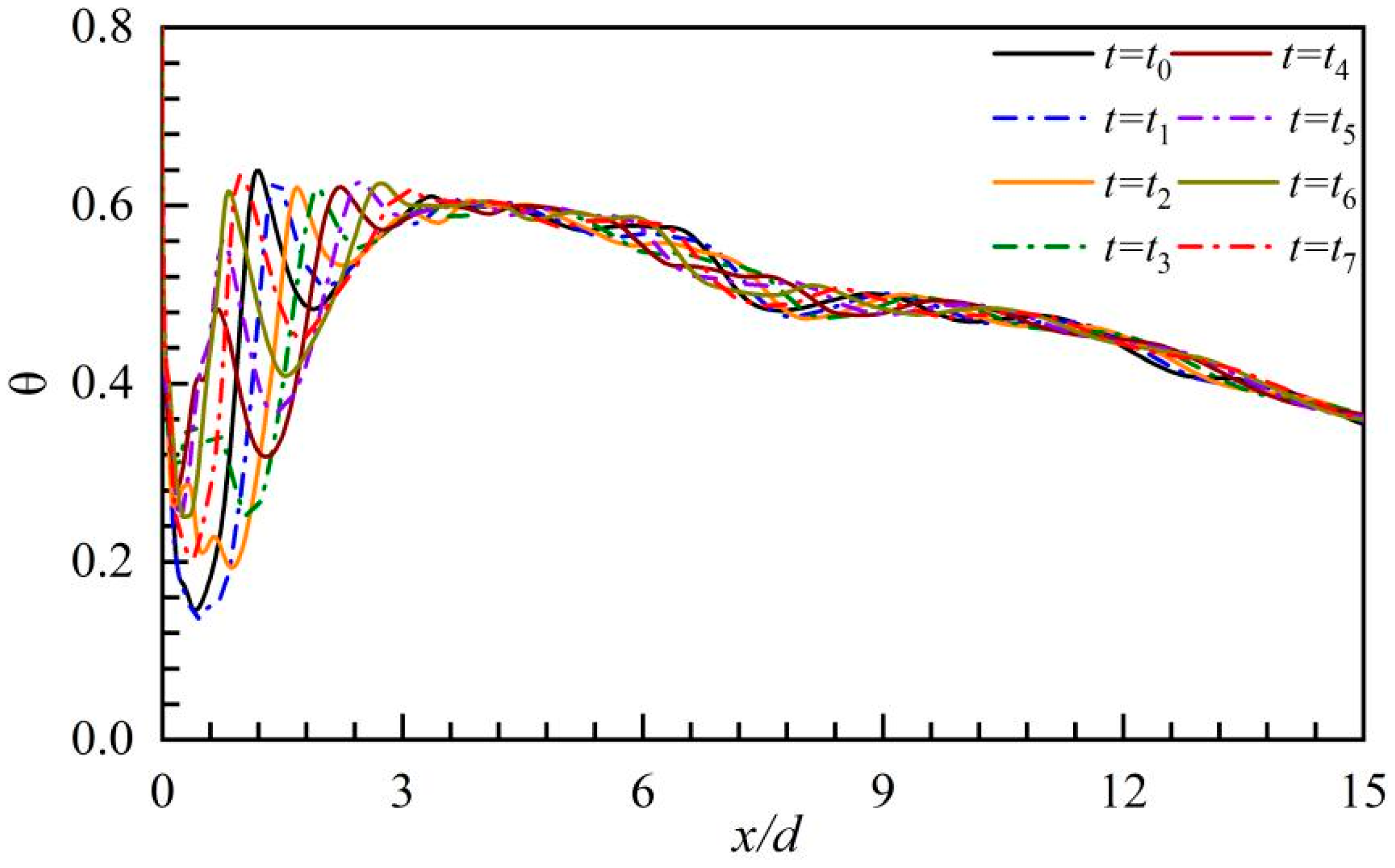
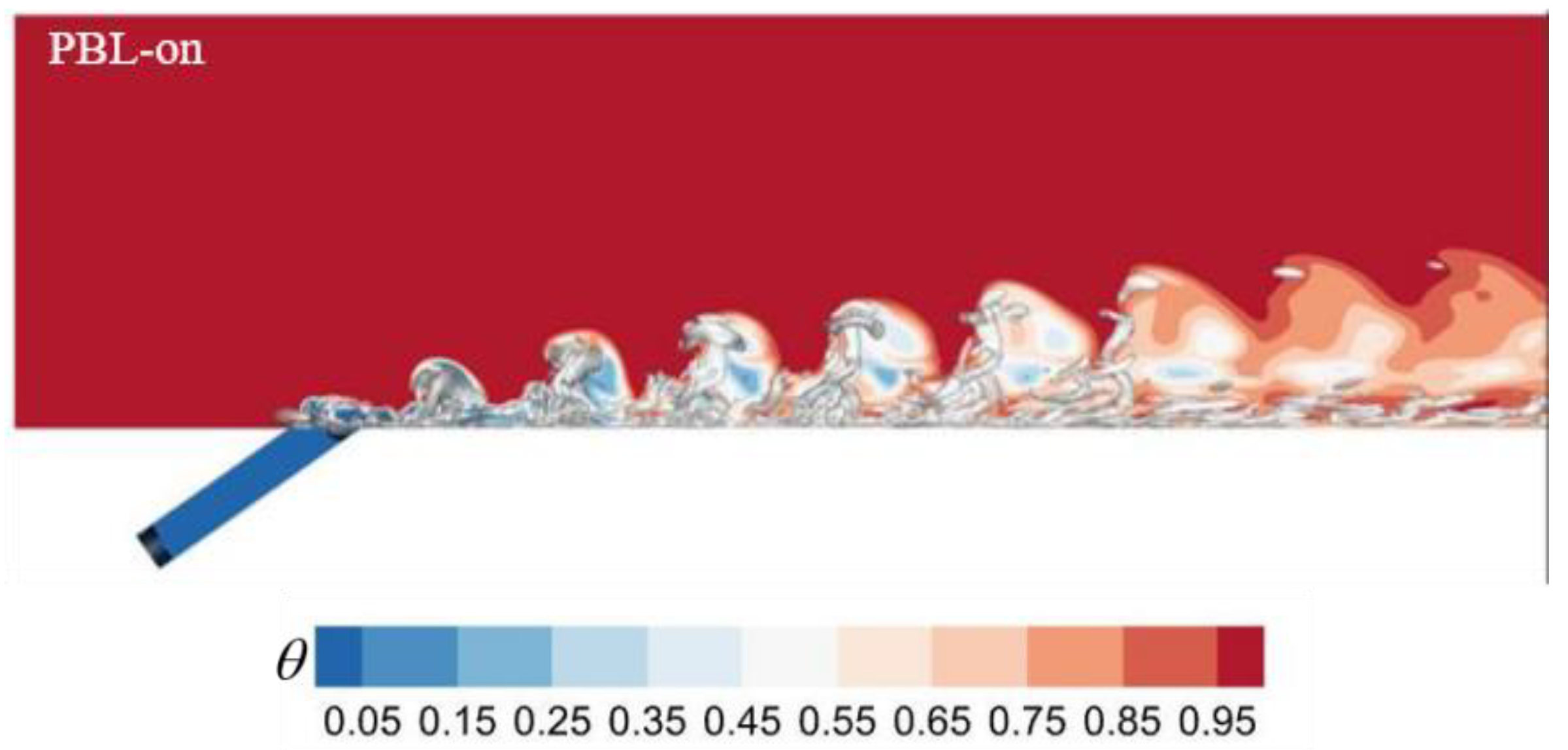
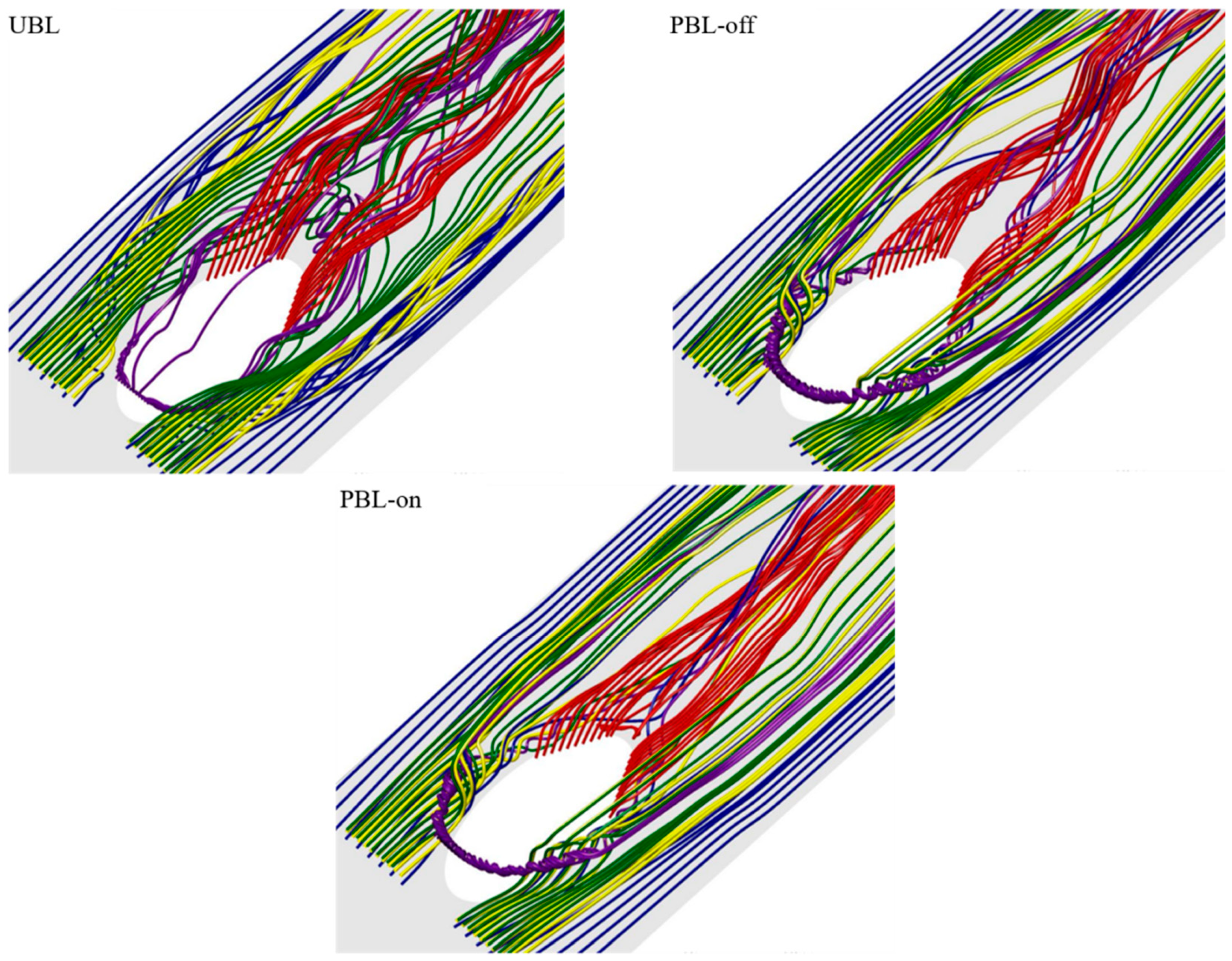
5.2. Instantaneous Flow Fields
6. Conclusions
- (1)
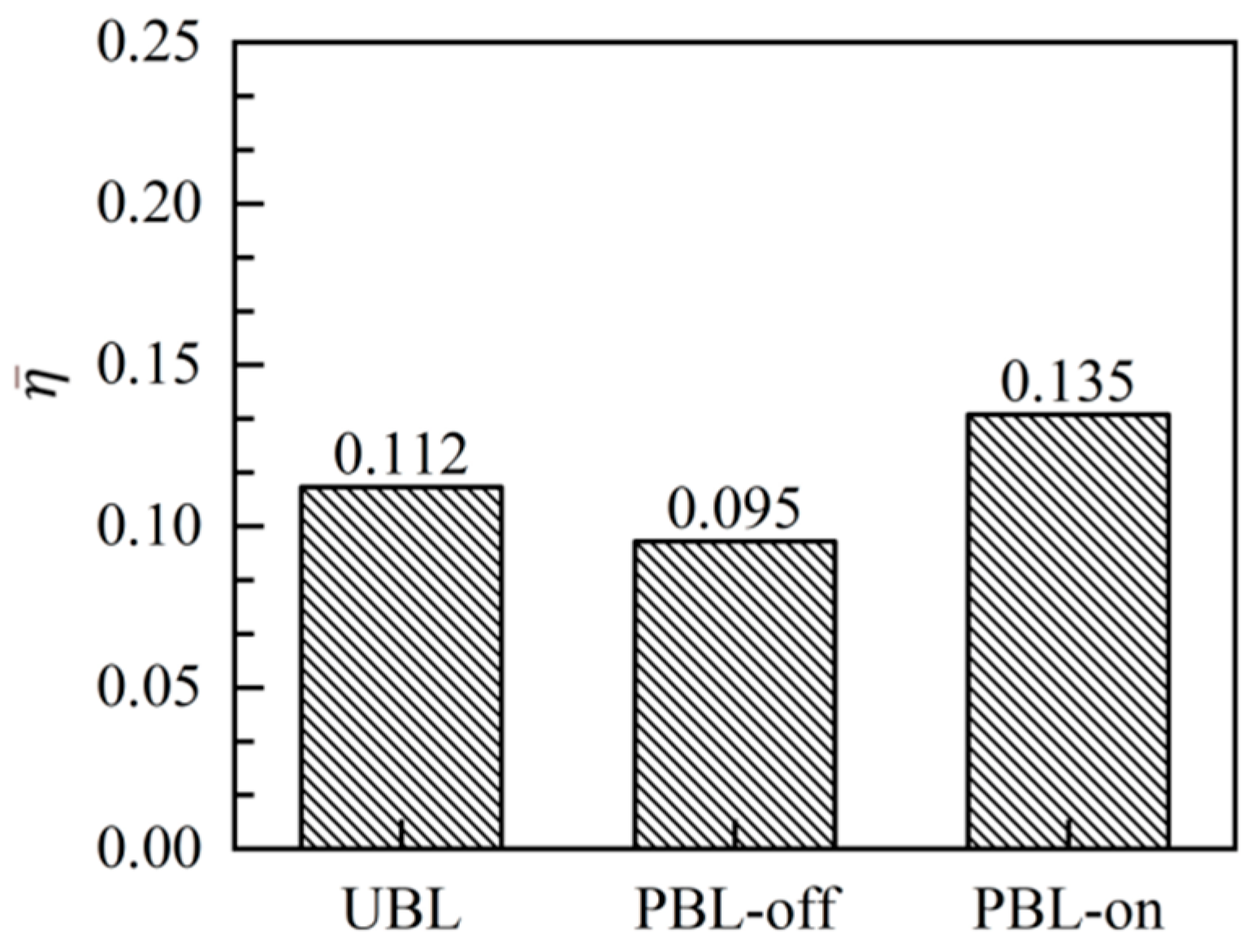
- The coolant pulsation might cause a slight reduction in the film cooling efficiency as the averaged pulsation BR was 1.0, while the PAA could effectively improve the pulsed film cooling efficiency and it would be superior to steady-state film cooling;
- (2)
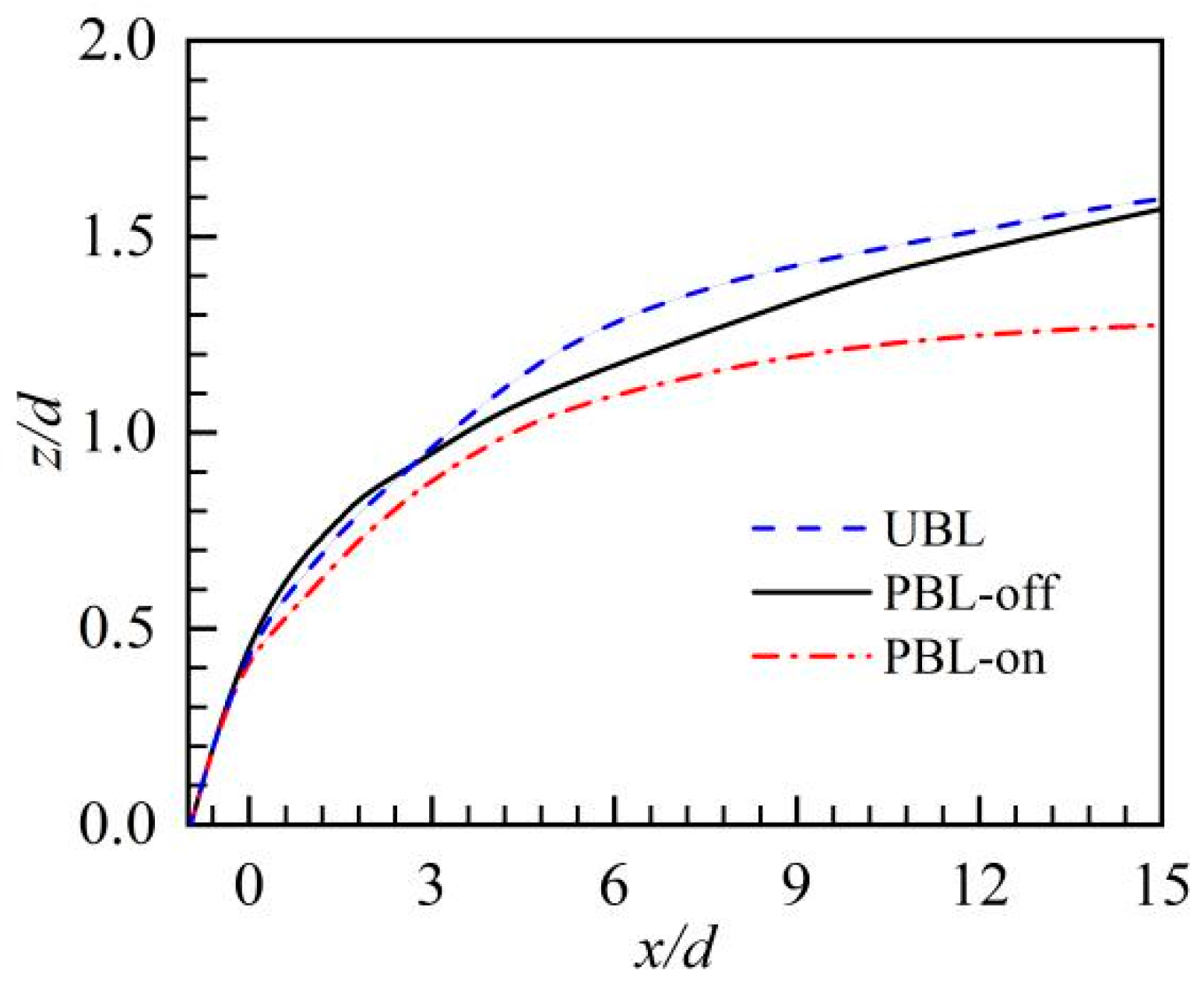
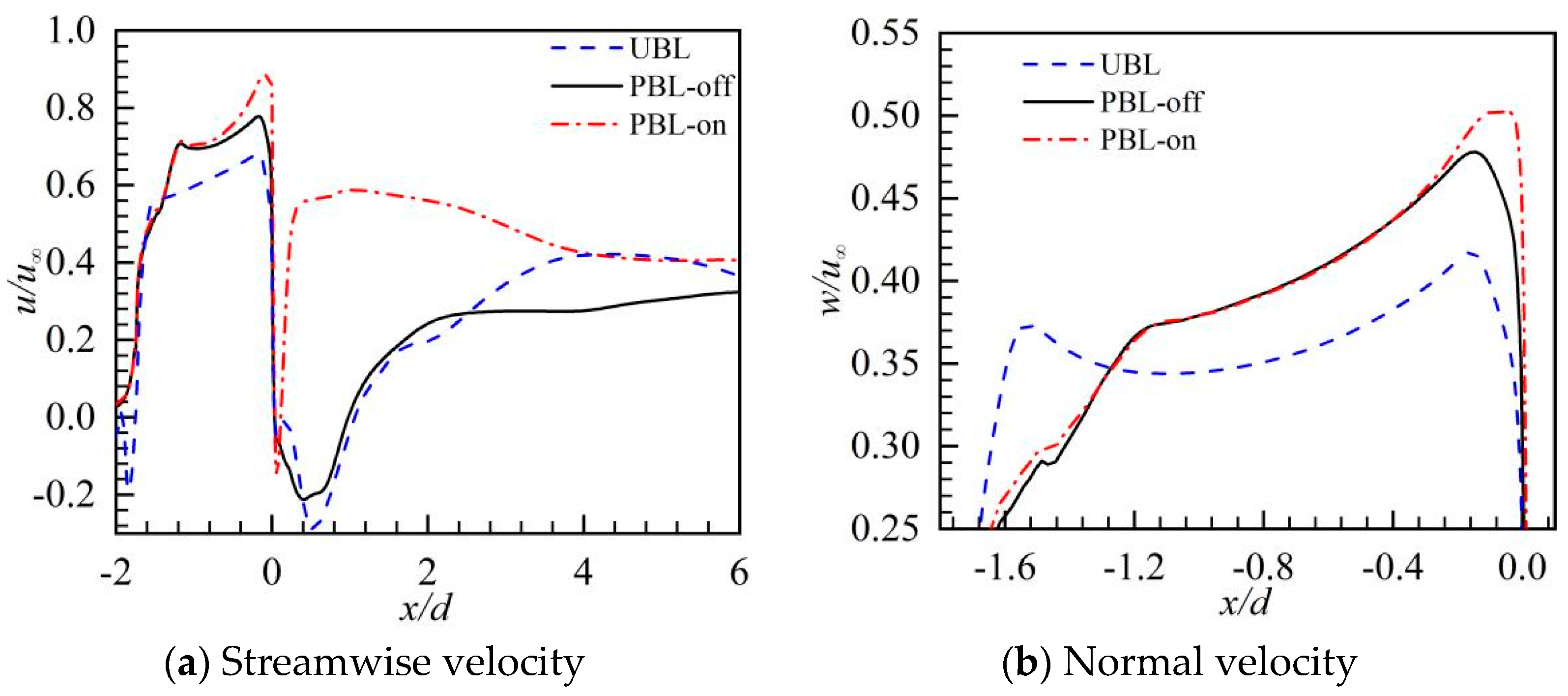
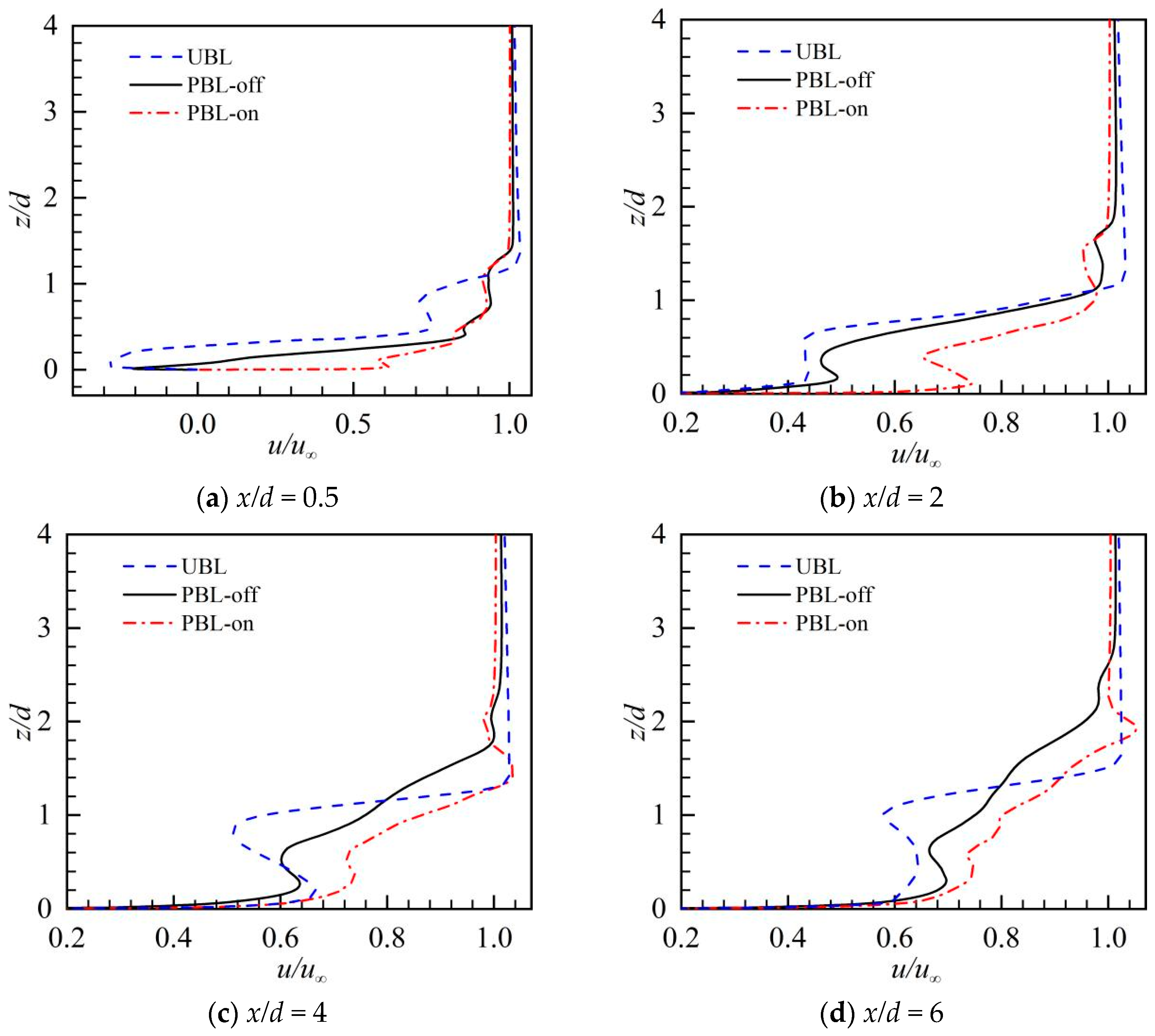
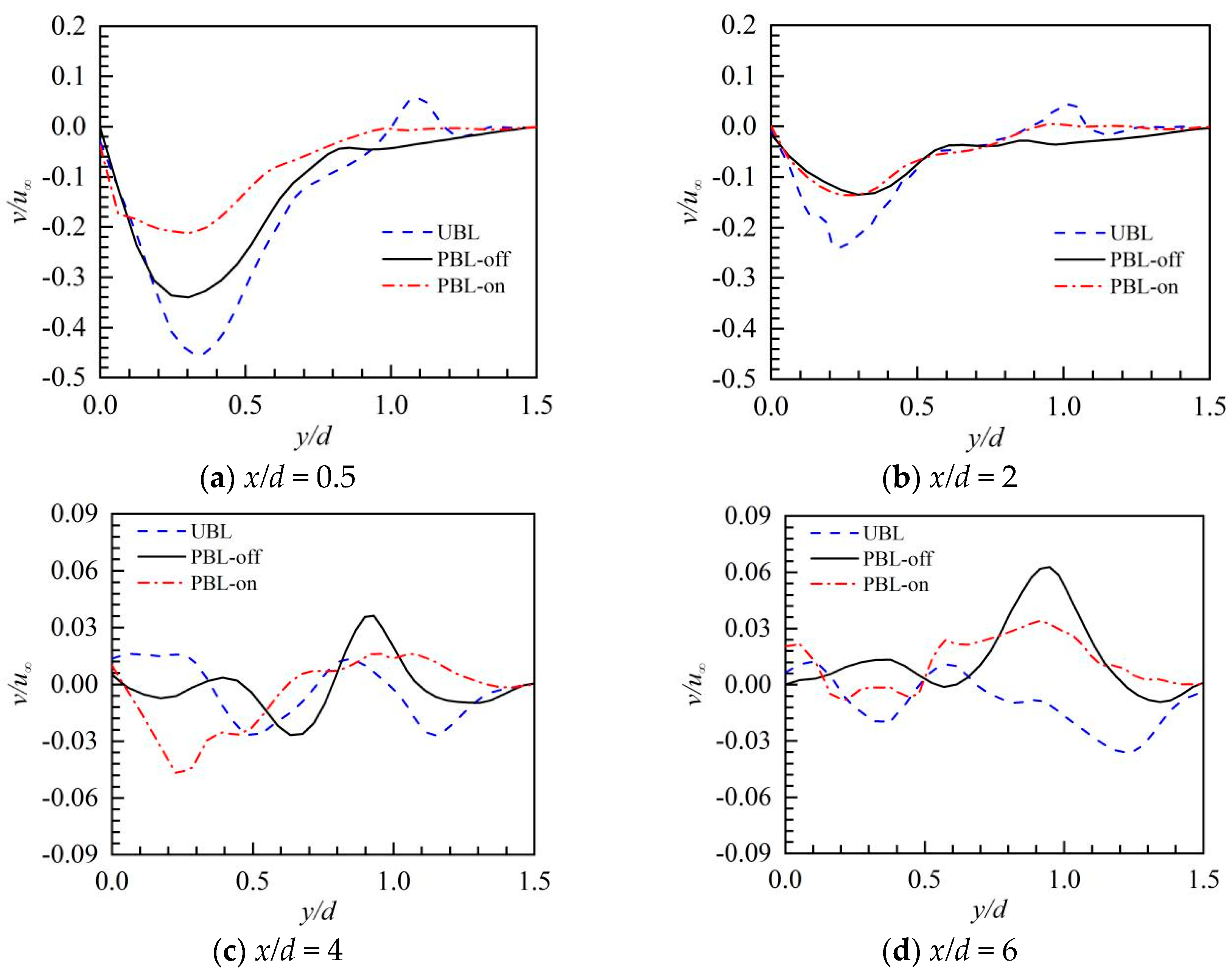
- The pulsed cooling jet can penetrate more deeply than steady-state film cooling in the near-hole region. Thus, the jet–crossflow interactions produced a large-scale CRVP, promoting the turbulent integration. Because of the downward force generated by the PAA, the penetration depth of the pulsed cooling jet was greatly reduced, which could be attributable to the downward force. The detrimental lift-off effect and entrainment of the CRVP were weakened.
- (3)
- Rather than hairpin vortices, intermittent coherent structure groups formed in the pulsed film cooling, and these groups also had upcast behavior and moved away from the wall surface while evolving downstream, thereby aggravating the turbulent integration of the coolant with the crossflow. The coherent structure groups were reduced in size and strength owing to the PAA, and their upcast behavior was attenuated; thus, the turbulent integration was suppressed and the film cooling efficiency was enhanced.
- (4)
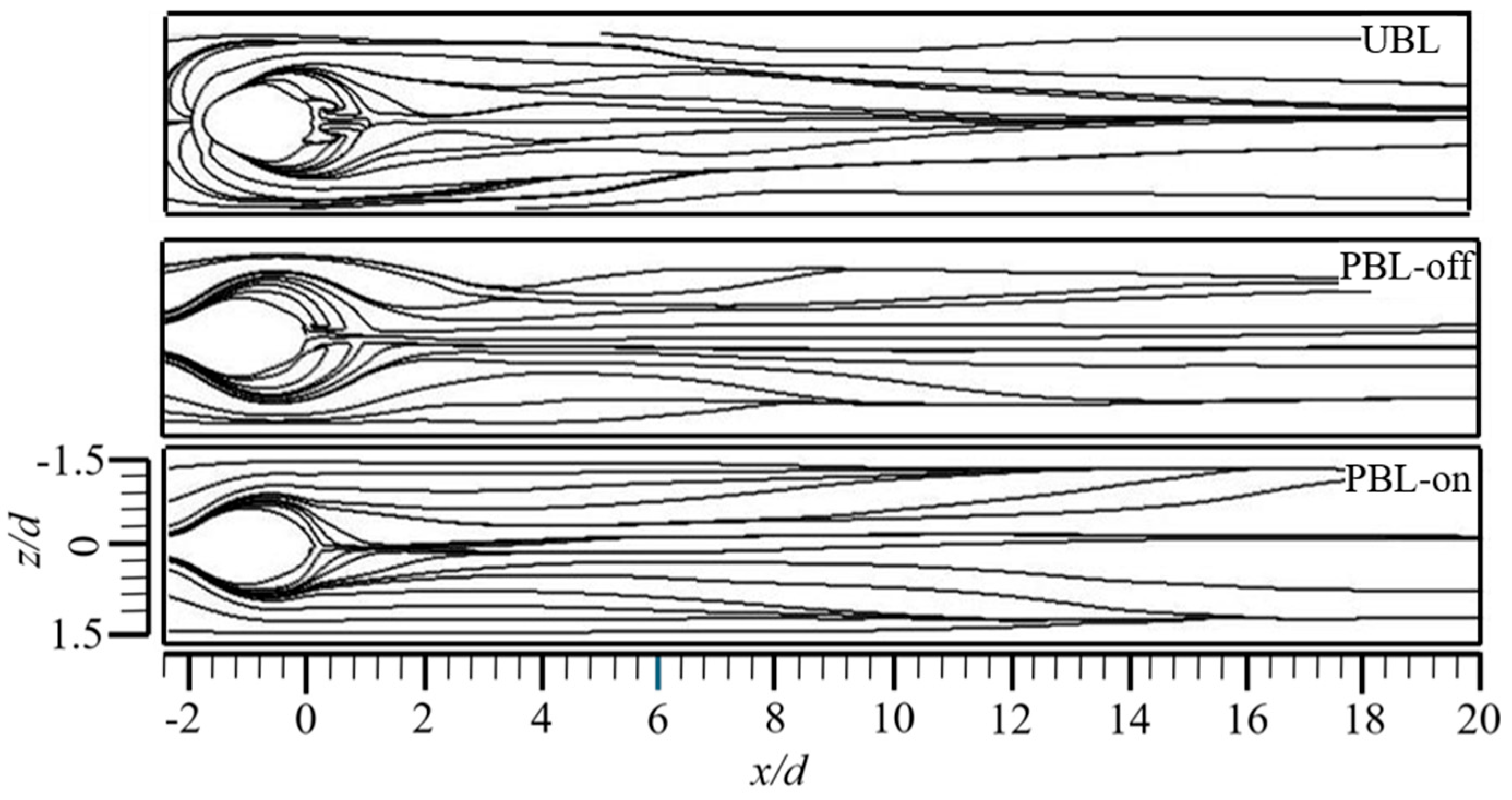
- The three-dimensional streamlines also confirmed that the PAA could effectively control the unsteady dynamic behavior of the LSCSs. The height of the three-dimensional streamlines was significantly reduced, indicating that the pulsed cooling jet flow was positioned close to the wall surface owing to the PAA.
- (5)
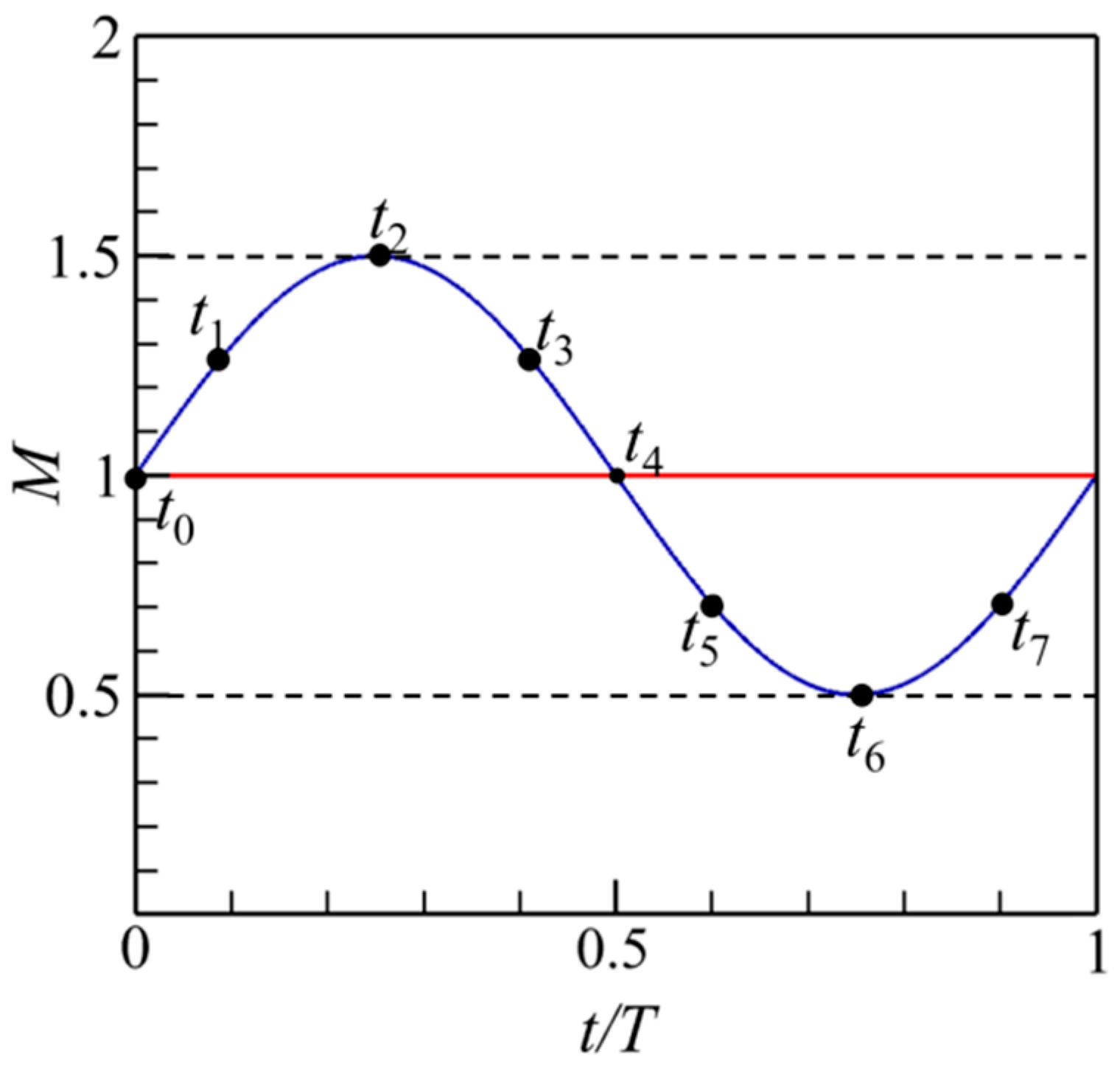
- Operating with an AC voltage of V(t) = Vmax × sin(2ft), where Vmax = 8 kV and f = 6 kHz, the PAA demonstrated compelling results. Importantly, the power supply characteristics (a high frequency of 6.0 kHz and a high voltage of 8.0 kVpp) translated into an estimated EHD force of about 2 MN/m3. Remarkably, the power consumption of the plasma actuator remained minimal, at approximately 0.75 watts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| E | electric field intensity (V/m) | Greek symbols | |
| Eb | breakdown electric field intensity (V/m) | ρ | gas density (kg/m3) |
| E0 | electric field intensity at the tip (V/m) | λ | wavelength of plasma actuator (m) |
| Es | electric field intensity at serrated edge (V/m) | α | intersection angle of actuator (°) |
| V0 | peak AC voltage (V) | β | angle of plasma force at the tip (°) |
| l | space between the two electrodes (m) | η | film cooling efficiency (-) |
| la | distance from the root (m) | ζ | collision efficiency (-) |
| f | pulsation frequency (Hz) | δ | thickness of boundary layer (m) |
| e | elementary charge (C) | ν | kinematic viscosity (m2/s) |
| ∆t | space of time (s) | νsgs | eddy viscosity (m2/s) |
| a | height of plasma region (m) | ϑ | applied voltage frequency (Hz) |
| b | length of plasma region (m) | Subscripts | |
| k | constants in plasma model (-) | aw | adiabatic wall |
| d | diameter of film-cooling hole (m) | ∞ | crossflow |
| x, y, z | cartesian coordinates (m) | c | jet flow |
| u, v, w | velocity component index (m/s) | lat | lateral-averaged cooling efficiency |
| T | local fluid temperature (K) | p | plasma actuation in a cycle |
| t | time (s) | ||
| k1, k2 | constants in plasma model (-) | ||
References
- Goldstein, R.J.; Eckert, E.R.G.; Burggraf, F. Effects of hole geometry and density on three-dimensional film cooling. Int. J. Heat. Mass Transf. 1974, 17, 595–607. [Google Scholar] [CrossRef]
- Bunker, R.S. A review of shaped hole turbine film-cooling technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Saumweber, C.; Schulz, A. Effect of geometry variations on the cooling performance of fan-shaped cooling holes. J. Turbomach. 2012, 134, 061008. [Google Scholar] [CrossRef]
- Kusterer, K.; Bohn, D.; Sugimoto, T.; Tanaka, R. Double-jet ejection of cooling air for impr-oved film-cooling. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar] [CrossRef]
- Shinn, A.F.; Vanka, S.P. Large eddy simulations of film-cooling flows with a micro-ramp vortex generator. J. Turbomach. 2013, 135, 011004. [Google Scholar] [CrossRef]
- Liu, C.L.; Ye, L.; Zhang, F.; Huang, R.; Li, B. Film cooling performance evaluation of the furcate hole with cross-flow coolant injection: A comparative study. Int. J. Heat Mass Transf. 2021, 164, 120457. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Ou, S.; Rivir, R.B. Effect of jet pulsation and duty cycle on film cooling from a single jet on a leading edge model. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. ASME Paper No. IMECE 2004-60466. [Google Scholar] [CrossRef]
- Coulthard, S.M.; Volino, R.J.; Flack, K.A. Effect of jet pulsing on film cooling—Part I: Effectiveness and flow-field temperature results. J. Turbomach. 2007, 129, 232–246. [Google Scholar] [CrossRef]
- Muldoon, F.; Acharya, S. DNS study of pulsed film cooling for enhanced cooling effecti- veness. Int. J. Heat Mass Transf. 2009, 52, 3118–3127. [Google Scholar] [CrossRef]
- Rutledge, J.L.; King, P.I.; Rivir, R.B. Influence of film cooling unsteadiness on turbine blade leading edge heat flux. J. Eng. Gas Turbines Power. 2012, 134, 071901. [Google Scholar] [CrossRef]
- Wang, Y.A.; Li, L.B.; Zhang, J.Z. Study on the interaction between coolant pulsation and recir- culation vortexes by large-eddy simulation. Aerosp. Sci. Technol. 2022, 130, 107951. [Google Scholar] [CrossRef]
- Babaee, H.; Acharya, S.; Wan, X. Optimization of forcing parameters of film cooling effecti- veness. J. Turbomach. 2014, 136, 061016. [Google Scholar] [CrossRef]
- Adamovich, I.; Baalrud, S.; Bogaerts, A.; Bruggeman, P.; Cappelli, M.; Colombo, V.; Czarnetzki, U.; Ebert, U.; Eden, J.; Favia, P. The 2017 Plasma Roadmap: Low temperature plasma science and technology. J. Phys. D Appl. Phys. 2017, 50, 323001. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. Single dielectric barrier discharge plasma enhanced aerodynamics: Physics, modeling and applications. Exp. Fluids 2009, 46, 1–26. [Google Scholar] [CrossRef]
- Benmoussa, A.; Rodrigues, F.F.; Páscoa, J.C. Plasma Actuators for Cycloidal Rotor Thrust Vectoring Enhancement in Airships. Actuators 2023, 12, 436. [Google Scholar]
- Benmoussa, A.; Pascoa, J.C. Performance improvement and start-up characteristics of a cyclorotor using multiple plasma actuators. Meccanica 2021, 56, 2707–2730. [Google Scholar] [CrossRef]
- Daraee, M.A.; Abbasi, S. A novel approach to performance improvement of a VAWT usingplasma actuators. J. Clean. Prod. 2023, 424, 138876. [Google Scholar] [CrossRef]
- Yang, P.Y.; Zhang, X.; Pan, C. The spatial-temporal evolution process of flow field generated by a pulsed-DC plasma actuator in quiescent air. Aerosp. Sci. Technol. 2021, 118, 107071. [Google Scholar] [CrossRef]
- Roya, S.; Wang, C.C. Plasma actuated heat transfer. Appl. Phys. Lett. 2008, 92, 231501. [Google Scholar] [CrossRef]
- Singh, K.P.; Roy, S. Modeling Plasma Actuators with Air Chemistry for Effective Flow Control. J. Appl. Phys. 2007, 101, 1233308. [Google Scholar] [CrossRef]
- Pescini, E.; Martínez, D.S.; De Giorgi, M.G.; Ficarella, A. Optimization of microsingle dielectric barrier discharge plasma actuator models based on experimental velocity and body force fields. Acta Astronaut. 2015, 116, 318–332. [Google Scholar] [CrossRef]
- Roya, S.; Wang, C.C. Numerical Investigation of three-dimensional plasma actuation for improving film cooling effectiveness. J. Thermophys. Heat Transf. 2013, 27, 489–497. [Google Scholar] [CrossRef]
- Yu, J.L.; He, L.M.; Zhu, Y.F.; Ding, W.; Wang, Y.Q. Numerical simulation of the effect of plasma aerodynamic actuation on improving film hole cooling performance. Heat Mass Transf. 2013, 49, 897–906. [Google Scholar] [CrossRef]
- Dai, S.J.; Xiao, Y.; He, L.M.; Jin, T.; Zhang, Q.; Hou, P.H.; Zhao, Z.C. Film-cooling of cylindrical hole with downstream surface dielectric barrier discharge actuators. Int. J. Heat Mass Transf. 2015, 90, 825–837. [Google Scholar] [CrossRef]
- Xiao, Y.; Dai, S.J.; He, L.M.; Jin, T.; Zhang, Q.; Hou, P.H. Investigation of film cooling from cylindrical hole with plasma actuator on flat plate. Heat Mass Transf. 2016, 52, 1571–1583. [Google Scholar] [CrossRef]
- Dolati, S.; Amanifard, N.; Deylami, H.M. Numerical study and GMDH-type neural networks modeling of plasma actuator effects on the film cooling over a flat plate. Appl. Therm. Eng. 2017, 123, 734–745. [Google Scholar] [CrossRef]
- Audier, P.; Fénot, M.; Bénard, N.; Moreau, E. Film cooling effectiveness enhancement using surface dielectric barrier discharge plasma actuator. Int. J. Heat Fluid. Flow. 2016, 62, 247–257. [Google Scholar] [CrossRef]
- Li, G.Z.; Zhang, H.J.; Yan, W.W. Control of the coherent structure dynamics of a film cooling flow by plasma aerodynamic actuation. Int. J. Heat Mass Transf. 2019, 137, 434–445. [Google Scholar] [CrossRef]
- Li, G.Z.; Wang, Q.Q.; Huang, Y.J.; Zhang, H.J. Large eddy simulation of film cooling effectiveness on a turbine vane pressure side with a saw-tooth plasma actuator. Aerosp. Sci. Technol. 2021, 112, 106615. [Google Scholar] [CrossRef]
- Jukes, T.N.; Choi, K.S.; Johnson, G.A.; Scott, S.J. Turbulent Drag Reduction by Surface Plasma through Spanwise Flow Oscillation. In Proceedings of the 3rd AIAA Flow Control Conference, Barcelona, Spain, 8–11 May 2006. AIAA 2006-3693. [Google Scholar]
- Dai, S.J.; Xiao, Y.; He, L.M.; Jin, T.; Zhang, Q.; Hou, P.H.; Zhao, Z.C. An Experimental Study of Plasma Aerodynamic Actuation on a Round Jet in Cross Flow. AIP Adv. 2015, 5, 037143-10. [Google Scholar] [CrossRef]
- Sinha, A.K.; Bogard, D.G.; Crawford, M.E. Film-cooling effectiveness downstream of a single row of holes with variable density ratio. J. Turbomach. 1991, 113, 442–449. [Google Scholar] [CrossRef]
- Kohli, A.; Bogard, D.G. Adiabatic effectiveness, thermal fields, and velocity fields for film cooling with large angle injection. J. Turbomach. 1997, 119, 352–358. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid. Flow. 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Electrohydrodynamic flow control with a glow-discharge surface plasma. AIAA J. 2000, 38, 1166–1172. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L. Overview of plasma flow control: Concepts, optimization, and applications. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. Paper No. 2005-0563. [Google Scholar] [CrossRef]
- Shyy, W.; Jayaraman, B.; Andersson, A. Modeling of glow discharge-induced fluid dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- Zhang, P.F.; Liu, A.B.; Wang, J.Z. Flow structures in flat plate boundary layer induced by pulsed plasma actuator. Sci. China Tech. Sci. 2010, 53, 2772–2782. [Google Scholar] [CrossRef]
- Rizzetta, D.P.; Visbal, M.R. Large eddy simulation of plasma-based turbulent boundary layer separation control. AIAA J. 2010, 48, 2793–2810. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 1988. [Google Scholar]
- Wang, C.H.; Wang, J.Z.; Feng, H.K.; Huang, Y. Large eddy simulation of film cooling flowfrom a fanshaped hole. Appl. Therm. Eng. 2018, 129, 855–870. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Hu, B.; Li, G.; Zhang, H. Large Eddy Simulation of Pulsed Film Cooling with a Dielectric Barrier Discharge Plasma Actuator. Aerospace 2024, 11, 28. https://doi.org/10.3390/aerospace11010028
Shen Z, Hu B, Li G, Zhang H. Large Eddy Simulation of Pulsed Film Cooling with a Dielectric Barrier Discharge Plasma Actuator. Aerospace. 2024; 11(1):28. https://doi.org/10.3390/aerospace11010028
Chicago/Turabian StyleShen, Zhou, Beimeng Hu, Guozhan Li, and Hongjun Zhang. 2024. "Large Eddy Simulation of Pulsed Film Cooling with a Dielectric Barrier Discharge Plasma Actuator" Aerospace 11, no. 1: 28. https://doi.org/10.3390/aerospace11010028
APA StyleShen, Z., Hu, B., Li, G., & Zhang, H. (2024). Large Eddy Simulation of Pulsed Film Cooling with a Dielectric Barrier Discharge Plasma Actuator. Aerospace, 11(1), 28. https://doi.org/10.3390/aerospace11010028