Model-Reference Reinforcement Learning for Safe Aerial Recovery of Unmanned Aerial Vehicles
Abstract
1. Introduction
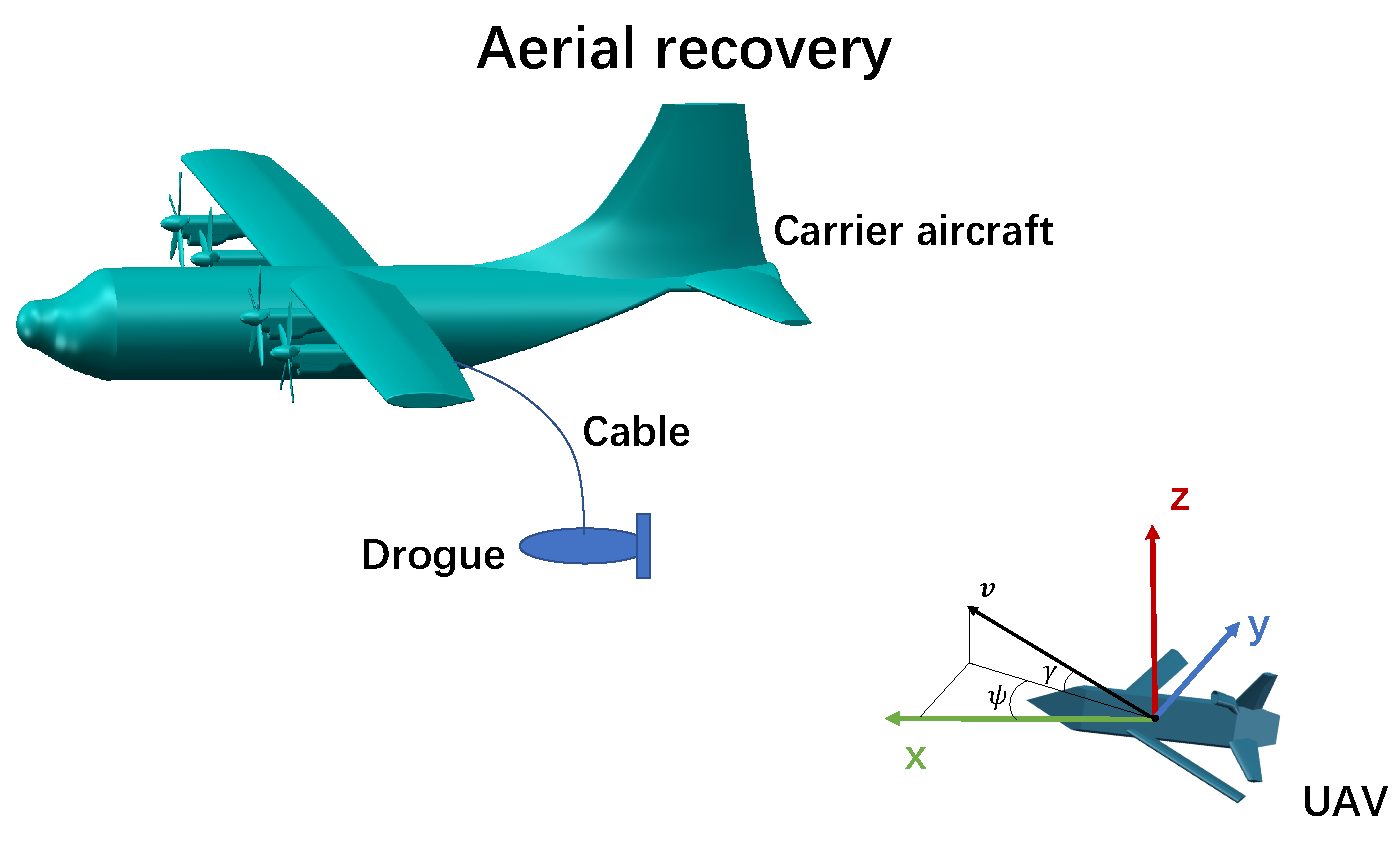
2. Problem Formulation
2.1. Dynamic Model for The UAV
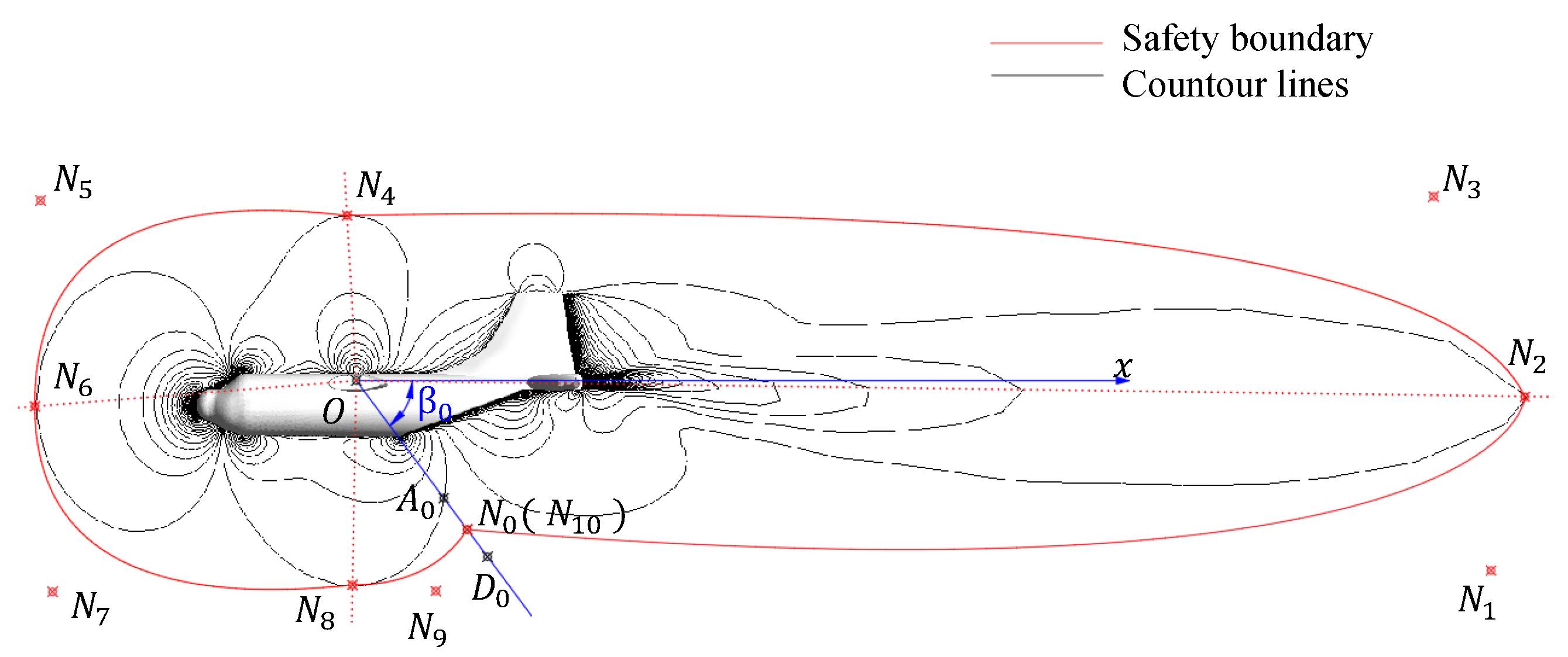
2.2. Hazard Area Concept
3. Establishment of Safety Constraint Model
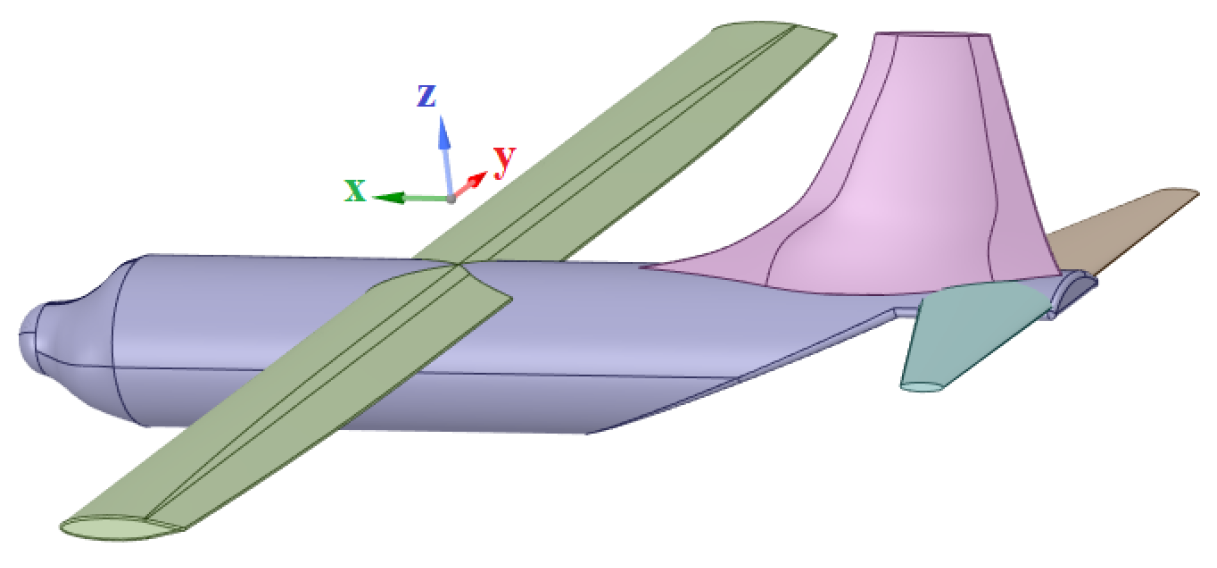
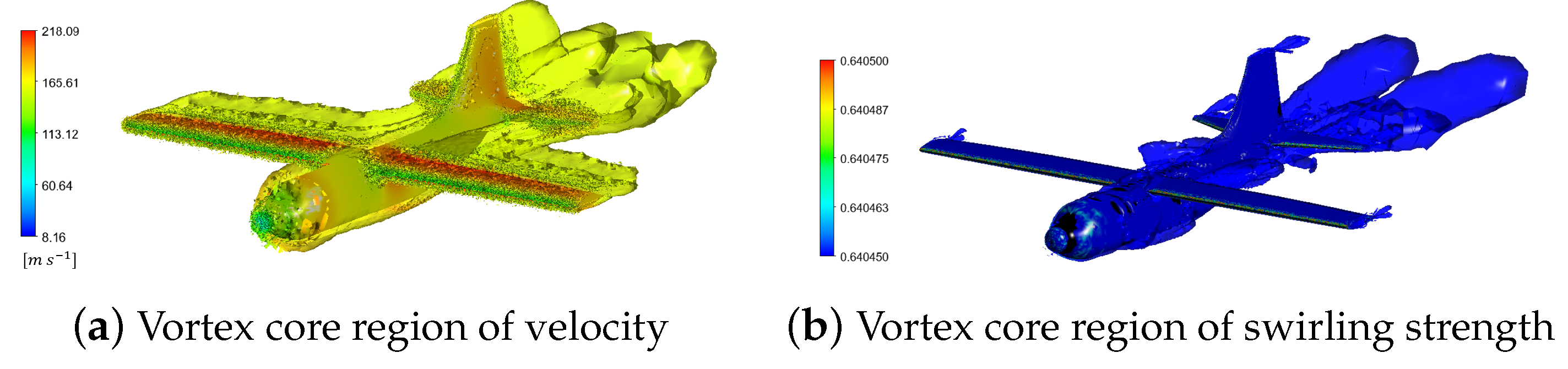
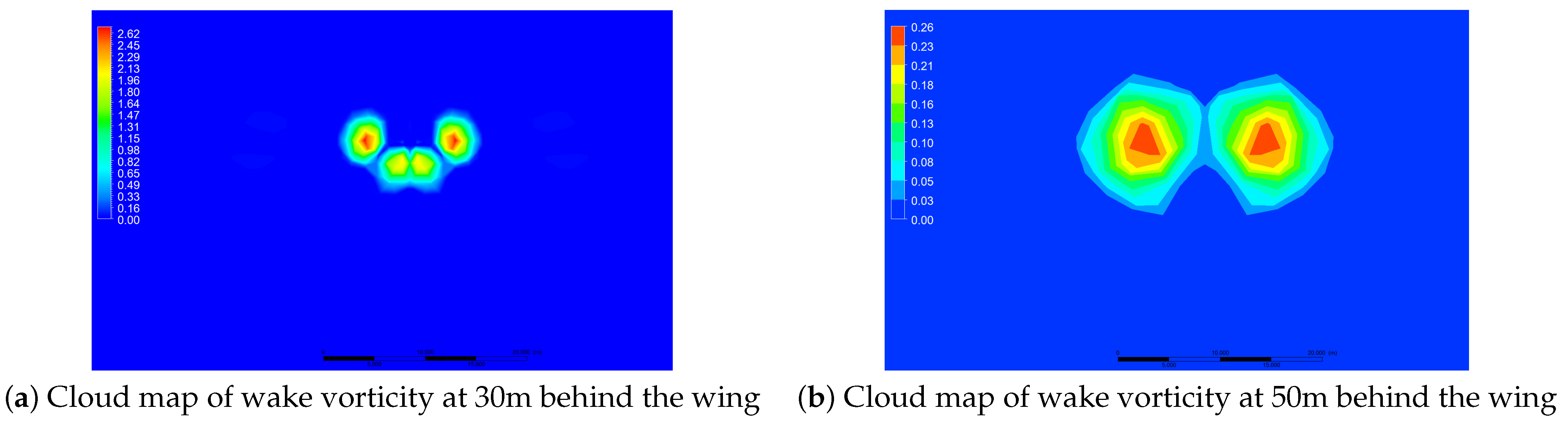
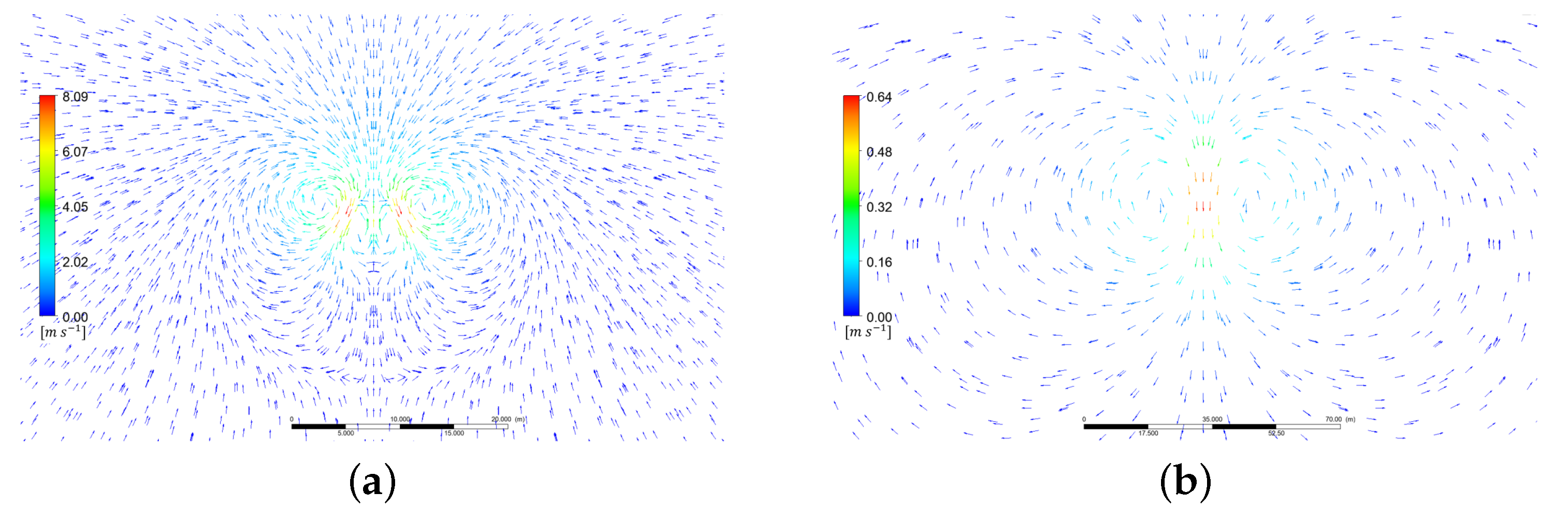
3.1. Finite Element Analysis
3.2. Establishment of the Safety Constraint Model
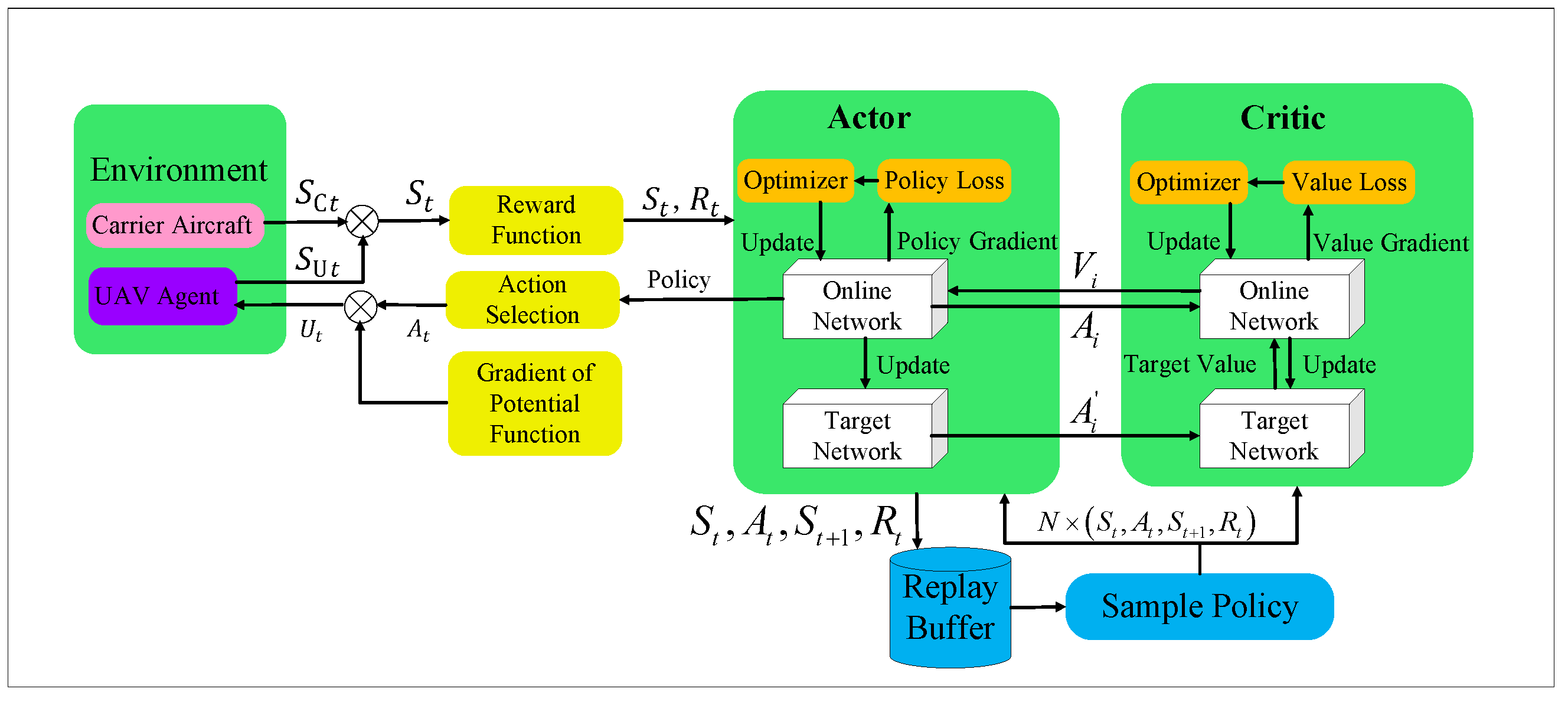
4. PRL Algorithms
4.1. Construction of Potential Function
4.2. Markov Decision Process
4.3. State and Action Settings
4.4. Setup of the RL
4.5. Rewards
4.6. Algorithm Design and Implementation
| Algorithm 1 PRL control algorithm |
| Initialize parameters , and |
| for all each iteration do |
| for all each environment step do |
| end for |
| for all each gradient step do |
| Sample a batch of data from |
| end for |
| end for |
| until training is done |
| Output optimal parameters , |
5. Performance Analysis
5.1. Converge Analysis
5.2. Stability Analysis
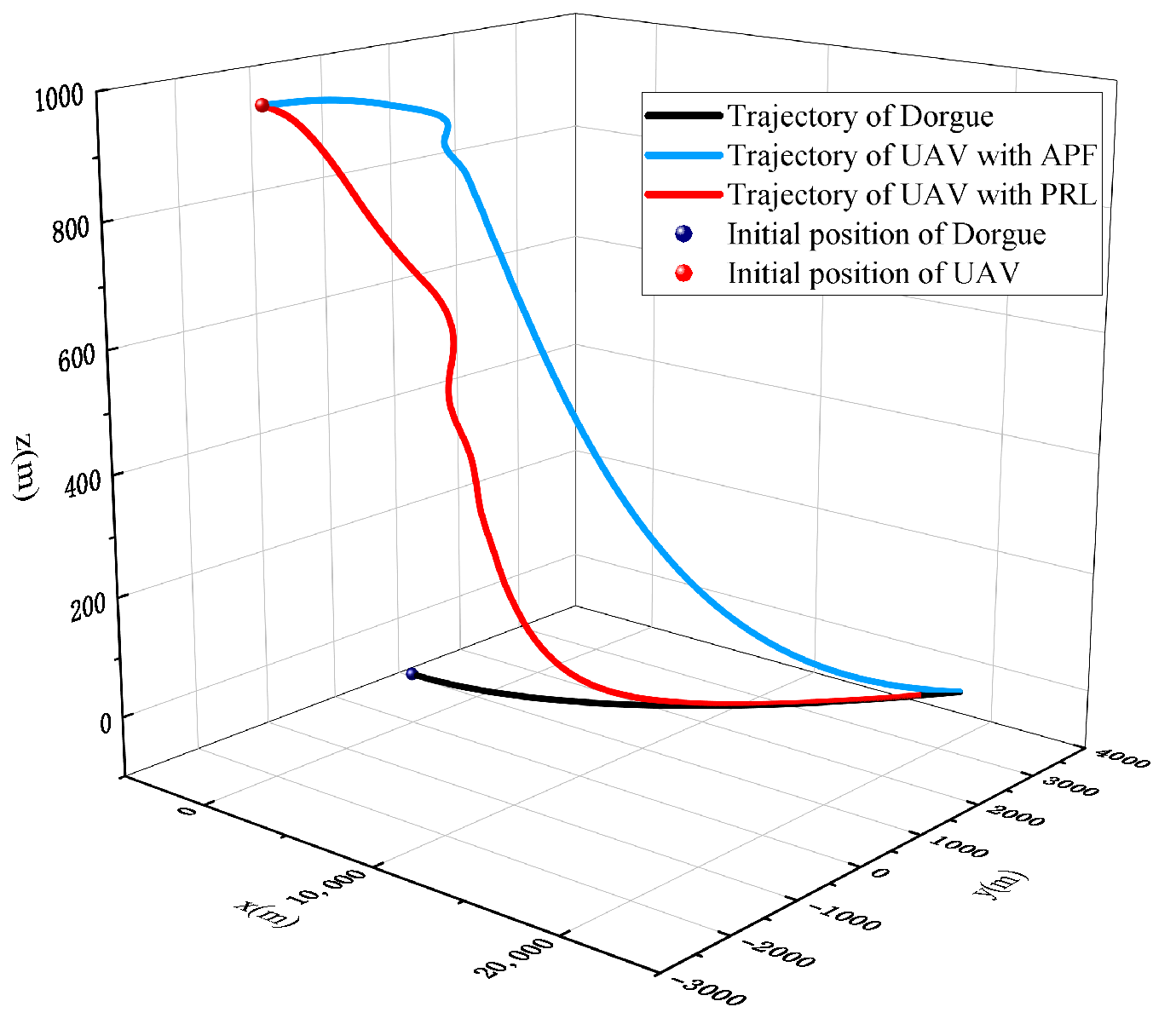
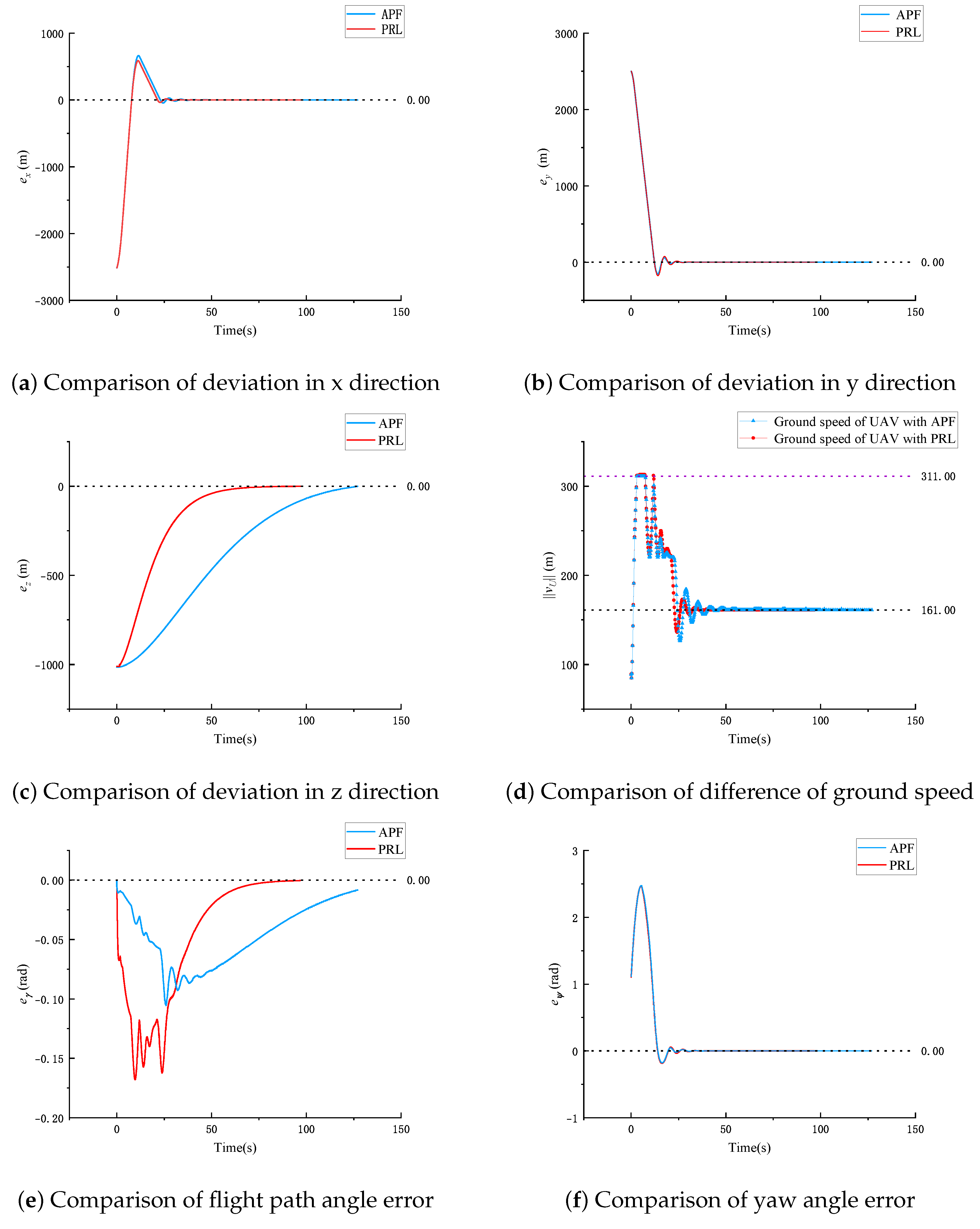
6. Simulations and Comparisons
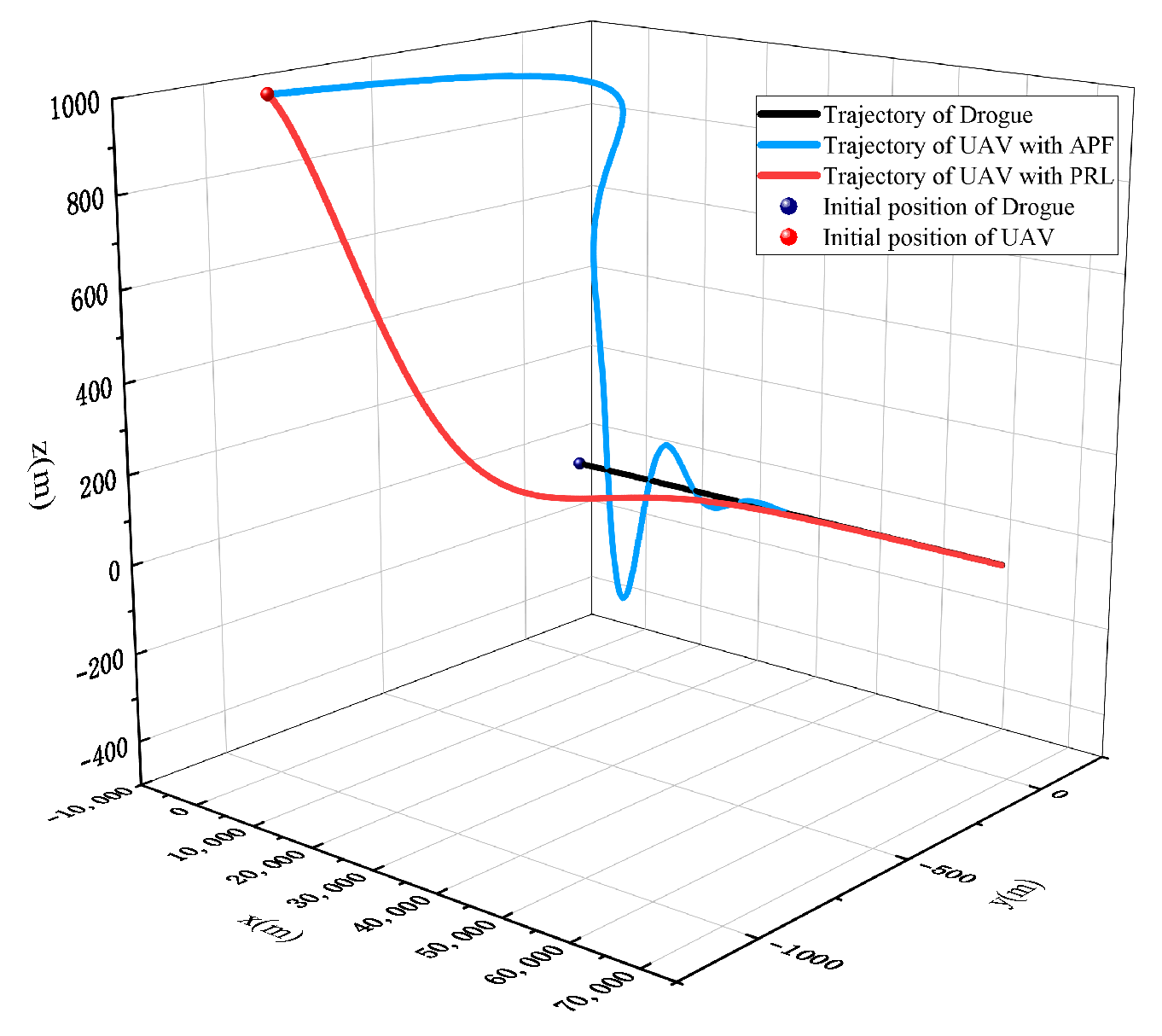
6.1. Rendezvous on Straight-Line Path
6.2. Rendezvous on Circular Path
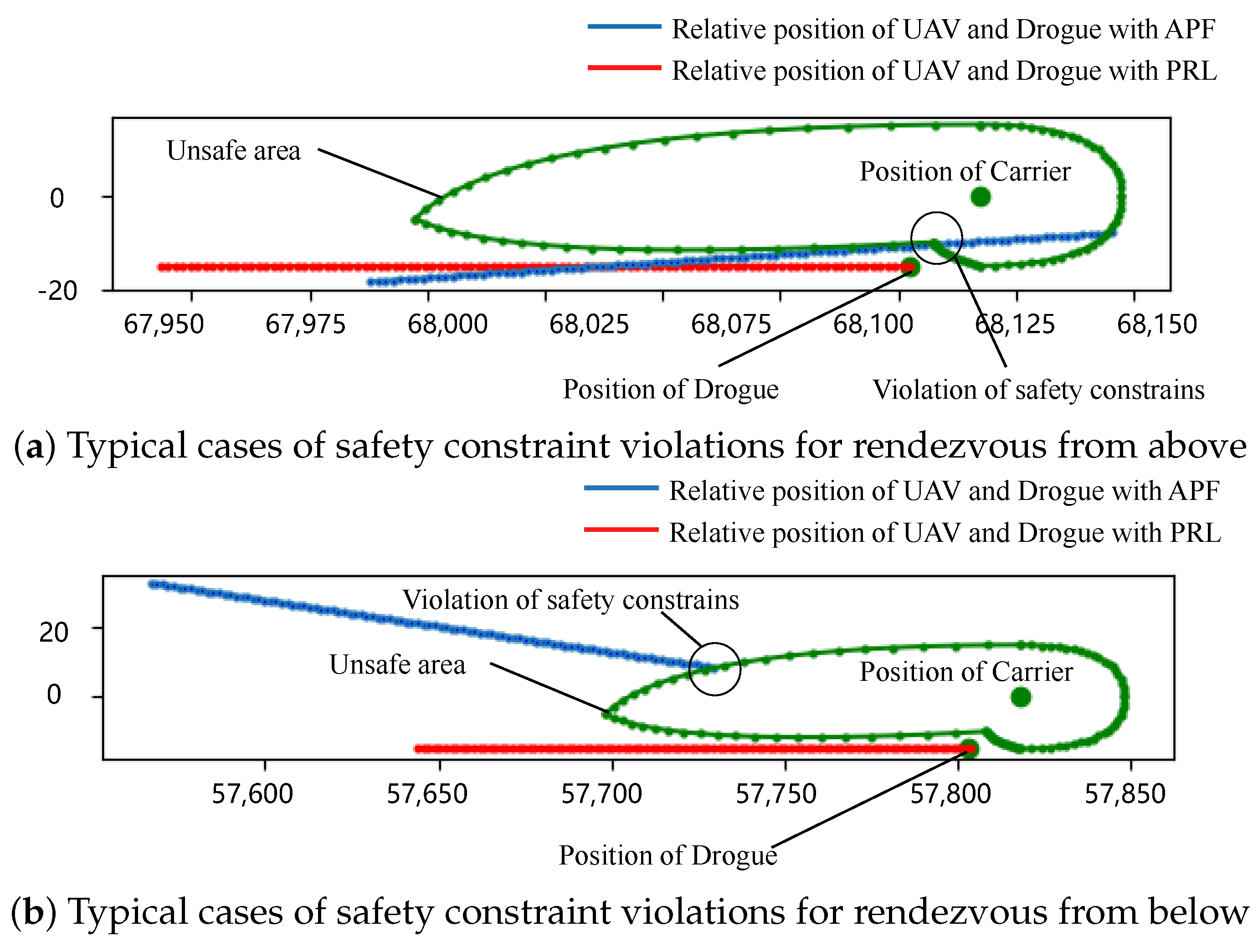
6.3. Security Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
Appendix D. Proof of Theorem 4
References
- Husseini, T. Gremlins are coming: Darpa enters phase III of its UAV programme. Army Technology, 3 July 2018. [Google Scholar]
- Nichols, J.W.; Sun, L.; Beard, R.W.; McLain, T. Aerial rendezvous of small unmanned aircraft using a passive towed cable system. J. Guid. Control. Dyn. 2014, 37, 1131–1142. [Google Scholar] [CrossRef]
- Hochstetler, R.D.; Bosma, J.; Chachad, G.; Blanken, M.L. Lighter-than-air (LTA) “airstation”—Unmanned aircraft system (UAS) carrier concept. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 July 2016; p. 4223. [Google Scholar]
- Wang, Y.; Wang, H.; Liu, B.; Liu, Y.; Wu, J.; Lu, Z. A visual navigation framework for the aerial recovery of UAVs. IEEE Trans. Instrum. Meas. 2021, 70, 5019713. [Google Scholar] [CrossRef]
- Darpa NABS Gremlin Drone in Midair for First Time. 2021. Available online: https://www.defensenews.com/unmanned (accessed on 1 July 2023).
- Gremlins Program Demonstrates Airborne Recovery. 2021. Available online: https://www.darpa.mil/news-events/2021-11-05 (accessed on 1 July 2023).
- Economon, T. Effects of wake vortices on commercial aircraft. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 1428. [Google Scholar]
- Wei, Z.; Li, X.; Liu, F. Research on aircraft wake vortex evolution and wake encounter in upper airspace. Int. J. Aeronaut. Space Sci. 2022, 23, 406–418. [Google Scholar] [CrossRef]
- Ruhland, J.; Heckmeier, F.M.; Breitsamter, C. Experimental and numerical analysis of wake vortex evolution behind transport aircraft with oscillating flaps. Aerosp. Sci. Technol. 2021, 119, 107163. [Google Scholar] [CrossRef]
- Visscher, I.D.; Lonfils, T.; Winckelmans, G. Fast-time modeling of ground effects on wake vortex transport and decay. J. Aircr. 2013, 50, 1514–1525. [Google Scholar] [CrossRef]
- Ahmad, N.N. Numerical simulation of the aircraft wake vortex flowfield. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference, San Diego, CA, USA, 24–27 June 2013; p. 2552. [Google Scholar]
- Misaka, T.; Holzäpfel, F.; Gerz, T. Large-eddy simulation of aircraft wake evolution from roll-up until vortex decay. AIAA J. 2015, 53, 2646–2670. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, N.; Yao, W.; Zhao, J.; Xu, S. Cooperative path planning for aerial recovery of a UAV swarm using genetic algorithm and homotopic approach. Appl. Sci. 2020, 10, 4154. [Google Scholar] [CrossRef]
- Luo, D.; Xie, R.; Duan, H. A guidanceaw for UAV autonomous aerial refueling based on the iterative computation method. Chin. J. Aeronaut. 2014, 27, 875–883. [Google Scholar] [CrossRef][Green Version]
- Zappulla, R.; Park, H.; Virgili-Llop, J.; Romano, M. Real-time autonomous spacecraft proximity maneuvers and docking using an adaptive artificial potential field approach. IEEE Trans. Control. Syst. Technol. 2018, 27, 2598–2605. [Google Scholar] [CrossRef]
- Shao, X.; Xia, Y.; Mei, Z.; Zhang, W. Model-guided reinforcementearning enclosing for UAVS with collision-free and reinforced tracking capability. Aerosp. Sci. Technol. 2023, 142, 108609. [Google Scholar] [CrossRef]
- Kim, S.-H.; Padilla, G.E.G.; Kim, K.-J.; Yu, K.-H. Flight path planning for a solar powered UAV in wind fields using direct collocation. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1094–1105. [Google Scholar] [CrossRef]
- Bonalli, R.; Hérissé, B.; Trélat, E. Optimal control of endoatmosphericaunch vehicle systems: Geometric and computational issues. IEEE Trans. Autom. Control. 2019, 65, 2418–2433. [Google Scholar] [CrossRef]
- Shi, B.; Zhang, Y.; Mu, L.; Huang, J.; Xin, J.; Yi, Y.; Jiao, S.; Xie, G.; Liu, H. UAV trajectory generation based on integration of RRT and minimum snap algorithms. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4227–4232. [Google Scholar]
- Wang, Z.; Lu, Y. Improved sequential convex programming algorithms for entry trajectory optimization. J. Spacecr. Rocket. 2020, 57, 1373–1386. [Google Scholar] [CrossRef]
- Romano, M.; Friedman, D.A.; Shay, T.J. Laboratory experimentation of autonomous spacecraft approach and docking to a collaborative target. J. Spacecr. Rocket. 2017, 44, 164–173. [Google Scholar] [CrossRef]
- Fields, A.R. Continuous Control Artificial Potential Function Methods and Optimal Control. Master’s Thesis, Air Force Institute of Technology, Wright-Patterson, OH, USA, 2014. [Google Scholar]
- Lu, P.; Liu, X. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization. J. Guid. Control. Dyn. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Virgili-Llop, J.; Zagaris, C.; Park, H.; Zappulla, R.; Romano, M. Experimental evaluation of model predictive control and inverse dynamics control for spacecraft proximity and docking maneuvers. CEAS Space J. 2018, 10, 37–49. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z. Adaptive backstepping control of spacecraft rendezvous and proximity operations with input saturation and full-state constraint. IEEE Trans. Ind. Electron. 2016, 64, 480–492. [Google Scholar] [CrossRef]
- Faust, A.; Oslund, K.; Ramirez, O.; Francis, A.; Tapia, L.; Fiser, M.; Davidson, J. PRM-RL: Long-range robotic navigation tasks by combining reinforcement earning and sampling-based planning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5113–5120. [Google Scholar]
- Williams, K.R.; Schlossman, R.; Whitten, D.; Ingram, J.; Musuvathy, S.; Pagan, J.; Williams, K.A.; Green, S.; Patel, A.; Mazumdar, A.; et al. Trajectory planning with deep reinforcementearning in high-level action spaces. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 2513–2529. [Google Scholar] [CrossRef]
- Dhuheir, M.; Baccour, E.; Erbad, A.; Al-Obaidi, S.S.; Hamdi, M. Deep reinforcement earning for trajectory path planning and distributed inference in resource-constrained UAV swarms. IEEE Internet Things J. 2022, 10, 8185–8201. [Google Scholar] [CrossRef]
- Song, Y.; Romero, A.; Müller, M.; Koltun, V.; Scaramuzza, D. Reaching theimit in autonomous racing: Optimal control versus reinforcementearning. Sci. Robot. 2023, 8, eadg1462. [Google Scholar] [CrossRef]
- Bellemare, M.G.; Candido, S.; Castro, P.S.; Gong, J.; Machado, M.C.; Moitra, S.; Ponda, S.S.; Wang, Z. Autonomous navigation of stratospheric balloons using reinforcementearning. Nature 2020, 588, 77–82. [Google Scholar] [CrossRef]
- Zhang, H.; Zongxia, J.; Shang, Y.; Xiaochao, L.; Pengyuan, Q.; Shuai, W. Ground maneuver for front-wheel drive aircraft via deep reinforcementearning. Chin. J. Aeronaut. 2021, 34, 166–176. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Wang, J.; Zhang, X. Deep-reinforcement-learning-based autonomous uav navigation with sparse rewards. IEEE Internet Things J. 2020, 7, 6180–6190. [Google Scholar] [CrossRef]
- Burda, Y.; Edwards, H.; Pathak, D.; Storkey, A.; Darrell, T.; Efros, A.A. Large-scale study of curiosity-drivenearning. arXiv 2018, arXiv:1808.04355. [Google Scholar]
- Pathak, D.; Agrawal, P.; Efros, A.A.; Darrell, T. Curiosity-driven exploration by self-supervised prediction. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–1 August 2017; pp. 2778–2787. [Google Scholar]
- Houthooft, R.; Chen, X.; Duan, Y.; Schulman, J.; Turck, F.D.; Abbeel, P. VIME: Variational information maximizing exploration. Adv. Neural Inf. Process. Syst. 2016, 29, 1–9. [Google Scholar] [CrossRef]
- Ng, A.Y.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the ICML, Bled, Slovenia, 27–30 June 1999; Volume 99, pp. 278–287. [Google Scholar]
- Yan, C.; Xiang, X.; Wang, C.; Li, F.; Wang, X.; Xu, X.; Shen, L. Pascal: Population-specific curriculum-based madrl for collision-free flocking with arge-scale fixed-wing UAV swarms. Aerosp. Sci. Technol. 2023, 133, 108091. [Google Scholar] [CrossRef]
- Schwarz, C.W.; Hahn, K.-U. Full-flight simulator study for wake vortex hazard area investigation. Aerosp. Sci. Technol. 2006, 10, 136–143. [Google Scholar] [CrossRef]
- Rossow, V.J. Validation of vortex-lattice method foroads on wings in ift-generated wakes. J. Aircr. 1995, 32, 1254–1262. [Google Scholar] [CrossRef]
- Schwarz, C.; Hahn, K.-U. Gefährdung beim einfliegen von wirbelschleppen. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2003, Jahrbuch 2003, Munich, Germany, 17–20 November 2003. [Google Scholar]
- Munoz, J.; Boyarko, G.; Fitz-Coy, N. Rapid path-planning options for autonomous proximity operations of spacecraft. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, ON, Canada, 2–5 August 2010; p. 7667. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcementearning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, PMLR, Vienna, Austria, 25–31 July 2018; pp. 1861–1870. [Google Scholar]
- Zhang, Q.; Pan, W.; Reppa, V. Model-reference reinforcementearning for collision-free tracking control of autonomous surface vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8770–8781. [Google Scholar] [CrossRef]
- Qi, C.; Wu, C.; Lei, L.; Li, X.; Cong, P. UAV path planning based on the improved ppo algorithm. In Proceedings of the 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), Qingdao, China, 26–28 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 193–199. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcementearning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Munoz, J.D. Rapid Path-Planning Algorithms for Autonomous Proximity Operations of Satellites. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2011. [Google Scholar]
- Bevilacqua, R.; Lehmann, T.; Romano, M. Development and experimentation of LQR/APF guidance and control for autonomous proximity maneuvers of multiple spacecraft. Acta Astronaut. 2011, 68, 1260–1275. [Google Scholar] [CrossRef]
- Lopez, I.; Mclnnes, C.R. Autonomous rendezvous using artificial potential function guidance. J. Guid. Control. Dyn. 1995, 18, 237–241. [Google Scholar] [CrossRef]



| Hyperparameters | Value |
|---|---|
| Sample batchsize | 512 |
| Learning rate | |
| Learning rate | |
| Discount factor | 0.99 |
| Neural network structure of policy | (256, 256) |
| Neural network structure of Value | (256, 256) |
| Time step (ms) | 10 |
| 0.2 | |
| [50.0, 5.0, 20.0, 20.0] |
| Method | PRL | APF |
|---|---|---|
| , m/s | ||
| , m/s | ||
| , rad | ||
| , rad | ||
| , Success rate |
| Method | PRL | APF |
|---|---|---|
| , m/s | ||
| , m/s | ||
| , rad | ||
| , rad | ||
| , Success rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Huo, M.; Yu, Z.; Qi, N.; Wang, J. Model-Reference Reinforcement Learning for Safe Aerial Recovery of Unmanned Aerial Vehicles. Aerospace 2024, 11, 27. https://doi.org/10.3390/aerospace11010027
Zhao B, Huo M, Yu Z, Qi N, Wang J. Model-Reference Reinforcement Learning for Safe Aerial Recovery of Unmanned Aerial Vehicles. Aerospace. 2024; 11(1):27. https://doi.org/10.3390/aerospace11010027
Chicago/Turabian StyleZhao, Bocheng, Mingying Huo, Ze Yu, Naiming Qi, and Jianfeng Wang. 2024. "Model-Reference Reinforcement Learning for Safe Aerial Recovery of Unmanned Aerial Vehicles" Aerospace 11, no. 1: 27. https://doi.org/10.3390/aerospace11010027
APA StyleZhao, B., Huo, M., Yu, Z., Qi, N., & Wang, J. (2024). Model-Reference Reinforcement Learning for Safe Aerial Recovery of Unmanned Aerial Vehicles. Aerospace, 11(1), 27. https://doi.org/10.3390/aerospace11010027






