Recent Advances in Airfoil Self-Noise Passive Reduction

Abstract

Airflow-induced noise prediction and reduction is one of the priorities for both the energy and aviation industries. This review paper provides valuable insights into flow-induced noise computation, prediction, and optimization methods with state-of-the-art efforts in passive noise reduction on airfoils, blades, and wings. This review covers the combination of several approaches in this field, including analytical, numerical, empirical, semi-empirical, artificial intelligence, and optimization methods. Under passive noise reduction techniques, leading and trailing edge treatments, porous materials, controlled diffusion airfoils, morphing wings, surface treatments, and other unique geometries that researchers developed are among the design modification methods discussed here. This work highlights the benefits of incorporating multiple techniques to achieve the best results concerning the desired application and design. In addition, this work provides an overview of the advantages and disadvantages of each tool, with a particular emphasis on the possible challenges when implementing them. The methods and techniques discussed herein will help increase the acoustic efficiency of aerial structures, making them a beneficial resource for researchers, engineers, and other professionals working in aviation noise reduction.

1. Introduction

With the development of high bypass ratio aeroengines, the dominance of jet engines in aircraft noise has diminished significantly, shifting the focus to other noise sources [1]. Noise reduction is crucial for passengers, cabin crew, and residents for reasons such as safety, performance, environmental impacts, regulatory compliance, and customer experience [2]. Today, the noise generated by the interaction between the airflow and different parts of the airframe is increasingly important [3,4]. Typical examples of this type of noise include the noise created by airfoils and other lifting surfaces, as well as the noise from the engine fan blades. A critical initial step in reducing noise levels is to understand the noise-generating mechanisms of these parts [5]. Much research has focused on quantifying flow-induced noise statistics and wall pressure fluctuations (WPF) due to Laminar and Turbulent Boundary Layers (LBL/TBLs) [6]. This section outlines diverse flow-induced noise sources and mechanisms in lifting devices. These mechanisms can be distinguished according to airflow conditions and aerodynamic phenomena on the Leading Edge (LE), Trailing Edge (TE), and surface of airfoils, wings, and blades.

LE noise is generally caused by different interactions of fluid flow with the LE. LE separation bubbles [7] might form around the sharp LE if the airfoil experiences laminar flow at moderate Reynolds numbers and high angles of attack (AoAs) (Figure 1c) [8]. When the airflow separates, vortices form and shed into the wake, generating unsteady fluctuations in air pressure. These pressure fluctuations are then responsible for producing sound waves, leading to the noise named LE noise [9]. Furthermore, upstream turbulence or time-dependent pressure variations [10] can trigger LE noise due to the ingested turbulence at higher Reynolds numbers [11].

TE noise, on the other hand, is generated at the rear edge of the airfoil. This noise is due to the interactions between the Boundary Layer (BL) and the TE [12], or the upper and lower surface flows as they rejoin at the airfoil TE [13] as Turbulence–Turbulence Interactions (TTI) [14]. These interactions lead to the formation of vortices, which produce pressure fluctuations and sound waves, resulting in TE noise [15]. TE noise is dominant at higher speeds and is generally more significant in thicker airfoils with blunter TEs [16]. The flow regime characteristics have direct correlations with TE noise mechanisms and the selection of noise reduction methods, consequently. The formation and shedding of turbulent eddies or vortices in the airflow are some of the dominant turbulent-TE noise sources in airfoils, with a significant impact on the Overall Sound Power Level (OSPL) [13].

Figure 1. Blade self-noise mechanisms are caused by different flow conditions. (a) TBL–TE noise, (b) LBL-VS noise, (c) separation-stall noise, (d) TE-bluntness-VS noise, and (e) tip vortex formation noise [13].

Figure 1. Blade self-noise mechanisms are caused by different flow conditions. (a) TBL–TE noise, (b) LBL-VS noise, (c) separation-stall noise, (d) TE-bluntness-VS noise, and (e) tip vortex formation noise [13].

In low to moderate Reynolds numbers, the LBL in the pressure side separation region amplifies the Tollmien–Schlichting (T–S) instability, which leads to the generation of laminar-TE noise [17,18]. T–S waves are characterized by small-amplitude oscillations in velocity and pressure fields within the boundary layer. These are moving wave bundles with modest streamwise scales, relatively wide spanwise scales, and exponentially increasing amplitudes as they travel downstream [19]. T–S waves are a result of the interaction between the smooth laminar (undisturbed) flow near the surface and disturbances in the flow, mostly due to imperfections or perturbations [20]. As the fluid flows over the surface, these disturbances can grow and evolve into more pronounced oscillations, eventually leading to the transition from a laminar flow to a turbulent flow [21]. This transition from laminar to turbulent flow is an important consideration in aeroacoustics as it leads to increased far-field noise emission [22]. On the other hand, when turbulent flow at higher Reynolds numbers interacts with the mean shear to produce unstable pressure fluctuations on the surface, the turbulent-TE noise starts forming [18].

Other noise sources include BL passing over the surface [23], tip vortices [24], and velocity fluctuations from vibrations on lifting surfaces [25]. Brooks et al. [13] categorized these noise generation mechanisms as TBL–TE, LBL Vortex-Shedding (LBL-VS), separation-stall, TE-bluntness-VS, and tip vortex formation (Figure 1). Section 2 presents an overview of different analytical, computational, and experimental techniques to evaluate the aerodynamics and aeroacoustics of lifting surfaces. Section 3 introduces modern metamodeling, prediction, and optimization techniques. Section 4 provides further exploration of passive noise reduction methods and related design changes. The paper will end with the conclusions and list of references in Section 5 and References part, respectively.

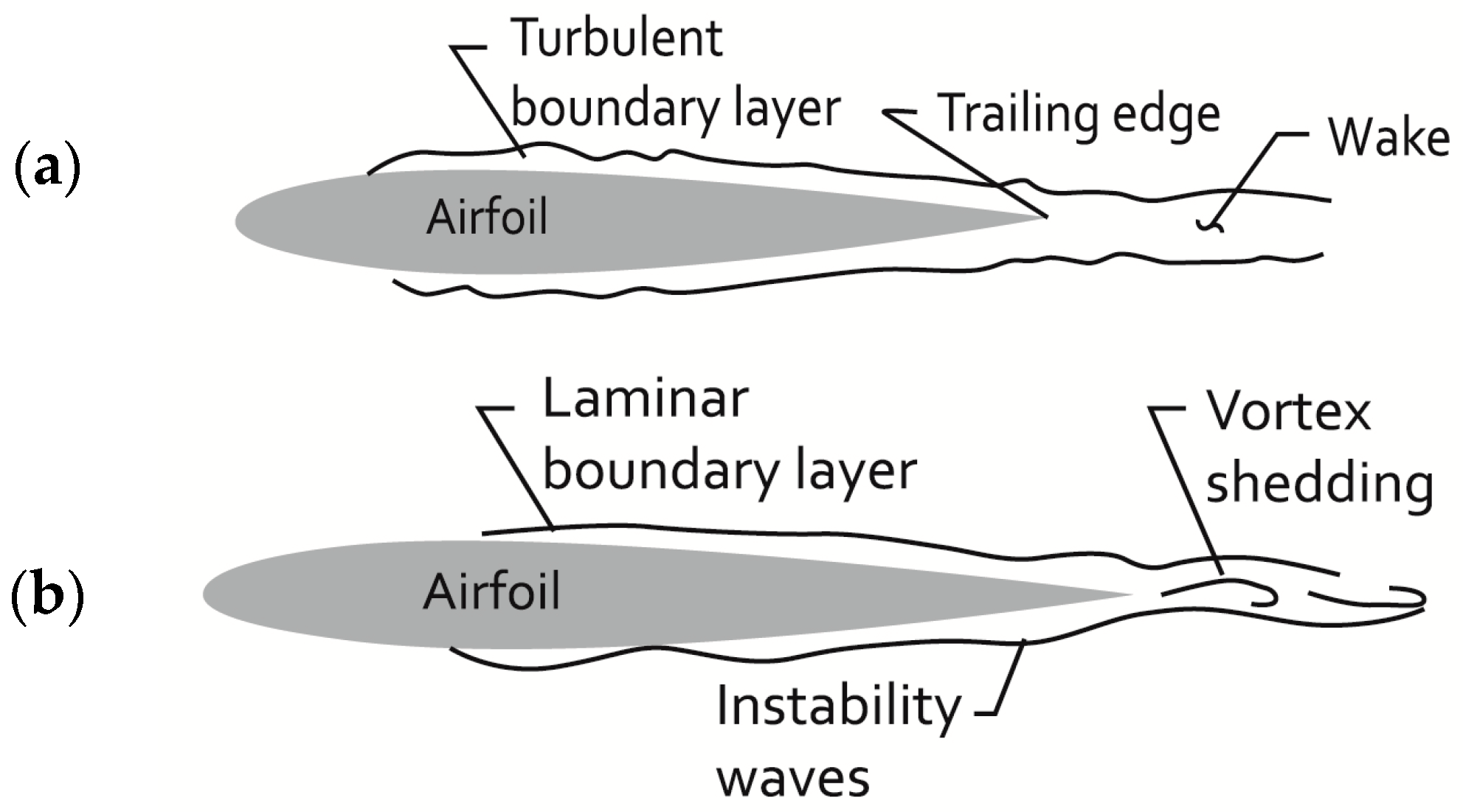
2. Aeroacoustic Methods

Several methods are utilized to model, compute, and predict flow-induced noise. These methods can be broadly categorized into analytical, numerical, integral-based flow/acoustic analogies, empirical and semi-empirical techniques, Computational AeroAcoustics (CAA) approaches, and compressible scale-resolving techniques [26,27]. A summary of the most popular techniques in each of these categories is discussed in this section. The first sub-section involves the most common analytical methods. The second sub-section is devoted to computational and numerical approaches. Empirical and semi-empirical approaches that employ presumptions from experimental findings to resolve the models are finally covered in the third sub-section.

2.1. Analytical Methods

There are various analytical methods that relate the acoustic field to the aerodynamic properties of the flow by solving integral [28,29] or Partial Differential Equations (PDEs) [30]. Integral-based methods are powerful in predicting noise in high-speed flows with high Reynolds numbers and are often employed in aeroacoustic simulations. Kirchhoff Formulation [31] and Lighthill Acoustic Analogy [32], the foundation of Ffowcs Williams–Hawkings (FW-H) [33] equations, are some examples of these analytical techniques. The FW-H model [33] is indeed one of the most well-known integral-based methods that predicts and analyzes monopole, dipole, and quadrupole sources of radiation that account for thickness noise, loading noise, and high-speed impulsive noise, respectively [34,35]. In specific cases, quadrupole sources are approximated by modeling permeable surfaces around physical noise sources to compute the far-field acoustic pressure [36]. To create a dispersed wave equation with sound sources, the FW-H equation revamps the Navier–Stokes equations and the continuity formula [37]. This equation adds arbitrary convective motion to the Lighthill–Curle theory of aerodynamic noise [32] to relate the fluctuating surface pressure distribution on an aerodynamic body or surface to the far-field Sound Pressure Level (SPL) it generates [38]. Specifically, the SPL at a distant point is linked to the time derivative of the normal component of the unsteady velocity on the surface, integrated over the surface of the body. It describes how the fluctuating surface pressure at the source generates sound waves that propagate away to the far field. The FW-H equation is particularly useful for predicting noise radiation from complex aerodynamic configurations and for understanding the noise generation mechanisms associated with fluid flow [39].

$$\frac{1}{{a_0}^2}\frac{{\mathsf{\partial }}^2{p}^{\prime }}{\mathsf{\partial }{t}^2}-{\nabla }^2{p}^{\prime }=\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}_i\mathsf{\partial }{x}_j}\left[T_{ij}H\left(f\right)\right]-\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}\left[P_{ij}{n}_j+\rho u_i\left(u_n-v_n\right)\delta \left(f\right)\right]+\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left[{\rho }_0{v}_n+\rho \left(u_n-v_n\right)\delta \left(f\right)\right]$$

(1)

In Equation (1), u_n and v_n are the fluid velocities in the direction normal to the integration surface and the normal velocities of i, respectively. δ(f) and H(f) are the Dirac delta function and the Heaviside function, respectively. ρ₀ is the density, and α₀ is the sound speed in the unbounded medium.

Green’s function [40,41,42,43] was also introduced as a solution for the FW-H equation [37] for computing the correlation of elastic or acoustic propagation in ideal lossless mediums [44]. Furthermore, Amiet [45,46,47] and Howe [48,49] simplified the process of defining sound dispersion by explaining the variation in the disturbance in the BL. By combining and extending the earlier analytical models, Grasso et al. [50] developed a thorough analytical method to model the wall-pressure fluctuations beneath a TBL. They obtained a revised Helmholtz equation for this purpose by Fourier transforming the Poisson equation, which controls pressure fluctuations in the wave number domain, and calculating it using the Green’s function [40,41,42,43] method. The authors analyzed the turbulence-mean shear and turbulence–turbulence interaction aspects that independently make up the differential equations’ terms under the assumption that the turbulent field has a joint normal probability distribution. This approach demonstrated that the most prominent factor in accurately depicting the wall-pressure spectrum is the functional characterization of the turbulence characteristics. Additionally, they pointed out that compared to DNS [51] results, the Prandtl theory [52] understates the correlation length.

2.2. Computational/Numerical/Scale-Resolving Approaches

There is a significant correlation between noise and turbulence, and most acoustic equations use the results from turbulence solvers to converge [53]. Here, hybrid methods with a dual-domain approach can ease the heavy calculation problem, especially for more complex geometries [54]. CAA is one branch of hybrid numerical methods known as the key to revealing this connection [55]. Boundary Element Method (BEM) [56], Panel/Viscous Vortex Particle Method [57,58], Finite Volume Method (FVM) [59,60], and Finite Element Method (FEM) [61] are some of the Computational Fluids Dynamic (CFD) solvers to feed CAA that work based on discretizing the domain into boundary surfaces and elements over which the governing PDEs are approximated.

According to the Reynolds number range, these methods tend to use compressible and incompressible solvers to compute the fluid flow. When compared to incompressible solutions, compressible solvers are significantly more complex. Low-Mach flows have a lower compressibility and a greater difference in scales between the turbulence and acoustic waves [62]. Compressible solutions, on the other hand, are usually utilized for higher Mach number flows, where compressibility is critical and the acoustic and turbulent scales are closer together. One approach to solving compressive flows is to first solve for the time-dependent incompressible flow and then calculate a density correction using the results from the turbulence flow and the related incompressible map [63]. However, in some cases, the requirement to keep big data sets is eliminated by simultaneously resolving the hybrid methods in the two domains, which increases their efficacy and readability [64].

Regardless of the compressibility of the flow, studying flow-induced noise on airfoils requires identifying at least a portion of the turbulent flow. In turbulence, there is a vast, continuous spectrum of spatial and temporal turbulence scales involved. The available range of various computing methods can be organized according to their ability to either model or resolve these turbulences. This range starts with RANS equations [65], which is a low-fidelity method that models the entire turbulence, and ends with the Direct Numerical Simulation (DNS) [66] method as the highest-fidelity approach that entirely resolves them. RANS models are based on time-averaging the Navier–Stokes equations and efficiently predicting mean flow behavior and some turbulent effects. However, they struggle to capture unsteady and large-scale turbulent structures. On the other hand, DNS requires significant computational resources and is not practical for industrial-scale problems. Employing low-fidelity aerodynamic solvers might result in erroneous or insensitive input to the aeroacoustic computations because of their nature of smoothing turbulence scales [67]. Therefore, using methods that do not average the pressure fluctuations is crucial. Martinez-Lera et al. [68] used various numerical methods with an incompressible LES to calculate the self-noise of a controlled-diffusion airfoil. To represent the auditory field with the Lighthill analogy [32], the authors used the finite element method and compared their findings to peers from a half-plane Green’s function [40,41,42,43]. According to their results, TE noise is predominant throughout a vast frequency range, whereas other sources of noise become more significant at higher frequencies.

Large Eddy Simulation (LES) directly resolves large-scale turbulent structures while modeling smaller scales. To further reduce the computational costs, scale-resolving RANS-LES approaches, commonly referred to as Embedded LES (ELES) or unstable RANS (URANS), are used. These solvers capture a broader range of turbulent flow scales than classic RANS simulations and have more affordable processing costs than LES [25]. Scale-resolving techniques maintain a balance between RANS and LES by resolving a certain portion of the turbulent scales in critical domains while modeling the smaller unresolved scales with RANS in other domains. There are different approaches to implementing scale-resolving techniques, including Wall-Resolved LES (WR-LES) [69], Wall-Modelled LES (WM-LES) [70], Scale-Adaptive Simulation (SAS), Zonal Detached ES (ZDES) [71], Detached ES (DES) [72], and Delayed Detached ES (DDES) [73,74]. The percentage of resolved turbulence, and consequently the accuracy and computational cost, decrease with this order [75,76]. Depending on the available resources and the complexity of the problem, researchers choose one of the available LES or hybrid methods.

2.3. Empirical/Semi-Empirical Approaches

A common approach to mapping airflow fluctuations is to use semi-empirical methods that combine empirical correlations with fundamental physical equations to accurately estimate aerodynamic properties. The Brooks, Pope, and Marcolini (BPM) model [13] is one of these semi-empirical methods that is founded on the aforementioned FW-H model. The BPM model is one of the most efficient semi-empirical models [77] developed to predict flow-induced noise, whose cornerstone is the spectral scaling of several airfoil self-noise systems. Brooks et al. [13] discussed five processes of airfoil self-noise to show that the most significant high-frequency noise source occurs when turbulent eddies in the BL grow over the airfoil’s surface and transfer over the TE. The BPM model is a prominent semi-empirical approach that divides the blades into two-dimensional airfoil sections to deliver the BL parameters and local relative velocities. The model adds the contributions from each element of the blades to predict the overall noise emission [78].

Since the Surface Pressure Fluctuation (SPF) acts as the input for the mentioned aeroacoustic functions, the calculation of the SPF is necessary as the foundation of noise analysis. There have been several semi-empirical wall-pressure spectrum (WPS) formulations produced, including Chase [79], Goody [80], and March [81] approaches. Rozenberg et al. [82] have expanded the Goody model [80] to account for the negative pressure gradient beneath the TBL as a scaling-based spectral model without contemplating the physics of the flow. These theories are founded on various geometrical and physical presumptions with empirical adjustments to some extent [27]. In the particular example of fixed wings, the noise mechanism is usually caused by the dispersion of BL turbulent energy into noise at the TE [83] or the separation of the LBL from the airfoil surface [84]. High Reynolds numbers cause a TBL to form over the surface of the wing, and due to the different sizes of the TBL eddies, the noise emitted is mostly broadband in character [85]. As a result, methods to decrease this noise source typically involve changing the LBL or TBL structure, its separation mechanism from the surface, and its scattering from the TE.

A two-dimensional TBL model, developed within a pressure gradient, was also the subject of semi-empirical model development by Kamruzzaman et al. [86] to ascertain wall pressure spectra. The authors employed wall-pressure tests covering a wide range of Reynolds numbers, both for equilibrium flat plates and non-equilibrium airfoils, at various AoAs. Through their investigation, the authors produced a simple function of the pressure ratio and BL timescales by combining the Rozenberg [82], Goody [80], and Chase–Howe [48,49,79,87] models to create a modified model. The model was also verified by predicting the TE noise spectra and the WPFs with an error of ±2 dB for the maximum noise level. Furthermore, Liu and Lee [88] looked at the impact of airfoil design elements on TE noise using Howe’s model [48,49] and Lee’s wall pressure spectral model [89]. To accomplish this, they parameterized an airfoil, beginning with a standard airfoil and then transforming it using a variety of design factors through a parametric airfoil design tool. Furthermore, to predict the airfoil TE noise, the authors employed a technique that blends an empirical wall-pressure spectral model with a noise dispersion model. They used Morris’ approach [90] to test the responsiveness of various factors and evaluate their respective impacts without the disadvantages of the one-factor-at-a-time methodology. Overall, the authors discovered that a decrease in the trailing boat-tail angle causes either an increase in lift-drag ratio or a noise reduction. Additionally, they verified these results using experimental data that supported the conclusions from their computational technique.

The TNO (Netherlands Organization for Applied Scientific Research) model [91,92] is another widely used method that uses a combination of analytical and numerical techniques to predict the effectiveness of noise control measures, such as barriers and enclosures [93,94,95]. While the TNO model has lower computational costs compared to methods that fully resolve all turbulent scales (as in LES), it does rely on the empirical assumption of Taylor’s hypothesis with the Navier–Stokes equations [96,97], which may limit its accuracy in certain flow conditions [98]. As a result, TNO is often used for industrial applications where computational cost efficiency is crucial, while LES or other more advanced turbulence models are employed for cases requiring higher accuracy and detailed turbulence modeling. The accuracy of the TNO modeling methodology depends on the tuning parameters derived from empirical data [25,99]. Ferret Gasch et al. [100] presented their findings on TE noise prediction using specialized aerodynamic and acoustic tests in three separate wind tunnel facilities for testing two slightly different wind turbine airfoils. The authors looked at patterns within the aeroacoustic noise analysis to gauge how sensitive the TNO and BPM models are to responding to even minor alterations of the design variables. Results reported significant variance in the acoustic results of various algorithms despite the agreement of the aerodynamic predictions. Both methods have built-in errors and dispersion that prevent them from achieving the desired precision. Therefore, one can conclude that additional experimental testing and more advanced simulation tools are required to evaluate TBL–TE noise accurately.

In aeroacoustics, the TNO model relies on sound propagation and transmission principles by considering the characteristics of the sound source, the environment, and the noise control measures. This model predicts the SPL reduction achieved by different noise control measures by considering the sound transmission loss of the control measure as well as the diffraction, reflection, and absorption of sound waves by the environment and the control measure. The near-surface pressure gradient along the TE serves as the noise source in the TNO model. To estimate the generated noise from airfoils caused by the interaction of the BL eddies with the TE, Fischer et al. [101] proposed a modification of the TNO model by resolving the Poisson equation with cross-correlation components for flow turbulence, in which the equations for the cross-correlation of turbulence are modeled. Results showed that predictions of surface pressure and the far-field noise spectrum obtained from the new model were more accurate. At the same time, it only costs marginally more to run than the TNO model, given that it is established as an analytical solution of the turbulence cross-correlation components.

In aeroacoustics, the TNO-Blake model [102,103,104] is a semi-empirical approach used to predict the noise generated by turbulent boundary layer interactions with solid surfaces by combining empirical data with theoretical formulations. Abid et al. [105] also looked at TNO-type models [102,106] to predict the surface pressure spectrum associated with TBL–TE noise. They employed flow models derived from XFOIL and Reynolds-averaged Navier–Stokes (RANS) [107] equations for two National Advisory Committee for Aeronautics (NACA) airfoils at varied AoAs and Reynolds numbers. The presence of the pressure gradient has a significant impact on airfoil BL flows. By scaling the integral correlation length with the kinematic shape factor, they introduced the impact of the pressure gradient in the velocity spectrum. This strategy was then used to develop a new and more accurate model based on Amiet’s theory [45,46,47], which considers the frequency dependency and the pressure/velocity gradient spectrum. Through another study, Abid et al. [108] developed a number of semi-analytical TE noise simulations of a NACA 0012 airfoil at three AoA and two Reynolds numbers by using the WM-LES [109,110,111,112] approach and a revised turbulence anisotropy model. As a modification, they enhanced the previously published TNO-type model [105] that they created using the XFOIL and RANS flow solutions. They sought to evaluate the noise predictions between the LES-FW-H scheme and Amiet’s TE noise model [45,46,47] by using an LES scale-resolving flow solver as the input for the acoustic models. The source statistical parameters for the TNO-type models included the mean flow profiles, two-point velocity, and pressure correlation length scales coupled with the coherence function in the airfoil BL. The authors demonstrated that the LES predictions of the mean velocity profiles and the WPS profiles matched both the experimental data and the predictions from the improved TNO model. They also compared the far-field noise spectra of the TNO models to the numerical solution generated by the FW-H approach. Thanks to the accurately reconstructed BL flow structure near the TE and other key elements of the noise model, the modified TNO model was shown to be more accurate in accordance with the LES-FW-H technique. Using this model, the authors could also utilize data-intensive optimization algorithms to evaluate the best conditions for minimizing the generated noise.

The TNO model has shown vast potential to match other models. In this context, Hornung et al. [14] recently proposed a model for TBL–TE noise prediction according to the Blake model deduction for TTI, which is disregarded in earlier models. Furthermore, Stalnov et al. [99] updated the TNO-Blake model to predict airfoil broadband self-noise generated by the interaction of a sharp TE with a TBL to lessen the dependency on so-called turning parameters. The authors developed the flat-plate theory with finite-chord effects to predict its eventual radiation to the distant field. They evaluated, measured, and predicted the surface pressure spectrum and found agreement in the mid-high frequency region within 2 dB. Herr et al. [113] presented their findings through the Benchmark Problems for Airframe Noise Computations (BANC) workshop. Through a collaborative effort with empirical statistical models on two separate wind tunnels and using three measuring methods, they sought to enhance and evaluate the current prediction capabilities in the field of aeronautical noise problems, with a focus on TBL-induced noise. The authors contrasted TNO-style models with more sophisticated modeling strategies such as hybrid CAA and lattice Boltzmann. They stated that more sophisticated techniques outperform, demonstrating the need for future advancement of TNO-type models to achieve the degree of precision necessary for industrial disciplines.

Noise emission reduction is considerably important in wind turbines since their blades usually have a high AoA and produce significant TE noise. The origin of this noise can be associated with changes in the BL wall pressure caused by turbulent vortices, which form due to shear, turbulence, and TTI. The effect of environmental factors on generated noise in wind turbine airfoils was the subject of a paper published by Tian et al. [114]. To predict noise patterns and amplitude modulation of wind turbines while considering wind shear and atmospheric turbulence, the authors used Amiet’s theory [45,46,47], Goody’s model [80], and Rozenberg’s model [82] to describe TE noise. After contrasting model predictions with existing experimental findings, the authors modified the model to account for rotating blades. Results reported a strong agreement at frequencies greater than around 1000 Hz, but they undervalued the levels at lower frequencies. They also applied the Monin–Obukhov similarity theory [115,116] to take wind shear and atmospheric turbulence influences into consideration. By doing so, the authors demonstrated that turbulent inflow noise considerably adds to the low-frequency noise emitted by wind turbines. Although the authors successfully predicted the sound power level spectrum, this study could potentially be developed further by adding wind tunnel experiments and field observations.

Yu et al. [117] investigated the TE noise phenomenon and suggested a wavelet-based beamforming approach to analyze flow fluctuations, transient flow dynamics, and their correlations. The authors performed transient acoustic imaging to interpret and examine the patterns and relationships of the TE noise in the time–frequency domain. Then, they verified this approach by providing the obtained velocity field by Particle Image Velocimetry (PIV), accompanied by the time–frequency analysis of acoustic measurements. Wind tunnel experiments were performed with a microphone array to map the noise produced on the TE. The study demonstrated how the spatial distribution of the disturbances inside the boundary and wake changes with time, resulting in intensity modulations of the TE noise. Furthermore, the position and source of the TE noise at various Reynolds numbers are visible from the association between the flow field and the acoustic pressure. Specifically, at lower Reynolds numbers, vortex separation is the primary source of the TE noise, while the BL instability plays this role at higher Reynolds numbers. Ryan Catlett et al. [118] also explored the unstable aerodynamic forces close to the TE of an airfoil at various Reynolds numbers. They developed a model to calculate fluctuating surface pressure using the velocity and steady versus unsteady surface pressures from three distinct TE designs. In addition, they extended Goody’s model [80] to offer an empirical model of the fluctuating pressure field based on non-dimensional variables that were affected by adverse pressure gradients. Schepers et al. [119] published the findings of a project to drastically reduce wind turbine aerodynamic noise while preserving aerodynamic performance. The authors used experimental data to validate the aeroacoustic wind turbine code SILANT [75] and modify the design. They demonstrated that the downward motion of the blade in the outboard portion of the blade produces most of the TE noise, which is generally accepted as the primary noise-generating component of current wind turbines. The authors employed a combined 2D model with precise turbulence property calculations while considering boundary-layer anisotropy to develop new aerodynamically and acoustically optimized airfoils for the outside portion of the turbine blade. The experimental results from wind tunnel testing showed that the new airfoils could reduce the generated noise while maintaining their aerodynamic performance.

Because of the high sensitivity and nonlinear complex interactions of parameters in aerodynamic and aeroacoustic modeling, the use of accurate and state-of-the-art testing is important for the validation of simulations and predictions. Wind tunnel tests play a key role in developing empirical methods in aeroacoustics. The accuracy of experimental tests in aeroacoustics depends on the quality of existing anechoic chambers while maintaining a standard flow regime. Al Tlua and Rocha [120] designed and tested an aeroacoustic wind tunnel with different anechoic chambers, using acoustic transparency tensioned cloth screens to provide a smooth flow surface and reduce interference effects. The test section was evaluated in a medium-speed closed-loop wind tunnel, showing comparable background noise to other facilities and demonstrating that sawtooth serrated TEs effectively reduce noise compared to a straight TE, as measured by the NACA0012 airfoil model benchmark test.

Aeroacoustics hinges on a multitude of factors and assumptions, including airfoil configuration, flow speed, angle of attack, Reynolds number, and surface roughness. These interrelated parameters complicate the identification of individual contributions and the establishment of clear causal relationships [121]. This section systematically outlines analytical, numerical, and empirical methodologies for predicting and assessing noise generated by fluid flows. Rooted in the fundamental equations of fluid dynamics, analytical methods elucidate core noise mechanisms. These approaches are well-matched to simple geometries and flow conditions, but their utilization frequently demands substantial computational resources. In contrast, computational or numerical approaches represent another category, enabling sophisticated simulations through techniques like CFD and direct DNS. These approaches accommodate intricate geometries and turbulent flows. Yet, accuracy challenges arise from the interplay of numerous parameters, underlying assumptions, and the size of resolved eddies [122,123]. Scale-resolving methods, a subset of numerical techniques, strive to encompass a range of turbulence scales, bridging the gap between conventional RANS and DNS methodologies [124]. Empirical or semi-empirical methods, the final category, leverage experimental data and correlations to estimate noise levels. These techniques capitalize on the connection between flow parameters and the resultant noise and provide reasonable assumptions for the needed constants. Consequently, all three approaches navigate an extensive parametric space. Extracting meaningful insights and precise predictions mandates meticulous design and meticulous interpretation of data. In summary, the calculation of airflow noise employs a spectrum of methodologies, each offering distinct advantages contingent on problem complexity and resource availability. However, the incorporation of advanced statistical techniques and sophisticated experimental setups becomes imperative to deal with the intricacies stemming from the multitude of involved parameters.

3. Supplementary Methods

Solving and evaluating potential solutions for multidisciplinary aeroacoustics problems incurs high computational costs due to their complexity. Hence, the adoption of modern techniques such as optimization and metamodeling appears essential to enhance aerodynamic and acoustic analysis capabilities [125,126].

3.1. Optimization Algorithms

Optimization algorithms are heuristic methods that increase the efficiency, precision, and robustness of the analyzed designs with a much lower computational cost compared to the more traditional methods discussed earlier [127]. The integration of optimization algorithms with analytical, numerical, and experimental tools seems vital to solving complex aerodynamic and aeroacoustic problems. These algorithms include various tools that mostly mimic natural [94,128] or industrial [129] appearances. This section shows how optimization methods enable researchers to handle the existing trade-off between multiple objectives in multidimensional problems [130], address data-driven problems, or even create innovative solutions [131]. Researchers have used different heuristic optimization algorithms, including population-based, nature-inspired, and gradient-based techniques, with the help of Artificially Intelligent (AI) techniques [132,133], and some of them will be discussed here.

One of the popular branches of heuristic optimization techniques is nature-inspired algorithms that include different techniques like Genetic Algorithm (GA) [134], Ant [135] or Bee [136] Colony, and Particle Swarm Optimization (PSO) [137]. The GA technique mimics the process of natural selection, using genetic operators such as selection, crossover, and mutation to evolve a population of potential solutions toward an optimal solution to a problem [138,139]. Using these nature-inspired techniques is highly beneficial in finding the absolute optimum design and avoiding local optimums. To identify the best low-noise airfoils, Volkmer et al. [140] employed a semi-empirical Kamruzzman’s wall pressure spectral framework [86], combined with an extended Amiet’s far-field noise model [45,46,47], along with a GA optimization [134]. They simulated the flow characteristics with low Reynolds numbers by encoding the models in XFOIL to determine the airfoil with the desired lift and the least amount of far-field noise. Comparisons between the results and the reference airfoil indicated that the optimal design significantly reduces TE noise while preserving the same aerodynamic properties. Without validating the aerodynamic portion, they used experimental data from the wind tunnel to confirm the acoustic portion of the conclusions. The authors also commented that semi-empirical models are often inaccurate compared to the collected data.

Another advantage of heuristic optimization methods is their considerable power in dealing with trade-off analysis and multi-objective optimization problems [141]. Ricks et al. [67] carried out a multi-objective shape optimization for airfoils based on CFD. The authors attempted to reduce the TE noise of an airfoil while maintaining aerodynamic performance using RANS CFD, Lee’s wall pressure spectral model [89], Amiet’s model [45,46,47], and GA [134]. They demonstrated a noise reduction of about 2 dB for a two-dimensional NACA 0012 airfoil, but the lift-to-drag ratio was slightly reduced because of that. The analysis could be more comprehensive if accompanied by experimental data to validate the high-fidelity results and optimization algorithm predictions. Furthermore, after emphasizing the importance of boat-tail angle on the generated noise at airfoils in a different work [88], Liu and Lee [142] used semi-empirical models and multi-objective optimization algorithms to improve a TE with a concave form, minimize the generated noise, and enhance the aerodynamic characteristics. The authors used Lee’s WPS model [89], Howe’s acoustic framework [48,49], the GA optimization tool, and the Kriging surrogate technique [126], together with the beginning point of three design parameters. Relative to the benchmark NACA 0012 airfoil, their study increased the lift-to-drag ratio while achieving approximately 4 dB in noise reduction.

Jim et al. [143] concentrated on optimizing the aerodynamics and aeroacoustics of a hypothetical low-drag, low-boom supersonic planform using Kriging-based Bayesian multi-objective optimization and the gradient-free GA algorithm (Figure 2). The authors investigated the use of Euler Computational Fluid Dynamics (CFD) with an enhanced version of the Burgers PDE solver [144,145] and an experimental parasitic drag addition to speed up the design space exploration and multi-objective optimization processes. They demonstrated that effective global optimization of the chosen aircraft design parameters is possible by combining the Kriging-based surrogate models [126] with the Anticipated Hyper-Volume Improvement (AHVI) performance indicator. They employed non-dominated sampling [146] alongside GA and local optimization techniques to explore the Kriging surrogates. The findings revealed a trade-off between designs with a higher lift-to-drag ratio and those producing lower noise at ground level. Additionally, results showed that properly placed wingtips can soften the undertrack signature and lessen the sonic boom.

PSO is another of the nature-inspired heuristic methods with a high capability for finding optimum conditions in continuous, feasible regions [94,147]. PSO is a population-based optimization algorithm that simulates the social behavior of birds or fish, where potential solutions, or so-called particles, move through the problem space towards better solutions by adjusting their positions based on their own experience and the best experience of other particles in the swarm [148]. PSO is highly capable of solving optimization problems in continuous, feasible regions. In this context, Li et al. [149] investigated a novel method for optimizing wind turbine blade design by enhancing structural integrity, power generation efficiency, and emitted noise. The authors used a multi-objective PSO technique in conjunction with FVM to improve both the aerodynamic and aeroacoustic performances of the blade while maintaining the strength and stiffness constraints. They took a regular blade from a 2 MW wind turbine as the reference case and used methods in MATLAB and ANSYS to optimize the performance. The authors reported that the optimization process resulted in a 3.1 dB reduction in blade noise and a 6.9% increase in the power coefficient.

Flaps are among other parts of the wing whose noise performance is immensely sensitive to the continuous changes in the design parameters. Providing improved designs for higher aeroacoustic and aerodynamic performance of flap arrangements with lower noise and more lift is one of the primary objectives in the paper published by Ju et al. [150]. The authors published a study on a hybrid method (Figure 3) for aerodynamic and aeroacoustic numerical optimization focused on a case study with a typically extended wing and flap design. To simulate the flow fields and perform the acoustic analogy, the authors used three-dimensional LES equations with a dynamic Smagorinsky sub-grid model [151], followed by the FW-H equation. Using wind tunnel tests, they also verified the numerical results. Additionally, they produced initial samples using the statistical Latin Hypercube Sampling (LHS) approach [152] and then used the PSO technique in conjunction with the Kriging surrogate model [126] to optimize the design. With a loss of lift-to-drag ratio (L/D) of less than 1%, the method achieved a reduction in the Overall Sound Pressure Level (OASPL) of far-field noise of about 4 dB.

A powerful technique used in aeroacoustic optimization problems is so-called Adjoint Optimization, which is a favored type of gradient-based optimization method [153]. This approach can address complex multi-objective problems in aerodynamics and aeroacoustics when applied to numerical simulation approaches, including LES and DNS. However, there are several challenges and limitations associated with the convergence of this method when coupled with scale-resolving approaches. These challenges include computational cost, time integration errors, sensitivity to initial vectors, inherent non-linearity and non-convexity, and a lack of adjoint-friendly codes [154,155]. To address these challenges and limitations, researchers and engineers often employ various techniques, such as algorithmic improvements, adaptive mesh refinement, turbulence model refinement, and sensitivity analysis verification [156,157]. Additionally, combining the Adjoint Optimization method with surrogate modeling techniques as efficient replacements for the original simulations or functions can help reduce the computational burden associated with scale-resolving simulations and improve convergence in practical engineering applications [158,159].

Despite the above-mentioned challenges, the Adjoint Optimization method remains a valuable tool for optimizing complex noise reduction problems. Zhou et al. [160] enhanced the noise created in the NACA 0012 airfoil by constructing an efficient optimization method in the open-source software built at Stanford University, SU2. In this regard, the use of shape optimization along the wing cord was shown to improve noise efficiency. In that study, a rod-and-wing design was investigated, with the rod upstream and the wing downstream. It was feasible to optimize the form of the airfoil with different degrees of freedom by creating FFD boxes around it. The optimization technique addressed the noise reduction issue for the 2D and 3D geometries, once without and once with constraints on the minimum lift coefficient. As a result of the optimization, waves were generated in the direction of the wing chord, causing the vortices that generate the noise to remain near the surface. According to the results, the LE should be more rounded in optimum conditions, while the wing thickness has not reduced considerably. However, while the authors have used mathematical constraints to limit the reduction in the lift coefficient owing to optimization, they have not indicated the changes in the drag coefficient, making the firmness of the produced results uncertain.

3.2. Metamodeling Algorithms

While most optimization techniques need to accumulate datasets to rely on, the expensive aeroacoustic analysis limits researchers’ ability to easily obtain this foundation [161]. Therefore, many researchers employed surrogate modeling techniques, also known as metamodeling, to approximate the behavior and eventually optimize these complex and computationally expensive simulations and functions [162,163,164]. Surrogate models are mathematical models or algorithms that cover a wide range of methods, including Polynomial Regression [165], Response Surface Methodology (RSM) [166], Kriging (Gaussian Process Regression) [141,167], Support Vector Regression (SVR) [168], Reduced-Order Modeling (ROM) [169], and Artificial Neural Networks (ANNs) [170,171]. These surrogate models can expand the size of datasets or serve as efficient replacements for the original simulations or analytical functions to significantly reduce computational costs while providing reasonably accurate predictions.

Reduced-order models (ROMs) help simplify high-fidelity, complex models and predict the behavior of the source models with the fewest computer resources. ROMs create physics-based computer models that are quick to analyze and trustworthy enough for different static, transient, linear, and nonlinear systems [172]. However, adopting ROM-compatible Computational Fluid Dynamics (CFD) simulation tools can be quite useful. Ansys Fluent can evaluate a design by capturing the accuracy of a 3D model using a ROM, while a complete 3D CFD analysis might take hours to simulate. Coupling this technique with aeroacoustic hybrid methodology is a decent method to address flow-induced noise reduction in different areas, from wind turbines to fixed wings or even the automotive industry [173].

The combination of ROMs and data-driven methodologies is known as a popular solution to bypass expensive and time-consuming high-fidelity CFD simulations. Li et al. [174] represented a real-time, data-intensive methodology for high-fidelity wing shape optimization. As a replacement for the computational fluid dynamic simulations, they built quick and precise data-based frameworks to perform aerodynamic assessments. The big database they used to train their models included samples with various flight heights, flying speeds, and aerodynamic design forms. These models proved to be accurate in comparison with fluid dynamics results. Additionally, they tested the models in several single-point, multi-point, and multi-objective optimization scenarios, which tended to be reliable in their predictions. This approach applies to other nonlinear and complicated engineering problems, like noise reduction in aerial structures. Brown et al. [175] used a ROM approach to predict the far-field noise generated by low-speed pusher-propeller configurations. The authors used a benchmark experimental setup to measure unsteady flow characterizations, on-blade pressure measurements, and the generated far-field noise. They then compared the test results with the estimated intermittent blade-loading data, resulting from the combination of FW-H calculations of acoustic sources with already-existing indicial gust-response functions. Results showed that the combination of high prediction accuracy and low computational cost of the discussed ROM system could be an advantage in aeroacoustic analyses.

Using ROMs, researchers can even enlarge the analysis domain by creating standalone applications to predict the overall scattered noise and bypass the considerable computational costs of simulating the design. Through a partnership with NASA, Lopes et al. [176] presented a comprehensive program to estimate airplane noise named ANOPP2. The authors created this architecture to ease combining acoustic methods with different fidelity levels through conventional and non-conventional investigations of aircraft noise. They built this model using a foundation of mixed-fidelity models that consider scattered sources, installation effects, and propagation across a non-uniform environment, including refraction and the impact of topography. Results were presented with model-scaled jet noise predictions utilizing high fidelity and ROMs as examples of how this application might provide predictions for model-scale test setups.

ANNs are one of the most widely used types of ROMs that researchers in fluid analysis use to forecast how well the suggested geometries would function [177]. Furthermore, another area for optimization algorithms to showcase their advantageous role is dealing with data-driven [4,178] and decision-making [179] problems, in which optimization tools can integrate ANN and machine learning models to improve the accuracy of predictions. Li et al. [180] published their investigations on deep learning-based geometric filtering ANN to design the optimum airfoil from a circle. Free-Form Deformation (FFD) boxes [181] around the base design gave them the needed degrees of freedom to filter out non-physical or unrealistic design shapes and generate the most functional possible airfoil. This method was tested on two single-objective and multi-objective design problems. Results demonstrate the proposed method can effectively improve optimization performance and reduce optimization time compared to traditional methods. For the single-objective optimization problem, the proposed method achieved a lower drag coefficient and a higher lift coefficient while reducing optimization time by 40%. For the multi-objective optimization problem, the technique found a Pareto-optimal set of designs, while the traditional method failed to find any acceptable solutions. With these results, the authors have highlighted the potential of deep learning techniques in improving the efficiency and effectiveness of aerodynamic shape optimization.

ANNs are suitable for expressing nonlinear functions and correlations in aeroacoustic problems since they can effectively encode information in a few latent variables [94]. Using flow modal decomposition and regression analysis, Lui et al. [182] proposed a numerical approach for building this form of fluid flow ROM model. They used spectral proper orthogonal decomposition to filter the proper orthogonal decomposition temporal modes and minimize the dimensions. The authors implemented the regression using a Deep Feed-forward Neural Network (DNN) in a setting akin to the sparse identification of nonlinear dynamics approach. They assessed the performance of the model on several test scenarios, including as a classic nonlinear oscillator, compressible flow through a cylinder, and turbulent flow around a plunging airfoil under dynamic stall, to optimize the DNN hyperparameters to produce the best ROMs. According to their findings, the ROM model accurately depicts the dynamics of several flow characteristics, and the DNN technique surpasses sparse regression in terms of the accuracy and stability of long-term predictions. Rastgoo et al. [183] suggested a forecasting strategy employing a hybrid ANN/optimization framework of the CatBoost algorithm to construct a technique for quick, efficient, and precise aeroacoustic design of airfoils. The authors adjusted CatBoost’s hyperparameters to improve prediction accuracy and speed. The authors used statistical assessment indicators like the coefficient of determination (R²), Root Mean Square Error (RMSE), Mean Squared Error (MSE), and Mean Absolute Error (MAE) to assess the precision of the hybrid models. Their findings demonstrate that, in comparison to other models, the CatBoost and Arithmetic Optimization Algorithm pair performs better and displays lower error values.

Although the ROMs have shown significant capabilities in capturing essential features of complex aeroacoustic problems while reducing computational costs, they have some limitations that should be considered. The challenges these models face are not limited to the accuracy of predictions or the validity of assumptions. Since the flow behavior changes significantly depending on the Reynolds number, ROMs are applicable to certain flow conditions whose data is available and valid for accurate extrapolation [184,185]. On the other hand, building reliable ROMs requires significant training and validation data from full-order simulations or experimental measurements with a proper Design of Experiments (DoE). Therefore, substantial computational cost is needed to build an accurate dataset that conveys any possible faults into the predicted models [186,187]. However, ROMs might not fully account for all aspects of turbulence, leading to potential inaccuracies in noise predictions. Nonetheless, it is worth emphasizing that while ROMs cannot replace aeroacoustics and numerical modeling, they can be regarded as reliable supplementary methods, as researchers still need expertise and hands-on knowledge in the field. Hence, despite these limitations, ROMs remain valuable tools for preliminary noise assessments and design optimization as they strike a balance between computational efficiency and accuracy, making them useful in various engineering applications.

4. Passive Noise Reduction Mechanisms

The noise reduction techniques are divided into active or passive flow management methods [188]. The active kind, such as plasma actuators or synthetic jets, involves the controlled alteration of flow-field parameters. On the other hand, passive techniques usually modify the shape or surface of the airfoil to reduce noise [189]. Because active noise control is usually more expensive and involves added maintenance requirements, passive noise control methods are more popular. Therefore, only the latter, with a focus on more recent advancements, is discussed in the current review study.

The design of an airfoil is the key parameter influencing the frequency and intensity of the generated noise in any flow condition. Design modifications of lifting parts are essential for passive noise reduction involving high-lift devices, wings, and blades. This task involves various techniques such as LE and TE treatments, controlled diffusion airfoils, porous materials, morphing wings, and surface treatments [190]. By combining these techniques with numerical, analytical, and experimental methods, engineers and researchers can predict and optimize airfoil designs. The following sections discuss these approaches and techniques.

4.1. Edge Treatment Methods

LE and TE noise are two distinct types of generated self-noise in different locations on the airfoil, resulting from various interactions between pressure fluctuations in wake and BL [191] and/or the surface [13]. The front edge of the airfoil causes LE noise with different phenomena. TE noise, on the other hand, is generated at the rear edge of the airfoil due to the interactions between the upper and lower surface flows as they rejoin at the airfoil TE. There are specific passive modifications for both TE and LE noise reduction explained in the subsequent subsections.

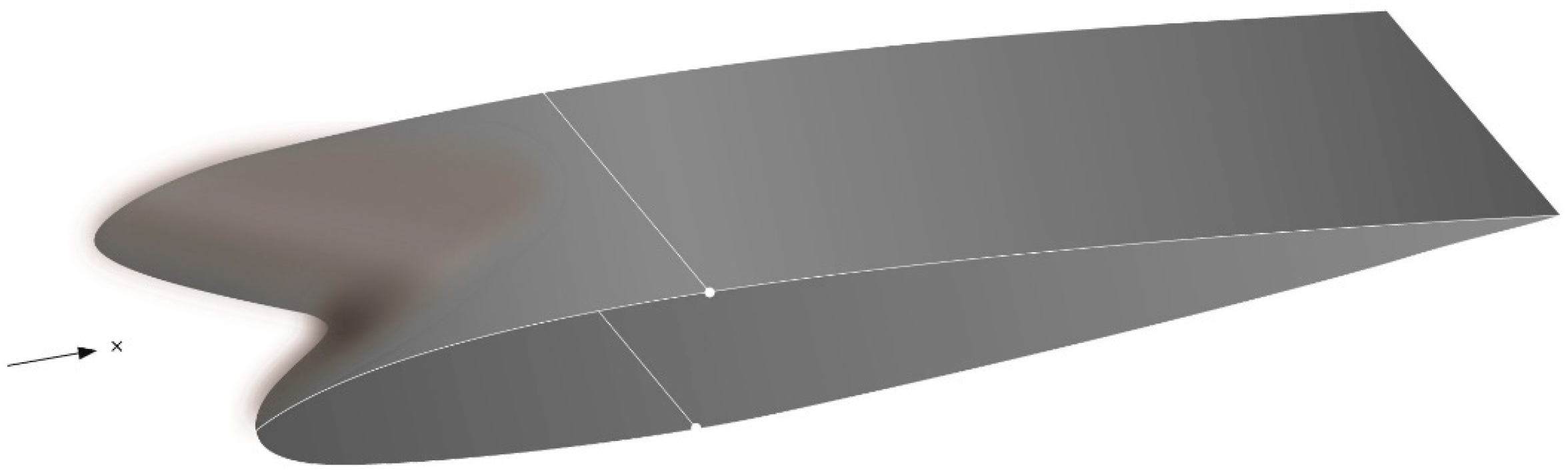
4.1.1. Leading Edge Treatments

There are several types of LE noise, with tonal, broadband, and screech frequencies, each with distinct characteristics depending on the airfoil shape, AoA, and flow regime [192,193,194]. Different flow–surface interactions and the corresponding phenomena cause LE noise, such as unsteady input turbulent fluctuation [195] and laminar flow separation [196]. Furthermore, the different types of LE noise can interact and combine in complex ways, contributing to the overall noise signature of an aerodynamic frame [197]. Some of the geometric design modifications that aim to reduce LE noise are discussed below.

LE modifications are among the most promising options for improving the overall noise characteristics of wings, and the researchers have introduced a wide variety of novel designs in this area. Kim et al. [198] performed research on optimizing the aerodynamic and aeroacoustic performance of a NACA 65-(12)10 airfoil by introducing sinusoidal Leading Edge Undulation (LEU) to the LE. The authors carried out wind tunnel tests with three alternative LE profiles. Not only were these improvements effective in improving the lift coefficient without compromising the drag coefficient, but they also displayed noise reduction effects through the entire frequency range. PIV measurements were also used to investigate the impacts of the LEU profile on TE on flow characteristics and discovered that turbulence generated at LEU peaks via the production of streamwise vortices aids in the reattachment of the flow whenever it separates.

As mentioned earlier, optimization methods for the airfoil profiles can be a game changer in airfoil design and the aerospace industry. With a focus on aerodynamic performance, Lu et al. [199] investigated the optimization of the bio-inspired wing with LE tubercles. Aiming to delay stall and increase lift, the authors generated a dataset containing random wavy configurations (Figure 4) using a parameterized approach with F-spline curves and evaluated those using CFD computations. The optimum designs were then achieved by employing the Non-dominated Sorting GA [134] and RSM [200] based on the Kriging Model [126].

An optimum LE serration geometry can significantly lower the total noise. Lyu et al. [201] offered a method to create an optimum LE profile with minimal overall noise deterioration at low frequencies by proposing an ogee-shaped serration profile. The authors demonstrated that the serration profile should not include stationary spots in order to obtain higher noise reduction at high frequencies. They showed that sharper serrations around the non-smooth points generate higher noise levels; therefore, they proposed stationary point-free piece-wise smooth curves. The authors verified these findings via experimental tests.

Because of its nature of creating semi-periodic shedding wakes, the rod-airfoil configuration is a popular geometry to benchmark the flow conditions and noise in turbomachinery devices [202,203]. This becomes more significant when considering that the impact of turbulent wake shed by an upstream rod causes aerodynamic excitation of the airfoils in turbomachinery systems. The generated turbulence results in unsteady loads on the airfoil, acting as dipole noise sources on the wing. Agrawal et al. [204] used incompressible LES followed by Curle’s acoustic analogy [205] to investigate the effect of sinusoidal serrated LE geometries (Figure 5) on generated wing noise. Based on their results, the far-field noise spectra were reduced in the mid-to-high-frequency ranges, given that the LE serrations decrease unstable loads on the airfoil, diminish coherence along the span, and enhance spanwise phase variation.

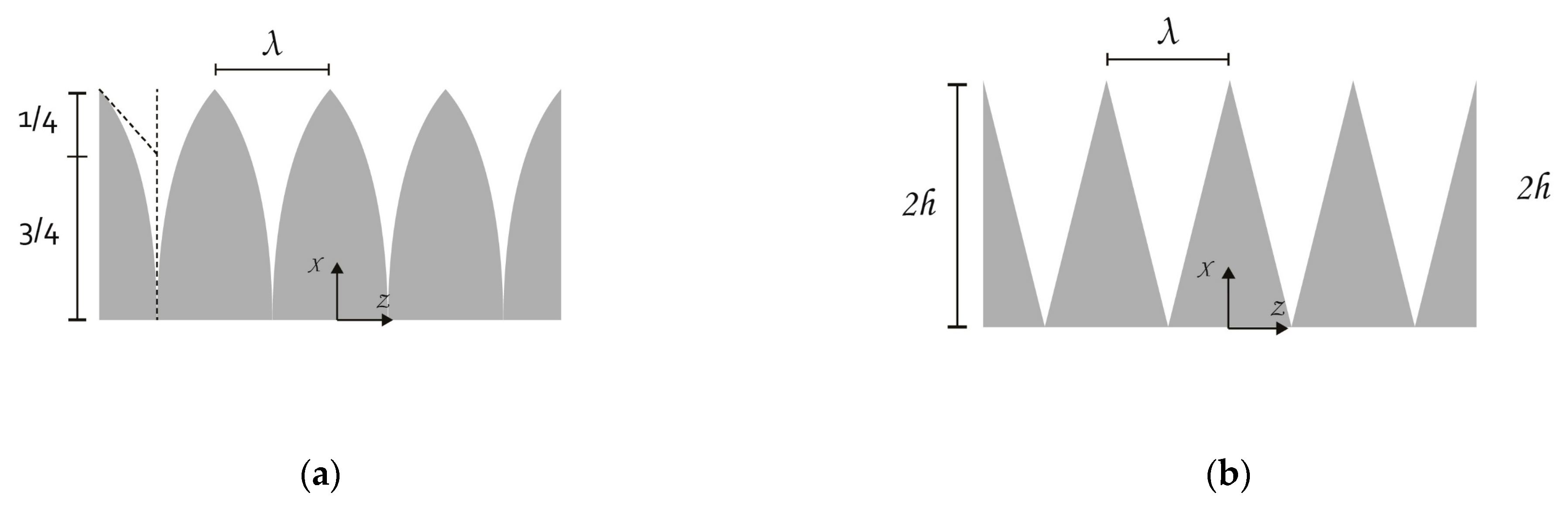
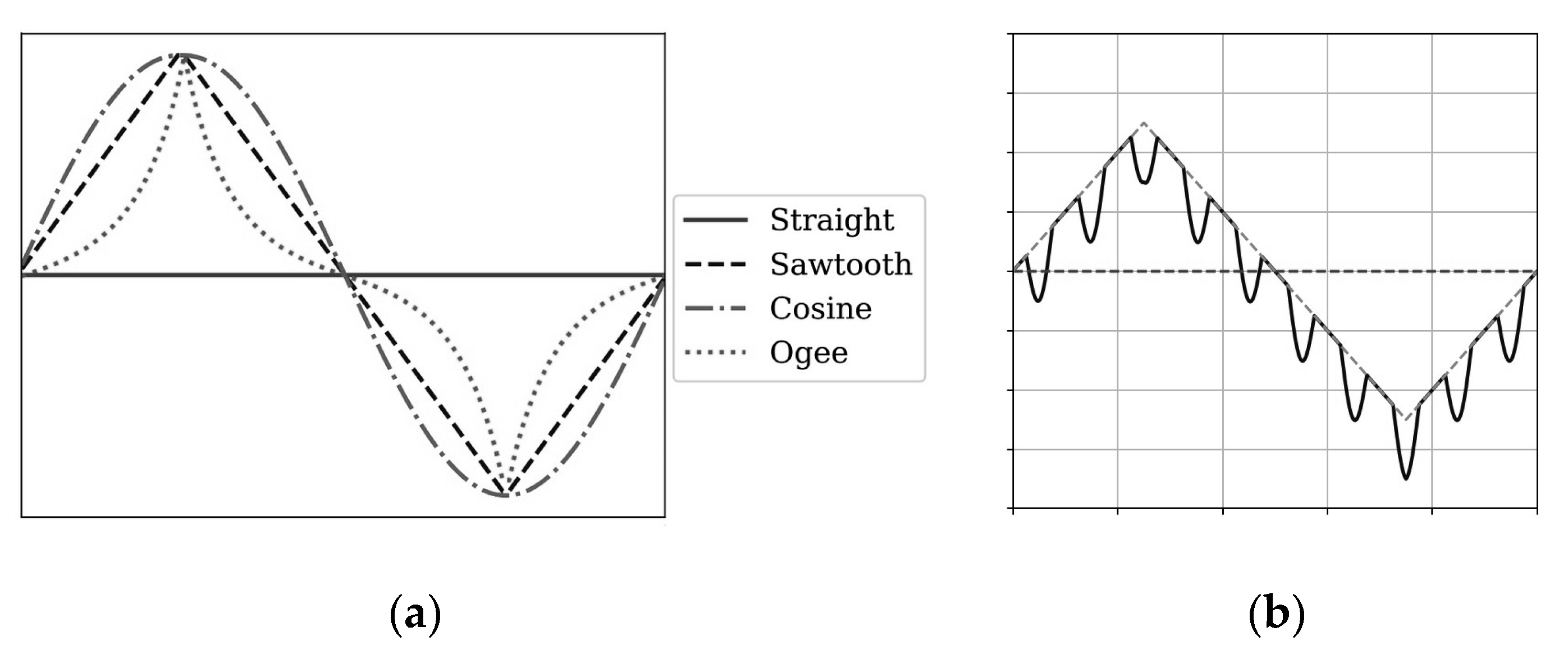
4.1.2. Trailing Edge Treatments

When fluid flows over a smooth TE, vortices tend to form at the edge due to the pressure difference between the upper and lower surfaces of the airfoil [206,207]. These vortices can create tonal noise as they shed and interact with the downstream flow [208]. TE serrations, also known as sawtooth or notched TEs, are a design feature to mitigate these noise sources [209]. These serrations are essentially small notches or teeth along the TE of an airfoil or blade, employed in engineering applications such as wind turbines [210], aircraft wings [211], and fan blades [212] to reduce aeroacoustic noise. In general, TE serrations offer a potential solution for decreasing aeroacoustic noise by disrupting vortex shedding, enhancing BL stability, and diffusing sound waves, as explained in the following:

• Vortex-Shedding Suppression: TE serrations can limit the VS process by breaking up the coherent vortex structures into smaller eddies that disrupt the periodic shedding of vortices and reduce tonal noise [213].
• Boundary Layer Stability: The TBL tends to be more stable and less prone to separation and associated noise generation [214]. Serrations can alter the airflow BL characteristics and trip the BL over the length of the serrations, which leads to a transition from laminar to turbulent flow closer to the TE [215].
• Noise Diffusion: The serrations create multiple smaller flow features along the TE instead of larger ones on a single sharp edge. This multiplicity of smaller eddies causes the sound waves generated by the airflow to diffract and scatter more, resulting in noise diffusion. The diffused noise is spread across a wider frequency spectrum, often leading to a reduction in overall noise levels [216].

In terms of profile and design footprint, TE serrations are divided into various forms such as simple, multi-height random [199], iron-shaped [217], tapered [218], asymmetric [213,219], and non-uniformly spaced [220]. All these profiles fall under the flat plate or non-flat serration TEs. The difference between these two types of designs is explained as follows:

• Flat-plate trailing edge

Flat-plate TE attachments are another call for splitters that are used for reducing aeroacoustic noise in low Reynolds numbers [221]. Serrated flat plate inserts, or even un-serrated ones, are among the most effective designs for noise reduction when attached to the wings [222]. The geometrical dimensions of splitters are critical to their noise reduction performance [223]. Jones and Sandberg [224] employed DNS to examine how the airflow through a NACA-0012 interacted and investigate how flat-plate TE splitters affected noise reduction. The authors studied TE splitters with and without serrations in both their long and short geometries. They reported that longer serrated TE splitters produce higher TE noise reduction.

Concerning non-serrated splitters, Song [225] explored the aerodynamic and aeroacoustic characteristics of a wind turbine airfoil. In particular, the author applied the Improved Delayed Detached Eddy Simulation (IDDES) approach to examine the TU Delft DU97-W-300 airfoil, modified to have a flat rear trailing edge or a non-serrated splitter plate. The results were then confirmed using experimental data, with a focus on the intensity and frequency of VS tonal noise from the trailing edge wake. The outcomes showed that adding a splitter plate to the trailing edge significantly influences the wake flows, resulting in decreased drag and noise levels.

Likewise, additional studies suggest that sawtooth edges are effective geometries for reducing synchronization between audio sources, resulting in an acoustic emission phase transition along the wetted edge [226,227,228]. Therefore, wideband noise is decreased as a result of the destructive acoustic interaction between these different dispersion sources [229,230,231]. However, the flat TE serrations (Figure 6) have inevitable negative impacts on the aerodynamic performance and the lifespan of the wings. Llorente et al. [232] showed that these add-on components might increase both lift and drag coefficients, but they do not have a considerable effect on the stall angle.

Chong et al. [233] presented the findings from an experimental investigation on turbulent flow over a flat plate configuration equipped with a serrated sawtooth TE to examine the impact on broadband noise. The authors used hot-wire anemometry, far-field microphones, near-field remote microphones, acoustic beamforming, and liquid crystal techniques for both wide-angle and narrow-angle sawtooth configurations. The study concentrated on the temperature and velocity characteristics of the TBL on a saw-toothed surface to determine the link between noise produced and near-field measurements. The BL was forced to be turbulent, and experimental methods were used to investigate the broadband noise sources at the saw-tooth-serrated TE. Here, the interaction between the local TBL and the vortical structures causes self-noise radiation. The effectiveness of the generated noise complies with the redistribution of turbulent shear stress and momentum transport around the sawtooth side edges and tip. The authors observed that the wall pressure Power Spectral Density (PSD) is lower between the sawtooth tips and side edges while it is still in the same frequency range. For the mechanisms behind the decrease in self-noise radiation, the correlation length in a sawtooth TE and the fluctuations of wall pressure PSD are only marginally significant. Additionally, the authors demonstrated that the prominent fluctuating components are primarily near the sawtooth tip. A higher frequency will cause these structures to change to sawtooth side edges and gradually vanish outside the frequency range, where noise reduction stops working.

Some noise reduction mechanisms can have unwanted side effects or even cause additional noise on the lifting surface at different frequencies. Tang et al. [234] published the results of a numerical analysis to check noise reduction mechanisms at low Mach numbers in wings with TE serrations. They used LES and the Lighthill–Curle technique [32,235] to predict changes in the aerodynamic field and sound sources caused by the TE serrations. According to their results, TE serrations prevent the formation of spanwise vortices while promoting the formation of streamwise vortices near the TE and wake. On the other hand, since other noise sources could partially obscure the noise-reduction advantages of the flat plate serrations, there might be some discrepancy between observed and predicted noise reductions. One example consists of the negative pressure gradient on the suction surface flat plate serrations, which may be large enough to cause turbulent dispersion and additional noise sources in certain conditions.

Gruber et al. [236] published a study on noise reduction mechanisms caused by serrations and proposed a relation between the TE geometry and the frequency and intensity of the scattered noise. Their experimental investigation on more than 30 different geometries showed that regardless of the dimensions of the serrations, the produced noise increases at frequencies higher than the related frequency to the Strouhal number equal to one. Furthermore, they showed that sharper serrations with higher height-to-pitch ratios are more efficient at reducing noise. Using hot-wire measurements, they located some noise sources in the early wake. By comparing results obtained from their data with Howe’s theory [48,49], they found that in addition to the increase in noise at high frequencies, the amount of noise reduction in practice is much lower than the value predicted by the theory.

Avallone et al. [237] investigated the iron-shaped curved TE far-field noise and flow field over this serration shape. The authors picked a triangular-shaped TE serration on a NACA 0018 airfoil as the case study to extract the spectra of the far-field broadband noise, to investigate directivity and flow field across the serration profile through numerical calculations using a compressible lattice Boltzmann solver [238]. When the chord-based Strouhal number is under 15, they claimed that the iron-shaped design (Figure 7) decreases far-field broadband noise by around 2 dB more than the traditional sawtooth serration while having equivalent strength at higher frequencies. Additionally, they demonstrated that the intensity and spectrum of the near-wall velocity profile and SPF are independent of the serration architecture but rather a function of the streamwise position. The authors also suggest that mitigation of the scattered noise at the root is the mechanism that causes improved noise reduction. By postponing the downward and outward flow movements at the roots, this phenomenon minimizes the interactions between the sides of the serration.

Another parameter that can alter the noise reduction in plate–plate TE inserts is their relative angle to the main airfoil. Woodhead et al. [239] evaluated the aeroacoustics characteristics of an asymmetric airfoil exposed to a range of positive and negative serrated TE lap angles. In the flap-down arrangement, they discovered that the blade loading turns into a problematic element that compromises the noise reduction efficacy throughout the whole frequency range. The authors looked at the flap-up layout in three frequency zones. The reduced cross flow at the sawtooth gaps altered the noise reduction in the lower frequency region. Reallocating the turbulent sources and shortening the turbulence spanwise length scales boosted noise reduction efficiency in the mid-frequency domain. Because the cross-flow and sawtooth shape do not interfere in the high-frequency band, noise reduction may also be enhanced there. Furthermore, in their study of the impact of adding varying serrated TE orientations on the self-noise radiation of an airfoil, Woodhead et al. [240] published another study with the experimental findings from wake flow measurements and aeroacoustic analysis. After examining five different serration-angle configurations, the authors discovered that, compared to a regular flat serration, a more intense spanwise deformation of the serration could exceed noise reduction efficiency in the middle to high-frequency ranges while remaining at the same level at low frequencies. Furthermore, Vathylakis et al. [222] covered the effect of serration flap angle on the generated self-noise of an airfoil. After evaluating various flap angles between −15 and 15 degrees, they reported that a positive flap angle (flap-up) is preferable to a negative flap angle (flap-down) for broadband noise reduction. The authors demonstrated that the best and worst flap angles are modest positive and negative values, respectively. This means that the serration effect is vulnerable to tiny changes in flap angle, and even a slight deviation could compromise the overall effectiveness of the self-noise reduction.

TE serrations can act as an effective solution for noise reduction. Therefore, obtaining their optimal dimensional parameters is a significant research goal to achieve maximum noise reduction. Kholodov et al. [241] published a paper investigating the effects of serration amplitude, length, slits, and shape function (Figure 8) on the amount of noise reduction in wings. The authors solved the surrogate-based optimization problem using Ayton’s analytical model [242,243] for both serrations with and without slits. According to their report, the amplitude and wavelength of the serrations have a non-linear effect on noise reduction. Generally, for a specific serration design, the highest noise reduction occurs when the serration amplitude and the wavelength are the highest and least possible amounts, respectively. This is while their ratio has no discernible effect on noise reduction. They also stated that the sharper serrations result in higher noise reduction. The authors reported that the optimum shape function of the serrations with the slowest noise also depends on their wavelengths. In general, when increasing the serration wavelengths, its optimal form gradually transitions from ogee to simple triangular form and then to sinusoidal or iron shape (Figure 8a). The impact of slits occurs when they are combined. The installed slits around the margins of serrations create extra modal scattering, while isolated ones do not have scattering effects. The authors demonstrated that optimum airfoils with the minimum possible serration wavelength result in a large 21 dB reduction in noise compared to the straight TE. Furthermore, it was concluded that the slits could further reduce the noise by up to 11 dB.

Ayton et al. [243] analytically investigated the aerodynamic noise due to a spanwise-variable TE while disregarding viscous and nonlinear effects. The Wiener–Hopf approach [244,245,246,247], along with a non-orthogonal coordinate transformation [248] and variable separation, contributed to the analytical development of the study. Their mathematical solution revealed the probable explanations behind the noise reduction for different serrated TEs, including sawtooth, slitted v/u-shaped root, chopped peak, and square wave designs. They showed increased destructive interference in the distant field, in which a transfer of acoustic energy from low cut-on modes to higher cut-off modes is a possible cause for the underlying noise reduction. By looking at separate test cases with TE designs at various frequency ranges, their analytical solution determined that the best TE shapes are those that boost destructive interference at lower frequencies. In comparison, the best ones at higher frequencies are the ones that encourage energy redistribution.

Noise can become a substantial variable in some cases, such as in the design of wind turbine blades, since their noise can be annoying, especially when installed in wind farms. TE noise and the Doppler amplification effect of the blade movement can combine to create a swishing sound in wind turbine blades [1]. In their paper, Zhou et al. [249] investigated the performance of wind turbine blades with an optimal design for TE serrations. They used the simulation tool Bladed and the airfoil analysis tool Rfoil to predict the aerodynamic performance of the wind turbine. The lift-to-drag ratio of the corresponding optimized serrations improved under most of the operational AoAs. They showed that adding optimum-designed TE serrations to the blades reduces noise while increasing power output at the expense of augmenting blade load.

Xue et al. [18] implemented experimental investigations in an anechoic wind tunnel to find the effects of different TE serrations on the generated noise from wind turbine blades. They used two distinct NACA airfoils and one base plate with different detachable sawtooth TEs as the three geometries employed in their studies. Results showed that the sawtooth TE could be used as an effective solution for noise reduction in mid-high-frequency wideband noise, especially in lower AoAs. Furthermore, they investigated the correlation of serration height, width, and the width-to-height ratio on noise reduction and reported that the former has the greatest impact. They also highlighted how important streamwise variable velocity at the serrated TE is to the effectiveness of noise reduction.

Nonetheless, serrated flat-plate TEs might change the wing footprint, which means that the overall airflow over the airfoil will probably differ from what it was before, and the aerodynamic characteristics of the airfoil will consequently change. They can even potentially increase the high-frequency noise because of improper alignment [250,251]. Furthermore, maintaining the structural integrity of the flat plate serration inserts for high-load operations is a challenging task that may hinder the broad use of this design in various industrial applications [252].

• Non-flat trailing edge

As previously mentioned, despite the fact that flat-plate serrations show potential for reducing tonal noise, their limited application range, potential misalignment issues, and changes to the airfoil footprint prevent them from being the best option in this regard. Therefore, using non-flat plate serrations (i.e., cutting the serration patterns directly into the airfoil body) is a better configuration to maintain structural integrity and the airfoil design.

For non-flat serrations, the geometric parameters, such as the length and angle of the serrations, will impact the ability to reduce noise. Chong et al. [253] published the results of an experimental investigation that attempted to lower airfoil self-noise with distinct non-flat sawtooth designs on the TE. Through wind tunnel testing, they investigated four different non-flat serrations on a NACA airfoil with embedded sensing holes on both surfaces of the mid-span plane along the chord to monitor the variations in wall pressure. They also used water tunnel experiments and non-dimensional calculations to show how the frequency of the vortices sinks with the TE shedding noise. Results show that non-flat serrated TEs can reduce the noise for both boundary-layer instability tonal noise and turbulent broadband noise [253,254]. However, the extraneous vortex noise exists at a narrowband frequency because of the relative bluntness at the serration roots [252,255]. Here, noise reduction was observed to be higher while using smaller serration angles, with a wide serration angle and a small serration length; however, this narrowband component seems to become less relevant [252,256]. By measuring the sound levels, the authors demonstrated that several sawtooth shapes offer considerable reductions in boundary-layer instability tonal noise while providing reasonable improvements in turbulent broadband noise over a wide range of velocities. They concluded that for a serrated TE to reduce boundary-layer instability tonal noise, boundary-layer detachment must occur before the start of the serrated TE. Furthermore, the serration angle (φ) must be sufficiently large to achieve more extensive flow mixing around the blunt roots. Results show that non-flat serrations outperform flat plate plugs in terms of noise performance at high frequencies. However, because the study involved aerodynamic and aeroacoustic measurements performed in different wind tunnels, they could not compare those directly to investigate noise generation mechanisms.

The use of non-flat plate serrations can be effective in reducing broadband noise across the frequency range; however, the total noise reduction is hampered by a significant amount of bluntness-induced narrowband VS noise, mostly at lower frequencies. Therefore, most of the published literature related to non-flat serration TE focuses on this aforementioned bluntness-induced noise. Analytical and experimental results published by earlier authors showed that TE bluntness noise happens if the TE thickness is greater than 20% of the thickness of the BL displacement [13,106,218].

When adopting non-flat TEs, bluntness-induced noise can be a substantial source of the noise. Al Tlua and Rocha [257] used empirical models combined with precise aeroacoustics measurements in a wind tunnel to examine the impact of TE bluntness on the production of airfoil tonal noise at various AoAs and up to medium Reynolds numbers. According to their findings for a straight TE, increasing the AoA causes the airfoil noise to transform from a broadband peak to an intense tonal noise, while increasing the Reynolds number has the opposite effect. The experimental data indicated that the amplitude of the prominent tonal peak drops and moves to higher frequencies as the Reynolds number is increased. In another study, the same authors [258] published a parametric optimization analysis of TE serrations in order to reduce TBL–TE noise. To explore the noise spectra generated by three distinct serration layouts, the authors employed the Howe semi-empirical model, accompanied by experimental wind tunnel tests. A NACA 0012 airfoil and modeled semi-infinite flat plates at zero AoAs and low Mach numbers were analyzed to investigate the effects of serration design parameters on the noise spectra. Their findings show that sawtooth-serrated TEs reduce noise more effectively than slitted or sinusoidal TE designs. Furthermore, Van Blitterswyk and Rocha [259] conducted research to understand the connection between wall pressure and turbulence for noise reduction strategies. They analyzed wall-pressure fluctuations induced by turbulent BLs using a high-resolution microphone array. The findings showed that turbulent activity in the buffer layer contributes significant energy to the wall-pressure spectrum at all frequencies. The authors showed that as the Reynolds number increases, low-frequency energy shifts to the logarithmic layer due to hairpin packets, and most of the broadband wall-pressure energy is concentrated within these packets, which retain their signature for several BL thicknesses.

Maddula et al. [260] used the BPM model to investigate the effect of TE thickness on the bluntness noise generated in the wind turbine blades. Using the original BPM model, they carried out modeling of the TE-bluntness-VS noise for a horizontal-axis wind turbine, with TE thicknesses between 0.1% and 0.5% of the local chord. The authors showed that the sound power level increases by roughly 17 dB for frequencies higher than 200 Hz when the TE height is raised from 0.1% to 0.5% of the local chord but reduces by 16 dB when the thickness is only 0.1% of the local chord. The TE bluntness noise predominates in the moderate-to-high-frequency region, as the blades are thicker. The OSPL simulation results were validated with peer data from land field measurements, with good agreement for the 10 kHz frequency, where the TE bluntness noise was prominent.

However, the BPM method is likely to over-predict the generated noise at high frequencies because of its inability to accurately predict noise from blunt TEs. To enhance this lack of accuracy, Wei et al. [261] proposed a modified formulation. Using a semi-empirical model and an advanced high-order CAA approach, the authors explored the intricacies of the bluntness-noise-generating process. They showed that bluntness noise deteriorates if the BL thickness exceeds the blunt TE thickness. Because the thickness of the blunt TE is usually thin, they also observed the VS behind the TE, which causes high-frequency noise. The authors used the second-order finite volume EllipSys code [262,263,264] to solve the incompressible Navier–Stokes equations [265,266] through 2D CAA calculations and a sixth-order optimized compact scheme to solve the acoustic equations. The results demonstrated that the blunt TE boosts high-frequency noise, shifting towards higher frequencies as free-stream speeds increase. The authors scaled the experimental data from a NACA 0012 airfoil to create the BPM model and interpolated between this airfoil and a flat plate extension to streamline other types of TE geometries. Consequently, they revised the general shape function suggested by the initial BPM model to look at how the shape function affects the TE tonal noise peak formed in the high-frequency portion of the sound spectrum. They used XFOIL to calculate the BL thickness fitted to the existing experimental data to obtain the SPL and the spectra, independent from the solid angle between the TE surfaces and as a function of Mach number, Strouhal number, BL displacement thickness, and other parameters.

The low-frequency narrowband bluntness-induced noise, produced at the sawtooth root, restricts the overall noise reduction in non-flat TEs. The key to solving this problem is to possibly reduce the blunt areas of the TE, which is a challenge when using non-flat serrations. Feng et al. [267] published their study on reducing this effect by adding wedge-shaped transition structures (Figure 9) within the sawtooth gaps. They simulated the flow around the airfoil with different heights for the wedge-shaped structures and employed the optimal configuration for verification test spectra using Welch’s method. Based on their report, this arrangement can weaken the VS noise by accelerating the fragmentation of large-scale spanwise vortices near the sawtooth root. Additionally, compared to the non-flat plate with serrated TE, this modification facilitates transverse flow. It lowers the broadband noise across most frequencies by creating counter-rotating oblique vortices farther forward within the sawtooth gap. The wedge-shaped design reduces the pressure difference between the upper and lower surfaces, and the generated oblique vortices promote transverse flow, which reduces the near-field surface pressure level. However, the effect of wedge heights on noise reduction is not linear. As the height increases, the noise reduction first increases and then decreases, with an optimal point occurring in between. This design suppresses the narrowband shedding noise.

4.2. Porous Materials

Another approach used for noise reduction in wings is the use of porous materials on the airfoil body. Mainly, when the TE is manufactured from porous materials, it is observed that the turbulent broadband noise at the TE might be reduced [268,269]. Although porous materials have been applied to the LE, TE, and even the full body of an airfoil, researchers have preferred focusing more on their noise reduction benefits in the TE alone [270,271,272]. The air flow resistivity describes a porous material by evaluating the pressure drop across the medium. In general, if the TE has a low flow resistivity, transverse flow is more likely to begin by through-flow at the porous medium close to the TE, resulting in a lower level of radiated broadband noise [273].

One of the pioneering studies on how porous surfaces impact noise generation in airfoils was published by Zamponi et al. [11]. By using a porous material in the airfoil, the scientists looked into the possibility of decreasing LE aeroacoustic-generated noise through turbulence interaction with the wing profile. Researchers sought to understand and explain the underlying physical processes and how porosity affects the properties of turbulence close to the surface. As a result, they compared the performance of a solid baseline airfoil with a porous NACA-0024 using melamine foam when both airfoils were exposed to turbulence produced by an upstream circular rod configuration. The authors employed hot-wire anemometry and LES to analyze the mean wall-pressure distribution along the airfoils. According to the results, the porous design kept the airfoil profile shape and permitted a dampening of velocity variations without significantly changing the upstream mean flow field. They reported that the porous material reduced the upwash component of velocity variations [274], which resulted in a considerable reduction in turbulent kinetic energy in the stagnation area. Porosity largely influenced the low-frequency region of the turbulent velocities’ power spectrum, according to comparisons of their power spectral densities for incoming turbulent velocities. These findings were corroborated by acoustic beamforming tests, which revealed a similar noise decrease. Based on these observations, the researchers offered an explanation of the phenomena related to turbulent interaction noise reduction with a porous airfoil using the theoretical justification from the Rapid Distortion Theory [275,276].

Conducting experimental tests can help better understand the effect of using these materials in different areas of the airfoil. Carpio et al. [277] used a microphone-phased array and measured far-field noise over identical airfoils with solid and porous TEs at various chord-based Reynolds numbers and AoAs to look into how the porous media affected noise radiation. They tested three metal foams with different cell diameters and a similar inner structure. Their observations showed that the distribution of pressure is unaffected upstream by the porous media. However, there is still a lift reduction due to the variated pressure distribution along the porous part. The authors discovered that raising the AoA reduces noise suppression relative to the solid TE arrangement. This effect is more conspicuous at higher frequencies than at lower frequencies. Furthermore, the reliance on noise reduction on the AoA is more pertinent when using materials with lower flow resistivity and bigger cell sizes. The study also showed that, at lower velocities, stretching the porous insert along the cord boosts noise attenuation in the low-frequency range.

In order to evaluate the noise reduction mechanism of porous materials, Chaitanya et al. [278] carried out an empirical investigation. By adding porosity to three different areas of a flat plate on the airfoil, the study intended to reduce the noise resulting from turbulence–airfoil interactions (Figure 10). The authors postulated two key processes to explain the observed narrow-band noise reduction spectra and the related noise peaks by examining the noise reduction spectra versus the geometrical characteristics of the porous surface. By measuring noise improvements on a realistic airfoil, the validity of these processes was verified. Furthermore, the authors claimed that using just one row of holes downstream of the airfoil LE is sufficient for achieving considerable noise reduction. The researchers also showed how to exploit downstream porosity to provide low-frequency noise reductions without boosting higher-frequency radiated noise.

Simulating the interaction of the porous material with the flow is one of the challenges in the prediction of its effects on the BL and the scattered noise. Teruna et al. [279] used Very Large Eddy Simulation (VLES) simulations with a lattice Boltzmann solver on a NACA 0018 airfoil to investigate the effect of a porous insert TE on turbulent boundary-layer noise. To simulate the porous TE insert, the authors used the material properties of metal foam, replaced it with fluid layers in the simulation, and achieved similar properties. They calculated the resulting noise with the FW-H analogy and compared the noise obtained from this configuration for different flight modes with the noise from a solid wing. By dividing the wing surface into smaller strips and examining the noise, the authors concluded that the noise sources on the porous TE are in opposite phases to each other, which makes them cancel each other out and reduce the overall noise generated.

In another study, Teruna et al. [270] utilized a lattice Boltzmann practice to investigate the aeroacoustics and aerodynamics of airfoils with LE porosity and LE serrations in order to find the variations in noise reduction between these two treatments. They discovered that the porous LE reduces noise by decreasing the surface pressure variations due to a lower blocking effect than the solid one. The LE serrations, on the other hand, encourage destructive interference from noise sources along the span. Both methods generate comparable broadband noise reduction, although the latter is more successful when applied to turbulent intake with tone characteristics. For aerodynamic performance, a cross-flow is present through the porous material under lifting conditions, resulting in a loss in lift and an increase in drag.

Considering NACA 0018 with solid and porous TE inserts as the case study, Carpio et al. [280] looked into the aeroacoustic domains. They developed porous trailing implants that occupied 20% of the chord using two metal foams with differing permeabilities to perform experiments at two different Reynolds numbers and a zero AoA. The authors reported that a porous insert with more permeability has a better noise reduction effect compared to a solid airfoil when the Strouhal number is greater than 0.26, while for lower Strouhal numbers, lower permeability is preferred. The authors measured lower turbulence intensity when metal foam with lower permeability was used. Accordingly, they reported that one of the strategies for reducing low-frequency noise is lowering velocity fluctuations, which is especially pertinent for metal foam inserts with lesser permeability.

As a novel use of porous materials, Ayton et al. [281] looked at how turbulence-induced noise on airfoils will be affected by the gradually variable chordwise porosity of a finite perforated plate, a nature-inspired porosity concept. They created the aeroacoustics model by applying the novel Mathieu function collocation [282,283] rather than the standard Wiener–Hopf methodology [244,245,246,247], which cannot accommodate chordwise-varying values. Through the aeroacoustics mathematical model, they discovered that plates with constantly increasing porosity from zero at the LE to a certain quantity at the TE, as opposed to plates with unchanging porosity, deliver lower levels of TE noise.

As mentioned earlier, although non-flat serrations are one of the most promising solutions in noise reduction on airfoils, bluntness-induced VS tonal noise is still one of the hampering factors that concern the designers when using this method. In another study, Vathylakis et al. [284] published the results of their investigations to reduce this part of the noise. The authors developed a solution in which porous metals, synthesized foams, or tiny brush packages that fill the spaces between neighboring sawtooth members would potentially suppress bluntness noise. To significantly increase the overall noise reduction in non-flat plate serrations, they thought of filling the solid serration gaps (Figure 11) with a porous material, which they named the poro-serrated technique. This technique was tested by adding porous metal foams with different transparency degrees to the non-flat serrated TEs. The simulations and experimental results demonstrated that this technique controls the VS tonal noise produced by the blunt regions and does not result in noise increases over the tested frequency range. Additionally, the authors researched the best porous material choice, which would more efficiently lower broadband noise. They used different materials as the porous media, which included direct and reversed configurations of nickel–chromium foams and melamine foams. Airflow resistivity, porosity, density, surface finish, cell size, and number are only a few of the many properties of these materials that can affect how well they reduce generated noise. The authors chose to introduce melamine foams, which produced superior results compared to the other options explored.

Poro-serrated TE configurations contain porous materials with flow-resistant material at the gaps between the teeth of a non-flat serrated-sawtooth TE, capable of enhancing the aeroacoustic performance of the structure. Chong et al. [1] published their study on optimizing this design and investigated the co-existence of multiple mechanisms for broadband noise reduction. It is normally expected that the use of porous materials in serration gaps hampers their noise reduction effectiveness while trying to limit the bluntness of the noise. Therefore, there should be a trade-off between these two methods to achieve the most noise reduction. The authors defined a formula to evaluate noise reduction, the Noise Performance Metric (NPM), which uses the ratio of generated noise for serrated and flat designs and shows their effectiveness. Results for different configurations were compared to find the optimum noise reduction. The authors characterized different possible designs based on the serration angle (θ) and flow resistance (σ) to classify their noise reduction abilities. They assumed that σ = 0 represents simple serrations without any porous media used, in which σ = ∞ corresponds to a straight TE without any serrations. They reported that using low-flow resistivity porous material in the saw gaps does not suppress the low-frequency VS tone at high velocity, but a reasonable broadband noise reduction is observed. On the other hand, there is no VS tone when filling a very high flow resistivity porous material at the gaps, while the serration impact on the broadband noise reduction is less effective. The authors stated that an optimal flow resistivity for the porous material exists in between that reduces the typical serrated TE broadband noise while entirely suppressing the VS tone. Through the investigated airfoil configurations, they concluded that θ = 10 and σ = 10 k is the optimal configuration, adding up to an additional 1.5 dB in noise reduction while retaining the serration effects. According to their study, during the pre-stall regime, the lift and drag coefficients continue to perform much as per the baseline, straight TE case.

4.3. Controlled Diffusion Airfoils

Due to their specialized design for subsonic and transonic flow conditions, Controlled Diffusion (CD) airfoils are crucial for civil aviation and noise reduction investigations. Depending on the Reynolds number and AoA, the generated broadband noise due to stall and separation might have different characteristics [285,286]. However, over the full range of airfoil operation for transonic flow conditions, these airfoils prevent considerable BL detachment by controlling the diffusion of the airfoil section [286]. A large number of investigations, here introduced, have been carried out on CD airfoils in order to define the noise signature and attempt to reduce it.

Sanjose et al. [287] employed the lattice Boltzmann technique to model a CD airfoil with a serrated TE at a large Reynolds number in an open-jet wind tunnel setting. They determined the aerodynamic and acoustic fields by analyzing the aerodynamic loads, BL formation, and near-wake flow while comparing their findings with experimental data from non-serrated airfoils. The authors claimed that despite the fact that the turbulent wall-pressure fluctuations on the suction side are hardly altered, a minor lift loss exists with the non-flat serrated edge. On the other hand, the serrations also reduced the observed minor vortex scattering on the pressure side of the simple airfoil.

In a different study, Moreau and Sanjose et al. [288] employed experimental, analytical, and computational approaches to explore the broadband noise reduction brought on by TE serrations for CD airfoils. They used the lattice Boltzmann method to replicate the open-jet wind tunnel installation effects with DNS resolution around the simple and serrated airfoils. Regarding loading, wall-pressure variations, and far-field noise, they reported excellent agreement between the simulation results and experiments. Howe’s model overestimated the observed noise reduction. In contrast, Lyu and Ayton’s [242,243,289] model offered comparable gains that are better in line with the experimental database, with the latter model even nearly matching the frequency range and the noise levels. Overall, they found the flow characteristics were rarely changed before upstream the serrations and accomplished noise reduction (5 to 15 dB) at high frequencies (800 to 4500 Hz) by altering the diffraction process. In a later study, Sanjose et al. [290] performed a DNS of the flow field around a controlled diffusion airfoil within an anechoic wind tunnel, using a lattice Boltzmann method to assess the simulation data against measurements of wall pressure, wake metrics, and far-field noise. These simulations reproduced high-amplitude acoustic tones, as seen in experiments that climb above a broadband hump.

Regarding aeroacoustically optimal airfoil design, Kholodov et al. [291] published a study on the optimization of airfoil TE serrations for broadband noise reduction. To compute and optimize the TE noise produced by a CD airfoil, they employed the nested optimization approach based on the results from Ayton’s analytical model [242,243]. The study demonstrated that a combination of slitted and sharp designs results in better noise reduction when using serrations. Furthermore, it was noted that for each given form, the global wavelength and depth of the serrations had a non-linear influence on the ultimate noise suppression. In a different study, Kholodov et al. [292] predicted an optimal TE serration geometry (Figure 12) for a CD airfoil to achieve broadband noise reduction. For the prediction of broadband noise, they used Ayton’s analytical model [242,243]. Additionally, for determining the aerodynamic performance, they used third-order B-spline parametric 3D geometrical and numerical RANS simulations. The authors also conducted a series of tests for DoE to build surrogate models based on the Gaussian Process approach for aerodynamic performance. They carried out a design using constant thickness and rounded roots and tips to avoid additional design variables and the complexities resulting from three-dimensional serrations. With the lift-to-drag ratio and the moment as constraints, an optimization process was designed to maximize noise reduction. According to their findings, the lift-to-drag ratio and the pitching moment vary nonlinearly as the size of the serrations changes, and the optimum design could reduce the airfoil self-noise by approximately 15% compared to the straight TE.

4.4. Morphing Wings

Morphing wings, often referred to as adaptive or shape-changing, are mostly bio-inspired structures that have the ability to dynamically modify their configuration or shape [293]. These wings are usually used to produce superior aerodynamic and aeroacoustic performance for various flight situations, duties, or needs. The adaptable nature of the morphing wings allows them to continually change the shape of different regions of the airfoil without gaps or ridges on the wing surface while in flight [294,295]. Morphing wings inherently have a wide range of degrees of freedom to change form and, consequently, a lot of room for aerodynamic and aeroacoustic optimization [296]. Therefore, most of the available literature focuses on an optimization point of view to enhance the noise characteristics of this type of wing. Bashir et al. [297] developed a hybrid optimization strategy based on a PSO algorithm mixed with a pattern search algorithm to efficiently exploit the best morphing configurations over a wide variety of AoAs. They utilized the Bezier-PARSEC parameterization approach [298] on the Morphing Trailing Edge (MTE) and Droop Nose Leading Edge (DNLE) of a UAS-S45 root airfoil to reduce the drag coefficient and maximize endurance as two single-objective optimization functions. In their study, the authors employed the low-fidelity 2D solver XFoil together with the high-fidelity CFD solver Ansys Fluent. This research resulted in a more than 20% increase in the maximum lift coefficient and a 3° delay in the stall angle, followed by a delay in LE separation.

Maintaining the aerodynamic performance of morphing wings during different flight conditions is one of the current challenges. In this regard, Bashir et al. [299] published a study to determine the optimal camber morphing of airfoils under various flying situations. They used the Black Widow Optimization (BWO) algorithm to maximize the lift-to-drag ratio for the cruise and climb phases. However, because the optimization framework focused on an aerodynamic standpoint, it did not include noise analyses. In an additional study [300], Bashir et al. reported on the results of shape optimization of a camber adaptive winglet. They employed the same optimization platform as before to reduce drag for climb flight circumstances and maximum endurance for cruise flight conditions and to investigate the influence of varied restrictions on optimization accuracy.

Responsive control methods are essential for morphing airfoils to retain their intended form according to flight conditions. Kammegne et al. [301] implemented a control system on a novel morphing wing structure with a built-in miniature electromechanical actuation mechanism and flexible skin. A database created via aerodynamic optimization for specific flying circumstances provided the four vertical actuator displacements that produced the new wing form over time. This approach and database could be beneficial in noise reduction studies since the flow conditions vary throughout the flight and are responsible for different noise levels. Furthermore, Valldosera et al. [302] developed a gradient-based shape design optimization method to enhance the aerodynamic characteristics of a morphing airfoil using Spalart–Allmaras turbulence equations [303] in the compressible steady RANS model. They sought to maximize the lift coefficient while adhering to the prescribed structural restrictions and providing a realistic, optimal design. After reaching the optimized airfoil, the authors conducted unsteady simulations to derive surface pressure distributions. They used the outcomes as inputs for the aeroacoustics modeling framework according to the Farassat formulation [304]. Although hindered by a significant drag coefficient increase owing to stall on the TE of the morphing airfoil, the design has proven advantageous for aeroacoustics performance since it generated lower noise for a similar lift coefficient compared to the standard flapped configuration.

The aeroacoustic performance of morphing wings, like their aerodynamic performance, is directly dependent on the control system. To create the modified deformation and ultimately generate an optimization framework for a customized morphing NACA 0012 airfoil, Schweikert et al. [305] utilized a modified category conversion and GA using data from Xfoil and ANSYS Fluent. Using a specific communication framework between the solvers, the authors applied multi-island GA optimization in Xfoil to find the global optimum conditions that initialize ANSYS Fluent. As a result of their study, in addition to the increase in the aerodynamic performance of the wing, the flow control delayed the transition from laminar to turbulent, inhibited separation of BLs, increased turbulent mixing, and eventually reduced noise.

Bao et al. [306] published their study on multi-objective optimization of the LE and TE on a variable camber airfoil. They used incompressible RANS equations in 2D and 3D simulations with turbulent, viscous incompressible flow to solve the multi-objective optimization problem and examine the airfoil’s aerodynamic and acoustic performances. A NACA 0012 symmetrical airfoil was analyzed using a pressure–velocity coupled solver and a second-order upwind scheme for discrete pressure, momentum, and turbulence transport equations. The calculated flow field was then used as input to the FW-H acoustic model in the Lighthill acoustic analogy [32] method. Four geometrical variables were involved in the optimization function, including rotation angles and deflection positions of the LE and TE. Using the Pareto frontier curve [307], they defined an objective function to maximize the lift coefficient and lift-to-drag ratio at a chosen AoA. The function was then solved using a coupled GA as the optimization method and a Deep Neural Network (DNN) as the predictor tool. The optimization resulted not only in improved aerodynamic performance but also reduced aerodynamic noise. However, the results showed that the optimum airfoil design depends on the designer’s expectations of aerodynamic or aeroacoustic performance and the bias towards them, as well as on the target frequency. The results showed that when low and medium frequencies are targeted, the noise will not increase and could potentially reduce at high frequencies. On the other hand, if focused on high frequencies, the noise reduces at high frequencies while the low-frequency noise increases.

One should not forget that reducing noise and increasing aerodynamic efficiency are usually trade-offs, and the optimal design can vary depending on the relative weight of each objective. Jawahar et al. [294] investigated the aeroacoustics and in-depth aerodynamic performance characteristics of an MTE configuration LES and the dynamic Smagorinsky sub-grid scale [151]. The authors demonstrated that the MTE airfoil has a more significant pressure differential between the suction and pressure sides, which results in a higher lift coefficient. Their findings also show that the MTE airfoil produces substantially more unsteady pressure changes than the Hinged Trailing Edge (HTE) airfoil in the TE area, which extends much further into the wake (Figure 13). Results for the PSD of WPF indicated that the MTE airfoil generates considerably higher values near the TE due to greater coherence in flow patterns. Using Curle’s example [308], the field noise measurements showed that MTE airfoils create larger values of OASPL due to more eminent surface pressure variations in the TE zone.

Not all morphing structures are made from hinged sections. Employing actuators hidden beneath the wing skin might offer a broader range of forms while better preserving the shape of the airfoil surface. Marouf et al. [309] published a study on the creation of smart wing configurations able to improve aerodynamic and aeroacoustic performances. The implanted actuators provided optimized deformations and vibrations to alter the local turbulence structures in order to boost lift, reduce drag, and enhance noise scattering across all stages of flight (including take-off, landing, and cruise). The authors used the outcomes of high-fidelity numerical simulations and empirical tests to demonstrate the effectiveness of this setup.

4.5. Other Design Techniques

Noise reduction methods with TE treatments are not limited to using sawtooth shapes. Novel designs and nature-inspired methods can be effective in this area. One bio-inspired design used to minimize airflow-induced noise is the finlet, which employs a decrease in spanwise correlation length and an increase in source ‘scattering edge’ separation distance as the two possible noise reduction mechanisms [310]. Gstrein et al. [311] examined the effect of finlets on TE noise reduction in a symmetric NACA 0012 airfoil (Figure 14). By examining far-field data and measurements of static/dynamic surface pressure collected at various chord-wise and spanwise locations, the authors evaluated the efficiency of this approach. The critical parameters for TE noise reduction, such as the spacing and height of the finlets and their relative locations relative to the TE, were identified by emphasizing the near-field dynamics in the zone between the finlets. Results reported a significant relationship between the finlet height and the TE’s BL thickness. The researchers discovered that the separation of small-scale turbulence structures from the airfoil surface seems to be the predominant mechanism leading to noise reduction. A position investigation also showed that moving the finlets upstream from the airfoil TE was more effective in TE noise reduction than the configuration with the finlets mounted flush with the TE.

Bluntness-induced noise remains one of the major drawbacks in noise reduction attempts, which is caused by the surface discontinuity at the airfoil TE. Salama and Rocha [312] numerically evaluated a noise-reducing airfoil TE design using finned serrations. This innovative method involves superimposing two distinct noise-reducing features that merge the noise-reduction properties of finlets and serrations. The channeling effect of the finlets prevents or reduces the unwanted VS phenomenon due to the bluntness at the serration roots. The authors assessed this design using Embedded Large Eddy Simulations (ELES) in conjunction with the Ffowcs Williams Hawkings model to compare its aerodynamics and aeroacoustics results to those of a flat TE airfoil. They demonstrated how this technique reduces the size of the vortices close to the TE by enhancing the flow mixing on the airfoil. The study also showed that this hybrid method considerably redistributes the turbulent kinetic energy adjacent to the airfoil TE surface, where the strong eddies are scattered away from the airfoil surface. Another way to mitigate the discontinuity of the airfoil consists of applying brush-type TE extensions. Herr et al. [218] investigated the noise reduction capability of this method using parametric research and experimental analysis of several configurations with different fiber diameters and brush lengths. The authors tested a zero-lift generic plate model in an open jet aeroacoustic wind tunnel with comparatively high Reynolds numbers to conduct the tests. Their results included aeroacoustics and aerodynamics measurements to develop the governing equations. They collected acoustic data using a directional microphone array. Measurements showed a considerable noise reduction potential of more than 10 dB. The tests showed that the chord length’s role in noise reduction is insignificant, while the decreased permeability of longer brushes results in more noise reduction than short ones. The authors also identified the importance of narrowband bluntness noise suppression and decreasing broadband noise due to the turbulent boundary-layer TE interaction. The test results showed that bluntness noise was significant even for extremely thin TEs. Furthermore, the authors supported the claim that Strouhal number scales TE noise frequencies and spectra, while the boundary-layer displacement thickness is not the most affecting factor in this regard.

Vortex Generators (VGs) aim to reduce noise by delaying the flow of the separation. Different VG designs are used in a variety of aerospace parts, including sections from jet nozzles with high Reynolds numbers [313,314] and in airfoils and flaps with moderate Reynolds numbers [315]. VGs are typically positioned on the suction side of wind turbine blades, 10% to 30% of the chord length away from the LE, to enhance the stall behavior of the blade and delay the separation [316]. VGs can be accompanied by other active or passive noise reduction methods to improve their noise reduction performance. Sundeep et al. [317] published an empirical study aiming to enhance the noise reduction capability of trailing-edge serrations using VGs. The authors evaluated the performance of VGs on a flat plate at different AoAs and flow speeds in the moderate Reynolds number range. Vane-type VGs were placed, with various heights to the BL thickness, along with the serration roots. Aeroacoustic and aerodynamic measurements near the trailing edge were carried out using a phased microphone array and a hot wire, respectively. Additionally, lift and drag forces were measured using load cells. Results showed a slight reduction in trailing edge noise across a broadband frequency range in the source-integrated noise spectra. The data also showed that the VGs produced streamwise vortices in the wake. It was discovered that these streamwise vortices mitigate the cross-flow produced at the serration roots, improving the serrations’ ability to dampen noise. Additionally, the lift and drag coefficients were little impacted by the presence of low-profile VGs.

A novel design modification concerning noise reduction is presented in the published research by Smith et al. [318]. Their study investigated the use of airfoils with spanwise wavy geometries to reduce TE noise and improve aerodynamic performance. Although the outcome of their work is reducing drag and TE noise, their novel design cannot be categorized under TE treatments since they have introduced the wavy surface of the airfoil as the solution instead. They compared four variants of the airfoil with different wavelengths of surface waves to a smooth airfoil and reported a maximum noise reduction of 17.7 dB. The enhancement is attributed to the reduced spanwise correlation of pressure fluctuations and modified BL dynamics. They also claimed that the wavy geometry reduces drag force by limiting flow separation on the suction side, leading to improved aerodynamic performance across a wider range of AoAs. Using bio-inspired wavy designs continues to be one of the favored bio-inspired noise reduction mechanisms among researchers. Wang et al. [319] introduced a novel biomimetic wavy concept on the entire airfoil to reduce noise. This proposed design included distinctive features such as LE waves, TE serrations, and surface ridges integrated into peer sections of a NACA 0012 airfoil (Figure 15). The authors employed LES simulations alongside the aeroacoustic analogy to assess the performance of this solution and compare it with the base airfoil. Simulations were performed at Reynolds number 1 × 10⁵ and 0 AoA. The results of the simulations revealed comprehensive OASPLs across diverse frequencies and at seven designated observer points around the biomimetic airfoil. Remarkably, the airfoil showcased a noteworthy decrease in SPLs, ranging from 13.1 to 13.9 dB, spanning all frequencies and observer points. Regarding the aerodynamic performance, the drag coefficient remained nearly unaffected despite the modifications. The reduction in noise was attributed to the biomimetic structures causing a shift in the shedding vortices, transforming them from the laminar mode seen in the base airfoil to more regular horseshoe-type vortices in the wake of the biomimetic airfoil. Furthermore, this design effectively lessened the spanwise correlation of the larger vortices, consequently managing the vortex-shedding noise surrounding the biomimetic airfoil.

Another modification to the design that has been made to decrease low-to-mid frequency range tonal VS noise at the TE zone is the inclusion of shallow dimples. This passive strategy diminishes the convective velocity of the streamwise convecting eddies and destroys the spanwise coherence [320]. Perry [321] used a dimple design (Figure 16) in his dissertation to manipulate the flow conditions on the wing surface. The author focused on exploring the use of shallow dimples and an airfoil to reduce aeroacoustic noise emissions. He used both RANS and LES models on a fixed Reynolds number of 4.8 × 10⁵ and with different dimple depth-to-diameter ratios (d/D), coverage areas, and AoAs for aerodynamic and aeroacoustic investigations. Eventually, the authors reported the best coverage area and d/D with the minimum aerodynamic impact and maximum aeroacoustic enhancement.

To subside the noise produced by the spanwise coherence of surface pressure variations on both the LE and TE of blades, Zhang et al. [322] developed a bio-inspired ridge-like structure on a NACA 0012 airfoil (Figure 17). At a freestream velocity of 20 m/s and an AoA of 0, this novel noise reduction configuration demonstrated a considerable peak noise reduction of roughly 26 dB and a more than 10 dB drop in the OASPL. The authors reported that the combination of ridge-like elements on the LEs and TEs decreases turbulent kinetic energy (TKE) near the airfoil surface and diminishes the spanwise consistency of surface pressure fluctuations. Furthermore, they showed that these ridge-like structures on the LE trigger a transition to migrate upstream. Additionally, they carried out a phase spectra analysis, which showed that fluctuating pressure signals on the outer surfaces of two adjacent ridge-like structures have opposite phases. This caused a significant amount of phase disruption in the biomimetic airfoil between these structures in the frequency range of 100 Hz to 800 Hz.

Riblets are renowned for their effectiveness as drag-reduction tools. A feasibility study by Muhammad et al. [323] examined the possibility of employing this design to reduce the accountable turbulent pressure sources for the airfoil self-noise radiation. According to the assessments of the boundary-layer profiles, riblets deduct the skin friction coefficient and turbulence intensity. Furthermore, the ribbed surface aided in the quicker dissipation of turbulence structures in the convective field. The study also showed that the riblets caused a minor decrease in the wall-pressure power spectral density at low and high frequencies, with an increase seen at mid-frequency ranges. The riblets showed a broad frequency range reduction in the lateral turbulence coherence length scale. According to the study, the riblet effect is significant, particularly in the low and high-frequency bands, for reducing TE self-noise.

The vortices generated at the wingtips are another source of noise in the wings. Engineers designed winglets to weaken these vortices and benefit from the operational reduction in tip vortex energy [324]. The design of the winglets and wingtips has an impact on the noise generated. Vaezi et al. [168] used AI approaches to examine the impact of operating and atmospheric factors on the aeroacoustic characteristics of a civilian aircraft wing. The authors studied simple and blended Boeing-737 wings that share identical airfoil profiles and wing geometric attributes, with the only difference being the presence of a winglet on one of them. They used commercial CFD simulations to solve the 3D turbulent viscous compressible flow with RANS equations combined with the k-ω SST turbulence model to study the influence of adjusting winglet cant angle during flight. The acoustic field was calculated by applying the broadband acoustic source model. Results showed that altering the winglet cant angle has a noticeable influence on the distribution of the Acoustic Power Level (APL), both around the wingtip and over the wingspan. Furthermore, the APL distribution on the top surface was strongly oscillatory, whereas the bottom area exhibited smoother behavior. The Multi-Layer Perceptron (MLP) ANNs were used to model the flow and predict the aeroacoustic performance. The analyzed parameters were the area-weighted average, integral, and maximum values of the APL, whose accuracy is tested by evaluation criteria such as Maximum Error Percentage, Mean-Squared Error (MSE), and Root Mean-Squared Error (RMSE). The authors classified the numerical samples using supervised learning and Cubic Support Vector Machine (C-SVM) [325] based on performance class definitions. Finally, they estimated the acoustic power level on the wing surface based on the flow properties using digital image processing coupled with Convolutional Neural Network and Deep Convolutional Neural Network (CNN-DCNN) [326] architecture with high accuracy. The results revealed that the winglet cant angle substantially influences the acoustic performance of the wing.

Since wingtip vortices are essentially spatial structures [327], they should be examined using three-dimensional models. Moreau et al. [328] concentrated on computational and experimental investigations of the noise produced by the airflow with a wall-mounted finite airfoil that has a flat-ended tip and a natural boundary layer transition (Figure 18). Both a single observer position and a microphone array were used by the researchers to quantify far-field noise. They evaluated several AoAs while varying the Reynolds numbers in the order of five to six. The findings showed that at non-zero AoAs, the airfoil produced a broadband noise in addition to a few distinct equispaced tones. Furthermore, the authors provided spectral data that showed the noise generated by three-dimensional vortex movement close to the flat tip and its connection zone with the wall. This was conducted to show how various flow characteristics affect the amount of noise the airfoil produces overall. The study demonstrated a relationship between the generation of tonal noise and the presence of a transitional flow condition close to the airfoil’s trailing edge. A spot of somewhat divided flow on the pressure surface was present along with this condition. The authors reported that as the AoA grew, the position of the separated flow zone and the origin of tonal noise also shifted. This change was linked to the impact of the flow field throughout the span of the airfoil tip. Additionally, when the airfoil aspect ratio is decreased, the tonal noise generation switches to lower Reynolds numbers and greater geometric angles of attack. The study also emphasized that there were significant differences between the creation of tonal noise and that of a two-dimensional airfoil.

Fleig et al. [329] presented another study to decrease the noise produced by the tip vortex. They looked at the underlying physical processes behind the broadband tip vortex that produced noise from whirling wind turbines. With a focus on the blade tip area, they used compressible LES and direct noise simulation to model the flow and acoustic field around a wind turbine blade. They also used the FW-H acoustic analogy to describe the far-field aerodynamic noise. Instead of utilizing the real tip shape in this case, they used an ogee-type tip shape (Figure 19), which was successful in lowering the OSPL by 5 dB at frequencies over 4 kHz.

High-lift devices, like slats and flaps, are a major source of noise [330]. Yamamoto et al. [331] focused their research on the generated noise from slats, which are often used during take-off and landing. Since this source of noise is related to the turbulence downstream of the shear-layer reattachment point, the authors considered increasing the distance between this area and the TE as a possible solution. They proposed this change either by increasing the TE length or adding a bump on the lower surface of the slat. The flap side-edge noise is another important source of noise in civil aircraft, and flap-tip fences are the parts that aim to reduce this type of noise. Burghignoli et al. [332] published a paper on the aeroacoustics of flaps and the noise control these components offer. The authors reproduced take-off and landing conditions under different critical flow speeds and AoAs by testing a scaled-down model of a civil aircraft in a subsonic wind tunnel. Using a phased-microphone array, they evaluated pressure fluctuations to identify the noise sources. To extract the sound source patterns and the combined spectrum in specific areas, they analyzed the data using conventional beamforming and the Clean Subtraction of the Continuum (CLEAN-SC) algorithm [333], which is a signal processing tool used to remove interference and noise from images. The authors also explored directivity effects by shifting the microphone array in different axial orientations that correlate to various aircraft polar angles. After extending the wind tunnel data to full size and projecting it to flying conditions, they finally computed the Effective Perceived Noise Level (EPNL). The results showed that flap-tip fences can be effective in reducing noise generated by wings, with a maximum reduction of 1.5 dB. However, it is highlighted that the aerodynamic impact of these fences should be carefully evaluated.

Among the parameters affecting the generated self-noise, the sweep angle and wall-pressure statistics are the focal points in the study by Grasso et al. [334]. They conducted an analytical investigation using Amiet–Schwarzschild’s [45,46,47,335] method to determine how sweep angle affected the free-field noise exposure from the TE of an isolated airfoil. Additionally, they looked at how the density’s spanwise wavenumber of the wall-pressure power spectral distribution affected the radiated noise. The authors used Corcos’ model [336], and the results showed that the directivity of airfoil TE noise is influenced by the sweep angle of the airfoil and the statistics of the wall pressure. These factors can affect the strength and directionality of noise radiation from airfoils, with implications for aircraft design and noise reduction.

4.6. Surface Treatments

The employment of the aforementioned attachments, such as finlets, serration, or porous surfaces, has been found to be effective in lowering airfoil self-noise, although they are typically incompatible with the streamlined airfoil body [323]. In addition to these airfoil design modifications, a few other factors influence the formation of the BL and its development over the airfoil surfaces. Among these, the surface interaction with the BL has an obvious effect on the BL and the generated noise. As mentioned earlier, TS wave amplification is one of the noise sources, and specially designed surfaces are used as a remedy to delay or manage this phenomenon [337,338]. Nature has inspired many studies on the self-noise reduction of aerial structures. For example, birds whose flight has evolved for easy hunting are a good choice for researchers seeking silent aerial creatures [339]. Inspired by the velvety structures on the surface of an owl’s wing, Zhou et al. [340] studied the effect of these surfaces on the noise produced and the BL flow of a flat plate model. For this purpose, the authors conducted simulations and experimental tests in an ultra-quiet wind tunnel at low speed. The results showed that velvet surfaces can play a considerable role in reducing the flow-induced noise. In general, they concluded that velvety structures increase low-frequency noise below a cross-over Strouhal number while decreasing noise levels at higher frequencies. The results also showed that the velvety surfaces alter the BL’s thickness, turbulence distribution, and non-dimensional velocity distribution since this coating prevents or reduces VS despite the blunt TE.

Through another bio-inspired design, Wang et al. [341] investigated the noise reduction ability and revealed the noise reduction mechanism of the multiple coupling elements inspired by owl wings. To understand how the connected segments reduce noise, they rebuilt the bionic airfoils with three different non-smooth structures of the LE. They employed the LES method with FW-H acoustic analogy theory to analyze the noise scattering mechanism. The bio-mimetic airfoil designs included sinusoidal, serrated, and iron-shaped LE serrations and surface ridges. Among these, they reported the one with iron-shaped LE serrations as the most effective design for noise reduction. Here, the bio-mimetic structures alter the streamwise vortices, which causes the typical large-scale tubular vortices to split into smaller horseshoe vortices. Additionally, the change in time-averaged vorticity in the space field and the reduction in the spanwise correlation coefficient both supported the attenuation of sound sources.

BL separation is a source of aeroacoustic instabilities and the generated self-noise in the wings [342,343]. Laminar flows separate faster from the surface, while turbulent flows tend to follow the airfoil surface more. One way to delay the flow separation phenomenon is by transforming the flow regime from laminar to turbulent, called tripping [344]. Surface structural components, surface roughness, or implanted spanwise turbulators can trigger this to occur. To predict the possible effects of tripping on the TE noise of an airfoil, Winkler et al. [345] employed a variety of techniques. They case-studied a NACA 6512-63 airfoil installed at zero AoAin in the narrow stream of an open-jet acoustic-insulated wind tunnel. They added tripped sections on both sides of the airfoil to interfere with the airfoil BL. The noise sources of the airfoil TE flow were also calculated using incompressible LES and compared with compressible DNS. The acoustic far-field pressure was predicted using FW-H and Amiet’s analytical acoustic analogies. The authors claimed that the trip geometry had no discernible impact on the generated noise. The far-field acoustic pressure, however, is overestimated and more closely mimics the laminar instability noise from the not-tripped airfoil if the boundary-layer trips are not sufficiently thick in the computational model or absent at all.

The surface–flow interactions have considerable impacts on boundary-layer transitions and the generated noise in areal structures [346]. To reveal details of these influences, Volkmer et al. [347] published computational and experimental results from three different blade modification methods for noise reduction in a small wind turbine. The suggested remedies include blade profile optimization, BL tripping, and serrations on the TEs of the blades. The authors used two Bezier curves of sixth order to define the two-dimensional airfoil profile. They executed an evolutionary optimization algorithm with aerodynamic and performance constraints to produce the optimal airfoil profile, which yields the minimum OASPL at an observer point. They tested the solutions experimentally and measured, statistically analyzed, and compared shaft power and sound power over long periods to reveal the aerodynamic noise attenuation mechanisms. The outcomes confirmed that even though both the trailing and tripping edge serrations, to a greater or lesser extent depending on the design and relative thickness of the blade profile, diminish the produced self-noise, they inevitably lower output shaft power. The hybrid approach, which included the best-possible blade profiles without trips but with TE serrations, offered the best balance between noise suppression and a drop in the aerodynamic efficiency of the turbine.

The noise signature is very sensitive to the lifting surface texture, to the extent that even the cleaning degree of the airfoil can impact the generated self-noise. Oerlemans et al. [348] performed acoustic field measurements on a three-bladed wind turbine to identify the noise sources and determine if the TE noise from the blades was predominant. To evaluate the dispersion of the noise sources in the rotor plane and on each blade, a wide horizontal microphone array was installed around one rotor diameter downstream from the turbine to record the generated noise and the operation parameters of the turbine simultaneously. The authors investigated the effect of blade surface roughness by cleaning one blade, tripping another, and leaving the last one untreated. Their findings demonstrated that the noise level scales with the local flow speed to the fifth power, meaning that the outside portions of the blades generate more noise. They also reported that the tripped blade produced higher noise levels than the other two. The study concluded that broadband TE noise is the predominant noise source, whereas narrowband analysis shows TE bluntness noise not to be considerable.

This section reviews a variety of passive noise reduction techniques. Design modifications for noise reduction on airfoils offer promising solutions to enhance the acoustic performance of airfoils and lifting surfaces. LE and TE serrations disrupt flow separation and turbulence to reduce noise levels. Porous materials contribute to noise reduction through sound absorption, flow control, and wake interaction. Controlled diffusion airfoils with gradual pressure changes promote smoother flow, minimizing noise from vortices and turbulence. Surface treatments control boundary layer conditions, suppressing turbulence and noise interactions. While these advancements show great potential, they come with certain challenges. Integrating new technologies may increase complexity and cost. Maintaining the structural integrity and durability of morphing components can also be a concern. Additionally, design trade-offs are necessary to ensure optimal aerodynamic performance and noise reduction. Despite these challenges, design modifications represent significant steps towards quieter and more environmentally friendly air transportation.

5. Conclusions

This paper provides an overview of recent advances in passive noise reduction methods applied to airfoils, wings, and blades. The discussed literature included theoretical, computational, and experimental methods, in addition to the applications of ROMs, AI, and optimization techniques in passive noise reduction. Regarding design techniques, the authors have discussed various solutions, such as LE/TE treatments with flat and non-flat serrations, controlled diffusion airfoils, porous materials, morphing wings, and surface treatments.

In general, each of the techniques discussed here allows for the reduction in generated noise with the evaluation of appropriate design parameters. It is important to note that the effectiveness of the mentioned passive noise reduction methods can vary based on the specific airfoil design, application, and operating conditions. Furthermore, a combination of these methods, or tailoring them, can help meet the requirements of a particular airfoil application. However, there is a trade-off between the aerodynamic and aeroacoustic performances, and even between reduced noise in some frequencies and the higher generated noise in other frequencies due to design modifications. These methodologies can be categorized based on their application within specific frequency ranges and flow regimes. For instance, in the context of laminar airflow with Reynolds numbers below approximately order 10⁵ and smaller-scale geometries, the underlying mechanisms leading to noise reduction differ from those applicable to transitional flows within the Reynolds number range of the order between 10⁵ and 10⁶, as well as turbulent flows characterized by Reynolds numbers exceeding approximately order 10⁶ (

Table 1. Summary of passive noise reduction methods.

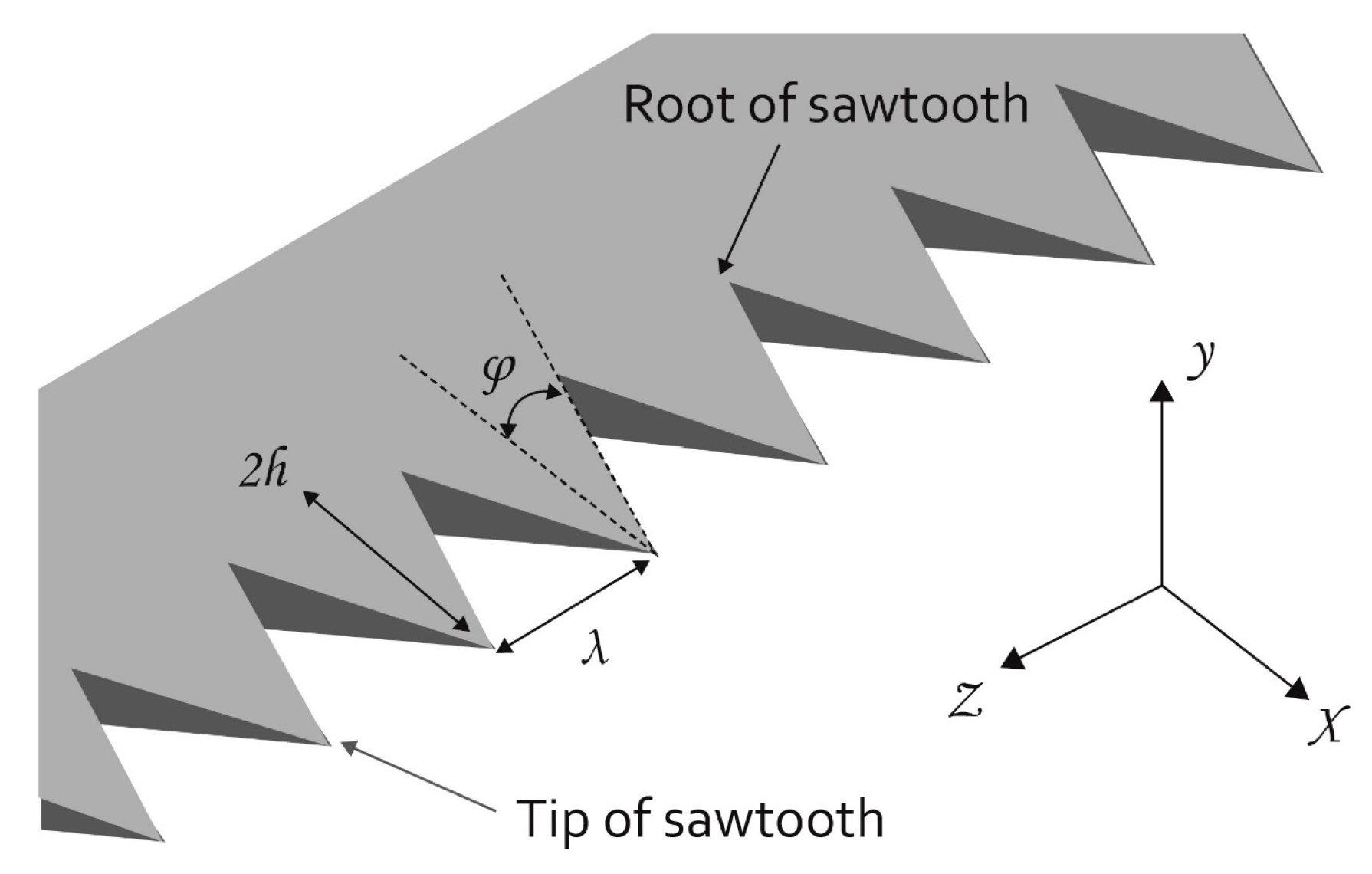
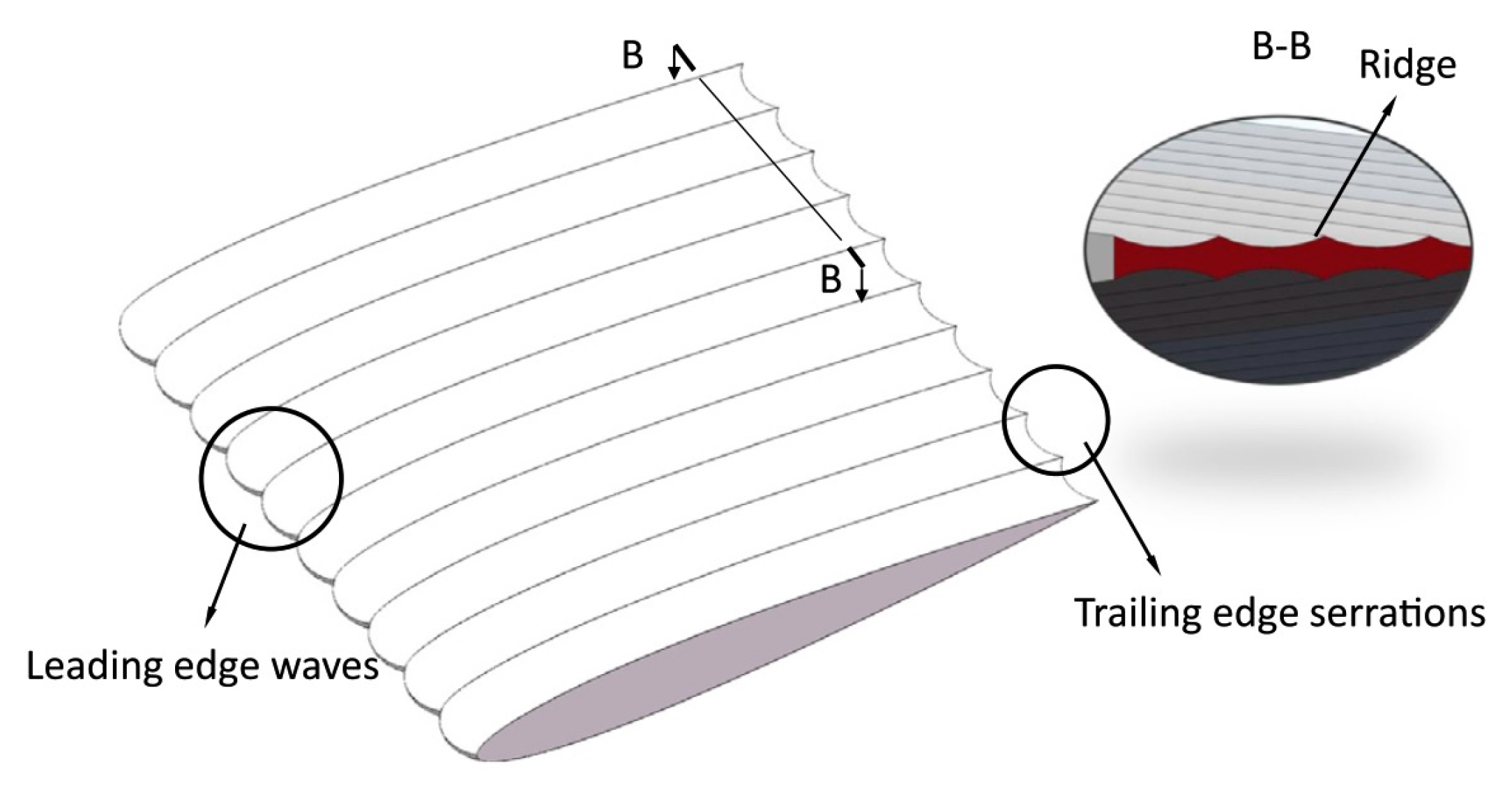
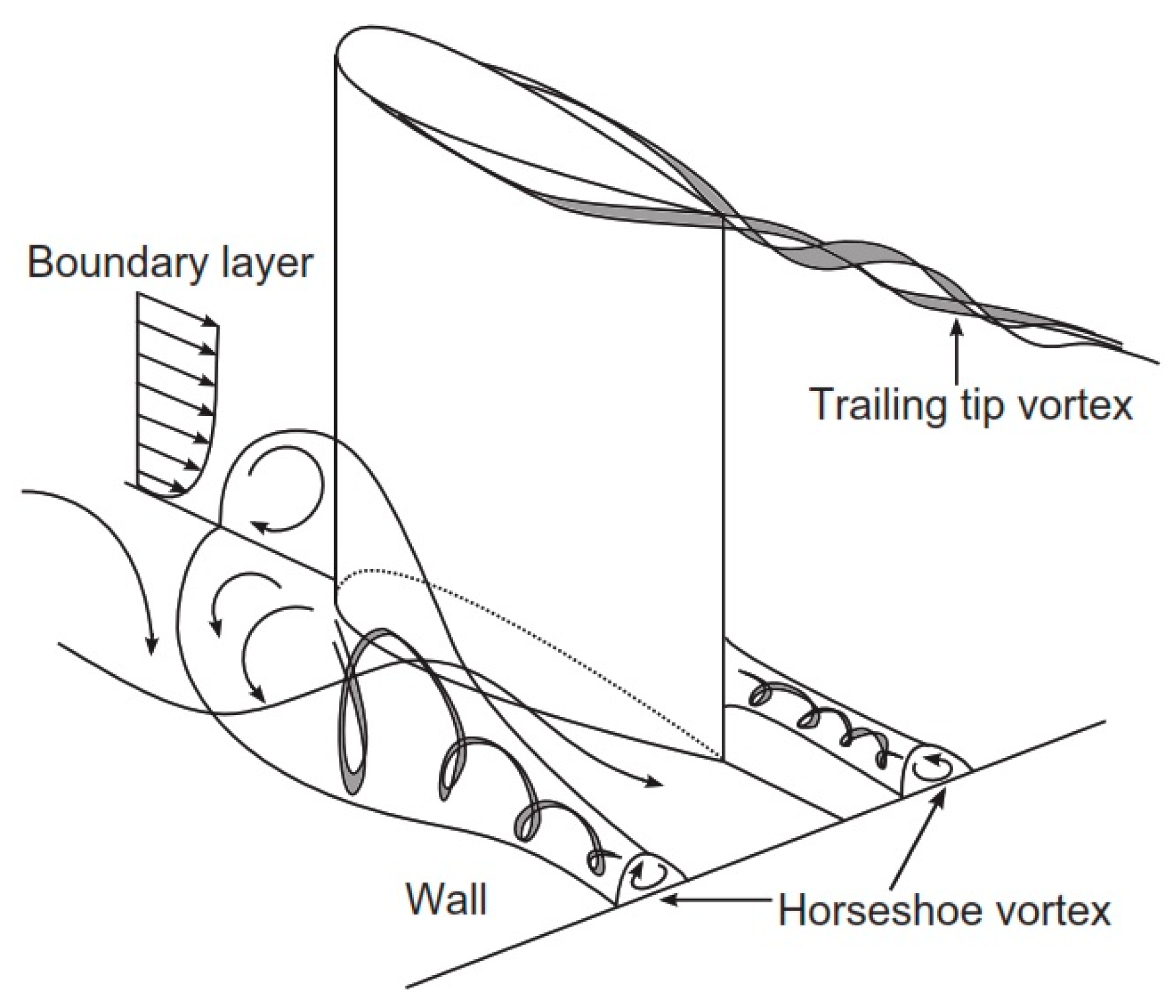
Method	Mechanism	Frequency Range	Reynolds Number
Leading-Edge Serrations	Disrupt the formation of LE vortices. Delay separation	Low-to-mid frequency range	Low to moderate Reynolds numbers
Trailing-Edge Serrations	Disrupting the formation of turbulent VS, Breaking large vortices into smaller-scale ones	A wide frequency range, especially tonal noise in the mid-frequency range	Moderate to high Reynolds numbers
Porous Materials	Flow Reshaping and Wake Interaction	Low-to-mid frequency range	A wide range of Reynolds numbers
Controlled Diffusion Airfoils	Controlling the flow separation and preventing the formation of noise-inducing vortices	A wide frequency range, including both low and high-frequency components	Moderate to high Reynolds numbers
Morphing Airfoil	Smooth Shape Transitions and BL control	A wide frequency range, mostly effective on low-frequency components	The applicability of morphing airfoils depends on their structural design and the targeted Reynolds number range
Surface Treatments	Control BL behavior and trip the laminar flow	High-frequency components, particularly those associated with BL turbulence	A wide range of Reynolds numbers

). Therefore, it seems that a synthetic use of different noise reduction techniques/devices can be beneficial to achieve further noise reduction in a wider frequency region. Table 1 presents a summary of the passive noise reduction methods discussed in this paper.

The theoretical and computational models used in noise prediction require data from accurate modeling of the turbulent surface pressure spectra and SPL. Computational methods, ranging from low- to high-fidelity models, can be practical for providing this data. Medium-fidelity models based on RANS have also been used for this purpose, although RANS may not accurately generate the pressure fluctuations data needed for precise noise modeling due to its averaging. While limitations remain in accurately modeling the turbulent surface pressure spectra and pressure fluctuations, advancements in processor hardware have enabled the growing use of high-fidelity models, such as LES or DNS. These models provide an even better understanding of flow physics in various design concepts, offering promising opportunities for further advancements in aeroacoustics research. On the other hand, acoustic models, such as Amiet’s and FW-H models, are widely used for noise predictions and have been modified to account for novel TE shapes. Experimental studies have also played a key role in generating new solutions for noise reduction and evaluating the effectiveness of various noise reduction devices.

Passive noise reduction will remain a key section in aeroacoustics, and the information discussed here contributes to the ongoing efforts of researchers and engineers in the field of noise reduction, lighting the way for future innovations and advancements in aircraft noise reduction technologies. The authors hope this review will be beneficial to researchers, engineers, and enthusiasts in this field of noise reduction, the environmental impact of high-lift devices, and a more sustainable future for air travel.