A Novel Digital Twin Framework for Aeroengine Performance Diagnosis

Abstract

Aeroengine performance diagnosis technology is essential for ensuring flight safety and reliability. The complexity of engine performance and the strong coupling of fault characteristics make it challenging to develop accurate and efficient gas path diagnosis methods. To address these issues, this study proposes a novel digital twin framework for aeroengines that achieves the digitalization of physical systems. The mechanism model is constructed at the component level. The data-driven model is built using a particle swarm optimization–extreme gradient boosting algorithm (PSO-XGBoost). These two models are fused using the low-rank multimodal fusion method (LWF) and combined with the sparse stacked autoencoder (SSAE) to form a digital twin framework of the engine for performance diagnosis. Compared to methods that are solely based on mechanism or data, the proposed digital twin framework can effectively use mechanism and data information to improve the accuracy and reliability. The research results show that the proposed digital twin framework has an error rate of 0.125% in predicting gas path parameters and has a gas path fault diagnosis accuracy of 98.6%. Considering that the degradation cost of a typical flight mission for only one aircraft engine after 3000 flight cycles is approximately USD 209.5, the proposed method has good economic efficiency. This framework can be used to improve engine reliability, availability, and efficiency, and has significant value in engineering applications.

1. Introduction

Aeroengines, particularly high-bypass-ratio turbofan engines, serve as the primary power sources for aviation transportation [1]. Aeroengines play crucial roles in improving fuel efficiency and cost-effectiveness. Engine Original Equipment Manufacturers (OEMs) strive to enhance the fuel mileage per unit of energy by continuously improving the engine design, increasing the combustion efficiency, and reducing the aerodynamic drag [2]. This not only reduces the operating costs for airlines, but also decreases the reliance on finite fossil fuel resources, promoting the sustainable development of the aviation industry. However, prolonged operation in high-temperature and high-pressure environments leads to performance degradation over time. This deterioration can result in decreased performance, malfunctions, and even system failure, posing a significant threat to flight safety and reliability [3]. The maintenance services and component replacement costs associated with aviation engines are substantial. For instance, the price of a single turbine blade can reportedly reach up to approximately USD 10,000 [4]. Consequently, the development of an accurate, reliable, and efficient aviation engine health management system is crucial. Engine gas path performance diagnosis technology has emerged as a key focus in the development of engine health management systems and is currently a prominent area of research [5].

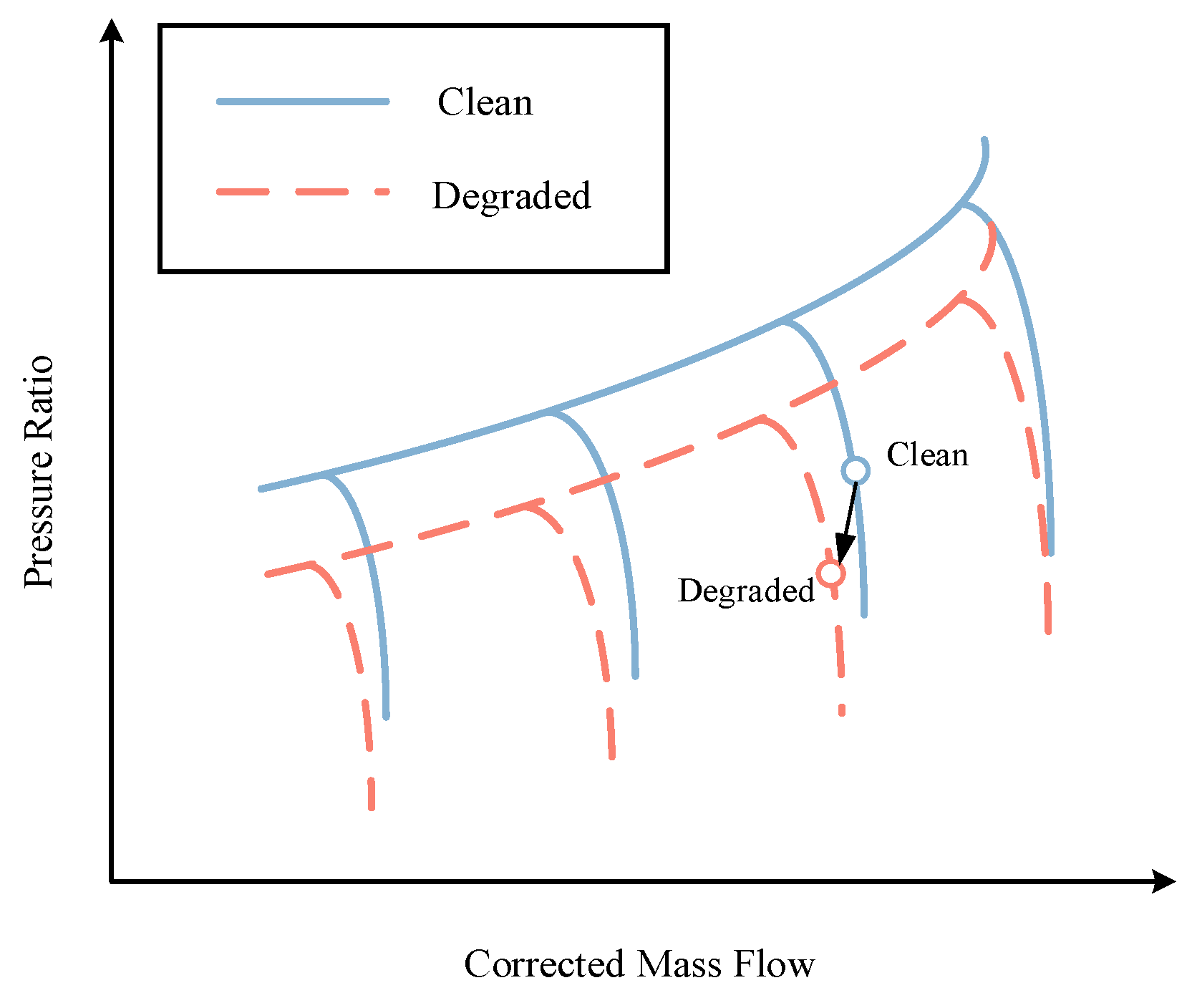
Gas path faults can be categorized into two main types: gradual degradation faults and abrupt mutation faults [6]. During the engine’s prolonged operation, the component performance gradually deteriorates, leading to faults such as corrosion, erosion, fouling, and increased blade tip clearances. Abrupt mutation faults mainly include damage from internal and external objects, such as hail or bird strikes. These faults can cause a rapid decline in the component performance within a short period and may even lead to in-flight shutdowns [7]. Typically, gas path faults primarily target the rotating components of the engine’s gas path, such as the fan, compressor, and turbine. Currently, most engine gas path performance diagnostic techniques are developed based on the Gas Path Analysis (GPA) theoretical framework. The derived methods can be broadly categorized into two classes: model-based and data-driven approaches [8].

Model-based approaches aim to establish accurate mechanism models based on the actual characteristics of the engine. Such methods extract gas path information from multiple engine operating points to track the engine’s dynamic processes and state changes, enabling real-time fault diagnosis and prediction [9]. For instance, Aretakis et al. [10] developed a multi-fault equation model by extracting gas path information from multiple engine operating points. Ogaji et al. [11] optimized the diagnostic errors for multiple engine operating points using genetic algorithms. Ying et al. [12] addressed the issue of incomplete measurement parameters for engine fault diagnosis by utilizing multiple engine operating points. Li et al. [13,14,15] improved the diagnostic and predictive range of the model by adjusting the engine performance characteristics under “off-design” conditions. Tsoutsanis et al. [16] employed elliptical transformations to scale, shift, and rotate the speed lines in component characteristic maps, enhancing the transient diagnostic accuracy of the mechanism model. Subsequently, Tsoutsanis et al. [17,18] optimized the diagnostic scheme for transients using local window regression methods. Song et al. [19] developed a diagnostic model for a three-axis engine with turbine cooling, demonstrating its diagnostic accuracy during transients. Kim et al. [20] proposed a transient adaptive approach to predict potential faults during the early testing phase of an engine. Chen et al. [21] introduced a sequential-based transient diagnostic method that is applicable to hydrogen-powered engines. In summary, the advantages of model-based approaches include their ability to predict a wide range of operating conditions with limited data. However, these approaches require specialized knowledge for development, and the extraction of engine operating points from a large volume of measurement data may lead to unnecessary information loss.

Data-driven methods, at their core, extract high-dimensional feature vectors that characterize the engine’s health state from existing experience and data. In contrast to model-based approaches, data-driven methods do not require extensive knowledge of engine physics [22]. For instance, Zhou et al. [23] employed support vector machines (SVMs) for engine gas path fault diagnosis. Park et al. [24] optimized the accuracy of artificial neural networks (ANNs) in predicting engine operating characteristics. Tamilselvan et al. [25] utilized deep belief neural networks (DBNs) for the fault classification of engine health states. Bai et al. [26] employed convolutional neural networks (CNNs) for fault detection in engine combustion chambers. Luo et al. [27] used autoencoders (AEs) to detect anomalies in the engine gas path. Lu F et al. [28] proposed a multi-rate sensor fusion approach using information filters for estimating aeroengine performance degradation. Although data-driven models offer robustness and real-time capabilities, they are essentially mathematical “black boxes” that lack explicit physical information, making it challenging for engine operators to interpret their underlying mechanisms. Moreover, the generalization of data-driven models is difficult to ensure due to factors such as component degradation and operating conditions, thereby limiting the applicability of data-driven methods.

Currently, the concept of digital twins has emerged as an innovative approach. Digital twin technology combines the physical and digital worlds by creating virtual replicas of physical entities. These replicas are used for the simulation, optimization, and prediction of various scenarios and situations, resulting in improved efficiency and cost reduction [29]. In the field of aeroengines, digital twin technology is still in its developmental stage. For instance, Fentaye et al. [30] proposed a gas path performance diagnostic method that combines SVM and ANN. LU et al. [31] introduced a diagnostic method based on DS evidence theory and data fusion. Xiong et al. [32] presented a digital twin framework that integrates data with LSTM, a deep learning method, for engine maintenance decision making. Zhou et al. [33] developed an engine health assessment system by combining the Kalman filter (KF) with LSTM and incorporating CNN. Envelope et al. [34] developed an adaptive correction method for turbofan engines based on an LSTM neural network and the hybrid optimization method. However, most of these studies focus on the fusion of data-driven models without fully leveraging the complementary advantages of mechanism models and data-driven models. Currently, there is a lack of sufficient research on how to effectively utilize digital twin technology to integrate mechanism models and data-driven models [35].

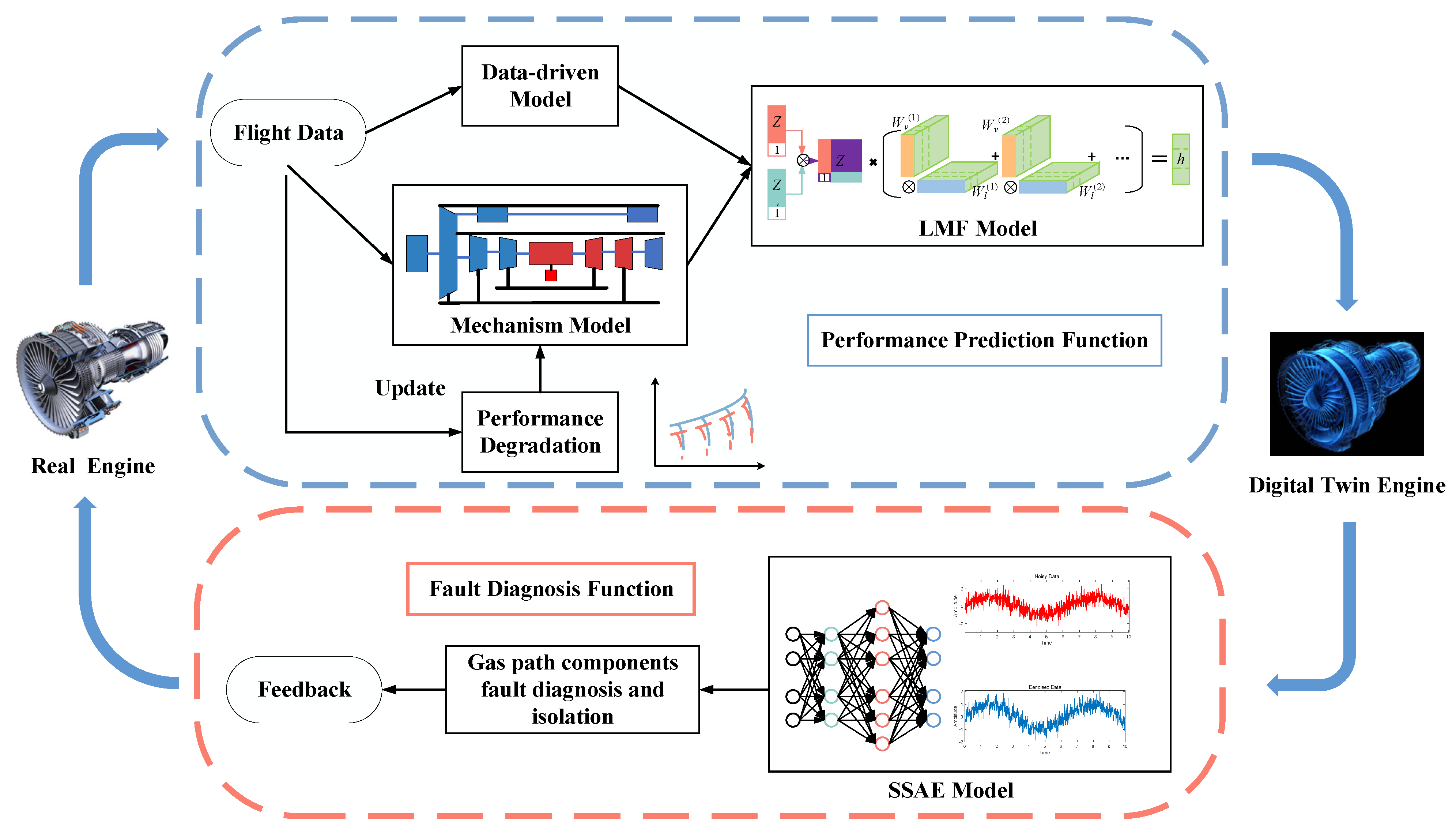
To address the limitations of previous methods for performance diagnosis in aeroengines, this study proposes a novel digital twin framework that is specifically designed for twin-spool turbofan engines. The proposed digital twin framework combines the advantages of mechanism models and data-driven models to achieve more accurate results. This research aims to explore the application of digital twin technology in gas path performance diagnosis for turbofan engines and contribute to this growing research field. The main contributions are as follows:

• The proposed digital twin framework provides a new approach for effectively integrating mechanism models and data-driven models in engine performance diagnosis.
• The proposed digital twin framework incorporates the strengths of mechanism models and data-driven models, allowing for continuous updates to follow engine performance changes while ensuring high-precision monitoring. Compared to purely model-based or data-driven methods, the proposed digital twin framework exhibits a higher prediction accuracy and diagnostic precision.
• Serving as a more reliable and efficient tool for gas path diagnosis, the proposed digital twin framework enables more intuitive monitoring of the engine health and provides more effective technical support for establishing engine health management systems.

2. Methodology

2.1. Component-Level Mechanism Model

The research in this paper focuses on a typical high-bypass-ratio twin-spool turbofan engine. Initially, it is necessary to establish mechanism models for each key component to describe their motion and energy conversion processes. Subsequently, based on the principle of mass flow balance, dynamic equations can be formulated to connect the inputs and outputs of the components, thereby describing the transfer and conversion of energy throughout the entire system [36]. Through this approach, the components can be interconnected to form a complete mechanistic model of the engine. The mechanical structure of the twin-spool turbofan engine is illustrated in Figure 1, where “Inlet” represents the inlet duct, “FAN” denotes the fan, “LPC” stands for the low-pressure compressor, “HPC” signifies the high-pressure compressor, “Combustion chamber” represents the combustion chamber, “HPT” refers to the high-pressure turbine, “LPT” denotes the low-pressure turbine, “Nozzle1” corresponds to the core nozzle, “Bypass” represents the bypass duct, “Nozzle2” signifies the bypass nozzle, “N₁” denotes the high-pressure spool, and “N₂” represents the low-pressure spool.

Table 1. Design point performance.

Parameter	Value	Unit
Thrust	95.31	kN
Total flow rate	322.65	kg/s
Total pressure ratio	33.8
SFC	10.17	g/(kN·s)

presents the design point performance of this engine, while

Table 2. Meaning of station number of each section of engine.

Number	Significance
amb	Ambient
13	Bypass
18	Bypass nozzle outlet
2	FAN outlet
25	Low-pressure compressor outlet
3	High-pressure compressor outlet
4	Combustion chamber outlet
45	High-pressure turbine outlet
5	Low-pressure turbine outlet
8	Nozzle outlet

provides the definitions of the station numbers.

2.1.1. Thermodynamic Calculation of Gas Path Components

For the sake of brevity, only the calculation methods for rotating components are provided here. The calculations for the three types of compressors (FAN, LPC, and HPC) are similar, so this paper provides a unified description. The component characteristic parameters of the compressor are obtained from the component characteristic map. Therefore, the thermodynamic calculations of the compressor can be expressed as follows:

$$N_{\mathrm{cor}}=N\times \sqrt{288.15/T_{in}}$$

(1)

$$(W_c,{\pi }_c,{\eta }_c)=f(N_{\mathrm{cor}} ,{\beta }_c)$$

(2)

In Equations (1) and (2), N_cor represents the non-dimensional speed corresponding to the compressor, N represents the actual physical speed of the compressor, β_c represents the auxiliary coordinate on the compressor characteristic map, W represents the mass flow rate at the compressor outlet, π_c represents the pressure ratio of the compressor, and η_c represents the efficiency of the compressor. The total temperature T_c and total pressure P_c at the compressor outlet section can be calculated as follows:

$$T_c=T_{in}\times [1+({{\pi }_c}^{\frac{\gamma -1}{\gamma }}-1)/{\eta }_c]$$

(3)

$$P_c=P_{in}\times {\pi }_c$$

(4)

In Equations (3) and (4), the subscript “in” represents the compressor inlet. Therefore, the power consumed by the compressor per second can be calculated as follows:

$$P_{\mathrm{c}}=C_P{W}_c(T_c-T_{in})$$

(5)

In Equation (5), C_P represents the air’s specific heat capacity at constant pressure.

While the thermodynamic calculations for LPT resemble those of HPT, this paper will focus solely on the calculation methods for HPT. By considering the parameters at the outlet section of the combustion, the physical speed of the high-pressure shaft (N₂), and the auxiliary coordinate (β_t) on the HPT component characteristic map, the component characteristic parameters for the HPT can be obtained from the map. Therefore, the thermodynamic calculations of the turbine can be expressed as follows:

$$N_{\mathrm{HPT}\mathit{cor}}=N_2\times \sqrt{\frac{288.15}{T_4}}$$

(6)

$$(W_{45},{\pi }_{\mathrm{H}\mathrm{P}\mathrm{T}},{\eta }_{\mathrm{H}\mathrm{P}\mathrm{T}})=f(N_{\mathrm{H}\mathrm{P}\mathrm{T}cor},{\beta }_t)$$

(7)

In Equations (6) and (7), N_HPTcor represents the non-dimensional speed of HPT, W₄₅ represents the mass flow rate at the outlet of HPT, π_HPT represents the HPT pressure ratio, η_HPT represents the HPT efficiency, and β_t represents the HPT auxiliary coordinate on the HPT map. Therefore, the total temperature and total pressure at the outlet section of HPT can be calculated as follows:

$$T_{45}=T_4\times [1-(1-{{\pi }_{\mathrm{H}\mathrm{P}\mathrm{T}}}^{\frac{{\gamma }_g-1}{{\gamma }_g}})/{\eta }_{\mathrm{H}\mathrm{P}\mathrm{T}}]$$

(8)

$$P_{45}=P_4/{\pi }_{\mathrm{H}\mathrm{P}\mathrm{T}}$$

(9)

In Equations (8) and (9), γ_g represents the specific heat ratio of the gas. Therefore, the power generated per second by HPT can be calculated as follows:

$$P_{\mathrm{HPT}}=C_{PG}{W}_{45}(T_4-T_{45})$$

(10)

2.1.2. Steady-State and Dynamic Balance Calculation

The engine operating state can be divided into two types, steady-state and transient conditions, so the engine mechanism model should have simulation functions for the steady-state and transient conditions. The engine mechanism model takes H, Ma, and W_f as inputs. Based on the thermodynamic calculations of the key components in the aeroengine gas path as described earlier, the equilibrium equations for the steady-state and transient conditions are solved using the Newton–Raphson method [37]. In order to complete the overall simulation of the aeroengine gas path, the power balance and the gas mass flow continuity principle are considered. The equilibrium equations for the aeroengine under steady-state conditions can be expressed as follows:

$$(W_{2\mathrm{inner}}-W_2)/W_2=0$$

(11)

$$(W_2-W_{25})/W_{25}=0$$

(12)

$$(W_{25}-W_3)/W_3=0$$

(13)

$$(W_3+W_f-W_{45})/W_{45}=0$$

(14)

$$(W_{45}-W_5)/W_5=0$$

(15)

$$(W_{13}-W_{18})/W_{18}=0$$

(16)

$$(W_5-W_6)/W_6=0$$

(17)

$$(P_{\mathrm{HPC}}-P_{\mathrm{HPT}}\times {\eta }_{N_2})/(P_{\mathrm{HPT}}\times {\eta }_{N_2})=0$$

(18)

$$(P_{\mathrm{FAN}}+P_{\mathrm{LPC}}-P_{\mathrm{LPT}}\times {\eta }_{N_1})/{(P}_{\mathrm{LPT}}\times {\eta }_{N_1})=0$$

(19)

For the engine transient process, the power is determined by the rotational speed, acceleration, and moments of inertia of the engine rotors. Equations (18) and (19) can be modified as follows:

$$\frac{d{N}_1}{dt}=\frac{P_{\mathrm{LPT}}\times {\eta }_{N_1}-P_{\mathrm{FAN}}-P_{\mathrm{LPC}}}{N_1{J}_L}{\left(\frac{30}{\pi }\right)}^2$$

(20)

$$\frac{d{N}_2}{dt}=\frac{P_{\mathrm{HPT}}\times {\eta }_{N_2}-P_{\mathrm{HPC}}}{N_2{J}_H}{\left(\frac{30}{\pi }\right)}^2$$

(21)

In Equations (20) and (21), J_L represents the low-pressure shaft moment of inertia, and J_H represents the high-pressure shaft moment of inertia.

2.1.3. Mechanism Model Solving Process

The steady-state and transient simulation process of the mechanism model based on component-level modeling is illustrated in Figure 2. After inputting the flight control parameters, the mechanism model performs thermodynamic calculations for each gas path component and solves the corresponding equilibrium equations under steady-state and transient conditions using the Newton–Raphson method [38]. In the steady-state mode, the equilibrium equations described in Equations (11) to (19) are computed, and the gas path parameters at each engine station corresponding to the equilibrium state are outputted. For the transient mode, the current accelerations of the high-pressure and low-pressure rotors are obtained by solving Equations (20) and (21). If the simulation time is not completed, the computation of the next moment’s rotor speeds is continued. The transient process is repeated continuously until the prediction task for all time points in the transient process is completed, and finally, the gas path parameters at all time points are outputted.

2.2. Data-Driven Model

2.2.1. Extreme Gradient Boosting Machine (XGBoost)

In this study, to construct a highly accurate data-driven model, we selected an Extreme Gradient Boosting Machine (XGBoost) to fulfill the predictive functionality. XGBoost, proposed by Chen et al. [39] in 2016, is an optimized implementation of gradient boosting trees. XGBoost is an efficient, robust, accurate, and scalable machine learning algorithm that has been widely applied in various engineering domains. The specific description of the XGBoost algorithm is as follows [40]:

$$y_i^{\ast }=\varphi \left(x_i\right)=\sum _{k=1}^K{f}_k\left(x_i\right), f_k\in F$$

(22)

In Equation (22), x_i is drawn from a dataset D = {(x_i, y_i)} that contains n samples with m features. K represents the additive function, and F represents the space of regression trees. f_k represents the function to the decision tree. The XGBoost model reduces the error of the ensemble of trees through the objective function, which is calculated as follows:

$$L^{\left(t\right)}=\sum _{i=1}^{n}l\left(y_i,y_i^{\ast \left(t-1\right)}+f_t\left(x_i\right)\right)+\mathsf{\Omega }\left(f_t\right)$$

(23)

In Equation (23), l represents a convex objective function used to determine the error between the predicted values and the actual values. y_i represents the actual value, y^*_i represents the predicted value, t represents the number of iterations to minimize the error, and Ω represents the penalty function.

2.2.2. Data-Driven Model Framework Based on PSO-XGBoost

XGBoost has multiple parameters that need to be tuned, including tree depth, learning rate, regularization parameters, etc. Therefore, in this study, Particle Swarm Optimization (PSO) [41] is used to optimize the hyperparameters of XGBoost. In the PSO algorithm, individuals are called particles, and each population consists of N particles that are randomly initialized in the D-dimensional search space. Each particle is represented by two vectors: the velocity vector and the position vector. The update process can be divided into three parts: The first part is the inertia term, which allows particles to retain their previous velocities, representing “memory”. The second part is the self-awareness component, where particles update their positions based on their individual best-known positions. The third part involves information exchange and cooperation among particles, representing the “social” aspect.

Figure 3 illustrates the framework flow of developing a data-driven model based on PSO-XGBoost. The initial XGBoost model is developed first, followed by the optimization of its hyperparameters using PSO. The PSO algorithm optimizes the hyperparameters of the XGBoost model by allowing the particles to fly in the search space and exchange experiences to determine the best values for these hyperparameters [42]. For each particle’s new position, their fitness is calculated based on the optimization results of the XGBoost model. The hyperparameters are continuously optimized until the optimal data-driven predictive model is obtained.

2.3. Multimodal Fusion Model

In general, multimodal fusion refers to the process of integrating and interacting information from two or more different modalities. Modality refers to the manner in which something happens or exists, while multimodality refers to the combination of different modalities. Research in this field mainly focuses on the processing of three modalities: image, text, and speech. The reason for multimodal fusion lies in the fact that different modalities present information in different ways, leading to variations in the observation perspective of phenomena. As a result, there are cross-modal and complementary phenomena, and there may even be multiple ways of interaction between modalities. By appropriately handling multimodal information, richer feature information can be obtained, thereby improving prediction accuracy [43]. Mechanistic models and data-driven models reflect the performance of an engine from different perspectives and can be seen as forms that carry different modalities of information about the engine. Through multimodal fusion, mechanistic models and data-driven models can be comprehensively utilized to obtain more comprehensive and accurate predictions and diagnostic results for engine performance.

2.3.1. Multimodal Fusion Using Tensor Representations

Tensor representation has gained widespread attention due to its ability to capture multimodal interactions. To construct such tensor representations, the outer product operation of the input modalities can be utilized [44]. The expression for the input tensor Z is as follows:

$$Z={\otimes }_{m=1}^M{z}_m,z_m\in R^{d_m}$$

(24)

In Equation (24), ${\otimes }_{m=1}^M$ denotes the tensor outer product over a set of M indexed vectors, where z_m represents the input representations. The input tensor Z is then transformed by a linear layer g to generate the vector representation, which is expressed as follows:

$$h=g\left(Z;W,b\right)=W\times Z+b, h,b\in R^{d_y}$$

(25)

In Equation (25), W represents the weights and b represents the bias. Figure 4 illustrates the tensor fusion process in the case of bimodal (dual-modal) inputs. The number 1 in the figure represents the dimension.

2.3.2. Low-Rank Multimodal Fusion (LMF)

Taking into account the limitations of tensor-based fusion methods in handling a large number of modalities, this paper introduces the concept of low-rank factorization [45]. By decomposing the weight tensor of the tensor representation into low-rank tensor representations, and by utilizing parallel decomposition of the low-rank weight tensor and the input tensor, tensor-based fusion can be computed. The key idea is to perform separate linear transformations on each modality and then perform multidimensional dot product operations, summing the results of multiple low-rank vectors to reduce the number of parameters in the model [46]. This approach reduces the number of parameters and improves computational efficiency. The M (where M represents the number of input modalities) order tensor can be decomposed into a vector representation in the following form:

$$W_k=\sum _{i=1}^R{\otimes }_{m=1}^M{w}_{m,k}^i, w_{m,k}^i\in R^{d_m}$$

(26)

In Equation (26), the rank of the tensor is given by the minimum value of R obtained from the decomposition, and the decomposition factors of the original tensor with rank R are denoted as {{wⁱ_m,k}^M_m=1}^R_i=1. Therefore, the low-rank weight tensor can be modified as follows:

$$W=\sum _{i=1}^r{\otimes }_{m=1}^M{w}_m^i$$

(27)

The LMF method utilizes each rank r to reconstruct the low-rank W_k, and these vectors are recombined and concatenated to form the low-rank factors for each of the M modalities. Therefore, Equation (25) can be rewritten as follows:

$$h=\left(\sum _{i=1}^r{\otimes }_{m=1}^M{w}_m^i\right)\ast Z$$

(28)

By introducing low-rank factors for the computation of weight matrix W, Equation (28) can be further rewritten as follows:

$$h=\sum _{i=1}^r{\left[\underset{m=1}{\overset{M}{\bigwedge }}\left[w_m^1,w_m^2,\dots ,w_m^r\right]\ast z_m^{\wedge }\right]}_i$$

(29)

In Equation (29), $\underset{m=1}{\overset{M}{{\displaystyle \Lambda }}}$ represents the product of elements in a sequence.

Figure 5 illustrates the process of the weight tensor W low-rank factorization in a bimodal scenario. The number 1 and 2 in the figure represents the dimension. As seen in Figure 5, the low-rank factors are concatenated into an M-th order tensor, which is used to perform element-wise multiplication and summation along the first dimension of the surrounding matrix. Compared to the vector-set representation, h is computed via mode-specific factorizations and parameterized by an M-th order tensor, greatly reducing the dimensionality increase for tensors Z and W.

2.4. Fault Diagnosis Model

2.4.1. Sparse Stacked Autoencoder Network (SSAE)

In this study, the research adopts stacked sparse autoencoder (SSAE) for the modeling process. SSAE is a deep network structure formed by SAE. It takes the features extracted from the previous layer and feeds them into the next layer, enabling deep learning of data features at different scales. The structure of the network is illustrated in Figure 6 [47].

SSAE is composed of N stacked SAE, and the parameters in the network can be represented as follows: the number of nodes in the input layer is n, the number of hidden layers is N, the number of nodes in the hidden layers is s = [s₍₁₎, s₍₂₎, …, s_(l)], the weight matrices are represented as w = [w⁽¹⁾, w⁽²⁾, …, w^(l+1)], and the bias matrices are represented as b = [b⁽¹⁾, b⁽²⁾, …, b^(l+1)]. The encoding process can be written as follows:

$$\begin{gathered} h^{\left(t\right)}=f\left(z^{\left(t\right)}\right);\forall t=1, 2,\dots ,l \\ \begin{array}{c}{z}^{\left(t\right)}=w^{\left(t,1\right)}{h}^{\left(t-1\right)}+b^{\left(t,1\right)}\end{array} \end{gathered}$$

(30)

The decoding process can be written as follows:

$$\begin{gathered} h^{\left(t+l+2\right)}=f\left(z^{\left(t+l+2\right)}\right);\forall t=1, 2,\dots ,l \\ \begin{array}{c}{z}^{\left(t+l+3\right)}=w^{\left(l+2-t,2\right)}{h}^{\left(t+l+2\right)}+b^{\left(l+2-t,2\right)}\end{array} \end{gathered}$$

(31)

2.4.2. Training Process of SSAE

Figure 7 illustrates the learning process of SSAE [48]. The overall training of SSAE can be divided into multiple subnetworks, sequentially training each subnetwork layer by layer until all hidden layers reach an optimal state. Then, the model parameters are updated through backpropagation using the global loss function. Firstly, the original sample data are fed into the first autoencoder of the network, and this layer’s subnetwork is trained. The updated weight set w⁽¹⁾ = [w^(1,1), w^(1,2)] and bias set b⁽¹⁾ = [b^(1,1), b^(1,2)] are obtained. Then, the output values of the non-linear mapping function in the first layer are used as inputs for the next autoencoder to train the second autoencoder. The updated weight set w⁽²⁾ = [w^(2,1), w^(2,2)] and bias set b⁽²⁾ = [b^(2,1), b^(2,2)] for the second layer subnetwork are obtained. This process continues layer by layer until all subnetworks are trained, resulting in w = [w^(1,1), w^(2,1), …, w^(l,1), w^(l+1,1)] and b = [b^(1,1), b^(2,1), …, b^(l,1), b^(l+1,1)]. Finally, all the subnetworks are concatenated, and the global loss function is used to adjust the weights (w) and biases (b).

3. Digital Twin Framework Functions and Processes

3.1. Mechanism Model Update for Performance Degradation

As the engine operates continuously, its performance is bound to decline over time. However, most engine gas path diagnostic models are designed to analyze the initial benchmark performance of the engine, making it difficult to track the deterioration of the engine over its lifespan. Therefore, it is crucial to regularly update the engine’s benchmark performance to enhance the accuracy of diagnosis. The GPA theoretical framework assumes that the characteristic curves in the component characteristic maps do not change their shape after performance degradation of engine gas path components [8]. The degradation is represented as a slight translation of the characteristic lines in the characteristic map from the initial clean state, as shown in Figure 8 [49]. The arrows in the figure represent the trend trajectory of degradation. This study uses the degradation factor (DF) to quantify the degree of degradation, which is defined as follows:

$$DF=\frac{X_D}{X_C}\times 100\%$$

(32)

In Equation (32), X represents the gas path component characteristic parameters corresponding to the mass flow, pressure ratio, and efficiency. The subscripts D and C indicate the degraded and clean states, respectively.

In practical engineering, the gas path component characteristic parameters are often not directly measurable. Therefore, it is necessary to select the appropriate gas path measurement parameters as target parameters based on the actual sensor configuration to reverse engineer the engine gas path components’ degradation condition. This study utilizes the PSO algorithm introduced in Section 2.2.2 to calculate the DF and periodically update the mechanism model. Figure 9 illustrates the process of updating the mechanism model for engine performance degradation. First, the velocity and position of individuals in the particle swarm are initialized. The PSO is then employed to calculate the new DF, which is then incorporated into the mechanism model to perform thermodynamic performance calculations. The objective function (OF) is obtained, which represents the discrepancy between the gas path measurement parameters obtained from the mechanism model and the actual gas path measurement parameters. The formula for OF is as follows:

$$OF=\frac{1}{n}\frac{1}{m}\left[\sum _{j=1}^n\sum _{i=1}^m\left|\frac{p_{\left(pre\right)i,j}-p_{\left(act\right)i,j}}{p_{\left(act\right)i,j}}\right|\right]$$

(33)

In Equation (33), m represents the number of gas path measurement parameters used, and n represents the number of operating conditions involved in the engine model correction calculation. P(pre) represents the gas path measurement parameters calculated using the engine thermodynamic model, and P(act) represents the target gas path measurement parameters. Finally, it is determined whether the current OF satisfies the termination condition. If so, the process of updating the mechanism model for engine performance degradation stops. Otherwise, the PSO continues the calculation. Through the aforementioned process, the mechanism model can periodically track the degradation of engine performance and update the DF of the mechanism model. Additionally, the updated mechanism model can continue to maintain high accuracy in predicting engine gas path measurement parameters, effectively assisting engine maintenance personnel in maintenance operations.

3.2. Gas Path Fault Diagnosis

According to the GPA theory introduced in Section 3.1, engine gas path faults can also be viewed as a specific type of gas path component degradation. The gas path faults in this paper mainly focus on slow time degradation, including fouling, erosion, etc., and the degradation is ultimately manifested as changes in the gas path measurement parameters (temperature and pressure) [50]. Figure 10 illustrates the information transfer process between the engine gas path measurement parameters and fault diagnosis in the GPA theory, indicating a close relationship between the engine gas path measurement parameters and the gas path faults. Therefore, diagnosing engine gas path faults using engine gas path measurement parameters is feasible. However, the available recorded fault data in practical engineering are limited. Currently, most studies implant engine fault rule libraries into engine models to simulate post-degradation component characteristic maps and obtain gas path measurement parameters after faults. Based on this, various gas path component faults are simulated [51]. To construct more realistic fault scenarios, the relationship between typical physical faults and component characteristic parameters is referenced from reference [52] (as shown in

Table 3. Relationship between the physical faults and health parameters.

Fault Type	Flow Capacity (A)	Isentropic Efficiency (B)	Ratio A:B	Range
Compressor fouling	↓	↓	~3:1	(0, −7.5%), (0, −2.5%)
Turbine fouling	↓	↓	~2:1	(0, −4%), (0, −2%)
Turbine erosion	↑	↓	~2:1	(0, 4%), (0, −2%)

), and a fault rule library is built accordingly. In Table 3, ↓ represents a decrease, ↑ represents an increase. The decrease in the pressure ratio and flow characteristics resulting from gas path faults is assumed to be the same. Since this study mainly focuses on the digital twin method for diagnosing the performance of rotating components in aeroengines, sensor faults are not within the scope of this study. Assuming that gas path faults occur in the FAN, LPC, HPC, HPT, and LPT, the probability of multiple components experiencing multiple faults simultaneously is very low. Therefore, this study primarily investigates nine fault cases, which are listed in

Table 4. Cases based on cause–effect scenario.

Case	FAN Fouling	LPC Fouling	HPC Fouling	LPC Erosion	HPT Fouling	LPT Fouling	LPT Erosion
1	×
2		×
3			×
4				×
5					×
6						×
7	×	×			×		×
8	×	×	×	×		×
9	×	×	×		×		×

. In Table 4, × ndicates the fault categories included in the case.

3.3. Digital Twin Process

Figure 11 illustrates the proposed digital twin framework for aeroengines, which adopts a closed-loop form and consists of multiple mechanism and algorithm models, forming two functional modules: engine performance prediction and fault diagnosis. These two modules drive each other through information transfer, achieving a virtual mapping between the real engine and the digital twin engine. Firstly, the mechanism model and data-driven model are built using flight data, which are the core of the engine performance prediction module. The data-driven model adopts the PSO-XGBoost model, which effectively extracts engine performance information from the flight data. The mechanism model is constructed based on the aerothermal principles introduced in Section 2.1, representing another mode of information. Additionally, the mechanism model can adaptively update performance degradation to ensure its applicability and reliability. The LWF model, as the core of the engine digital twin fusion, is used to achieve multimodal information fusion between the data-driven model and the mechanism model, enabling the mapping of information between the real physical engine and the virtual simulated engine. Since the LWF model integrates the modal information from both models and possesses the characteristic of mechanism model updating, it can provide more accurate data information, enabling engine performance prediction and condition monitoring. Moreover, the multimodal fused engine information is combined with the SSAE model to achieve engine fault diagnosis and isolation, providing timely feedback to the real physical engine and assisting the engine flight control system in making correct decisions.

4. Case Study

4.1. Gas Path Parameters Prediction Verification

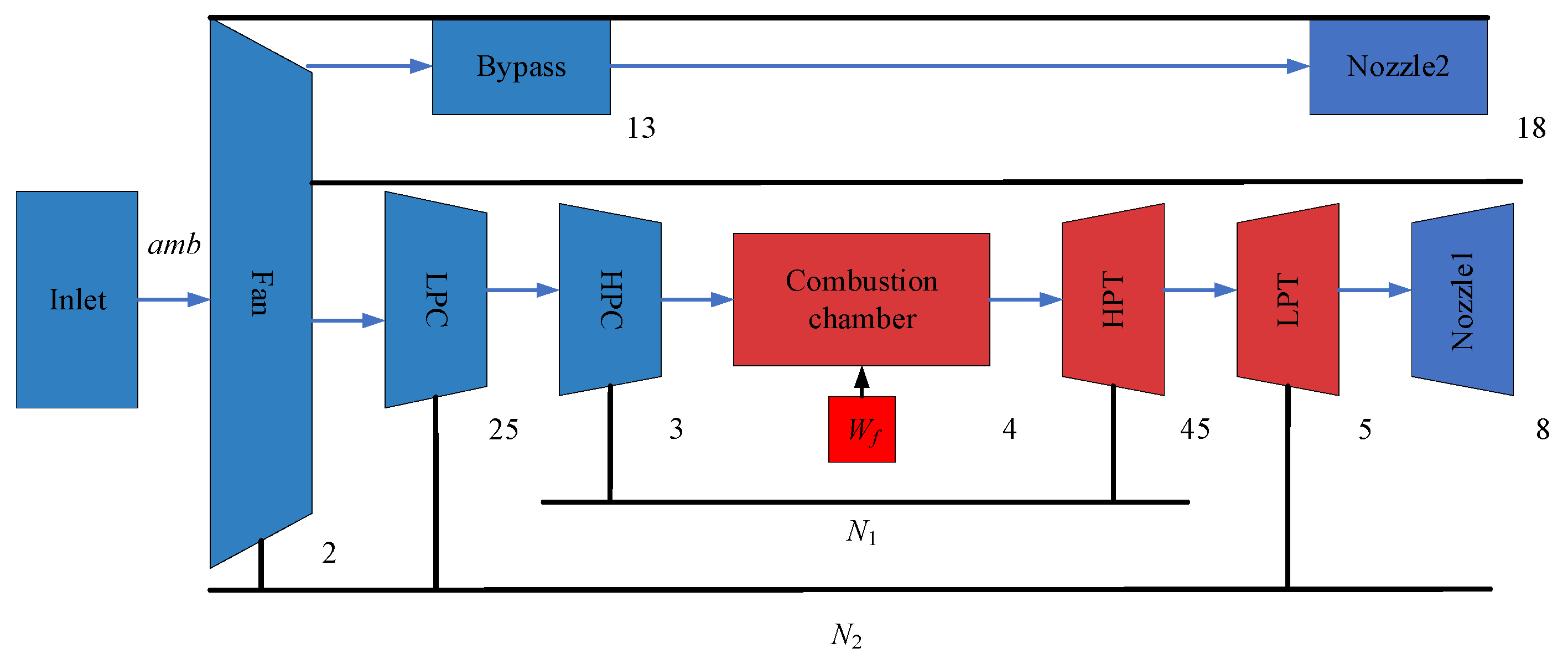
Due to the difficulty of obtaining long-term operational data for engines, this study utilizes the mechanism model for the simulation to obtain “real” engine degradation data. Previous research has demonstrated the feasibility of this verification method [53,54,55]. Section 2.1 introduced the relevant information regarding the aeroengine applied in this study. The typical performance degradation trend for a turbofan engine defined in the literature [56,57,58] was selected to simulate the degradation behavior during long-term engine operation. It is assumed that all five rotating components experience simultaneous performance degradation, and the propagation trend of performance deterioration can be described using an exponential function based on flight cycles. The degradation propagation function used in this study is defined as follows:

$$DF=(2-\mathit{exp}\left(a\ast t^b\right))\times 100\%$$

(34)

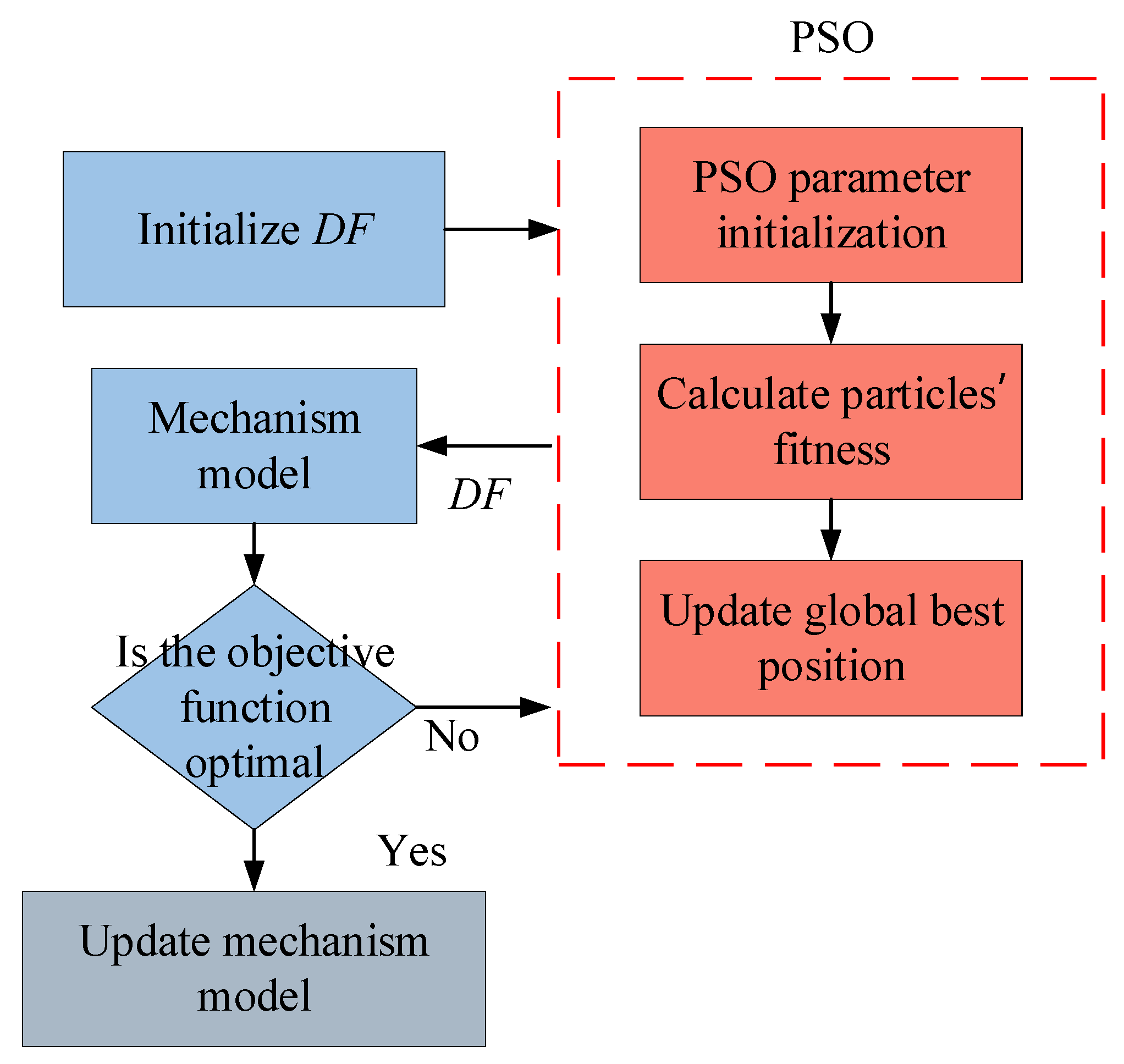
In Equation (34), a represents the degradation rate of DF, t represents the number of flight cycles, and b represents the flight cycle exponent coefficient.

Table 5. Degradation propagation and related coefficients.

Component	Health Parameter	Coefficient	Value
FAN	DFm	a	0.01
		b	0.14675
	DFη	a	0.01
		b	0.11878
LPC	DFm	a	0.01
		b	0.1571
	DFη	a	0.01
		b	0.1088
HPC	DFm	a	0.01
		b	0.25236
	DFη	a	0.01
		b	0.29621
HPT	DFm	a	0.01
		b	0.10705
	DFη	a	0.01
		b	0.1516
LPT	DFm	a	0.001
		b	0.16544
	DFη	a	0.01
		b	0.008

presents the coefficient values of “a” and “b” for the five rotating components’ performance degradation propagation exponential functions, which describe the degradation propagation pattern with respect to the flight cycles. The propagation pattern assumes a maximum of 6000 flight cycles, indicating that the engine is considered to have failed after reaching 6000 flight cycles. In this study, the actual engine’s performance degradation corresponds to 3000 flight cycles, and the DF corresponding to 3000 flight cycles is injected into the mechanism model to obtain the “real” flight data.

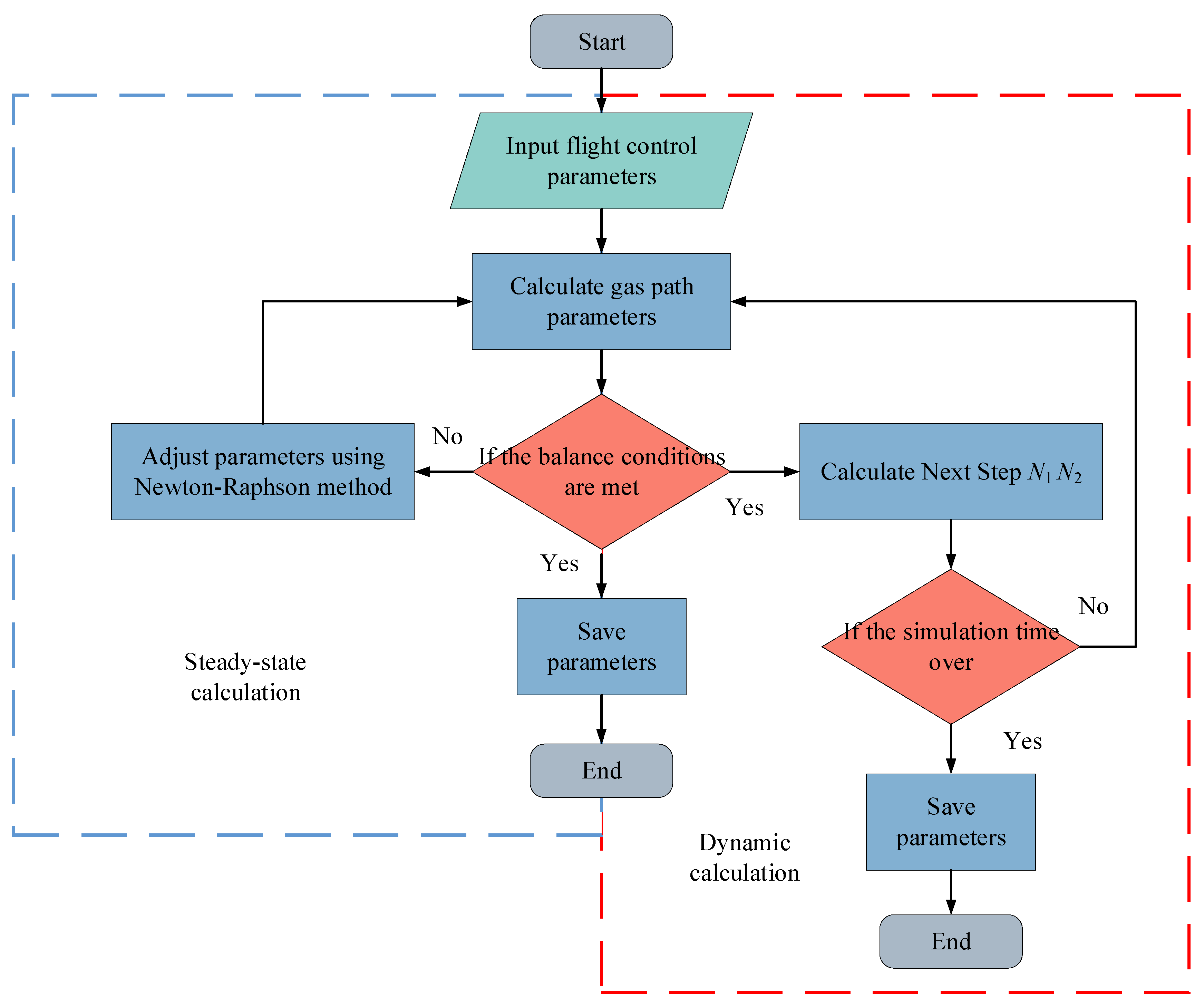
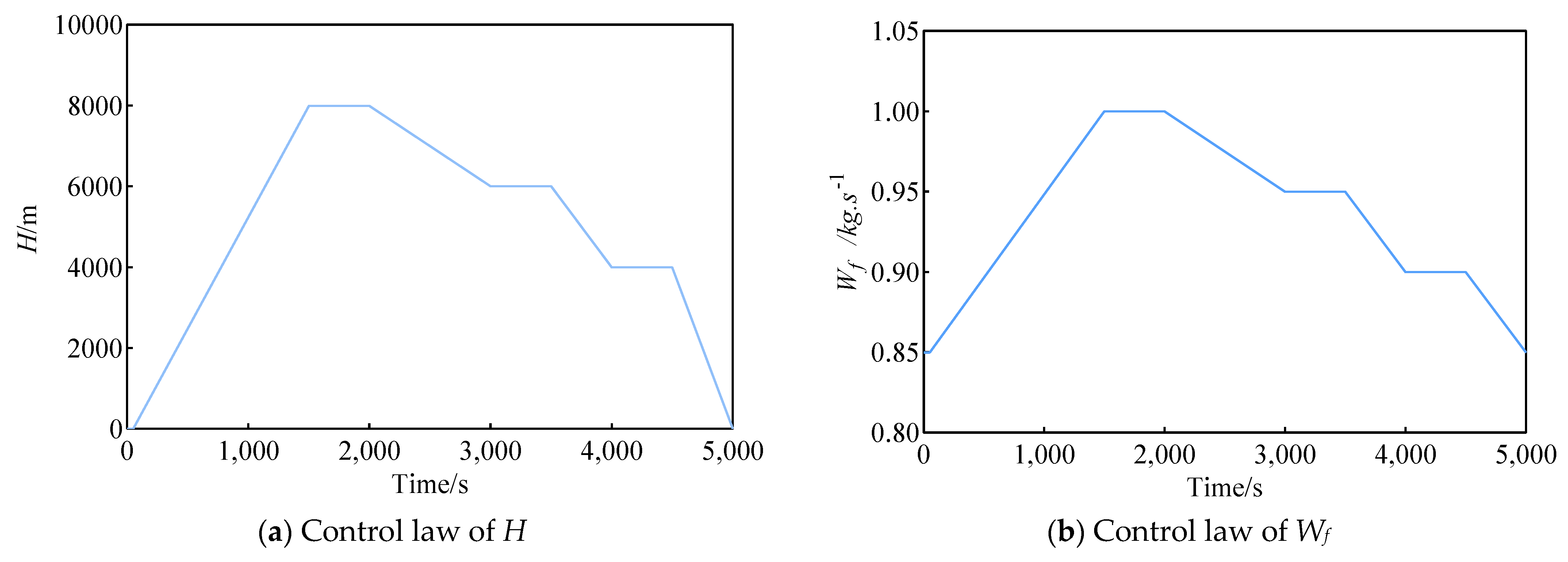
To validate the reliability of the proposed digital twin framework, the method was tested following the process framework depicted in Figure 11. Considering the specific engine information and actual sensor measurement conditions, the measurement noise was added to the simulated data to better mimic the engine’s flight conditions. Assuming that the measurement noise follows a normal distribution,

Table 6. Measurement parameters and noise level description.

Parameters	Definition	Reference Noise Level
N1	LP spool speed	0.25%
N2	HP spool speed	0.25%
T2	Fan outer exit temperature	0.75%
T25	LPC exit temperature	0.75%
T3	HPC inlet temperature	0.75%
T5	LPT exit temperature	0.75%

lists the gas path parameters used in this study and their corresponding noise levels. In this study, we intentionally introduced a small deviation as simulated noise after applying noise reduction techniques. However, it is important to note that the primary focus of this study does not encompass the investigation of the impact of measurement noise on the model accuracy. Additionally, as the inputs for the mechanism model and data-driven model are the flight control data (H, Ma, and W_f), to make the study case more realistic, we simulated the typical flight trajectory of a commercial twin-spool turbofan engine, and the variations of the flight mission control data are shown in Figure 12. From Figure 12, it can be observed that except for the cruise phase, H keeps changing, while W_f gradually increases during the climb phase. The mechanism model generates the corresponding flight data based on this flight control pattern, with one data point generated per second. The data-driven model utilizes the generated flight data as training samples, while the mechanism model updates the performance degradation by extracting the engine operating points from the flight data.

Figure 13 illustrates a comparison of the output results from different models. It can be observed from Figure 13 that the mechanism model without degradation updates exhibits significant errors compared to the actual engine output. Although the mechanism model with degradation updates can better reflect the changing trend of the gas path parameters, there are still certain deviations in its output. This is because the mechanism model considers relatively ideal conditions and cannot differentiate the influence of factors such as the measurement noise and external environment in the data, thus making it difficult to achieve an accurate prediction of the engine gas path parameters. On the other hand, the data-driven model shows good predictive results, effectively reflecting the changing trend of the gas path parameters in the aeroengine. This is because the data-driven model can dynamically learn based on historical and current data, providing stronger real-time capability. Moreover, the data-driven model can incorporate the influence of the measurement noise and external factors during the learning process. However, the data-driven model is a black-box model that cannot provide the changing trend of the engine’s unmeasurable data (such as the component characteristic parameters). In comparison, the digital twin approach demonstrates the best prediction results for the gas path parameters, which are closer to the actual data. Furthermore, to better demonstrate the superiority of the proposed digital twin framework, we compared the mean absolute percentage error (MAPE) of the predicted values from different models. The formula for calculating the MAPE is as follows:

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{1}{n}\sum _i^n\left|\frac{y_i-y_i^{\ast }}{y_i}\right|\times 100\%$$

(35)

where y_i and y^*_i represent the actual value and predicted value of the i-th data sample, respectively.

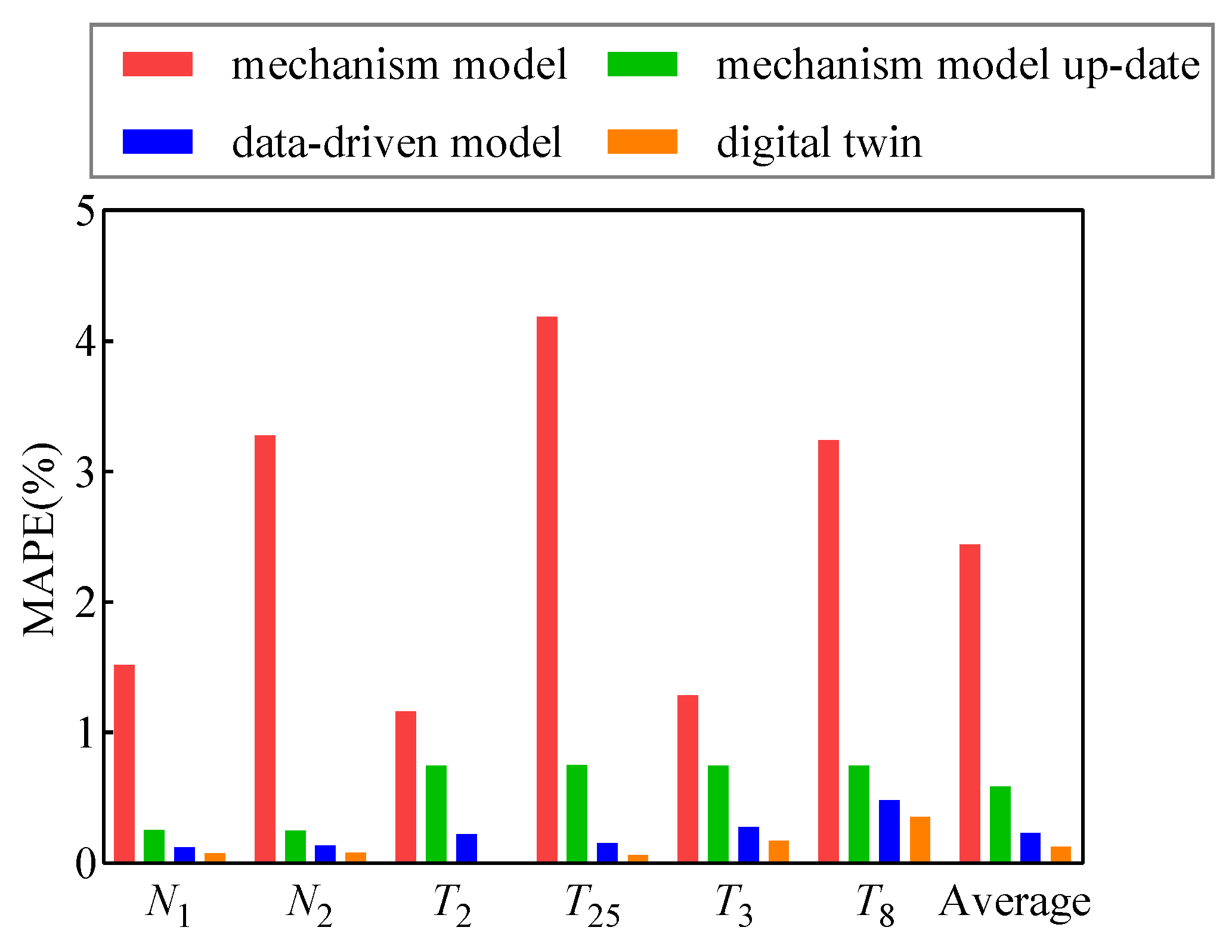
Figure 14 and

Table 7. The MAPE of different model outputs.

Model	N1	N2	T2	T25	T3	T5	Average
mechanism model	1.516%	3.276%	1.162%	4.184%	1.286%	3.235%	2.443%
mechanism model update	0.251%	0.249%	0.749%	0.752%	0.748%	0.748%	0.583%
data-driven model	0.122%	0.137%	0.223%	0.152%	0.278%	0.481%	0.232%
digital twin	0.076%	0.081%	0.011%	0.061%	0.171%	0.352%	0.125%

present the MAPE of the gas path measurement parameters obtained using different models. It can be observed that the mechanism model without performance degradation updates exhibits significant errors compared to the actual engine outputs, with a maximum MAPE of 4.184% and an average MAPE of 2.443%. In contrast, the mechanism model with performance degradation updates shows fewer prediction errors, with an average MAPE reduced to 0.583% compared to the original mechanism model. This indicates that the mechanism model with performance degradation updates can achieve a higher accuracy in real-time condition monitoring. The overall MAPE of the data-driven model is 0.232%, while the digital twin model achieves an even lower overall MAPE of only 0.125%. It can be seen that the digital twin method has smaller errors compared to the mechanism model and the data-driven model, demonstrating a significant improvement in the prediction performance. Although the MAPE of the data-driven model is higher than that of the digital twin method, its prediction results are significantly better than the mechanism model. This is because the mechanism model can reflect the trend of the engine performance changes but cannot handle small measurement deviations or noise in the actual measurements. On the other hand, the data-driven model can absorb the influence of noise during the learning process, but as a black-box model, it cannot reflect the degradation of the unmeasurable parameters (such as the mass flow, pressure ratio, and efficiency) of the engine, which hinders the representation of the performance change trends. The proposed digital twin framework incorporates information from both the mechanism model and the data-driven model, leveraging the advantages of both modalities to achieve high-precision predictions while continuously tracking the performance changes in the engine. This provides a more effective basis for subsequent gas path fault diagnosis.

4.2. Gas Path Fault Diagnosis Verification

Through the case study in Section 4.1, we validated the accuracy of the digital twin framework in predicting the aeroengine gas path parameters. It can more accurately simulate the actual engine’s gas path measurement parameters, making it suitable for engine condition monitoring. However, due to the difficulty in obtaining the actual fault data for aeroengines, we also use a mechanism model here to simulate the engine’s gas path fault data and combine it with the SSAE model to perform a gas path fault diagnosis for the engine, thus achieving an integrated digital twin framework for aeroengine performance diagnosis. In this setup, we still set the actual engine with a performance degradation corresponding to 3000 flight cycles and generate gas path fault data using the mechanism model as described in Section 3.2. Based on the degradation rates in Table 3, we randomly generate the performance parameters of each gas path component within the degradation range to create a dataset for validating the gas path fault diagnosis functionality. The data in the dataset are engine sensor information, which were processed according to the noise levels in Table 6. A total of 2700 data samples were collected, with 300 samples for each type of fault, and each fault sample is independent of the others.

To better validate and evaluate the diagnostic performance of the proposed digital twin framework, we additionally include a comparison with DBN [25], CNN [26], and SSAE models that are built solely using engine sensor information. These models have been widely applied in practical engineering and have demonstrated excellent performance. Unlike the SSAE model that is used in the digital twin framework, they utilize only a single modality of information.

Table 8. The network structures of these neural networks.

Network	Network Structure
SSAE	6 layers of modules
digital twin + SSAE	6 layers of modules
DBN	1 hidden layer and 1 visible layer
CNN	3 convolution layers and 2 fully connected layers

presents the network structure information for these models.

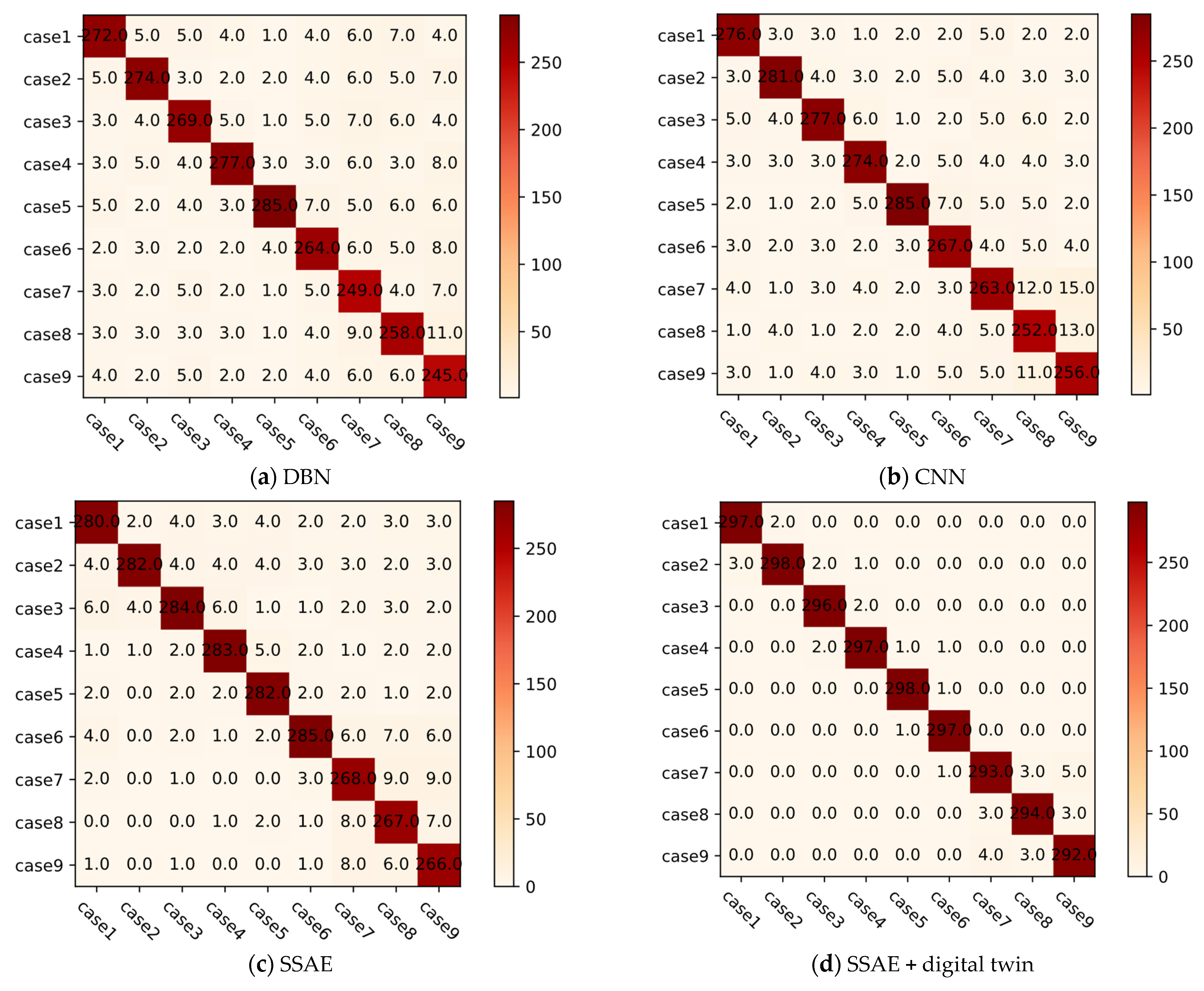
Figure 15 illustrates the diagnostic confusion matrices corresponding to various deep learning networks and the digital twin framework, while

Table 9. Diagnostic accuracy and CPU time of each approach.

Approach	Total Accuracy (%)	CPU Time (s)
DBN	88.6%	52.11
CNN	90.1%	69.39
SSAE	92.5%	47.25
SSAE + digital twin	98.6%	93.96

summarizes their overall diagnostic accuracy and CPU processing time. From Figure 16d, it is evident that the SSAE + digital twin framework can clearly distinguish between the nine fault types, with only a small number of fault samples causing confusion. However, in the three fault cases (Case 7, Case 8, and Case 9) involving multiple coupled gas path faults, there are relatively more instances of confusion. This is because extracting multiple fault features becomes more challenging. For the proposed SSAE + digital twin framework in this paper, Case 7, Case 8, and Case 9 have seven, six, and eight misclassified fault samples, respectively. Specifically, in Case 7, three fault samples are misclassified as Case 8, and four fault samples are misclassified as Case 9. In Case 8, three fault samples are misclassified as Case 7, and three fault samples are misclassified as Case 9. In Case 9, five fault samples are misclassified as Case 7, and three fault samples are misclassified as Case 8. However, the misclassified fault samples constitute only a small portion of the overall samples, and compared to the other three methods, the number of misclassified fault samples is significantly reduced.

According to the data in Table 9, it can be observed that the overall diagnostic accuracies of the DBN, CNN, and SSAE are 88.6%, 90.1%, and 92.5%, respectively. Among them, the SSAE has a higher accuracy compared to the DBN and CNN. This is because the SSAE applies sparsity constraints to the outputs of each hidden unit, limiting the model’s complexity and reducing the risk of overfitting, thereby improving the generalization performance of the model. The overall accuracy of the digital twin + SSAE method reaches 98.6%, significantly outperforming the three aforementioned methods.

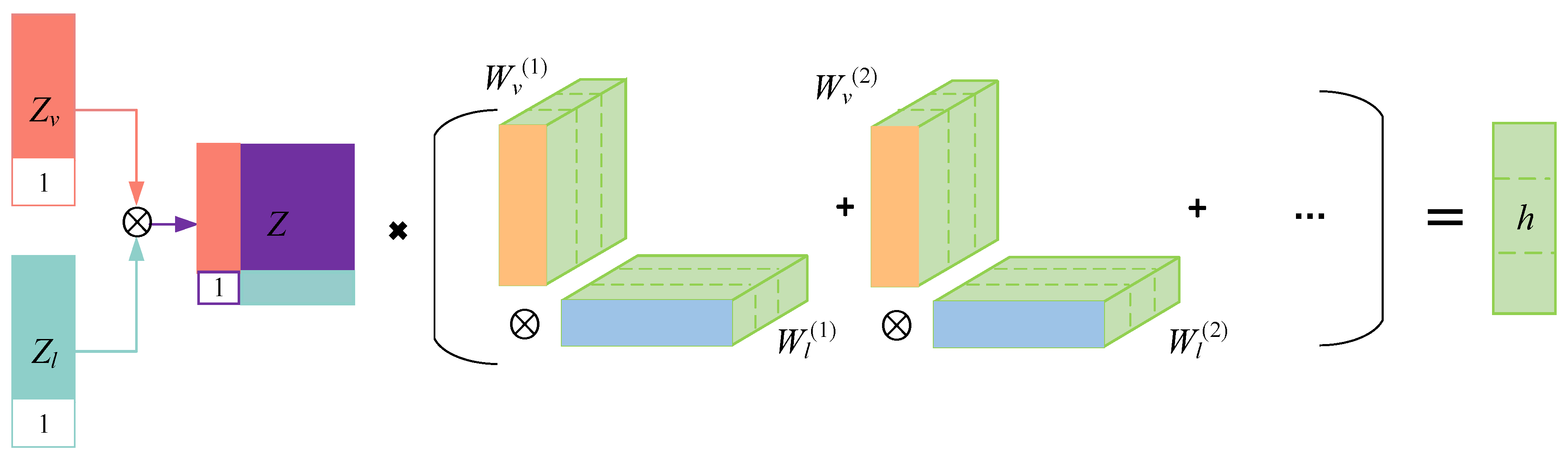
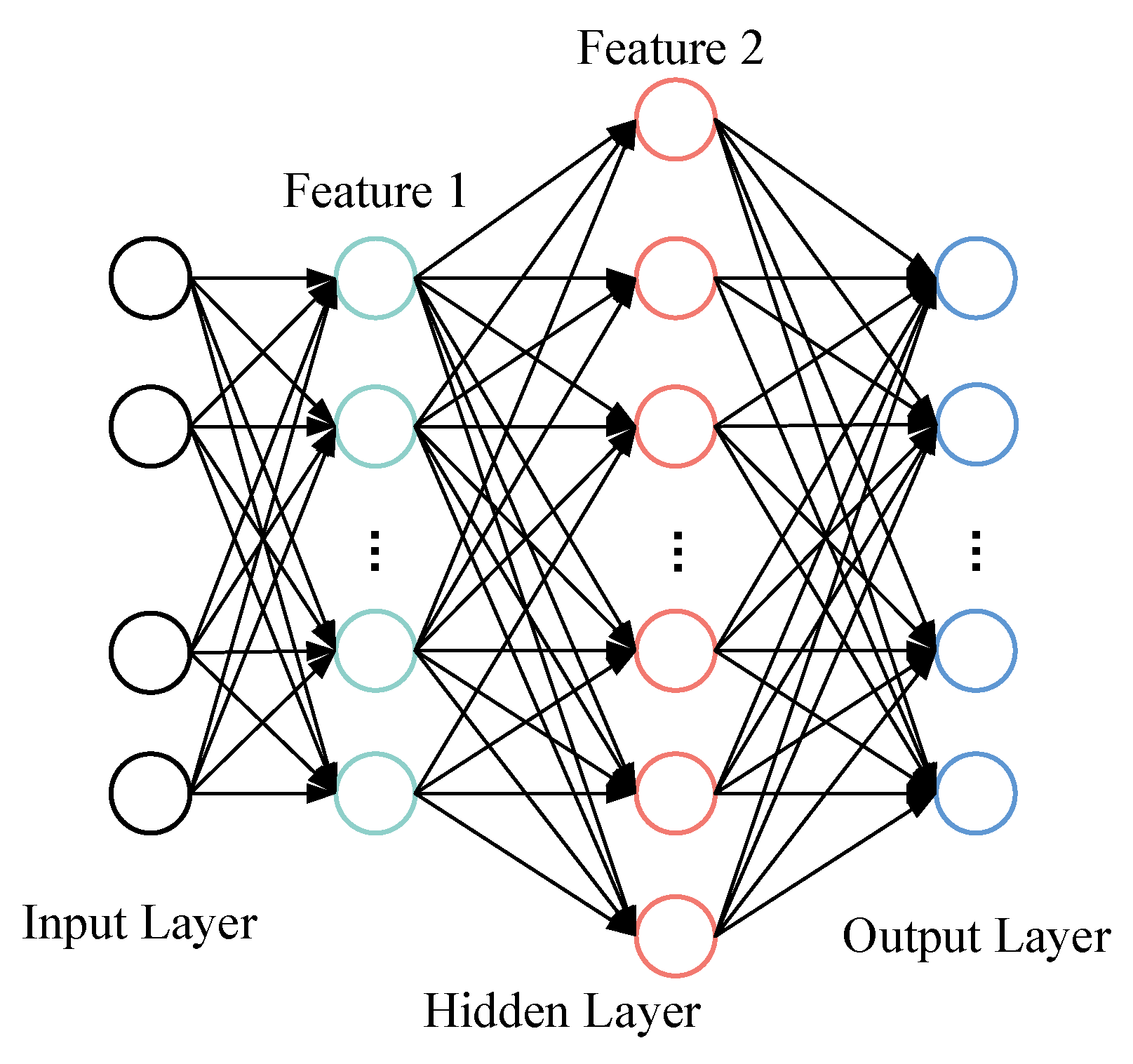
The SSAE plays a central role in the digital twin framework for gas path fault diagnosis. Through the multimodal data fusion in the digital twin framework, the accuracy of the SSAE is significantly improved. Compared to the DBN, CNN, and SSAE, the proposed digital twin + SSAE method achieves improvements of 10%, 8.5%, and 6.1% in the overall accuracy, respectively. This indicates a significant enhancement in the diagnostic performance of the SSAE through the fusion of multimodal data in the digital twin framework. The digital twin framework, unlike single-modal information-based gas path fault diagnosis methods, effectively extracts valuable features from the engine gas path data from different modalities through the LWF method. This improves data reliability and enhances the accuracy of the gas path fault diagnosis in engines by leveraging the fusion of multimodal information.

In terms of the diagnostic time, all the methods were run on a computer with an AMD Ryzen 9 3900X CPU and 32 GB of memory. The SSAE showed the shortest CPU computation time, with 47.25 s. The DBN and CNN had CPU computation times of 52.11 s and 69.39 s, respectively. The proposed digital twin + SSAE method had the longest CPU computation time, which was 93.96 s. This is understandable, as the digital twin framework processes more information from different modalities. However, it still demonstrates a fast computation time, requiring only 0.0348 s to process the diagnosis for a single engine operating point. Considering the trade-off between the performance prediction accuracy, diagnostic accuracy, and computation time, the proposed aeroengine digital twin framework has clear advantages over the other models and is suitable for aeroengine performance diagnosis tasks.

4.3. Economic Evaluation of Gas Path Performance Degradation

During actual flight, aircraft engines typically maintain a constant takeoff weight, necessitating a consistent level of thrust. Consequently, assuming that the engine maintains a certain thrust throughout different flight stages, engine degradation will cause an increase in the fuel flow rate as a control measure to compensate for the reduced performance. The following equation presents the formula for calculating the additional fuel volume (W_fe) generated by the flight mission due to degradation:

$$W_{fe}=\sum _i^n\left[\left(W_{fd}-W_f\right)\times T_i\right]$$

(36)

In the equation, W_fd represents the fuel flow rate of the engine after degradation, T_i represents the total duration of the flight mission, and i represents the i-th flight phase among n flight segments. The calculation method for the additional fuel cost (C_f) incurred by the entire airline fleet due to engine degradation is

$$C_f=W_{fe}\times F_{up}\times TNumE$$

(37)

In the formula, F_up represents the fuel price, and TNumE represents the total number of engines in the entire fleet.

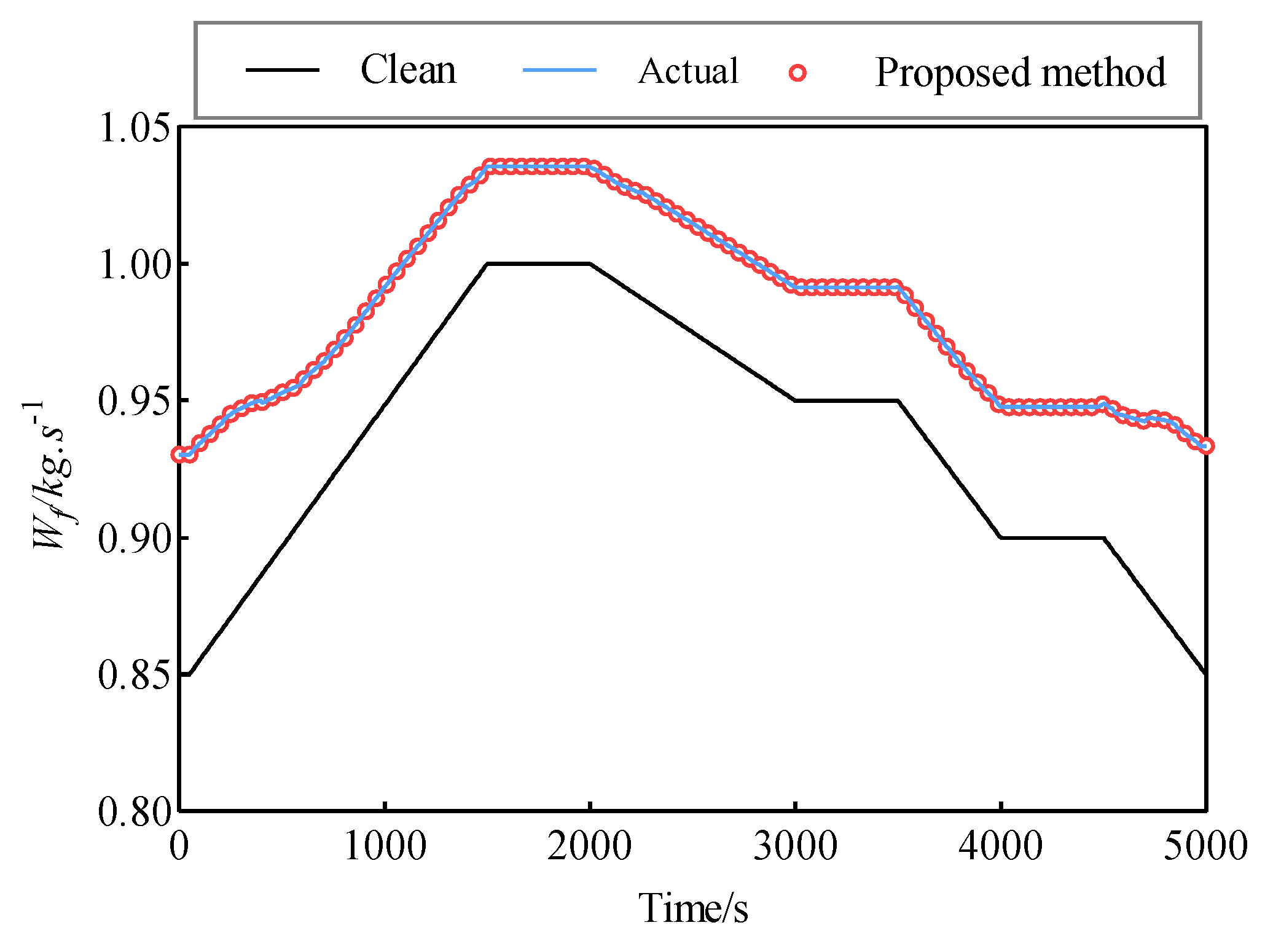
This study involves the estimation of the flight trajectory, as illustrated in Figure 12, and utilizes the DF injection mechanism model for 3000 flight cycles to determine the corresponding fuel flow rate while maintaining the same thrust as in a clean state. In Figure 16, a comparison of the fuel consumption using the digital twin method is shown for both the clean and degraded states, demonstrating highly accurate prediction results. Based on the current market price of aviation fuel, which is approximately USD 0.887/kg, and using formulas (36) and (37), the additional fuel cost (C_f) for the next engine in the flight cycle due to degradation is approximately USD 209.5. This significant increase in the fuel cost highlights the detrimental impact of aviation engine degradation on the economy of engine users. In conclusion, this study demonstrates that aviation engine degradation can have a substantial negative effect on operational costs for engine users, emphasizing the importance of monitoring and managing the engine health to mitigate these economic implications.

The aeroengine gas path diagnosis technology is of significant importance in reducing maintenance costs and improving the economic efficiency of engines. This research can be applied to analyze the performance degradation trends of engine health conditions, enhance the thermal efficiency of engines, and optimize flight missions. Additionally, this research holds the potential to contribute to improving maintenance decision making, prolonging the service life of aeroengines, and ensuring the safety and reliability of aviation operations.

5. Conclusions

This paper summarizes previous research progress on engine gas path diagnosis and proposes a digital twin framework for aeroengines. The framework combines a low-rank multimodal fusion mechanism model and a data-driven model. The mechanism model is constructed based on component-level models of the engine, providing steady-state and transient functionalities, while the data-driven model is developed using the PSO-XGBoost model. These two models provide engine information in different modes, and the features of both modes are fused using the LWF method to form the corresponding virtual engine. Additionally, the diagnosis of the engine gas path faults is accomplished by combining the SSAE with another method, resulting in a complete digital twin framework. The main feature of this method lies in its integration of the advantages of different models, enabling accurate prediction and fault diagnosis with a high precision and computational efficiency. It also takes into account the long-term degradation of the engine, which is suitable for flight missions. The feasibility of this method is verified through case studies, leading to the following conclusions:

• The mechanism model updated with performance degradation achieves a significant improvement in the total MAPE, decreasing from 2.443% to 0.583%, and the overall MAPE of the data-driven model is 0.232%. The proposed digital twin framework achieves an overall MAPE of only 0.125%. Compared to the mechanism model and the data-driven model, the digital twin framework exhibits a significantly improved prediction accuracy for aerodynamic parameters across the entire flight mission, enabling continuous updates as the engine operates over the long term, and better reflecting the engine’s health condition.
• Compared to three deep learning models, DBN, CNN, and SSAE, the proposed digital twin framework demonstrates distinct advantages in diagnostic accuracy, achieving overall accuracy improvements of 10%, 8.5%, and 6.1%, respectively, with an overall diagnostic rate of 98.6%. In terms of the diagnostic time, the digital twin framework performs comparably to the other models.
• This study presents an estimation method for calculating the fuel cost incurred by engine degradation and assesses the resulting typical flight mission loss, which amounts to approximately USD 209.5 per engine after undergoing 3000 flight cycles. The proposed digital twin framework for aeroengines accurately tracks the engine’s degradation and enables gas path diagnosis under a flight mission, providing effective data support for engine health management. In conclusion, this framework contributes to improving maintenance decision making, ensuring the reliability and safety of aviation operations, and reducing engine operating costs.