Abstract
Airlines optimize flight trajectories in order to minimize their operational costs, of which fuel consumption is a large contributor. It is known that flight trajectories are not fuel-optimal because of airspace congestion and restrictions, safety regulations, bad weather and other operational constraints. However, the extent to which trajectories are not fuel-optimal (and therefore CO-optimal) is not well known. In this study, we present two methods for optimizing the flight cruising time by taking best advantage of the wind pattern at a given flight level and for constant airspeed. We test these methods against actual flight trajectories recorded under the In-service Aircraft for a Global Observing System (IAGOS) programme. One method is more robust than the other (computationally faster) method, but when successful, the two methods agree very well with each other, with optima generally within the order of 0.1%. The IAGOS actual cruising trajectories are on average 1% longer than the computed optimal for the transatlantic route, which leaves little room for improvement given that by construction the actual trajectory cannot be better than our optimum. The average degree of non-optimality is larger for some other routes and can be up to 10%. On some routes, there are also outlier flights that are not well optimized; however, the reason for this is not known.
1. Introduction
Optimizing flight trajectories is an important activity for airlines. Generally speaking, airlines will seek to minimize their overall operating costs which, for a given flight, depend on both factors independent of the flight trajectory, such as landing fees, and factors dependent on the flight trajectory such as fuel consumption, en route charges and flight time (as the latter may feed back on the availability of the aircraft, staff costs and operations). Airlines operate under multiple constraints including air traffic regulations, airport slot time, airspace availability, flight safety and regulations, passenger comfort, etc. Flight planning and optimal trajectory computations are therefore strategic activities for airlines and how exactly they do it remains confidential to some extent. Dalmau et al. [1] showed that the optimal flight trajectory could differ significantly whether en route charges are accounted for or not because these are more expensive over some countries than others. EUROCONTROL [2] estimated an average fuel inefficiency of between 8.6% to 11.2% from take-off to landing on flights within the EUROCONTROL Network Manager area in 2019. This said, fuel costs are known to be a significant expense for airlines so we expect flight trajectories to be fuel-optimized to some extent, especially long-haul flights, despite the other costs and constraints under which airlines operate. It is therefore in the interest of airlines to exploit fully the three-dimensional wind field to minimize their fuel consumption. Improvements in the atmospheric observing system, data assimilation techniques and numerical weather prediction models have gone a long way to provide accurate forecasts of the wind field at cruising altitudes on lead times of a few hours to a few days. Although trajectories are already well wind-optimized, Wells et al. [3] argued that further savings were achievable using flights between London (LHR) and New York (JFK) as an example. They estimate potential savings of 2.5% for eastbound flights and 1.7% for westbound flights, assuming a constant airspeed of 240 m s and a constant flight level. The Air Traffic Management (ATM) community has also developed indicators to measure inefficiencies in the ATM system. Liu et al. [4] computed the horizontal en route inefficiency as the deviation of the actual flown distance relative to the shortest ground distance (also called the geodesic or great circle). Prats et al. [5] and Kuljanin et al. [6] estimated inefficiencies, expressed in extra kg fuel burned, and separated them between horizontal and vertical components during the strategic and tactical layers of the flight planning. Unlike Liu et al., they estimate the inefficiencies against a wind-optimized trajectory without considering en route charges. Wells et al. [7,8] further showed that airspeeds can be adjusted to some extent within a flight to “take optimal advantage of the wind field” and probably the temperature field as well. However, they found the additional advantage of varying airspeed to be rather small at 0.5% for transatlantic flights compared to constant airspeed trajectories.
A wind-optimized flight trajectory is also one that minimizes CO emissions. There is thus a synergy between minimizing fuel cost and minimizing the CO emissions of a particular flight. However, CO is not the only pollutant emitted by aircraft. There is increasing awareness of the importance of non-CO effects [9] and regulatory bodies have started to scope how non-CO effects can be embedded in existing or forthcoming policy instruments for climate mitigation [10,11]. These non-CO effects include the NOx effects on ozone (O) and methane (CH), aerosols, contrails and induced cirrus that stem from the emission of water vapour (and aerosols) and their mixing in the atmospheric environment. The radiative effects of contrails and induced cirrus are known to be highly variable in space and time, and it is suspected that a small fraction of flights are responsible for a large fraction of the radiative forcing attributable to contrails and induced cirrus [12,13]. There is intense research activity to understand the potential for contrail avoidance through flight rerouting [14,15,16,17,18]. This is a very challenging objective that requires an accurate forecast of contrail-prone conditions, and in particular of ice-supersaturated regions, an ability to optimize flight trajectories within operational constraints, and the right choice of climate cost function(s) [19,20,21]. A prerequisite to investigating flight trajectory optimization that combines CO and non-CO effects is to demonstrate an ability to compute fuel-optimized trajectories. Reconstructing aircraft trajectories may also be important for verification of CO emissions by airlines. This study therefore aims to revisit optimized trajectories in comparison to actual flight trajectories in a more systematic way than was done before.
Various techniques of varying complexity have been proposed to optimize flight trajectories against a particular cost function. Zermelo [22] proposed a numerical solution by solving a differential equation on the aircraft heading angle, , known as Zermelo’s equation. A similar approach was proposed by Sawyer [23], who solved an equation that links the rate of change of to the curvature of the wind. This method forms the basis of the Met Office routing algorithm as implemented by Lunnon and Marklow [24] and used by Irvine et al. [25]. Parzani et al. [26] developed a Hamilton–Jacobi–Bellman approach for coordinated optimal aircraft trajectory planning. Yamashita et al. [27,28] implemented a genetic algorithm to optimize flight trajectory in the ECHAM climate model and used such a model to design aircraft routing strategies according to weather patterns [29]. Simorgh et al. [30] summarized in their Table 1 the different techniques which are being used for flight trajectory optimization, which they categorized into direct optimal control, genetic algorithm, brute force algorithm and non-linear algorithms. They also implemented a heuristic algorithm based on an augmented random search that exploits the computing power of graphics processing units. It is important for such algorithms to be robust because the wind field can have a lot of structure on the horizontal and there could be many local minima to a trajectory optimization. To our knowledge, there has been no intercomparison of flight trajectory optimization algorithms and there is a lack of validation of such algorithms.
Our ultimate goal is to quantify the potential for minimizing the total aviation cost using optimal trajectories and simulate an actual system with uncertainties in order to verify it. This study represents an intermediate step with several objectives. First, we would like to compare two optimization methods against each other and against actual trajectories. Second, we quantify the degree of non-optimality of flight trajectories. The two optimization algorithms are based on a standard minimization algorithm (Sequential Least SQuares Programming) and an implementation of the Zermelo method. We assess the algorithms against the actual trajectories of flights from the In-service Aircraft for a Global Observing System (IAGOS). The methodology and data used are described in Section 2 while the results are presented and discussed in Section 3.
2. Data and Methodology
2.1. Problem to Solve and Simplifying Assumptions
We seek to compute the fastest trajectory to fly from point P to point P across a wind field. In the following, we make a number of simplifying assumptions. We focus on the cruising phase of the flight to avoid any operational constraint with the take-off and landing phases of the flight. Thus, P and P are taken to be the beginning and end of the cruising phase of the flight. We also assume a constant aircraft airspeed and flight level. These assumptions are discussed further in Section 4.
2.2. Data
We apply our optimization methods on the flights that contribute to the In-service Aircraft for a Global Observing System (IAGOS) European Research Infrastructure [31]. Only long-haul flights with a cruising flight phase longer than 2500 km are selected. For each IAGOS flight, we identify the cruising phase as datapoints for which the pressure is less than 350 hPa and the absolute difference in pressure between two successive datapoints is less than 50 Pa after application of a 1D Gaussian filter with standard deviation of 40. These parameters are dependent on the temporal resolution of the IAGOS data which is currently 4 s. The screening works well to remove the steep pressure changes during the take-off and landing phase but not the pressure changes associated with changing flight levels during the cruising phase (see Figure S1). It should be noted that the IAGOS flights come from a limited number of airlines (Air France and Cathay Pacific in 2018; Lufthansa, China Airlines and Hawaiian Airlines in 2018 and 2019; only Lufthansa and Hawaiian Airlines in 2020 and 2021; see Table S1). Therefore, our results may not be representative of all the world’s airlines and flight routes.
We use wind data from version 5 of the European ReAnalysis (ERA5) project of the European Centre for Medium range Weather Forecasts (ECMWF). The data are extracted from the MARS archive at the 0.25 × 0.25 horizontal resolution, hourly temporal resolution and on Pressure Levels (PL). PL relevant for this study are 300, 275, 250, 225, 200 and 175 hPa. The hourly data combine the 6-hourly analysis and its subsequent forecast. We consider time variations in the wind field at the hourly resolution during the flight duration in a simple manner as explained in the next subsection.
2.3. Reprojection
The first step of our method is to rotate the sphere so that the shortest route from P to P is located on the Equator of the rotated sphere. In this way, we can treat equally any route without having to worry about the singularities at the poles. Indeed, it is very unlikely, not to say impossible, that an optimal trajectory deviates by more than 90 from the geodesic. This is done by defining a new North Pole, P, which is such that
where O is the Earth’s center and × denotes the cross product of two vectors. We use the cartopy package in Python to rotate the sphere so that P is the new North Pole. We then use the transform_points and transform_vectors methods of the cartopy package to interpolate datapoint coordinates and wind vectors onto the rotated sphere. The new pole P is located in the northern hemisphere if P is eastward of P and in the southern hemisphere if is westward (here, eastward and westward refer to the shortest way of going from P1 to P2). In this way, the longitude of P in the rotated grid is always less than the longitude of P, while the latitudes of P and P are zero by construction. The two components of the wind are then interpolated onto a regular latitude-longitude grid with the same 0.25× 0.25 resolution as that of the original grid. It should be noted that the minimization procedure is performed entirely on the rotated sphere. The solution of the problem can be reprojected on the original, unrotated sphere although there is no need to do so in our study since we compute all our statistics on the rotated sphere. The reprojection on the rotated sphere accounts for the small non-sphericity of the Earth as the cartopy package of Python uses the WGS84 coordinate system by default. Thus, the flown distance between P1 and P2 also accounts for the non-sphericity of the Earth.
In a second step, we discretize the shortest route (or great circle) along the Equator in n segments with a uniform resolution of about 50 km. This provides a set of longitudes for for which we need to find a set of latitudes for . The coordinates of P and P are (, ) and (, ).
The ERA5 wind field is four-dimensional but we make two simplifying assumptions. First, we do not seek to optimize the flight level and its variations in time. The optimal flight level depends not only on the wind field but also on the plane and flight characteristics. We consider the flight level to be known and we select the ERA5 pressure level that is closest to the average flight pressure as provided by IAGOS for the cruising phase. We do not interpolate the wind field on the vertical. Second, we approximate the time variations of the wind field by attributing one time to each longitude of the grid:
where and are the times of beginning and end of the cruising phase and the overbar denotes the closest round hour. The same time is allocated to all latitudes of a given longitude band. This approximation is a simple way to take into account the temporal variations of the wind field between the beginning and end of the cruising without selecting times dynamically in our optimization procedures. Like for the pressure level, we do not interpolate between times but select the closest time available in ERA5.
2.4. Cost Function
Finding the optimal trajectory requires defining the cost function that we seek to minimize. Here, the cost function is defined simply as the square of the flight time assuming a constant airspeed of the aircraft of 240 m/s (or 864 km/h). It is computed along the discretized trajectory:
where is the distance of segment i and is the groundspeed of the aircraft for that segment, which itself is computed as
with the airspeed of the aircraft (assumed constant), the wind speed and the supplement of the angle between the aircraft and wind vectors. It should be noted that the estimate of the groundspeed as a function of the plane bearing (and its derivatives as used in the Zermelo method) assumes sphericity of the Earth. The error caused by this approximation is likely to be very small as the coordinate system for each flight is rotated (using an ellipsoid-aware algorithm) such that it lies along the Equator.
The flight time is computed for the cruising phase only. It should be noted that in order to focus on the properties of the trajectory and maintain consistency between the different approaches, we do not use the actual flight time of the IAGOS trajectory when comparing with that of our optimized trajectories. Instead, we recompute the flight time of the IAGOS trajectory with the Equations above and with the same longitudinal resolution.
2.5. Gradient Descent
The first optimization method is based on a classical gradient descent method to minimize the cost function defined in Section 2.4. We use the Sequential Least SQuares Programming (SLSQP) method of the Python scipy package to minimize the square of flight time between P and P (see Section 2.4). As the function to be minimized is not convex, there is no guarantee that we find the global minimum. To maximize our chance to find the global minimum, the minimization procedure is repeated p times with different initial conditions, , for the control vector and we keep the smallest of all the minima. The initial conditions are set to:
with (in degrees) and , where / and denote float and Euclidian divisions, respectively. This makes a grand total of p = 1 + 14 × 3 = 43 optimizations for each flight. The maximum number of iterations was set to 100 as it was found to represent a good compromise between accuracy and computational cost.
2.6. Zermelo Method
The second optimization method is an adaptation of the Zermelo equation, solved using a simple forward Euler method. The solution is found following the “shooting” method, where trajectories with a range of initial directions are produced either side of the great-circle route between P and P [32]. For trajectory pairs that fall either side of P, a further search is performed between these pairs to locate an optimal trajectory.
By construction, the Zermelo solution starts exactly from P but it does not end exactly in P. In order to obtain a trajectory that ends exactly in P, we stretch slightly the Zermelo solution for each trajectory that passes within 75 km of P:
where and are the coordinates of the P point and N is the number of segments of the Zermelo trajectory (which is generally different from n).
It should be noted that the Zermelo method is applied in the same framework (Section 2.3 and Section 2.4) as the gradient descent method, which means that both methods share the same wind field and cost function. The results of the two methods are thus fully comparable.
3. Results
3.1. Timings
We have run both the gradient descent and Zermelo methods for all IAGOS flights longer than 2500 km in the years 2018 and 2019 (pre-COVID) and 2020 and 2021 (which encompass the COVID period with much-reduced air traffic). However, we focus in this study on the 2019 year only as this is the latest year with a number of IAGOS flights in excess of 1000 flights (see Table S1). However, we have processed all IAGOS flights from 2018 to 2021 to test the robustness of our procedure. The flights are categorized from their regions of origin and destination as per Figure S2.
The two methods differ in their computational time, accuracy and success rate. The Zermelo-based solution is by far the quickest of both methods with an average runtime of ∼6 s per flight (range 4 to 15 s) on a 2.8 GHz AMD EPYC 7402P CPU (see Figure S3). In contrast, the gradient descent method takes an average execution time of 450 s per flight (range 300 to 600 s). As it depends on a Python optimizer, there is little room for speeding up the algorithm without a major revamping of the code. We have already greatly optimized the wind extraction along the trajectory using numpy and xarray built-in methods, which benefited both methods. The number of optimizations for each flight (which is currently 43) can be decreased by selecting the most promising initial conditions but we have not performed a full sensitivity study on this. We have tried to decrease the maximum number of iterations below 100 but this decreased the accuracy of the solution.
The gradient descent method always converges to a solution but there is no guarantee that it is the optimal solution. Indeed, quite often the Zermelo solution is a little better than the gradient descent method, but only by about 0.1%, which is essentially negligible and gives confidence that both algorithms work when they are in agreement. The disadvantage of the Zermelo method, as implemented in this study, is that it sometimes fails to find the global optimum or does not find an optimum for longer routes. We consider that the Zermelo method fails if it finds a solution that is 2% longer than the gradient descent method. The success rate of the Zermelo method is ∼95% for the 2019 IAGOS flights. In the following, we present statistics of the gradient descent method only.
3.2. Statistics
Figure 1 shows the flight time differences between our optimum and the recomputed IAGOS flight time for the transatlantic flight route (Europe to North America, or westbound flights, and North America to Europe, or eastbound flights). It can be seen that with only one exception, the optimum found is faster than the actual IAGOS flight, which is as expected because we compute the flight time using the same metric that has served for the optimization. The two methods agree fairly well with each other, with the Zermelo method finding a slightly more optimal solution but sometimes failing. When assessed against the gradient descent method, we find the IAGOS flight to be only ∼1% slower than the optimum trajectory on average for both eastbound and westbound transatlantic flights (see column IAGOS/Quickest in Table 1). However, we can see in Figure 1 that a few IAGOS flights can be up to 4–5% slower than the optimum. There are many reasons why IAGOS flights are non-optimal. Firstly, as mentioned above, we assess the IAGOS flights against our own metric; therefore, it can only be slower (except if our optimization algorithm fails to find a global optimum). For instance, we assume a constant (average) flight level whereas actual flights increase their flight level along the trajectory. Secondly, operational routing has to rely on weather forecast rather than reanalysis, as is the case here, which may result in a suboptimal route. Thirdly, there are operational constraints (i.e., flight tracks to be used over the North Atlantic) which we do not consider here. It is difficult to quantify the relative impact of these three effects. The second one is thought to be small because operational routing is often adjusted until shortly before departure and benefits from the latest forecasts that are close to the (re)analysis. Flight tracks over the North Atlantic ocean are also thought to be a rather weak constraint because they are adjusted every day on the basis of the preferred routes that airlines communicate to air traffic control agencies. Therefore, with a 1% difference, IAGOS flights can be considered as being fairly well optimized. The flights that are 3 to 5% below optimality would be worth investigating as they represent a potential for improving fuel efficiency. This is in contrast with the finding from Wells et al. [3] who find a larger potential for improving efficiency of transatlantic flights. The differences between their and our conclusions could be due to the way the flight times are computed, the fact that they consider the end-to-end trajectory while we only consider the cruising phase, or the representativeness of the flights being considered in terms of routes or airlines.
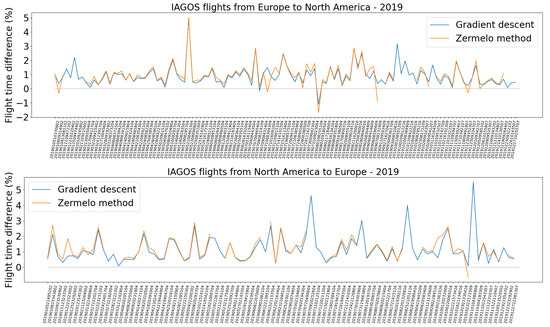
Figure 1.
Relative difference in flight time for our time-optimized trajectories relative to the actual IAGOS recomputed time for our two optimization methods and for 2019 Europe to North America (top panel) and North America to Europe (bottom panel) IAGOS flights. Negative values indicate that the IAGOS trajectory is faster. The orange line is interrupted for cases for which the Zermelo method has failed. The labels on the x-axis corresponds to the IAGOS flight ID in format YYYYMMDDHHMMZZZZ with YYYY being the year, MM the month, DD the day, HH the hour, MM the minute of take-off and ZZZZ the IAGOS measurement package number.

Table 1.
Statistics of the trajectory times for 2019 by regions of origin and destination (see text for more explanation). The ratios correspond to the ratios of average flight times, rather than the average of the ratios.
The near-optimality of flights that we observe for the transatlantic route does not translate for all routes. Figure 2 expands the statistics to all 2019 IAGOS flights and shows only a small fraction of flights above the 5% inefficiency rate. Considering all 2019 IAGOS flights, we find that IAGOS flights are 2.14% below the optimum. However, there are large differences among the routes (see Table 1). Among the least efficient routes are South-East Asia to Asia (ratio of 1.080), Asia to South-East Asia (ratio 1.096), Europe to South-East Asia (ratio 1.055), Europe to Asia (ratio 1.041), Europe to Middle East (ratio 1.039) and Middle East to Europe (ratio 1.034). We note that the number of flights considered may be low; hence, the above ratios may not be representative. Some of these differences are clearly due to air traffic control restrictions due to political or safety reasons. This appears to be the case for the routes involving Asia, with restrictive air corridors in India and China, and some routes potentially crossing conflict regions (e.g., Libya, Syria, eastern Ukraine). This finding is consistent with that of Liu et al. [33] who found longer actual airborne times in China and in the United States for the same origin–destination distance.
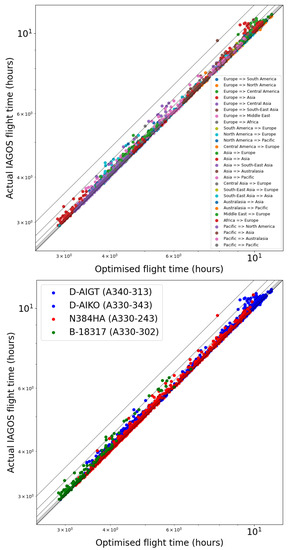
Figure 2.
Scatter plot of all 2019 IAGOS flight times versus the corresponding optimal flight time for the cruising fraction of the trajectory. Flights are colour-coded by route (upper panel) and aircraft (lower panel). In addition to the 1:1 line (thicker line) are shown the 1.01:1, 1.02:1, 1.05:1, 1.1:1, and 1.2:1 lines. D-AIGT, D-AIKO and D-AIHE belong to Lufthansa, N384HA belongs to Hawaiian Airlines and B-18317 belongs to China Airlines.
As some parametrizations for fuel consumption [34] depend only on flown distance, irrespective of whether the flight or the route considered meet headwind or tailwind, we find it useful to introduce several hypothetical flight times and compare them. We first compute the flight cruise time in the absence of wind, , which corresponds simply to the great circle distance divided by the airspeed. We then compute the flight cruise time for the great circle in the presence of wind, . The ratio / measures how the dominant winds affect the average flight time on a given route. The ratio / measures by how much optimizing the trajectory by accounting for the wind field can speed up the flight compared to the great circle route. Finally, we can decompose the ratio / as
where we have omitted the subscript for clarity. Table 1 shows this decomposition for the different routes categorized from the IAGOS flights. Beyond the / which has been already discussed, we can see that wind-optimization allows 1–4% faster trajectories compared to the great circle, while there are much larger variations due to the dominant wind as evident from the / ratio.
3.3. Examples of Time-Optimized Trajectories in Comparison to Actual Trajectories
Figure 3 shows examples of time-optimized trajectories for westbound and eastbound transatlantic flights operated by Lufthansa. On the top panels, the IAGOS flights are very well optimized and within 1–2% of our optimum. On the lower panel, we selected two outliers for which the IAGOS flights are less well optimized. In the case of the westbound flight, the IAGOS trajectory has many angles especially towards the end. The eastbound flight misses the wavy pattern of the jet stream, especially during the first half of the trajectory.
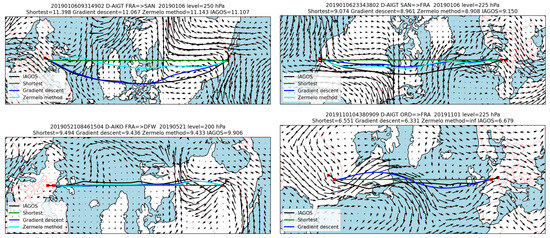
Figure 3.
Examples of time-optimized trajectories (cyan blue and dark blue curves) along with the actual IAGOS trajectory (black curve) for transatlantic routes. The shortest route for the cruising segment is represented by a straight green line on the longitude–latitude projection of the rotated sphere. The trajectories read from left to right, with the airports and start and end of cruising shown with red crosses. Some information is provided on top of each panel: IAGOS flight ID, departure airport arrival airport, flight code, date, average pressure level in hPa, shortest, quickest (×2) and actual flight times in decimal hours.
Examples of trajectories between Europe and Asia are shown on Figure 4. As these routes are essentially continental, they are subject to many operational constraints with e.g. the Himalayan mountain range and partly closed Chinese airspace, which results in non-optimal routes. It should be noted that the flights are for 2019 when the Ukrainian airspace was avoided by Western airlines.
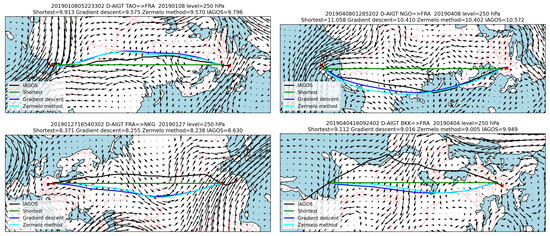
Figure 4.
Same as Figure 3 but for Europe-Asia routes.
The two flight trajectories on the India-Asia route shown in Figure 5 reveal substantial suboptimality which is recurrent in this part of the world probably because of restrictions in the Chinese airspace.
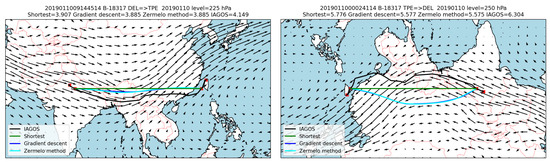
Figure 5.
Same as Figure 3 but for India-Asia routes.
The Pacific routes shown on Figure 6 contrast a trajectory that is very well optimized with three trajectories that are far from their respective optima. We observe that trajectories by Hawaiian Airlines are less well optimized than those by Lufthansa despite routes that are essentially over the ocean. It would be interesting to understand whether there are operational constraints that justify such route choices or whether fuel saving can be realised.
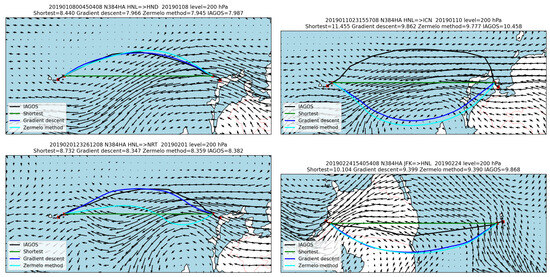
Figure 6.
Same as Figure 3 but for Pacific routes.
4. Discussion and Conclusions
In this study, we have developed, presented and tested two methods to optimize flight trajectories. The methods are currently restricted to the cruising phase and assume a constant flight level and airspeed of the aircraft. The two methods agree very well with each other, which lends confidence that we have a working solution for trajectory optimization. However, one method is less robust in that it can occasionally find a local optimum or fail altogether to find an optimum. The two methods can be used together to increase their robustness.
We find that IAGOS trajectories are well optimized on some routes, in particular the transatlantic routes between Europe and North or South America, but less well optimized on some other routes, especially routes within Asia or between Europe and Asia. This is likely to be due to airspace restrictions and narrow air flight corridors that require flying some detours. We also observe some flights that are outliers, in that they are very far from the optimum trajectory. The reason for such outliers is not known but could be due to airspace congestion, operational constraints, bad weather or imperfect flight planning. Such outliers would need to be studied in more detail with the relevant airlines.
It is worth revisiting the assumptions made in this study. Some assumptions are expected to have very small or insignificant impacts on our calculations. This is the case of neglecting the non-sphericity of the Earth or the lack of temporal interpolation from hourly-resolved wind field. Other assumptions are worth revisiting in future work. Indeed, we assume a constant airspeed during cruising. To test this assumption, we have analyzed time variations in the groundspeed and airspeed of the IAGOS aircraft during the cruising phase. We found that the airspeed for the cruising phase presents a mode at 240 m/s across all IAGOS flights of 2019, thus justifying our value. We also found that the standard deviation of the airspeed during the cruising phase of a given flight is generally much less than the standard deviation of the groundspeed. On average for all 2019 IAGOS flights, the standard deviation of the airspeed within a flight is 1.32 m/s compared to 4.88 m/s for the groundspeed. This also justifies our assumption of a constant airspeed for this study. However, a more appropriate constant Mach number [35] or a varying airspeed that seeks to minimize fuel consumption should be used in future studies. A constant flight level is another assumption that will need to be relaxed in future work on contrail avoidance. The difficulty though is to consider a fuel flow model that is accurate enough to capture the fuel cost of changing flight altitude several times during the cruising phase.
Finally, when considering more complex trajectory optimizations that include the climate impacts of NOx and contrails, special attention will be paid to the sensitivity of the results to the choice of climate cost function, their time horizons and the uncertainties in the model prediction of the climate effects (and in particular the prediction of the ice-supersaturated regions).
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/aerospace10090744/s1, Figure S1: Cross-section of the flight pressure along the longitude of a sampled IAGOS flight from Frankfurt to Detroit airports; Figure S2: World regions considered to categorize IAGOS flights by origin and destination airports; Figure S3: Computational time as a function of individual flights for the Europe to North America 2019 IAGOS flights and for our two optimization methods; Table S1: Total and screened number of IAGOS flights considered in this study for the different years in the period 2018 to 2021 and the different IAGOS-equipped aircraft.
Author Contributions
Conceptualization, O.B. and E.G.; Methodology, O.B., E.G. and N.B.; Software, O.B., E.G. and J.K.; Validation, O.B., E.G. and J.K.; Formal Analysis, O.B.; Investigation, O.B.; Resources, O.B. and N.B.; Data Curation, H.C.; Writing—Original Draft Preparation, O.B.; Writing—Review and Editing, E.G., N.B., H.C. and J.K.; Visualization, O.B.; Supervision; Project Administration, N.B.; Funding Acquisition, O.B. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
O. Boucher, N. Bellouin and J. Karadayi acknowledge support from the French Ministère de la Transition écologique et Solidaire (grant no. DGAC 382 N2021-39), with support from France’s Plan National de Relance et de Resilience (PNRR) and the European Union’s NextGenerationEU. E. Gryspeerdt was supported by the Royal Society University Research Fellowship—Tracking Aviation and Shipping Impacts on Clouds (URF/R1/191602). We acknowledge the strong support of the European Commission, Airbus and the airlines (Deutsche Lufthansa, Air France, Austrian, Air Namibia, Cathay Pacific, Iberia, China Airlines, Hawaiian Airlines, Eurowings Discover, and Air Canada) that have carried the MOZAIC or IAGOS equipment and performed the maintenance since 1994. IAGOS has been funded by the European Union projects IAGOS–DS and IAGOS–ERI. Additionally, IAGOS has been funded by INSU-CNRS (France), Météo-France, Université Paul Sabatier (Toulouse, France) and Research Center Jülich (FZJ, Jülich, Germany). The IAGOS database is supported in France by AERIS (https://www.aeris-data.fr).
Informed Consent Statement
Not applicable.
Data Availability Statement
ERA5 meteorological data can be downloaded from the European Centre for Medium Range Weather Forecast (https://doi.org/10.24381/cds.bd0915c6). Data last accessed on 2 December 2022. IAGOS data are available from the IAGOS data portal (https://doi.org/10.25326/20). We use IAGOS data accessed on 1 February 2023. Our code, with a sample IAGOS flight data, is available on https://github.com/OB-IPSL/FlightTrajectories.git, version of 7 August 2023 was used for this article.
Acknowledgments
Damien Boulanger, Sophie Cloché and the ESPRI team are acknowledged for their help with the management of the IAGOS and ERA5 data.
Conflicts of Interest
O. Boucher receives consulting fees as a member of the Stakeholder Committee of Groupe ADP. The authors declare no other potential conflict of interest.
References
- Dalmau Codina, R.; Melgosa Farrés, M.; Vilardaga Garcia-Cascón, S.; Prats Menéndez, X. A fast and flexible aircraft trajectory predictor and optimiser for ATM research applications. In Proceedings of the International Conference on Research in Air Transportation, Catalonia, Spain, 25–29 June 2018. [Google Scholar]
- Eurocontrol. Environmental Assessment: European ATM Network Fuel Inefficiency Study. Technical Report, Eurocontrol, 8 December 2020. Available online: https://www.eurocontrol.int/publication/environmental-assessment-european-atm-network-fuel-inefficiency-study (accessed on 22 August 2023).
- Wells, C.A.; Williams, P.D.; Nichols, N.K.; Kalise, D.; Poll, I. Reducing transatlantic flight emissions by fuel-optimised routing. Environ. Res. Lett. 2021, 16, 025002. [Google Scholar] [CrossRef]
- Liu, Y.; Hansen, M.; Ball, M.O.; Lovell, D.J. Causal analysis of flight en route inefficiency. Transp. Res. Part Methodol. 2021, 151, 91–115. [Google Scholar] [CrossRef]
- Prats, X.; Dalmau, R.; Barrado, C. Identifying the sources of flight inefficiency from historical aircraft trajectories. A set of distance- and fuel-based performance indicators for post-operational analysis. In Proceedings of the 13th USA/Europe Air Traffic Management Research and Development Seminar, Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Kuljanin, J.; Pons-Prats, J.; Prats, X. Fuel-based flight inefficiency through the lens of different airlines and route characteristics, A post-operational analysis for one day of traffic at the ECAC area. In Proceedings of the 14th USA/Europe Air Traffic Management Research and Development Seminar, Virtual Event, 20–23 September 2021. [Google Scholar]
- Wells, C.; Kalise, D.; Nichols, N.; Poll, I.; Williams, P. The role of airspeed variability in fixed-time, fuel-optimal aircraft trajectory planning. Optim. Eng. 2023, 24, 1057–1087. [Google Scholar] [CrossRef]
- Wells, C.A.; Williams, P.D.; Nichols, N.K.; Kalise, D.; Poll, I. Minimising emissions from flights through realistic wind fields with varying aircraft weights. Transp. Res. Part Transp. Environ. 2023, 117, 103660. [Google Scholar] [CrossRef]
- Lee, D.; Fahey, D.; Skowron, A.; Allen, M.; Burkhardt, U.; Chen, Q.; Doherty, S.; Freeman, S.; Forster, P.; Fuglestvedt, J.; et al. The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef]
- Niklaß, M.; Dahlmann, K.; Grewe, V.; Maertens, S.; Plohr, M.; Scheelhaase, J.; Schwieger, J.; Brodmann, U.; Kurzböck, C.; Repmann, M.; et al. Integration of Non-CO2 Effects of Aviation in the EU ETS and under CORSIA, Final Report, Climate Change 00/2019. Technical Report, German Environment Agency. 2019. Available online: https://www.umweltbundesamt.de/publikationen/integration-of-non-co2-effects-of-aviation-in-the (accessed on 30 June 2023).
- EASA. Updated Analysis of the non-CO2 Climate Impacts of Aviation and Potential Policy Measures Pursuant to the EU Emissions Trading System Directive Article 30(4). Technical Report, EASA, August 2020. Available online: https://www.easa.europa.eu/en/document-library/research-reports/report-commission-european-parliament-and-council (accessed on 30 June 2023).
- Teoh, R.; Schumann, U.; Stettler, M. Beyond contrail avoidance: Efficacy of flight altitude changes to minimise contrail climate forcing. Aerospace 2020, 7, 121. [Google Scholar] [CrossRef]
- Teoh, R.; Schumann, U.; Gryspeerdt, E.; Shapiro, M.; Molloy, J.; Koudis, G.; Voigt, C.; Stettler, M.E.J. Aviation contrail climate effects in the North Atlantic from 2016 to 2021. Atmos. Chem. Phys. 2022, 22, 10919–10935. [Google Scholar] [CrossRef]
- Sridhar, B.; Ng, H.K.; Chen, N.Y. Aircraft trajectory optimization and contrails avoidance in the presence of winds. J. Guid. Control Dyn. 2011, 34, 1577–1584. [Google Scholar] [CrossRef]
- Lim, Y.; Gardi, A.; Sabatini, R. Modelling and evaluation of aircraft contrails for 4-dimensional trajectory optimisation. SAE Int. J. Aerosp. 2015, 8, 248–259. [Google Scholar] [CrossRef]
- Zou, B.; Buxi, G.; Hansen, M. Optimal 4-D aircraft trajectories in a contrail-sensitive environment. Netw. Spat. Econ. 2016, 16, 415–446. [Google Scholar] [CrossRef]
- Rosenow, J.; Fricke, H.; Luchkova, T.; Schultz, M. Minimizing contrail formation by rerouting around dynamic ice-supersaturated regions. Aeronaut. Aerosp. Open Access J. 2018, 2, 105–111. [Google Scholar] [CrossRef]
- Yin, F.; Grewe, V.; Frömming, C.; Yamashita, H. Impact on flight trajectory characteristics when avoiding the formation of persistent contrails for transatlantic flights. Transp. Res. Part Transp. Environ. 2018, 65, 466–484. [Google Scholar] [CrossRef]
- Irvine, E.A.; Hoskins, B.J.; Shine, K.P. A simple framework for assessing the trade-off between the climate impact of aviation carbon dioxide emissions and contrails for a single flight. Environ. Res. Lett. 2014, 9, 064021. [Google Scholar] [CrossRef]
- Grewe, V.; Matthes, S.; Frömming, C.; Brinkop, S.; Jöckel, P.; Gierens, K.; Champougny, T.; Fuglestvedt, J.; Haslerud, A.; Irvine, E.; et al. Feasibility of climate-optimized air traffic routing for trans-Atlantic flights. Environ. Res. Lett. 2017, 12, 034003. [Google Scholar] [CrossRef]
- Yin, F.; Grewe, V.; Castino, F.; Rao, P.; Matthes, S.; Dahlmann, K.; Dietmüller, S.; Frömming, C.; Yamashita, H.; Peter, P.; et al. Predicting the climate impact of aviation for en-route emissions: The algorithmic climate change function submodel ACCF 1.0 of EMAC 2.53. Geosci. Model Dev. 2023, 16, 3313–3334. [Google Scholar] [CrossRef]
- Zermelo, E. Über die Navigation in der Luft als Problem der Variationsrechnung. Jahresber. Der Dtsch.-Math.-Ver. 1930, 39, 44–48. [Google Scholar]
- Sawyer, J.S. Pressure-pattern flying. Weather 1948, 3, 290–294. [Google Scholar] [CrossRef]
- Lunnon, R.; Marklow, A. Optimization of time saving in navigation through an area of variable flow. J. Navig. 1992, 45, 384–399. [Google Scholar] [CrossRef]
- Irvine, E.A.; Shine, K.P.; Stringer, M.A. What are the implications of climate change for trans-Atlantic aircraft routing and flight time? Transp. Res. Part Transp. Environ. 2016, 47, 44–53. [Google Scholar] [CrossRef]
- Parzani, C.; Puechmorel, S. On a Hamilton-Jacobi-Bellman approach for coordinated optimal aircraft trajectories planning. Optim. Control Appl. Methods 2018, 39, 933–948. [Google Scholar] [CrossRef]
- Yamashita, H.; Grewe, V.; Jöckel, P.; Linke, F.; Schaefer, M.; Sasaki, D. Air traffic simulation in chemistry-climate model EMAC 2.41: AirTraf 1.0. Geophys. Mod. Dev. 2016, 9, 3363–3392. [Google Scholar] [CrossRef]
- Yamashita, H.; Yin, F.; Grewe, V.; Jöckel, P.; Matthes, S.; Kern, B.; Dahlmann, K.; Frömming, C. Newly developed aircraft routing options for air traffic simulation in the chemistry–climate model EMAC 2.53: AirTraf 2.0. Geophys. Mod. Dev. 2020, 13, 4869–4890. [Google Scholar] [CrossRef]
- Yamashita, H.; Yin, F.; Grewe, V.; Jöckel, P.; Matthes, S.; Kern, B.; Dahlmann, K.; Frömming, C. Analysis of aircraft routing strategies for North Atlantic flights by using AirTraf 2.0. Aerospace 2021, 8, 33. [Google Scholar] [CrossRef]
- Simorgh, A.; Soler, M.; González-Arribas, D.; Linke, F.; Lührs, B.; Meuser, M.M.; Dietmüller, S.; Matthes, S.; Yamashita, H.; Yin, F.; et al. Robust 4D climate-optimal flight planning in structured airspace using parallelized simulation on GPUs: ROOST V1.0. Geosci. Model Dev. 2023, 16, 3723–3748. [Google Scholar] [CrossRef]
- Petzold, A.; Thouret, V.; Gerbig, C.; Zahn, A.; Brenninkmeijer, C.A.M.; Gallagher, M.; Hermann, M.; Pontaud, M.; Ziereis, H.; Boulanger, D.; et al. Global-scale atmosphere monitoring by in-service aircraft—current achievements and future prospects of the European Research Infrastructure IAGOS. Tellus 2015, 67, 28452. [Google Scholar] [CrossRef]
- Williams, P.D. Transatlantic flight times and climate change. Environ. Res. Lett. 2016, 11, 024008. [Google Scholar] [CrossRef]
- Liu, K.; Zheng, Z.; Zou, B.; Hansen, M. Airborne flight time: A comparative analysis between the U.S. and China. J. Air Transp. Manag. 2023, 107, 102341. [Google Scholar] [CrossRef]
- Seymour, K.; Held, M.; Georges, G.; Boulouchos, K. Fuel estimation in air transportation: Modeling global fuel consumption for commercial aviation. Transp. Res. Part Transp. Environ. 2020, 88, 102528. [Google Scholar] [CrossRef]
- Poll, D.; Schumann, U. An estimation method for the fuel burn and other performance characteristics of civil transport aircraft in the cruise. Part 1: Fundamental quantities and governing relations for a general atmosphere. Aeronaut. J. 2021, 125, 257–295. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).