Optimal Collaborative Scheduling of Multi-Aircraft Types for Forest Fires General Aviation Rescue
Abstract
:1. Introduction
2. Optimization Model of General Aviation Collaborative Scheduling in Forest Fires under Multi-Aircraft Types Conditions
2.1. Model Description and Assumptions
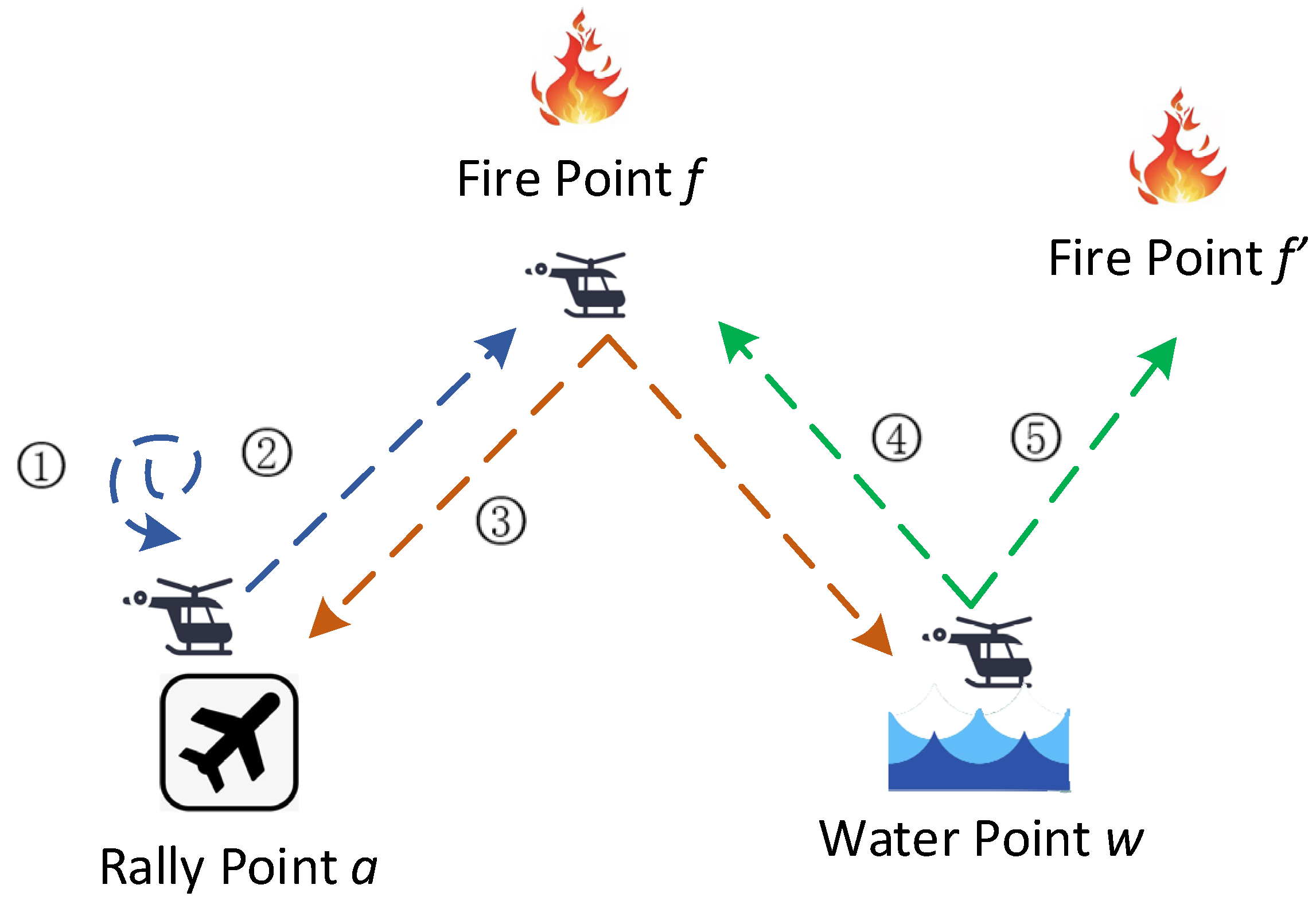
- When coordinating the scheduling of general aviation rescue aircraft, a multi-to-one approach is used. This means that several rescue aircraft can be sent to the same fire point at the same time to extinguish the fire.
- When carrying out the tasks, the rescue aircraft maintains a constant flight speed through direct flight mode.
- The number and location of aircraft rally, fire, and water points can be determined in advance.
- The number and type of rescue aircraft that can be scheduled at each rally point are determined.
- The amount of water required to extinguish the fire at the fire point can be determined in advance.
- Each rescue aircraft can only rescue one fire point in a cycle.
2.2. Model Description and Assumptions
2.3. Model Building
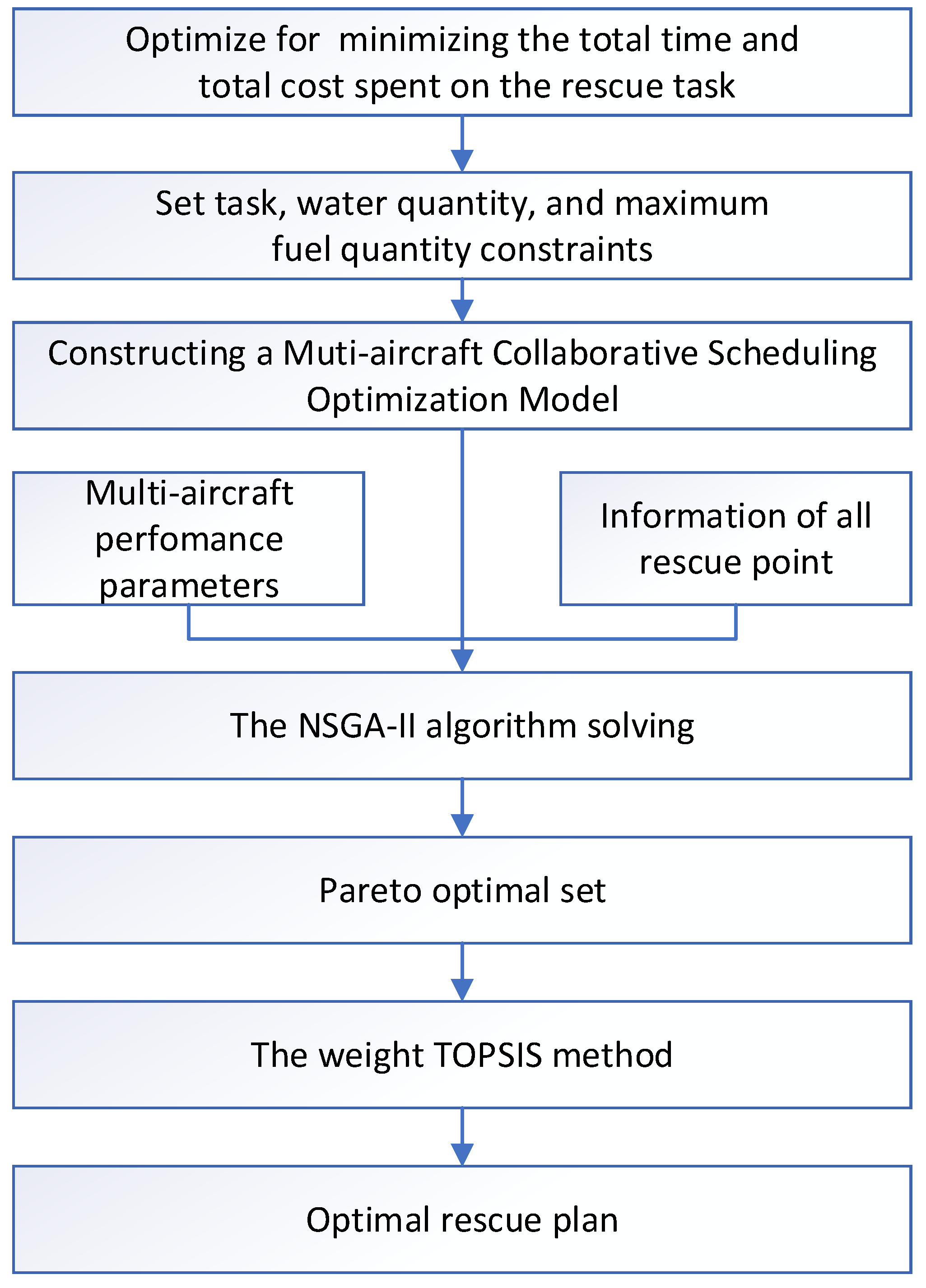
3. Multi-Aircraft Collaborative Scheduling Optimization Model Solving
3.1. NSGA-II Algorithm for Solving the Optimal Solution Set
3.1.1. NSGA-II Algorithm Solution Idea
3.1.2. NSGA-II Algorithm Design
3.2. Weight TOPIS Method for Solving the Optimal Solution
4. Simulation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Wu, M.; Chen, T.; Gao, X.; Zhao, Q. Research on unmanned aerial vehicle optimization and combination scheduling based on forest fire hotspot data. For. Surv. Plan. 2022, 47, 65–69. [Google Scholar]
- Zhu, X.; Qu, J.; Xu, C. Design of an integrated command system for forest fire rescue. Fire Sci. Technol. 2022, 41, 1287–1290. [Google Scholar]
- Maraş, E.E.; Dönmez, K.; Emecen, Y. GIS-Based Determination of the Optimal Heliport and Water Source Locations for Forest Fire Suppression Using Multi-Objective Programming. Aerospace 2023, 10, 305. [Google Scholar] [CrossRef]
- Ai, H.; He, X.; Liu, Q.; Hu, M. General aviation mountain rescue safety trajectory planning model. J. Saf. Environ. 2023, 23, 506–514. [Google Scholar]
- Zhou, Y. Research on Intelligent Scheduling Model and Algorithm for Low-Altitude Rescue; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2014. [Google Scholar]
- Shao, Q.; Liang, B.; Zhu, Y.; Zhang, H.; Zhang, J. Optimization Simulation Research on Civil Aviation Emergency Dispatch of Disaster Relief Supplies. J. Wuhan Univ. Technol. (Inf. Manag. Eng. Ed.) 2015, 37, 503–508. [Google Scholar]
- Li, G.; Ma, L. Scheduling of civil aviation emergency relief supplies based on improved genetic algorithm. Comput. Simul. 2015, 32, 104–107+111. [Google Scholar]
- Tang, Z.; Zhou, Y. Research on civil aviation emergency material scheduling under the constraint of guarantee capacity. Electron. Technol. Softw. Eng. 2016, 14, 196–198. [Google Scholar]
- Wu, H. Research on Site Selection and Emergency Dispatching of Low Altitude Rescue Landing Sites; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2020. [Google Scholar]
- Zhang, Q.; Jin, Y.; Qin, S. Optimization of cooperative helicopter rescue scheduling. Chin. J. Saf. Sci. 2019, 29, 180–186. [Google Scholar]
- Liu, Q.; He, X.; Ai, H.; Liu, Y.; Li, H. Research on general aviation rescue scheduling model based on rescue efficiency. Pract. Underst. Math. 2020, 50, 115–126. [Google Scholar]
- Liu, H.; Chen, Z.; Tian, Y.; Wang, B.; Yang, H.; Wu, G. Evaluation method for helicopter maritime search and rescue response plan with uncertainty. Chin. J. Aeronaut. 2021, 34, 493–507. [Google Scholar] [CrossRef]
- Zhang, M.; Li, S.; Li, B. An air-ground cooperative scheduling model considering traffic environment and helicopter performance. Comput. Ind. Eng. 2021, 158, 107458. [Google Scholar] [CrossRef]
- Xue, Y.; Gao, Y.; Tian, Y.; Liu, H.; Wang, X. Helicopter Rescue for Flood Disaster: Scheduling, Simulation, and Evaluation. Aerospace 2022, 9, 822. [Google Scholar]
- Liu, Z.; Han, W.; Wu, Y.; Su, X.; Guo, F. Automated Sortie Scheduling Optimization for Fixed-Wing Unmanned Carrier Aircraft and Unmanned Carrier Helicopter Mixed Fleet Based on Offshore Platform. Drones 2022, 6, 375. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.; Tian, Y.; Li, X.; Shang, Y. Hierarchical Optimization of Scheduling Scheme for Mixed Helicopter Fleet in Disaster Relief. Arab. J. Sci. Eng. 2023, 48, 7195–7206. [Google Scholar] [CrossRef]
- Song, Y.; Sun, P. Scheduling strategy of emergency material air launching force considering the urgency of the affected area. Sci. Technol. Eng. 2023, 23, 4011–4018. [Google Scholar]
- Wang, B. The role and development direction of aviation emergency rescue system in emergency management. In China Fire Protection Association, Proceedings of the 2022 China Fire Protection Association Science and Technology Annual Conference Proceedings, Online, 28–31 December 2022; Emergency Management Press: Beijing, China, 2022; Volume 8. [Google Scholar]
- Zhang, X. Strengthening the construction of aviation emergency rescue system. China Emergency Management News, 14 March 2023. [Google Scholar]
- Du, X.; Zhang, N.; Meng, F.; Wang, J. Improvement of NSGA2 algorithm to solve flexible job shop scheduling problem. Comb. Mach. Tools Autom. Mach. Technol. 2022, 05, 182–186. [Google Scholar]
- Qu, J.; Zhu, X.; Xu, C. Rasterized modeling of general aviation rescue flight airspace for forest fires. Sci. Technol. Eng. 2023, 23, 6271–6277. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwl, S.; Meyarivan, T.A.M.T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Khodashenas, M.; Najafi, S.E.; Kazemipoor, H.; Sobhani, M. Providing an integrated multi-depot vehicle routing problem model with simultaneous pickup and delivery and package layout under uncertainty with fuzzy-robust box optimization method. Decis. Mak. Appl. Manag. Eng. 2023, 6, 372–403. [Google Scholar] [CrossRef]
- Abiodun, F.T.; Ismail, F.S. Pump scheduling optimization model for water supply system using AWGA. In 2013 IEEE Symposium on Computers & Informatics (ISCI); IEEE: Piscataway, NJ, USA, 2013; pp. 12–17. [Google Scholar]
- Tang, J.; Xu, C. Forward and reverse courier logistics distribution path planning based on multi-objective optimization genetic algorithm. Highlights Sci. Eng. Technol. 2023, 31, 23–28. [Google Scholar] [CrossRef]
- Asanjarani, A.; Dibajian, S.H.; Mahdian, A. Multi-objective crashworthiness optimization of tapered thin-walled square tubes with in dentations. Thin-Walled Struct. 2017, 116, 26–36. [Google Scholar] [CrossRef]
- Gong, L.; Zhang, J. Research on multi-objective optimization model and algorithm of emergency production task based on NSGA-II. Oper. Res. Manag. 2019, 28, 7–13. [Google Scholar]
- Wang, Z.; Wang, H.M.; Wang, Z.J.; Xiang, S. Multi-objective optimization of propeller airfoils for general-purpose aircraft. J. Aerosp. Dyn. 2023, 1–11. [Google Scholar] [CrossRef]
- Ghaseminejad, A.; Kazemipoor, H.; Fallah, M. Modeling the robust facility layout problem for unequal space considering health and environmental safety criteria under uncertain parameters. Decis. Mak. Appl. Manag. Eng. 2023, 6, 426–460. [Google Scholar] [CrossRef]
- Li, Z.; Peng, X.; Lu, R.; Qi, Y.; Guo, H.; Lin, Y. Comprehensive evaluation of the quality of statutory infectious disease reporting in Yunnan Province in 2021 by the weighted TOPSIS method and the weighted rank-sum ratio method. Pract. Prev. Med. 2023, 30, 504–508. [Google Scholar]
- Ren, L.; Li, F.; Wang, Y.; Dai, Y.; Yang, H.; Xu, Z. Multi-objective optimization of injection molding quality based on TOPSIS grey relational analysis. China Plast. 2022, 36, 96–102. [Google Scholar]
- Chen, G.; Li, J.; Zhang, J. Evaluation of drug utilization of recombinant human coagulation factor VIIa based on weighted TOPSIS method. J. Pharmacoepidemiol. 2023, 32, 384–390. [Google Scholar]
- Liu, L.; Wan, X.; Li, J.; Wang, W.; Gao, Z. An Improved Entropy-Weighted Topsis Method for Decision-Level Fusion Evaluation System of Multi-Source Data. Sensors 2022, 22, 6391. [Google Scholar]


| Parameters | Significance |
|---|---|
| The set of rally points, . | |
| The set of fire points, . | |
| The set of rescue aircraft, . | |
| the set of task execution cycles, , . | |
| The set of water point, . | |
| the set of water required to extinguish all fires. | |
| The time it takes for the aircraft with the longest task time to complete the task among all rescue aircraft. | |
| The time for aircraft to execute the entire firefighting task | |
| The time for aircraft to execute the nth cycle of tasks. | |
| The cost for all aircraft to execute the entire firefighting task. | |
| The cost for aircraft to execute the nth round of tasks. | |
| Sub-task 1, a 0-1 variable, where 1 means that aircraft did not execute a flight task in the nth round, and 0 otherwise. | |
| Sub-task 2, a 0-1 variable, where 1 means that aircraft flew from rally point to fire point to execute a fire extinguishing task in the nth round, and 0 otherwise. | |
| Sub-task 3, a 0-1 variable, where 1 means that aircraft flew from fire point to rally point to execute a fire extinguishing task in the nth round, and 0 otherwise. | |
| Sub-task 4, a 0-1 variable. Aircraft flies from fire point to water point to fetch water after completing the fire extinguishing task in the nth round and then flies back to fire point to execute the fire extinguishing task, which is 1, otherwise 0. | |
| Sub-task 5, a 0-1 variable. Aircraft flies from fire point to water point to fetch water after completing the fire extinguishing task in the nth round and then flies back to fire point to execute the fire extinguishing task, which is 1, otherwise 0. | |
| The distance from rally point to fire point . | |
| The distance from fire point to water point . | |
| The preparation time for aircraft to execute tasks from the rally point each time. | |
| The additional time required for aircraft to fetch and spray water each time. | |
| The flight cost per minute of aircraft flight. | |
| The fixed cost of aircraft to execute tasks from the rally point. | |
| The flight speed of aircraft . | |
| The water capacity of aircraft . | |
| The flight fuel consumes per minute of aircraft . | |
| The maximum fuel capacity of aircraft . |
| Information | Fire Point 1 | Fire Point 2 | Fire Point 3 |
|---|---|---|---|
| Distance from Rally Point 1/km | 111.22 | 36.22 | 237.06 |
| Distance from Rally Point 2/km | 124.72 | 83.82 | 158.20 |
| Distance from Rally Point 3/km | 63.73 | 73.44 | 140.59 |
| Distance from Water Point/km | 133.85 | 59.04 | 90.22 |
| Required Fire Extinguishing Water Volume/tons | 24 | 18 | 18 |
| Aircraft Type | Performance Parameters | Cost Parameters | ||||
|---|---|---|---|---|---|---|
| Flight Speed/(km/h) | Water-Carrying Capacity/Tons | Take-Off Preparation Time/min | Fuel Capacity/L | Take-Off Cost/CNY | Flight Cost/(CNY/km) | |
| Heavy Aircraft | 150 | 3 | 30 | 2450 | 1500 | 15 |
| Light Aircraft | 200 | 1.5 | 20 | 1530 | 1000 | 10 |
| Parameter | NSGA-II | AWGA |
|---|---|---|
| T | 1.1629 | 1.1499 |
| hv | 0.01984 | 0.01568 |
| S | 0 | 636.4562 |
| NPS | 4 | 3 |
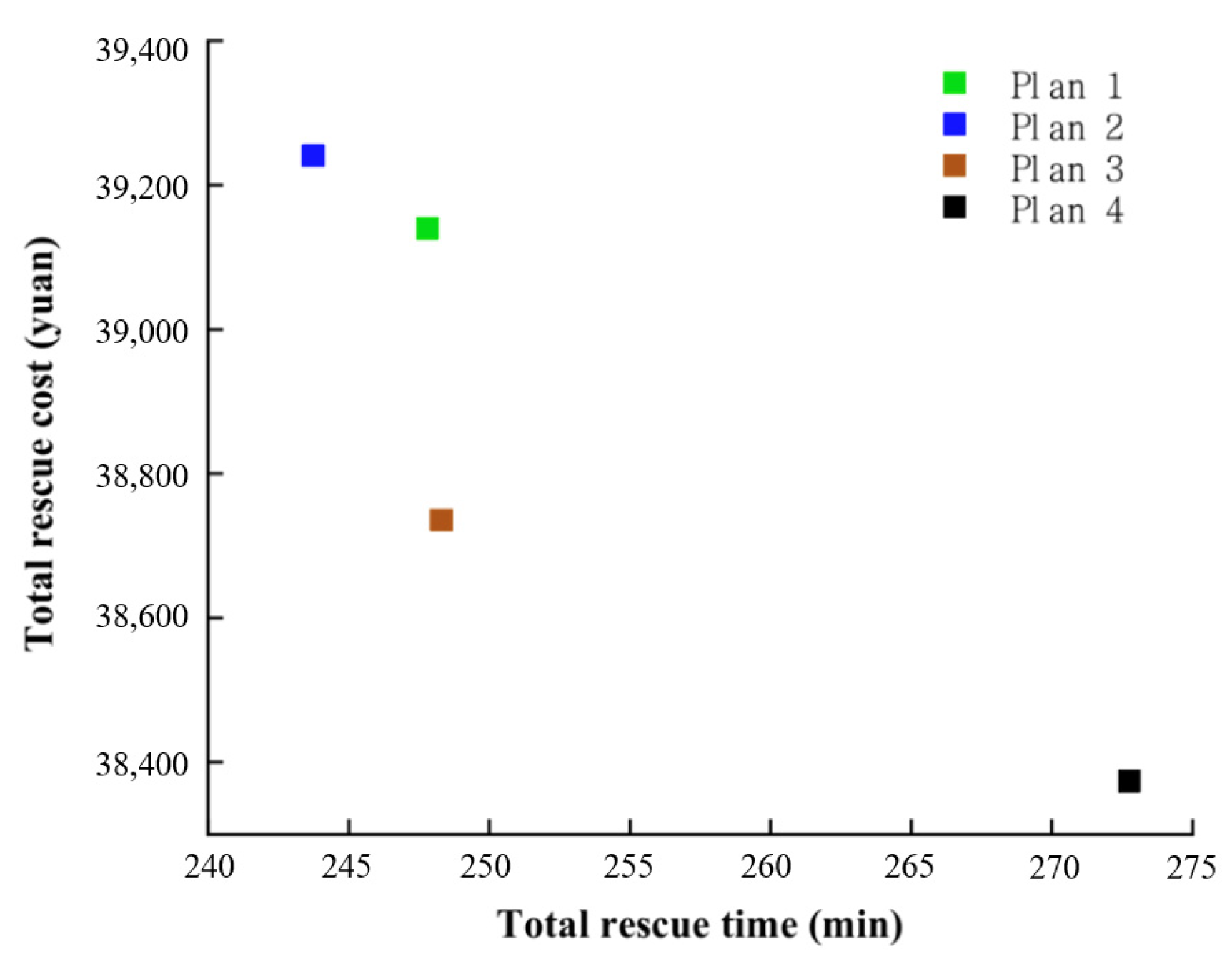
| Objective Function | Plan 1 | Plan 2 | Plan 3 | Plan 4 |
|---|---|---|---|---|
| Total Rescue Time/min | 243.7536 | 248.3136 | 247.8112 | 272.756 |
| Total Rescue Cost/yuan | 39,240.702 | 38,735.806 | 39,139.494 | 38,373.226 |
| Plan 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rally Point | Rally Point 1 | Rally Point 2 | Rally Point 3 | |||||||||
| Aircraft Type | H | H | L | L | L | H | L | L | L | L | L | L |
| Cycle 1 | 2 | 2 | 0 | 1 | 1 | 3 | 3 | 0 | 1 | 1 | 1 | 1 |
| Cycle 2 | 3 | 3 | 0 | 3 | 3 | 2 | 1 | 1 | 3 | 3 | 1 | 1 |
| Cycle 3 | 2 | 2 | 0 | 1 | 1 | 2 | 2 | 1 | 1 | 3 | 1 | 1 |
| Plan 2 | ||||||||||||
| Rally Point | Rally Point 1 | Rally Point 2 | Rally Point 3 | |||||||||
| Aircraft Type | H | H | L | L | L | H | L | L | L | L | L | L |
| Cycle 1 | 1 | 2 | 0 | 2 | 1 | 1 | 3 | 0 | 1 | 1 | 1 | 3 |
| Cycle 2 | 3 | 3 | 0 | 3 | 3 | 2 | 1 | 1 | 3 | 3 | 3 | 1 |
| Cycle 3 | 2 | 2 | 0 | 1 | 1 | 2 | 2 | 0 | 1 | 3 | 1 | 1 |
| Plan 3 | ||||||||||||
| Rally Point | Rally Point 1 | Rally Point 2 | Rally Point 3 | |||||||||
| Aircraft Type | H | H | L | L | L | H | L | L | L | L | L | L |
| Cycle 1 | 2 | 2 | 0 | 1 | 1 | 1 | 3 | 0 | 1 | 1 | 1 | 3 |
| Cycle 2 | 3 | 3 | 0 | 3 | 3 | 2 | 1 | 1 | 3 | 3 | 3 | 1 |
| Cycle 3 | 2 | 2 | 0 | 1 | 1 | 2 | 2 | 1 | 1 | 3 | 1 | 1 |
| Plan 4 | ||||||||||||
| Rally Point | Rally Point 1 | Rally Point 2 | Rally Point 3 | |||||||||
| Aircraft Type | H | H | L | L | L | H | L | L | L | L | L | L |
| Cycle 1 | 2 | 2 | 0 | 1 | 1 | 1 | 3 | 0 | 1 | 1 | 1 | 1 |
| Cycle 2 | 3 | 3 | 0 | 3 | 3 | 3 | 1 | 1 | 3 | 3 | 1 | 1 |
| Cycle 3 | 2 | 2 | 0 | 1 | 2 | 2 | 2 | 0 | 1 | 3 | 1 | 1 |
| Plan | Rank | |||
|---|---|---|---|---|
| Plan 1 | 0.500 | 0.866 | 0.634 | 2 |
| Plan 2 | 0.249 | 0.786 | 0.759 | 1 |
| Plan 3 | 0.458 | 0.747 | 0.620 | 3 |
| Plan 4 | 0.866 | 0.500 | 0.366 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Huang, Y.; Yin, Z.; Qin, L. Optimal Collaborative Scheduling of Multi-Aircraft Types for Forest Fires General Aviation Rescue. Aerospace 2023, 10, 741. https://doi.org/10.3390/aerospace10090741
Pan W, Huang Y, Yin Z, Qin L. Optimal Collaborative Scheduling of Multi-Aircraft Types for Forest Fires General Aviation Rescue. Aerospace. 2023; 10(9):741. https://doi.org/10.3390/aerospace10090741
Chicago/Turabian StylePan, Weijun, Yuanjing Huang, Zirui Yin, and Liru Qin. 2023. "Optimal Collaborative Scheduling of Multi-Aircraft Types for Forest Fires General Aviation Rescue" Aerospace 10, no. 9: 741. https://doi.org/10.3390/aerospace10090741
APA StylePan, W., Huang, Y., Yin, Z., & Qin, L. (2023). Optimal Collaborative Scheduling of Multi-Aircraft Types for Forest Fires General Aviation Rescue. Aerospace, 10(9), 741. https://doi.org/10.3390/aerospace10090741





