Abstract
This study considers the problem of injecting a spacecraft into an elliptic, repeating-ground-track orbit about Mars, starting from a 4-sol highly elliptical orbit, which is a typical Martian capture orbit, entered at the end of the interplanetary transfer. The final operational orbit has apoares corresponding to the maximum (or minimum) latitude, and nine nodal periods are flown in 5 Martian nodal days. The orbit at hand is proven to guarantee coverage properties similar to the Molniya orbit about Earth; therefore, it is especially suitable for satellites that form constellations. Low-thrust nonlinear orbit control is proposed as an affordable and effective option for orbit injection, capable of attaining significant propellant reduction if compared to alternative strategies based on chemical propulsion. This work introduces a new, saturated feedback law for the low-thrust direction and magnitude that is capable of driving the spacecraft of interest toward the operational orbit. Remarkable stability properties are proven to hold using the Lyapunov stability theory. Because no reference path is to be identified a priori, this technique represents a viable autonomous guidance strategy, even in the case of temporary unavailability of the low-thrust propulsion system or in the presence of widely dispersed initial conditions and errors on estimating orbit perturbations. Monte Carlo simulations prove that the feedback guidance strategy at hand is effective and accurate for injecting a spacecraft into the desired, repeating-ground-track operational orbit without requiring any reference transfer path.
1. Introduction
Mars represents a primary objective in the forthcoming space exploration programs. Several scientific missions are planned or currently ongoing, with the prospect of carrying out the first human mission in the next two decades. A satellite constellation capable of supplying continuous, global coverage over the great majority of Mars would represent a precious asset as a communications infrastructure useful to orbiters, probes, and instruments located on the surface while extending the existing capabilities of NASA’s Deep Space Network. Several goals were defined [1] for a satellite constellation about Mars, including the global coverage over a specified time span and the maximization of the communication and navigation performance across all latitudes.
Nann et al. [2] designed a constellation of eight satellites mainly devoted to carrying out radio occultation measurements, with reconfiguration capabilities aimed at providing navigation services. Bell et al. [3] proposed four configurations of microsatellite constellations using low-altitude, inclined orbits. Each configuration is composed of six satellites and ensures satisfactory navigation and communication performance, with special regard to the equatorial region. However, continuous coverage is not guaranteed, and the maximum revisit even reaches 8 h while exceeding 2 h over the great majority of the Martian surface. Kelly and Bevilacqua [4] proposed a constellation of 15 satellites that ensures global and continuous coverage of the entire Martian surface, using 5 equally spaced, inclined orbit planes. Most recently, Pontani et al. [5] designed a constellation composed of 12 satellites released in 4 distinct orbit planes. While three satellites travel an areostationary orbit, the remaining nine satellites are released in three repeating, circular, quasi-synchronous, inclined orbits. This configuration was proven to guarantee global and continuous coverage while ensuring repetition and predictability of the visible passes as well as the visibility of multiple satellites. While the preceding contributions deal with the constellation of satellites that travel circular orbits, the scientific literature also includes relevant contributions that consider eccentric-orbit constellations. Tundra and Molniya [6,7] inclined orbits are especially suitable for the coverage of high-latitude regions. Palmerini and Graziani [8] propose highly elliptical polar orbits for global-coverage constellations, whereas Draim [9] introduced the polyhedral elliptic-orbit constellation. The same author also designed the Ellipso configuration [10], composed of elliptic orbits and a single circular, equatorial, medium-altitude orbit. Pontani and Teofilatto [11] used a correlation-based approach to design elliptic-orbit constellations composed of a reduced number of satellites and tailored to continuous regional coverage.
To ensure repetition and predictability of the visible passes, this study considers repeating-ground-track, quasi-synchronous orbits at the critical inclination as a convenient option for Martian constellations. Moreover, the low-thrust transfer to this orbit is investigated, with the use of nonlinear orbit control, starting from the ESA 4-sol orbit [12], which is entered after planetary capture. Orbit dynamics about Mars is modeled with the inclusion of the most relevant perturbations, i.e., several harmonics of the areopotential, together with the gravitational pull due to the Sun as a third body and solar radiation pressure. Low-thrust propulsion has recently gained increased relevance in space mission design because it allows substantial propellant savings at the price of increasing (even considerably) the time of flight. Nonlinear orbit control provides feedback guidance for the low-thrust direction and magnitude, only relying on the instantaneous state (position and velocity) of the spacecraft, without any need for a precomputed transfer path. This strategy can be regarded as a viable alternative to optimal control, especially in those mission scenarios where uncertainties on the initial state or technological failures can occur. Although optimal control outperforms nonlinear orbit control, the performance penalty associated with the use of feedback guidance in place of optimal control can be considerably reduced through proper tuning of the control gains [5]. Nonlinear orbit control was already proven to be very effective for Earth orbit transfers and maintenance [13] and constellation deployment [5,14]. This research aims at extending the range of application of nonlinear orbit control to elliptic orbits with some prescribed, time-varying orbit elements. Numerical simulations are being presented, assuming either nominal or nonnominal flight conditions, i.e., stochastic failures of the propulsion system, errors in estimating orbit perturbations, and significant displacements of the initial conditions from the nominal values, due to injection errors at the planetary capture.
In summary, the major objectives of this work are (i) the identification of a repeating-ground-track, quasi-synchronous, elliptic orbit suitable for Martian constellations, (ii) the related coverage analysis, with a special focus on high-latitude regions, (iii) the extension of nonlinear orbit control to the case of target elliptic orbits with some time-varying orbit elements, and (iv) the numerical testing of the nonlinear feedback strategy for satellite deployment, both in nominal and nonnominal flight conditions.
2. Orbit Dynamics
In recent years, low-thrust propulsion has gained increased relevance in space mission design. In fact, for specified mission profiles and payloads, low-thrust propulsion allows substantial propellant savings at the price of increasing (even considerably) the time of flight. Recently, nonlinear control was proven to be an effective option for real-time feedback guidance in orbit transfers, as well as for orbit maintenance [5,13,14,15].
2.1. Modified Equinoctial Elements
Modified equinoctial elements are used to describe the dynamics of the spacecraft, modeled as a point mass. The orbital motion of the vehicle is mainly affected by the Mars gravitational field. Therefore, the spacecraft dynamics can be investigated by employing a perturbed two-body problem model, with the inclusion of the most relevant orbit perturbations. Fundamental planetary parameters are reported in Appendix A. The space vehicle is assumed to be equipped with a steerable, throttleable low-thrust propulsion system to perform the orbit injection maneuvers. Nonlinear orbit control using low-thrust propulsion is being employed for the purpose of driving a spacecraft toward some operational conditions and maintaining it in the desired orbit, compensating for perturbations. The operational conditions can be expressed in terms of osculating orbit elements.
Orbit dynamics can be described in terms of osculating orbit elements, i.e., semimajor axis a, eccentricity e, inclination i, right ascension of the ascending node (RAAN) , argument of periapsis , and true anomaly f. However, the Gauss equations [16,17], which govern the time evolution of the classical orbit elements, become singular in the presence of a circular or equatorial orbit (and when an elliptic orbit transitions to a hyperbola). For these reasons, the modified equinoctial elements [18,19] are chosen, in conjunction with the semilatus rectum (parameter), used in place of a. The six elements are defined as
These elements are nonsingular for all Keplerian trajectories, with the only exception of equatorial retrograde orbits (). If , the instantaneous radius is . Letting , the governing equations for the modified equinoctial elements can be written as
where represents the Martian gravitational parameter, whereas the expression of is [5,14]
Vector a represents the -vector of the non-Keplerian acceleration that affects the spacecraft’s motion. Its components, denoted with , are the projections of a into the local vertical local horizontal (LVLH) rotating frame aligned with , where unit vector is directed toward the instantaneous position vector r (taken from the Mars center), whereas is aligned with the spacecraft orbital angular momentum. Vector a includes both the thrust acceleration and the perturbing acceleration generated by the space environment. These two contributions can be distinguished, i.e., , where subscripts T and P refer respectively to thrust and perturbations. The perturbing acceleration is due to harmonics of the areopotential, third body gravitational attraction, and solar radiation pressure and must be projected in the LVLH-frame.
Let and represent the maximum available thrust magnitude and the initial mass. If denotes the mass ratio and T the thrust magnitude, for the following equation can be obtained:
where
Symbol c represents the effective exhaust velocity of the propulsion system. The magnitude of the instantaneous thrust acceleration is and is constrained to the interval , where . Moreover, the thrust acceleration can be expressed as , where has magnitude constrained to the interval .
In conclusion, the spacecraft dynamics is described in terms of the state vector , whereas the control vector is , directly related to the thrust acceleration. Equations (2), (3) and (5) represent the state equations.
2.2. Orbit Perturbations
An accurate dynamical model requires the introduction of the perturbing accelerations that affect the orbit dynamics about Mars. The most relevant perturbation included in the analysis of low-thrust transfers are
- (a)
- harmonics of the areopotential, with coefficient (i.e., , , , and ),
- (b)
- third body gravitational pull due to the Sun, and
- (c)
- solar radiation pressure.
It is worth remarking that the third body attraction due to the two Martian moons is negligible in comparison to that related to the Sun.
Correct modeling of these perturbations requires the definition of some useful reference frames. As a preliminary step, the Mars-centered inertial (MCI) frame is introduced. It is associated with the right-hand sequence of unit vectors , where identifies the equatorial plane, whereas is aligned with the Mars rotation axis and coincides with the so-called International Astronomical Union (IAU) vector of the date, corresponding to the intersection of the Martian equatorial plane with the Earth J2000 equatorial plane. Another useful frame (rotating together with the spacecraft) is associated with , where is directed along the local East direction, points toward the local North direction, and is aligned with the position vector (taken from the center of Mars). The local vertical local horizontal frame (LVLH) is associated with the triad , where is directed along the spacecraft angular momentum. Angles ξ (absolute longitude), ϕ (latitude), and ζ (heading) relate the MCI-frame to the -frame and to the -frame,
where denotes the matrix associated with the elementary rotation by angle χ about axis j. Moreover, an additional relation between the MCI-frame and the -frame can be written in terms of orbit elements,
Mars is not a perfectly spherical body, and its asphericity is modeled through spherical harmonics of the areopotential. In fact, the Martian gravitational field has the following general expression
where is represents the main contribution, while the second term can be written as
In Equation (10) is the Martian equatorial radius, are Legendre polynomials, are the coefficients associated with the harmonics, and are respectively the spacecraft latitude and geographical longitude, and r is the vehicle distance from the center of Mars. The term is responsible for the Keplerian gravitational acceleration, while produces the perturbing acceleration
The gravitational action of the Sun can be treated as a third body perturbation. If subscript 1 is associated with Mars and subscript 2 with the Sun, the perturbing acceleration can be expressed as [17]
where is the gravitational parameter of the third body, whereas is the position of the Sun with respect to Mars.
The spacecraft is subject to solar radiation pressure produced by the photons emitted by the Sun. The related perturbing acceleration can be evaluated using the following expression [20]:
In Equation (13) m is the vehicle mass and A its reference surface, is the unit vector pointing from the spacecraft toward the Sun, is the solar radiation pressure, and is the solar radiation pressure coefficient. Finally, ν is the shadow function, which can assume value 1, if the vehicle is illuminated, or 0 if it is shadowed. However, because the distance of Mars from the Sun is much greater than the typical radius of Martian orbits, the following approximation is adopted: .
2.3. Operational Orbit and Coverage Analysis
A mission devoted to telecommunications requires to cover the target region as long as possible. In particular, if the region of interest is located at high latitudes, a quasi-synchronous, elliptic Mars orbit, similar to an Earth Molniya orbit, is an interesting option. The apoapse must be sufficiently high to increase the duration of the visibility intervals. To do this, quasi-synchronism is enforced at apoapse, and this means that the satellite footprint at apoapse has the same velocity toward East as the corresponding point on the Martian surface. Moreover, desirable features of the orbit are (a) repetitiveness, which implies predictability of the performance, and (b) invariance with respect to the perturbation. For the purpose of constellation design, the solar radiation pressure and the third body gravitational pull due to the Sun are negligible. In contrast, the Mars oblateness ( zonal harmonic) produces significant effects on the orbit elements and is included in the model.
The quasi-synchronism condition can be expressed as
where denotes the instantaneous latitude, , whereas is the East component of velocity. Using the expressions for the spacecraft radius r and velocity magnitude v at apoapse, Equation (14) leads to the following relation between the semimajor axis and the other orbit elements :
Moreover, it is convenient that the orbit has repeating ground track [11]. This means that the spacecraft completes a number of nodal orbital periods every nodal days. The repetitiveness property is studied by considering the mean effect of the zonal harmonic. On average, the Martian oblateness yields the following time derivatives [16,20] of the right ascension of the ascending node (RAAN) , argument of perigee , and mean anomaly M:
In Equations (16)–(18) , , and are respectively the Martian equatorial radius, gravitational parameter, and oblateness coefficient. The parameter is introduced, to denote the number of orbits per nodal day,
In Equation (19) is the nodal day and is the nodal orbital period. To select the operational orbit, is regarded as a function of . Moreover, the critical inclination is selected, i.e., deg, to get (cf. Equation (17)), whereas the argument of periapse is set to . The latter value implies that apoapse corresponds to the maximum latitude and is aimed at guaranteeing long-duration coverage of high-latitude regions. The curve associated with deg is illustrated in Figure 1. The constraint on the minimum perigee altitude (200 km) is included in the analysis and reported in the plane (denoted with ). The value is chosen, i.e., the vehicle completes nine orbital periods in 5 nodal days, which corresponds to semimajor axis and eccentricity equal to 13,799 km and 0.698. The ground track associated with this orbit is portrayed in Figure 2, under the assumption of selecting RAAN and argument of latitude corresponding to zero geographical longitude and maximum latitude at the initial time.
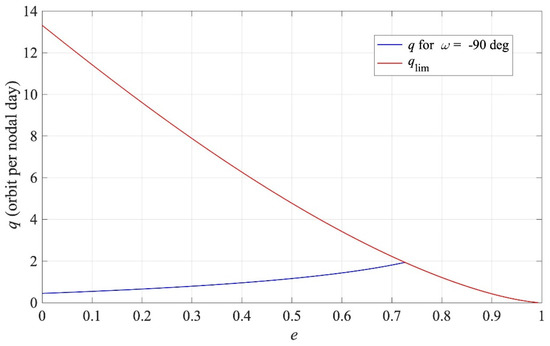
Figure 1.
Quasi-synchronous orbits: q as a function of the eccentricity.
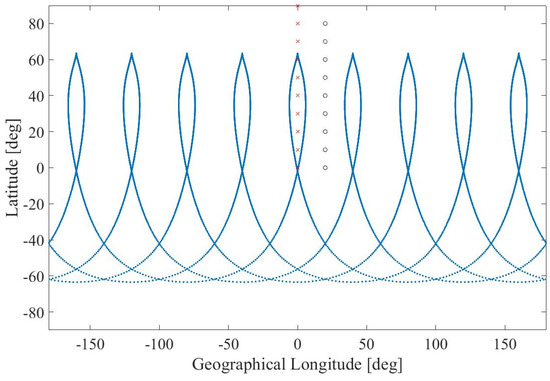
Figure 2.
Ground track of the operational quasi-synchronous, elliptic orbit.
Two satellites are assumed to describe the same ground track. The second vehicle is delayed by , i.e., half of the repetition period. Coverage analysis of this simple configuration aims at identifying (a) the minimum elevation for visibility, , for those longitudes where continuous coverage is ensured, and (b) the maximum revisit time, , for the remaining longitudes associated with discontinuous coverage. Both tasks (a) and (b) require obtaining the scheduling of the visible passes of the two satellites. However, due to the symmetry properties of the ground track, only a limited number of sample locations are to be considered to supply precise information on the global coverage properties. These sample locations are portrayed in Figure 3 (denoted with “x” and “o”) and lie along the symmetry meridians of the ground track. In fact, let and denote, respectively, the minimum elevation angle (task (a)) and the maximum revisit time (task (b)) over a repetition period, as functions of latitude, , and geographical longitude, . If is set to a specific value , then (and ) becomes a function of , and is continuous and locally even with respect to 18 values of , i.e., . These values correspond to the symmetry meridians of the ground track. This circumstance implies that the function (and ) has extremal values at these values of . As a result, for a given latitude , the minimum and maximum values of (and ) can be identified by considering only the locations marked with “o” and “x” in Figure 2.
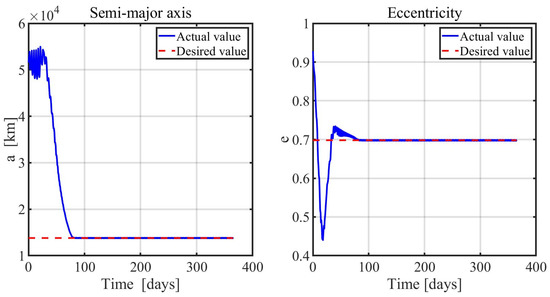
Figure 3.
Nominal conditions: semimajor axis (left) and eccentricity (right).
Visibility depends on the minimum elevation angle . In this study, two distinct values of are considered: (i) and (ii) . Continuous coverage is guaranteed for all locations with either (in case (i)) or (in case (ii)). For each latitude, two distinct longitudes are considered, i.e., those marked with “x” and “o” in Figure 2, and the maximum and minimum value of over a repetition period are reported in Table 1. The remaining latitudinal region is not covered uninterruptedly, and the maximum revisit times are identified and reported in Table 2. For only the revisit time when (case (ii)) is meaningful. Inspection of Table 1 and Table 2 points out that continuous coverage can be guaranteed by only two satellites in a relatively large latitudinal region, while the maximum revisit time remains sufficiently short at mid-latitudes (30 and 40 deg). Moreover, at high latitudes, the minimum elevation angle has only modest variations depending on geographical longitude. This property is apparent from inspection of Table 1, where the extremal values of are reported.

Table 1.
Extremals of the minimum elevation angle (deg), depending on latitude.

Table 2.
Maximum revisit time (min), depending on latitude and minimum elevation angle.
3. Nonlinear Orbit Control
In this section, nonlinear orbit control is introduced and described. It is aimed at identifying the thrust direction and magnitude to inject a spacecraft in a specified elliptic Martian orbit. The initial parking orbit is a typical ESA 4-Sol orbit [12], associated with the following orbit elements:
At the initial epoch , set to 16 April 2025 at 0:00 UTC, the true anomaly is assumed equal to 0 deg.
3.1. Operational Orbit
The desired orbit is defined by five orbit elements: semimajor axis, eccentricity, inclination, argument of perigee, and RAAN. The main effect of the zonal harmonic is the average linear time-variation of the RAAN, given by Equation (16). This means that desired RAAN of the operational orbit is
where is given by Equation (16) and subscript d refers to the desired (nominal) value of the respective orbit element. Moreover, as the critical inclination is selected, the perturbation yields no average change in the argument of periapse. Finally, the zonal harmonic generates no average variation of a, e, and i. In short, the desired orbit elements are
where for the RAAN, only the initial value is reported as it is time-varying.
The desired insertion conditions are expressed in terms of equinoctial elements. Because , one gets
To get the correct eccentricity and argument of periapse, using the definitions of l and m, the following relation is enforced:
leading to
The remaining conditions deal with the orbital plane orientation. The instantaneous direction of the spacecraft’s angular momentum, , is required to be aligned with the desired one, . The unit vector can be expressed in terms of and i, i.e., , leading to
After some steps, Equation (25) can be rearranged as
The final conditions (22), (24), and (26) can be incorporated as the three components of the vector and finally written as
The three (scalar) insertion conditions, written in the vector form (27), define the target set of the problem. It is worth noticing that is continuous and has continuous partial derivatives. Moreover, it is time varying due to .
3.2. Feedback Law and Related Stability Analysis
This section uses the Lyapunov direct method to identify a feedback control law aimed at driving the spacecraft toward the desired orbit injection conditions. Orbital motion is governed by Equations (2), (3), and (5). In particular, the non-Keplerian acceleration is written as the sum of thrust acceleration and perturbing acceleration, and Equation (2) becomes
For systems governed by Equation (28) with , the Jurdjevic–Quinn theorem [15,21] provides a feedback control law that drives the dynamical system to an arbitrary target state, making the controlled system Lyapunov-stable. On the other hand, if orbit perturbations are included in the model, a different approach can be adopted. A candidate Lyapunov function is introduced as
where K is a symmetric positive definite constant matrix. It is convenient to choose it as diagonal with positive elements that play the role of weights, to properly select in order to achieve the desired performance. It is straightforward to recognize that unless = 0. However, to be a Lyapunov function, must have a nonpositive time derivative, and this can be ensured through proper selection of the control action . The -vectors and are introduced as
Two propositions, proven in ref. [14], establish the conditions for V to be a Lyapunov function.
Proposition 1.
If and are continuous, is finite, unless , and , then the feedback control law
leads the dynamical system governed by Equations (2), (3), and (5) to converge asymptotically to the target set .
The previous proposition includes the hypothesis . If this condition is violated, the feedback control law is not feasible because would exceed the maximal value , i.e., the propulsive capability of the system. For this reason, when this occurs, an alternative saturated feedback law can be used.
Proposition 2.
If and are continuous, is finite, unless , and , then the feedback control law
leads a dynamical system governed by Equations (2), (3), and (5) to converge asymptotically to the target set .
In Equation (33) it is convenient to choose because this corresponds to the least value of . In conclusion, Propositions 1 and 2 lead to defining a feedback control law that identifies direction and magnitude of the thrust acceleration at each instant. This law can be written in compact form as
when the condition is violated, the thrust is turned off, i.e., . It is worth remarking that Propositions 1 and 2 provide some sufficient conditions for stabilizing the dynamical system of interest. This circumstance implies that the assumptions of Propositions 1 and 2 can be violated (in some time intervals) without necessarily compromising asymptotic convergence to the desired final condition.
To complete the stability analysis, the expressions for the components of must be found. After several analytical steps, omitted for the sake of brevity, one obtains
The attracting set collects all the dynamical states where . This condition is met if , i.e., if all the three components vanish, for any choice of the positive coefficients . While looking for conditions for states related to the attracting set, one must rule out those depending on , which is time-varying (also along the desired orbit). Clearly, if , then . Therefore, the attracting set certainly contains rectilinear trajectories (). It is straightforward to recognize that also in the target set . Moreover, regardless of if and , whose fulfillment is equivalent to . Moreover, the preceding two equalities also imply in Equation (37). In the latter equation, the remaining term
can be rewritten as
and is equal to zero, regardless of , only if and , i.e., .
In conclusion, the attracting set contains two subsets:
- rectilinear trajectories
- target set, i.e.,
Because the attracting set contains another subset other than the target set, asymptotic convergence toward the latter is only local, based on Lyapunov stability theorem. However, the equality can be considered again, to rule out, if possible, subset 1. The condition implies , i.e., while , where
Equation (40) yields three relations. Inspection of their closed-form expressions (obtained with MATLAB symbolic toolbox [22] and not reported for the sake of conciseness) leads to ruling out subset 1, associated with rectilinear trajectories. Therefore, only subset 2 (i.e., the target set) corresponds to an equilibrium condition. Therefore, global asymptotic convergence toward the target set is demonstrated.
As a final step, the vector , which appears in the definition of d, is to be analyzed, in order to verify the existence of possible singularity issues. Using the definitions of and G, the limit of as yields three closed-form analytical expressions for the three components. The second and the third component of the vector turn out to tend to zero, while the first component tends to
This section establishes some analytical conditions for convergence toward the operational orbit while neglecting the spacecraft shadowing. The unavailability of solar illumination may limit the onboard electrical power needed to operate the low-thrust system. If this occurs, electrical power must be switched off during eclipse intervals. The feedback law can easily take this into account. This is shown in ref. [13] for low Earth orbits. The major effect is an occasional and temporary violation of the boundary conditions along eclipse arcs. However, in the present research, the shadowing effect on the available electrical power is neglected, also because the initial orbit has a very high apoapse radius (while the final orbit is also highly eccentric), and the eclipse intervals seldom occur as a result.
4. Numerical Simulations
The nonlinear orbit control law presented in section III is implemented in MATLAB and numerically tested in order to evaluate its performance and capability to drive the spacecraft toward the desired final conditions. The simulations are performed assuming that the vehicle is equipped with an electric propulsive system, with the following two parameters:
- km/s, effective exhaust velocity
In the numerical simulations, canonical units are employed. In particular, by definition, the distance unit (DU) equals the Martian equatorial radius, whereas the time unit (TU) is chosen in such a way that . Moreover, for the solar radiation pressure, the value is assumed.
To avoid excessive propellant consumption, tolerances are introduced on the three components of such that
This means that, if all tolerances are met, the thrust is switched off.
Specifically,
The desired orbit is reached at the first occurrence of the three conditions (45), then the control law is used for orbit maintenance while compensating the perturbations. This second phase consists of repeating ignitions and shutdowns of low-thrust propulsion when at least one of the three conditions (45) is violated. Furthermore, the following weighting coefficients are used after extensive trial-and-attempt tuning: , , and . Simulations are propagated for one year to investigate orbit transfer and subsequent maintenance.
The results of the simulations are reported in Figure 3, Figure 4, Figure 5 and Figure 6. They show how the orbit control law succeeds in injecting the spacecraft into the desired orbit and manages to maintain it, despite orbit perturbations. Figure 3 and Figure 4 report the time histories of the semimajor axis, eccentricity, inclination, RAAN, and argument of periapse. Two phases, orbit acquisition, and maintenance, can be distinguished in the preceding plots. After a transient of 80 days, the spacecraft reaches the operational orbit, and the five orbit elements converge to their target value. Once the desired condition is achieved, it is kept with very good precision. Figure 5 (right) shows the time evolution of the mass ratio. In the latter plot, the distinction between the two phases is evident: orbital acquisition is more expensive, and the mass ratio decreases more rapidly as a result, whereas mass depletion is slower during orbit maintenance, as the propulsive system must only compensate for orbit perturbations. In this phase, all the orbital elements show oscillations within the prescribed tolerances. Figure 6 depicts the time history of the Lyapunov function, which drops to zero as the space vehicle reaches the target orbit. Figure 7 shows a three-dimensional illustration of the transfer trajectory, whereas Figure 8 and Figure 9 depict the thrust magnitude and angles, respectively, in a repetition period. Several gaps appear in the time histories of the thrust angles, corresponding to the coast arcs, in which the thrust direction is meaningless. Moreover, Figure 10 portrays the thrust magnitude during the maintenance phase, together with the true anomaly . Inspection of this figure reveals that a rather repeating pattern emerges for the thrust acceleration magnitude in relation to orbital motion.
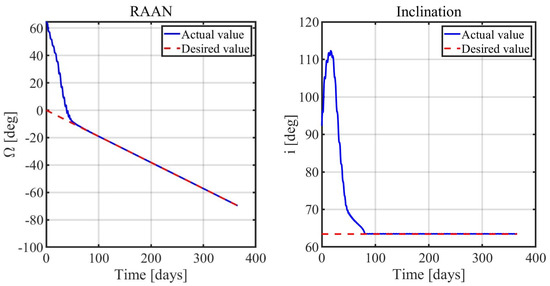
Figure 4.
Nominal conditions: inclination (left) and RAAN (right).
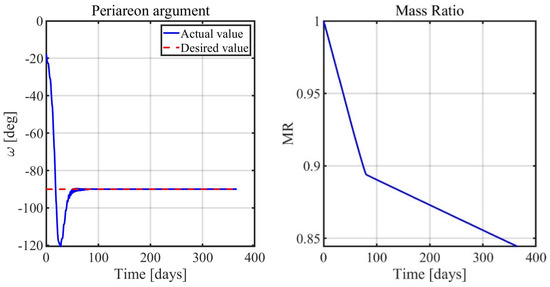
Figure 5.
Nominal conditions: argument of periapsis (left) and mass ratio (right).
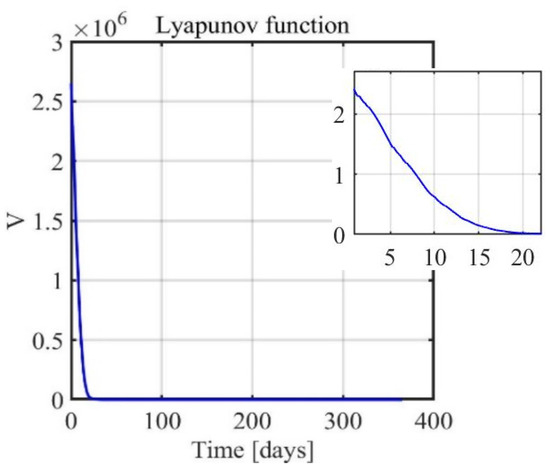
Figure 6.
Nominal conditions: Lyapunov function.
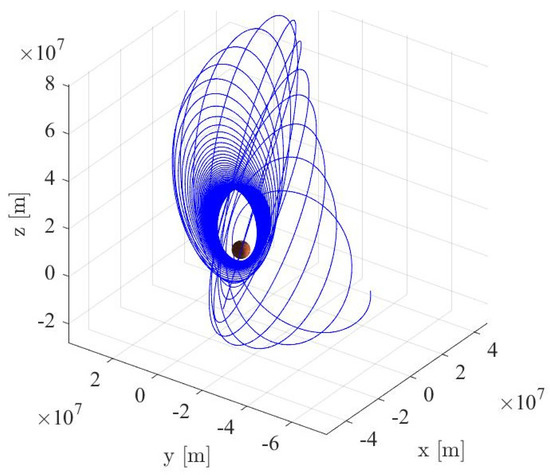
Figure 7.
Nominal conditions: transfer trajectory.
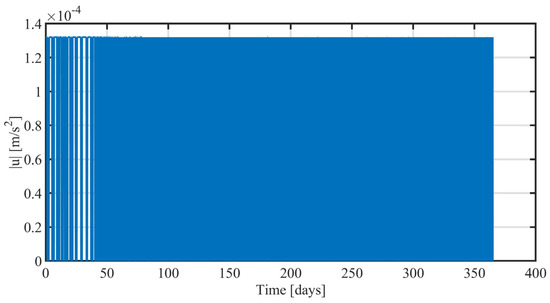
Figure 8.
Time history of the thrust acceleration magnitude.
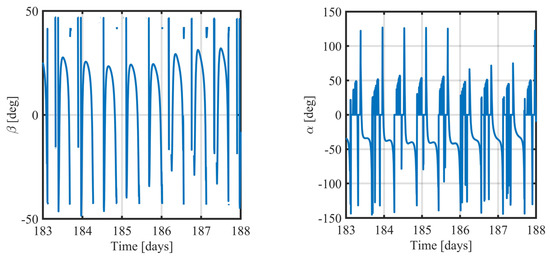
Figure 9.
Maintenance phase: time histories of the thrust angles.
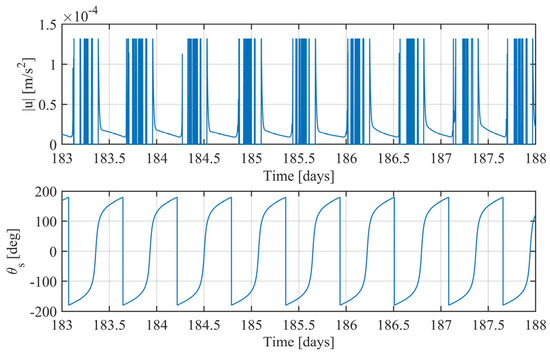
Figure 10.
Maintenance phase: time histories of the thrust acceleration magnitude (top) and the true anomaly (bottom).
Although this research adopts identical gains during the entire time of flight, it is worth remarking that the feedback gains can be changed during orbital maintenance. This strategy was shown to be convenient in the mission scenario described in ref. [23]. Moreover, after the orbit acquisition, different strategies for orbit maintenance may be applied on the basis of optimality or simple operational criteria. These alternative options can lead to propellant savings and are specifically relied on the acceptable tolerances on the orbit elements, which are in turn related to the prescribed mission specifications.
4.1. Orbit Injection with Temporary Propulsion Failure
One of the main advantages of driving the spacecraft with a closed-loop control law is that the guidance strategy is also effective in nonnominal conditions because the feedback control law is based on the actual state of the vehicle. For the purpose of underlining and using this property, stochastic temporary failure is introduced to point out the capability of the feedback strategy to drive the spacecraft toward the operational orbit also in this situation. More precisely, it is assumed that a random failure occurs during the orbital transfer, with starting time uniformly distributed in [0, 70] days. The propulsion system is unavailable for a random interval of time, with uniform distribution in [5, 10] days.
A Monte Carlo (MC) campaign, also termed MC 1, composed of 1000 simulations, is run to check if the feedback orbit control is capable of driving the vehicle toward the desired orbit, despite the temporary failure. This analysis leads to identifying the effect of the stochastic failure on the transfer duration and consumption. The results of the Monte Carlo analysis are described in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. For all the simulations, nonlinear orbit control succeeds in injecting the vehicle into the desired orbit in spite of the temporary failure. In fact, all the orbit elements converge to their desired value, ensuring the acquisition of the operational orbit in less than 95 days. Moreover, no impact with the Martian surface takes place, as shown in Figure 14 (the minimum altitude is 470 km). Table 3 reports the mean value and the standard deviation for the convergence time and the final mass ratio.
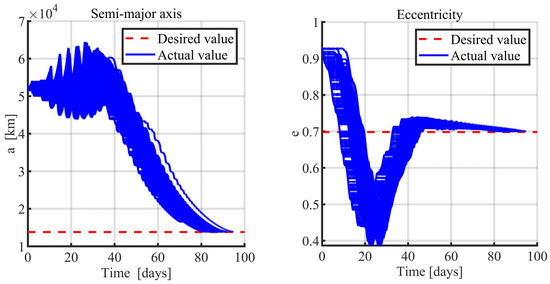
Figure 11.
Monte Carlo analysis 1: semimajor axis (left) and eccentricity (right).
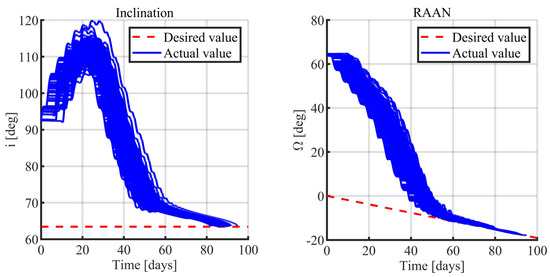
Figure 12.
Monte Carlo analysis 1: inclination (left) and RAAN (right).
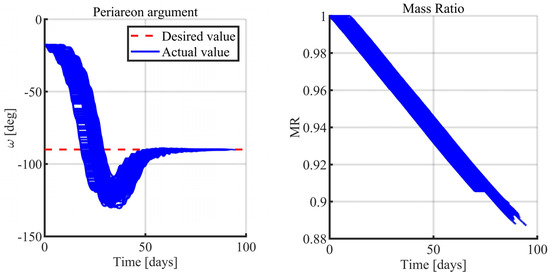
Figure 13.
Monte Carlo analysis 1: argument of periapsis (left) and mass ratio (right).
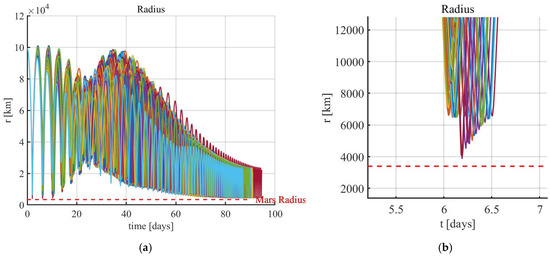
Figure 14.
Monte Carlo analysis 1: radius (a) and related zoom (b); the dotted line represents the Martian radius.
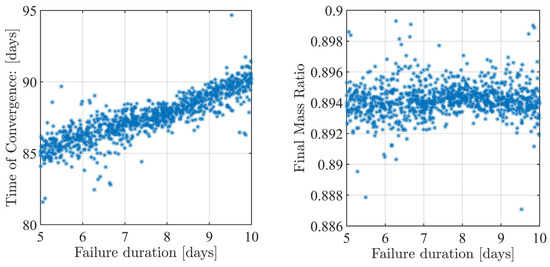
Figure 15.
Monte Carlo analysis 1: correlation analysis.

Table 3.
Monte Carlo analysis 1: time of convergence and final mass ratio.
Figure 15 is useful to underline the effects of the failure duration on the propellant consumption and on convergence time. A linear correlation appears between the time of convergence and failure duration, i.e., if the failure persists for more time, then the orbit transfer has a longer duration. On the other hand, the duration of the failure exhibits no apparent correlation with the final value of the mass ratio.
4.2. Orbit Injection with Dispersed Initial Conditions and Errors in Perturbation Estimation
The aim of this section is to show the effectiveness of feedback orbit control in the presence of dispersed initial conditions, which are representative of orbit injection errors at the planetary capture, and errors in estimating the orbit perturbations.
To model this, random displacements—with uniform distribution—on periares and apoares radii are assumed in place of semimajor axis and eccentricity. For each simulation, the latter orbit elements can be obtained once the periares and apoares radius is specified. The remaining orbit elements obey a normal distribution with mean value and standard deviation reported in Table 4, together with upper and lower bounds, for each variable.

Table 4.
Monte Carlo 2: mean value, standard deviations, and bounds for the stochastic initial orbit elements.
Moreover, errors in estimating the orbital perturbations are modeled as well. Each component of the perturbing acceleration is assumed to be
where and are six random variables, with uniform distribution in and , respectively, T is the time-varying orbital period associated with the instantaneous osculating orbit; symbol denotes the estimated value of the perturbing acceleration component, which is compensated through feedback control. It is apparent that the oscillating term that appears in Equation (46) represents the unmodeled perturbing acceleration component, with a magnitude up to 5% of the nominal value.
Even if the spacecraft starts its orbital transfer with nonnominal orbit elements, the closed-loop guidance strategy can be used to complete the orbit transfer. To prove this, a set of 1000 Monte Carlo simulations (campaign MC 2) is run with also the intent of obtaining information on propellant consumption and time of convergence.
The results of this study are summarized in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21: in all the 1000 simulations, the spacecraft successfully reaches the operational orbit. The orbit elements converge to the desired values, and the orbit acquisition is successfully completed. In Table 5, the mean value and the standard deviation of the convergence time and of the final mass ratio are reported. Figure 16, Figure 17 and Figure 18 witness the effectiveness and robustness of the guidance strategy at hand. Moreover, an inspection of Figure 19 reveals that no impact with the Martial surface occurs (the minimum altitude equals 804 km, i.e., the final, desired periapse altitude). Finally, Figure 20 depicts the time of convergence to the target set for all the simulations, whereas Figure 21 portrays the propellant fraction.
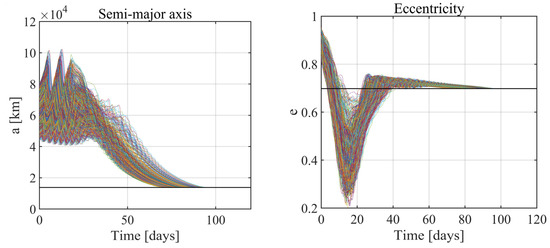
Figure 16.
Monte Carlo analysis 2: semi-major axis (left) and eccentricity (right).
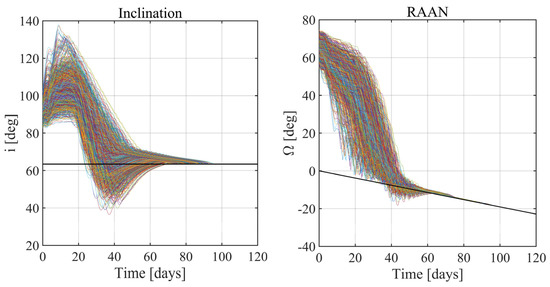
Figure 17.
Monte Carlo analysis 2: inclination (left) and RAAN (right).
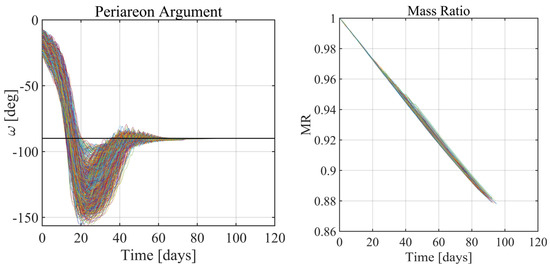
Figure 18.
Monte Carlo analysis 2: periareon argument (left) and mass ratio (right).
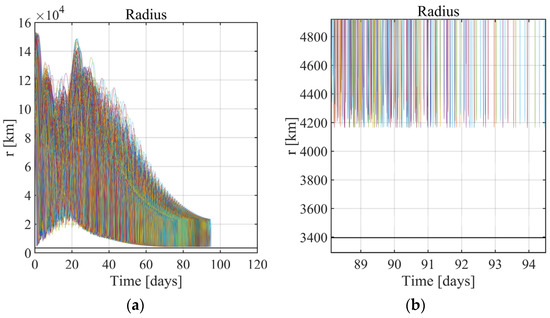
Figure 19.
Monte Carlo analysis 2: radius (a) and related zoom (b).
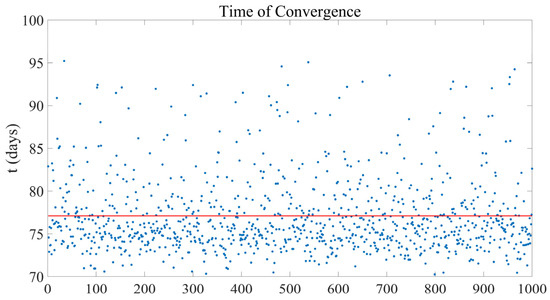
Figure 20.
Monte Carlo analysis 2: time of convergence.
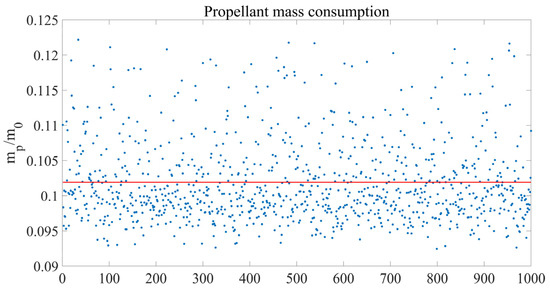
Figure 21.
Monte Carlo analysis 2: propellant mass consumption.

Table 5.
Monte Carlo analysis 2: time of convergence and final mass ratio.
5. Concluding Remarks
This research identifies a specific repeating-ground-track, quasi-synchronous orbit as a viable option for Martian constellations tailored to the continuous coverage of high-latitude regions. The orbit at hand is flown nine times in 5 nodal days. Coverage analysis reveals that two satellites are sufficient to ensure continuous global coverage at high latitudes. The maximum revisit time increases as the latitude decreases and can eventually be reduced by including additional satellites. Low-thrust propulsion, in conjunction with nonlinear orbit control, is proposed as a convenient option to perform the orbit transfer from the initial 4-sol orbit. In this framework, orbit dynamics about Mars are modeled with the inclusion of the most relevant perturbations, i.e., several harmonics of the areopotential, together with the gravitational pull due to the Sun as a third body. A saturated feedback law for the low-thrust magnitude and direction—with an upper bound on magnitude—is introduced and is proven to enjoy global stability properties. In particular, some sufficient conditions for the asymptotic convergence toward the operational conditions are presented. These conditions include the perturbing acceleration term and lead to identifying three types of transfer arcs: (a) maximum-thrust arcs, (b) time-varying, intermediate-thrust arcs, and (c) coast arcs. Specifically, this research extends the range of application of nonlinear orbit control to elliptic orbits with some prescribed, time-varying orbit elements. Monte Carlo simulations are run, assuming either nominal or nonnominal flight conditions, i.e., stochastic failures of the propulsion system, imperfect estimation of the orbit perturbations, or dispersed initial conditions, representative of possible injection errors at the planetary capture. The numerical results demonstrate that the low-thrust transfer strategy based on nonlinear orbit control is effective and needs a limited amount of propellant. Moreover, the feedback control law at hand does not require any offline reference trajectory; therefore, it is effective as an autonomous real-time guidance strategy, even in the presence of nonnominal flight conditions. A possible, though challenging, extension of nonlinear orbit control can be represented by the inclusion of the final position (along the operational orbit) in the target set. This would represent a valuable addition, very useful in challenging mission scenarios, such as orbit rendezvous.
Author Contributions
Conceptualization, M.P. (Mauro Pontani); methodology, R.S., M.P. (Mauro Pontani) and M.P. (Marco Pustorino); software, R.S. and M.P. (Marco Pustorino); validation, M.P. (Mauro Pontani); formal analysis, R.S., M.P. (Marco Pustorino) and M.P. (Mauro Pontani); investigation, R.S., M.P. (Marco Pustorino) and M.P. (Mauro Pontani); data curation, R.S. and M.P. (Marco Pustorino); writing—original draft preparation, R.S. and M.P. (Marco Pustorino); writing—review and editing, R.S. and M.P. (Marco Pustorino); visualization, R.S. and M.P. (Marco Pustorino); supervision, M.P. (Mauro Pontani). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data needed to reproduce the results are contained in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| reference surface | |
| solar radiation pressure coefficient | |
| nodal day | |
| coefficients of gravitational harmonics | |
| mean anomaly | |
| solar radiation pressure | |
| Martian equatorial radius | |
| thrust | |
| maximum available thrust | |
| nodal orbital period | |
| Martian gravitational potential | |
| Lyapunov function | |
| non-Keplerian acceleration vector | |
| desired semimajor axis | |
| perturbation acceleration | |
| thrust acceleration | |
| osculating eccentricity | |
| desired eccentricity | |
| true anomaly | |
| osculating inclination | |
| desired inclination | |
| modified equinoctial elements (MEE) | |
| instantaneous mass of the vehicle | |
| initial spacecraft mass | |
| mass time rate | |
| osculating semilatus rectum | |
| desired semilatus rectum | |
| position vector | |
| radius | |
| apoapse radius | |
| periapse radius | |
| actual time | |
| time of flight | |
| osculating RAAN | |
| desired RAAN | |
| heading angle | |
| Martian gravitational parameter | |
| shadow function | |
| absolute longitude | |
| latitude | |
| vector of final conditions | |
| osculating argument of periapse | |
| desired argument of perigee | |
| Martian angular rate |
Appendix A. Planetary Parameters of Mars
In this study, the following fundamental planetary parameters are used:
where the symbol denotes the characteristic geographical longitude associated with harmonic .
References
- Ely, T.A.; Anderson, R.; Bar-Sever, Y.E.; Bell, D.; Guinn, J.; Jah, M.; Kallemeyn, P.; Levene, E.; Romans, L.; Wu, S.-C. Mars Network Constellation Design Drivers and Strategies. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Girdwood, AK, USA, 16–19 August 1999; pp. 99–301. [Google Scholar]
- Nann, I.; Izzo, D.; Walker, R. A Reconfigurable Mars Constellation for Radio Occultation Measurements and Navigation. In Proceedings of the 4th International Workshop on Satellite Constellation and Formation Flying, Sao José dos Campos, Brazil, 14—16 January 2005. [Google Scholar]
- Bell, D.J.; Cesarone, R.; Ely, T.; Edwards, C.; Townes, S. Mars Network: A Mars Orbiting Communications & Navigation Satellite Constellation. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 18—25 March 2000. [Google Scholar]
- Kelly, P.W.; Bevilacqua, R. Constellation Design for Mars Navigation using Small Satellites. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1538. [Google Scholar]
- Pontani, M.; Pustorino, M.; Teofilatto, P. Mars Constellation Design and Low-Thrust Deployment Using Nonlinear Orbit Control. J. Astronaut. Sci. 2022, 69, 1691–1725. [Google Scholar] [CrossRef]
- Ulybyshev, Y.P.; Donianz, V.N. Elliptic Orbit Constellations for Regional Communication and Molniya–Zond Satellite Constellation. In Proceedings of the 53rd International Astronautical Congress, Houston, TX, USA, 10–19 October 2002. [Google Scholar]
- Ulybyshev, Y.P. Design of satellite constellations with continuous coverage on elliptic orbits of Molniya type. Cosm. Res. 2009, 47, 310–321. [Google Scholar] [CrossRef]
- Palmerini, G.B.; Graziani, F. Polar Elliptic Orbit for Global Coverage Constellations. In Proceedings of the AAS/AIAA Astrodynamics Conference, Scottsdale, AZ, USA, 1–3 August 1994; pp. 94–3720. [Google Scholar]
- Draim, J.E. Three- and Four-Satellite Continuous-Coverage Constellations. J. Guid. Control Dyn. 1985, 8, 725–730. [Google Scholar] [CrossRef]
- Draim, J.E. Design philosophy for the Ellipso satellite system. In Proceedings of the 17th AIAA International Communications Satellite Systems Conference and Exhibit, Yokohama, Japan, 23–27 February 1998. [Google Scholar]
- Pontani, M. Constellations of Repeating Satellites for Local Telecommunication and Monitoring Services. In Applied and Industrial Mathematics in Italy II; Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 2007; pp. 513–524. [Google Scholar]
- Cano, J.L.; Caramagno, A.; Catullo, V.; Cassi, C. ExoMars Mission Analysis and Design–Launch, Cruise and Arrival Phases. Adv. Astronaut. Sci. 2007, 127, 7–173. [Google Scholar]
- Pontani, M.; Pustorino, M. Nonlinear Earth orbit control using low-thrust propulsion. Acta Astronaut. 2021, 179, 296–310. [Google Scholar] [CrossRef]
- Pontani, M.; Teofilatto, P. Deployment strategies of a satellite constellation for polar ice monitoring. Acta Astronaut. 2022, 193, 346–356. [Google Scholar] [CrossRef]
- Gurfil, P. Nonlinear feedback control of low-thrust orbital transfer in a central gravitational field. Acta Astronaut. 2008, 60, 631–648. [Google Scholar] [CrossRef]
- Prussing, J.E.; Conway, B.A. Orbital Mechanics; Oxford University Press: Oxford, UK, 2013; pp. 46–54, 238–243. [Google Scholar]
- Schaub, H.; Junkins, J.L. Analytical Mechanics of Space Systems; AIAA Education Series; AIAA: Reston, VA, USA, 2009; pp. 574–597. [Google Scholar]
- Broucke, R.A.; Cefola, P.J. On the equinoctial orbit elements. Celest. Mech. 1972, 5, 303–310. [Google Scholar] [CrossRef]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics; AIAA Education Series; AIAA: Reston, VA, USA, 1987; pp. 484–503. [Google Scholar]
- Curtis, H.D. Orbital Mechanics for Engineering Students; Elsevier: Amsterdam, The Netherlands, 1987; pp. 479–541. [Google Scholar]
- Jurdjevic, V.; Quinn, J.P. Controllability and Stability. J. Differ. Equ. 1978, 28, 381–389. [Google Scholar] [CrossRef]
- MATLAB Symbolic Toolbox. Available online: https://it.mathworks.com/help/symbolic/ (accessed on 21 February 2023).
- Santoro, R.; Pontani, M. Orbit acquisition, rendezvous, and docking with a noncooperative capsule in a Mars sample return mission. Acta Astronaut. 2023; in press. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).