Abstract
Direct numerical simulations of non-premixed fuel-rich methane–oxygen flames at 20 bar are conducted to investigate the turbulent mixing burning of gaseous propellants in rocket engines. The reacting flow is simulated by using an EBI-DNS solver within an OpenFOAM frame. The transport of species is resolved with finite-rate chemistry by using a complex skeletal mechanism that entails 21 species. Two different flames at low and high Reynolds numbers are considered to study the sensitivity of the flame dynamics to turbulence. Regime markers are used to measure the probability of the flow to burn in premixed and non-premixed conditions at different regions. The local heat release statistics are studied in order to understand the drivers in the development of the turbulent diffusion flame. Despite the eminent non-premixed configuration, a significant amount of combustion takes place in premixed conditions. Premixed combustion is viable in both lean and fuel-rich regions, relatively far from the stoichiometric line. It has been found that a growing turbulent kinetic energy is detrimental to combustion in fuel-rich premixed conditions. This is motivated by the disruption of the local premixed flame front, which promotes fuel transport into the diffusion flame. In addition, at downstream positions, higher turbulence enables the advection of methane into the lean core of the flame, enhancing the burning rates in these regions. Therefore, the primary effect of turbulence is to increase the fraction of propellants burnt in oxygen-rich and near-stoichiometric conditions. Consequently, the mixture fraction of the products shifts towards lean conditions, influencing combustion completion at downstream positions.
1. Introduction
Methane is a promising propellant for the new generation of space propulsion systems [1,2]. Compared to kerosene, this fuel has superior cooling capabilities and a specific impulse [3]. In addition, it produces a negligible amount of soot [4] and displays low toxicity [2]. These characteristics confer a competitive edge to methane over the established propellants in the space industry, such as hydrazine or the previously mentioned kerosene [2,5]. Consequently, substantial research activities have been fostered over the last decade to investigate the usage of green propellants [6,7,8], particularly methane for space propulsion applications. Nevertheless, critical aspects related to turbulent ignition, mixing, and combustion challenge the development of new thrust chambers propelled by methane [9,10]. Computational fluid dynamics (CFD) software provides essential support in this process. The conventional methods applied therein, such as Reynolds-averaged Navier–Stokes (RANS) solvers, require turbulent combustion models to predict unclosed turbulent terms. This question has challenged the combustion community during the last century. Reacting flows escalate the inherent complexity of turbulence with the introduction of additional mechanisms of vorticity generation and dissipation [11,12]. Turbulence and combustion can promote or inhibit each other, depending on the overlap between their characteristic time and length scales [13,14,15]. Combustion in rocket engines is a particularly challenging case. Due to the high pressures and the absence of nitrogen, the flow’s reactivity is strongly accentuated, dwindling the chemical length and timescales [16]. As a consequence, the Damköhler number is very high, enabling the occurrence of exotic phenomena such as flame-generated turbulence [17,18] and intermittency between combustion in lean and fuel-rich conditions [19]. Knowledge of these phenomena is essential in the formulation of effective turbulent combustion models. Therefore, it is necessary to investigate the conditions in which the combustion of injected propellants develops in a rocket combustor. The present text addresses this question by using direct numerical simulations, representing turbulent mixing and combustion near the injection region of a methane–oxygen engine at high pressure. The resulting databases are post-processed to investigate the occurrence of combustion in different mixing configurations within this environment.
The rest of the paper is organized as follows: The next section provides a theoretical background, which provides necessary concepts concerning turbulence and non-premixed combustion. The third section describes the numerical simulation strategy. The numerical results are analyzed in the fourth section. Finally, the fifth section summarizes the concluding remarks of this research.
2. Theoretical Background
The present section introduces the basic notions that are required to discuss the results of the conducted numerical simulations. The text is structured in three parts. First, the basic concepts of turbulence for variable-density flows are presented. Second, the basic parameters for characterizing turbulent diffusion flames are presented. Third, the classification techniques of local combustion regimes are described, along with their phenomenological interpretation.
2.1. Turbulence
Turbulent flows are characterized by an unstable nature, which precludes reaching steady-state conditions. Due to their chaotic features [20,21], a statistical approach is deemed convenient. For a turbulent quantity , the most immediate indicator is its Reynolds number, i.e., time average, which is defined as follows:
In variable-density flows, such as turbulent flames, it is convenient to introduce density weighting to account for the specific volume variations. The Favre average [22] arises from the following consideration:
The averaged values can be taken as a reference to address the instantaneous values as fluctuations. Therefore, the Reynolds fluctuations are defined as and the Favre fluctuations as . Higher-order statistics are used to quantify the statistics of these fluctuations. The most relevant indicator is the turbulent kinetic energy, which is essentially the variance of the velocity fluctuations, as follows:
The turbulent kinetic energy is a fundamental manifestation of turbulence, as it indicates the magnitude of the flow unsteadiness and its influence on the momentum conservation equations. Therefore, it denotes the degree of forced convection, which is essential in turbulent combustion and mixing processes. Indeed, turbulent combustion models, such as the eddy dissipation concept (EDC) [23,24] and the flamelet model [25], contain implicit or explicit dependencies on the turbulent kinetic energy [26].
In turbulent premixed flames, turbulent kinetic energy enhances the burning rate, although the flame speed sensitivity to decreases with growing turbulence following the so-called bending effect [27]. This is caused by a change in the overlap between chemical and turbulent scales [28,29,30]. If the vortexes are significantly larger than the flame front, their effect on flame development is mainly an increase in the effective surface, due to wrinkling. If the turbulent structures are smaller, the enhancing effects of turbulence primarily occur in terms of diffusion increase. In both cases, it is expected that greater turbulence yields higher flame speeds. Nonetheless, previous research [31] has suggested the possibility of quenching in premixed flames with high turbulent intensity; however, there is no scientific consensus concerning this claim [32]. In diffusion flames, if the chemistry is very fast compared to the turbulence, an enhancement of the burning rate with respect to chemistry takes place [33]. This is primarily motivated by the fact that the mixing intensity grows with turbulent kinetic energy. However, if turbulence becomes significantly faster than the mixing process, it can disrupt the local diffusion flame structure producing local quenching [15].
2.2. Turbulent Diffusion Flames
In a diffusion flame, the oxidizer and the fuel are simultaneously mixing and reacting. The development of these processes is measured with the mixture fraction and the progress variable, which are briefly described in this sub-section.
The mixture fraction is used to assess the local mixing conditions, regardless of the combustion progress. For a chemical mixture consisting of species, this parameter is determined as follows:
where and stand for the mass fraction and the mixture fraction of the chemical species, respectively. The mixture fraction of a molecule is its hydrocarbon content mass fraction. For a generic chemical species with the formulation this parameter is determined as follows:
where , , and stand for the atomic mass weights of carbon, hydrogen, and oxygen, respectivley. As can be seen, the mixture fraction is zero when only the oxidizer is present, and it tends to unify when the mixture consists only of the fuel. Near the injection site, the mixture fraction profile presents sharp gradients, indicating the mixing of clusters with and . At downstream positions, the field is smoothed, tending to the global mixture fraction .
Besides the mixing of propellants, it is also necessary to evaluate the local development of chemical reactions. The progress variable is used for this purpose. For non-premixed combustion, the progress variable can be determined as follows, as suggested by Bray et al. [34]:
where is the reaction progress variable and is the equilibrium composition for the present mixture fraction. The reaction progress variable is a scalar that indicates the development of the combustion process. For methane combustion, the definitions devised by Pierce and Moin [35] are often used. However, in space propulsion applications, due to the absence of inert gases, high temperatures take place, with a significant proliferation of free radicals and hydroxyl molecules. For this reason, the mixture fraction definition used is the same in recent works [17,36], as follows:
where denotes the molecular weight of the chemical species. If the chemical reactions are very fast compared to the turbulent processes, then the progress variable and the mixture fraction are algebraically related [37]. Therefore, the progress variable dynamics are driven by the mixing intensity. This physical phenomenon is evaluated with the scalar dissipation of the mixture fraction, which is defined as follows:
where is the mass diffusivity of the reacting mixture. The scalar dissipation rate is analogous to the dissipation rate of the turbulent kinetic energy. Indeed, closure models [25,38,39] relate them as follows:
where denotes the length scale of the large eddies. In stable non-premixed flamelets with fast chemistry, the heat release rate scales with the scalar dissipation rate at stoichiometric conditions [33] are . Following (9), it is clear that the local mixing intensity and the burning rate are primarily driven by the turbulent kinetic energy.
In anchored flames with a stable recirculation zone, a standing flame can be maintained, regardless of the injection velocity, since continuous mixing is enabled near the injection posts. Therefore, as the velocity increases, the heat release rate grows as well, due to the greater rate of incoming fresh reactants. This fact can hinder the comparison between flames burning with different injection velocities. Such is the case for the numerical simulations performed in the present work. For this reason, the heat release rate should be normalized with the mean flow rate at the inlet to account for this fact. One possible normalization is as follows:
where is the specific energy content of methane () and is the volumetric flow rate at injection. This value has dimensions of 1/length, indicating the longitude required for the mixture to obtain all of the available energy. Therefore, one suitable reference value to normalize it is the laminar flame thickness at stoichiometric conditions, as follows:
The most important point of this normalization is the correction with respect to the incoming velocity, which allows the comparison of flows with different injection mass flow rates. More sophisticated normalizations might be possible, but the one presented in this paper suffices within the present work’s scope.
2.3. Flame Classification
For stability and performance purposes, liquid rocket engines typically operate in non-premixed conditions with fuel excess. Despite this global configuration, at local and instantaneous levels, combustion can take place in premixed and lean conditions as well. The occurrence of these processes is dependent on the turbulent mixing of the propellants. Direct numerical simulations allow the detailed observation of these local phenomena. The present sub-section discusses the objective criteria to quantify and classify the local burning regime based on the instantaneous physical fields. The presented methods will be applied to the output of the performed numerical simulations to investigate the occurrence of the different burning conditions.
2.3.1. Fuel-Rich vs. Lean
The classical procedure to calculate the stoichiometric ratio of a hydrocarbon is based on the assumption that the reactants are oxidized into a mixture that is entirely composed of water and carbon dioxide. For the case of methane, this corresponds to the following global reaction scheme:
which yields a stoichiometric mass O/F ratio of approximately 4, corresponding to . In atmospheric combustion applications that operate in lean conditions, this approximation is quite accurate, since the carbon monoxide content is very low compared to that of carbon dioxide. However, for combustion in space propulsion applications, fuel-rich mixtures are desired in order to maximize the specific impulse. In addition, the high temperatures significantly promote carbon monoxide generation. As a consequence, the equilibrium mass fraction of carbon monoxide significantly outweighs that of carbon dioxide. In an extreme case, the corresponding adjusted global reaction can be written as follows:
which implies a stoichiometric O/F of roughly 3, corresponding to . Besides the significant portion of carbon monoxide, additional particularities of combustion in the frame of space propulsion further entangle the equilibrium composition. Due to the high pressures and the absence of nitrogen, very high temperatures are reached in the flame (). Consequently, significant mass fractions of free radicals and hydroxyl are present at equilibrium. All of these substantial deviations from the assumption in (13) demand the redefinition of the stoichiometric condition. A reasonable criterion is to choose the O/F that maximizes the volumetric heat release. The integrated heat release rate is calculated as a function of the mixture fraction using Cantera [40] and a complex chemical mechanism [41]. The result is displayed in Figure 1. As can be seen, the mixture fraction that maximizes heat release takes place at values higher than the classical assumption of . More specifically, the maximum value is found at . This is in good agreement with the previous reasoning, since . Therefore, it can be expected that the redefined stoichiometric value is closer to the one in the assumption in Figure 1. Besides the graph in Figure 1, additional evidence for the better suitability of an as a stoichiometric value is provided in the discussion of the results.
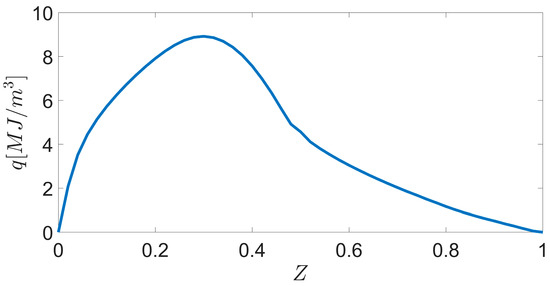
Figure 1.
Integral volumetric heat release as a function of the mixture fraction for methane–oxygen combustion at 20 bar.
The shift in the maximum heat release is relevant, since most models for non-premixed combustion require knowledge of the properties at stoichiometric conditions. Within the present work, it is assumed that the stoichiometric mixture fraction in high-pressure methane–oxygen combustion corresponds to . It is important to note that this specific definition is assumed to address the decoupling between the local maximum heat release and the standard stoichiometric oxidizer-to-fuel ratio. From a global standpoint, the classical definition should be considered.
2.3.2. Flame Index
In burning devices that operate in non-premixed conditions, the reacting flow simultaneously displays both premixed and non-premixed configurations at a local level. These variations are driven by the local mixing conditions, which can enable premixed combustion despite the predominant diffusive nature of the flame. Regime markers can be used to identify the local burning regime. The most commonly used marker is the flame index as defined by Yamashita et al. [42], as follows:
The original formulation has been re-normalized so that zero corresponds to non-premixed conditions and unity corresponds to premixed conditions. The relationship between this numerical value and the local combustion regime can be easily deduced by the physical meaning of the mathematical expression. If the gradients of the fuel and the oxidizer are aligned, then the local mixing conditions can be deemed premixed. Contrarily, the opposed gradients of the reactants correspond to a counterflow non-premixed configuration. There are several available definitions of a flame index that have been proposed in recent works [43,44,45,46,47,48]. These markers have been extensively reviewed in a recent study [49], where it was found that most definitions yield similar classifications overall. In the frame of the present work, the definition of Yamashita et al. was the one considered, due to its simplicity and extended usage.
An example of the different classifiers presented in this section can be visualized in Figure 2. In this figure, the instantaneous detail of the shear layer for one of the simulated flames is displayed. This graph shows the flame index, mixture fraction, and temperature in order to illustrate the different regimes in which combustion can take place in space propulsion applications. As can be seen, the central region of the shear layer presents the classical counterflow structure of a diffusion flame. Heat release is concentrated in the nearby stoichiometric conditions, where the local O/F maximizes the reacting capabilities of the flow. However, in certain positions far away from the stoichiometric line, the gradients of methane and oxygen are aligned, denoting local premixed combustion. This circumstance is very specific to space propulsion applications. Due to the absence of nitrogen, the flammability limits are significantly widened, enabling combustion in extremely fuel-rich and/or oxygen-rich conditions. Direct numerical simulations enable accessibility to every relevant physical field. Therefore, they offer the possibility to study the occurrence of these events and how they influence the combustion development process.
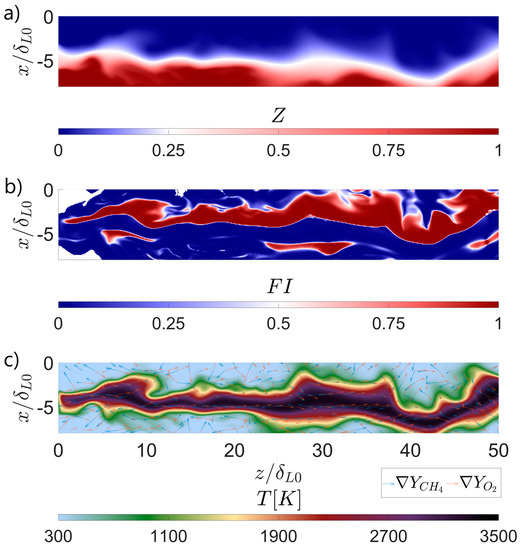
Figure 2.
Example of instantaneous flame classification parameters in a reacting shear layer: mixture fraction (a), flame index (b), and temperature, unity fuel, and oxidizer gradients (c). Only the x and z components of the normalized gradients are displayed.
3. Numerical Simulation Case Setup
The numerical simulations aim to represent the turbulent combustion process that occurs in modern rocket engines in locations near to injection and far away from walls. The turbulent reacting flow is resolved with the compressible solver EBI-DNS [50,51,52,53], which is embedded in the open-source software OpenFOAM [54,55]. This code uses an implicit scheme to resolve the transient conservation equations for mass, momentum, energy, and species with the finite volume method (FVM) [56,57]. EBI-DNS has been applied and validated in several combustion-related problems in recent years [58,59,60,61,62]. A recent study by Zirwes et al. [63] comprehensively assessed the numerical accuracy of this solver for a wide variety of setups, with different reactive and compressibility features. This research shows that EBI-DNS is capable of providing results that are comparable with high-fidelity explicit solvers under a wide range of scenarios. Direct validation of DNS for space propulsion applications is unfeasible, due to the prohibitive computational cost that would be required for a complete system simulation. This difficulty can be addressed by applying convenient normalizations over the results of a reduced engine instance. Following such an approach, a good agreement between experimental and simulated combustion completion points was reported in a previous research paper [64].
The Cantera [40] routines are used for the computation of detailed chemistry and transport properties, using the mixture-averaged transport model described by Kee et al. [65]. The reaction mechanism developed by Slavinskaya et al. [41] is used to determine the chemical source terms of methane combustion using the finite-rate method. This skeletal mechanism consists of 21 species and 97 reactions, and it was devised for combustion in high-pressure space propulsion applications. This mechanism has been applied in several numerical studies of combustion for scale rocket combustors [66,67]. Despite the relatively high complexity of the used reaction scheme, the formation of large aromatic compounds and soot has not been considered. Such a simplification is appropriate for methane combustion, where soot formation is negligible. Nonetheless, it is important to keep in mind the possibility of soot-related phenomena being ignored in the fuel-rich side of the flame. The relevant data concerning combustion are provided in Table 1.

Table 1.
Main turbulence and combustion parameters of the simulated flame.
The inlet boundary conditions at the injection site in the main simulation are patched using the results of a precursor simulation. In this prior simulation, periodic synthetic turbulence is generated at the inlet via the procedure described in [68]. This scheme is derived from the original formulation proposed by Kraichnan and the subsequent improvements suggested by Shur et al. [69] and Morsbach et al. [70]. These methods are based on discretizing a reference turbulent kinetic energy spectrum in harmonics with random amplitude and phases. These waves are thereafter superposed to provide a synthetic velocity field that complies with the prescribed 2nd order turbulent statistics. The statistics were selected to resemble the output of RANS simulations for a scale methane rocket combustor discussed in a previous work [71]. The described simulation strategy is summarized in Figure 3.
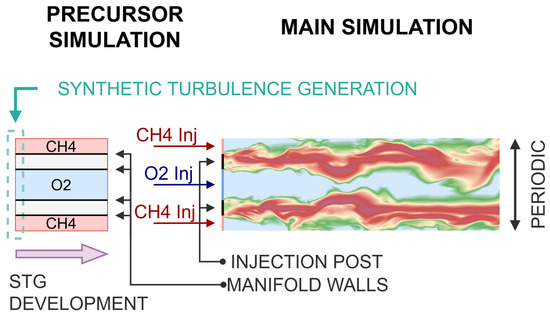
Figure 3.
Scheme of the conducted simulation strategy.
Due to the high computational cost associated with DNS, the hydraulic diameter of the injector is one order of magnitude smaller than the actual setup. As a consequence, the global Reynolds number and the turbulent Reynolds number are smaller than the reference device. Despite this shift, most of the relevant turbulent and chemical features are preserved. Therefore, the simulations can be assumed to capture the relevant aspects of turbulent mixing and combustion. Relevant turbulent flow parameters at the injector plane are provided in Table 2.

Table 2.
Main turbulence and combustion parameters of the simulated flame.
The main simulation comprises a volume of 0.3 × 0.2 × 3 mm, resolved with 144 × 216 × 2160 cubic cells with identical geometry. Periodicity is imposed in the directions perpendicular to the injection. The grid size is small enough to resolve the smallest Kolmogorov eddies in both of the simulations, following the standard requirements [72]. The flame front is resolved with varying resolutions, since the flame front thickness varies. The chosen grid size ensures a resolution of the instantaneous flame front realizations in the order of 10 cells. This is generally enough, although a higher resolution would be desirable. The convergence of the turbulent statistics for the used setup has been addressed in a prior work [36]. The effect of increasing the resolution is marginal. More specifically, a grid size 2.5 times larger yields maximum errors in the order of 5% and axially averaged properties below 1%. A finer grid (halving the cell volume) leads to discrepancies in the axially averaged properties in the order of 0.5%. Therefore, it can be concluded that the resolution of the used mesh is high enough to allow the usage of the simulation results for turbulence research purposes. The timestep size is chosen in an adaptive fashion to ensure that the maximum acoustic CFL number is below 0.9. This corresponds to maximum convective CFL numbers in the order of 0.05 for and 0.25 for . Moreover, due to the implicit nature of the used solver, the fulfillment of the general condition is not required to achieve numerical stability. Such low CFL numbers, coupled with the cubic spatial differentiation scheme, ensure the minimization of numerical dissipation, as discussed elsewhere [62].
4. Results Analysis
This section is devoted to the discussion and analysis of the results obtained in the performed numerical simulations. The discussion is structured in three parts. The first and second sub-sections i.e., Section 4.1 and Section 4.2, discuss the overall results of simulations and respectively. The flame development is discussed from a phenomenological standpoint to identify the main events and the driving physical mechanisms. In the third sub-section (i.e., Section 4.3), the different interactions between turbulent mixing and combustion are discussed in order to investigate the sensitivity of the burning process, with respect to the turbulent kinetic energy.
4.1. Simulation
The Simulation is characterized by low inlet turbulence, with a flow behavior close to laminarity. An example of instantaneous flame development can be observed in Figure 4. In this illustration, the flame classification is displayed at the top, and both a positive and a negative heat release rate can be visualized at the center and bottom, respectively.
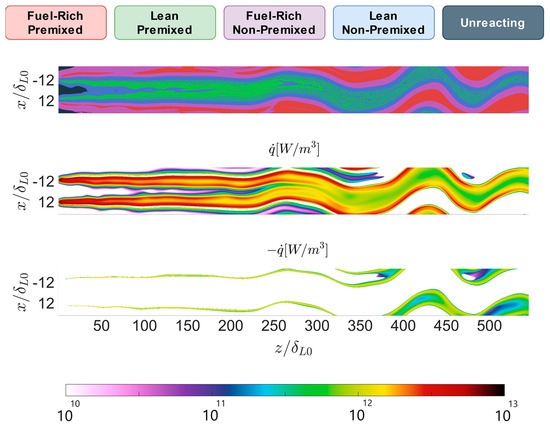
Figure 4.
Example of instantaneous flame classification and heat release rate for simulation .
The flow structure near injection resembles a triple flame, with a non-premixed branch surrounded by lean and fuel-rich premixed branches. Negative heat release can be observed in the transition from fuel-rich premixed to fuel-rich non-premixed conditions. This process is on account of the cracking reactions, which can lead to endothermic results due to the formation of larger hydrocarbons (especially ethylene). The fuel-rich premixed branch displays a discontinuous axial development, with local breakups. This is caused by the forced advection of methane into the flame core. Due to its higher diffusivity, methane benefits more than oxygen from the moderate turbulence. This different sensitivity to turbulence shifts the local O/F in the thick premixed regions outside of the flammability limits. Contrarily, the lean premixed branch displays a more stable configuration. As expected, most of the heat release is obtained from the non-premixed flamelets. Nevertheless, a significant amount of combustion occurs in the lean premixed side, while both of the shear layers are still present. This trend is interrupted by , when both of the shear layers merge into a single structure. From this point, the combustion at the lean core significantly decreases, and the majority of chemical reactions develop on the non-premixed side.
Figure 5 was elaborated to statistically summarize the observed processes. The right manifold can be used to investigate the probability of occurrence of the different classifications. Most of the observations take place in non-premixed conditions, ranging from moderately lean to significantly fuel rich. This is in good agreement with the example in Figure 4, where it can be observed that the non-premixed flamelet is predominant. There is a significant portion of data in the premixed conditions with extremely lean and fuel-rich mixtures. However, only the lean premixed regions deliver heat release rates in the same order of magnitude as the non-premixed flamelets. Intermediate flame indexes are rather unusual. This is due to the quasi-bimodal distribution of the flame index, which can be observed in the examples in Figure 2 and by other researchers [49]. These graphs provide valuable insights concerning the overall combustion process. However, it is important to remark on their strong dependency on geometry. For example, if the simulation domain were significantly longer, the statistics would shift toward equilibrium conditions. This would imply a greater concentration of points towards , with a lower averaged heat release rate.
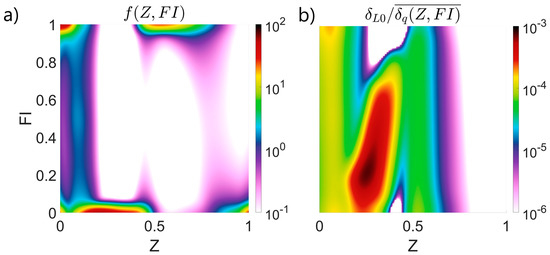
Figure 5.
Statistical distribution of the normalized heat release rate, with respect to the local combustion regime for Simulation : Joint probability density as a function of the flame index and the mixture fraction (a) and the average heat release rate as a function of the flame index and the mixture fraction (b).
4.2. Simulation
An analogous analysis was conducted with the database of Simulation . Unlike , this simulation presents a Reynolds number high enough to display fully turbulent features. An example of an instantaneous flame classification and heat release rate is shown in Figure 6.
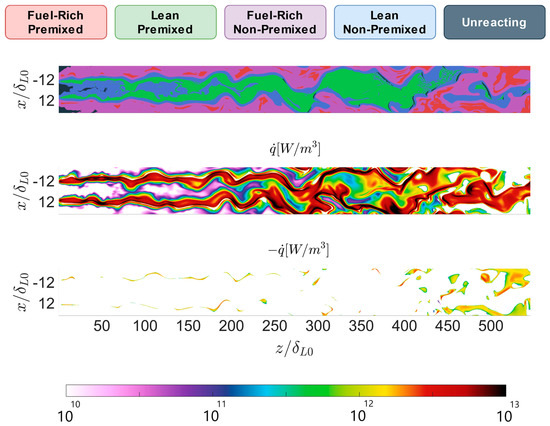
Figure 6.
Example of instantaneous flame classification and heat release rate for simulation .
As can be seen, there is a greater disruption in the fuel-rich premixed region, as this combustion regime only occurs in isolated regions. This is caused by the greater turbulent kinetic energy, which, furthermore, promotes the transport of methane into the flame core. Another remarkable fact is that the negative heat release caused by cracking reactions near to the injection site takes place intermittently. These variations are caused by the flame stretching, which can locally promote or inhibit the heat transfer from the warm products to the cold methane. If heat transfer is promoted, the initial transitory ethylene formation is dampened, due to the local enhancement of the burning rate. The opposite occurs if the flame stretching defocuses the local heat fluxes from the products to the reactants. This effect is discussed in greater detail in the following sub-section. Negative heat release can be observed at downstream positions as well; however, this result is mainly motivated by recombination reactions of the combustion products.
Overall, the absolute heat release rate is substantially larger in compared to . This is mainly a consequence of the greater mass flow rate of the propellants, which enhances the incoming rate of fresh reactants and the turbulent kinetic energy , which is proportional to the scalar dissipation rate . Nevertheless, the flow in simulation is able to keep up a significant burning rate in the flame core, with lean premixed conditions following the merging of the shear layers. To complete this section, the 2D joint functions are displayed in Figure 7. Few differences can be observed in the 2D joint probability density function. The most remarkable one is the greater prevalence of lean premixed configurations. This is caused by the greater presence of this regime at downstream positions, as can be seen by comparing Figure 4 and Figure 6. Concerning the normalized heat release, it can be seen that it is higher overall, regardless of the considered configuration. However, the enhancements are more remarkable in the lean regions. The differences in the heat release trends are discussed in greater detail in the following sub-section.
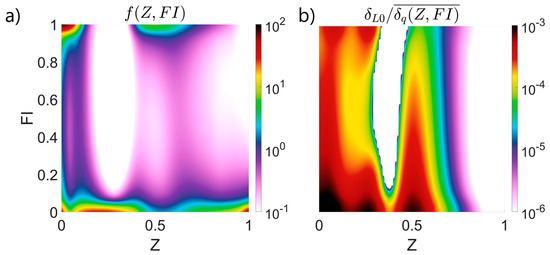
Figure 7.
Statistical distribution of the heat release rate, with respect to the local combustion regime for simulation : Joint probability density as a function of the flame index and the mixture fraction (a) and the average heat release rate as a function of the flame index and the mixture fraction (b).
4.3. Comparison
Despite the remarkably different flow characteristics, for both of the flames, the chemistry remains very fast compared to the turbulence. To prove this claim, the progress variable, as a function of the mixture fraction, is represented in Figure 8. As can be seen, both of the flames follow the trend expected for fast chemistry [33,37]. Flame displays a slight deviation, due to its higher turbulent kinetic energy, but the differences are negligible overall. The maximum value of the progress variable is obtained at , which further supports the discussed necessity to consider a shift in the stoichiometric value. The maximum variance of the progress variable conditional to is in the order of , corresponding to , while, for the rest of the domain, holds. Therefore, it can be assumed that combustion is limited by mixing, since, for a given mixture fraction, the corresponding progress variable is reached almost immediately. The turbulent timescales near injection can be used to examine the validity of the flamelet assumption as well. The mean turbulent timescale in this region is in the order of and for simulations and , respectively. Since the chemical timescale is in the order of 2 , it is evident that chemistry is significantly faster in both cases. These points are crucial for the interpretation of the results discussed in this section. Since the local heat release rate , which scales with , is essentially dependent on the mixture fraction dynamics. Therefore, the influence that turbulence exerts on the flame development occurs in terms of heat and mass transfer enhancements caused by forced convection.
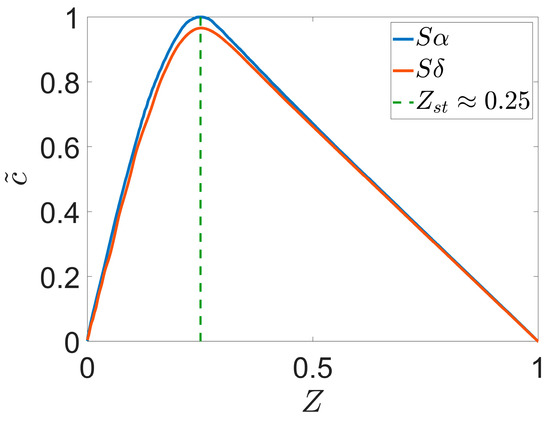
Figure 8.
Progress variable as a function of the instantaneous mixture fraction.
To further study the influence of turbulence in the mixing process, the probability distributions in Figure 5 and Figure 7 are compared. To assess the sensitivity of these joint distributions, with respect to inlet turbulence, the relative increase is displayed in Figure 9. This graph provides a rough indication of the effects that a turbulence enhancement has with respect to mixing. As can be seen, there is a greater amount of data toward the horizontal center. This is due to improved mixing, which promotes the concentration of data, with respect to the global mixture fraction, i.e., . However, the probability of presenting extreme conditions, i.e., ), is enhanced as well. The motivation for this difference is the smaller residence time of the molecules in simulation . Since turbulence and mean velocity increase simultaneously, the enhanced mixing is accompanied by a shorter stay time, which increases the possibility of an unmixed cluster reaching the outlet. These effects illustrate that, although these comparative analyses provide valuable information, they should be approached carefully and critically.
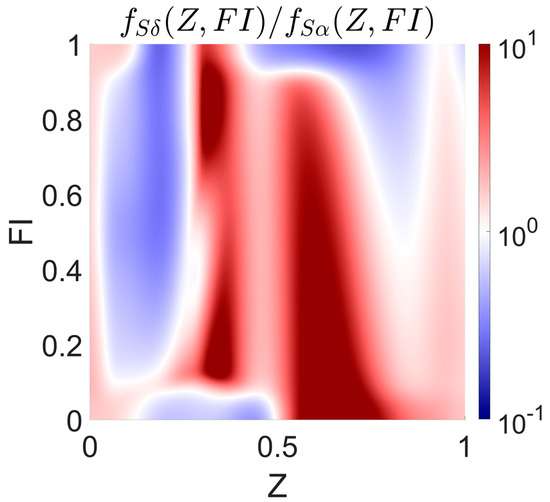
Figure 9.
Relative probability density increase in Simulation , with respect Simulation as a function of the mixture fraction and the flame index .
To study the variations in heat release, this value was averaged conditionally to the mixture fraction for both of the simulations. The result is displayed in Figure 10. As can be seen, provides a higher heat release overall, with the only exception being the extremely lean regions.
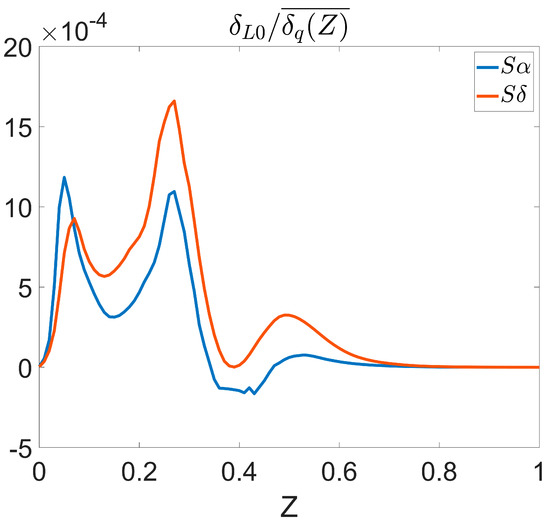
Figure 10.
Average normalized heat release rate conditional to the mixture fraction or the simulated flames.
Thanks to the fact that and are algebraically related, most of the dependencies with the geometry and residence time are eliminated. Therefore, the differences in Figure 10 are linked to the mixing enhancement driven by turbulence. These effects are strongly dependent on which part of the flame is considered. To simplify the phenomenological description, the different trends are commented on in two different positions: near injection and downstream (where both of the shear layers have merged). The physical driving mechanisms in both of these cases are commented on in the text below.
4.3.1. Near Injection Mixing
To approach the turbulent mixing dynamics near injection, details of the simulated flame are presented in Figure 11. In this figure, the instantaneous stoichiometric line is presented along with the line marking the instantaneous border between the premixed and non-premixed classifications. Therefore, the region between these two isolines corresponds to the lean side of the local diffusion flame. Overall, flame exhibits a greater amount of normalized heat release. presents similar values in the stoichiometric line, but it only keeps up in the stretched regions due to the enhanced convection. Moreover, in these positions, the negative heat release caused by cracking reactions can be suppressed thanks to the high local curvature, which fosters the heat transfer from the stoichiometric line to the fuel-rich zone. Indeed, it can be seen that the regions with non-negative heat release only appear where there is significant stretching.
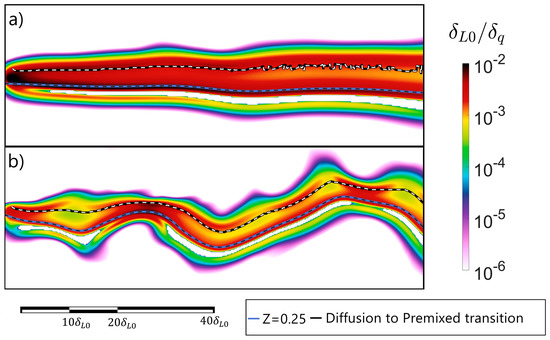
Figure 11.
Detail of heat release near injection: Simulation (a) and simulation (b).
4.3.2. Downstream Mixing
The flame development dynamics are dramatically altered once the merging of the shear layers takes place. To study the driving mechanisms, details of the local heat release for both simulations are presented in Figure 12. In this illustration, the transparency is varied in order to identify the local burning regime. As can be seen, the lean side of the diffusion flame generates similar heat release in both of the simulations, although, in Simulation , the observed values are slightly larger.
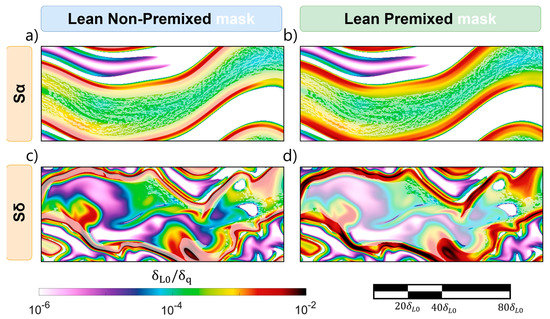
Figure 12.
Details of normalized heat release right after the reactive shear layers merge: Simulation with a mask indicating lean non-premixed regions (a), Simulation with a mask indicating lean premixed regions (b), Simulation with a mask indicating lean non-premixed regions (c), and Simulation with a mask indicating lean premixed regions (d).
The main differences between the simulations take place at the flame core, where the mixture fraction is significantly below its stoichiometric value. In Simulation , intermittency between premixed and non-premixed combustion can be observed. This result points to unstable burnability, due to insufficient mixing intensity. This behavior contrasts with what is observed in , where the flame core burns mostly in the premixed conditions. There, the heat release greatly varies between the two flames, since it depends on the local strain and availability of reactants. In both cases, a heat release rate drop can be observed from the lean edge of the diffusion flame to the oxygen core. However, heat release near the diffusive region is significantly larger in , and the values decrease faster. This decreasing trend is motivated by the lower availability of burnable reactants, as the mixture fraction tends to . Although heat release at the core is smaller in Simulation , the significantly higher burning rate close to the diffusive side enables a greater heat release in lean conditions overall. This process is behind the trend observed in Figure 10 towards the lean side.
The differences in the burning rate between the simulations are primarily driven by the different evolution of the scalar dissipation. To discuss the influence of this variable, instantaneous 2D cuts of its value are displayed in Figure 13.
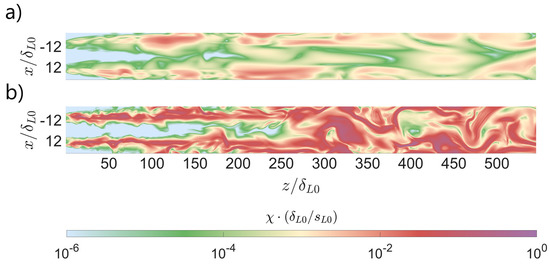
Figure 13.
Instantaneous scalar dissipation rate: Simulation (a), Simulation (b).
As expected, the scalar dissipation rate is greater in overall. This is caused by the larger turbulent kinetic energy at the inlet. The most remarkable difference between the simulations corresponds to the behavior following the merging of the shear layers. In Simulation , the mixing intensity decreases after the shear layers collapse. Contrarily, in , an increase in scalar dissipation follows the merging of the shear layers. This is motivated by the larger wrinkling of the shear layer, due to the integrated effects of the turbulence departing from the injection site. In , the shear layers are mostly aligned with the injection direction and, consequently, between themselves. Therefore, their merging produces little additional shear, and global dissipation dominates. Nevertheless, in , turbulence has enough energy to create substantial oscillations of the diffusive flame structures prior to their merging. In such a scenario, the collapse becomes more abrupt, enhancing the local mixing intensity. This phenomenon enables larger heat release rates, as premixed combustion becomes viable at the core, as displayed in Figure 12 for . If the scalar dissipation rate becomes too small, the possibility of combusting in a premixed condition in a stable way is disabled. This is evident in , but it can occur in localized regions in as well, as can be observed in Figure 6 and Figure 12.
5. Conclusions
Non-premixed methane–oxygen turbulent diffusion flames were studied using direct numerical simulations with finite-rate chemistry. The main purpose of this research was to study the flame development in the frame of modern space propulsion systems. A novel definition of the stoichiometric oxidizer-to-fuel ratio was proposed to capture the effects of significant carbon monoxide formation. The proposed definition is better suited to reaction engines, since the amount of carbon dioxide in equilibrium is small compared to carbon dioxide, altering the main assumption in which the classical definition of stoichiometric conditions is grounded.
The redefined stoichiometric value was used in conjunction with flame regime markers to classify the local combustion regime. Therefore, two main degrees of freedom were considered: fuel-rich vs. oxygen-rich and premixed vs. non-premixed conditions. The statistics of the heat release rate were analyzed conditional to these conditions, with varying Reynolds numbers, to investigate the influence of turbulence in the flame development process. This investigation was performed by a comparative analysis of one mildly turbulent flame () and one fully turbulent one (). For both of the flames, the chemistry was very fast compared to the turbulence. Therefore, combustion progress is limited by mixing, and differences in the heat release dynamics can be primarily attributed to the forced convection variations. It has been found that, despite the eminent non-premixed configuration of the burning device, a significant amount of heat release occurs in lean premixed conditions. This process occurs primarily at the flame core, following the merging of the shear layers. With growing turbulence, this merging becomes more abrupt, due to the increased decorrelation between the two interacting diffusive flame structures.
The results presented here point out several challenges concerning combustion in systems that resort to using oxygen as an oxidizer. Due to the wider flammability limits, combustion in lean premixed conditions can become significant. This effect indicates the necessity to consider a combination of premixed and non-premixed combustion models in turbulent combustion simulations for space propulsion systems. In addition, the definition of the stoichiometric conditions should be redefined to account for the large amount of carbon monoxide in equilibrium.
Author Contributions
Conceptualization, D.M.-S. and A.S.; methodology, D.M.-S. and O.H.; software, A.S.; validation, D.M.-S. and A.S.; formal analysis, D.M.-S.; investigation, D.M.-S.; resources, A.S.; data curation, D.M.-S.; writing—original draft preparation, D.M.-S.; writing—review and editing, D.M.-S.; visualization, D.M.-S.; supervision, O.H. and M.T.; project administration, O.H.; funding acquisition, A.S. and O.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bayerische Forschungsstiftung (BFS), “Weiterentwicklung der CFD-Simulationsmethoden für H2-O2-Hochduck-Dampfgeneratoren zur Stromnetzstabilisierung”. Project number: AZ-1517-21.
Data Availability Statement
The authors will share the used datasets upon reasonable request.
Acknowledgments
The authors thank the Leibniz-Rechenzentrum (LRZ) for providing the computational resources for performing the numerical simulations and post-processing. Special thanks go to Martin Ohlerich for his decisive aid and support that allowed this project to make the most of SuperMUC NGen’s capabilities. This research was founded by the Bavarian Research Foundation (Bayerische Forschungsstiftung), within the project “-Brennkammer im Kraftwerk”, with reference Grant No. AZ-1517-21.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haeseler, D.; Bombelli, V.; Vuillermoz, P.; Lo, R.; Marée, T.; Caramelli, F. Green Propellant Propulsion Concepts for Space Transportation and Technology Development Needs. In Proceedings of the 2nd International Conference on Green Propellants for Space Propulsion, Sardinia, Italy, 7–8 June 2004. [Google Scholar]
- Sackheim, R.L.; Masse, R.K. Green Propulsion Advancement: Challenging the Maturity of Monopropellant Hydrazine. J. Propuls. Power 2014, 30, 265–276. [Google Scholar] [CrossRef]
- Turner, M.J.L. Liquid Propellant Rocket Engines. In Rocket and Spacecraft Propulsion; Springer: Berlin/Heidelberg, Germany, 2009; pp. 67–108. [Google Scholar]
- Nickerson, G.R.; Johnson, C.W. A Soot Prediction Model for the TDK Computer Program. In Proceedings of the AIAA/SAE/ASME/ASEE 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Ciezki, H.K.; Zhukov, V.; Werling, L.; Kirchberger, C.; Naumann, C.; Friess, M.; Riedel, U. Advanced Propellants for Space Propulsion—A Task within the DLR Interdisciplinary Project “Future Fuels”. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain, 1–4 July 2019. [Google Scholar]
- Kajon, D.; Liuzzi, D.; Boffa, D.; Rudnykh, M.; Drigo, D.; Arione, L.; Ierardo, N.; Sirbi, A. Oxygen-methane combustion studies in the In Space Propulsion Programme. In Proceedings of the 4th European Conference for Aerospace Sciences (EUCASS), Madrid, Spain, July 2019. [Google Scholar]
- Ciezki, H.N.M.; Werling, L. Trends in Research and Development on Green Chemical Propulsion for Orbital Systems. In Proceedings of the 7th International Conference on Recent Advances in Space Technologies, RAST 2015, Istanbul, Turkey, 16–19 June 2015. [Google Scholar]
- Werling, L.; Freudenmann, D.; Ricker, S.C.; Wilhelm, M.; Lauck, F.; Strauss, F.; Manassis, K.; Kurilov, M.; Petrarolo, A.; Hörger, T.; et al. Research and Test Activities on Advanced Rocket Propellants at DLR’s Institute of Space Propulsion in Lampoldshausen. In Proceedings of the 9th European Conference for Aeronautics and Space Sciences, Lille, France, 27 June–1 July 2022. [Google Scholar]
- Haidn, O.; Ordonneau, G.; Soller, S.; Onofri, M. Development of the liquid oxygen and methane M10 rocket engine for the Vega-E upper stage. In Proceedings of the 8th European Conference for Aerospace Sciences, Saint Petersburg, Russia, 4–8 July 2011. [Google Scholar]
- Haidn, O.J.; Celano, M.P.; Luo, M.; Roth, C.; Silvestri, S.; Slavinskaya, N.A. On Methane/ Oxygen Combustion for Rocket Applications. In Proceedings of the International Symposium on Innovation and Prospects of Liquid Propulsion, Xi’an, China, 4–6 September 2016. [Google Scholar]
- Friedrich, R. Modelling of Turbulence in Compressible Flows. In Transition, Turbulence and Combustion Modelling: Lecture Notes from the 2nd ERCOFTAC Summerschool held in Stockholm, 10–16 June 1998; Springer: Dordrecht, The Netherlands, 1999; pp. 243–348. [Google Scholar] [CrossRef]
- Echekki, T.; Mastorakos, E. Concepts, Governing Equations and Modelling Strategies. In Turbulent Combustion; Springer: Dordrecht, The Netherlands, 2011; pp. 19–39. [Google Scholar]
- Chakraborty, N.; Katragadda, M.; Cant, R.S. Statistics and Modelling of Turbulent Kinetic Energy Transport in Different Regimes of Premixed Combustion. Flow Turbul. Combust. 2010, 87, 205–235. [Google Scholar] [CrossRef]
- Chakraborty, N. Influence of Thermal Expansion on Fluid Dynamics of Turbulent Premixed Combustion and Its Modelling Implications. Flow Turbul. Combust. 2021, 106, 753–848. [Google Scholar] [CrossRef]
- Cuenot, B.; Poinsot, T. Effects of curvature and unsteadiness in diffusion flames. Implications for turbulent diffusion combustion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1994; Volume 25, pp. 1383–1390. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D. A Flame Control Method for Direct Numerical Simulations of Reacting Flows in Rocket Engines. Master’s Thesis, Institute of Space Propulsion, Technical University of Munich, Munich, Germany, 2021. [Google Scholar]
- Martinez-Sanchis, D.; Banik, S.; Sternin, A.; Sternin, D.; Haidn, O.; Tajmar, M. Analysis of turbulence generation and dissipation in shear layers of methane–oxygen diffusion flames using direct numerical simulations. Phys. Fluids 2022, 34, 045121. [Google Scholar] [CrossRef]
- Martínez-Sanchis, D.; Sternin, A.; Tagscherer, K.; Sternin, D.; Haidn, O.; Tajmar, M. Interactions Between Flame Topology and Turbulent Transport in High-Pressure Premixed Combustion. Flow Turbul. Combust. 2022, 109, 813–838. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D.; Sternin, A.; Shvab, J.; Haidn, O.; Hu, X. An Eddy Dissipation Concept Performance Study for Space Propulsion Applications. Aerospace 2022, 9, 476. [Google Scholar] [CrossRef]
- Ruelle, D. Strange attractors as a mathematical explanation of turbulence. In Statistical Models and Turbulence: Proceedings of a Symposium Held at the University of California, San Diego (La Jolla) 15–21 July 1971; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Favre, A. Problems of Hydrodynamics and Continuum Mechanics; SIAM: Philadelphia, PA, USA, 1969. [Google Scholar]
- Magnussen, B.F. On the Structure of Turbulence and a Generalized Eddy Dissipation Concept for Chemical Reaction in Turbulent Flow. In Proceedings of the Nineteenth AIAA Meeting, St. Louis, MO, USA, 12–15 January 1981. [Google Scholar] [CrossRef]
- Magnussen, B.F. The Eddy Dissipation Concept—A Bridge Between Between Science and Technology. In Proceedings of the ECCOMAS Thematic Conference on Computational Combustion, Lisbon, Portugal, 21–24 June 2005. [Google Scholar]
- Peters, N. Laminar diffusion flamelet models in non-premixed turbulent combustion. Prog. Energy Combust. Sci. 1984, 10, 319–339. [Google Scholar] [CrossRef]
- Veynante, D.; Vervisch, L. Turbulent Combustion Modeling. Prog. Energy Combust. Sci. 2002, 28, 193–266. [Google Scholar] [CrossRef]
- Nivarti, G. The Bending Effect in Turbulent Flame Propagation. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Damköhler, G. Der einfluss der turbulenz auf die flammengeschwindigkeit in gasgemischen. Z. Elektrochem. Angew. Phys. Chem. 1940, 46, 601–652. [Google Scholar]
- Nivarti, G.; Cant, S. Direct Numerical Simulation of the bending effect in turbulent premixed flames. Proc. Combust. Inst. 2017, 36, 1903–1910. [Google Scholar] [CrossRef]
- Nivarti, G.V.; Cant, S. Scalar transport and the validity of Damköhler’s hypotheses for flame propagation in intense turbulence. Phys. Fluids 2017, 29, 085107. [Google Scholar] [CrossRef]
- Bradley, D. How fast can we burn? In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1992; Volume 24, pp. 247–262. [Google Scholar] [CrossRef]
- Driscoll, J.F. Turbulent premixed combustion: Flamelet structure and its effect on turbulent burning velocities. Prog. Energy Combust. Sci. 2008, 34, 91–134. [Google Scholar] [CrossRef]
- Bilger, R.W. The Structure of Diffusion Flames. Combust. Sci. Technol. 1976, 13, 155–170. [Google Scholar] [CrossRef]
- Bray, K.; Domingo, P.; Vervisch, L. Role of the progress variable in models for partially premixed turbulent combustion. Combust. Flame 2005, 141, 431–437. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D.; Sternin, A.; Haidn, O.; Tajmar, M. Turbulent combustion statistics in a diffusion flame for space propulsion applications. Phys. Fluids 2022, 34, 125115. [Google Scholar] [CrossRef]
- Burke, S.P.; Schumann, T.E.W. Diffusion Flames. Ind. Eng. Chem. 1928, 20, 998–1005. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Poinsot, T.; Veynante, D. Turbulent non premixed flames. In Theoretical and Numerical Combustion; Aquaprint: Bordeaux, France, 2012; pp. 287–348. [Google Scholar]
- Goodwin, D.; Moffat, H.; Speth, R. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics and Transport Processes Version 2.3.0b. 2017. Available online: https://zenodo.org/record/48735 (accessed on 1 January 2023).
- Salavinskaya, N.A.; Haidn, O.J. Reduced Chemical Model for High Pressure Methane Combustion with PAH Formation. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Yamashita, H.; Shimada, M.; Takeno, T. A numerical study on flame stability at the transition point of jet diffusion flames. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1996; Volume 26, pp. 27–34. [Google Scholar] [CrossRef]
- Fiorina, B.; Gicquel, O.; Vervisch, L.; Carpentier, S.; Darabiha, N. Approximating the chemical structure of partially premixed and diffusion counterflow flames using FPI flamelet tabulation. Combust. Flame 2005, 140, 147–160. [Google Scholar] [CrossRef]
- Nguyen, P.-D.; Vervisch, L.; Subramanian, V.; Domingo, P. Multidimensional flamelet-generated manifolds for partially premixed combustion. Combust. Flame 2010, 157, 43–61. [Google Scholar] [CrossRef]
- Som, S.; Aggarwal, S. Effects of primary breakup modeling on spray and combustion characteristics of compression ignition engines. Combust. Flame 2010, 157, 1179–1193. [Google Scholar] [CrossRef]
- Wu, H.; Ihme, M. Compliance of combustion models for turbulent reacting flow simulations. Fuel 2016, 186, 853–863. [Google Scholar] [CrossRef]
- Wan, K.; Vervisch, L.; Xia, J.; Domingo, P.; Wang, Z.; Liu, Y.; Cen, K. Alkali metal emissions in an early-stage pulverized-coal flame: DNS analysis of reacting layers and chemistry tabulation. Proc. Combust. Inst. 2018, 37, 2791–2799. [Google Scholar] [CrossRef]
- Butz, D.; Hartl, S.; Popp, S.; Walther, S.; Barlow, R.S.; Hasse, C.; Dreizler, A.; Geyer, D. Local flame structure analysis in turbulent CH4/air flames with multi-regime characteristics. Combust. Flame 2019, 210, 426–438. [Google Scholar] [CrossRef]
- Zirwes, T.; Zhang, F.; Habisreuther, P.; Hansinger, M.; Bockhorn, H.; Pfitzner, M.; Trimis, D. Identification of Flame Regimes in Partially Premixed Combustion from a Quasi-DNS Dataser. Flow Turbul. Combust. 2021, 1006, 373–404. [Google Scholar] [CrossRef]
- Zhang, F.; Bonart, H.; Zirwes, T.; Habisreuther, P.; Bockhorn, H.; Zarzalis, N. Direct Numerical Simulation of Chemically Reacting Flows with the Public Domain Code OpenFOAM. In High Performance Computing in Science and Engineering ‘16; Springer: Berlin/Heidelberg, Germany, 2015; Volume 14, pp. 221–236. [Google Scholar]
- Zirwes, T.; Zhang, F.; Denev, J.A.; Habisreuther, P.; Bockhorn, H. Automated Code Generation for Maximizing Performance of Detailed Chemistry Calculations in OpenFOAM. In High Performance Computing in Science and Engineering ‘17; Springer: Berlin/Heidelberg, Germany, 2018; pp. 189–204. [Google Scholar]
- Zirwes, T.; Zhang, F.; Denev, J.A.; Habisreuther, P.; Bockhorn, H.; Trimis, D. Improved Vectorization for Efficient Chemistry Computations in OpenFOAM for Large Scale Combustion Simulations. In High Performance Computing in Science and Engineering ‘18; Springer: Berlin/Heidelberg, Germany, 2019; pp. 209–224. [Google Scholar]
- Zirwes, T.; Zhang, F.; Habisreuther, P.; Denev, J.A.; Bockhorn, H.; Trimis, D. Implementation and Validation of a Computationally Efficient DNS Solver for Reacting Flows in OpenFOAM. In Proceedings of the 14th World Congress on Computational Mechanics, Virtual Congress, 11–15 January 2021. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Weller, H.; Tabor, G.; Jasak, H.; Fureby, C. OpenFOAM; OpenCFD Ltd.: Bracknell, UK, 2017. [Google Scholar]
- McDonald, P.W. The Computation of Transonic Flow Through Two-Dimensional Gas Turbine Cascades. In Proceedings of the ASME 1971 International Gas Turbine Conference and Products Show, Houston, TX, USA, 28 March–1 April 1971. [Google Scholar]
- Maccormack, R.; Paullay, A. Computational efficiency achieved by time splitting of finite difference operators. In Proceedings of the 10th Aerospace Sciences Meeting, San Diego, CA, USA, 17–19 January 1972. [Google Scholar]
- Zhang, F.; Zirwes, T.; Nawroth, H.; Habisreuther, P.; Bockhorn, H.; Paschereit, C.O. Combustion-Generated Noise: An Environment-Related Issue for Future Combustion Systems. Energy Technol. 2017, 5, 1045–1054. [Google Scholar] [CrossRef]
- Zhang, F.; Zirwes, T.; Habisreuther, P.; Bockhorn, H. Effect of unsteady stretching on the flame local dynamics. Combust. Flame 2017, 175, 170–179. [Google Scholar] [CrossRef]
- Zirwes, T.; Häber, T.; Zhang, F.; Kosaka, H.; Dreizler, A.; Steinhausen, M.; Hasse, C.; Stagni, A.; Trimis, D.; Suntz, R.; et al. Numerical Study of Quenching Distances for Side-Wall Quenching Using Detailed Diffusion and Chemistry. Flow Turbul. Combust. 2020, 106, 649–679. [Google Scholar] [CrossRef]
- Zhang, F.; Zirwes, T.; Häaber, T.; Bockhorn, H.; Trimis, D.; Suntz, R. Near wall dynamics of premixed flames. Proc. Combust. Inst. 2021, 38, 1955–1964. [Google Scholar] [CrossRef]
- Zirwes, T.; Zhang, F.; Habisreuther, P.; Hansinger, M.; Bockhorn, H.; Pfitzner, M.; Trimis, D. Quasi-DNS Dataset of a Piloted Flame with Inhomogeneous Inlet Conditions. Flow Turbul. Combust. 2019, 104, 997–1027. [Google Scholar] [CrossRef]
- Zirwes, T.; Sontheimer, M.; Zhang, F.; Abdelsamie, A.; Pérez, F.E.H.; Stein, O.T.; Im, H.G.; Kronenburg, A.; Bockhorn, H. Assessment of Numerical Accuracy and Parallel Performance of OpenFOAM and its Reacting Flow Extension EBIdnsFoam. Flow Turbul. Combust. 2023, 111, 567–602. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D.; Sternin, A.; Santese, T.; Haidn, O.J. The role of turbulence in the characteristic velocity and length of rocket combustors. Aerosp. Sci. Technol. 2023, 134, 108158. [Google Scholar] [CrossRef]
- Kee, R.; Coltrin, M.; Glarborg, P. Chemically Reacting Flow: Theory and Practice; Wiley: London, UK, 2005. [Google Scholar]
- Winter, F.F.; Perakis, N.; Haidn, O.J. Emission imaging and CFD simulation of a coaxial single-element GOX/GCH4 rocket combustor. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Perakis, N.; Rahn, D.; Haidn, O.J.; Eiringhaus, D. Heat Transfer and Combustion Simulation of Seven-Element O2/CH4 Rocket Combustor. J. Propuls. Power 2019, 35, 1080–1097. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D.; Sternin, A.; Sternin, D.; Haidn, O.; Tajmar, M. Analysis of periodic synthetic turbulence generation and development for direct numerical simulations applications. Phys. Fluids 2021, 33, 125130. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. Synthetic Turbulence Generators for RANS-LES Interfaces in Zonal Simulations of Aerodynamic and Aeroacoustic Problems. Flow Turbul. Combust. 2014, 93, 63–92. [Google Scholar] [CrossRef]
- Morsbach, C.; Franke, M. Analysis of a Synthetic Turbulence Generation Method for Periodic Configurations. In Direct and Large-Eddy Simulation XI; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 169–174. [Google Scholar]
- Sternin, A.; Perakis, N.; Celano, M.P.; Haidn, O. CFD-analysis of the effect of a cooling film on flow and heat transfer characteristics in a GCH4/GOX rocket combustion chamber. In Space Propulsion 2018; 3AF: Sevilla, Spain, 2018. [Google Scholar]
- Yeung, P.K.; Pope, S.B. Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 1989, 207, 531–586. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).