Abstract
The search for a rational design subspace of aircraft configurations can be addressed by using the advanced morphological approach (AMA). It allows the decomposition of design problems into functional and/or characteristic attributes and their technological implementation options. These are systemized in a morphological matrix (MM). Based on expert evaluations of each option, an exhaustive space is generated containing option combinations as possible solutions. Therefore, extensive MMs lead to immense solution spaces that are hard to analyze. However, removing attributes without justification might leave potential rational solutions out of scope. In this context, a sensitivity analysis technique is suggested based on analysis of variance (ANOVA) tests for use with the AMA. It can be applied to assess the sensitivity of solution scores against the attribute options and their importance. As a result, optimization of the MM and solution space can be achieved and improvement proposals can be drawn for future problem statements with the AMA. This is demonstrated on the data from a previously conducted AMA workshop on the conceptual design of a search and rescue aircraft.
1. Introduction
Aviation’s contribution to the CO2 footprint was estimated to be around in 2000 [1]. The European authorities have set highly ambitious goals requiring the reduction of aviation-generated emissions by 2050, namely and for CO2 and NOX per passenger kilometer, respectively, as well as noise reduction [2]. In order to assure the realization of such intentions, it is necessary to not rely solely on incremental technology improvement, which is reported to yield a yearly fuel consumption saving per passenger-kilometer between 1960 and 2014 [3]. These trends increase the significance of the search for new aircraft concepts and disruptive technologies. However, the identification and fixation of new optimal vehicle configurations in such a concise time frame requires a series of innovations in the early stages of the aircraft design process as well. Particularly, these should address challenges such as (a) the consideration of disruptive and/or unconventional technologies lacking deterministic performance and test data; (b) extensive generation of concept ideas to expand the designer’s horizon; (c) handling uncertainties during design stages with scarce information on the aircraft; (d) derivation of reliable qualitative technology evaluations; (e) impossible mathematical definition of an objective function for an optimization process [4]; and (f) the simultaneous consideration of components and technologies even from different aircraft classes (e.g., fixed wing lift generation and aerostats).
These aspects are targeted by the advanced morphological approach (AMA) [4]. It uses the concept of structural decomposition originating from the general morphological analysis (MA) to obtain notable system attributes and their corresponding alternative constructive options (which constitute the morphological matrix (MM)), evaluate these, and generate an extended solution space for further analysis. In order to cover innovative technologies lacking quantitative design or test data, expert knowledge is used as a scientific basis for the qualitative scoring. The technology evaluation is conducted in the form of expert workshops that are specially designed and dedicated for the conceptual aircraft design with the AMA. For the purpose, a full-scale structured expert judgment elicitation (SEJE) method has been developed with an appropriate questionnaire, uncertainty modeling, workshop and problem structure, as well as data post-processing [5]. The methodology has been applied and iteratively developed on two use cases so far: the conceptual design of a search and rescue (SAR) aircraft [6] and the conceptual design of wing morphing architectures [5]. On a global scale, the desired output of the AMA is a reduced design subspace of rational configurations for further consideration. Hence, the method could be seen as a step prior to the application of multidisciplinary aircraft optimization (MDAO) methods by setting the optimally chosen boundaries for parametric optimization.
In order to improve the robustness and the general application of the method, it is currently necessary to study the sensitivity of the main process outputs as well as to define universal guidelines for the AMA problem definition regardless of the use case. The current work focuses on the development and application of a sensitivity analysis (SA) approach as well as on the resulting improvements. Further benefits of the AMA process could be drawn by considering it in the paradigm of data models and as a milestone for the future development of digital expert systems.
For these purposes, one could consider the following view on the process: based on a MM as an input of the design problem, the experts help obtain solutions with final scores on the defined criteria. In other words, a certain MM (input) can be mapped to solutions and their scores (output) by a function that contains the expert opinions. As such, the function also reflects their diverse professional background and entire cognitive complexity of decision-making, along with the data post-processing of the AMA. Such a point of view resembles a typical data model structure as known from the machine learning (ML) domain. At the same time, it can be seen as a development milestone of an expert system in aircraft design. Expert systems represent computer software used to solve quantitative and qualitative tasks not only by leaning on a knowledge base originating from expert statements, but also aiming to “reproduce the problem-solving behavior of an expert” [7]. Although it is not the current aim to develop a full-scale expert system or ML data model, approaching the problem in this paradigm helps discover new aspects and improvement opportunities for the problem statement, the results, and the methodology itself. In addition, morphological approaches can be successfully integrated into knowledge-based engineering (KBE) systems. This is also due to the fact that KBE systems refer to expert systems [8,9]. According to Tripathi [10], “a rule-based expert system contains a knowledge base, inference engine, knowledge retrieval, explanation tools, and user interface” [10]. Furthermore, the use of the AMA as KBE in aerospace was considered in Reference [11].
In this context, one seeks to study the influence of the input system attributes on the variation of the solution scores. The findings have the potential to optimize the MM size and the results. The optimization of the input variables is defined as “feature selection” or “feature extraction” in the ML domain [12]. For this purpose, the analysis of variance (ANOVA) statistical test is used to estimate the significance with which the variation of attribute options justifies the variance of solution scores according to the separate criteria.
This approach has been applied to the results of the first AMA workshop on the conceptual design of a SAR aircraft. It demonstrates not only the SA of the results but also the diagnostic role it can play for the detection of problem formulation flaws and their correction. In particular, the main objectives can be summarized as follows:
- Representation of AMA design problem data as a data model;
- Development of a SA approach for the sensitivity estimation of solution criteria scores against MM attributes;
- Use of the SA results as a feature selection and method diagnosis tool;
- Improvement and optimization of the problem statement and/or other steps of the methodology based on the SA results.
1.1. Advanced Morphological Approach
The AMA by Rakov and Bardenhagen [4] is an extension of the MA and adapts the structural decomposition and synthesis to conceptual design problems in aerospace. The classical MA was developed by Fritz Zwicky [13] around the mid-twentieth century and applied by him to the classification of celestial bodies [14] and aircraft engines [15]. The main AMA steps are depicted in Figure 1. The method allows one to structure and analyze the design problem by decomposing it into attributes associated with major system functions. Additionally, sets of alternative technological options are selected that are able to fulfill the corresponding attribute functions. The attributes and the options are summarized in an MM. An important extension feature of the AMA is the qualitative assessment of each option according to pre-defined criteria. The combinations of all options and their scores from different attributes into solutions yield an exhaustive solution space that might bring into consideration advantageous yet previously unknown concepts. In a next step, solution space clustering is performed, which aids to distinguish configurations with similar scores—especially helpful in vast solution spaces. This allows the designer to focus on a subset of promising concepts in order to proceed with parametric optimization within this limited yet optimal subspace. This output paves the way for further application of MDAO methods for parametric optimization within the discovered design subspace. The positioning of the method in the scientific context and its comparison to similar approaches is discussed in Reference [16].
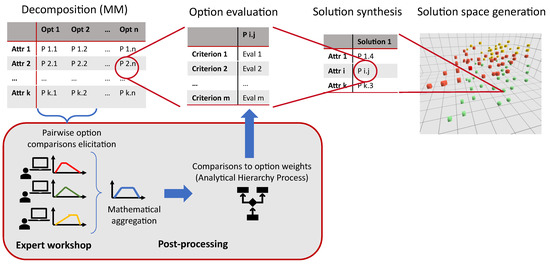
Figure 1.
Main steps of the enhanced AMA including the workshop. MM—morphological matrix; Attr.—attribute; Opt.—option; Eval.—evaluation. Reprinted from [5].
1.2. Conducted Workshop
As shown in Figure 1, the technology evaluations are obtained from dedicated expert workshops, which implement a SEJE methodology specifically developed for the conceptual aircraft design with the AMA. The workshop methodology, its justifications, and applications are described in References [5,6]. The current work conducts the SA approach on the results of the first AMA workshop, which focused on the conceptual design of a SAR aircraft [6]. The defined mission implies the following aspects:
- Transport/deployment/retrieving capabilities in remote and/or high mountain areas;
- Short takeoff and landing distances, low speed flight (hover capabilities are considered an advantage);
- Payload: 5 passengers or cargo/medical equipment (equivalent mass);
- Range: 200 km;
- Cruise altitude: 0–5 km;
- Stormy weather flight capabilities (wind gusts, heavy rain).
The MM with the selected attributes and options is presented in Figure 2. These were evaluated by the experts according to the following criteria:
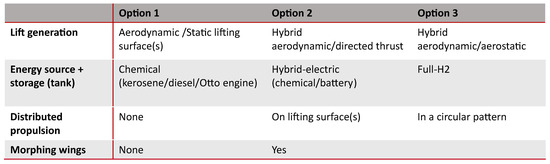
Figure 2.
Morphological matrix for the conceptual design of of a SAR aircraft. Reprinted from [6].
- Mission performance;
- CO2/NOx emissions;
- Direct operating cost (DOC).
As stated in the definition of the workshop methodology in Reference [6], the evaluations of the MM options are structured in a hierarchy and are processed with the analytical hierarchy process (AHP) by Saaty [17]. The hierarchy defined for the current use case is shown in Figure 3. Such a structure implies pairwise evaluations of the elements from a given level according to the elements of the level above. Subsequently, the AHP algorithm allows one to calculate the global option weights according to each criterion from their pairwise comparisons. The application of the AHP within the AMA design process as well as the uncertianty modeling for the option evaluations are presented in more detail in Reference [18].
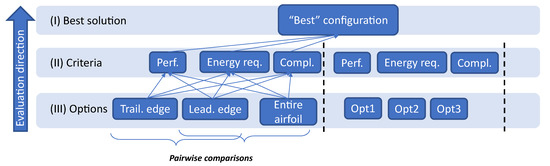
Figure 3.
Initial hierarchy structure of the use case for the use with the analytical hierarchy process. Reprinted from [6].
As one of the main purposes of the first workshop was methodology testing, it did not assume the exhaustive definition and solution of a full-scale conceptual design problem. Hence, the MM and the criteria represent only a subset of the aspects necessary for a full-scale design process.
The workshop involved five experts from the field of aircraft design and lightweight aerostructures and resulted in 350 obtained technology comparisons from all participants together. The solution space comprised 54 generated solutions containing all possible option combinations (no inconsistent combinations) [6]. Considering the qualitative assessments of mostly disruptive technologies with no statistical/historical test data, a full-scale data-based validation of the obtained evaluations could not be performed. However, a qualitative verification of the solution scores and their location in the solution space was conducted [6]. Because the extensive study of this aspect was left out of scope at the time, a thorough data quality study will be prioritized in future work.
2. Fundamentals
2.1. Machine Learning Data Models and Feature Selection
In order to describe which advantages could be expected by applying feature selection in the form of SA, it is first necessary to briefly introduce the scientific context of ML. As a branch of artificial intelligence, it aims to identify and use relationships among data by systematically applying algorithms [12]. Such an approach allows the computer to learn on given data without being programmed to [19]. In particular, it allows it to detect complex relationships from extensive datasets, which could be irretrievable by purely empirical formulas and therefore remain utterly challenging for human detection. ML models are built by training algorithms on known datasets in order to predict the outcome from previously unseen input data [20]. The ML models are also seen as a representation of the generated/learned knowledge [21]. Therefore, one could summarize the main concept of ML models as the attempt to obtain a simultaneously precise and generalized function or mapping F of given input parameters vector (denoted in this paper as independent variables (IVs)) onto a certain output quality , denoted as dependent variable (DV)—see Equation (1).
In order to improve the generalization capability of the model, it is necessary to include IVs that exhibit certain influence on the DV. Otherwise it might be necessary to optimize the model by removing, editing, or combining some IVs. This process of optimizing the input variables is denoted as dimensionality reduction or feature selection [12]. It can be conducted by different means depending on the type of data model and variables in question; however, one often tends to study the influence and the relationship of the separate IVs and the DV.
Although the current article does not aim to build a ML data model, this representation will aid in using the advantages of feature selection and optimization of AMA design problems.
2.2. Representation of the AMA Design Process as a Data Model
Using the concepts from the previous subsection, the AMA design process will be represented as a data model in terms of IVs and DVs. This consideration is depicted in Figure 4, which illustrates the main AMA steps and their role for the new representation.
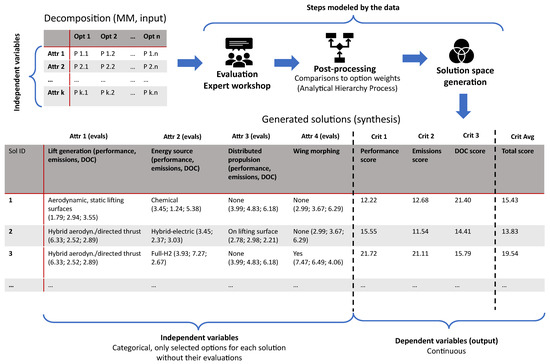
Figure 4.
A representation of the AMA design problematic as a data model on the use case of the SAR aircraft conceptual design. MM — morphological matrix; Attr.—attribute; Opt.—option; Eval.—evaluation; Sol.—solution.
The attributes from the MM are defined as the vector of IVs , which are each categorical and contain the corresponding technological options. The options are used as alternative categories without directly involving their weights derived from the workshop. The numbers in brackets next to the options stand for the scores (or global weights) according to the criteria performance, emissions, and DOC, as obtained from the AHP output.
At the same time, the criteria scores of the generated solutions as well as their total scores are defined as DVs . These are derived as the sums of the scores of the selected options for the corresponding solution. Based on these, different data models are defined for further investigation, which are summarized in Table 1.

Table 1.
Definition of data model representations.
Such definition of the IVs and DVs allows one to represent all AMA steps in between, including the SEJE and the problem hierarchy processing, as data model mapping. Hence, the mapping can be described as a function of the MM as input, in order to approximate the solution scores as output (Equation (2)).
2.3. Analysis of Variance (ANOVA)
In order to conduct feature selection within the AMA design process, it is necessary to study the importance of the input attributes for the solution scores. This is done by selecting an appropriate SA technique suitable to the input and output data types.
Handoko [22] notes the following main SA types in a very extended summary: derivative based (local SA), regression-based, variance-based, value of information-based, the screening method, the active subspace method, meta-modeling-based methods, etc.
The requirements set by the AMA design problem are:
- Input: MM attributes as categorical variables;
- Output: solution scores as continuous variables;
- Purpose: output variance explanation by the input variance.
The defined purpose is justified by the fact that the solution scores are in the form of qualitative data that has to be explained by the selected attribute options as categorical data.
To fulfill this need, the ANOVA method has been selected, which represents one of the most common statistical approaches to test whether the variances of three or more data groups are different [23,24]. This is done by conducting a statistical F-test of a hypothesis regarding the groups’ means , as defined in Equation (4) [24]— being the null hypothesis stating that all means are equal and defining the alternative hypothesis that some means might differ.
The derivation of conclusions on groups’ variances based on their means is explained in more detail in Reference [24]. The conducted F-test implies the comparisons of variances among groups and within groups, which is reflected in Equation (5) [24,25].
The following notation is used:
- : mean of the group i;
- : number of observations in group i;
- : overall mean;
- K: number of groups;
- : the jth observation of group i.
For the statistical test, a significance threshold of is used, which means that in order to reject the null hypothesis, a p-value corresponding to the calculated F-value of is required [25].
According to the general definition of ANOVA, it is subject to the following assumptions, which have to be confirmed [23,25]:
- Independent samples—because the evaluations of the technology options have been obtained from expert elicitation and not derived from other data, these are considered as independent data in this work.
- Normality—the data originate from a normally distributed population. This assumption will be checked during the application of ANOVA by means of the Anderson–Darling statistical test. However, multiple sources [23,26,27] state the relative robustness of the ANOVA F-test to non-excessive violations of this assumption.
- Homoscedasticity or homogeneity of variance—this requires that the studied data groups exhibit the same variance. This assumption is checked by applying the Levene test.
Even in the case of adoption of the alternative hypothesis, the researcher does not possess further data on the influence of each data group on the dependent variable—all that is known is that some variances might be different. In order to obtain more information on the impact of the separate groups, the so-called post-hoc tests are suggested [24,25]. However, as the obtained evaluations from the experts already represent the individual influence of each data group, such tests become obsolete in the current work.
One could argue that the ANOVA statistical test is used for datasets containing independent and dependent variables from different sources that in turn require the investigation of the relationships with ANOVA. This is not the case for an AMA design problem, as the solution scores (DVs) are calculated from the elicited option evaluations, hence a dependence is certain. However, the advantage of applying ANOVA in this case can be justified by the fact that the input data are defined as the MM attributes—categorical data containing the options as alternative categories instead of their corresponding (continuous) evaluations. In this context, it is of interest to investigate the influence of the attributes as categorical variables directly on the solution scores according to the separate criteria as well as their total scores.
The main ANOVA test types one distinguishes between are the so-called one-way and multiple-way ANOVA [23,25]. Whereas the one-way test studies the influence of a single categorical variable on a given output, the two-way ANOVA allows the simultaneous involvement of multiple categorical variables as well as their interactions. As the workshop use case and data have not implemented option and attribute interactions, only one-way ANOVA tests have been carried out in this work. This decision is also justified with the aim to yield a better transparency and overview of the results.
2.4. Used Software
The statistical tests have been conducted in the present work using the following packages in the Python programming language:
- statsmodels [28]—implementation of the ANOVA and Anderson–Darling tests;
- SciPy [29]—implementation of the Levene statistical test.
3. Methodology
The SA approach used in this work can be described in the following steps:
- Representation of the AMA design process as a data model. This involved the definition of independent and dependent variables (explained in Section 2.2).
- Checking the ANOVA assumptions, including normality test on the continuous DVs via the Anderson–Darling statistical test, as well as Levene statistical test to check the similarity of variances of the data from the separate groups.
- Conduction of the ANOVA test—obtaining of the F- and p-values.
- Results evaluations.
- Optimization of the MM and eventually the solution space. Eventual removal or combination of variables with less significance for the model. Additionally, a reevaluation of the problem statement and the hierarchy might be a possible solution in order to optimize the design process.
4. Results
The ANOVA statistical test was first conducted for the initially obtained results of the first AMA workshop. The findings have pointed out the necessity to improve the problem definition, which was then carried out. Subsequently, the ANOVA tests were repeated on the improved workshop results, which were then analyzed. These steps are presented in the following subsections.
4.1. Application on the Initial Workshop Data
Table 2 contains a summary of the ANOVA tests applied to the initial results of the first AMA workshop. Beforehand, the assumptions of the ANOVA test were checked. All data groups passed the Levene statistical test, stating that they all comply with the condition of having the same variance within the corresponding attribute. Furthermore, the p-values of the Anderson–Darling normality tests for all DVs are presented under the corresponding criteria columns in Table 2. Only the mission performance solution scores comply with the statistical significance threshold of . However, based on the robustness of ANOVA regarding the deviation from normal distribution noted in Section 2.3, one could accept the moderate deviation of the emissions criterion and the total score, whereas the p-values of 41–52% of the emission, DOC, and total scores signify a lower reliability of the ANOVA test for these criteria. Table 2 also includes the ANOVA test results for each defined data model, namely the F- and p-values of the corresponding test. The F-values can be interpreted as the amount of variance in the DVs explained by the variance of the corresponding IV. These are plotted in Figure 5a–d and can also be interpreted as the relative importance of the categorical attribute for the criteria scores of each solution.

Table 2.
Application of the ANOVA test on the initial results of the first AMA workshop.
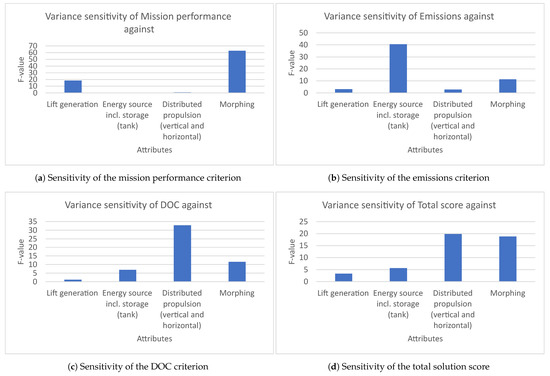
Figure 5.
ANOVA test results from the initial workshop data.
In this case, one could underline the unexpected outcome when comparing the importance of certain attributes. In particular, Figure 5a exhibits a higher variance portion of the mission performance scores explained by the wing morphing variation than by the selected type of lift generation. Furthermore, one recognizes the largest importance of the distributed propulsion and wing morphing for the solution total score than the rest of attributes in Figure 5d. The subsequent data analysis of the option evaluations against the performance criterion (resulting from the expert workshop) yields larger score ranges for morphing options than for lift generation types. This fact brings to light the lacking weighting of these attribute scores when composing the total criterion score of each solution. This is reflected in the hierarchy structure defined for the problem statement of the first workshop, as presented in Figure 3. Hence, when applying the AHP, the evaluation scale is the same, however left without the “importance” of the different attributes for the corresponding criterion.
This finding represents an example of the SA contribution to problem statement diagnosis and to the use case and result optimization.
4.2. Improvement of the Workshop Problem
Considering the previously discovered flaw of the initial problem statement, a potential idea would be to define the attributes as an additional hierarchy level in Figure 6. However, the AHP method would then imply the evaluation of the option importance according to the attributes and not the criteria. Instead, an improved hierarchy structure was elaborated, shown in Figure 6. The presented diagram suggests the attachment and multiplication of the attribute weights against the criteria to the corresponding options. This involved the application of the workshop methodology on the assessment of the attributes, namely the elicitation of their pairwise comparisons from experts, the application of the AHP, and the obtaining of their global weights according to the same criteria. Subsequently, this output is used as weights on the initial option assessments and is multiplied with the corresponding values of the option global weights obtained previously.
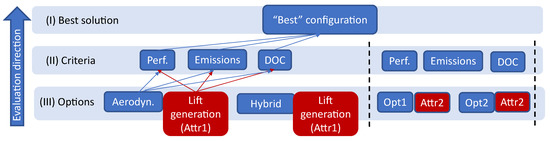
Figure 6.
Improved hierarchy structure of the problem statement by attaching and multiplying the weights of the attribute weights with the corresponding option scores.
Because the initial workshop was conducted earlier, the necessary additional evaluations were elicited from a single researcher with expertise in aircraft design. One should acknowledge that this correction does not represent a full-scale workshop extension due to the involvement of a single participant instead of the original expert panel. However, this simplification still allows one to roughly verify the SA through ANOVA tests.
The results of the ANOVA tests on the improved workshop results are shown in Table 3 and Figure 7a–d. These exhibit attribute importance that reflects common expectations better. The p-values confirm the normality distribution of the separate criteria scores, which is partial only for the case of the total score with . One observes wide ranges for both F- and p-values. This can be justified by the fact that the IVs and the DVs do not come from independent datasets, the relationship of which might require examination. Instead, the DVs are directly derived from the IVs, therefore exhibiting unquestionable dependence, reflected in the pronounced extreme values of the statistics. This leads to undoubted statistical significance by extremely low p-values for some attributes and reduced significance for others with p-values high above the threshold of .

Table 3.
Application of the ANOVA test on the improved workshop results.
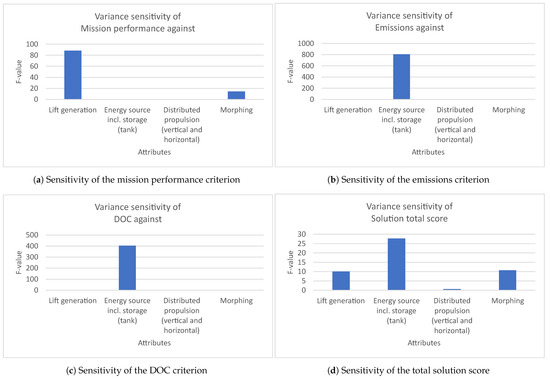
Figure 7.
ANOVA SA of the improved workshop results.
The mission performance score is mostly influenced by the lift generation type and moderately influenced by wing morphing. At the same time, the energy source shows the highest importance for emissions and DOC, being the only statistically significant attribute for these criteria. These findings are also reflected in the attribute importance for the solution total score, where the energy source selection remains the most important factor, almost three times as important as lift generation or wing morphing. These are followed by the availability of distributed propulsion.
5. Discussion
The results of the SA through ANOVA tests have demonstrated the benefit for the AMA design process diagnostics and optimization.
As previously noted, the DVs were directly derived from the IVs. However, this statement does not correspond to some p-values in Table 3, which indicate lacking statistical significance of some IVs. This can be explained by the lower influence of these attributes in comparison to others, and the one-way ANOVA recognizes this utterly low explained variance as statistically insignificant, however, not absent.
The derived importance differences of the attributes is a direct result of the subjective expert evaluations—higher difference among the option assessments of a given attribute increases its importance regarding the rest. The hypothesis behind the expert workshop states that qualitative expert knowledge could be used as a scientific basis for conceptual design problems lacking quantitative statistical and test data. In this context, the obtained data are not based on any empirical calculations, but solely reflect the experts’ professional experience expressed as qualitative technology evaluation.
Nevertheless, the results can still be explained from a physical point of view. For this purpose, one can take a closer look at the separate experts’ evaluations and their corresponding justifications given during the workshop for the two hierarchy levels separately—first the comparisons of the options according to the criteria and then of the attributes. On the option level, the mission performance assessments of the distributed propulsion options are very close. This was explained by the trade-off between the hover advantage on the one hand and the increased system complexity and weight on the other hand. At the same time, a bigger impact on mission performance would be caused by changing the lift generation options, especially considering the specific character of a SAR mission (e.g., required landing distance of a vertical takeoff/landing and a fixed-wing aircraft, non-conventional landing sites, extreme weather conditions, etc.). On the attribute level, wing morphing is considered a sub-architectural component of lift generation, therefore receiving a lower importance than the latter. These are example justifications from the workshop aiming to illustrate the logic used and support the obtained results.
The extremely low importance of the distributed propulsion according to all criteria as well as for the total score signifies low difference in the workshop evaluations of its options. The aim of the problem statement and the MM is to introduce attributes and options contributing to a wider diversity in the scores of the final solutions. For this purpose, one could either (a) define different/additional options to this attribute or (b) remove the attribute from the MM in order to improve the efficiency of the entire AMA process.
The varying importance of the attributes brings forward the aims of the problem definition and MM elaboration, namely the necessity to develop concrete methodological steps to select attributes and options with possibly higher influence on the criteria scores.
It is important to point out that the change in results after the hierarchy correction did not involve any manipulation of the obtained expert evaluations. Instead, the same evaluation process was executed for an additional hierarchy level. Namely, the attributes were evaluated according to the given criteria using the same questionnaire design. Instead of altering the initial results, the adjusted hierarchy represent a further iteration of the design process. Precisely this conclusion indicates one of the benefits of the sensitivity analysis, namely the diagnostics of the problem statement and the urge to rethink the correctness of the setting. Hence, the sensitivity analysis can be considered as an expansion and correction of the general approach.
The conducted modification of the hierarchy structure also resulted from the SA. It indicates that the hierarchies for the application of the AHP should be carefully elaborated for each use case depending on the system level of the option components, their contribution to the criteria, and potential option interaction. Hence, additional guidelines for the definition of such hierarchies are required due to their influence on the final results.
6. Conclusions
The AMA design process brings forward the advantages of qualitative technology evaluation and the generation of a solution space for a given design problem/MM. The assessments are obtained from dedicated expert workshops and are processed in order to assign criteria weights to each option. One of the current challenges of the methodology is the overall analysis and robustness of the process and the design space.
In this context, the current work has demonstrated the use of SA of an aircraft design space through ANOVA statistical tests within the AMA design process. In particular, the sensitivity of generated solutions criteria scores against system attributes of the MM is studied. The approach not only yields benefits for the importance comparison of the attributes, but also contributes to the overall AMA design process diagnostic and optimization.
For this purpose, an AMA use case has been observed from the view point of a data model, as known from the ML domain. Such a view of the design problem allows one to recognize the application potential of feature selection analysis and the identification of variables from the dataset. In this context, system attributes from the MM have been defined as IVs and the criteria scores of generated solutions as DVs.
The considered use case originates from the first conducted AMA expert workshop, resulting in a solution space for a SAR aircraft design. In this context, the solution scores according to the criteria mission performance, CO2 and NOX emissions, and DOC have been defined as the DVs. The aim of the work is to study their sensitivity against the alternative input technologies, namely the MM system attributes lift generation, energy source, distributed propulsion, and wing morphing, defined as categorical IVs. The continuous character of the DVs and the categorical type of the IVs required the application of the ANOVA statistical test for the investigation of the portions of explained variance in the outputs.
The results revealed unexpected distribution of importance among the attributes for the solution scores and led to the correction of the problem definition hierarchy. After multiplying the option weights with the newly obtained attribute weights in this improvement step, the qualitative results corresponded to the expectations.
The benefits of such SA through ANOVA tests can be summarized as follows:
- Obtaining of attribute importance for the output in the form of generated solution scores;
- Diagnostics of the defined problem statement, MM, and hierarchy;
- Optimization of the selected attributes—removal, combination, or interactions within the hierarchy;
- Verification opportunity of the intermediate steps of the AMA design process, including the qualitative expert evaluations and the data post-processing.
This way, the demonstrated SA approach represents a consecutive contribution to the robustness and analysis of the AMA design process. It revealed vital steps to be defined in the future, such as concrete guidelines for the definition of MM attributes and options, as well as the elaboration of problem hierarchy structures.
In this regard, the presented SA method could be used as an integral part of every following design use case with the AMA. Taking into account the previously noted aspects, it could serve as a means of verification of the conducted strategy and lead to (a) further conceptual design iterations of the same use case with more relevant system attributes and (b) quality improvement through the lessons learned of each new design task with the AMA.
The relationship between the input (MM attributes) and output (solution scores) of the AMA design process brings the research one step closer to development of digital expert systems. In the future, these could be able to model the complex steps conducted within the AMA, e.g., the workshop conduction, expert reasoning, and the entire post-processing of the workshop results and use it as a digital knowledge basis for further challenges and upcoming innovations in aerospace.
Author Contributions
Conceptualization, V.T.T., D.R., and A.B.; methodology, V.T.T. and D.R.; software, V.T.T.; validation, V.T.T. and A.B.; formal analysis, V.T.T.; investigation, V.T.T.; resources, D.R. and A.B.; data curation, V.T.T.; writing—original draft preparation, V.T.T. and D.R.; writing—review and editing, D.R. and A.B.; visualization, V.T.T.; supervision, D.R. and A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) grant number 443831887.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data can be made available on demand.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytical hierarchy process |
| AMA | Advanced morphological approach |
| ANOVA | Analysis of variance |
| DOC | Direct operating cost |
| DVs | Dependent variables |
| FS | Feature selection |
| IVs | Independent variables |
| MA | Morphological analysis (classical) |
| MDAO | Multidisciplinary aircraft optimization |
| ML | Machine learning |
| MM | Morphological matrix |
| SA | Sensitivity analysis |
| SAR | Search and rescue |
| SEJE | Structured expert judgment elicitation |
References
- Skeie, R.B.; Fuglestvedt, J.; Berntsen, T.; Lund, M.T.; Myhre, G.; Rypdal, K. Global temperature change from the transport sectors: Historical development and future scenarios. Atmos. Environ. 2009, 43, 6260–6270. [Google Scholar] [CrossRef]
- European Commission. Directorate General for Research and Innovation. In Flightpath 2050: Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; Publications Office: Luxembourg, 2012. [Google Scholar]
- Kharina, A.; Rutherford, D. Fuel Efficiency Trends for New Commercial Jet Aircraft: 1960 to 2014; White Paper; The International Council on Clean Transportation: Washington, DC, USA, 2015. [Google Scholar]
- Bardenhagen, A.; Rakov, D. Analysis and Synthesis of Aircraft Configurations during Conceptual Design Using an Advanced Morphological Approach; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth e.V.: Bonn, Germany, 2019. [Google Scholar] [CrossRef]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Structured Expert Judgment Elicitation in Conceptual Aircraft Design. Aerospace 2023, 10, 287. [Google Scholar] [CrossRef]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Improvement and Testing of the Advanced Morphological Approach in the Domain of Conceptual Aircraft Design; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth e.V.: Bonn, Germany, 2022. [Google Scholar] [CrossRef]
- Prince, M.E.; NASA. Expert System Technology; Research Reports: NASA; Marshall Space Flight Center: Huntsville, AL, USA, 1987.
- Rocca, G.L. Knowledge based engineering: Between AI and CAD. Review of a language based technology to support engineering design. Adv. Eng. Inform. 2012, 26, 159–179. [Google Scholar] [CrossRef]
- Häußler, M.; Borrmann, A. Knowledge-based engineering in the context of railway design by integrating BIM, BPMN, DMN and the methodology for knowledge-based engineering applications (MOKA). J. Inf. Technol. Constr. 2021, 26, 193–226. [Google Scholar] [CrossRef]
- Tripathi, K. A Review on Knowledge-based Expert System: Concept and Architecture. IJCA 2011, 4, 21–25. [Google Scholar]
- Bardenhagen, A.; Pecheykina, M.; Rakov, D. Advanced Morphological Approach for Knowledge-Based Engineering (KBE) in Aerospace. In Advances in Artificial Systems for Medicine and Education II; Hu, Z., Petoukhov, S.V., He, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 902, pp. 495–505. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015. [Google Scholar] [CrossRef]
- Zwicky, F. Discovery, Invention, Research-through the Morphological Approach; The Macmillan Company: Toronto, ON, Canada, 1969. [Google Scholar]
- Zwicky, F. Morphological Astronomy; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 1957. [Google Scholar] [CrossRef]
- Zwicky, F. Morphology and Nomenclature of Jet Engines. Aeronaut. Eng. Rev. 1947, 6, 6. [Google Scholar]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Creation of innovative concepts in Aerospace based on the Morphological Approach. Iop Conf. Ser. Mater. Sci. Eng. 2022, 1226, 012029. [Google Scholar] [CrossRef]
- Saaty, T. Decision-Making. Analytic Hierarchy Process; Radio i Svyaz: Moscow, Russia, 1993. [Google Scholar]
- Todorov, V.T.; Rakov, D.; Bardenhagen, A. Enhancement Opportunities for Conceptual Design in Aerospace Based on the Advanced Morphological Approach. Aerospace 2022, 9, 78. [Google Scholar] [CrossRef]
- Nagy, Z. Artificial Intelligence and Machine Learning Fundamentals; Packt Publishing: Birmingham, UK, 2018; OCLC: 1085904815. [Google Scholar]
- Jung, A. Machine Learning: Foundations, methodologies, and applications. In Machine Learning: The Basics; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Kononenko, I.; Kukar, M. Machine Learning and Data Mining: Introduction to Principles and Algorithms; Horwood Publishing: Chichester, UK, 2007. [Google Scholar]
- Handoko, B. Sensitivity analysis and its role in expert judgement. Ph.D. Thesis, The University Of Sheffield: Sheffield, UK, 2022. [Google Scholar]
- Stahle, L.; Wold, S. Analysis of variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar] [CrossRef]
- Kim, T.K. Understanding one-way ANOVA using conceptual figures. Korean J. Anesthesiol. 2017, 70, 22. [Google Scholar] [CrossRef] [PubMed]
- Herzog, M.; Francis, G.; Clarke, A. Understanding Statistics and Experimental Design: How to Not Lie with Statistics; Springer: New York, NY, USA, 2019. [Google Scholar]
- Feir-Walsh, B.J.; Toothaker, L.E. An Empirical Comparison of the Anova F-Test, Normal Scores Test and Kruskal-Wallis Test Under Violation of Assumptions. Educ. Psychol. Meas. 1974, 34, 789–799. [Google Scholar] [CrossRef]
- Blanca, M.J.; Alarcón, R.; Arnau, J. Non-normal data: Is ANOVA still a valid option? Psicothema 2017, 29, 552–557. [Google Scholar] [CrossRef] [PubMed]
- Seabold, S.; Perktold, J. statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).